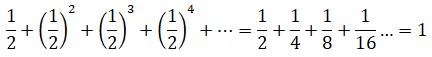Leibniz

José Muñoz Santonja

Introducción

Historiador, ingeniero de minas, poeta, diseñador, geólogo, diplomático, músico, alquimista, casamentero político, agricultor, bibliotecario... ¿Se puede dar mayor diversidad? Pues todas esas actividades las llevó a cabo Gottfried Wilhelm Leibniz. No en vano, debido a la variedad de disciplinas en las que influyó su legado, ha sido calificado de «último gran genio universal». El filósofo francés del siglo XVIII Denis Diderot, a pesar de tener en su discurso filosófico opiniones contrarias a las del pensador alemán, dijo lo siguiente: «Quizá nunca exista un hombre que haya leído tanto, estudiado tanto, meditado más y escrito más que Leibniz Lo que ha elaborado sobre el mundo, sobre Dios, la naturaleza y el alma es de la más sublime elocuencia». Y añadió más adelante descorazonado: «Cuando uno compara sus talentos con los de Leibniz, tiene la tentación de tirar todos sus libros e ir a morir silenciosamente en la oscuridad de algún rincón olvidado».
Leibniz fue un febril escritor de libros, memorándums y cartas. Su producción bibliográfica fue tal que no solo muchas de sus obras principales aparecieron después de su muerte, sino que aún no se ha publicado una edición completa de sus escritos. Pero fueron sus trabajos en filosofía y ciencia, especialmente en matemáticas, los que lo encumbraron.
Sin duda, lo que hizo entrar a Leibniz en la historia de la ciencia con letras de oro fue su aportación al estudio del cálculo infinitesimal. Desarrolló esta materia de forma simultánea con Newton, lo que constituyó una gran polémica de su época. En la actualidad, la idea que tenemos del cálculo está más cerca de la concepción que tenía el matemático inglés, pero la notación que usamos es la creada por Leibniz. Además, fue él quien se preocupó por estudiar a fondo las propiedades y buscar ejemplos y aplicaciones para el cálculo, apoyado en esta ardua labor por los hermanos Bernoulli, célebres matemáticos suizos.
El cálculo infinitesimal es una de las herramientas más poderosas con las que cuenta la matemática. Gracias a él pudieron resolverse, de una forma fácil y general, algunos de los problemas científicos que se habían tratado desde los antiguos griegos. En primer lugar, permitió el estudio de la variación constante de ciertos elementos, algo parecido a lo que haría el velocímetro de un coche; en particular, fue aplicado en el estudio de los cuerpos en movimiento. También vino a simplificar el cálculo de la recta tangente a una curva, lo que tuvo inmediata aplicación, por ejemplo, en cuestiones de óptica. Otro tipo de problemas que permitió afrontar fue el de la optimización, es decir, hallar en qué condiciones se podía obtener un valor máximo o mínimo, una herramienta muy utilizada actualmente en economía. Y la cuarta gran cuestión que resolvió fue la del cálculo de áreas y volúmenes de elementos que no son geométricamente regulares. Sus aplicaciones actuales en la vida cotidiana son muy amplias: en el diseño de teléfonos móviles o aviones, en transporte, meteorología... En general, podemos encontrar este tipo de cálculo en cualquier proceso en el que haya una evolución constante de la energía utilizada, el estudio del proceso de una epidemia o la distribución de cualquier tipo de población.
Las aportaciones matemáticas de Leibniz no se redujeron únicamente al cálculo, sino que también trabajó y dejó su impronta en otros campos: se planteó problemas filosóficos, utilizando aspectos probabilísticos y combinatorios para estructurarlos y siguiendo las pautas prescritas por el filósofo y teólogo mallorquín Ramón Llull. Pero lo que hizo que comenzara a ser conocido y aceptado en los círculos científicos fue la invención de una máquina mecánica de calcular que perfeccionaba el anterior invento de la Pascalina del matemático francés Blaise Pascal. Fue, además uno de los pioneros en el uso del sistema binario, que se encargó de fijar, relacionándolo con los hexagramas del I Ching chino.
Otra de sus facetas, la de diplomático, estuvo favorecida por la convulsa época en que le tocó vivir, caracterizada por grandes cambios políticos, militares, culturales, sociales, religiosos y, sobre todo, científicos. Cuando nació estaba agonizando la Guerra de los Treinta Años (1618-1648), que cambiaría el panorama político de Europa, con la Paz de Westfalia (1648) el Sacro Imperio entró en decadencia al tiempo que emergía Francia como el reino más poderoso de Europa. Tras el remado de Luis XIII, regido por la novelesca figura del cardenal Richelieu, apareció en escena Luis XIV, el «Rey Sol», quien, con la ayuda del cardenal Mazarino primero, y después como monarca absoluto, no escondió sus ansias de expansión. El monarca comenzó con una profunda reforma de su propio país; fomentó la economía, favoreciendo la industria nacional, y también la política colonial en América, y estableció unas excelentes infraestructuras, así como la creación de un ejército permanente, entre otros cambios. Después dirigió su atención al resto de Europa. Primero, declaró la guerra a los Países Bajos, que en la Paz de Westfalia se habían descolgado firmando la tregua por separado con España. En ese conflicto (1672-1678) contó con la ayuda de Inglaterra y algunos principados germánicos como aliados.
Más tarde, con el fin de combatir la belicosa política francesa, se creó la Liga de Augsburgo (1688-1697), cuyos integrantes eran el Sacro Imperio, Inglaterra, Suecia y España. Finalmente, la guerra concluyó con la rúbrica de la Paz de Ryswick (1697). En el siglo XVIII Francia volvió sus intereses hacia España. En ese complicado escenario, dadas sus notables dotes diplomáticas, la intervención de Leibniz se requirió en varios de los conflictos; participó en el proceso de consultas diplomáticas e incluso llegó a escribir informes sobre cómo aprovechar los recursos materiales y humanos en una guerra que parecía imposible de terminar.
Leibniz fue deudor de la profunda transformación que se produjo durante el Renacimiento en el dominio del pensamiento, la religión y las artes, que supuso una mayor libertad de espíritu, y a la postre posibilitó la Reforma protestante y con ello las futuras guerras de religión. La segunda mitad del siglo XVI fue realmente una edad de oro para las artes. Basta citar algunos de los nombres que encontramos en esa época para reconocer el impresionan el nivel al que se llegó en la cultura; Molière, Shakespeare, Swift, Cervantes, Velázquez, Rubens, Rembrandt, Vivaldi, Bach, Händel... Y en el terreno del pensamiento nos encontramos a Spinoza, Hobbes, Locke, Bacon o Arnauld, entre otros.
Sin embargo, la mayor evolución se produjo seguramente en el campo científico. En apenas año y medio, la ciencia había avanzado mucho más que en toda su historia. Esa revolución científica sentó las bases para una futura revolución industrial, y la ciencia pasó de ser meramente teórica, como en la antigua Grecia, a adquirir un carácter eminentemente práctica. Para comprobar la importancia de dicha revolución, basta citar algunos de los hitos conseguidos: la ley de la caída libre de los cuerpos de Galileo, las leyes del movimiento planetario o las lentes astronómicas de Kepler, la de los gases de Boyle, el cálculo de la velocidad de la luz por Römer, la teoría ondulatoria de Huygens, el barómetro de Torricelli, la descripción de la circulación de la sangre por Harvey o el descubrimiento de los microorganismos por Leeuwenhoek. Estos logros espectaculares de la ciencia se consiguieron no porque los científicos del siglo XVII fueran más capaces que sus predecesores, sino porque vieron el mundo con ojos nuevos. Abandonaron la estricta rigidez griega y comenzaron a investigar sin dar tanta importancia a la rigurosidad de la demostración. Se impuso el lema « primero inventar, después demostrar».
Eli filósofo Francis Bacon, firme defensor de la investigación empírica, apoyaba al científico de laboratorio. En su obra Nueva Atlántida. (1626) planteaba una sociedad utópica dirigida por científicos, que sería ridiculizada en Los viajes de Gulliver (1726), de Jonathan Swift, pero que sirvió de inspiración para muchas sociedades o círculos científicos que florecieron en el siglo XVII y que permitieron el intercambio de experiencias científicas y resultados.
Precisamente, otro de los factores que hicieron posible la gran revolución científica fue el gran desarrollo de las matemáticas. Se abandonó la rigidez geométrica griega y se dio el gran salto al álgebra y al análisis, que revolucionarían el mundo matemático, y el científico en general. Se consideró que las leyes matemáticas eran la base de la naturaleza.
Muchas áreas que hoy día son ciencias independientes, en el siglo XVII formaban parte de las matemáticas aplicadas, como puede verse en El curso o El mundo de las matemáticas, publicado en 1674 por el matemático francés Claude-François Milliet Deschales, en el que se trataban los siguientes temas matemáticos: aritmética, trigonometría, logaritmos, geometría práctica, álgebra, teoría de las cónicas y de los indivisibles, mecánica, estática, geografía, magnetismo, ingeniería civil y militar, carpintería, talla de piedras, hidrostática, movimiento de fluidos, hidráulica, construcción de barcos, óptica, perspectiva, música, astronomía, con la construcción de relojes de sol, astrolabios, calendarios y horóscopos. El descubrimiento de la geometría analítica por parte de Fermat y Descartes abrió el camino al cálculo infinitesimal.
Fue en este contexto en el que vivió y trabajó Leibniz, cuyo genio resultó ser tan vasto y sus intereses intelectuales tan variados, que puede encontrarse su impronta en innumerables campos. Lo mismo actuaba como un ingeniero inventando sistemas para extraer material de las minas o para el riego de jardines, que investigaba propiedades de los productos químicos recién descubiertos, como el fósforo, o relacionaba su filosofía con el movimiento de cuerpos.
Puede imaginarse la variedad de intereses que abarcaba el intelecto del genio alemán si vemos las propuestas que preparó para su audiencia con el emperador Leopoldo I: el Colegio Imperial de Historia, la reforma de la moneda, la reorganización de la economía, la mejora del comercio y la manufactura textil, la creación de un fondo para seguros e impuestos sobre vestidos de lujo y de un archivo estatal central, la firma de un concordato de estado y la creación de una biblioteca de referencia general, así como una propuesta para el alumbrado de las calles de Viena con lámparas de aceite de colza.
Leibniz, en definitiva, fue un optimista acérrimo que pensaba que vivía en el mejor de los mundos posibles, y nunca se desanimaba en ninguno de los múltiples proyectos en que se enfrascaba y no salían adelante. Durante toda su vida tuvo una completa dedicación al estudio, como servicio a la humanidad.

Cronología

1646	El 1 de julio nace Gottfried Wilhelm Leibniz en Leipzig, Alemania.
1661	Comienza sus estudios superiores en la Universidad de Leipzig, donde se especializa en Filosofía. Tras pasar un semestre en la Universidad de Jena, regresa a Leipzig y se especializa en Derecho.
1666	Publica su primara obra filosófica: Disertatio de arte combinatoria, inspirado probablemente en Ars Magnus de Ramón Llull.
1667	Se gradúa como doctor en Derecho en la Universidad de Altdorf.
1668	Comienza a trabajar \|para el elector de Maguncia
1672	Viaja a París para presentar un proyecto elaborado con el barón Johann Christian von Boineburg.
1673	Viaja a Londres, donde asiste a reuniones de la Royal Society y presenta su máquina aritmética y sus resultados con la suma de series infinitas.
1676	Es nombrado consejero del duque de Hannover, cargo que mantendrá hasta su muerte.
1679	Comienza el proyecto de explotación de las minas del Alto Harz, para la que había diseñado una serie de bombas de extracción y molinos de viento.
1684	En la revista Acta Eruditorum aparece un artículo de Leibniz donde explica d nuevo cálculo infinitesimal.
1685	Recibe el encargo de realizar una historia de la casa Brunswick- Luneburgo, lo que le mantendrá ocupado hasta el final de sus días, sin llegar a concluir la obra.
1692	Hanover pasa a convertirse en electorado alemán y Leibniz participa en varias partes del proceso.
1698	Tras la muerte de! duque Ernesto Augusto, su hijo Jorge Luis le sucede como elector de Hannover. Leibniz no tiene mucha sintonía con él.
1700	Se crea la Academia Prusiana de las Ciencias, Leibniz es su primer presidente.
1710	Se publica Teodicea: Ensayos sobre la bondad de Dios, la libertad del hombre y el origen del mal, donde recoge muchas de sus conversaciones con la reina Sofía Carlota en Charlottenburg.
1714	Publica la Monadología, resumen de sus posiciones filosóficas.
1716	Publica su obra principal sobre China, Discurso sobre la teología natural de los chinos . En ella defiende a China como un pueblo civilizado a la altura de Europa. Tras sufrir varios episodios de gota, muere el 14 de noviembre en Hannover.

Capítulo 1
El diseñador de calculadoras

Desde el principio de los tiempos, el hombre ha usado las matemáticas para contar y operar. Conforme los cálculos aumentaban en cantidad y calidad, se buscaron medios para agilizar los procesos y hacerlos más eficientes. Así surgieron, por ejemplo, el ábaco o los logaritmos. En el siglo XVII aparecieron una serie de máquinas mecánicas que mejoraban la rapidez y precisión en las operaciones, como fue la máquina aritmética de Leibniz.

Los padres con hijos pequeños suelen «martirizar» a los invitados con anécdotas realizadas por sus retoños para exponer lo listos, imaginativos, espabilados y geniales que son. Con el tiempo esas anécdotas quedan reducidas a la memoria de los ancestros, y únicamente sirven para hacer enrojecer de vergüenza al ya no tan retoño en cualquier reunión con familiares, amigos o compañeros de trabajo.
Si la persona destaca en cualquier disciplina, esas anécdotas infantiles se incorporan a su biografía para reforzar la impresión de hallarse ante un niño prodigio, algo que en no pocos casos llega a ser real. El ejemplo más conocido en el mundo de las matemáticas es el alemán Carl Friedrich Gauss, que en 1787, cuando tenía tan solo diez años, resolvió un complicado ejercicio propuesto en clase. Su profesor pidió que sumaran los 100 primeros números naturales. Gauss presentó en su pizarra la solución en cuestión de segundos.
El método seguido fue el siguiente. Gauss se dio cuenta que si escribía los números ordenados del 1 al 100 y debajo los volvía a escribir del 100 al 1, sumando cada dos elementos superior e inferior siempre se obtiene 101:

Como hay 100 sumandos, la suma de esas dos series de números sería 10100, y como hay dos sumas, en definitiva la suma de los 100 primeros números valdría:

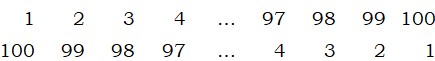
100×101/2 = 5050

Se había dado cuenta de que la primera cifra (uno) y la última (cien) sumadas daban la misma cantidad (ciento uno) que la segunda y la penúltima, y el razonamiento se podía proseguir sin problema, o sea, 1 + 100= 2 + 99 = 3 + 98 =...= 50 + 51 = 101, con lo que tenía 50 parejas de números que sumaban 101 y cuyo producto es 5050.
Como veremos en el siguiente capítulo, la suma de grandes series de números tuvo gran interés para los matemáticos del siglo XVII.
Aunque las anécdotas en la vida de Leibniz no son tan llamativas, también hay autores que lo consideran un niño prodigio. A la edad de dos años, trepó a una mesa alta mientras estaba al cuidado de una tía y, de pronto, perdió el equilibrio y cayó desde una altura considerable, terminando sentado en el suelo, sin ningún daño y riéndose del lance. Su padre pensó que estaba protegido por los cielos y envió inmediatamente un emisario a la iglesia para que se dieran gracias al terminar el servicio. Seguramente su padre pensó que ese detalle era una muestra de que su hijo estaba respaldado por la providencia, y por tanto predestinado a hacer grandes cosas. No se equivocaba.

§. Nace el genio
El 1 de julio de 1646 vino al mundo Gottfried Wilhelm Leibniz en la ciudad alemana de Leipzig, en el estado de Sajonia, uno de los principales centros comerciales de Europa desde el siglo XII. Esta ciudad era famosa por su gran cantidad de talleres de imprenta, hasta el punto de que llegó a competir con Frankfurt en el siglo XVIII en el arte de la impresión, de modo que se podían conseguir buenos libros con relativa facilidad.
Leipzig era un importante centro para la enseñanza y la ciencia desde el Renacimiento, y con una destacable vida cultural. Su universidad, fundada en 1409, es la segunda más antigua de Alemania, solo detrás de la de Heidelberg. En el momento del nacimiento de Leibniz, su padre, Friedrich Leibniz, era vicedecano de la Facultad de Filosofía, además de profesor de Filosofía Moral en la universidad. También ejercía de registrador, abogado y notario. Era natural de Altenberg, una pequeña localidad distante unos cuarenta kilómetros de Leipzig. Su madre, Anna Deuerlin, pertenecía a la nobleza de Leipzig.

§. El gran autodidacta
Entre 1663 y 1663 Gottfried Wilhelm cursó sus estudios básicos en la Escuela de San Nicolás de Leipzig. Durante aquellos años saciaba su sed de saber con el legado bibliotecario de su padre, y aprendió latín por sus propios medios gracias a los clásicos latinos y a los padres de la Iglesia.

Estatua de Leibniz en Leipzig, su ciudad natal, obra de Ernst Julius Hähnel (1611-1691).

Ya con doce años dominaba el latín y balbuceaba el griego, que había estudiado durante un par de años en la escuela. Se afirma que con solo trece años, al caer enfermo un compañero que debía recitar un poema en una conmemoración escolar, Leibniz compuso y recitó un poema en hexámetros latinos.

Grabado que muestra la Universidad de Jena hacia 1600, donde Leibniz pasó un semestre en 1665 y tuvo le oportunidad de conocer a Erhard Weigel

Durante los últimos años escolares, Leibniz descubrió la lógica aristotélica y llegó a dominarla hasta el punto de que sabía aplicar las reglas a casos particulares, algo inalcanzable para sus compañeros de clase. Este aprendizaje fue el que hizo florecer la gran inventiva de Leibniz y, al descubrir las limitaciones de dicha lógica silogística, comenzó a plantearse preguntas sobre las ideas nuevas que asaltaban su mente. Se enfrascó en el estudio de la teología y la metafísica, algo que impregnaría toda su obra. Se centró especialmente en el estudio de los grandes polemistas, tanto católicos como protestantes.
En la Pascua de 1661, Leibniz comenzó sus estudios en la Universidad de Leipzig, centrándose en el estudio de la filosofía, sobre todo en Aristóteles y se adentró en la obra de Euclides. Hasta ese momento no había tomado contacto con lo que hoy llamaríamos ciencia.
Tuvo como profesor de Filosofía a Jacob Thomasius, quien fundó en Alemania el estudio científico de la historiar de la filosofía y a quien Leibniz estimó durante toda su vida Thomasius dirigió su trabajo para la obtención del grado de bachiller en Filosofía, que consiguió en 1663. El ensayo, de título « Disputación metafísica sobre el principio de individualización », estableció las bases para el desarrollo posterior de su filosofía.
Aunque se inició en el mundo de la filosofía a través de los clásicos, por aquella época comenzó a tomar contacto con la nueva filosofía, tal como el mismo Leibniz recordada, pocos años antes de su muerte, en una carta a Nicolás Rémond, primer consejero del duque de Orleans:

Siendo aún niño estudié a Aristóteles y los escolásticos mismos (... ). Después, ya liberado de la trivial filosofía escolar, caí en los modernos, y recuerdo que me paseaba solo por un bosquecillo cerca de Leipzig, llamado de Rosenthal, a la edad de quince años, para deliberar si debía conservar las formas sustanciales. Al fin prevaleció el mecanicismo, que me llevó a aplicarme a las matemáticas.

Su interés por la filosofía mecanicista fue lo que le hizo comenzar a tener más en consideración las matemáticas. Pasó un semestre de 1663 en Jena, una población del estado de Turingia, cuya universidad es una de las de mayor tradición cultural y científica de Alemania. En ella se relacionó con Erhard Weigel, profesor de Matemáticas de gran renombre, además de filósofo moral y actualizador del derecho natural.

Retrato de autor desconocido de Erhard Weigel, matemático y filósofo alemán que fue un gran oro motor del conocimiento científico en Alemania. Como profesor de Leibniz, lo Inició en la escueta pitagórica.

Weigel había publicado años antes una obra en la que intentaba una reconciliación entre Aristóteles y los filósofos modernos, como Francis Bacon (1561-1626), Thomas Hobbes (1588-1679) o Pierre Gassendi (1592-1655), cuya filosofía se basaba en el método matemático.
Leibniz solía asistir en Leipzig a encuentros con otros estudiantes para intercambiar ideas y discutir sobre libros, y durante el tiempo que pasó en Jena se hizo miembro de la sociedad académica Societas Quarentium, donde tenían lugar reuniones semanales dirigidas por Weigel.
A lo largo de toda su vida, Leibniz apoyó y promovió este tipo de asociaciones, en especial las sociedades científicas por toda Europa.

§. Camino hacia el doctorado
Leibniz volvió a Leipzig para especializarse en Derecho y en febrero de 1664 se convirtió en maestro en Filosofía con el trabajo titulado « Muestra de cuestiones filosóficas tomadas del derecho», donde relacionaba la filosofía y el derecho, pues defendía que sin la filosofía, la mayoría de las cuestiones planteadas en derecho no tendrían solución. Quería, además, ayudar a disipar el desprecio que los estudiantes de Derecho solían tener por la filosofía.
Nueve días después de la lectura de su obra, murió su madre. Compartió la herencia con su hermana y una tía casada con el especialista de derecho Johann Strauch, que supo ver las grandes capacidades del muchacho y lo apoyó documentándolo sobre legislación. Esta ayuda le sirvió para preparar su disertación «De conditionibus», con la que obtuvo el grado de bachiller en Derecho. En este trabajo Leibniz desarrolla aspectos jurídicos con un marcado sesgo matemático y filosófico. Plantea una ley sujeta a una condición y estudia los distintos casos. Si la condición es imposible, la ley es nula y le asigna el valor 0. Si no está claro si puede suceder o no, entonces la considera como condicional y le asocia una fracción entre 0 y 1, supongamos 1/2. Si por el contrario la condición se cumple seguro, lo que él definía como necesaria, la ley es cierta y le asocia el valor 1. Los valores de dicha ley corresponderían a la siguiente tabla:

Es fácil encontrar relación con el cálculo de probabilidades. Esta relación matemática y científica estaría presente constantemente en la obra filosófica de Leibniz.
En 1666 fue rechazado en su intento de conseguir el grado de doctor en Derecho por su juventud, ya que el doctorado favorecía el nombramiento de profesor ayudante, y había muchos aspirantes de mayor edad para las doce plazas disponibles. En octubre de 1666 se matriculó en la Universidad de Altdorf, perteneciente a la república de Nüremberg, donde presentó el trabajo, finalizado en Leipzig, «Sobre casos difíciles en derecho», y cinco meses después ya tenía el grado de doctor. Rechazó la invitación para formar parte de la Universidad de Altdorf, pues opinaba que la revolución científica que tenía en mente no podía hacerse en el seno de la universidad.
Conviene mencionar ciertos aspectos sobre los estudios universitarios de la época. Actualmente, cada vez aparecen carreras nuevas con mayor grado de especialización, y en las que todos pueden encontrar los aspectos en los que quieren formarse, siempre que la nota de selectividad lo permita. Pero en el siglo XVII la oferta de titulaciones era muy escueta. En el Renacimiento solo existían tres titulaciones superiores: Teología, Derecho y Medicina. Por eso muchos científicos de la época realizaron estudios de medicina, pues eran los que más se acercaban a sus aspiraciones, y en donde podían conseguir la mejor formación científica en ese momento. Como Leibniz se formó en derecho, a pesar de su interés por la metafísica y las matemáticas, su formación en el campo científico no era todo lo buena que él deseaba, algo que comprobaría cuando comenzó a relacionarse con los científicos de otros países.

§. Las combinaciones filosóficas
Aunque esta obra pretende desarrollar aspectos científicos, no podemos dejar totalmente de lado los filosóficos, pues la relación entre ambos es estrecha cuando empiezan a aparecer aspectos matemáticos y físicos para explicar la filosofía.

Ramón Llull
Ramón Llull o Raimundo Lulio (ca. 1232-1315) fue un filósofo, teólogo, místico y misionero mallorquín a quien se considera inventor de la rosa de los vientos y de un aparato para situar las estrellas en el cielo nocturno llamado nocturlabio.
Al nacer, el Reino de Mallorca acababa de ser anexionado a la corona de Aragón por el rey Jaime I. En esa época, en Mallorca convivían sin problemas las tres grandes culturas, cristiana, judía y árabe, por lo que Llull creció en un ambiente de tolerancia, enriquecido culturalmente.
Tuvo puestos de confianza en la corte de Aragón, llegando a ser mayordomo real y senescal del futuro rey Jaime II de Mallorca. Con treinta años abandonó sus puestos y a su familia para predicar por los caminos mientras estudiaba teología y árabe. Posteriormente se recluyó en un monasterio para aprender latín, gramática y filosofía. Su mente tenía tres ideas fijas: la cruzada en Tierra Santa, la conversión de los infieles y la propagación de un método de demostración racional de las verdades de la fe.
Orden franciscana
En 1295 ingresó en la orden franciscana para ser tenido más en cuenta que un mero laico. Predicó en las puertas de mezquitas y sinagogas, con poco éxito. Asistió al Concilio de Vienne, convocado en 1308 por el papa Clemente V. Viajó de misionero a África, donde tuvo bastantes problemas, hasta el punto de morir en Túnez en 1315, al parecer linchado por una turba de musulmanes. Tras su muerte fue nombrado beato. Escribió multitud de libros de temáticas muy diversas, como gramática, educación, caballería, ciencia o filosofía. Alcanzó tal fama que se le conoció comoDoctor Iluminatus, Doctor Inspiratus o Doctor Archangelicus (para diferenciarlo de Tomás de Aquino, que recibió el título de Doctor Angelicus).

No olvidemos que Leibniz había decidido adoptar una filosofía mecanicista en la que las ciencias son inherentes a su desarrollo.
Uno de los filósofos que influyó a Leibniz en su juventud fue Ramón Llull, y sobre su obra vamos a resaltar algunos aspectos que nos pueden dar una idea de por dónde se desarrollará su filosofía. Pero antes veamos un aspecto matemático que aparecerá en ella.
Podemos considerar la combinatoria como aquella parte de las matemáticas que estudia la forma en que se pueden elegir, agrupar y ordenar una serie de objetos. Nos proporciona fácilmente la cantidad de posibilidades que podemos obtener al escoger unos objetos de entre un conjunto de ellos. La combinatoria está presente en muchas situaciones de nuestra vida cotidiana. Cuando entre un grupo de amigos o compañeros de una empresa se plantea en Navidad hacer el «amigo invisible», el orden en que salen los nombres para hacer el regalo es una permutación del orden de las personas que van eligiendo. Los tres libros que elegimos al azar para llevárnoslos de vacaciones son una combinación de los muchos posibles entre los que los elegimos. En una carrera de las olimpiadas en la que participan 8 corredores, las formas en que puede quedar el medallero es una variación, de esos elementos, de los que seleccionamos tres.
Como vemos por los ejemplos anteriores, en las permutaciones elegimos todos los elementos y los ordenamos de distinta forma. Para hallar la cantidad posible de situaciones resultantes basta hallar el factorial de esa cantidad. El factorial de un número natural n, que se representa por n!, es el producto de los números naturales desde el 1 hasta ese número:

n ! = n×(n-1)×(n-2)× ...×3×2×1

Por ejemplo, si tenemos cinco libros que vamos a colocar en una estantería sin fijar ningún orden concreto, la cantidad de formas en que pueden quedar sería:

5! = 5×4×3×2×1 = 120 ordenaciones distintas.

Basta pensar que en el primer lugar puede quedar cualquiera de los cinco libros. Por cada una de esas posibilidades, en el segundo lugar podemos colocar cualquiera de los cuatro libros restantes; en la siguiente, cualquiera de los tres restantes, y así hasta el último lugar, en que solo hay una posibilidad, pues ya solo queda un libro.
El caso de las variaciones es parecido al anterior importa el orden en que se seleccionan los objetos, pero no se seleccionan todos. Por eso para hallarlas no tenemos que llegar hasta 1 en el producto final. Supongamos que en el estante solo vamos a colocar dos libros de los cinco que tenemos. Si realizamos un razonamiento parecido al anterior, el número de selecciones posibles será 5×4 = 20. En general, la cantidad de variaciones de n elementos de los que tomamos solo r vendrá dada por la expresión:

en total r factores comenzando en n y disminuyendo una unidad cada vez.
Por último, en las combinaciones no nos importa el orden, solo queremos saber cuántas formas distintas hay de elegir un subconjunto de un conjunto de objetos dados. Por ejemplo, si tenemos un conjunto de monedas en las que hay una sola de cada tipo, desde 1 céntimo de euro hasta una de 2 euros, si nos dan tres monedas no nos importa el orden en que las recibamos; la cantidad total que vamos a tener al final será la misma si nos dan primero una moneda de euro, otra de 2 céntimos y otra de 50 céntimos, que si primero nos dan la de 2 céntimos, después la de 50 céntimos y por último la de euro.
Para hallar las combinaciones de n objetos tomados de r en r utilizamos la siguiente expresión:

La expresión siguiente es equivalente a un cociente entre factoriales llamado número combinatorio:

Así, si quisiéramos calcular cuántos grupos de tres libros podemos elegir entre quince posibles, tendríamos que calcular el número combinatorio de 15 sobre 3, lo que nos daría:

Pero la combinatoria no se utiliza solo en matemáticas, como podría pensarse, sino que se usa en muchas otras disciplinas casi desde el principio de los tiempos. Hay autores que hablan de permutaciones ya en antiguos textos asirios o en las fuentes mágicas griegas. En los documentos judaicos se plantea que las letras del alfabeto están revestidas de poder místico, y que combinando adecuadamente símbolos y signos se puede llegar a obtener cualquier criatura. En el propio Talmud, la Biblia judía, se afirma que combinando letras dotadas de valor numérico es posible construir la estructura del mundo. La Cábala, que podemos considerar como una línea de pensamiento mediante la que se pretenden descubrir aspectos relacionados con el hombre, como por qué existe, cuál es el propósito de su vida, etc., es una ciencia de los números, En ella se estudian letras y números, tratándolos mediante tres procedimientos: la Gematría (ciencia del valor numérico de las letras), la Notariken (ciencia de las letras primera, media y final de las palabras) y la Termurah (ciencia de la permutación y combinación de las letras). Algo similar ocurre en la cultura árabe, en la que a partir de las 28 letras que forman su alfabeto, simbolizando cada una de ellas un número entero, se abren una infinidad de combinaciones, dando lugar a la gran riqueza de la civilización islámica.

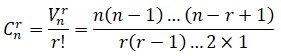
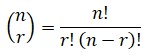
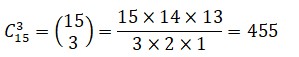
§. «Ars Magna»
El objetivo del arte filosófico de Ramón Llull era crear un instrumento para la conversión de judíos y árabes; quizá por ello estudió a fondo sus estructuras básicas y, por tanto, tuvo una clara influencia de ambas culturas para crear su filosofía. Sin pretender un estudio filosófico de su obra, queremos señalar aquellos aspectos relacionados con la ordenación y que influyeron en Leibniz.
Ars magna (Gran obra), obra de Llull publicada en 1308, tiene como objetivo último conocer a Dios. Está planteada en forma de una lógica combinatoria, tanto inventiva como demostrativa, Trata de encontrar todos los conocimientos a partir de unas cuantas nociones y principios, que por combinación pueden llegar a conseguir todas las ciencias. Ars magna está íntimamente relacionada con el cálculo lógico, y plantea que la lógica no solo sirve para establecer la validez de los razonamientos, sino para inventar razonamientos nuevos mediante combinaciones de dios.
Distingue una serie de principios, absolutos y relativos. Los primeros corresponden a los atributos de Dios, mientras que los segundos se refieren a conceptos de relación entre objetos.
Llull relaciona el alfabeto con los atributos de Dios. Hace corresponder la A al propio Dios y las siguientes letras a las distintas dignidades de Dios, que serian las siguientes:

Si realizamos ahora combinaciones de estos elementos de dos en dos, obtendríamos el siguiente total de juicios posibles:

según vemos en la tabla siguiente:

Como complemento, Llull creó una serie de cuatro figuras axiomáticas, mezclando unos principios con otros.
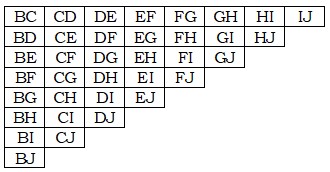
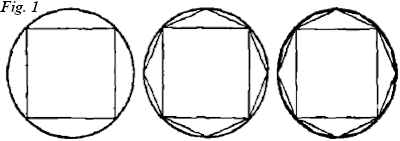
La razón es que necesitaba realizar de una forma mecánica lo que sus escasos conocimientos matemáticos no le permitían. Una de ellas correspondía a la tabla anterior. Otra era un círculo como el de la figura 1, dividido en nueve compartimentos en los que aparecían los principios absolutos.

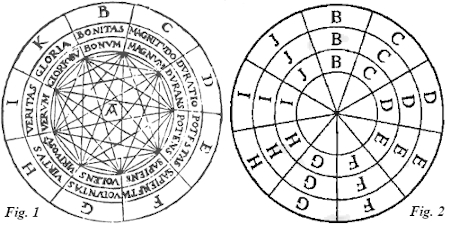
Figuras pensadas por Ramón Llull para su máquina lógica, incluida en su Ars Magna.

En ese círculo todas las dignidades equidistan por igual del centro, donde se sitúa Dios. Debajo de cada una de las letras aparecía un sustantivo y un adjetivo, de forma que cada división está unida a las otras ocho para indicar todas las combinaciones posibles que se podían obtener al girar el círculo.
De esta forma se pueden mezclar, convirtiéndose los sustantivos en adjetivos y obteniendo, por ejemplo, bondad grande o grandeza buena.
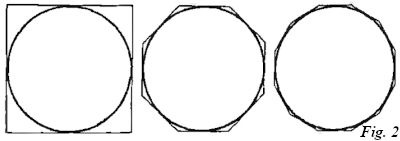
Otra de las figuras era una especie de máquina combinatoria en la que existían tres círculos concéntricos, de los cuales el menor giraba sobre el mediano y este sobre el mayor, que era fijo. De esa forma tomaba los conceptos que quedaban alineados en los discos. Podemos ver ese diseño en la figura 2.

§. «Dissertatio De Arte Combinatoria»
Está aceptado que Llull influyó en Leibniz, aunque este era crítico con la obra del primero, llegando a indicar que su arte:
Es solo sombra del verdadero arte combinatorio Se halla tan aleado de ese arte como lo está el fanfarrón del hombre elocuente, y al mismo tiempo, sólido.
Sin embargo varios autores afirman que a Leibniz le apasionó Ars Magna, y que le sirvió de base para su idea de arte combinatoria Leibniz publicó en 1666 su obra Dissertatio de arte combinatoria, en la que presentaba nuevos resultados en lógica y matemáticas. Era la primera vez que se utilizaba la palabra combinatoria en el sentido que la utilizamos en la actualidad. Aunque en su madurez Leibniz se arrepintió de haber publicado esta obra, al no considerarla un trabajo muy elaborado, es claro que en ella se presentan sus intereses filosóficos y los caminos por los que iban a dirigirse sus descubrimientos, a pesar de que aun no se había decidido por dedicarse a ninguna ciencia en concreto. Para Leibniz las aplicaciones filosóficas eran aún más importantes que las matemáticas. No es de extrañar, ya que varios filósofos consideraban que las matemáticas desvirtuaban el sentido de las cosas naturales y, por tanto, pervertían la filosofía natural. Entre ellos podemos citar a los italianos Pico della Mirandola (1463-1494) y Giordano Bruno (1548-1600).
En esta obra Leibniz desarrolla una idea de sus tiempos de escuela: usar la combinatoria para conseguir un alfabeto del pensamiento humano, lo que más tarde llamaría Scientia generalis. Siguiendo a Llull, Leibniz pensaba que al igual que partiendo del alfabeto, mediante combinaciones y permutaciones, se podía obtener cualquier palabra o frase, a partir de conceptos simples y fundamentales se podían llegar a conseguir todas las verdades surgidas de esas relaciones. El principio fundamental de la metafísica de Leibniz fue considerar que todas las proposiciones lógicas podían reducirse a la combinación adecuada de un sujeto y un predicado. Planteaba una lógica del descubrimiento o invención, en oposición a una lógica demostrativa en la línea de otros filósofos clásicos.
Las combinaciones en general eran nombradas por Leibniz con la palabra complexiones, y utilizaba la palabra combinationes para las elecciones de dos en dos objetos. Cuando se trataba de tres objetos utilizaba la palabra consternationes o consnationes, y así sucesivamente.
Aparecen en su obra aplicaciones de la combinatoria al derecho, a la música e incluso a la teoría aristotélica de la generación de los elementos, a partir de las cuatro cualidades primarias: frío, caliente, húmedo y seco. Al tomar esas cualidades de dos en dos obtenía las siguientes combinaciones diferentes:

aunque despreciaba aquella en la que aparecían cualidades opuestas, como frio y caliente o húmedo y seco. De las cuatro restantes obtenía los elementos básicos: agua, aire, fuego y tierra.
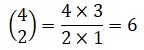
Leibniz buscaba, en definitiva, un método que le permitiera de forma general trabajar con las ideas de una forma científica, para razonar y demostrar mediante operaciones similares la aritmética y el álgebra.

§. Nuevos encargos
Tras conseguir el grado de doctor, Leibniz decidió emprender un viaje por diversos países europeos, pero no llegó muy lejos. Pasó unos meses en Nüremberg porque ingresó en una sociedad alquímica. Aunque en la actualidad pensamos en la alquimia como en una seudo-ciencia, en el siglo XVII era una actividad aceptada por los científicos. La alquimia fue la precursora de la propia química actual, que comenzarla a desarrollarse en ese siglo, a partir de los trabajos del irlandés Robert Boyle (1627-1691). Leibniz comentaría años más tarde que fue en Nüremberg donde aprendió los conocimientos básicos de química, que utilizaría luego para pruebas que le propusieron los príncipes con quienes se relacionó.
Durante el viaje escribió una obra de título Nuevo método de aprendizaje y enseñanza de la jurisprudencia , dedicada al elector de Maguncia, Juan Felipe de Schönberg, con la idea de conseguir un puesto en la corte. En ella planteaba el derecho desde un punto de vista filosófico. Señalaba dos reglas fundamentales en la jurisprudencia: no aceptar ningún término sin definición y no aceptar ninguna proposición sin demostración. Tras presentar la obra personalmente al elector, consiguió ser contratado para ayudar al consejero de la corte, Hermann Andreas Lasser, en la redacción de un nuevo código civil adaptado a las nuevas necesidades del Estado.
Una persona fundamental en la vida de Leibniz fue el barón Johann Christian von Boineburg (1622-1672), ministro del elector de Maguncia. A partir de 1668 Leibniz, que se había instalado en dicha ciudad, tuvo una gran relación con el barón, llegando a intimar tanto con él como con su familia. Mientras colaboraba con Lasser, Leibniz realizó trabajos esporádicos para Boineburg, entre otros de secretario, bibliotecario o abogado. Durante esos años, redactó escritos a petición del barón sobre diversos temas, especialmente filosóficos y políticos. Veamos uno de ellos.
En aquella época la corona de Polonia había quedado libre por abdicación del rey Juan Casimiro y el conde palatino, o palstgrave, de Neuburg pretendía el trono. Solicitó ayuda a Boineburg para que fuera a defender su causa en Polonia, y este encargó a Leibniz un trabajo que defendiera las aspiraciones del palstgrave. Leibniz escribió bajo el nombre de un desconocido noble polaco una obra en la que partía del concepto de demostración matemática en la ciencia, en la línea de Galileo Galilei (1564-1642) o René Descartes (1596-1650), entre otros, y aplicaba ese desarrollo a la elección del futuro rey. Llegaba, claro está, a la conclusión de que la persona más indicada era el palstgrave de Neuburg. En el desarrollo de la obra usaba los razonamientos éticos y políticos manejándolos como elementos de un cálculo de probabilidades. Podemos considerar que esa fue la primera vez que Leibniz se adentró en el mundo diplomático, algo que sería una constante a lo largo de toda su vida, Boineburg y Leibniz coincidían en muchos pensamientos. Aunque el barón era católico y Leibniz luterano, ambos abogaban por la reunificación de las Iglesias católica y protestante. Esta idea estuvo en la intención de Leibniz siempre y la planteó en todos los lugares en los que podía conseguir algún tipo de apoyo.
En 1669 dieron fruto sus contactos con el elector de Maguncia y fue nombrado para el Alto Tribunal de Apelación, del que formó parte hasta 1672. Años después volvería a actuar de Jurista en Hannover. A pesar de su grado de doctor en Derecho, no le atraía especialmente ese mundo, pues si bien admiraba a los jueces, menospreciaba la labor de los abogados, razón por la cual nunca se dedicó profesionalmente al derecho.
En 1670, Leibniz fue con Boineburg a Bad Schwalbach, una ciudad balneario donde el barón seguía regularmente un tratamiento de aguas, En esa ocasión comenzó a fraguarse lo que sería la primera misión diplomática de importancia que realizaría Leibniz en su dilatada carrera. El rey francés Luis XIV (1638-1715), con claras tendencias expansionistas, tenía la intención de invadir los Países Bajos. Leibniz imaginó una posibilidad de desviar su ansia conquistadora, de Europa y redirigirla hacia Egipto, lo que se llamó el Proyecto egipcio o Consilium aegyptiacum. La idea de desviar los conflictos internos europeos a otras partes del mundo no era nueva, ya que Leibniz se basó en un proyecto parecido del siglo XIV planteado al papa por el veneciano Marino Canuto.
Se preparó un plan secreto para presentar el proyecto en la corte francesa. De sus conversaciones con Boineburg, Leibniz elaboró un escrito, pero aunque el objetivo último seguía siendo evitar el ataque francés contra los Países Bajos, la redacción final planteaba más bien una cruzada general contra los infieles. Quedaba tan diluida la idea original que casi ni se citaba Egipto. Este escrito fue enviado al rey de Francia a principios de 1672, y el ministro de Asuntos Exteriores francés, quizá al no tener clara cuál era la propuesta, pidió más información e invitó a Boineburg a asistir a la corte, en persona o a quien designara para ello. El barón nombró a Leibniz como representante en Francia para plantear más claramente su idea. En marzo partió hacia París.
Además del objetivo de las negociaciones de paz en Europa, Leibniz llevaba otros ocultos Boineburg le había encargado que abogara ante el rey el pago de una serie de rentas y pensiones que se le adeudaban. Por otro lado, Leibniz deseaba visitar París, donde podía entrar en contacto con grandes nombres del panorama filosófico y científico francés. Su reclusión en Maguncia le impedía tomar contacto directo con los importantes personajes que estaban revolucionando la cultura científica. Leibniz siempre defendió que si hubiese podido asistir antes a París, sus capacidades se habrían ampliado y habría estado más en disposición de perfeccionar y renovar 1a ciencia, que es lo que en realidad pretendía con su trabajo.
Un año antes Leibniz se había carteado con Pierre de Carcavi (1600-1684), bibliotecario real, y le había hablado de la máquina aritmética en la que estaba trabajando. Supo que Carcavi estaba realizando gestiones para invitar a Leibniz a entrar en la Academia de las Ciencias de París. El propio Carcavi le escribió invitándolo a enviar un ejemplar de su máquina para mostrársela a Jean-Baptiste Colbert (1619-1683), ministro de Luis XIV. Esta relación con las sociedades científicas fue la que abrió el mundo al genio de Leibniz.

§. Los intercambios científicos
Hoy día hay personas que se dedican profesionalmente a la investigación y reciben su salario como investigadores. A veces trabajan en las universidades, en laboratorios, en grandes hospitales, o en empresas como las dedicadas a la informática o la telefonía Pero lo que suele caracterizar a todos ellos es que viven de esa labor. Pero eso no siempre ha sido así. En los siglos XVI y XVII, muchos de los grandes personajes que desarrollaron sus avances durante la revolución científica tenían otros trabajos para subsistir. La mayoría de las personas dedicadas a las ciencias eran teólogos, diplomáticos, juristas, sacerdotes, arquitectos, etc. No existían los científicos profesionales, salvo algunos pocos afortunados que podían estar a las órdenes de algún rey o mandatario importante. Podemos citar a Pierre de Fermat (1601-1666), que era abogado y empleado en una oficina del Gobierno; John Wallis (1616-1703) era criptógrafo; Antón van Leeuwenhoek (1632-1723), que fue el primero en descubrir los microorganismos en el microscopio, era comerciante textil, y el filósofo Baruch de Spinoza (1632-1677) era pulidor de lentes.
Además, la mayoría de científicos eran prácticamente autodidactas. En general, las universidades iban mucho más atrasadas que la evolución de las ciencias, por lo que, salvo excepciones, la formación más avanzada había que conseguirla fuera de la universidad. John Wallis, en referencia a su formación, decía:
Las matemáticas en aquel tiempo se consideraban raramente entre nosotros como algo académico; más bien se miraban como algo mecánico.
Las matemáticas casi se consideraban patrimonio de los comerciantes más que de los científicos. Por eso, quien deseaba introducirse en las ciencias más avanzadas lo que hacía era acercarse a algún científico importante y convertirse en su discípulo, para adentrarse en los conocimientos que no podía encontrar en otro lado.
Otro aspecto dificultoso para el desarrollo de la ciencia era el aislamiento de los científicos. Hoy, gracias a los nuevos medios de comunicación, cualquier suceso ocurrido en un país es inmediatamente conocido en el mundo entero. Pero en el siglo XVI no era así: un nuevo descubrimiento podía tardar meses o años en ser conocido por el resto de los científicos. Esto se agravaba por la rivalidad entre las diferentes naciones.
Al comienzo del siglo XVII no existían cauces que permitieran un intercambio rápido y eficiente de ideas entre los intelectuales y científicos de la época. Conscientes de esta carencia, grupos de científicos comenzaron a reunirse e intercambiar experiencias y resultados en reuniones o a través de cartas que se leían en ellas. Una de las personas más importantes en esos momentos fue el teólogo Marín Mersenne, monje de la orden de los mínimos. Compañero de estudios de Descartes, Mersenne escribió varios libros sobre filosofía y música, y es recordado en el mundo de la matemática por los llamados números primos de Mersenne.

Los números primos de Mersenne
Se suelen llamar números de Mersenne aquellos que son una unidad menos que una potencia de base 2, es decir, los números de la forma 2 ⁿ-1 (por ejemplo: 3, 7, 15, 31, 63, 127...), y de ellos, los que sean primos reciben el nombre de primos de Mersenne (de los anteriores serian: 3, 7, 31 y 127), Marín Mersenne (1588-1648) presentó estos números, que posteriormente fueron llamados así en su honor, en la obra Cognitata phiysico-mathematica, publicada en 1641. En ella incluía vanas propiedades de dichos números, que no pudieron ser demostradas hasta tres siglos después. También incluía una serie de números primos de Mersenne hasta el exponente n =2 57, que tenía varios errores, como se comprobó más tarde.
Los números primos en la actualidad.
La era electrónica permitió que a partir demediados del siglo XX se pudieran encontrar nuevos números primos cada vez más grandes, usados hoy día en las comunicaciones para hacer más seguro el acceso a las cuentas bancadas o los intercambios de información en Internet. En los últimos sesenta años, el mayor número primo conocido casi siempre ha sido de Mersenne. En la actualidad se conocen un total de 47 números y el mayor es un número con casi 13 millones de cifras. No se sabe cuántos números primos de Mersenne pueden existir, aunque la conjetura es que son infinitos.

Para Mersenne los científicos debían trabajar en comunidad, consultando y comparando sus experimentos y descubrimientos. Pensemos que en esa época los conocimientos de los gremios artesanales solo pasaban, a veces con gran secretismo, a los aprendices que entraban en dichos gremios. La idea de Mersenne era que los conocimientos debían circular libremente y ser aprovechados por todos aquellos interesados en hacer avanzar la ciencia.
Creó lo que se conoce como círculo de Mersenne, una especie de club matemático que se reunía en la propia celda del monje. A él pertenecieron, entre otros, Descartes, Pascal, Roberval, Desargues, Fermat y Gassendi. Aunque el grupo se creó como Academia Mersenne, más adelante se unió a otro grupo similar organizado por los hermanos Pierre y Jacques Dupuy, bibliotecarios reales. A este segundo grupo asistía gente de muchas disciplinas más variadas que las matemáticas, aunque también pertenecieron, Huygens, Oldenburg y Gassendi. La unión de los dos grupos pasaría a llamarse Academia Parisiensis y sería el germen de lo que se convertiría posteriormente en la Academia de Ciencias de París.
Otro grupo similar, aunque un poco más avanzado el siglo, se reunió en torno al filósofo y teólogo Nicolás Malebranche (1638- 1715), quien fue profesor de Matemáticas y miembro de la congregación del Oratorio de San Felipe Neri. En el oratorio organizó reuniones, en la línea de Mersenne, para intercambiar descubrimientos matemáticos. Pertenecieron a este círculo Pierre Varignon, el marqués de L'Hôpital o Johann Bernoulli. Malebranche fue un gran divulgador de la obra de Descartes y Leibniz y editor del libro de L'Hôpital, él primero que se publicó sobre el nuevo cálculo infinitesimal.
En Inglaterra, el político inglés Francia Bacon (1561-1626), más filósofo que científico, abogó por la importancia de la ciencia de laboratorio, que estaba desprestigiada como mera artesanía, y también por los intercambios intelectuales. Siguiendo sus consejos se creó un grupo de científicos alrededor del diácono alemán afincado en Inglaterra, Theodore Haak (1605-1690). Este grupo, conocido como Grupo 1645, se reunía inicialmente en Cambridge, pasando posteriormente a Londres, y sería el germen del que nacería la Royal Society.
Las publicaciones de Malebranche tuvieron mucho interés, pues en esa época era complicado editar libros de ciencia y especialmente de matemáticas, puesto que acostumbraban a tener una tirada limitada y no solían ser negocio. El astrónomo alemán Johannes Kepler (1571-1630), que consideraba que los libros de matemáticas eran bastante complicados de entender y por eso tenían poco público, comentaba:
Muy duro destino es hoy día el de escribir libros matemáticos y, sobre todo, astronómicos (...) y por ello hay poquísimos lectores buenos. Yo mismo, que soy considerado como un matemático, tengo que hacer un esfuerzo para leer mi obra.
La cosa se complicaba porque había personajes reacios a publicar sus resultados, como por ejemplo Pierre de Fermat, que jamás escribió un libro con sus avances. Muchas veces los científicos no querían publicar para no entrar en polémica con otros científicos, que fue lo que le ocurrió inicialmente a Isaac Newton tras su enfrentamiento con Robert Hooke (1636-1703) por sus resultados sobre óptica. Por tanto, era corriente que los resultados no se publicaran como libro, sino que se dieran a conocer a través de cartas a amigos y conocidos. Muchas veces había descubrimientos que se quedaban en los papeles y sólo eran revelados tras la muerte del autor. Otros científicos eran reticentes a publicar algo si no estaba totalmente terminado. Esto le ocurría a Christiaan Huygens (1629-1695), que además de una gran inventiva, tenía un sentido estético de la matemática que hacía que solo publicara los trabajos que consideraba perfectos, por lo que no era raro que otros se adelantaran con resultados parecidos, y después surgieran grandes polémicas sobre quién había sido el primero en descubrir el resultado, como sucedió con la invención del cálculo infinitesimal, que enfrentó a Newton y a Leibniz.
La costumbre entre científicos que no tenían cierta amistad era enviarse sus escritos a través de una tercera persona, que ejercía como testigo de lo que se estaba intercambiando. Esta labor de conexión entre científicos, especialmente de distintos países, la realizó, por ejemplo, Mersenne. Henry Oldenburg (1619-1677) sirvió de nexo de unión entre Newton y Leibniz en el intercambio de resultados. Esta era además una forma de reivindicar los propios descubrimientos, ya que en las sociedades solían quedar constancia de ellos antes de que pudieran ser publicadas y dados a conocer al gran público.

§. Las sociedades científicas en el siglo XVII
Pero los estamentos que realmente favorecieron la extensión de la ciencia moderna por toda Europa fueron las sociedades científicas y sus medios de difusión: las revistas científicas, que permitieron la difusión de todos los descubrimientos en cualquier rama de la ciencia. La primera academia científica, concebida como lugar de reunión de intelectuales para el intercambio de experiencias y conocimientos, se fundó en 1603 en Roma por el científico y noble Federico Cesi (1585-1630), la Accademia dei Lincei (Academia de los Linces), que duró hasta 1630; su miembro más famoso fue Galileo Galilei. En 1657 se creó en Florencia la Accademia del Cimento (Academia del Experimento) fundada por Femando II, duque de Toscana, y el príncipe Leopoldo, que solo duró diez años. Entre sus miembros destacan los alumnos de Galileo, el matemático Vincenzo Viviani (1622-1703) y el físico Evangelista Torricelli (1608-1647), inventor del barómetro, el instrumento para medir la presión atmosférica.
Pero la sociedad científica más importante del momento, y una de las que ha continuado su labor hasta la actualidad, es la Royal Society, fundada en 1660 a partir de los grupos de Londres y Oxford Sus miembros se reunían una vez a la semana para tratar temas de filosofía natural y sus materias relacionadas: medicina, mecánica, óptica, geometría... En 1662 se nombró un encargado de experimentos con el fin de presentar resultados en cada reunión, y la primera persona sobre quien recayó esta labor fue Robert Hooke. Para dejar bien claro que el avance de la ciencia provendría de las evidencias experimentales, más que de la opinión de personas influyentes, la sociedad tomó el lema Nullius in verba, es decir, « En palabras de nadie». Miembros de ella durante esa época fueron Robert Boyle, Robert Hooke, Gottfried Leibniz, John Wallis, Isaac Newton, Christiaan Huygens y Antón van Leeuwenhoek. A partir de 1663, el nombre oficial pasaría a ser Royal Society of London for Improving Natural Knowledge (Real Sociedad de Londres para el Avance de la Ciencia Natural) La sociedad recibió el prestigioso premio Príncipe de Asturias en 2001 en la modalidad de Comunicación y Humanidades.

Grabado que muestra la Universidad de Jena hacia 1600, donde Leibniz pasó un semestre en 1665 y tuvo le oportunidad de conocer a Erhard Weigel

En 1666 fue creada en Francia, por el ministro de Luis XIV, Jean-Baptiste Colbert, y con el apoyo expreso de la Corona, la Académie des Sciencies, que indicaba en su segundo artículo fundacional cuál era su objetivo prioritario: «Animar y proteger el espíritu de la investigación, y contribuir al progreso de las ciencias y sus aplicaciones».
Durante la Revolución francesa fueron suprimidas todas las academias, pero años después se creó el Instituto Nacional de Ciencias y Artes, que recogía el espíritu de todas las antiguas academias literarias, artísticas y científicas.
Pertenecieron a él las personalidades científicas más importantes de la época, como Descartes, Pascal o Fermat Igual que en la Royal Society, era costumbre invitar a científicos de otros países a pertenecer a la academia En 1699, la academia francesa invitó a los ocho primeros miembros extranjeros: Isaac Newton y Gottfried Leibniz, los hermanos Johann y Jakob Bernoulli, Vincenzo Viviani, el astrónomo polaco Johannes Hevelius, el naturalista neerlandés Nicolás Hartsoeker y el matemático, físico, médico y filósofo alemán Ehrenfried Walther von Tschirnhausen.
Aparte de las sociedades científicas, merece la pena llamar la atención sobre la importancia que alcanzaron algunas colecciones particulares, que recibían el nombre de gabinetes de curiosidades o cuartos de maravillas, y en los que se podía encontrar cualquier cosa Mersenne tenía un gabinete particular con instrumentos de física Uno de los más famosos fue el del jesuita Atanasio Kircher (1601-1680), que tema un gabinete en Roma con fósiles, cristales, dientes y cuernos de rinoceronte, entre otros elementos.

§. Leibniz y las academias científicas
Gottfried Wilhelm Leibniz no solo perteneció a las academias científicas más importantes del siglo XVII, sino que apoyó y animó la creación de muchas otras sociedades.
En 1700, el príncipe Federico III (1657-1713), elector de Brandeburgo, creó la Academia Prusiana de las Ciencias, más conocida como Academia de Berlín, a instancias de Leibniz, que fue nombrado presidente. Ya tres años antes, al plantear Sofía Carlota de Hannover, duquesa de Brunswick-Luneburgo, y futura reina de Prusia, la creación de un observatorio astronómico en Alemania, Leibniz, gran amigo de la duquesa, sugirió ampliar el proyecto y crear una academia en la línea de las de París y Londres.
Leibniz, al ser invitado a Berlín para presidir la academia, redactó una serie de escritos indicando cómo debía ser el enfoque de la nueva sociedad. Bebía desarrollar tanto teoría como práctica, para que se beneficiaran de sus informaciones no solo las artes y ciencias del país, sino también las industrias y el comercio. La sociedad científica debería dedicarse especialmente a las ciencias fundamentales, como las matemáticas y la física, aunque en esa partición incluía más de lo que puede pensarse hoy en día. Leibniz dividía las matemáticas en cuatro partes: la geometría, incluyendo el análisis; la astronomía y sus campos relacionados (geografía, cronología, óptica); la arquitectura (civil, militar, naval), que comprendía también la pintura y la escultura, y la mecánica, con sus aplicaciones tecnológicas. Por su parte, la física incluía la química y los reinos animal, vegetal y mineral.
Preocupado por la financiación de la academia, Leibniz consiguió para la sociedad la elaboración y venta, en exclusiva, de calendarios astronómicos. Más adelante presentó un proyecto de sericultura (cría del gusano de seda) para conseguir fondos y asegurar la peí-vivencia económica de la academia. En ese sentido, planeó la plantación y cuidado de árboles de morera en los jardines reales de Potsdam. Aunque el proyecto no terminó de salir adelante, Leibniz llegó a realizar experimentos en sus propios jardines.
También intentó potenciar otras academias en Dresde o en Viena, pero los proyectos no fructificaron.

§. Revistas científicas
Aunque los descubrimientos se daban a conocer en las reuniones de las sociedades, se echaba en falta un medio eficaz de comunicación que sirviera para difundir más ampliamente los grandes avances en la ciencia moderna.
La primera revista científica que puede tener esa consideración fue el Journal des Sçavans, aparecida en París en enero de 1665. Sin embargo, no era propiamente una revista únicamente científica, ya que aparecían artículos de legislación o también obituarios de personas famosas. Fue fundada por el asesor del Parlamento Denis de Sallo bajo el patrocinio del ministro Colbert. En ella se dieron a conocer varios de los descubrimientos de Leibniz, pero también información sobre trabajos de Descartes, Hooke, Huygens y otros. Durante la Revolución francesa, la revista desapareció y, aunque surgió de nuevo a finales del siglo XVIII, se convirtió en una revista eminentemente literaria.
Por tanto, la revista científica por antonomasia, y la más importante durante mucho tiempo, fue Philosophical Transactions, que vio su primer número en marzo de 1665. Aun siendo desde el primer momento el órgano de difusión de la Royal Society, se trataba de un trabajo personal del secretario de la sociedad, Henry Oldenburg, quien comprendió claramente la necesidad de encontrar un recurso que permitiera hacer llegar los avances de la ciencia a todos los interesados. Oldenburg publicó la revista a sus expensas con el acuerdo de la Royal Society, pensando que sería un negocio rentable, algo que resultó bastante desacertado, Posteriormente en el siglo XVIII, la revista pasó a ser el boletín oficial de la sociedad.
«No hay nada más necesario para promover los avances de los asuntos filosóficos que la comunicación de los mismos.»
Henry Oldenburg, carta de presentación de Philosophical Transactions.
Esta revista fue la primera que planteó las normas de control que existen actualmente en todo tipo de revista científica. Aparte de la prioridad científica del artículo, Oldenburg enviaba los originales a diversas personas para que evaluaran el interés o no de su publicación.
A instancias de Leibniz, en 1682 comenzó a publicarse en Leipzig la revista Acta Eruditorum, fundada por el científico alemán Otto Mencke (1644-1707), aunque su impresión, con dificultades, sólo sobrevivió hasta 1782. Se editaba en latín, idioma común que todos los científicos de la época entendían, por eso tuvo una amplísima difusión. Leibniz fue un colaborador habitual de esta publicación y, revisando los distintos números de la revista, se puede comprobar la gran variedad de temas que le interesaban. Su primer artículo trataba sobre la cuadratura aritmética del círculo, pero en otros números encontramos artículos sobre óptica, descuento de facturas, mecánica de planos inclinados o resistencia de vigas.
Leibniz creó una revista anual que recogiera artículos, reseñas bibliográficas y resultados interesantes de los miembros de la Academia de Berlín. El primer número de dicha publicación, con el título de Miscellanea Beroniliensia, apareció en 1710. Una gran parte de los artículos eran del propio Leibniz, que escribía de cosas tan diversas como su máquina aritmética, artículos de matemáticas y mecánica, el estudio del origen de las naciones a través de la lingüística o los descubrimientos del fósforo o la aurora boreal. A pesar de su interés en la publicación, no contó con muchas colaboraciones.
Como hemos visto, Leibniz comenzó a abrirse camino en estas sociedades gracias a su máquina mecánica. Es interesante que veamos la evolución de las herramientas mecánicas de cálculo hasta aquella época.

§. Calcular más eficientemente
Desde que el ser humano comenzó a contar fue aplicando esas operaciones a todos los niveles de la vida cotidiana. Al avanzar la civilización, las operaciones se ampliaron y hubo que realizar cuentas cada vez más laboriosas en el comercio, los viajes, el estudio de los astros, etc. Al ampliarse y complicarse el número de operaciones, el hombre imaginó medios para realizarlas de una forma más rápida y segura. Así, aparecieron las máquinas de calcular con el objetivo de mecanizar unos instrumentos de cálculo, que permitieran eliminar o paliar los errores a los que estaba expuesto todo cálculo manual.
Los primeros intentos de ayudamos con elementos que nos permitieran contar y operar fueran «digitales». Hay países donde se utilizan los dedos para hacer operaciones más complicadas que meras sumas y restas. Por ejemplo, para operar rápidamente por 9 hay una regla que consiste en extender las dos manos y comenzar a contar desde un extremo, usualmente el izquierdo, y doblar el dedo correspondiente al valor por el que queremos multiplicar el 9. Para el resultado basta contar los dedos que hay antes del doblado, que será la cifra de las decenas, y los posteriores al doblado, lo que nos daría las unidades. En la figura 3 vemos que el resultado de multiplicar 9×4 es igual a 36.
«No es digno de hombre notable perder su tiempo en un trabajo de esclavos, el cálculo que podría confiarse a cualquiera con la ayuda de una máquina.»
Gottfried Wilhelm Leibniz.
Si queremos multiplicar dos números mayores que 5, basta doblar en cada una de las manos los dedos correspondientes al resultado de restarle 6 a cada número a multiplicar. Se suman los números doblados de ambas manos y se multiplica por diez, y a eso se le suma el producto del número de dedos Que hay levantados en ambas manos.

En la figura 4 podemos ver el resultado de multiplicar 8 (8 - 5 = 3 dedos doblados, en este caso en la mano derecha) ×9 (9 - 5 = 4 dedos doblados): como tenemos siete dedos doblados, y dos levantados en una mano y uno en la otra, el producto de 8 × 9 = 7 × 10 + 1 × 2 = 72.

§. Los ábacos
Los sistemas babilónico, maya, egipcio, griego o romano, entre otros, permitían el recuento, pero eran complicados a la hora de calcular. Basta pensar en el producto de XDI por XXI utilizando números romanos. Pero como la ingeniería o el comercio debían seguir adelante, hubo que inventarse métodos que permitieran realizar los cálculos que la civilización demandaba. Así apareció la primera máquina de calcular de la historia: el ábaco.
Con pequeñas diferencias y alguna que otra variante, el ábaco apareció casi a la vez en todos los continentes hace más de 3000 años. Ha sido, además, el artilugio más longevo, ya que se ha utilizado en algunos países hasta bien entrado el siglo XX.
Posiblemente en su origen se limitaran a una serie de marcas en la arena, en la que se colocaban una serie de calculus (piedrecillas en latín, de donde procede la palabra cálculo). Después su diseño varió, con la aparición de una serie de varillas en las que insertaban unas cuentas con las que se realizaban las operaciones.

Figura 5. Ilustración de un ábaco romano. Sus columnas representan las unidades, decenas, centenas mediante los símbolos romanos I, X y C. seguidos de unidades, decenas y centenas de millar. Le parte de la derecha se usaba para representar fracciones.

En la figura 5 se observa una reproducción de un ábaco romano. En él aparecen una serie de líneas verticales, en las que cada cuenta tiene el valor de una unidad en la parte inferior y de cinco unidades en la superior. Por eso el valor que puede tener cada una de las cuentas varía según el lugar y la posición en que se muevan.
Los símbolos que aparecen corresponden a los iniciales en el sistema de numeración romano, que evolucionó con los años hasta llegar, en el Renacimiento, a las formas que usamos hoy día. Algunos ábacos romanos disponían de líneas especiales para trabajar las fracciones.

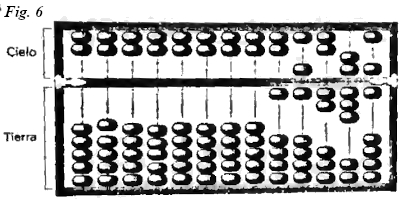
Ábaco chino, se lee de derecha a izquierda, siguiendo el orden decimal: unidades, decenas, etc. Las bolas se contabilizan junto a la barra central. En el ábaco ilustrado aparece representado el número 16 336, ya que en las decenas, al haber dos bolas de cinco unidades, equivale a una unidad superior.

El ábaco más conocido en la actualidad es el chino, llamado suanpan, localizable en tiendas de regalos. Tal como vemos en la figura, consta de un recuadro de madera con una serie de varillas separadas en dos partes. La superior, que se llama cielo, tiene dos cuentas, cuyo valor es de 5 unidades correspondientes, y en la inferior, la tierra, hay cinco bolas, cada una con un valor de 1 unidad. La forma de contar es acercar las cuentas correspondientes a la barra de división central. De derecha a izquierda aparecen las unidades, decenas, centenas, unidades de millar, etc. Cada vez que se completan diez unidades de un nivel se eliminan y se añade una al nivel superior.
El ábaco japonés o soroban, es parecido al chino, pero en el cielo solo hay una cuenta y en la tierra cuatro, suficientes para realizar operaciones en base 10. Por último, el ábaco ruso o tchotu consta de varillas en las que hay 10 bolas sin separación.
El ábaco fue durante siglos 1a máquina por excelencia para realizar cálculos; incluso existía la profesión de abaquista, que era el que realizaba cálculos utilizando esta herramienta. Cuando en Europa comenzó a introducirse las cifras indo-arábigas, hubo una gran resistencia por parte de los abaquistas a abandonar el modo clásico de cálculo. Es conocida la ilustración realizada por Gregor Keisch para la obra Margarita philosophica, donde se enfrentan un abaquista, en este caso Pitágoras, y Boetius, un algorista que utilizaba las nuevas cifras indo-arábigas para calcular. A pesar de su utilidad, el sistema de numeración indo-arábigo no terminó de implantarse completamente en Europa hasta el siglo XVI

§. Napier: tablillas y logaritmos
Hasta el siglo XVII no apareció un nuevo invento en el afán humano por realizar cálculos más fácilmente. En 1617 el matemático escocés John Napier (también conocido por Neper) publicó una obra, que se llegó a conocer como Rabdologia, en la que presentaba una serie de tablillas que permitían convertir los productos en sumas y las divisiones en restas y que se llamaron huesos de Napier.

John Napier
Napier (1550-1617) barón de Merchiston, fue teólogo y matemático. A pesar de que su gran pasión era la religión, y consideraba las matemáticas como un entretenimiento, ha pasado a la historia de la ciencia como el creador de los logaritmos, herramienta en la que trabajó más de veinte años y que dio a conocer en 1614 en su obra Mirifici logaritmorum canoniss descriptio. Los logaritmos que planteó no estaban basados en ninguna base determinada, pero el matemático inglés Henry Briggs lo convenció para modificar la escala a la base 10. El propio Napier calculó el logaritmo decimal de los mil primeros números. Basándose en la misma idea de encontrar una herramienta para simplificar las operaciones aritméticas, publicó en 1617 la obra Rabdiologiae seu numerationes per virgulas libri duo , en la que presentaba lo que se conoce como las tablillas de Napier. También dejó para la historia varios resultados interesantes en el campo de la trigonometría, tanto plana como esférica.

El invento consistía en una serie de tablillas en las que aparecían en columna diez cuadrados, divididos en dos partes por un trazo diagonal, salvo el primero. En cada tablilla aparecía la tabla de multiplicar de un número, es decir, aparecía en el cuadro inicial una cifra y debajo su doble, su triple, su cuádruple y así sucesivamente hasta llegar al valor de multiplicar la cifra por 9.

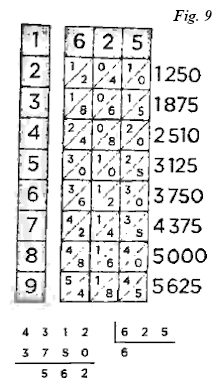
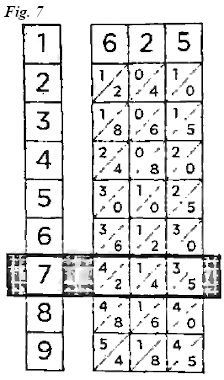Bastaba colocar en una caja las tablillas correspondientes a uno de los valores que se quería multiplicar y comprobar los valores que quedaban a la altura del otro valor que se quería multiplicar. En ese caso bastaba sumar las cifras que estaban en la misma diagonal y nos salía el valor del producto. Así, para multiplicar el número 625 por 7, la fila correspondiente al número 7 de la multiplicación nos daría los valores 4 para las unidades de millar, 3 = 2 + 1 para las centenas, 7 = 4 + 3 para las decenas y 5 para las unidades. Es decir, el producto sería 625 × 7= 4.375. Podemos comprobarlo en la figura 7.
Sí se quieren multiplicar números mayores, basta seleccionar cada fila de las cifras del segundo factor y sumar, escalonadamente, los números obtenidos por el método anterior.
Para multiplicar 2134 por 732 debemos distribuir las tablillas tal como aparecen en la figura 8.
Sumaríamos los valores correspondientes a cada factor. Debemos tener en cuenta que cuando sumamos en diagonal y suma más de nueve, como ocurre en las decenas del producto 2134 x 3, colocamos en su lugar las unidades y las decenas de ese resultado se añaden a la unidad siguiente.

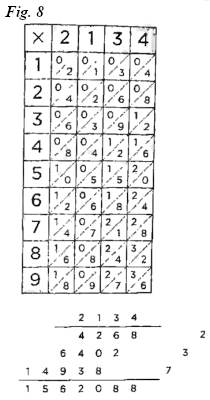Como podemos apreciar en el proceso anterior, el producto se reduce a realizar una serie de sumas, ya que los productos por cada cifra ya los tenemos en la tablilla. Para hacer la división se hace un proceso inverso, restando. Si quisiéramos dividir 4312 entre 625, colocaríamos las tablillas correspondientes al divisor (625) y realizaríamos todas las operaciones correspondientes a la multiplicación de cada línea para encontrar la cifra inferior más cercana al dividendo (4312), en este caso 3750, y así obtendríamos el cociente (6), como podemos observar en la figura 9. Finalmente, para bailar el resto de la división, deberíamos restar a 4312 el valor 3 750, lo que nos da un resultado de 562.
También es posible realizar, de una forma más complicada, potencias, raíces cuadradas y cúbicas con las tablillas.
Napier hubiese pasado a la historia de las matemáticas aun sin haber creado estos artilugios para operar rápidamente. En un libro publicado arios antes, en 1614, presentaba su obra más importante: los logaritmos. Se trata de una regla de cálculo que permite convertir los productos en sumas, las divisiones en restas y las potencias en productos. La simplificación de las operaciones fue algo de mucha utilidad,

sobre todo en los cálculos astronómicos. El gran matemático francés Pierre-Simon de Laplace (1749-1827) dijo al respecto:
«Con la reducción del trabajo de varios meses de cálculo a unos pocos días, el invento de tos logaritmos parece haber duplicado la vida de los astrónomos».
El logaritmo en una base cualquiera a de un número b se define como aquel valor al que hay que elevar el número a para obtener el b. Expresado en símbolos sería:

log_ab = x → ax = b

Por ejemplo, el logaritmo en base 3 de 81 vale 4 (log₃ 81 = 4), ya que 3⁴ = 81.
El logaritmo es una operación inversa de la potencia, igual que la resta es una operación inversa de la suma.

Grabado realizado por Gregor Reisch para su obra Margarita philosophica (1508). Muestra el enfrentamiento entre a un abaquista (Pitágoras) y un algorista (Boetlus), que usa las cifras indo-arábigas para calcular.

Si tenemos el valor de una suma y conocemos el valor de uno de los sumandos, hallar el otro sumando equivale a restarle a la suma el valor del sumando conocido; luego son operaciones inversas. Del mismo modo, si conocemos el valor de una potencia y conocemos el exponente de la potencia, hallar la base equivale a la radicación, es decir, a hallar la raíz de grado igual al exponente del valor de la potencia. Si lo que conocemos es la base, hallar el exponente se convierte en el logaritmo de esa base del valor de la potencia Como la suma de dos números tiene la propiedad conmutativa, el orden de los sumandos no altera la suma, esta operación solo tiene una operación inversa. Como la potencia no es conmutativa, existen dos operaciones inversas según no se conozca la base o el exponente de la potencia.
Junto con los logaritmos de base 10, que se suelen abreviar simplemente como log, sin indicar la base, los más usados son los logaritmos en base e, un número trascendente de la misma familia que el más conocido π. Estos logaritmos reciben, en honor a Napier, el nombre de logaritmos neperianos y suelen representarse por ln.
Las propiedades fundamentales en las que se basa el cálculo con logaritmos son las siguientes, que se verifican para cualquier base:
1. El logaritmo del producto de dos números es igual a la suma de los logaritmos de los dos factores: log (a×b) = log a + + log b.
2. El logaritmo del cociente de dos números es igual a la diferencia entre el logaritmo del numerador menos el logaritmo del denominador

log (a/b) = log a - log b

3. El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base: log a^b = b×log a .
En estas propiedades se observa claramente que las operaciones se sustituyen por otras de un nivel de dificultad inferior. Inicialmente, para poder aplicar los logaritmos era necesario trabajar con tablas de logaritmos.
Los logaritmos se aceptaron enseguida por los matemáticos de la época, que supieron reconocer el avance que representaban. Se comenzaron a buscar aplicaciones y, unos pocos años después, se idearon herramientas mecánicas que aplicaban esos principios.
Se considera al astrónomo y matemático inglés William Oughtred (1574-1660) como el primero que utilizó la letra griega π para representar el cociente entre la longitud de una circunferencia y su diámetro. También se le atribuye el uso del símbolo × para indicar el producto, y las abreviaciones sen y cos para las razones trigonométricas seno y coseno. Pero por lo que pasó a la historia fue por la invención de la regla de cálculo en 1621. Ideó un par de tablillas en las que aparecían los valores de los logaritmos y permitían hacer productos y divisiones deslizando una tablilla sobre otra y realizando sumas y restas. Lo curioso fue que la primera vez que comercializó la regla de cálculo le dio una estructura circular, en la que existían una serie de discos concéntricos, en donde estaban situados los logaritmos y que giraban alrededor del centro. Este artilugio recibe normalmente el nombre de regla de cálculo circular.

Regla de cálculo circular, artilugio ideado por William Oughtred en 1621.

Sin embargo, el diseño básico que tuvieron las reglas de cálculo fue el de una barra fija con una regleta movible en su interior. En las reglas de cálculo más modernas, tanto la barra fija como la regleta movible están calibradas con varias líneas divididas en partes proporcionales. Con ellas no solamente se pueden calcular logaritmos, sino también potencias, inversos y razones trigonométricas.
Las reglas de cálculo han sido las herramientas utilizadas diariamente por arquitectos, ingenieros y otros profesionales hasta el último tercio del siglo XX, en que comenzaron a popularizarse las calculadoras científicas que incluían ya los cálculos logarítmicos.

§. Las máquinas mecánicas
Pocos años después, el alemán Wilhelm Schickard (1592-1635) crearía la considerada como primera máquina mecánica de la historia Fue profesor de arameo y hebreo, ministro luterano, teólogo, topógrafo, astrónomo y matemático. Entre 1613 y 1619 ejerció de diácono en Nürtingen, donde entró en contacto con Kepler. Este solicitó ayuda a Schickard, que tenía fama de excelente grabador, para que le preparara una serie de grabados y xilografías para su obra Harmonice mundi. También le pidió ayuda en el cálculo de una serie de tablas. De esta relación surgió la idea en Schickard de crear una máquina para mecanizar los cálculos astronómicos que estaba realizando. El propio Schickard explicaba cómo le había surgido la idea en una carta a Kepler en 1623:
Lo que se ha hecho mediante el cálculo, yo he intentado hacerlo, usando la mecánica He ideado una máquina compuesta de once ruedas dentadas completas y seis incompletas; esta calcula instantánea y automáticamente a partir de números dados, mientras los suma, resta, multiplica y divide.

Prototipo de la máquina aritmética inventada por Leibniz. Biblioteca Nacional de la Baja Sajonia, en Hanover.

Así diseñó una máquina basada, como la regla de cálculo, en los logaritmos. Consistía en una serie de cilindros que rotaban en una estructura parecida a una antigua máquina registradora. La máquina, que bautizó como reloj de cálculo, no llegó a construirse completamente pues se encargó un ejemplar para Kepler, pero un incendio destruyó el prototipo. En el siglo XX, siguiendo los esquemas de Schickard, se construyeron algunos ejemplares de la máquina.

§. La Pascalina
La siguiente máquina conocida fue creada por el matemático francés Blaise Pascal, que la diseñó en 1642 pata ayudar en los cálculos que tenía que realizar su padre, jefe de recaudación de impuestos para Normandía Podía realizar sumas y restas.
Estaba formada por una serie de ruedas conectadas entre sí y divididas en 10 partes, del 0 al 9. Cada vez que una rueda daba una vuelta completa, la rueda siguiente avanzaba un lugar. Para restar bastaba girar la rueda en dirección contraria y, tras completar una vuelta, se restaba una unidad del círculo siguiente. El diseño consistía en una caja en forma de paralelepípedo con una serie de ruedas enlazadas entre sí. Cada una de ellas representaba una de las unidades correspondientes; unidades, decenas, centenas, etc. Hoy en día es posible encontrar en algunos comercios o en Internet máquinas aditivas basadas en la misma idea.
El propio Pascal creó una empresa para fabricar ejemplares de la Pascalina, como se llegó a conocer su invento, Al ser la fabricación totalmente manual, el precio del producto final era tal que nunca se convirtió en negocio. Se llegaron a fabricar alrededor de medio centenar de máquinas, de las que quedan algunas en la actualidad en museos de la ciencia.
A mediados de la década de 1660 nos encontramos nuevas máquinas, en este caso ideadas por el matemático Samuel Morland (1625-1695), que además fue diplomático, espía, académico y sobre todo inventor, llegó a diseñar estufas portátiles de vapor y bombas de agua.

Blaise Pascal
Pascal (1623-1661), físico, matemático y filósofo, comenzó a frecuentar desde muy joven los ambientes científicos e intelectuales de la época, entrando a formar parte del círculo de Mersenne. Con solo diecisiete años redactó un ensayo sobre las cónicas en el que ya aparece el que se conoce como teorema de Pascal, sobre geometría proyectiva, Trabajó sobre el vacío, reproduciendo el experimento de Evangelista Torricelli, y la presión atmosférica, campo en el que llegó a ser el primero en realizar un estudio completo sobre la hidrostática.

La Pascalina, la máquina de calcular ideada por Pascal
También desarrolló resultados en dinámica de fluidos, en particular al descubrir la ley de los vasos comunicantes, más conocida como ley de Pascal. Calculó el área de la curva cicloide, un problema fundamental en el desarrollo del cálculo infinitesimal. El Caballero de Meré, un noble aficionado a los juegos de azar, planteó a Pascal un problema sobre dados: ¿qué era más probable, sacar al menos un seis en cuatro lanzamientos de un dado, o sacar un doble seis en veinticuatro lanzamientos de dos dados? De la correspondencia entre Pascal y el matemático francés Pierre de Fermat nacería el cálculo de probabilidades. También desarrolló el que actualmente se conoce como triángulo de Pascal, cuyas filas nos dan todos los números combinatorios que tienen el mismo numerador. Este triángulo es una herramienta muy útil para el cálculo de desarrollo de potencias. Pero indudablemente, el invento más conocido de Pascal es su máquina de calcular, la Pascalina, con la que se podían realizar sumas y restas.

Morland conocía la máquina de Pascal y al parecer también la diseñada por Rene Grillet de Reven, relojero de Luis XIV, que se considera basada en la de Leibniz. Llegó a diseñar tres máquinas de cálculo, una para realizar cálculos trigonométricos, otra sumadora y otra que permitía productos y divisiones. Estas dos últimas máquinas fueron dadas a conocer en su libro Descripción y uso de dos instrumentos aritméticos .
La máquina sumadora tenía una serie de ruedas como la de Pascal, pero eran independientes. Cada una de ellas tenía unido un pequeño círculo que contabilizaba el número de vueltas completas que había dado el disco grande, y esas vueltas había que añadirlas posteriormente a mano. Estaba diseñada para operar en el sistema monetario inglés. Está considerada como la primera calculadora de bolsillo.
La máquina multiplicativa se basaba en las mismas ideas que las tablillas de Napier. Estaba compuesta por una placa plana provista de varios puntos, donde se podían colocar una serie de discos intercambiables, algunos de los cuales permitían calcular raíces cuadradas y cúbicas. Los discos eran, básicamente, una versión circular de las tablillas de Napier. Se cree que su diseño está inspirado en otra máquina creada en 1659 por el italiano Tito Livio Burattini (1617-1681).

§. La máquina aritmética de Leibniz
Todas las máquinas de aquella época seguían la misma estructura que la máquina de Pascal; por eso, la máquina aritmética que diseñó Leibniz significó un avance significativo con respecto a los otros artilugios contemporáneos. Aunque inicialmente partió de la misma idea que Pascal, pronto comprendió que para poder dar el salto de sumas y restas a operaciones más complicadas se necesitaba un mecanismo más potente y sofisticado.
Es posible que el diseño de esta máquina ya lo tuviera Leibniz a principios de la década de 1670. Durante su primera visita a París consultó los legados de Pascal, por lo que seguramente estudió su máquina calculadora.
Aunque inicialmente la denominó Staffelwalze ( Stepped Reckoner, en inglés), algo así como «calculador escalonado», más adelante se referiría a ella como máquina aritmética.
Se componía de dos partes, una superior, fija, y otra inferior, que disponía de un carro movible.
Pero la gran genialidad consistía en una serie de cilindros sobre los que estaban insertadas un total de nueve varillas de diferente longitud (véase la figura). El cilindro iba montado sobre un eje y estaba en contacto con una rueda dentada, fijada a un eje paralelo al anterior.

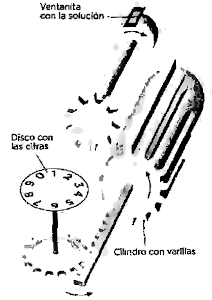
Mecanismo de la máquina aritmética de Leibniz. Era la primera máquina da este tipo que permitía realizar las cuatro operaciones aritméticas básicas.

Al girar el disco correspondiente a las cifras, el cilindro avanzaba o retrocedía, de manera que una rueda dentada accionada por el cilindro se movía en (unción de las varillas que hubiesen quedado a su altura. Esta rueda giraba un último disco en el que aparecía la solución, que podía verse en una ventanita de la caja.
La máquina utilizaba tres tipos de ruedas: de suma, multiplicando y multiplicador. Haciendo interactuar unas con otras permitía sumas, restas, productos y divisiones.
La primera máquina que Leibniz presentó en las sociedades científicas era un prototipo realizado en madera con problemas de funcionamiento. No pudo conseguir demostrar que realizaba los cálculos para los que estaba diseñada, principalmente por defectos de fabricación. Más tarde encontró un relojero mecánico que consiguió fabricarle una máquina de metal que funcionaba.
Aunque ya a mediados de la década de 1670 Leibniz disponía de una máquina que realizaba las cuatro operaciones, estuvo perfeccionándola durante toda su vida. Años más tarde intentó diseñarla de forma que trabajara en sistema binario, pero la gran cantidad de cilindros que se necesitaban para operaciones medianas le obligó a desechar la idea.
En aquella época, las máquinas mecánicas solían adolecer del mismo problema: eran complicadas y muy costosas, cuando no imposibles de fabricar, pues la tecnología de la época no podía dar salida a los diseños que generaban las mentes de esos genios. Aunque las primeras máquinas aparecieron a principios del siglo XVII, se tardaría dos siglos en que comenzaran a extenderse y popularizarse, tras ser comercializadas eficientemente. En concreto, hasta 1822 no se comercializó la primera máquina mecánica, la Arithmometer, ideada por el francés Charles Xavier Thomas de Colmar (1785- 1870), que fue nombrado caballero de la Legión de Honor por dicho invento.
Igual que Isaac Newton comenzó a ser conocido en los ambientes científicos de la época a través de la creación de su telescopio reflector, la máquina aritmética de Leibniz, junto con algunos escritos sobre el movimiento, permitieron que el nombre de Gottfried Wilhelm Leibniz comenzara a ser citado en las principales academias científicas del momento.

Capítulo 2
Y el cálculo se hizo

Las ciencias, y en concreto las matemáticas, gozaron de un impresionante auge en los siglos XVI y XVII. Una gran parte de esta mejora sustancial fue debida a la fundamentación del cálculo infinitesimal. Se resolvieron todos los problemas clásicos y se afrontaron otros nuevos que proporcionaban la naturaleza y el mundo físico. Aunque Newton y Leibniz son considerados los fundadores de este cálculo, se apoyaron en muchos otros importantes matemáticos de estos siglos.

Leibniz llegó por primera vez a París a finales de marzo de 1672 para abogar por el proyecto egipcio elaborado con el barón Von Boineburg. Quería conseguir audiencia en la corte para plantear sus propuestas con el fin de desviar las ansias bélicas de Francia frente a los Países Bajos. Al llegar a París, Inglaterra ya había entrado en guerra con los Países Bajos y Francia lo haría a la semana siguiente, por lo que sus intenciones carecían de sentido. Aun así, insistió en su labor diplomática para conseguir, al menos, que Alemania no se viera envuelta en el conflicto.
Tras seis meses esperando ser recibido en la corte con pocas posibilidades de éxito, Melchior Friedrich von Schönborn, sobrino del elector de Maguncia y yerno de Boineburg, se trasladó a París acompañado de Phillip Wilhelm, hijo del barón. El objetivo de Von Schönborn era participar en las negociaciones oficiales de paz y proponer la realización de un congreso para la paz en Colonia. Tras no conseguir ningún efecto positivo, Von Schönborn viajaría más tarde a Inglaterra con Leibniz.
La muerte de Boineburg el mes siguiente significó un duro golpe para Leibniz, pues tenía una gran amistad con él y le había servido bien en muchas ocasiones. El barón le había apoyado en el desarrollo de sus trabajos y sobre todo le había conseguido contactos con científicos, políticos y hombres de estado, hasta el punto de conseguirle el puesto de consejero del elector de Maguncia. El propio Leibniz hablaba de Boineburg como « uno de los más grandes hombres de este siglo, que me honró con una amistad muy especial ».

§. Conversaciones con científicos
Durante la espera para poder entrevistarse con miembros del Gobierno francés, Leibniz aprovechó las oportunidades que una urbe como París le ofrecía y se entrevistó con importantes científicos e intelectuales que estaban en ese momento en la ciudad.
En el verano de 1672, visitó al gran científico neerlandés Christiaan Huygens, cuya obra conocía en parte. En esta primera reunión, Leibniz le mostró el primer modelo de máquina aritmética, aún enmadera e imperfecto. Huygens escribió más adelante a Oldenburg, comentando que la máquina era un gran adelanto, aun a pesar de necesitar ser perfeccionada
También le presentó un método para sumar series infinitas, uno de los problemas que más desarrollaron los matemáticos de esa época. Huygens le aconsejó que consultara las obras de los matemáticos ingleses John Wallis, a quien conoció en su posterior viaje a Londres, y Grégoire de Saint-Vincent (1584-1667), cuya obra consultaría en la biblioteca real.
Otra reunión importante fue con el bibliotecario real Pierre de Carcavi, que tenía mucho interés en conocer la máquina aritmética de la que Leibniz le había hablado. También realizó para él algunos encargos, como una evaluación sobre una obra relacionada con el vacío escrita por el físico alemán Otto von Guericke (1602-1686). Este científico fue el inventor de la bomba de vacío y quien, en 1654, realizó el célebre experimento conocido como las esferas de Magdeburgo. Unió dos semiesferas de 50 centímetros de diámetro y dentro de ellas hizo el vacío. En cada lado de la esfera resultante colocó ocho caballos tirando para separar las dos semiesferas, pero no lo lograron
Tras fracasar la misión diplomática en Francia, Leibniz recibió la orden de acompañar a Von Schönborn a Inglaterra y después volver a Maguncia pasando por los Países Bajos, con el objetivo de conseguir que ambas naciones iniciaran conversaciones de paz. Por tanto vistió a Londres a principios de 1673.

Christiaan Huygens
Nacido en La Haya, Huygens (1629-1695) fue uno de los principales científicos de la época. Destacó en matemáticas, física y astronomía. Tuvo gran amistad con el filósofo y matemático René Descartes, que visitaba a menudo a su padre, y que ejerció una influencia palpable en el enfoque de sus investigaciones. Como embalador de los Países Bajos, visitó ciudades importantes, entre ellas Copenhague, Roma y Paris, donde se instaló en 1660. Al año siguiente viajó a Londres, y allí consiguió ingresar en la Royal Society. En 1666 regresó a la capital francesa para encargarse de la coordinación de la Academia de Ciencias de París. Por entonces conoció a uno de sus más brillantes discípulos: Leibniz. En 1689 regresó a su ciudad natal, donde residiría hasta su muerte, aunque previamente pasó algunos años de nuevo en Londres, donde conoció el otro gran genio, Isaac Newton.
Logros científicos
Fue un gran pulidor de lentes y construyó muchos telescopios, algunos de gran tamaño. Localizó un anillo alrededor de Saturno, descubierto por Galileo sin concretar los resultados, y descubrió el satélite Titán. Cuando la Agencia Espacial Europea mandó una sonda para investigar Titán la llamó, en su honor, Sonda Huygens. En matemáticas fue uno de los pioneros del cálculo de probabilidades y estudió longitudes y áreas de diversas curvas, como la cisoide o la cicloide, curvas que allanaron el camino hacia el cálculo infinitesimal. También trabajó aspectos de mecánica, especialmente la teoría de oscilación a partir de péndulos o el principio de conservación de las fuerzas vivas. En óptica desarrolló la teoría ondulatoria de la luz.

Una vez en Londres se reunió con el teólogo y diplomático alemán Henry Oldenburg, firme defensor de la filosofía natural, lo que hoy llamaríamos ciencia. Oldenburg convocó una sesión de la Royal Society para que Leibniz pudiera presentar su máquina aritmética. Durante su estancia en Londres, Leibniz pudo asistir a varias de las reuniones de la Royal Society, aunque casualmente no estuvo en una en la que Hooke lanzó serios comentarios negativos sobre la máquina, que como ya hemos comentado, no funcionaba correctamente.
Robert Hooke fue uno de los científicos experimentales más importantes de la historia. Abarcó multitud de campos científicos y fue nombrado, entre otros cargos, director de experimentación de la Royal Society en 1662, con el cometido de presentar semanalmente resultados científicos de lo más variopinto, y en 1677, secretario de la misma institución. Con una gran inventiva, pero poca capacidad para desarrollar los temas de una forma rigurosa, Hooke afirmaba haber tenido las ideas sobre los grandes descubrimientos de la época, pero sin llegar a rematarlos, antes que quienes los desarrollaron y los hicieron públicos. Esto hizo que constantemente estuviera envuelto en polémicas sobre el descubrimiento de muchos resultados. Fue especialmente llamativo el enfrentamiento con Isaac Newton por la paternidad de la ley de gravitación universal. Hasta tal punto llegó el odio entre ellos, que tras su muerte Newton hizo destruir todos los retratos existentes de Hooke, por lo que hoy no se tienen imágenes seguras de él.
De todos modos, la satisfacción de Leibniz por su participación en las reuniones de la sociedad fue tal que solicitó su admisión antes de abandonar Londres, siendo aceptado como miembro a mediados de abril.
En una reunión con Samuel Moriand, se hicieron demostraciones de sus respectivas máquinas de calcular. También visitó a Robert Boyle, quien le presentó al matemático John Pell (1611-1685), con quien discutió sobre los métodos para hallar sumas de términos y acerca del método de diferencias inventado por Leibniz para el cálculo de series.
Antes de abandonar Inglaterra le llegó la noticia de la muerte del elector de Maguncia, por lo que la misión diplomática que tenía entre manos quedó en suspenso. Eso le permitió no tener que viajar a los Países Bajos y poder volver a París.

§. Consejero en la corte de Hanover
En 1675 Leibniz se encontraba en París, pero sin una ocupación clara. Era evidente que quería quedarse en la capital francesa para estar en contacto con la revolución científica que se estaba gestando allí; por eso había rechazado el puesto de secretario del primer ministro del rey de Dinamarca y el de consejero del duque Juan Federico de Hannover, ofrecimiento que él mismo había favorecido al escribirle al duque hablándole de las actividades y contactos realizados tanto en París como en Londres. A finales de año intentó conseguir una plaza remunerada en la Academia de Ciencias de París, tras quedar una plaza vacante por el fallecimiento del matemático Gilles de Roberval (1602-1675), pero la academia consideró que con Huygens y Cassini ya tenían cubiertos los puestos de extranjeros contratados.
Le escribió al duque Juan Federico de Hannover, con el pretexto de hablarle de su máquina aritmética, que ya había recibido grandes elogios en la academia al presentar un ejemplar que funcionaba correctamente, y aprovechó para aceptar el cargo que se le había ofrecido meses atrás. En enero de 1676 se hizo cargo del puesto de consejero, mientras que recibía también el nombramiento de consejero del nuevo elector de Maguncia.
Leibniz intentó no dejar París y viajaba de vez en cuando a Hannover y a Maguncia para seguir con sus relaciones políticas y no perder el contacto directo con la academia y con los científicos y filósofos que visitaban la ciudad; así podría informar de los avances más importantes a sus patronos. Durante meses hubo varios requerimientos por parte de Hannover para que se trasladara inmediatamente a la ciudad, a lo que Leibniz respondió dando largas.
Al final le plantearon un ultimátum, ya que Leibniz, además de consejero, se iba a hacer cargo del puesto vacante de bibliotecario de la biblioteca ducal. Este puesto le hizo visitar muchos lugares para comprar bibliotecas particulares en las que podría haber libros interesantes para la del duque. También era su intención estar en contacto con eruditos de diversos países y recopilar los nuevos descubrimientos en la biblioteca.
Por fin, a principios de octubre de 1676 abandonó París para ya no regresar jamás. El viaje lo realizó desde Calais, pasando por Londres, donde se entrevistó de nuevo con Oldenburg, a quien le mostró su prototipo perfeccionado de máquina aritmética, y también con el bibliotecario de la Royal Society, el matemático John Collins, que quedó muy impresionado por los conocimientos de Leibniz.

§. Las series infinitas
Aparte de su máquina, uno de los primeros resultados que Leibniz dio a conocer en la Royal Society fue un método para hallar la suma de series de infinitos términos.

La suma de los términos de la serie geométrica
La primera suma de infinitos términos de la que se tiene conocimiento corresponde a la llamada serie geométrica. Ya hay resultados para esa serie en el Papiro Rhind. La serie consiste en hallar la suma de las infinitas potencias cuya base sea un número menor que uno. El ejemplo más común sería la suma de la serle geométrica de razón 1/2:

es conocida y manejada por los alumnos de secundaria. Para hallar el valor de la suma tenemos que sumar n términos de la serie geométrica, y a continuación multiplicamos la misma suma por la razón r. Luego restamos las dos expresiones:
De esta manera, podemos despejar S y así podemos obtener el valor de la suma que estábamos buscando:
Si consideramos ahora que d es un valor menor que 1 y que en lugar de sumar n términos sumamos infinitos, el valor rⁿ^{+ 1} se convierte en cero y, por tanto, la suma se reduce a:
S = 1/(1 - r)

Los matemáticos habían buscado siempre fórmulas que permitieran sumar con facilidad un gran número de términos. Ya en la antigüedad se conocía la suma de los términos de las series de primeras potencias: n, n² y n³.

Pero desde el principio los matemáticos tenían mucho interés en estudiar el caso concreto en que la suma de infinitos términos diera un valor finito. Demócrito y Arquímedes, por ejemplo, trabajaron en dicho problema.
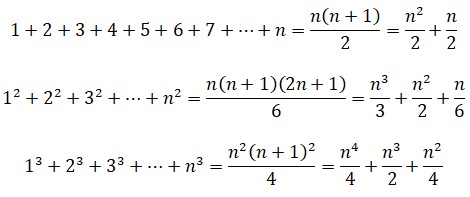
A partir de la serie geométrica

en la Edad Media se investigaron las series de potencias que intercambian entre sí la base y el exponente, es decir, las series del tipo

aunque pronto se vio que si el exponente r era positivo y n era un número entero, la suma se convertía en infinito. En el caso de que el exponente r fuera negativo, se obtenían potencias de fracciones menores que la unidad, es decir, la suma

con r mayor que la unidad.
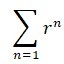
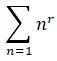
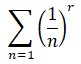
El francés Nicolás de Oresme (1323-1382) proporcionó muchos resultados sobre series y fue el primero en demostrar que la serie armónica, es decir, la serie anterior para r = 1, era divergente, por lo tanto la suma de una gran cantidad de términos tendía a infinito. En esa época, las demostraciones se hacían de forma literal, describiendo los pasos que se seguían en el proceso de demostración, pero nosotros vamos a ver ese ingenioso razonamiento utilizando símbolos más corrientes. Lo que hizo Oresme fue agrupar términos; de esa manera tenía el primer término, los dos siguientes, los cuatro siguientes, los ocho siguientes y así sucesivamente:

Así se obtiene una serie de fracciones todas mayores que 1/2; por ello, la suma de la serie se puede hacer más grande que cualquier número que se indique sin más que tomar suficientes términos de la serie.
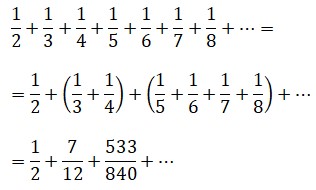
El matemático y astrónomo indio Madhava de Sangamagrama (1350-1425) descubrió, entre otras series infinitas, las de las funciones trigonométricas del seno y del coseno. También encontró la serie de la arcotangente:

Años más tarde el matemático y astrónomo escocés James Gregory (1638-1675) redescubrió esta serie y, a través de él, la conoció Leibniz, quien la utilizó para hallar una aproximación del número π, con el inconveniente de que se acerca muy lentamente a ese valor. Se conocía como serie de Gregory-Leibniz, aunque otros autores la conocen en la actualidad como serie de Madhava-Leibniz:

Tanto Newton como Leibniz encontraron el desarrollo en serie de potencias del resto de funciones trigonométricas.
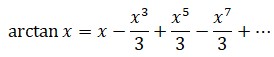
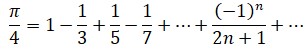
El cálculo de cifras correctas del número π ha sido una búsqueda constante de los matemáticos de todas las épocas. Este número se define como el cociente entre la longitud de una circunferencia y su diámetro. Muchos han intentado hallar la mayor cantidad de cifras y uno de los métodos usados ha sido el de las series numéricas, de forma que a medida que se van calculando más términos, van apareciendo mayor cantidad de cifras decimales exactas.
Las series no siempre han sido sumas. Por ejemplo, el matemático François Viéte (1540-1603), uno de los precursores del álgebra actual, presentó el primer producto infinito que se acercaba al valor de π mediante la siguiente expresión:

Por su parte el propio Gregory, intentando calcular el área del círculo de forma analítica, llegó a otra expresión para el cálculo de π

En el siglo XVII tuvieron gran auge las sumas de series infinitas de potencias, que servían para buscar las cuadraturas de figuras limitadas por distintos tipos de curvas, es decir, el área encerrada por una curva no limitada por segmentos.
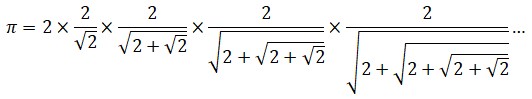
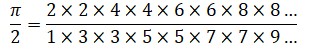
LEIBNIZ Y LAS SERIES INFINITAS
Cuando en 1672 Leibniz visitó a Huygens en París, le habló sobre un método que había inventado para hallar sumas de series de números, que consistía en considerar diferencias entre los términos de la sucesión. Si tenemos una serie de términos a₀ < a₁ < a₂ < a₃ < a_n, consideramos las diferencias b₁ = a₁ - a₀; b₂ = a₂ - a₁; b₃= a₃ -a₂;... y entonces de la suma nula

a₀ - a₀ + a₁ -a_l +a₂ - a₂+ … +a_n - a_n = a₀ +b₁ + b₂ + ... + b_n - a_n = 0,

de donde se sigue que la suma de diferencias es igual a:

b₁ + b₂ + b₃ + ... + b_n = a_n - a₀

Leibniz defendió que su método de diferencias se podía utilizar para hallar la suma de cualquier serie de números que estuviesen construidos según una regla, e incluso para series infinitas siempre que fueran convergentes.
En esa misma reunión Huygens le planteó un problema a Leibniz, que él ya habla solucionado, para que probara su método, la suma de los inversos de los números triangulares, es decir, la serie siguiente:

1 + 1/3 + 1/6 + 1/10 + …

Leibniz partió de la suma de los inversos anterior y dividió por dos cada término, descomponiendo las fracciones en diferencia de dos: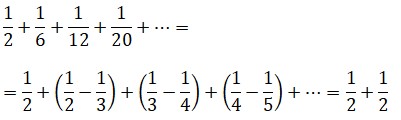

por lo que la serie buscada tiene el valor de 2×(1 + 1).
También se debe a Leibniz lo que se conoce como criterio de convergencia de series alternadas, es decir, aquellas en que se alternan los términos que van sumando y restando. Básicamente será una expresión de la forma:

El criterio apareció por primera vez en una carta dirigida a Johann Bernoulli (1667-1748) en 1713.
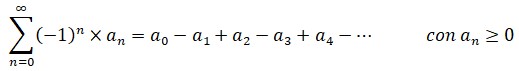
Para muchos matemáticos, los criterios de convergencia que utilizaban se basaban en hallar sumas parciales de una serie de términos, por ejemplo n, intentando hallar una expresión simplificada que dependiese de n y después estudiar qué ocurriría si el número de términos aumentaba hasta el infinito. Pero no todos los matemáticos estaban de acuerdo con este proceso, dado que aparecían los llamados disparates lógicos, es decir, series que con un procedimiento divergían, mientras que si se utilizaban otros procedimientos, se podían conseguir valores adecuados para la suma.
Uno de los principales disparates de la época era sumar la serie alternada en la que a_n = 1 para todo n. Es decir, estamos hablando de la serie:

Si tomamos un número par de términos, la suma parcial vale 0, mientras que si tomamos un número impar, la suma parcial vale 1. Leibniz llegó a asignar a esa suma el valor de 1/2.
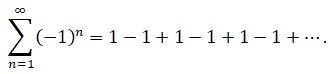
Un razonamiento simple para llegar a esa solución sería el siguiente:
S = 1 - 1 + 1 - 1 + 1 - 1 + 1-...= 1 - (l - l + l - l + l - 1 + ...) = l - S,
de donde si despejamos obtenemos que 2S = 1 y, por tanto, la suma buscada sería S = 1/2.
En su visita a Robert Boyle, Pell le indicó a Leibniz que el matemático François Regnault ya había publicado un método general para interpolar series mediante diferencias. Leibniz consultó la obra, comprobando que su método difería del de Regnault, y redactó un escrito para ser presentado en la Royal Society. Su trabajo no despertó ningún entusiasmo, ya que no presentaba ningún resultado nuevo e incluso fue acusado de plagio. El propio Leibniz reconoció después que no había ningún resultado novedoso y que lo interesante era el nuevo método presentado.
El rechazo a su obra le hizo comprender que tenía grandes carencias en sus conocimientos matemáticos, al desconocer mucho de lo que ya se había publicado. Por eso dedicó casi un año a reforzar sus conocimientos. Cuando abandonó París, había dejado sus intereses en el mundo del derecho y de las polémicas diplomáticas en Alemania, y se dedicó al estudio de la matemática más actual.

§. Una nueva ocupación
Cuando abandonó París, Leibniz ostentaba ya el cargo que ocuparía el resto de su vida: consejero de los distintos duques de Hanover. Desde 1677 fue consejero privado del duque Juan Federico, puesto de más confianza y más remunerado. Al encontrarse sin problemas financieros, pudo dedicar los esfuerzos que le permitía su ocupación a investigar los aspectos científicos que le interesaban, que eran prácticamente todos. Aunque inicialmente aceptó el puesto a regañadientes, más tarde expresó su satisfacción por el cargo que desempeñaba.
En su cargo de bibliotecario del duque planteó ampliar la biblioteca para cubrir todos los campos más importantes del conocimiento, abogando más por la calidad que por la cantidad y para ello ofrecía su experiencia y sus contactos con estudiosos de todas las disciplinas. Gracias a esta ocupación viajó a otras ciudades para comprar bibliotecas en las que había libros interesantes para la biblioteca ducal. Por ejemplo, en 1678 visitó Hamburgo para comprar la biblioteca de Martin Fogel, discípulo del naturalista alemán Joachim Jungius (1587-1657).
A su vuelta preparó para el duque una serie de escritos con temas tan diversos como la forma de mejorar la administración pública, la organización de archivos, la práctica de la agricultura y el trabajo en granjas. En ellos insistía en que para contribuir al bienestar del pueblo se debía tener una idea clara de cuáles eran los recursos de que se disponía, tanto humanos como naturales. Además de los escritos, le presentó al duque una idea que había comenzado a rondar por su mente: la de crear una academia de ciencias en Alemania. Para ello planteaba una serie de inventos a fin de mejorar la producción minera, y sacar de ahí financiación para crear la institución.
A pesar de estar instalado en Hanover, Leibniz no perdió el contacto con los intelectuales y científicos de Londres y Paria; continuaba recibiendo información sobre los avances de la ciencia y escribiéndose con personajes influyentes de la sociedad. Por ejemplo, durante esa época se carteó con Henri Justel (1620-1693), secretario del rey francés, aunque después se mudó a Inglaterra Para Justel realizó una breve y precipitada investigación sobre la historia de los condes de Löwenstein. Ese fue el primer trabajo histórico que realizó Leibniz, y en cierta forma presagiaba la que sería la gran ocupación de su vida.

§. Bajo un nuevo patrón
Al duque Juan Federico lo sustituyó su hermano Ernesto Augusto (1629-1698), duque de Brunswick-Luneburgo, que sería el primer príncipe elector de Hanover, es decir, una de las personas que se encargaba de elegir, en su momento, al emperador alemán.
Tras su llegada a Hanover, Leibniz conoció a Sofía de Wittelsbach (1630-1714), esposa de Ernesto Augusto. Sofía era hija de Federico V, rey de Bohemia, y de Isabel Estuardo, princesa de Baviera, Escocia e Inglaterra, además de nieta de Jacobo I de Inglaterra y V de Escocia. Por lo tanto, por línea directa, fue pretendiente al trono de Gran Bretaña, pues era la descendiente protestante más directa de la reina de Inglaterra y solo su muerte, dos meses antes que la reina Ana Estuardo, impidió que gobernara. Su hijo Jorge Luis llegó a alcanzar el trono de Inglaterra con el título de Jorge I.
La relación de Leibniz con Sofía se fue haciendo más estrecha con los años y llegaron a tener una gran amistad. La princesa tenía unas grandes inquietudes intelectuales que abarcaban multitud de temas y sobre los que discutía, con un alto nivel, con Leibniz, de lo que da fe la amplísima correspondencia existente. La propia Sofía comentó que le era de gran agrado la correspondencia que mantenía con Leibniz, así como sus encuentros. Trataban principalmente temas de religión, política y filosofía, temas que habla tratado con el duque Juan Federico, pero por los que su sucesor no mostraba ningún interés.
Leibniz fue ratificado en sus ocupaciones, y realizó un informe para el nuevo duque comentando detalles de su carrera, lo que hoy diríamos su currículo, y una serie de proyectos que tenía en mente. Propuso ampliar la biblioteca ducal con un laboratorio y un museo y la creación de una imprenta ducal. En un escrito dirigido al primer ministro, Franz Ernest von Platen (1631-1709), se ofreció para elaborar una historia de la casa de Brunswick- Luneburgo. Seguramente no era consciente del berenjenal en el que se metía, ya que ese proyecto lo martirizó el resto de su vida.

§. Nuevos proyectos
A pesar de los múltiples encargos que recibía del duque, Leibniz tenía fuerzas y capacidad para seguir produciendo avances en muchos aspectos de la ciencia.

Grabado realizado por Theobald Freiherr von Oer (1807–1885) que muestra a la reina Sofía Carlota de Prusia, durante la inauguración de la Academia da Berlín, da la que fue su primer presidente.

En 1681 Otto Mencke visitó Hannover y se reunió con Leibniz para hablar sobre la edición de la revista Acta Eruditorum, y le solicitó que enviase alguno de sus escritos para publicarlos en la revista. Además de sus propias obras, Leibniz también hizo reseñas de algunos textos, como por ejemplo uno de John Wallis que versaba sobre álgebra y otro del matemático Jacques Ozanam en el que exponía sus tablas trigonométricas.
Siguió redactando escritos para el duque sobre los aspectos más diversos, como métodos para mejorar la organización y el ánimo del ejército, proponiendo favorecer la salud física y psíquica de los soldados; para ello sugería dotarlos de alimentación, ropa y medicinas adecuadas, y emplearlos, en época de paz, en trabajos para la comunidad, como la edificación de fortificaciones, el drenaje de pantanos, y en proyectos de canalización, de modo que eso haría más llevadera la rutina del entrenamiento militar. Presentó un proyecto con medidas preventivas de carácter político para combatir la epidemia que asolaba en esos momentos Europa, dado que los médicos no habían conseguido encontrar métodos para erradicarla. Propuso impedir el paso a personas contaminadas y aislarlas para que no extendieran la infección.
Por encargo del consejero ducal, Otto Grote, preparó un memorándum sobre la ampliación del número de electorados alemanes. Existían ocho electorados, cinco católicos y tres protestantes. En el escrito abogó por la creación de un noveno electorado, en este caso protestante. Después de varios años, en 1692 se consiguió por fin que el duque Ernesto Augusto fuera declarado príncipe elector. Leibniz participó en el proyecto desde el principio hasta el final, pues una vez concedido el electorado, diseñó una medalla conmemorativa, y elaboró también el discurso, que contenía un resumen histórico, que Otto Grote leería cuando recogiera el título de manos del emperador.
Leibniz era requerido para cualquier asunto político en Hannover. La princesa Sofía aprovechó uno de los viajes de Leibniz por Italia para que intercediera por una alianza política mediante matrimonio entre Carlota Felicidad, hija mayor del duque Juan Federico, con el duque Rinaldo de Módena, y de paso también consiguió los esponsales de la hija pequeña del duque, Guillermina, con el rey de Hungría y futuro emperador José I de Habsburgo.
Aparte de sus estudios científicos, la labor más importante que emprendió durante esos años fue, como ya se ha comentado, la elaboración de una historia de la casa de Brunswick-Luneburgo para el duque. Leibniz opinaba que la historia y la genealogía se habían convertido en una ciencia, y que por tanto se necesitaba una documentación fiel basada en las fuentes primitivas de información y en los autores de la época. De esta manera consiguió del duque una pensión vitalicia y liberado de otras tareas ordinarias para dedicarse casi en exclusiva a ese menester.
Pero además, en esa época, ya hacía años que había realizado el descubrimiento con el que pasaría a la historia de las matemáticas entre los más excelsos: el cálculo infinitesimal.

§. Las matemáticas en la antigua Grecia
Los griegos crearon las matemáticas como ciencia. Las civilizaciones anteriores las habían utilizado para aplicarlas a problemas prácticos de la vida cotidiana. Por ejemplo, los egipcios usaban el teorema de Pitágoras para construir un ángulo recto y con él poder reconstruir las lindes de los cultivos inundados por el Nilo. Los griegos estudiaban las matemáticas como objetivo en sí mismas, sin importarles su utilidad. Esto no quiere decir que no usaran también sus conocimientos para solucionar situaciones concretas, sino que diferenciaban muy bien lo que podríamos decir teoría de la práctica. Por ejemplo, los griegos diferenciaban entre la aritmética, que era la teoría abstracta de números, y la logística, los propios cálculos en sí mismos, es decir, la aritmética aplicada. Consideraban importante el estudio de la matemática en sí misma y a ello dedicaron sus escritos y, en cierta forma, despreciaban la otra matemática, la aplicada, la que solucionaba los problemas diarios.
En época más moderna, en el apogeo de Alejandría, los científicos griegos, sin dejar de lado el cultivo de la ciencia pura, comenzaron a desarrollar también la ciencia aplicada. Los alejandrinos inventaron bombas para elevar agua desde los pozos, poleas y sistemas de engranajes para mover grandes masas, utilizaron la fuerza del agua y del vapor para mover vehículos, el fuego para conseguir estatuas móviles o utilizar el aire comprimido para lanzar objetos a grandes distancias.
Mientras que en las civilizaciones anteriores los conocimientos se adquirían a través de la experiencia, la inducción o la experimentación, los griegos potenciaron sobre todo la deducción. A partir de una serie de conceptos se deducían nuevos resultados aplicando un riguroso razonamiento deductivo. Por ejemplo, Apolonio (ca. 262 aC.-ca. 190 a.C.), en su libro Secciones cónicas, presentó 487 proposiciones deducidas a partir de los axiomas recogidos en los Elementos de Euclides.
El principal objetivo de los griegos era el deseo de comprender el mundo físico, pues consideraban que las leyes matemáticas eran la base de la naturaleza y eran imprescindibles para estudiar el universo. Era un modo de abordar la naturaleza de una forma crítica y racional
Los matemáticos griegos eran muy rigurosos en sus presentaciones. Debían demostrar sus razonamientos de forma exhaustiva, sin dejar posibilidad a ningún resquicio. Rigurosidad que no se volvió a conseguir en las matemáticas hasta el siglo XIX. Pero al ser tan rigurosos, presentaban los trabajos terminados tan perfectos que no habla forma de entender cómo habían llegado a esos resultados. Se llegó a creer que esto era debido a que tenían una gran inventiva, una idea feliz que les hacía encontrar resultados que después eran demostrados de forma exhaustiva. Muchos matemáticos a partir del Renacimiento estaban convencidos de que los griegos debían de tener algún método, pero que lo mantenían oculto. Lo podemos ver claro en el siguiente comentario de Descartes:

Así como muchos artesanos ocultan el Secreto de sus inventos, Pappus y Diofanto, temiendo tal vez que la facilidad y la sencillez de su método le hicieran perder su valor, prefirieron, para excitar la admiración de todos, presentaron como productos de su ingenio algunas verdades estériles muy sutilmente deducidas, en lugar de mostrar el método de que se servían.

El palimpsesto de Arquímedes
Un palimpsesto es un texto escrito en pergamino que se ha borrado y sobre el que se ha escrito otro texto para aprovechar el material.
Gracias a uno de ellos conocemos una de las obras más importantes de Arquímedes. Muchas de las obras del genio de Siracusa se mantuvieron para la posteridad a través de copias árabes y latinas. Sin embargo, los matemáticos de los siglos XVI en adelante echaban en falta conocer cuál era el método que utilizaba para llegar a sus creaciones. Sus libros estaban llenos de demostraciones esquemáticas y completas, pero no se sabía cómo había llegaba a esos resultados antes de demostrarlos. Se pensaba que no tenía ningún método para llegar a sus ideas brillantes, o si lo tenía, no lo había dejado para la posteridad.
«El método»
En 1906, el filólogo danés Johan Ludwig Heiberg recibió noticias de un palimpsesto con contenido matemático existente en el convento del Santo Sepulcro de Constantinopla. Utilizando técnicas fotográficas consiguió capturar y copiar el texto original oculto, y lo que halló fueron varías obras de Arquímedes. El texto original era una copia, realizada en el siglo X, de algunas de las obras de Arquímedes que se había reutilizado para unos escritos religiosos. La mayoría se conocían, pero incluía la única copia conocida de la obra Sobre el método relativo a los teoremas mecánicos , más conocida como El método. Esta obra es una carta de Arquímedes a Eratóstenes en la que explicaba su método para llegar a dichos resultados, que posteriormente demostraba con el máximo rigor. En el libro, Arquímedes utiliza una mezcla de razonamientos infinitesimales y mecánicos para hallar áreas y volúmenes. La idea de considerar una superficie compuesta por segmentos o un volumen compuesto por superficies no volverla a aparecer en el mundo matemático hasta dos mil años más tarde, en pleno siglo XVII. La creencia general es que si esta obra hubiese sido conocida como otros escritos de Arquímedes, el cálculo infinitesimal hubiese aparecido mucho antes en la historia.

La matemática más desarrollada para la obtención del cálculo se dio en la época alejandrina, cuando matemáticos como Arquímedes, Eratóstenes, Hiparco o Pappus obtuvieron muchos resultados para el cálculo de longitudes de curvas, áreas y volúmenes. Aunque durante muchos siglos se hablará de cuadratura para referirse al área o cubicación para el volumen. Según Pappus, matemático alejandrino del siglo III-IV, las curvas se podían clasificar en:

Planas, que se construían a partir de rectas y círculos.
Cónicas, que eran lugares sólidos provenientes del cono.
Lineales, que eran todas las demás curvas que no podían resolverse por los métodos anteriores, como espirales, concoides, cisoides, etc. Estas curvas no solían ser tratadas.

Muchos matemáticos griegos fueron precursores del actual cálculo. Por ejemplo, Pappus mencionaba al matemático Zeodoro, quien en un libro sobre figuras isoperimétricas planteaba teoremas como los siguientes:

Entre los polígonos de n lados con el mismo perímetro, el polígono regular es el que tiene mayor área.
Entre los polígonos regulares con igual perímetro, el que tiene más lados tiene mayor área.
El círculo tiene mayor área que un polígono regular del mismo perímetro.
De todos los sólidos con la misma superficie, la esfera tiene el mayor volumen.

Este tipo de situaciones forman parte de los problemas de máximos y mínimos.
No se puede hablar del cálculo infinitesimal sin comenzar hablando del mayor matemático de la antigüedad y uno de los mayores matemáticos de la historia, comparable a Newton o Gauss. Arquímedes (ca. 287 a.C.-ca. 212 a.C.) nadó en Siracusa, una colonia griega de Sicilia, y era hijo del astrónomo Fidias. Estudió en Alejandría y regresó a Siracusa, donde desarrolló su genio hasta su muerte. Tenía una inteligencia fuera de lo normal y una gran amplitud de intereses, y gustaba de trabajar tanto los aspectos teóricos como los prácticos. Su importancia la demuestra una frase del filósofo y escritor Voltaire: « Hay más imaginación en la cabeza de Arquímedes que en la de Homero ».
Aparte de las matemáticas, trabajó y desarrolló el estudio de la estática y la palanca. Es famosa su frase: « Dadme un punto de apoyo y moveré el mundo». Fue el creador de la hidrostática, al menos la parte que trata sobre los cuerpos que flotan en el agua. Uno de los principios más conocidos por todo el mundo es el de Arquímedes, que indica que cualquier cuerpo sumergido en un líquido experimenta una fuerza de abajo arriba igual al volumen del liquido desalojado.

«Quien comprenda a Arquímedes y Apolonio admirará menos los logros de los hombres más ilustres de su tiempo.»
Gottlieb Wilhelm Leibniz

Este principio se relaciona con una de las supuestas anécdotas de Arquímedes. Hierón, el tirano de Siracusa, encargó una corona y entregó una determinada cantidad de oro, pero cuando la corona fue entregada, el tirano no estaba convencido de si el orfebre habría utilizado todo el oro o lo habría mezclado con plata. Consultado Arquímedes, comenzó a pensar en el problema y encontró la solución mientras se bañaba en su casa, con lo que salió directamente del baño y corrió por las calles de Siracusa gritando «¡Eureka!» («¡Lo he encontrado!»). Como conocía la densidad del oro y de la plata, le bastó sumergir objetos de oro y plata del mismo volumen y estudiar el líquido desalojado en función del peso. Así descubrió que la corona había sido depredada añadiéndole una aleación.
Las obras de Arquímedes eran ensayos cortos que trataban puntualmente sobre aspectos geométricos. Los propios títulos nos indican claramente la temática; Sobre la cuadratura de la parábola, Sobre la esfera y el cilindro, Sobre las espirales, Sobre la medida del círculo. Sobre los cuerpos flotantes, Sobre el equilibrio de los planos, etc. Algunos de sus libros se han perdido, por ejemplo, los escritos sobre gravedad, palancas u óptica.
Pero fue su capacidad como inventor lo que lo hizo famoso en su época. En su juventud construyó un planetario donde simulaba el movimiento de los planetas mediante un mecanismo hidráulico. Diseñó un juego compuesto de poleas que le permitió botar un barco del rey Hierón con una sola mano. Inventó gran cantidad de instrumentos militares que impidieron durante años que Siracusa fuese conquistada por los romanos, entre ellos la utilización de grandes espejos para quemar las naves enemigas a gran distancia. Fue el creador del tornillo de Arquímedes (véase la figura), un ingenio manual para extraer agua de pozos y cisternas consistente en un mecanismo con forma de espiral dentro de un cilindro.

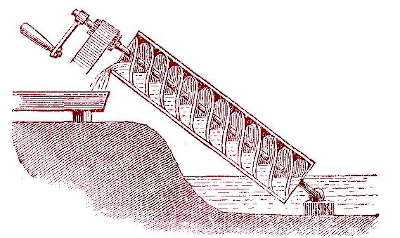
Tornillo Arquímedes. Aunque su invención se atribuye comúnmente el sabio griego, se cree que ya era empleado en el antiguo Egipto

A pesar de su dedicación a los inventos, estos eran, según el historiador Plutarco, en la obra que dedicó a la vida de Marcelo, el general que conquistó Siracusa, una mera « diversión para el geómetra». El propio Plutarco nos explica cuáles eran los intereses del genio:
Aunque sus descubrimientos le proporcionaron un nombre y una fama, no humana sino divina, no quiso dejar ningún tratado sobre ellos, sino que, considerando la ingeniería y todo arte utilitario como innoble y vulgar, ponía su ambición solamente en aquellas materias cuya belleza y sutilidad no están mezcladas con la necesidad, y que no pueden compararse con las otras, ofreciendo una disputa sobre la materia y la demostración, donde la primera proporciona fuerza y belleza, y la segunda, precisión y poder en grado sumo, porque es imposible encontrar en la geometría proposiciones más difíciles e importantes tratadas en términos más puros y más netos.
Arquímedes utilizaba el método de exhaución para demostrar rigurosamente sus resultados. En su escrito Sobre la esfera y el cilindro, el primer axioma que plantea es que de todas las líneas que tienen los mismos extremos, la línea más corta es la línea recta.

Grabado en el que se puede apreciar la estrategia de Arquímedes para destruir las naves romanan con los rayos solares.

Incluye otros axiomas referidos a longitudes de curvas y superficies. Con estos axiomas comparaba perímetros de polígonos inscritos y circunscritos con el círculo.

§. No todo es geometría
En la parte geométrica los griegos tenían la limitación de considerar solo aquellas figuras construibles con regla y compás. Por eso, se encontraban limitados por los famosos problemas bélicos: la duplicación del cubo, la cuadratura del círculo y la trisección del ángulo.
La matemática griega no presentaba métodos generales útiles para resolver problemas distintos. Además, al supeditar el rigor matemático a la geometría, las demostraciones fueron cada vez más elaboradas y complicadas. Eso les impidió avanzar más en el desarrollo del cálculo.

El método de exhaución
Método debido al matemático griego Eudoxo de Cnido (ca. 390 a.C.-ca. 337 a.C.). Consiste en aproximar el área desconocida que se desea calcular por áreas mayores y menores que se acercan a la buscada todo lo que se quiera. El método se basa en lo que se conoce como principio de Eudoxo. que aparece mencionado en los Elementos de Euclides:
Dadas dos magnitudes desiguales, si de la mayor se resta una magnitud mayor que su mitad y de lo que queda otra magnitud mayar que su mitad y se repite continuamente este proceso, quedará una magnitud menor que la menor de las magnitudes dadas.
Veamos cómo hallar el área del círculo (figura 1). Para ello inscribimos un cuadrado (con superficie mayor que la mitad del círculo) y se le resta su área al círculo. De los segmentos circulares, construimos triángulos sobre el punto medio y luego restamos el área de esos triángulos. Esto último se vuelve a hacer con los segmentos circulares restantes y así sucesivamente se llega tan cerca del área de! circulo como se quiera.
Se puede apreciar en las imágenes que lo que se hace es insertar polígonos con cada vez mayor número de lados y cuya área cada vez está más cerca de la buscada. Se razona igual desde un cuadrado exterior (figura 2).
De esta forma se va acotando e! valor del área circular por arriba y por abajo.

Al principio, la aritmética griega estaba condicionada a la geometría, pues los matemáticos la reducían al cálculo de cantidades geométricas o trigonométricas. Más adelante, la aritmética y el álgebra comenzaron a desarrollarse como materias independientes, Matemáticos de la época cristiana, como Herón de Alejandría (siglo I), Nicómaco de Gerasa (siglo II) o Diofanto de Alejandría (ca. 200-ca. 298), desarrollaron aspectos aritméticos y algebraicos sin limitaciones geométricas. Nicómaco, que sigue la tradición pitagórica, publicó su trabajo Introductio arithmetica, considerado el equivalente a los Elementos de Euclides para la aritmética.
Por su parte, el punto álgido del álgebra griega se alcanzó con Diofanto, de cuya obra se conserva muy poco. Su Aritmética, de la que se conserva solo la mitad, consiste en una serie de ejercicios dirigidos a la enseñanza del álgebra. En su obra encontramos ejercicios que parecen sacados de un texto actual de secundaria. Un ejemplo sería «encontrar dos números cuya suma sea 20 y su producto 96». La forma en que lo resolvió Diofanto podía ser la siguiente, usando nuestra terminología actual. La suma es 20 y el producto 96; se considera 2x, que es la diferencia entre el número mayor y el menor; por tanto ambos números serían 10 + x y 10 - x, y su producto (10 + x) (10 - x) = 100 - x² = 96, x² = 4 y por tanto x = 2, ya que los griegos no consideraban soluciones negativas. Es decir, los números buscados son 12 y 8.
A partir del siglo VII la cultura griega desapareció arrollada por los árabes. Los romanos, junto con los cristianos y los árabes, se esforzaron por hacer desaparecer toda la ciencia griega y, en gran parte, lo consiguieron. Miles de manuscritos fueron quemados y buena parte del saber científico desapareció. Durante un milenio no se aportó nada nuevo en geometría. Hasta prácticamente 1600 no se comenzaron a desarrollar aspectos nuevos en ese campo.
A mediados del siglo XVI comenzaron a extenderse por Europa traducciones latinas de los principales textos griegos, recuperados por los sabios árabes, que fueron acogidas con entusiasmo por los matemáticos de la época. Se comenzaron a estudiar detenidamente los resultados y demostraciones desarrolladas por los griegos. La admiración de los matemáticos de los siglos XVI y XVII por los conocimientos griegos era innegable.

§. La evolución del álgebra
Aunque la geometría se estancó durante un milenio, el avance del álgebra fue fundamental para el desarrollo posterior del cálculo. El álgebra seguía íntimamente unida a la geometría. El matemático Mohamed ib Musa Al-Khwarizmi (780-850) desarrolló su obra en Bagdad y de su nombre se deriva la palabra algoritmo. También se deben a él las palabras guarismo y álgebra. Muchos autores consideran, por ello, a Al-Khwarizmi como el padre del álgebra. Sin embargo, el método que usaba para resolver sus ecuaciones seguía siendo fundamentalmente geométrico, las soluciones se encontraban completando cuadrados.
Uno de los personajes más importante del siglo XVI, que puso las bases para lo que vendría después, fue François Viéte, ya mencionado anteriormente. Retomó el análisis geométrico de los griegos, pero a partir del álgebra. Comenzó a simbolizar las expresiones utilizando letras para representar los parámetros de una ecuación, diferenciando entre parámetros constantes y variables. Hizo más hincapié en los métodos de resolución que en la propia solución del problema. De esa forma se pasó del estudio de problemas particulares al desarrollo de métodos generales, algo fundamental para desarrollar el cálculo infinitesimal Su trabajo fue el que abonó el camino para la aparición de la geometría analítica.
Dado que las cantidades simbólicas que utiliza Viéte pueden considerarse como longitudes de segmentos o medidas de ángulos, y las operaciones simbólicas pueden considerarse, a su vez, como construcciones geométricas, las soluciones obtenidas pueden ser vistas no solo como problemas numéricos, sino también geométricos.

§. Cambio de enfoque
Durante el Renacimiento las artes y la literatura tuvieron un notable desarrollo, mientras que los aspectos científicos quedaron algo más abandonados. Francis Bacon es considerado uno de los creadores del método científico. En su obra Nueva Atlántida los gobernantes eran los científicos, que acumulaban el conocimiento científico y tecnológico. Muchas sociedades científicas se inspiraron en dicha obra. Bacon se quejaba de que la sociedad estaba preparada para las humanidades y los metafísicos, mientras que dejaba de lado al sabio de laboratorio. Un siglo más tarde, abundarían las obras sobre resultados experimentales.
La forma de afrontar el desarrollo de las matemáticas a partir de mediados del siglo XVI cambió radicalmente respecto al enfoque griego. Aparecieron nuevos problemas, procedentes de las ciencias y de las necesidades prácticas. Las matemáticas se volcaron hacia el mundo físico. Poco a poco la ciencia se basó cada vez más en principios matemáticos y, como contrapartida, las matemáticas cada vez se basaron más en la ciencia para justificar sus nuevos campos de estudio.
Los matemáticos de la época eran grandes científicos y desarrollaban su saber en muchos campos diferentes. Descartes comentaba que las matemáticas eran la ciencia del orden y la medida, y comprendían, además del álgebra y la geometría la astronomía la música la óptica y la mecánica Los pilares del sistema mecánico de Newton fueron la fuerza y el movimiento. Los dos grandes motores que hicieron avanzar la ciencia en esa época fueron la astronomía y la mecánica impulsadas por Galileo y Kepler. Tenemos así la aplicación, por ejemplo, de las cónicas a las ciencias de la naturaleza las elipses son trayectorias de planetas y las parábolas trayectorias de proyectiles.
Se abandonó el rigor griego en beneficio del empirismo. Para Galileo era tan importante taparte deductiva como la experimental. A diferencia de los griegos, interesaba más el descubrimiento de nuevos resultados que la fundamentación rigurosa de dichos resultados. Siempre habría tiempo después para el rigor, puesto que lo importante era el descubrimiento en sí. El convencimiento de que los resultados que mostraban podían ser después demostrados rigurosamente mediante los métodos griegos, queda patente en el siguiente texto de Huygens:
No es de gran interés el que demos una demostración absoluta, después de haber visto que una perfecta demostración puede ser dada. Concedo que debería aparecer en una forma clara, ingeniosa y elegante, como en todos los trabajos de Arquímedes. Pero lo primero y más importante es el método de descubrimiento mismo.

Retrato da Leibniz hacia 1700, obra de Christoph Bernhard Francke. Museo Herzog Anton Ulrich, Braunschweig.

Pero al plantear los descubrimientos de una forma empírica, sin la rigurosidad griega, algunos resultados no eran aceptados o creaban mucha controversia en otros científicos.
Otro aspecto fundamental fue considerar que los problemas no debían plantearse de forma independiente.

Las coordenadas cartesianas
La idea fundamental de la geometría analítica reposa en las coordenadas cartesianas, llamadas así en honor a Descartes.
Todo punto del plano se representa con dos números, que hacen referencia a su situación en el plano. El sistema de ejes cartesianos consiste en dos rectas perpendiculares que se cortan en un punto, el origen de coordenadas. Al graduar las rectas, a cada punto le corresponden dos valores numéricos medidos sobre ambos ejes. El primero se mide en el eje horizontal, llamado eje de abscisas, y el segundo en el eje vertical, llamado eje de ordenadas. Un punto general se escribirla, por tanto, P(x,y), siendo x la abscisa e y la ordenada.
Las dos rectas, al cortarse, dividen el plano en cuatro reglones que reciben el nombre de cuadrantes, que se numeran de la I a la IV, comenzando por el que los puntos tienen ambas coordenadas positivas y siguiendo en el sentido contrario a las agujas del reloj (figura 1). Sin embargo, la expresión inicial de los ejes no era así. Fermat definió las coordenadas de la siguiente forma: la posición de un punto P venia dada por dos longitudes, una medida en horizontal desde el punto O hasta un punto I y otra medida oblicuamente desde I hasta P (figura 2). Esas medidas serian nuestras actuales x e y. Como se ve no aparecen determinados los ejes ni hay medidas negativas.

Descartes planteaba que los problemas con una misma estructura deben resolverse por un método común.

§. La geometría analítica
El gran salto para pasar de la geometría al álgebra se dio con la creación de la geometría analítica, que permite sustituir las curvas por sus ecuaciones para trabajar directamente en la resolución algebraica Una curva, desde el punto de vista de la geometría analítica, es cualquier lugar geométrico, es decir, el conjunto de puntos que cumple una condición, que lleva asociada una ecuación algebraica. Como muchos otros casos en esa época, la geometría analítica fue descubierta de forma independiente por dos autores, cuyos resultados no eran exactamente iguales. Los padres de la criatura fueron los franceses Pierre de Fermat (1601-1665) y René Descartes (1596-1650).
Fermat, considerado por algunos como el príncipe de los aficionados, pues en realidad ejercía de magistrado y se dedicaba a las matemáticas en su tiempo libre, realizó importantes descubrimientos en teoría de números, en especial el famoso «último teorema de Fermat», que tardó más de tres siglos en ser demostrado. Realizó también aportaciones a la óptica. Aparte de la geometría analítica fundó, junto con Blaise Pascal, la teoría de la probabilidad. No publicó ningún resultado en vida, por lo que su obra debe buscarse en las cartas y escritos que intercambiaba con amigos y conocidos.
Descartes, filósofo, físico y matemático, trabajó la geometría, partiendo, como Fermat, de los clásicos. En 1637, publicó su gran obra, El discurso del método, en la que presentaba su filosofía y que incluía tres anexos donde presentaba su obra científica: «Dióptrica», «Meteoros» y «Geometría».
Se planteó una de las grandes polémicas del siglo, sobre quién había sido el primero en descubrir esta geometría. Por un lado, en la obra de Fermat Introducción a los lugares planos y sólidos, escrita en 1629 pero no publicada hasta 1679, Fermat ya presenta las ideas básicas de su geometría analítica, que casualmente es mucho más cercana a la idea que tenemos actualmente. Por su parte, el científico neerlandés Isaac Beeckman (1588-1637), considerado como uno de los pioneros en el estudio del vacío termométrico, amigo y profesor de Descartes desde 1619, comentaba que en aquella época su alumno ya tenía en mente un método para resolver todos los problemas que se pudieran proponer en geometría.
Al parecer, Fermat llegó primero a desarrollar la geometría, pero Descartes fue el primero en publicarla, algo muy corriente en la época. Pero como se habían intercambiado información de forma epistolar a través de Mersenne, surgieron las acusaciones de plagio, parece evidente que ambos llegaron a sus conclusiones de forma independiente, pues sus enfoques son distintos. Descartes parte del lugar geométrico y estudia su ecuación, mientras que Fermat parte de la ecuación y estudia qué curva la cumple y cuáles son sus propiedades. Es recorrer el camino entre geometría y álgebra de forma opuesta.

§. Los cimientos del cálculo
El primero que intentó avanzar en el método del cálculo, siguiendo un método riguroso al estilo griego, fue Bonaventura Cavalieri (1598-1647), discípulo de Galileo. En 1635 publicó su obra Geometría superior mediante un método bastante desconocido, los indivisibles de los continuos . Cavalieri planteaba que todas las figuras están formadas por una serie de elementos básicos, que él llama indivisibles. Es decir, un área está formada por un número indefinido de segmentos paralelos (véase la figura), y un volumen, por áreas planas paralelas.
Los indivisibles son los elementos mínimos en que puede descomponerse un elemento. En Exercitationes geometricae (1647) expuso la idea de que una línea está compuesta de puntos, como una sarta de cuentas; un plano está hecho de líneas, como fibras en un vestido, y un sólido está formado por áreas planas, como las hojas de un libro.

Cualquier área está formada por un número indefinido de segmentos paralelos

Gracias a esta idea, Cavalieri consiguió hallar la cuadratura, es decir, el área, de las curvas del tipo x^k para los valores de k hasta 6 y 9. En nuestra notación moderna, Cavalieri demostró que: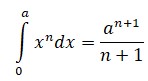

Enunció él conocido como principio de Cavalieri:
«Si dos figuras planas (o sólidas) tienen igual altura, y las secciones hechas por rectas paralelas (o planos paralelos) a las bases y a igual distancia de ellas están siempre en una misma razón, entonces las figuras planas (o sólidas) están también en esa razón».
En la figura 1 podemos ver el caso concreto de dos triángulos con la misma base y misma altura, en los que los indivisibles son iguales, luego su área es la misma.

A pesar de las críticas que recibió el método de Cavalieri, no respaldado con el rigor clásico, muchos matemáticos continuaron en la misma senda de los indivisibles. Fermat, Torricelli, Pascal o Roberval también plantearon métodos parecidos, aunque sustituyendo las líneas por otros elementos geométricos, como rectángulos, triángulos, paralelepípedos o cilindros.
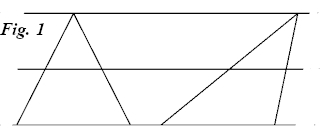
Gilles de Roberval, uno de los miembros fundadores de la Academia de Ciencias de París, sustituyó las líneas de Cavalieri por rectángulos infinitesimales, con lo que su método se acercó bastante al usado hoy en día.
Trazaba un conjunto de rectángulos de la misma anchura y suponía que el área bajo la función podía acercarse al área de esos rectángulos, cuando la anchura fuese muy pequeña.

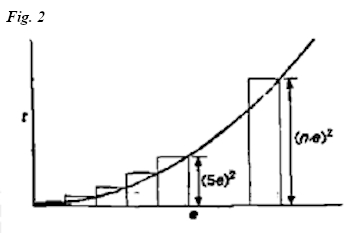
Método de Cavalieri para hallar al área da una parábola.

Para hallar el área bajo una parábola, por ejemplo, seguía el método que se ve en la figura 2. En nuestra escritura actual se trataría de hallar ^α∫₀x²dx. Consideramos n rectángulos de amplitud e. Por tanto, el rectángulo correspondiente al rectángulo de la posición t, tendrá de base e y de altura el valor de la parábola en su abscisa t×e. Luego su área será e×(t×e)²= t²e³.
Si sumamos todos los rectángulos el área será:

A = e×e² + e(2e)² + e×(3e)² + ... + e×(ne)² =

= e³ + 4e³ + 9e³ + … + n²×e³ = e³×(l + 4 + 9 + ... + n²).

La suma de los cuadrados de los números ya era conocida y valía: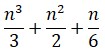

y si llamamos a a la suma de las n anchuras de los rectángulos, es decir, a×ne, por tanto:

e = a /n

y la expresión anterior se convertía en:

Como se supone que n es un número suficientemente grande para que sea buena la aproximación, las fracciones con n en el denominador pueden despreciarse, lo que lleva implícito una aproximación al paso al límite, y nos queda que el área bajo la parábola es:

a³ /3

§. Los gigantes
Hubo otros matemáticos que se acercaron tanto a la definición estricta del cálculo infinitesimal, que pusieron la alfombra por la que Newton y Leibniz entraron en la historia.
El matemático inglés John Wallis, criptógrafo real, presentó en 1656 su obra principal Arithmetica infinitorum, en la que presentaba, a partir de los trabajos de Descartes y Cavalieri, su método de infinitésimos. Wallis calculó la cuadratura de la hipérbola, es decir, las curvas cuyas ecuaciones son de la forma

1/x^r

con r distinto de 1.
En su método utilizaba una representación más aritmética que geométrica, como también hicieron en parte Fermat y Roberval. Para hallar el área encerrada por la curva y = x³, Wallis consideró la relación entre triángulos y cuadrados de la misma longitud de base. En ellos trazó todas las líneas que lo pueden formar, en el sentido de los indivisibles, y sumó las medidas de su valor cúbico, pues queremos trabajar con x³. De esa forma, construyó la siguiente relación: Si solo hay dos líneas, en el triángulo tendremos las longitudes asociadas con 0 y 1, mientras que en el cuadrado las dos líneas valdrán 1, luego tendremos la relación:

Si consideramos tres líneas, las longitudes de las que están en el triángulo serían 0, 1 y 2, mientras que las del cuadrado, en los tres casos, valdrían 2. Si consideramos cuatro líneas (véase la figura), en el triángulo tenemos medidas de 0, 1, 2 y 3, mientras que en el cuadrado todas las líneas miden 3:

Como se puede apreciar, a medida que se va aumentando el número de líneas el resultado es siempre la fracción 1/4 más una fracción cada vez más pequeña Al aumentar el número de líneas, llegará un momento en que esa segunda fracción sea menor que cualquier número que fijemos, y por tanto prácticamente cero, por lo que el área de la curva es 1/4.

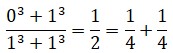
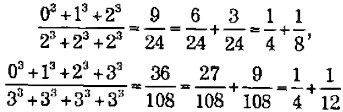
Método de Wallis para hallar la relación entre un triángulo y un cuadrado cuando se tienen cuatro líneas.

El personaje más importante en el que se apoyaron Newton y Leibniz fue el inglés Isaac Barrow (1630-1677), teólogo y matemático, profesor de Newton en la cátedra lucasiana de Matemáticas de Cambridge. Publicó varias obras con las lecciones que impartía y en concreto su obra, matemática principal, Lectiones opticae et geometricae (1669), escrita con la supervisión de Newton y en la que desarrolló su análisis. Si su supeditación a la geometría no hubiese sido tan excesiva, Barrow podría haber sido el fundador del cálculo.
Un repaso a dicha obra nos da una idea de todo lo que se conocía ya en relación con el cálculo: obtención de tangentes, diferenciación del producto y cociente de funciones, diferenciación de potencias de x, rectificación de curvas, cambios de variables en una integral definida o la diferenciación de funciones implícitas. Barrow fue además consciente de que los problemas de cuadraturas y los de cálculo de tangentes eran inversos, algo ya planteado por el escocés James Gregory, pero que había pasado desapercibido. Barrow lo planteó de forma geométrica y solo para algunas funciones.

§. Los problemas del cálculo
Uno de los aspectos más relacionados con las matemáticas era el del movimiento. Pensemos que muchos matemáticos consideraban una curva como un punto en movimiento. Dos cuestiones destacaban en relación con el movimiento: hallar la velocidad y la aceleración de un objeto cuando se conoce la distancia que recorre en función del tiempo, y el problema inverso, conocida la aceleración, hallar la velocidad y la distancia recorrida. Sin embargo, lo que realmente constituía un gran desafío era averiguar cuál era la velocidad instantánea Si hemos recorrido 90 kilómetros en una hora, sabemos que la velocidad media de ese recorrido es 90 km/h, pero muy posiblemente en esa hora unas veces habremos llevado más velocidad y otras menos. De forma análoga, si conocemos la velocidad en un instante y el tiempo de circulación, tampoco podemos saber la distancia recorrida, porque esa velocidad cambia de un instante a otro. Para pasar de la variación media a la instantánea debemos hacer un proceso de paso al límite, desconocido en el siglo XVII.
El segundo gran desafío era hallar la tangente a una curva. La aplicación física de ese cálculo era inmediata en los estudios de óptica. En los problemas de lentes es importante saber el ángulo con el que un rayo incide sobre la lente, pues será el mismo que el del rayo refractado. El ángulo se mide con respecto a la dirección normal, es decir, la perpendicular a la recta tangente en el punto en el que incide. También en el movimiento, la dirección de un móvil en cualquier punto por el que circule, es la de la tangente a la trayectoria que lleva. Se puede pensar en un experimento muy fácil para comprobarlo: si atamos un peso a una cuerda y la hacemos girar rápidamente alrededor de nuestra mano, cuando soltemos la cuerda el peso no seguirá girando, sino que se desplazará en la dirección tangente a la circunferencia descrita en el preciso momento en que la soltemos.
Para los griegos, la tangente a una curva era aquella recta que tenía un único punto común con la curva, y quedaba toda ella a un mismo lado.

Las curvas mecánicas: la cicloide
Para los griegos, las curvas podían ser planas, las que podían obtenerse solo con regla y compás, cónicas, que se obtienen seccionando un cono, o lineales, las no incluidas en los grupos anteriores y que necesitaban algún medio mecánico para su construcción.
Galileo le dio el nombre de cicloide, aunque ya Mersenne había proporcionado una definición de la curva y algunas de sus propiedades. Roberval consiguió hallar la cuadratura de un trozo de cicloide y aunque intentó encontrar un método para dibujar la tangente, fue Fermat quien lo logró, Pascal planteó un desafío para hallar el área de cualquier segmento de una cicloide y el centro de gravedad de un segmento. De todos los que respondieron, Pascal valoró especialmente el trabajo de Christopher Wren. Por su parte; Huygens planteó el problema de encontrar una curva, con un mínimo o punto más bajo, de forma que si se deja caer una bola rodando sin rozamiento por esa curva por efecto de la gravedad, tarda el mismo tiempo en llegar al punto más bajo desde cualquier punto donde se comience; llamó a la curva tautócrona. Pascal demostró que la solución era una cicloide invertida. La curva alcanzó tal fama que salió citada en Los viajes de Gulliver. Leibniz renombró las curvas; llamando algebraicas a las geométricas y cambiando el nombre de mecánicas por trascendentes. Esa terminología aún se usa en la actualidad.

Pero en el siglo XVII se planteó en términos de movimientos y fuerzas. Así, Roberval consideró que sobre un punto que se moviera tendrían influencia dos fuerzas, una horizontal y otra vertical. La diagonal del rectángulo formado por las dos rectas, daría la dirección de la recta tangente (véase la figura).

Dirección de la tangente según Roberval.

El tercer y gran desafío era el cálculo de máximos y mínimos. Este problema era de aplicación a muchas situaciones cotidianas. Se suele considerar que los problemas de este tipo comenzaron cuando Kepler estudió tas formas óptimas que debían tener los toneles de vino, demostrando que de todos los paralelepípedos rectos de base cuadrada y la misma superficie, el cubo es el que guarda el mayor volumen. Este tipo de problema también tenía aplicaciones en el lanzamiento de proyectiles y en el movimiento de los planetas.
El cuarto problema era el de las medidas que comprendían la rectificación de curvas, es decir, transformar un trozo de curva en un segmento con la misma longitud, con lo que se podía saber lo que medía ese trozo de curva,- la cuadratura de una curva, es decir, el área limitada por esa curva y la cubicación de un cuerpo, es decir, el volumen encerrado dentro del cuerpo. Dentro de este grupo de problemas se incluían el del cálculo de los centros de gravedad de los cuerpos o la atracción gravitatoria entre ellos.

§. Y llegaron los genios
Prácticamente casi todos los grandes matemáticos del siglo XVII aportaron algo a la construcción del cálculo. De forma desorganizada, casi todo estaba ahí, Fermat, por ejemplo, utilizó el mismo método para obtener tangentes y valores extremos, máximos o mínimos, es decir, la derivada. Torricelli comprobó que, en casos particulares, los problemas de movimiento, es decir, el cambio relativo, era el inverso del problema de cuadraturas. Gregory demostró que los problemas de la tangente y el área eran recíprocos, igual que Barrow.
Hacía falta que llegara alguien con mejor vista para darse cuenta de las relaciones claras que había entre los problemas. Tanto Newton como Leibniz dieron el salto cualitativo en la creación del cálculo con dos aspectos fundamentales. En primer lugar, dieron con un método que era general, que se podía aplicar a cualquier tipo de problema. En segundo lugar, pusieron de manifiesto que los problemas de tangentes y de cuadraturas eran inversos, por lo que para resolver uno de ellos bastaba invertir el método para hallar el otro. Ese resultado es lo que se conoce como teorema fundamental del cálculo. Por ello, después de Leibniz y Newton, los cuatro problemas del cálculo quedaron reducidos únicamente a dos: problemas de derivación e integración.
Además, plantearon el cálculo completamente desligado de la geometría. Con ellos, el cálculo se convirtió en una ciencia independiente, que trabajaba con conceptos algebraicos, lo que permitía plantear un método que sirviera para cualquier tipo de función o de problema.

Isaac Newton
Newton (1642-1727) fue matemático, físico, filósofo, alquimista, teólogo e inventor. Estudió en la Universidad de Cambridge, donde asistió a las clases de Barrow, a quien sustituyó como profesor.
En 1665, regresó a su pueblo natal tras cerrarse la universidad debido a la peste que asolaba Inglaterra. Durante dos años de vacaciones forzosas, Newton alumbró lo que sería la obra más importante del siglo XVII. Trabajó en tres grandes campos, la óptica, la gravedad y los movimientos de los cuerpos, y por último, el cálculo infinitesimal. Siempre fue reacio a publicar sus resultados, pues no quería entrar en polémicas, y prefería mandar sus descubrimientos mediante escritos a otros científicos. Esto le llevó a publicar algunos de sus hallazgos muchos años después de haberlos descubierto, lo que planteó ciertos problemas de paternidad.
Los «Principia»
En 1686 aparecería el primero de los tres tomos de la obra que revolucionarla la ciencia: Philosaphiae naturalis principia matemática ( Principios matemáticos de la filosofía natural ), más conocida por Principia. En ella incluía la celebérrima ley de la gravitación universal.
En 1696 abandonó la enseñanza y se convirtió primero en interventor, y más tarde en director de la Casa de la Moneda de Londres, puesto desde el que dirigió el cambio de sistema monetario en Gran Bretaña. En 1703 fue elegido presidente de la Royal Society, cargo que mantuvo hasta su muerte. Durante una breve época fue parlamentarlo y recibió el título de sir en 1705 de manos de la reina Ana,

A pesar de la agria polémica sobre quién inventó antes el cálculo infinitesimal, los enfoques de Leibniz y Newton son distintos. Newton calculaba la derivada y la primitiva ayudándose de incrementos infinitamente pequeños, mientras que Leibniz trabajaba directamente con esos incrementos, lo que para él eran los diferenciales. Por otro lado, Newton siempre trabajó las derivadas e integrales en términos de cambio relativo entre las variables, mientras que Leibniz enfocaba su trabajo mediante las sumatorias de términos para hallar áreas o volúmenes, en la línea de las sumas de indivisibles de Cavalieri. Además, Newton utilizó con profusión las series para representar funciones, mientras que Leibniz trabajó más directamente con la expresión general de la función. EL científico alemán se preocupó asimismo de desarrollar reglas de cálculo y fórmulas de aplicación, algo que el inglés no tuvo en cuenta. Y la última gran diferencia hace referencia a la notación. Mientras que Leibniz se esforzó en buscar una notación adecuada y fácil de utilizar, Newton no se preocupó del tema. Hoy día usamos la notación que creó Leibniz, a pesar de que la concepción del cálculo de Newton sea más cercana a la nuestra.
Este divulgó su cálculo a partir de varios escritos. El primero fue De analysi per aequations numero terminurom infinitas, escrito en 1669 pero publicado en 1711; el segundo fue el libro Methodus fluxiorum et serierum infinitorum, terminado en 1671 pero no publicado hasta 1736. En esta obra define sus elementos fundamentales, los fluyentes y las fluxiones. Define los primeros como cantidades variables, ya que consideraba las rectas, planos y volúmenes como un movimiento continuo de puntos, rectas y superficies. Al cambio relativo de ese fluyente lo llama fluxión. Corresponderían aproximadamente a nuestras variables y funciones y sus derivadas respectivas. Si x e y son fluyentes, sus fluxiones las denota por

. La fluxión de la fluxión, lo que sería la derivada segunda, se representa por

, y así sucesivamente. Define asimismo el momento de un fluyente, que representa por o, como un cambio muy pequeño de la variable, un intervalo infinitamente pequeño de cambio.
En un tercer artículo, De cuadratura curvarum, escrito en 1676 y publicado en 1704 como apéndice de su obra de óptica, Newton modificó en parte su enfoque infinitesimal, acercándose más a la idea intuitiva de limite.
Veamos cómo utilizaba Newton estos elementos para hallar una derivada. Partamos de la función y = xⁿ. Newton dice que si la variable x fluye, es decir, cambia infinitesimalmente a + o, la función se convertirá en (x + o)ⁿ. A continuación, desarrolla este binomio, obteniendo la serie:

Si restamos a esa expresión el valor y = xⁿ, tenemos entonces que el incremento de la variable x, es decir, o, es equivalente al incremento de la variable y, es decir.

y si simplificamos esa equivalencia por el incremento, nos queda que 1 es equivalente a la expresión'.

Y, como el propio Newton dice: « Ahora dejemos que estos incrementos se desvanezcan», es decir, todos los términos con el incremento desaparecen al hacer tender este valor a cero. De esa forma la relación que nos queda es 1 a xⁿ^-1

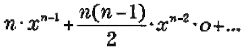
§. El cálculo de Leibniz
Sobre 1675 ya aparecían en las notas de Leibniz las ideas que le llevarían, con muchos cambios por el camino, a su concepción del cálculo. Sin embargo, parece que las ideas que lo pusieron en marcha ya las tenía previamente. En su obra Dissertatio de arte combinatoria trabajó con sucesiones y con diferencias de términos. Partía, por ejemplo, de la sucesión de cuadrados 0,1, 4, 9, 16, 25,...
Las primeras diferencias serian 1, 3, 5, 7, 9,... Las segundas diferencias serían 2, 2, 2, 2, 2,... y las terceras serían todas nulas.
Si se tomaran las potencias terceras, todas las cuartas diferencias serían nulas y así sucesivamente.
Comprobó que al sumar los primeros términos de las primeras diferencias, da el término siguiente de la sucesión original, es decir, si se suman los dos primeros términos 1 + 3 = 4, que es el tercer término de la sucesión. Si se suman los tres primeros l + 3 + 5 = 9, es decir, el cuarto término, y así sucesivamente.
De esa forma, el cálculo infinitesimal de Leibniz tiene su base en las sumas y diferencias de sucesiones. La suma nos daría el cálculo integral, es decir, el área comprendida por la curva, y las diferencias, la derivada.
Leibniz consideró que las curvas estaban formadas por infinitos segmentos rectilíneos, infinitesimales que darían lugar a las tangentes a la curva. Con lo que en cada punto tendríamos el valor de la x, de la y y del segmento correspondiente de la curva; es decir, en el fondo, lo que tendríamos serían sucesiones de números en las que se podían aplicar las sumas y diferencias.
En el primer artículo que publicó sobre el cálculo en 1684 en la revista de Acta Eruditorum, de titulo Un nuevo método para los máximos y mínimos, que no se detiene ante cantidades fraccionarias o irracionales, y es un singular género de cálculo para estos problemas , Leibniz presentó su método y lo aplicó para resolver un problema planteado por el cartesiano Florimon de Beaune: encontrar las curvas de subtangente constante. Veámoslo en nuestra notación actual.

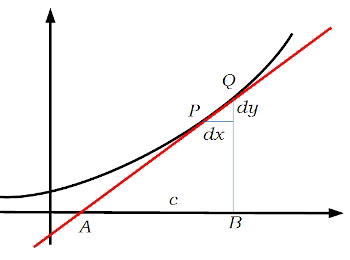
Triángulo característico de Leibniz, donde aparece la tangente a una curva y su subtangante

La subtangente es la proyección sobre el eje X de la medida desde donde la tangente corta el eje X hasta el punto de tangencia; en la figura de la página siguiente sería la medida AB, que queremos que sea constante e igual a c. En esta demostración Leibniz utilizó lo que conoce como triángulo característico, que también habían utilizado Pascal y Barrow, de catetos dx y dy y como hipotenusa uno de los segmentos infinitesimales que componían la curva.
La medida BQ corresponde a y, y por tanto, como el triángulo ABQ es semejante al triángulo característico, tenemos que se cumple que

de donde

e integrando esa expresión

y, por tanto, las curvas de subtangente constante son las de expresión

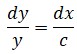
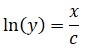
y = e^x^/c

es decir, las exponenciales.
Veamos la forma en que Leibniz deducía la derivada de un producto a partir de un texto extraído de un manuscrito de 1675:
d(xy) es lo mismo que la diferencia entre dos xy adyacentes, de los cuales uno será xy y el otro (x + dx) (y + dy). Entonces

d(xy) - xy = (x + dx)(y + dy)xy = xdy + ydx + dxdy

y esto será igual a xdy + ydx si la cantidad dxdy es omitida, la cual es infinitamente pequeña con respecto a las restantes cantidades, porque dx y dy se suponen infinitamente pequeños.
Hoy día se acepta que Newton fue el primero en desarrollar los principios del cálculo, y Leibniz el primero en publicar resultados. Ambos llegaron de forma independiente apoyándose en los mismos fundamentos: Descartes, Fermat, Cavalieri, Pascal, Walis, Barrow, etcétera

§. La polémica del cálculo
Ya en 1674, Leibniz citaba de pasada en una caita a Oldenburg que habla realizado la cuadratura aritmética del círculo con un método general que había encontrado, y en 1676 le indicaba que había descubierto un método para resolver cuadraturas que podía generalizarse, pero no especificaba mucho más. Ese mismo año llegó a París, vía Londres, el noble sajón Walter von Tschimhaus con cartas de presentación de Oldenburg para Leibniz y Huygens. Von Tschimhaus trabajó un tiempo con Leibniz, por ejemplo, en unos manuscritos de Pascal que después desaparecieron y solo nos queda información por el trabajo de Leibniz. Por los escritos, estaba claro que Tschimhaus no tema ningún interés en el cálculo infinitesimal, por lo que no podría haber informado de nada a Leibniz. Tschimhaus defendía que todo lo realizado por Barrow y otros matemáticos ingleses eran derivaciones de lo aportado por Descartes y para contrarrestar esta opinión Collins elaboró un escrito de unas cincuenta páginas conocido por Historiola en el que explicaba el cálculo desarrollado por Barrow y Newton. Envió un extracto en 1675 a Tschimhaus y Leibniz, aunque este ya dominaba su propio cálculo.
Cuando Leibniz abandonó París en octubre de 1676, pasó una semana en Londres camino de Hannover, y Collins, a la sazón bibliotecario de la Royal Society, permitió a Leibniz copiar extractos de su Historiola y del escrito De analysi, del propio Newton.
A lo largo de la historia, Newton y Leibniz se cartearon varias veces a través de Oldenburg. El 6 de agosto de 1676, Oldenburg le envió a Leibniz una carta de Newton, conocida como epístola prior, a través de Samuel König, que estaba de visita en París; la carta se traspapeló y no le llegó hasta el 26 de ese mes. En la carta, Newton se centraba especialmente en el teorema del binomio y presentaba varios resultados, todos conocidos ya por Leibniz, sin explicar en ningún momento los métodos por los que había llegado a ellos. Leibniz le contestó al día siguiente, comentándole que su método era diferente. En el juicio sobre el descubrimiento del cálculo se insistió en que Leibniz había tenido casi tres semanas para estudiar atentamente la carta antes de responder.
En 1677 le llegó una. segunda carta de Newton, la epístola posterior, en la que le explicaba todo su trabajo sobre las series infinitas y le hablaba también de su cálculo, aunque se lo presentó mediante un criptograma, basado en palabras latinas, que decía lo siguiente:

La base de estas operaciones es suficientemente obvia, pero debido a que no puedo seguir ahora con la explicación, he preferido dejarla oculta: 6accd et 13efí713l9n4o4orr4s8tl 12vx.

Ese galimatías significaba, traducido de la frase latina:

«Siendo dada una ecuación cualquiera que incluye un cierto número de cantidades fluyentes, encontrar las fluxiones y viceversa».

Esto se completaba con otro anagrama más extenso, que incluso después de descifrado, daba poca información a quien no tuviese ya conocimientos del tema.

«Los segundos inventores no cuentan para nada.»
Isaac Newton, en referencia a Leibniz tras la polémica la polémica de la maternidad del cálculo infinitesimal.

Desde su primer artículo de 1684, Leibniz tuvo problemas de autoría, y aunque insistió en que su método era distinto y que lo había encontrado antes de consultar ningún escrito de Newton, cosa que demostraban las cartas escritas a Oldenburg, no sirvió de nada. El asunto se enconó cuando Nicolás Fatio de Duilier, discípulo de Newton, llegó a acusar a Leibniz de plagio.
Las acusaciones comenzaron a ir y venir entre el continente y la isla, y los matemáticos a tomar partido por unos y otros. Hasta tal punto llegó la polémica que Leibniz solicitó una comisión de la Royal Society para dilucidar quién tenía razón en esa discusión. La comisión, creada casualmente por Newton, que en ese momento era presidente de la sociedad científica, llegó a la conclusión de que la prioridad era del inglés.
Debido a esta disputa los científicos ingleses y el resto de los europeos rompieron relaciones y dejaron de intercambiar información. Los científicos del continente siguieron a Leibniz y los ingleses a Newton, pero como el cálculo del inglés era mucho más geométrico que el del alemán, esto significó una rémora para la matemática inglesa, que quedó retrasada respecto al continente.
El método de Leibniz fue rápidamente aceptado por los matemáticos del continente europeo. Los «apóstoles» más eficientes de esta conversión fueron los hermanos Jacob y Johann Bernoulli, los primeros de una larga familia de importantes matemáticos. Aunque el trabajo de Leibniz era original y rico en resultados, era un poco incompleto y, a veces, complicado de seguir. Por fortuna, los hermanos Bernoulli lo organizaron y le dieron una estructura sólida, aportando multitud de ejemplos y desarrollos nuevos. Leibniz llegó a reconocer el gran trabajo realizado por los Bernoulli, e incluso recalcó que fueron los primeros en utilizar el nuevo cálculo para resolver problemas físicos.
Jacob (1654-1705) fue autodidacta y bebió de las principales fuentes del cálculo: Descartes, Wallis y Barrow. Fue profesor de Matemáticas en la Universidad de Basilea. Le explicó matemáticas a su hermano Johann y ambos comenzaron a trabajar sobre el cálculo de Leibniz. En 1690 publicó en Acta Eruditorum un artículo en el que hablaba de sus propios métodos del cálculo y resolvía un problema propuesto por Leibniz tres años antes: « Encontrar la curva, situada en un plano vertical, según la cual un punto material desciende alturas iguales en tiempos iguales ».
Por su parte, Johann (1667-1748), conocido como el pendenciero, tenia mayor inteligencia e inventiva que su hermano. Fue un gran geómetra, aunque poco modesto, pues en su lápida grabó la frase: « Aquí yace el Arquímedes de su tiempo». Fue un firme defensor de Leibniz e impulsor de sus reclamaciones de fundador del cálculo. Se enemistó con varios matemáticos, especialmente su hermano Jacob y su hijo Daniel. Fue profesor de Euler y le explicó el cálculo al marqués de L'Hôpital, un competente matemático.
Efectivamente, Guillaume François Antoine, marqués de L'Hôpital (1661-1704), contrató a Johann para que le explicara los entresijos del cálculo infinitesimal. Con lo aprendido en sus clases, publicó el primer libro de la historia en el que se hablaba del cálculo: Análisis de los infinitamente pequeños para el entendimiento de las líneas curvas (1696). L'Hôpital lo publicó sin autoría y en la presentación comentaba su dependencia de Johann, aunque la mayoría de resultados que aparecían en el libro eran del propio Bernoulli.
Ambos hermanos resolvieron multitud de problemas utilizando el nuevo cálculo: rectificación de curvas, cálculo de curvaturas, envolventes y evolutas, puntos de inflexión. Jacob trabajó especialmente con la espiral logarítmica y la admiraba de tal forma que acabó inscrita en su lápida. Lamentablemente el cantero tenía menos conocimientos que él y le hizo pasar a la posteridad con una espiral de Arquímedes en su lápida
Una de las formas en que más se extendió el cálculo fue a base de desafíos. Lanzar un problema para que los restantes matemáticos lo solucionaran era un método muy corriente en la época.
En el artículo de Jacob de 1690, donde resolvía el problema propuesto por Leibniz, planteaba también un desafío: encontrar la forma que toma una curva perfectamente flexible y homogénea por la acción solo de su peso, si está atada por sus extremos. La solución es la curva conocida como catenaria. Fue resuelto por su hermano Johann, además de Huygens y Leibniz. El propio Leibniz publicó más tarde, en 1692, un artículo en el Journal des Sçavans donde volvía a dar la solución y explicaba cómo utilizar la catenaria en navegación.
En 1696, Johann Bernoulli lanzó un reto al mundo matemático, especialmente inglés, con el fin de probar quién estaba a la altura del nuevo cálculo. Pedía encontrar la curva por la que un cuerpo desciende entre dos puntos, no alineados vertical ni horizontalmente, en el menor tiempo posible. Esta curva recibe el nombre de braquistócrona. Antes de finalizar el plazo previsto, solo Leibniz había presentado una solución, que consideraba el problema muy bello y hasta el momento desconocido. El propio Leibniz pidió que se ampliara el plazo para que otros matemáticos pudieran presentar la solución. Tras el nuevo plazo solo se habían presentado cinco soluciones: Leibniz, los hermanos Bernoulli, L'Hôpital y una solución anónima presentada en Inglaterra. Después de estudiar dicha solución, el propio Johann indicó: « Por las garras se conoce al león». La solución era, por supuesto, de Newton. Por tanto, todas las soluciones usaban el nuevo cálculo. Por cierto, la curva que resuelve ese problema es también la cicloide invertida.

Capítulo 3
Códigos antiguos y modernos

Hoy día no concebimos nuestra vida cotidiana sin los ordenadores. Pero para entendemos con ellos tenemos que manejar su idioma, el sistema binario, aunque sea de manera inconsciente. Quien sentó las bases actuales de ese sistema fue Leibniz, que lo relacionó con los antiguos hexagramas del I Ching, un libro oracular chino. También se preocupó de otros tipos de lenguajes, e incluso se planteó crear uno universal para expresar matemáticamente todas las ideas.

Un proyecto que le creó a Leibniz muchos quebraderos de cabeza fue gestionar la extracción en unas minas en el Alto Harz, al sur de la ciudad de Goslar, a unos 100 kilómetros de Hannover. Esas minas tenían grandes filones de plata, cobre, hierro y plomo, Leibniz tenía varias ideas para perfeccionar la tecnología minera.
Tras visitar Hamburgo en 1678, entre los escritos que preparó para el duque incluyó un proyecto en el que trabajaba desde su estancia en París, con el objetivo de utilizar las hoy llamadas energías renovables para mejorar la extracción de mineral. Leibniz diseñó bombas y molinos de viento que permitieran usar la energía eólica e hidráulica para optimizar el drenaje de las minas. Las bombas aprovechaban gran parte de la energía que se perdía por fricción, y necesitaban poco mantenimiento. El diseño de los molinos permitía que funcionaran incluso con vientos de poca intensidad y con mayor rendimiento que los convencionales. La idea era usar los molinos todo el tiempo que se pudiera y complementarlo con la energía hidráulica cuando fallaran, consiguiendo un flujo de energía constante en cualquier época del año para elevar el agua y realizar las restantes operaciones mineras, pues en épocas de sequía, no se podía garantizar el funcionamiento de las minas.
La idea real de Leibniz, según informó al duque, tras el visto bueno al proyecto, es que parte de las ganancias se invirtieran en investigación en minería, pero parte de ellas irían a la financiación de la Academia de Berlín, que tenía en esos momentos en mente. Aunque el proyecto inicialmente no fue muy bien visto, especialmente por el gasto que significaría la construcción de tanta herramienta nueva, Leibniz argumentó en contra de todas las protestas, y recibió a finales de 1679 el beneplácito del duque para el acuerdo con la Oficina de Minas, que junto al duque y el propio Leibniz, financiarían el proyecto.
Desde el principio todo fueron problemas. Al manifiesto rechazo entre los funcionarios de las minas, que lo consideraban un intruso sin los conocimientos necesarios, se unieron las inclemencias del tiempo y especialmente las rachas de ausencia de viento. Al parecer, Leibniz había pasado por alto estudiar las variaciones y direcciones del viento en la zona. Otra dificultad era la construcción de los elementos diseñados, pues en varias ocasiones, al no seguir correctamente las indicaciones, las máquinas no funcionaban de manera adecuada y había que corregirlas una y otra vez.
Ante el aumento de los costes, que en 1683 eran ya de casi ocho veces lo previsto, el duque planteó cancelar el proyecto, pero Leibniz insistió en seguir un año más, pagando de su propio bolsillo, para demostrar que seguía siendo viable. Tuvo que replantearlo por completo y perfeccionar los molinos, de forma que se pudieran construir a mitad de precio. Incluyó un mecanismo de velas que se plegaban y desplegaban según las necesidades, y planteó la posibilidad de optimizar las bombas de extracción inyectando aire comprimido, aunque ambas ideas no prosperaron. Más adelante, ante la escasez de viento en la zona, diseñó unos molinos horizontales, en lugar de verticales, que pudiesen aprovechar todo tipo de viento, funcionar en cualquier momento y soportar las tormentas. Pero su rendimiento era la tercera parte de los tradicionales, por lo que tampoco resultaron viables. Definitivamente, en 1686 se abandonó el proyecto.
La minería no era un entretenimiento más entre la gran cantidad de temas que trató Leibniz; muy al contrario, fue uno de sus preferidos. Durante los seis años que duró el proyecto, Leibniz llegó a pasar más de la mitad del tiempo en Harz, lo que da una idea del ingente trabajo que supuso. Además, siempre tuvo en mente mejorar la extracción. En 1680, cuando aún tenía esperanza en el éxito del proyecto, escribió al duque que se podrían conseguir grandes beneficios de un acuerdo con los neerlandeses, para refinar la ganga procedente de las minas de oro y plata de Sumatra, propiedad de la Compañía Neerlandesa de las Indias Orientales. Un año más tarde, aconsejaba al duque en otro escrito un acuerdo con el emperador y el elector de Sajorna, para llevar una opinión conjunta a la conferencia política que se iba a celebrar en Frankfurt sobre el aumento del precio de la plata.
Una vez abandonado el proyecto, Leibniz, que aún confiaba en que se reconocería que sus ideas eran interesantes, no dejó de lado el perfeccionamiento de los métodos de extracción de mineral. Diseñó un mecanismo consistente en una serie de contenedores encadenados, que estarían subiendo y bajando continuamente, posibilitando la extracción de ganga Así se eliminaba el tremendo gasto de energía para elevar el contenedor de ganga desde las entrañas de la mina, pues a veces pesaba más la cadena para la extracción que la propia cantidad de desecho extraída. Su idea tuvo la misma nula acogida que el resto de los avances que ideó.

§. Leibniz historiador
En 1685, Leibniz obtuvo el encargo definitivo de realizar una historia de la casa de Brunswick-Luneburgo, su trabajo más importante a partir de ese momento. Su idea era que se podría trazar la historia retrocediendo hasta más o menos el año 600 d.C., pero para ello había que acudir a las fuentes originales, que estaban en los monasterios.
A principios de 1687 estaba investigando por los alrededores de Hannover, y a finales de año emprendió un viaje por el sur de Alemania y Austria. En abril de 1688 hizo un descubrimiento en Augsburgo que amplió bastante sus expectativas. En el monasterio benedictino de dicha localidad pudo consultar el códice Historia de Guelfis principibus, en el que encontró las pruebas que relacionaban a los güelfos, creadores del ducado de Brunswick-Luneburgo, con la casa de Este, nobles italianos del ducado de Ferrara y Módena.

La casa de Este
La casa de Este, de origen francés, se dividió en dos: la casa de Welf-Este, conocida como casa de Welf, y la casa de Fulco-Este, que se convirtió en la casa de Este italiana. Durante las guerras entre güelfos y gibelinos, que tuvieron lugar en la Baja Edad Media, se apoderaron en 1240 de Ferrara, que era un feudo papal, convirtiéndose en 1352 en vicarios papales.
En 1288 se anexionaron Módena, aunque hasta 1482 no recibieron el titulo de duques de Módena y Regio de manos de Federico III de Habsburgo, emperador del Sacro Imperio Romano y archiduque de Austria. Esta familia dio grandes mecenas para el arte del Renacimiento y llegó a estar emparentada con familias italianas muy importantes, como los Borgia o los Sforza. Cuando en 1597 se agotó la línea sucesoria directa, el papa volvió a incorporar Ferrara a los Estados Pontificios y el poder de la casa de Este comenzó a declinar. De la rama más antigua de la familia salieron duques de Baviera, de Sajonia y los de la casa de Brunswick y Luneburgo.

Esto hizo que el viaje tuviera que ampliarse por Italia, en especial a Módena, donde también organizó el enlace político.
La labor histórica de Leibniz fue mucho más complicada de lo esperado inicialmente. En 1691 le comentó al duque que la obra podría estar acabada en un par de años si conseguía colaboración, cosa que obtuvo con la contratación de un secretario. No obstante, sí bien es verdad que tres tomos vieron la luz, la obra no llegó a terminarse nunca. Aunque sí escribió sobre parte de lo descubierto. En 1695, con motivo del enlace matrimonial entre la casa de Brunswick-Luneburgo y la de Este en Módena, Leibniz diseñó una medalla conmemorativa de la nueva unión de las casas después de más de seis siglos, y escribió una obra editada en Hannover, de título Lettre sur la connexion des Maisons de Brunswick et d'Este, en la que exponía lo descubierto en sus pesquisas históricas.
En todos esos viajes se entrevistó con intelectuales y científicos, visitó museos y recogió información sobre aspectos muy diversos, por ejemplo, sobre fósiles, que después aparecería en su obra Prologoea. También estuvo varias semanas, en calidad de invitado, en casa del landgrave Ernesto de Hessen-Rheinfels, con quien departió sobre temas de historia y religión, con especial hincapié en su proyecto, siempre presente, de la reunificación de la iglesia católica y protestante. Incluso consiguió su gran deseo de ser recibido en audiencia por el emperador alemán Leopoldo I,

«En el ámbito del espíritu, busca la claridad; en el mundo material, busca la utilidad»
Gottfried Wilhelm Leibniz

Durante su estancia en Roma pudo visitar la Biblioteca Vaticana, donde encontró manuscritos que corroboraban los descubrimientos hechos en Augsburgo También coincidió con la muerte del papa Inocencio XI, que estaba a favor de la reunificación de las iglesias. En esas fechas comenzó a leer los Principia de Newton, tal como indican las anotaciones que realizó en su propio ejemplar.

La casa donde vivió Leibniz en Hannover hasta su muerte.

A pesar de su labor para el elector, Leibniz siguió acumulando cargos que no le obligaban a una presencia física constante. En 1691 pasó a ser director de la biblioteca de Wolfenbüttel, en la Baja Sajonia, cargo que mantuvo hasta su muerte. Aunque se debía encargar de la planificación a largo plazo, no era un trabajo para el día a día. En 1693 y a publicó una primera obra, Codex juris Pentium diplomaticus, en la que recopilaba documentos constitucionales de los siglos XII al XIV, la mayoría inéditos.
En 1696 fue nombrado consejero privado de justicia, un puesto cuya categoría era un poco inferior a la de vicecanciller. Sobre esas fechas realizó un proyecto para la instalación de fuentes en el jardín de Herrenhausen, en Hannover, lo que demuestra que Leibniz siempre tenía presente los aspectos prácticos y tecnológicos, y que seguía interesado en todo tipo de proyectos.
A principios de los ochenta intentó conseguir una copia de la olla a presión con válvula de seguridad, que había inventado Denis Papin (1647-1717) y que permitía aprovechar los huesos para elaborar comida. Papin era físico e inventor, y había tenido que emigrar a Inglaterra y Alemania por problemas religiosos. Aparte de su marmita o digestor, como la llamaba, inventó un submarino, una catapulta y una máquina para elevar agua con aplicación en molinos o fuentes. El invento de la olla a presión inspiró a Leibniz para escribir una obra satírica, en la que unos perros defienden su derecho a los huesos, amenazado por la utilización de la olla a presión.
Durante 1696 y 1697, su principal tarea diplomática consistió en obtener para el duque de forma permanente el obispado de Osnabrück, que ya llevaba personalmente el duque Ernesto. Este obispado tenía la característica de que era gobernado de forma alterna por un obispo católico y un conde protestante tras la Paz de Westfalia.

§. Cuestiones religiosas
Leibniz recibió en su vida muchos cargos de importancia. Especialmente fue consejero de grandes personalidades. Pero hubo otros puestos que se le ofrecieron, dentro de actividades que le eran muy gratas, y que no aceptó por no abandonar sus creencias. Por ejemplo, se le ofreció un cargo en la Biblioteca Vaticana, pero como requisito debía convertirse al catolicismo y no lo aceptó. Igual le pasó en 1698, cuando le ofrecieron ser bibliotecario en París. A través de su amigo el landgrave Ernesto recibió la oferta de ser canciller de la diócesis de Hildesheim, ciudad de la Baja Sajorna, pero la rechazó debido a sus ocupaciones y a su religión.
Muchos de los personajes con quienes tuvo contacto intentaron convertido al catolicismo, especialmente el landgrave Ernesto de Hessen-Rheinfels, pero Leibniz siempre se negó. Pensaba que la Iglesia era irrefutable en cuestiones de fe, pero que existían multitud de temas científicos y filosóficos que no contradecían ni las Sagradas Escrituras ni ningún concilio ecuménico, y que, sin embargo, eran rechazados por la Iglesia incluso cuando podía demostrarse que eran verdaderos. Él mismo decía que si hubiese sido criado dentro de la Iglesia católica, no la abandonaría; pero que al haberse criado en el luteranismo, no podía aceptar esas contradicciones.
A pesar de todo, durante toda su vida siguió abogando por la reunificación de ambas confesiones. Buscó apoyos allí donde pudo, pues era consciente de que si no se conseguía involucrar al papa, al emperador o a algún príncipe gobernante, no habría posibilidad de lograrlo. Durante su vida realizó muchos escritos en defensa de esa idea, como Sistema, theologicum, obra que planteaba la reunificación desde el punto de vista de un católico y que no se publicó hasta 1845.
Durante su estancia en Viena se acercó a visitar a su amigo el obispo Cristóbal de Rojas y Spínola, con quien se había reunido varias veces en Hannover, ya que este visitaba la ciudad para tratar distintos temas, a veces relacionados con el emperador o con la reunificación de los teólogos protestantes. El obispo estaba en la misma línea que Leibniz de abogar por la reunificación de las confesiones, y le mostró la documentación que había intercambiado con el papa y algunos cardenales en ese sentido. A través de Rojas, Leibniz entró en contacto con varios funcionarios importantes de la corte imperial, que le abrieron el camino para ser recibido en audiencia por el emperador.
Tras terminar sus pesquisas en Italia, su intención era regresar a Hannover, después de casi tres años de viaje. Pero el duque Ernesto Augusto le encargó que realizara una serie de recados en Viena. Volvió a entrevistarse con Rojas y plantearon apoyar un acercamiento diplomático conjunto por parte de los electores de Brunswick-Luneburgo y Sajonia frente al emperador, que había manifestado su rechazo al proyecto de reunificación religiosa.

§. Nuevos contactos científicos
La labor científica de Leibniz durante esos años fue incansable. Seguía carteándose con científicos de muchos países y mandando artículos a casi todas las revistas importantes del momento. Amargamente se quejaba en carta a algún amigo de que en Hannover no tenía nadie con quien hablar de temas importantes. En 1689, a su paso por Roma, fue elegido miembro de la Academia Físico- Matemática.
También continuaba con sus polémicas con otros intelectuales por temas científicos y filosóficos. Durante toda su vida, Leibniz fue bastante crítico con la filosofía y ciencia de Descartes. Aunque ya había expresado en muchos escritos su disconformidad con su filosofía, en marzo de 1686 publicó en Acta Eruditorum un artículo con un título muy explícito: « Breve demostración de un error notable de Descartes», en el que lo atacaba directamente. Meses más tarde apareció una traducción francesa en la revista neerlandesa Nouvelles de la république des lettres, realizada por el abad Catelan, acérrimo cartesiano que criticaba a Leibniz planteando que era él quien erraba. Esto le permitió al alemán publicar una respuesta en la misma revista. Tras algunas controversias más que aparecieron por parte de uno y otro en ese mismo medio, Leibniz le planteó un desafío a Catelan: que utilizara el método cartesiano para encontrar la curva de caída uniforme, es decir, la catenaria. El abad nunca respondió, pero sí se publicó una solución de Huygens, aunque sin demostración. Leibniz publicó la solución junto con la demostración en un artículo de 1689 en Acta Eruditorum.
En 1690 retomó su contacto con Londres a través de Henri Justel, bibliotecario real.

Explicación de la aritmética binaria, el artículo que Leibniz envió a la Academia de Ciencias de París.

Le pedía información sobre los últimos descubrimientos, ya que la última revista que había recibido databa de 1678. Dos años más tarde, a través de Justel, entró en contacto con el astrónomo Edmund Halley (1656-1742), por aquel entonces secretario de la Royal Society. Ya por esa época, Fatio de Duillier había puesto en marcha la polémica acerca de la paternidad del cálculo al mostrar, en carta a Huygens, la extrañeza porque Leibniz no hubiese mostrado el reconocimiento a Newton al publicar sus artículos sobre el cálculo. En 1693 Leibniz le mandó la primera carta directa a Newton, quien le contestó pasado un tiempo al haberse extraviado su carta, y sin mostrar ningún tipo de animosidad.
En 1687 comenzó su fructífera correspondencia con los hermanos Bernoulli, y en 1692 comenzó a cartearse con el marqués de L'Hôpital, ya un experto en cálculo tras haber leído y entendido el artículo de Leibniz publicado en 1688, además de haber recibido clases de Johann Bernoulli. En sus cartas se contaban sus proyectos y L'Hôpital le habló en particular del texto que estaba escribiendo, y que publicó en 1696, sobre el cálculo diferencial, al que estaba previsto que le siguiera otro sobre el cálculo integral. En el prólogo del libro, L'Hôpital comentaba que Leibniz había reconocido en uno de sus artículos que Newton había descubierto algo similar a su cálculo, aunque la notación de Leibniz era de aplicación más rápida y fácil.

§. Aspectos médicos
Hay pocos temas en los que Leibniz no mostrara algún tipo de interés: literatura, teatro, ópera, diseños tecnológicos, organización militar... Casi todo lo imaginable llamaba su atención. Y como no podía ser menos, también se interesó por la medicina.
Intentaba estar al tanto de los avances médicos y aconsejar mejoras en una ciencia que aun estaba en un estado muy elemental. Pensemos que no hacía ni cien años que se había descubierto la circulación de la sangre, o que aún se tardarían casi dos siglos en la simple idea de que los médicos debían lavarse las manos antes de una operación. Cuando en 1691 recibió información desde Inglaterra a través de Justel de un remedio para la disentería, no descansó hasta conseguirlo, la ipecacuana, procedente de América, y abogar por su utilización en Alemania.
Un par de años después, en escrito enviado a la princesa Sofía, hacía una serie de recomendaciones sobre medicina, que hoy en día nos parecen evidentes. Para avanzar en la medicina había que facilitar la investigación médica y la difusión de los resultados. Era fundamental que el diagnóstico fuera previo al tratamiento. Había que observar los síntomas de la enfermedad y llevar una historia escrita de su evolución y de la respuesta al tratamiento del paciente. Se debían divulgar informes de los casos más interesantes, y para ello era importante que los hospitales tuvieran financiación y personal adecuados. Defendía la necesidad de una medicina preventiva y la creación de un Consejo de Salud, integrado por políticos y médicos que plantearan una serie de medidas para enfermedades de gran extensión social, como las periódicas epidemias.
Otro tema que trató, a partir de sus conversaciones con el médico Bernardino Ramazzini (1633-1714), al que conoció en Módena, fue la importancia de las estadísticas médicas. Leibniz estaba convencido de que la difusión de dichas estadísticas podía producir una ostensible mejora, pues los médicos estarían en mejor disposición a la hora de enfrentarse a las enfermedades más usuales. Sobre ese tema insistió en distintos foros, incluso propuso al Journal des Sçavans que las publicara anualmente siguiendo el modelo establecido por Ramazzini.

Bernardino Ramazzini
Ramazzini (1633-1714) fue un médico y filósofo nacido en Carpí, ciudad próxima a Módena. Realizó sus estudios de medicina en Parma, y comenzó a ejercer en su ciudad natal. En 1671 se trasladó a Módena, donde fue ayudante del médico personal de Francesco II de Este. En 1682 fue contratado como profesor de Teoría de la Medicina en la Universidad de Módena. En 1700 se trasladó a la Universidad de Padua, de la que llegó a ser decano. Perteneció a muchas sociedades médicas y a la Academia de Berlín por recomendación de Leibniz, que entonces era su presidente. Ha pasado a la historia de la medicina por ser el primero que se dedicó, de forma exhaustiva, al estudio de las enfermedades laborales, que recogió en su obra principal De morbis artificum diatriba (Discurso de las enfermedades de los artesanos), publicada en 1700. Fue el primero que estudió las dolencias de los enfermos interesándose por la profesión que ejercían. Llegó a recoger multitud de datos y presentó la enfermedad no como una dolencia que afecta a un individuo, sino a todo un grupo laboral.

§. El estudio de las lenguas
Leibniz tenía gran facilidad para las lenguas. En su juventud estudió latín y griego de forma casi autodidacta, y escribió artículos en latín, francés y alemán-, incluso publicó alguno en italiano con buen manejo del idioma. También estaba interesado en el estudio de las lenguas. Partía del convencimiento de que debió existir un lenguaje original del que habían partido todos los demás, y que debían quedar retazos de ese idioma primigenio en todas las lenguas existentes. Para comprobarlo recopiló ejemplos lingüísticos de todo el mundo. Defendía además que el estudio de las lenguas debía ser complementario al de la historia, y servir de complemento al estudio del origen y las migraciones de los pueblos.
En 1696, con idea de promover el estudio de la lengua alemana, propuso la creación de la Sociedad Alemana en Wolfenbüttel bajo la dirección del duque Antonio Ulrico, que gobernaba junto con su hermano Rodolfo Augusto. Ambos eran amigos de Leibniz.
Una de sus obras más importantes en ese ámbito fue Unvorgreiffliche Gedanken, betreffend die Ausübung und Verbesserung der teutschen Sprache ( Reflexiones provisionales sobre el uso y el perfeccionamiento de la lengua alemana ), escrita en 1697 y publicada en 1717. En ella aboga por convertir la lengua alemana en vehículo de expresión cultural y científico y advertía que desde la Guerra de los Treinta Años el idioma alemán se había degradado y estaba en peligro de ser corrompido por el francés.
Pero a Leibniz no solo le importaban las lenguas existentes, también estaba en disposición de crear su propia lengua, relacionada con las matemáticas. Ya en la escuela había tenido la idea de crear un alfabeto universal, idea que desarrolló parcialmente en su De combinatoria. Leibniz planteaba un alfabeto del pensamiento humano, lo que le llevó al concepto de característica universal. De la misma manera que las palabras se forman por combinaciones de letras, a partir de un pequeño número de ideas simples se podían construir las ideas más complejas. En su lenguaje universal las ideas estarían formadas por combinaciones de signos, que serían los componentes de esa idea. Si además se planteaba una serie de reglas para combinar esos signos, se podrían realizar razonamientos igual que se hace un cálculo numérico. En varias cartas en las que trataba el tema, ponía como ejemplo de característica universal la escritura china.
En 1678 redactó el escrito Lingua generalis, donde representaba las ideas simples mediante números primos, y las ideas que se deducían de ellas mediante el producto de esos números, Para entender el lenguaje, se debían conocer las ideas simples y tener destreza en descomponer los números para hallarlas Para convertir los números en un lenguaje hablado, utilizó una idea del lingüista escocés George Dalgamo (1626-1687): las vocales representaban los números 1,10,100,1000 y 10000, y los números del 1 al 9 eran las primeras consonantes, b-1, c-2, d-3, f-4, etc., Así, el número 245 se expresaría por cifega. La permutación de las sílabas daría lugar al mismo número, es decir, 245 también podría ser fegacl.
Más tarde abandonó la idea por encontrarla demasiado complicada, y adoptó otro esquema basado en el latín, En su nuevo enfoque había que reducir todos los conceptos a sus elementos más simples, representarlos por símbolos y crear otros símbolos para las combinaciones de los anteriores. Para hacer esto planteaba que había que elaborar una enciclopedia que recogiera todo el conocimiento existente. Llegó incluso a escribir una introducción para la enciclopedia y realizó estudios para hacer aplicaciones del método, intentando plantear un cálculo lógico y una geometría encaminadas a la característica universal, Finalmente, el proyecto no llegó a concretarse.

§. Un lenguaje muy actual
Aunque en la historia existen algunos intentos aislados de crear un sistema binario, quien sistematizó un sistema de base dos tal como lo conocemos hoy día fue Leibniz. No sabemos exactamente en qué momento desarrolló la idea, pero ya en 1682 había escrito sobre las posibilidades del sistema, e incluso había estudiado el diseño de la máquina aritmética en binario, aunque tuvo que desistir por la gran cantidad de engranajes que requería.

Durante una fuerte tormenta en uno de los viajes de Leibniz a Italia, los supersticiosos marineros querían arrojarlo por la borda por ser protestante. Pero como sabía italiano, se puso a rezar y salvó tu vida.

Nuestro sistema decimal, de base 10, dispone de diez dígitos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. Si agrupamos más de 9 elementos, como ya no disponemos de más dígitos distintos, pasamos a una unidad de carácter superior, la decena, y así el elemento posterior a 9 se representa por 10, es decir, una decena y cero unidades. De la misma forma, si añadimos una unidad más a un grupo de 99 elementos, obtenemos una centena, que se representa por 100, y así sucesivamente.
En un sistema binario, o de base dos, solo tenemos dos dígitos: 0 y 1. Por eso, cuando queremos representar elementos superiores a 0 o 1, debemos usar también unidades de rango superior. Por ejemplo, para representar el valor 2 usamos la notación 10, una unidad de segundo grado y cero unidades de primer grado. Un número en binario está compuesto de una serie de ceros y unos. Los primeros números en binario aparecen en la siguiente tabla:

Para pasar de un número decimal a forma binaria, lo que debemos hacer es dividir entre 2 los restos de las divisiones serán los ceros y unos, que se deben ordenar del último al primero, Veamos cómo convertir el número 54 en binario, que será 54= 110110:

Para pasar de binario a decimal, debemos tener en cuenta la descomposición del número. En decimal, el número 2537 es igual a:

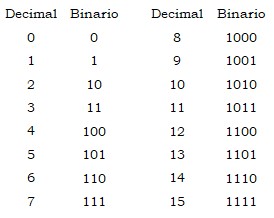
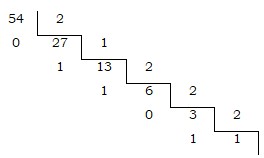
2357 = 2000 + 300 + 50 + 7 = 2×1000 + 3×100 + 5×10 + 7×1=

= 2×10³ + 3×10² + 5×10¹ + 7×10⁰.

De forma análoga, el número 110110 es equivalente a:

110110 = 1×2⁶ + 1×2⁴ + 0×2³ + 1×2² + 1×2¹ + 0×2⁰ =

= 32 + 16 + 0 + 4 + 2 + 0 = 54.

Durante una visita a Wolfenbüttel en 1696, le presentó su sistema al duque Rodolfo Augusto, que quedó muy impresionado, Leibniz diseñó una moneda en la que en el anverso llevaba una imagen del duque y en el reverso una alegoría de la creación en relación con los números binarios. En concreto, había grabado una tabla con los números del 0 al 15 y sus correspondientes valores binarios, así como ejemplos de suma y multiplicación de binarios.
Leibniz veía en ese sistema una representación de su propia filosofía, y una analogía de la creación continua de las cosas a partir de la nada. También lo relacionaba con la creación del mundo. Al principio no había nada, el 0, y en el primer día solo estaba Dios. Después de 7 días, dado que el 7 en notación binaria era el 111, ya existía todo, pues no hay ningún cero.
Cuando en 1700 fue escogido como miembro extranjero de la reconstituida Academia Real de Ciencias de París, Leibniz envió un escrito presentando el sistema binario. Sin embargo, aunque los académicos mostraron interés por el descubrimiento, encontraron que era muy complicado de manejar y aguardaron a que Leibniz presentara ejemplos de su aplicación. Varios años después volvió a presentar su estudio, que tuvo mejor acogida, pero esta vez lo relacionó con los hexagramas del I Ching. Envió también un artículo de título Explicación de la aritmética binaria para ser publicado en la Historie que editaba la academia
Hoy en día el sistema binario es la base de toda la informática. Los ordenadores trabajan en ese sistema y todo aquello que pasa por un soporte digital, como las imágenes, vídeos, telecomunicaciones…
[… faltan 2 páginas en el original]
…gran éxito, ya que la misión católica no había avanzado mucho en ese aspecto.
Leibniz publicó su obra principal sobre China pocos meses antes de morir, con el título Discours sur la idéologie nalurelle des chináis (Discurso sobre la teología natural de los chinos). En ella defendía que los antiguos chinos habían creado una religión natural que era compatible con el cristianismo. Mostró aquellos aspectos de la filosofía china antigua que eran compatibles con la suya propia. Y en la última parte exponía su sistema binario y su relación con el I Ching. También indicaba dos puntos importantes que hacían de China un pueblo civilizado a la altura de Europa: sus tres mil años de crónicas históricas, más tiempo que en Europa, y un avance importante en la filosofía práctica (educación, asuntos civiles, relaciones personales) y en las ciencias, solo superadas por la ciencia europea

§. El «I-Ching» y el sistema binario
El I-Ching, o Libro de las mutaciones, es un antiguo tratado chino que sirve para hacer predicciones. Se trata de una especie de oráculo que nos indica cosas que pasarán relacionadas con la familia y otros aspectos, aunque también es una obra que desarrolla la filosofía taoísta del ying y el yang. Inicialmente escrito por el emperador mítico Fu-Hsi alrededor de 2400 a.C., después se fue ampliando en épocas posteriores, por ejemplo, por Conflicto en el año 500 a.C.
Su interpretación se basa en una serie de símbolos, cada uno de los cuales tiene distintos significados dependiendo del aspecto que se estudie. Estos símbolos están formados por líneas continuas y discontinuas, agrupadas en trigramas, variaciones con repetición de esos dos elementos tomados de tres en tres. Los ocho trigramas posibles aparecen en la figura siguiente:

Si unimos entre sí dos trigramas de todos los modos posibles, obtenemos los 64 hexagramas posibles, formados per seis líneas. Aunque Bouvet pensó que era creación del propio Fu-Hsi, fue el filósofo chino Shao Yong (1011-1077) quien ordenó los hexagramas en una distribución que recuerda al sistema binario. En la figura siguiente podemos ver parte de esa posible relación. Aunque los chinos no conocían el cero, si consideramos que la línea partida es el cero y la continua el uno, podemos ver los primeros números binarios codificados:

De esa manera, se puede asociar un número en binario desde el 0 hasta el 63. Basta hacer corresponder al hexagrama el código binario y convertirlo en decimal. Por ejemplo, el hexagrama de la figura siguiente representaría el valor:

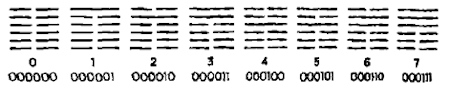
101001₍₂ = 1×2⁶ + 0×2⁴ + 1×2³ + 0×2² + 0×2¹, + 1×2⁰ =

= 32 + 8 + 1 = 41.

§. La notación matemática
Es normal que las cosas que hemos conocido desde pequeños las aceptemos como si siempre hubiesen estado ahí. Elementos como Internet, los teléfonos móviles, los ordenadores o incluso la televisión parece que son inventos que existen desde hace muchísimos años, aunque muchos hemos vivido las épocas en que no existían. Con los símbolos que utilizamos en la ciencia pasa lo mismo. Estamos acostumbrados a escribir y operar números y funciones con símbolos, que pensamos que se han utilizado siempre, cuando, por ejemplo, los números indo-arábigos que usamos como numeración principal se han utilizado durante menos tiempo que los números romanos.
En los siglos XVI y XVII, una de las dificultades para intercambiar resultados o para entender lo que habían desarrollado otros científicos era precisamente la inexistencia de una notación clara y unificada
Los símbolos + y - para las operaciones de sumar y restar no comenzaron a usarse hasta el siglo XV en Alemania. Incluso durante bastantes años hubo países, como España, donde se siguieron utilizando los símbolos p y m (iniciales de plus y minus). El uso del signo × para la multiplicación se asocia a Oughtred, el inventor de la regla de cálculo.
El uso de la barra para indicar la división se considera un invento árabe, y fue Fibonacci (ca 1170-ca 1250) quien la extendió por Europa. Como curiosidad, fue en el siglo XIX cuando el matemático inglés Augustus de Morgan (1806-1871) comenzó a utilizar la versión a/b por motivos de tipografía, ya que en los libros la expresión

ocupa tres líneas, mientras que la otra solo ocupa una.
Newton fue el primero que utilizó las potencias para representar fracciones y raíces. Así, utilizaban a^-1 para la expresión 1/a y a^3/5 para ⁵√3. El símbolo √ para las raíces, como deformación de la letra r, comenzó a utilizarse en el siglo XVI.
El inglés Robert Recorde (1510-1558) fue el primero en utilizar el símbolo =, pues decía que no había nada más igual que dos líneas paralelas, aunque tardó casi un siglo en ser aceptado como símbolo general. Descartes, por ejemplo, usaba el símbolo ∝ (el símbolo real es con la abertura a la izquierda). Los símbolos < y > para indicar menor y mayor no se usaron basta principios del XVII por el inglés Thomas Harriot (1560-1621).
Otro elemento importante para el cálculo fue el concepto de función. Se asigna al francés Nicolás de Oresme (1323-1382) una primitiva idea de función, que él definía así « Todo lo que varía, se sepa medir o no, lo podemos imaginar como una cantidad continua representada por un segmento ». Pero fue Descartes quien comenzó a manejar el concepto como una relación entre dos variables que, representada, daba lugar a una curva. Él fue también el primero que utilizó las primeras letras del alfabeto para indicar constantes y las últimas para indicar variables, como hacemos actualmente.
La primera idea clara de relación funcional se debe al escocés James Gregory, que indicaba que una variable dependía de varias expresiones si se podía obtener de ellas mediante cualquier operación imaginable.

§. La notación de Leibniz
Leibniz fue una persona muy cuidadosa con la notación elegida y dedicaba mucho tiempo a perfeccionarla. Fue el primero que usó el punto (∙) para indicar el producto, pues el símbolo × podía confundirse con la variable. También fue el primero en utilizar el símbolo: para la división, por una justificación visual igual a la que usó años más tarde Morgan. Sus palabras exactas fueron: a dividido por b es comúnmente denotado por

sin embargo, muy a menudo es deseable evitar esto y continuar en el mismo renglón, usando la interposición de dos puntos, de manera que a: b indique a dividido por b.
El suizo Johann Heinrich Rahn había usado unos cuantos años antes el símbolo (:) como notación para la división. Este símbolo fue adoptado por Inglaterra, y de esa manera se suele usar en los países anglosajones, mientras que en la mayoría de los otros países se usa la notación de Leibniz.
Él fue también la primera persona en utilizar la palabra función en sus escritos, aunque no era todavía el concepto que nosotros utilizamos. Fue Johann Bernoulli el primero que utilizó la palabra dando una definición concreta; « Una función de una variable es definida como una cantidad compuesta de alguna manera por una variable y constantes », entendiendo que esa «de alguna manera» puede ser tanto algebraica como trascendente. También fue el primero en utilizar las palabras constante, variable y parámetro.
Respecto a la notación del cálculo, Leibniz comenzó utilizando la abreviatura omn para el cálculo del área, es decir, la integral. Esa abreviatura había sido utilizada por Cavalieri y provenía del latín omnia lineas (todas las líneas) puesto que su área salía de sumar todas las líneas formadas por los Indivisibles. En un manuscrito de 1675, Leibniz decidió cambiar omn por el símbolo que solemos utilizar actualmente ∫. Sin embargo, el primero que utilizó la palabra integral fue Jakob Bernoulli en un artículo aparecido en Acta Eruditorum en 1690, el primero en que presentaba su cálculo.
Leibniz había estudiado que omn aumentaba su valor, ya que se sumaba, y su operación inversa, la derivada, debía disminuir. En cierta forma, las omn sumaban y la operación inversa restaba, por eso para esa segunda operación utilizó la d de diferencia. Inicialmente Leibniz escribía la d en el denominador.
Según Leibniz: «Esto se obtendrá por el cálculo contrario, esto es, supongamos que ∫l = ya. Sea l = ya/d, entonces justo como ∫ incrementa, así d disminuirá, las dimensiones».
Poco después ya colocaba la d en el numerador.
En el primer artículo sobre el cálculo de 1684 ya aparecía la d para indicar diferenciación, y en el segundo de 1686 ya aparecía el símbolo ∫ e incluso aparecía dx dentro de la integral.

§. Un nuevo duque
Desde que en 1676 pasó a ser consejero de la casa de Brunswick- Luneburgo en la corte de Hannover, Leibniz había dedicado muchos esfuerzos a servir a los duques respectivos en todo aquello que le encargaban, proponiendo muchas veces temas que consideraba que podían ser de interés. Tuvo libertad y respaldo para dedicarse a proyectos que había considerado interesantes. Además, la labor de atención a los encargos del duque le permitió dedicar tiempo a sus estudios y sus relaciones con científicos, técnicos, teólogos y filósofos de muchos países.
Muchos proyectos presentados al ducado fueron bien recibidos y apoyados personal y económicamente. Pero eso iba a cambiar radicalmente, planteándole muchos quebraderos de cabeza y sinsabores en los años que le quedaban de vida.
En junio de 1698 murió, después de una larga enfermedad, el duque Ernesto Augusto, el gobernante durante cuyo mandato el ducado de Brunswick-Luneburgo había pasado a convertirse en electorado. Lo sustituiría su hijo Jorge Luis, quien llegaría a ser el rey Jorge I de Gran Bretaña. Las relaciones con el nuevo duque no fueron nunca lo cordiales que habían sido con su padre y su tío, hasta el punto de que cuando Jorge se trasladó a Inglaterra, impidió que Leibniz viajara con él, obligándolo a permanecer en el continente.

Capítulo 4
No solo de matemáticas se nutre el genio

En el siglo XVII todavía existían "virtuosi", que desarrollaban grandes ideas tanto en la teoría como en la práctica abarcando inquietudes muy diversas. Un ejemplo claro fue Leibniz, un pionero de la geología y la paleontología, ciencias que estaban naciendo. Además, aportó todo su genio al campo de la mecánica, especialmente la dinámica, con el estudio de las fuerzas que influyen en el movimiento.

El 23 de junio de 1698 falleció el elector Ernesto Augusto, que fue sustituido por su hijo Jorge Luis. Leibniz fue refrendado en su puesto y aunque al principio nada pareció cambiar, las relaciones personales con el nuevo elector nunca fueron tan fluidas como con sus antecesores. Este nunca apoyó decididamente las múltiples actividades a que se dedicaba Leibniz.
Su trabajo principal siguió siendo la elaboración de la historia de la casa de Brunswick-Luneburgo, pero tras ocho años, aún no se veían resultados tangibles de su trabajo. Aunque Leibniz en todo momento informaba de los lugares que visitaba y de las acciones que llevaba a cabo, el elector siempre manifestó sus quejas sobre su trabajo. En una carta a su madre, Sofía, se quejaba de que nunca sabía dónde estaba Leibniz, que siempre hablaba de los invisibles libros en los que trabajaba.
En 1698 y 1700 editó y publicó dos volúmenes de crónicas históricas alemanas inéditas, con el título de Accesiones historicae. También publicó la primera recopilación de documentos de la biblioteca de Wolfenbüttel.
Desde 1698 recibió invitaciones de Sofía Carlota para visitar Berlín, pero no consiguió permiso hasta dos años después, cuando el propio elector de Brandeburgo lo reclamó para encargarle la dirección del proyecto de la nueva Academia Prusiana de las Ciencias.
En esa época, Leibniz ya tenía una edad avanzada y durante el resto de su vida tuvo problemas de salud. Eran frecuentes sus dolores de cabeza y fiebres. Los últimos años padeció gota y artritis. Muchas de esas enfermedades le impidieron viajar como hubiera querido, y le sirvieron de excusa, reales muchas veces, para no regresar inmediatamente a Hannover cuando lo requería el elector.
Durante su visita a Berlín, Leibniz intentó conseguir ayuda de Philippe Naudé (1654-1729), matemático de la corte, para seguir con el estudio del sistema binario. En esos años buscó varias veces la colaboración de algún matemático joven que le ayudara a terminar estudios que le resultaban muy laboriosos. Recibió unas tablas numéricas realizadas por Naudé en notación binaria, que incluían los números hasta el 1023, es decir, los que se pueden escribir con un máximo de diez cifras. Leibniz estudió por columnas las series de formación que tenían las cifras de esos números. Así, en la primera columna los números alternaban las cifras 01, en la segunda columna se repetían las series 0011, en las terceras 00001111 y así sucesivamente. También realizó estudios respecto a la variación en múltiplos. Con todo ese material escribió Ensayo de una nueva ciencia de los números, que envió a la Academia de Ciencias de París con motivo de su elección como miembro extranjero. Es curioso que en la carta adjunta a esa obra comentase que ese sistema no estaba pensado para cálculos prácticos.
En 1669, se había publicado el tercer volumen de Opera mathematica, la gran obra de John Wallis. En él se incluía la correspondencia entre Leibniz y Newton a través de Oldenburg, en concreto las epístolas prior y posterior. Aunque Leibniz había dejado la selección de cartas a Wallis, no quedó muy disgustado con el resultado. No le gustó nada el trabajo de Fatio de Duillier, en el que presentaba a Leibniz como el segundo inventor del cálculo. Mantuvo otra discusión con el matemático autodidacta Michel Rolle (1652-1719), que atacó el cálculo de Leibniz indicando que la noción de derivada era confusa, y rechazó la idea de infinitésimos de órdenes superiores. La respuesta en la academia la dio el matemático Pierre Varignon (1654-1722), quien llegó a afirmar que Rolle no tenía ni idea sobre el cálculo que estaba rechazando.

§. La discípula real de Leibniz
Leibniz guardó una gran amistad con la electora Sofía, esposa del elector Ernesto Augusto, y con su hija, la princesa Sofía Carlota, esposa del elector de Brandeburgo, quien se proclamó rey de Prusia en enero de 1701. Aunque Sofía Carlota siempre había visto a Leibniz como amigo de su madre, pronto comenzó a considerarlo como su propio amigo y maestro. En una carta de 1699 le decía que la podía considerar como discípula. A partir de 1700, cuando Leibniz la visitó por primera vez en su palacio de Lützenburgo (actual Charlottenburg), fue invitado con asiduidad a Berlín para charlar de multitud de temas con la reina. Frecuentemente se reunían para tratar temas filosóficos, religiosos y políticos. En los años siguientes le escribió en numerosas ocasiones, con contenido de temas filosóficos en su mayoría, pues era reacio a enviar temas matemáticos que eran complicados para alguien sin formación.
En 1704 conoció a la princesa Carolina de Ansbach, que se casaría con el hijo de Jorge Luis, Jorge Augusto, quien sustituiría a su padre, primero como elector de Hannover y posteriormente como rey de Inglaterra.
Por desgracia, la relación con su discípula no duró mucho, ya que el 1 de febrero de 1705 moría la reina Sofía Carlota.

§. La diplomacia que no cesa
Por petición del emperador Leopoldo I, se reunió en Viena con el obispo Von Buchaim para tratar el tema de la reunificación de las iglesias católica y protestante. También había tenido reuniones con el capellán de la corte de Brandeburgo, Jablonski, para intentar reunificar las sectas luterana y reformada, algo que parecía incluso más difícil que la reunificación con los católicos, Leibniz continuó con estas negociaciones diplomáticas hasta su muerte, ya que en 1716, su último año de vida, volvió a reunirse con Jablonski a petición del rey Federico Guillermo I de Prusia, para intentar la reunificación de ambas confesiones y entrar en negociaciones con la Iglesia anglicana, aprovechando que el elector de Brandeburgo se había convertido en rey de Inglaterra, y por tanto, en cabeza de la Iglesia anglicana, pero sin abandonar su religión, lo que le daba ciertas esperanzas de conseguir resultados favorables. Sin embargo, el desinterés del rey por el tema hizo que la misión no prosperase.
A principios de la década 1670, la labor diplomática más importante en la que estuvo inmerso fue apoyar las aspiraciones de la electora Sofía a la corona de Inglaterra. Ya en 1698 hizo llegar al rey inglés Guillermo III la propuesta de que se nombrara a Sofía con derecho a la línea sucesoria, así como el matrimonio del duque de Gloucester con la princesa de Hannover. Sofía, debido a su avanzada edad, no mostraba mucho entusiasmo por la sucesión, por lo que realmente fue Leibniz quien más se esforzó en las negociaciones. En 1701 el Parlamento inglés promulgó el Acta de Establecimiento, garantizando la corona inglesa a los descendientes protestantes de la casa de Hannover.
También medió entre las casas de Hannover y Brandeburgo, enfrentadas con Wolfenbüttel, que tenía una alianza de neutralidad con Francia y había creado un gran ejército. En ese tiempo se creó una gran alianza contra Francia, formada por Inglaterra y los Países Bajos, con el apoyo de Austria, Dinamarca, Prusia, Hannover y el Palatinado. En 1702 comenzó la guerra entre los aliados y Francia. Leibniz redactó un informe aconsejando aspectos que favoreciesen las condiciones militares y el desarrollo de la guerra; la coordinación entre estrategias y recursos, el cuidado médico de los soldados o la creación de dos cuarteles generales, uno imperial y el otro neerlandés, eran algunas de sus apreciaciones.
También abogó en favor de la sucesión austríaca en España, mediante uno de los recursos que más le gustaban: una carta, supuestamente escrita por un habitante de Ámsterdam en este caso, en respuesta a un ciudadano de Amberes. Ambas cartas fueron ampliamente difundidas.
En 1713 se reunió en Karlsbad con Pedro I de Rusia, tras aceptar una invitación del propio zar, y aprovechó para interceder por una alianza entre el zar y Austria que permitiera al emperador terminar con la guerra contra Francia. Ya el año anterior, en la boda de Alejandro y Carlota, Leibniz se había entrevistado con el zar, quien le había encargado el desarrollo de las ciencias en Rusia, otorgándole el título de consejero privado ruso de justicia, con un salario fijo anual, y encargándole además la elaboración de propuestas para reformar el derecho y la justicia en Rusia.

Pedro I de Rusia
Pedro I (1672-1725) fue el zar que reformó Rusia, transformándola en un país más cercano a las naciones europeas occidentales de la época. Subió al trono con diez años, pero intrigas palaciegas lo relegaron a un segundo plano, En 1694, dio un golpe de Estado y se coronó como zar de Rusia. A partir de ese momento, comenzó una reforma profunda de la nación en la línea que imperaba en el resto de Europa, que conocía bien gracias a sus múltiples viajes por Francia, Austria, Alemania, etc. Potenció el desarrollo industrial, especialmente en los sectores minero y metalúrgico. Realizó también grandes reformas económicas que le permitieron financiar una agresiva política exterior, apoyada por la creación de un alistamiento obligatorio en el ejército, que reorganizó. Modificó la vida cotidiana de sus súbditos, obligando a abandonar muchas de las costumbres ancestrales rusas. Se enfrentó a Suecia en la conocida como Guerra del Norte, conquistando grandes territorios del Báltico, lo que le valió el apelativo de El Grande, con el que pasó a la historia.

Los temas concretos que presentó al zar fueron el estudio de la declinación magnética a lo largo de toda Rusia y entablar relaciones con China para que la cultura y ciencia chinas llegaran a Europa.

§. La historia avanza
Tras la visita a Karlsbad se desplazó a Viena, sin notificarlo a Hannover, de donde recibía órdenes perentorias del elector para que regresase a la ciudad. Desde allí escribió una carta al primer ministro de Hannover, Andreas Gottlieb von Bernstorff, en la que informaba de que el emperador le había ofrecido acceso a su biblioteca particular, pues pensaba que una historia de la casa de Brunswick- Luneburgo no podía hacerse sin hacer una historia del Imperio.
A pesar de las continuas recriminaciones, el trabajo realizado por Leibniz empezó a dar sus frutos. En junio de 1707 apareció el primer volumen de Scriptorum bruresvicensia illustrantium, editado por el propio Leibniz. Tuvo que pagar a sus ayudantes, adelantar los costes de imprenta del segundo volumen y comprar una serie de ejemplares para ser distribuidos, gastos que recuperó con bastantes esfuerzos.
El segundo volumen salió en 1710, un año bastante prolífico para Leibniz, pues también publicó el primer número de Miscelánea Berolonensia, la revista de la Academia de Berlín, y una de sus principales obras filosóficas, la Teodicea. El año siguiente apareció el tercer volumen de la historia.
Leibniz había previsto que la historia se completara con otros dos volúmenes. A finales de 1714 tenía previsto terminar el primero, que llegaría hasta los comienzos de la casa actual, y el segundo volumen en breve después de este. Pero por desgracia, su muerte impidió que la historia se completara. No obstante, en 1749 su secretario Eckhart publicó cuatro volúmenes sobre el origen de los güelfos como introducción a la historia.
Una vez que el rey Jorge I estaba en su trono, Leibniz intentó ser nombrado historiógrafo de Inglaterra, pues aducía que en su estudio había tenido que investigar también aspectos de las casas inglesas. Pero no logró el puesto porque le quedaba poco más de un año de vida, y en ese momento el rey no confiaba en que pudiese terminar la historia de la casa de Brunswick-Luneburgo por las múltiples actividades que realizaba.
En 1703 había conseguido de la reina Sofía Carlota, la patente para la sedicultura en Prusia, a fin de financiar la Academia de Berlín, tema que siempre tuvo presente, pues en 1707 presentó un escrito al rey con nuevos métodos para drenar pantanos, de forma que parte de los beneficios repercutieran en la sociedad.
Leibniz aspiraba a muchos puestos vacantes. En 1704 solicitó ser vicecanciller de Hannover, pero el elector pensaba eliminar el puesto, igual que había desaparecido el de canciller cuatro años antes. También solicitó la alcaldía de Ilfeld, uno de los cargos que también desempeñaba el antiguo vicecanciller. En 1709, dadas las continuas tensiones con el elector, llegó incluso a proponer a su amigo el duque Antonio Ulrico que lo tomara a su servicio.
Cuando en 1711 se coronó al nuevo emperador Carlos VI, Leibniz movió todos los hilos a su alcance para obtener el cargo de consejero privado imperial, que finalmente logró al año siguiente, aunque con la desagradable sorpresa de que era un puesto honorífico sin remuneración. Sin embargo, más adelante consiguió una cuota anual, que en algunos momentos desaparecía y entonces debía volver a insistir de nuevo para recobrarla.

§. Las obras filosóficas
En el siglo XVIII Leibniz escribió sus obras más importantes, que reflejan la evolución de su filosofía desde sus primeros balbuceos juveniles. La primera referencia sería Teodicea: Ensayos sobre la bondad de Dios, la libertad del hombre y el origen del mal , obra publicada en dos volúmenes en 1710 como homenaje a Sofía Carlota, en la que recoge muchas de sus conversaciones con la reina en Charlottenburg e incluye referencias a las polémicas teológicas de la época. Su fundamento es que vivimos en el mejor de los mundos posibles, y que la maldad del mundo no está reñida con la bondad divina. Hoy día la teodicea es una rama filosófica, también llamada teología natural, que pretende la demostración racional de la existencia de Dios. La Teodicea fue caricaturizada por Voltaire, admirador de Newton, en su obra Cándido.
La Teodicea y el De combinatoria fueron las únicas obras filosóficas de Leibniz publicadas en vida del autor, las demás fueron póstumas. En 1686 escribió Discurso de metafísica, su primera gran obra filosófica, en la que recogía todas sus ideas hasta el momento sobre Dios, el mundo y el hombre, relacionados entre sí. Ahí aparecían ya sus ideas de sustancias simples y compuestas, que germinarían en las mónadas, especialmente rechazaba las leyes cartesianas de conservación del movimiento, al mismo tiempo que promovía su idea de fuerza viva, germen de la energía cinética. La obra no fue publicada hasta 1846.
En 1714, Leibniz escribió en Viena dos de sus trabajos: Principios de la naturaleza y de la gracia, fundados en la razón , publicado en 1718, y sobre todo la Monadología, obra de su etapa de madurez, en la que presentaba, de forma bastante esquemática, un resumen de toda su filosofía. Fue escrita para su amigo Nicolás Remond, quien años antes había animado a Leibniz a escribir sobre la teología natural china. Redactada en francés, no tenía título y el editor que la publicó por primera vez en 1720, por cierto en alemán, fue el que se lo puso.
En ambas obras presentó su idea de sustancias simple y compuesta. En el primer punto de la Monadología podemos leer:

La mónada de que hablaremos aquí no es otra cosa que una sustancia simple, que forma parte de los compuestos; simple, es decir, sin partes.

Y en el punto tercero la ejemplifica en la naturaleza:

Ahora bien, allí donde no hay partes tampoco hay extensión, ni figura, ni divisibilidad posibles. Y estas mónadas son los verdaderos átomos de la naturaleza y, en una palabra, los elementos de las cosas. {... j Cabe afirmar, por lo tanto, que las mónadas no pueden comenzar ni acabar más que de repente, esto es, no pueden comenzar, a no ser por creación, ni acabar, a no ser por aniquilación; lo que es compuesto, por el contrario, comienza o acaba por partes.

Presenta estas mónadas como una especie de puntos metafísicos sin forma ni tamaño. Por tanto; deben diferenciarse en alguna cualidad para dar lugar a formas diferentes al componerse. Además, no cambian por ningún agente externo, sino por causas internas, llama percepción al estado de relación de cada mónada con las demás, y al proceso interno que hace cambiar la percepción lo llama apetición o apetitos.
A partir de estos conceptos divide las mónadas en tres clases: mónadas que solo tienen percepción sin conciencia; mónadas en las que la percepción va acompañada de conciencia, que serían las que corresponderían a los animales, y aquellas que además incluyen el razonamiento, que es lo que llama alma razonable o espíritu, y que sería característico del ser humano.

§. La idea de átomo
Desde la prehistoria los hombres descubrieron, al trabajar los metales, que había elementos que se transformaban en otros. Tales de Mileto (ca. 620 aC.-ca 546 aC.) fue el primero que se planteó si cualquier sustancia podía convertirse en otra siguiendo una serie de pasos. Si ello era posible, tenía que existir un elemento básico que estuviera presente en todos los elementos. Consideró que ese elemento era el agua, de ahí que su máxima filosófica fuera «Todo es agua». Anaxímenes de Mileto (585 aC.-524 aC.) planteó que ese elemento era el aire y Heráclito de Éfeso (535 aC.-484 aC.) propuso el fuego. Empédocles (ca 495 aC.-ca 435 aC.), discípulo de Pitágoras, pensó que no debería ser un solo elemento y propuso los cuatro elementos básicos: agua, aire, fuego y tierra
Por su parte, Aristóteles (384 aC.-322 aC.) tomó estos resultados y añadió un quinto elemento, el éter. Los griegos no aceptaban el vacío, y por ello debía existir un elemento entre la tierra y el Cielo. La influencia de Aristóteles fue tal, que durante veinte años la concepción sobre la composición de la materia siguió sus pautas.
No obstante, entre los griegos se produjo un interesante debate sobre la divisibilidad de la materia. Unos defendían que la materia se podía dividir indefinidamente y cualquier elemento que se obtuviera, por pequeño que fuese, podía volverse a dividir, idea defendida por Aristóteles. Otra corriente indicaba que en la división se llegaría a una partícula minúscula que ya no podría ser dividida más; esta corriente recibió el nombre de atomismo y su principal valedor fue el tracio Demócrito (460 aC.- 370 aC.), que llamó átomos a esas partículas indivisibles e indicó que toda la materia está formada por átomos.

Robert Boyle
Boyle (1627-1691) fue un químico inglés que estudió las transformaciones que la presión provocaba en los gases. El fruto de dichas investigaciones fue una ley que indica que el volumen es inversamente proporcional a la presión, descubierta también de forma Independiente por el francés Edme Mariotte (1620-1684), por lo que hoy se conoce como ley de Boyle-Mariotte, estudiada en la enseñanza secundaria. En 1661 escribió El químico escéptico, obra por la que es considerado el padre de la química moderna. En ella defiende que la materia está formada por grupos de átomos en movimiento, y que las colisiones entre ellos son las que dan lugar a los fenómenos que observamos. Realizó investigaciones sobre la propagación del sonido, la densidad relativa, la refracción en cristales y descubrió la intervención del oxígeno en la combustión y la respiración

Sin embargo, la figura de Aristóteles fue tan inmensa que el atomismo fue casi desterrado del pensamiento griego; se mantuvo gracias a Epicuro (341 a.C.-270 aC.), cuya filosofía tuvo muchos seguidores. Otro personaje de relevancia, el poeta romano Lucrecio, del siglo I a-C., difundió el atomismo de forma didáctica en su poema De rerum natura (Sobre la naturaleza de las cosas).
Durante veinte siglos, las ideas de Aristóteles rigieron el pensamiento científico. La alquimia fue la disciplina que se dedicó al estudio de la transformación de unos elementos en otros, bien por la búsqueda de elementos concretos como el oro, o como aplicación en la medicina, como hicieron Avicena (981-1037) o Paracelso (1493-1541). Pero sucedió un hecho curioso. Uno de los primeros libros que se publicó tras la invención de la imprenta fue precisamente el poema de Lucrecio, por lo que el atomismo volvió a coger fuerza en toda Europa
La figura fundamental de esa época fue Robert Boyle, con quien Leibniz se reunió varias veces en Londres y con quien mantuvo correspondencia hasta su muerte. Esa línea de pensamiento fue, muy posiblemente, la que dio pie a la creación de las mónadas.

§. El interés por la formación de la tierra
El hombre siempre ha sentido curiosidad por saber cómo se habían formado los distintos elementos que constituyen la Tierra. Aunque ya en la Grecia antigua hubo personas interesadas en el estudio de estos elementos, se suele considerar que fueron los filósofos árabes los primeros en comenzar a investigar sobre el tema. Avicena, por ejemplo, explicó cómo se formaban las montañas y el origen de los terremotos. Pero en la Edad Media, el término geología todavía se utilizaba para indicar el estudio de todo lo terrenal en oposición a lo divino.
La geología moderna comenzó su andadura en el siglo m Abraham Ortelius (1527-1598) es el primero que aportó la hipótesis de la deriva continental, lo que daría pie a la tectónica de placas actual. Aunque sin duda la figura más importante en este campo fue Nicolás Steno, el padre de la geología moderna, pues fue el creador de las leyes por las que se rige la estratigrafía, la ciencia que estudia la superposición de capas o estratos de la Tierra.
Eli geólogo danés Konrad von Gesner (1515-1565) es considerado el fundador de la paleontología. Publicó una obra capital en dicha disciplina: De omni rerumfossillium genere, gemmis, lapidibus, metallis, et huiusmodi ..., en la que separaba los fósiles de forma orgánica de las gemas y minerales a través de ilustraciones. Robert Hooke utilizó el microscopio para comparar la estructura de las maderas fósiles con las actuales, y presentó sus resultados en la obra Micrographia , de 1665. También estudió los amonitas y los conectó con el nautilo actual, además de ser un precursor en la teoría de la evolución de las especies.
El físico jesuita Atanasio Kircher (1601-1680) planteó que la Tierra es un astro en evolución y mostró lo que en su opinión, errónea por cierto, es el Interior de la Tierra.

Nicolás Steno
Nacido en Copenhague. Steno (1638- 1686) fue un anatomista, y científico en general, que fundó las bases de la estratigrafía moderna, al defender que las capas de la corteza terrestre son producto de la sedimentación marina: cada capa es anterior a la que tiene encima y posterior a la inferior, en la que se apoya. También postuló que cada estrato se crea horizontalmente. y cuando están inclinados es porque son debidos a movimientos posteriores. A su vez, distinguió entre rocas primitivas, las anteriores a las plantas y animales, y rocas secundarias, que se sobreponen a las anteriores y contienen fósiles. Comparó fósiles de conchas marinas con especies vivas, y entre especies de agua dulce y marina. Todo ello está recogido en la que puede considerarse su obra maestra: De solido intra solídum naturaliter contento dissertationis prodromus ( Discurso preliminar de una disertación sobre los cuerpos sólidos de manera natural contentaos en un sólido , 1668), por la que es considerado el padre de la geología moderna. También elaboró algunas leyes sobre cristalografía y fue el descubridor de la glándula parótida.

Según él, los volcanes eran los respiradores de los fuegos internos. No obstante, su gran aportación fue hacer hincapié en la idea de la observación y el estudio de los movimientos de la Tierra.
Hasta ese momento, la creencia generalizada acerca de la aparición de fósiles, tan alejados del mar, era achacada al diluvio universal Fue el conde de Buffon (1707-1788) quien comenzó a criticar dicha teoría. Su teoría era que la erosión y la transformación geológicas eran debidas al agua y el fuego, y además dividió la evolución de la naturaleza en siete épocas, desde la creación del planeta hasta la aparición del hombre. Buffon reconoció en su Historia natural la contribución de Leibniz a la embrionaria geología.

§. El precursor geológico
Leibniz demostró siempre un gran interés por el estudio de la evolución de la Tierra y de las especies. En sus viajes siempre se interesaba por las colecciones de curiosidades, donde podía observar fósiles y restos minerales. Durante su estancia en Harz visitó cuevas en las que encontró huesos y dientes de animales prehistóricos. También recogió muchos ejemplares en sus viajes por Alemania e Italia.
En Hannover conoció a Steno, y también leyó a Kircher. Todos estos conocimientos desembocaron en la elaboración de su obra principal sobre el tema: Protogaea, escrita en 1691 y publicada en 1749; no obstante, en 1693 salió una referencia en Acta Eruditorum. También incluyó un resumen sobre su teoría de la evolución de la Tierra en Teodicea. Su idea era que el estudio histórico que estaba llevando a cabo debería comenzar con una exposición geográfica y geológica. En la obra hablaba de una nueva ciencia, que él llama geografía natural, y que correspondería a nuestra actual geología.
Protogea es la primera obra que engloba buena parte de los grandes temas geológicos: el origen del planeta Tierra, la formación del relieve, las causas de las mareas, de los estratos y de los minerales, y el origen orgánico de los fósiles. Leibniz admite el origen ígneo del planeta y la existencia de un fuego central, tal como defendía Descartes. Pero a diferencia de este, que indicaba que el fuego era el causante de las transformaciones terrestres, Leibniz también consideraba el agua como agente geológico.
En su opinión, las montañas eran debidas a erupciones anteriores al diluvio, provocado no solamente por las lluvias, sino por la irrupción de aguas del subsuelo. Hablaba además del agua y el viento como moldeadores del relieve y distinguía entre rocas ígneas y sedimentarias.
Fue también uno de los pioneros de la teoría de la evolución, al considerar que el hecho de que los animales existentes no fueran iguales a los fósiles encontrados era debido a que las especies se habían transformado por las constantes revoluciones geológicas.

§. El estudio del movimiento
Posiblemente la ciencia que más avanzó durante los siglos XVI y XVII fue la mecánica, el estudio de los movimientos en sus múltiples aspectos. En esa época se planteó un estudio matemático serio de dichos fenómenos, a raíz del cual se creó la formulación fundamental para desarrollar la mecánica, que afecta a todos los ámbitos de la naturaleza.
Dentro de esta ciencia existen dos grandes ramas: la cinemática , que trata del estudio del movimiento sin tener en cuenta las fuerzas que actúan en el proceso, y la dinámica, que se fundamenta en las causas que producen ese movimiento. Todos los grandes científicos de la época realizaron sus aportaciones a la mecánica, especialmente a su segunda rama.
En el siglo VI, un seguidor de Aristóteles, de nombre Filopón, acuñó el término ímpetus para señalar las fuerzas impresas en los cuerpos, las causantes del movimiento. En la Edad Media, los escolásticos defendían que el movimiento es causa de una fuerza, y que se mantiene mientras esta actúa, extinguiéndose cuando cesa. En la física moderna, por el contrario, se considera que el movimiento se conserva sin necesidad de una fuerza constante que actúe sobre el móvil.
Aunque muchos autores pensaban que ese ímpetus se conservaba indefinidamente si no encontraba resistencia, Nicolás de Oresme (ca, 1323-1382] creía que era una fuerza que se agotaba espontáneamente. Esta idea le permitía explicar los movimientos de los péndulos, resortes o cuerdas vibrantes. Por su parte, el escolástico francés Jean Buridan (1300-1368) aplicó el ímpetus para estudiar la caída de los cuerpos y el desplazamiento de proyectiles. Según decía:
Cuando un motor mueve un cuerpo móvil imprime un cierto ímpetus o fuerza motriz que actúa en la dirección hacia la que el motor movía el móvil, sea arriba o abajo, lateralmente o en círculo.
Pero quien realmente estableció las bases de la dinámica moderna fue Galileo Galilei. Estudió también la caída de cuerpos y el movimiento de proyectiles. Al principio aceptaba, como se hacía desde Aristóteles, que cuando un cuerpo cae va aumentando su velocidad hasta que llega un momento en que alcanza una velocidad constante de caída. Más tarde sus experimentos le llevaron a describir el movimiento uniformemente acelerado. Dado que era muy complicado estudiar un cuerpo en caída libre, lo que hizo fue experimentar con bolas que caían por planos inclinados.
Las leyes que rigen un movimiento con aceleración constante son bastante conocidas en la actualidad. Si consideramos que s representa la distancia recorrida, t el tiempo, v₀ la velocidad inicial, v la final y a la aceleración, las fórmulas fundamentales son:

No obstante, quien calculó el valor de la constante de la gravedad para las caídas fue Huygens, que lo situó en g = 9,81 m/s ².
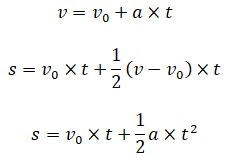
Galileo planteó las siguientes leyes del movimiento:

Cualquier cuerpo en movimiento sobre un plano horizontal sin rozamientos continuará moviéndose indefinidamente con la misma velocidad (ley de inercia),
En caída libre en el vacío, todos los objetos [independientemente de su masa] caen una distancia determinada en el mismo tiempo.
El movimiento de un objeto en caída libre, o rodando sobre un plano inclinado, es uniformemente acelerado, es decir, se obtienen incrementos iguales de velocidad en tiempos iguales.

La segunda ley chocaba con la intuición, así que para confirmarla realizó, supuestamente, el famoso experimento en la Torre de Pisa, que consistía en dejar caer dos objetos de diferente masa para averiguar si llegaban a la vez al suelo. Si bien es verdad que la fuerza de gravedad actúa más en el cuerpo con más masa, como esa fuerza es igual al producto de la masa del cuerpo por la aceleración, esta última es constante en el caso de ambos cuerpos.

Izquierda: Retrato de Leibniz obra de Johann Friedrich Wentzel, pintado en torno 1700, actualmente en el Archiv der Berlin Branderburgischen Akademia der Wisenschafen. Derecha: Tumba de Leibniz en la Neustädte Kirche, iglesia luterana de Hannover. La sencillez del sepulcro que contiene los restos de uno de los científicos más brillantes de su tiempo, además de haber sido hombre de estado, contrasta con el boato de la tumba del otro gran genio de la época, Isaac Newton, enterrado en la abadía de Westminster, junto a otros grandes genios ingleses de todas las épocas. Otro tanto puede decirse de sus entierros: mientras el del inglés fue tan multitudinario como el de un rey, al de Leibniz solo asistieron su secretarlo y los familiares más cercanos.

La obra principal de Galileo fue Discursos y demostraciones matemáticas relativas a des nuevas ciencias pertenecientes a la mecánica y a¡ movimiento local. escrita mientras permanecía recluido por su disputa con la Inquisición y que tuvo que ser publicada en los Países Bajos en 1638. La obra se presenta como una charla entre tres personajes; Salviati, que representa el punto de vista galileano, Simplicio, que defiende el punto de vista aristotélico, y Sagrado, un sujeto independiente y de mentalidad abierta, con ganas de aprender. Fue ampliamente difundida por Mersenne. Planteaba que si un cuerpo se desplaza por un plano horizontal, su movimiento uniforme se extiende indefinidamente, pero si el plano se acaba, sobre el cuerpo se aplica la fuerza de la gravedad, que le obliga a ir hacia abajo. De esa forma nacía el movimiento compuesto, que aplicó a los proyectiles: presentan los dos movimientos, el horizontal de avance y el vertical de atracción. También incluyó los dos movimientos más simples, el uniforme sin fuerza y el uniformemente acelerado, en el que el peso actúa como una aceleración constante.
Su discípulo Torricelli, el iniciador de la hidrodinámica, desarrolló la dinámica de los Discursos. Demostró la igualdad de las velocidades a lo largo de diferentes planos inclinados, que partían todos de la misma altura. Otro de sus seguidores, Pierre Gassendi (1592-1665), realizó un experimento que consistía en lanzar una piedra desde lo alto del mástil de un barco en movimiento. Según la intuición, la piedra debería caer alejada del mástil, pues el barco estaba en movimiento, pero comprobó que caía al mismo pie, con lo que demostraba que el movimiento es relativo y depende del sistema en que nos encontramos. Esto venía a solucionar la polémica de por qué los pájaros no se quedaban rezagados si la Tierra estaba en movimiento.
Descartes también estudió el movimiento, que definía así:

«El movimiento no es otra cosa que la acción, por la cual un cuerpo pasa de un lugar a otro».

Para él el movimiento era relativo y debía ser definido en su relación entre cuerpos:

El movimiento es la traslación de una parte de la materia, o de un cuerpo, de la vecindad de los cuerpos que lo tocan inmediatamente, y que consideramos como un reposo, a la vecindad de otros.

Estudió también las fuerzas que se utilizan para elevar cuerpos en el espacio, indicando que:

La fuerza que puede levantar un peso de 100 libras a la altura de 2 pies, puede también levantar uno de 200 a la altura de 1 pie. |...| Esa fuerza tiene siempre dos dimensiones, es decir, el producto de un peso por la altura.

Si en vez de peso hablamos de masa, esa fuerza definida corresponde a lo que entendemos hoy por energía potencial de un cuerpo.
Debido al rechazo absoluto del vacío, Descartes defendía que el espacio estaba lleno de porciones de materia, que interactuaban al chocar, por lo que no aceptaba la fuerza o acción a distancia. Para explicar la gravedad, por ejemplo, hablaba de la propagación de impulsos a través de una materia etérea que llenaba el espacio. Las leyes del movimiento de Descartes eran:

Un cuerpo no cambia de movimiento (o reposo) sino por choque con otro cuerpo.
Cada parte de la materia tiende a moverse en línea recta, salvo choque con otros cuerpos.
Cuando un cuerpo choca con otro, no puede transmitirle movimiento a menos que pierda otro tanto del suyo, ni puede privarle de él a menos que aumente el suyo en la misma proporción.

Complementaba la última ley con una serie de reglas, donde estudiaba los distintos tipos de choque. Pero como no indicaba si eran elásticos o inelásticos y no consideraba las direcciones, la mayoría no son ciertas.
Lo que definía como cantidad de movimiento, el producto de la masa por la velocidad, era un número y defendía que se conservaba. Algo erróneo si no se considera la dirección de la velocidad.
Con la intención de aclarar la confusión entre choques, en 1668 la Royal Society invitó a sus socios a estudiar los problemas derivados de estas situaciones, llegándose a la conclusión de que en los choques, la cantidad de movimiento solo se conserva si se atiende a la dirección y el sentido de las velocidades, es decir, se trabaja con su carácter vectorial, no como un escalar.

Vista de la Universidad de Hannover, que a partir de 2006 pasó a llamarse Universidad Gottfried Wilhelm Leibniz.

A esa invitación respondieron John Wallis, con el estudio de los choques inelásticos; Christopher Wren, con el del choque elástico, aunque sin basarlo en una verdadera demostración, y por último Huygens, que trató el choque elástico a partir del principio de inercia, de un principio de relatividad y del postulado de que dos cuerpos iguales con velocidades iguales que chocan directamente rebotan con la misma velocidad. Su estudio sobre los choques entre cuerpos desiguales apareció póstumamente en 1700.
Huygens descubrió las leyes de la fuerza centrípeta, aquella que retiene a un cuerpo que se mueve girando alrededor de un centro. Demostró que en un movimiento circular, la fuerza centrípeta es a la total (m×a) como el perímetro (la longitud 2πr) es al radio, de donde obtenía F_c = 2πr×m×v/t y, y como

sustituyendo, llegamos a la fórmula que dio Huygens:

De la expresión anterior y de la tercera ley de Kepler, según la cual la es inversamente proporcional al r³, Newton dedujo en su ley de gravitación universal que la fuerza de atracción de dos masas era inversamente proporcional al cuadrado de la distancia:

donde G es la constante de gravitación universal.
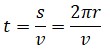
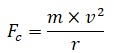
«La fuerza ejercida entre dos cuerpos de masas m₁ y m ₂, separados una distancia d es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia.»
Newton, ley de gravitación universal.
Newton, aparte de revolucionar el mundo gravitatorio, también estudió los choques sin elasticidad y defendió la necesidad de fuerzas externas para crear o destruir movimiento, cambiando la dirección o la rapidez. El matemático inglés consideraba tres fuerzas distintas:

Vis insita o inerte: Es un poder de resistencia de todos los cuerpos, en cuya virtud persevera cuanto está en ellos por mantenerse en su estado actual, ya sea de reposo o movimiento uniforme en línea recta.
Vis impresa: Es una arción ejercida sobre el cuerpo para cambiar su estado.
Vis centrípeta: Es aquella por la cual los cuerpos son arrastrados o impelidos, o tienden de cualquier modo hacia un punto como hacia un centro.

Pone como ejemplos de esta última la gravedad o la fuerza que atrae al hierro hacia el imán. Es la que hace que los planetas giren alrededor del Sol en lugar de seguir en línea recta. Esta fuerza centrípeta, que nombró Newton en honor a Huygens, crea movimiento y actividad en el cosmos, y la considera como una reacción a la fuerza centrífuga.
Por su parte, Newton también planteó tres leyes del movimiento:

Todo cuerpo persevera en su estado de reposo o movimiento uniforme rectilíneo salvo que fuerzas impresas tiendan a cambiar su estado.
El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la que se imprime dicha fuerza.
Con toda acción ocurre siempre una reacción igual y contraria; o sea, las acciones mutuas de los cuerpos siempre son iguales y dirigidas hacia partes contrarías.

§. El dinámico Leibniz
En 1669 Leibniz estudió los trabajos de Wallis, Wren y Huygens sobre choques. Luego publicó su primera obra sobre el movimiento; Nuevas hipótesis físicas (1671), en la que trataba el problema del continuo, pues defendía, como los escolásticos, que la naturaleza no avanzaba mediante saltos. Tomaba el término conatus en el sentido de Hobbes, como una tendencia innata a continuar el movimiento en línea recta. Por eso, un cuerpo que abandona un recorrido circular lo hace a través de su tangente.
A finales de la década de los ochenta escribió Dinámica. Sobre la fuerza y las leyes de los cuerpos naturales.
En la obra atacaba a Descartes planteando que no es la cantidad de movimiento lo que se conserva en el universo. Para ello ponía un ejemplo (ver figura), que también incluyó en su Discurso de metafísica.

Leibniz propuso que se necesita la misma fuerza para un cuerpo de una libra (A) a cuatro pies de altura que un cuerpo de cuatro libras (a) a un pie de altura.

Descartes decía que se debía utilizar la misma fuerza para subir un cuerpo de 1 libra de peso a una altura de 4 pies que una masa de 4 a una altura de 1. Por tanto, los cuerpos A y a deberían tener la misma fuerza al caer. Aplicaba la ley de Galileo según la cual la velocidad es proporcional a la raíz cuadrada de la altura de caída. Según esto, al final de la caída, la velocidad de A será el doble que la de a y por tanto la cantidad de movimiento de A será la mitad que la de a, lo que contradecía el postulado de Descartes.

«Es una de mis más importantes y mejor verificadas máximas el que la naturaleza no realiza saltos. A esto lo he denominado la ley de la continuidad.»
Leibniz, sobre la ley de la continuidad del movimiento.

Leibniz defendía que lo que se conservaba era el producto de la masa por la velocidad al cuadrado (mv²), lo que él llama vis viva. Esta fuerza viva es el doble de lo que hoy conocemos por energía, cinética, algo que ya había defendido Huygens. Más adelante, en 1840, se plantearía la ley de conservación de la energía tal como hoy la consideramos, en la que se verifica que la suma de las energías potencial y cinética de un cuerpo es una constante. En la Dinámica planteaba sus dos leyes principales, la de la conservación de la filena viva y la de la continuidad del movimiento.
En 1692 escribió Ensayo de dinámica, en el que recogía y organizaba todas sus ideas sobre dinámica. En él habla de la diferencia entre fuerza estática o muerta, y fuerza cinética o viva Pone como ejemplo de la primera la tendencia centrífuga y la gravedad, manteniendo que en los choques la fuerza es viva, y surge de una infinidad de impresiones de la fuerza estática La obra no se publicó hasta 1860, pero Leibniz presentó varios resúmenes en forma de artículos en Acta Eruditorum.
Leibniz consideró por tanto la fuerza en un doble sentido. Por un lado, una fuerza pasiva o materia prima, que residía en la masa y que nunca aparecía aislada en la naturaleza Y por otro, una segunda fuerza viva o activa, que era la que daba el movimiento.
Esta segunda fuerza se dividía a su vez en dos: una fuerza primitiva, que existía en cada cuerpo en sí mismo, y una fuerza derivativa, que se consigue por el choque entre cuerpos, y que según él era la única que interviene en el movimiento.

§. Se acerca el final
Los tres últimos años de la vida de Leibniz fueron bastante duros. En marzo de 1714 murió su gran amigo el duque Antonio Ulrico, que durante muchos años lo había respaldado ante el emperador y defendido frente al elector. En junio del mismo año perdió a su gran amiga y valedora, la electora viuda Sofía de Hannover. Ya solo le quedaba la princesa Carolina, con quien solía charlar igual que lo había hecho antes con las dos electoras.
Cuando un par de meses después de Sofía murió Ana, la reina de Inglaterra, el elector Jorge Luis pasó a convertirse en el rey Jorge I de Gran Bretaña, por lo que se trasladó con su corte, incluido su hijo Jorge Augusto, el nuevo príncipe de Gales, a Inglaterra Leibniz, que se encontraba en Viena desde hacía meses sin poder viajar debido a problemas de salud, hizo el esfuerzo de trasladarse a Hannover para despedirse del elector, pero llegó cuando ya había partido hacia las islas.
Aunque intentó viajar a Inglaterra junto a la princesa Carolina el mes siguiente, tuvo que desistir por problemas de salud. Más tarde recibió cartas del ministro Bernstorff instándole a no viajar a Inglaterra y a que se centrara en la interminable historia. A principios de 1715 el propio rey le envió una orden para que no hiciera ningún viaje largo hasta terminar el trabajo histórico.
De esta manera, Leibniz pasó los últimos años de su vida sin ninguno de sus grandes amigos, con su movilidad cada vez más menguada, y viendo que el tiempo pasaba sin poder terminar su ingente labor.
También comenzó una discusión con el capellán del rey, Samuel Clarke, amigo de Newton, quien ya había tenido un encontronazo dialéctico con la princesa Carolina sobre la filosofía de Leibniz. En las cinco cartas que envió a Clarke, Leibniz atacaba la filosofía de Newton, indicando que sus errores principales eran, primero considerar que Dios necesitaba un órgano sensorial para percibir las cosas, pues en ese caso, los objetos percibidos no dependían totalmente de Dios y este no podía haberlos creado. En segundo lugar, defendía que en el mundo había siempre la misma cantidad de fuerza o vis viva, que pasaba de unas partes a otras según las leyes de la naturaleza, y que no necesitaba que Dios, como defendían los newtonianos, actuara de vez en cuando para hacer que todo marchara bien. La última carta que le envió Clarke le llegó pocos días antes de su muerte, por lo que fue la disputa con la que se despidió de este mundo.
En julio de 1716 el rey Jorge visitó Hannover y pasó unos días descansando en Bad Pyrmont. Leibniz lo acompañó en todo momento, y al parecer había desaparecido la tensión anterior entre ellos.
Sin embargo, la reconciliación le sirvió de poco, ya que el 14 de noviembre Leibniz murió en su casa, dejando como único heredero a su sobrino Friedrich Simón Löffler. Ya a principios de ese mes la gota le había afectado las manos, lo que le impidió seguir escribiendo y los médicos no pudieron hacer nada por él.
Según nos cuenta Johann Georg von Eckhart, secretario de Leibniz y el primero de sus biógrafos, a su funeral solo asistieron los amigos y familiares más cercanos. Aunque se había avisado a la corte, no apareció ningún representante, pese a encontrarse bastante cerca, lo que puede deberse a la idea bastante extendida de que Leibniz no era creyente. Su entierro fue el de una persona insignificante, y sus contemporáneos de Hannover no lo tuvieron en mucha consideración, ya que solo a finales del siglo se colocó en su memoria un busto en mármol blanco con la inscripción «Genio Leibnitii ». Las academias y sociedades a que perteneció no realizaron ningún acto en su honor, aunque aparecieron necrológicas en muchas de las revistas científicas de las que fue colaborador.
Hasta medio siglo después de su muerte no comenzó a revalorizarse su figura, en particular cuando se comenzaron a publicar algunos de sus ensayos y su correspondencia con grandes personalidades, y a que Kant estudió a fondo su filosofía.
En la actualidad su fama es mucho mayor que en vida, de lo que da fe la asignación del nombre de Leibniz a un cráter de la Luna en 1970, que en 1985 se creara en Alemania el premio Leibniz, considerado como uno de los principales para las contribuciones científicas, o que en 2006 la Universidad de Hannover pasara a denominarse Universidad Gottfried Wilhelm Leibniz.

Lecturas recomendadas

Aiton, E. J., Leibniz. Una biografía, Madrid, Alianza, 1992.
Bell, E. T., Los grandes matemáticos, Buenos Aires, Losada, 2010,
Boyer, C. B., Historia de la matemática, Madrid, Alianza, 1986.
Chica, A., Descartes. Geometría y método, Madrid, Nivola, 2001.
Duran, A. J., Historia, con personajes, de los conceptos del cálculo, Madrid, Alianza, 1996.
González Urbaneja, P.M., Las raíces del cálculo infinitesimal en el siglo XVII, Madrid, Alianza, 1992.
Holton, G., Introducción a los conceptos y teorías de las ciencias físicas , Barcelona, Reverté, 1988.
Muñoz, J., Newton. El umbral de la ciencia moderna, Madrid, Nivola, 1999.
Newman, J. R., Sigma. El mundo de las matemáticas, Barcelona, Grijalbo, 1968.
Stewart, I, Historia de las matemáticas, Barcelona, Critica, 2008,
Taton, R, Historia general de las ciencias, Barcelona, Orbis, 1988.
Torra, V., Del ábaco a la revolución digital Algoritmos y computación , Barcelona, RBA, 2011.
Torrija, R., Arquímedes. Alrededor del círculo, Madrid, Nivola, 1999.