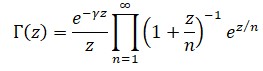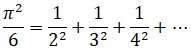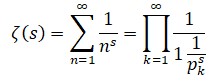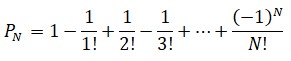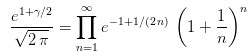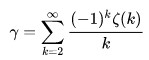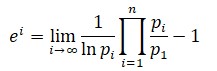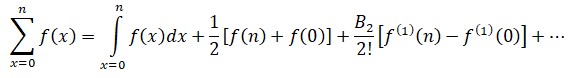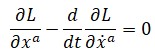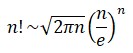Leonhard Euler - Joaquin Navarro Sandalinas

Euler

Joaquin Navarro Sandalinas

Introducción

En 2007 se conmemoró a nivel mundial el tricentenario del nacimiento de un suizo universal: el matemático, físico e ingeniero Leonhard Euler. Organismos y particulares procedentes de casi todos los rincones del mundo científico impulsaron actos conmemorativos —congresos, simposios, publicaciones— destinados a poner de relieve la importancia de la aportación intelectual de Euler. Sus impulsores no dudaron en situarlo a la altura de la de auténticos gigantes de la ciencia como Newton o Einstein en amplitud y consecuencias.
Aunque este tipo de comparaciones son siempre odiosas, no es exagerado afirmar que la obra de Euler es, en su conjunto, de un valor solo superado por un pequeñísimo número de científicos en toda la historia. Aunque su nombre está por siempre asociado al análisis —la rama de las matemáticas que estudia los «flujos», es decir, los fenómenos continuos, y que abarca las series, los limites y el cálculo diferencial—, realizó aportaciones fundamentales en geometría y teoría de números; creó de la nada una nueva área de investigación, la teoría de grafos; publicó infinidad de estudios fundamentales sobre temas tan diversos como la hidrodinámica, la mecánica, la astronomía, la óptica, la ingeniería naval o la tecnología de los ejes y los engrandes; escribió obras de divulgación científica y dedicó atención a juegos y pasatiempos matemáticos. En el curso de todo ello encontró tiempo para renovar buena parte de la notación matemática de la época y aproximarla a la forma con que hoy día la emplea la comunidad científica
Si de esta enumeración se desprende una sensación de acumulación un tanto caótica el culpable no es otro que el propio Euler. Aunque publicó no menos de una docena de libros, entre los cuales algunos de los más importantes de la historia de las matemáticas —sobre todo, su inigualada trilogía de textos sobre análisis Introductio in analysins infinitorum (Introducción al análisis del infinito), Institutiones calcuii differentialis (Fundamentos de cálculo diferencial) e Institutiones calcuii integralis (Fundamentos de cálculo integral)—, buena parte de su obra apareció de forma aislada, en artículos, sin que sea posible hallar en ella continuidad alguna de intereses a través de las diferentes épocas de su vida. Tan pronto abordaba un problema candente en teoría de números —el problema de Basilea, cuya resolución en 1735 le otorgó la fama— como se «descolgaba» con una fórmula que relaciona de forma inesperada las caras, los vértices y las aristas de un poliedro, uno de los resultados en geometría más profundos de todos los tiempos. Euler creó de forma compulsiva, acorde con las exigencias particulares de una mente excepcional y única.
A la extraordinaria multiplicidad de intereses de Euler hay que sumar un segundo factor que dificulta aún más la labor de hacerse una idea cabal de la obra del matemático suizo: su no menos extraordinaria abundancia productiva En efecto, Euler fue uno de los matemáticos más prolíficos, sino el que más, de toda la historia Sus escritos están parcialmente clasificados por Gustaf Eneström, y se identifican, como si fueran de un músico famoso, por su número de opus. Mozart tiene su número K. (de Köchel) y Euler, su número E. (de Eneström); los números E. se detienen en el 866. Esta labor dista de estar completada; todo y con eso, la edición de sus obras completas (Opera omnia), en curso de publicación desde 1911, se prevé que ocupe unos 90 volúmenes de aproximadamente 450 páginas. Euler mismo decía que su lápiz se le desbocaba y escribía más rápido que él. Solo la correspondencia de Euler encontrada hasta el momento asciende a casi 3000 cartas. Sus artículos y libros representan, más o menos, un tercio del total de las matemáticas, física e ingeniería mecánica escritas entre 1726 y 1800. Esta fecundidad resulta tanto más sorprendente si se tiene en cuenta que Euler fue tuerto durante más de 36 años (como atestigua su retrato más célebre, de 1753), y ciego de ambos ojos durante los siguientes 22.
Si hay que juzgar por las circunstancias que rodearon su entorno, Euler vivió en la época apropiada. El siglo XVIII ha sido denominado «de las luces», pues en dicho período buena parte del mundo occidental evolucionó hacia las formas propias del mundo moderno y se liberó de las «tinieblas» del pasado. Este proceso se ha atribuido en gran parte al avance progresivo e imparable de la razón ilustrada. En el ámbito específico de la ciencia, este avance se benefició de dos innovaciones destacadas: las academias nacionales de ciencias y las revistas científicas. La trayectoria profesional de Euier estuvo siempre al amparo de las primeras, instituciones nacidas en su mayor parte durante el siglo XVII, pero que alcanzaron la mayoría de edad en el siguiente gracias al apoyo de monarcas ilustrados, ansiosos por prestigiar sus países mediante el mecenazgo de la ciencia y el conocimiento en general.
La otra circunstancia que modeló irreversiblemente el modo de hacer ciencia fue la aparición de las publicaciones científicas periódicas. Con la excepción de los libros, muchos de los cuales tenían que ser financiados por sus propios autores, los descubrimientos científicos se habían venido difundiendo hasta entonces por procedimientos lentos e inseguros como las cartas o los viajes. La aparición sucesiva de revistas como Philosophical Transactions, Comptes rendus, Mémoires de l‘Académie o Journal de Crelle fueron poniendo al alcance de todos lo que antes solo era accesible a unos pocos. Euler, en particular, hizo uso amplísimo de este medio.
En la vida de Euler pueden distinguirse cuatro grandes períodos: el primero o de formación, hasta 1727; los catorce años transcurridos en San Petersburgo en el seno de la Academia de Ciencias fundada por Pedro el Grande; su época en la Academia de Ciencias en Berlín, hasta 1766; y el retorno a Rusia, donde falleció, La primera etapa, marcada por su encuentro con los hermanos Bernoulli, quienes despertaron su interés por el análisis, concluye con uno de los hallazgos más importantes de Euler, la fórmula que lleva su nombre, y que relaciona, apoyándose en la constante matemática e, los números complejos (i) y las funciones trigonométricas seno y coseno:

e^xi = cos x + i sen x.

El número e, base de los denominados logaritmos naturales, iba a tener numerosas apariciones en la obra de Euler, hasta el punto de que en ocasiones se denomina «número de Euler». Sobre la base de esta fórmula Euler desarrollará, décadas más tarde, buena parte de su trabajo en análisis.
La primera etapa en Rusia tal vez sea la más fecunda de la trayectoria científica de Euler. Como es de esperar en el marco de una obra tan prolífica, la cantidad de hallazgos que se condensan en este período son tan numerosos como extraordinarios. Solo en el campo del análisis incluyen el cálculo preciso del número e, así como la determinación de muchas de sus propiedades; el descubrimiento de la función gamma (Γ), que permite interpolar valores de un determinado tipo de funciones y que se encuentra presente tanto en combinatoria, probabilidad y teoría de números como en física; la fórmula de Euler-Maclaurin para el cálculo de sumas e integrales; y la solución (y posterior generalización de los resultados) del problema de Basilea que se interroga por la suma de la serie:

Corresponden también a esta época importantes trabajos en teoría de números tales como el establecimiento de la constante de Euler-Mascheroni o el estudio de los llamados números de Fermat, así como la solución, en 1736, del problema de los puentes de Königsberg, el hallazgo que daría pie a la creación de una rama totalmente nueva de las matemáticas, la teoría de grafos.
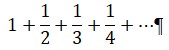
En 1741 Euler aceptó el ofrecimiento de Federico II el Grande, rey de Prusia, y se instaló en Berlín. El ritmo de sus aportaciones continuó imparable, y entre ellas se cuentan la fórmula de los poliedros, que relaciona las caras (C), aristas (A) y vértices (V) de un poliedro de una forma tan sencilla como absolutamente inesperada por los geómetras de la época:

C - A + V = 2;

así como, también en el campo de la geometría, la determinación de la recta de Euler. Son, asimismo, de esta época sus trabajos acerca de la conjetura de Goldbach, la más célebre de la teoría de números tras el teorema de Fermat o sus aportaciones al cálculo de variaciones, de fundamental importancia en física. En lo que respecta al análisis, fue en Berlín donde redactó los tratados que se mencionaban al principio de esta introducción, acaso la cumbre de su genio. Y todo ello sin contar su producción en ingeniería y mecánica.
La cuarta y última etapa de su vida tuvo como escenario, nuevamente, San Petersburgo. A pesar de haber superarlo la cincuentena y con los graves problemas de visión anteriormente mencionados, Euler prosiguió con el flujo constante de artículos hasta prácticamente el día de su muerte. Convertido ya en una leyenda en vida entre la comunidad matemática, sus trabajos de esta época se centraron sobre todo en la teoría de números y, en particular, los números primos (y otros conceptos asociados como los números de Mersenne o los números amigos), las ecuaciones diofánticas y las particiones. También tuvo tiempo para cuestiones más ligeras, como los cuadrados mágicos y otros temas de recreación matemática; para idear un juguete infantil (el disco de Euler) que ha llegado hasta nuestros días y para redactar una deliciosa obra divulgativa sobre cuestiones de mecánica y astronomía que dedicó a la princesa de Anhalt-Dessau, un clásico en su género

Cronología

1707	El 15 de abril nace Euler en Basilea, Suiza.
1720	Tutelado por Johann Bernoulli, ingresa en la universidad de Basilea con solo trece años.
1723	Recibe el título de Magister filosofía con un estudio comparativo entre las ideas de Descartes y Newton
1727	Emigra a Rusia al no conseguir una plaza como profesor de física en la universidad, de Basilea.
1731	Es nombrado profesor de Física en la Academia de ciencias de San Petersburgo. Su ascensión en la jerarquía de la Academia le convierte en una figura respetable entre los científicos.
1734	Se casa con Katharlna Gsell, hija de un pintor de la Academia, con quien tendrá trece hijos, aunque solo sobrevivirán cinco.
1735	Empieza a perder progresivamente la visión de un ojo, lo que no le impide, sin embargo, hacerse famoso en el mundo científico tras la resolución del problema de Basilea.
1738	Publica su primer libro, Mecanica, sive motus srientia analytica exposita, y acrecienta su fama con la resolución del problema de los puentes de Königsberg.
1741	Atendiendo a la llamada del rey de Prusia, Federico II, Euler y su familia se trasladan a Berlín, donde desempeñará un cargo en la Academia de la ciudad.
1742	Euler y Goldbach plantean en su correspondencia la que posteriormente se ha denominado conjetura de Goldbach.
1748	Publica una de sus obras más importantes, Introductio in analysins infinitorum, donde trata principalmente las funciones matemáticas.
1755	Publica otra de sus obras fundamentales, Institutiones calculi dijferentialis, que versa sobre cálculo diferencial.
1766	Euler abandona Berlín y regresa a Rusia, impulsado por la falta de entendimiento con Federico II
1768-70	Publica la tercera y última de sus grandes obras en el ámbito del análisis, Institutiones calculi integralis,
1771	Euler se queda ciego definitivamente al sufrir cataratas en su ojo sano, lo que no hace sino realzar su capacidad para el cálculo mental.
1783	El 18 de septiembre muere en San Petersburgo como consecuencia de una hemorragia cerebral.

Capítulo 1
Basilea, cuna de un gran matemático

La ciudad suiza era un buen lugar donde arrancar una carrera científica, particularmente en matemáticas. Centro intelectual do primer orden, con la primera universidad del país, en ella vivían varios miembros de la familia Bernoulli, la saga de matemáticos más eminente de la historia. Los Bernoulli acogieron bajo su protección al joven y prometedor Euler y le inculcaron un amor al análisis que ya no le abandonaría.

Basilea es una ciudad suiza enclavada de un modo privilegiado casi en la frontera alemana y en la francesa, a orillas del alto Rin, un poco antes de llegar a las cataratas que lo convierten en innavegable. Actualmente, su conturbación abarca casi tres cuartos de millón de habitantes, una excelente universidad, la más antigua de Suiza, y un buen número de recuerdos históricos, pues nacieron o vivieron en ella personalidades del renombre de Vesalio, Jung, Erasmo, Nietzsche y Paracelso, amén de varios miembros de la extraordinaria familia Bernoulli. En la actualidad, el más conocido de los hijos de Basilea es el tenista Roger Federer, gracias al cual la ciudad goza de fama universal. Los ciudadanos más ilustrados prefieren a Erasmo de Rotterdam, quien, aunque no nació en Basilea, sí que residió y murió allí. Sin embargo, los científicos, y en especial los matemáticos, no dudan considerar como hijo predilecto de Basilea a otro personaje distinto, nacido hace más de tres siglos, que responde al nombre de Leonhard Euler.
Euler, quien era matemático e ingeniero, físico, astrónomo, filósofo, arquitecto, músico y, ocasionalmente, teólogo, fue uno de los científicos más importantes del siglo XVIII y uno de los más prolíficos de la historia. Numerosos conceptos matemáticos llevan su nombre y, aunque seria un ejercicio muy pesado de erudición dar una lista completa de todos, sirvan, a modo de ejemplo, los siguientes: fórmula de Euler, ángulos de Euler, característica de Euler-Poincaré, recta de Euler, sumación de Euler-Maclaurin, teorema de Euler-Lagrange, teorema de Euler para las rotaciones de un sistema de coordenadas, teorema de Euler para el triángulo, circuito y camino euleriano, círculo de Euler, ladrillo de Euler... Y así hasta contar más de 140, dependiendo de las fuentes consultadas.

§. Euler y los Bernoulli
La de Euler era una familia corriente. Su padre, Paulus Euler, era un pastor calvinista, y su madre, Margaretha Brucker, un ama de casa convencional, hija de otro pastor. Euler fue el mayor de cuatro hermanos, de los cuales dos eran mujeres, Anna María y María Magdalena. El tercero, Johann Heinrich, adquiriría un cierto renombre como pintor.
Paulus Euler tenía una buena base matemática, pues había sido alumno de una figura distinguida, Jakob Bernoulli (1654- 1705), el iniciador intelectual de una después famosa camada de científicos distinguidos, los Bernoulli. Asimismo, Paulus Euler había sido condiscípulo y amigo de otro Bernoulli, Johann (1667- 1748), hermano de Jakob (pero trece años más joven). El 15 de abril de 1707 nació Euler. El deseo confesado de su padre era que se convirtiera también en pastor y «apacentara», llegado el momento, a sus propias ovejas. Pero el destino le tenía reservada otra suerte.
El joven Leonhard ya destacaba en la escuela en lenguas: se expresaba en alemán y francés; dominaba el latín, y profundizaba con notables resultados en griego y hebreo, como cabía esperar, de un futuro hombre de Dios, y se adentraba en la filosofía.
Parece que Euler aprovechó la amistad de su padre con Johann Bernoulli para conseguir que este le diera clases informales de matemáticas los sábados; y la realidad se impuso: el joven Euler tenía una disposición natural fenomenal para las matemáticas, algo que resultaba evidente para su profesor, a la sazón una de los principales matemáticos del mundo.

La familia Bernoulli
Existe un cierto consenso en considerar a cuatro matemáticos como el Olimpo anterior al siglo XXI Arquímedes, Newton, Euler y Gauss, cuando se pretende mencionar a un quinto todo se complica.
Muchos votarían por un matemático multifronte, formado por toda una familia: los Bernoulli.
Su impronta se nota en más de un siglo, pues padres, hijos y hermanos componen el árbol familiar.

Grabado de 1874 que muestra a Johann y Jakob Bernoulli trabajando en problemas geométricos.
En la familia eran frecuentes los rifirrafes producidos sobre todo por cuestiones matemáticas, algunos de los cuales habían tenido serias consecuencias, como cuando Jakob, el primero de la saga, hizo un testamento donde prohibía expresamente que se mostraran sus papeles científicos a su hermano Johann, o cuando este acusó a su propio hijo Daniel de plagio en cuestiones de hidrodinámica. Durante más de un siglo (de hecho. 105 años consecutivos), la titularidad de la cátedra de matemáticas de Basilea fue ostentada por un Bernoulli, y hasta mediados del siglo XX, es decir, durante más de 250 años, en dicha ciudad, siempre hubo un Bernoulli ocupando una cátedra.

Importancia de los Bernoulli
Algunas de las aportaciones más destacadas de los Bernoulli son el uso extensivo de las coordenadas polares, el estudio a fondo de la lemniscata y la espiral logarítmica, numerosos problemas de teoría de probabilidades y de series, el célebre teorema de la hidrodinámica que lleva su nombre y la regla de L'Hôpital. El análisis matemático experimentó un gran avance gracias al trabajo de esta familia y, a través de la influencia de Johann, se convirtió en la gran especialidad de Euler.
El grado de precocidad de Euler resulta evidente a la vista de sus primeros logros: universitario a los trece años, en 1723 recibía su título de Magister en filosofía mediante una especulación sobre los universos teóricos resultantes de seguir a Newton o a Descartes. Johann Bernoulli, quien seguía supervisando sus progresos y cuyo carácter no era nada propenso a elogiar a sus conocidos científicos, consideraba a Euler un genio en ciernes.

§. Johann Bernoulli. El análisis y la braquistócrona
Influencia básica en la formación y algunos de los intereses posteriores de Euler, la figura de Johann Bernoulli merece un inciso que de justa medida de su talla científica. Matemático extraordinario, quizás el más notable de la saga Bernoulli, Johann estaba predestinado por su padre a ser comerciante y, luego, médico. Sin embargo, terminó dedicándose a las matemáticas, como su hermano mayor Jakob, en quien siempre encontró apoyo, aunque su relación fraternal estaba teñida de rivalidad y puntuales desacuerdos.
Johann era un hombre muy competitivo y bastante fanfarrón, y entró en multitud de polémicas y disputas, incluso con sus familiares. Cuando descubría algo pretendía poseer siempre la prioridad del descubrimiento, aunque otros lo hubieran descubierto de manera independiente y, muchas veces, con anterioridad. También se le ha acusado de hacer suyos, de modo malintencionado, hallazgos de terceros.
En cualquier caso, Johann no solo fue un gran matemático, sino una auténtica bendición para los historiadores, a quienes ha provisto de un número inagotable de anécdotas, como la que protagonizó con el marqués de L'Hôpital (1661-1704). Este era un noble adinerado y un excelente matemático, quien cerró un acuerdo económico-intelectual un tanto peculiar con Johann Bernoulli: a cambio de dinero, el marqués obtuvo el derecho de acceder y exhibir como propios los descubrimientos de Johann. Herramientas del análisis matemático tan fundamentales como la denominada regla de L'Hôpital vieron la luz asociadas al nombre del marqués, si bien, en realidad, las había desvelado Johann Bernoulli. El magnífico libro del marqués de L'Hôpital, L'Analyse des Infiniment Petits pour l'Intelignce des lignes Courbes (Análisis de los ínfnitamente pequeños para el entendimiento de las líneas curvas) fue saludado en su día como una obra estupenda, pero hoy se sabe que los auténticos derechos de autor habían de ser compartidos. Muerto el marqués, Johann Bernoulli no pudo resistirse a reivindicar lo que realmente era suyo, pero tuvo que esperar bastante a que la posteridad le diera la razón.
En junio de 1696, antes de que naciera Euler, Johann planteó en las páginas del Acta Eruditorum de Leipzig, la primera revista científica de la historia, un desafío a sus colegas: dados dos puntos A y B, con A situado a distinta altura que B, encontrar la trayectoria descrita por un cuerpo sometido a la única fuerza de la gravedad que va de un punto a otro en el menor tiempo posible. Como es natural, Johann ya contaba con su solución (la cual posteriormente se supo que no era del todo correcta), y el desafío en cuestión iba encaminado a poner a prueba a sus colegas, y, en particular, a su hermano Jakob. En mayo de 1697, en el Acta Eruditorum, se publicaron los resultados correctos que coincidían en proclamar a la curva cicloide de extremo en A y altura máxima en B como la curva buscada (véase la figura).

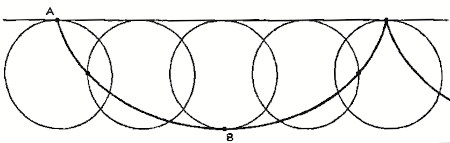
La cicloide es la curva descrito por un punto fijo da una circunferencia al rodar siguiendo una línea recta.

Entre otras figuras eminentes encontraron la solución Leibniz y Jakob Bernoulli. Una solución magistral, pero anónima, fue enviada desde la Royal Society de Londres. Johann la leyó y reconoció, acertadamente, que tras ella se escondía la mano genial del gran Newton. «Conozco al león por sus garras» parece que fueron sus palabras, frase que hizo fortuna y que se ha convertido en un elogio paradigmático de Newton.
La cicloide es, como se ha visto, una curva braquistócrona (del griego brachistos, «más corto» y chronos, «tiempo»), y con el nombre de problema de la braquistócrona ha pasado a la historia toda esta secuencia de acontecimientos. Muchos años más tarde, el propio Euler volvió sobre la cicloide y la braquistócrona en el marco del cálculo de variaciones, una poderosa técnica que él mismo y Giuseppe Luigi Lagrange (1736-1813) habían puesto en marcha, y que se ha revelado como fundamental para el desarrollo de la mecánica

§. Los inicios de un genio
Johann Bernoulli intentó convencer a Euler padre de que el futuro de su hijo no estaba en el sacerdocio y la teología; lo suyo eran las matemáticas. Como ya se ha visto, Euler hijo apuntaba alto, muy alto.
En 1726, cuando Euler contaba apenas diecinueve años, ya ostentaba el título de doctor. Dirigida por Johann, su tesis, para darle un nombre actual a su escrito, versaba sobre la propagación del sonido, y se llamaba muy apropiadamente, De sono. Era un texto pensado para servirle de base a Euler para opositar a una plaza profesoral que había quedado vacante en la universidad de Basilea La juventud de Euler hacía poco probable que accediera al puesto, y, como era de esperar, no lo consiguió.

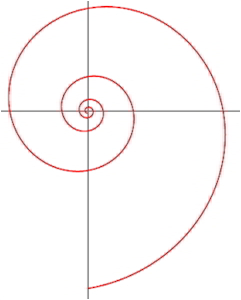
La espiral de Jakob Bernoulli
Jakob Bernoulli había quedado seducido, como solo puede quedarlo un auténtico geómetra, por las propiedades y el aspecto de la espiral logarítmica, esa curva retorcida cuya ecuación simplificada obedece, en coordenadas polares, a la expresión r = a^π con el radio r igual a una potencia de exponente igual al ángulo π y que se denomina spira mirabilis («espiral maravillosa)»).

La espiral logarítmica no posee principio ni fin, y se encuentra en la naturaleza en forma aproximada, como en la espiral de los huracanes o la de algunas galaxia».
Hasta tal punto llegó su obsesión que solicitó formalmente que una tal espiral, adecuadamente esculpida, adornara su tumba junto a las palabras Eadem mutata resurgo («Muto y vuelvo a resurgir como antes»), y dicho y hecho, solo que no contaba con el cantero responsable de esculpir la lápida fúnebre. En lugar de una espiral logarítmica, sobre la tumba figura una espiral de Arquímedes, pues para el cantero en cuestión, al parecer, todas las espirales eran iguales. Conociendo el fuerte carácter del hermano menor de Jakob, a quien este había transmitido su afición por la espiral, es de desear que Johann no coincidiera en la otra vida con el artesano.

En la lápida da Jakob Bernoulli no se esculpió una espiral logarítmica, sino una espiral de Arquímedes» (véase la parte inferior de la imagen), en la que las volutas son equidistantes.

En 1727, participó en el Grand Prix de la Academia de las ciencias de París con el propósito de debatir los mejores puntos donde ubicar los mástiles de una embarcación. Es casi imposible no ver la ironía del hecho de que se presentara para un premio de espíritu inequívocamente náutico un Euler inequívocamente «de secano». Como hace notar su biógrafo, Emil A. Felmann, la mayor masa de agua que Euler había visto en su vida era el Rin, por lo que la auténtica navegación, como a todo buen suizo, le quedaba un poco lejos. Sea como fuere, Euler se presentó al concurso y, aunque no ganó, conquistó un envidiable accésit compartido y una cierta fama en la comunidad científica El ganador del concurso fue el eminente catedrático francés de veintiocho años, Pierre Bouguer, especialista indiscutido en hidrodinámica. Habiéndose leído con provecho obras de Varignon, Galileo, Descartes, Newton, van Schooten, Hermana, Taylor, Wallis y Jakob Bernoulli, el joven y prometedor Euler empezaba a ofrecer destellos de su genio.
Mientras tanto, varios destacados nombres de la comunidad matemática internacional, en su mayoría de origen alemán o en la órbita de influencia cultural germánica, estaban tejiendo una sutil tela de araña desde Rusia con el objetivo de «fichar» a la joven promesa; en particular Christian Goldbach (1690-1764), con quien Euler mantenía correspondencia desde hacía unos años y del que se hablará en páginas posteriores.
El zar de Rusia, Pedro I (1672-1725), llamado «el Grande», era un hombre de ideas pro-occidentales y progresistas. Uno de los modos con los que Pedro I pensaba occidentalizar su vasto reino y situarlo en el mapa de los dominios civilizados era la creación de una Academia de ciencias rusa, al estilo de las Academias de París o Berlín o de la Royal Society, joyas del pensamiento ilustrado de su tiempo.
Para levantar su academia, Pedro I encomendó a sus agentes la búsqueda de talentos dispuestos a emigrar a Rusia. Tanto Nicolaus II como Daniel Bernoulli, dos de los cuatro hijos de Johann, con quienes Euler había desarrollado una gran amistad y que se encontraban ya en Rusia, en la futura sede de la academia, San Petersburgo, recomendaron vivamente el fichaje del joven Euler con el beneplácito de Goldbach. La súbita muerte de Nicolaus II, víctima de un ataque de apendicitis, dejó una inesperada vacante, que le fue ofrecida rápidamente a Euler, quien aceptó. En realidad lo hizo a regañadientes, pero la falta evidente de perspectivas inmediatas en Basilea fue determinante para que decidiera instalarse en Rusia.

Pierre Bouguer, padre de la arquitectura naval
El nombre de Pierre Bouguer (1698-1758) raramente aparece en los libros de matemáticas, a excepción de los dedicados a su aplicación en hidrografía, donde Bouguer es tenido por toda una autoridad y conceptuado como uno de los padres indiscutidos de la arquitectura naval.
Este científico bretón, destacó por su precocidad; a los quince años dominaba de tal manera los conocimientos fisicomatemáticos que sucedió a su propio padre, uno de los mejores especialistas de su época, al frente de su cátedra de hidrografía al quedar vacante por la muerte de su progenitor.

Estatua de Pierre Bouguer junto al rio Loira, erigida en Le Croisic, su lugar de nacimiento.
En 1727, con menos de treinta años. Bouguer ganó el Grand Prix de la Academia de las ciencias de París con una memoria sobre la óptima disposición de los mástiles de un buque, galardón que conseguiría en dos ocasiones más. Euler, quien quedó segundo en el citado certamen, consiguió doce Grand Prix a lo largo de su vida.
El legado de Bouguer
Recién cumplida la treintena, Bouguer realizó contribuciones importantísimas a la fotometría analizando la disminución de la luz al atravesar capas de aire. En 1747, inventó el heliómetro, que fue mejorado luego por Joseph Fraunhofer (1787-1826) y tantos avances ha permitido a la espectrografía y la física en general. A los treinta y siete años se embarcó con Charles-Marie de La Condamine y Louis Godin en una expedición científica a Perú destinada e medir un grado del meridiano terrestre próximo al ecuador, que culminó en la determinación del ensanchamiento ecuatorial del globo terráqueo. También, dio a conocer una anomalía gravitatoria, que lleva su nombre, la anomalía de Bouguer. En 1746 publicó su Traité du navire (Tratado del navío), considerado el tratado cumbre de la literatura naval de la época, donde se mide la estabilidad de un navío por la posición de su metacentro o centro de la carena. Elegido miembro de la Royal Society. Bouguer ascendió metafóricamente a la gloria celestial en forma de cráteres lunares y marcianos, pues dos de estos accidentes geográfico-astronómicos fueron bautizados con su nombre en su honor. Sin embargo, la comunidad matemática le recordará siempre por algo bastante trivial, pero extraordinariamente útil: Bouguer introdujo, en 1752, los símbolos '≤' y '≥'.

§. El legado de Euler a la notación matemática
La labor fundamental de Euler en el ámbito de la notación matemática arrancó ya en Basilea, antes de emprender su viaje a Rusia, y al estar repartida a lo largo y ancho de su vida, es adecuado ofrecer un resumen de la misma antes de emprender nuestro propio viaje por la vasta obra del matemático suizo.
En un sentido general, el objetivo de la notación es el de crear un lenguaje sintético que permita sustituir ventajosamente largas secuencias de palabras por símbolos y variables simbólicas. En términos no matemáticos, una buena notación establece unas reglas comunes de «buenas prácticas», pues permite entendemos los unos a los otros. La notación actual no es perfecta, pero sí ha evolucionado de muy antiguo. Permite tratar casi todo con una admirable economía de medios.
Por ejemplo, si se intenta leer un texto clásico de matemáticas, anterior a François Viéte (1540-1603), inventor de la terminología moderna en álgebra, resulta evidente la complejidad de la tarea. Al no emplear símbolos los conceptos deben expresarse en lenguaje llano y las repeticiones son constantes y pesadas. Una muestra: El teorema de Pitágoras podría enunciarse hoy de la siguiente manera:

En el triángulo de lados a, b y c, A = 90° → a² = b² + c²

Mientras que la versión equivalente de Euclides, dividida en dos partes (libro I, proposiciones 47 y 48), dice:

En los triángulos rectángulos el cuadrado del lado opuesto al ángulo recto es igual a la suma de los cuadrados de los lados que comprenden el ángulo recto.
Si en un triángulo el cuadrado en uno de sus lados iguala a la suma, de los restantes dos lados del triángulo, entonces el ángulo contenido por los restantes dos lados del triángulo es recio.

Se trata de un caso bien elemental, y es patente el progreso experimentado gracias al uso de símbolos.

Uno de los retratos más conocidos de Leonhard Euler, realizado en 1753, Euler vivía entonces en Berlín, por Jakob Emanuel Handmann, donde ya puede apreciarse el defecto en la vista que le afligía desde 1735. Euler perdió primero la visión de un ojo y luego la del otro, pero continuó su labor matemática sin interrumpirla.

Entre las notaciones que Euler popularizó o creó y que se siguen utilizando en la actualidad destacan las siguientes:
1. π: ningún símbolo aportado por Euler ha tenido tanta' fortuna como π, el símbolo ideado para designar un número: la relación entre la longitud de una circunferencia y su diámetro, un número irracional y trascendente de valor aproximado π = 3,1415926535... La letra griega pi fue usada por primera vez por el galés William Jones (1675- 1749), quien la utilizó por ser la inicial griega de la palabra «periferia», pero fue Euler quien la popularizó a partir de la publicación, en 1748, de su famoso libro Introduction in analysins infinitorum.
2. La constante e, la letra e la empleó Euler para bautizar a la constante que designa a la vez la base de los logaritmos naturales —Euler denominó con la letra e dicha base ya en 1731, en una carta a Goldbach—, el límite:

y la suma de la serie infinita:

Sin embargo, no será hasta la publicación de la ya mencionada Introduction cuando Euler profundizó en las ideas alrededor de e, calculando incluso 26 dígitos:

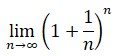
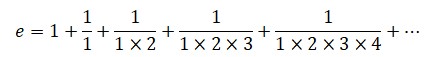
e = 2,71828182845904523536028747...

No se sabe con exactitud a qué obedece la elección de la letra e por parte de Euler. No es cierto, como algunos afirman, que la eligiera por ser la inicial de su nombre o de la palabra «exponencial».3. i: durante la mayor parte de su vida, Euler, quien no contaba con el concepto riguroso y correcto de límite, escribía:

para indicar lo que hoy se escribiría como:

En este ejemplo, la letra i representaba el papel de un número infinito. Pero en 1777 había cambiado de idea y empleó i para representar la unidad imaginaria de los números complejos, i = √-1. El artículo de 1777 no se publicó hasta 1794, pero lo hizo suyo Gauss y con él toda la comunidad matemática. Euler eligió la i por ser la inicial de la palabra «imaginario».
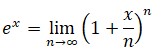
4. y = f(x): Euler fue el primero en utilizar el concepto moderno de función, ligando el valor de entrada x con el de salida y, a través de una correspondencia que se denominaría f. El dominio y la imagen de f quedan claramente establecidos. Su uso ya aparece en los Commentarii academiae scientiarum imperialis Petropolitanae, primera revista publicada por la Academia de San Petersburgo, de 1734-1735. Aunque el modo moderno de concebir las funciones discrepa ligeramente del euleriano, puede atribuirse a Euler un gran paso adelante en lo que concierne a claridad conceptual y expositiva.
5. Σ (= sigma): fue escogida por Euler para indicar una suma de una sucesión de números sujeta a alguna condición, que acostumbra a explicitarse escribiéndola debajo y encima del símbolo. El caso general de una suma de elementos x_i

para indicar lo que hoy se escribiría como:

donde i es un «contador» de sumandos que va de m a n, se escribe:

Sigma es la letra «s» griega, inicial de «suma», así que la utilización de una sigma es bastante lógica. Euler calculó a lo largo de su vida centenares de sumatorios, muchos de ellos infinitos. Cuando n- w, se dice que el sumatorio es una serie. Quizá el más famoso sumatorio de Euler, en su sencillez, sea el del «problema de Basilea», que Euler resolvió en 1735, en plena efervescencia creativa (y que se examina en detalle en el capítulo siguiente):

Nadie esperaba que el número π jugara un rol en la solución de este sumatorio, y su «aparición» provocó una auténtica conmoción en el mundo científico.
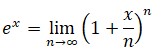
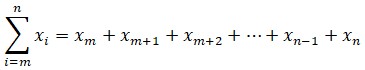
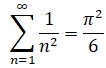
6. Uso de mayúsculas y minúsculas: en un triángulo cualquiera, los lados se designan con letras minúsculas, y los ángulos opuestos con las mismas letras, pero mayúsculas (figura 1).

De modo similar, se designan por R y r, respectivamente, los radios de las circunferencias circunscrita (figura 2) e inscrita (figura 3).
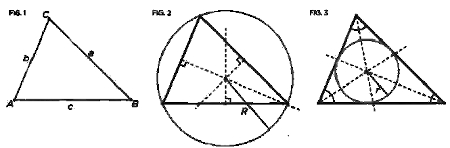
7. Uso en las fórmulas de las primeras letras del alfabeto a, b, c, d... (normalmente en minúsculas) para designaren tas ecuaciones a las cantidades conocidas, mientras se reservan las últimas, x, y, z, v... para las cantidades desconocidas o incógnitas.
8. Uso de las formas abreviadas del latín sin, cos, tang., cot, sec, y cosec. Euler las utilizó por primera vez en 1748 en su libro Introductio in analysins infinitorum, para designar las funciones trigonométricas. Luego cada lengua ha procedido a adaptar ligeramente estas denominaciones, aunque son ya casi universales en su forma inglesa, y que en dicha lengua y en expresión funcional se leen sin x, cos x, tan x (o tg x), cot x, sec x y cosec x (o csc x).
9. Notación para las diferencias finitas: las diferencias finitas son un instrumento de cálculo que guarda un cierto parecido con las derivadas. Eso sí, el concepto de límite y los llamados infinitésimos no están presentes. Las diferencias finitas aparecieron ya con Newton (1642-1727), James Gregory (1638-1675) y Colin Maclaurin (1698-1746) y permiten calcular polinomios desconocidos a partir de sus valores, así como interpolar y estudiar sucesiones y series, La aparición de los ordenadores ha representado un incremento de su interés.
Euler dedicó considerables esfuerzos a las diferencias finitas, y la notación con la que se presentan hoy en los libros es suya. En el caso más sencillo de todos, una simple sucesión (u_i), la diferencia de dos términos sucesivos se denomina ∆:

∆u_k = u_k₊₁ -u_k

Las sucesivas diferencias finitas (de segundo orden, ∆², de tercer orden ∆³, de cuarto orden ∆⁴ etc.) se definen a partir de las de primer orden ∆ de modo recursivo, cada una partiendo de la anterior:

∆^pu_k = ∆(∆^p^-1u_k)

De esta manera ya se tienen recogidas todas las diferencias finitas, del orden que sea: ∆, ∆², ∆³... y se puede operar con ellas.

§. Una primera aportación fundamental: números complejos y logaritmos negativos
En una serie de trabajos iniciados en sus días de Basilea, Euler dio con una fórmula para los números complejos que se haría célebre y la empleó para dar con el valor de una entidad matemática desconocida hasta ese momento; los logaritmos negativos.
Como ya se ha señalado, Euler utilizó la letra i para representar un número imaginario, el número √-1. Desde entonces, en cualquier fórmula aritmética en la que figure i se ha de entender, i = √-1.
En el curso de sus trabajos en Basilea, Euler descubrió esta fórmula:

e^xi = cos x + isen x,

y jugó con ella, como solo él, el gran malabarista de los símbolos supo hacer. De esta simple expresión simbólica, conocida como fórmula de Euler de los números complejos o simplemente como fórmula de Euler, y que relaciona la exponenciación compleja con la trigonometría, nació, como se verá en el capítulo tercero, buena parte del análisis matemático de siglos posteriores.
En la época de Euler estaban muy de moda los logaritmos, una herramienta de cálculo descubierta en el siglo XVI cuyas potencialidades, sin embargo, no fueron explotadas hasta la llegada del matemático suizo. Definámoslos: si a es un número positivo, llamado base, y N, un número positivo, si:

N = ax,

se llama a a, el logaritmo de N, y se escribe x = log N. Es decir

N = a log N.

Cuando la base es la constante e, se acostumbra a poner ln N en lugar de log N.

«Señores: esto es seguramente cierto, es absolutamente paradójico, no lo podemos entender y no sabemos lo que significa, pero lo hemos demostrado, y por consiguiente sabemos que debe ser la verdad.»
Benjamín Peirce (1809-1880), profesor de Harvard, enfrentado a la llamada «fórmula de Euler de los números complejos.

Ahora bien, el número -1 puede escribirse como -1 = -l + 0i, y estudiarlo así, como un número complejo. Operemos con él en el seno de la fórmula de Euler

-1 = -1 + 0i = cos π + i sen π =e^πi

Fijémonos ahora en el principio y final de esa igualdad y calculemos el logaritmo natural:

ln (-1) = ln (eπi) = πi

Euler obtuvo así un valor definido para el logaritmo natural de -1, un número negativo.
El suizo detuvo aquí su maquinaria mental y partió de viaje a San Petersburgo. No fue hasta 1751, casi un cuarto de siglo más tarde, que Euler dio a conocer este resultado, junto a muchos otros, en su forma correcta, con la publicación de su magistral libro Introductio in analysins infinitorum (Introducción al análisis del infinito).
Como los guerreros partos de la Antigüedad, que disparaban sus dardos en plena retirada, Euler se marchó a Rusia y dejó abierta la cuestión de los logaritmos negativos, pero eso sí, mostrando ya sus armas futuras.

Capítulo 2
Series, constantes y funciones: Euler en Rusia

Con apenas veinte años, Euler se incorporó a la Academia de Ciencias de San Petersburgo. Se abría así un período creativo sin parangón en la historia de las matemáticas que tendría como fruto la función gamma (Γ), la fijación de la constante e y otros importantes trabajos en análisis y teoría de números, así como la resolución de dos problemas de gran relevancia futura; el de Basilea y el de los puentes de Königsberg.

Euler viajó a Rusia en 1727 sin mucho entusiasmo, pues aparte del rigor del clima, se dirigía a trabajar a un país atrasado y donde se hablaba y escribía en otra lengua e incluso en otro alfabeto. Esto último se demostró que carecía de importancia, pues Euler, quien tenía una gran facilidad para los idiomas —dominaba latín, griego, francés y alemán—, añadió el ruso al repertorio de los que hablaba, leía y escribía. En ello se distinguía además, y favorablemente, de los otros miembros extranjeros que atrajo la Academia de ciencias de San Petersburgo. He aquí a un sabio extranjero con el que se podía hablar y entender, a quien era posible escribir, y que se molestaba en entender y saberse expresar en la lengua local. Además sabía de todo y todo despertaba su curiosidad. Nombrado, uno de sus muchos títulos, miembro de la Academia de Cartografía, se maravillaba de sus logros y los comparaba muy favorablemente con la cartografía occidental, que era la que había conocido hasta entonces.
Cuando Euler llegó a San Petersburgo coincidió allí con talentos como Christian Goldbach y Daniel Bernoulli, así como con otros sabios, muchas de los cuales de procedencia y lengua germanas. Euler había sido contratado para enseñar aplicaciones matemáticas y mecánicas a la fisiología, pero pasó rápidamente de ser un joven empleado del departamento médico (1727) a profesor de matemáticas (1733), con un intermedio como profesor de física (1731). La transferencia fundamental de fisiología a física fue fruto de las peticiones insistentes a la Academia de sus colegas Jakob Hermann (1678-1733) y Daniel Bernoulli.
La estancia de Euler en Rusia trabajando para la Academia fue fructífera; ascendió rápidamente y trabó gran amistad con Daniel Bernoulli y con el secretario perpetuo de la Academia, Christian Goldbach. Escribía mucho, descubría cosas nuevas constantemente y empezaba a labrarse una fama internacional considerable. En 1733 su posición y sueldo le permitían mantener casa y familia, y se casó con Katharina Gsell, la hija de un pintor de la Academia. Del matrimonio nacieron trece hijos, aunque solo cinco sobrevivieron.
En 1735, Euler padeció una fuerte infección ocular. Algunos afirman que enfermó a consecuencia del estrés producido por un trabajo urgente relacionado con el cálculo de la latitud de San Petersburgo. Sea como fuere, el caso es que se quedó momentáneamente ciego del ojo derecho, y aunque en un principio se fue recuperando poco a poco, a los tres años recayó y perdió de modo definitivo 1a visión de ese ojo.

La academia de San Petersburgo
El zar Pedro I puso el punto de mira del progreso de su imperio en la instrucción pública y la difusión del conocimiento. Tras sus viajes a través de Europa en los que trabó una buena amistad con Leibniz, decidió en 1724-1725 la creación de la Academia de ciencias, la Academia Scientiarum Imperialis Petropolitanae, afincada en la capital real, San Petersburgo. La Academia estaba basada en las normas y estructura de la Academia de París, y dependía, como ella, de la protección y el subsidio reales. La historia de la Academia de ciencias fue un tanto azarosa en ese periodo inicial, y a los tumbos obligados por la incierta política rusa de aquel entonces, constelada de niños con títulos reales, regentes y zarinas, hay que añadir las intrigas internas y luchas por el poder dentro de la propia institución. Los miembros de extracción extranjera, sobre todo germanos, se enfrentaban por la supremacía a los miembros rusos, quienes se sentían postergados. Todo ello terminó determinando que Euler, un tanto preocupado por el cariz que tomaban tas cosas, aceptara cambiar San Petersburgo por Berlín, y emigrar de una academia a otra.

Su ánimo, no obstante, no se resintió por su irremediable disminución de la visibilidad, si se considera cierta la afirmación atribuida a Euler: «Mejor, así no me distraeré tanto».

«Calculaba sin esfuerzo aparente, como otros hombres respiran o como las águilas se sostienen en el aire.
Françoise Jean Dominique Arago (1788-1853)

En 1738 consiguió el Grand Prix de la Academia de París -—al que también habían aspirado Voltaire y Émilie de Breteuil, la marquesa de Chátelet— con un ensayo sobre el fuego. Dos años después, en 1740, volvió a obtener el galardón —frente a Daniel Bernoulli y Colin Maclaurin—, esta vez con una memoria sobre el flujo y reflujo de las mareas.

§. La función gamma
Al poco de llegar a San Petersburgo, Euler emprendió el imparable camino de descubrimientos sorprendentes que marcaría su existencia. El primero de sus grandes momentos parece haber sido la creación de la función Γ (Γ es el símbolo de la letra mayúscula griega gamma), una herramienta básica del análisis matemático. Alrededor de 1720 ya aparece la sombra de Γ en la correspondencia con Daniel Bernoulli y Christian Goldbach, pero no es hasta 1729 que Euler la define por primera vez; la define pero no la bautiza, pues no es hasta 1814 que Adrien-Marie Legendre (1752-1833) la denomina gamma y la escribe de esta forma; Γ(x).
La función gamma está presente muchas veces como componente de las distribuciones de probabilidades, y son multitud los especialistas en física que usan dicha función; de hecho acostumbra a estar presente en los fenómenos que implican algún tipo de integración de carácter exponencial, tan frecuentes en el mundo atómico; también es moneda corriente en astrofísica y en dinámica de fluidos, así como en el estudio de los fenómenos sísmicos. También en matemáticas la función gamma tiene aplicación en múltiples áreas, de modo notable en combinatoria y muy en especial al estudiar la función zeta de Riemann, de fundamental importancia en el estudio de los números primos.
El objetivo de Euler fue resolver una cuestión de lo que entonces se llamaba interpolación y que consistía en, conociendo los valores extremos de una variable, deducir valores intermedios de un modo natural y sin artificios. Veamos un ejemplo. El llamado factorial de un número natural, denominado en aritmética n!, y usado por primera vez por Christian Kramp (1760-1826), es el nuevo número:

n! = n×(n-1)×(n-2)…3×2×

que consiste en el producto de todos los números naturales menores o iguales a n. Su crecimiento es espectacular, como puede verse en la siguiente tabla: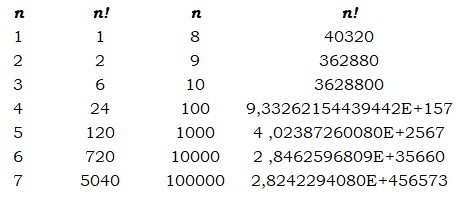

El factorial es discontinuo y solo está definido entre números naturales; «interpolar» el factorial era prolongar el factorial hasta encontrar una función continua f(x), de modo que al tomar x el valor entero n se obtuviera f(n).
Un ejemplo casi trivial se halla en el concepto de cuadrado de un número. Dado un número entero n está bien definido su cuadrado n²= n×n. El concepto es «interpolable» a cualquier número real x sin más que poner f(x) = x².
Euler «interpoló» el factorial n! y encontró, en 1729, una función continua f(x) que actuaba como el factorial cuando x = n era entero, la llamaremos r(at) que es su denominación actual Γ(x).
Euler definió el valor de Γ(x) en cada punto x por lo que hoy llamaríamos limite:

definición sustituida en la actualidad por la fórmula integral:

que es más sencilla y manejable y es válida, además, en el campo de los números complejos.
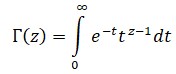
Cuando se estudia a fondo, de la Γ(x) resultan todo tipo de fórmulas muy sugestivas para una mente matemática como:

que relaciona a gamma con pi y con funciones trigonométricas.

Las otras gammas
Hay varios modos de definir Γ(x). En el siglo pasado hizo fortuna la fórmula de Karl Weierstrass (1815-1897), que pone de relieve a la constante de Euler (γ, llamada también gamma, aunque con minúscula):
Esta función cumple que:

Una fórmula que se deduce con el auxilio de la función gamma es la célebre fórmula de Stirling (1692-1770), paradigma para muchos de la belleza simbólica, pues en su enunciado intervienen de manera armónica las constantes π, e y el número n en varias formas:

Por último, pero no menos importante, un vínculo entre la función gamma: y la zeta, ζ(z), esta última de fundamental importancia en teoría de números y, en particular, en el fascinante campo de los números primos:

§. La función beta
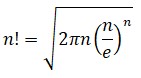
Euler, al estudiar la función gamma, se vio abocado a estudiar también otra función, llamada beta y representada por la letra B. Hay varias formas de definir esa nueva función, que es también muy útil en análisis; uno de los modos es recurrir al cálculo integral:

si las partes reales de x e y son estrictamente positivas.
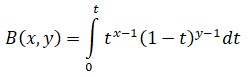
Y otro es recurrir a la función gamma, ya definida previamente:

§. Los números de Fermat
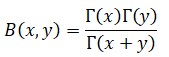
Tras abordar el estudio de las funciones gamma y beta, Euler desplazó su atención a la teoría de números, en uno de esos bruscos cambios de objetivo tan definitorios de la trayectoria científica del suizo.

La madre de todas las funciones
En matemáticas la reina de las funciones, la que centra la atención de más especialistas y que consume más bytes de literatura electrónica es la función zeta. Su denominación procede de la letra griega ζ (zeta) y fue Euler quien la empleó por primera vez generalizando el llamado problema de Basilea, el primer resultado matemático que le dio fama. Euler demostró que la suma infinita de los inversos de los cuadrados es π²/6:
y posteriormente consiguió generalizar el resultado considerando la siguiente función:
que puede tomar cualquier valor x en el campo R de los números reales. Euler calculó muchos valores de la función zeta, aunque incluso en la actualidad se desconoce un método directo para hallar infinitos de esos valores. El propio Euler encontró un modo de convertir la suma infinita de ζ en producto infinito, obteniendo, gracias a su habilidad algebraica para la manipulación de fórmulas, la expresión:
donde los distintos p_k recorren exclusivamente el campo de los números primos. De este modo puso al descubierto un vínculo inesperado de la función zeta con dichos números. Con las herramientas especializadas del análisis superior, puede trasladarse la función zeta al campo complejo, tomando los valores de s, ya no en R, entre los números reales, sino en el campo complejo, C. La función zeta fue ampliada a este campo y estudiada, en principio, por el gran matemático alemán Bernhard Riemann (1826-1866). Esta es la función conocida hoy como función zeta de Riemann y en ella se inscribe la llamada hipótesis o conjetura de Riemann, un enunciado desconcertante, todavía no demostrado, que constituye lo que se considera actualmente como problema pendiente número uno de la matemática contemporánea. La hipótesis de Riemann forma parte de los siete problemas del milenio cuya resolución premia la fundación Clay con un millón de dólares cada uno.

En concreto, se ocupó de una cuestión que había dejado abierta un siglo antes el francés Pierre de Fermat (1601-1665). Los vínculos de Euler con Fermat son muy estrechos. Si se sigue la trayectoria euleriana a través de la teoría de números se apreciará que la tarea fundamental de Euler parece haber sido la de solventar, uno tras otro, los problemas dejados sin resolver por Fermat, tarea tanto más laboriosa cuanto que Fermat guardaba por escrito pocas de las incógnitas que solucionaba, pues escribía comentarios en los mismos textos que leía y analizaba, acostumbrando a plantear a los demás colegas los problemas que resolvía como desafíos a la inteligencia de los amigos.
Uno de los más interesantes temas numéricos heredado de Fermat es el de los números que llevan su nombre, los números -de Fermat, que se denotan con la letra F y se definen por

Para n = 0, 1, 2, 3, 4, se tiene:

que son todos números primos. El siguiente número de Fermat es este:

y no era ilógico conjeturar que también fuera primo, como los anteriores. Algo más aventurado, aunque muy poco más para los estándares de su tiempo, era conjeturar, como hizo Goldbach, que todos los números de Fermat eran primos, reafirmando lo que había creído el propio Fermat Goldbach le comunicó a Euler la conjetura en 1729 y, en 1732, Euler ya había encontrado la solución: F₅ no era primo, sino compuesto. Más en concreto:

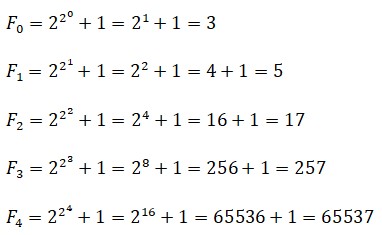
F₅ = 4294967297 = 641×6700417

La primera reacción que despierta este resultado es de asombro, pues el esfuerzo que requiere lograr la factorización por el modo convencional, probando a dividir por 2, 3, 5, 7, 11, 13, etc., y recorriendo hacia arriba la escalera infinita de los primos, es colosal.
Profundizando un poco más en las maniobras de Euler, puede rastrearse su método, y de paso, su genialidad. Poco a poco, merodeando por el resbaladizo terreno de la divisibilidad, llegó a la conclusión, nada fácil, de que cualquier divisor de F₆debía ser de la forma 64n +1; de manera que ya no tenía que lidiar, uno por uno, con todos los divisores primos, sino solo con los números 65 (n = 1), 129 (n = 2), 193 (n = 3), etc. descartando además los que no son primos.

Fierre de Fermat
Hombre de leyes de profesión, muchas veces se le ha llamado «el rey de los diletantes», pues cultivó las matemáticas solo como pasatiempo, Fermat contribuyó de forma fundamental al nacimiento de la geometría analítica y al desarrollo del cálculo de probabilidades y de la óptica.
En este campo estudió la reflexión y refracción de la luz, aspectos que consideró inmersos entre los fenómenos de máximos y mínimo.
Si sentando así las bases del cálculo diferencial, del que fue uno de los más notables precursores. Lo que más fama le dio fueron sus trabajos en teoría de números, donde puso de relieve muchas de sus admirables facultades y métodos de trabajo. No acostumbraba a poner por escrito sus razonamientos, por lo que anotaba, mientras le cabían, sus ideas en el margen de los libros que leía, Sin embargo, su ascenso a la fama universal proviene de pretender haber demostrado el teorema: «Para n>2, no existen enteros positivos no nulos, x, y y z tales que x^n,+y^n,=zⁿ». Conocido por el último teorema de Fermat, último, porque siempre quedaba pendiente de prueba, Fermat había manifestado, y muy probablemente se equivocó, que, en el curso de sus lecturas, había encontrado una demostración maravillosa pero que no le cabía en el margen del libro que estaba leyendo. El teorema fue probado en 1995 por Andrew Wiles (n. 1953).

Para n = 10 el cálculo da 64×10 + l=641, y resulta una división exacta.
Hasta hoy no se ha encontrado ningún otro número de Fermat primo. Todos los que se conocen —o sea, que han sido estudiados— son números compuestos. Se ha comprobado que de F₅a F₃₂, que es un número enorme, no hay ningún primo. Pero eso no quiere decir que ya no los habrá; que los haya o no es una simple conjetura y, en matemáticas, las conjeturas son verdaderas o falsas si y solo si se demuestran o se refutan.

§. El bautizo de un número
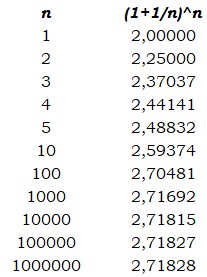
En paralelo a su trabajo sobre los números de Fermat, y nuevamente en el marco de su fértil correspondencia con Goldbach, Euler puso nombre a una constante numérica que, como ya se ha apuntado en el capítulo anterior, iba a erigirse en pieza clave de su trabajo en teoría de números: la constante e. La primera aparición de e con la denominación con que ha llegado a nuestros días fue en una carta de 1731. Esta constante es, seguramente, la más conocida después de π, y vale en primera aproximación:

e = 2,718281828459045235360287471352662497757247...

En la actualidad se conocen de e más de 1000000000000 de dígitos decimales. No obstante le dio nombre y lo empleó para toda clase de desarrollos y aplicaciones, Euler no fue en puridad su «descubridor»; e nació mucho antes, pero con otro nombre y un poco «de tapadillo», como se verá.
El número e proviene del campo de los logaritmos, como Euler puso de relieve. El vínculo entre uno y otro, explicado con más detalle en el Anexo 1, pasó desapercibido a la comunidad matemática durante cerca de un siglo. En descargo de los contemporáneos del suizo, hay que decir que el número e iba a revelarse a lo largo de los años como una constante especialmente escurridiza Uno de los primeros en acercarse a e fue Grégoire de Saint-Vincent (1584-1667) quien, en 1647, se enfrentó a la hipérbola equilátera, de ecuación y = 1/x, y cuyo gráfico en coordenadas cartesianas puede apreciarse en esta página Saint-Vincent calculó el área limitada entre 1 y otro punto cualquiera t del eje horizontal X, es lo que en lenguaje moderno equivale a integrar la curva entre 1 y t.
Si se integra entre 1 y t, resulta

y cuando se toma el valor t = e, se tiene ln t = ln e = 1. Así pues, e es el valor del eje horizontal X para el que el área señalada en el gráfico vale 1, definición adoptada más tarde por el propio Euler, pero sobre la que Saint-Vincent pasó de largo.

Tampoco Christiaan Huygens (1629-1695) prestó mucha atención a e a pesar de que en uno de sus razonamientos se vio obligado a obtener 17 dígitos del logaritmo decimal de e. Pero como los necesitaba para otra cosa y no para fijarse específicamente en e, pues también pasó de largo.
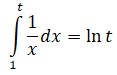
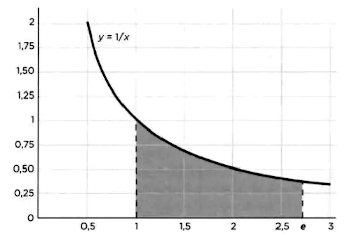
Quien no pasó de largo fue Jakob Bernoulli, aunque no tomó el sendero de los logaritmos, sino otro distinto, más «terrenal». En 1683, Bernoulli se interesó por el interés compuesto de un depósito de capital. Se puede seguir de modo aproximado sus mismos pasos, aunque en lenguaje moderno. Si se deposita, un capital C a un interés anual i, al cabo de un año el dinero se habrá convertido en:

C + C_i = C(1+i)

Si el interés se calculara dos veces al año en lugar de una vez, se debería dividir el interés por 2 y capitalizar el dinero dos veces. Por tanto, al cabo del año se tendría un capital más intereses igual a: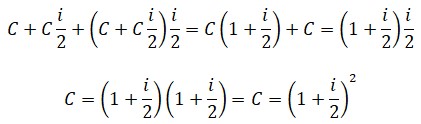

Si se repite la operación n veces, se observa, siguiendo el patrón, que el capital se convierte en:

Repitiendo la operación infinitas veces el interés sería instantáneo y en el actual lenguaje de los límites (prescindiendo de la magnitud de i, que no es importante en el planteamiento del problema) se llegaría al final con el límite:

Al verificar el límite se constata que este existe e, incluso, se puede uno acercar a su valor con un simple cálculo:

Jakob Bernoulli, sin la ayuda de los modernos instrumentos de cálculo, llegó hasta las primeras líneas de la tabla anterior, y su actuación ha de calificarse de extraordinaria teniendo en cuenta el nivel de las matemáticas de su tiempo. Según sus cálculos, el límite estaría entre 2 y 3. Ahora se sabe ya que:

Jakob Bernoulli, de una sola vez, había encontrado a e, aunque no le dio nombre, y por primera vez en la historia había hecho un hallazgo aplicando el concepto, hasta entonces desconocido, de límite.
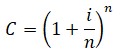
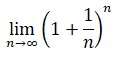
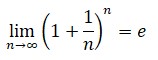
Por desgracia, también por esta vez la constante e se encontraba huérfana de auténtico reconocimiento, pues Jakob no vinculó su constante-límite con los logaritmos.
El número e encontró su primer nombre, la letra b, cuando Leibniz en 1690 la identificó así en una carta a Huygens. A partir de ahí, e comenzó a existir. Alguien le había otorgado un nombre, aunque este no fuera el definitivo.

El número e y los sombreros
Jakob Bernoulli no solo se topó con la constante e en el interés compuesto; un acertijo, o más bien, un problema de probabilidades y sombreros, le hizo moverse en torno a e. Pierre Raymond de Montmort (1678-1719) y Jakob Bernoulli se enfrentaron al siguiente enigma: N invitados asisten a una fiesta y entregan sus sombreros al criado en el vestíbulo. Todo estaba preparado para guardarlos cuidadosamente en cajas etiquetadas de antemano, evitando los errores de pertenencia, pero a última hora enferma el criado encargado del asunto y tiene que ser sustituido por otro, que desconocedor de la identidad de los invitados, va disponiendo los sombreros al azar en las cajas. El problema acontece cuando los visitantes se van y el criado les entrega un sombrero. Unos recibirán el suyo y otros no. ¿Cuál es la probabilidad del desastre total, es decir, de que ningún sombrero vaya a parar a su dueño? La respuesta es:
una magnitud que se parece mucho a la suma cuyo límite es e. De hecho, su límite es precisamente l/e. Si la fiesta es multitudinaria y N muy grande:
P_N = 1/e = 36.79%.

Relacionarla con los logaritmos era una cuestión de tiempo, y su lento paso concluyó en 1731, como ya hemos mencionado, con la carta de Euler a su corresponsal Goldbach. A partir de entonces y en especial en una serie de artículos escritos de 1736 en adelante, Euler llamó oficialmente e a la constante, la identificó, relacionó el límite de Jakob Bernoulli con los logaritmos, dio de estos una definición moderna, otorgó a e su lugar como base de los logaritmos naturales y, en una palabra, llevó a e a la inmortalidad, calculando incluso sus primeras 18 cifras decimales posiblemente mediante la suma directa de los veinte primeros términos de una serie descubierta por él mismo:

Si fuera así se trataría de una hazaña extraordinaria, casi un imposible; pero Euler demostró en tantas ocasiones una capacidad de cálculo tan sobrehumana que muchos se sienten inclinados a creer en tal procedimiento.
La elección por parte de Euler de la letra e, y no de otra, ha generado mucha especulación. A pesar de algunas creencias muy extendidas, Euler no eligió la «e» por ser la inicial de la palabra «exponencial», y, ni mucho menos, porque fuera la inicial de su propio apellido. Al parecer la iba a llamar a, pero esa notación estaba ya «ocupada» en sus cálculos por otra magnitud. En cualquier caso, lo cierto es que Euler nunca explicó las razones de su elección.
Mucho de lo que Euler desentrañó acerca de e lo publicó en 1748, en su obra magna Introductio in analysin infinitorum, escrita en su etapa berlinesa Entre otras notables aportaciones, Euler estableció de modo definitivo que el logaritmo y la exponenciación son procedimientos inversos el uno del otro, lo que significa que:

y=a^x si y solo si x = log_ay,

fórmula válida para cualquier base a, incluida la base e, a = e.
Otro hecho que cae en el terreno del análisis se refiere a la exponenciación en base e: la función f(x) = e^x coincide con su propia derivada:

La conslante e es un número trascendente, es decir, no puede obtenerse mediante la resolución de una ecuación algebraica con coeficientes racionales. El primer paso para demostrar la trascendencia de un número es probar su irracionalidad (se dice que un número es irracional cuando no se puede expresar por la razón de dos enteros), cosa nada fácil y que Euler no pudo llevar a cabo. Sin embargo, se quedó bastante cerca, pues pudo encontrar la siguiente fracción continua:

Al demostrar fehacientemente que no terminaba nunca, probó que (e - 1)/2 era irracional. Finalmente, Charles Hermite (1822-1901) demostró en 1873 la trascendencia de e.
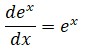
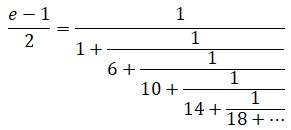
Además de la de Euler, otras expresiones comunes de e en forma de fracción continua son:

En tiempos recientes ha crecido en el ámbito de la teoría de números el interés por averiguar si una constante es normal; ¿es e normal? Normal significa, en este contexto, que los dígitos de e, cuando la constante se la expresa en cualquier base numérica, guardan un equilibrio estadístico: tomados de uno en uno, en grupos de dos, de tres ó como sea, la probabilidad de aparición en la secuencia numérica de e es siempre equitativa.
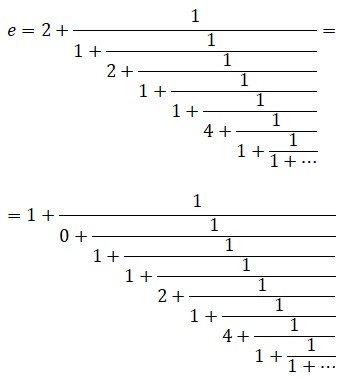
Pues bien, hay constantes normales y anormales, pero e parece ser normal. Pero eso es solo una conjetura, pues nadie lo ha podido demostrar hasta hoy.

Los arcos del colegio de las teresianas de Barcelona, obra de Antonio Gaudí (izquierda), o el gran arco del Gateway Arch de St. Louis (arriba derecha) son ejemplos invertidos de la vulgar curva catenaria formada por los cables colgantes (derecha abajo). Dicha curva tiene una expresión que involucra al número e.

Ejercicios de memoria con el número e
Existe un deporte matemático denominado mnemonics, que consiste en recitar cuantas más cifras decimales posibles de una constante numérica. Como recordar decimales como simple ejercicio de memoria puede ser aburrido, las reglas de mnemonics prescriben recordar frases o versos creados a propósito. El número de letras de cada palabra se identifica con la secuencia numérica decimal que se quiere recordar. Por ejemplo, en el caso del verso «Con diez cañones por banda», del poeta español José de Espronceda:
puede identificarse con la secuencia 34735; es mucho más fácil de recordar el verso que el número, pues las palabras poseen un sentido. Recordar cifras del número a tiene muchos seguidores; practicar mnemonics con las cifras de la constante e es menos conocido, pero no menos atractivo. En Internet existen frases (en Inglés) como esta:
We present a mnemonic to memorize a constant so exciting that Euler exclaimed: '!' when first it was found, yes, loudly '!'. My students perhaps will compute e, use power or Taylor series, and easy summation formula, obvious, clear, and elegant!
donde el signo «!» representa por convenio al dígito cero. Si se cuentan las diferentes cifras correspondientes a palabras consecutivas, se obtendrá la secuencia:
2718281828459045235360287471352662497757
que resume las 40 primeras cifras.

§. La constante de Euler-Mascheroni
Hay tres constantes matemáticas que destacan por encima de todas las demás y que están muy relacionadas con Euler. La más famosa es π, y después, e. La tercera es conocida con la letra griega γ, y aunque Euler ya la definió en 1734, tres años después de hacer lo propio con el número e, comparte la paternidad del hallazgo con el matemático italiano Lorenzo Mascheroni, por lo que γ es denominada constante de Euler-Mascheroni. Un poco injustamente, como han hecho notar algunos especialistas, pues el mérito más relevante de Mascheroni parece haber sido calcularla, en 1790, con 32 decimales..., y tres errores: en el 19, 20 y 21.
Se trata de una constante puramente aritmética; si tomamos en consideración la antiquísima serie armónica:

se constata que es divergente, es decir, que el límite de su suma tiende a ∞ (la primera prueba rigurosa de ello se atribuye a Jakob Bernoulli).
Euler tuvo la idea de comparar el crecimiento de esta serie divergente con el ln(n). Si se hace la resta:

término a término, se obtiene:

Esta diferencia se estabiliza y, en el límite, da una cantidad constante:

Lo que buscaba Euler era un modo de describir el crecimiento de la serie armónica, y concluyó que tenía un crecimiento logarítmico. Euler denominó a esa constante con la letra mayúscula G, por lo que el uso de la letra griega γ se debe posiblemente a Mascheroni (1790). Euler la computó en 1736 hasta la cifra 19 usando una fórmula propia, los llamados números de Bernoulli, B_n, si lo hubiera intentado por la vía convencional de sumar términos de la serie armónica y restar el logaritmo hubiera fracasado; con todo, y ser un calculista fantástico, pues la convergencia de la serie de la definición es lentísima.
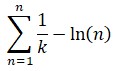
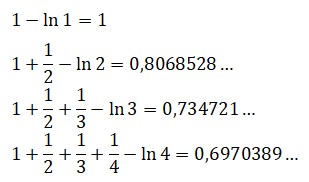
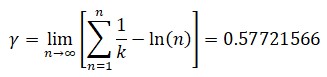
El alemán Weierstrass encontró que la definición de Γ(x) dada por Euler era equivalente a la derivada:

Γ'(1) = -γ

lo que permite establecer una inesperada relación entre la función gamma y la constante de Euler-Mascheroni.
De la constante γ no se sabe casi nada; ni siquiera si es racional o irracional, y, como es lógico, se desconoce si es trascendente. Sí se sabe que en el caso de que sea racional, lo que pocos especialistas creen, su denominador tendría por lo menos 244663 dígitos en base 10, un número que de reproducirse al mismo tamaño que el presente texto ocuparía casi todo este libro.
La constante y aparece con frecuencia en análisis (como en las llamadas funciones de Bessel) y tiene aplicaciones en mecánica cuántica, en especial en la regularización dimensional de los diagramas de Feynman, claves en electrodinámica.
Sin embargo, no hace falta ir tan lejos para encontrarse con γ. Si se coleccionan cromos, de esos que aparecen en los paquetes de chicle o que se encontraban en las tabletas de chocolate, el coleccionismo pasa a ser un hábito inequívocamente euleriano. Si la colección completa es de n cromos, se necesitan aproximadamente N compras del producto que los contiene para tenerlos todos:

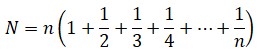
Lorenzo Mascheroni
La primera vocación de este sacerdote y matemático italiano (1750-1800) fue la poesía. Su adscripción política era más bien liberal y afrancesada, por lo que en 1797 fue nombrado diputado en Milán; fue enviado entonces a París para colaborar con Legendre en la implantación del Sistema Métrico Decimal, pero a causa de la ocupación austríaca de Milán ya no pudo regresar a su patria, pues murió al año siguiente.

Un conocido problema del libro de Mascheroni es el problema de Napoleón (pues se dice que fue Napoleón quien se lo planteó al matemático) que consiste, en cada una circunferencia, determinar los cuatro vértices de un cuadrado usando solo el compás.
En 1797 publicó su obra magna, Geometría del compasso(Geometría del compás), y su prólogo, en verso, estaba dedicado a su amigo Napoleón, quien era, además, un matemático aficionado, como demuestra el teorema que lleva su nombre. En esta obra demuestra que la exigencia griega de admitir solo construcciones geométricas usando en exclusiva la regla y el compás era menos estricta de lo que se creía: sobra la regla, pues todo lo construible lo es usando solo el compás. Esta tesis, hoy bastante trivial, era sorprendente en su época; en enunciarla, sin Mascheroni saberlo, le había precedido el matemático danés Georg Mohr (1640-1697), quien la publicó en Euclides dánicas (Euclides danés; en 1672). Su conexión con Euler, y la inmortalidad matemática, le llegó con su libro Adnotationes ad calculum intégrale Eulerí (Anotaciones de cálculo integral de Euler), que. aunque no aportó avances significativos, contiene la constante γ y su cálculo (erróneo) con 32 decimales. Desde entonces a γ se la denomina constante de Euler-Mascheroni.

Si se intenta resolver el problema haciendo suma y hay suficientes cromos, se tardará muchísimo y los errores se irán acumulando (incluso usando una calculadora de bolsillo). Es más aconsejable recurrir a Euler y sumar solo dos cosas:

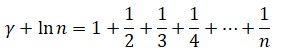
La constante γ y los números primos
La constante γ es mucho menos frecuente que π o e. No es difícil hallar una fórmula que relacione a las tres:
El propio Euler encontró conexiones entre γ y la función zeta, como:
y hay fórmulas que conectan directamente a γ con los números primos, como la fórmula de Franz Mertens (1840-1927):
donde los p son solo números primos. Ya tenemos a γ, la función zeta y los números primos involucrados. Cabe poca duda de que la tercera constante de Euler es importante, y que lo será aún más.

El logaritmo lo dará la calculadora y en cuanto a γ, aquí aparece con cincuenta decimales:

0,57721566490153286060651209008240243104215933593992,..

Otro ejemplo algo más abstracto sería el siguiente: si se quiere saber cuántos divisores de n hay en promedio entre 1 y n, se puede emplear la expresión ln n + 2γ -1. Se trata de una aproximación, tanto más exacta cuanto más grande se hace n y más divisores tiene.

La fórmula de Euler-Maclaurin, en detalle
La expresión de la fórmula de Euler-Maclaurin puede resultar intimidante. En su forma más usual se presenta como:
donde los B_k, son los números Bernoulli y las f⁽ⁿ⁾ son las sucesivas derivadas de f. Una aplicación de la fórmula consiste en hacer n = ∞, con lo que en la izquierda puede colocarse una serie, y, en ocasiones, mejorar su convergencia. Euler utilizó este truco en el problema de Basilea, como se verá más adelante.

§. Una suma que suma lo insumable
En 1735, la última de las grandes aportaciones de Euler en el campo del análisis durante su primera estancia rusa es una fórmula de gran utilidad que permite calcular de modo aproximado una integral a base de sustituirla por una suma, o calcular aproximadamente una suma sustituyéndola por una integral. Descubierta también de forma independiente por el escocés Colin Maclaurin, la denominada fórmula de Euler-Maclaurin funciona como sigue: dada una función f(x), cuando se habla de sumarla, se suele pensar en dos cosas, vagamente relacionadas, pero distintas. Cuando se la restringe a valores enteros se obtiene una suma:

y cuando se la suma para todo x se obtiene una integral:

Parece evidente que hay algún vínculo entre s(n) e i(n), pero la primera es una suma discreta, mientras la segunda es continua. La fórmula de Euler-Maclaurin es un resultado que permite, en muchos casos, pasar de un lugar al otro. Si se conoce s(n), permite evaluar i(n), y si se conoce i(n) se puede calcular s(n).

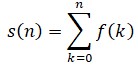
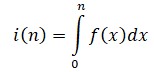
§. El problema de Basilea: el principio
A su llegada a San Petersburgo el salario de Euler era de 300 rublos, e incluía alojamiento, leña para el hogar y aceite para las lámparas. Tras acceder en 1733 al cargo de profesor de matemáticas que había dejado vacante Daniel Bernoulli, la Academia aumentó su estipendio a 600 rublos, una cantidad que se vería nuevamente incrementada ese mismo año gracias a las clases y exámenes que empezó a impartir, a propuesta del barón Von Münnich, en la escuela local de cadetes. La seguridad económica derivada de sus nuevas responsabilidades permitió a Euler contraer matrimonio con Katharina Gsell, hija de Georg Gsell, un pintor de origen suizo empleado en la Academia de arte por expreso deseo del zar Pedro I, la ceremonia tuvo lugar el 27 de diciembre de 1733, y la joven pareja se trasladó al poco a una casa de madera, «extremadamente bien amueblada», en palabras del propio Euler, ubicada en la isla de Wassiljevski, a poca distancia de la sede de la Academia de Ciencias. Un año después veía la luz el primer hijo del matrimonio, Johann Albrecht, que fue apadrinado por Von Korff, a la sazón presidente de la Academia. Este hecho atestigua la gran estima en que se tenía a Euler en el seno de la institución, lo que no resulta de extrañar vistas las aportaciones hechas hasta el momento por el matemático suizo. Sin embargo, lo mejor estaba aún por llegar. Apenas un año después, en 1735, Euler iba a deslumbrar a toda la comunidad matemática con un destello de genio: la solución al problema de Basilea.
En los países anglosajones hay un gusto bastante extendido por lo que allí se llama los Top Ten. Son muchos los libros o programas de televisión dedicados a glosar los 10 primeros de cualquier tema. Inmersos en esta tradición se han elaborado incluso listas de realizaciones científicas, clasificadas por su belleza intrínseca, su repercusión práctica o su altura intelectual. Una de esas listas se realizó sobre cuál era la mejor de las muchas aportaciones de Euler. Con otras figuras no hubiera podido hacerse, pues hubiera faltado material para llegar a los 10 temas, pero con Euler no hay peligro: presenta resultados suficientes para una lista larguísima. Y bien, ¿cuál ocupó la primera posición? Pues la fórmula

que expresa, precisamente, la solución al problema de Basilea El origen del problema es desconocido pero obedece a una duda razonable. Conocida desde antiguo la serie armónica, que es la serie que corresponde a la suma de los inversos de los números:

y sabido que es divergente, parece lógico preguntarse a continuación por la suma de los inversos de los cuadrados, que parece convergente, pero que no se sabe a qué número exacto converge:

Y ni siquiera se sospecha. Si se suman experimentalmente varios miles de términos de esa serie, se nota que se aproxima a un cierto valor, pero también se cae en la evidencia de que la serie converge muy lentamente, tanto que resulta casi impensable pasar de los dos decimales de aproximación.
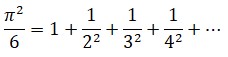
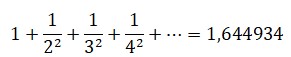
Parece ser que fue el sacerdote y matemático italiano Pietro Mengoli (1626-1686) el primero en referirse al problema de Basilea, pero fue Johann Bernoulli quien lo dio a conocer a Euler, quien ya en 1729 lo mencionaba en una carta a su colega Goldbach. En 1730 el problema ya estaba en las mentes de todos los matemáticos y ejercía entre ellos un atractivo similar al que ejercería el denominado último teorema de Fermat.
Euler abordó el tema tan seriamente que se cuenta con varias demostraciones suyas de la solución. Todas son muy ingeniosas y algunas muy seductoras para los profesionales del análisis, en especial] una de ellas, publicada en 1741 y que hace referencia a técnicas del cálculo integral, la demostración considerada «canónica» es la que los expertos denominan tercera demostración, y es la más elegante desde el punto de vista del lector no especializado. Se encuentra bosquejada en el anexo 2.

«He encontrado ahora y contra todo pronóstico una expresión elegante para la suma de la serie que depende de la cuadratura del círculo... He encontrado que seis veces la suma de esta serie es igual al cuadrado de la longitud de la circunferencia cuyo diámetro es 1.»
Leonhard Euler

La resolución del problema fue algo inesperado por la comunidad científica, y la noticia de la solución al problema de Basilea dio la vuelta al mundo; una vuelta extremadamente modesta, ya que el mundo era entonces bastante restringido, el mundo culto mucho más y los medios de comunicación, salvo el correo, de alcance muy limitado.
Euler preparó el camino a su solución con cálculos y maniobras preliminares. Por ejemplo, recurrió a sumaciones previas propias del método de Euler-Maclaurin para probar, antes de empezar, una aproximación mejor que 1,64. A base de ingenio, Euler encontró hasta seis cifras exactas y se situó en el punto de partida con:

Por otra parte, a alguien acostumbrado a las potencias de π y con una memoria tan fabulosa como la suya, no debió escapársele que 1,644934 se parecía mucho a π²/6. De manera que hay que suponer que, al iniciar el espinoso camino, ya sabía de antemano dónde iba a desembocar, una ventaja que no tenía ninguno de sus contemporáneos. Se supone que el ingenio de Euler ahorró el equivalente de sumar unos 30 000 términos de la serie original.

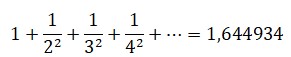
§. El problema de Basilea: el final
Una vez resuelto el problema de Basilea estrictamente dicho, Euler no se detuvo aquí. Regresemos a la función zeta, de la que ya se habló en el capítulo anterior.

Para x = 1, se obtiene la serie armónica, y para x = 2, la serie del problema de Basilea. Euler profundizó en la cuestión y, a partir de sus trabajos con el problema de Basilea, obtuvo expresiones para las series de potencias pares:

hasta ζ(26), con fórmulas cada vez más aparatosas en las que el número π; aparecía siempre elevado a la potencia n que corresponde a ζ(n). En 1739, Euler llegó a una expresión general:

que involucraba a los números B_k, los números de Bernoulli, j. sobre los que se tratará en el capítulo 4.
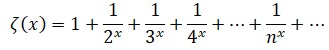
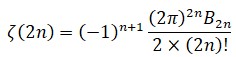
Los números B_k se van haciendo cada vez mayores e intratables; para hacerse una idea de ello basta con transcribir el miembro cincuentavo:

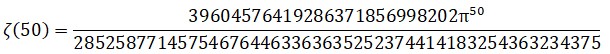
El primer programa informático de la historia
Ada Byron (1815-1852), conocida más tarde por Ada King, condesa de Lovelace al contraer matrimonio con William King, era hija de lord Byron, al que ni siquiera llegó a conocer, pues sus padres se separaron al mes de su nacimiento. No tuyo que superar ninguna dificultad para cultivar sus dotes matemáticas, pues su madre las consideraba un eficaz antídoto contra las posibles veleidades literarias de su hija; el odio por la vida y obra de su ex-marido era profundo y persistente. La figura central en la vida científica de Ada fue el célebre matemático Charles Babbage (1791-1871), responsable del desarrollo de la primera computadora de la historia.

La máquina analítica da Charles Babbage para la que Ada King desarrolló un programa para calcular los números da Bernoulli.
Ada creó para la máquina un algoritmo recurrente que, una vez implementado con tarjetas perforadas permitían el cálculo automático de los números de Bernoulli. El procedimiento ideado por Ada es, desde el punto de vista informático, un auténtico programa, el primero de la historia. En los años 80 del siglo XX el Ministerio de Defensa de Estados Unidos denominó ADA a su lenguaje computacional MIL-STD-1815 (el número coincide con el año de nacimiento de Ada) en homenaje a su persona.

De hecho, el primer software de la historia, es decir, el primer programa destinado a efectuar un cálculo automático en un computador calculaba los números de Bernoulli por un procedimiento recurrente. Lo llevó a cabo Augusta Ada King, condesa de Lovelace, en 1843, e iba destinado a funcionar —y era informáticamente impecable— con el computador mecánico de Charles Babbage.
Los valores impares de ζ(n) son muy difíciles de calcular y en la actualidad se sigue luchando con ellos. Como es natural, el primero coincide con la serie armónica:

Y el tercero, que es un número irracional, se denomina constante de Apéry:

Euler aún dio un paso más, un paso casi de visionario. Se adentró progresivamente en los dominios de la función zeta, y, por consiguiente, en el terreno de los números primos, al transformar la suma infinita de su función ζ(n) en un producto que involucraba a los números primos. Quien lo desee puede seguir con profundidad a Euler en su camino en el anexo 3.

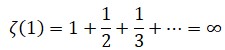
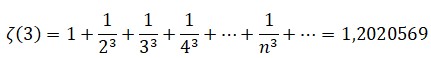
§. Los puentes de Königsberg
En los primeros meses de 1735, Euler cayó víctima de una enfermedad cuya naturaleza es imposible determinar a partir de las fuentes biográficas de las que se dispone, pero que se sabe cursó con una «fiebre feroz» que llegó a amenazar su vida. Tras congratularse de su recuperación, tanto en su nombre como en el de «los matemáticos de todo el mundo», Daniel Bernoulli le confesó que «nadie guardaba esperanzas de que se recuperara de ella [la enfermedad]». Como consecuencia del episodio, el ojo derecho de Euler quedó seriamente afectado, y tres años más tarde perdía su uso definitivamente. Todo y con ello, Euler siguió trabajando a su ritmo acostumbrado, y apenas un año después abordaba una cuestión radicalmente distinta a sus trabajos anteriores, el conocido como problema de los puentes de Königsberg. Hay matemáticos que sitúan este particular episodio en la cima de los descubrimientos de Euler, lo que es una distinción extraordinaria. ¿Por qué? Es un problema geométrico que no parece geométrico, pues no implica figura reconocible ni medida alguna: se razona solo sobre la posición de determinadas líneas y puntos y sobre el modo de ir de unos a otros. Es una fascinante historia sobre algo poco corriente.
En la época de Euler, Königsberg era una ciudad de la Prusia más oriental, situada en aguas bálticas. Denominada en la actualmente Kaliningrado, es mucho mayor, pertenece al territorio ruso y es un enclave geográfico situado entre Polonia y Lituania, fruto de las guerras más que de la historia.

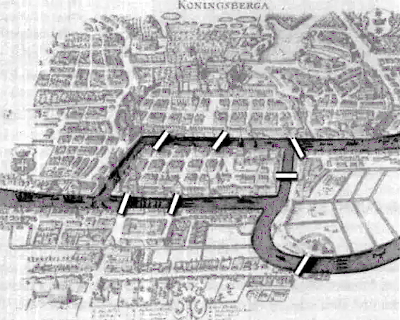
Grabado de la ciudad de Königsberg en la época de Euler, con detalles de los siete puentes

Como hoy, la ciudad estaba regada por el rio Pregel, cuyos brazos, al atravesarla, definían una isla y tres masas de tierra, que quedaban separadas por sus aguas, pero conectadas por siete puentes; estos permitían a sus habitantes atravesar el río y pisar tierra firme, tal y como se observa en la ilustración de la página anterior.
Tan idílico escenario ya determinaba numerosos paseos posibles a través de la ciudad y cruzando los puentes, pero algunos paseantes se preguntaron por la posibilidad de convertirlo en ciclo cerrado, a saber, ¿era posible pensar en un paseo que empezara y terminara en el mismo lugar, pero que solo pasara una vez por cada puente? Eso ya no es un simple paseo, sino un acertijo matemático.
Pasear de todos los modos posibles no es una tarea imposible. Al fin y al cabo, tan solo hay siete puentes y resultan unos cuantos miles de paseos a seguir. Pero la situación sería algo kafkiana porque, cualquier camino elegido, se partiera del punto del que se partiera, si pasaba por un puente una sola vez, desembocaría pertinazmente en un punto diferente del de partida. Podía sospecharse, con cierta razón, que el paseo buscado era tan inaccesible como el castillo del autor checo en su conocida narración.
En tiempos de Euler no era raro el planteamiento de enigmas semejantes, los cuales, con suerte, se resolvían y se convertían en cabezas de puente de teorías matemáticas. Que llegaran a convertirse en iniciadores de toda una rama, rica y frondosa, de las matemáticas ya era menos común, pero eso es lo que ocurrió precisamente con los puentes de Königsberg.
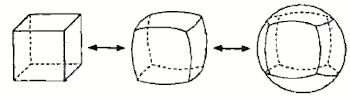
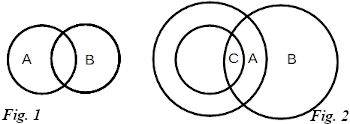
Euler tuvo la idea de, a partir de la representación esquemática de la ciudad (figura 1), prescindir de la forma de todos las componentes y sustituirlos por un grafo, de manera que se consideren los puntos de tierra como vértices y los puentes como camino (figura 2). Razonando de modo exclusivo sobre el grafo resultante, Euler extrajo sus conclusiones.
Un grafo es un dibujo en forma de red, que consta de dos partes: los puntos llamados nodos o vértices y los trayectos entre ellos, denominados aristas o arcos.
El grado de un nodo es el número de arcos que concurren en un nodo.

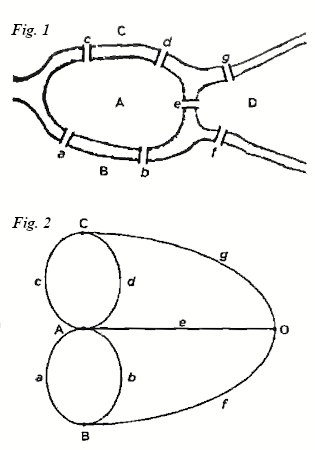
El problema de los puentes de Königsberg pretendía encontrar un circuito euleriano.

Del camino seguido por el paseante se dirá que es un camino eule- riano cuando permita discurrir por dicho itinerario pasando una sola vez por cada arco. El camino será un circuito euleriano (figura 3) cuando empiece y termine el recorrido en el mismo nodo. Esto es, precisamente, que sea un circuito euleriano, lo que define para muchos lo que sería un «paseo perfecto».

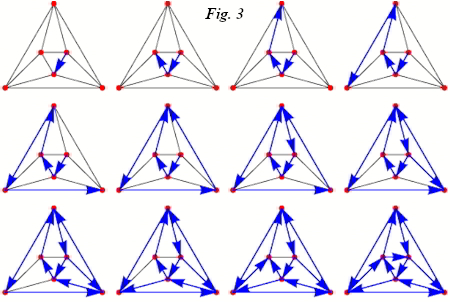
Un circuito euleriano empieza y termina en el mismo punto pasando una sola vez por todos los arcos o aristas del grafo, en este caso en forma de octaedro.

Así pues, lo deducido por Euler puede escribirse así: Llamemos n al número de nodos de grado impar.
a. Si n = 0 el grafo contiene al menos un circuito euleriano.
b. Si n = 2 hay al menos un camino euleriano pero no un circuito.
c. Si n > 2 no hay ni camino ni circuito.
Dado que, en el caso que nos ocupa, n = 4, los paseantes de Königsberg se quedaron sin «paseo perfecto». Si le hubiesen preguntado a Euler, les podría haber dicho que la adición o supresión de un simple puente habría hecho su problema resoluble.

§. Un problema relacionado: el paseo del caballo

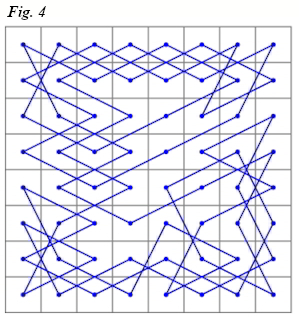Otra cuestión también estudiada por Euler y que de algún modo se relaciona con el tema de los grafos es el problema de ajedrez del paseo del caballo, abordado en 1759 en Solution d'une question curieuse que ne paraît soumise á aucun analyse (Solución a una cuestión curiosa que no parece sujeta a ningún análisis). El problema consistía en, partiendo de cualquier punto del tablero de ajedrez, conseguir un recorrido para el caballo de manera que pisara todas las casillas. Euler encontró la solución, poniendo de paso el fundamento a los posteriormente denominados grafos hamiltonianos, que presentan caminos que pasan una sola vez por cada vértice y vuelven al punto de partida (figura 4).

§. El nacimiento de la topología
Euler denominó geometriam situs a las cuestiones relacionadas intelectualmente con la de los puentes, pero fue Johann Benedict Listing (1808-1882) quien acuñó, en 1847, el término de topología que permanece en la actualidad. La topología es una robusta rama de las matemáticas que agrupa conceptos considerados en general poco geométricos, como dentro y fuera, cerca y lejos, orientable y no-orientable, conexo y no-conexo, fronterizo o no, continuo y discontinuo, entre otros. La topología se ocupa de cuestiones en apariencia alejadas, de lo que tradicionalmente se entiende por matemáticas. Así, en su marco han encontrado solución problemas tan dispares como saber cuál es el número mínimo de colores para pintar cualquier mapa convencional; son 4.

Teorema de la bola peluda
Representemos intuitivamente una esfera recubierta por pelos lisos y lacios, suponiendo que en cada punto de la esfera crece un pelo. A continuación, se considerará la proyección sobre el plano tangente a la esfera en el punto en que crece el pelo, el conjunto de estas proyecciones es semejante a un campo de vectores tangentes a la esfera, lo que se denomina espacio tangente. El objetivo es «peinar» estos pelos alisándolos sobre la superficie de la bola pero evitando las discontinuidades, es decir, el peinado no puede tener raya; ningún pelo puede cambiar bruscamente de dirección con respecto a los otros. El teorema afirma entonces que es imposible peinar todos los pelos sin que en el total de la esfera nos veamos obligados a hacerlo con raya. Cualquier intento causará al menos un rizo o remolino. Basta con echar un vistazo a la realidad que nos rodea para comprobar el teorema: si pretendemos peinar a un niño sin raya (un occipucio con el típico remolino), siempre aparecerá un remolino en algún lugar.

También se ha demostrado rigurosamente que siempre hay dos puntos antípodas sobre la superficie terrestre con igual presión y temperatura, o que cuando se arruga un folio y se superpone a uno liso, siempre hay un punto del primero que cae exactamente sobre el punto equivalente del segundo. También dentro de esta rama se ha desarrollado él divertido teorema de la bola peluda, que trata el concepto de dirección de un modo típicamente topológico.
Euler hizo algo más que intentar explicar el universo conocido: abrió las puertas de uno desconocido.

§. Los primeros libros de Euler
Durante su primera estancia en Rusia, Euler redactó sus primeros tratados. Los libros son densos, pero de lectura fácil, y en ellos ya brillan la excelente organización y el estilo, mostrando la legendaria claridad expositiva y amenidad de Euler. De esta época es Mechanica sive motos scientia analylice expósita (Mecánica o ciencia analítica del movimiento) donde desarrolla los aspectos físico-mecánicos de una masa puntual. Lo novedoso es que lo hace con las armas del cálculo diferencial e integral, pues lo corriente era darle a la mecánica un tratamiento puramente sintético y geométrico. En su obra aparecen ya las ecuaciones diferenciales, las masas puntuales y el movimiento de cuerpos elásticos y el de los fluidos, de manera que los tomos constituyen el primer tratado moderno de mecánica racional. Lagrange los ponderó como «la primera gran obra donde el análisis ha sido aplicado a la ciencia del movimiento».
Asimismo, dedicó un tratado a la música, Tentamen novae theoriae musicae (Una tentativa para una nueva teoría de la música) que, aunque data de 1731, no se publicó hasta 1739. Esta obra, que forma equipo con otras similares de la misma época de Mersenne, Descartes o D'Alembert, trata de la naturaleza, generación y percepción del sonido, del placer musical y de la teoría matemática de los temperamentos.
Scientia navalis (Ciencia naval) fue la primera gran obra euleriana dedicada a la ciencia naval, que cubre tanto los principios básicos de la hidrostática, la estabilidad de los buques y los conocimientos prácticos de la construcción naval y la navegación.
Asimismo, escribió memorias y artículos sobre navíos y navegación donde abordaba procedimientos alternativos de navegación que iban desde las máquinas impasibles de movimiento perpetuo a la aprovechable energía del oleaje. Lo más interesante era la utilización de un sistema de palas, premonitorio de las ruedas motrices. En 1773, como se verá, regresó al tema.
Durante los últimos años de su primera estancia en Rusia, Euler se encargaba de gran cantidad de actividades en el seno de la academia; se ocupaba de los problemas de jardinería e ingeniería, y escribía sus propios trabajos al tiempo que leía y supervisaba los ajenos. Era miembro de la comisión de medidas. Se encargaba incluso de anotar los manuscritos que llegaban a la Academia sobre la cuadratura del círculo, y de comprar papel y lápiz. Lo que más trabajo le dio fue la revisión de la cartografía rusa, por la que, sin embargo, sentía una gran admiración.
Tanta y tan variada actividad profesional como la que hemos repasado en el capítulo no impedía a Euler ver lo delicado de la situación política del país. A la guerra ruso-otomana que en 1739 acababa de terminar, se sumaba el descontento de la aristocracia local con respecto a la nutrida presencia germana en los más altos cargos del gobierno y la burocracia. Con el acceso al poder de Isabel, la hija de Pedro, en 1740, el temor de que se emprendieran fuertes purgas contra la élite de origen germano, y por extensión, con todos los extranjeros, impulsó a Euler a aceptar la oferta de empleo de la Academia de Ciencias Prusiana, con sede en Berlín.

Capítulo 3
Berlín, capital del análisis

Siendo ya una personalidad científica de primera fila, Euler atendió la llamada de Federico II, el rey ilustrado de Prusia, Su obra de esa época se abrió a otras disciplinas, como la geometría, la mecánica de fluidos o la ingeniería, pero nunca abandonó su énfasis en el análisis, al que dedicó una tema de obras para la eternidad y el estudio de un tema fundamental: el cálculo de variaciones.

«Señora, he llegado de un país donde las personas son ahorcadas si hablan» fue la respuesta de Euler a Sophia Dorothea, la reina madre del rey de Prusia cuando esta, amablemente, le reprochó a Euler su escasa participación en una conversación palaciega.
En 1741, Euler había regresado al calor de la Europa tradicional, al centro del universo iluminista y uno de los focos de irradiación de la cultura occidental, a Berlín, a la capital del reino de Prusia, donde imperaba la voluntad del más liberal de los reyes de Europa, Federico II el Grande (1712-1786). Allí coincidió con luminarias tales como François Mane Arouet (1694-1778), más conocido como Voltaire, el músico Johann Joachim Quantz (1697- 1773), el pensador Emmanuel Kant (1724-1804) o el polifacético Johann Wolfgang von Goethe (1749-1832).
A la llegada de Euler, Federico II andaba embarcado en unas escaramuzas locales por Silesia, por lo que el suizo tuvo que vivir de los préstamos de diversos conocidos hasta el regreso real, en 1746. Mientras tanto, Euler adquirió un terreno y una casa, plantó patatas y otros vegetales de subsistencia en su jardín, y se dedicó al trabajo científico como empleado de la Societas Regia Scientiarum.
Esta era una institución fundada en 1700 por el rey Federico I, por iniciativa de Leibniz. Sufrió un pequeño declive durante los años en que pasó a depender de Federico Guillermo I, quien no compartía el interés de su antecesor por las cuestiones intelectuales ni, en general, por nada que no le reportase un provecho político o militar inmediato. Por fortuna para la pervivencia de la institución, Federico II, terminados los combates en Silesia, se dedicó a cuidarla y la mantuvo en el lugar que se merecía.
Cuando Federico regresó, Euler ya había presentado un montón de artículos y había escrito varios libros. Por entonces, el presidente de la Academia era Pierre Louis Moreau de Maupertuis, y Euler dirigía la sección de matemáticas, aunque también se ocupaba, entre otras cosas, de las finanzas, la astronomía, la ingeniería y la botánica. De acuerdo con el historiador Adolf P, Yushkevich:(...) supervisó el observatorio y los jardines botánicos; seleccionó el personal, supervisó varias cuestiones financieras, y, en particular, logró la publicación de varios calendarios y mapas geográficos, cuya venta era una fuente de ingreso para la Academia. El rey también encargó a Euler problemas prácticos, tales como el proyecto en 1749 para corregir el nivel del canal de Finow (...) En tal período también supervisó el trabajo de las bombas y tuberías del sistema hidráulico de Sanssouci, la residencia real de verano.Sin embargo, el monarca no estaba satisfecho con respecto a sus méritos, como demuestran estas líneas de una carta suya a Voltaire:

Quería tener una bomba de agua en mi jardín: Euler calculó la fuerza necesaria de las ruedas para elevar el agua a una reserva, desde la que caería después a través de canalizaciones para finalmente manar en el palacio de Sanssouci. Mi molino fue construido de forma geométrica y no podía elevar una bocanada de agua basta más allá de cinco pasos hacia la reserva. ¡Vanidad de las vanidades! ¡Vanidad de la geometría!

En 1747, Euler fue nombrado miembro de la Royal Society; en 1748, ganó nuevamente el Grand Prix de la Academia de ciencias de París con una memoria sobre el problema de los tres cuerpos, cuyo contenido orientó a Alexis Claude Clairault (1713-1765) en sus propios trabajos en este campo. En 1758, fue nombrado académico por la Academia parisina, de manera que en Euler ya convergían todos los nombramientos honoríficos posibles.
Tal era su fama que cuando el ejército ruso invadió Alemania en 1760 y dañó gravemente una propiedad que el sabio suizo tenía en Charlottenburg, el general del ejército invasor, Gottlob Curt Heinrich von Tottleben, se apresuró a indemnizar a Euler y pedirle disculpas por los hechos proclamando «Yo no hago la guerra a la ciencia»; también la emperatriz rusa Isabel le envió 4000 coronas para resarcirlo de sus perjuicios.
Alrededor de 1750 alcanzó gran notoriedad la disputa acerca de la prioridad del principio de mínima acción, que König atribuía a Leibniz y Maupertuis, a sí mismo. Parece que Euler también lo había descubierto por su cuenta, pero no lo hizo público para no disgustar al que nominalmente era su jefe. Voltaire tomó partido por König y, en 1752, escribió un relato irónico (Diatriba del doctor Akakia) donde ridiculizaba a Maupertuis. Federico zanjó la polémica expulsando a Voltaire del reino, y Maupertuis, muy afectado por los hechos, se marchó de Berlín.
A partir de ese momento, todo quedó en manos de Euler, pero, a pesar de ello, no fue nombrado presidente de la Academia. En primera instancia, Federico le ofreció el puesto a Jean-Baptiste le Rond D'Alembert, una figura de prestigio inmaculado, pero con el que Euler no tenía muy buena relación. Euler se veía ya bajo la férula de otro francés; incluso mencionó que la Academia de Berlín corría el riesgo de convertirse en una copia de la francesa; y lo cierto era que los sucesivos nombramientos reales de miembros franceses —sobre todo filósofos— apuntaban en esta dirección. Pero en el curso de sus negociaciones para su nombramiento, D'Alembert se entrevistó con un resignado Euler y se quedó muy impresionado. Aquel científico de aspecto tosco tenía una memoria incomparable, dominaba todos los campos y era un prodigio matemático, por lo que resultaba incomprensible no promocionar a semejante talento. D'Alembert rechazó muy cortésmente el puesto de presidente de la Academia y le sugirió al rey que nombrara a Euler, un sabio de prestigio mundial, que, además, ya tenía en su casa Pero, como se ha dicho, las virtudes personales de Euler no incluían 1a conversación ocurrente, la discusión constante de materias artísticas, literarias o filosóficas ni las maneras cortesanas, que tanto agradaban a Federico II, quien las prefería a los conocimientos científicos de su «Cíclope matemático», mote con que designaba a Euler en su correspondencia con Voltaire. El rey desoyó el consejo de D’Alembert y se nombró a sí mismo presidente de la Academia, lo que al parecer desagradó a Euler.
A partir de ese momento, la relación se agrió; Euler, quien recibió cantos de sirena desde Rusia, decidió volver a emigrar, pero el rey Federico no se lo puso fácil; en aquel tiempo no se abandonaba así como así el servicio de un monarca, y el rey le dio largas. Finalmente, Euler fue autorizado a irse.

§. Una fórmula de Euler para poliedros
De entre todos los trabajos de Euler en su etapa berlinesa, hay uno que destaca por su difícil clasificación dentro del «mapa» de las matemáticas de su época. Al final del capítulo anterior esbozábamos los principios de un rama novedosa de las matemáticas, la teoría de grafos, inaugurada por el propio Euler con su trabajo sobre los puentes de Königsberg, y del área más general en la que aquella se inscribe, la topología. Primero de forma privada, en cartas a diversos corresponsales en 1750-1751, y públicamente en un artículo de 1758, Euler regresó a esta segunda, con un resultado extraordinario: su fórmula para poliedros convexos de C caras, A aristas y V vértices:

C - A + V = 2.

A principios de la década de 2000, los lectores de la prestigiosa revista Mathematical inlelligencer votaron para establecer las que eran, en su opinión, las más bellas fórmulas matemáticas de la historia; esta fórmula sobre poliedros obtuvo el segundo lugar, por detrás de otra también estrechamente asociada con Euler, e^πi + 1 = 0.
La expresión numérica C - A + V es, como se diría hoy, un invariante topológico. Un invariante topológico es aquella propiedad de una superficie que se conserva sin importar las sucesivas transformaciones a las que se somete dicha superficie; en concreto, las que resultan de deformarla sin romperla. La superficie de la que la fórmula de Euler es un invariante topológico, es la esfera y, por ende, lo es también de cualquier poliedro tridimensional homeomorfo a ella, es decir, de los cuerpos que pueden obtenerse de deformar la esfera sin romperla.
La fórmula C - A + V = 2 se acostumbra a designar como fórmula de Euler-Descartes, ya que, aunque fue Euler quien la dio a conocer al mundo oficialmente, René Descartes (1596-1650) ya la había descubierto en 1649, en realidad descubrió otra cosa que implicaba el resultado de Euler, aunque murió antes de poder publicarla.

§. Características de un poliedro
Tómese un poliedro convexo cualquiera; en realidad, lo que Euler enunció vale para cualquier poliedro, deformable en uno convexo, con tal que esté formado por una sola pieza, no por dos poliedros unidos por un punto o por un segmento, y que no tenga agujeros.

Llamemos V, A y C al número de vértices, aristas y caras de un poliedro de las características mencionadas más arriba. Euler constató, como se ha visto, que se verifica:

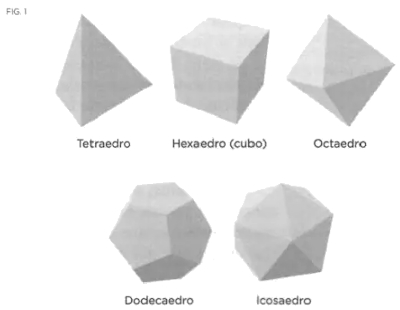
C - A + V = 2.

Esta sorprendente relación es válida siempre, hay que insistir, cualquiera que sea la forma del poliedro, por intrincado que sea su diseño y por estrambóticas que sean sus caras (con una excepción: los poliedros «estrellados» cuyas caras se interpenetran). La observación de Euler no es nada evidente, aunque puede ser comprobada fácilmente, tanto en los armónicos y simétricos sólidos platónicos (figura 1), como en cualquier «desgarbado» poliedro como el que se ilustra en la figura 2.
Se trata de una fórmula numérica, independiente de las características puramente geométricas de la figura. No depende de la forma del poliedro, pues es una propiedad de cualquier poliedro convexo sin agujeros.
Actualmente, se consideran a nivel elemental ya no simples poliedros, sino superficies, que se denominan S, con agujeros y sin ellos, y el número Χ(S) = C - A + V se conoce como característica de S. Para las superficies homeomorfas a la superficie esférica, como los poliedros, la característica vale 2. Para el toro (figura 3), o la botella de Klein (figura 4), y demás superficies homeomorfas a ellos, la característica vale 0. Para superficies tridimensionales de género g, el género g viene a ser algo así como el número de agujeros que tiene S, se verifica:

Χ(S) = C - A + V = 2 - 2g

y a la característica se la llama característica de Euler-Poincaré.

La homeomorfía
La denominación puede sonar extraña» pero el significado de homeomorfía (del griego homoiós, «misma» y morphé, «forma») es bien conocido por los matemáticos. Se refiere a toda cosa que se pueda derivar de otra (y viceversa) por simple deformación, sin rotura, de modo continuo. Por ejemplo, el cubo de la figura es homeomorfo a una esfera.
Los matemáticos, en especial los topólogos, llaman a esos cuerpos, que se transforman el uno en el otro por simple deformación, sin rotura, cuerpos homeomorfos. Un ejemplo clásico de figuras homeomorfas o topológicamente equivalentes son una taza y una rosquilla, pues pueden deformarse continuamente el uno en el otro.
La taza y la rosquilla son homeomorfos por una razón geométrica tan impensada como la que ambos tengan un solo agujero, Se dice que el número de agujeros de una superficie es un invariante topológico, pues no varía cuando media una homeomorfía.

Es una expresión que ha hecho fortuna en matemáticas y forma parte de disciplinas tan abstractas como el álgebra homológica. La fórmula:

C - A + V = 2 - 2g

fue enunciada explícitamente en 1813, por Simón Antoine Jean L'Huillier (1753-1840). Su origen es, como hemos visto, inequívocamente euleriano.

§. Regreso a la teoría de números: la conjetura de Goldbach
La correspondencia de Euler con Goldbach no se resintió del traslado del primero a Berlín y así, en una carta, fechada el 7 de junio de 1742, al año de la llegada de aquel a la capital prusiana, Goldbach le sugería que todo entero par era la suma de dos enteros, p y q, donde o valían 1 o eran primos impares. El intercambio de ideas continuó hasta que Euler dio con una formulación de la sugerencia que sería definitiva y cuyo enunciado es quizá la conjetura más famosa de toda la historia después del teorema de Fermat:
Todo entero par mayor que 2 puede expresarse como suma de dos primos.
Es la conjetura de Goldbach, llamada así en honor de quien la planteó, aunque fuera con otras palabras. Se la conoce también como conjetura fuerte de Goldbach en contraposición a la conjetura débil de Goldbach, matemáticamente más sencilla, que postula:

Todo número impar mayor que 7 puede escribirse como suma de tres primos impares.

La conjetura fuerte implica la débil, pero no al revés. La demostración es relativamente sencilla; si n es impar y mayor que 7, es que n = p + 3 > 7, y, por tanto, p es par y p > 7 - 3 = 4. Si se cumple la hipótesis fuerte de Goldbach, p es suma de dos primos, además, impares, pues, p > 2 y par. Por tanto n = p + 3, con p igual a la suma de dos primos impares. Luego, n es suma de tres primos impares, como se quería demostrar. La conjetura fuerte implica la débil.
La conjetura fuerte de Goldbach parece cumplirse para cualquier número par, e incluso, de más de una manera:

En diversos sitios de Internet, se hallan sumas de tipo Goldbach destinadas a demostrar que la conjetura se cumple siempre, con independencia del número par que se elija Por ejemplo, el 1000:

1000 = 179 + 821 = 191 + 809 = 431 + 569 = -19 + 1019.

Asimismo, se puede elegir una suma con primos impares, uno negativo, para ver que la conjetura de Goldbach va más allá de los simples números naturales. Incluso pueden hallarse en Internet programas informáticos para proporcionar sumas de Goldbach para cualquier número razonable que se elija siempre y cuando no sean números muy grandes. También se pueden hallar sumas de Goldbach que involucran parejas de primos increíblemente desiguales en tamaño, como por ejemplo esta;

389965026819938 = 5569 + 389965026814369.

En esta pareja, hallada hace poco por el numerólogo Jorg Richstein, uno de los dos sumandos es de 4 dígitos, mientras que el otro tiene 15 y ambos son primos.

Christian Goldbach
Matemático originario de Prusia (1690-1764), residió la mayor parte de su vida en Rusia y trabajó como cazatalentos para la Academia de San Petersburgo, donde también desempeñó el cargo de secretario. Amigo de Leibniz, Abraham de Moivre. Nicolaus Bernoulli (y otros miembros de su distinguida familia) y Euler, apoyó fuertemente la candidatura de este a un puesto en la academia y fue un elemento determinante en su viaje a Rusia. Llegó a ejercer la tutoría del zarevich Pedro II y desempeñó altos puestos en el ministerio ruso de asuntos exteriores, donde trabajó como criptógrafo. Dedicó sus esfuerzos profesionales a muchos ámbitos y legó algún resultado perdurable en el campo de las series, sobre todo trabajando en colaboración con Euler La personalidad de este último parece haberlo estimulado de un modo especial} pocos conocen, por ejemplo, que Goldbach, seguramente no capacitado para resolverlo, fue quien interesó a Euler por el problema de Basilea, cuya solución haría a este famoso, La correspondencia entre Euler y Goldbach, extensa y repleta de matemáticas, llega casi a las 200 cartas. El aprecio que Euler sentía por Goldbach queda de manifiesto al elegirlo padrino de su primogénito.
Influencia de la conjetura de Goldbach
Actualmente. Goldbach es recordado no por sus teoremas, sino por la conjetura que lleva su nombre. En 1992, apareció la novela El tío Petros y la conjetura de Goldbach, de Apóstolos Doxiadis; el editor Faber and Faber ofreció un premio de un millón de dólares, válido por dos años, a todo el que encontrara una solución. Con toda probabilidad sabía que no iba a recibir respuesta. La conjetura, hasta ahora, solo se ha probado en la ficción; en una película española, la habitación de Fermat, dirigida, en 2007, por Luis Piedrahíta y Rodrigo Sopeña.

Hasta la actualidad nadie ha podido probar ninguna de las dos conjeturas. La «débil» puede considerarse casi demostrada, pues se sabe que es cierta para todos los números mayores que 10¹³⁴⁶. Para poder presumir de que la conjetura débil de Goldbach está probada, hay que proceder a demostrarla en los casos pendientes: empezar con 7 y llegara 10¹³⁴⁵, un salto de complejidad que llevaría a cualquier máquina existente que intentara realizar el cálculo un tiempo, contado en segundos, superior al número de átomos del universo.
Con la conjetura «fuerte» de Goldbach, la situación está más clara: no existe prueba alguna Ni Euler pudo con ella Se ha podido comprobar, con supercomputadores Cray, para números enormes, hasta 10¹⁸, pero la prueba permanece en el limbo de los desafíos intelectuales sin resolver.
Se ha llegado a resultados admirables, como el del matemático chino Chen Jingrun (19:13-1996), quien probó ya, en 1966, que todo número lo bastante grande se podía descomponer en suma de otros dos, uno primo y el otro producto de, a lo más, dos primos.

§. El cálculo de variaciones: máximos y mínimos
El cálculo de variaciones puede considerarse una generalización del cálculo, y por tanto, se incluye firmemente en el campo del análisis. Se ocupa de encontrar el camino, curva, superficie, etc., para la cual una función determinada posee un valor estacionario; normalmente, un valor máximo o uno mínimo.
Es de fundamental importancia en física y, en particular, en ámbitos prácticos como la elasticidad o la balística, de gran interés ya en la época de Euler. No es de extrañar que Euler llegará a él, en 1744, a los tres años de establecerse en Berlín, desde el estudio de la física; en concreto, como se verá, del principio de mínima acción en el ámbito de la mecánica.
Como casi todos los grandes temas de las matemáticas, el tema general de los máximos y mínimos viene de muy lejos.
Se puede pensar en un problema típico, el problema —o mejor dicho, leyenda— de Dido. Dido, reina de Tiro, tras huir acompañada de sus últimos fieles, llegó a las costas de la ciudad que sería su reino, Cartago. Allí, suplicó a Jaibas, el rey del lugar, un pedazo de tierra donde poder asentar a su gente y este se lo concedió, pero con una condición; los dominios de Dido serían aquellos que la reina consiguiera encerrar dentro de una simple piel de toro. Para hacer la explicación más fácil, se puede suponer que la costa es recta, sin golfos, ni bahías, ni cabos, ni promontorios.
La reina empezó por cortar en una tira finísima la piel en cuestión y la convirtió en una cinta de longitud considerable, que unió por los extremos (figura 5); luego, aplicó la condición básica de los isoperímetros, es decir, de las superficies de igual longitud de frontera. Una parte de la frontera era el mar; el resto de frontera debía contener el área máxima La solución es que la cinta de piel de toro adopte la forma de una semicircunferencia con el centro en la costa (figura 6).

El problema de Dido es un problema de perímetros iguales típico, como muchos que se dan en el mundo físico. Forma parte de una clase más extensa de problemas, que en el fondo se parecen, pues lo que se está buscando es un extremo —máximo o mínimo— dadas unas condiciones iniciales inamovibles.
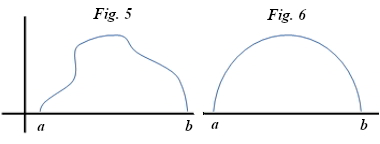
Un ejemplo muy claro es de origen antiquísimo, pues ya se lo planteó Herón de Alejandría (ca. 10-70) con la reflexión de la luz. Se apercibió de que el camino a seguir por un rayo que va de A a B reflejánd ose en un espejo sigue la trayectoria en que el trayecto es mínimo (figura 7).

El trayecto de un rayo de luz reflejado en una superficie que va de A a B mide lo mismo que la recta que va de A a B. Por tanto, el espacio recorrido K mínimo.

Con el tiempo, Fermat emitió su ley de refracción, (llamada ley de Snell), que dice que

n₁senθ₁ = n₂senθ₂

Y aquí ya no era mínimo el espacio recorrido, o no exactamente. Lo que era mínimo era el tiempo empleado por el rayo de luz para ir de A a B, y el espacio era en realidad, como se diría hoy, una función del tiempo: e = v×t, siendo v la velocidad del rayo de luz en el medio que lo refractaba. Y de este modo ya se está haciendo mínima una función: f(t) = v×t (figuras 8 y 9).

Pierre de Maupertuis
Aunque su familia edificó su fortuna en la piratería, su padre era un ex-corsario ennoblecido, y se le presentaron oportunidades profesionales en la milicia.
Pierre Louis Moreau de Maupertuis (1698-1759) se decidió por la ciencia, destacando como matemático, físico, naturalista y astrónomo, seguidor de las teorías newtonianas, Maupertuis emprendió una expedición a la lejana Laponia para recolectar datos sobre la medida del meridiano terrestre y concluyó que la Tierra estaba achatada por los polos, confirmando así la teoría de Newton. Maupertuis también fue el primero en enunciar el principio de mínima acción. Algunos historiadores han puesto en duda la prioridad de Maupertuis pues sostienen que el principio ya era conocido y utilizado por Euler. Las relaciones entre Maupertuis, una de las figuras más destacadas de la Academia prusiana, y Euler, atravesaron momentos de considerable tensión, Maupertuis escribiría, acerca del suizo:
«Euler... es en su conjunto un personaje extremadamente peculiar... un hombre incansablemente fastidioso, al que le gusta meterse en todos y cada uno de los asuntos, aunque la forma de la Academia y las directrices de nuestro rey prohíban esta clase de intromisiones».

La mencionada «variación» no es más que un instrumento imaginario de cálculo. Si y(x) es la curva que, pasando por (a, y(a)) y (b, y(b)), satisface las condiciones buscadas, la variación es la curva ligerísimamente alterada, «variada», a la que se designa con el símbolo 6 delante (figura 10).

En 1744-1746, Maupertuis enunció su principio de mínima acción, que se podría traducir como «la naturaleza es ahorrativa en sus acciones», pues siempre las «lleva a cabo» siguiendo la mínima acción posible.
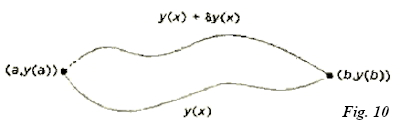
La «acción» es una magnitud definible. Un modo de describirla, aunque no el único, es la suma del momento de las fuerzas implicadas multiplicada por el camino recorrido, y es eso lo que debe ser mínimo.
Euler expuso su propia versión del principio en 1744, en un artículo titulado Método para hallar líneas curvadas que gozan de propiedades de máximo o mínimo, al que los historiadores suelen referirse por el comienzo del título latino original, Methodus, y de esta versión será la que partirá el cálculo de variaciones moderno.

«Dado que la textura del universo es la más perfecta y la obra de un Creador sapientísimo, nada sucede en el universo sin obedecer alguna regla de máximo o mínimo.»
Leonhard Euler.

En 1755 un matemático italiano de solo diecinueve años, Giuseppe Luigi Lagrange, escribió una extensa carta a Euler en que resolvía un problema perfeccionando su sistema del cálculo de variaciones. Lagrange publicó su método en 1772 con la bendición de Euler, que reconoció la valía del trabajo.
Explicado en términos actuales, el cálculo de variaciones consiste en poner analíticamente en marcha el principio de mínima acción. Se empieza por escribir el llamado lagrangiano del sistema, al que llamaremos L y que es igual a L = C - P, diferencia entre las energías cinética C y la potencial P. El lagrangiano es un funcional, una función de funciones. Si nos circunscribimos al caso más trivial, en el que solo hay un camino que es una función x(t) del tiempo, el lagrangiano es de la forma L(x,ẋ, t), donde se indica con la notación newtoniana ẋ a la derivada primera de x.
La integral de acción adopta la forma:

y eso es lo que hay que minimizar (y en ciertos casos, maximizar). Aunque de formas distintas, tanto Euler como Lagrange llegaron a unas ecuaciones diferenciales (habitualmente hay varias) del tipo:

que en la actualidad se denominan ecuaciones de Euler-Lagrange y que dejan el problema reducido a resolverlas.

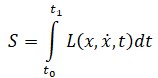
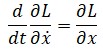
D'Alembert y su principio
D'Alembert (1717-1785) formuló en 1743, en el Traité de dynamique (Tratado de dinámica), el principio que lleva su nombre; este es una afirmación de la mecánica analítica que postula que en un sistema dinámico todo movimiento virtual permitido por las ligaduras entraña un trabajo nulo. Dicha formulación permite orillar el principio de mínima acción o del mínimo esfuerzo y le vincula con Euler, pues conduce matemáticamente a las ecuaciones de Euler-Lagrange:
una fórmula fundamental de la mecánica clásica, donde L es el lagrangiano y las x^a las llamadas coordenadas generalizadas del sistema.
Un sabio de la época
D'Alembert era hijo ilegítimo del caballero Dostouches, aunque nunca fue reconocido. Su nombre proviene a medias del de la iglesia en cuyos escalones lo abandonaron (St. Jean-le-Rond) y de un supuesto satélite de Venus (Alembert). Editó, junto con Denis Diderot (1713-1784) la traducción del inglés de la Cyclopaedia de Ephraim Chamberí, que más tarde se reconvirtió en l'Enciclopédie, pues la re-redactó y amplió con unos 1700 artículos nuevos, matemáticos, filosóficos, literarios y musicales, incluyendo su célebre y liberal Discours prélíminaire (1751). Tras ingresar en la Academia de ciencias de Berlín, en la Royal Society, en la Academia de Ciencias de París y en la Academia Francesa de la Lengua, fue nombrado secretarlo de esta en 1772. Como matemático D'Alembert aportó la primera prueba (errónea y posteriormente corregida por Gauss) del teorema fundamental del álgebra «todo polinomio real de grado n tiene n ceros en el cuerpo complejo». También aportó un magnifico criterio de convergencia de series y, en física teórica, el llamado operador de D'Alembert. En teoría de la probabilidad se le recuerda por la martingala de D'Alembert. Compitió con Euler en la mejora de las lentes astronómicas.

Las ecuaciones de Euler-Lagrange figuran en todos los textos avanzados de análisis, y transforman la integral de acción en unas simples condiciones, simples relativamente, en derivadas parciales. Constituyen el punto central del cálculo de variaciones y puede consultarse el anexo 4 para ver su deducción formal.

§. Euler y la geometría
Cuando Euler residía en Berlín, acostumbraba a enviar algunos artículos a la Academia de San Petersburgo, en especial de aquellos temas cuyas raíces se hundían en cuestiones anteriores publicadas allí, es decir, si alguno de sus artículos elaborados en Berlín trataba de un tema ya estudiado en Moscú, el artículo nuevo se enviaba a Moscú. En 1763, Euler presentó Solutio facilis problematum. quorundom geometricorum difficillimorum (Una solución fácil para un problema muy difícil de geometría), un escrito puramente geométrico, euclidiano y complicado, que se publicó en 1767, cuando Euler ya había regresado a San Petersburgo.
En él, Euler demostró por primera vez que en todo triángulo que no fuera equilátero, en cuyo caso todo degenera en un punto, el ortocentro (O; punto del triángulo donde se cortan las tres alturas), el circuncentro (C; punto del triángulo donde se cortan las tres mediatrices) y el baricentro, también llamado centroide (B; punto del triángulo donde se cortan las tres medianas) están sobre la misma línea, la llamada posteriormente recta de Euler. El incentro (punto de intersección de las tres bisectrices) está en la línea solo si el triángulo es isósceles; si no, no. Del centro del círculo de Euler (CE), se habla unas líneas más adelante.
No solo se verifica que O, B y C están alineados, sino que además se cumple una relación métrica precisa:

2d (B,C) = d (B,O).

Es decir, la distancia entre el baricentro y el ortocentro siempre es el doble de la distancia entre el baricentro y el circuncentro (figura 11).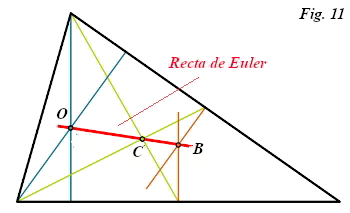

Aunque, como ya se comentó, el incentro no está en la recta de Euler salvo si el triángulo es isósceles, Euler ideó una fórmula que da la distancia d entre ambos puntos, el incentro y el circuncentro:

d² = R×(R - 2r)

donde R y r son los respectivos radios de los círculos circunscrito e inscrito.
Transcurrido un tiempo desde 1767, Karl Wilhelm Feuerbach (1800-1834) y Olry Terquem (1762-1862) hallaron el círculo de centro CE, que se conoce como circulo de Euler.

Se trata de un círculo que pasa por los nueve puntos siguientes; los puntos medios de cada lado del triángulo; los tres pies de las tres alturas y, por último, el punto medio del segmento que va de cada vértice al ortocentro (figura 12).

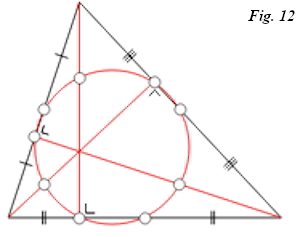
El techo del estadio olímpico de Münich es una superficie mínima. y para diseñarla se echó mano del cálculo de variaciones.

Los centros de un triángulo
Se llama centro de un triángulo a todo punto P que desde el punto de vista geométrico es poseedor de una propiedad privilegiada en referencia a determinadas líneas (alturas, medianas, bisectrices, etc.) y define circunferencias u otras figuras sencillas, sujeto de propiedades curiosas relacionadas con el triángulo de partida.
Esta sería una definición muy vaga si no se añadiera la condición de que P fuera invariante respecto de simetrías, rotaciones y dilataciones.
Un ejemplo de tales centros de un triángulo son los ya clásicos baricentro, ortocentro, circuncentro e incentro. Pero hay muchos más centros. El artículo de Euler sobre los centros de un triángulo provocó la sorpresa entre los geómetras, quienes creían haberlo dicho casi todo de los puntos privilegiados de un triángulo; en su época y años posteriores los geómetras descubrieron muchos centros más. De hecho, en la actualidad hay webs especializadas en la enumeración y estudio de tales centros, como la Clark Kimberling's Encyclopedia of Triangle Centers, que menciona más de 3500 puntos.

En 1750, Euler dio a conocer el megascopio, un aparato de proyección para cuerpos opacos. Estaba formado por dos espejos reflectores cóncavos y dos lámparas que iluminaban el objeto y provocaban su proyección.

Como cabe suponer, los centros de un triángulo no constituyeron el único centro de interés geométrico de Euler. Se podrían citar muchos otros temas, pero hay uno que destaca por su gran dificultad, sin comparación posible con lo simple del enunciado.
En 1751, Euler propuso por carta a Goldbach lo siguiente: averiguar, dado un polígono convexo cualquiera de n lados, el número de modos de dividirlo en n-2 triángulos mediante diagonales que no se corten y si diferentes orientaciones se cuentan separadamente.

Un sello italiano ilustra una de las cimas intelectuales de Euler, el concepto de característica de un poliedro.

Además, se da otra relación relativa a las distancias:

d (CE,O) = d (CE,C).

«La naturaleza de algunos de sus más sencillos descubrimientos es tal que uno bien puede pensar en el fantasma de Euclides diciendo “Pero ¿cómo no se me ocurrió?".»
H.S.M. Coxete» en relación al trabajo de Euler.

Polígonos de 4, 5 y 6 lados mostrando todos los casos posibles de división en triángulos con diagonales que no se cortan.

En el fondo, lo que Euler se estaba preguntando era por el número de cortes de través que había que darle a un «pastel» poligonal, como se ilustra en esta página Se trata de un complicado problema de combinatoria, cuya solución es C_n_-2, donde:

§. El Euler menos conocido
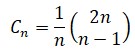
Euler se interesaba por todo y escribía artículos sobre casi todo. Muchos eran de difícil clasificación en cualquier categoría del conocimiento conocido hasta entonces; porque, ¿dónde incluir temas como los posibles paseos cruzando a través de los puentes de Königsberg? Otros sí encontraban acomodo preciso entre los conocimientos de la época, como las pensiones, solo que no eran cuestiones de primerísima fila. Un breve itinerario por esos escritos de difícil calificación ofrece una visión más precisa de la variedad extraordinaria de la obra de Euler.
Euler ingeniero
Las contribuciones eulerianas a la ingeniería práctica tienden a ser menospreciadas, en parte por los prejuicios de Federico II, quien suponía que todo lo que emprendían sus subordinados, ya fueran generales, jardineros o científicos, tenía que funcionar, pues para eso les pagaba. Los ingenieros de Su Majestad, y Euler era el jefe de todos ellos, no eran una excepción, y si, por ejemplo, el agua no fluía adecuadamente en los surtidores de uno de sus jardines era porque los diseñadores y constructores eran incompetentes. Un error en el cómputo de la presión del agua era inconcebible e imperdonable.
No obstante, Euler trabajaba, y mucho, en problemas prácticos de ingeniería y, aproximadamente en 1744 (aunque no se publicó hasta 1757), hizo una aplicación de su cálculo de variaciones a la sobrecarga de peso de objetos sobre los pilares que los sostienen. Es lo que en la jerga técnica se denomina pandeo, una variante sencilla de la deformación.
Imaginemos una columna, como la que se ilustra en la página siguiente, sometida a una carga axial concéntrica, q, es decir, a una carga ejercida sobre el centro de gravedad de su sección transversal Euler dio con una fórmula:

que gobierna el pandeo, en la que F es la fuerza o carga axial, E el módulo de elasticidad, I el momento de inercia del área, L la longitud entre los apoyos de la columna y K un factor empírico que está en función de las condiciones de soporte de los extremos de la barra o columna que se deforma. El producto KL determina la longitud efectiva de la misma.

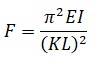
Deformación o pandeo de una columna por efecto de una carga.

Euler y la mecánica de fluidos
En 1757 Euler publicó el artículo Principes généraux du mouvement des fluidez (Principios generales del movimiento de los fluidos), donde aparecían por primera vez sus ecuaciones, que, en dinámica de fluidos, son las que describen el movimiento de un fluido que no se puede comprimir y que está desprovisto de viscosidad.
El fluido de Euler era lo que hoy se llamaría un fluido ideal. En realidad lo que se someterá ahora a consideración no son ya fluidos ideales, sino las ecuaciones de Euler expuestas en su enunciado moderno.
Laplace (1749-1827) añadió una parte significativa a las ecuaciones primigenias de Euler, al apuntar una componente adiabática (es decir, supuso que la cantidad de calor del sistema era constante). En lenguaje tensorial actual las ecuaciones se escriben:

Ahí ρ es la densidad del fluido, v su velocidad vectorial, E la energía total por unidad de volumen y p la presión. Se supone que la viscosidad del flujo es irrelevante, lo que no es cierto en formulaciones más avanzadas, como las ecuaciones de Navier-Stokes. A medida que las ecuaciones se hacen más sofisticadas para acercarse a la realidad, es lógico que supongan menos cosas. Las ecuaciones de Navier-Stokes sí son ecuaciones célebres, pues su solución es uno de los problemas del Milenio, según el Instituto Clay, y está premiada con un millón de dólares.

Las computadoras han añadido algo insuperable a las ecuaciones de Euler-Navier-Stokes; ahora se puede simular el comportamiento mecánico de un fluido, aunque todavía no se pueda ni soñar en resolver de modo exacto las ecuaciones que rigen su movimiento.

El teorema de Bernoulli de la hidrodinámica es deducible de las ecuaciones de Euler por simple integración. Así que no se puede dudar de que las ecuaciones de Euler son importantes, pues de días se deduce d principio del vuelo con alas de un cuerpo más pesado que el aire. Las ecuaciones de Euler de la mecánica de fluidos se aplicaron en su día al estudio de objetos tan dispares como la gran mancha roja de Júpiter, la circulación sanguínea o la aerodinámica de los automóviles, y en la actualidad siguen siendo utilizadas. Euler estudió con detenimiento las turbinas movidas por fluidos en una memoria específica de 1756, y su aporte no ha sido todavía superado.
Las ecuaciones de Euler son ecuaciones diferenciales no lineales, y, a veces, de muy difícil estudio. El advenimiento de las computadoras, con su tremenda capacidad de cálculo, ha abierto a los físicos la oportunidad de buscar soluciones numéricas aproximadas. Quizá no se pueda obtener una solución elegante y exacta, pero se puede obtener una excelente solución aproximada
Ecuaciones de Cauchy-Riemann
Desde un punto de vista histórico, estas ecuaciones analíticas fueron ya tratadas por D'Alembert en 1752 y por Euler, quien las desarrolló al trabajar en varios campos, como en la hidrodinámica. Ya figuran con claridad en 1777 en medio de otras expresiones analíticas, aunque no se publicaron sino tras la muerte de Euler.
Las ecuaciones son igualdades entre derivadas parciales y funcionan como sigue: supongamos que una función f(x+ iy) de variable compleja puede dividirse en una parte real y otra imaginaria:

f(x + yi) = u (x,y) + i v(x,y).

Y que tanto u como v son diferenciables como funciones de dos variables en el campo real R; entonces, sus derivadas parciales cruzadas cumplen: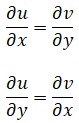

Y viceversa, en el sentido de que si u y v son diferenciables como funciones reales (pueden ser diferenciables en el campo complejo C y no serlo en R) y se verifica la anterior igualdad de derivadas, entonces f es diferenciable y f = u+iv.
Estas ecuaciones aparecen en las primeras páginas de cualquier libro actual de análisis complejo y son muy familiares para los estudiantes de física o ingeniería.
Juegos, loterías y seguros de vida
Euler también tuvo tiempo para ocuparse de cuestiones de estadística y probabilidades. Sus investigaciones no fueron tan abundantes como en otros campos, pero merece la pena mencionarlas. Muchas de ellas tuvieron lugar durante su estancia en Berlín y figuran, en algunos casos, entre su correspondencia con el monarca Federico II.
Algunas de ellas entran en el terreno de los juegos de azar y de las apuestas, pues este era un ámbito científicamente valorado; de hecho numerosas cuestiones que posteriormente adquirirían gran importancia se dilucidaron en este terreno. Como otros matemáticos de renombre tales como Johann Heinrich Lambert (1728-1777) o Pierre-Simon Laplace, Euler se ocupó de juegos de cartas como el treize («13»), también conocido como rencontré («coincidencias»).

La princesa y los silogismos
Euler escribió más de 200 cartas a la princesa Anhalt-Dessau, sobrina de Federico, que en 1768 serían recopiladas en un volumen titulado Lettres á une princesse d'Allemagne sur divers sujets de physique et de philosophie (Cartas a una princesa alemana sobre distintos temas de física y de filosofía). Hasta en una obra, aparentemente tan ligera, Euler consigue sorprender al estudioso. En ciertos puntos (cartas 102-105) discursea sobre los silogismos, y, para explicarse con propiedad, se vale de gráficos como los de las figuras 1 y 2.
Estos gráficos pueden recordar a los diagramas de Venn, aunque de hecho, John Venn (1834-1923) y Euler no idearon sus diagramas exactamente con el mismo significado. Lo que Venn representarla según la figura 3. Euler lo dibujaba como en la figura 4. Venn utilizaba un fragmento de diagrama aun cuando estaba vacío, mientras que Euler, que no pensaba en términos de conjuntos, no contemplaba esa eventualidad. Venn no denominaba a sus diagramas «diagramas de Venn», como en la actualidad, sino «diagramas de Euler».
No hace falta mencionar, pues, cuál fue su fuente inspiradora.

También se adentró en el campo de las loterías numéricas, que aparecieron por aquel tiempo, así como en el de los seguros de vida y las estadísticas de vida y muerte. Las pensiones y las anualidades que hay que pagar para recibir una pensión se derivan de estas estadísticas, pues el importe de las pensiones y anualidades está en función de la mayor o menor probabilidad de fallecer.
Asimismo, se ocupó de la teoría de errores, aunque no fue hasta el desarrollo de la técnica de los mínimos cuadrados, emprendida por Gauss, cuando se convirtió en una auténtica teoría Hay que tener presente que el error en las medidas se computaba en la época por la inedia de los errores; como los había positivos y negativos arabos se compensaban, con lo cual no se entraba de verdad en' la naturaleza del error y en su corrección efectiva.
Libros de menor envergadura
Euler escribió durante su etapa prusiana otros libros comparativamente menores en el contexto de su vasta obra. En 1744, apareció uno sobre trayectorias de planetas y cometas, Theoria motuum planetarum et cometarum (Teoría de los movimientos de planetas y cometas) y en 1746, un tratado de óptica, que trata de la luz y los colores, Nova Theoria lucis et colorum (Una nueva teoría de la luz y los colores). Euler, siguiendo a Christiaan Huygens (1629-1695), se decanta por la hipótesis ondulatoria, que prevalecerá frente a la teoría corpuscular hasta el advenimiento de la mecánica cuántica.
En 1745 se publicó la traducción alemana de Euler del libro inglés New Principles of Gunnery (Nuevos principios de artillería), de Benjamín Robins (1707-1751), con tal cantidad de comentarios, correcciones y complementos que el libro es prácticamente nuevo.
En 1765, cuando Euler ya casi tenía un pie en Rusia, apareció Theoria motus corporurn solidorum seu rigidorum (Teoría del movimiento de cuerpos sólidos y rígidos), su segundo tratado de mecánica. Es una mejora lógica de su primer tratado —donde se aplicaban por primera vez las técnicas del análisis matemático a la mecánica—, pues contiene las posteriormente denominadas ecuaciones diferenciales de Euler del movimiento de un sólido rígido sometido a fuerzas externas, y los ángulos de Euler, conectados al uso de dos sistemas de coordenadas, uno fijo y otro ligado al cuerpo en movimiento, con lo que el movimiento se descompone ya lógicamente en lineal y rotacional. Todos los expertos destacan la originalidad de algunas aportaciones, como el tratamiento del eje de rotación de una simple peonza, que introduce de modo natural la nutación y precesión de los equinoccios.
Ya se ha comentado que la cartografía fue otra de las pasiones de Euler, tras años de colaboración en la Academia de San Petersburgo en la elaboración de un Atlas de Rusia, este finalmente vio la luz en 1745, con 20 mapas. Euler estaba muy orgulloso del resultado y remarcaba que dicho atlas situaba la cartografía rusa por delante de la alemana.
Sin embargo, a pesar de su extensa productividad, no hay que caer en el error de pensar que todo lo que Euler escribió era definitivo. Sus escritos padecen de un mal inevitable en su tiempo, la falta de auténtico rigor en las operaciones y definiciones, lo que, frecuentemente, da la impresión de que todo se sostiene porque funciona, no porque quede probado. En realidad, el siglo XIX dedicará muchas energías a fundamentar las atrevidas intuiciones eulerianas dando lugar a conceptos que como el límite, la convergencia o la continuidad vayan cubriendo los agujeros argumentales de muchas proposiciones. Las matemáticas se harán más aburridas, pero también más fiables.

§. Una trilogía magistral; la cumbre del análisis
Aunque la obra de Euler abarca una enormidad de campos distintos y escribió sobre todo lo que despertaba su interés, muchos le siguen distinguiendo como el padre del análisis matemático moderno, concediéndole a esta faceta de su personalidad el carácter de trazo dominante. En el apartado anterior se ha explorado el trabajo de Euler en cálculo de variaciones; acaso espoleado por ese éxito, en los años siguientes el suizo procedió a condensar y estructurar sus vastos conocimientos en análisis en forma de diversos tratados.
En 1748, publicó Introductio in analysin infinitorum (Introducción al análisis del infinito), una obra maestra en dos volúmenes, que junto con Institutiones calculi differentialis (Fundamentos de cálculo diferencial), de 1755, y los tres volúmenes de Institutiones calculi integralis (Fundamentos de cálculo integral), de 1768-1770, conforman una trilogía sin parangón en el mundo científico moderno. La aparición de estos textos marcó un antes y un después, especialmente, en el análisis. François Arago (1786-1853) denominó a Euler «el análisis encamado», y el historiador matemático Cari Benjamín Boyer (1900-1976) ensalzó estos libros hasta situarlos a la altura de los de Euclides (Elementos), Newton (Principia), Gauss (Disquisitiones) o Descartes (Géometrie), e incluso, los antepuso en cuanto a importancia pedagógica Escribió Boyer:

Puede decirse que Euler hizo por el Cálculo de Newton y Leibniz lo que Euclides había hecho con la geometría de Eudoxo o lo que Viéte hizo por el álgebra de Cardano y Al-Kwarismi; Euler tomó el cálculo diferencial de Leibniz y el método de las fluxiones de Newton y los integró en una rama más general de las matemáticas, que desde entonces recibe el nombre de Análisis, es decir, el estudio de las funciones y los procesos infinitos.

El cambio no solo contempló los contenidos, sino también la notación. Es un ejercicio aleccionador leer ahora estos libros y darse cuenta de que casi se entienden sin tropiezos. Además, Euler escribió todos sus escritos de forma muy comprensible.
Clifford Truesdell (1919-2000), el eminente físico estadounidense, afirmó al respecto:

Euler fue el primero en el mundo occidental que escribió matemáticas de un modo abierto, fácil de leer. Enseñó a su época que el cálculo infinitesimal era algo que cualquier persona inteligente podía, con aplicación, aprender y usar. Era justamente famoso por la claridad de su estilo y por su honestidad para con el lector acerca de las dificultades cuando se presentaban

Algunas de las aportaciones de Euler en el campo del análisis son de interés solo para el especialista y nos limitaremos a enumerarlas; es el caso de las series hipergeométricas, las series q, las funciones hiperbólicas trigonométricas, las ecuaciones diferenciales, las funciones elípticas o las integrales complejas.
Una base en la que se asienta una de las novedades relevantes de entre todos los logros contenidos en Introductio in analysin infinitorum es fórmula de De Moivre, que un analista moderno escribiría así:

y que De Moivre, en 1730, había escrito de un modo un tanto aparatoso pero acorde con los usos notacionales de la época:

Euler utilizó, sin aportar demostración alguna, la fórmula que manejó De Moivre, jugó algebraicamente con ella, la combinó con la fórmula de Euler, que había desarrollado ya en sus días en Basilea, como se vio en el capítulo 2, y que recordamos aquí:

y dedujo, usando las simples reglas de la exponenciación, la expresión que hoy día escribiríamos:

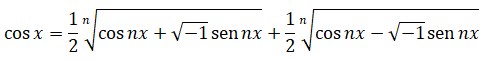
Abraham de Moivre
Nacido en 1667, en la región francesa de Champagne, su carrera se desarrolló en Gran Bretaña, donde se exilió huyendo de la persecución religiosa de los protestantes, que tuvo lugar cuando Luis XIV revocó el edicto de Nantes en 1665. Vivió en Londres, un poco con estrecheces, dando clases en los cafés o ganándose la vida con su habilidad en el ajedrez. Se hizo muy amigo de Edmund Halley (1656-1742) y de Newton, con quien tomaba café cada día. y del que se dice que respondía a quienes le preguntaban sobre aspectos de cálculo: «Pregúnteselo a Mr. De Moivre, que sabe de esas cosas más que yo».
Tales amistades, junto con las de Leibniz, Euler y los Bernoulli, no le sirvieron, no obstante, para encontrar un trabajo estable. Fue un excelente matemático, no en vano es el responsable de introducir en probabilidad y estadística la independencia de sucesos, acercándose mucho al concepto de distribución de los valores estadísticos en forma de campana de Gauss. Estudió también las anualidades, tema que desarrolló en Annuities in life (Anualidades en vida), aparecido en 1724, a partir de un trabajo de Halley. En análisis puro, se le debe una primera formulación del valor aproximado del factorial de un número. Más tarde esa fórmula se conocerá universalmente como aproximación de Stirling:
Sin embargo, su contribución más notable fue su fórmula de los números complejos, que hoy enunciaríamos, en notación moderna, como:
Soltero y pobre, siempre recordó con el orgullo del exiliado que la Academia de ciencias de París lo había elegido en 1754 miembro extranjero asociado. Murió en Londres, pero lo curioso es que se dice que predijo el día de su propia muerte. Se apercibió que cada día dormía 15 minutos más que el anterior, así que hizo la cuenta… y calculó que fallecería el día en que durmiera 24 horas: el 27 de noviembre de 1754. Su cálculo fue exacto.

Euler llegó a estos resultados, y a otros de suma importancia también, partiendo de la simple serie de Taylor.

En el anexo 5 se muestra con mayor detalle el modo en que Euler dedujo su fórmula de esta última expresión.
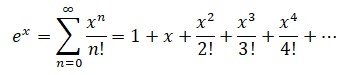
Si damos a x el valor del número pi (π) en el marco de la fórmula de Euler se tiene que

y cambiando de lado al -1:

eⁱ^π + 1 = 0

Esta ecuación, conocida como identidad de Euler, está considerada por muchos matemáticos como la más hermosa de toda la disciplina.
También en Introductio in analysin infinitorum puede encontrarse el auténtico concepto de logaritmo, en una forma que resuelve el tema de los logaritmos negativos que Euler arrastraba desde su juventud en Basilea. Euler lo definía correctamente como la operación inversa de la exponenciación, o sea:

lo cual lleva a que el logaritmo en el campo complejo tenga infinitos valores que solo difieren en un múltiplo par de n, o sea 2kπ. En particular.

lo que conduce a expresiones como:

Asimismo, en este libro se introduce el número e, la fórmula de De Moivre, las series de potencias sen x y cos x, la idea de función, muchas series de potencias (entre otros, se resuelve por otra vía el problema de Basilea), etc.
También se explican, y sistematizan los primeros pasos de la geometría analítica, impecablemente engarzados en los conceptos del análisis. Se pueden encontrar entre los temas las coordenadas oblicuas y polares, las transformaciones de coordenadas, las asíntotas, las curvaturas, la intersección de curvas, las tangentes, y un largo etcétera. No solo se tratan los conceptos de forma moderna, sino que se lleva a cabo una auténtica labor de fusión de los puntos de vista de Newton y Leibniz y queda claro definitivamente que diferenciación e integración son acciones inversas la una de la otra; caras enfrentadas de la misma moneda.
En Institutiones calculi differentialis y en Institutiones calculi integralis se estudian primordialmente las series, las fracciones continuas, las ecuaciones diferenciales, incluidas las derivadas parciales, los máximos y mínimos, etc.
Euler mantuvo durante toda su vida un pugilato intelectual con las series numéricas, sumas infinitas de las que se ignoraba si eran convergentes o no, y, en caso de que lo fueran, se desconocía hacia qué convergían, qué suma representaban. En algunos casos la divergencia era clara, como en la llamada serie armónica.

que el matemático italiano Retro Mengoli agrupó así

demostrando que su suma era infinita. Sin embargo, otras eran desconcertantes. Tomemos por ejemplo:

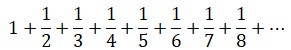
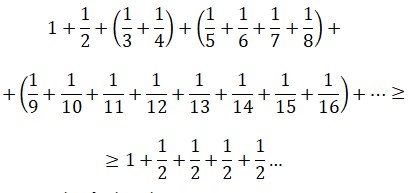
1 - 1 + 1 - 1 + 1 - 1 +. ..,

que agrupada así parece dar 0:

(1 - 1) + (1 - 1) + (1 - 1) +...= 0,

pero agrupada así parece dar 1:

(1 + 1) - (1 + 1) - (1 + 1) -...= 1.

Ni lo uno ni lo otro, pues Eider prefería partir, como otros matemáticos de la época, de la bien conocida serie:

para tomar el valor x = -1 y concluir que:

así que ni 1 ni 0; Euler sostenía que el total era un medio.
Al arsenal de series ya sumadas por aquel entonces, como:

Euler añadiría poco a poco una gran cantidad de resultados propios: su contribución al problema de Basilea; su método de sumación, denominado de Euler-Maclaurin, que mejoraba la convergencia, en caso de que la hubiera (ambos vistos en detalle en el capítulo anterior); la transformación de series mediante las diferencias finitas y sucesivas; e importantes aportaciones al estudio de las series divergentes. De hecho, en 1755, es decir en una época en que no existía todavía el concepto de límite, ya distinguía correctamente entre series convergentes y divergentes.
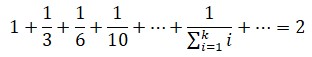
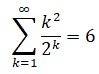
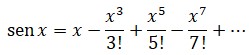
Entre las series sumadas por Euler se encuentran:

Además, Euler descubrió dos series; una fue la siguiente expresión como serie de potencias;

y la otra, la primera serie de Fourier de la historia, que Euler desveló en 1744 en una carta a Goldbach, y, por tanto, mucho antes de que Joseph Fourier (1768-1830) emprendiera sus famosos trabajos. En realidad, antes de que ni siquiera tuviera ocasión de nacer

La aportación de Euler al dominio de las series es enorme y su exposición en detalle no es el fin de este libro. Baste decir que solo Carl Gustav Jakob Jacobi (1804-1851) y Srinivasa Aiyangar Ramanujan (1887-1920) están a su altura en cuanto a la relevancia de sus aportaciones en esta materia.
Otro de los campos que cultivó Euler fue el de las ecuaciones diferenciales. Quizá su aportación más conocida, aunque una de las más elementales, sea el método de Euler, que permite aproximarse a la soluciones de una ecuación diferencial de primer orden.

Capítulo 4
Segunda estancia en Rusia: Euler y la teoría de números

Euler, aquejado de fuertes problemas de visión, pudo haber hecho de su segunda estancia en Rusia un retiro dorado, pero nada más lejos de la realidad. Decidido a que la muerte le sorprendiera trabajando se centró en la teoría de números, y engarzó una serie de resultados notables relativos a los números primos, de Mersenne y de Bernoulli, así como a las ecuaciones diofánticas y las particiones. También halló tiempo para estudiar las matemáticas lúdicas e incluso escribir libros de divulgación.

El regreso de Euler a Rusia, en 1766, estuvo presidido por el deseo de la zarina, Catalina II, de prestigiar de nuevo la Academia. De hecho, Euler no había roto los vínculos con Rusia durante el periodo en que residió en Berlín. Es sabido que envió numerosos artículos a la Academia de San Petersburgo cuando las cuestiones tratadas en los mismos eran continuación lógica de artículos publicados en Rusia la primera vez. Por otra parte, siguió recibiendo estipendios de origen ruso en pago a temas puntuales, como cuestiones de carácter militar, y ponía bajo su protección y tutela a alumnos rusos que habían sido enviados a estudiar a Occidente. A cambio de sus contribuciones científicas a la academia de San Petersburgo, Euler recibió de Rusia en 1742 —residiendo en Berlín— el compromiso de una pensión. Una singular anécdota permite no solo conocer un detalle concreto del segundo viaje de Euler a Rusia, sino también lo emponzoñadas que estaban las relaciones con su patrón anterior. Así, en una carta escrita por Federico este se regocijaba de la pérdida de una serie de notas personales del matemático a causa del naufragio del barco que las conducía a San Petersburgo con las palabras siguientes:

«Es un hecho lamentable, porque de ellas podrían haber salido seis tomos de tratados llenos de números de principio a fin, y ahora, con toda probabilidad, Europa se va a ver privada de una lectura tan placentera».

El sueldo que se le asignó a su llegada a Rusia (3000 rublos) era magnífico, e incluso la zarina le ofreció un cocinero de su propia casa real, la directora de la Academia, nombrada por Catalina II, era la princesa Dashkova, y su aprecio por Euler se manifestó en otra celebrada —y documentada— anécdota. En el curso de cierta sesión de la Academia, la princesa acompañó al sabio hasta la sala de sesiones. Entonces, un profesor que se daba mucha importancia solicitó sentarse en el sillón de honor, cerca de la presidencia. La princesa, con exquisita educación, se dirigió entonces a Euler «Siéntese donde usted quiera, señor, pues el lugar que elija ya sabemos que será el más distinguido, el primero de todos».
Sin embargo, no todo fueron buenos momentos. La primera de sus tragedias de este periodo fue la ceguera. Euler se sometió a una operación quirúrgica para tratar una catarata en su ojo sano; aunque al principio todo fue bien, se le declaró posteriormente un absceso del que no se trató a tiempo y que acabó provocándole la pérdida de la visión. En 1771 ya estaba virtualmente ciego de ambos ojos. No obstante, su ritmo de trabajo no disminuyó e, incluso, puede afirmarse que su productividad en este segundo periodo ruso es la más alta de su vida. Pero dicha productividad no pudo conseguirla solo; la historia ha conservado el nombre de alguno de los auxiliares de Euler de la última época, muchos de ellos excelentes matemáticos, como Georg Wolfgang Krafft, Mikhail Evseyevich Golovin, Stepan Runiovsky, S. K. Kotelnikov y Petr Inokhodtsev. Algunos de sus auxiliares fueron especialmente relevantes: su hijo mayor Johann Albrecht, su nieto político Nicolaus Fuss y el matemático y astrónomo germano Anders Lexell.
El primogénito de Euler. Johann Albrecht (1734-1800), fue matemático y miembro de la Academia de Berlín desde 1754 y catedrático de física de la Academia de San Petersburgo desde 1765. Fue un excelente científico a juzgar por los siete galardones que recibió de academias diferentes en el curso de su vida profesional.
La mano derecha de Euler fue Nicolaus Fuss (1755-1826), un matemático que ascendió de asistente y secretario personal a profesor en la escuela de Infantería y secretario permanente de la Academia de San Petersburgo. En 1784 se casó con una nieta de Euler y estuvo presente en su casa el mismo día en que falleció.

Una anécdota famosa
A un personaje de la talla de Euler es normal que le atribuyan un buen numero de anécdotas Lo malo de las anécdotas en general es que su atribución acostumbra a ser directamente proporcional a lo extravagante del personaje y su verificabilidad, inversamente proporcional a la distancia en el tiempo en que vivió.

Retrato de Denis Diderot, considerado el padre y supervisor de la Enciclopedia
La que viene a continuación se incluye por la buena fama del narrador, D. Thiebault (1733-1807), un cronista por lo general creíble y veraz que aunque no estaba presente en la ocasión dice habérsela oído explicar a varios testigos, y porque goza de gran popularidad El protagonista de la historia es el escritor y filósofo francés Denis Diderot (1713-1784), padre y supervisor de la Enciclopedia. Diderot, quien estaba de visita en Rusia, fue invitado a debatir en la corte sobre la existencia de Dios. Al parecer el muy creyente Euler disponía de una prueba irrefutable. Diderot acudió a la reunión y contempló como Euler avanzaba hasta él para enunciar su argumento:
«Señor, luego Dios existe, responded».

Diderot, que no entendía gran cosa de matemáticas, no respondió y permaneció callado. Los cortesanos presentes interpretaron el silencio como imposibilidad de responder a la contundencia del argumento, y se mofaron de Diderot quien, avergonzado, regresó a Francia. Hasta aquí el relato.
La otra cara del relato
La historia ha encontrado con cierta rapidez resquicios por donde introducir un deje de verdad. La «ecuación» de la frase no tiene valor matemático alguno. Además. Diderot no era un ignorante en matemáticas pues poseía una excelente formación como matemático aficionado, por tanto, la pretendida frase de Euler le habría sonado como lo que era en realidad, un galimatías sin sentido, y así lo habría dicho. Además, uno no se imagina al muy serio y respetuoso Euler prestándose ante un sabio como Diderot a una maniobra tan burda En lo único en que la historia es cierta es en lo tocante al regreso de Diderot a Francia.

Suyo es un magnífico elogio fúnebre, un texto extenso y conmovedor sobre la vida y obra de quien fue el abuelo de su esposa.
Por último, Anders Lexell (1740-1784) fue colaborador de Euler en sus últimos tiempos y estuvo también presente en el momento de su muerte. Lexell se ocupaba entonces, junto con Euler y Fuss, del recién descubierto planeta Urano, y llegó a prever con sus cálculos la existencia de Neptuno.
Otra de las desgracias que le aconteció en este período fue el incendio de su casa en 1771, que a punto estuvo de costarle la vida; la intervención de su sirviente Peter Grimm (otras fuentes hablan de un simple compatriota de Basilea), que lo sacó a hombros, fue decisiva. La casa fue levantada de nuevo en piedra con fondos que provinieron parcialmente de la emperatriz.

Curvas y engranajes
En 1754, Euler publicó en la Academia de Berlín unas memorias sobre los engranajes, tema que retomó en 1765, a caballo entre Berlín y su segunda etapa rusa, en Supplementum de figura dentum rotarum, que versaba sobre los dientes de un engranaje giratorio.
En la figura 1 puede observarse un engranaje con dientes triangulares, pero los simples triángulos no son suficientes; el perfil de los dientes es fundamental, y en la figura 2, inspirada en los trabajos de Euler, se aprecia el perfil óptimo. Cuando el perfil de los dientes está formado por curvas involutas de una circunferencia —aquellas que resultan de trazar el camino qué recorre al desenrollarse el extremo de una cuerda previamente enrollada a la circunferencia—, la relación entre sus respectivas velocidades de rotación se mantiene constante a medida que se produce el deslizamiento.
Los dientes tienen una tangente común y el engranaje no vibra; no se pierde energía en ruidos y el desgaste se minimiza. Euler no solo fue el primero en explorar el campo de las curvas involutas, sino que sus ideas llevaron a desarrollar posteriormente las ecuaciones de Euler-Savary, utilizadas hoy en día para trabajar en cuestiones de curvatura.
Dientes de las sierras.
Junto a los engranajes, Euler también se interesó por tos dientes de la sierras (figura 3) tema al que le dedicó, en 1756, un articulo de 25 páginas.
En él aparecen fórmulas que tienen presentes el número de dientes, su ángulo de inclinación. la penetración del diente en la madera, etc. Sin embargo, algunas de las conclusiones del estudio resultan ahora sorprendentes, pues Euler recomendaba usar sierras de 1.20 m y recurrirá equipos reducidos de aserradores.
En la figura un dibujo basado en el estudio de los dientes de sierra llevado a cabo por Euler.

El tercer y más importante suceso que marcó su vida fue el fallecimiento, en 1773, de su esposa Katharina tras casi 40 años de matrimonio. Euler volvió a casarse, esta vez con su cuñada Abigail.
A pesar de estos sobresaltos, Euler siguió con su ritmo de publicaciones. Aunque ya había realizado importantes aportaciones en teoría de números con anterioridad, como por ejemplo en su trabajo sobre constantes numéricas, o el llevado a cabo alrededor de la constante de Goldbach y los números de Fermat, los historiadores coinciden en señalar que la mayor parte de esa contribución se produjo en los últimos años de su vida Es justo señalar que todas estas aportaciones a esta rama de las matemáticas —no especialmente apreciada en su tiempo— serían más que suficientes para (consagrar a un matemático.

§. Euler y las ecuaciones diofánticas
Euler hizo importantes contribuciones al estudio de las ecuaciones diofánticas ya en el año 1736. Estas constituyen un punto central en la teoría de números. Una ecuación diofántica es una ecuación con coeficientes enteros y en la que solo se consideran posibles soluciones también enteras. Su nombre proviene del matemático griego Diofanto de Alejandría, quien fue el primero en estudiarlas.
Euler no fue impermeable a su encanto, ya que buena parte de su empeño numérico era la resolución de problemas heredados de Fermat, y Fermat sentía un atractivo irresistible por Diofanto y su campo de actividades. Pero el fruto no estaba todavía maduro para que Euler lo recogiera, y faltaban muchas armas poderosas para abordar sistemáticamente las ecuaciones diofánticas, como la geometría algebraica o las integrales elípticas, que estaban todavía en sus albores. Aunque Euler tanteó las fronteras del imperio de Diofanto, no lo conquistó. Quizá lo más recordado en este terreno sea la demostración del caso n = 3 que dio Euler del último teorema de Fermat. Este establecía la imposibilidad de resolver la ecuación diofántica xⁿ + yⁿ = zⁿpara n = 3, pero Euler demostró la imposibilidad para n = 3. Parece que la demostración, que ya encontró en 1735, contenía un error, pero el propio Euler la corrigió. Además, mientras estudiaba otra categoría de números confirmó la solución para n = 4, que ya había establecido el propio Fermat. La solución universal para cualquier n tuvo que esperar a Andrew Wiles, a finales del siglo XX.
Euler también se interesó por la denominada ecuación de Pell, la ecuación diofántica de la forma

y² =Ax² + 1

donde A es un número entero concreto, no una incógnita. Esta ecuación fue solucionada por Lagrange, quien desarrolló ampliamente el procedimiento de las fracciones continuas investigadas por Euler. Su denominación actual procede de un error de Euler, quien, al parecer, confundió a John Pell (1610-1685) con el matemático William Brouncker (1620-1684), padre universalmente aceptado de la famosa ecuación.

Diofanto y sus ecuaciones
Diofanto de Alejandría (ca. 200/214-ca. 284/298) es conocido por ser el padre de las ecuaciones diofánticas. Aunque en la actualidad se denominan así a las ecuaciones algebraicas, de una o más incógnitas, donde todos los coeficientes son enteros y donde solo se admiten soluciones también enteras, Diofanto admitía también números racionales. Se supone que vivió ochenta y cuatro años, pues entre las pocas cosas que se han conservado de Diofanto figura su epitafio, que hace referencia a su edad. Dice así:
Yace aquí Diofanto, la roca mirad;
mediante arte algebraico, te dice su edad
un sexto de su vida fue niñez y alegría,
y un doceavo adolescente, mientras su barba crecía,
y después de un séptimo, Diofanto casaría
Pasaron cinco, años y un hijo nació.
Pero fue desgraciado pues ese hijo murió, cuando tenía la mitad de los años que su padre vivió.
Durante cuatro años más su consuelo halló,
en la ciencia del número y entonces murió.
Deshaciendo la madeja y escribiendo la ecuación diofántica escondida en estas palabras, se llega a:
y a la solución buscada, x = 84.
Diofanto y Fermat
Otra circunstancia determinante en la popularidad de Diofanto es e! planteamiento del último teorema de Fermat. La larga historia se puede resumir de modo abreviado como sigue: en tiempos de Fermat se editó casi todo lo poco que ha llegado de Diofanto en forma de traducción latina realizada por Claude Joseph Bachet de Méziriac. Fermat tenía por costumbre leer los libros y comentarlos al margen de los mismos. En un lugar determinado del texto encontró una proposición de Diofanto que le dio pie a enunciar lo que luego sería el último teorema de Fermat, un enunciado de aspecto inocente, de planteamiento sencillo y del que Fermat escribió que poseía una demostración maravillosa, que no transcribía por no disponer el libro de margen suficiente. Aireada esa pretensión por el hijo de Fermat, nadie fue capaz de encontrar prueba alguna hasta finales del siglo XX (Andrew Wiles, 1995).
Diofanto escribió once libros de aritmética, de los que solo han llegado seis (otros cuatro de atribución dudosa). Contiene más de 100 problemas de carácter «diofántico», pero no es posible encontrar tras ellos método alguno, sino una formidable exhibición de ingenio.

Julia Robinson (1919-1985) resolvió, gracias a él, el décimo problema de Hilbert, uno de los más preciados de la matemática contemporánea, que se interrogaba sobre la existencia de un algoritmo capaz de determinar si una ecuación diofántica cualquiera tenía soluciones en los enteros, resultando que no.

Una conjetura de Euler sobre ecuaciones diofánticas
Una famosa conjetura euleriana, de su segunda etapa rusa, fechada en 1769, hace referencia a la ecuación diofántica:

x⁴+ y⁴ + z⁴ = u⁴,

y, simplificando, diremos que postula la inexistencia de enteros x, y, z y u que cumplan la igualdad.

Una conjetura sobre sumas de potencias
El matemático francés Augustin-Louis Cauchy (1789-1857) es recordado como un gran talento, pues a él se deben multitud de descubrimientos, teoremas y conceptos; pero hay otros puntos de su personalidad, su piedad acaso excesiva, su descuido a la hora de reconocer el trabajo de otros colegas, que son algo así como el «lado oscuro» de una personalidad controvertida. Una de las anécdotas que cuentan de él muestran su rostro más simpático, más burlón, el inimitable ésprít francés. Según la historia, o con mayor probabilidad, la leyenda, Cauchy, quien recibía muchos manuscritos para evaluarlos, dio con uno que pretendía probar, en el mejor estilo de Fermat, que no existían enteros x, y, z,u, que satisficieran le ecuación diofántica:
x³ + y³ + z³ = u³.
Cauchy estaba aquel día de buen humor, porque antes de leer el artículo ya tenía escrita la respuesta, que ocupaba una sola línea. Lo que respondió concisamente Cauchy fue:
3³ + 4³ + 5³ = 6³.
pues, en efecto, 27 +64 +125 = 216, como cualquier alumno de primaria puede comprobar.

Durante mucho tiempo se creyó que la conjetura era cierta, hasta que el matemático americano Noam Elides (n. 1966) la refutó al publicar en 1988 un contraejemplo:

2682440⁴ +15365639⁴ +18796760⁴ = 20615673⁴.

Y no solo eso, sino que Elides también probó que había infinitas soluciones esencialmente distintas, aunque la más pequeña de ellas involucraba unas setenta cifras. Ello demuestra que ningún resultado conjeturado puede darse por bueno, por evidente que parezca y por mucho que se avance en su comprobación. En la actualidad hay incluso una web rusa que recopila los contraejemplos a la fallida conjetura de Euler.

§. Particiones
A lo largo de toda su trayectoria científica, Euler dedicó considerables esfuerzos a las particiones. Aunque el concepto básico de «partición» es elemental, las matemáticas necesarias para su estudio a fondo son de gran complejidad. Su exposición excede los objetivos de este libro, por lo que el tema se trata someramente.
Tomemos un número entero positivo cualquiera, pequeño para que sea manejable, como por ejemplo, 7; ¿de cuántas maneras se puede descomponer en partes que restituyan el número original? Como es natural, se meten en el mismo paquete aquellas particiones que solo difieren en el orden pero no en las cantidades, es decir, que particiones como 7 = 5 + 1 + 1 y 7 = 1 +5 + 1 se consideran equivalentes y se cuentan solamente una vez. Así, pues, tenemos para el número 7:

Total: 15. Escribamos p(7) = 15. Esta primera aproximación ya muestra que partir un número es una tarea laboriosa y que el resultado no es evidente. Si se calculan los primeros valores de p(x) da:

donde no se atisba regularidad ninguna, salvo que p es creciente. Puede comprobarse que:

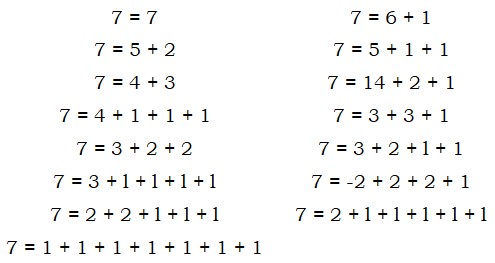
p(100) = 190569292.
Se ha llegado a resultados increíblemente largos y a distinciones tan sutiles como las particiones pares e impares (que solo contienen números pares o impares), o a idear complicados instrumentos aritméticos.

Srinivasa Aiyangar Ramanujan
Matemático indio (1887-1920), su procedencia lejana, lo novelesco de su historia personal y su extraordinario talento introdujeron una nota exótica en el mundo científico de su tiempo. Nació en Erode, del estado de Tamil Nadu, y era hijo de su ambiente, muy religioso, y obsesivo con las cuestiones alimentarias, Genio matemático autodidacta, aconsejado por algunos amigos, envió por correo cartas a la metrópoli británica exponiendo sus resultados. Una de sus misivas llegó a la manos de Godfrey Harold Hardy (1877-1947) quien, junto con su amigo y colaborador John Littlewood (1885-1977), analizaron su desconcertante contenido, que comprendía de todo: presuntos descubrimientos que ya habían sido «descubiertos» antes —incluso por el propio Hardy-' y fórmulas nuevas que denotaban una capacidad matemática excepcional. Invitado por Hardy, Ramanujan viajó por fin a Inglaterra para trabajar y llegó a ser nombrado miembro del Trinity College de Cambridge y de la Royal Society. Muchos de sus resultados figuran todavía en cuadernos de notas sin desentrañar por completo, pero en lo que todos han coincidido es en la belleza, profundidad, ingenio y novedad de los mismos. Amplió el trabajo de Euler en el tema de las particiones, del que se ocupó a fondo; no en vano, mucho de lo que se sabe en la actualidad de este campo es fruto de sus investigaciones. Gracias al genio hindú de Ramanujan, se dispone de una estimación «sencilla» del número de particiones para cualquier número:
que puede llevarse a cabo con una simple calculadora. Si se desearan cifras exactas en lugar de estimaciones, también se pueden conseguir, pero de una forma algo más complicada.

Mucho del extraordinario trabajo de Euler se apoya en las técnicas desarrolladas por Abraham de Moivre, consistentes en jugar con las series de potencias. Obtenía así lo que modernamente se han denominado funciones generadoras, que no son otra cosa que ingeniosos trucos algebraicos encaminados a imitar la realidad. En 1742, Euler ya concibió la idea de encontrar una función generatriz de las particiones, y tras largos años de trabajo llegó, a partir de la serie:

a la fórmula:

Se puede comprobar, desarrollando el producto infinito de la derecha, que aparecen las diferentes particiones del número n en la forma, disimulada, de todas las agrupaciones de exponentes inferiores a n que suman n. Por ejemplo, si tomamos n = 4, vemos cuántos x⁴ se generan:

Resulta 5x⁴ y, naturalmente, p(4) = 5.
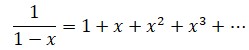
De ahí Euler infirió un modo de calcular p(n), aunque por desgracia es un método recurrente, y solo permite calcular p(n) si se conocen los valores anteriores:

p(n) = p(n - 1) + p(n - 2) - p(n - 5) - p(n - 7) +

+ p(n - 12) + p(n - 15) - p(n - 22) -...

§. Números de Bernoulli
Llamados así en honor a Jakob Bernoulli, pues fue el primero que los trató en 1713, en Ars conjectandi (Arte de conjeturar).
Uno se encuentra con estos números al calcular las sumas de potencias de los enteros positivos:

1 + 2²+ 3² + 4² +… + k²

1 + 2³+ 3³ + 4³ +… + k³

1 + 2⁴+ 3⁴ + 4⁴ +… + k⁴

1 + 2⁵+ 3⁵ + 4⁵ +… + k⁵

o, expresado al modo euleriano, las sumas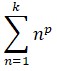

. Se tiene que: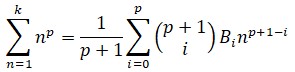

donde los B_i son los números de Bernoulli. Para clarificar la fórmula de más arriba, se propone un ejemplo sencillo, por ejemplo, la suma de los primeros cuadrados. Aplicando la fórmula y poniendo p = 2 en ella, se obtiene:

Euler calculó los treinta primeros números de Bernoulli, una tarea de gran magnitud si se tiene en cuenta que el treintavo es de este tamaño

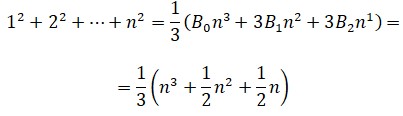
8616841276005
14322

Los números de Bernoulli terminaron apareciendo en la expresión que Euler dedujo para ζ(2n), en el curso de sus investigaciones posteriores al problema de Basilea y que era:

Los números de Bernoulli también aparecen en la moderna expresión de la fórmula de sumación de Euler-Maclaurin, aunque Euler no se apercibió de ello cuando usó la fórmula para tantear el valor de:

y averiguar sus seis primeras cifras decimales.

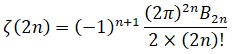
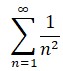
§. Euler y el estudio de los números primos
Aunque no llegó a desentrañar sus misterios, Euler investigó bastante sobre los números primos, incluidos otros conceptos íntimamente relacionados como la función φ, los números de Mersenne o la ley de reciprocidad cuadrática.

«Los matemáticos han intentado en vano, hasta la actualidad, descubrir algún orden en la secuencia de números primos, y tenemos razones para creer que se trata de un misterio que la mente humana nunca resolverá.»
Leonhard Euler

En Variae observationes circa, series infinitas (Varias observaciones sobre series infinitas), publicado en 1744, Euler incluyó una de las fórmulas más aclamadas en el reino de los primos, la fórmula del producto de Euler, cuya deducción figura en el anexo 3 de este libro:

Cuando se hace s = 1, a la izquierda se tiene la serie armónica, que tiende a infinito. Por consiguiente, el resultado de la derecha también debe hacerlo. Pero si es así, no puede ser un producto finito, pues daría lugar a un producto también finito. Así, es un producto infinito y hay, pues, infinitos factores; y como cada factor conlleva un número primo, hay infinitos primos. He aquí cómo Euler encontró otra prueba de la infinitud de los primos.
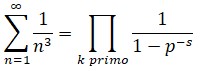
Sin embargo, Euler buscó algo más profundo; la densidad de los primos. Ya sabemos que son infinitos, pero ¿cuán infinitos? Euler probó que la serie, limitada a denominadores primos:

que es una subserie de la serie armónica;

es también divergente. Y aún probó más; si bien la serie armónica diverge más o menos como el logaritmo de n, la serie de los inversos de los números primos todavía diverge más lentamente. Lo hace como el logaritmo del logaritmo de n.
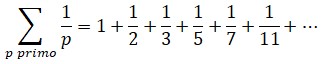
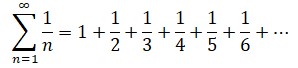
Las ideas de Euler, quien es considerado como iniciador de las técnicas del análisis en teoría de números, fueron desarrolladas primero por Legendre y luego por Gauss, verdaderos iniciadores del estudio del teorema de tos números primos, que dice:

donde π(x) es el número de primos menores que x. Dicho teorema fue demostrado de manera independiente por los matemáticos Charles-Jean de la Vallée Poussin (1866-1962) y Jacques Hadamard (1865-1963) en 1896. Bernhard Riemann extendió las ideas de Euler al terreno de los números complejos gracias a la ampliación a los números complejos, C, de la euleriana función zeta, vista en el capítulo 2, que Euler solo había definido en el conjunto de los números reales, R. De ahí se saltó a la denominada teoría analítica de números y en la era moderna, a la nunca probada hipótesis de Riemann.
La función φ
En aritmética se aprende no solo el concepto de número primo, sino el concepto de primos entre sí (o primos relativos). Se dice que dos números enteros positivos, p y q, son primos entre sí cuando no tienen divisores comunes; salvo el número 1, que los divide a todos. Por ejemplo, 14 y 15 son primos entre sí, pues aunque ninguno de ellos es primo, no poseen divisores comunes, salvo el 1:

14 = 2×7

15 = 3×5.

Otro modo de decirlo mismo, pero más moderno, es acudir al máximo común divisor. Es lo mismo decir que p y q son primos entre sí que decir que mcd (p, q) = 1. La función que Euler denominó φ(n) se define como el número de elementos del conjunto de números menores que n que son primos entre sí con n.
Practiquemos con los diez primeros números:

La función φ(n) se denomina función indicatriz; no se trata solo de un «juguete aritmético» más o menos interesante, sino de un instrumento al que puede sacársele mucho partido; uno de los teoremas más importantes de la teoría de números, el llamado pequeño teorema de Fermat, involucra a la función φ.
Contrariamente a lo acostumbrado en sus trabajos, la notación de la función φ no se debe a Euler.
Euler demostró que si p y q son primos entre sí, entonces se verifica:

φ(p,q) = φ(p) φ(q)

Y, también, que si p es primo; φ(p) = p - 1.
Asimismo, es de Euler, aunque bastante anterior, el resultado de que si p y q son primos entre sí, se verifica el llamado pequeño teorema de Fermat:

p^φ(q) ≡ 1 mod q

donde mod q significa «módulo q» y quiere decir que p^φ(q) y 1 dejan el mismo resto al dividirse por q. Este teorema fue demostrado por Euler en 1736, en Theorematum Quorundam ad Numeros Primos Spectantium Demonstratio (Una prueba de ciertos teoremas sobre números primos), y se presentaba antes en la forma restringida que le dio Fermat. Si se supone además que q es primo, entonces se verifica φ(q) = q - 1 y se tiene el enunciado original de Fermat:

p^q-¹ ≡ 1 mod q

con q primo y p y q primos entre sí Euler ofreció no menos de tres demostraciones concretas de este teorema, aunque es casi seguro que no sabía que Fermat era uno de los padres del teorema original.
El moderno sistema de encriptación RSA, el sistema de clave pública más utilizado, tiene en este teorema su base más firme, como puede comprobarse en el anexo 6.
Los números de Mersenne
Euler quiso descubrir números primos de gran tamaño. Muchos fueron los matemáticos que hasta entonces habían supuesto, erróneamente, que los números M_p de la forma M_p= 2^p^-1, siendo P un primo, eran todos primos. Pietro Cataldi (1548-1626) probó, en 1588, que M₁₇y M₁₉ eran primos por el procedimiento un tanto rudimentario, pero estándar, de intentar dividirlos por los primos inferiores a su raíz cuadrada.

Marin Mersenne
Marín Mersenne (1508-1648) fue sacerdote, músico, matemático, filósofo y teólogo, aunque su gran vocación era la música, disciplina a la que dedicó una gran parte de sus esfuerzos, no en vano se le conoce en muchas fuentes como «el padre de la acústica», Estableció las leyes fundamentales de la vibración de las cuerdas y se ocupó de multitud de problemas armónicos e instrumentales. Se dice que en la segunda suite de Ottorino Respighi, Antiche arie e danze per liuto, se reproduce un fragmento compositivo suyo, se ocupó también a fondo de los telescopios y de sus espejos, llegando a ser considerado una autoridad. Actuó, sobre todo a través de su abundante correspondencia, como una especie de centro neurálgico receptor y emisor de novedades científicas en un tiempo en el que escaseaban las publicaciones de este tipo. Interesado por casi todo, conoció y cultivó la amistad o el contacto con multitud de intelectuales de su tiempo, en particular de Descartes, quien era compañero de estudios suyo. Racionalista y reflexivo, combatió con energía las creencias más irracionales como la cabalística o la magia. Se interesó mucho por las matemáticas, y además de editar varios textos de autores clásicos, como Arquímedes o Euclides, dedicó atención al mundo numérico. Es ahí donde reside su importancia para los historiadores y por eso los números que estudió, los números M_p de la forma:
M_p = 2^p -1
Se denominan números de Mersenne. Existe un generador de números pseudo-aleatorios, relacionado con los primos de Mersenne, que lleva su nombre; el Mersenne twister.

Más tarde, Marín Mersenne, a quien se debe la M de tales números, dio una lista de presuntos primos que posteriormente se demostró bastante inexacta, pues sobraban M₆₇ y M₂₅₇, y faltaban M₈₁, M₈₉, y M₁₀₇. En la actualidad, el récord está en el M_43112609 que tiene 12978189 dígitos y cuya expresión ocuparía más de 50 libros como el presente.
Euler demostró que M₃₁ era primo en 1772, aunque es muy probable que ya lo hubiera averiguado antes. Lo curioso es que hubo que esperar más de un siglo para que Édouard Lucas (1842- 1891) encontrara, en 1876, el siguiente en el tiempo, M₁₆₇ (M₆₁ y M₈₉)también son primos, pero se descubrieron con posterioridad.) Así, el récord del primo mayor estuvo en poder de Euler durante aproximadamente 104 años.
La reciprocidad cuadrática
La reciprocidad cuadrática, todo un cuerpo de doctrina aritmética plasmado por Gauss de modo brillante en las Disquisitiones arithmeticae (Disquisiciones de aritmética), fue iniciada por Legendre y Euler, este último en una carta a Goldbach, en 1742. Para empezar, definamos primero el lenguaje, es decir, los símbolos de Legendre

Supongamos p y q primos impares distintos y:

Con esta notación Gauss, y no Euler, llegó a demostrar que:

Lo cual puede reunirse (no fácilmente) en una sola fórmula. Gauss descubrió todo lo anterior a los diecinueve años y lo tenía en tal aprecio que lo calificó de aurum theorema, «el teorema áureo».

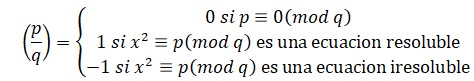
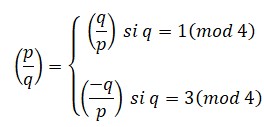
Adrien-Marie Legendre
La vida profesional de Legendre (1752- 1833) empezó bajo los mejores auspicios, pues era un hombre muy bien dotado intelectualmente y poseía una fortuna propia que le permitía dedicarse a su trabajo sin coerciones externas. Su progreso como matemático fue asentándose a medida que transcurrían los años. Al lado de Laplace, realizó importantes trabajos astronómicos, inventando lo que luego se llamaron polinomios de Legendre; se sumergió en el poco conocido territorio de las funciones elípticas y en la teoría de números, donde creyó haber resuelto la entonces magna cuestión de la reciprocidad cuadrática. Pero su investigación contenía algunos agujeros, tal y como puso de manifiesto años más tarde Carl Friedrich Gauss. Sus trabajos astronómicos determinaron su nombramiento como miembro de la Royal Society. Fue designado para trabajar en la comisión encargada de poner las bases del Sistema Métrico Decimal uno de los programas de racionalización que se impulsaron tras la revolución francesa. Aunque comulgaba con muchas de las ideas revolucionarias, tuvo que ocultarse en los tiempos del terror, y por esa época perdió su fortuna personal. Reescribió entonces y publicó los Elementos de Euclides bajo un punto de vista y un lenguaje modernos, obteniendo un éxito editorial resonante y duradero. El recién llegado Napoleón lo tomó bajo su protección, y Legendre, ya académico y consagrado, se dedicó por un tiempo al movimiento de los cometas, lo que dio origen al método de los mínimos cuadrados para calcular trayectorias, adelantándose esta vez a Gauss. De esta época datan sus estudios sobre la distribución de los números primos, que conjeturó obedecían a la ley asintótica:
Este valor, muy próximo al óptimo actual, conduciría luego al teorema fundamental de los números primos. También en este terreno Gauss llegó el primero, pero no publicó nunca sus resultados.
Los últimos años de Legendre
El último período de su vida lo dedicó a las funciones elípticas, pero en una forma ya entonces obsoleta debido a las aportaciones de Niels Abel (1802-1829) y Carl Gustav Jakob Jacobi (1804-1851). Trató también las geometrías no euclídeas, quedándose a las puertas de desentrañar sus secretos. Todavía probó el último teorema de Fermat para n = 5. En 1824 se enfrentó al ministro del interior de Luis XVIII y fue privado de su pensión. El gobierno posterior de Luis Felipe de Orleans volvió a pagarle, pero solo una parte; no obstante, le concedieron la Légion d'Honneur, Legendre no murió en la indigencia, pero conoció la pobreza. Un triste final para un científico que posee un cráter lunar dedicado a su memoria, una calle en París y una placa recordatoria en la torre Eiffel.

§. Números amigos y números perfectos
Diremos que un divisor d de un número cualquiera n es un divisor no trivial de n, si 1 ≤ d ≤ n. El divisor n, será el divisor trivial de n.
En 1747 apareció documentada una primera intervención seria de Euler en el terreno de los números amigos. Dos números son amigos si sumados los divisores no triviales del uno dan el otro y viceversa.
Es un concepto de «amistad» muy aritmético que se enriende con un ejemplo; tomemos los números 220 y 284: los divisores no triviales de 220 son 1, 2, 4, 10, 11, 20, 22, 44, 55 y 110; los correspondientes de 284 son 1, 2, 4, 71 y 142.
Se cumple que:

220 = 1 + 2 + 4 + 10+ 11 +20 + 22 + 44 + 55 + 110 = 284

284 = 1 + 2 + 4 + 71 + 142 = 220.

Los números 220 y 284 son amigos. En el reino numérico, la amistad es un fenómeno nada común. Si se hubiera realizado la prueba con cualquier otra de las 19 880 parejas posibles inferiores a 284, no se hubiera encontrado ninguna otra. De hecho, en época de Euler solo se conocían tres parejas amigas: (220,284), (17296, 18416) y (9363584,9437056), encontradas por Thabit ibn Qurra (836-901), Fermat y Descartes.
Euler, en un primer artículo, daba ya 30 parejas nuevas pero no demasiadas pistas de por dónde discurrían sus pensamientos. Luego elevó su aportación a 90 números amigos. La pareja (1184, 1210) fue descubierta en el siglo XIX por un modesto cultivador de las matemáticas, Niccoló Paganini.
Se ha comprobado ya que no hay demasiadas parejas amigas: el húngaro Paul Erdös (1913-1996) probó en su día que la densidad de números amigos en el conjunto N es cero. Con la ayuda de las computadoras se ha llegado a las decenas de millón de parejas amigas. Más adelante volvió Euler sobre el tema, con su acostumbrada perspicacia, y legó un criterio suficiente para construir números amigos:
Los números N = 2ⁿpq y N = 2ⁿr son amigos si p, q y r son primos, de la forma:

con n >m > 0.
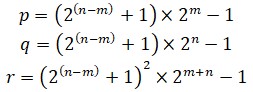
La condición sugerida por Euler es suficiente pero no necesaria. No proporciona todas las parejas amigas, pero es un paso importante.
Números perfectos
Están estrechamente relacionados con los números amigos. Un número se dice que es perfecto cuando es amigo de sí mismo. Eso quiere decir que un número es perfecto cuando es igual a la suma de sus divisores no triviales; es lo que sucede con 6 o 28, por ejemplo, que cumplen:

6 = 1 + 2 + 3 =6

28 = 1 +2 + 4 + 7 + 14 = 28.
El siguiente número perfecto es el 496 que todavía es accesible con simple lápiz y papel.
Hasta 2012 se habían encontrado 47 números perfectos, y el octavo lo descubrió Euler. He aquí los diez primeros:

El número p de la tabla tiene su significado. Todos los números perfectos de la relación y, de hecho, todos los que se han descubierto hasta hoy, son de la forma 2^p^-1 (2^p-1) donde M_p = 2^p -1 es un primo de Mersenne. Euclides ya incluyó en sus Elementos que si 2^p -1 es primo, 2^p^-1 (2^p-1) es par y perfecto. El mérito de demostrar el teorema reciproco es de Euler, aunque la demostración apareció póstumamente.
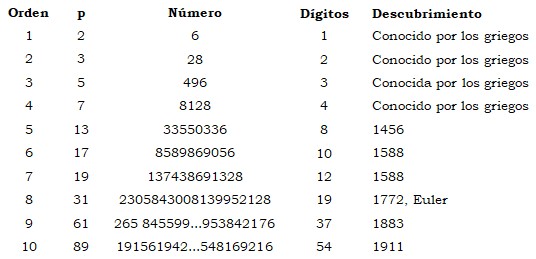
Lo que no se ha encontrado nunca es un número perfecto impar, por más que las computadoras han buscado hasta 10³⁰⁰. Tampoco se sabe si hay infinitos números perfectos, otra de las grandes incógnitas de la teoría de números.
En Internet se puede encontrar hasta el número 24 de los números perfectos y tiene 12003 dígitos.

§. Ladrillo de Euler
Llamado también cuboide, el ladrillo de Euler es un prisma rectangular de lados a, b y c, en el que tanto los lados como las diagonales de las caras son números enteros. Eso equivale a que tales elementos satisfacen un sistema de ecuaciones diofánticas:

Euler no inventó dicho «ladrillo», pero en 1770 y 1772 encontró dos ecuaciones que proporcionaban infinitos ladrillos, pero no todos. Hasta el momento el menor ladrillo encontrado tiene por lados 240, 117 y 44.
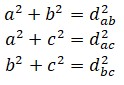
Cuando la diagonal espacial del cuboide, no la de las caras, sino la espacial, es también entera, al ladrillo se le llama cuboide perfecto, aunque de momento, y se llevan buscando más de 250 años, no se ha encontrado ninguno.
De todas maneras, se ha llegado bastante cerca del cuboide perfecto; se ha encontrado un cuboide con un a de 68162 dígitos, un b de 56802 y un c de 56803, que proporciona una diagonal espacial que solo difiere de un número entero en 10^-60589 = 0,000000...00001, con 60589 ceros tras la coma decimal).

§. Un paseo por el Euler recreativo
Ya se ha dicho que las matemáticas llamadas hoy recreativas fueron el detonante de muchas teorías importantes en el pasado y que la consideración de mero pasatiempo de que gozan ahora no ha sido siempre la misma. Eminentes sabios dedicaron en el pasado muchas energías a temas como los juegos de naipes, dados, cuadrados mágicos y todo tipo de acertijos sin experimentar rubor alguno por hacerlo y sin sentir que perdían el tiempo.

El cuadrado mágico que se reproduce en Melancolía de Albrecht Durero, es de orden 4 y un número clave 34.

Un desahogo aritmético extendido fueron los cuadrados mágicos. Se trata de disposiciones cuadradas de n números (n se dice que es el orden del cuadrado), que no se repiten, usualmente, en la misma fila o en la misma columna, y que suman (la suma S se denomina constante mágica) la misma cantidad cuando se las suma fila a fila, columna a columna y siguiendo las diagonales.
Los cuadrados mágicos forman parte de una clase más general, los llamados cuadrados latinos, denominados así porque Euler los denotaba con caracteres latinos. Euler dedicó bastante reflexión a los cuadrados latinos en su artículo Investigaciones sobre una nueva especie de cuadrados mágicos, de 1782. Un cuadrado latino es un cuadrado de lado n (los algebristas prefieren hablar de una matriz de orden n) de manera que en cada casilla anida un símbolo (que puede ser un número) que aparece una vez sola en cada fila y columna.

El número de cuadrados latinos crece de modo fenomenal a medida que aumenta n:

En la actualidad los cuadrados latinos tienen su aplicación científica más comente en la elaboración de códigos correctores de errores, en agronomía, en el diseño de experimentos, en análisis estadístico y en ramas más clásicas de las matemáticas como la teoría de números, la de grupos, la informática o la teoría de grafos y la combinatoria.
Solo citar también, porque las matemáticas involucradas son ya de carácter superior, que completar un cuadrado latino incompleto, cualquiera que sea el cuadrado, es un problema de planteamiento sencillo, pero para el que no parece existir algoritmo de solución alguno. Es, por tanto, un problema NP-completo en la jerga de la teoría de la complejidad.
Un tipo especial de cuadrados latinos son los cuadrados grecolatinos, como el de la figura 1.

Euler los llamaba grecolatinos poique para describirlos con claridad usaba caracteres de ambos tipos, griegos y latinos. Los cuadrados grecolatinos son hijos de dos cuadrados latinos más simples.

Mucho antes que Euler, no obstante, existían los cuadrados grecolatinos, encarnados en simples juegos de naipes; la disposición de cartas que aparece en la figura 2, de Jacques Ozanam (1640-1718), muestra palos y figuras sin que figuren repetidos en ninguna fila o columna.
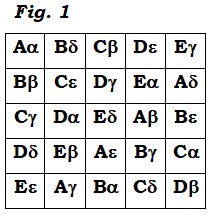
Para este caso, simetrías aparte, hay 144 soluciones.
No fue tan afortunado Euler cuando abordó el problema de los 36 húsares, de estructura similar (figura 3).

El problema funciona como sigue: de seis regimientos se seleccionan seis oficiales, cada uno de graduación distinta,^- ¿es posible disponerlos en una formación cuadrada de manera que no coincidan en la misma fila o columna miembros de igual regimiento o graduación?
Euler probó a hacerlo y fracasó, por lo que conjeturó que el problema carecía de solución. De hecho, conjeturó que no existía ningún cuadrado grecolatino de orden n = 4x + 2, cualquiera que fuera x. Su conjetura permaneció como tal durante más de un siglo hasta que la probó el matemático francés Gastón Tarry (1843-1913); lo curioso es que Tarry construyó todos los cuadrados posibles para el orden n - 6, y comprobó que la respuesta era negativa.

Posteriormente, en 1960, una computadora encontró un cuadrado grecolatino de orden 10 (figura 4). Así pues, la conjetura de Euler era cierta para n = 6, pero ya no lo era para n = 10 (y sucesivos, como se demostró luego).

El sudoku
Quizás uno de los pasatiempos más conocidos actualmente sea el sudoku, un juego que data del año 1979, cuando hizo su aparición en la publicación Dell pencil puzzles and word games, de donde saltó al Japón con el nombre de sudoku («números sueltos») y de ahí a la fama universal. El sudoku no es un juego de origen japonés, como generalmente se cree, sino que es norteamericano.
El sudoku hunde sus raíces en Euler y los cuadrados latinos. Un sudoku no es más que un cuadrado latino de orden 9, que contiene 9 subcuadrados. Dentro de estos pueden disponerse los nueve dígitos habituales (figura 5).
El disco de Euler

Entre 1761 y 178], a Euler debió de apetecerle volver por unos momentos a su niñez. No solo se ocupó de los cuadrados mágicos, que constituyen una forma de entretenimiento, sino que también data de esta época la invención de un juguete; el disco de Euler.
Tomemos una simple moneda, pongámosla vertical sobre la mesa y hagámosla girar de súbito alrededor de su eje vertical como se muestra en la figura 6.
La moneda girará primero alrededor de su eje vertical; luego, a medida que su energía cinética se vaya disipando, irá cediendo a la atracción de la gravedad e inclinándose hacia el suelo, la mesa o la superficie sobre la que se sostenga. Pero no caerá súbitamente porque el momento de rotación tenderá a conservarla de pie. La duración del giro puede ser larga, incluso larguísima si el rozamiento es mínimo, pues entonces la energía se disipa más lentamente. Por eso cuando se utiliza el disco como juguete, la superficie de giro se incluye en el paquete de ventas y ambos objetos, disco y superficie de giro están muy pulidas (son de acero cromado) y casi no producen roce. El disco va colapsando en su giro, pero ya no lo hace sobre un eje vertical, sino por un eje que se desplaza perpendicularmente al eje de tangencia (que a su vez va describiendo una curva alrededor del centro inicial), y termina por caer con un repiqueteo característico (figura 7).
Muchos investigadores han examinado el comportamiento a fondo del disco de Euler y han llegado a predecir con bastante exactitud el momento en el que el juguete entra en el período de repiqueteo anunciador del fin de todo movimiento; parece ser que ello sucede cuando la moneda gira unas 100 veces por segundo. Entonces sobreviene una singularidad y es el fin de la diversión.
Algunos se habrán apercibido que se ha imitado, con una simple moneda, el lentísimo fenómeno astronómico de la precesión de los equinoccios. Ese era el auténtico interés de Euler.

§. Los últimos libros de Euler
Ningún estudio de la obra de Euler puede dejar de citar los libros importantes aparecidos en esta última época. Uno de ellos, Lettres a une princesse d’Allemagne sur divers sujets de physique et de philosaphie, publicado en 1768, consta de 234 cartas dirigidas a la princesa de Anhalt-Dessau, y explora todo el universo científico, con incursiones de carácter pío y filosófico, dando a una persona ilustrada, pero sin formación científica, su visión sobre el universo y sus entresijos. No todo el mundo entendió que Euler dedicara su tiempo a la divulgación. El propio Daniel Bernoulli, que siempre fue un amigo muy respetado, le reprendía instándole a ocuparse de «más sublimes materias».
Otro libro de importancia, de 1770, es Vollständige anleitung zur algebra (Instrucción completa en álgebra), un libro de álgebra ideal páralos que se estrenan en la disciplina, y que se convirtió en un auténtico best seller, traduciéndose a varias lenguas. En él se explican, con extraordinaria claridad y método, las operaciones numéricas, los polinomios, las series elementales, las progresiones, los desarrollos en números decimales y las ecuaciones. Casi al principio, Euler introduce ya los números complejos y opera con ellos siempre que puede, considerando a los «números imaginarios» como creaciones legítimas del intelecto, objeto de estudio matemático al margen de su significado práctico.
Entre 1769 y 1771 aparecieron tres sólidos tomos dedicados a la óptica, los tres volúmenes de la Dioptricae, que son tratados muy prácticos que pretenden, sobre todo, mejorar el funcionamiento de los instrumentos ópticos por antonomasia, microscopios y telescopios. El trato que se le da a los sistemas lenticulares y a la aberración, tanto esférica como cromática, es muy acertado. Las conclusiones son contrarias al criterio de Newton de que no se podía combatir con lentes la aberración cromática. Un experimentador inglés, John Dollond (1706-1761), demostró la certeza de las tesis eulerianas que recomendaban el uso de dos vidrios distintos para construir lentes acromáticas.
Ya se ha comentado anteriormente el interés que Euler profesó a las cuestiones astronómicas, en concreto, a la teoría de los tres cuerpos, el movimiento cometario y el estudio de la Luna.

Grabado realizado por el artista J. Chapman, que muestra en un primer plano a un Euler ya anciano.

Su gran centro de atención terminó siendo el movimiento de la Luna. En 1770 añadió otro Grand Prix a su lista cuando, conjuntamente con su hijo Johann Albrecht, fue galardonado por un ensayo sobre el problema de los tres cuerpos aplicado al movimiento lunar, en 1748 Euler ya había ganado uno sobre el mismo tema; pero no pareció haberse fatigado por la materia, pues, en 1772, lo volvió a ganar sobre la misma cuestión y esta vez lo compartió con Lagrange.
Sin embargo, quedaron sueltos unos flecos importantes y Euler analizó nuevamente, en 1772, las muchas irregularidades del movimiento de la Luna dedicándole un libro de 791 páginas, Theoria motuum lunae (Teoría del movimiento de la Luna), Escrito en dos partes, la segunda presenta casi solo tablas de situación —una de ellas ocupa 144 páginas—, obtenidas a través de métodos innovadores y cálculos muy laboriosos, en las que se tienen en cuenta las elongaciones del Sol y la Luna, la excentricidad, el paralaje o la inclinación del plano orbital lunar.

Tumba de Euler, situada en el Monasterio de Alejandro Nevski, de San Petersburgo.

Aunque para llevar a cabo esta ingente labor se rodeó de sus mejores colaboradores, no deja de ser un ejercicio intelectual de gran mérito.
En 1773 regresó de nuevo a los temas navales con Theorie complete de la construction el de la manoeuvre des vaisseaux (Teoría completa de la construcción y de la maniobra de los buques), que sorprende por su casi ausencia de fórmulas matemáticas.

§. El día en que Euler dejó de calcular
La muerte sobrevino a Euler, rico, respetado, en algunos ambientes directamente reverenciado, mientras trabajaba. Según el relato del historiador Adolf-Andréi Pávlovich Yushkévich. La muerte de Euler a los 78 años, fue así:

El 18 de septiembre de 1783, Euler invirtió la mayor parte del día del modo usual. Dio su lección de matemáticas a uno de sus nietos, hizo algunos cálculos con la tiza sobre dos pizarras sobre el movimiento de los globos aerostáticos; luego discutió con Lexell y Fuss el reciente descubrimiento de Urano. Sobre las cinco de la tarde sufrió una hemorragia cerebral y dijo solo «Me estoy muriendo» antes de perder la consciencia. Murió alrededor de las once de la noche

El relato debe de ser bastante fiel, pues entre los artículos póstumos, terminados por su hijo, figura el de los globos Montgolfier, los globos aerostáticos. Que su muerte fue súbita y que Euler se apercibió de ella también ha sido corroborado por más de un testigo. Tras el fallecimiento del sabio, llegó la hora de los elogios fúnebres. Los más notables, auténticas biografías laudatorias de regular extensión, son dos. Fueron escritos, el primero, por su nieto político Fuss, a quien le correspondía por derecho propio, dado su parentesco y el alto cargo que desempeñaba en la Academia. El otro lo escribió el marqués de Condorcet (1743-1794) para la Academia francesa. La línea final del elogio de Condorcet es bella y elocuente y podría aplicarse en cierto sentido al presente volumen. Termina diciendo: «Dejó de calcular y dejó de vivir»

Anexo

1. Los logaritmos y Napier
Puede considerarse a sir John Napier (1550-1617) como el inventor de los logaritmos. Este procedió a dibujar dos rectas planas del siguiente modo: primero dibujó un segmento de extremos A y B; en paralelo, dibujó una recta sin fin de inicio en A'. Luego supuso que un móvil se deslizaba a través de la recta sin fin con velocidad constante. A cada punto X' de la recta le hizo corresponder un punto X del segmento AB, pero no de cualquier modo: X se movía con una velocidad igual a la distancia XB. Llamando x = BX e y = A'X', Napier creó su logaritmo:

y = log x

Napier tomó AB = 10⁷, lo que conduce a unas igualdades algebraicas un tanto complicadas. Si N es un número y L es el logaritmo, Napier calculó N = 10⁷(1-10^-7)^L. De todo ello se deduce:

Y, como se ve, ya ha aparecido la constante e, pues:

En muchos tratados antiguos —y no tan antiguos— se habla de logaritmos neperianos o naturales, identificación algo confusa pues los logaritmos naturales son los de base e, mientras que los ideados por Napier estaban (casi) en base 1/e. Son prácticamente lo mismo, pues solo difieren en un signo no en el valor absoluto:

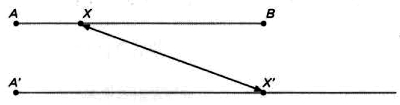
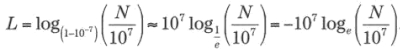
log_eN = log_1/e N

En la actualidad, para todo número real positivo N, cuando N = a^L, decimos que L es el logaritmo de N en base a. Escribimos entonces

L = log_aN.

Si uno se detiene a pensar, se comprobará que el logaritmo de la base es siempre 1, lo que resulta una propiedad fundamental.
Las bases más utilizadas son a = 10, a = 2 y a = e. Los logaritmos en base 10 se denominan logaritmos decimales, los de base 2, binarios; y los de base e, logaritmos naturales. Si se elije e como base, la escritura normalmente aceptada es ln N, en lugar de log N.
Lo relevante del concepto de logaritmo es que facilita el cálculo puramente aritmético. Ello se deduce de que:

y, por tanto, el logaritmo de un producto es la suma de los logaritmos de los factores.
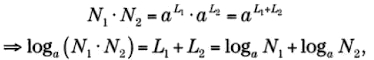
Si se tienen tabuladas ambas magnitudes, números y logaritmos decimales, pueden sumarse los logaritmos y acudir a las tablas para conocer sin dificultades el producto. Aunque en la actualidad son las calculadoras electrónicas las que proporcionan directamente los productos sin esfuerzo, en la época en la que estas no existían, sustituir una multiplicación ardua, cuando el producto original era muy grande, por una suma sencilla, era algo de una relevancia extraordinaria.
2. El problema de Basilea
Sigamos los vericuetos de su razonamiento, aunque sepamos por adelantado que diversos pasos presentan algún problema y necesitan ser pulidos. El propio Euler lo hizo a posteriori.
Si partimos de la conocida serie de Taylor

sabemos que se anula si se anula x, es decir que sen x = 0 cuando x = 0, ± π, ± 2π, ± 3π,...
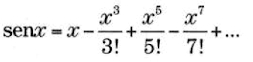
De modo que, suponiendo que una serie se comportará como un polinomio, ya que de hecho es un polinomio larguísimo, la aplicación del teorema fundamental del álgebra la convertirá en producto de monomios del tipo x - α., donde α es una solución. Procedamos:

Ahora K es una constante numérica desconocida. Operando a la derecha:

se observa que cada término de la forma x² - λ²π² de la derecha es cero. Ahora bien, eso solo sucede si y solo si:

Reescribimos, pues, los términos de la derecha en la forma:

Ahora dividimos por x.

Y como

concluimos que K= 1. Así que queda:

que es una serie igual a un producto infinito. Ningún problema, según Euler. Efectuamos ordenadamente el producto y separamos los términos (infinitos) en x² del producto de la derecha. Queda la igualdad:

Y dividiendo ambos lados por -x²/π² se obtiene:

como queríamos averiguar.
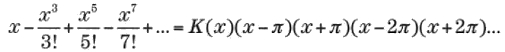
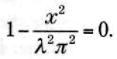
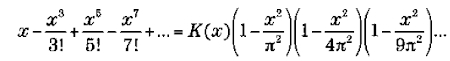
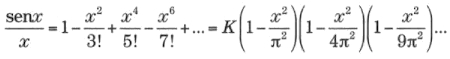
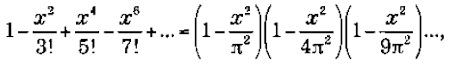
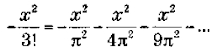
3. La función zeta y los números primos
Euler es quien demostró en primer lugar la equivalencia entre ζ(s) como serie de potencias y ζ(s) como producto infinito. Llamemos p_k al k-ésimo número primo; entonces se verifica:

A continuación, se puede ver cómo llegar a esa igualdad:

Para quienes conozcan el análisis complejo por el procedimiento estándar, la función zeta puede prolongarse como función meromorfa a todo el plano complejo con un solo polo en s = l, donde el residuo es 1. Esta es la función zeta (zeta = ζ) a la que se refería Riemann y objeto asimismo de la célebre hipótesis de Riemann.
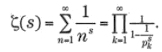
4. Las ecuaciones de Euler-Lagrange
Para simplificar la exposición en la medida de lo posible, se partirá del supuesto de que las funciones involucradas satisfacen todas las condiciones de continuidad y derivabilidad necesarias.
Llamaremos S al funcional (función de funciones) al que aplicamos el cálculo de variaciones y x₁, x₂ a los extremos de la función incógnita:

Supondremos que f₀, es la solución y que el funcional posee un mínimo en esa ubicación; llamaremos α(x) a una función (es la que haremos «variar») que se anule en los extremos, x₁, x₂. Como en f₀ el funcional posee un mínimo:

en un entorno def₀ entorno pequeño, cercano a cero. La «variación»:

debe, pues, cumplir

Recordemos ahora que:

y apliquemos la regla de derivación en cadena y las sustituciones oportunas.
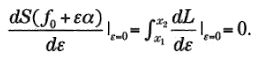
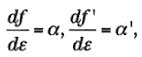
Obtenemos:

y aplicando la integración por partes y las sustituciones de la fórmula anterior

Como el término inicial es cero, el final también, y concluimos que:

Y ya se tienen las ecuaciones de Euler-Lagrange, que, en el mundo real, acostumbran a desembocar en ecuaciones diferenciales de segundo orden.
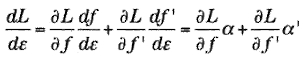
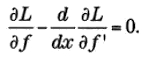
5. Los números complejos
Euler dedujo su primera fórmula fundamental, de la que fue extrayendo otras, de simples series de Taylor.
Recordemos que las potencias de i se comportan así:
Y recordemos también que los desarrollos en serie de potencias, o desarrollos en series de Taylor de las potencias de base e, y las funciones trigonométricas del seno y del coseno son:

Y recordemos también que los desarrollos en serie de potencias, o desarrollos en series de Taylor de las potencias de base e, y las funciones trigonométricas del seno y del coseno son:

Operando:

6. Criptografía y el pequeño teorema de Fermat
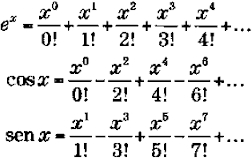
Sea M un mensaje y E su encriptación. Supondremos que ambos son números naturales. Llamemos f a la función que va de M a E: f(M) = E. Para codificar M, el codificador y el descifrador del mensaje seleccionan dos números primos muy grandes, p y q, y definen el módulo, al que llamaremos n poniendo n = p q, suponiendo n > M. Se elije un e, con 1 < e < φ(n) y e primo entre sí con φ(n). La clave pública está formada por n y e, y la conoce todo el mundo. Como n es tan grande y no está factorizado, p y q son una incógnita inextricable. Se tiene E = f(M) ≡ M^e (mod n). Denominamos clave privada al par n,d, donde d se elije de manera que de ≡ 1 (mod φ(n)). Como p y q son primos, y pq = n, se tiene que φ(n) = (p - l)(q - 1); si no se conocen p y q, y es prácticamente imposible conocerlos, no puede conocerse tampoco φ(n). Así que no se puede conocer d. Pero el descifrador sí que posee d, pues conoce p y q, y, por tanto, puede proceder al descifrado: E^d ≡ (M^e)^d (mod n) ≡ M^ed (mod n) ≡ M^Nφ(n)+¹ (mod n), N ∈ ℕ. Se aplica entonces el pequeño teorema de Fermat. Si a = M^N (a es, casi seguro, primo entre sí con n), aplicando el teorema: E^d ≡ Ma^φ(n) (mod n) ≡ M (mod n) = M, ya que M < n, como se ha supuesto al principio. De esta explicación se puede extraer que crear una clave es relativamente fácil, pues solo se necesitan dos números primos grandes, p y q, y romperla, muy difícil.

Lecturas recomendadas

Bell, E.T., Los grandes matemáticos, Buenos Aires, Losada, 2010.
Boyer, C., Historia de la matemática, Madrid, Alianza Editorial, 2007.
Bradley, R., Sandifer, E. (editores), Leonhard Euler: life, work and legacy, Amsterdam, Elsevier B.V., 2007.
Dunham, W., Euler, el maestro de todos nosotros, Madrid, Nivola,2000.
Galindo, A et al., La obra de Euler: tricentenario del nacimiento de Leonhard Euler (1707-1783), Madrid, Instituto de España, 2009.
Stewart, I., Historia de las matemáticas, Madrid, Crítica, 2008.
Vargas, G., Calzada, G., Euler, el matemático, Madrid, El rompecabezas, 2011.