
Breve historia de las matemáticas
Jacqueline Stedall
Durante la redacción de esta obra, dedicada a un tema tan amplio, me he inspirado enormemente en otros autores que también se han enfrentado al desafío de ofrecer textos imaginativos e inspiradores.
En los últimos años he tenido el privilegio de trabajar en la edición deThe Oxford Handbook of the History of Mathematics y del BSHM Bulletin (la revista de la Sociedad Británica para la Historia de las Matemáticas). Ambas tareas me permitieron trabajar de cerca con más de ochenta autores que han escrito sobre la historia de las matemáticas desde perspectivas muy variadas, y de cada uno de ellos he aprendido algo. Gran parte de ese trabajo lo realicé junto a Eleanor Robson, una gran amiga y compañera a la que agradezco enormemente las horas de compañía y debate con las que me ayudó a trazar el paisaje que he intentado plasmar en este libro. En particular me apoyé en la investigación y la experiencia de Markus Asper, Sonja Brentjes, Christopher Cullen, Marit Hartveit, Annette Imhausen, Kim Plofker, Eleanor Robson, Corinna Rossi, Simón Singh, Polly Thanailaki, y Benjamin Wardhaugh; los libros y artículos de estos autores y algunos otros figuran en el apartado dedicado a lecturas adicionales del final de este volumen.
La colección de cuadernos de copiado para niños de John Hersee que se menciona en el capítulo 4, es propiedad de la Asociación de Matemáticas (Mathematical Association), y se encuentra en la Biblioteca David Wilson de la Universidad de Leicester. Agradezco a Mary Walmsley y Mike Price, archivistas de dicha asociación, la generosa hospitalidad y colaboración que me brindaron durante esa parte de mis indagaciones. Asimismo agradezco a Joanna Parker, del Worcester College, Oxford, que me permitiera consultar la copia de John Aubrey del cuaderno de notas de Anne Ettrick. Me siento en deuda con Andrew Wiles, Christopher Cullen, Eleanor Robson y Adam Silverstein por darse el trabajo de revisar los detalles de los capítulos 1, 2, 4 y 5, respectivamente. Mi agradecimiento más sincero a todos ellos y a aquellos otros que aportaron agudos comentarios sobre aspectos diversos del texto: los lectores anónimos de Oxford University Press, Peter Neumann, Harvey Lederman, Jesse Wolfson y todos los miembros de mi familia más próxima, algunos de los cuales jamás habían pensado en leer sobre la historia de las matemáticas hasta ahora.
Las matemáticas tienen una historia que se remonta como mínimo a 4.000 años atrás y que alcanza a todas las civilizaciones y culturas. Incluso en una obra tan concisa como este libro, sería posible perfilar algunos acontecimientos y descubrimientos matemáticos decisivos siguiendo un orden más o menos cronológico. De hecho, tal vez sea eso lo que espera la mayoría de los lectores. Sin embargo, una exposición de ese tipo puede plantear diversos problemas.
El primero es que esos discursos suelen dar una versión «progresivista» de la historia de las matemáticas, donde el pensamiento matemático parece progresar y ascender imparable hacia los fantásticos logros de la actualidad. Por desgracia, esas colecciones de signos de avance suelen pasar por alto las complejidades, errores y callejones sin salida que forman parte inevitable de cualquier actividad humana, incluidas las matemáticas; en ocasiones, los fracasos son tan reveladores como los éxitos. Además, al definir las matemáticas actuales como el referente a partir del cual deben valorarse los esfuerzos previos, es fácil acabar considerando las aportaciones del pasado como empeños valerosos, pero en última instancia desfasados. En cambio, para observar cómo se llegó a tal o cual hecho o teorema, hay que detenerse a contemplar los descubrimientos en el contexto del tiempo y lugar en el que surgieron.
Otro problema sobre el que me extenderé más adelante, radica en que las exposiciones cronológicas presentan muy a menudo los descubrimientos como «saltos de trampolín» donde se enuncian uno detrás de otro, sin las importantísimas conexiones que mantienen entre ellos. La finalidad del historiador no consiste únicamente en recopilar listas cronológicas de grandes acontecimientos, sino en desvelar las influencias e interacciones que condujeron hasta ellos. Este será un tema recurrente en este libro.
Un tercer problema consiste en que los hechos y descubrimientos cruciales se suelen asociar con personas clave. Además, en la mayoría de las historias de las matemáticas, casi todas esas grandes figuras vivieron en Europa occidental a partir del siglo XVI y fueron varones. Esto no siempre se debe a una concepción eurocentrista o sexista por parte de los autores. El vertiginoso desarrollo de las matemáticas en la cultura masculina de Europa a partir del Renacimiento dio lugar a una gran cantidad de material que los historiadores han considerado, con razón, digno de estudio; además, disponemos de una abundancia de fuentes procedentes de la Europa de ese periodo, a diferencia de las poquísimas fuentes (en términos relativos) que se conservan de Europa, China, India o América premedievales. Por suerte, la disponibilidad y accesibilidad de fuentes procedentes de esas otras zonas está empezando a aumentar.
Sin embargo, sí que es un hecho que centrarse en los grandes descubrimientos excluye la experiencia matemática de la mayoría de la especie humana: mujeres, niños, contables, profesores, ingenieros, obreros industriales y demás, incluso a menudo de continentes y de siglos enteros. Está claro que no debe ser así. Sin negar el valor de ciertos hallazgos notables (y este libro comienza con uno de ellos), tiene que haber formas de reflexionar sobre la historia teniendo en cuenta a las numerosas personas que practican las matemáticas, y no solo a unas pocas. Poco puede hacer este libro para enmendar el sesgo masculino que manifiestan la mayoría de las historias de las matemáticas, pero sí puede dedicar algo más que meras palabras huecas a las matemáticas de continentes distintos del europeo, e intentar analizar cómo, dónde y por qué las matemáticas fueron utilizadas por personas cuyos nombres no figurarán jamás en las historias convencionales. Pero para ello se precisa un análisis distinto del cronológico habitual.
El modelo alternativo que yo propongo seguir gira en torno a temas, en lugar de periodos o épocas. Cada capítulo se centrará en dos o tres casos ilustrativos, elegidos no porque sean de alguna manera amplios o exhaustivos, sino con la esperanza de que inspiren ideas e interrogantes y maneras nuevas de pensar. Pero a la vez que he seguido las pautas recién expuestas, he procurado, siempre que ha sido posible, señalar contrastes o semejanzas entre las diversas historias, de forma que los lectores puedan interconectar al menos algunos de los aspectos de la larguísima historia de las matemáticas. He intentado mostrar no solo cómo abordan los historiadores profesionales de la actualidad su disciplina, sino también que los legos en la materia puedan reflexionar sobre la historia de las matemáticas.
Espero, pues, que este libro ayude a los lectores a reconocer la riqueza y la diversidad de la actividad matemática a lo largo de la historia humana, teniendo presente que se trata de un libro breve dedicado no solo a algunas matemáticas del pasado, sino a la historia de las matemáticas en sí como disciplina académica moderna.
Capítulo 1
Las matemáticas: mitos e historia
No es frecuente que un viejo problema matemático peliagudo sea noticia, pero en 1993 los periódicos británicos, franceses y estadounidenses anunciaron que un matemático de 40 años llamado Andrew Wiles había presentado una demostración de un problema de 350 años de antigüedad conocido como el último teorema de Fermat, durante una conferencia en el Instituto Isaac Newton de Cambridge. Luego resultó que el anuncio había sido un tanto prematuro: las 200 páginas de matemáticas de Wiles contenían un error que precisó un tiempo para enmendarlo, pero dos años después la demostración era segura. La historia de la lucha de nueve años que mantuvo Wiles con aquel teorema se convirtió en el tema de un libro y de una película de televisión en la que Wiles acababa contando entre lágrimas cómo llegó a su logro final.
Una razón indudable por la que aquel fragmento de la historia de las matemáticas llamó la atención de la gente fue la figura del propio Wiles. Durante los siete años previos a aquella conferencia en Cambridge, se había dedicado casi en exclusiva y en completo aislamiento a las profundas y complejas matemáticas relacionadas con el teorema. Así que aquella era una historia perfecta para la gente habituada a los mitos occidentales: el héroe solitario que lucha contra la adversidad para alcanzar un objetivo difícil. Hasta aparecía una princesa al fondo: solo su esposa conocía los verdaderos propósitos de Wiles, y fue la primera en recibir la demostración completa como regalo de cumpleaños.
Pero hubo una segunda razón: aunque la posible demostración del último teorema de Fermat solo fuera comprensible para quizá no más de veinte personas en todo el mundo, el teorema en sí es fácil de enunciar. A Wiles lo fascinó ya cuando sólo tenía 10 años, y hasta quienes han olvidado hace mucho la mayoría de las matemáticas que aprendieron alguna vez, entienden de qué va; volveremos a ello en un momento.
Pero antes, nótese que la primerísima frase de este capítulo menciona expresamente a tres personas: Wiles, Newton y Fermat. Es algo propio de las matemáticas: en esta disciplina es práctica universal asignar a teoremas, conjeturas o edificios el nombre de alguien de la tribu. Y esto es así porque la mayor parte de los matemáticos es muy consciente de que constantemente se basan en el trabajo realizado por sus predecesores o colegas. En otras palabras, las matemáticas son una disciplina intrínsecamente histórica en la que los esfuerzos del pasado rara vez se pierden de vista. Para empezar a conocer las cuestiones que se plantean los historiadores de las matemáticas, nos remontaremos a los orígenes más remotos del último teorema de Fermat a partir de aquella conferencia celebrada en un salón de actos de Cambridge en 1993.
Fermat y su teorema
Pierre de Fermat, nacido en 1601, pasó toda su vida en el sur de Francia. Tras formarse en leyes, se convirtió en consejero del Parlamento de la ciudad de Toulouse, órgano judicial de una gran área circundante. En su tiempo libre, que era poco, Fermat se dedicaba a las matemáticas y, como estaba lejos de los círculos intelectuales más activos de París, lo hizo casi en completa soledad. Durante la década de 1630 mantuvo correspondencia con matemáticos más alejados a través de Marín Mersenne, fraile mínimo de París, pero durante la década de 1640 aumentaron las presiones políticas sobre su persona y volvió a recluirse en el aislamiento matemático. Fermat consiguió algunos de los resultados más relevantes de las matemáticas de principios del siglo XVII, pero la mayoría de las veces solo se dignó a revelar golosos fragmentos menores sobre ellos. Una y otra vez prometía a sus destinatarios entrar en detalles en cuanto dispusiera de la calma suficiente para ello, pero esa tranquilidad nunca llegaba. A veces enviaba una sola frase sobre lo que había descubierto, o planteaba desafíos que evidenciaban con claridad las ideas sobre las que estaba trabajando, pero sin revelar los resultados conseguidos con tanto esfuerzo.
La primera pista sobre su último teorema apareció en uno de esos desafíos, enviado a los matemáticos ingleses John Wallis y William Brouncker en 1657; ninguno de los dos supo ver qué se traía entre manos, y lo desestimaron por considerarlo indigno de su condición. El enunciado completo del teorema no apareció hasta después de la muerte de Fermat, anotado en el margen de su ejemplar de la Aritmética de Diofante, cuando Samuel, hijo de Fermat, publicó algunos de sus apuntes y documentos. Antes de remontarnos otro paso en el tiempo para ver qué había en Diofante para inspirar a Fermat, es necesario hacer una breve digresión matemática para conocer el último teorema de Fermat.
Uno de los enunciados matemáticos que casi todos recordamos de nuestra etapa escolar es el teorema de Pitágoras, que dice que el cuadrado del lado más largo de un triángulo rectángulo, la hipotenusa, es igual a la suma de los cuadrados de los dos lados más cortos, los catetos. La mayoría de la gente también recordará que si los dos lados más cortos miden 3 y 4 unidades de largo, entonces el lado más largo medirá 5 unidades, puesto que 32 + 42 = 52. Esta suerte de triángulo se conoce como triángulo 3-4-5, y se puede usar para trazar ángulos rectos sobre el terreno mediante un trozo de cuerda, o en libros de texto para plantear problemas que se pueden resolver sin recurrir a una calculadora. Hay muchos otros conjuntos de tres números enteros que cumplen la misma relación: es fácil comprobar que 52 + 122 = 132, por ejemplo, o que 82 + 152 = 17 2. Estos conjuntos, que a veces encontramos escritos como (3, 4, 5), (5, 12, 13), etcétera, se conocen como ternas pitagóricas, y existe una cantidad infinita de ellos.
Supongamos ahora que, tal como les gusta hacer a los matemáticos, retorcemos un poco las condiciones para ver qué ocurre. ¿Y si en lugar de tomar los cuadrados de cada número, tomamos los cubos? ¿Encontraremos ternas de números (a, b, c) que cumplan la igualdad a3 + b3 =c3? ¿Y si nos animamos un poco más y buscamos ternas que cumplan la igualdad a7 + b7 = c7 o incluso am + bm = cm? La conclusión a la que llegó Fermat es que no tiene sentido ni intentarlo: no existen ternas de este tipo con ninguna potencia mayor que dos. Y, como otras muchas veces, dejó para los demás el trabajo de esclarecer los detalles. Esta vez la excusa que puso no fue el tiempo, sino el espacio: había descubierto una demostración maravillosa, afirmaba, pero el margen existente en la Aritmética de Diofante era demasiado exiguo para anotarla.
El margen en cuestión era la página 85 de la edición que hizo Claude Gaspar Bachet en 1621. La Aritmética había cautivado a los matemáticos europeos desde que en 1462 se había redescubierto en Venecia una copia manuscrita, escrita en griego. Sobre el propio Diofante nadie sabía nada, y poco más se conoce hoy. El manuscrito lo menciona como Diofante de Alejandría, así que podemos suponer que vivió y trabajó durante una parte considerable de su vida en esa ciudad de lengua griega del norte de Egipto. Si era nativo de allí o si procedía de otro lugar del mundo mediterráneo, no lo sabemos. Y las estimaciones de sus fechas no son más que suposiciones. Diofante menciona una definición de Hipsicles (alrededor del año 150 a. C.) en su obra, mientras que Teón (alrededor del año 350 d. C.) cita un resultado de Diofante. Ambas referencias temporales sitúan a Diofante dentro de una horquilla cronológica de 500 años, pero no tenemos nada mejor.
Comparada con los textos de geometría conservados de otros matemáticos griegos, la Aritmética es una obra muy inusual. Su tema de estudio no es la geometría, pero tampoco lo es la aritmética de los cálculos cotidianos. En realidad es un conjunto de sofisticados problemas relacionados con números enteros o fracciones que deben cumplir ciertas condiciones. El octavo problema del libro segundo, por ejemplo, pide al lector que divida «una potencia de dos en dos potencias de dos». Para la finalidad que perseguimos aquí, podemos traducir esa expresión a otra más moderna y comprobar que la pregunta de Diofante estaba relacionada con las ternas pitagóricas, donde cualquier número elevado a dos (en la notación recién utilizada, c2) se puede dividir o separar en dos números más pequeños elevados a dos (a2 + b2 ). Diofante mostraba una manera ingeniosa de lograrlo cuando el número más grande elevado al cuadrado es 16 (en cuyo caso, la respuesta implica fracciones); y después pasaba a otra cosa.
Sin embargo, Fermat vaciló en este punto y debió de preguntarse lo obvio: ¿podrá ampliarse el método? ¿Es posible dividir un número elevado al cubo en dos números elevados al cubo? Esta fue exactamente la pregunta que planteó Fermat a Wallis y Brouncker en 1657 (y a la que Wallis respondió con enojo que estas preguntas «negativas» son absurdas, después de que Fermat le comunicara que no es posible). En realidad, lo que Fermat planteaba en aquel margen no se aplicaba únicamente a números elevados al cubo, sino a cualquier potencia mayor que dos, mucho más de lo que pedía Diofante.
En las líneas anteriores ha aparecido otro nombre, así que daremos otro paso atrás en el tiempo para remontarnos desde Diofante hasta Pitágoras, quien se cree que vivió en la isla griega de Samos hacia el año 500 a. C. A pesar de ser una fecha tan remota, es probable que muchos lectores hayan oído hablar más de Pitágoras que de Diofante. De hecho, la pregunta que más me formulan como historiadora de las matemáticas es: «¿Abarca usted toda la historia desde Pitágoras?». Es cierto que el teorema de Pitágoras se conoce desde hace mucho tiempo, pero lo decepcionante es que no hay ningún indicio que lo vincule a Pitágoras. Es más, apenas hay signos que permitan relacionar nada con Pitágoras. Si Diofante es una figura desdibujada, Pitágoras está sepultado bajo una cortina de mito y leyenda. No disponemos de textos escritos ni por él ni por sus discípulos más inmediatos. Los testimonios más antiguos que se conservan sobre su vida proceden del siglo tercero antes de Cristo, unos 800 años después de su existencia, y proceden de autores que aspiraban a forjar sus propios ejes filosóficos. Los supuestos viajes que realizó a Babilonia o a Egipto, donde se decía que había aprendido geometría, probablemente no fueran más que invenciones de esos escritores para potenciar el prestigio y la autoridad de Pitágoras. En cuanto a las supuestas actuaciones o creencias de sus discípulos, puede que tengan algún fundamento, pero es imposible confirmarlas a ciencia cierta. En resumen, Pitágoras se convirtió, literalmente, en una figura legendaria a quien se le atribuyen muchas cosas, pero de la que, en realidad, se sabe bien poco.
Las vidas de estos cuatro hombres, Pitágoras, Diofante, Fermat y Wiles, abarcan más de 2.000 años de historia de las matemáticas. Ciertamente podríamos encontrar ideas matemáticas similares en la historia de cada uno, aunque entre ellos medien varios siglos de separación temporal. ¿No permitiría eso trazar la historia del último teorema de Fermat desde sus orígenes hasta su final? La respuesta es «no», y por varias razones, además. La primera es que uno de los cometidos del historiador consiste en separar la ficción de los hechos, y el mito de la historia. Esto no quiere decir que haya que despreciar el valor de la ficción ni del mito: ambos encarnan los relatos con los que las sociedades se definen y entienden a sí mismas, y pueden tener un valor inmenso y duradero. Sin embargo, el historiador no debe permitir que esos relatos enturbien las pruebas que tal vez conduzcan hacia otras interpretaciones. En el caso de Pitágoras, resulta bastante sencillo ver cómo y por qué los relatos aparentemente sólidos están hilados con la más fina de las hebras, pero en el caso de Andrew Wiles, donde los hechos parecen estar delante de nuestra vista, resulta mucho más difícil. La verdad de casi cualquier historia suele ser más compleja de lo que imaginamos en un principio, o de lo que nos hacen creer a veces los autores, y las historias relacionadas con las matemáticas y los matemáticos no son una excepción. Lo que resta de este capítulo analiza algunos mitos y trampas habituales en las historias de las matemáticas; por comodidad, los he apodado «relato torre de marfil», «relato a saltos» y «relato elitista». El resto del libro ofrece algunos planteamientos alternativos.
Relato torre de marfil
Uno de los rasgos más extraordinarios de la historia de Wiles es que se recluyera deliberadamente durante siete años para dedicarse a demostrar el último teorema de Fermat sin interrupciones ni interferencias. También Fermat fue un solitario indiscutible, separado por la distancia geográfica, si no por algo más, de quienes podrían haber comprendido y apreciado su trabajo. Asimismo hemos hablado de Diofante y de Pitágoras sin ninguna alusión a sus contemporáneos. ¿De verdad fueron estos cuatro hombres genios aislados que abrieron nuevas sendas por sí solos? ¿Es así como deben practicarse las matemáticas o como mejor se desarrollan? Volvamos a Pitágoras para, esta vez, avanzar hacia delante.
Las historias sobre Pitágoras sostienen con insistencia que fundó o reunió a su alrededor una comunidad o hermandad con la que compartía determinadas creencias religiosas y filosóficas, y tal vez también algunas indagaciones matemáticas. Por desgracia, los relatos sostienen también que aquella hermandad estaba sometida a un estricto secreto que, por supuesto, abre la puerta a una especulación continua acerca de sus actividades. Sin embargo, aunque solo hubiera un grano de verdad en esas narraciones, parece que Pitágoras era lo bastante carismático como para atraer a discípulos. Es más, el mero hecho de que su nombre haya perdurado induce a pensar que fue respetado y venerado durante su vida, y que no fue ningún ermitaño.
Algo mejor podemos ubicar a Diofante, quien habría podido disfrutar de la compañía de otros eruditos en la ciudad de Alejandría. También es casi seguro que hubo tenido acceso a libros traídos de otras partes del mundo mediterráneo en las bibliotecas de algunos templos o en colecciones privadas. Es posible que inventara él mismo los problemas de la Aritmética, pero también es igualmente posible que los recopilara en un solo volumen a partir de otras fuentes diversas, ya fueran orales o escritas. Uno de los temas recurrentes de esta obra es que las matemáticas pasan continuamente de una persona a otra de forma oral. Es casi seguro que Diofante, al igual que cualquier otra persona con creatividad matemática, comentara sus problemas y soluciones con algún maestro o con sus propios alumnos. Por tanto, no debemos imaginarlo como una figura silente que escribió sus libros en privado, sino como ciudadano de una urbe donde se valoraba el aprendizaje y el intercambio intelectual.
Ni siquiera Fermat, confinado en Toulouse y sometido a los rigores del trabajo político a jornada completa, estuvo tan aislado como podría parecer de entrada. Una de las amistades que entabló durante sus primeros estudios en Burdeos fue Etienne d’Espagnet, cuyo padre había sido amigo del jurista y matemático francés François Viète. Las obras de Viète, raras, pero accesibles por esa vía para Fermat, ejercieron una gran influencia en su desarrollo como matemático. Otro amigo y también consejero en Toulouse fue Pierre de Carcavi quien, al mudarse a París en 1636, informó allí sobre Fermat y sus descubrimientos.
Gracias a Carcavi, Marin Mersenne oyó hablar de Fermat, quien a través de Mersenne mantuvo correspondencia con Roberval, probablemente el mejor matemático de París en aquel tiempo, y con Descartes, en los Países Bajos. Más tarde comunicó algunos de los hallazgos surgidos de su estudio de Diofante a Blaise Pascal, en Rúan, y a John Wallis, en Oxford. De modo que, incluso Fermat, alejado de núcleos importantes del conocimiento, mantuvo contacto con una red de correspondencia que se extendía por Europa, una comunidad virtual de eruditos que más tarde recibió el nombre de República de las letras.
En el caso de Wiles resulta mucho más fácil detectar las fisuras en el relato del «genio solitario». Wiles estudió en Oxford y Cambridge, y con posterioridad trabajó en Harvard, Bonn, Princeton y París. En todos esos lugares formó parte de prósperas comunidades matemáticas.
El detonante matemático que acabó orientando sus intereses hacia el último teorema de Fermat provino de una conversación casual con un compañero matemático de Princeton; cuando cinco años después necesitó un empujón nuevo, asistió a un congreso internacional para enterarse de las reflexiones más recientes sobre el tema; cuando necesitó ayuda técnica con un aspecto importante de la demostración, reveló su secreto a un colega, Nick Katz, y compartió el material en cuestión durante un curso de posgrado, aunque al final se quedó sin ningún asistente, excepto Katz; dos semanas antes de que hiciera pública toda la demostración en tres conferencias en Cambridge, Inglaterra, pidió a un compañero, Barry Mazur, que la comprobara; la demostración final se sometió a la supervisión de otras seis personas; y cuando se detectó un error, Wiles pidió a uno de sus antiguos alumnos, Richard Taylor, que lo ayudara a resolverlo. Es más, durante los años que dedicó a conseguir la demostración, Wiles nunca dejó de enseñar a sus alumnos o de asistir a los seminarios en su departamento universitario. En definitiva, aunque pasó muchas horas a solas, también estaba inmerso en una comunidad que le permitió hacerlo, y que, cuando él la necesitó, acudió en su ayuda.
Los años de aislamiento de Wiles llaman la atención no porque sea lo normal en un matemático en activo, sino porque fueron algo excepcional. Las matemáticas son esencial y necesariamente una actividad social a todos los niveles. En todos los departamentos de matemáticas del mundo hay espacios comunes, ya sean rincones o salas, provistos de algún tipo de superficie para escribir, de forma que los matemáticos puedan compartir ideas mientras toman el café o el té que los propulsa. Los estudiantes de idiomas o de historia rara vez colaboran para escribir artículos conjuntos, ni tampoco se les insta a hacerlo, pero los de matemáticas sí realizan con frecuencia trabajos fructíferos juntos, durante los cuales se iluminan y aprenden entre sí. Y es que, a pesar de los avances de la tecnología moderna, las matemáticas se siguen aprendiendo no tanto en los libros sino más bien a través otras personas, a través de conferencias, seminarios y clases.
Relato a saltos
En la historia que hemos perfilado antes sobre el último teorema de Fermat, Pitágoras, Diofante, Fermat y Wiles se muestran no solo asilados durante su propia existencia, sino también unos de otros, como piedras que sobresalen sobre la superficie de un río en la que no destaca nada más. Si los relatos torre de marfil presentan a los matemáticos aislados de sus grupos y comunidades sociales, la versión a saltos de la historia los aísla de su pasado. Como se supone que el pasado es el objeto de la historia, parece extraño obviar grandes trozos de ella, pero existe una cantidad sorprendente de historias generales de las matemáticas que se exponen a saltos. Volvamos a examinar, pues, más de cerca nuestro relato y los huecos que contiene.
Si Pitágoras y Diofante son figuras un tanto desdibujadas, también lo es el intervalo temporal que medió entre ambos. Es posible que Diofante no oyera hablar jamás de Pitágoras, pero es casi seguro que conocía el teorema de Pitágoras, si no a través de algún texto del propio Pitágoras, sí a través de la obra de Euclides, quien vivió alrededor del año 250 a. C.
Aparte de esta fecha, muy aproximada, no sabemos más sobre Euclides que sobre Diofante, pocos siglos posteriores, pero su obra maestra, los Elementos, se conservó y se convirtió en el libro de texto con mayor vigencia en toda la historia, ya que se usó en las escuelas para enseñar geometría incluso hasta bien entrado el siglo XX. Los Elementos son una recopilación exhaustiva de la geometría de la época de Euclides que presenta los teoremas en un cuidadoso orden lógico, y el penúltimo teorema del primer libro es el teorema de Pitágoras, el cual se demuestra con esmero por construcción geométrica. Es razonable suponer que Diofante tuviera acceso en Alejandría a los Elementos, y es posible que el teorema de Pitágoras lo animara a pensar en las ternas pitagóricas. Sin embargo, también es posible que la inspiración le llegara de otras fuentes de las que ya no tenemos noticia.
Los primeros siglos transcurridos entre Diofante y Fermat son casi tan difíciles de completar, siquiera con la imaginación, como los que precedieron a Diofante. Sabemos que la Aritmética de Diofante se escribió en sus orígenes en trece libros, de los que solo perduraron los seis primeros en griego; no sabemos cómo ni por qué. (En 1968 se descubrió un manuscrito árabe en Irán que se considera una traducción de los libros IV a VII, pero los especialistas no se ponen de acuerdo sobre la fidelidad de ese texto a la obra original). Por suerte, esos seis libros se conservaron para el mundo de lengua griega en Bizancio (más tarde Constantinopla, hoy Estambul), y con el tiempo se llevaron copias a Europa occidental. Tal como ampliaremos luego en el capítulo 6, un erudito alemán apodado Regiomontano vio una de ellas en Venecia en 1462 y creyó que contenía los orígenes de una estrafalaria disciplina que era conocida en Europa como «álgebra». Un siglo después, el ingeniero y algebrista italiano Rafael Bombelli estudió un manuscrito de la Aritmética en el Vaticano y suspendió el trabajo que estaba realizando en su propio libro sobre álgebra para incluir problemas de Diofante. La primera edición impresa se publicó en Basilea en 1575, en latín, editada y traducida por Wilhelm Holtzman (Guilielmus Xylander), un estudioso humanista que describió la obra como «inigualable, con la verdadera perfección de la aritmética». Los problemas de Diofante siguieron intrigando a quienes se topaban con ellos, y así, en 1621 Claude Gaspard Bachet de Méziriac realizó una nueva edición de la Aritmética en latín en París. Esta es la edición que tenía y que anotó Fermat.
No es demasiado difícil rellenar el hueco que existe entre Fermat y Wiles. El último teorema, publicado por Samuel Fermat en 1670, parece no haber provocado intentos serios de resolverlo en el siglo XVII, pero en el siglo XVIII llamó la atención de Leonhard Euler, el matemático más versátil y prolífico de la época, quien hizo algunas incursiones en los casos más sencillos del problema. En 1816, la Academia de Ciencias de París ofreció un premio a quien consiguiera resolverlo. Esto alentó a Sophie Germain, quien había logrado cierto éxito con algunas partes del mismo y cuyo trabajo aprovecharon y ampliaron otros.
Al margen de eso, el problema se volvió muy conocido y, con los años, inspiró cientos, cuando no miles, de supuestas soluciones de profesionales y de aficionados por igual. La mayoría de aquellas tentativas eran incorrectas e inútiles, pero algunas depararon descubrimientos matemáticos relevantes de por sí, que Wiles conocía. Cuando al fin se animó a desarrollar su propia demostración, empleó algunas de las matemáticas más avanzadas del siglo XX que por entonces se sabía que guardaban relación con el último teorema de Fermat: la conjetura Taniyama-Shimura, desarrollada por dos matemáticos japoneses en la década de 1950, y el método de Kolyvaguin-Flach, desarrollado por Víctor Kolyvaguin (ruso) y Matthias Flach (alemán) en la década de 1980. Nótese una vez más la propensión de los matemáticos a incluir los nombres de sus predecesores en el registro histórico. Repárese también en la compleja red de relaciones históricas que hay detrás de un único teorema.
En términos generales, cuanto más nos remontamos en la historia, más difícil resulta seguir el camino que hay entre una piedra y la siguiente para cruzar el río, sobre todo si gran parte de los datos se han borrado hace mucho tiempo. Pero si no se intenta, no hay historia, tan solo una serie de anécdotas en las que aún se basan con demasiada frecuencia muchas de las historias de las matemáticas habituales.
Relato elitista
Aunque apenas sabemos nada sobre las vidas de Euclides o Diofante, hay algunas cosas que se pueden afirmar con seguridad: que ambos eran personas formadas y que sabían escribir con fluidez en griego, la lengua culta del Mediterráneo oriental; que ambos tuvieron acceso a textos matemáticos anteriores a ellos; que ambos eran capaces de comprender, ordenar y ampliar algunas de las matemáticas más avanzadas de su tiempo; y que las matemáticas sobre las que escribieron no tenían ningún valor práctico, sino que eran meros ejercicios intelectuales. La cantidad de hombres dedicados a este tipo de matemáticas no podía ser grande, ni tan siquiera en una ciudad como Alejandría. De hecho, se calcula que en cualquier época no hubo más que un puñado de ellos en todo el mundo de lengua griega. En otras palabras, tanto Euclides como Diofante formaban parte de élites matemáticas muy reducidas.
Un instante de reflexión basta para darse cuenta de que por entonces se utilizaban muchas más matemáticas que aquellas sobre las que ellos escribieron. La sociedad griega, igual que cualquier otra, tenía tenderos y sirvientes, agricultores y constructores, y muchas otras personas que realizaban mediciones y cálculos a diario. Casi no sabemos nada sobre sus métodos porque aquella gente aprendía y enseñaba sobre todo de forma práctica y oral. Tampoco estaba organizada por escuelas o gremios, aunque conocemos el nombre de un grupo, el harpenodaptai, o estiradores de cuerdas’. Por su propia naturaleza, sus matemáticas apenas dejaron rastro. Las señales que utilizaban o las marcas grabadas en madera, piedra o arena se desechaban en cuanto dejaban de tener utilidad, y es indudable que no se guardaban en las bibliotecas. En cualquier caso, aquellas actividades las realizaban personas de un nivel social bastante bajo, y tenían poco o ningún interés para los intelectuales de las academias.
Cuando los historiadores de las matemáticas hablan de las «matemáticas griegas», como ocurre con frecuencia, casi siempre se refieren a los sofisticados textos escritos que nos han llegado de Euclides, Arquímedes, Diofante y otros autores, no de las matemáticas cotidianas o corrientes de los hoi polloi (la gente común). Pero esto ha empezado a cambiar hace poco. Los historiadores han empezado a reconocer que las matemáticas griegas exquisitas encuentran sus raíces en las matemáticas prácticas de todos los días del Mediterráneo oriental, aunque autores posteriores se distanciaran de esas raíces para desarrollar un tipo de matemáticas más formal e «inútil».
También hay algo más que debe hacernos desconfiar de la expresión general «matemáticas griegas». Diofante vivió en Alejandría, Egipto; Arquímedes vivió en Siracusa, en la isla de Sicilia; Apolonio, otro gran matemático «griego», vivió en Pérgamo, región que ahora pertenece a Turquía; en otras palabras, aunque todos escribieron en lengua griega, ninguno procedía de la zona que hoy se conoce como Grecia. De hecho, hasta donde sabemos, es posible que Diofante naciera y se criara en el norte de África. Y, a pesar de todo, las «matemáticas griegas», tan alabadas por los europeos del Renacimiento, acabaron considerándose fundamentalmente «europeas».
El absurdo de incluir a Alejandría en Europa se torna más manifiesto cuando se tiene en cuenta la exclusión de España, en el extremo opuesto del continente. España pertenecía al islam a comienzos del siglo VIII, y, por tanto, disfrutaba de la rica cultura y sabiduría del mundo islámico. Sin embargo, a menudo leemos que fue Fibonacci quien introdujo los números arábigos en Europa, autor que escribió en Pisa, Italia, a comienzos del siglo XIII, como si su utilización en España a lo largo de dos siglos antes de él no contara en absoluto, y como si de alguna manera España no formara parte verdaderamente de Europa. Quienes defienden la causa de las matemáticas elitistas han tendido de manera natural a incluir en su versión de la historia todo lo que diera autoridad y prestigio a su idea, dejando de lado otros hechos incómodos.
Dondequiera que se practiquen las matemáticas, casi siempre nos encontramos con algunos individuos avezados y admirados, pero siempre hay muchos más que jamás entrarán en los anales de la historia. Si volvemos a analizar la situación en tiempos de Fermat, apenas encontramos diferencias. Durante su vida, Francia era especialmente rica en cuanto a actividad matemática selecta; podríamos nombrar hasta tres o cuatro parisinos de la talla de Fermat. Siendo generosos, tal vez hubiera otros tantos entre los Países Bajos e Italia juntos, y hasta uno o dos en Inglaterra, pero no más. Sin embargo, a medida que se descendía por la escala social, la actividad matemática estaba más generalizada de lo que parece. Búsquedas electrónicas recientes en material digitalizado han revelado que hasta una cuarta parte de los libros publicados en Inglaterra en los siglos XVI y XVII hacían alusión a las matemáticas de un modo u otro, aunque solamente fuera de pasada. Es más, hubo un aumento progresivo de los libros orientados a comerciantes o artesanos interesados en adquirir unos conocimientos matemáticos básicos.
Antes de concluir este capítulo, analicemos más en detalle uno de ellos; al fin y al cabo, no hay mejor manera de estudiar la historia de las matemáticas que ahondando en las fuentes originales. La obra The Pathway to Knowledge, de Robert Recorde, se publicó en Inglaterra en 1551, unos cincuenta años antes de que naciera Fermat. Durante gran parte de su vida, Recorde ejerció como médico. En 1549 fue nombrado interventor de la Real Casa de la Moneda de Bristol, y dos años después, inspector de las minas de plata de Irlanda. Por desgracia, durante aquel periodo cosechó enemigos políticos y acabó en la prisión de King’s Bench, en Southwark, donde falleció en 1558 a la edad de 48 años. Sin embargo, durante esta etapa también publicó la mayoría de las obras matemáticas por las que es recordado en la actualidad.
Recorde, formado en Oxford y Cambridge, dominaba el latín y el griego con fluidez, pero tomó la atrevida decisión de escribir sus textos matemáticos en inglés. En concreto, intentó acercar las matemáticas de Euclides (uno de los matemáticos más excelsos) al hombre común. No fue tarea fácil: por un lado, la mayoría de los artesanos ingleses jamás había oído hablar de la disciplina formal llamada «geometría», aunque pudieran estar bien familiarizados con plomadas y reglas de medir; por otro lado, sencillamente no había palabras en inglés para nombrar tecnicismos tales como «paralelogramo» o «segmento». Recorde abordó ambos problemas con imaginación y habilidad.
A lo largo de un extenso prefacio fue describiendo la clase de hombre a quien la geometría sería «muy necesaria», y abarcaba desde los estratos sociales más humildes hacia arriba. En la base de la pirámide se encontraban los «ignorantes» que trabajaban la tierra; incluso ellos, afirmaba Recorde, tenían un conocimiento instintivo de la geometría, pues sus zanjas no se derrumbaban ni sus pajares se venían abajo. Al ascender hasta los comerciantes, Recorde aportaba una larga lista en verso de aquellos para quienes la geometría era indispensable: mercaderes, navegantes, sastres, zapateros, tejedores, y concluía diciendo:
Porque no ha habido industria tan ingeniosa todavía, tan necesaria para el hombre, como la buena geometría.
Recorde también consideraba la geometría indispensable en medicina, teología y justicia, aunque sus argumentos se volvían bastante más artificiales y menos convincentes a medida que ascendía por la escala social.
La empatía de Recorde con el hombre común se aprecia con más claridad cuando trata la geometría en sí: su exposición es un ejemplo de buena pedagogía en un lenguaje llano con multitud de ejemplos y diagramas útiles. Muy al comienzo enseña la construcción de Euclides mediante regla y compás de un ángulo recto. Sin embargo, si esto resulta demasiado complejo, ofrece una propuesta alternativa: toma una línea y marca en ella tres, cuatro y cinco unidades respectivamente; a continuación utiliza esas longitudes para formar un triángulo. El ángulo situado entre los lados cortos será recto. No se trata de una construcción euclídea clásica: es un método para hombres prácticos, para «estiradores de cuerdas».
La lista de la gente que usa las matemáticas a diario (en las aulas, en casa o en el trabajo) en el siglo XXI sería mucho más larga que la que confeccionó Recorde. Estoy pensando en mi madre, Irene, que a sus 89 años no se fiaba ni de los bancos ni de los ordenadores, pero llevaba un registro escrupuloso de cada penique de sus gastos domésticos en libretas esmeradamente anotadas; o en mi amiga Tatjana, que siempre me repite que no era buena en matemáticas en el colegio, pero que elabora edredones con diseños complejos (véase la figura 1).

Figura 1. Colourwash («aguada de color»), de Tatjana Tekkel Peppé, a quien, según ella misma, no se le dan bien las matemáticas.
Es evidente que sabe hacer triángulos rectángulos. De hecho, su intuición para el teselado y la proporción tal vez la cualifiquen como representante actual de los harpédonaptai.
En las historias elitistas no hay espacio para Irene o Tatjana: las mujeres, en particular, tienen que llegar como mínimo al nivel de Sophie Germain para que se las empiece a tener en cuenta. Pero sin la actividad de la gente que practica y enseña matemáticas a todos los niveles, la elite no podría florecer.
Más allá de las cumbres eminentes que ocupan Wiles, Fermat o Diofante, se extienden inmensas llanuras de actividad matemática apenas exploradas en las historias generales sobre esta materia. Parte del objetivo de este libro es recuperar el equilibrio y reivindicar las matemáticas para los hombres, las mujeres y los niños de la calle; revisar la historia de las matemáticas desde perspectivas nuevas.
Capítulo 2
¿Qué son las matemáticas y quiénes son los matemáticos?
En el capítulo anterior di por hecho que los lectores entienden que las «matemáticas» son más o menos la disciplina que estudiaron con ese nombre en el colegio, y que los «matemáticos» son las personas que siguen estudiándola en la edad adulta. En cambio, la historia nos obliga a reflexionar sobre ambos términos con más detenimiento; aunque también la experiencia: cuando en mi época de docente me veía enseñando en una misma mañana lecciones sobre porcentajes, teoremas de la circunferencia y cálculo diferencial, me preguntaba cómo aquel conjunto improbable de temas había acabado confluyendo bajo el título único de «matemáticas». Probablemente la mayoría de la gente coincida en que las matemáticas se basan en propiedades espaciales y numéricas, pero ¿qué serían entonces los sudoku? ¿Son un ejercicio matemático o no? He oído a especialistas en matemáticas explicar con idéntica vehemencia que sí lo son y que no lo son.
Retrocedamos hasta un principio. La palabra griega mathemata significaba tan solo «lo aprendido», a veces en términos generales y otras en una relación más específica con la astronomía, la aritmética o la música. El término griego intervino en la etimología del vocablo moderno «matemáticas», y sus análogos en otras lenguas europeas (mathematics, mathématiques, Mathematik, matemático, etc.). Sin embargo, el significado de la palabra matemáticas adquirió y atravesó numerosas variaciones a lo largo de los siglos, tal como veremos a continuación. Y eso considerando el tema tan solo desde un punto de vista europeo. Si nos remontamos uno o dos milenios, antes de que la cultura europea se volviera dominante, ¿encontramos términos equivalentes al nuestro de «matemáticas» en chino, támil, maya o árabe? Y, en tal caso, ¿qué textos o actividades englobaban esos términos? El estudio exhaustivo de esta cuestión llevaría toda una vida a un ejército de especialistas, pero aquí, como en otras partes del libro, unos cuantos ejemplos ilustrativos servirán para conocer qué interrogantes deben plantearse y qué tipo de respuestas pueden surgir de ellos.
En busca de algunos significados de suán
A partir de historias escritas por autoridades públicas chinas durante el periodo que va desde un poco antes del año 200 a. C. hasta el año 200 d. C. (las dinastías Qin y Han), descubrimos algo más de 20 personas consideradas instruidas en algún aspecto del suán,![]() . Como sustantivo, suán puede aludir a una serie de pequeñas varillas hechas de madera, de metal o de marfil, que se manipulan sobre una superficie plana para llevar la cuenta de los números de un cálculo; pero también puede referirse al acto de usar esas varillas. Aquí hay, pues, indicios de actividad matemática, pero no sabremos mucho más si no descubrimos de qué clase de cálculos se trataba.
. Como sustantivo, suán puede aludir a una serie de pequeñas varillas hechas de madera, de metal o de marfil, que se manipulan sobre una superficie plana para llevar la cuenta de los números de un cálculo; pero también puede referirse al acto de usar esas varillas. Aquí hay, pues, indicios de actividad matemática, pero no sabremos mucho más si no descubrimos de qué clase de cálculos se trataba.
En el caso de muchos de los especialistas mencionados en los registros oficiales, parece que el suán guardaba una relación muy estrecha con los sistemas astronómicos o calendáricos conocidos como lí,![]() . Todas las sociedades premodernas usaron las posiciones del Sol, la Luna y los planetas para concretar instantes temporales favorables y fechas para la práctica de ritos religiosos y para sembrar cosechas, así que quienes sabían emitir predicciones correctas a partir de datos astronómicos eran indispensables para los dirigentes y gobernantes. De ahí que a menudo se asocie el suán con el lí en las historias de la China imperial temprana. Sin embargo, esos mismos registros también revelan que el suán era importante para temas más terrenales, como llevar la contabilidad y repartir recursos.
. Todas las sociedades premodernas usaron las posiciones del Sol, la Luna y los planetas para concretar instantes temporales favorables y fechas para la práctica de ritos religiosos y para sembrar cosechas, así que quienes sabían emitir predicciones correctas a partir de datos astronómicos eran indispensables para los dirigentes y gobernantes. De ahí que a menudo se asocie el suán con el lí en las historias de la China imperial temprana. Sin embargo, esos mismos registros también revelan que el suán era importante para temas más terrenales, como llevar la contabilidad y repartir recursos.
A comienzos de la década de 1980 se descubrió un nuevo documento del periodo en torno al año 200 a. C., que desvela algo más sobre el empleo delsuán en aquella época. Ese texto, que se conoce como Suán shií shü, ![]() , está grabado sobre 190 tiras de bambú, cada una de ellas de 30 cm de largo, que en su origen se encontraban unidas entre sí por los laterales con cuerda anudada, de forma que pudieran enrollarse todas juntas como una alfombra. La última palabra, shü, significa escritos’, a veces ‘libro’. El término del centro, shü, puede interpretarse en general como ‘número’. Sin embargo, lo más relevante para nuestro cometido es el significado de la combinación suán shu.
, está grabado sobre 190 tiras de bambú, cada una de ellas de 30 cm de largo, que en su origen se encontraban unidas entre sí por los laterales con cuerda anudada, de forma que pudieran enrollarse todas juntas como una alfombra. La última palabra, shü, significa escritos’, a veces ‘libro’. El término del centro, shü, puede interpretarse en general como ‘número’. Sin embargo, lo más relevante para nuestro cometido es el significado de la combinación suán shu.
Los escritos del Suán shu contienen unos 70 problemas con instrucciones para resolverlos. Incluyen multiplicaciones con números enteros y fracciones; reparto de ganancias de acuerdo con las cantidades aportadas por distintas personas; consideración de la parte que se desperdicia en la producción de materias primas; cálculo del total a partir del precio de una cantidad dada; cálculo de impuestos; hallar las cantidades de ingredientes en una mezcla; convertir una cantidad de materia prima en un número de productos acabados; comprobar la duración de un viaje; cálculo de volúmenes y áreas; conversión de unidades.
Por tanto, la mayor parte de los problemas del Suán shií shü se basa en actividades y transacciones cotidianas. Está escrito en un estilo muy directo: cada problema va acompañado de «pregunta», «resultado» y «método». Veamos dos «problemas de puestos aduaneros» del segundo capítulo:
Un zorro, un gato montes y un perro pasan por un puesto aduanero: les cobran una tasa de 111 monedas. El perro le dice al gato montés: «Tu piel vale el doble que la mía; ¡así que debes pagar el doble que yo!»; y lo mismo le dice el gato montés al zorro. Pregunta: cuánto paga cada animal. Resultado: el perro paga 15 monedas y 6/7 de moneda; el gato montés paga 31 monedas y 5 partes; el zorro paga 63 monedas y 3 partes. Método: cada uno es el doble que el otro y juntos dan lugar a 7 unidades como divisor; multiplica cada uno por el impuesto para obtener el dividendo; cuenta uno por cada vez que el dividendo contenga al divisor.
Un hombre que transporta grano entero (desconocemos la cantidad) pasa por tres puestos aduaneros. Cada puesto exige unos aranceles de una parte de tres. Al final, al hombre le queda un dóu de grano entero. Pregunta: ¿cuánto grano transportaba al principio? Resultado: el grano que tenía ascendía a 3 dóu, 3 shéng y 3/4. Método: parte de uno y multiplícalo por dos tres veces para obtener el divisor. Vuelve a partir de un dóu de grano entero y multiplícalo por tres. Vuelve a multiplicarlo por tres y por el número de veces que pasa los puestos para hallar el dividendo.
Las respuestas son correctas, pero las descripciones del «método» no son muy esclarecedoras, y es probable que estuvieran pensadas para complementarlas con explicaciones orales. Las instrucciones se dan únicamente para los números que responden la pregunta formulada, pero cualquier lector preparado sería capaz de adaptarlos a problemas similares, así que, en este sentido, enseñan técnicas generales. No obstante, el texto no aspira a que el lector comprenda el razonamiento que hay detrás del método, sino tan solo que sea capaz de aplicarlo.
Problemas parecidos y otros análogos aparecen en un texto posterior, el Jiü zhang suán shü,![]() , escritos sobre suán shu en nueve apartados y que suele conocerse como «Los nueve capítulos». Las historias oficiales revelan que el texto estuvo en uso a comienzos del segundo siglo de nuestra era. Sin embargo, igual que en el caso de los Elementos de Euclides, que data de unos tres o cuatro siglos antes, no tenemos ninguna información sobre el autor o la composición de «Los nueve capítulos», ni sobre el texto original. La única versión que nos ha llegado es la que dejó Liú Huí,
, escritos sobre suán shu en nueve apartados y que suele conocerse como «Los nueve capítulos». Las historias oficiales revelan que el texto estuvo en uso a comienzos del segundo siglo de nuestra era. Sin embargo, igual que en el caso de los Elementos de Euclides, que data de unos tres o cuatro siglos antes, no tenemos ninguna información sobre el autor o la composición de «Los nueve capítulos», ni sobre el texto original. La única versión que nos ha llegado es la que dejó Liú Huí, ![]() , en el año 263 d. C. Hasta la transcripción y publicación del contenido del Suán shu shü en el año 2000,
, en el año 263 d. C. Hasta la transcripción y publicación del contenido del Suán shu shü en el año 2000,
«Los nueve capítulos» eran el texto extenso más antiguo dedicado al suán. Así que, el hallazgo del Suán shií shu no solo permite establecer importantes comparaciones entre ambos textos, sino que también ofrece a los historiadores un conocimiento mucho más profundo de los usos del suán durante los primeros años de la China imperial.
Incluso a partir de este brevísimo apunte queda claro que el término suán no guardaba relación con ninguna disciplina general que pudiéramos englobar bajo el término único de «matemáticas». Más bien alude a técnicas y habilidades susceptibles de ponerse en práctica en diversos contextos; desde aplicaciones del U, hasta cálculos astronómicos requeridos en la corte, o el más mundano suán shií. Volviendo ahora al Occidente latino, ¿es posible diferenciar un conjunto de actividades asociadas al término «matemáticas»?
En busca de algunos significados de matemáticas
Hacia el año 100 d. C., el autor romano Nicómaco nombró cuatro disciplinas relacionadas con la multitud y la magnitud: la aritmética, la música, la geometría y la astronomía. Para Nicómaco, la aritmética -el estudio de las multitudes (o números)- y la geometría -el estudio de las magnitudes- eran las fundamentales; la música era la ciencia de las relaciones que mantienen las multitudes entre sí, mientras que la astronomía se ocupaba de magnitudes en movimiento. Cuatro siglos después, el filósofo Boecio describió el conjunto de estas disciplinas como el quadrivium. Éstas unidas al trivium, consistente en la gramática, la lógica y la retórica, conformaban las siete artes liberales del currículo académico medieval. El propio Boecio escribió tratados sobre aritmética y música que se estudiaban en las universidades europeas durante la época medieval. Algunos textos de geometría también se le atribuían a él, aunque su verdadera autoría es incierta; Boecio, como Pitágoras, se convirtió en una figura mítica a quien resultaba cómodo atribuirle obras posteriores.
La aritmética y la geometría siguen siendo la esencia de las matemáticas (recodemos que son las actividades practicadas por Irene y Tatjana), pero la astronomía y la música han seguido su propio camino por separado. La ruptura se produjo en el siglo XVII, cuando se volvió cada vez más difícil reconciliar la teoría matemática con la actividad musical, y cuando la astronomía batalló para liberarse de su larga vinculación histórica con la astrología y convertirse en una disciplina respetable por derecho propio.
En cualquier caso, en el Renacimiento la división cuádruple de Nicómaco era demasiado rígida para adecuarse a las múltiples actividades matemáticas que empezaron a surgir en respuesta al veloz crecimiento de la riqueza, el comercio y los viajes. En un prefacio a la primera traducción al inglés de los Elementos de Euclides, en 1570, John Dee propuso un esquema básico de las artes matemáticas y las ciencias (véase la figura 2). La aritmética y la geometría siguen siendo las materias cruciales, pero ahora la geometría -que responde a preguntas como «¿cuánta distancia?», «¿cuánta altura o profundidad?», «¿cuánta anchura?» ha dado lugar a la geografía, la corografía, la hidrografía y algo llamado «estrataritmetría».
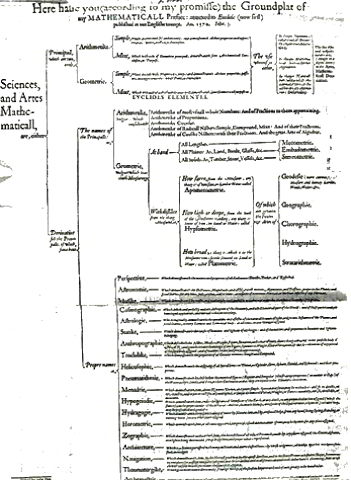
Figura 2. Esquema básico que propone John Dee en su prefacio a los Elementos de Euclides, 1570.
Además, da una larga lista de materias consideradas «derivadas» tanto de la aritmética como de la geometría, que incluye la astronomía y la música, entre otras. El lector moderno tendrá alguna idea sobre qué eran la perspectiva, la cosmografía, la astrología, la estática, la arquitectura y la navegación, pero probablemente se sentirá igual de perplejo que los lectores de la época ante la «antropografía», la «pneumatitmia», la «arquimaestría» y otras ramas insólitas del saber. De hecho, la opacidad de la materia en cuestión y las claras divisiones entre apartados y subapartados inducen a pensar que la sistematización de Dee, al igual que los esquemas mucho más simples de Nicómaco y Boecio, constituyó más un ejercicio filosófico que una verdadera clasificación de las prácticas existentes.
Entonces, ¿cómo descubrir con más precisión en qué consistía la actividad matemática en Europa occidental durante los siglos transcurridos entre los años 500 y 1500 d. C.? ¿Podemos estudiar las matemáticas igual que el suán? Es decir, ¿podemos indagar en el significado de la palabra analizando los contextos en los que se usó? Han perdurado muchos más textos procedentes de este periodo de Europa occidental que de los primeros tiempos de la China imperial, así que es imposible estudiarlos todos, pero como primera aproximación examinaremos una historia de las matemáticas compilada por el erudito neerlandés Gérard Jean Vossius, De scientiis mothematicis, publicada en Ámsterdam en 1649, sobre todo la parte dedicada a autores británicos. Tal vez resulte extraño que recurra a un estudioso neerlandés para buscar información sobre la historia intelectual británica, pero gran parte de lo que cuenta Vossius sobre autores británicos se basa en una obra anterior del anticuario inglés John Leland.
En 1533, poco antes de la disolución de los monasterios, Enrique VIII encargó a Leland que visitara las bibliotecas y los centros de enseñanza del reino para confeccionar un listado con sus colecciones de libros. A lo largo de los dos o tres años siguientes, Leland reunió en una lista las posesiones bibliográficas de unas 140 fundaciones religiosas. La ulterior dispersión y pérdida de libros lo apenó enormemente: en 1536 se quejó a Thomas Cromwell de que
los alemanes, conscientes de nuestra desidia [indolencia] y negligencia, mandan aquí a diario jóvenes estudiosos que los expolian y los arrancan de las bibliotecas.
Leland aportó el registro más reciente y más completo de lo que contenían las bibliotecas. Pensaba confeccionar un diccionario de autores británicos, con unas 600 entradas, pero por desgracia padeció demencia antes de acabarlo. Sin embargo, su inestimable aportación obtuvo el reconocimiento de otros historiadores, y gran cantidad de autores posteriores, como Vossius, se basaron directa o indirectamente en sus hallazgos.
El autor inglés más antiguo que menciona Vossius es Beda, quien escribió alrededor del año 730 d. C. y figura tanto en astronomía como en aritmética. Beda, que pasó la mayor parte de la vida en el monasterio de Jarrow, en el nordeste de Inglaterra, es muy conocido como comentarista bíblico e historiador eclesiástico, pero pocos lo considerarían hoy un astrónomo. En cambio, los textos que se le atribuyen se consideran dedicados a la Luna y sus ciclos, la fecha de la Pascua, los planetas y el zodiaco, el uso del astrolabio, y el cálculo del equinoccio vernal. Es posible que muchos de esos textos fueran atribuidos erróneamente a Beda por comentaristas posteriores, pero lo cierto es que le interesó mucho el cálculo de la fecha en la que caería la Pascua, que era tan crucial para los cristianos como lo había sido el cálculo correcto del solsticio de invierno para los primeros emperadores chinos. Tampoco es que fuera un cálculo sencillo: la Pascua debía caer el primer domingo posterior a la primera luna llena después del equinoccio de primavera, así que para calcular bien la fecha había que conocer los ciclos solares y lunares, entre los cuales no existe una correlación natural. La coexistencia de dos tradiciones cristianas en el norte de Inglaterra, la irlandesa y la romana, había dado lugar a discrepancias cronológicas que acabaron resolviéndose con el sínodo de Whitby en 664. Es posible que no fuera el propio Beda quien realizara los cálculos necesarios, pero era consciente de lo que estaba en juego. Los cálculos de las fechas eclesiásticas acabaron conociéndose como computus, y fueron esenciales durante toda la época medieval.
Después de Beda y su pupilo Alcuino de York, no aparecen más nombres ingleses en el relato de Vossius durante más de cuatro siglos, hasta que llegamos a Adelardo de Bath, en torno al año 1130. Adelardo, que parece haber viajado a Francia, Sicilia y Siria, fue uno de los primeros traductores de fragmentos de los Elementos de Euclides del árabe al latín, y también se cuenta que escribió sobre el astrolabio.
Solo en los siglos XIII y XIV empiezan a aparecer nombres (y sus supuestas fechas) con más frecuencia, todos ellos dentro de los apartados de astronomía o astrología: Juan de Sacrobosco (1230), cuyos escritos sobre la Tierra y su lugar en el universo fueron una parte esencial del currículo universitario a lo largo de cuatro siglos; Roger Bacon (1255), definido como astrólogo; Walter Oddington (1280), del que se dice que escribió sobre el movimiento de los planetas;
Robert Holcot (1340), de Northampton, quien parece que escribió sobre el movimiento de las estrellas; John Eastwood (1347), astrólogo; Nicholas Lynne (1355), astrólogo; John Killingworth (1360), astrónomo; Simón Bredon (1386), del que se dice que escribió sobre medicina, astrología y astronomía; John Summer (1390), astrólogo, y otros más. Después, en el siglo XV los nombres vuelven a desaparecer. Claramente, el siglo XIV fue un momento álgido de estudios astronómicos y astrológicos, a lo que tal vez contribuyó el terrible impacto de la peste negra en 1348. Muchos de los mencionados pertenecían a órdenes religiosas, como la de los franciscanos, dominicos o carmelitas. Bastantes estaban vinculados, además, a Oxford, sobre todo al Merton College, y algunos de sus escritos se han conservado hasta nuestros días en las bibliotecas de Oxford. Y todos ellos cruzaron en ambos sentidos la desdibujada frontera entre la astronomía y la astrología.
En contraste con esta constelación de astrónomos, no figuran escritores ingleses en ninguno de los capítulos que Vossius dedica a la música, la óptica, la geodesia, la cosmografía, la cronología y la mecánica; tan solo aparecen mencionados Gervasio de Tilbury y Roger Bacon dentro de la geografía, como cartógrafos. Por tanto, al mirar hacia atrás desde la perspectiva del siglo XVI en busca de los escritos matemáticos de la Inglaterra medieval, los temas imperantes son el computus y la astrología.
En cambio, en otras zonas de Europa el panorama fue muy distinto. En Italia, por ejemplo, situada en el centro del Mediterráneo occidental, el comercio estaba más generalizado y era más complejo que en el norte de Europa; en el siglo XIII vivió la proliferación de escuelas de ábaco para enseñar a los niños la aritmética comercial e incluso un poco de álgebra rudimentaria (como la resolución de algunas ecuaciones básicas). El texto de partida fue el Líber abací (‘Libro del ábaco’) de Leonardo de Pisa, más tarde conocido como Fibonacci. El Líber abaci contiene cientos de problemas comerciales. Veamos dos de ellos:
Cuatro hombres crean una compañía en la que el primero de ellos aporta 1/3 del total, otro da 1/4, el tercero pone 1/5 y el cuarto contribuye con 1/6, y entre todos obtienen unos beneficios de 60 soldi; se requiere saber cuánto gana cada uno. El problema en realidad es igual que si decimos que cuatro hombres compran un puerco por 60 soldi, y que el primero quiere quedarse un tercio del cerdo; el segundo, un cuarto; el tercero, un quinto; y el cuarto, un sexto...
El propio Leonardo da dos versiones del problema; desde un punto de vista matemático, también es equivalente al del zorro, el perro y el gato montés del Suán shií shü.
El siguiente problema refleja las inquietudes imperantes en la Italia contemporánea y tipifica cientos de problemas sobre conversión de monedas o materiales. Al mismo tiempo, evidencia que unos diez siglos después de Diofante, en Alejandría aún se practicaba la otra clase de aritmética.
Además, 11 rollos genoveses [de paño] valen 17 carats en Alejandría; ¿cuánto valen 9 rollos florentinos? Como los 11 rollos y los 9 rollos no usan la misma medida de peso, hay que convertir los 11 rollos genoveses en rollos florentinos, o los 9 rollos florentinos en rollos genoveses, de forma que ambos estén expresados en rollos florentinos o en rollos genoveses; pero como la conversión a rollos florentinos es fácil, cada rollo genovés es 1/6 + 2 rollos florentinos, hay que multiplicar los rollos genoveses por 1/6 + 2 para obtener 5/6 + 23 rollos florentinos...
A pesar de todos sus conocimientos, Vossius y sus fuentes del norte de Europa nunca habían visto el Líber abaci; Vossius sabía de él únicamente de oídas, y confundió la fecha en dos siglos. Seguramente la actividad matemática estaba muy localizada.
Pero también estuvo muy vinculada al tiempo. Durante la época medieval, la mayoría de las categorías inventadas más tarde por Dee y Vossius habrían sido muy redundantes, al menos en Inglaterra. A finales del siglo XVI, cuando también Inglaterra entró a formar parte del vasto mundo, dejó de ser así. Thomas Harriot, cuyos trabajos datan de alrededor de 1600, dejó textos sobre óptica, balística, alquimia, álgebra, geometría, navegación y astronomía. Al mismo tiempo, su contemporáneo Simón Stevin publicó en los Países Bajos sobre los mismos temas, aunque reemplazando la navegación por problemas más pertinentes (para él) sobre esclusas y compuertas. El computus y la astrología dejaron paso a las prácticas matemáticas de un nuevo orden mundial.
¿Qué son las matemáticas?
Entonces, ¿qué han sido las matemáticas a lo largo de la historia si, en realidad, nunca existió tal entidad? A estas alturas está claro que la actividad matemática ha adoptado muchas formas, que se encuentran ligeramente conectadas entre sí por el hecho de que implican algún tipo de medición o de cálculo.
Una respuesta más precisa depende en gran parte del momento y el lugar. Aunque hay algunos hilos comunes: todas las sociedades organizadas necesitan regular el comercio y el calendario, que en términos muy generales eran los objetivos del suán shií y del suán h, respectivamente, en los inicios de la China imperial, o del ábaco y el computus en la Europa del siglo XIII. Sin embargo, es muy probable que quienes practicaban aquellas técnicas diversas pertenecieran a niveles sociales muy diferentes. La enseñanza del suán shu y del ábaco estaba pensada para comerciantes y funcionarios, mientras que el suán lí y el computus provenían de especialistas de alto rango en China, y de monjes y eruditos en la Europa medieval. Durante muchos siglos se repitió en numerosos contextos una diferenciación en cuanto a categoría y respeto entre quienes estaban lo bastante formados como para dedicarse a las matemáticas «elevadas», que suelen requerir cierto grado de pensamiento abstracto, y los comerciantes o artesanos que trabajaban con las matemáticas «corrientes» o «vulgares».
A medida que las sociedades se volvieron más complejas, también lo hicieron sus necesidades matemáticas. La larga lista de categorías que propuso Dee (aunque algunas fueran redundantes) indica una gran cantidad de actividades que requerían conocimientos matemáticos. El conjunto de estas materias se conocía como «matemáticas mixtas», lo que indica que las matemáticas eran una parte integral de cada una de ellas (que no es exactamente lo mismo que el concepto posterior de las «matemáticas aplicadas», donde las matemáticas se usan para analizar cuestiones ajenas a ella misma).
No hay ninguna razón para pensar que las lecciones que se enseñaban en los comienzos de la China imperial y en la Europa medieval no alcanzaran también a otras sociedades: no existe un corpus único de conocimientos que podamos llamar adecuadamente matemáticas, pero sí podemos identificar muchas disciplinas y actividades matemáticas. Y siempre ha dependido del momento y el lugar que unas fueran consideradas más relevantes o prestigiosas que otras.
¿Quién es un matemático?
Ahora que hemos empezado a identificar la variedad de actividades que han conformado las matemáticas, podemos decir quién se puede considerar o no matemático. Tanto Pitágoras, como Diofante, Fermat y Wiles suelen catalogarse como matemáticos, y los tres primeros, ya fallecidos, figuran en la obra de referencia habitual en lengua inglesa, titulada Biographical Dictionary of Mathematicians. Sin embargo, ninguno de ellos habría aceptado la etiqueta que les han impuesto. No tenemos ni idea de cómo se habría definido a sí mismo Pitágoras, de haberlo hecho de algún modo. Diofante probablemente se habría calificado de aritmético, pero no como experto en la aritmética cotidiana del suán shu o el ábaco, sino de la «aritmética elevada», que estudia algunas de las propiedades más ocultas y difíciles de los números naturales. Fermat, por su parte, se habría considerado a sí mismo un «geómetra», porque por entonces la geometría era la rama más acreditada y respetable del quadrivium. Esa fue la descripción estándar de un matemático académico en Francia hasta bien entrado el siglo XIX. De los cuatro, sospecho que tan solo Wiles se habría definido a sí mismo como matemático.
En la actualidad, la disciplina de las matemáticas es muy reputada, incluso venerada, pero con lo que acabamos de decir en este capítulo se ve con claridad por qué no fue siempre así. Juan de Salisbury sostuvo en el siglo XII que la práctica de la mathematica, la lectura del futuro en las posiciones de las estrellas y planetas, provenía de una fatídica familiaridad entre hombres y demonios, y que esta, junto con la quiromancia (leer las manos) y el augurio (interpretar el vuelo de las aves), era una fuente del mal. En 1570, Girolamo Cardano, médico y autor de uno de los textos sobre álgebra más destacados del Renacimiento, fue encarcelado por levantar un horóscopo de Cristo; Thomas Harriot, arrestado en 1605 acusado de colaborar con los organizadores de la Conspiración de la Pólvora, fue cuestionado, no tanto por la pólvora en sí como por el hecho de tener un horóscopo de Jacobo I colgado en la pared; y a finales del siglo XVII John Aubrey escribió acerca de William Oughtred, clérigo rural y profesor de matemáticas, que «la gente del campo lo creía capaz de conjurar». En la Europa premoderna, la práctica de las «matemáticas» no estaba exenta de peligros, ni para quienes las realizaban ni para sus supuestos objetos de trabajo.
De hecho, el término «matemático» empezó a usarse con regularidad en los textos matemáticos ingleses a partir del año 1570. Al principio se empleaba sobre todo con autores extranjeros, pero después se extendió a dos contextos curiosamente sin ninguna relación entre sí: la artillería y la astrología. Tras la Restauración inglesa de 1660, empezó a utilizarse de manera más general con autores que escribían sobre aritmética y geometría, pero continuó usándose con astrólogos; al mismo tiempo, las predicciones de las mathematicks se convirtieron en objeto habitual de sátiras y burlas. La dilatada y persistente asociación de las matemáticas con la astrología explica por qué los académicos preferían evitar el término. Cuando Henry Savile creó dos cátedras matemáticas en Oxford en 1619, de geometría y de astronomía, lo hizo con órdenes estrictas de que esta última no debía incluir astrología judiciaria. En la actualidad, Cambridge alberga una Cátedra Lucasiana de Matemáticas, pero su equivalente en Oxford es la Cátedra Saviliana de Geometría. Y si nada obliga a pensar que la asociación de las matemáticas con la predicción y el influjo fue un fenómeno exclusivamente europeo, vale la pena tener en cuenta que el término chino moderno para matemáticas, shu xué,![]() , se ha relacionado tradicionalmente con el estudio de los números en el contexto de la adivinación.
, se ha relacionado tradicionalmente con el estudio de los números en el contexto de la adivinación.
En resumen, los «matemáticos», en el sentido actual del término, son un invento moderno europeo. A lo largo de la dilatada historia de la práctica matemática, han existido durante poco más que un mero abrir y cerrar de ojos, y para percibir correctamente la historia de las matemáticas es esencial no proyectar su imagen hacia el pasado. Esta es la razón por la que los historiadores prefieren usar descripciones más específicas, como «amanuense», «cosmógrafo» o «algebrista», o términos más generales, como «persona que practica las matemáticas». Una cosa está clara: la historia de las matemáticas no es la historia de los matemáticos.
Capítulo 3
¿Cómo se difunden las ideas matemáticas?
El capítulo anterior contiene varios análisis muy generales de la actividad matemática en distintos momentos y lugares. Esta es una de las maneras de estudiar la historia de las matemáticas: ver qué hacía la gente en realidad. Pero los historiadores siempre se plantean interrogantes adicionales: no solo qué sabían las personas, sino también cómo lo transmitían a sus coetáneos y a sus descendientes; cómo se difundían las ideas matemáticas de un individuo a otro, de una cultura a otra, o de una generación a otra. (Recordemos las preguntas planteadas en el capítulo 1: ¿cómo supo Fermat de Diofante, o Wiles de Fermat?). Una ampliación de estas preguntas nos lleva a plantearnos cómo acceden los propios historiadores a las matemáticas del pasado: qué fuentes tenemos, de qué manera han llegado hasta nosotros, hasta qué punto son fiables, y cómo aprendemos a leerlas.
En el presente capítulo veremos que en ocasiones las ideas matemáticas han recorrido largas distancias temporales y espaciales, pero también que, con mucha frecuencia, no ocurrió así.
Fragilidad, escasez y oscuridad
Quienes se hayan conformado pensando que las matemáticas empezaron con Pitágoras tal vez sientan un poco de vértigo al descubrir que ya se practicaban matemáticas complejas más de mil años antes en Egipto y en la región que hoy es Iraq. Las civilizaciones egipcia y babilónica del segundo y primer milenios antes de Cristo estaban bastante próximas entre sí, pero sabemos mucho más sobre las matemáticas de esta última que sobre las de la primera, por la simple razón de que las tablas de arcilla que se usaban como soporte de la escritura a lo largo de las orillas del Tigris y el Éufrates eran robustas y duraderas, mientras que los papiros de la región del Nilo no lo eran. En excavaciones de Iraq se han encontrado miles de tablillas, muchas de ellas con contenidos matemáticos, y es muy probable que queden muchas más enterradas si aún no las han pulverizado el paso de los tanques o no han sido saqueadas en medio del caos de las recientes guerras. En Egipto, por su parte, la cantidad de textos y fragmentos matemáticos que han perdurado se puede contar con los dedos de tres manos, y están desperdigados por miles de años de historia. Su equivalente en Gran Bretaña lo constituirían algunos textos que datan de alrededor de la época de la conquista normanda y algunos más del siglo XIX. Es evidente que los textos egipcios aportan una idea muy escasa, pero al mismo tiempo dejan mucho espacio para especular y fabular sobre la actividad matemática egipcia.
En India, el sudeste de Asia y América del Sur, la situación se asemeja mucho a la de Egipto: las condiciones climáticas destruyeron con rapidez los materiales naturales, como la madera, la piel o los huesos, así que los historiadores han tenido que afanarse mucho con muy pocos textos mal conservados.
Es evidente que la escasez de material distorsiona nuestra visión del pasado. Debemos preguntarnos si lo que sobrevive es representativo de lo que se ha perdido, sabiendo que cualquier nuevo hallazgo (como el Suán shu shü en China) podría alterar radicalmente nuestra percepción de toda una cultura matemática. Al mismo tiempo, la falta de textos tal vez haya tenido algo de positivo, puesto que ha obligado a los historiadores a ampliar la búsqueda de posibles fuentes. Los registros oficiales, por ejemplo, pueden desvelar el tipo de cálculos y de mediciones que se realizaban en la vida cotidiana. Los restos arqueológicos nos han permitido conocer mejor cómo se proyectaban y construían los edificios y, por tanto, qué cálculos requirieron (ya que no disponemos de datos directos sobre qué cálculos se efectuaron para construir Stonehenge o las pirámides). Restos tan diversos como pinturas, narraciones o poemas también pueden dar pistas sobre los conocimientos matemáticos de una época.
Muchos textos antiguos se escribieron en alfabetos y lenguas ya extintas en la actualidad, y el proceso de traducirlos está plagado de dificultades. Sigue habiendo muy pocos especialistas con los conocimientos lingüísticos necesarios y con suficiente valentía para enfrentarse a textos matemáticos, y realizan una labor sumamente delicada. Cualquier traducción de una lengua a otra corre el riesgo de destruir parte de la esencia del original, pero la traducción de textos matemáticos añade una dificultad adicional: la de conseguir que los conceptos específicos de otra cultura sean comprensibles para el público actual. ¿Qué haría un lector convencional, por ejemplo, con el siguiente pasaje del texto indio Brahmasphutasiddhánta del año 628 d. C.:
La altura de una montaña multiplicada por un multiplicador dado es la distancia a una ciudad; esto no se borra. Cuando se divide entre el mismo multiplicador más dos se obtiene el salto que da uno de los dos que hacen el mismo viaje.
Para entender este problema hay que saber que un viajero desciende una montaña y recorre a pie una llanura para llegar a una ciudad, mientras que otro viajero da un salto mágico desde la cima, lo que lo levanta a una altura vertical mayor que la de la montaña, y desde ahí vuela por la hipotenusa hasta la ciudad, pero de forma que recorre la misma distancia que el otro. Esto bien pudo ser un problema típico para un estudiante de la época (en otra versión se habla de monos que brincan por los árboles), y probablemente se explicaba de forma oral, pero para un lector del siglo XXI sin conocimientos de sánscrito o de las convenciones matemáticas en la India del siglo VII, resulta de entrada simplemente incomprensible.
Así que una traducción literal de un texto original no dirá mucho a un lego en la materia. El método ancestral al que han recurrido traductores (o copistas) para resolver el problema consiste en añadir notas o diagramas explicativos: todos los textos matemáticos importantes han acumulado capas de comentarios de esta manera. Otro sistema consiste en traducir el texto a la notación matemática moderna. Quien lo intente con el problema de los dos viajeros que descienden de la montaña seguramente lo verá mucho más claro. El empleo de la notación algebraica moderna puede servir como método preliminar para entender las matemáticas del pasado, pero no debe confundirse nunca con lo que el autor original intentó hacer «en realidad», ni con lo que habría hecho en caso de contar con la ventaja de una buena formación actual. En el mejor de los casos, esa modernización oscurece el método original y, en el peor, puede dar lugar a graves malentendidos.
Los textos egipcios que se han conservado del segundo milenio antes de Cristo, por ejemplo, están en escritura hierática, una escritura cursiva que reemplazó a la jeroglífica en el uso cotidiano desde alrededor del año 2000 a. C. en adelante. Se tradujeron al inglés o el alemán a comienzos del siglo XX, y durante muchos años se tomaron como traducciones de referencia. Sin embargo, los contenidos se tradujeron no solo, por desgracia, a las lenguas modernas, sino también a las matemáticas modernas. Así, por ejemplo, se afirma con frecuencia que los egipcios asignaban un valor de 3.16 al número que ahora simbolizamos mediante π, el factor que da el área de un círculo al multiplicarlo por el cuadrado de su radio (la fórmula moderna se escribiría A = πr2). Cuando se analizan los textos en los que se basa esta afirmación, descubrimos que no cuentan con que el lector multiplique el radio al cuadrado por ningún número en absoluto, sino que le enseñan a hallar el área reduciendo el diámetro en 1/9 para, a continuación, elevarlo al cuadrado. Unas cuentas con papel y lápiz revelan que con eso se obtiene que el área del círculo es 256/81 por el radio al cuadrado, de ahí el valor mágico de 256/81 = 3.16... Pero «reducir y elevar al cuadrado» no es lo mismo que «elevar al cuadrado y multiplicar», aunque con ello se llegue casi a la misma respuesta: el método es bastante diferente, y los historiadores deben fijarse justamente en los métodos para comprender el pensamiento matemático de las culturas precedentes.
La traducción de textos babilónicos ha tenido una historia parecida. En este caso, las lenguas de partida eran la sumeria (una lengua sin ninguna relación con idioma actual alguno) y la acadia (precursora del árabe y el hebreo); la escritura de ambas es cuneiforme, tallada en arcilla húmeda con un junco afilado. Durante la década de 1930, Otto Neugebauer y François Thureau-Dangin tradujeron y publicaron gran cantidad de textos matemáticos, y durante muchos años se pensó que el trabajo ya estaba más o menos hecho. Sin embargo, aquellas primeras traducciones convertían con demasiada frecuencia las técnicas de cálculo mesopotámicas en sus equivalentes algebraicos modernos, lo que oscurecía la naturaleza verdadera de lo que el amanuense original pensaba y hacía en realidad, al tiempo que confería a los cálculos un aire bastante primitivo. A partir de la década de 1990 muchas de las tablas volvieron a traducirse de nuevas prestando mucha más atención a la lengua original. Las palabras que literalmente significan «partir en dos» o «añadir», por ejemplo, expresan acciones físicas que se pierden en las traducciones abstractas «dividir entre dos» o «sumar», y permiten hacerse una idea mucho más acertada de la forma en que se entendían o enseñaban los problemas.
Leer y traducir textos solo es una parte, si bien crucial, del trabajo de los historiadores de las matemáticas antiguas. La otra consiste en interpretarlos dentro de su contexto particular. A veces resulta simplemente imposible: muchos textos de Oriente Próximo hallados o redescubiertos en el siglo XIX -incluidos casi todos los textos hieráticos egipcios que se conservan y cientos de las antiguas tablillas cuneiformes babilónicas- fueron cambiando de manos en los mercados de antigüedades sin ninguna información conocida sobre su procedencia. Por desgracia, hoy en día aún se compran y venden de este modo numerosos objetos saqueados o robados.
La fragilidad y la escasez de textos matemáticos apenas mejoran a medida que avanzamos desde el mundo de la antigüedad hacia el periodo medieval. Ni siquiera los documentos conservados deliberadamente en bibliotecas están siempre seguros. Existen diversos testimonios, imposibles de confirmar ya, sobre la destrucción de la Biblioteca de Alejandría en tiempos de conflicto y, desde luego, sería un lugar tan vulnerable a los incendios como cualquier biblioteca antigua que albergara libros o manuscritos. A los usuarios de la Bodleian Library de Oxford aún se les impone el juramento de «no traer a la biblioteca o encender dentro de ella ningún fuego o llama, y a no fumar en su interior», un recordatorio de aquellos días en que estas acciones podían resultar tan letales para los libros como para las personas.
Ya hemos hablado de los esfuerzos de John Leland para catalogar todo lo que contenían las bibliotecas monásticas, pero no consiguió conservar más que una porción de las colecciones cuando aquellas bibliotecas acabaron destruidas y su contenido, diseminado. Pero también había otros peligros: el Merton College de Oxford tiró gran cantidad
de volúmenes manuscritos durante el siglo XVI cuando se modernizaron, y los cambió por libros impresos, y aunque algunos fueron rescatados por coleccionistas avispados, muchos seguro que no lo fueron. Y John Wallis lamentó con amargura en 1685 (igual que Leland más de un siglo antes) el robo de material valioso: dos prefacios del siglo XII, escribió, fueron «arrancados con posterioridad (por alguna mano desconocida), y sustraídos» de un manuscrito en el Corpus Christi College. Él confiaba en que «quienquiera que los tenga, haga el favor de devolverlos (de un modo u otro)», pero fue una esperanza vana: los prefacios siguen desaparecidos.
Las colecciones privadas de documentos también eran vulnerables: John Pell, temiendo por los textos matemáticos de su amigo recién fallecido Walter Warner, escribió en 1644:
No es pequeña la preocupación que siento por que todos los documentos del señor Warner, y no pocas de mis aportaciones en ellos, sean incautados y divididos sin criterio matemático alguno entre los confiscadores y acreedores, que sin lugar a dudas decidirán por una vez en su vida hacer de astrólogos [1] y, tras sus cálculos, votarán que todos ellos sean arrojados al fuego.
Los libros impresos están tan expuestos como los manuscritos al fuego, las inundaciones, los insectos y las negligencias humanas, pero como hay más copias, tienen más posibilidades de sobrevivir. Sin embargo, es poco probable que los que nos han llegado sean representativos de lo que existió una vez. Es más fácil que perdure un volumen caro procedente de la biblioteca de un caballero, que las gastadas tablas de cálculo de un comerciante, pero seguramente aquel revelará menos sobre qué se leía y usaba en realidad.
La reconstrucción fiel del pasado suele ser como intentar armar un rompecabezas al que le faltan la mayoría de las piezas y sin imagen para guiarse en la caja. Y, a pesar de todo, curiosamente tenemos textos matemáticos que se han conservado durante siglos o incluso milenios. En su mayoría, los contenidos tienen un interés puramente histórico: nadie calcula ahora con fracciones egipcias, salvo como ejercicio escolar, y el único vestigio que queda del sistema sexagesimal babilónico es nuestra curiosa división de las horas en 60 minutos, y de la circunferencia en 360 grados. Otros textos, en cambio, se han mantenido mucho más vivos a través de su uso y traducción constantes, y en ocasiones hasta es posible trazar una línea casi continua de ascendencia desde el pasado hasta el presente. El ejemplo más destacado lo constituyen los Elementos de Euclides, mencionado aquí ya más de una vez, y sin el cual ninguna historia de las matemáticas puede estar completa. Un estudio de lo que a veces se denomina la «historia de transmisión» de los Elementos revela mucho sobre cómo pueden conservarse, revisarse y difundirse las ideas matemáticas.
Conservación a través del tiempo
Lo que acabamos de comentar sobre la fragilidad de las fuentes egipcias se aplica por igual a textos procedentes del mundo antiguo en lengua griega, también escritos sobre papiros. A partir de referencias contemporáneas a algunas de sus obras, partimos del supuesto de que Euclides escribió alrededor del año 250 a. C., pero el volumen más antiguo que se conserva de los Elementos data del año 888 d. C., lo que significa más de mil años de copias y recopias, con todo lo que eso conlleva de errores, cambios y «mejoras». ¿Cómo sabemos que el texto que tenemos ahora se parece en algo al original? La respuesta es que no lo sabemos.
En el caso de los Elementos, contamos con comentarios extensos de algunos escritores griegos posteriores, como Papo (320 d. C.), Teón (380 d. C.) y Proclo (450 d. C.), que nos dicen cómo era el texto en los siglos IV o V de nuestra era. Estos hombres vivieron mucho más cerca de la época de Euclides que nosotros, pero, aun así, varios siglos después de que se escribieran los Elementos por primera vez. A falta de este tipo de referencias, la única manera que tienen los historiadores de acercarse al original consiste en confeccionar un «árbol genealógico» de los manuscritos conservados, observando, por ejemplo, en qué lugar se han copiado errores o modificaciones de un texto a otro. De este modo confían en llegar hasta una «copia maestra», pero se trata de un trabajo muy laborioso sin ninguna garantía de que acabe llevándonos hasta una fuente auténtica y única.
Ese primer manuscrito conservado de los Elementos, del año 888 d. C., se escribió en griego y se preservó en Bizancio. Pero a medida que el islam se expandió por las regiones del Mediterráneo donde se hablaba el griego antiguo, el texto también se tradujo al árabe. Es fácil imaginar las dificultades a las que se enfrentaron los primeros traductores al árabe al comparar su tarea con la que realizó Robert Recorde varios siglos después: es improbable que el árabe, una lengua de tribus nómadas, contara con palabras propias para nombrar los conceptos abstractos de la geometría euclídea. Sin embargo, las traducciones al árabe salvaron muchos textos de la extinción.
La mayoría de las traducciones medievales de los Elementos al latín se realizaron, por tanto, a partir de fuentes en árabe desde España o Sicilia. Adelardo de Bath, que apareció ya en el capítulo anterior, fue uno de esos traductores, y hubo muchos otros en el siglo XII, eruditos del norte de Europa que viajaron al sur en busca de los conocimientos que pudieran encontrar allí. Con el tiempo, a medida que el aprendizaje del griego se fue recuperando lentamente, también empezaron a efectuarse traducciones directas a partir de fuentes griegas.
Una vez que se instauró la imprenta, en el siglo XV, la supervivencia de los Elementos de Euclides quedó garantizada para la posteridad. Fue uno de los primeros libros de matemáticas que se imprimió, en una bella edición de 1482, la cual mantenía las tradiciones de la producción de manuscritos: sin portada con el título (porque lo tradicional en los manuscritos era que los autores firmaran la obra al final y no al principio), y unas delicadas ilustraciones iluminadas (véase la figura 3).
Durante el siglo XVI, las ediciones impresas se sucedieron con rapidez, al principio en latín y griego, pero después también en varias lenguas vernáculas. Robert Recorde incluyó la mayoría del material de los cuatro primeros libros de los Elementos en The Pathway to Knowledg, en 1551, y material adicional, más complejo, de los últimos libros en su última obra The Whetstone of Witte, en 1557.

Figura 3. Primera página de la primera edición impresa de los Elementos de Euclides, de 1482.
La primera traducción al inglés íntegra de los Elementos se publicó en una edición de lujo de Henry Billingsley en 1570; contiene el «esquema básico» de John Dee y también es el primer texto en inglés conocido que exhibe el término «matemático» en la portada.
A lo largo de los cuatro siglos posteriores hubo muchas más traducciones y ediciones que los editores adaptaron a las necesidades de la época. A mediados del siglo XX, los Elementos se retiraron al fin de los programas de estudios escolares (aunque no sus contenidos: los niños aún aprenden a trazar triángulos y a biseccionar ángulos en los colegios). Sin embargo, no ha desaparecido del dominio público. Una versión interactiva actual es la innovación más reciente en la larga tradición de traducciones y adaptaciones de los Elementos para cada nueva generación.
Los Elementos han tenido un alcance y una longevidad únicos, pero la historia de su conservación es la típica de muchos otros textos griegos, incluida la Aritmética de Diofante que inspiró el último teorema de Fermat. La mayoría de los textos clásicos tiene una historia similar de citas tempranas, traducciones al árabe, traducciones posteriores al latín, y publicación ulterior impresa de las fuentes griegas conservadas. Solo ha habido una excepción: el redescubrimiento casi milagroso a comienzos del siglo XX de un texto perdido de Arquímedes, apenas perceptible bajo escritos y pinturas posteriores en las páginas de un libro de oraciones bizantino. Estos hallazgos son rarísimos, y vuelven a recordarnos la cantidad de textos matemáticos de todas las culturas que se han perdido.
Conservación en la distancia
A pesar de la fragilidad de los documentos escritos, la difusión de las matemáticas se ha producido, no solo a través de largos periodos de tiempo, sino a veces a lo largo de enormes distancias, y en ocasiones de ambos modos. Partiremos de un misterio.
Este es el comienzo de un problema de una tablilla de la antigua Babilonia que ahora se encuentra en el Museo Británico (BM 13901):
Sumé el área y el lado del cuadrado y daba 0;45.
Recurriendo a la técnica sobre la que advertimos antes, introduciremos la notación algebraica para ver de qué va el problema. Si el lado de un cuadrado es l, entonces su área será l2. El número 0;45 es una transcripción moderna que se puede interpretar como 45/60 o 3/4. Por tanto, el enunciado se puede escribir en términos actuales mediante la ecuación l2 + l = 3/4. La técnica babilónica para hallar la longitud del lado de un cuadrado implicaba la partición y la reordenación de figuras geométricas; para una persona experimentada, esto podía reducirse a una serie de instrucciones breves, una receta que garantizaba llegar a la respuesta.
Consideremos ahora este problema en un texto sobre el mismo tema de Al-fabr wa-l-muqdbala (Compendio sobre cálculo algebraico y reducción) compuesto por al-Juarismi (al-Jwárizmí) en Bagdad alrededor del año 825 d. C.
Un cuadrado y 21 unidades es igual a 10 raíces.
En este caso las «raíces» son las raíces cuadradas del cuadrado en cuestión, así que, si volvemos a usar la notación moderna, vemos que el problema se puede escribir como l2 + 21 = 10l. En otras palabras, esto guarda una relación muy directa con el problema de la antigua Babilonia que se escribió más de dos mil quinientos años antes. Pero, además, al-Juarismi daba una receta muy parecida para hallar la respuesta. Su texto tuvo tanta influencia que su título dio nombre a toda la disciplina, conocida hoy como álgebra.
¿Es una coincidencia que el mismo tipo de problema con la misma suerte de solución reapareciera tantos siglos después en la misma parte del mundo? No hay ningún signo de que hubiera continuidad a lo largo de los años, como sí ocurre con los Elementos de Euclides, al menos no dentro del Iraq antiguo o islámico. Sin embargo, sí tenemos indicios de que las ideas se difundieron desde la cultura babilónica tardía hasta India, y de que las matemáticas se propagaron más tarde en la dirección opuesta, desde India hacia Bagdad. Es muy posible que problemas como los comentados aquí formaran parte de esa corriente; no podemos afirmar nada, solo podemos especular. Pero vale la pena repasar lo que sabemos con más seguridad.
Desde el año 500 a. C. hasta el 330 a. C., el antiguo Iraq y el noroeste de India eran los confines del Imperio persa, tras lo cual, durante un breve espacio de tiempo, esa misma región estuvo gobernada por Alejandro Magno. Las pruebas de la asimilación de las matemáticas babilónicas en India son indirectas, pero muy claras, sobre todo en cálculos astronómicos: se aprecia en el uso indio de las medidas en base 60 para el tiempo y los ángulos, y en métodos similares para calcular la duración de la luz del día a lo largo del año. (En India, igual que en otras sociedades tempranas, era esencial la medición exacta del tiempo con fines rituales y de otros tipos). Más tarde hubo traducciones al sánscrito de textos astronómicos o astrológicos griegos, así que la «cuerda» griega, utilizada para medir la altura
astronómica, se convirtió en la base del «seno» indio. La escasez de textos indios antiguos impide saber qué otros conocimientos pasaron al Occidente, y sin duda también en la dirección opuesta: unos pocos fragmentos astronómicos del Irán preislámico, por ejemplo, sugieren la repercusión que tuvieron allí los textos en sánscrito.
Hacia el final del siglo vi (o incluso mucho antes) se desarrolló en partes de India central un sistema para escribir números que solo utilizaba diez dígitos junto con un sistema de valores posicionales. Es difícil exagerar la trascendencia que tuvo aquello. En términos actuales significa poder escribir cualquier número de cualquier tamaño (grande o pequeño) usando únicamente diez símbolos: 0, 1,2, 3, 4, 5, 6, 7, 8, 9. El término «valor posicional» significa que el 2 y el 3 adoptan valores distintos en 200 003 y en 302, porque se encuentran en posiciones diferentes. En ambos casos los ceros sirven como marcadores de posición, de forma que no confundamos 200 003 con 23, o 302 con 32. Una vez comprendido este sistema, unas breves reglas de adición y multiplicación, siempre las mismas, se pueden aplicar a números de cualquier tamaño. Por supuesto, a lo largo de la historia ha habido muchas otras maneras de escribir números, pero todas ellas requieren la invención de más y más símbolos nuevos a medida que los números van creciendo, y ninguno de ellos sirve para efectuar cálculos con lápiz y papel: intente sumar un par de cantidades escritas en números romanos, XXXIV más XIX, por ejemplo, sin convertirlos a algo más familiar.
Los numerales indios o hindúes, como acabaron denominándose, se conocían en partes de Camboya, Indonesia y Siria ya en el siglo VII: fueron muy elogiados por el obispo sirio Severo Sebokht, por ejemplo. Hacia el 750 el islam se había difundido por la región del antiguo Imperio persa (y más allá); y hacia el 773 los números hindúes habían llegado a Bagdad en tratados astronómicos traídos desde India al califa al-Mansur.
Hacia el año 825, al-Juarismi -al que ya conocimos como autor de Al-fabr- escribió un texto sobre el uso de los numerales indios. El original se perdió, pero sus contenidos se pueden recuperar a partir de traducciones posteriores al latín. En primer lugar enseñaba a escribir los diez dígitos, en sus formas arábigas en lugar de sánscritas, con una explicación cuidadosa del valor posicional y el uso correcto del cero; a eso le seguían instrucciones para sumar y restar, doblar y reducir a la mitad, multiplicar y dividir, algunas enseñanzas sobre fracciones incluido el tipo sexagesimal, e indicaciones para obtener raíces cuadradas. El texto de al-Juarismi estableció las pautas de los textos aritméticos durante siglos: su estructura aún se aprecia con claridad en muchos de los textos europeos del siglo XVII, aunque por entonces aquel material ya se había ampliado mucho. De momento, no obstante, quedémonos con los numerales indios o, tal como se los conoce hoy en día, los numerales indoarábigos, y con el avance de su propagación hacia el oeste.
Hacia finales del siglo X, aquellos números llegaron a España, en el otro extremo del mundo islámico, desde India, y adquirieron la forma árabe occidental que prefiguró los numerales occidentales modernos, en lugar de su forma árabe oriental, que aún se emplea en países de lengua árabe. Y desde España se fueron difundiendo poco a poco hacia el norte, hasta llegar a Francia e Inglaterra. Uno de los mitos relacionados con estos números es que fueron introducidos en la Europa cristiana por un monje llamado Gerberto -que más tarde fue papa con el nombre de Silvestre II-, quien había visitado España antes de 970. Es cierto que Gerberto usó esos numerales sobre contadores de ábaco, pero ese débil indicio difícilmente permite atribuirle la introducción de esos números en el resto de Europa: desconocemos si conocía los métodos relevantes de cálculo o si se limitó a usar esos numerales como meros símbolos decorativos; tampoco sabemos cuánto se conoció o utilizó su ábaco; y, además, tuvo que haber más viajeros que llegaran a España y también se llevaran consigo algún conocimiento sobre esos numerales para compartirlo con sus amistades. Lo más probable es que el conocimiento de esos numerales se propagara poco a poco y de manera fragmentaria hasta que su utilidad acabara encontrando un reconocimiento más generalizado.
Lo que sí sabemos es que unas tablas astronómicas procedentes de España -las Tablas Toledanas- se adaptaron para Marsella en 1140 y para Londres en 1150. Las instrucciones para utilizarlas se tradujeron del árabe al latín, pero no las tablas en sí: ¿quién iba a querer convertir los farragosos números romanos en columnas enteras de números formados por dos dígitos que medían grados, minutos y segundos? Igual que fueron tablas astronómicas las que llevaron los numerales indios hasta Bagdad, también fueron tablas las que los transportaron más tarde hasta el norte de Europa: para los astrónomos, aquellos numerales no solo eran útiles, sino cruciales para entender las observaciones de otras personas.
De un modo más prosaico, el conocimiento de esos numerales y de los métodos de cálculo asociados a ellos también tuvo que propagarse hacia el oeste y el norte a través del comercio. Los cruzados, por ejemplo, debieron de toparse con ellos a partir de finales del siglo XI. Sin embargo, a diferencia de las tablas astronómicas, los registros de compras y ventas eran efímeros y se perdieron hace mucho tiempo.
Hacia el siglo XII, se escribieron textos específicos para explicar los nuevos numerales y los métodos de cálculo asociados a ellos. Uno de ellos fue el Líber abaci de Leonardo de Pisa, que circuló por Italia, pero no por el norte de Europa. En Francia e Inglaterra se han encontrado, en cambio, textos en latín llamados «algorismos», un nombre derivado de la deformación de las palabras con las que solían comenzar esos textos, Dixit Algorismi, que se traduciría como ‘Según dijo al-Juarismi’. Al igual que el tratado original de al-Juarismi, aquellos textos en latín enseñaban a escribir los numerales y a realizar aritmética básica con ellos. Un ejemplo especialmente bonito compuesto en el norte de Francia por Alexandre de Villedieu es el que se conoce como «Carmen de algorismo», cuyas primeras líneas podrían traducirse así:
Este arte se denomina algorismus, y en él se usan dos veces cinco números indios:
0.9.8.7.6.5.4.3.2.1
Alexandre continúa explicando la relevancia de la posición de cada numeral:
Si colocas cualquiera de ellos en el primer lugar, significa simplemente él mismo: si lo sitúas en el segundo, es él mismo diez veces.
A pesar de sus ventajas evidentes, la adopción de los numerales fue lenta, pero no, tal como se ha insinuado a veces, por sus orígenes orientales y no cristianos, sino porque para el uso cotidiano aún servía bien el viejo sistema romano junto con cálculos realizados con los dedos y pizarras para contar. Además, el aprendizaje de los nuevos numerales no resultaba fácil a todo el mundo: todavía en el siglo XIV o XV, un monje del monasterio benedictino de Cavenso en Italia numeró algunos de sus capítulos del 30 en adelante como XXX, XXXI, 302, 303, 304..., pero con el paso del tiempo los numerales indoarábigos acabaron reemplazando a todos los demás, y cuando alcanzaron el oeste de América prácticamente completaron su circunnavegación del mundo.
Se pueden contar otras historias sobre la forma en que se difundieron las matemáticas a lo largo de grandes distancias. Las matemáticas tradicionales chinas, por ejemplo, fueron adoptadas por los vecinos inmediatos de China, y no hay duda sobre los intercambios que también hubo con India, aunque ninguno con Occidente hasta la llegada de los jesuitas en el siglo XVII, quienes llevaron allí los Elementos de Euclides. Tales movimientos continuaron en tiempos más recientes: en el siglo XIX las matemáticas europeas se trasladaron desde sus grandes centros en Francia y Alemania hacia la periferia de Europa, los Balcanes en un extremo, y Bretaña en el otro, y más tarde hasta Estados Unidos, y con el tiempo a todos los países del mundo. Esta difusión es característica de la era moderna, pero en el ámbito de las matemáticas las ideas llevan mucho tiempo viajando.
No nos olvidemos de las personas
En este capítulo he descrito cómo han sobrevivido algunas matemáticas del pasado, aunque de forma fragmentada, durante largos periodos de tiempo y en ocasiones también a lo largo de grandes distancias. Un término que suele utilizarse para referirse a estos desplazamientos de las ideas matemáticas es «transmisión», pero a mí no me convence nada: aparte de recordar a las antenas de radio, induce a pensar que los emisores lanzaron a propósito sus ideas y descubrimientos hacia las generaciones futuras. Pero rara vez ocurrió así. En la mayoría de los casos las matemáticas se anotaban para usos privados o para contemporáneos inmediatos del autor, y su supervivencia mucho más allá fue en buena medida accidental. También he procurado evitar hablar de que las ideas se propagan sin más, cual malas hierbas de jardín con capacidad propia para diseminarse.
Al contrario, todo intercambio matemático, ya fuera grande o pequeño, se debió a la intervención humana. Detrás de las largas historias temporales recién comentadas se ocultan innumerables interacciones y transacciones minúsculas. Ya hemos vislumbrado algunas de ellas: emisarios indios que se presentan ante el califa de Bagdad; un escriba bizantino que copia un manuscrito seguramente apenas comprensible para él; comerciantes florentinos que regatean en los mercados de Alejandría; un bibliotecario que en esa misma ciudad de Alejandría catalogó meticulosamente un milenio antes los rollos que tenía a su cargo, y tal vez, al igual que John Leland más tarde, se angustió ante la idea de su destrucción; Fermat enviando sus cartas con una esperanza vana a Wallis en Oxford; Wiles comunicando por primera vez su demostración en una conferencia, e informando de su corrección ulterior a través del correo electrónico. Las ideas matemáticas solo circulan porque la gente reflexiona sobre ellas, las comenta con otras personas, las anota y conserva documentos relevantes. Sin las personas, no se produce ninguna difusión de las ideas matemáticas.
Capítulo 4
El aprendizaje de las matemáticas
Un hecho que se pasa por alto con facilidad es que el mayor colectivo de practicantes de las matemáticas en las sociedades modernas está formado no por adultos, sino por escolares. Un joven de cualquier lugar del mundo lo bastante afortunado como para tener acceso a la educación probablemente pase una cantidad considerable de tiempo aprendiendo matemáticas; en los países desarrollados, esa cantidad suele ascender a entre dos y tres horas lectivas semanales durante diez años o más.
Teniendo esto en cuenta, sorprende un tanto recordar que la inclusión de las matemáticas dentro del currículo escolar es un fenómeno moderno. Hacia 1630, por ejemplo, John Wallis, más tarde titular de la Cátedra Saviliana de Geometría en Oxford, no aprendió aritmética ni en el colegio ni en Cambridge, sino de la mano de su hermano pequeño, quien estudió para dedicarse al comercio; treinta años después, el inteligente e instruido Samuel Pepys, también formado en Cambridge y miembro de la Armada, tuvo dificultades para aprender las tablas de multiplicar. Sin embargo, la mayoría de las sociedades civilizadas ha considerado importante la transmisión de los conocimientos matemáticos al menos a unos pocos individuos de la generación siguiente.
Un estudio de lo que se enseñaba y de cómo se enseñaba revela con bastante claridad qué aspectos de las matemáticas se consideraban relevantes, y con qué finalidad. En este capítulo analizaremos dos ejemplos bastante bien documentados: un aula en Nippur, en el sur de Iraq, algo antes del año 1740 a. C., y otra de la Academia Greenrow de Cumbria, en el norte de Inglaterra, algo después del año 1800 de nuestra era.
Una clase de matemáticas en Babilonia
La antigua ciudad de Nippur, situada en las marismas del Éufrates, a medio camino entre las actuales ciudades de Bagdad y Basora, fue un importante centro religioso construido alrededor de un conjunto de templos dedicados al dios Enlil. Al igual que las abadías y monasterios de la Europa medieval posterior, los templos babilónicos recibían sustanciosas ofrendas y controlaban la tierra y el trabajo, así que necesitaban escribas formados capaces de realizar registros escritos y cálculos. Es por tanto probable que los niños destinados a ejercer esa profesión, que solía recaer sobre determinadas familias, empezaran a instruirse a una edad temprana.
Una pequeña casa de ladrillos de adobe de Nippur, que ahora se conoce como Casa F, parece haber sido una de las diversas escuelas de escribas de la ciudad. Próxima a un templo dedicado a la diosa Inanna, la Casa F se construyó por primera vez algo después del año 1900 a. C. y se usó como escuela poco antes del año 1740 a. C. Igual que todas las construcciones hechas con ladrillos de adobe, precisaba un mantenimiento regular, y cuando dejó de usarse como escuela, se reconstruyó cuatro o cinco veces. Para ello, los albañiles aprovecharon centenares de tablillas escolares desechadas que incorporaron al suelo, a las paredes y al mobiliario del nuevo edificio. Otras tablillas parcialmente destruidas se han encontrado mezcladas con grandes cantidades de arcilla sin utilizar en contenedores de reciclaje.
Mientras se usó como escuela, la Casa F estaba dividida en tres o cuatro estancias interiores y dos patios que albergaban bancos y los contenedores de reciclaje. Por desgracia, desconocemos los nombres y edades de los alumnos, que seguramente no serían más de uno o dos cada vez, ni sabemos con qué frecuencia, ni durante cuánto tiempo ocupaban los bancos del patio. Sin embargo, el método que seguían para utilizar las tablillas ha permitido a los expertos en escritura cuneiforme reconstruir su currículo.
Muchas de las tablillas de la Casa F son planas por un lado (el anverso) y ligeramente redondeadas por el otro (el reverso). El anverso contiene en la parte izquierda un modelo de texto escrito por un profesor y copiado en la parte derecha por el alumno. Por su parte, el reverso redondeado de la tablilla contiene pasajes más largos de material aprendido con anterioridad, reescrito para volver a practicarlo o tal vez como ejercicio memorístico. A partir de unas 1500 tablillas de este tipo de Nippur, cada una de ellas con material «anterior» y «posterior», Niek Veldhuis consiguió discernir en la década de 1990 un orden coherente en el currículo básico, que comenzaba con técnicas elementales de escritura y finalizaba con los inicios de la Sumeria literaria. Al aplicar la misma metodología a unas 250 tablillas análogas procedentes de la Casa F, Eleanor Robson logró hacer lo mismo con el currículo de esta escuela en particular, y descubrir así la relevancia que tenían las matemáticas en él.
Los primeros pasos de los alumnos consistían en aprender la técnica correcta para escribir signos cuneiformes y combinarlos para formar nombres de personas. Adquirían vocabulario escrito a través de listas de palabras, que empezaban con árboles y objetos de madera, después cañas o juncos, embarcaciones, objetos de cuero y metal; animales y carnes; piedras, plantas, peces, aves y prendas de vestir; etcétera. En esta fase también se introducía ya algún vocabulario matemático, con medidas de capacidad para buques, de peso para árboles y piedras, y de longitud para varas de medir de caña o junco. Más tarde también aparecían otras unidades en listas especializadas de pesos y medidas.
Después, el alumno debía aprender de memoria listas de recíprocos (pares de números que al multiplicarlos dan 60), y más de 20 tablas de multiplicar convencionales. Una lista de recíprocos, por ejemplo, podía comenzar así
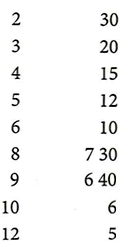
(En la aritmética sexagesimal, que todavía utilizamos en la actualidad con las horas, minutos y segundos, 7 30 equivale a 7 + 1/2, y 6 40 a 6 + 2/3). Las tablas de multiplicar requerían gran capacidad memorística. La tabla de multiplicar del 16 40, por ejemplo, empezaba así:

Se ha calculado que podría tardarse un año en aprender el conjunto completo de tablas y otros ejercicios escolares. En esta etapa, los alumnos también empezaban a escribir frases completas en sumerio, algunas de ellas con unidades de medida aprendidas con anterioridad.
Solo después de todo lo anterior, y con un nivel de sumerio más avanzado, los estudiantes empezaban a realizar cálculos propios de recíprocos que no figuraban en las tablas convencionales. Una de las pocas tablillas «avanzadas» que se conservan de la Casa F contiene alguno de los cálculos utilizados para hallar el recíproco de 17 46 40 (la respuesta es: 3 22 30). Estos cálculos figuran escritos en la misma tablilla que un extracto de una obra literaria conocida como «El consejo de un supervisor a un joven escriba», la cual incluye algunas líneas moralistas basadas en los recuerdos que conserva el supervisor de sí mismo cuando era un joven estudiante:
Como un junco que brota, di un brinco y me puse a trabajar.
No me desvié de las instrucciones de mi maestro; no me puse a hacer cosas por mi cuenta.
Mi mentor se mostró encantado con el trabajo que realicé sobre lo que me había encargado.
La mayoría de los textos avanzados procedentes de la Casa F no son matemáticos sino, como «El consejo del supervisor», composiciones literarias. Sin embargo, muchos contienen referencias a los usos de la literatura y los números para la administración justa de la sociedad. En estas líneas, extraídas de un himno a Nisaba, la diosa protectora de los escribas, la alaban por brindar sus dones al rey:
Una vara y una cuerda de medir de lapislázuli, un cayado y una tabla de escribir que otorga la sabiduría.
Una clase de matemáticas en Cumbria
La Academia Greenrow fue fundada en 1780 por John Drape en Silloth, en la costa noroeste de Inglaterra, pocos kilómetros al sur de la frontera con Escocia. Al igual que la escuela de la Casa F de Nippur, la Academia Greenrow también fue algo así como una empresa de tradición familiar. El padre de Drape, conocido como John Draper, había regentado con anterioridad una escuela en Whitehaven, unos 50 kilómetros al sur de esa misma costa, la cual había fomentado disciplinas relevantes para «el comercio y la navegación»; además, Draper había publicado dos libros de texto para uso de sus pupilos: The Young Students Pocket Companion, or Arithmetic, Geometry, Trigonometry, and mensuration, Calculated for the Improvement of Youth at School (1772) y The Navigators veni-mecum: or a Complete System of the Art of Navigation (1773). Tras la muerte de Draper, su hijo John heredó sus libros, sus instrumentos matemáticos y algunas propiedades que le permitieron fundar la Academia Greenrow unos años más tarde. Cuando falleció el propio Drape en 1795, la escuela pasó a manos de otro miembro de la familia, Joseph Saúl, pariente de la esposa de Drape, quien permaneció al frente de la misma durante casi 50 años. El currículo se amplió para incluir estudios de griego, español y escritura, pero la Academia Greenrow, como su antecesora Whitehaven, siguió prestando especial atención a los estudios matemáticos.
La escuela atrajo a chicos procedentes no solo de la región, sino de todas partes de Inglaterra y hasta del otro lado del océano. En ella ingresaron niños de 9 años, y hasta uno de 6. Aunque a veces también se formaron allí jóvenes de veintipocos años, sin embargo, la mayoría de los alumnos rondaba los 14 o 15 años de edad. Los registros de 1809 revelan que uno de los alumnos más jóvenes, Rowland Cowper (de 11 años), y uno de los más mayores, James Irving (de 23), siguieron el mismo currículo básico de inglés, escritura y aritmética. La mayoría del resto de alumnos estudiaba dibujo y francés o latín, junto a una gran variedad de temas matemáticos. El currículo que siguió John Coleman (de 15 años) era el habitual: inglés, francés, escritura, dibujo, aritmética, geometría, medidas,
agrimensura, contabilidad, trigonometría esférica, astronomía, mecánica, álgebra y geometría euclídea. Otras asignaturas matemáticas ofertadas eran marcación (gnomónica), calibración, y fortificación, aunque George Peat (que tenía 16 años y al parecer era un alumno especialmente capacitado) también recibió lecciones de secciones cónicas y fluxiones (la versión newtoniana del análisis matemático).
Pero tenemos la suerte conocer más cosas sobre Greenrow que meras listas de asignaturas. Antes de morir en 2005, el profesor de matemáticas John Hersee recopiló más de 200 libros matemáticos de copiado escritos por alumnos de colegios de toda Inglaterra y Gales entre 1704 y 1907. No se trataba de libros de ejercicios como los actuales; los alumnos no desaprovechaban el preciado papel en practicar una y otra vez ejercicios similares, sino que copiaban con esmero ejemplos de problemas estándar y con ello confeccionaban una colección de ejemplos ya resueltos que podían servirles de consulta en cualquier momento de su vida futura. Muchos de aquellos ejemplos procedían de libros de texto populares en la época, sobre todo del veterano The Tutor Assistant, de Francis Walkingame (publicado por primera vez en 1751), pero muchos otros debieron de ser inventados por los propios profesores para sus alumnos.
La recopilación de Hersee incluye cinco cuadernos de matemáticas de Robert Smith de los años 1832 y 1833 (véase la figura 4). A lo largo de esos dos años, Robert llenó casi 1700 páginas con ejemplos matemáticos, así que tenemos una idea muy detallada de lo que estudió. Estos libros no fueron los primeros que escribió Robert porque para entonces ya había superado las operaciones básicas de la suma, la resta, la multiplicación y la división.

Figura 4. Portada del libro de aritmética de Robert Smith, Academia Greenrow, 1832.
El cuaderno más antiguo conservado, de 1832, comienza con la regla de tres. Esta fue la regla que permitió a innumerables generaciones de estudiantes resolver problemas como: A hombres cavan una zanja en B días, ¿cuánto tardarán C hombres en realizar el mismo trabajo? La regla se llama así porque a partir de tres cantidades conocidas (A, B y C) hay que hallar una cuarta cantidad (la respuesta). Esta regla es originaria de India y probablemente viajó hacia Occidente con los numerales indios; estuvo omnipresente durante siglos en textos de aritmética islámicos y europeos.
La regla de tres se aprendía de memoria: igual que en Babilonia, no se esperaba que los escolares ingleses del siglo XIX «hicieran cosas por su cuenta». Para resolver el problema recién mencionado, se les enseñaba que debían multiplicar B por C y dividir el resultado entre A para obtener la respuesta correcta. Aunque, por supuesto, siempre había variantes para pillar al alumno incauto: Robert Smith tuvo que aprender la regla de tres directa, la regla de tres inversa y la regla de tres compuesta. Estos contenidos aparecen seguidos de, entre otros, canjes, interés, la regla de sociedades (reparto de beneficios), fracciones simples, fracciones decimales y progresiones aritméticas y geométricas. Un segundo cuaderno -escrito al parecer el mismo año y dedicado a un conjunto análogo de temas- vuelve a comenzar con la regla de tres y termina con progresiones y duodecimales. Estos dos libros parecen consecutivos, ya que el propio Robert los etiquetó como Vol. I y Vol. II; no está claro por qué trabajó dos veces materias similares.
Muchos de los ejemplos que utilizó proceden de Walkingame; este, por ejemplo, es uno de los dos únicos problemas sobre permutaciones (el otro trata sobre la cantidad de variaciones que se pueden lograr al hacer sonar 12 campanas):
Un joven que llegó a la ciudad para una buena biblioteca hizo un trato con la persona que lo hospedaba. Le pagaría 40 libras por la comida y el alojamiento durante todo el tiempo que consiguiera sentar a la familia (compuesta por 6 personas aparte de él) en distintos lugares de la mesa a la hora de comer. ¿Cuánto tiempo conseguirá quedarse por 40 libras?
Robert escribió la solución correcta (1×2×3×4×5×6×7 = 5040 días) inmediatamente después de la pregunta, pero a continuación, siguiendo a Walkingame a rajatabla en este punto, pasó sin más a las fracciones simples.
Entre los dos libros de aritmética de Robert del año 1832 hay casi 900 páginas; además, llenó casi 500 páginas más de un tercer cuaderno titulado «Geometría trigonometría medición y agrimensura», que contiene algunos de los esbozos bellamente dibujados y pintados que parecían fomentarse en Greenrow (véase la figura 5).

Figura 5. Un problema de trigonometría ilustrado y resuelto por Robert Smith, Academia Greenrow, 1832.
El siguiente libro, con la portada «Aritmética de Robert Smith Green-Row 1833» trata de «Cuestiones Prácticas sobre reglas comunes». Son especialmente interesantes las preguntas que se conocen como «recibos de partidas», porque los alumnos solían reemplazar los nombres y fechas de Walkingame por los suyos propios. Así, el comienzo del primer recibo de Robert dice:
Green Row 13 de julio de 1832
Sr. Thos Nash
Compra de Robert S Smith
8 pares de medias de estambre a 4 chelines y 6 peniques el par, hacen un total de 1 libra, 16 chelines y 0 peniques
5 pares de medias de hilo a 3 chelines y 2 peniques cada par, hacen un total de 15 chelines y 10 peniques
Otras fechas que figuran en otros recibos son de julio y de agosto de 1832, lo que sugiere que seguramente Robert escribió este libro a lo largo de 1832, y que no lo empezó, sino que lo terminó de escribir en 1833, la fecha de la primera página. El nombre de Thomas Nash aparece en otro lugar al final del primer libro de Robert, junto con el de Robert Reid, lo que insta a pensar que pudieron ser sus profesores; Robert Reid vuelve a figurar aquí debiendo
18 yardas de lazo fino a 0 libras 12 chelines y 3 peniques por yarda, hacen un total de 11 libras 0 chelines y 6 peniques 5 pares de guantes de piel fina a 2 chelines y 3 peniques el par, hacen un total de 11 chelines y 3 peniques
y así sucesivamente.
El segundo libro completado en 1833 trataba sobre «Medición de sólidos». Incluye sofisticados cálculos de volúmenes y áreas de superficie de los cinco sólidos regulares (tetraedro, cubo, octaedro, dodecaedro, icosaedro), pero también cálculos habituales de albañiles, canteros, carpinteros, pizarreros, pintores, vidrieros, plomeros y otros, con las unidades adecuadas en cada caso. Robert aprendió que los pintores, por ejemplo, calculan las superficies de «revestimiento, puertas, contraventanas» en yardas cuadradas, pero que «siempre hay que restar los huecos de chimenea y otros vanos».
Las niñas
He dudado si insertar un apartado dedicado a un grupo de personas que conforma la mitad de la humanidad como si fuera una minoría, pero es imposible eludir la realidad de que durante la mayoría de la historia, en la mayoría de las sociedades no se consideró necesario, o ni siquiera apropiado, instruir a las niñas y, desde luego, no en materias como las matemáticas u otras de carácter científico. Por consiguiente, no es raro que haya habido muy pocas mujeres matemáticas notables, de la misma manera que apenas ha habido mujeres escritoras, juristas o doctoras. Esta circunstancia tuvo que frustrar de algún modo a muchos miles de mujeres inteligentes. No obstante, de tanto en tanto hubo alguna que tuvo la oportunidad -o se la creó por sí misma- de aprender matemáticas.
Algunas de esas mujeres fueron aquellas con suficiente dinero o esparcimiento como para entregarse al estudio de lo que quisieran. Un ejemplo temprano lo encarnó la emperatriz china Déng, ![]() , quien al final del siglo i d. C. recibió lecciones de suán shù.. Pero lo que resulta más curioso, por lo inusual en la época, es que su maestra también fue una mujer llamada Bán Zháo,
, quien al final del siglo i d. C. recibió lecciones de suán shù.. Pero lo que resulta más curioso, por lo inusual en la época, es que su maestra también fue una mujer llamada Bán Zháo, ![]() . Mucho más tarde, en la década de 1640, la princesa Isabel de Bohemia y la reina Cristina de Suecia recibieron enseñanzas de Descartes, aunque tal vez les interesara más su filosofía que sus matemáticas. Un siglo después, el matemático más prolífico de Europa, Leonhard Euler, escribió más de 200 cartas sobre cuestiones matemáticas y científicas a la princesa de Anhalt-Dessau, sobrina de Federico el Grande de Prusia. Las cartas, publicadas en francés, ruso y alemán, y más tarde también en inglés, se siguen publicando en la actualidad.
. Mucho más tarde, en la década de 1640, la princesa Isabel de Bohemia y la reina Cristina de Suecia recibieron enseñanzas de Descartes, aunque tal vez les interesara más su filosofía que sus matemáticas. Un siglo después, el matemático más prolífico de Europa, Leonhard Euler, escribió más de 200 cartas sobre cuestiones matemáticas y científicas a la princesa de Anhalt-Dessau, sobrina de Federico el Grande de Prusia. Las cartas, publicadas en francés, ruso y alemán, y más tarde también en inglés, se siguen publicando en la actualidad.
Sin embargo, la vía de acceso a las matemáticas más habitual entre las mujeres corrientes eran las enseñanzas del padre, el marido o un hermano. En el siglo XIX a. C., por ejemplo, hubo dos mujeres escribas en la ciudad babilónica de Sippur, las hermanas Inana-amaga y Nig-Nanna. Parece más que probable que aprendieran la profesión de su padre, Abba-tábum, que también era escriba. Dos milenios después, la emperatriz Déng y sus hermanos recibieron su primera instrucción de su padre, aunque al parecer su madre lo consideraba una pérdida de tiempo para una niña. La profesora que tuvo la emperatriz Déng más adelante, Bán Zháo, era hermana del erudito Bán Gil, ![]() , cuya obra conocía ella lo bastante bien como para acabarla después de la muerte de aquel, incluido un tratado de astrología.
, cuya obra conocía ella lo bastante bien como para acabarla después de la muerte de aquel, incluido un tratado de astrología.
Tal vez la pareja de padre e hija más conocida de las matemáticas sea la formada por Teón e Hipatia a finales del siglo IV en Alejandría; sin embargo, no conservamos escritos de la propia Hipatia, solo relatos indirectos sobre su vida y su muerte, alrededor de la cual se ha acumulado mucha leyenda.
La instrucción de las niñas dentro de la familia continuó hasta comienzos de la era moderna. John Aubrey, quien escribió en la década de 1670 sobre su fallecido amigo Edward Davenant, vicario de Gillingham en Dorset, señaló su amor por las matemáticas, aunque «al ser un hombre santo era reacio a publicar, porque el mundo no debía saber a qué dedicaba la mayor parte de su tiempo». Davenant había enseñado álgebra no solo a Aubrey, sino también a sus propias hijas:
Siempre estaba dispuesto a enseñar y formar. Me hizo el favor de ser el primero en instruirme en álgebra. Sus hijas también eran algebristas.
Sabemos que Edward Davenant enseñó álgebra a su hija mayor, Anne, porque en 1659 Aubrey, ávido recopilador de todos los asuntos humanos, copió los contenidos del cuaderno de la chica. Anne nació antes de 1632 (año de nacimiento de su hermana pequeña Katherine) y contrajo matrimonio con Anthony Ettrick en 1650, así que probablemente aprendió álgebra a principios de la década de 1640. La copia que realizó Aubrey de aquel cuaderno comienza con
Transcribí este álgebra a partir del anuario manuscrito de la señora Anne Ettrick, la hija mayor del doctor Davenant, logista excelente.
Los problemas más antiguos del cuaderno de Anne, y el latín en el que ella los escribió, son los habituales de un joven principiante. En uno de ellos, por ejemplo, varias niñas pasean cuando se les acerca un joven y les dice en latín: «Saludos, doce doncellas». A lo que una de las muchachas responde de inmediato (y también en latín): «Multiplicadas por cinco superamos la cifra de doce en la misma cantidad que ahora no llegamos a ella». Pregunta para el lector: «¿Cuántas muchachas eran?». Varias páginas después vemos que Anne trabaja un problema cuya forma y solución había planteado ya al-Juarismi en Bagdad ocho siglos antes: qué número multiplicado por 6 y sumado a 16 da como resultado su propio cuadrado (en notación moderna se escribiría 6x + 16 = x2). Por último, hacia el final del cuaderno, tanto el latín como las matemáticas se vuelven más maduros. El penúltimo problema procede directamente de la Aritmética de Diofante: divide 370 en dos cubos cuyas raíces cuadradas sean números enteros que sumados den 10. Tal como consiguió resolver Anne, la respuesta correcta es 73 + 33. En este caso los números se escogieron con la intención de que arrojaran una solución sencilla, pero el problema se torna imposible si se reemplaza 370 por un cubo perfecto tal como acababa de descubrir Fermat, en esa misma época, pero lejos de allí, en Toulouse.
Bien entrado el siglo XVIII, las niñas solo tenían posibilidad de recibir instrucción matemática si, como la emperatriz Déng o Anne Davenant, gozaban del privilegio de tener un elevado nivel social o unos padres comprensivos.
Sophie Germain, una de las personas decisivas para avanzar en la resolución del último teorema de Fermat, disfrutó de ambas cosas. Nació en una familia adinerada y culta de París en 1776, y tenía solo 13 años cuando estalló la Revolución francesa. Confinada en su casa, se entretenía en la biblioteca de su padre, donde descubrió las matemáticas, una disciplina que sus padres en un principio no consideraban adecuada para ella, aunque más tarde transigieron en vista de su determinación. A los 18 años consiguió hacerse con apuntes de la recién inaugurada École Polytechnique y, aunque no le permitían asistir a las clases, presentó trabajos bajo el seudónimo de «Monsieur le Blanc» a uno de los mejores profesores de la École, Joseph-Louis Lagrange. Cuatro años después mantuvo correspondencia con otro grande de las matemáticas alemanas, Carl Friedrich Gauss, también bajo el mismo seudónimo. A ambos, a Lagrange y Gauss, los honra que siguieran admirando sus matemáticas y su fortaleza incluso después de descubrir su verdadera identidad.
Sophie luchó contra los elementos durante la mayor parte de su vida; nunca recibió la formación que habría tenido cualquier niño varón con su mismo talento, y su trabajo se vio arruinado a menudo por estar incompleto o por adolecer de errores. Jamás obtuvo un título oficial. Y, sin embargo, tras su muerte en 1831, Gauss señaló que merecía un título honorario de Gotinga, por entonces uno de los centros matemáticos más importantes de Europa.
Los artículos o carteles sobre «mujeres en las matemáticas» siempre incluyen a Hipatia y Sophie Germain, por desgracia no porque fueran típicas de su tiempo y lugar, sino justamente porque no lo fueron. Las mujeres olvidadas, como Bán Zháo o Anne Davenant son, en general, mucho más representativas de la relación que mantuvieron las mujeres con las matemáticas y con la formación matemática.
En el siglo XIX, la situación de las niñas en Europa occidental mejoró poco a poco, hasta que empezaron a beneficiarse en mayor número de la educación escolar básica. Los cuadernos de copia de niñas son minoritarios en la recopilación de Hersee, pero los pocos que hay tienen gran valor para conocer qué tipo de matemáticas se enseñaba a las niñas en diversos colegios de Inglaterra y Gales.
En 1831, el año anterior a que Robert Smith empezara a escribir los libros ya mencionados en Greenrow, Eleanor Alexander trabajó la reducción («Convierte a farthings[2] la cantidad de 30 libras con 1 chelín y 1/4») y la regla de tres («Si 7 yardas de paño cuestan 3 libras con 10 chelines, ¿cuánto costarán 65 yardas?») en la Escuela Fairwater, sita en un valle al norte de Newport en Gales del Sur. Todo su cuaderno de copia, formado por 127 páginas, consiste tan solo en estos dos tipos de ejercicios
Tres años después, a comienzos del otoño de 1834, Ann Weetman, en Appleton-le-Moors, cerca de York, empezó a trabajar la obra The Tutors Assistant, de Walkingame (véase la figura 6). Sus primeros ejercicios están fechados, así que sabemos que dedicó unos diez días a las sumas simples, pero un mes entero a la multiplicación. Después de Navidad trabajó en sumas compuestas (de dinero, de medidas de telas, de medidas de tierras, de medidas de cerveza, etcétera) y a finales de marzo llegó a los «recibos de partidas».

Figura 6. Primera página del libro de ejercicios de Ann Weetman, fechada el -0 de octubre de 1834 (Oct 20th 1834).
En su caso, los 8 pares de medias de estambre eran para la señora de Wm G. Atkinson (¿su profesora?), mientras que el señor Henry Weetman (¿su padre?, ¿su hermano?) compraba 15 yardas de satén.
En abril de 1837 había superado la «práctica», un método basado en el conocimiento de las fracciones de pesos y medidas estándar (véase la figura 7).
Su libro termina, tras 250 páginas, el 10 de mayo de 1837, momento en que había trabajado el manual de Walkingame hasta llegar al interés compuesto.

Figura 7. Una de las últimas páginas del libro de ejercicios de Ann Weetman, fechada el 12 de abril de 1837.
En total, fueron tres años, bastante menos de lo que había completado Robert Smith en unos pocos meses, aunque sigue siendo una cantidad de matemáticas muy respetable.
Veinte años después, Elisabeth Attersall, de Stainfield, en Lincolnshire, también trabajó el manual de Walkingame, desde la suma compuesta hasta la regla de tres («Si pagaste 1 libra, 1 chelín y 8 peniques por 3 libras de café, ¿cuánto tendrás que pagar por 29 libras y 4 onzas?»). En su caso, los 8 pares de medias de estambre fueron para la señora Chappell el 22 de octubre de 1850.
En cambio, la señorita I. Norman siguió un régimen ligeramente distinto en 1861 en la Dorset Street Academy del señor Ingleson en Hulme, Manchester. Su libro de copia llevaba impreso el nombre de la escuela sobre papel azul claro con márgenes señalados mediante dobles líneas rojas. En la primera página, la señorita Norman escribió «Aritmética progresiva», pero, por desgracia, no llegó muy lejos: cada una de las 60 páginas del libro está llena de multiplicaciones o divisiones de libras, chelines y peniques («¿Cuánto pagaré por 4767 yardas de tela a 7 8/9 peniques por yarda?»).
Elizabeth Dawson, en la Escuela Carshield de Northumberland, trabajó mucho un año más tarde en la regla de tres y mucho más aún en la Práctica; para hallar «el valor de 7234 yardas a 6 chelines y 8 peniques cada una», por ejemplo, usaba un dato conocido por todos los escolares británicos antes de 1971, que 6 chelines y 8 peniques eran 1/3 libras. Mucho menos sencillo para ella era, sin embargo, hallar el precio de 65 pies y 3 + 1/4 pulgadas a 3 chelines y 7 + 3/4 peniques por pie.
Desde abril de 1866, Isabella Lund, alumna de la Escuela de Gramática de Bolton-le-Sands en Lancashire (fundada en un principio exclusivamente para niños), solo tardó algo más de un año en progresar desde las sumas simples hasta la regla de tres.
Un año después, la señorita G. Jones, en la Escuela de Gramática Femenina de Ribston Hall, en Gloucester, fue rellenando poco a poco 20 páginas de recibos o facturas; sus 8 pares de medias de estambre fueron para una tal señora Jenkins en julio de 1868.
Los libros de copia de las niñas que acabamos de mencionar son algunos de los que se conservan con el nombre de su autora, la escuela y la fecha; sin un análisis más detenido no se puede concluir que sean representativos. Sin embargo, sí apuntan a que la enseñanza matemática de las niñas se centraba sobre todo en cuestiones prácticas (nada de Euclides aquí); es más, comparado con la enseñanza actual, el ritmo de su aprendizaje parece haber sido desesperantemente lento y repetitivo. Aún así, las niñas que escribieron esos cuadernos fueron alfabetizadas y aprendieron de números, nada que ver con las generaciones de mujeres que las precedieron.
No obstante, el tránsito de una instrucción básica en matemáticas a una formación universitaria requería una fuerza de voluntad especialmente acusada. Acabaremos este apartado comparando dos mujeres que lograron llegar a lo más alto dentro de los sistemas educativos de sus países respectivos. Flora Philip en Escocia y Florentia Fountoukli en Grecia.
Flora Philip fue una de las primeras mujeres que se graduó en la Universidad de Edimburgo, en 1893, aunque para entonces ya llevaba siete años perteneciendo a la Sociedad Matemática de Edimburgo. De hecho, había conseguido la mayor parte de sus conocimientos matemáticos, no en la universidad, sino a través de la Asociación de Edimburgo para la Formación Universitaria de las Mujeres, que se había fundado en 1867 para ofrecer a las mujeres una formación más allá del nivel escolar, en paralelo a la que ofrecía la universidad a los hombres. Las matemáticas se incluyeron desde bien pronto en los cursos de la Asociación, aunque no sin cierta oposición por parte de quienes las consideraban «absolutamente ajenas al pensamiento de una dama». El objetivo consistía en enseñar las mismas matemáticas que se impartían en la universidad pero, como muchas de las mujeres tenían una formación escolar deficiente, nunca alcanzaban un nivel tan alto como el de los cursos de la universidad. Aun así, enseñaban geometría euclídea, álgebra, trigonometría y secciones cónicas. La cantidad de mujeres que asistía a los cursos solía ser muy baja, pero, tal como señaló una de las asistentes, «el celo y la aplicación de la clase compensa doblemente su reducido número». Más tarde se introdujo un curso superior más avanzado, que Flora Philip completó con éxito en 1886, el año que ingresó en la Sociedad Matemática de Edimburgo. Para cuando consiguió graduarse en la universidad, en 1893, ya llevaba un tiempo enseñando en la Escuela Femenina de St. George, una escuela fundada por la Asociación. Sin embargo, aquel mismo año se casó, y a partir de entonces se retiró tanto de la vida académica como de la Sociedad Matemática de Edimburgo.
La carrera de Florentia Fountoukli, nacida en 1869 en Atenas, transcurrió paralela a la de Flora en muchos sentidos. Mientras Flora estudiaba matemáticas con la Asociación de Edimburgo en la década de 1880, Florentia Fountoukli se estaba sacando el diploma de maestra de escuela en la Escuela Normal Arsakeion para niñas de Atenas. Tras obtenerlo, la junta directiva de las Escuelas Arsakeion le concedió financiación para estudiar pedagogía en Berlín durante un año. A continuación solicitó una ampliación para titularse en Zúrich en matemáticas, pero la junta la desestimó. (Su hermano Michael, en cambio, sí se hizo matemático y trabajó más tarde en Hamburgo). Florentia volvió a enseñar en la Escuela Arsakeion de Corfú, durante los mismos años que Flora enseñaba en St. George. En 1892, justo cuando Flora se matriculó en la Universidad de Edimburgo, Florentia se matriculó en el departamento de matemáticas de la Universidad de Atenas y fue la primera mujer en hacerlo. Sin embargo, a diferencia de Flora, ella no parece haberse graduado, sino que siguió enseñando en una escuela femenina de Atenas que fundó y regentó junto con su amiga Irene Prinari. En 1899 empezó a firmar como Fountoukli-Spinelli, lo que sugiere que pudo contraer matrimonio con Loudovikos Spinelli, otro profesor, pero no hay datos claros. Por desgracia, a finales de la década de 1890, antes de que llegara a cumplir los 30, comenzó a sufrir problemas de salud y se marchó a vivir a Italia, donde falleció en 1915.
Tanto Flora como Florentia tuvieron que luchar para recibir la formación que deseaban. No obstante, las universidades de Edimburgo y Atenas se adelantaron a muchas otras. La Universidad de Cambridge no admitió mujeres como miembros de pleno derecho hasta 1947.
Autodidactas
Hasta hace dos siglos, solo un número reducido de niñas recibía algún tipo de formación matemática en cualquier lugar del mundo. Pero incluso en el caso de los niños, la enseñanza obligatoria de las matemáticas ha sido un fenómeno bastante reciente. Tal como vimos con Wallis y Pepys, en la Inglaterra del siglo XVII era posible superar toda la formación escolar y universitaria sin apenas aprender matemáticas. Así que, quienes tenían un talento o un interés especial por la materia, fueron en gran medida y en su mayoría autodidactas. Fue el caso de Fermat, quien aprendió algunas de las matemáticas más avanzadas de su tiempo con libros del padre de su amigo Etienne d’Espagnet en Burdeos. También fue el caso de Newton, uno de los matemáticos más sobresalientes del siglo XVII. Es posible que Newton aprendiera algunas matemáticas elementales en la escuela de gramática de Grantham, en Lincolnshire, pero aprendió mucho más de Sus propias lecturas mientras permaneció en Cambridge en la década de 1660. Muchos años después contó a un amigo cómo había leído la Geometría de Descartes, que había vuelto a publicarse en latín unos años antes. Mucha gente reconocerá las dificultades de leer un extraño texto nuevo sobre matemáticas; pero tal vez menos gente haya igualado la tenacidad y perseverancia propia de Newton.
Compró la Geometría de Descartes y la leyó por su cuenta. Cuando llevaba 2 o 3 páginas no logró entender nada más, así que volvió a empezar y llegó 3 o 4 páginas más allá, hasta que se topó con otro punto difícil, así que volvió a empezar y avanzó algo más, y siguió procediendo de este modo hasta dominarla en su totalidad.
Por los manuscritos que se han conservado de Newton, sabemos que actuó de manera similar con otros textos contemporáneos, y que trabajó con el material que encontraba en ellos para desarrollar unas matemáticas mucho más avanzadas que las de cualquiera de sus predecesores.
En el siglo XVII y parte del XVIII, una persona lo bastante motivada aún podía leer y entender casi todo el conjunto de la bibliografía matemática que había en circulación. Incluso a comienzos del siglo XIX, Sophie Germain consiguió aprender por sí sola algunas de las matemáticas más avanzadas de su tiempo, pero perteneció casi a la última generación con posibilidades de lograrlo. En el siglo XX esto apenas era viable, salvo, tal vez, en el caso de prodigios con una intuición matemática muy excepcional, como el matemático autodidacta indio Ramanujan. Es indudable que Andrew Wiles no aprendió solo; superó los numerosos años de formación reglada que se necesitan en la actualidad para iniciar incluso a los mejor dotados en algunos de los problemas, técnicas y convenciones de la disciplina. Hace mucho tiempo que quedaron atrás los días de las matemáticas «de aficionados», en los que casi cualquiera podía atreverse con un problema de vanguardia, como el último teorema de Fermat.
Sin embargo, de cuando en cuando los escritores siguen inventando relatos ficticios de individuos que, a partir de los escritos de otra persona, consiguen aprender matemáticas lo bastante bien como para entender y ampliar la obra de aquella. Una de esas historias es la de Mrs Einstein («La señora Einstein»), de Anna McGrail, y otra más reciente es la obra de teatro Lo prueba (Proof), de David Auburn. En ambos casos, las protagonistas son hijas de matemáticos (un tema que ya hemos visto en la vida real) que consiguen formarse solas hasta los altísimos niveles de la obra de sus padres. Por desgracia, la realidad de las matemáticas modernas es que esas hazañas son hoy extremadamente improbables.
¿Para qué aprender matemáticas?
Dada la enorme cantidad de energía humana empleada a lo largo de los siglos para enseñar o aprender matemáticas, parece un tanto perverso preguntarse «¿para qué?». Sin embargo, las respuestas a este interrogante han cambiado mucho con el paso del tiempo. Los textos sumerios del segundo milenio antes de Cristo dejan claro que el aprendizaje de las letras y los números era esencial para la justa administración de la sociedad, aunque los niños que ocupaban los incómodos bancos del patio de la Casa F pudieran percibirlo como un ideal algo lejano.
Dos mil años después, niños de edades similares formados en las escuelas de ábaco de la Italia del siglo XIII aprendían, como sus homólogos babilónicos precedentes, a manejar números, pesos y medidas, pero por razones distintas: no para el bien de la sociedad en su conjunto, sino para que estuvieran mejor preparados como individuos y desempeñar correctamente las tareas comerciales que estaban destinados a realizar. La importancia de las competencias matemáticas para el individuo se aprecia de nuevo en el prefacio de la obra The Pathway to Knowledg de Robert Recorde, donde figura una larga lista de oficios y trabajos específicos que requieren un conocimiento de la geometría.
En los textos de Recorde, sin embargo, también se vislumbra otra razón para estudiar matemáticas: aguzar el intelecto. Recorde no fue el primero en apuntar esto: algunos acertijos matemáticos atribuidos a Alcuino de York, en el siglo VII, se titularon «Propuestas de Alcuino para aguzar la juventud» (Propositiones Alcuiní ad acuendos jovenes).
La idea de que las matemáticas debían aprenderse, como el latín o el griego, para potenciar el intelecto ha perdurado desde entonces. Después de todo, es muy probable que la mayoría de la población dominara al final de la infancia las matemáticas necesarias para la vida cotidiana, en esencia medir el tiempo y contar. Pocos adultos necesitan alguna vez usar el teorema de Pitágoras, resolver ecuaciones de segundo grado o biseccionar un ángulo, pero a casi todos nos lo han enseñado alguna vez. Se podría decir (y yo lo diría) que aprender un idioma extranjero o estudiar historia también sirven para fomentar la memoria, el razonamiento y el análisis, pero estas materias nunca han alcanzado el prestigio de las matemáticas, y en la actualidad son asignaturas optativas, y no obligatorias, en el currículo escolar británico.
Tal vez sea la mera longevidad de las matemáticas lo que las ha convertido en una parte integral de la formación de cualquier niño o niña actual. Aunque también es verdad que quienes hayan de progresar hasta alcanzar los límites de la disciplina deberán, cual jóvenes músicos, empezar pronto y practicar con regularidad.
Capítulo 5
Las matemáticas como medio de vida
Cualquier matemático que aspire a explorar territorios nuevos necesita tiempo para pensar y garabatear signos, además de algún tipo de apoyo financiero. Volvamos por un momento a quienes nos encontramos en el primer capítulo.
No tenemos ni idea de cómo se ganaba la vida Diofante; tal vez, igual que muchos con dotes matemáticas, ejerciera la docencia. Muchos de los matemáticos más conocidos del siglo anterior a Fermat también enseñaron matemáticas, pero a menudo tan solo como ocupación secundaria: Girolamo Cardano y Robert Recorde eran médicos, aunque Recorde también trabajó durante gran parte de su vida en la administración de la Real Casa de la Moneda y de Minas; tanto Rafael Bombelli como Simón Stevin estuvieron empleados en proyectos de ingeniería; François Viète, al igual que Fermat, era jurista y consejero; Fermat se ha descrito a menudo como matemático «aficionado», pero vivió en una época en la que había tan pocos profesionales, que el concepto de aficionado carecía de sentido. Wiles, por el contrario, solo se puede calificar como profesional absolutamente reconocido y pagado por trabajar a tiempo completo en la investigación y la enseñanza de las matemáticas.
A lo largo de los siglos han cambiado mucho las ocupaciones desempeñadas por los matemáticos. Es muy probable que un matemático moderno trabaje en la docencia, las finanzas o la industria, actividades todas ellas organizadas desde las instituciones. También puede haber alguien dispuesto a pagar por recibir conocimientos matemáticos quizá para instruirse o para aprender contabilidad, pero solo dan trabajo a un número reducido de personas.
En el primer milenio de nuestra era, el panorama era muy distinto. El poder económico y político en la mayoría de Europa y Asia estaba concentrado en manos de reyes, obispos, califas y mandatarios. Quienes querían vivir de sus dotes intelectuales, incluidas las matemáticas, procuraban ponerse al servicio de un patrón lo bastante poderoso para mantenerlos y protegerlos. Se trataba de un mecenazgo que podía adoptar diversas formas. En este capítulo veremos, en primer lugar, cómo se desarrolló en la vida de tres eruditos de los siglos x y xi en las tierras dominadas entonces por el islam.
Tipos de mecenazgo
Thabit ibn Qurrá nació en el año 826 d. C. en la ciudad de Harrán, muy cerca de la actual frontera entre Turquía y Siria, y pasó los primeros años de su vida allí como cambista de moneda. No era musulmán, sino que pertenecía a la secta local de los sabianos. Tan solo unos años antes, el califa abasí al-Mamún había fundado en Bagdad la biblioteca conocida como Bayt al-Hikmah (‘Casa de la sabiduría’) con el objeto de preservar y traducir al árabe textos en griego, sánscrito o persa. Los conocimientos de griego y árabe de Ibn Qurrá -junto con el dominio que tenía del sirio, su lengua materna- llamaron la atención del matemático Muham- mad ibn Musa de Bagdad, cuando pasó por la ciudad de Harrán a su regreso de Bizancio. Por desgracia, desconocemos la fecha de aquel encuentro, pero podemos suponer que Ibn Qurrá era aún bastante joven, puesto que, tras la invitación de Ibn Musa, se trasladó a Bagdad, donde aprendió matemáticas y astronomía con Ibn Musa y sus dos hermanos (conocidos por el nombre colectivo de Banu Musa).
En los años siguientes, Ibn Qurrá se convirtió en uno de los sabios más respetados de Bagdad. Escribió sobre medicina, filosofía y religión, pero en la actualidad se lo recuerda sobre todo por sus trabajos de matemáticas y astronomía. Tradujo al árabe varios tratados de Arquímedes, y escribió mucho sobre temas que también habían interesado a Arquímedes, como mecánica y problemas relacionados con áreas, superficies o volúmenes de figuras curvas. También comentó el Almagesto de Tolomeo y escribió sobre geometría esférica y astronomía, en especial sobre el movimiento y la altura aparente del Sol, y el movimiento de la Luna y los cinco planetas conocidos entonces. Asimismo estudió con detenimiento los Elementos de Euclides; su intento de demostración de uno de los postulados de Euclides, el de las líneas paralelas, se volvió a usar en Oxford en el siglo XVII. Ibn Qurrá también desarrolló sus propias demostraciones del teorema de Pitágoras, una de las cuales se muestra en la figura 8.
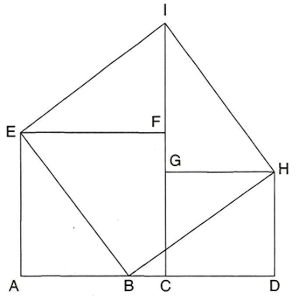
Figura 8. Demostración del teorema de Pitágoras del sabio Thabit ibn Qurrá: un sencillo razonamiento de recorta-y-pega evidencia que IHBE = EFCA + GHDC.
Ibn Qurrá permaneció en Bagdad hasta su fallecimiento en el año 901. Mantuvo su unión con los hermanos Banu Musa durante muchos años y enseñó a los hijos de Ibn Musa. Durante los diez últimos años de su vida, se convirtió en un asiduo de la corte del califa al-Mu’tadid; era tal su cercanía al mandatario que, según un apunte biográfico del escritor del siglo XII al-Qifti, estaba autorizado a «sentarse en su presencia siempre que quisiera». Con posterioridad también su hijo Sinan y dos de sus nietos fueron eruditos muy conocidos.
En lo que sabemos de la vida de Ibn Qurrá podemos diferenciar dos rasgos cruciales. Uno es una red de enseñanza y aprendizaje urdida entre amigos y familias que, en este caso, unió a miembros de la familia de Ibn Musa con los de
la familia de Ibn Qurrá. A lo largo de este libro ya hemos encontrado relaciones personales tan estrechas en varias ocasiones. La segunda característica, más específica del tiempo y el lugar de Ibn Qurrá, es la protección y el mecenazgo que halló primero de Banu Musa, y más tarde del mismísimo califa.
Otro erudito fue Abü ‘r-Raihán Muhammad ibn Ahmad al-Birünl, generalmente conocido como al-Biruni y nacido setenta años después de la muerte de Ibn Qurrá en un extremo más apartado de los territorios islámicos y en un mundo menos estable.
Su ciudad natal, a orillas del río Amu Daría, se encuentra dentro del actual Uzbekistán, y hoy en día lleva el nombre de Biruni. Fue instruido por el matemático y astrónomo Abu Nasr Mansur, con quien siguió trabajando más tarde en su vida. De joven ya usó observaciones solares para calcular latitudes de ciudades locales, pero su actividad se vio interrumpida por el estallido de una guerra civil en 995 que lo obligó a huir. Sabemos algo sobre los grandes desplazamientos que realizó durante los treinta años siguientes a partir de sus precisas observaciones de eclipses. En ocasiones trabajó en la región situada al sur del mar Caspio, cerca de la actual Teherán, donde es conocido por haber dedicado un texto sobre cronología al mandatario ziyarí de la región, Qabus. En otros momentos residió en su región natal, al principio bajo la protección del emir samánida Mansur II, y después, a lo largo de catorce años, bajo la de Abu 1-Abbas Mamun.
Este último periodo de relativa estabilidad concluyó en el año 1017, con la invasión de la región por parte de la dinastía gaznávida, con base en lo que ahora es el oeste de Afganistán. Al parecer, al-Biruni cayó prisionero y después vivió
muchos años cerca de Kabul o en la propia capital, Gazni, unos 100 kilómetros al sur. Su relación con el sultán Mahmud no está clara: se quejó del mal trato recibido, pero más tarde sufragó algunos de sus estudios. También logró viajar al norte de la India, que había caído igualmente bajo el dominio gaznávida, y escribió mucho sobre la región y su religión, sus costumbres y su geografía. Tras la muerte de Mahmud en 1030, al-Biruni quedó a las órdenes de Masud, hijo de Mahmud, y bajo el mandato de un tercero, Mawduder, hijo de Masud, tras el asesinato de este en 1040. Al-Biruni murió en Gazni en 1050.
A lo largo de una vida azotada por sucesivos cambios dinásticos, al-Biruni fue un erudito entregado y un autor prolífico. Alrededor de la mitad de sus obras versó sobre astronomía y astrología, y el resto trata sobre matemáticas, geografía, medicina, historia y literatura. Por desgracia solo ha perdurado una parte de lo que escribió.
El tercer sabio matemático que consideraremos aquí es Ornar ibn Ibrahim Jayyam Nishapurí, más conocido en occidente como Omar Jayyam. Nació poco antes del fallecimiento de al-Biruni en Nishapur, en el noreste de la actual Irán. Su nombre apunta a que venía de una familia dedicada a la construcción de tiendas. Por entonces, esta región iraní estaba gobernada por los selyúcidas, una dinastía de origen turco. De joven, al-Jayyam viajó hacia el este hasta llegar a Samarcanda, donde escribió un importante tratado sobre ecuaciones que dedicó al cadí, Abu Taher. Más tarde pasó muchos años en Isfahán, donde, bajo la protección del sultán Malik Shah y de su visir Nizam al-Mulk, dirigió el observatorio y la recopilación de tablas astronómicas. Durante este mismo periodo escribió comentarios a la obra de Euclides, tal como había hecho Ibn Qurrá antes que él. Por desgracia, el observatorio se cerró en 1092, tras el asesinato de Nizam al-Mulk y la muerte de Malik Shah. Con el tiempo, después de varios cambios en el poder, al-Jayyam abandonó Isfahán. Tras pasar una temporada en Marv, situada casi a medio camino entre Isfahán y Samarcanda, acabó regresando a Nishapur, donde falleció en 1131.
No me resisto a incluir aquí una de sus Robaiyyat (Cuartetas) en una de sus traducciones más recientes [3]:
La eternidad: misterio que ignoramos tú y yo, acertijo que nunca tú y yo descifraremos.
Deciden nuestras vidas por detrás del telón; cuando caiga el telón, ni tú ni yo estaremos.
Estos tres casos simplificados no revelan todo lo que se podría decir sobre la práctica matemática bajo las dinastías islámicas medievales, pero al menos perfilan algunos detalles generales. Uno es que, así como unos pocos siglos antes los autores matemáticos griegos procedían de todas partes del Mediterráneo oriental menos de la propia Grecia, quienes escribieron textos matemáticos en árabe estuvieron dispersos por una región aún más vasta que abarcaba desde la actual Turquía hasta la actual Afganistán, pero no en Arabia en sí; por esta razón los historiadores prefieren considerarlos autores «islámicos» en lugar de «árabes», pero tal como revela el ejemplo de Ibn Qurrá, no todos eran musulmanes, ni sus textos matemáticos guardaron relación con sus creencias religiosas. Sin embargo, todos residieron en sociedades dominadas por las costumbres y la cultura islámicas, así que seguramente este calificativo sea mejor que cualquier otro.
Otro aspecto destacado es la precariedad de la sabiduría en un mundo con rápidos cambios de mandatarios y dinastías. El hecho de que un niño o un joven de talento viera reconocidas y favorecidas sus dotes matemáticas dependía ya entonces de la suerte y de las circunstancias, tal como ocurrió con Ibn Qurrá y al-Biruni. Por tanto, su capacidad para estudiar o viajar podía depender en gran medida del favor y la financiación de un dirigente cuyo propio futuro era muy incierto. Al-Biruni parece haber destacado especialmente en el disfrute o el mantenimiento del favor de los dirigentes de dinastías enemigas. A pesar de esas dificultades, la producción de algunos de estos sabios fue tanto prolífica como variada. Quienes escribían sobre astronomía y astrología también podían escribir sobre geometría esférica y trigonometría, o sobre los Elementos de Euclides o las obras de otros autores griegos, o sobre aritmética y álgebra, o sobre geografía, historia, música, filosofía, religión o literatura.
Por último, cabría preguntarse qué ganaba el protector con estas actuaciones. Cada caso difería mucho del resto; de hecho no existía ninguna palabra específica en las sociedades islámicas para nombrar la relación que hemos calificado aquí de mecenazgo. Como hemos visto ya en China y Europa, los mandatarios solían valorar a los expertos en matemáticas por su capacidad para calcular fechas propicias. En algunos casos también esperaban sacar un beneficio a largo plazo, incluso eterno, de su apoyo a las buenas obras: contar con los servicios y la compañía de prodigios intelectuales sería una fuente de satisfacción y una señal de prestigio.
Desde finales del siglo XII aproximadamente, los eruditos empezaron a ocupar con más frecuencia puestos remunerados en instituciones académicas sufragadas, las madrasas, que los hizo menos dependientes de los caprichos y preferencias de cada mandatario particular. Sin embargo, para estudiar más de cerca el paso del mecenazgo a la contratación profesional nos desplazaremos ahora a la Inglaterra de una época algo posterior.
Del mecenazgo a la profesionalización
Los cuarenta años transcurridos desde 1580 hasta 1620 fueron un periodo de transición en Inglaterra; aún existía el mecenazgo, pero al mismo tiempo empezaban a vislumbrarse los primeros signos de desplazamiento hacia puestos remunerados por la administración pública. Las trayectorias que siguieron Thomas Harriot, William Oughtred y Henry Briggs ilustran algunas de las posibilidades y oportunidades disponibles en Inglaterra en aquel momento para las dotes matemáticas.
Thomas Harriot, nacido en 1560, estudió en Oxford entre los años 1577 y, tal vez, 1580. No se tituló en matemáticas (no existía tal cosa), pero es posible que aprendiera algo sobre la materia de algunos tutores o a través de sus lecturas personales. Mejor documentado está su interés por la exploración y la navegación, interés que también parece haber adquirido en Oxford, seguramente en las clases del aventurero Richard Hakluyt. Durante la década de 1580, Harriot trabajó bajo el patrocinio de Walter Raleigh, por entonces muy interesado en las posibilidades de colonización en América. En 1585 Harriot zarpó hacia las costas de la actual Carolina del Norte en un viaje financiado por Raleigh, una expedición de un año que acabó en fracaso, pero que permitió a Harriot y a su amigo John White traer consigo gran cantidad de información valiosa y bellos dibujos de la gente, la flora y la fauna de la región. Por desgracia, también trajo una afición al tabaco que acabaría matándolo.
Antes del viaje, Raleigh había encargado a Harriot que enseñara navegación a los marineros, aunque, lamentablemente, el texto que escribió está perdido en la actualidad. A su regreso, siguió viviendo bajo el patrocinio de Raleigh, al principio en las haciendas que este poseía en Irlanda (otra aventura colonial), y más tarde en la casa que el propio Raleigh tenía en Londres, Durham House, a orillas del Támesis. Precisamente el tejado de Durham House fue el que usó Harriot para realizar sus primeros experimentos sobre caída de cuerpos, durante los cuales comparó lo que tardan en caer bolas de metal y bolas de cera. Harriot siguió al lado de Raleigh hasta el mismo día en que este fue ejecutado en 1618: se conservan algunos apuntes sobre las últimas palabras que pronunció Raleigh desde el patíbulo manuscritos por Harriot entre sus documentos personales y matemáticos.
A principios de la década de 1590 Harriot encontró un segundo patrón en Henry Percy, noveno conde de Northumberland. Harriot pasó los treinta años restantes de su vida en la casa que tenía Percy en Londres (Syon House, en Middlesex, a orillas del Támesis), o en su casa de campo (Petworth House, en Sussex). Por desgracia, ninguno de los mecenas de Harriot sorteó con éxito las tensiones políticas y religiosas del momento: Percy, igual que Raleigh, pasó muchos años encarcelado en la Torre de Londres. Aun así, le dio a Harriot un sueldo y la libertad de dedicarse a los estudios de su elección. Harriot nunca perdió su interés por los problemas de navegación marítima; también se interesó más tarde por la astronomía y, al mismo tiempo que Galileo, usó un telescopio para observar manchas en el Sol y los cráteres de la Lima. A través de uno de sus amigos de Oxford, Nathaniel Torporley, logró hacerse con las obras matemáticas de Viète (de gran influencia más tarde en Fermat), así que fue uno de los primeros de todo el mundo -y sin duda de Inglaterra- en valorar y ampliar algunas de las interesantes novedades matemáticas que se estaban desarrollando en Francia.
Harriot no publicó ninguno de sus hallazgos. Como contaba con un sueldo privado garantizado, no tuvo ninguna necesidad ni de demostrar nada ni de ganarse la vida de otro modo. Tampoco ejerció la docencia, aunque sí discutió sus ideas dentro de su círculo de amistades. En cierto modo, la obra de Harriot tuvo muy poca influencia inmediata; desde luego, no causó el revuelo intelectual que levantó Galileo más tarde. Por otra parte, su libertad para trabajar como quiso le permitió explorar gran cantidad de temas, algunos de ellos bastante difíciles, y desarrollar sus investigaciones hasta llegar a algunas conclusiones importantes. Hoy en día hablaríamos de una investigación ilimitada.
La obra de Harriot bien podría haberse perdido, pero por suerte fue tan conocido entre sus contemporáneos que sus papeles se conservaron después de su muerte en 1621, y algunas de las ideas que contenían siguieron circulando entre sus sucesores durante muchos años. En este aspecto puede decirse que Harriot alentó, aunque fuera indirectamente, tanto el debate matemático como el respeto por los estudios matemáticos y científicos que medio siglo después caracterizaron a la Royal Society recién fundada. De hecho, fue tanta la fama de Harriot que, durante sus diez primeros años de existencia, la Royal Society promovió más de una vez el estudio de los documentos que se conservaban de él.
Menos creativo que Harriot, pero en ciertos aspectos con la misma relevancia para el florecimiento ulterior de las matemáticas en Inglaterra, fue William Oughtred. Nacido en 1573, Oughtred solo era un poco más joven que Harriot, pero lo sobrevivió unos cuarenta años. Desde 1610 o antes, Oughtred fue clérigo de Albury en Surrey; no parece haberse movido más de allí con posterioridad salvo para visitas ocasionales a Londres. Adquirió prestigio como profesor de matemáticas, tanto para niños como para adultos.
Al igual que Harriot, también él encontró un mecenas aristócrata: Thomas Howard, conde de Arundel, cuya sede en West Horsley distaba tan solo unos pocos kilómetros de Albury. Oughtred instruyó al hijo de Howard, William, al igual que a los hijos de otros señores de la zona. A través de Howard también conoció a un pariente de la familia, sir Charles Cavendish, que con el tiempo acabó erigiéndose en una figura importante para las matemáticas inglesas de este periodo. Cavendish no era especialmente bueno en matemáticas, pero, por alguna razón, sentía fascinación por ellas y recopiló e intentó entender con avidez los libros y escritos más novedosos sobre la materia. Tras la muerte de Harriot, por ejemplo, copió apartados completos de los manuscritos de Harriot, a pesar de que, según admitía él mismo, «sospecho que no lo entiendo todo». Fue Cavendish quien llevó a Oughtred la obra de Viète desde Francia, igual que Torporley se la había llevado a Harriot.
También fue Cavendish quien animó a Oughtred a escribir su primer libro de texto, dedicado a su alumno de 14 años William Howard. La obra, publicada a comienzos del año 1631, acabó conociéndose por su título abreviado, Clavis mathematicae («La clave de las matemáticas»), y circuló una y otra vez, hasta editarse cinco veces en latín y dos veces traducida al inglés. El contenido era elemental, una introducción a la aritmética y el álgebra, pero por entonces los libros de texto escritos por Recorde tenían casi un siglo de antigüedad y había una necesidad desesperada de algo nuevo. Así, cuando se incorporaron profesores nuevos a la Universidad de Oxford tras los años de guerra civil, estos eran o bien alumnos o bien lectores de Oughtred, e introdujeron de inmediato el Clavis en Oxford, con lo que se convirtió en el primer libro de matemáticas que imprimió la universidad. Casi todos los matemáticos relevantes del siglo XVII, y muchos que no lo fueron, se iniciaron con el Clavis, entre ellos Christopher Wren, Robert Hooke e Isaac Newton. Así que, aunque Oughtred nunca realizó ninguna gran aportación personal a las matemáticas y solo enseñó a un nivel bastante elemental, favoreció de forma indirecta, al igual que Harriot, la difusión y el desarrollo de la pericia matemática en los albores de la Inglaterra moderna.
Con todo, ni Harriot ni Oughtred habrían podido hacer lo que hicieron sin contar con el respaldo de tres aristócratas que alentaron su trabajo: Henry Percy, Thomas Howard y Charles Cavendish; aunque un miembro posterior de la familia Cavendish dio nombre al Laboratorio Cavendish de Cambridge, pero las familias Percy y Howard no suelen relacionarse con la ciencia o las matemáticas, pero sin la convicción y el apoyo intelectual y financiero de estos tres hombres, la emergencia de una comunidad matemática significativa en Inglaterra durante la primera mitad del siglo XVII habría tardado mucho más en llegar.
Al mismo tiempo, y como contraste, no deberíamos pasar por alto ciertos logros contemporáneos adicionales. En el año 1597, el legado que dejó el comerciante y financiero Thomas Gresham pagó siete conferencias públicas (una para cada día de la semana) sobre astronomía, geometría, física (medicina), legislación, teología, retórica y música. La institución Gresham College (que ha perdurado hasta la actualidad y aún ofrece conferencias públicas) fue especialmente relevante para la consolidación de la comunidad matemática londinense; los encuentros celebrados después de las conferencias a lo largo de la década de 1650 favorecieron la creación de la Royal Society unos años más tarde. Veinte años después de la instauración de las conferencias en el Gresham College, Henry Savile fundó las cátedras de geometría y astronomía en Oxford. Durante muchos años hubo gran movilidad entre los cargos en Gresham y en Oxford. En concreto, el primer profesor de geometría de Gresham, Henry Briggs, se convirtió también en el primer titular de la Cátedra Saviliana de geometría en Oxford.
Briggs, procedente de Halifax, en Yorkshire, era casi de la misma edad que Harriot e ingresó en el St. Johns College de Cambridge en 1577, el mismo año que Harriot se inscribió en Oxford. Sin embargo, a diferencia de Harriot, siguió una carrera universitaria que lo llevó a enseñar en Cambridge primero medicina y más tarde matemáticas, hasta que se trasladó al Gresham College en 1597. Allí se quedó veinte años hasta que ocupó la Cátedra Saviliana de Oxford, donde permaneció hasta su muerte en 1630.
Briggs y Harriot forman una pareja fascinante; un gran misterio de la historia de las matemáticas de este periodo es si llegaron a conocerse alguna vez. Tendrían que haberlo hecho. Durante los años previos y posteriores a 1600, Briggs, igual que Harriot, se interesó mucho por problemas sobre navegación. En 1610, mientras Harriot observaba manchas solares, Briggs trabajó en eclipses. Cuando John Napier desveló su «maravilloso invento» de los logaritmos en 1614, ambos, Harriot y Briggs, se enteraron enseguida. Briggs viajó de inmediato a Escocia para visitar a Napier, y lo ayudó a desarrollar mejor su trabajo; Harriot había dejado de realizar grandes viajes ya, y empezaba a estar muy enfermo, pero hizo anotaciones sobre los logaritmos; es casi seguro que reparó en su relevancia para buena parte de su propio trabajo anterior.
Es inevitable pensar que con Harriot, como con Napier, Briggs habría podido entablar largas y fructíferas conversaciones. También es fácil que ocurriera, puesto que durante los veinte últimos años de la vida de Harriot no residieron muy lejos el uno del otro: Harriot en la Syon House, y Briggs cerca de Bishopsgate, a algo menos de un kilómetro de la Torre de Londres, donde Harriot visitaba con regularidad a Raleigh y Percy. Pero no hay ningún indicio de que coincidieran alguna vez; sus círculos de amistad y esferas de influencia eran muy diferentes: Briggs estaba contratado por una institución pública, mientras que Harriot trabajaba de manera privada en su propia casa. Un tratado de Briggs sobre «El paso del noroeste hacia el Mar del Sur a través del continente de Virginia», que sin duda habría interesado a Harriot, se publicó en 1622, un año después del fallecimiento de Harriot, y la Arithmetica logarithmica de Briggs no salió a la luz hasta 1624. Lo que sí se sabe es que durante la década de 1620, Briggs mantuvo contactos con Nathaniel Torporley, amigo de Harriot, y estaba al tanto de los intentos para publicar algunos de los apuntes de Harriot, pero él mismo murió en 1630, un año antes de la publicación póstuma de la Praxis de Harriot. Así que, en la imprenta, como en la vida, navegaron cerca sin llegar a abordarse.
Las vidas de Harriot y Briggs presentan un contraste pertinente entre las viejas costumbres del mecenazgo y la nueva vida de los matemáticos profesionales, con una remuneración acorde a unas obligaciones claras, sobre todo en el ámbito de la docencia. Esta última, por supuesto, sería la senda del futuro.
Instituciones, publicaciones y congresos
La vida de Joseph-Louis Lagrange, uno de los matemáticos más excelsos del siglo XVIII, resume algunas de las nuevas posibilidades que se abrieron ante los matemáticos de talento en Europa occidental 150 años después de las muertes de Briggs y Harriot.
Lagrange nació en 1736 en Turín, en el seno de una familia franco-italiana (su nombre de pila fue Giuseppe Lodovico Lagrangia). A los 17 años de edad descubrió su predilección por las matemáticas, y dos años después fue elegido para enseñar en la Real Escuela de Artillería de Turín. Lagrange aún vivía con su familia en su ciudad natal, pero su intelecto ya había empezado a viajar más lejos. Poco antes de aceptar el puesto docente, Lagrange había enviado parte de su obra a Leonhard Euler, director de matemáticas en la Real Academia de las Ciencias de Berlín. El envío adicional de misivas a Euler no tardó en dar como resultado la elección de Lagrange como miembro extranjero de la Academia. Al mismo tiempo, el propio Lagrange fundó en compañía de otros su propia sociedad científica en Turín, una de las muchas instituciones de este tipo que se crearon en las ciudades de Europa occidental durante la década de 1750 y predecesora de la actual Academia de Ciencias de Turín.
El florecimiento de las sociedades y academias científicas constituye uno de los rasgos definitorios de la historia intelectual del siglo XVIII. La Royal Society de Londres se había fundado en 1660, y la Academia de Ciencias de París, en 1699; las siguió la Academia Prusiana de las Ciencias en 1700 -reestructurada como Real Academia de las Ciencias de Berlín en 1740- y la Academia de las Ciencias de San Petersburgo, que se fundó siguiendo el modelo parisino en 1724. Estas instituciones ofrecían empleo a un número reducido de matemáticos y científicos, pero su influencia tuvo más relevancia porque sus encuentros regulares facilitaban un foro para la presentación y discusión de la investigación más puntera. Los artículos presentados durante esos encuentros se publicaban después en las actas o memorias de las academias; este proceso duraba algún tiempo, pero los volúmenes resultantes acababan circulando entre lectores de toda Europa, y a través de las páginas de las publicaciones de las academias se realizaban numerosos intercambios importantes. Lagrange publicó la mayoría de sus estudios tempranos en los Mélanges de Turin, la revista de su sociedad en Turín.
Además, la Academia de París también instauró una tradición de preguntas con premio que podían responderse en el plazo de dos años. Lagrange envió preguntas para los premios de 1764 (sobre por qué la Luna muestra siempre la misma cara) y de 1765 (que ganó él mismo, sobre el movimiento de los satélites de Júpiter). Fue durante esta época cuando empezó a ser conocido y respetado por los principales matemáticos de Europa; Jean le Rond D’Alembert, por ejemplo -que había ejercido con anterioridad como editor científico de la Encyclopédie- se esforzó por conseguirle un puesto fuera de Turín. En 1766, Euler abandonó Berlín para incorporarse a la Academia de San Petersburgo y anunció que conseguiría una plaza para Lagrange en Rusia, pero Lagrange ocupó el puesto que había tenido Euler en la Academia de Berlín.
La larga relación entre Euler y Lagrange, iniciada antes de que Lagrange cumpliera los 20 años, prosiguió, pues, de manera estrecha en la distancia. Euler, el matemático más prolífico del siglo XVIII, lanzaba una intuición brillante detrás de otra, pero no siempre persistía en ella lo bastante como para desarrollarla antes de pasar al siguiente asunto que le cautivaba la imaginación. La persona que muy a menudo seguía su estela hasta convertir ideas a medias en teorías sólidas y bellas era Lagrange. Sin embargo, nunca llegaron a encontrarse; de hecho, Lagrange siempre mantuvo una respetuosa distancia con Euler, a quien consideraba su antecesor y superior. Así, se negó a competir directamente con él por el premio de París de 1768 (sobre el movimiento de la Luna), aunque al final acabaron compartiendo el premio de 1772 sobre un tema similar. Lagrange permaneció veinte años en Berlín, un periodo durante el cual realizó numerosas publicaciones (en francés) en las Mémoires de la Academia.
Tras el fallecimiento de Federico el Grande, quien había otorgado un apoyo enorme a la Academia de Berlín, Lagrange volvió a trasladarse, esta vez a la Academia de París, a donde llegó en 1787. Dos años después, todas las instituciones de Francia se sumieron en el caos de la Revolución, pero Lagrange se las arregló para conservar durante aquellos años la cabeza y la reputación. En 1795, la Academia quedó abolida y reemplazada por el Instituto Nacional; Lagrange fue elegido director de la división dedicada a las ciencias físicas y matemáticas.
Al mismo tiempo, la necesidad acuciante de profesores e ingenieros bien formados que tenía la Revolución condujo a la fundación de instituciones nuevas, en particular la École Polytechnique en 1794 y la École Nórmale para la instrucción de profesores en 1795. Lagrange enseñó en ambas. La École Polytechnique acabaría convirtiéndose en la institución educativa más prestigiosa de comienzos del siglo XIX en París. A cualquier persona que haya estudiado matemáticas más allá del nivel escolar le sonarán casi con seguridad los nombres de Lagrange, Laplace, Legendre, Lacroix, Fourier, Ampère, Poisson y Cauchy, todos ellos formados y examinados durante los primeros años de la École Polytechnique. Además, la École publicaba sus apuntes de clase en cahiers que se usaban como libros de texto en toda Francia, sobre todo por quienes aspiraban a ser admitidos en ella como alumnos.
Lagrange falleció en 1813. Durante los primeros dos tercios de su carrera, transcurridos entre Turín y Berlín, fomentó y aprovechó las academias nacionales y sus respectivas revistas, instituciones que habían hecho mucho por alentar y divulgar la investigación de vanguardia. Durante sus últimos años en París, Lagrange presenció el ascenso de una nueva clase de institución, diseñada para ofrecer un nivel alto de formación matemática y científica a la mayoría de los estudiantes con capacidad. A diferencia de las universidades, la École Polytechnique ofrecía una instrucción muy específica y práctica que permitiría a sus graduados consolidar los logros de la Revolución y del Imperio napoleónico ulterior.
Pero por si la historia de las instituciones resultara un tanto impersonal, no perdamos de vista las estrechas relaciones personales que también se dieron a lo largo de la vida de Lagrange, sobre todo con Euler y D’Alembert. Cuando Lagrange murió, su protégé Augustin-Louis Cauchy, hijo de un amigo de la familia, iniciaba su larga carrera y acabaría convirtiéndose en una figura notable de las matemáticas francesas hasta su fallecimiento en 1857. Es posible trazar vínculos ininterrumpidos de amistades personales y de colaboraciones en las matemáticas de Europa occidental desde Leibniz a finales del siglo XVII hasta Lagrange o Cauchy a mediados del XIX, pasando por la familia Bernoulli y por Euler.
Hacia la época del fallecimiento de Lagrange, empezaron a producirse cambios en su antigua ciudad de residencia, Berlín. En 1810 Wilhelm von Humboldt fundó la Universidad de Berlín como una institución que no se limitara a transmitir los conocimientos acumulados, sino que también promoviera y facilitara estudios nuevos. Los profesores de la universidad alemana tenían libertad para contratar a su antojo y decidir así la orientación y el énfasis de sus departamentos. En las universidades alemanas se crearon grupos de investigación, conferencias y formación doctoral antes de 1900; ahora todas las universidades del mundo las imitan en mayor o menor medida. En este sentido, todos los matemáticos académicos, Andrew Wiles entre ellos, son producto de la Alemania decimonónica.
La publicación de la investigación matemática también cambió. En los siglos XVII y XVIII, la mayoría de los artículos matemáticos se publicaba en revistas académicas. El primer artículo matemático impreso aparecido en la revista Philosophical Transactions of the Royal Society, que salió en 1668; fue escrito por William Brouncker, por entonces presidente de la Royal Society. Aquel artículo solo tenía cuatro páginas e iba yuxtapuesto a cartas al editor sobre «Detalles de química, medicina y anatomía», sobre «La variedad de pleamares anuales» y algunas notas diversas sobre nuevos libros publicados. Más tarde las revistas se organizaron mejor: el Acta eruditorum, por ejemplo, tenía secciones independientes sobre medicina, matemáticas, filosofía natural, derecho, historia, geografía y teología; pero las revistas científicas siguieron siendo durante todo el siglo XVIII publicaciones sobre disciplinas muy variadas, y las matemáticas solo eran una más entre todas ellas.
La primera revista dedicada en exclusiva a las matemáticas, Amales de mathématiques purés et appliquées, fue fundada y editada por Joseph Gergonne en Francia en 1810, y acabó conociéndose como la «revista de Gergonne». Nótese aquí la primera aparición de la diferenciación entre matemáticas puras y aplicadas. La revista de Gergonne duró solo hasta 1832, pero para entonces August Crelle ya había creado, en 1826, su equivalente alemana con un título paralelo; la revista Journal für die reine und angewondte Mathernatik («revista de Crelle») existe aún hoy. Y lo mismo ocurre con la publicación que reemplazó a la revista de Gergonne, editada por primera vez por Joseph Liouville en 1836 con el título Journal de mathématiques purés et appliquées («revista de Liouville»). La publicación de revistas matemáticas ha seguido proliferando y aumentando desde entonces. Hoy en día las revistas ya no están especializadas en matemáticas en general, sino en las disciplinas y subdisciplinas de la materia. Una de mis preferidas es Journal of ill-Posed and Inverse Problems, pero hay muchas más.
Cualquier profesión moderna se identifica con unas instituciones especializadas, asociaciones profesionales y encuentros y congresos regulares, y las matemáticas también. Los congresos internacionales o incluso nacionales no existían en la época de Lagrange, pero hoy desde luego que sí, y acaparan al menos una parte del tiempo de todos los matemáticos académicos. En particular, los especialistas en matemáticas siempre están dispuestos a celebrar los aniversarios importantes de los demás; otro signo de la intensa cohesión social de esta disciplina.
El primer Congreso Internacional de Matemáticas se celebró en Zúrich en 1897, y a él acudieron representantes de varios países europeos y de Estados Unidos. El segundo congreso, celebrado en-París en 1900 para que coincidiera con la Exposición Universal, se recuerda sobre todo por una conferencia que dio el matemático alemán David Hilbert, durante la cual apuntó los 23 problemas que él consideraba que habrían de resolver los matemáticos a lo largo del nuevo siglo (aunque la demostración del último teorema de Fermat no figuraba entre ellos). Después de 1900 se celebraron congresos cada cuatro años salvo durante las dos guerras mundiales. Sin embargo, la exclusión de los matemáticos de Alemania, Austria, Hungría, Turquía y Bulgaria durante la década de 1920 y la ausencia de quienes se oponían a esta medida, suscitó el debate de si aquellos congresos podían ser considerados de carácter internacional.
La relación de las ciudades que acogieron los congresos desvela cómo fue aumentando la naturaleza global de la investigación matemática. Hasta la década de 1960 todos los encuentros se celebraron en Europa occidental, Canadá o Estados Unidos, pero el congreso de 1966 se celebró en Moscú y el de 1982, en Varsovia. El primer país asiático en celebrar uno fue Japón, en 1990, seguido por China en 2002 e India en 2010. Cuando Wiles anunció su demostración del último teorema de Fermat en su ciudad de residencia, Cambridge, también habría podido hacerlo ante audiencias similares en Pekín, Madrid o Hyderabad, sedes de los tres congresos más recientes. Las matemáticas son hoy, no ya una disciplina altamente especializada, sino también absolutamente internacional.
En este punto hemos alcanzado la cima de la pirámide matemática, la compacta comunidad de profesionales asociada a las palabras «matemáticas» y «matemáticos». Sin embargo, comparada con la cantidad de gente que practica matemáticas con regularidad, desde los escolares en adelante, esta comunidad de profesionales es minúscula, y el número de mujeres que hay en ella es todavía más insignificante.
Cabe preguntarse por qué las mujeres siguen teniendo una representación tan baja. La respuesta a esta pregunta no es sencilla, pero debemos recordar que como en la mayoría de las esferas profesionales, las reglas fueron pensadas por y para hombres, y es posible que algunas mujeres perciban el ambiente un tanto enrarecido en la cúspide de la pirámide y la compañía no siempre grata. Si dejamos las matemáticas de elite para los historiadores de elite, esta cuestión apenas tiene relevancia. De igual modo que las matemáticas han tenido muchas manifestaciones, las vidas matemáticas también se han vivido de múltiples maneras, y ninguna de ellas es más válida o correcta que las demás.
Capítulo 6
Las matemáticas por dentro
Hasta ahora he evitado entrar demasiado en tecnicismos matemáticos, y tampoco entraremos mucho en ellos en este capítulo, pero un historiador de las matemáticas está obligado a tratar no solo el contexto social de los textos matemáticos escritos en el pasado, sino también el máximo posible de sus contenidos. Esto es más fácil de decir que de hacer. A un nivel determinado, las matemáticas del pasado pueden parecer sencillas comparadas con lo que se espera, por decir algo, de un universitario actual. La dificultad del historiador no suele radicar tanto en entender las matemáticas en sí como en meterse en la mente y el universo matemático de alguien de otra época.
A modo de ejemplo, reflexionemos unos instantes sobre el teorema de Pitágoras, mencionado varias veces ya a lo largo de este libro. La demostración de Euclides del teorema de Pitágoras se ilustra en la figura 9. Consiste en trazar los cuadrados de los tres lados del triángulo rectángulo y en dividir en dos partes el lado más largo para comprobar que cada una de esas partes es igual a uno de los dos cuadrados menores.
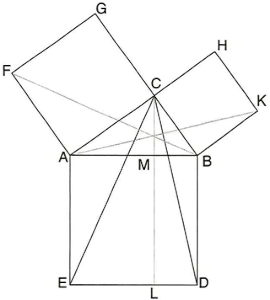
Figura 9. Demostración de Euclides del teorema de Pitágoras: AFGC = AMLE y CHKB = BDLM.
Los detalles los mostró mediante colores con gran ingenio Oliver Byrne en 1847, con la demostración casi sin palabras que aparece en la figura 10. Un rasgo crucial de esta demostración es que sirve para cualquier triángulo rectángulo, tenga la forma que tenga (de hecho, la versión interactiva de David Joyce te permitirá estirar y encoger a tu antojo el triángulo de partida siempre que conserve el ángulo recto). En otras palabras, la demostración no depende de unas medidas determinadas; no implica ninguna aritmética y, desde luego, nada de álgebra. Esto mantiene por completo el estilo de los Elementos: Euclides permitía a sus lectores el uso de regla y compás, pero no de calculadora.
La demostración de Thabit ibn Qurrá, que aparece en la figura 8, también se basa en geometría de recorta-y-pega para demostrar que el cuadrado grande se puede construir de forma que cubra los dos pequeños. Para Euclides e Ibn Qurrá, la lógica subyacente al teorema y su demostración era geométrica.
Consideremos ahora la técnica moderna para etiquetar los lados del triángulo como a, b y c y para escribir el teorema como a2 = b2 + c2. ¿Reproduce esta expresión el teorema que tenía Euclides en mente? En cierto sentido, sí. Sabemos que el área de un cuadrado de lado a es a2, así que la fórmula es una manera muy concisa de resumir un hecho geométrico. Hasta hay una continuidad en el lenguaje: usamos el mismo término «cuadrado» para nombrar la cantidad a2y para la figura geométrica de cuatro lados iguales. Pero en otro sentido, no. Esa fórmula procede de una cultura matemática muy diferente a la de Euclides, que nos ha enseñado a usar letras para representar longitudes y que hasta nos permite olvidarnos de la geometría y limitarnos a manipular las letras de acuerdo con sus propias reglas. Por tanto, si queremos, podemos reescribir la fórmula anterior comoc2= a2 - b2 = (a - b)(a + b), lo cual sigue siendo cierto, pero ya no tiene ninguna relevancia obvia para un triángulo rectángulo.
El paso del razonamiento geométrico hacia la manipulación algebraica no es trivial: requiere cierto esfuerzo aprender a hacerlo. Históricamente, la transición de una cultura matemática dominada por la geometría hacia otra en la que empezó a imponerse el lenguaje del álgebra sucedió en Europa occidental en el siglo XVII. (Fermat fue uno de los primeros matemáticos que experimentó con esa posibilidad, aunque más tarde también lamentó con tristeza cualquier desviación de la manera tradicional de hacer las cosas).
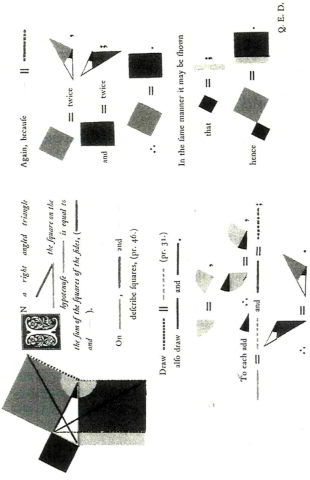
Figura 10. Demostración de Oliver Byrne del teorema de Pitágoras.
Los historiadores han estudiado este periodo en profundidad, ya que los cambios fueron determinantes para el desarrollo de las matemáticas modernas. Pensar que la versión algebraica del teorema de Pitágoras es en esencia idéntica a la versión geométrica equivale a ignorar el mar histórico que las separa, un mar que sólo se cruzó gracias a la labor acumulativa de muchos pensadores individuales.
Reinterpretación
El ejemplo que acabamos de considerar es una reinterpretación matemática consistente, en este caso particular, en partir de un teorema geométrico y reinterpretarlo desde un punto de vista algebraico. Esto es algo que se hace mucho en matemáticas; de hecho, partir de un trabajo anterior, propio o de otra persona, analizarlo, extenderlo y resolverlo bajo unas condiciones nuevas es una de las principales herramientas que se usan en matemáticas para avanzar en esta disciplina. Sin embargo, una cosa es que los propios matemáticos reescriban las viejas matemáticas, y otra cosa es que lo hagan los historiadores. Cuando se volvió a descubrir la Aritmética de Diofante en Europa durante el Renacimiento, resultó ser una fuente tan rica de problemas que experimentó varias reinterpretaciones, tanto matemáticas como históricas. Veamos en primer lugar algunas de las matemáticas.
Ya hemos dicho que Fermat extendió el problema II.8 y lo puso a prueba con números elevados al cubo o incluso a potencias más altas, y no solo elevados al cuadrado. Veamos ahora otra reinterpretación de principios del siglo XVII de otro problema de Diofante, esta vez procedente del matemático inglés John Pell.
Pell, nacido en Southwick, Sussex, en 1611, fue coetáneo tanto de Harriot como de Oughtred (con quienes nos cruzamos en el capítulo 5), aunque era unos cincuenta años más joven. Se formó en la recién creada Escuela de Gramática Steyning, unos pocos kilómetros al norte de Southwick, y más tarde en el Trinity College, Cambridge. Con posterioridad regresó a Sussex y enseñó en una escuela experimental de Chichester hasta su cierre unos años más tarde. Pell dedicó entonces varios años a buscar un puesto remunerado o bien un mecenas, pero no encontró nada que se adecuara a su particular temperamento. A finales de 1643 lo contrataron en el Gymnasium de Ámsterdam, y dos años después en el Ilustre Colegio de Breda, donde permaneció hasta 1652.
Durante este periodo, Pell prestó mucha atención a Diofante. Lo sabemos porque a comienzos de la década de 1640 Pell había conocido a sir Charles Cavendish (de quien también hablamos en el capítulo 6) y ambos intercambiaron correspondencia durante los años que Pell pasó en los Países Bajos. Cada cual tenía su propio concepto de lo que era una relación de mecenazgo matemático: Cavendish solicitaba a Pell que lo ayudara con lo que no había entendido durante su lectura matemática más reciente, y Pell respondía diligente. Es evidente que Cavendish tenía un concepto elevado de las capacidades de Pell y esperaba que publicara ciertos libros importantes, entre ellos una nueva edición de Diofante «que», según escribió, «estoy deseando ver». Por desgracia, Pell tenía una incapacidad casi patológica para acabar o publicar lo que fuera, pero hay signos de que al menos empezó a trabajar en esa edición; esos signos provienen de las voluminosas anotaciones que dejó Pell (miles de páginas que ahora se han reunido en más de 30 extensos volúmenes en la British Library).
Pell estuvo tan interesado en Diofante porque había desarrollado un método para resolver problemas que él consideraba perfecto para las cuestiones que figuran en la Aritmético. El método era el siguiente: primero y para cualquier interrogante, anotar las cantidades que se desconocen y las condiciones que se plantean en líneas numeradas; segundo, trabajar de forma sistemática desde las condiciones hasta la respuesta requerida. Para asegurarse de que el trabajo avanza como debe, se expone en tres columnas, con los números de línea en la estrecha columna central. La columna de la izquierda de cada línea contiene una instrucción breve; la columna de la derecha muestra el resultado obtenido con esa instrucción. El conjunto completo se parece y se percibe como un algoritmo de ordenador actual.
Para ver cómo se aplicaría este método a la obra que escribió Diofante en la antigüedad, veamos la interpretación que hace Pell del problema IV. 1 de la Aritmética: hallar dos números cuya suma da un número dado y cuyos cubos suman otro número dado. Diofante estableció que la suma de esos números era 10 y que la suma de sus cubos daba 370, justo el problema que más tarde estudió la joven Anne Davenant instruida por su padre. Pell lo resolvió con su particular estilo. Sus primeras dos líneas son las siguientes, en las que llama a los números desconocidos a y b:
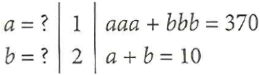
Después, siguiendo al pie de la letra a Diofante, Pell introdujo un tercer número, c, y supuso que a = c + 5, de manera que, necesariamente, b = 5 - c. Las dos siguientes líneas son
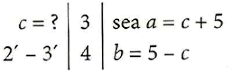
donde 2’ - 3’ no tiene otro significado más que restar la línea 3 a la línea 2. Ya está todo preparado y se puede empezar a trabajar. Quien quiera seguir los detalles debe saber que la instrucción de Pell 3’@3 significa «hallar el cubo de la línea 3», mientras que 10’ω2 significa «hallar la raíz cuadrada de la línea 10». Otra convención que siguió Pell es la de cambiar las letras minúsculas por mayúsculas cuando se descubren sus valores.

Las últimas cuatro líneas son una comprobación de que el problema está bien resuelto:
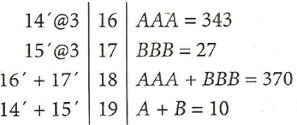
Da la impresión de que Pell había planeado reescribir los seis libros de la Aritmético a su estilo, pero si llegó a completar el proyecto alguna vez, el manuscrito se perdió. Aun así, muchos de sus contemporáneos se quedaron impresionados con su método. Su amigo John Aubrey hasta inventó un verbo nuevo en latín para referirse a él: pelliare, o sea «pelliar» o «al estilo de Pell».
A partir del ejemplo anterior queda claro que Pell no creía en el derroche de palabras: la única que aparece en sus 19 líneas de trabajo es «sea» (en realidad la escribió en latín: sit). Pero si desaparecen las palabras, debe haber símbolos que las sustituyan, y en esto Pell era un maestro de la inventiva. Los símbolos @ y <v que permiten mantener la concisión en la primera columna dejaron de usarse hace mucho tiempo, pero su símbolo para la división aún sigue entre nosotros.
La inventiva para la notación fue una de las grandes dotes de Pell, y para ello siguió lo que por entonces ya era casi una tradición inglesa. En 1557 Robert Recorde había ideado el signo = basándose en dos líneas paralelas «porque no hay dos cosas que puedan ser más iguales». Por su parte, alrededor de 1600 Thomas Harriot había añadido los signos de desigualdad “<” y “>”, y la convención de escribir ab para indicar a multiplicado por b. En 1631 William Oughtred introdujo el signo ×, aunque rara vez lo utilizó; también defendió con entusiasmo una notación «con una presentación clara a la vista durante todo el curso y proceso de cualquier operación y razonamiento». Está claro que Pell opinaba lo mismo, que su método representaba el razonamiento con claridad ante la vista sin necesidad de ninguna explicación adicional. Por tanto, sus esfuerzos para «pelliar» a Diofante revelan más sobre las aspiraciones de los algebristas ingleses de comienzos del siglo XVII, que sobre Diofante y su Aritmética.
Pero esto también se da con las reinterpretaciones históricas en lugar de las matemáticas: suelen revelar más sobre quien interpreta que sobre lo interpretado. Las historias que han circulado a lo largo de los siglos sobre los orígenes del álgebra, por ejemplo, han registrado no solo el hecho histórico en sí, sino también los conocimientos contemporáneos de cuando se escribieron.
El álgebra llegó por primera vez a regiones no islámicas de Europa occidental a finales del siglo XII a través de traducciones de la obra Al-fabr wal-muqabala, de al-Juarismi, pero en el siglo XVI ya se había olvidado aquella historia inicial, si es que en algún momento llegó a conocerse debidamente. Así y todo, se reconocían los orígenes islámicos de la materia, aunque solo fuera a través de los extraños términos «álgebra» y «almucábala» asociados a ella. Así que a principios del siglo XVI los autores atribuían la invención del álgebra a «une nome Arabo di grande intelligentia» (‘una personalidad árabe de gran inteligencia’), otras veces a un tal Algeber (en realidad, Jabir ibn Aflah, astrónomo musulmán español del siglo XII sin ninguna relación con el tema), o al vago nombre de «Maumetto di Mose Arabo» (una traducción de «el árabe Muhammad ibn Musa»).
En cambio, en 1462 el erudito alemán Johannes Müller -a menudo conocido como Regiomontano por el nombre latinizado de su ciudad natal, Königsberg- examinó un manuscrito de la Aritmético de Diofante en Venecia y tres años después, mientras daba una conferencia en Padua, describió su contenido como «la flor de toda la aritmética... que hoy recibe el nombre árabe de álgebra». Su disertación no se publicó hasta 1537, pero muy poco después otros autores empezaron a retomar el mismo tema: que el álgebra había sido una invención de Diofante y que «los árabes» no la adoptaron hasta más tarde. Es comprensible que aquellas historias encontraran aceptación en una época en que el pedigrí griego confería una respetabilidad y un estatus inmediatos. El hecho de que los problemas tratados por Diofante difirieran, tanto en estilo como en contenido, de los hallados en los textos islámicos no parece haber impedido a nadie pensar que los últimos tenían que derivarse de algún modo de los primeros. Incluso hoy, que existe una apreciación mucho mayor de las matemáticas que heredó Europa occidental del mundo árabe, se sigue considerando a veces a Diofante como el fundador del álgebra. Este debate podría seguir y seguir, pero debemos intentar entender el asunto desde un punto de vista matemático.
Es cierto que Diofante escribió muchos problemas del tipo «halla un número» que pueden resolverse con facilidad mediante los métodos algebraicos modernos, tal como demuestra el ejemplo de Pell, pero también planteó muchos otros problemas «indeterminados», es decir, que tienen más de una solución posible. En esos casos, Diofante solía quedarse satisfecho si a través de algún método concreto lograba alcanzar alguna de esas respuestas. De hecho, su obra está repleta de ideas, algunas de ellas muy ingeniosas, que funcionan tan solo para preguntas específicas, a diferencia de las reglas más generales de los textos de álgebra posteriores procedentes del mundo islámico.
También se ha afirmado que Diofante usó una notación simbólica elemental al escribir, por ejemplo, q para representar un número desconocido y A Y para su cuadrado, pero ahora se ha demostrado que esas abreviaturas de los términos griegos arithmos (‘número’) y dynamis (‘cuadrado’), respectivamente, fueron introducidas por copistas del siglo IX y no se pueden atribuir en absoluto a Diofante. Por último, las matemáticas derivadas de la aritmética han sido absorbidas por la teoría de números moderna, mientras que los textos islámicos de al-fabr dieron lugar de una manera mucho más directa al álgebra de Europa occidental.
Creo que el término «álgebra» debería reservarse para aludir a las reglas y procedimientos que los propios actores describieron como al-yabr o «álgebra», y que no deberíamos imponer esos términos, ni la historia que arrastran consigo, a un autor que desarrolló su labor dentro de una tradición anterior y muy diferente.
¿Quién fue el primero...?
La cuestión que acabamos de analizar -¿quién inventó el álgebra?- es una de las típicas que suelen plantearse los historiadores de las matemáticas, quienes a menudo se creen capaces de decir quién fue la primera persona que descubrió o inventó determinadas ideas. Salvo en los casos más simples, estas cuestiones son difíciles de responder. Consideremos, por ejemplo, el descubrimiento del análisis matemático. Esta es la rama de las matemáticas que se puede usar para describir y predecir cambios. Hoy en día se usa en biología, medicina, economía, ecología, meteorología y cualquier otra ciencia que funcione con sistemas interactivos complejos. Por tanto, es bastante razonable pretender saber quién inventó el análisis matemático.
La respuesta corta sería que lo inventaron dos personas casi a la vez pero por separado: Isaac Newton desde Cambridge y Gottfried Wilhelm Leibniz desde París. Los historiadores modernos ya no lo discuten porque contamos con los manuscritos de ambos, y en ellos se ve con exactitud cuándo y en qué orden desarrollaron sus ideas. Asimismo se aprecia que siguieron procedimientos muy diferentes y que cada cual ideó un vocabulario y una notación propios (Leibniz hablaba de «diferenciales» mientras que Newton lo hacía de «fluxiones»; Leibniz inventó la notación habitual en la actualidad dx/dt, mientras que Newton usó x, menos común hoy en día).
En cambio, para sus contemporáneos la historia no estaba nada clara. Los hechos esenciales son que Newton desarrolló su versión del análisis matemático durante 1664 y 1665 (antes de su vigésimo tercer cumpleaños), pero luego no hizo nada con él. A comienzos de la década de 1670 ya se había enfrascado en una trifulca intelectual con Robert Hooke sobre sus descubrimientos de óptica, y puede que temiera arriesgarse a tener otra por el análisis matemático. En cualquier caso, por entonces había centrado su interés en la alquimia, la cual lo tendría ocupado durante la siguiente década.
En cambio, en 1673 Leibniz, que entonces residía en París, empezó a trabajar de manera independiente en algunos de los mismos problemas que habían intrigado previamente a Newton, y publicó su primer artículo sobre análisis matemático en 1684, al cual le siguieron otros durante la década de 1690. Al parecer, Newton les prestó muy poca atención, probablemente porque consideró los primeros trabajos de Leibniz bastante triviales comparados con lo que él mismo había llegado a alcanzar. Sin embargo, algunas amistades de Newton lo vieron de otra manera, y en el cambio de siglo algunos de sus seguidores ingleses empezaron a sospechar, no ya que Newton había sido el primero, sino también que Leibniz bien podría haber robado a Newton el germen de sus ideas. No ayudó en la defensa de Leibniz el hecho de que hubiera visto algunos de los documentos de Newton cuando estuvo en Londres en 1675 y que recibiera cartas de Newton en 1676, pero lo que sacó de ellos y la relación que mantenían con lo que ya había descubierto no lo sabía nadie en realidad, excepto el mismo Leibniz.
Tanto Newton como Leibniz evitaron la confrontación directa, pero permitieron que esa batalla la libraran sus secuaces, especialmente beligerantes en ambos bandos. Al final, en 1711, Leibniz apeló a la Royal Society, de la cual era miembro, para que arbitrara la disputa. Newton, como presidente de la misma, creó una comisión que apenas necesitó reunirse porque el propio Newton ya estaba ocupado en la redacción de su informe. Tal como era de esperar, falló en su favor. Y como también era de esperar, aquello no puso fin al asunto: la disputa prosiguió hasta después del fallecimiento de Leibniz en 1716. Y esa disputa explica por qué en 1809 el escolar inglés George Peat, en Cumbria, estudió una asignatura llamada «fluxiones» en lugar de estudiar una llamada «calculus».
Aquella fue una historia nada edificante de la que nadie salió bien parado. Si la hemos vuelto a contar aquí es para hacer hincapié en lo difícil que era para todo el mundo en aquel entonces llegar al fondo de la cuestión: nadie conocía todos los hechos; además, era difícil saber si el debate se centraba en el análisis matemático en su conjunto o en algunos aspectos particulares (Leibniz acusó a los ingleses de fluctuar a este respecto); y, como puede ocurrir con las disputas, se deslizaron varias discrepancias que nunca formaron parte de la discusión original. Sin embargo, otro detalle de la historia es que las pruebas últimas de la verdad no provienen de lo que la gente de la época escribió o dijo, lo que casi siempre era parcial (en ambos sentidos de la palabra), sino de los manuscritos matemáticos en sí.
En matemáticas no es nada infrecuente -tal como ocurrió con el análisis matemático- que dos personas desarrollen ideas similares más o menos al mismo tiempo. Una vez realizado el trabajo de base, cualquier matemático puede hacer uso de él con la misma facilidad que otro, y entonces resulta muy difícil saber a quién le corresponde el mérito, sobre todo si ambos han mantenido algún contacto entre sí. Este fue precisamente el motivo por el que Wiles se encerró con tanto celo durante los años que trabajó en el último teorema de Fermat.
En el caso del análisis matemático hay suficientes indicios documentales para que los historiadores esclarezcan qué sucedió en realidad, pero no siempre es así. A principios del siglo XIX los matemáticos Bernard Bolzano, desde Praga, y Augustin-Louis Cauchy, desde París, también desarrollaron ideas muy similares, Bolzano en 1817 y Cauchy en 1821. ¿«Copió» Cauchy a Bolzano o no? El trabajo de Bolzano se publicó en un periódico bohemio poco conocido al que, sin embargo, Cauchy tenía acceso desde París. Pero, por otra parte, ambos pudieron basarse por separado en la obra previa de Lagrange. También debemos tener en cuenta los indicios circunstanciales sobre la manera de trabajar de Cauchy, que muy a menudo consistía en tomar buenas ideas de otros y desarrollarlas en profundidad. En definitiva, ante la falta de pruebas en uno u otro sentido, simplemente no lo sabemos.
Otro problema a la hora de esclarecer quién fue la primera persona que realizó un descubrimiento consiste en definir en qué creemos que consiste el descubrimiento en sí. ¿En qué instante preciso de la historia podemos decir, por ejemplo, que surgió el análisis matemático, en oposición a una maraña de ideas relacionadas que poco a poco empezaron a cobrar sentido, primero para Newton, y después para Leibniz?
Tal como acabamos de ver, resulta igual de difícil discernir cuándo empezó el álgebra o en qué lugar el teorema de Pitágoras se convirtió en un teorema formal en oposición a una realidad útil conocida por los constructores. Casi todas las matemáticas nuevas se asientan sobre trabajos anteriores, y a veces sobre varias ideas concurrentes. Uno de los cometidos de los historiadores consiste en rastrear los antecedentes de una técnica o de un teorema particular, pero no para decir quién fue la primera persona que los concibió, sino para entender con mayor claridad cómo han evolucionado las ideas matemáticas con el paso del tiempo.
Hasta que todo cuadra
El estilo deductivo sistemático de Euclides, mediante el cual todo teorema se demuestra cuidadosamente a partir de los teoremas y definiciones que lo preceden, se ha considerado durante siglos la regla de oro del proceder matemático. Pero incluso Euclides resultó no ser infalible. Ya en el siglo v d. de C. surgieron interrogantes sobre uno de los postulados de Euclides que se mostraron difíciles de responder. El postulado problemático se conoce a veces como el postulado de las paralelas; se puede expresar de maneras diferentes, pero la más simple dice que si tenemos una recta l en un plano, y un punto P situado fuera de ella, solo existe una recta que pase por P y que sea paralela a l.
La mayoría de nosotros no tendrá dificultades para aceptar esta afirmación, que tiene como consecuencia que los ángulos de un triángulo sumen 180 grados, y la mayoría de nosotros tampoco tiene inconveniente en aceptar también esto. Sin embargo, muchos de los comentaristas de Euclides pensaban que el postulado de las paralelas no debe considerarse un postulado, sino un teorema, es decir, que debería poder demostrarse de algún modo a partir del resto de definiciones y de postulados. Thabit ibn Qurrá y Ornar Jayyam fueron algunos de los que lo intentaron; también probó John Wallis desde Oxford en 1663, y más tarde, en 1733 otro matemático poco conocido llamado Gerolamo Saccheri, catedrático de matemáticas en Pavía, en el norte de Italia, probó con un enfoque distinto: estudió qué ocurriría si suponía que los ángulos de un triángulo suman más o menos de 180 grados, esperando, por supuesto, que los resultados fueran absurdos y que, por tanto, ello condujera a descartar semejante supuesto de partida. Pero estaba equivocado. Al admitir que los ángulos suman menos de 180 grados se llegaba a algunos resultados extraños, pero consistentes.
Cien años después, Nikolai Ivanovich Lobachevski, catedrático de la Universidad de Kazán, en Rusia, y János Bolyai, de la ciudad actualmente llamada Cluj-Napoca, en el norte de Rumania, llevaron mucho más lejos aquellas ideas (otro ejemplo de un hallazgo independiente pero más o menos simultáneo); ambos repararon en que se puede construir un tipo de geometría aceptable desde un punto de vista matemático aunque definitivamente no sea euclídea. Esta idea dejó asombrados a los pensadores del siglo XIX: una consecuencia era que nadie podía saber si el mismísimo espacio infinito es euclídeo o no, de igual manera que recorrer a pie una calle no revela si la Tierra es esférica o plana. Se suponía que las matemáticas arrojaban verdades irrefutables sobre el mundo, pero de pronto esas verdades empezaron a parecer menos fiables.
Uno de los resultados de todo esto fue que los matemáticos empezaron a estudiar con más detenimiento sus supuestos esenciales, formalmente conocidos como «axiomas». De hecho, a finales del siglo XIX y comienzos del XX, se produjo una vuelta al estilo euclídeo más puro y se revisaron ramas enteras de las matemáticas para asentarlas sobre bases axiomáticas que les impusieron un rigor lógico desconocido en matemáticas desde la época de la antigua Grecia. Desde el siglo II a. C. hasta el XIX d. C., la mayoría de las matemáticas se habían desarrollado de un modo completamente aleatorio. La verdad es que los matemáticos no realizan descubrimientos creando axiomas y reflexionando de manera lógica sobre ellos, sino respondiendo de forma imaginativa a los problemas que les interesan, planteando cuestiones en direcciones nuevas, o estableciendo conexiones inesperadas y novedosas entre partes de las matemáticas aparentemente distintas. Por supuesto, deben hacer XIII uso correcto de sus conocimientos y experiencias, y al final deben llegar a un razonamiento irrefutable llamado «demostración», tal como hizo Wiles durante las conferencias que dio en Cambridge, pero es probable que ese resultado se aparte un tanto de los razonamientos iniciales y del arduo trabajo que les sigue casi indefectiblemente.
El descubrimiento del análisis matemático que hemos tratado en el apartado anterior es un ejemplo excelente de matemáticas carentes por completo de lógica durante su concepción. La idea general se basaba en lo que los matemáticos del siglo XVII denominaban «cantidades infinitamente pequeñas». Sin embargo, la pregunta que hay que hacerse en relación con una cantidad infinitamente pequeña es si llega a tener algún tamaño. Si lo tiene, no puede ser «infinitamente pequeña»; pero si no tiene ningún tamaño, entonces ni siquiera existe y no se puede usar de ninguna manera práctica en nuestros cálculos. Esto tal vez suene un tanto puntilloso, más parecido a un debate como el de la cantidad de ángeles que pueden bailar en la punta de una aguja que a uno matemático. Pero es importante, porque las discusiones sobre cantidades infinitamente pequeñas dan lugar a contradicciones con mucha rapidez, y como las matemáticas se consideran un edificio lógico unificado, una sola contradicción desmorona todo el conjunto. (Por eso los matemáticos plantean a menudo una contradicción de manera deliberada, tal como probó a hacer Saccheri, cuando pretenden demostrar que algo es imposible, una técnica denominada reductio ad absurdum).
Tanto Newton como Leibniz fueron muy conscientes de la paradoja de lo infinitamente pequeño e hicieron lo posible para lidiar con ella, Newton afrontándola de cara, y Leibniz dando un rodeo. Sus sucesores también repararon en ella, no solo matemáticos, sino también gente bien formada. El obispo George Berkeley, por ejemplo, en su libro titulado The Analysis: A Discourse Addressed to an Infidel Mathematician («El analista: discurso dirigido a un matemático infiel») planteó si los matemáticos, que tanto afinan en cuestiones religiosas, ¿son estrictamente escrupulosos en su propia ciencia? ¿No se someten a la autoridad, no aceptan cosas basándose en la fe y no creen cosas inconcebibles?.
¿Detuvieron estos problemas a los matemáticos en su búsqueda? No, porque desde bien pronto en el desarrollo del análisis matemático reconocieron su potencial y se esforzaron por aplicarlo, con gran éxito, a rayos de luz, cadenas colgantes, objetos que caen, cuerdas que vibran y muchos otros fenómenos del mundo físico. Difícilmente habrían renunciado a todo eso por lo que consideraban una dificultad más metafísica que matemática.
Transcurrieron unos 150 años hasta que se encontró una solución del problema que resultara satisfactoria para la mayoría de la gente, siguiendo métodos demasiado técnicos para exponerlos aquí; sin embargo, durante esos mismos 150 años las matemáticas avanzaron más allá de toda expectativa, a pesar del tambaleó de sus cimientos.
Algo parecido ocurrió en el siglo XIX. En 1822, Joseph Fourier, profesor de la École Polytechnique de París, publicó un tratado sobre la difusión del calor, su Théorie analytique de la chaleur. En él, Fourier investigó la idea de usar sumas infinitas de senos y cosenos para describir distribuciones periódicas; estas sumas infinitas se conocen ahora como «series de Fourier», y tienen gran cantidad de aplicaciones en ingeniería y física. Sin embargo, la deducción original de Fourier estaba plagada de errores e incoherencias. Algunas de ellas se anulaban entre sí, pero Fourier pasó por alto muchas otras, si es que llegó a percibirlas en algún momento. En otras palabras, la teoría inicial de las series de Fourier no tenía una base más firme que la que había tenido el análisis matemático, y a pesar de ello, al igual que el análisis matemático, resultó ser una herramienta inmensamente rica y útil. Pero, como sucedió con el análisis, muchos matemáticos posteriores a Fourier se vieron obligados a dedicar gran cantidad de tiempo a resolver las lagunas.
Estos no son ejemplos excepcionales. Como hemos visto, Wiles, matemático mucho más competente que Fourier, también se vio obligado a seguir un proceso muy similar para enmendar un error, aunque en su caso solo le llevó dos años, no un siglo. Casi cualquier descubrimiento matemático nuevo parte de un estado tosco e inmediato y debe mejorarse y refinarse antes de poder presentarlo al resto de la comunidad matemática, no digamos ya para enseñárselo a quienes se inician en la materia.
La mayoría de los libros de texto modernos siguen el mismo patrón que los Elementos de Euclides, empiezan por un principio simple a partir del cual van edificando las matemáticas siguiendo un curso lógico continuado.
En otras palabras, dejamos (o esperamos) que los alumnos sigan un camino despejado que los primeros exploradores ni siquiera atisbaron. Si los estudiantes tuvieran la oportunidad de remontarse hasta los descubrimientos originales, seguramente encontrarían algo muy distinto: un proceso de ensayo y error, falsos puntos de partida y callejones sin salida; ideas a medio hacer, desarrolladas a medias para que fueran otros quienes las completaran; ideas mejor concebidas refinadas con los meses o los años; y todo ello adaptado al final por docentes que tal vez no tengan capacidad para innovar, pero dotados con la capacidad igualmente importante de saber explicar las cosas a quienes empiezan.
En otras palabras, la exposición pulida de los libros de texto dice muy poco acerca de la intuición y el trabajo arduo, la imaginación y el esfuerzo aplicados a las matemáticas en un primer momento. Eso es tarea del historiador.
Capítulo 7
La historiografía evolutiva de las matemáticas
Las formas de hacer y pensar la historia de las matemáticas han cambiado mucho durante los últimos siglos, algunas debido a cambios generales en la historia intelectual, y otras siguiendo cambios específicos dentro de las matemáticas. Como vimos en el capítulo 2, el procedimiento que siguió John Leland en la década de 1550, a quien siguió Gérard Jean Vossius un siglo después, consistía en registrar la mayor cantidad de datos posibles sobre autores, fechas y textos, pero sin analizar en absoluto el contenido de esos textos. Sin embargo, a finales del siglo XVII, cualquier persona interesada en las matemáticas sabía que el poder, el alcance y las técnicas de la disciplina estaban avanzando con rapidez: «La geometría avanza cada día», escribió Joseph Glanville en 1668, mientras que pocos años después John Wallis elogió «el progreso y el avance» que había llevado al álgebra hasta «la altura a la que se encuentra ahora».
El siglo XVIII, la época de la Encyclopédie, presenció la publicación de dos obras relacionadas con la historia de las matemáticas: la Histoire des mathématiques de Jean-Étienne Montucla, publicada en París en 1758 (ampliada a cuatro volúmenes entre 1799 y 1802), y el Mathematical and Philosophical Dictionary de Charles Hutton, que incluía varios artículos históricos, publicado en Londres en 1795.
Sin embargo, a finales del siglo XIX, el foco se apartó, como en otros campos de estudio, de los testimonios indirectos hacia ediciones académicas y traducciones de textos antiguos y medievales (igual que había ocurrido durante el Renacimiento). Por tomar ejemplos de obras ya comentadas con anterioridad aquí: la primera traducción al inglés de la Aritmética de Diofante fue publicada por Thomas Heath en 1885; la edición de Heath de los Elementos de Euclides, basada en los mejores estudios existentes por entonces, apareció en 1908; y la traducción de Louis Charles Karpinski del Al-fabr de al-Juarismi a partir de una versión medieval en latín, apareció pocos años después, en 1915. Estas ediciones eran y siguen siendo inestimables: ni la Aritmética ni el Al-fabr habían estado disponibles con anterioridad en inglés, y los Elementos de Heath siguen siendo hoy la edición de referencia en esa lengua.
Sin embargo, los historiadores modernos también tratan esas ediciones con cautela. El ensayo de Heath sobre la Aritmética se titula Diophantus of Alexandria: A Study in the History of Greek Algebra («Diofante de Alejandría: un estudio de la historia del álgebra griega»), un título que plantea interrogantes ya señalados en este libro. Es más, un crítico de la edición de Heath de Apolonio ha observado que «gracias a la condensación hábil y a la sustitución con notación moderna de las demostraciones de la obra, ocupa menos de la mitad de espacio que el original». Una vez más, el historiador seguramente no agradece a Heath esta capacidad, y preferiría ver el texto sin comprimir y Ubre de los anacronismos de la notación moderna. Sin embargo, muchas de las obras sobre historia de las matemáticas surgidas a comienzos del siglo XX, realizadas a menudo por matemáticos en lugar de historiadores, seguían un procedimiento muy similar, consistente en partir de textos originales escritos en jeroglíficos egipcios o en sumerio, sánscrito o griego para traducirlos a los símbolos y conceptos de las matemáticas modernas. Las razones de aquellos traductores no eran de por sí reprochables: para comprender ideas que de entrada parecen completamente desconocidas, es natural intentar relacionarlas con algo más familiar; el riesgo está en que al final esas ideas desconocidas acaban considerándose sin más representaciones arcaicas de lo que ahora podemos hacer, a nuestro entender, de una manera más eficiente. De este modo, la historia se reescribe a partir de nuestra propia perspectiva en lugar de hacerse a partir de los autores originales.
Los historiadores de las matemáticas antiguas son los primeros que se rebelan contra las distorsiones introducidas por la modernización, y durante la década de 1990 encabezaron la forma de intentar recuperar y conservar, en la medida de lo posible, el idioma y el pensamiento de los originales. De acuerdo con la reflexión tan citada ahora de Reviel Netz, editor y traductor de Arquímedes:
La función de una traducción académica, a mi entender, consiste en eliminar todas las barreras relacionadas con el idioma extranjero en sí, y en dejar intactas todas las demás.
Esto obliga al lector actual de textos matemáticos históricos a realizar un esfuerzo mucho mayor que el lector de hace cincuenta años, pero los beneficios en cuanto a percepción histórica son incomparablemente mayores.
Quienes trabajan con escritos matemáticos antiguos también han encabezado el avance en otros aspectos de la historiografía, en parte debido al desorden con que se fue acumulando su material de estudio en épocas pasadas. Una única tablilla de arcilla, por ejemplo, revela muy poco si no se sabe dónde o cuándo se escribió. Esa información es esencial para hacerse una idea de cómo se relaciona un texto concreto con otros hallados en la misma zona o en cualquier otro lugar. Muchas tablillas aparecidas en las primeras excavaciones se depositaron en museos con una información mínima sobre su procedencia, o bien se vendieron en el mercado de antigüedades sin más, lo que complica sobremanera que los historiadores deduzcan de ellas información que nos pueda resultar útil ahora.
Por fortuna, los arqueólogos de hoy registran con sumo cuidado su ubicación y su entorno antes de extraer cada capa de restos. Además, la tecnología moderna también ha permitido avances en la lectura de textos escritos con pluma y luego borrados o deteriorados. El trabajo realizado con el texto redescubierto de Arquímedes que se menciona en el capítulo 3 ha sido especialmente notable a este respecto. Los especialistas han conseguido leer buena parte del texto original, pero, además, han identificado al escriba que pulió el pergamino y escribió sobre él: se trata de Ioannes Myronas, quien trabajó en Constantinopla durante la Cuaresma de 1229. Es muy conveniente que la recuperación del texto y la recuperación de la historia del texto vayan de la mano.
Los historiadores de las matemáticas se han ido apartando de una concepción puramente «interna» que considera los progresos matemáticos como resultado de sí mismos, con independencia de influencias externas. Tal como hemos evidenciado una y otra vez a lo largo de este libro, la actividad matemática ha tenido manifestaciones muy diversas a lo largo de los siglos, todas ellas condicionadas por cada sociedad y cada cultura.
Pero no debemos mezclar las cosas: lo habitual es que los matemáticos se enfrasquen en un problema concreto, no porque pueda resultar útil o porque alguien se lo pida, sino porque el problema en sí atrapa su imaginación. Eso fue lo que les pasó a Newton y Leibniz con el análisis matemático, a Bolyai y Lobachevski con la geometría no euclídea, o a Wiles con el último teorema de Fermat. En esos casos, el avance depende en primer lugar y por encima de todo de un compromiso profundo y concentrado con las matemáticas, y en este sentido se puede afirmar que la creatividad matemática es un proceso interno. Pero las cuestiones matemáticas que se consideran relevantes en una época o un lugar determinados, la forma en que han surgido, la manera en que se conciben e interpretan, todo eso está influido por multitud de factores externos a las propias matemáticas: factores sociales, políticos, económicos y culturales. El contexto se ha vuelto tan importante para el historiador como el contenido.
Otro cambio significativo que se ha producido en los últimos años ha sido el reconocimiento cada vez mayor de que las matemáticas practicadas por un pequeño número de figuras célebres no ha reflejado (aunque sí ha configurado) la diversidad de la actividad y la experiencia matemática en otros niveles de la sociedad. La historia de las matemáticas no exquisitas ha sido uno de los temas esenciales de este libro.
Los historiadores de las matemáticas, igual que los especialistas en muchas otras disciplinas, también se han vuelto mucho más sensibles a cuestiones de género y étnicas. Los estudios de culturas anteriores o externas a la Europa occidental actual se vieron limitados en el pasado por la falta de fuentes, o por barreras lingüísticas, pero estas circunstancias están empezando a cambiar porque las imágenes en Internet, las nuevas traducciones y las glosas de especialistas están facilitando mucho el acceso a fuentes originales, tanto desde un punto de vista intelectual como material. De ahí que las matemáticas del pasado ya no se contemplen como meras precursoras de las matemáticas actuales, sino como una parte integral de su propia cultura contemporánea.
Como en todas las disciplinas académicas florecientes en nuestros días, quienes se dedican a la historia de las matemáticas deben traspasar fronteras. De hecho, uno de los grandes placeres de trabajar en la materia es que se aprende de la experiencia de especialistas en arqueología, archivología, sinología, clasicismo, orientalismo, medievalismo, historia de la ciencia, lingüística, historia del arte, crítica literaria, conservación de museos y muchas otras materias. La diversidad de las fuentes originales también ha experimentado un incremento similar, y ya no se restringe a los libros o manuscritos que en algún momento exponían las ideas más novedosas, sino que incluyen correspondencia, diarios, apuntes, libros de ejercicios, instrumentos de medida, máquinas para calcular, dibujos, bosquejos, agendas y novelas.
Estas últimas tal vez puedan extrañarnos, pero quienes escriben novelas pueden ser los registradores más sagaces y elocuentes de las ideas matemáticas contemporáneas; quien tenga interés en explorar este tema encontrará más información en el apartado dedicado a «lecturas adicionales».
Los interrogantes que se han planteado los historiadores a lo largo de los últimos cincuenta años han cambiado y se han diversificado a la vez. Ya no basta con limitarse a preguntar quién descubrió qué y cuándo. También queremos conocer las prácticas matemáticas realizadas por grupos de personas o individuos aislados, y por qué. ¿Qué influencias históricas o geográficas intervinieron? ¿Cómo contemplaban las actividades matemáticas tanto quienes las practicaban, como los demás? ¿Qué aspectos se valoraban especialmente? ¿Qué medidas se tomaban para conservar o transmitir los conocimientos matemáticos? ¿Quién las costeaba? ¿Cómo gestionaban los matemáticos su tiempo y sus conocimientos? ¿Cuáles eran sus motivaciones? ¿Qué produjeron? ¿Qué hicieron con ello? Y ¿con quién debatieron, colaboraron o razonaron durante todo el proceso?
Casi todas las respuestas a la mayoría de estas preguntas son difíciles de encontrar con cierto grado de certidumbre. Los historiadores de las matemáticas, al igual que el resto de historiadores, trabajan con indicios escasos a partir de los cuales deben reconstruir con sumo cuidado historias incompletas sobre el pasado. Sigue valiendo la pena intentarlo por todo lo que podemos aprender sobre esta actividad humana tan antigua y extendida como la literatura o la música, y que se ha manifestado con una variedad tan inmensa de formas culturales: la práctica y la creación de las matemáticas.
1. Las matemáticas: mitos e historia
Fuentes primarias:
Recorde, Robert, The Pathway to Knowledg (Londres, 1551); reimpresión minuciosa de Gordon y Elizabeth Roberts (TGR Renascent Books, 2009).
Fuentes secundarias:
Asper, Markus «The two cultures of mathematics in ancient Greece», en Eleanor Robson y Jacqueline Stedall (edit.), The Oxford Handbook of the History of Mathematics (Oxford University Press, 2009), pp. 107-132.
Singh, Simón, El enigma de Fermat (Editorial Planeta, 1998).
Wardhaugh, Benjamín «Mathematics in English printed books, 1473-1800: a bibliometric analysis», Notes and Records ofthe Royal Society, 63(2009): 325-38.
2. ¿Qué son las matemáticas y quiénes son los matemáticos?
Fuentes primarias:
The Suan shu shu, writings on reckoning: a translation of a Chinese mathematical collection of the second century BC, with explanatory commentary, trad. de Christopher Cullen (Needham Research Institute, 2004).
Fibonaccis Líber abad: Leonardo Písanos book of calculation, trad. L. E. Segal (Springer, 2002).
Fuentes secundarias:
Cullen, Christopher, «People and numbers in early imperial China», en Eleanor Robson y Jacqueline Stedall (edit.), The Oxford Handbook ofthe History of Mathematics (Oxford University Press, 2009), pp. 591-618.
Lloyd, G. E. R., «What was mathematics in the ancient world?», en Eleanor Robson y Jacqueline Stedall (edits.), The Oxford Handbook ofthe History of Mathematics (Oxford University Press 2009), pp. 7-25.
Wardhaugh, Benjamin, «Poor Robin and Merry Andrew: mathematical humour in Restoration England», BSHM Bulletin, 22(2007): 151-9.
3. ¿Cómo se difunden las ideas matemáticas?
Fuentes primarias:
Los trece libros de los Elementos de Euclides en MS D’Orville 301, extraído de 888,
http://www.claymath.org/library/historical/euclid/ último acceso en noviembre de 2011.
Joyce, David, «A Quick Trip through the Elements», compilado en 2002, http://alephO.clarku.edu/~djoyce/java/elements/trip .html, último acceso en enero de 2012.
Barrow-Green, June ««Much necessary for all sortes of men»: 450 yesar of Euclids Elements in English», BSHM Bulletin, 21(2006): 1-25.
Imhausen, Annette, «Traditions and myths in the historiography of Egyptian mathematics», en Eleanor Robson y Jacqueline Stedall (edit.), The Oxford Handbook ofthe History of Mathematics (Oxford University Press, 2009), pp. 781-800.
Katz, Victor (ed.), The mathematics of Egypt, Mesopotamia, China, India, and Islam: a sourcebook (Princeton University Press, 2007).
Netz, Reviel y Noel, William, El código de Arquímedes: la verdadera historia del manuscrito que podría haber cambiado el rumbo de la ciencia (Temas de Hoy, 2007).
Robson, Eleanor, Mathematics in ancient Iraq: a social history (Princeton University Press, 2006).
Rossi, Corinna, «Mixing, building, and feeding: mathematics and technology in ancient Egypt», en Eleanor Robson y Jacqueline Stedall (edit.), The Oxford Handbook ofthe History of Mathematics (Oxford University Press, 2009), pp. 407-28.
Wardhaugh, Benjamín, How to read historical mathematics (Princeton University Press, 2010).
4. El aprendizaje de las matemáticas
Fuentes primarias:
Cuadernos de copia de la colección de John Hersee que posee la Mathematical Association, en la biblioteca David Wilson Library de la Universidad de Leicester.
Fuentes secundarias:
Hartveit, Marit, «How Flora got her cap», BSHM Bulletin, 24(2009): 147-58.
Robson, Eleanor, Mathematics in ancient Iraq (Princeton University Press, 2008).
Thanailaki, Polly «Breaking social barriere: Florentia Fountoukli (1869-1915)», BSHM Bulletin, 25(2010): 32-8.
5. Las matemáticas como medio de vida
Brentjes, Sonja, «Patronage of the mathematical Sciences in Islamic societies», en Eleanor Robson y Jacqueline Stedall (edit.), The Oxford Handbook of the History of Mathematics (Oxford University Press, 2009), pp. 301-27.
6. Las matemáticas por dentro
Fuentes primarias:
Euclides, The fírst six books ofthe Elements of Euclid, bellamente reproducidos en color a partir del original de Oliver Byme de 1847 por Wemer Oechslin y Petra Lamers-Schutze (Taschen, 2010).
Euclides, Elements, edición coloreada de Oliver Byrnes de 1847 combinada con la versión interactiva de David Joyce de 2002 http://www.math.ubc.ca/~cass/Euclid/byrne.html , último acceso en enero de 2012.
Fuentes secundarias:
Van Brummelen, Glen, «Filling in the short blanks: musings on bringing the historiography of mathematics to the classroom», BSHM Bulletin, 25(2010): 2-9.
7. La historiografía evolutiva de las matemáticas
Mann, Tony, «From Sylvia Plath’s The Bell Jar to the Bad Sex Award: partial account of the uses of mathematics in fiction», BSHM Bulletin, 25(2010): 58-66.
Relación de ilustraciones
1. Colourwash («aguada de color»), de Tatjana Tekkel Peppé a quien, según ella misma, no se le dan bien las matemáticas
© Fotografía de Jonathan Peppé
2. Esquema básico que propone John Dee en su prefacio a los Elementos de Euclides, 1570
© The British Library Board
3. Primera página de la primera edición impresa de los Elementos de Euclides, de 1482
© Wikipedia Commons
4. Portada del libro de aritmética de Robert Smith, Academia Greenrow, 1832
© Fotografía Mary Walmsley
5. Un problema de trigonometría ilustrado y resuelto por Robert Smith, Academia Greenrow, 1832
© Fotografía Mary Walmsley
6. Primera página del libro de ejercicios de Ann Weetman, fechada el 20 de octubre de 1834 («Oct 20th 1834»).
© Fotografía Mary Walmsley
7. Una de las últimas páginas del libro de ejercicios de Ann Weetman, fechada el 12 de abril de 1837 («April 12 1837»).
© Fotografía Mary Walmsley
8. Demostración del teorema de Pitágoras del sabio Thabit ibn Qurrá
9. Demostración de Euclides del teorema de Pitágoras
10. Demostración de Oliver Byrne del teorema de Pitágoras © Wikipedia Commons
Notas: