El geómetra revolucionario
Félix García
Litton dejó dicho:
"El pasado no ha muerto mientras los libros vivan.
Y yo añado ahora:
"El futuro vivirá aún cuando yo muera. Quedarán mis libros A todos los que los lean.
El geómetra trata siempre de representarse más o menos las figuras que estudia, pero sus representaciones no son para él más que instrumentos.
Henri Poincaré
Se dice que Euclides triunfó en un punto: en su forma de trabajar con las rectas paralelas. Y no intentó encubrir por medio de un axioma plausible su incapacidad para demostrar cierta propiedad de las líneas coplanarias. Dejó sin demostrar su V postulado, el que conocemos como postulado de las paralelas, probando realmente su recíproco, exponiéndose al ridículo por ello. Se hicieron vanos intentos a lo largo de la historia para eliminar este postulado de la herencia de sus Elementos, primero deduciendo postulados equivalentes y luego tratando de demostrar éstos. En palabras de Herbert Westren: “La venganza de Euclides llegó con el descubrimiento de la geometría no euclídea en el siglo XIX, cuando se hallaron motivos fundamentales de dicho postulado”.
Gauss fue uno de los interesados por la geometría en general y por la no euclídea en particular. Y en relación con esta última también debemos agregar a la lista al inglés Wallis y al italiano Saccheri, entre otros varios. Fueron todos ellos los precursores de esa nueva geometría que apuntaba a convertirse en el hallazgo más importante desde los tiempos de los primeros geómetras de Mesopotamia, Grecia y Egipto. De nuevo, todos ellos se preocuparon por el aparente misterio que encerraba el postulado de las paralelas: era como un curioso elemento áspero dentro de la suave y bien armada lógica de los antiguos, cuya eliminación parecía tan deseable. Gauss fue el primero, aunque por caminos diferentes y al mismo tiempo que lo hicieron el húngaro Bolyai y el ruso Lobachevski, en ofrecer una explicación satisfactoria de la anomalía, como lo demuestra su diario. No obstante, el asunto lo guardó para sí. Temió verse sometido al ridículo por los seguidores de la filosofía kantiana. La realidad fue que el interés se extendió naciendo una nueva rama de la geometría que conocemos como geometría hiperbólica. No fue una simple novedad en las matemáticas, fue una auténtica revolución. Se opuso, pero de forma muy práctica, a Euclides y, aún más, a las opiniones de la generación que la vio nacer. Se abolía así su dictadura y se destruía para siempre la concepción kantiana del espacio.
Verdaderamente fue éste uno de los casos más notables entre todos los descubrimientos que ha apuntado la ciencia. En el curso de unos veinte años, varios hombres, de forma independiente unos de otros, como hemos dicho, conciben la chocante idea de desechar el V postulado y comenzar a trabajar de forma no euclídea. Eso no se le había ocurrido antes a nadie, a pesar de los muchos matemáticos que se habían ocupado precisamente en este problema.
Las geometrías no euclídeas constituyeron la infraestructura para que otras ciencias y técnicas nos sorprendieran con avances espectaculares. Además, el promotor de los métodos proyectivos, el inglés Arthur Cayley, mostró que las geometrías básicas no euclídeas, es decir, las hiperbólicas desarrolladas por Bolyai y Lobachevski, y la geometría elíptica, creada por Riemann, podían derivarse también como casos especiales de la geometría proyectiva. No es de extrañar que Cayley dijera en este sentido que: “La geometría proyectiva es toda la geometría”.
Los grandes matemáticos a caballo entre el siglo XIX y el XX, como Poincaré, Klein y Fuchs, idearon modelos que hacían más transparentes las teorías de la geometría no euclídea, sus propiedades y resultados, con lo que a partir de ellos emergieron nuevos estudios matemáticos.
Transcurrió mucho tiempo desde su muerte hasta que János Bolyai fuera reconocido internacionalmente como auténtico descubridor de la geometría absoluta, tipo de geometría no euclídea que llega más lejos que la hiperbólica de Lobachevski. Trataremos en esta obra de analizar las causas de este destierro científico de Bolyai y mostrar su dura y difícil labor a pesar de las discrepancias que tuvo con su padre y del alejamiento que sufrió, en un principio, por parte de matemáticos insignes de su época como Gauss.
András Prékopa y Emil Molnár aseguran que “János Bolyai es la figura más grande en la historia de la matemática húngara”. Y basan esta afirmación categórica en que supo resolver un viejo problema de la geometría que tenía más de dos mil años: el problema de las paralelas. Aunque es verdad que la gloria de su descubrimiento debe ser compartida con Lobachevski. Algunos historiadores de la ciencia matemática están de acuerdo en asegurar que tal descubrimiento significa una gran revolución en la geometría. A partir de ahí ha quedado más claro que geometría y realidad pueden ser cosas diferentes y que, por tanto, la geometría no pertenece a las ciencias naturales, entre las que nació en Egipto y Grecia.
Desde hace ya mucho tiempo las geometrías no euclídeas han tenido entrada en las matemáticas como rama indiscutible de las mismas. Y ha ocurrido que los matemáticos se han habituado rápidamente a las nuevas ideas representadas por esas geometrías. En un principio la cosa fue más difícil con los físicos, pero el profundo y atrevido discurso de Riemann con motivo de la presentación de su tesis doctoral en 1854, Sobre las hipótesis que yacen en el fondo de la geometría, abrió la puerta y mostró aquí el camino debido, aunque éste no fuera frecuentado hasta el siglo XX con los intentos de encontrar nuevas teorías para la gravitación, para la cosmología y para las mediciones astronómicas. Y hace algunos años añadía Paul Karlson:
“lo más difícil es, como de costumbre, contentar a los filósofos, pero esto no es cosa que pueda exigirse ni esperarse, por lo cual la discusión sobre la posibilidad de un Universo no euclídeo todavía no se ha acallado”.
La geometría de Bolyai-Lobachevski ha permitido el desarrollo de las teorías de la física ya dentro del siglo XX y ha servido de base para ampliar muchos campos de las matemáticas y de otras ciencias. El propio Einstein hizo uso implícito de la geometría hiperbólica en sus teorías sobre la trayectoria de la luz proveniente de las estrellas lejanas.
No ha resultado fácil encontrar información de base y contrastada para acometer esta biografía de János Bolyai y completarla con sus trabajos y obras matemáticas. Hemos recurrido a muchas fuentes que tratan la cuestión de una forma parcial, algunas de ellas con datos más bien de poca relevancia o que no profundizan en su vida, hechos y obra. En otros casos hemos podido deducir información valiosa, sobre todo al examinar textos clásicos o de autores prestigiosos y especialistas en las matemáticas. He aquí cómo hemos conseguido adentrarnos en el tema.
Los aniversarios cien, ciento cincuenta y doscientos del nacimiento de Bolyai siempre se han conmemorado con una serie de conferencias impartidas en húngaro. El primero fue celebrado en Kolozsvár y los dos últimos en Budapest. El bicentenario resultó especial, no sólo por el número de años transcurridos desde 1802, sino también porque la investigación de Bolyai había alcanzado auténtica carta de naturaleza en el mundo de las matemáticas. En esta ocasión, la Academia Húngara de Ciencias y otras instituciones de Hungría y de fuera de ese país organizaron una conferencia internacional, que se celebró del 6 al 12 de junio de 2002 en la sede central de la Academia en Budapest, para tratar exclusivamente sobre la geometría hiperbólica. Las ponencias fueron recogidas en un valioso volumen que además de rendir tributo al gran científico ha servido para exponer todos sus logros de forma contrastada.
Capítulo 1
La invención de la geometría
Deja que el hombre se dedique al arte que conoce. Cicerón, Disputaciones tusculanas, I, XVIII
§. Los geómetras de la Grecia antigua
“La geometría encarna una forma de racionalidad que se encuentra en diversos aspectos de la civilización griega antigua, como el urbanismo, las artes o las teorías políticas. No obstante, es una disciplina relativamente reciente; no tiene ni dios, ni musa. En este universo, el estudio de las figuras, de su construcción y de su medida, ha seguido un camino original desde el siglo V antes de nuestra era. Su evolución no se puede disociar de la ciudad de Alejandría, cuyas instituciones eruditas, como fueron su Museo y su Biblioteca, han determinado lo que ha llegado hasta nosotros: algunos tratados y una tradición de problemas que, por su rigor y riqueza, suscitan aun hoy día la curiosidad del lector”.
Éstas son algunas de las frases con las que Bernard Vitrac, investigador francés del CNRS, prologa un extenso capítulo dedicado a la Invención de la geometría por los griegos y su posterior evolución.
La geometría suministra el primer ejemplo histórico de la presentación axiomática de una disciplina matemática. Ahora bien, el conjunto clásico de postulados sobre el que Euclides fundamentó su sistema ha resultado insuficiente para la deducción de los conocidos teoremas de la llamada geometría euclídea; por eso, y como veremos más adelante, ha sido revisado y completado, e incluso cambiado en tiempos recientes, como nos muestran las geometrías no euclídeas.
Hoy día disponemos de varios sistemas adecuados de postulados tanto para la geometría euclídea como para las no euclídeas. El más relacionado con el sistema de Euclides es probablemente el de Hilbert.
Los pueblos antiguos concibieron el espacio pero sin el número. Ha sido en época más moderna, principalmente con René Descartes, cuando surgió la relación entre el número y el espacio a través de las coordenadas. Por ello los antiguos no tuvieron más remedio que partir de propiedades experimentales que consideraban falsamente como evidentes, para todo aquello que tuviera que ver con la razón pura, y se esforzaron en agruparlas en proposiciones coherentes. Filosofía que, incluso hoy día y en ciertos temas, aún conservamos. No cabe duda de que si se tiene en cuenta que ellos ignoraban el método adecuado, entonces los resultados que obtuvieron de esa ignorancia resultan de lo más admirable para la época. Pero esto no debe perpetuar tales hábitos. No debe confundirse el interés histórico con la formación del ingenio, ya que ello nos encadenaría, por ejemplo, a Viète en lo relacionado con el álgebra o a Euclides en lo que se refiere a la geometría. Esos vínculos fueron rotos por geómetras como Bolyai.
En los orígenes de la geometría se observa, desde nuestra perspectiva actual, la confirmación del fundamento experimental al que nos hemos referido, así como el carácter social de la ciencia matemática.

Pitágoras (detalle del cuadro La escuela de Atenas de Rafael).
La geometría nació cuando se tuvo necesidad práctica de ella, por ejemplo, en el valle del Nilo hace más de cuatro mil años para restablecer el amojonamiento de las tierras después de una inundación o en China, aunque allí el nivel de conocimientos no pasó de un simple empirismo. También en Mesopotamia despiertan esos albores trasladados al resto del mundo por los fenicios. Pero como advierte Babini:
“entre la época de los papiros egipcios y la época a la que pertenecen las primeras noticias de un saber griego, transcurre más de un milenio, lapso en el cual el mar Egeo es teatro de acontecimientos en gran parte todavía desconocidos”.
Cuando irrumpe en el escenario la Grecia antigua, su ciencia se construye con ayuda de sacerdotes y escribas egipcios y caldeos y se siente atraída por los descubrimientos más simples de la geometría. Primero Tales y después Pitágoras son los personajes a los que es preciso atribuir la gloria de quienes, a partir de las cosas más simples, han sido capaces de abstraer los conceptos de línea, ángulo y superficie. Fueron los auténticos inventores de la prueba deductiva, tanto en geometría como en matemáticas. El teorema de Pitágoras se presenta como una cosa absolutamente nueva en la historia de la humanidad, con la que la ciencia parece anunciarse sirviéndose de la geometría, que, a su vez, se compone de leyes y de teorías.
En opinión de Tobías Dantzing (manifestada en su obra El número, lenguaje de la ciencia),
“la mentalidad general de los griegos permanece encerrada en una singular contradicción. Por una parte, su Universo no comprendía más que cosas inmediatamente accesibles a los sentidos; por otra, su talante de espíritu era esencialmente aristocrático, ya que tenían por banales y vulgares ocupaciones tales como la de artesano, por muy ingeniosos y elegantes que fueran los procedimientos que se emplearan”.
§. Geometría y civilización
En lo que concierne al origen de la geometría, la explicación que tiene actualmente más adeptos fue propuesta por el historiador griego Heródoto de Halicarnaso en el siglo V antes de nuestra era. Cuenta las guerras entre griegos y persas, lo que le sirve para describir las costumbres y las instituciones de los pueblos. El Libro II, Euterpe, está consagrado a Egipto y contiene la mención más antigua de la palabra griega geometría en dialecto jónico, que es el empleado por Heródoto. Los sacerdotes egipcios le confiaron el siguiente secreto del rey Sesostris[1]:
“Los sacerdotes también me dijeron que este rey repartió el suelo entre todos los egipcios, concediendo a cada habitante un lote cuadrangular de extensión uniforme; y, con arreglo a esta distribución, fijó sus ingresos, al imponer el pago de un tributo anual. Ahora bien, si el río se le llevara a alguien parte de su lote, el damnificado acudía al rey y le explicaba lo sucedido; entonces, el monarca enviaba a algunas personas a inspeccionar y medir la disminución que había sufrido el terreno para que, en lo sucesivo, pagara una parte proporcional del tributo impuesto. Y, a mi juicio, para este menester se inventó la geometría, que pasó luego a Grecia. Pues el polo, el gnomon y la división del día en doce partes los griegos lo aprendieron de los babilonios”.
Heródoto añade en otra parte que los griegos, no especifica quién, importaron ese conocimiento a su país. Proclo, tal vez siguiendo la opinión de Eudemo de Rodas, afirma que se trató de Tales.
Como hemos visto, Heródoto emplea en su descripción la palabra geometría, 𝛾𝜀𝜔μ𝜀τρια, constituida por el prefijo griego geo, 𝛾𝜀𝜔, la tierra, y por el verbo medir, μ𝜀τρ𝜀ω: medición de la tierra.

Platón (detalle del cuadro La escuela de Atenas de Rafael).
Con ello surge además la idea de que la geometría ha nacido de la agrimensura. Dado que la ciencia geométrica también parece haberse utilizado en Egipto para medir la altura de la gran pirámide, surge la tesis de que existe, en su origen, una relación directa entre la geometría y la determinación indirecta de distancias inaccesibles. Parece que fue Tales quien midió la altura de la pirámide en presencia del rey Amasis. Caben otras definiciones, esta vez ya de los griegos. Aristófanes, célebre poeta cómico ateniense, en su obra Las nubes dice que la geometría
“es la medida de toda la tierra habitada, no de un pequeño territorio que se distribuye en partes en una colonia”.
La tradición griega antigua relaciona esta geometría, a la que también llamó geografía, con otros personajes como Anaximandro de Mileto (siglo VI antes de nuestra era), y Heródoto se burla de las primeras cartas jónicas del mundo debido a las numerosas y arbitrarias simetrías que contenían. A partir de esa época, existen dos formas de considerar el desarrollo de la geometría: unas veces reseñando su modesto origen empírico, la agrimensura, otras, su implicación en las investigaciones más especulativas de la información sobre la naturaleza, como la estructura geométrica del cosmos, la descripción y carta del mundo habitado. La sombra de esta doble faceta se ha prolongado hasta nuestros días.
La geometría ha constituido siempre una ciencia que no se contenta con medir sino que además compara figuras: en cuanto a la forma, estudia la semejanza; en cuanto a la magnitud, compara longitudes y áreas; en cuanto a la posición, trata de tangencias, de relaciones, como inscrito o circunscrito. En los Elementos de Euclides nos volveremos a encontrar con esta dualidad entre las características geométricas de los objetos y las relaciones entre objetos.
§. Euclides
Hacia finales del siglo IV a.C. la ciencia matemática emigró de Grecia a Egipto. Alejandro Magno había conquistado el mundo griego con sus victorias y concibió la idea de crear un gran imperio.

Euclides (detalle del cuadro La escuela de Atenas de Rafael).
Pero murió joven, a los 33 años. Durante su visita a Egipto fundó la ciudad de Alejandría, situada en el litoral occidental del delta del Nilo, ciudad que se convirtió en la más Importante del mundo mediterráneo. Pasó a ser el centro del nuevo comercio entre Europa, Arabia y la India y geográficamente era el lugar de reunión adecuado para griegos, judíos y árabes.
Los alejandrinos supieron atraer a su ciudad a los científicos más destacados de su tiempo. Durante siglos continuó siendo el centro espiritual del mundo, y en el primer siglo de su existencia vivieron allí los tres matemáticos más grandes de la Antigüedad: Euclides, Arquímedes y Apolonio.
Euclides fue el primer guía de la escuela alejandrina. Se le describe como un hombre apacible y mesurado, lleno de buena voluntad con todo aquel que se propusiera mejorar las matemáticas. Sintió mucho respeto y reconocimiento por los que le precedieron, de forma que trató de modificar lo menos posible sus obras. Se dice que era muy retraído hacia todos los trabajos que realizaba y de los resultados que alcanzaba, de tal forma que sus contemporáneos y sucesores tenían la inclinación a olvidar al hombre frente a su obra. Así, cuando hablaban de Euclides pensaban, casi como hacemos hoy día, en sus trabajos y, ante todo, en sus Elementos, y poco en el propio sabio. En la Edad Media se llegó a más, negándose casi por completo la propia existencia del hombre: parecía que Euclides no hubiera vivido.
No siempre los matemáticos son tan modestos ni saben anteponer, de la manera que lo hizo Euclides, las cosas a sus propios méritos. Así, por ejemplo, se cuenta de Sturm, especialista francés en álgebra y teoría de números, y del que procede un importante teorema relativo a las funciones algebraicas conocido ya durante su vida con el nombre de teorema de Sturm, que en sus últimos años y durante la docencia de sus lecciones, decía con toda seriedad: Ahora, señores, llegamos a un bello teorema cuyo nombre tengo el honor de llevar. De Euclides no se hubiera podido pensar una manifestación semejante: su modestia, unida a un rigor inflexible y la máxima veneración por la ciencia, le impedían hablar de otra cosa que no fueran sus hechos, sus trabajos.
Su obra cumbre se caracterizaba por el rigor de la sistematización. En los Elementos, según comentario de Proclo
“concluía muchas cosas comenzadas y, además de esto, apoyaba en demostraciones irrefutables lo que sus antecesores sólo habían demostrado a la ligera”.
A este mismo respecto, decía Lagrange que
“aprender geometría sin conocer a Euclides sería como querer aprender latín o griego en los libros modernos escritos en esos idiomas sin consultar los textos originales”.
No es nuestro objetivo hablar de la obra de Euclides más allá de lo relacionado con la geometría. Sólo reseñar unas notas sobre el maestro. El tratado Elementos es uno de los escritos matemáticos antiguos más voluminosos. Uno de los méritos más notables que como autor tiene Euclides en la obra fue haber distribuido la materia que contenía de acuerdo con unos criterios muy determinados, además de haberla dotado de una estructura deductiva local. Los resultados están agrupados en función de los objetos a los que se refiere. Se distinguen tres grandes subconjuntos: los libros de la geometría plana, los libros de la aritmética y los libros de la estereometría. Todo ello equivale al estudio de la figura plana, del número y de la figura sólida.

Las proposiciones 5, 6 y 7 del Libro II de los Elementos de Euclides en la edición de E. Ratdolt (Venecia, 1482).
Esta clasificación en elementos conduce a resaltar las figuras más simples, como son los triángulos, cuadrados, rectángulos, los paralelogramos y el trapecio, en los libros I y II; el círculo y los segmentos, en el libro III; y los polígonos regulares inscritos o circunscritos en un círculo, en el libro IV. Una distribución semejante emplea para las figuras sólidas.
Pero Euclides triunfó en un punto: en su forma de trabajar con líneas paralelas. Y nos interesa resaltar esta cuestión puesto que será nuestro punto de apoyo y arranque para lo que pretendemos describir y desarrollar hasta llegar a relatar la vida y la obra de János Bolyai. Por ello, es necesario aclarar que Euclides no intentó encubrir por medio de un axioma plausible su incapacidad para demostrar cierta propiedad de las líneas paralelas coplanarias. Muchos de sus otros supuestos, o bases necesarias para sus argumentos, eran tales que dispondrían razonablemente del asentimiento general. Pero en el caso de las líneas paralelas comenzó con un supuesto elaborado que conocemos como el postulado de tas paralelas: si una línea recta corta a otras dos líneas rectas de manera que los dos ángulos interiores que se forman en el mismo lado no sumen más de dos ángulos rectos, esas líneas rectas prolongadas continuamente se cortarán a la larga en el lado en el que los ángulos son menores que dos rectos.
Dejando esto sin demostrar, y probando en realidad su recíproco, Euclides se expuso al ridículo y a los ataques. Seguro que sus críticos dirían que éste no era un supuesto adecuado como los otros suyos, sino más bien susceptible de demostración. La venganza de Euclides llegó, como se dijo anteriormente, con el descubrimiento de las geometrías no euclídeas en el siglo XIX de la mano de Gauss, Bolyai y Lobachevski.
Capítulo 2
Biografía de los Bolyai
Quienes no aspiran a nada, no arriesgan nada y no sirven para nada.
Beaumarchais
§. La familia Bolyai: los orígenes
Según el profesor húngaro, miembro de la Academia Húngara de Ciencias, Andrés Prékopa, es mucha la información que se tiene de los dos Bolyai, padre e hijo: “Fue Ferenc Schmidt, un arquitecto de Temesvár (hoy Timisoara) y después de Budapest, el primero, el más cuidadoso y esforzado investigador de sus obras y de sus vidas”. Su padre, Antal Schmidt, también arquitecto, coincidió con János cuando trabajaba como ingeniero militar en Temesvár, entre los años 1823 y 1826.
HoüelGuillaume Jules Hoüel nació el 7 de abril de 1823 en Thaon, región de Calvados, Francia, y falleció el 14 de junio de 1886, en Périers-sur-le-Dan, Francia. Fue alumno del liceo de Caen y más tarde del colegio Rollin. En 1843 entra en la Escuela Normal Superior donde se gradúa.
Será profesor en Burdeos, Pau y Caen. En 1855 obtiene su doctorado en la Sorbona de París por sus investigaciones sobre mecánica celeste. En 1859 dirigirá la cátedra de matemática pura en la Facultad de Ciencias de Burdeos.
Publicó un trabajo sobre geometría en 1863, cuando aún desconocía las investigaciones sobre geometría no euclídea llevadas a cabo por János Bolyai, aunque sí estaba al tanto de los trabajos que se desarrollaban en Europa alrededor de la teoría de las paralelas. Comenzó a interesarse por la geometría de Bolyai y Lobachevski al conocer el trabajo de ambos, sirviendo de traductor al francés de los trabajos más importantes tanto de Bolyai como de Beltrami, Helmholtz y Riemann.
A sugerencia de Hoüel, Ferenc Schmidt reunió cierto material de los trabajos de Bolyai que más tarde le sirvió para redactar la primera biografía de János.
Hoüel construyó tablas de logaritmos y trabajó sobre las perturbaciones planetarias.
Además, Ferenc pudo escuchar cosas muy interesantes acerca de János de la propia boca del padre de éste y no ahorró esfuerzos para reunir toda la información que le fue posible sobre los Bolyai. Su mejor pasatiempo fueron las matemáticas y las ciencias naturales. Mantuvo correspondencia con científicos de distintos países del occidente europeo, solicitándoles cualquier información sobre libros científicos publicados en sus respectivos países. Los datos recogidos por Ferenc se encuentran en su obra, publicada en 1868, titulada: Sobre la vida y los trabajos de los dos matemáticos húngaros Farkas y János Bolyai de Bolya.
Veamos en primer lugar de quién y de dónde proceden las más importantes fuentes biográficas de los Bolyai para, de ese modo, fundamentar las relaciones científicas entre padre e hijo, y las que mantuvieron con otros matemáticos de su época. Guillaume Jules Hoüel, profesor de historia de las matemáticas en Burdeos, se convirtió en uno de los primeros descubridores del trabajo de János Bolyai y fue la conexión francesa de la que se sirvió Ferenc Schmidt. Hoüel tradujo al francés el Apéndice de János añadiéndole la biografía preparada por Schmidt. Este último facilitó la mayor parte de la información recibida a Paul Stäckel, que la recogió en su obra en dos volúmenes Farkas y János Bolyai. Investigaciones geométricas.
§. Farkas Bolyai
Las vidas de padre e hijo estuvieron siempre ligadas por el lazo común de la ciencia, especialmente de las matemáticas. Por ello comenzaremos hablando de Farkas, nombre que significa lobo en húngaro. También se le cita con frecuencia por la traducción alemana de su nombre: Wolfgang. Durante su juventud estuvo aquejado de una enfermedad en los ojos, lo que le hizo desarrollar una memoria prodigiosa. Su dominio de la aritmética y de las lenguas le convirtió en preceptor del hijo de un noble a la temprana edad de doce años.
Los Bolyai eran húngaros originarios de la Transilvania, provincia rumana desde el tratado de Trianón de 1920. El padre de János nació el 9 de febrero de 1775 en Bolya, cerca de Nagyszeben. Provenía de una familia de Hungría de antiguo linaje. Sus antecesores tomaron posesión del castillo fortificado de esa ciudad a principios del siglo XIV. Algunos miembros de su familia fueron valientes soldados pero, en la primera mitad del siglo XVII, un tal János Bolyai perdió el castillo durante su cautiverio en Turquía. A partir de ahí, la fortuna de los Bolyai fue poco a poco perdiéndose y Gaspar Bolyai, padre de Farkas, heredó únicamente una pequeña porción de tierra cerca de Bolya. A esa finca se le unió posteriormente otra cercana a Domáld, villa próxima a Marosvásárhely (actualmente la ciudad rumana de Tárgu Mures), perteneciente a la herencia de Krisztina Pávai Vajna, esposa de Gaspar. Vásárhely fue el nombre primitivo de Marosvásárhely y era la ciudad más grande del pueblo szákely, los húngaros del extremo este de Transilvania.
Farkas asistió, entre los 6 y los 13 años, al colegio luterano y calvinista de Nagyenyed. Además, el barón Simón Kemény pagó a Farkas los servicios educativos de su hijo, entablándose entre ambos jóvenes una buena amistad, de manera que a partir de 1790 estudiaron juntos durante cinco años en la Escuela Calvinista de Kolozsvár. En esa época el talento de Farkas para las matemáticas fue desarrollándose progresivamente, aunque también mostraba verdadero interés por la música, en especial por el violín, el dibujo y el teatro, para el que escribió varias obras además de trabajar como actor. En el otoño de 1795 Farkas dejó Nagyenyed y se trasladó a Gotinga para proseguir allí sus estudios. Fue acompañado por su amigo y compañero, Simón Kemény hijo. Pero cayó enfermo y tuvo que regresar de nuevo a Hungría, aunque por poco tiempo: en la primavera del año siguiente se reunió de nuevo con Simón. Estuvieron varios meses en Jena y más tarde, en octubre del mismo año, entró en la Universidad de Gotinga. El hecho de ser un estudiante becado dentro de la universidad le aseguró a Farkas la posibilidad de pagar los costes de su mantenimiento y de seguir estudiando y aprendiendo. Todos los que conocieron a Farkas decían de él que era un hombre de pensamiento profundo y de carácter bonachón.
Fue precisamente en Gotinga donde Farkas, a sus diecinueve años, encontró a Gauss, el príncipe de los matemáticos, con el que hizo una perdurable amistad. Después de la muerte de éste último, la rica y fructífera correspondencia mantenida entre ambos constituiría una colección de documentos extremadamente valiosos para la historia de las matemáticas. Farkas envió en 1855 las cartas que había recibido de Gauss al profesor Wolfgang Sartorius von Waltershausen, que en aquel entonces estaba trabajando en una biografía de Gauss. Señalada su amistad con el príncipe de los matemáticos, Farkas fue el único hombre que supo comprender sus consideraciones metafísicas acerca de la matemática.

Farkas Bolyai
Después de algunos años transcurridos en Gotinga, Farkas regresó a Kolozsvár en 1799. Comenzó trabajando como tutor familiar y luego contrajo matrimonio con Susana Árkosi Benkó, hija de un enfermero y barbero. La pareja se movió muy pronto de Kolozsvár a Domáld, donde permaneció hasta el otoño de 1802. Poco después regresaron de nuevo a Kolozsvár, en espera del nacimiento de su primogénito János, nacimiento que ocurrió el 15 de diciembre de ese año.
En enero de 1804 Farkas ya había obtenido una plaza como profesor de matemática, física y química en el Colegio Calvinista Reformado de Marosvásárhely, plaza que conservaría durante 47 años hasta su retiro en 1851. El colegio donde Farkas ejerció su docencia había sido construido a mediados del siglo XIV, en parte sobre las ruinas de la iglesia de San Nicolás destruida hacia el 1600. La escuela comenzó a impartir clases en el siglo XV1I1 cuando los estudiantes calvinistas fueron expulsados de Sárospatak donde habían estado instalados.

El Colegio Calvinista Reformado de Marosvásárhely donde estudió János Bolyai .
El matrimonio Bolyai tuvo, además de János, una hija que falleció a edad muy temprana. El matrimonio no fue nada feliz debido, según comentarios del propio Farkas, a que su suegra era la causante de frecuentes disgustos entre la pareja, además de que pretendía separarlo de su mujer. Por otra parte Susana era neurótica, mal que se manifestó ya en los primeros años de casados. El matrimonio fue a peor desde 1817. Ella falleció en 1821, después de largos sufrimientos.
Volviendo a la vida de Farkas como profesor, añadir que éste era pagado por sus clases en trigo, vino, sal, cerdo, cordero y leña. Le concedieron además una casa con jardín y una paga dineraria.
Farkas se casó por segunda vez en 1824 con Teresa Somorjai Nagy, que era veintidós años más joven que él. Era hija de un tendero de Marosvásárhely. Tuvieron dos hijos, Gergely y Berta. Esta última falleció a los pocos años de su nacimiento. Teresa era también de salud delicada y murió joven, en 1833. En cualquier caso, fue un matrimonio mucho más tranquilo y relajado que el primero.
Farkas Bolyai fue un hombre muy inteligente, uno de los matemáticos más importantes de Hungría y un precursor, como veremos, del descubrimiento de las geometrías no euclídeas. Se interesó toda su vida por los fundamentos de la geometría y en especial por el axioma de las paralelas. Después de publicar varios manuales escolares, entre 1832 y 1833 da a luz su obra didáctica Tentamen, escrita en latín en dos volúmenes. Su título completo es Tentamen juventutem studiosam in elementa matheseos purae introducenci (Intento de introducir a la juventud estudiosa en los elementos de la matemática pura). Estaba dedicado a los alumnos de las clases superiores de su colegio y en esta obra prueba a establecer de forma rigurosa y sistemática los fundamentos de la geometría, de la aritmética, del álgebra y del análisis, es decir, constituía un resumen de toda la matemática de su tiempo. Gauss comentó positivamente el alto grado de precisión que se notaba en este trabajo.
Farkas fue elegido miembro correspondiente de la Academia de Ciencias de Hungría el 9 de marzo de 1832, pero no en el departamento de matemáticas, sino en el de ciencias naturales. La base para su elección fue la publicación en 1830 de su libro Elementos de aritmética. Parece que esa asignación a un departamento que realmente no era el suyo se debió a que la citada obra de Farkas había sido la única, hasta la fecha, redactada en húngaro y no en latín, como era el caso del Tentamen. La Academia de Ciencias era la sucesora reciente de otra sociedad dedicada a promover y desarrollar la lengua húngara, lo cual podría explicar la actitud del secretario del tribunal, Gábor Dóbrenti, de no incluirlo en el departamento de matemáticas, puesto que las anteriores obras de Farkas estaban todas ellas escritas en latín: contaba, pues, nada más que con una obra meritoria para obtener la plaza.
Farkas Bolyai no sólo era un talento para las matemáticas, también hay que resaltar otras cualidades propias de un auténtico genio en otras muchas labores. Así, por ejemplo, debido a la escritura de obras para el teatro, consiguió alcanzar un puesto en la historia de la literatura húngara. Por sus conocimientos de música acostumbraba a impartir clases privadas de ese arte e incluso dio conferencias sobre teoría de la música. Era un buen conocedor de lenguas: se desenvolvía con gran soltura en húngaro, alemán, latín y rumano, además de poseer conocimiento de otras varias. Era el invitado favorito de la alta sociedad local al haberse convertido en un divertido y gran conversador.
Otro de los pasatiempos favoritos de Farkas fue el diseño de estufas y hornos. Habiendo oído que la construcción de estufas económicas figuraba en la agenda de una reunión internacional a celebrar en Viena, puso manos a la obra con el objetivo de resolver el problema e inventó varios tipos de estufas, algunas de las cuales construyó él mismo. Como consecuencia, esas estufas estuvieron de moda en Transilvania durante mucho tiempo.
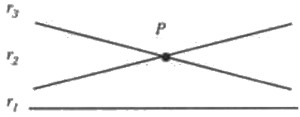
El axioma de las paralelasMuchos matemáticos han tratado en todas las épocas de deducir este postulado de los anteriores establecidos por Euclides. Pero todo ha sido en vano. Lo único que consiguieron fue elaborar enunciados equivalentes. Tal es el caso de Proclo, Saccheri, Lambert, Legendre, Lagrange y también Farkas Bolyai que, en su obra Tentamen, lo enunció así: “tres puntos no alineados pertenecen a una misma circunferencia"
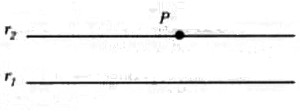
En su Tratado de geometría métrica, el gran matemático e ingeniero español Pedro Puig Adam escribe que “la necesidad de un axioma como éste para fundamentar la teoría del paralelismo fue advertida por Euclides, cuyo postulado fue enunciado de otra manera”. El enunciado equivalente al de Euclides que nos da el profesor Puig Adam, y también otros muchos, es como sigue: “por un punto exterior a una recta pasa una sola paralela a ella”. Este postulado permite asegurar la existencia de una paralela r2, y sólo una, por un punto exterior O a una recta r1.
Como puede apreciarse, este postulado afirma dos cosas: primera, la existencia de una recta que pasa por el punto exterior a otra dada y que es paralela a ella y, en segundo lugar, que esa recta es única. Entonces, ese postulado puede negarse todo él o sólo la segunda parte. Trabajando con la segunda alternativa, han nacido las geometrías no euclídeas.
En la misma obra citada se nos dice: “la forma poco intuitiva que tiene el postulado de Euclides, en comparación con los restantes que este geómetra estableció al comienzo de sus famosos Elementos, motivó, sin duda, que el propio Euclides hiciera el menor uso posible de él y que los geómetras posteriores se esforzaran en hallar del mismo una demostración ”. Durante más de veinte siglos se ha tratado de dar consistencia lógica a las geometrías no euclídeas, es decir, las que niegan tal postulado.
Otro de sus logros fue la construcción de un asiento con ruedas que se podía conducir con la ayuda de un volante y mover con los pies. Y también una casa colocada sobre ruedas y recubierta con techumbre de madera, precursora de las casas móviles.
En un determinado momento, se publicó una vacante en Transilvania para inspector general de bosques, plaza a la que se
presentó con el fin de aliviar sus penurias económicas. No fue admitido, pero debido a la preparación que tuvo que realizar, alcanzó un cierto grado de experiencia en técnicas forestales y fue capaz de escribir el primer libro sobre el tema en húngaro.
Farkas Bolyai falleció el 20 de noviembre de 1856. Según Orbán Balázs, fue su voluntad que no se hiciera ceremonia alguna, sólo el “sonar de la campana de la escuela. En su tumba no figuran ni epitafios ni inscripciones, sólo se plantó sobre ella un manzano que tenía en sus tierras, porque el famoso profesor Bolyai había sido también un especialista en horticultura. Su hijo János le tuvo en gran estima y consideración, y esa estima, según veremos más adelante, fue recíproca a pesar de las varias discusiones que mantuvieron ambos. Después del funeral, János dedicó a su padre un opúsculo.
§. Los primeros estudios
János Bolyai es una de las figuras más grandes y relevantes de la matemática húngara y tuvo una carrera fulgurante como matemático; muchos opinan que es el Copérnico de la geometría. Las obras publicadas de János quedan casi reducidas a un simple apéndice de veintiséis páginas en las que se pone fin a veintidós siglos de investigación infructuosa sobre el V postulado de Euclides o axioma de las paralelas. A János se le debe el establecimiento de la primera geometría no euclídea. Con este trabajo rompe uno de los monopolios de la geometría y prepara el camino para que la humanidad considere el espacio de diferente manera a como lo venía haciendo durante siglos.
János nació el 15 de diciembre de 1802 en la casa que sus abuelos maternos tenían en Kolozsvár. Pensaron que en esa ciudad su madre dispondría de mejores cuidados médicos que en Domáld, donde habían estado residiendo hasta el momento de acercarse el parto.
Su padre prestó la máxima atención en primer lugar al desarrollo físico de su hijo y se encargó luego personalmente, como había hecho el padre de Blaise Pascal, de su formación matemática: primero la salud, luego la ciencia.
Esto escribe Szénássy sobre la infancia de János: “A la edad de cuatro años podía distinguir ciertas figuras geométricas, conocía la función seno y era capaz de identificar las principales constelaciones. A los cinco años aprendió a leer por sí solo. Estuvo muy por encima de la media a la hora de aprender lenguas, principalmente el alemán, y música, de forma que a los siete años era capaz de tocar el violín haciendo tales progresos en este instrumento que muy pronto interpretó difíciles obras de concierto”. János no asistió a la escuela hasta que cumplió nueve años; hasta entonces recibía clases de los mejores estudiantes de la escuela de Marosvásárhely, excepto en el caso de las matemáticas, de cuya enseñanza se encargó su propio padre.
A los catorce años János era ya un maestro en la matemática superior, como el cálculo diferencial e integral, y en la mecánica. Se había convertido en un lingüista de excepción, hablando nueve idiomas extranjeros, entre ellos el chino y el tibetano. Todo esto está documentado en una carta que su padre dirigió a Gauss en 1816.

Sello postal emitido por Hungría en recuerdo de János Bolyai, parece que el retrato pudiera no ser el suyo.
Cuando a los doce años se convirtió en un colegial normal, pudo matricularse directamente en cuarto debido a la formación y conocimientos que ya había adquirido: los tres primeros cursos le fueron convalidados. Hizo su examen final en junio de 1817. Había llegado el momento de pensar en la formación universitaria de János.
Por un artículo de Samu Benkó, titulado “Gotinga, Gauss y Erdély”, podemos tener una visión de la relación existente entre la Universidad de Gotinga y los naturales de Transilvania, acercándonos así al problema de la educación superior en aquella Europa del Este que le tocó vivir a János. Esa universidad era famosa por la libertad de pensamiento, que encajaba bien con la libertad religiosa que se vivía en los hogares de Transilvania, lo que animaba a las familias a enviar a sus hijos a Gotinga. Entre los numerosos alumnos que asistieron a sus aulas ya nos hemos referido al caso de Farkas Bolyai como uno de los más conocidos y renombrados. También Gauss estuvo allí. Sin embargo la educación universitaria era cara, especialmente allí, de tal forma que si una familia perseguía una educación superior para su hijo, debía ser pudiente o bien encontrar un protector que ayudara e incluso cubriera los gastos. Los historiadores también mencionan que en la mayor parte de las universidades se permitían la bebida y los duelos, y el comportamiento irresponsable estaba de moda, todo lo cual causaba un cierto recelo en las familias a la hora de enviar a sus hijos a cualquier universidad. Parece sin embargo que en Gotinga la moral no estaba tan relajada como en otras universidades debido a que los claustros ejercían una cierta vigilancia sobre el cumplimiento de las reglas establecidas. A finales del siglo XVIII la mayor parte de los estados comenzó, de alguna manera, a regular la vida de las universidades aunque, por otra parte, no estaba permitido que los gobiernos violasen la autonomía de la vida académica.
§. A la búsqueda de una universidad
En Transilvania no había universidades, y las de Pest o Viena no enseñaban matemáticas por carecer de profesores especializados en la materia o, si había alguno, no eran de la suficiente confianza de Farkas como para poner bajo su tutela el genio de su joven hijo. La única alternativa era enviar a János a Gotinga, junto a Gauss. No se sabe con certeza si le fue ofrecida una beca a Farkas para su hijo János por parte de una familia bien situada económicamente que le hubiera facilitado suficiente dinero para vivir y estudiar con desahogo. Pero lo cierto es que Farkas prefirió seguir con sus planes de enviar a su hijo a la casa de Gauss: la vida en las universidades alemanas, como hemos dicho, era lo suficientemente disoluta. János tenía quince años en 1817.
El 10 de abril de 1816, Farkas escribió a su amigo Gauss pidiéndole que János viviera con él durante tres años para que así recibiera la mejor formación posible en matemáticas. Incluso le habló de reembolsarle los gastos que se produjeran. Pero parece que Farkas le exigió demasiado a Gauss, que rechazó la idea. ¿Cuáles fueron esas exigencias? Preguntarle por la moral de su hija, para que nunca resultase peligrosa para János, estar satisfecho y no quejarse por nada, disfrutar de buena salud y tener una esposa excepcional como mujer y de carácter estable. Por todo lo anterior, Gauss nunca contestó a esa carta.
§. János comienza los estudios de ingeniero militar
Después de este intento fallido, surgió en Farkas la idea de que János estudiase en Viena, concretamente en la Academia de Ingenieros Militares. De hecho, visitó esa academia en uno de los viajes que hizo a Gotinga, quedando altamente impresionado, tanto que se hubiera matriculado él mismo en ella. El problema era cómo reunir inmediatamente el dinero necesario para pagarle a su hijo los estudios en esa institución. Hasta ver cómo solucionaba las cuestiones presupuestarias tuvo que comenzar matriculando a János en 1817 en la Facultad de Artes de la Escuela de Marosvásárhely, graduándose el 30 de junio de 1817. Algo más tarde, el director de la institución, conde Miklós Kemény, junto con otros benefactores, facilitó el dinero suficiente para que János pudiera comenzar sus estudios como ingeniero militar. Una vez pasado el correspondiente examen de admisión en 1818, János seguirá un programa de ocho años en la Imperial y Real Academia de Ingenieros Militares. Se podía ingresar en el cuarto curso o en alguno de los anteriores, dependiendo de la formación que poseyera el aspirante: János siguió la opción avanzada y finalizó cuatro años después, a pesar de una cierta aversión por la disciplina militar. Ingresó por tanto como cadete de ingenieros en el ejército austro-húngaro. Ahora bien, tuvo que hacer frente a otros gastos que no llegaban a cubrirse con la asignación del conde y de los otros amigos, por lo que recayó en su propio padre esa financiación extra, tarea nada fácil dada la situación económica por la que atravesaba Transilvania por culpa de las guerras mantenidas con Francia desde 1792.
János fue un excelente estudiante, clasificado por muchos profesores como el primero, aunque otros le consideraban el segundo, quizá debido a sus dificultades con el dibujo, materia que se asegura que le aburría. No olvidó en ningún momento el deporte, no bebía alcohol ni café, sólo agua, y nunca fumaba. El violín seguía siendo su mayor pasión, interpretando varios conciertos durante su estancia en Viena.
§. Graduación en Viena como ingeniero militar
Se graduó el 6 de septiembre de 1822, pero, debido a su alto interés por las materias y por ser uno de los dos alumnos más aventajados, se le permitió proseguir estudios un año más. A principios de septiembre de 1823 fue nombrado subteniente y asignado a la dirección de la fortificación de Temesvár. Se retirará, como veremos, en 1833 con el grado de capitán.
A principios de 1825 János visitó a su familia en Marosvásárhely, donde tuvo un gran éxito: la sociedad aristocrática quedó fascinada por su personalidad y por la elegancia del joven oficial. Su padre estaba feliz por tener un hijo que se había convertido en un genio de las matemáticas, no sólo por los conocimientos adquiridos en la escuela de Viena sino también porque sabía de las investigaciones que, sobre la teoría de las paralelas, venía haciendo desde 1820, estando ya en la Academia de Ingenieros. En una carta que Farkas escribe a Pál Bodor el 27 de febrero de 1825 le comenta que János es un joven elegante, decidido y con una naturaleza muy fuerte. Además, János era un excelente practicante de esgrima y era famoso en ese arte desde sus años de estudiante. Se cuenta que una vez, durante su estancia en Arad, trece oficiales de caballería le retaron a un juego que János aceptó. Las condiciones eran que cada dos lances ganados por su parte, él podría tocar el violín. Venció en los trece retos. Si la historia fuera cierta, dado que las espadas empleadas por los oficiales de caballería eran muy pesadas, significaría que János era de una complexión física extremadamente fuerte.
En 1826 János fue trasladado a Arad y la suerte quiso que allí se encontrara con Johann Wolter Eckwehr, que había sido uno de sus profesores de matemáticas en la academia, y con el que, además, había sostenido una rica correspondencia. Ahora era su superior inmediato. János le pasó un manuscrito en alemán con sus investigaciones relativas a la geometría no euclídea. Por desgracia, este manuscrito se ha perdido. Cinco años más tarde, en 1831, János fue nuevamente trasladado, esta vez a Lemberg (actual ciudad ucraniana de Lviv), y en 1832 a Olmütz, (la actual ciudad checa de Olomouc) último destino en su carrera militar.
Estando en Arad, János padeció de fiebre persistente. Casi con seguridad cogió la malaria, debido a la extrema humedad de los suburbios de la ciudad. Más tarde también sufrió de cólera, de manera que su salud se deterioró de forma significativa. Además, en su traslado de Lemberg a Olmütz tuvo la desgracia de que el carruaje en el que viajaba sufriera un accidente a causa del cual se hirió en la cabeza. Comenzaba a no sentir interés por su carrera militar, estaba aburrido y cansado de la rutina de los escritos, informes y de la elaboración de planos que debía hacer a diario. Dedicaba su tiempo libre a resolver problemas de matemáticas. Con el fin de dedicarse de lleno a sus investigaciones solicitó una baja temporal del servicio por tres años, baja que le fue denegada. Finalmente, en 1833, fue separado del servicio con una pensión de capitán de segunda clase. Puede que hubiera una segunda razón para esa jubilación prematura del servicio. De camino desde Lemberg a Olmütz, János tuvo una discusión con los aduaneros de frontera por negarse a abrir su equipaje y los oficiales le denunciaron a las autoridades.
§. De nuevo en la vida civil
János se fue a vivir a la casa que su padre tenía en Marosvásár- hely, pero sólo por una temporada, ya que un año más tarde, en 1834, se trasladó a Domáld donde permaneció hasta 1846. La familia había heredado allí una finca de la madre de Farkas. A partir de 1834 János cohabitó con Rosalía Kibédi Orbán. Su matrimonio legal no era posible al no poder reunir el dinero de un depósito, el dinero de un aval, que le fue requerido cuando era oficial del ejército. Su padre nunca aprobó enteramente esa unión y consideró que su hijo estaba manchando la buena reputación que siempre tuvo en la comunidad en la que vivía. Tuvieron dos hijos: Dénes y Amalia. Uno de sus descendientes, su tataranieto János Bolyai, vive en Edelény (Hungría). Debido a la pensión insuficiente y quizás también a la mala gestión económica del dinero percibido, la finca y casa en la que habitaba la pareja con sus hijos se convirtió en una carga con el paso del tiempo y ellos mismos llegaron a vivir en una auténtica penuria.
En 1846 János se trasladó de nuevo con su familia a Marosvásárhely para agradar a su padre, disgustado, y no le faltaba razón, por lo que él consideraba una mala gestión de la finca de Domáld. La finca sería luego arrendada.
Durante la guerra de independencia, en 1849, dejó de tener vigencia la exigencia del aval, por lo que János y Rosalía pudieron casarse legalmente el 18 de mayo de 1849. El ejército nunca reconoció, sin embargo, la legalidad de ese matrimonio. Pero esa vida en común y legal no durará mucho tiempo.

La tumba de los Bolyai en Marosvásárhely.
En 1852 János abandona a su familia, pensando quizá que con ello se congraciaría con su padre, dejando la casa a su esposa, a la vez que una considerable cantidad de dinero para el mantenimiento de sus hijos. No obstante, nunca dejó de protegerlos. Su salud comenzó a deteriorarse, por lo que tuvo que pagar los cuidados de una sirvienta, Julia Szóts. Esa economía escasa, y el hecho de haber fallecido su padre, le movió a vender sus bienes de Domáld y repartirse las ganancias con su hermanastro Gergely.
§. Muerte de János Bolyai
El 27 de enero de 1860, Julia Szóts escribió a Gergely comunicándole que János estaba muy enfermo, por lo que debía venir urgentemente. Habiendo firmado ya la carta, miró a su patrón. “Mientras escribía esta carta, ha muerto, por lo que no hay nada más que decir: el capitán se ha ido”. Una neumonía fue la causa, arrebatándole de este mundo a la edad de 57 años, un mundo que no supo reconocer en ningún momento ni su sabiduría ni su genio prematuro.
En la celebración del funeral sólo estuvieron tres personas civiles, además de la obligatoria escolta militar. Por Kiss, un estudioso de la vida y obra de János Bolyai, sabemos que al final del informe del registro que obra en la iglesia calvinista de la localidad donde falleció, se añadieron las siguientes frases: “Fue un famoso matemático de mente preclara. Fue el primero entre los primeros. Ha sido una pena que su talento fuera sepultado de forma inusual”.
No ha llegado hasta nosotros retrato alguno de János. Parece haber existido sólo un cuadro vestido de uniforme, pero él mismo lo cortó en trozos con su propia espada. Actualmente ha ganado aceptación la opinión de que uno de los relieves de la parte superior de la fachada del Palacio de Cultura de Marosvásárhely corresponde a su efigie. Hay seis relieves, con los correspondientes nombres sobre cinco de ellos; bajo el sexto se inscribió el nombre de János Bolyai. También podría corresponder a Gyórgy Klapka, general del ejército revolucionario húngaro. Se sabe que János y Gyórgy eran muy parecidos. Kinga Széchenyi fabricó en 2002 una placa de János Bolyai para conmemorar el cien aniversario de su nacimiento.

Relieve de la parte superior de la fachada del Palacio de Cultura de Marosvásárhely que parece ser una imagen fiel de János Bolyai .
Un cráter recuerda en la Luna el nombre de Bolyai y, justamente al lado de éste, otro lleva el nombre de otro insigne húngaro, Eötvös, famoso por su invención del péndulo de torsión en 1891, para medir los cambios de la fuerza de la gravedad.
§. El trabajo científico de János Bolyai
Desde 1820, estudiando ya en Viena, János retomó el mismo camino que había apasionado a su padre: el postulado V de Euclides, tratando de reemplazar el axioma de las paralelas por otro que pudiera deducirse de los anteriores, es decir, demostrarlo. Efectivamente, llegará a la conclusión cierta de que el postulado V es independiente de los que le preceden. Con ello comenzó a desarrollar las ideas básicas de la geometría hiperbólica.
Farkas, no obstante, alertó a su hijo y le indujo a abandonar esa investigación. En su emotiva carta del 4 de abril de 1820, en la que revela un patetismo desmesurado, le decía: “No debes intentar ese camino hacia las paralelas: yo lo conozco hasta su final. He atravesado esa noche sin fondo que extinguió toda la luz y toda la alegría de mi vida. ¡Por Dios! Te suplico que abandones las paralelas, aborrécelas como si fuera una pasión indecente, te pueden privar (como me ha ocurrido a mí) de tu tiempo, de tu salud, de la tranquilidad de espíritu y de la felicidad de tu vida Yo ya me convertí en un mártir que deseaba suprimir la imperfección de la geometría y retorné purificado al mundo. Realicé monstruosos y enormes trabajos, mis creaciones son mejores que las de otros y no por eso he logrado una completa satisfacción. Retorné cuando me di cuenta de que ningún hombre ha sido capaz de encontrar el fondo de esa noche. Y retorné desconsolado y lleno de una gran pena. He viajado por todos los escollos de este infernal mar Muerto y siempre he vuelto con el mástil roto y las velas rasgadas [...]. Arriesgué atolondradamente mi vida y mi felicidad. Aut Caesar aut nihil [0 César o nada, divisa de César Borgia]”.
Roberto Bonola, en su Geometrías no euclidianas, nos ha dejado un testimonio que no hemos encontrado en ningún otro informe posterior relativo a la obra de János. Parece que en el tiempo que estuvo en Viena János entabló cierta amistad con C. Szász, y esa relación y las conversaciones científicas que mantuvieron condujeron a Bolyai a crear su Ciencia absoluta del espacio. Bonola añade, incluso, que se debe a Szász la idea de considerar la paralela a una recta por un punto exterior a la misma como la posición límite de la secante a la recta dada que gira alrededor de ese punto exterior. Por ello, esa secante límite, esa paralela, recibió el nombre de paralela asintótica o, simplemente, asíntota a la recta dada. Así termina Bonola, en el libro citado, este pasaje: “Habiendo Szász abandonado Viena a principios de 1821 para encargarse de la enseñanza del derecho en el colegio de Nagy-Enyed, János queda solo para proseguir con sus especulaciones. Hasta el año 1820 estuvo dominado por la idea de encontrar una demostración al axioma XI, siguiendo un camino análogo al de Saccheri y Lambert. Bien pronto cree haber conseguido su objeto, como se deduce de la correspondencia con su padre”. János llamó axioma XI en sus trabajos al V postulado de Euclides.
El 3 de noviembre de 1823, casi un año después de graduarse en la escuela militar de Viena, János escribía desde Temesvár a su padre una carta en la que, quizás un poco prematuramente, le decía cosas como las siguientes:
“¡Mi querido y buen padre! Tengo tanto que escribirle acerca de mis nuevos hallazgos que, por el momento, no puedo discutirlos aquí en profundidad, así que se los voy a escribir sólo en una cuartilla. Espero su respuesta a mi carta de dos folios y tal vez no le hubiera escrito antes de recibir su respuesta si no deseara mandarle la carta que he escrito a la baronesa, que le ruego le haga llegar [...]. Estoy decidido a publicar ahora una obra sobre la teoría de las paralelas, apenas haya ordenado la materia y las circunstancias me lo permitan. Por el momento no he encontrado aún el camino definitivo, pero he descubierto cosas tan hermosas que yo mismo me he quedado sorprendido de ellas [...]. Sería una pérdida eterna si se perdieran. Cuando las veáis, querido padre, vos mismo las reconoceréis. Ahora no puedo añadiros nada más; sólo esto: he creado un mundo nuevo y diferente a partir de la nada. Todo lo que os he dicho hasta ahora no es más que un castillo de naipes comparado con una torre. Estoy tan persuadido de que esto me dará gloria, como si eso ya hubiera sucedido”.
Terminaba con la siguiente posdata:
“He osado, padre mío, juzgar estos trabajos de mi espíritu absolutamente y con convicción antes que tú; no temo de ti ninguna interpretación falsa (que ciertamente yo no merecería), lo que significa que, desde cierto punto de vista, te considero un segundo yo.
Como hoy sabemos y reconocemos, ese mundo nuevo y diferente al que se refiere János en su carta es el mundo mágico de la geometría absoluta, de la geometría hiperbólica. Evidentemente, Bolyai había creado un mundo abstracto y había adoptado una aproximación al problema enteramente original estudiando las consecuencias que podían derivarse de negar el V postulado, es decir, de suponer que por un punto exterior a una recta pasan infinitas rectas paralelas a la dada. Quedó perplejo de la coherencia que lograba en sus deducciones, es decir, de la coherencia contenida en su nueva geometría.
En la misma carta, y antes de comenzar a contarle sus hallazgos sobre las paralelas, János también hace alusión al teorema del binomio: “Primero de todo, voy a responderle sobre el teorema del binomio. Para exponentes enteros positivos, la prueba es perfecta como usted la ha escrito, pero se necesita conocer la forma de las series para utilizarla en la prueba”. Sigue después una discusión sobre el teorema para exponentes no enteros, refiriéndose a la prueba de su padre y haciendo alusión a las de Lacroix y Vega: “Acerca de todas estas cosas, seguiremos discutiendo; también lo estudiaremos para exponentes negativos ”.
Cuando Farkas leyó la carta de su hijo, le surgió el deseo de incluir la teoría de János en su publicación Tentamen. Se justifica diciéndole que “las ideas pasan fácilmente de uno a otro y cualquiera puede anticiparse en publicarlas [...]. Cuando el tiempo ha hecho madurar las cosas, esas cosas aparecen en distintos lugares, tal como hacen las violetas con la luz del comienzo de la primavera”. Y termina: “puesto que toda lucha científica es una gran guerra a la que no se sabe cuando seguirá la paz, se debe, cuando se pueda, vencer en la lid, puesto que aquí la victoria corresponde al primero”. En este sentido su padre tenía razón, aun considerando que el lugar donde aparecerían las teorías de János no sería el mejor para llamar la atención de la comunidad matemática internacional de aquel tiempo.
Después del envío de esta carta a su padre, János escribió otra en alemán, dando a conocer los resultados que había descubierto, a su antiguo profesor Eckwehr de Viena, supervisor suyo más tarde, en 1826, en Arad.
Hechas algunas mejoras a la teoría, visitó a su padre en Marosvásárhely a principios de 1825, pero se marchó decepcionado por el poco entusiasmo que su progenitor mostraba hacia sus investigaciones. ¿Había sido Farkas capaz de comprender la nueva geometría de su hijo?
Las tres geometríasLa geometría, llamémosla clásica, que se basa y admite el axioma de las paralelas o postulado V de Euclides, recibe el nombre de geometría euclídea.
A principios del siglo XIX, los matemáticos Gauss, Lobachevski y János Bolyai, por separado, demostraron la posibilidad de construir una geometría coherente reemplazando la geometría basada en la paralela única de Euclides por otra, donde era posible trazar un número infinito de paralelas a una recta por un punto exterior a ella. Esta geometría no euclídea se conoce con el nombre de geometría de Bolyai-Lobachevski o también geometría hiperbólica Es una geometría cuya referencia, modelo o espacio podría ser un círculo plano en el que las rectas son cuerdas de su circunferencia. El primer trabajo de Lobachevski sobre esta geometría se ha perdido. En 1836 apareció, escrita en ruso, su obra definitiva Nuevos elementos de geometría con una teoría completa sobre las paralelas. Sin embargo, el tratado más completo sobre esta teoría se publicó en ruso y en francés con el título Pangeometría.
La geometría que el matemático alemán Bernhard Riemann, discípulo y continuador de Gauss, mostró hacia 1860, también no euclídea, es una geometría en la que no existen las rectas paralelas. Se trata de una geometría basada en la esfera en la que las líneas rectas son círculos máximos de la misma. Recibe el nombre de geometría de Riemann o geometría elíptica La teoría de la relatividad de Einstein se basa en esta última geometría riemanniana.
Siguiendo con la referencia a las cónicas para darles nombres a las geometrías, la geometría euclídea, la intermedia entre las dos anteriores, también recibe el nombre de geometría parabólica.
János volvió a visitar a su padre a principios de 1831, cuando viajaba con destino militar a Lemberg. En aquel momento Farkas ya había tenido tiempo de comprender el significado de lo que su hijo le había dicho años antes. Entonces sí, le recomendó escribir lo antes posible un apéndice, el Appendix, a su Tentamen. El acontecimiento más importante fue la publicación de ese apéndice, cuya preimpresión se hizo en latín en 1831. El primer volumen del Tentamen, escrito también en latín, se encuadernó junto con el apéndice aportado por János y se publicó en 1832. Un año más tarde aparecía el segundo volumen. Curiosamente, la fecha del Tentamen con su respectiva licencia, el imprimatur, corresponde al 12 de octubre de 1829. La extensión del escrito de János no supera las veinticuatro páginas. El título completo de este opúsculo era: Appendix, scienciam spatii absolute veram exhibens: a ueritate aut falsitate Axiomatis XI Euclidei (a priori haud unquam decidenda) independentem; adjecta ad casum falsitatis, quadratura circuli geométrica. Podríamos traducirlo así: Appendix, la ciencia absoluta del espacio independiente de la uerdad o falsedad del axioma XI de Euclides (que nunca se podrá establecer a priori); seguido de la cuadratura geométrica del círculo, en el caso de la falsedad del axioma XI. Y termina este largo y completo título: Auctore Johanne Bolilla de eadem, Geometrarum in Exercitu Caesareo Regio Austríaco Castrensium Capitaneo.
Nos advierte Babini en su obra ya citada: “Bolyai da el nombre de absoluto a sus consideraciones porque se refieren a las propiedades geométricas independientes del postulado, verdades o teoremas que son válidos tanto para la geometría ordinaria como para la geometría más general que él ha construido”.
János Bolyai nunca intentó remitir su trabajo a las revistas u otras publicaciones matemáticas líderes y conocidas de la época, a pesar de las conexiones y posibilidades que su padre tenía, sobre todo por su amistad con Gauss. Tal vez influyera en esta decisión el hecho de no haber conseguido, como veremos más adelante, el total beneplácito de Gauss a sus teorías, al menos en los primeros momentos.
El Appendix fue publicado varias veces en húngaro y en otros idiomas, incluso se tradujo al inglés en 1891, obra acometida por George Bruce Halsted, de Texas, en cuyo prefacio escribe: “Estas son las dos docenas de páginas más extraordinarias de la historia del pensamiento”. También Bonola realizó una versión inglesa en 1911a partir de su original en italiano.
Las ideas fundamentales se expresaban en 43 proposiciones, un conjunto de definiciones sobre rectas paralelas, demostrando que si el postulado V se cumplía en una región del espacio también se cumpliría en todo él y viceversa. Da indicaciones concretas para construir las figuras geométricas correspondientes a su nueva geometría y, en particular, un cuadrado y un círculo de igual superficie. János llega a esta alternativa: o bien el axioma de las paralelas es cierto o bien la cuadratura del círculo es posible y ello casi cincuenta años antes de que Lindemann cierre el problema de la cuadratura del círculo en la geometría euclídea demostrando la trascendencia del número n.
§. La comunicación con Gauss
Farkas envió una copia del escrito de su hijo a su amigo Gauss, casi al mismo tiempo que se publicaba por primera vez en abril de 1831. Le pedía su opinión sobre el trabajo de János. Esa copia parece haberse perdido, pero sí se conserva la carta que la acompañaba, fechada el 20 de junio de 1831.
Farkas remitiría una segunda copia del trabajo a Gauss el 16 de enero de 1832. Éste escribió poco después a uno de sus amigos: “considero a este joven geómetra Bolyai como un genio de primera clase”. En la contestación a Farkas Bolyai no fue, sin embargo, tan adulador. La carta que envió el 6 de marzo de 1832, mes y medio después de recibir el envío, es ampliamente conocida. En una de las partes más devastadora, Gauss escribe:
“Respecto al trabajo de tu hijo comienzo por decirte, aunque te sorprenderás por un momento, que si yo lo alabara, ello comportaría alabarme a mí mismo, porque el contenido completo del trabajo, el camino seguido por tu hijo y las conclusiones a las que llega, coinciden casi exactamente con mis propias ideas, que han ocupado mi pensamiento durante los pasados treinta o treinta y cinco años. Esto me ha dejado, en efecto, estupefacto”.
Y luego añade que él también había intentado escribir esas ideas para que no desaparecieran con su muerte.
¿Por qué esta falta o, al menos, debilidad de reconocimiento de Gauss hacia el trabajo de János? Desde 1817, Gauss no tenía duda alguna sobre la coherencia de la geometría no euclídea, que él ya conocía y parece que dominaba. No publicó nada sobre el tema por el miedo al qué dirán y a que se burlaran de él, sufriendo las consecuencias e influencia del kantismo, que consideraba al espacio euclídeo como una necesidad inevitable del pensamiento.

Carta autógrafa de Gauss a Taurinus fechada el 8 de noviembre de 1824.
Por eso, en la carta dirigida a Farkas añade: “Me sorprende en exceso que me despojen de ese trabajo pero, al mismo tiempo, me siento particularmente dichoso de saber que la fatiga de una redacción [en alusión a lo que podía haber sido su propia publicación de la teoría] me ha sido evitada por el hijo de mi viejo amigo, que me ha adelantado de tan excelente manera”. Por otra parte, Gauss ya había declarado su conocimiento de estas teorías en una carta enviada el 8 de noviembre de 1824 al matemático alemán Taurinus, aunque en otra, escrita al también matemático y astrónomo alemán Christian Ludwig Gerling, reconocía que sus ideas de 1798 estaban muy lejos de la madurez que se podía apreciar en las de János. Taurinus es también considerado como un precursor de Lobachevski y Bolyai en lo que a geometrías no euclídeas se refiere.
En la carta aludida, Gauss invitaba a János a resolver ciertas cuestiones en su geometría, como la de encontrar el volumen de un tetraedro o la obligatoriedad de demostrar la posibilidad de un plano, considerando que la definición ordinaria del plano estaba poco cuidada.
Aunque de algún modo Gauss había alabado el trabajo de Bolyai, el hecho de enterarse de que conocía la mayor parte de sus resultados desestabilizó a János. Lo tomó como un duro palo que lo convirtió en una persona irritable y poco tratable. Las posteriores alabanzas no aliviaron en modo alguno la pena que la carta causó al joven Titán, como le llaman sus compatriotas contemporáneos. Poco a poco su salud, física y psíquica, se fue deteriorando y ello le indujo a alejarse de su padre. Además, ese deterioro le hizo abandonar la carrera militar el 16 de junio de 1833, convirtiéndose en un pensionista en la reserva.
§. Los concursos y los pesares. Aceptación de la nueva geometría
En 1837 ocurrió un hecho significativo en la vida de los Bolyai. La Sociedad Científica de Leipzig anunció un concurso sobre los fundamentos de la teoría de los números imaginarios. Los Bolyai tuvieron conocimiento de este anuncio pocos días antes de su fecha límite, en el mes de noviembre de ese año. No obstante, padre e hijo presentaron trabajos al concurso. Otro participante fue Ferenc Kerekes, de la escuela de Debrecen. Los Bolyai no ganaron, mientras que Kerekes fue merecedor de la mitad del premio establecido. El trabajo de János, conocido como Responsio, se basaba en los mismos principios utilizados por Hamilton, fundador de la teoría de los números complejos. Aunque János presentó este trabajo en 1837, su teoría ya estaba completa en 1831, mucho antes, por tanto, de que Hamilton hiciera pública su investigación en la Academia de Dublín. János produjo otros descubrimientos matemáticos que se han presentado y discutido en “Notas sobre las investigaciones de János Bolyai relativas a la teoría de números”, un artículo publicado por Elemér Kiss en la revista Historia Mathematica.
El año 1848 sorprendió a János con la llegada del trabajo de Lobachevski, aparecido en 1829 y publicado más tarde en alemán en 1840, y cuyo contenido coincidía en gran parte con su Appendix. Su primera reacción fue pensar que había sido víctima de un plagio. Más tarde fue capaz de reflexionar y sacar sus propias conclusiones sobre el trabajo, que fueron recogidas en 1902 por Stäckel y Kürschák: “Comentarios de János Bolyai sobre las investigaciones de Nicolás Lobachevski relativas a las paralelas”. Ya se ha dicho que János concluyó el esquema de su trabajo sobre las paralelas en 1823 y el texto completo en alemán tres años más tarde. Dado que este último se ha perdido, y que el primero es sólo un informe del descubrimiento redactado en una carta, no existen documentos anteriores relativos a su descubrimiento que no sean su Appendix. Por otra parte, también es cierto que Lobachevski impartió una conferencia en 1826 sobre un tema relacionado en la Universidad de Kazán, donde fue profesor y rector. Según Elemér Kiss, si se analiza el título de la memoria, parece que Lobachevski únicamente intentaba demostrar el V postulado.
Debemos añadir que la comunidad científica cercana a los Bolyai no se mostró demasiado interesada por el trabajo de János. Algo parecido le ocurrió a Lobachevski con alguno de sus escritos, según expresa él mismo en su libro publicado en 1840. Éstas son algunas frases contenidas en la carta que Farkas envió a Gauss el 3 de octubre de 1836: “Aquí nadie necesita las matemáticas; aparte de mis alumnos, sólo algunas personas sienten algo hacia esa ciencia”. La historia y la propagación del descubrimiento de las teorías de János acontece, más bien, fuera de su patria. La clasificación de los trabajos de Gauss hecha después de su muerte en 1855 juega un importante papel en ese descubrimiento. Entre esos papeles se encontraron los trabajos de Bolyai y de Lobachevski, así como ciertas cartas escritas y recibidas por Gauss, que fueron clasificados por Wolfgang Sartorius von Waltershausen, profesor de matemáticas en Gotinga, a quien Farkas Bolyai había enviado las cartas que Gauss le había dirigido a él, de forma que también fueron incluidas en esa clasificación. A partir de ahí, el panorama comenzó a aclararse. Así, las primeras palabras de aprecio publicadas se debieron a Baltzer, profesor de matemáticas en Dresde. Fueron incluidas en su trabajo, muy bien conocido en aquella época, Los elementos de las matemáticas. En el mismo año, Hoüel, profesor en Burdeos, publicó en francés su versión completa del Appendix junto con un artículo que contenía una biografía de Bolyai debida a Ferenc Schmidt. Al profesor Hoüel se debe la siguiente apreciación sobre la negligencia de los húngaros con su compatriota Bolyai: “Me siento afligido al ver lo poco que Hungría aprecia los descubrimientos científicos que se producen en su suelo”.
Si lo dicho anteriormente demuestra más bien el interés de la comunidad científica por la labor de Gauss en la geometría no euclídea, en el año 1868 se despertó también el interés por las investigaciones de Bolyai. Ese año, un artículo del italiano Beltrami contiene un modelo de la geometría hiperbólica de Bolyai-Lobachevski, modelo con el que podía demostrarse que los axiomas de su geometría estaban exentos de contradicciones.
Aislado del mundo y de otros científicos, y aunque continúa desarrollando teorías matemáticas por su cuenta mientras vive en Domáld, János no volverá a publicar ninguno de los resultados de sus investigaciones. Uno de sus últimos trabajos, comenzado en 1834, se refiere a la axiomatización de todas las matemáticas, especialmente de la geometría. Al incluir en esos estudios nociones sobre el invariante topológico, una concepción rigurosa de los números complejos como pareja de números reales, se estaba anticipando a su tiempo.
Abandonó las matemáticas y, en una patética búsqueda de la perfección, se consagró a la elaboración de una lengua universal, lo que hoy llamaríamos un esperanto, partiendo del magiar, lengua que consideraba un modelo de armonía vocálica.
Se dice que dejó más de 20.000 páginas manuscritas con material de sus trabajos sobre matemáticas. Investigaciones actuales, como veremos, totalizan unas 17.000 páginas. Se encuentran en la biblioteca Bolyai-Teleki de la ciudad rumana de Tárgu Mures. En 1945 se abrió una universidad en Cluj que llevaba su nombre. Fue cerrada en 1959 por el gobierno de Ceaucescu.
§. El descubrimiento y la clasificación de la obra de János Bolyai
József Eötvös, político, ministro y literato húngaro, supo comprender la importancia de la obra científica de Bolyai. Con su apoyo fue posible el traslado a Pest de todas las cajas que contenían las obras de János. Allí fueron depositadas en los archivos de la Academia, donde permanecieron un cuarto de siglo. Un comité se encargó, aunque con escaso éxito, de identificar los resultados escondidos entre las páginas. Fue durante ese tiempo cuando Ferenc Schmidt encontró entre la documentación la célebre carta que János escribió a su padre el 3 de noviembre de 1823 dándole cuenta de que había “encontrado un mundo nuevo y diferente Más tarde apareció en Marosvásárhely otra parte de los trabajos con contenido matemático, escritos después del Appendix. Fueron los siguientes: Responsio, el material enviado al concurso de la Sociedad Científica Jablonowski de Leipzig, Suplementos al Appendix, el cálculo del volumen del tetraedro en geometría hiperbólica, Estudios en ausencia de contradicciones y comentarios sobre la geometría de Lobachevski.
EötvösEl barón József Eötvös de Vásárosnamény nació en Buda el 13 de septiembre de 1813 y falleció en Pest el 2 de febrero de 1871.
Después de recibir una esmerada educación, como correspondía a su rango, su padre le introdujo en la vida política de Hungría. Pasó varios años en Europa occidental, donde tuvo la oportunidad de empaparse de las nuevas ideas literarias y políticas, así como también del romanticismo reinante.
A su vuelta a Hungría colaboró con periódicos, como Pesti Hírlap, y escribió novelas y comedias. Fue considerado como uno de los principales escritores y políticos en su tierra natal y ostentó el cargo de ministro de educación y religión pública.
Pasó al exilio en Münich al dimitir el presidente Lajos Batthyány durante la turbulenta época de la Guerra de la Independencia. Regresó a Hungría en 1851, no volviendo a participar en la vida política hasta pasados dieciséis años. Se dedicó a la literatura, siendo elegido presidente de la Academia Húngara en 1866. Más tarde, en 1867, volvió a formar parte del gobierno de Gyula Andrássy, repitiendo como ministro de educación y religión pública.
El 3 de mayo de 1879 se erigió una estatua en su honor en Pest.
El profesor de historia de Kolozsvár Samu Benkó ordenó los manuscritos con la ayuda de Gusztáv Abafáy. Emplearon en esa labor dieciséis años clasificando unas 14.000 páginas. Le sirvió de pauta la utilización de ciertas palabras clave que Bolyai escribía en la parte inferior de algunas páginas y que luego repetía en la parte superior de la página siguiente. Una vez leídos los manuscritos, Benkó publicó en 1968 un libro titulado Confesiones de Jónos Bolyai, que contiene textos no matemáticos.
El profesor Elemér Kiss, en 1990, leyó 3.000 páginas de material matemático manuscrito informando de su contenido en un libro y en varios artículos en 1999. En el manuscrito, Kiss descubrió nuevos y muy significativos resultados matemáticos de János, tales como ciertos teoremas relativos a la teoría de números publicados 38 años después de su muerte. Actualmente, ese tratado sirve aún como material de texto. En diciembre de 1997, con motivo del 195 aniversario del nacimiento de János Bolyai, Elemér publicó Mathematical Gems from the Bolyai Chests, cuyo contenido abarca los trabajos de János sobre teoría de números y álgebra.
János Bolyai escribió algunos de sus manuscritos en papeles que contenían, además, otra información no relacionada con el propio tema, como, por ejemplo, carteles de teatro, la parte interior de los sobres o libros de notas de su hijo. Por lo tanto, a la lectura del material hay que añadirle la propia interpretación del contenido, todo lo cual ha constituido un trabajo difícil y duro. Actualmente está en marcha la publicación de todos sus manuscritos bajo la dirección editorial de Samu Benkó.
Capítulo 3
La evolución de la geometría no euclídea
En la teoría de las paralelas no hemos conseguido llegar hasta ahora más allá de Euclides. Esta es la parte vergonzosa de la matemática que, tarde o temprano, habrá de tomar otra forma.
Gauss
§. Los Elementos de Euclides. La teoría de las paralelas
Recordemos que la geometría práctica comenzó con la agrimensura en Mesopotamia y Egipto, alcanzando un buen nivel hace más de cuatro mil años.
Más tarde, los griegos elevaron esta técnica al nivel de ciencia y las leyes de esa ciencia matemática fueron ordenadas por Euclides y desarrolladas mediante una red metódica de conclusiones lógicas.
Los Elementos de Euclides son una pieza maestra utilizada como fuente del conocimiento geométrico durante más de dos mil años. El mayor mérito de ese trabajo lo constituye la uniformidad de su sistema lógico, basado en unas pocas proposiciones que, a través de un razonamiento deductivo, conducen a nuevas nociones que se van construyendo una sobre otra; también contiene definiciones y teoremas. Algunas proposiciones iniciales son postulados. Dice Poincaré a este respecto: “toda conclusión supone premisas, esas premisas o son evidentes por sí mismas y no tienen necesidad de demostración o bien no pueden ser establecidas más que apoyándose en otras proposiciones, y como no se podría remontar uno así hasta el infinito, toda ciencia deductiva, y la geometría en particular, debe descansar sobre un cierto número de axiomas indemostrables".
Euclides define los conceptos de punto y línea recta. Un “punto es lo que no tiene partes”; una “línea recta es aquella que yace por igual respecto de los puntos que están en ella”. Demuestra también, enunciándolo explícitamente, que “la suma de los ángulos de un triángulo es dos rectos”, pero no lo formula como haríamos nosotros hoy día con la notación α + β + γ = 180°. Otro ejemplo es el teorema de Pitágoras, que Euclides enuncia sirviéndose de cuadrados construidos sobre los catetos y la hipotenusa de un triángulo rectángulo:
“En los triángulos rectángulos el cuadrado del lado que subtiende el ángulo recto es igual a los cuadrados de los lados que comprenden el ángulo recto”.
El insigne profesor Alberto Dou comenta en su sencilla y atractiva obra Fundamentos de la matemática: “Naturalmente que como toda obra humana, sujeta a la ley de la historia, la matemática griega y en particular los Elementos tienen sus insuficiencias”. Y así señala como defectos más notables los cometidos por razón de las definiciones, alude a la poca claridad que resulta de la deficiente distribución de los postulados y axiomas, comenta la insuficiente lista de postulados y señala también la existencia de algunos errores de razonamiento.
Axiomas, proposiciones y teoremasAxioma o postulado es una relación que enlaza los conceptos primitivos. Sólo la experiencia o la intuición son indispensables para plantearlos o enunciarlos. Empleando la vía deductiva, y con rigor lógico matemático, se deducen de ellos las proposiciones o relaciones ciertas. Con las proposiciones se construyen los primeros teoremas y con ellos y sus conclusiones se llega a establecer una doctrina.
Algunos precisan una cierta diferencia entre postulado y axioma, señalándola de la manera que sigue. Un postulado es una premisa, un punto de partida arbitrario cuya verdad o falsedad no se pone en cuestión, es decir, son proposiciones que no son evidentes, pero que no pueden demostrarse, por ejemplo: “por un punto exterior a una recta no se puede trazar más que una paralela a ella”. Un axioma es una proposición obvia por sí misma, indemostrable y evidente: “el todo es mayor que la parte”.
El conjunto de axiomas que sirven para fundamentar una ciencia recibe el nombre de sistema de axiomas.
La axiomática es la ciencia que tiene por objeto determinar los sistemas de axiomas apropiados a una disciplina determinada y concreta. De ella opina Hilbert: “Esta ciencia no aspira a descubrir proposiciones nuevas o más generales sobre una verdad matemática, sino que sólo pretende investigar con toda certeza qué suposiciones primordiales son necesarias y suficientes para el fundamento de aquella verdad; una exploración sobre el fundamento de las ciencias particulares”.
Ya nos hemos referido a Euclides y a su V postulado, que volvemos a enunciar en su forma original:
“Si una recta al incidir sobre dos rectas hace los ángulos internos del mismo lado menores que dos rectos, las dos rectas prolongadas indefinidamente se encontrarán en el lado en el que están los [ángulos] menores”.
Este célebre postulado ha tenido una vida agitada a lo largo de la historia de las matemáticas. Algunos llegaron a pensar que no era cierto. Proclo era de otra opinión: “debe ser borrado por completo de los postulados porque se trata de un teorema lleno de dificultades, que Ptolomeo se propuso resolver en un libro, y su demostración requiere varias definiciones y teoremas”. Más aún: “la proposición recíproca es efectivamente demostrada por el propio Euclides como un teorema”. Proclo debe aludir, con toda seguridad, a la proposición 17 de los Elementos, que dice: “En todo triángulo dos ángulos tomados juntos de cualquier manera son menores que dos rectos”. Y ello, porque el V postulado equivale a decir que las rectas convergentes, al llegar a encontrarse por el lado que corresponda a los ángulos cuya suma sea menor que dos rectos, forman un triángulo (Wallis, Legendre).
Pero Proclo todavía va más lejos o, si se quiere, más cerca de las geometrías no euclídeas: “En este caso, el hecho de que las rectas convergen cuando los ángulos son menores que dos rectos, es cierto y necesario. Por el contrario, la afirmación de que como convergen más y más a medida que se prolongan llegarán alguna vez a encontrarse es una afirmación verosímil, pero no es necesaria a falta de un argumento que pruebe que esto es verdad acerca de las líneas rectas. El hecho de que haya algunas líneas que se aproximen indefinidamente, pero sin tocarse [asíntotas], por más improbable y paradójico que parezca, también es cierto y está completamente comprobado en relación con líneas de otro tipo. ¿Por qué en el caso de las rectas no es posible lo mismo que ocurre con las líneas mencionadas?”
Este V postulado del que estamos hablando ha adoptado diferentes formas a lo largo de la historia y dependiendo de los diversos autores, formas todas ellas equivalentes entre sí y equivalentes al propio postulado. Reproducimos algunas de ellas. Bonola en 1911 y Stäckel en 1914 han tratado en profundidad muchas de esas reformulaciones equivalentes del axioma del paralelismo que han ido apareciendo, así como los intentos de su demostración.
- Las rectas no equidistantes convergen en una dirección y divergen en la opuesta (Thabit ibn Qurra, c. 826-901).
- Por un punto exterior a una recta sólo cabe trazar una paralela (Ptolomeo y Alhacén, c. 905-1041).
- Todos los puntos equidistantes de una línea recta, situados a un lado determinado de ella, constituyen una línea recta (Clavius, 1574).
- Sobre una recta finita siempre se puede construir un triángulo semejante a un triángulo dado (Wallis, 1663, y Legendre, 1824).
- La suma de los ángulos de cualquier triángulo es igual a dos ángulos rectos (Saccheri, 1733).
- En todo cuadrilátero que tenga tres ángulos rectos, el cuarto ángulo también es recto (Clairaut, 1741, y Lambert, 1766).
- Se puede construir un triángulo cuya área sea mayor que cualquier área dada (Gauss, 1799).
- Dados tres puntos no alineados, siempre será posible construir una circunferencia que pase por todos ellos (Legendre, 1824, y Farkas Bolyai, 1832).
El profesor Dou asegura, y es opinión universal, que: “El quinto postulado parece un teorema que debería poderse demostrar partiendo de los postulados explícitos de Euclides y de las veintiocho primeras proposiciones del libro primero de los Elementos, los cuales son demostrados sin emplear el quinto postulado: así lo pensaron eminentes matemáticos a lo largo de todos los siglos, hasta hace poco más de un siglo en que los matemáticos empezaron a sospechar que el tal postulado era independiente de los demás, y hace menos de un siglo se dio la primera demostración matemática, o mejor, metamatemática, de que, efectivamente, era imposible demostrar el quinto postulado sin suponer algo que fuera equivalente al postulado que quería demostrarse”.
El sistema axiomático de HilbertEn 1899 el matemático alemán y profesor en Gotinga David Hilbert (1862-1945) formuló un sistema axiomático que resulta matemáticamente correcto y satisface todas las condiciones de exactitud. Se trata de un sistema falto de contradicción en sí mismo, lógicamente necesario y lo más sencillo posible. Bolyai, Lobachevski y Gauss no siguieron, sin embargo, esta axiomática; se movieron dentro del sistema contenido en los Elementos.
Eso no significa que los teoremas descubiertos por los tres matemáticos no sean ciertos, quiere decir que los viejos teoremas y sus pruebas deben colocarse bajo una nueva perspectiva y deben mostrarse de diferente manera. En tiempos de Bolyai era suficiente para la evidencia la sola apreciación visual de una aserción. Por ejemplo, un punto C está entre los puntos Ay B si los tres están situados en la misma línea. En el sistema axiomático de Hilbert el concepto de orden forma parte también del sistema axiomático.
Los axiomas de Hilbert se agrupan en cinco categorías: (1) Axiomas de incidencia. Coinciden con los contenidos en los Elementos. (2) Axiomas de orden. No se encuentran en la sistematización de Euclides. (3) Axiomas de congruencia. También se encuentran en los Elementos. (4) Axioma del paralelismo. Existe uno sólo y coincide con el V de los Elementos, aunque enunciado de forma diferente. (5) Axiomas de continuidad. Son dos y están también enunciados en los Elementos.
El sistema axiomático anterior determina la geometría euclídea y uno de los modelos que mejor se adapta a este sistema es el plano de Descartes, en el que los objetos geométricos se crean y representan mediante números. Por ejemplo, un punto es un par ordenado de números (x,y) y una recta es el conjunto de pares (x,y) que satisfacen la ecuación y = ax + b.
La geometría euclídea plana es la geometría ordinaria, la que estudiamos en los años previos a la universidad.
David Hilbert puso el punto y final al difícil conjunto de cuestiones que planteaba la axiomática. El abandono de la intuición, que en Euclides llegaba ya hasta el punto de no apoyarse nunca en el sentido común, ni en lo intuitivamente claro, en Hilbert se lleva a cabo radicalmente, y las reglas de combinación de la lógica asumen el único papel director.
Este V postulado o axioma de las paralelas difiere de los cuatro primeros en el sentido de que no es posible comprobar su validez empíricamente, es decir, no es una verdad geométrica decidible. Hasta los tiempos de Bolyai, Lobachevski y Gauss, el postulado fue considerado un defecto de la teoría geométrica, existiendo un sentimiento universal de que podría deducirse de los cuatro axiomas anteriores.
§. Los precursores de la geometría no euclídea
No existe una opinión unánime en la historia de las matemáticas reciente sobre quién es considerado precursor o quién fundador de la geometría no euclídea hiperbólica. Una consideración muy extendida es la de que existen dos grupos de precursores y uno sólo de descubridores. En el primer grupo de precursores estarían Saccheri, Lambert, Legendre y Farkas Bolyai; en el segundo, Schweikart, Taurinus y Gauss. Los descubridores serían Bolyai y Lobachevski. Stäckel y Engel incluyen, sin embargo, a Gauss en el grupo de los descubridores. Una tercera opinión es la de Bonola, para el que existen dos grupos de descubridores: aquel en el que están incluidos Schweikart, Taurinus y Gauss, y un segundo con Bolyai y Lobachevski.
A continuación vamos a describir muy brevemente algunos de los resultados de los precursores incluidos en los dos grupos establecidos anteriormente.
Gerolamo Saccheri (1667-1733) fue un matemático italiano perteneciente a la orden de los jesuitas, profesor de lógica en Turín y más tarde de matemáticas en Pavía. Publicó dos estudios: Euclides ab ovni naevo vindicatus (Euclides redimido de todo error), que versaba sobre la prueba del V postulado, y otro, anterior en el tiempo, donde planteaba una geometría no euclídea según la cual, en el plano, por un punto exterior a una recta no existía paralela alguna. En este trabajo también trató de demostrar el V postulado de forma indirecta pero, en lugar de llegar a una contradicción, el trabajo le condujo a sentar los principios de la geometría elíptica.

Portada de la obra de Saccheri.
El punto fundamental de partida fue su cuadrilátero birrectángulo isósceles, es decir, el cuadrilátero ABCD en el que sobre los extremos de la base AB se trazan dos lados iguales, AD y BC, que forman con ella ángulos rectos, mientras que los ángulos formados con la paralela CD a la base han de ser iguales obviamente, pero pueden ser rectos, agudos u obtusos.

El cuadrilátero de Saccheri.
Bajo las hipótesis de ser rectos, agudos u obtusos, Saccheri demuestra que, de ser cierta cualquiera de ellas en su cuadrilátero, entonces también lo será en cualquier otro. De ahí también se deduce que si en un triángulo la suma de sus ángulos es igual, menor o mayor que dos rectos, entonces eso también se verificará para todos los triángulos. Además, el primer resultado notable es el siguiente: según que en el cuadrilátero se verifique la hipótesis de ángulos rectos, agudos u obtusos, se tendrá, respectivamente, que AD = BC, AD < BC, AD > BC.
Estos resultados constituyen un teorema importante y, a la vez, bello de la geometría absoluta, en el que no se considera ni niega la validez del V postulado. Pero al final de su libro, publicado el mismo año de su muerte, como conclusión de sus trabajos, Saccheri facilita una prueba simple pero errónea del V postulado. Imre Tóth es de la opinión de que lo hizo así por miedo a la inquisición.
Johann Heinrich Lambert (1728-1777) fue matemático y filósofo de origen suizo, aunque vivió la mayor parte de su vida en Berlín. Su trabajo Teoría de las paralelas fue publicado después de su muerte, en 1786.
A semejanza de Saccheri, Lambert utilizó como figura fundamental el cuadrilátero, pero esta vez se trataba de un trirrectángulo, es decir, un rectángulo con tres ángulos rectos y un cuarto que podía ser recto, obtuso o agudo.

Johann Heinrich Lambert
La primera hipótesis conduce al sistema euclídeo, la segunda conduce a una contradicción (con lo que Lambert, como ya había hecho Saccheri, la declara falsa) y con la tercera descubre que la deficiencia o defecto de un polígono de n lados, es decir, la diferencia entre 2(n - 1) rectos y la suma de los ángulos del polígono, es proporcional a su área.
También descubrió que el área de un triángulo puede obtenerse a través de la utilización del área del triángulo esférico. Partiendo del área de un triángulo esférico, Lambert encontró el área del triángulo plano, siempre suponiendo la hipótesis del ángulo agudo. Si designamos por 𝛼, 𝛽 y 𝛾 los ángulos de un triángulo esférico, entonces su área vale
r2 × (𝛼 + 𝛽 + 𝛾 - π),
siendo r el radio de la esfera. Sustituyendo en la fórmula anterior r por ir (siendo i la unidad imaginaria) se obtiene
r2 × (π - 𝛼 - 𝛽 - 𝛾),
es decir, el valor del área de un triángulo plano, siempre según la tercera hipótesis de ángulo agudo. Es curioso que el propio Lambert considerara que el resultado que había obtenido era absurdo ya que, como él mismo dejó escrito, no existen los círculos o las esferas con radio imaginario.
Los objetos de HilbertHilbert admite la existencia de ciertos objetos que pueden describirse mediante las palabras punto, recta, plano y otras semejantes. Entre esos objetos se establecen ciertas relaciones mediante un sistema axiomático correcto donde pueden encontrar uso otros conceptos como estar, entre, congruente con, etc. Por medio de esas relaciones, y sólo a partir de ellas, se definen otros objetos como punto y recta. Entonces, todo contenido intuitivo, como ocurría con Euclides, carece de interés, es decir, desaparece. Se puede, desde luego, representar bajo dichas palabras lo que siempre, y en la geometría euclídea también, se ha entendido por punto, recta o plano. Pero de la misma forma también se pueden entender como puntos las personas, los números o los colores. Resulta completamente indiferente: sólo será necesario que la interpretación sea conciliable con el sistema de axiomas establecido.
Con la ayuda de estos axiomas se puede construir ahora una geometría absoluta, común a todas las geometrías posibles, incluso a la euclídea. Los objetos tales como el punto o la recta, definidos mediante las relaciones de los axiomas (definidos por tanto implícitamente), quedan ligados, relacionados. De las proposiciones así logradas se van extrayendo consecuencias y, paso a paso, se va edificando un sistema de teoremas. Sólo queda una laguna sin cubrir: supongamos una recta r1 y un punto P exterior a ella; sea r2 otra recta incidente con el punto P. Entonces, cabría preguntarse si es posible trazar esta segunda recta r2 de forma que no corte a la primera. Y también si la recta r2 será única o existirán varias. Los axiomas admitidos hasta aquí no se refieren en absoluto a ello y, por lo tanto, en la geometría absoluta tampoco podremos deducir ningún teorema sobre el particular.
Cabe decidir el camino mediante el establecimiento de un nuevo y último axioma.
Si decimos entonces que por el punto P hay exactamente una recta, es decir, una y sólo una recta r2 que no corta a la recta dada, nos habremos decidido por Euclides y, con ello, por la intuición, ya que esa proposición constituye el axioma de las paralelas y, admitido éste, nos encontramos con la geometría euclídea ordinaria con sus conocidos teoremas.
Dos rectas paralelas a r1 por P.Si establecemos como nuevo axioma: existen dos rectas r2 y r3 que pasan por P y no cortan a r1, habremos vuelto la espalda a Euclides y de la geometría absoluta habremos ido a la geometría no euclídea o hiperbólica. De igual forma que antes, también con el nuevo axioma de las dos paralelas se puede construir consecuentemente una geometría rigurosa que conducirá a una multitud de curiosos teoremas, muchos de los cuales coincidirán con los euclídeos y otros, como es natural, serán generalizaciones de nueva índole.
Uno de los hallazgos más importantes de Lambert fue la medida de las magnitudes geométricas. En la geometría euclídea, longitud, área y volumen son magnitudes aditivas, es decir, una longitud, por ejemplo, que resulta de la unión de otras longitudes es la suma de las longitudes individuales. Lo mismo puede decirse de las áreas y de los volúmenes. Por lo tanto, a la medida corresponde un significado relativo: depende de la unidad de medida adoptada. En la geometría basada en el cumplimiento de la tercera hipótesis de ángulo agudo (que se puede enunciar de la forma equivalente: la suma de los ángulos de un triángulo es menor que dos rectos) se le puede conferir un significado absoluto, es decir, existe una única medida aditiva.
La principal contribución de Adrien-Marie Legendre, matemático y geómetra, fue su magnífico libro Elementos de geometría, rival en su época de los Elementos. Es importante advertir que Legendre también descubrió el teorema de Saccheri, por lo que hoy día se conoce como el teorema de Saccheri-Legendre.
Farkas Bolyai trató intensamente de probar el V postulado. En su obra Tentamen elaboró redacciones equivalentes, de las cuales extraemos dos: “cuatro puntos que no están en un plano están en una esfera",“tres puntos que no están en una recta están en una circunferencia.
Abriremos el segundo grupo de precursores con Ferdinand Kart Schweikart (1780-1859), matemático y jurista alemán, contemporáneo de Gauss, que fue profesor de leyes en Marburg.

David Hilbert
En 1819, a través de un amigo común, Gerling, matemático también en Marburg, envió a Gauss un breve manuscrito con las siguientes notas (extraído de Bonola, Geometrías no euclidianas):
“Existen dos tipos de geometría: una geometría en sentido estricto, la euclídea, y una geometría astral (astralische Grössenlehre).
Los triángulos, en esta última, tienen la particularidad de que la suma de sus tres ángulos no es igual a dos ángulos rectos.
Sentado esto, se puede demostrar rigurosamente:
- Que la suma de los tres ángulos de un triángulo es menor que dos ángulos rectos.
- Que esta suma es tanto menor cuanto mayor es el área del triángulo.
- Que la altura de un triángulo rectángulo isósceles, aun creciendo cuando crecen los lados, sin embargo no puede superar a determinado segmento, que yo llamo constante.
- El cuadrado, en consecuencia, tiene la forma que se indica en la figura.
El cuadrado astral de Schweikart. - Si esta constante fuese para nosotros el semieje terrestre (y en consecuencia, toda línea recta trazada entre estrellas fijas que distan entre sí 90° fuera tangente a la esfera terrestre) sería infinitamente grande respecto a las dimensiones que se presentan en la vida cotidiana.
- La geometría euclídea se verifica en la hipótesis de que la constante sea infinitamente grande. Sólo entonces es verdad que la suma de los tres ángulos de todo triángulo es igual a dos rectos, y esto se deja demostrar fácilmente tan sólo si se admite como dato que la constante sea infinitamente grande.”
Según investigadores y comentaristas de nuestros días como András Prékopa, la respuesta de Gauss no fue en absoluto favorable a lo expuesto por Schweikart. Bonola, sin embargo, opina que “ensalzó el trabajo de Schweikart y declaró estar de acuerdo con todo lo que contenía”, además de decir que él también había desarrollado la geometría astral. Termina la carta exponiendo, aunque sin prueba alguna, que en esa geometría el área del triángulo hiperbólico es proporcional al defecto del ángulo (π - 𝛼 - 𝛽 - 𝛾), siendo la cota superior de esa área:
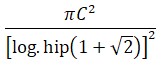
C es la llamada constante universal de Schweikart, constante que corresponde a un ángulo de paralelismo de 45°, y representa el límite de la altura de un triángulo rectángulo isósceles cuando la longitud de sus lados tiende a infinito. Hoy sabemos que esa cota puede alcanzarse cuando todos los lados son asintóticos entre sí. Esa constante C está relacionada con otra, k, del propio Gauss. Más adelante veremos la relación entre ambas.
Para finalizar señalaremos que no sabemos por qué Gauss escribió en la fórmula anterior log.hip, logaritmo hiperbólico (otro nombre para logaritmo natural o neperiano) en lugar de simplemente log.
Schweikart no nos ha dejado publicación alguna.
Franz Adolph Taurinus (1794-1874) nació en Bad König, Alemania, y falleció en Colonia. Era sobrino de Schweikart, quien le influyó para que trabajara en el problema de las paralelas. En 1825 publicó Teoría de las paralelas con contenidos no euclídeos. Rechazaba la hipótesis de ángulo obtuso y se inclinó por la de ángulo agudo, tal como habían hecho Saccheri y Lambert. Encontró la relación entre la constante C y la constante k (utilizada por Gauss para expresar la longitud de la circunferencia), que corresponde al área del triángulo:
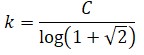
Publicó esta fórmula en su libro Geometriae prima elementa en 1826. Taurinus llegó muy lejos en lo que llamó geometría logaritmo- esférica, basada siempre en la hipótesis de ángulo agudo, obteniendo muchas fórmulas trigonométricas bajo esa hipótesis. Pero no aceptó la nueva geometría como una posible geometría del espacio en el sentido físico.
Gauss nunca publicó nada sobre la geometría no euclídea. Sus resultados se han reconstruido partiendo de su legado, contenido en cartas enviadas a otras personas. A Barna Szénássy se le debe mucha de esa información, que publicó entre los años 1977 y 1980.
Es importante mencionar que en la segunda mitad del siglo XIX Bolyai se vio relegado a un segundo plano en comparación con Lobachevski. El italiano Beltrami, entre otros, despertó el interés de la comunidad científica por los descubrimientos de Bolyai y fue a principios del XX cuando el panorama realmente cambia y comienza a aclararse, al menos en Europa. Sin embargo, debido a las conferencias y congresos celebrados con motivo del doscientos aniversario (1977) del nacimiento de Gauss, así como las comunicaciones y publicaciones producidas a tal efecto, tanto Bolyai como Lobachevski han quedado de nuevo ensombrecidos. Incluso hoy día existen ciertas corrientes que aseguran que Gauss es el verdadero descubridor de la geometría no euclídea. En sentido contrario opina su primer biógrafo, Sartorius von Waltershausen, quien afirma que Gauss sólo estuvo interesado por la geometría euclídea[2].
En el legado de Gauss se dan 25 ocasiones en las que claramente se observa su preocupación por los fundamentos de la geometría, tanto euclídea como no euclídea. Sus notas sobre estas cuestiones completan 12 páginas. Por otra parte, en su diario se puede leer una nota con la siguiente frase: “Hemos hecho excelentes progresos en los fundamentos de la geometría”. Gauss fue, tal vez, el primero en ofrecer una explicación satisfactoria al postulado de las paralelas, y su diario demuestra que ello aconteció pronto en su carrera científica. Pero Gauss era un hombre prudente, especialmente cuando trabajaba con novedades extrañas y desconcertantes. Durante muchos años guardó el asunto para sí hasta descubrir que otros, como János Bolyai, estaban pensando en las mismas cosas.
Algunas notas de Gauss parecen atestiguar que conocía completamente el libro de Lambert Teoría de las paralelas. Puede que lo pidiera prestado a la biblioteca de la Universidad de Gotinga durante su época de estudiante. Gauss formuló un concepto de paralelas que, indudablemente, es similar a los de Bolyai y Lobachevski. Ya hemos dicho que en su carta escrita a Schweikart evitó la prueba del valor de la cota superior del área del triángulo hiperbólico. Sí envió a János un esquema de prueba incluido dentro de sus comentarios sobre el Appendix. En otra carta dirigida a Schumacher tampoco incluyó la prueba de la longitud de la circunferencia correspondiente al círculo hiperbólico. Por último, entre los años 1840 y 1846, Gauss hizo varios comentarios al trabajo de Lobachevski, todos ellos muy válidos, pero siempre basándose en las ideas ya incluidas en el Appendix. Por consiguiente, desde antes de la publicación del Appendix, cuya reimpresión se hizo en 1831, pocos resultados pueden atribuirse a Gauss.
Hemos dicho que Gauss conocía el libro de Lambert. Sin embargo, sabemos por los escritos de János Bolyai cuáles eran los primeros libros sobre la teoría de las paralelas que Gauss conocía, y el de Lambert no figura entre ellos. Así que, o Gauss nunca le mencionó a Farkas Bolyai la existencia del libro de Lambert, o bien el padre, conociéndolo, no le dijo nada a János. Parece que esta segunda hipótesis debe excluirse. Resulta más verosímil que la discusión entre Gauss y Farkas no fuera lo suficientemente profunda y Gauss no mencionara todo lo que sabía acerca del problema de las paralelas. Es importante notar esto porque algunos autores alegan que János Bolyai publicó lo que había oído decir a su padre acerca de Gauss. También existen muchos argumentos contrarios que refutan esta alegación[3].
§. Los juicios de Kant. Influencia en los geómetras de su tiempo
Esto escribe Gauss acerca de Kant en la carta que envía a su amigo Schumacher el 1 de noviembre de 1844:
“Se ve el mismo tipo de cosa [incompetencia matemática] en los filósofos contemporáneos Schelling, Hegel, Nees von Essenbeck y sus seguidores. ¿No te ponen los pelos de punta con sus definiciones? Lee en la historia de la filosofía antigua lo que los grandes hombres de aquel tiempo, como Platón y otros, produjeron en el dominio de las explicaciones. Pero con Kant las cosas van a menudo mucho mejor. Según mi opinión, su distinción entre proposiciones analíticas y sintéticas es una de aquellas cosas que, o desembocan en una trivialidad o son falsas”.
Cuando Gauss escribía esto ya tenía conocimiento de la geometría no euclídea, que es en sí misma una refutación suficiente de algunas afirmaciones de Kant sobre espacio y geometría.
Para nuestros propósitos, lo que nos interesa de la filosofía de Kant son sus ideas sobre el espacio y el tiempo, porque esas ideas, como casi todas las suyas, tuvieron una gran influencia en los científicos de la época.

Immanuel Kant
La filosofía crítica se propone resolver el problema del conocimiento, analizando nuestras facultades y sus formas esenciales, para averiguar su valor en la adquisición de la certeza, y separar el elemento subjetivo, fenómeno, del elemento objetivo, noúmeno. El hecho de conocer es, para Kant, innegable, por eso no investiga la posibilidad, preguntando si es posible, sino el modo, inquiriendo cómo es posible. Entonces, los conocimientos que adquirimos son de dos clases:
- Conocimientos a posteriori: son los que provienen de la experiencia, tienen como punto de origen la materia, se adquieren por la sensibilidad y su carácter es contingente (pueden suceder o no) e individual.
- Conocimientos a priori: son los que provienen de la propia facultad cognoscitiva, nacen en el fondo de nuestra alma, preceden a toda experiencia, su carácter es necesario y universal, y tienen como base ciertas denominaciones innatas que Kant llama formas a priori, por ser apriorístico el conocimiento que engendran.
Para explicar debidamente la función del entendimiento, que es la facultad de juzgar, Kant expone la teoría del juicio, conservando su manía apriorística y atendiendo para su clasificación a la relación necesaria o contingente entre el sujeto (del que se afirma o niega algo) y el predicado (lo que se afirma o niega del sujeto) en una proposición. Incluiremos aquí sólo tres clases de los juicios de Kant.
- Juicios analíticos: son aquellos en los que el predicado está contenido en la esencia del sujeto, y analizando éste se encuentra aquél. Son necesarios y conocidos por la razón a priori, es decir, antes de toda experiencia. Por ejemplo: la circunferencia es redonda es un juicio analítico porque examinando el sujeto, la circunferencia, encontraremos en él como nota esencial la redondez.
- Juicios sintéticos: son aquellos en los que el predicado no está incluido en la esencia del sujeto, de cuyo análisis racional no fluye el concepto atribuido. Estos juicios son contingentes y conocidos a posteriori por la experiencia. Por ejemplo: este círculo es de hierro. Aunque la razón examine el concepto círculo no encontrará la cualidad férrea que se le atribuye, y será preciso comprobar la afirmación por la experiencia. De acuerdo con Kant, los juicios matemáticos son todos sintéticos. Hubo quien criticó, como el matemático y lógico alemán Gottlob Frege, esta distinción, porque lo importante en matemáticas son las pruebas y no el contenido de las proposiciones.
- Juicios sintéticos a priori: según Kant, son aquellos juicios en los que el predicado no está incluido esencialmente en el sujeto (son pues sintéticos), pero al mismo tiempo son universales y necesarios, y su conocimiento procede de la razón (son inherentes a nuestro propio espíritu) y no de la experiencia (son pues a priori). Por ejemplo: siete más cinco igual a doce: la línea recta es la distancia más corta entre dos puntos.
Otro de los conceptos que define Kant es la intuición. La sensibilidad es una facultad meramente receptiva. Existen en nosotros multitud de impresiones o sensaciones visuales, auditivas, etc. La sensibilidad se representa en esas sensaciones a través de dos formas a priori: el espacio y el tiempo, verificándose en nosotros el fenómeno de conocer, sin darnos derecho a afirmar que los objetos son como los conocemos, sino únicamente a afirmar el hecho subjetivo del conocimiento. Estos conocimientos de la sensibilidad se llaman intuiciones sensibles.
Espacio y tiempo son dos conceptos universales y necesarios, luego no provienen de la experiencia, que es particular y contingente. Es decir, espacio y tiempo son formas a priori de la sensibilidad, correspondiendo el espacio a la externa y el tiempo a la interna. En particular, Kant establece que la geometría es un campo que determina las características del espacio sintéticamente y a priori, es decir, inherente en nosotros antes de cualquier experiencia adquirida sobre un objeto, teniendo un papel coordinador en el desarrollo de la forma de nuestra percepción externa. Dicho de otro modo, el espacio de ninguna manera va unido a los objetos, sólo existe para el hombre. Conocemos las cosas no como son en sí mismas (noúmeno), sino como se nos aparecen (fenómeno).
En su tesis, Kant admite que es posible que la estructura del espacio pueda ser diferente de la representada por la geometría euclídea. Pero más tarde abandona ese punto de vista y en la Crítica de la razón pura se inclina por mantener que la estructura del espacio es euclídea. Puede encontrarse esta argumentación cuando discute sobre las diferencias entre los métodos de la filosofía y los de las matemáticas.
Si se tiene en cuenta la opinión de ciertos autores, la geometría de Bolyai y de Lobachevski supone el criticismo del concepto kantiano del espacio; para otros es la refutación del concepto. Ésta es su argumentación: si en nuestra mente existe sitio para las geometrías euclídea e hiperbólica, no es posible que nuestro concepto del espacio sea a priori en nuestra mente, independientemente de nuestras experiencias acerca de los objetos.
Indudablemente, el carácter absoluto que Kant otorga a la geometría euclídea en su filosofía demuestra ser un callejón sin salida, no tanto por lo que representa la geometría de Bolyai- Lobachevski, sino por los resultados de la física obtenidos en el siglo XX. Sin embargo, la visión de Kant de que el espacio es euclídeo se puede aislar de sus otras visiones relativas al espacio, que son sutiles y diferentes de la susodicha opinión contraria. Kant no niega el hecho de que también se pueda formular sobre el espacio más de una teoría matemática abstracta.
Sin embargo, en la época de Gauss, Bolyai y Lobachevski, la filosofía de Kant era considerada como el soporte definitivo de la geometría euclídea. Al contrario que Gauss, que tuvo miedo de publicar sus resultados por los posibles ataques que podía recibir de los beodos, Bolyai y Lobachevski fueron unos revolucionarios que revelaron con coraje sus convicciones científicas al mundo entero.
Capítulo 4
El Appendix y otros trabajos de Bolyai
Verdaderamente, lo que más placer proporciona no es el saber, sino el estudiar; no la posesión, sino la conquista; no el estar aquí, sino el llegar allá.
Gauss
§. La ciencia absoluta del espacio
Nos hemos referido en otro lugar a la obra escrita de János Bolyai y a su inclusión como apéndice en la de su padre, Tentamen. Nos adentraremos ahora en el contenido de ese trabajo que János tituló La ciencia absoluta del espacio.
También nos hemos referido ya en el capítulo anterior al concepto de geometría absoluta. Lo analizaremos de nuevo aquí relacionándolo con la geometría no euclídea descubierta por Bolyai.
¿Qué nos quiere significar János Bolyai con el nombre de geometría absoluta? ¿Cuál es el alcance de esta nueva geometría? El concepto de geometría absoluta fue introducido por Bolyai en el punto §15 de su Appendix:
Considerando §§ 13 y 14, el sistema de geometría que descansa sobre la hipótesis de la certeza del axioma XI de Euclides se denomina Σ el sistema apoyado en la hipótesis contraria es S.
Todos los conceptos que no se diga expresamente que pertenezcan a Σ o a S, se sobreentiende que se enuncian absolutamente, es decir, son considerados ciertos tanto para Σ como para S.

Guardas escritas por el propio János Bolyai en el ejemplar del Appendix que se conserva en la Academia de Ciencias Húngara.
Por lo tanto, los teoremas de esta nueva geometría absoluta son aquellos que no dependen de la hipótesis que se haga al considerar una única paralela (euclídea) o varias paralelas (no euclídea) a una recta por un punto exterior a la misma. Como consecuencia, esta geometría se llama así porque es común a todas las geometrías posibles y, en particular, va más lejos que la geometría hiperbólica. Y esta es la geometría de János Bolyai.
El Appendix consta de 43 secciones desarrolladas en 29 páginas. Esas secciones se reparten en distintas familias de contenidos. Las deducciones, así como la metodología seguida, se basan en las matemáticas de siglos anteriores, sobre todo en la geometría de Descartes y el cálculo diferencial e integral de Newton y Leibniz.

Portada original de la versión del Appendix de 1897.
Los contenidos del Appendix los podemos distribuir en las siguientes secciones:
- Definición de las paralelas y de sus propiedades independientes del postulado euclídeo.
- Círculo y esfera de radio infinito. La geometría sobre la esfera de radio infinito es idéntica a la geometría plana ordinaria.
- La trigonometría esférica es independiente del postulado de Euclides. Demostración directa de las fórmulas.
- Trigonometría plana en el caso no euclídeo. Aplicaciones al cálculo de las áreas y de los volúmenes.
- Problemas resolubles elementalmente. Construcción de un cuadrado equivalente a un círculo, en la hipótesis de ser falso el V postulado.
Vamos a hacer un extracto del Appendix, comentando únicamente alguno de sus apartados.
Figuras geométricas en el ejemplar del Appendix que se conserva en la Academia de Ciencias Húngara.
Comienza dando una definición de todos los conceptos básicos que utilizará más adelante, así como los signos para representarlos, como por ejemplo recta AB, segmento y rayo (vector), plano, semiplano, perpendicularidad ⊥, paralelismo ∥, etc.
En primer lugar, al rechazar Bolyai el V postulado debe definir el paralelismo. Lo hace de la siguiente manera. Consideremos una recta r, y un punto P fuera de ella. Si, comenzando en P trazamos una semirrecta r2 que corte a r1 según un sentido de ésta (izquierda), moviendo esa intersección hacia el infinito, existirá una posición límite en la que la semirrecta r2 ya no corte a r1. Podemos hacer lo mismo en el otro sentido de r1 empleando para ello la semirrecta r3. Si prolongamos también ambas semirrectas en los otros sentidos desde P, entonces obtendremos dos rectas, las cuales serán paralelas a r1. Si estas rectas son distintas, entonces existirán infinitas rectas entre las dos r2 y r3 que no cortarán a r1. Además, todas ellas tendrán una perpendicular común d con r1. La geometría correspondiente a este caso recibe el nombre de geometría hiperbólica, con ángulo de paralelismo α.
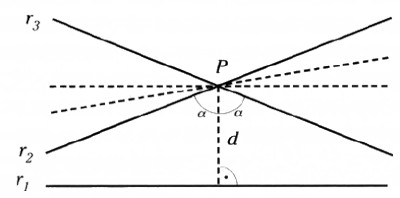
Las paralelas de Bolyai.
Las rectas r2 y r3reciben el nombre de paralelas asintóticas o paralelas límite. Todas las demás situadas entre ellas son las hiperparalelas. La recta d es la perpendicular a r1 por P.
Es necesario tener en cuenta que el concepto de recta de Bolyai no es el que estamos acostumbrados a manejar, aunque lo hayamos representado así en la figura. Las rectas de la geometría de Bolyai-Lobachevski pueden ser cualquier objeto geométrico que satisfaga los axiomas que se establezcan.
La redacción textual con la que Bolyai define el paralelismo en su primer apartado del Appendix es la siguiente:
“Si el rayo [semirrecta] AM no es cortado por el rayo BN, situado en el mismo plano, pero sí es cortado por todo rayo BP comprendido dentro del ángulo ABN, entonces llamaremos al rayo BN paralelo al rayo AM; y eso se designa por BN ∥ AM.”
Reproducción de la figura original del Appendix con la definición de paralela.
Como ya hemos dicho anteriormente, Bolyai desarrolló la geometría absoluta, que es independiente del V postulado. El siguiente teorema pertenece a la geometría del plano absoluto: si un punto P dista d de la recta r y α es el ángulo comprendido entre la recta incidente con P perpendicular a r y la recta paralela límite a r, entonces se verifica que:
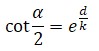
siendo k una constante universal (cualquiera) independiente de la elección que se haga para r y P, y que puede valer incluso infinito, en cuyo caso regresaríamos a la geometría euclídea. En efecto, basta hacer en la fórmula anterior α = 90° para obtener k = ∞.
Además, puede observarse que el ángulo de paralelismo depende de la distancia d del punto P a la recta r.
Bolyai desarrolló también la geometría hiperbólica y la aplicó a) cálculo de longitudes y áreas. Por ejemplo, la longitud de una circunferencia de radio r, en la geometría hiperbólica, vale:
![]()
siendo k, de nuevo, la constante universal. Realizando las transformaciones convenientes, esta fórmula equivale al recíproco de la curvatura del espacio. Si hacemos en ella k → ∞, entonces el valor de ese límite es 2πr, es decir, la longitud de la circunferencia en la geometría euclídea.
Uno de los teoremas más bellos de la geometría absoluta de Bolyai, relativo a los triángulos rectilíneos, es el siguiente: los senos de los ángulos de un triángulo son proporcionales a las longitudes de las circunferencias cuyos radios son iguales a los lados opuestos a los respectivos ángulos, tanto en Σ como en S. Si se designan por A, B y C los ángulos, por a, b y c los lados y por Or la longitud de la circunferencia de radio r, entonces el teorema establece que:
Oa : Ob : Oc = sen A : sen B : sen C
La longitud de una circunferencia de radio r la designa Bolyai como la periferia del segmento igual a r.
Bolyai define la L-línea, para nosotros horociclo en el plano, y el concepto análogo de horosfera en el espacio. Son, respectivamente, las posiciones límite del círculo y de la esfera cuando el radio es infinito.
Si α, β y γ son los ángulos de un triángulo, entonces su suma en el plano euclídeo es π, mientras que en la geometría hiperbólica es α + β + γ = π. Ya hemos dicho que la diferencia π – (α + β + γ) recibe el nombre de defecto del triángulo. Bolyai demuestra que el área A del triángulo vale:
A = k2 (π – (α + β + γ)))
Ya dijimos que esta fórmula había sido conocida por Lambert, pero fue Bolyai quien hizo una demostración de la misma en su Appendix.
Por último, otro interesante teorema de Bolyai es el siguiente: sean a y b dos lados de un triángulo rectángulo y c su hipotenusa, entonces:
![]()
de donde se puede deducir en el límite la fórmula de Pitágoras c2 = a2 + b2, haciendo en la de Bolyai k → ∞.
Bolyai incluye al final de su obra construcciones pertenecientes a la geometría hiperbólica. Con estas frases termina el Appendix:
Queda por probar la imposibilidad de decidir (sin usar ninguna suposición) cuál, entre Σ los varios S, existe: lo cual, sin embargo, se reservará para una ocasión más idónea.
De acuerdo con el profesor Montesinos, “Bolyai estaba psicológicamente convencido de la consistencia de los sistemas S y Σ. Se plantea el problema de probarla, pero lo deja para el futuro.
En esto Bolyai, como Gauss y Lobachevski, se diferencian netamente de los anteriores cultivadores de la geometría no euclídea; a saber, en que estaban convencidos de su coherencia interna, mientras que los anteriores siempre buscaban una contradicción, para establecer una demostración del axioma de las paralelas”.
§. Investigaciones sobre la teoría de números
El interés de János Bolyai por la teoría de números se remonta a su juventud, cuando con sólo 13 años, hablando ya latín, leyó un ejemplar de Disquisitiones arithmeticae de Gauss. Éste envió y dedicó el libro a su amigo de universidad Farkas Bolyai en 1803. János adquirió un segundo ejemplar en Viena, glosado por él y que se encuentra actualmente en la biblioteca Teleki-Bolyai de Marosvásárhely. Además, lo cita con suma frecuencia en sus propios trabajos sobre números y lo calificó en su día como colosal. Se trataba de un trabajo de Gauss de gran calidad y, sobre todo, anticipado a su tiempo. Gauss le comentó a Farkas el 2 de septiembre de 1808 que únicamente seis matemáticos de aquel entonces habían sido capaces de comprender su contenido. Para los Bolyai, esta publicación fue su pequeño compañero y un manual de referencia que estudiaron completamente.
Algunos biógrafos de János Bolyai advierten del poco éxito que logró en sus trabajos sobre la teoría de números. Sin embargo, sus manuscritos parecen afirmar lo contrario. En ellos demuestra un gran interés por esa teoría y además tuvo ideas originales con las que se adelantó a otros matemáticos posteriores. Veamos algunos ejemplos.
Uno de los primeros teoremas encontrado en el legado de Bolyai es el siguiente: si p y q son primos y a es un entero que no es múltiplo ni de p ni de q, y se cumple que:
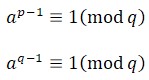
entonces se cumple también que:
![]()
Líneas manuscritas de Bolyai con la redacción de su teorema.
Éste es el mismo teorema que James Hopwood Jeans (1877-1946), físico, astrónomo y matemático británico, publicó décadas más tarde, concretamente en 1898. Debería llamarse, por tanto, teorema de János Bolyai.
En algún momento Bolyai pensó que podría encontrar la fórmula de los números primos apoyándose en las teorías de Fermat; no fue así. Por ello probó a demostrar su recíproco.
Como resultado, halló la relación (1) escrita anteriormente.
Haciendo en ella α = 1, y con repetidos intentos, obtuvo los números p = 11 y q = 31, encontrando así el pseudoprimo más pequeño con respecto a 2, que es 341, y para el que se verifica que:
![]()

James Hopwood Jeans
Con la fórmula (1) y otras operaciones, Bolyai dedujo muchos números pseudoprimos, como:
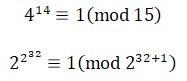
Las investigaciones sobre los números pseudoprimos alcanzaron su mayor desarrollo en el siglo XX y han jugado un papel muy significativo en la criptografía.
Otro ejemplo de la dedicación de János a esta teoría es el caso del teorema de los dos cuadrados de Fermat: todo número primo de la forma 4k + 1 (k ∈ N) puede escribirse como suma de dos cuadrados. El teorema fue planteado por Fermat y demostrado cien años más tarde por Euler. Farkas tuvo acceso a esta prueba y le pidió a su hijo que tratara de hallar una demostración más sencilla que la de Euler. En muy poco tiempo János lo consiguió y envió a su padre una carta con cuatro demostraciones distintas. Nadie ha conseguido una solución más brillante al problema de Fermat que János Bolyai.
En 1844, G. Eisenstein demostró también el teorema de Fermat, pero utilizando números complejos.

Escrito de Bolyai relacionado con el teorema de Fermat.
János también trató con otros problemas de la teoría de números, como la ecuación de Pell, los números de Fermat (Fn= 2(2)^n +1 , n ∈ N ) o las ecuaciones diofánticas exponenciales. Puede afirmarse que Bolyai fue uno de los primeros en tratar este tipo de ecuaciones, aunque no alcanzara conclusiones significativas.
Por último, vale la pena mencionar la construcción por Bolyai del siguiente cuadrado mágico:
§. La divisibilidad en el campo complejo
En un principio János Bolyai admitió que la teoría de los números imaginarios no estaba clara para él, que la consideraba como algo inútil, y por tanto la abandonó. Pero más tarde conoció la expresión ![]() lo que le indujo a estudiar y tener una idea clara de los números complejos. En este sentido intercambió correspondencia con su padre y cuando se enteró del concurso organizado por la Sociedad Científica Jablonowski sobre la construcción de números complejos, Bolyai escribió una breve comunicación titulada Responsio, que envió a Leipzig en 1837.
lo que le indujo a estudiar y tener una idea clara de los números complejos. En este sentido intercambió correspondencia con su padre y cuando se enteró del concurso organizado por la Sociedad Científica Jablonowski sobre la construcción de números complejos, Bolyai escribió una breve comunicación titulada Responsio, que envió a Leipzig en 1837.

El cuadrado mágico de Bolyai.
No obstante, los trabajos de János relacionados con los números complejos no se limitan al Responsio. Profundizando en sus manuscritos nos encontramos también con teorías relativas a la divisibilidad en este campo. Aunque es notorio que fue Gauss el primero en publicar esta teoría en los años 1831 y 1832, las notas de Bolyai demuestran que, de forma independiente, concibió también las propiedades de la divisibilidad en el campo complejo. Leyendo sus notas, parece que desarrolló sus propias teorías a partir de 1820.
Ya hemos señalado de alguna manera el interés que Bolyai manifestó por los números primos. En el caso de los primos complejos, distingue tres categorías: los primos racionales, como ±2, ±3, ±5,... que él llama números principales-, los números del anillo K de los enteros complejos, como 1 + i, 1 + 2i, 2 - 3i, 6 - i... que denomina números primos perfectos-, y los números primos tanto del anillo de los racionales como del anillo de los complejos, tales como 3, 7, 11, ..., 4m + 3, que denomina números primos absolutos.
Tal como decía Gauss, Bolyai asegura que los números primos complejos son:
Los números (1 + i), (1 - i), (-1 + i), (-1 - i).
Los números primos racionales que tienen la forma 4m + 3.
Los factores complejos de los números primos racionales de la forma 4m + 1.
Los manuscritos descubren la demostración de todos los casos.
§. Las investigaciones sobre el álgebra
Pocos conocen la dedicación de János Bolyai a la resolución de problemas de álgebra. También obtuvo importantes resultados en este campo, como demuestran varias monografías, principalmente en la resolución de ecuaciones algebraicas de orden superior.
El estudio de sus manuscritos revela dos etapas en esta investigación. En la primera, Bolyai, como muchos otros antes que él, elige el camino equivocado para tratar de resolver las ecuaciones algebraicas de grado quinto. Incluso llegó a pensar que había descubierto el método para resolver las ecuaciones de cualquier grado. Después de varios intentos infructuosos, ya en la segunda etapa de su investigación, abandonó el camino erróneo, llegando por su cuenta al conocido teorema de Ruffini-Abel, en el que se demuestra la imposibilidad de encontrar expresiones basadas en radicales para hallar las soluciones de una ecuación de grado quinto o superior. En uno de sus manuscritos, refiriéndose a este asunto, dice: “A partir de 1837 me llamó la atención este problema”. Aunque Bolyai era contemporáneo de Abel, debido a su aislamiento nunca conoció sus trabajos y teorías a este respecto, como tampoco las de Galois, que no fueron publicadas hasta 1846 de la mano de Liouville. Sus dos fuentes de información fueron su padre, con el que se formó en las matemáticas desde que era un niño, y la biblioteca de Marosvásárhely, donde encontró varios trabajos que estudió con el máximo interés. En ese centro fue precisamente donde János leyó el libro de Gauss Disquisitiones arithmeticae, así como su tesis doctoral presentada en 1799, donde prueba, por vez primera, el principio del álgebra clásica. Ahí es donde, con toda probabilidad, comenzó el interés de Bolyai, ya que Gauss expresaba sus dudas acerca de la resolución de las ecuaciones de grado superior. En el mismo centro también debió de leer la obra de Ruffini relativa a su teorema.
Consta que János Bolyai se percató de los fallos cometidos por Ruffini en sus razonamientos, ya que en sus manuscritos se han encontrado frases como ésta: “Como la aserción de Ruffini necesita todavía una prueba, trataré de demostrar la imposibilidad por otro camino”, que parece probar que estaba en el camino correcto. Su teorema lo enunció así: “Encontrar una solución algebraica de la ecuación general de grado superior al cuarto, es decir, al menos de grado cinco, es imposible”.
En nuestros días, los compatriotas de Bolyai dedicados a la investigación de la matemática y de sus obras advierten, como Elemér Kiss, de la Universidad Sapientia, que "la historia de la matemática ignora que hubo un matemático húngaro en el siglo XIX capaz de resolver uno de los problemas más importantes de la matemática".
Capítulo 5
Los modelos de la geometría hiperbólica
Fórmate tú en vez de esperar a que te formen y modelen. Herbert Spencer
§. Introducción
Hemos visto que Bolyai y Lobachevski fueron los descubridores de la geometría hiperbólica, primera geometría que se apartaba de la praxis de Euclides. Sin embargo, ninguno de estos dos grandes personajes de las matemáticas probó que su nueva geometría estuviera libre de contradicciones. Esa ausencia de contradicción puede probarse utilizando modelos, es decir, objetos matemáticos y sus relaciones mutuas, de manera que el conjunto satisfaga los axiomas establecidos en la geometría hiperbólica. Como dice Alberto Dou: “ayudará a la comprensión [...] el tener presente modelos de la geometría del ángulo agudo o hiperbólica.
Este modelo puede realizarse en superficies sumergidas en el espacio euclídeo de tres dimensiones y dotadas, por tanto, de la métrica subordinada por el espacio euclídeo tridimensional en las superficies modelo”. La geometría euclídea está basada en un modelo tan sencillo como es el constituido por una superficie plana.
Bonola introdujo una serie de conceptos en relación con los modelos, que vamos a recoger en este texto. Y advierte que para una superficie cualquiera que no sea plana es necesario comprobar hasta qué punto es posible fundamentar sobre ella una geometría análoga a la del plano.
“Por dos puntos A y B de la superficie pasa generalmente una línea bien determinada que le pertenece, la cual marca sobre la superficie la mínima distancia entre los dos puntos. Tal línea es la geodésica que une los dos puntos dados. Si se trata, por ejemplo, de una esfera, la geodésica que une dos puntos (no extremos de un diámetro) es un arco del círculo máximo por ellos determinado”.
Nos habla después del concepto de igualdad para poder comparar la geometría del plano con la equivalente sobre la superficie elegida. Según Bonola, a este concepto de igualdad se puede llegar de una manera intuitiva admitiendo que la superficie que elijamos para contener el modelo yazca sobre una hoja flexible e inextensible.
“Parece natural comparar las geodésicas de aquella [la superficie elegida] midiendo las distancias sobre la superficie con las rectas de éste [del plano], y también considerar como [geodésicamente] iguales, sobre una superficie, a dos figuras trazadas en ella que puedan hacerse corresponder punto a punto, de modo que las distancias geodésicas entre los pares de puntos correspondientes sean iguales”.
Un ejemplo sencillo es el basado en una superficie cilíndrica, conseguida arrollando (flexionando sin extender) una cuartilla por los dos extremos laterales. Si sobre esa superficie tomamos un segmento (una geodésica), ese segmento puede aplicarse, hacerse corresponder, punto a punto con otro segmento del plano. Lo mismo para una recta u otra figura, como un triángulo: en un caso tendremos el triángulo geodésico y en el otro, el triángulo plano correspondiente. Es verdad que los dos triángulos no son iguales al considerar el espacio común en el que residen.
El conjunto de conceptos antes enunciado, aplicable a una superficie cualquiera, supone el punto de arranque para producir una geometría sobre la superficie.
“Volviendo a una superficie cualquiera, el sistema de convenciones antes indicado da origen a una geometría sobre la superficie, que consideraremos siempre por regiones convenientemente limitadas (regiones normales). Dos superficies aplicables una sobre otra con una flexión sin extensión tendrán la misma geometría; así, por ejemplo, sobre una superficie cualquiera cilíndrica, y en general sobre una superficie cualquiera desarrollable, se tendrá una geometría semejante a la de una superficie plana”.
La geometría de Riemann, llamada geometría elíptica, es otro ejemplo de geometría sobre una superficie. En este caso el modelo es la esfera, en la que todas sus rectas son los círculos máximos de la misma. Pues bien, Bonola advierte que la geometría de la esfera nos proporciona otro ejemplo de geometría sobre una superficie distinta de la del plano, siendo imposible aplicar una porción de esfera sobre una superficie plana.
“Todavía entre la geometría plana y la esférica tenemos, sin embargo, una notable analogía. Esta analogía halla su fundamento en el hecho de que la esfera puede moverse libremente sobre sí misma, precisamente como el plano, así que para las figuras iguales sobre la esfera valen proposiciones en todo análogas a los postulados de la congruencia sobre el plano”.
Es fundamental para proseguir que introduzcamos un concepto nuevo propio de las curvas y de las superficies: la curvatura. Intuitivamente, curvatura de una curva en uno de sus puntos significa el desvío que experimenta en ese punto respecto de la dirección recta, es decir, de la tangente en ese punto.
Por ello, una circunferencia tiene una curvatura constante, pero una elipse, no: es más curvada cerca de los extremos del eje mayor y menos cerca del eje menor. En cada punto de una curva donde se calcule su curvatura existe un círculo llamado círculo osculador, círculo distinto de un punto a otro. Si su radio es R, el valor de la curvatura en ese punto será 1/R, de donde se deduce que cuanto mayor sea el radio del círculo osculador, menor será la curvatura.
Si se trata de una superficie, la cosa se complica un poco más. Supongamos que queremos calcular la curvatura de una superficie en un punto P. Trazaríamos por P la recta normal (perpendicular) n a la superficie y por esa normal haríamos pasar un haz de planos, es decir, un conjunto de planos que se corten todos ellos en la recta n. Cada plano seccionará a la superficie en una curva que naturalmente será plana. Entre esas curvas existirán dos que se cortarán según un ángulo recto, y cada una de ellas tendrá su propia curvatura en el punto P, curvatura que será máxima o mínima. El producto de ambas define la curvatura de la superficie en P.
Conocidos someramente estos conceptos, añadamos lo que expresa Bonola como aplicación de la curvatura:
“A fin de que una superficie convenientemente limitada pueda moverse, con flexión sin extensión, sobre sí misma como la superficie plana, es preciso que un cierto número K, invariante respecto a las susodichas flexiones, tenga un valor constante en todos los puntos de la superficie. Este número ha sido introducido por Gauss con el nombre de curvatura".
Es posible construir superficies con curvatura constante dependiendo del valor dado a K.
- Si hacemos K = 0, obtenemos superficies desarrollabas que pueden aplicarse en el plano. El plano es un ejemplo de superficie de curvatura constante de valor 0. Su círculo osculador tiene un radio infinito.
- Si K > 0, obtendríamos superficies que pueden aplicarse sobre una superficie esférica de radio √(1/K). La esfera sería un ejemplo.
- Si K < 0, obtendríamos superficies aplicables sobre la pseudoesfera.
Más adelante volveremos sobre la pseudoesfera (y cómo se construye) que, como hemos dicho, tiene una curvatura constante negativa.
“Entre la geometría sobre una superficie de curvatura constante y la de una porción de plano, tomadas una y otra con las convenientes limitaciones, existe una analogía, que podemos poner en evidencia traduciendo las primeras definiciones y propiedades de una en las de la otra, como se indica sumariamente en las contraposiciones de frases que se observan en el siguiente cuadro:
| a) | Superficie. | Región de plano. |
| b) | Punto. | Punto. |
| c) | Geodésica. | Recta. |
| d) | Arco de geodésica. | Segmento rectilíneo. |
| e) | Propiedades lineales de la geodésica. | Postulados relativos a la ordenación de los puntos sobre la recta. |
| f) | Dos puntos determinan una geodésica. | Dos puntos determinan una recta. |
| g) | Propiedades fundamentales de la igualdad de arcos geodésicos y de ángulos. | Postulados de la congruencia segmentaria y angular. |
| h) | Si dos triángulos geodésicos tienen iguales dos lados y el ángulo comprendido, también los restantes lados y ángulos son iguales. | Si dos triángulos rectilíneos tienen iguales dos lados y el ángulo comprendido, también los restantes lados y ángulos son iguales.” |
Antes de describir los modelos correspondientes a la geometría hiperbólica, transcribimos el siguiente párrafo con el que Bonola finaliza las cuestiones anteriores, antes de estudiarlas y compararlas con el plano euclídeo:
“Síguese de aquí que se pueden considerar comunes a la geometría de las superficies en cuestión todas aquellas propiedades pertenecientes a regiones limitadas del plano, que en el sistema euclídeo son independientes del postulado de las paralelas y en cuya demostración no se hace uso del plano completo (por ejemplo, de la infinidad de la recta)”.
A continuación presentaremos algunos modelos para entender la geometría hiperbólica.
§. El modelo de Beltrami
Beltrami creó un modelo de geometría hiperbólica. Utilizó para ello el trabajo desarrollado por el profesor de matemáticas polaco Ferdinand Minding en 1868, en el que estudiaba, entre otras cosas, la geometría diferencial de las superficies de curvatura constante. El modelo en cuestión está constituido por la pseudoesfera, que es la superficie de revolución cuya generatriz es la tractriz.
Pseudoesfera y tractriz.
La tractriz es una curva tal que el segmento de recta tangente comprendido entre un punto cualquiera de la curva y su eje (asíntota) es constante, es decir, ese segmento de tangente conserva su longitud. El giro de la tractriz sobre su eje, tomado como eje de revolución, genera la pseudoesfera, superficie de curvatura constante negativa. La tractriz fue descubierta por el arquitecto francés Perrault en el siglo XVII.
Christiaan Huygens denominó a la tractriz (traktorien) curva del perro: si un perro P1 persigue a otro P2 que se mueve sobre una recta, estando P1 fuera de la misma, entonces la distancia P1P2 es constante y por lo tanto P1 describe una tractriz.

Eugenio Beltrami
Éstas son algunas características de la pseudoesfera. Un punto hiperbólico es cualquier punto de la pseudoesfera. Un segmento de recta sobre la pseudo-esfera que pasa por dos puntos de la misma, se caracteriza por ser el camino más corto entre esos dos puntos y, por lo tanto, es una geodésica. Dos rectas geodésicas cualesquiera nunca se cortarán en más de un punto. Por un punto exterior a una recta sobre la pseudoesfera pasan, al menos, dos paralelas. Por último, los lados de un triángulo sobre la pseudoesfera son segmentos de geodésica y la suma de sus ángulos, como corresponde a esta geometría hiperbólica, es menor de 180°.
La geometría construida sobre la superficie de la pseudoesfera cumple con todos los postulados de Euclides a excepción, naturalmente, del postulado de las paralelas.
§. El modelo de Klein
Otro modelo adaptado a la geometría hiperbólica se debe a Christian Félix Klein, aunque actualmente también se conoce con el nombre de modelo de Beltrami-Cayley-Klein. La geometría Bolyai-Lobachevski puede definirse, por consiguiente, utilizando este modelo que consiste en un plano formado por todos los puntos de un círculo, pero excluyendo los correspondientes a la circunferencia del mismo.
Entonces, punto es cualquier punto interior a la circunferencia, como el P. Las rectas son las cuerdas de la misma, excluyendo sus puntos extremos como, por ejemplo, las AB, AC o BD.
Puntos del infinito de ese plano son todos aquellos situados en la circunferencia.

Christian Félix Klein
Dos rectas serán paralelas si tienen el mismo punto del infinito o, lo que es igual, si tienen un extremo común. Son paralelas a la AB, las AC y BD, y ambas pasan por un punto P exterior a AB.
Así que en esta superficie se cumple que por un punto exterior P a una recta existen, al menos, dos paralelas, las que cortan a la recta dada en sus extremos pasando por P. Todas las demás rectas del haz P son las hiperparalelas a AB.
Modelo de Beltrami-Cayley-Klein
Sobre la superficie utilizada en este modelo también se cumplen todos los axiomas de Euclides con excepción, de nuevo, del V postulado.
§. Modelo hiperbólico de Poincaré
Los dos modelos de Poincaré, el de disco y el de semiplano, son mucho más simples que el de Beltrami. Vamos a describir cada uno de ellos.
En el modelo de disco, el plano está constituido por los puntos interiores a un círculo y, como antes, los puntos de la circunferencia exterior no pertenecen al plano hiperbólico y se denominan puntos límite del infinito de ese plano. Las rectas son arcos circulares situados dentro del círculo que cortan ortogonalmente a la circunferencia de los puntos límite del infinito. Naturalmente, también son rectas los diámetros. Por lo tanto, cada recta tiene dos puntos límite.

Henri Poincaré
En cuanto a las distancias, efectivamente, la más corta entre dos puntos límite es precisamente el arco circular ortogonal a la circunferencia del modelo en los puntos límite citados.
En el otro modelo, el de semiplano, el plano está constituido por un semiplano del que la recta origen, AB, es la de los puntos límite del infinito.
Modelo de disco de Poincaré.
Los puntos son aquellos que pertenecen a la parte superior del semiplano. Las rectas son semicircunferencias ortogonales a la recta límite que encuentran a ésta en dos puntos, P¡ y P2, y que, por consiguiente, tengan su centro en esa recta límite. También será recta hiperbólica toda recta euclídea perpendicular a la recta límite.
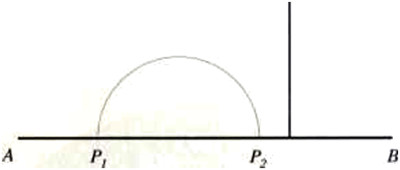
Modelo de semiplano de Poincaré.
El mundo de la geometría hiperbólica ha ejercido, y aún ejerce, una gran influencia, no sólo entre los científicos sino también entre los artistas. Por ejemplo, el holandés Maurits Escher dibujó y gravó distintas configuraciones dentro de un círculo.

Autorretrato de Maurits Cornelis Escher. De la litografía Mano con globo reflectante (1935).
En algunas de ellas, rellenaba ese círculo con círculos cada vez más pequeños que se iban aproximando a la periferia. En el entorno inmediato a la periferia, Escher colocaba minúsculos circulitos y, aun así, no era posible rellenar totalmente el círculo original de partida.
Modelo circular de Escher (Limite circular III).
- Babini, José, Historia sucinta de la matemática. Colección Austral, Espasa- Calpe, 1958.
- Barbarin, Paul, La géométrie non euclidienne. Gauthier-Villars et Cié, Éditeurs, tercera edición, 1928, reimpresión de Éditions Jacques Gabay, París.
- Beltrami, Eugenio, Opere matematiche. Universidad de Roma, tres volúmenes, 1902-1910.
- Beltrami, Eugenio, “Saggio di interpretazione della geometría non-euclidea”. Giornale di matematiche VI, 284-312.
- Benkó, S., The confessions of Jónos Bolyai. Irodalmi Konyvkiadó, Bucarest, 1968.
- Bolyai, Farkas, Tentamen. Academia Húngara de Ciencias, 2a edición, Budapest.
- Bolyai, János, La Science absolute de l’espace. Traducción del latín por Hoüel, Burdeos.
- Bolyai, János, The Science absolute of space. Traducción del latín de George Bruce Halsted, 4a edición, Austin, Texas, 1896.
- Bonola, Roberto, Geometrías no euclidianas. Espasa-Calpe Argentina, Buenos Aires-México, segunda edición, 1951.
- Dou, Alberto, Fundamentos de la matemática. Editorial Labor, 1970.
- Euclides, Elementos, Libros 1-IV. Biblioteca Clásica Gredos, Madrid, 2000.
- Fernández, Santiago, Lobachevski, un espíritu indomable. Editorial NIVOLA, Madrid, 2004.
- Fuchs, Walter, El libro de la matemática moderna. Omega, Barcelona, 1969.
- Les génies de la Science n° 21, noviembre 2004-febrero 2005.
- Kant, Emmanuel, Crítica de la razón pura. Clásicos Bergua, Madrid, 1970.
- Karlson, Paul, La magia de los números. Editorial Labor, 1960.
- Kiss, Elemér, “Notes on János Bolyai’s Researches in Number Theory”. Historia Mathematica 26, 68-76.
- Newman, James R., El mundo de las matemáticas. Grijalbo, Barcelona- México D.F., 1968.
- Poincaré, Henri, La ciencia y la hipótesis. Colección Austral, Espasa-Calpe, 1963.
- Prékopa, A., Molnár, E. (editores), Non-Euclidean Geometries. Springer, 2006.
- Real Academia de Ciencias Exactas, Físicas y Naturales, Historia de la matemática en el siglo XIX, Ia Parte. Madrid, 1992.
Notas: