
El pequeño libro de los agujeros negros
Steven Gubser y Frans Pretorius
Si hay algún fenómeno de la Física y la Astronomía que intriga y fascina al hombre, este es el de los agujeros negros, y fue Albert Einstein, cuando hace más de cien años elaboró la Teoría de la Relatividad, el primer científico que predijo su existencia como solución a sus ecuaciones. Steven S. Gubser y Frans Pretorius arrojan luz sobre uno de los mayores misterios del universo a través de ejemplos creativos y accesibles.
Tanto los agujeros negros como las ondas gravitatorias son consecuencias de la teoría general de la relatividad de Einstein. La relatividad general predice qué tipo de ondas gravitatorias debería ver el detector LIGO en caso de que colisionen dos agujeros negros, y el chirrido registrado el 14 de septiembre de 2015 estaba maravillosamente cerca de lo esperado. Esto no solo supone la justificación de unas ideas teóricas preciadas desde hace mucho tiempo; esta primera detección también augura una nueva era de la astronomía de ondas gravitatorias. Los detectores LIGO han visto un suceso del tipo de los que habíamos soñado durante décadas. Ahora queremos explorar un nuevo jardín entero de sorpresas gravitacionales.
La ciencia no suele implicar certezas matemáticas, así que debemos preguntarnos cuán seguros estamos de que el LIGO interpretó correctamente que el pequeño chirrido era el eco distante de una fusión de agujeros negros que ocurrió hace mil millones de años. En breve, la respuesta es «bastante seguros». Todo parece encajar. La señal fue percibida por ambos detectores. No puede explicarse por ninguna otra cosa que estuviera ocurriendo en la zona. Y es lo bastante fuerte como para verse con la tecnología actual, pero demasiado débil para observarse con la tecnología previa. La hipótesis de una fusión de agujeros negros hace mil millones de años no entra en conflicto con nuestro entendimiento general de la astrofísica y la cosmología. El punto clave es que tenemos esperanzas fundadas de ver más sucesos de ese tipo. De hecho, el LIGO anunció un segundo suceso confirmado que ocurrió el día de Navidad de 2015, y un tercero ocurrido el 4 de enero de 2017. Estos sucesos son comparables, a rasgos generales, al primer descubrimiento, y deberían darnos mucha más confianza en que el LIGO está verdaderamente observando fusiones de agujeros negros. En conjunto, creemos estar presenciando el amanecer de una nueva era de la astrofísica observacional: una era en la que los agujeros negros tendrán un papel central.
En este libro describimos los agujeros negros, por un lado como objetos físicos cuya existencia está ya casi por encima de toda duda, y por otro como laboratorios teóricos que nos permiten afilar nuestra comprensión no solo de la gravedad, sino también de la mecánica cuántica y la física térmica. La explicación de la relatividad especial y la relatividad general dibujan el escenario en los capítulos 1 y 2. En los capítulos restantes procedemos a discutir los agujeros negros de Schwarzschild, los agujeros negros rotatorios, las colisiones de agujeros negros, la radiación gravitatoria, la radiación de Hawking y la pérdida de información.
Entonces, ¿qué es un agujero negro? Esencialmente, es una región del espacio-tiempo hacia la que la materia es arrastrada y de la que escapar es imposible. Enfoquemos la discusión en los agujeros negros más simples, conocidos como agujeros negros de Schwarzschild (en honor de su descubridor, Karl Schwarzschild). «Todo lo que sube debe bajar», dice el dicho. Dentro de un agujero negro de Schwarzschild rige una afirmación más fuerte: «Nada puede subir, todo debe bajar». Pero no estamos seguros de adonde conduce esa bajada finalmente. La hipótesis más simple, dadas las matemáticas que subyacen a los agujeros negros de Schwarzschild, es que un núcleo terrible e infinitamente comprimido de materia mora en su centro. Colisionar con ese núcleo es el final de todo. Es incluso el final del tiempo. Esta hipótesis es difícil de probar, porque ningún observador que se introduzca en un agujero negro podrá jamás mandar de vuelta un informe de lo que ve.
Antes de que sigamos explorando los agujeros negros de Schwarzschild más a fondo, demos un paso atrás para considerar la gravedad en algunas de sus formas más suaves. Desde la superficie de la Tierra, si aplicamos a un objeto una velocidad hacia arriba lo bastante grande, el objeto seguirá moviéndose hacia arriba para siempre. La velocidad mínima para que ocurra esto se llama velocidad de escape, y es de unos 11,2 kilómetros por segundo si ignoramos la fricción del aire. En comparación, es difícil para una persona tirar una bola a más de 45 metros por segundo, menos del 0,5 % de la velocidad de escape. La velocidad inicial en un rifle de alta energía es de unos 1,2 kilómetros por segundo: algo más del 10 % de la velocidad de escape. Entonces, lo que queremos decir con «todo lo que sube debe bajar» es que la gravedad terrestre es fuerte comparada con la fuerza con la que podemos tirar objetos hacia arriba con métodos ordinarios.
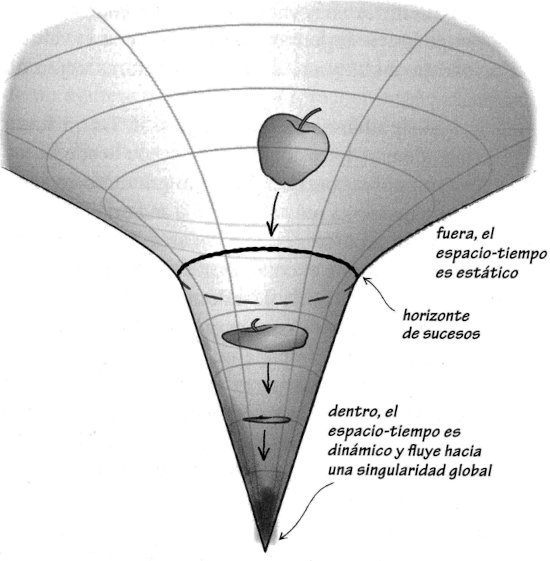
Figura 0.1. Corte de una representación esquemática de la geometría de un agujero negro. Fuera del horizonte y lejos de él, el espacio-tiempo es plano. Al irse acercando al horizonte, se vuelve cada vez más curvo, pero todavía sigue siendo independiente del tiempo, o estático. Al cruzar el horizonte, sin embargo, el espacio-tiempo se hace dinámico: con el fluir del tiempo, dos de las dimensiones espaciales (que tienen la geometría de una esfera) se comprimen, mientras que la tercera (no mostrada) se alarga, hasta que todo el espacio se estira y comprime en una singularidad infinitamente larga y delgada.
Los cohetes son el medio actual para vencer a la gravedad terrestre y mandar objetos al espacio. Para escapar de la gravedad de la Tierra, no es estrictamente necesario que el cohete supere los 11,2 kilómetros por segundo (aunque algunos cohetes lo hacen). También se puede hacer que el cohete viaje a una velocidad inferior, pero tenga el suficiente combustible para seguir empujando hacia arriba hasta que alcanza una altitud donde el campo gravitacional terrestre es sustancialmente más débil. La velocidad de escape desde esas altitudes es correspondientemente más pequeña. En otras palabras, un cohete diseñado para llevar una sonda espacial enteramente fuera del campo gravitatorio terrestre debe superar la velocidad de escape en el punto donde sus motores dejan de funcionar.
Ahora nos podemos preguntar: ¿y si la Tierra fuera mucho más densa? La velocidad de escape desde la superficie sería mayor, porque el campo gravitatorio sería más intenso. La forma más densa de la materia ordinaria en el universo conocido se da en las estrellas de neutrones. Allí se empaqueta el equivalente a una masa solar y media en una esfera de solo 12 kilómetros de radio, aunque este radio no se puede medir con mucha precisión. La materia ordinaria está completamente aplastada contra la superficie por la tremenda fuerza gravitatoria, que es algo así como 100000 millones de veces más fuerte que el campo gravitatorio terrestre. Si asumimos un radio de 12 kilómetros, la velocidad de escape se aproxima al 60 % de la velocidad de la luz.
Pero ¿por qué pararse ahí? Como experimento mental, podemos imaginar que comprimimos una estrella de neutrones aún más. Si comprimimos una estrella de neutrones hasta un radio de unos 4,5 kilómetros, la velocidad de escape alcanza a la velocidad de la luz. Si viajamos más allá de ese punto, la gravedad cambia por completo de carácter. Ya no es posible para ninguna forma de materia resistir al tirón gravitatorio. Moverse hacia delante en el tiempo significa moverse hacia dentro en el radio. Escapar es imposible. Esto es un agujero negro.
El objetivo central de los primeros capítulos de este libro es hacer más precisa la idea de un agujero negro. Un concepto clave que exploraremos es la idea del horizonte de sucesos, que es la «superficie» de un agujero negro. Es una superficie en el sentido geométrico de ser un lugar bidimensional en el espacio tridimensional. Por ejemplo, en el caso más simple de un agujero negro de Schwarzschild, el horizonte es una esfera perfecta cuyo radio se llama radio de Schwarzschild. Lo extraño del horizonte de un agujero negro es que (al menos según el conocimiento convencional) no es la superficie de nada en particular. En el momento en que lo atraviesas, no notas nada especial. El único problema surge cuando intentas darte la vuelta y volver afuera. Por muy duro que lo intentes —usando un cohete, un cañón láser o lo que sea—, y por mucha ayuda que obtengas del exterior, es imposible volver afuera del horizonte, o incluso mandar una señal de socorro al exterior para avisar de que estás atrapado. De manera poética, podemos pensar en el horizonte de un agujero negro como si fuera el borde de una cascada, a partir del cual el espacio-tiempo se precipita ineluctablemente hacia abajo hasta una singularidad que destruye todas las cosas.
Los agujeros negros son más que un experimento mental. Se piensa que ocurren en el universo en al menos dos situaciones. Una se refiere a las líneas generales de la discusión anterior sobre las estrellas de neutrones. Cuando las estrellas grandes agotan su combustible nuclear, se colapsan sobre sí mismas. Este colapso es un proceso desordenado en el que una gran cantidad de materia resulta escupida hacia el universo circundante, en una explosión llamada supernova. (De hecho, se piensa generalizadamente que las supernovas tienen un papel crucial como distribuidoras de metales y otros elementos moderadamente pesados por todo el universo). Pese a ello, aún queda atrás tanta masa que es imposible que una estrella de neutrones se forme y permanezca estable. En vez de eso, la masa remanente se colapsa para formar un agujero negro cuya masa es de al menos unas cuantas veces la masa del Sol. Los agujeros negros cuyas fusiones fueron observadas por el LIGO eran algo más masivos, pero todavía pudieron producirse concebiblemente por colapso estelar.
Se piensa que unos agujeros negros mucho mayores existen en el centro de las galaxias. La forma exacta en que se formaron estos agujeros negros es más misteriosa y puede estar relacionada con la materia oscura, con la física del universo muy joven, o con ambas. Los agujeros negros del centro de las galaxias son tremendamente masivos, con masas de miles a miles de millones de veces la masa del Sol. Se piensa que uno de ellos está en el centro de la Vía Láctea, y que tiene unos 4 millones de masas solares. Muy bien podemos preguntarnos: ¿cómo podemos estar seguros de que hay un agujero negro si ninguna señal puede escapar del horizonte de un agujero negro? La respuesta es que los objetos cercanos responden al tirón gravitatorio del agujero negro. Registrando el movimiento de las estrellas cercanas al centro de la Vía Láctea, podemos saber con certeza que allí hay un objeto muy masivo y muy denso. No podemos probar así que se trata de un agujero negro. Lo que podemos decir es que, si no es un agujero negro, debe de ser algo mucho más extraño. En resumen, los agujeros negros son la posibilidad más simple, y el consenso actual es que existen en el centro de muchas, si no la mayoría de las galaxias.
Los agujeros negros son un laboratorio teórico tremendamente útil porque son matemáticamente simples, comparados con la mayoría de los objetos astrofísicos. Las estrellas son verdaderamente complicadas. Las reacciones nucleares en el núcleo de las estrellas les aportan su poder. La materia dentro de las estrellas experimenta unas presiones y unas dinámicas de fluidos que podemos simular numéricamente, pero desde luego no comprender por completo. Y las estrellas tienen unas dinámicas de superficie que son probablemente tan complicadas como la meteorología de la Tierra. Un agujero negro, en comparación, es maravillosamente simple. En ausencia de otra materia, los agujeros negros deben asentarse en alguna de unas pocas formas definitivas, todas las cuales se comprenden explícitamente como geometrías curvas que resuelven las ecuaciones de la relatividad general de Einstein. Desde luego, la materia que cae complica la imagen, pero tenemos un entendimiento tolerablemente bueno de cómo se comporta la materia ordinaria cuando cae hacia un agujero negro. En nuestros días, incluso tenemos un buen entendimiento numérico de lo que pasa cuando un agujero negro colisiona con otro, y uno de los objetivos centrales del capítulo 6 de este libro es explicar cómo se ha alcanzado este entendimiento, y lo que significa para experimentos como el LIGO.
Las cosas empiezan a resultar extrañas al saber que los agujeros negros no son realmente negros. Utilizando la mecánica cuántica, Stephen Hawking mostró que los agujeros negros tienen una temperatura definida, relacionada con su gravedad de superficie. De hecho, hay un campo entero de estudio, conocido como termodinámica de los agujeros negros, donde las propiedades geométricas de los agujeros negros se ponen en correspondencia precisa con las propiedades que nos resultan familiares del estudio del calor: temperatura, energía y entropía. Incluso existe la propuesta de que los agujeros negros de partes distantes del universo pueden tener interiores solapantes, y de que esos interiores solapantes contribuyen a codificar un efecto cuántico llamado entrelazamiento. Ofreceremos una introducción a estas cuestiones en el capítulo 7.
Los agujeros negros siguen hoy capturando la imaginación de los científicos. Los astrónomos buscan evidencias cada vez más precisas de las propiedades de los agujeros negros rotatorios, y ahora esperan con ansiedad colaborar con los observatorios de ondas gravitatorias para comprender los cataclismos asociados a las fusiones de agujeros negros. Y esto es solo el principio de la astronomía de ondas gravitatorias, con un esfuerzo mundial en proceso para construir una red de detectores en Estados Unidos (los dos detectores LIGO en Hanford, Washington, y Livingston, Luisiana), Europa (Virgo y GEO600), Japón (KAGRA) y la India (LIGO India). Entretanto, los teóricos de cuerdas estudian los agujeros negros a mayor número de dimensiones no solo como una forma de sondear efectos cuánticos en la gravedad, sino también como análogos de aspectos de la física tan diversos como las colisiones de iones pesados, los fluidos viscosos y los superconductores. Y los agujeros negros nos inspiran a todos a considerar las cuestiones más extrañas: ¿podrán algún día los agujeros negros resultarnos de utilidad? ¿Qué hay dentro de ellos realmente? ¿Cómo sería caer dentro de un agujero negro? De hecho, ¿sería posible que ya hubiésemos caído dentro de uno y no nos hubiésemos dado cuenta?
Capítulo 1
Relatividad especial
Para entender los agujeros negros tenemos que aprender algo de relatividad. La teoría de la relatividad se divide en dos partes: especial y general. Albert Einstein halló la teoría especial de la relatividad en 1905. La teoría trata sobre objetos que se mueven unos respecto de otros, y con la forma en que la experiencia del espacio y el tiempo de un observador depende de cómo se esté moviendo. Las ideas centrales de la relatividad especial se pueden formular en términos geométricos usando un bello concepto llamado espacio-tiempo de Minkowski.
La relatividad general subsume la relatividad especial e incluye también la gravedad. La relatividad general es la teoría que necesitamos para entender realmente los agujeros negros. Einstein desarrolló la relatividad general durante un periodo de varios años que culminó en un artículo de finales de 1915, en el que presentaba las denominadas ecuaciones de campo de Einstein. Estas ecuaciones describen cómo la gravedad distorsiona el espacio-tiempo de Minkowski para dar una geometría espaciotemporal curva, por ejemplo la geometría del agujero negro de Schwarzschild que describiremos en el capítulo 3. La relatividad es más simple y fácil que la relatividad general porque omite la gravedad; es decir, la gravedad se ignora, o se considera un efecto demasiado débil como para resultar significante.
La relatividad especial incluye la fórmula E = mc2, que relaciona la energía E, la masa m, y la velocidad de la luz c. Esta es una de las ecuaciones más famosas de toda la física, y posiblemente de todo el entendimiento humano. E = mc2 hizo posible prever el formidable poder de las armas nucleares, y también está en el corazón de nuestras esperanzas, aún incumplidas, de tener una fuente de energía limpia basada en la fusión nuclear. E = mc2 resulta también muy importante para la física de los agujeros negros. Por ejemplo, la energía equivalente a tres masas solares eyectada por la primera colisión de agujeros negros observada es una ilustración primordial de la equivalencia entre la masa y la energía. Para hacernos una idea del cataclismo que supuso esta colisión, consideremos que la masa que se convierte en energía en la explosión de una bomba nuclear (asumiendo un rendimiento de 400 kilotones) no pasa de unos meros 19 gramos.
La relatividad especial está estrechamente relacionada con la teoría del electromagnetismo de James Clerk Maxwell. De hecho, una pista temprana de la visión relativista del espacio y el tiempo emergió a finales del siglo XIX con las llamadas transformaciones de Lorentz, que explican cómo las percepciones que los observadores tienen de los fenómenos electromagnéticos dependen de cómo los observadores se estén moviendo. El fenómeno electromagnético más familiar es la luz, que es una onda viajera de campos eléctricos y magnéticos. Una consecuencia de la teoría de Maxwell es que la luz tiene una velocidad definida. La relatividad se construye alrededor de la idea de que esa velocidad es una verdadera constante, independiente del movimiento del observador.
El movimiento de los observadores se describe en la relatividad especial en términos de marcos de referencia. Para hacernos una idea de lo que es un marco de referencia, pensemos en un tren de alta velocidad. Si todos los pasajeros van sentados y todos los equipajes guardados, cualquier cosa en el tren es estacionaria respecto al propio tren. Pero este se mueve deprisa respecto a la Tierra. Supongamos que se mueve en línea recta a velocidad constante. Para ofrecer una descripción totalmente precisa de los marcos de referencia, tendríamos que estipular la ausencia de cualquier campo gravitatorio significativo. Por ejemplo, en vez de que el tren se desplace a velocidad constante por la superficie de la Tierra, tendríamos que considerar una nave espacial moviéndose por inercia a velocidad constante en el espacio vacío. Pero el campo gravitatorio de la Tierra es lo bastante débil para que, para nuestros objetivos actuales, podamos ignorar sus efectos en el tren y trabajar con la teoría especial de la relatividad, en lugar de con la teoría general.
Si no miramos por la ventana, es difícil decir lo deprisa que se está moviendo el tren. En caso de que este tenga una magnífica suspensión y las vías estén muy niveladas, y de que las persianas de todas las ventanas estén echadas, sería imposible saber que se está moviendo en absoluto. El tren aporta un marco de referencia: el que los pasajeros usan normalmente para juzgar si algo se está moviendo dentro del tren. No pueden saber (en la situación ideal recién descrita) si el tren entero se está moviendo. Pero, desde luego, saben si alguien está andando por el pasillo, porque esa persona se está moviendo respecto a su marco de referencia. Más aún cualquier fenómeno físico, como bolas que se caen o peonzas que giran, se comportaría del mismo modo, según observa cualquier observador en el tren, tanto si el tren se está moviendo como si no. En resumen, pues, un marco de referencia es una manera de mirar el espacio y el tiempo que se asocia a un observador, o a un grupo de observadores, en un estado de movimiento uniforme. Movimiento uniforme significa que el tren no está acelerando, ni frenando ni girando.
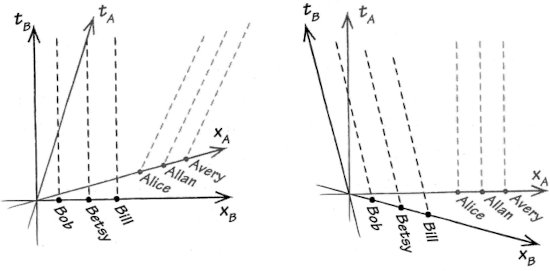
Figura 1.1. Izquierda: el espacio-tiempo de Minkowski, donde se muestran tres observadores estacionarios en el sistema de referencia B, y otros tres que se mueven adelante en el sistema de referencia A. Derecha: una perspectiva distinta del espacio-tiempo de Minkowski, en que los observadores del sistema B se mueven hacia atrás, y los observadores del sistema A permanecen estacionarios.
Si el tren está haciendo alguna de estas cosas, los pasajeros lo notarán; por ejemplo, la aceleración rápida les empuja atrás en sus asientos, mientras que la deceleración rápida les arroja hacia delante.
Imaginemos que nuestro tren pasa por una estación sin parar ni reducir su velocidad. Los pasajeros del tren, digamos Alice, Alian y Avery, son observadores en un marco de referencia móvil al que llamaremos el marco A. Mientras, sus amigos Bob, Betsy y Bill están en el andén, un marco de referencia estacionario al que llamaremos el marco B. Para dibujar estos marcos de referencia, ponemos la posición del marco B en el eje horizontal, y el tiempo del marco B en el eje vertical, y mapeamos las trayectorias de nuestros observadores a través del espacio y el tiempo, de modo que, a lo largo del tiempo, los observadores del marco B permanecen siempre en las mismas posiciones del marco B, mientras que los observadores del marco A se mueven hacia delante. El diagrama resultante es de hecho ¡el espacio- tiempo de Minkowski! La palabra espacio-tiempo se refiere al hecho de que estamos mostrando el espacio y el tiempo en el mismo diagrama. Es posible adoptar una perspectiva diferente sobre el espacio-tiempo de Minkowski, de modo que los observadores del marco A se muestren como estacionarios, mientras que los observadores del marco B se mueven hacia atrás. Volveremos a esta perspectiva más adelante.
La relatividad especial depende del postulado de que la velocidad de la luz es constante. En otras palabras, se supone que la velocidad de la luz es la misma cuando la miden los observadores del tren que cuando la miden los observadores del andén. Si no fuera así, bastaría medir la velocidad de la luz para que un observador pudiera decidir en cuál de los dos marcos de referencia está situado. Pero un principio central de la teoría de la relatividad es que la física debe ser la misma en cualquier marco de referencia, de modo que no puedas decidir en qué marco estás mediante ninguna medición física. Según este principio, no puedes elegir un marco y decir: «Permanecer en este marco es lo que significa estar estacionario; el movimiento consiste en estar en un marco diferente». Lo único que podemos decir es: «Cualquier marco es tan bueno como cualquier otro; la única idea de movimiento que podemos permitir es el movimiento de un observador respecto a otro». En otras palabras, los estados de movimiento no son absolutos; son relativos. Así que ha sido un error referirse al marco A como móvil y el marco B como estacionario. Lo único que podemos decir realmente es que se están moviendo uno respecto al otro. (La idea de que el marco B estaba estacionario parecía natural, sin embargo, porque estamos pensando implícitamente en el movimiento respecto a la Tierra).
La intuición que acabamos de explicar sobre el movimiento relativo parece de sentido común, y debemos preguntarnos cómo es posible que obtengamos alguna ventaja de ella para asuntos relacionados con la naturaleza profunda del espacio y el tiempo. El ingrediente clave es la teoría del electromagnetismo de Maxwell. Lo que nos dice esta teoría (entre otras cosas) es que, si Alice saca un puntero láser y manda un pulso de luz hacia delante, hacia el morro del tren, y Bob hace lo mismo, los dos pulsos de luz viajan exactamente a la misma velocidad. Esto vuelve a parecer una afirmación inocua, ¡pero no lo es! Por ejemplo, si hacemos que el tren viaje al 99 % de la velocidad de la luz (obviamente no sería un tren estadounidense), ¿no debería Bob medir que el pulso láser disparado por Alice viaja a casi el doble de la velocidad de la luz? Después de todo, Alice se está moviendo hacia delante al 99 % de la velocidad de la luz respecto a Bob, y su pulso láser se mueve hacia delante a la velocidad de la luz respecto a ella, así que parece que Bob debería medir que el pulso láser de ella se mueve hacia delante al 199 % de la velocidad de la luz. Pero, según el electromagnetismo, ¡no lo hace! Bob mide que el pulso láser se está moviendo precisamente a la misma velocidad de la luz, respecto a él mismo, que registraría Alice si midiera su movimiento respecto a ella misma.
¿Cómo es esto posible? La respuesta es que Alice y Bob miden el paso del tiempo de manera diferente, y también miden la longitud de manera diferente. Los detalles de cómo pasa esto están codificados en la transformación de Lorentz, que es una expresión matemática que relaciona el tiempo y la longitud en el marco A con el tiempo y la longitud en el marco B. Una transformación de Lorentz es fácil de dibujar utilizando el espacio-tiempo de Minkowski. Antes de la transformación de Lorentz (la parte izquierda de la figura 1.1), podemos pensar que el marco B está estacionario, y que el marco A se está moviendo hacia delante. Después de la transformación de Lorentz (la parte derecha de la figura 1.1), ¡el marco A está estacionario y el marco B se mueve hacia atrás! Una transformación de Lorentz no es más que el cambio de perspectiva entre el informe que ofrecería Bob pensando que su marco es estacionario, y el que ofrecería Alice pensando que el de ella es el estacionario.
Entre las consecuencias esenciales de la transformación de Lorentz están la dilatación del tiempo y la contracción del espacio. Empezaremos describiendo la dilatación del tiempo porque es más sencilla de explicar. Supongamos que al mediodía del viernes te montas en un tren en el Empalme de Princeton. Por conveniencia, diremos que este tiempo y lugar corresponden al origen del espacio de Minkowski, donde los ejes t y x se cruzan. Añadamos que por el Empalme de Princeton pasan trenes rápidos y lentos; los hay que van al norte hacia Nueva York, y otros que van al sur hacia Filadelfia; y tú puedes decidir cuál quieres coger. Lo que vas a hacer es subir al tren durante una hora exacta según tu reloj, y entonces te bajas y marcas adonde has llegado. Es evidente que si tomas un tren rápido llegarás más lejos. Pero cuidado con asumir que llegarás exactamente el doble de lejos si tomas un tren que va el doble de rápido. La parte delicada es que has ido en el tren durante una hora exacta según tu propio reloj. La velocidad de un tren es algo que los observadores estacionarios respecto al suelo van a medir, y sus relojes corren un poco distinto que los tuyos porque están en un marco de referencia distinto.
Así que, ¿dónde terminaréis? Más en general, si tú y una pandilla de amigos tomáis trenes diferentes (que salen todos del Empalme de Princeton al mismo tiempo), ¿adonde iréis todos a parar? La respuesta es que todos iréis a parar a algún punto de una hipérbola en el espaciotiempo de Minkowski (véase la figura 1.2). En otras palabras, la hipérbola es el conjunto de todas las posibles posiciones finales que podéis alcanzar tras una hora exacta de vuestro propio tiempo de viaje. Una posible posición final es el mismo Empalme de Princeton, exactamente a la una de la tarde según el tiempo del Empalme de Princeton. La forma de llegar allí tras una hora es que seas lo bastante tonto como para pasar una hora en un tren que no se mueve en absoluto. En esa situación, por supuesto, es la una de la tarde en tiempo del Empalme de Princeton cuando llegas, porque tu marco de referencia es el mismo que el de la estación, de modo que tu reloj va exactamente sincronizado con el tiempo de la estación. Pero, si montas en un tren que realmente va a algún sitio, tu reloj corre más lento que el tiempo de la estación, de modo que cuando te bajas tras una hora del tiempo de viaje que percibes, el reloj de la estación marca en realidad un tiempo más tardío del que tú piensas que debería ser. Este efecto «más tardío del que tú piensas», conocido como dilatación del tiempo, se registra en el espacio- tiempo de Minkowski mediante la forma en que la hipérbola se curva hacia arriba (en la dirección del tiempo) según viajas a posiciones cada vez más lejanas de tu punto de partida[1].
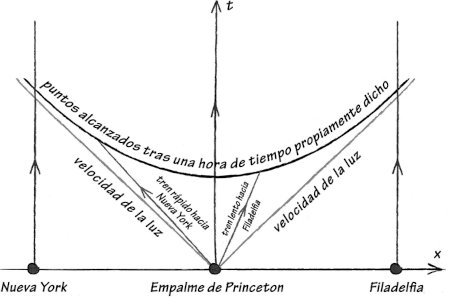
Figura 1.2. Los trenes desde el Empalme de Princeton. La curva que comprende los puntos que se alcanzan tras una hora de tiempo propiamente dicho es una hipérbola.
El espacio-tiempo de Minkowski se llama a veces geometría hiperbólica, en referencia al tipo exacto de hipérbola que hemos discutido.
En el espacio-tiempo de Minkowski, visualizamos la velocidad constante de la luz dibujando rayos de luz a un ángulo exacto de 45° respecto al eje vertical del tiempo. Date cuenta de que la hipérbola de los posibles puntos de llegada para cualquier viaje en tren de una hora está totalmente incluida en la región de espacio-tiempo que queda entre los dos rayos de luz que emanan del origen. Esta es la manera en que el espacio- tiempo de Minkowski codifica la afirmación de que ninguno de nuestros trenes puede ir más deprisa que la luz.
Puede parecer que nuestro tratamiento de la dilatación del tiempo no tiene mucho que ver con las transformaciones de Lorentz. Pero sí que tiene. Para verlo, volvamos a llamar marco A al marco de referencia del tren, y marco B al marco de referencia de la Tierra. Supongamos que Alice pasa una hora en el marco A mientras va del Empalme de Princeton a Nueva York. Entretanto, Bob y sus amigos permanecen estacionarios respecto a la Tierra. ¿Cómo deberían calcular Bob y sus amigos el tiempo de llegada de Alice? No resultaría muy útil que Alice les llamara al llegar, porque la señal que ella usaría solo podría viajar a la velocidad de la luz, y Bob y sus amigos tendrían que hacer un cálculo basado en la hora a la que reciben la llamada, la velocidad de la señal y la distancia a Nueva York para estimar cuándo ha llegado Alice. Todo eso suena demasiado complicado. Así que Bob imagina una manera mejor de hacerlo. Sincroniza su reloj con el de uno de sus amigos, digamos Bill, y luego Bob y Bill se apostan en las estaciones del Empalme de Princeton y Nueva York, respectivamente. Bob mide la hora en que Alice sale, y Bill mide cuándo Alice llega. No se requiere ningún teléfono. Puede parecer dificultoso sincronizar los relojes de manera fiable entre observadores distantes, pero una buena estrategia sería que tanto Bob como Bill partieran desde el punto medio entre el Empalme de Princeton y Nueva York, sincronizaran sus relojes cuando aún estuvieran juntos y luego caminaran a velocidades idénticas hasta sus respectivas estaciones, todo ello mucho antes de que Alice tomara su tren.
En todo este relato sobre el viaje en tren de Alice, el marco A está claramente privilegiado, porque Alice no necesita a ningún amigo para calcular la duración de su viaje, mientras que Bob y Bill tienen que cooperar para hacer sus medidas del tiempo. El intervalo de tiempo que mide Alice se llama tiempo propiamente dicho porque ella lo mide mientras permanece en una localización fija en su marco de referencia (el marco A). El intervalo de tiempo que miden Bob y Bill es tiempo dilatado, que siempre debe ser mayor que el tiempo propiamente dicho. El tiempo dilatado forma parte de la manera en que se relacionan las perspectivas A y B del espacio-tiempo. La transformación de Lorentz entre el marco A y el marco B contiene la dilatación del tiempo, entre otras cosas.
Se puede utilizar un tratamiento similar para describir la contracción del espacio. En vez de un viaje en tren, imaginemos que Bob, Bill y Alice van a los Juegos Olímpicos, donde Alice espera batir el récord de salto de pértiga. Su secreto es que puede correr muy deprisa, al 87 % de la velocidad de la luz. (Por alguna razón, Alice deja los cien metros lisos para Usain Bolt, pese a que ella podría hacerlos en 0,4 microsegundos). Alice elige una pértiga de 6 metros; es más larga que la que usan la mayoría de los saltadores, pero después de todo Alice es una chica excepcional. Bob y Bill no pueden creerse que Alice esté usando una pértiga tan larga, así que deciden medirla mientras Alice hace su carrera para el salto, agarrando la pértiga perfectamente horizontal. Está claro que Bob y Bill se enfrentan a un trabajo duro. ¿Cómo pueden hacer esa medida, realmente? Esto es lo que se les ocurre. Primero, sincronizan sus relojes. Luego se apostan a unos metros de distancia (menos de 6 metros) uno del otro, y acuerdan que, exactamente al mismo tiempo, van a mirar delante y a anotar qué parte de la pértiga ven. Después de muchos intentos, consiguen organizarse de modo que Bob vea la cola de la pértiga mientras Bill ve la punta frontal. Entonces miden a qué distancia están uno del otro. La respuesta es que están a solo tres metros uno del otro. Concluyen, razonablemente, que la pértiga de Alice mide 3 metros. Se acercan a Alice y le explican lo que han descubierto. Ella se queja de que no pueden haberlo hecho bien, así que recluta a sus dos amigos, Alian y Avery, que corren con ella (parece ser que también son muy buenos corredores) y miden la pértiga en el marco de referencia de ella. La respuesta que hallan es que la pértiga tiene 6 metros de larga.
De nuevo, el marco A es el privilegiado en este tratamiento, porque es el marco en el que la pértiga de Alice permanece estacionaria. La longitud de la pértiga, medida en el marco A, se llama longitud propiamente dicha. Medida en el marco B siempre es más corta, y se llama longitud contraída. La dilatación del tiempo y la contracción de la longitud están estrechamente vinculadas, como podemos apreciar en nuestro ejemplo si consideramos lo que Alice diría de su experiencia mientras corre hacia el listón. Según ella mide en su marco de referencia, llegar al listón le lleva solo la mitad de tiempo del que habrían medido Bob y Bill mediante el protocolo que vimos antes en el contexto del viaje en tren de Alice a Nueva York. La dilatación del tiempo, por tanto, implica un factor dos para la carrera de Alice al 87 % de la velocidad de la luz: los observadores del marco A dicen que la pértiga tiene 6 metros, y los observadores del marco B dicen que tiene 3. Generalizando, la dilatación del tiempo y la contracción de la longitud siempre implican el mismo factor, llamado a veces el factor de Lorentz.
Parece haber una desconexión entre nuestro tratamiento de la relatividad especial, que se centra en la geometría del espacio-tiempo, y la famosa ecuación E = mc2. Vamos a intentar salvar esa desconexión considerando una derivación parcial de E = mc2en que los pasos más importantes se pueden ilustrar de manera geométrica. Nuestro argumento es solo una derivación parcial porque implica algunas aproximaciones y otro par de fórmulas que no vamos a justificar aquí.
El primer paso es expresar en una ecuación qué es realmente la masa. La mejor ecuación que podemos usar es p = mv,donde p es la cantidad de movimiento (también llamada momento lineal, o momentum) y v es la velocidad de un cuerpo masivo que se mueve lentamente y cuya masa es m. La relación p = mv viene directamente de la mecánica newtoniana, y podemos utilizarla siempre que v sea muy inferior a la velocidad de la luz. El siguiente paso es relacionar la energía con algo. Aquí vamos a tener que aceptar como un acto de fe otro resultado, en este caso del electromagnetismo: el momento p de un pulso de luz se relaciona con su energía Emediante la ecuación p = E/c.Como ya sabemos, los pulsos de luz tienen la peculiaridad de que se mueven a una velocidad fija en cualquier marco de referencia. Esto es muy distinto a la forma en que se comportan los objetos masivos. En un marco de referencia dado, los objetos masivos pueden estar quietos, o pueden moverse a una velocidad v que —según la relatividad especial— debe siempre ser menor que la velocidad de la luz.
Ahora conocemos la cantidad de movimiento de un objeto masivo (p = mv) y la cantidad de movimiento de un pulso de luz (p = E/c).Pero no podemos igualar esos dos momentos, porque los objetos masivos ¡son distintos de los pulsos de luz! En vez de eso, lo que tenemos que hacer es imaginar cómo construir un objeto masivo a partir de pulsos de luz. Solo entonces podremos usar nuestras ecuaciones de la cantidad de movimiento para inferir E = mc2.
La idea crucial es la siguiente. Pongamos dos espejos de reflexión perfecta exactamente uno en frente del otro, y hagamos que dos pulsos de luz idénticos reboten una y otra vez entre los espejos de tal forma que siempre viajen en direcciones opuestas. Proponemos que este montaje es, en efecto, un cuerpo masivo. Supongamos que los espejos son muy ligeros, tan ligeros que podemos ignorarlos en los cálculos de la masa y la energía. Entonces, la energía de nuestro cuerpo masivo es el doble de la energía de uno de los dos pulsos de luz. Su cantidad de movimiento es exactamente cero, porque un pulso de luz tiene cantidad de movimiento hacia arriba en el mismo instante en que el otro la tiene hacia abajo, y esas cantidades de movimiento hacia arriba y hacia abajo se cancelan mutuamente. Se cancelan porque el cuerpo en su conjunto no tiene movimiento hacia ningún lado; solo se mueven sus partes.
Para llegar al argumento correcto que conduce a E = mc2, lo que necesitamos es persuadir a todo nuestro artilugio de que se ponga en movimiento. Simplifiquemos la discusión registrando el movimiento de uno solo de los dos pulsos de luz. Si registráramos ambos, obtendríamos simplemente el doble de energía y el doble de masa. Centrarnos en un solo pulso también simplificará nuestro tratamiento, que hace que el movimiento del artilugio sea lateral respecto al movimiento original arriba y abajo del pulso de luz que estamos registrando. Una vez que tenemos ambos movimientos en funcionamiento, el pulso de luz ya no viaja solo arriba y abajo. También se desplaza un poco de manera lateral. Y aquí es donde hace su entrada la geometría. El movimiento lateral del pulso de luz tiene una velocidad v, mientras que su movimiento arriba y abajo tiene una velocidad c. (En realidad, su movimiento arriba y abajo es un poco más lento que c, porque la velocidad total del pulso de luz es c; para la exactitud que necesitamos aquí, podemos ignorar este detalle). Otra forma de expresarlo es que una fracción (v/c) del movimiento del pulso de luz ocurre lateralmente. Así que parece razonable postular que la cantidad de movimiento lateral plateral del fotón es una fracción v/c de su momento total p = E/c. Es decir, plateral = Ev/c2. Ahora afirmamos que plateral = mv lo que tiene sentido, puesto que platerales la cantidad de movimiento lateral del artilugio completo (si registramos solo uno de los pulsos), y estamos pensando que el artilugio es un cuerpo masivo. Si ahora combinamos las dos maneras de escribir plateral,obtenemos Ev/c2= mv. Eliminando v a los dos lados, obtenemos —redoble de tambor— ¡E = mc2!
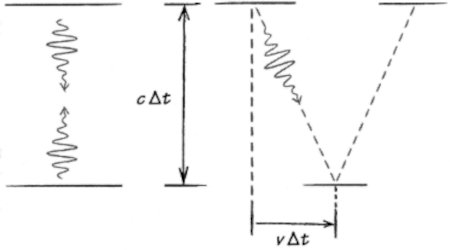
Figura 1.3. Izquierda: dos pulsos de luz idénticos viajan arriba y abajo entre dos espejos. Derecha: los espejos se mueven hacia la derecha con una velocidad v. En el tiempo Δt que le lleva a uno de los pulsos de luz llegar de un espejo al otro, el pulso de luz viaja una distancia aproximada cΔt hacia abajo o hacia arriba, y una distancia vΔt lateralmente.
Se podría objetar que nuestro artilugio de luz y espejos es muy diferente de los objetos masivos de la experiencia diaria. Pero no es cierto, realmente. Los protones y los neutrones constituyen la mayor parte de la masa de cualquier material cotidiano, y pueden entenderse aproximadamente como pequeñas regiones del espacio-tiempo en las que tres cuarks sin apenas masa están rebotando a una velocidad cercana a la de la luz. Si esto fuera todo, la masa del protón provendría enteramente del movimiento de sus cuarks constituyentes, al igual que la masa del artilugio de luz y espejos vendría de los pulsos de luz. Pero la verdad es que eso no es todo: los cuarks interactúan con fuerza entre ellos, y esas interacciones también contribuyen de manera significativa a la energía total del protón, y por tanto a su masa total. Pese a todo, el origen esencial de la mayoría de la masa de la materia cotidiana tiene más que ver con nuestro análisis del artilugio de luz y espejos que con ninguna masa intrínseca de los constituyentes fundamentales de la materia.
Cuanto más avanzamos con la relatividad especial, más claro queda que la teoría del electromagnetismo de Maxwell es un precursor esencial de ella. Más aún, ¡es en muchos sentidos un precursor de la relatividad general! Acabemos este capítulo con una visita guiada por los puntos culminantes de la asombrosa teoría de Maxwell.
Antes de que el electromagnetismo se desarrollara correctamente, la gente entendía la atracción entre cargas positivas y negativas como algo parecido a lo que Newton entendía por atracción gravitatoria entre la Tierra y el Sol. Dicho mal y pronto, en realidad no comprendían ninguna de las dos. Newton sabía que no lo entendía. Acerca de su cruzada para discernir el origen de la atracción gravitatoria, dejó escrito: «Hasta ahora no he podido descubrir de forma empírica la razón de estas propiedades de la gravedad, y no voy a simular ninguna hipótesis». (Esto es una traducción aproximada del original en latín de Newton). Newton, por supuesto, tenía una ley cuantitativa de enorme utilidad, que describía la fuerza del tirón gravitatorio. En concreto, sabía que la atracción gravitatoria se debilitaba como el inverso del cuadrado de la distancia entre los cuerpos masivos. La fuerza atractiva entre cargas positivas y negativas sigue una pauta similar, proporcional al inverso del cuadrado de la distancia. Pero tanto Newton como sus muchos sucesores se sentían incómodos con el mero hecho de que existiera cualquier fuerza que actuara a distancia. Dicho de otro modo, resulta raro que una fuerza que actúa sobre un objeto venga causada por la existencia de otro objeto muy lejano. Michael Faraday abanderó la resolución moderna de ese enigma. Según sus ideas, un objeto cargado crea campos eléctricos y responde también a ellos, y esos campos se propagan por el espacio según las cuatro ecuaciones cuya forma final descubrió finalmente Maxwell.
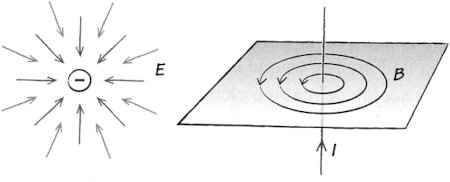
Figura 1.4. Izquierda: el campo eléctrico E cerca de una carga negativa apunta en todas partes hacia dentro. Derecha: un cable que lleva una corriente I crea un campo magnético B que circula alrededor de él.
En el esquema de Faraday, las cargas negativas no atraen directamente a las positivas. Lo que ocurre es que una carga negativa orienta el campo eléctrico circundante de modo que apunte directamente hacia ella. El campo eléctrico tira a su vez de una carga positiva que está a cierta distancia de la negativa, y el resultado neto es que la carga positiva se ve arrastrada hacia la carga negativa. También podemos decir que la carga positiva orienta el campo eléctrico circundante para que apunte directamente en dirección contraria a ella, y el campo eléctrico ejerce a su vez un tirón sobre la carga negativa. Ambos efectos ocurren a la vez. Si lo único que vemos son las cargas, concluiremos (correctamente) que sienten fuerzas iguales y opuestas que las mueven a juntarse. Lo importante de la idea de Faraday es que esas fuerzas solo surgen a través de la acción del campo eléctrico, que tiene una existencia independiente de cualquier carga que lo haya generado.
Similares argumentos sirven también para las fuerzas magnéticas y los campos magnéticos. Sin entrar en detalles, las cargas eléctricas en movimiento crean, y responden a, los campos magnéticos, que se propagan por el espacio de la forma que dictan las ecuaciones de Maxwell. Un ejemplo de especial importancia son los campos magnéticos que se forman alrededor de un cable con corriente eléctrica. La corriente eléctrica es el movimiento de cargas microscópicas dentro del cable, así que esto no es más que un caso particular de la regla general de que las cargas en movimiento generan campos magnéticos.
Al igual que ocurre con los campos eléctricos, se supone que los campos magnéticos tienen algún tipo de existencia independiente de la configuración concreta de cargas en movimiento que los producen. Para entender lo que queremos decir con esto, consideremos un montaje usado por Maxwell durante el desarrollo de la forma final del electromagnetismo. Pongamos dos placas metálicas paralelas que no se tocan y soldemos un cable a cada una. Este sistema se conoce como un condensador. Hagamos que una corriente eléctrica fluya hacia una placa alejándose de la otra. Este flujo causa un incremento de carga positiva en una placa (en realidad, una deficiencia creciente de electrones) y un incremento igual de carga negativa en la otra placa (una superabundancia de electrones). Como consecuencia del cada vez mayor desequilibrio de carga en las placas, se produce entre ellas un campo eléctrico creciente. Ese campo eléctrico fluye de la placa cargada positivamente hacia la placa cargada negativamente, y a medida que las cargas de las placas crecen en magnitud, otro tanto ocurre con la magnitud del campo eléctrico.
Ya sabemos que un campo magnético se genera alrededor de un cable que lleva corriente. En nuestro caso, un campo magnético se genera alrededor de los cables que llevan la corriente al condensador. Pero ninguna corriente fluye de una placa a la otra, y a un observador descuidado le parecería por tanto que no habría que esperar ningún campo magnético entre las placas. Para Maxwell, esto no se conciliaba muy bien con lo que entendía de los condensadores, y entonces propuso una solución asombrosa: que un campo eléctrico creciente genera un campo magnético circulante del mismo modo en que lo hace una corriente. Esta idea es un paso importante desde la noción original de que las cargas producen campos y responden a ellos, porque ahora podemos ver que los campos producen campos.
En realidad, ya se comprendía antes (por Faraday) que un campo magnético creciente genera un campo eléctrico circulante; este es, esencialmente, el principio en que se basan los generadores eléctricos. Dos de las cuatro ecuaciones de Maxwell formalizan esas dos relaciones recíprocas entre los campos eléctricos y magnéticos. Las otras dos ecuaciones son más simples, y afirman que los campos magnéticos no tienen fuentes ni sumideros, y que las únicas fuentes y sumideros del campo eléctrico son las cargas eléctricas positivas y negativas. Todas las ecuaciones de Maxwell son ecuaciones diferenciales, lo que significa que se basan en la tasa de cambio de los campos eléctricos y magnéticos en el tiempo, además de la forma en que estos campos varían en el espacio. Las ecuaciones diferenciales dependen del modo en que se comportan los campos en una pequeñísima vecindad del espacio-tiempo. No hay acción a distancia en las ecuaciones de Maxwell. Todo ocurre localmente, en términos de cómo los campos vecinos empujan y tiran uno de otro.
El mayor triunfo de Maxwell fue mostrar que sus ecuaciones implicaban la existencia de la luz. La luz, según Maxwell la entendía, es una combinación de campos eléctricos y magnéticos fluctuantes, donde la variación espacial del campo eléctrico causa la variación temporal del campo magnético y viceversa. Las constantes físicas incluidas en las ecuaciones de Maxwell describen la fuerza de las interacciones electrostáticas y magnéticas, pero cuando se combinan de manera correcta ofrecen una predicción numérica de la velocidad de la luz: una predicción que se puede verificar experimentalmente.
Si miramos adelante en este libro, querremos comprender dos conexiones esenciales entre el electromagnetismo y la relatividad general: ambas teorías implican el concepto de campo de Faraday, y ambas culminan en ecuaciones diferenciales para el comportamiento de unos campos que implican alguna forma de radiación. En el caso de la radiación electromagnética, los campos eléctricos engendran campos magnéticos y viceversa, en una cascada autosostenida a través del espacio-tiempo que se describe en las ecuaciones de Maxwell. Esta cascada tiene una longitud de onda característica, a través de la cual los campos eléctricos y magnéticos varían de cero a su valor máximo, vuelven por el cero hasta otro máximo, y otra vez a cero.
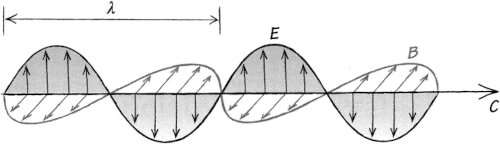
Figura 1.5. Un rayo de luz es una perturbación viajera de campos eléctricos E y campos magnéticos B, todos moviéndose en la misma dirección a la velocidad de la luz c. Si interpretamos que el dibujo es a escala, la longitud de onda A que se muestra es de varios centímetros, que está en el rango de las microondas, un poco más corta que las longitudes de onda que hallamos dentro de un homo de microondas típico.
La luz visible es un caso especial en que la longitud de onda mide más o menos media micra (o media milésima de milímetro). Las longitudes de onda más largas conducen a la luz infrarroja, las microondas y las ondas de radio, mientras que las longitudes de onda más cortas dan lugar a la luz ultravioleta, los rayos X y los rayos gamma.
Einstein descubrió las análogas gravitatorias de las ecuaciones de Maxwell, y esas son el principal contenido de la teoría general de la relatividad. En las ecuaciones de Einstein, los campos son más extraños que los campos eléctricos y magnéticos: sorprendentemente, son la curvatura del propio espacio-tiempo. Otra gran sorpresa es que la relatividad general puede describir los objetos masivos en términos de pura geometría. Esto difiere mucho del electromagnetismo, donde las cargas siguen siendo fundamentales todo el tiempo. Esos objetos masivos puramente geométricos son los agujeros negros.
En la relatividad especial, el espacio-tiempo es un escenario vacío. Los observadores y los rayos de luz se mueven en él, y podemos hablar con sensatez sobre el tiempo entre dos sucesos o la distancia entre dos objetos, siempre que tengamos en mente ideas como el tiempo propiamente dicho, el espacio propiamente dicho, la dilatación del tiempo y la contracción de la longitud. La creencia central de que todo movimiento es relativo pone de manifiesto lo muy vacío que está realmente el espacio-tiempo. Si hubiera algo ahí fuera, algún tipo de éter estacionario que llenara todo el espacio- tiempo, podríamos desarrollar la noción del movimiento absoluto, trabajado siempre en el propio marco de referencia del éter y describiendo los objetos como estacionarios o móviles respecto al éter estacionario[2].
La relatividad general implica una actitud distinta al respecto. El espacio-tiempo es ahora el protagonista. Se curva en respuesta a los cuerpos masivos de una manera controlada por las ecuaciones de campo de Einstein, que toman la forma
Gμν = 8πGNTμν/c4
Echemos un primer vistazo a lo que significan los símbolos de esta ecuación. Los subíndices en letras griegas μ y ν son los sellos distintivos de la denominada notación de tensores, que nos permite escribir las diez distintas ecuaciones de campo de una tacada. El tensor de Einstein Gμν es una descripción de la curvatura del espacio-tiempo. El tensor de energía-impulso (o de energía-momento) Tμν describe la presencia de materia. En el espacio vacío, calibraríamos Tμν = 0. La constante de Newton GN describe la fuerza con que la materia influye en el espacio-tiempo. Como siempre, c es la velocidad de la luz. El factor 8π, donde π = 3,14159..., es una constante no muy importante. Podríamos redefinir GN de modo que incluyera el 8π, pero no lo hacemos porque GN aparece también en la descripción newtoniana de la gravitación, de modo que se ha hecho tarde para cambiar su significado.
Como estudiantes de la relatividad, nos podemos preguntar: ¿cómo es posible que la relatividad general subsuma a la relatividad especial a la vez que otorga un papel tan activo al espacio-tiempo? La respuesta es que, en la mayor parte de las circunstancias, la gravedad es realmente débil. Si ignoramos la gravedad por completo, podemos volver a pensar en el espacio-tiempo de Minkowski, que no tiene curvatura y codifica la mayor parte de lo que hace a la relatividad especial funcionar como lo hace. En concreto, el espacio-tiempo es el mismo antes y después de la transformación de Lorentz, que es la forma matemática de decir que todos los marcos de referencia son equivalentes. En presencia de gravedad, se pierde la equivalencia de los marcos de referencia (al menos en el sentido usual de la relatividad especial), porque el cuerpo que gravita convierte en especial un marco de referencia. El lector recordará que tocamos este mismísimo punto en el capítulo 1, cuando describimos por primera vez el marco B de Bob como estacionario, cuando de hecho solo es estacionario respecto a la Tierra.
Incluso cuando la gravedad está presente, a menudo podemos apañarnos con la relatividad especial en regiones pequeñas del espacio-tiempo. Esto se debe a que la gravedad curva el espacio-tiempo solo un poco, y si nos centramos en objetos y sucesos que están lo bastante cerca en el espacio y el tiempo, podemos describirlos con un excelente grado de aproximación como si el espacio-tiempo fuera plano. Por ejemplo, pensemos en disparar una bala a una manzana justo cuando se acaba de desprender del árbol. Tenemos que admitir que la gravedad está operando, y si le damos el suficiente tiempo, causaría que la manzana cayera con alguna velocidad medible. Pero en el breve tiempo que le lleva a la bala pasar a través de la manzana, la aceleración gravitatoria es tan débil que no entra en escena de forma significativa. Si vamos a hacernos preguntas sobre el tiempo propiamente dicho y el tiempo dilatado transcurridos mientras la bala pasa a través de la manzana, la relatividad especial nos bastará.
Para hacernos una idea de lo muy diferentes que son las cosas cuando la gravedad es importante, imaginemos una bala disparada a través de un agujero negro. ¡Eso no funcionaría! Una vez que la bala cruza el horizonte del agujero negro, se ha ido para siempre, y ninguna parte de ella saldrá por el otro lado. Esto no se debe en realidad a que los agujeros negros sean grandes: seguiría siendo cierto incluso para un agujero negro del tamaño de una manzana. Los agujeros negros son unas regiones del espacio-tiempo tan altamente curvadas que secuestran el futuro de todo objeto que cae en ellos. (Por cierto, un agujero cuyo horizonte tenga el tamaño de una manzana tendría una masa de unas cinco veces la de la Tierra).
Para empezar, afilemos nuestra intuición sobre la relatividad general considerando la gravedad en situaciones en que es bastante débil, como la gravedad que experimentamos aquí en la Tierra. Nos quedan aún algunos conceptos ciertamente extraños a los que debemos acostumbrarnos, entre los que destaca una nueva forma en que el tiempo pasa más deprisa o más despacio dependiendo de tu posición en un pozo gravitatorio. Al final del capítulo, nos centraremos en el poderoso lenguaje de la geometría diferencial mientras revisitamos las ecuaciones de Einstein en su gloria plena. Solo mediante este lenguaje podremos articular por entero las ideas de los siguientes capítulos: en concreto, la geometría del espacio-tiempo curvo que constituye un agujero negro.
En la medida de lo posible, seguiremos pistas sobre cómo desarrollar la relatividad general a partir de analogías con el electromagnetismo. Para ello, tenemos que empezar de algún modo con el concepto de campo y llegar a unas ecuaciones de campo que implican radiación. Nuestro objetivo final, las ecuaciones de campo de Einstein, son ecuaciones diferenciales formuladas localmente en términos de cómo trocitos vecinos de espacio- tiempo curvo empujan y tiran uno de otro. Pero abordar la historia entera y complicada del espacio-tiempo fuertemente curvado es justo lo que no queremos hacer ahora mismo, y por eso restringiremos la atención de momento a lo que llamamos «gravedad ordinaria». Esto quiere decir que trata de la gravedad en situaciones donde los cuerpos de interés se mueven unos respecto a otros mucho más despacio que la velocidad de la luz, y ninguno de ellos es lo bastante denso para formar un agujero negro. El sistema solar es un lugar de este tipo, como lo es la mayoría de nuestra galaxia, excepto cerca de estrellas colapsadas y agujeros negros como el que acecha en el centro de la galaxia.
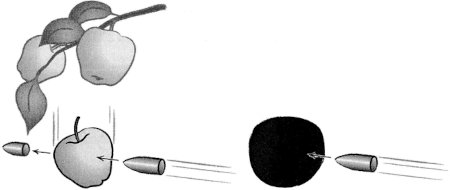
Figura 2.1. Izquierda: una bala pasa a través de una manzana justo cuando empieza a caerse de la rama. La relatividad especial basta para describir esta situación, porque la gravedad es tan débil y tiene tan poco tiempo para actuar que no supone ninguna diferencia. Derecha: una bala se dispara hacia un agujero negro cuyo horizonte tiene el mismo tamaño que la manzana. ¡La bala nunca sale por el otro lado!
Al tratar la gravedad ordinaria, nos estamos restringiendo a las situaciones en que el espacio-tiempo es casi plano, aunque no del todo.
La manifestación más simple del concepto de campo en electromagnetismo es el campo eléctrico que media la atracción de las cargas positivas y negativas. Nuestro primer paso hacia la relatividad general es aprender cómo la gravedad ordinaria puede explicarse en términos de una propiedad como el campo eléctrico: una propiedad que tiene sentido en todo el espacio-tiempo, haya o no cuerpos gravitatorios en la vecindad. Estamos, en resumen, tratando de hallar la respuesta que se le escapó a Newton cuando escribió sobre el origen de la gravedad: «No formulo ninguna hipótesis».
La respuesta es el propio tiempo. De forma más precisa, la gravedad ordinaria surge por desplazamiento gravitatorio al rojo, que es la forma en que el tiempo pasa más lento cuando estás cerca de un cuerpo masivo. El desplazamiento gravitatorio al rojo fue observado directamente por primera vez por Robert Pound y Glen Rebka, en un experimento que describiremos enseguida. El desplazamiento gravitatorio al rojo es sutil (alrededor de una parte en mil millones en la superficie de la Tierra), pero es lo bastante grande para ser un efecto importante en el diseño de los satélites del sistema de posicionamiento global (GPS en sus siglas inglesas). Los satélites están notablemente más arriba en el pozo gravitatorio de la Tierra de lo que estamos nosotros en la superficie, y en consecuencia sus relojes corren más deprisa que los nuestros. La medida precisa del tiempo es crucial para que el sistema GPS determine las posiciones con gran exactitud, y los efectos relativistas se han empotrado cuidadosamente en el sistema.
El flujo del tiempo también es esencial para entender los agujeros negros. Como veremos con más detalle en el capítulo 3, el espacio-tiempo cerca de un agujero negro se distorsiona tanto que el tiempo, según lo definimos normalmente, se detiene por completo cuando alcanzas el horizonte. Según vayamos describiendo las propiedades detalladas del desplazamiento gravitatorio al rojo, será bueno que tengamos en mente que todos los argumentos que hagamos son aplicables a los espacio-tiempos de los agujeros negros, siempre que no nos aventuremos demasiado cerca del horizonte. En el capítulo 3 completaremos nuestro tratamiento de un agujero negro metiéndonos más aún dentro de su pozo gravitatorio, hasta que por fin seamos destruidos por la singularidad de su centro.
La idea de que el tiempo se ralentiza cerca de un cuerpo masivo parece un tanto resbaladiza. ¿Cómo podemos saber que eso está ocurriendo? ¿Y por qué demonios eso ejerce un tirón gravitatorio sobre otros cuerpos masivos? El experimento de Pound-Rebka nos ofrece una respuesta muy bella a la primera pregunta. Responder a la segunda nos conducirá finalmente a la noción fundamental de una geodésica del espacio-tiempo.
Pound y Rebka midieron el desplazamiento gravitatorio al rojo utilizando —¿qué si no?— un pulso de luz. Sabían por su investigación anterior con isótopos radiactivos que el hierro-57 (una forma de hierro con 26 protones y 31 neutrones) puede absorber y emitir un fotón con una frecuencia extremadamente bien definida, cercana a 3 trillones de hercios. Por comparación, una emisora de radio emite a una frecuencia mucho menor, de unos 100 millones de hercios. Un hercio es una oscilación por segundo, y un millón de hercios significa un millón de oscilaciones por segundo. Para nuestros objetivos, nos bastará pensar en el hierro-57 como en un relojito minúsculo que hace tic 3 trillones de veces por segundo. Estos tics se pueden observar a distancia porque el fotón emitido por el hierro-57 los lleva de un lugar a otro. Pound y Rebka enviaron fotones emitidos por el hierro-57 desde la base hasta el tejado de una torre, de poco más de 22 metros de alta. Contaban con un método para medir la frecuencia de los fotones en el tejado de la torre con una exactitud extraordinaria. Su método de medición era análogo a la manera en que se sintoniza una radio para recibir una emisora concreta en vez de cualquier otra que emita a una frecuencia distinta. Lo que hallaron fue que la frecuencia era menor en el tejado de la torre que en la base. Esa reducción en frecuencia es exactamente la que predice el desplazamiento gravitatorio al rojo.
Del experimento de Pound-Rebka ya podemos obtener un indicio de por qué el desplazamiento gravitatorio al rojo tiene algo que ver con el tirón gravitatorio.
Para hacerlo, necesitamos otra de las percepciones de Einstein (en este caso basada en las ideas de Max Planck): que la energía de un fotón es proporcional a su frecuencia.
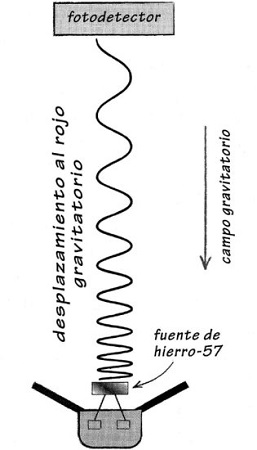
Figura 2.2. Representación esquemática del experimento Pound-Rebka. Fotones procedentes del hierro-57 se envían hacia arriba, contra el tirón de la gravedad. Un fotodetector situado a mayor elevación determina que están desplazados al rojo gravitatoriamente. Una mayor longitud de onda significa una luz más roja. El desplazamiento al rojo del experimento real es mucho más sutil de lo que hemos dibujado aquí.
Así, cuando la frecuencia disminuye, la energía disminuye. En realidad, tiene sentido que la energía de un fotón decrezca a medida que viaja hacia arriba, porque, para subir, tiene que luchar contra el tirón de la gravedad. No puede perder energía por deceleración: en la relatividad general, como en la relatividad especial, la luz siempre viaja a la misma velocidad. En lugar de ello, su pérdida de energía viene codificada por su frecuencia gravitatoriamente desplazada al rojo.
Tras haber conocido la dilatación del tiempo en el capítulo 1, podrías sospechar que el desplazamiento gravitatorio al rojo ocurre porque las cosas que caen en un pozo gravitatorio acumulan algo de velocidad en el proceso, y la dilatación del tiempo resultante es de lo que hablamos cuando hablamos de desplazamiento gravitatorio al rojo. No es así. El desplazamiento gravitatorio al rojo es algo nuevo y distinto. Los dos relojes de Pound y Rebka estaban estacionarios respecto a la Tierra.
El desplazamiento gravitatorio al rojo nos rodea por completo. Por ejemplo, tu cabeza envejece más deprisa que tus pies debido al desplazamiento gravitatorio al rojo (a menos que estés tumbado). Al igual que la dilatación temporal, el efecto es numéricamente muy pequeño en la experiencia diaria: por ejemplo, durante toda tu vida, tu cabeza envejece solo unas décimas de microsegundo más que tus pies. Para obtener un efecto más pronunciado, tendrías que estar en un campo gravitatorio mucho más intenso que el que ofrece la Tierra. Por ejemplo, si pudieras estar con los pies solo unos centímetros por encima del horizonte de un agujero negro cuya circunferencia es igual a la de la Tierra, tus pies envejecerían bastante más despacio que tu cabeza, que está más de un metro sobre el horizonte. Por supuesto, estar en ese entorno sería una experiencia absolutamente devastadora. Solo estamos tratando de posibilidades conceptuales.
¿Cómo explicamos los fenómenos gravitatorios más cotidianos, como las manzanas que caen y los planetas que orbitan, usando la idea de que la causa original de la gravedad es la forma en que el tiempo pasa más lento cerca de los cuerpos masivos? Tenemos que dar un rodeo por las ideas que popularizó satíricamente el lema panglossiano: «Todo marcha bien en el mejor de los mundos posibles». Los científicos y matemáticos de tiempos de Voltaire, en particular Joseph-Louis Lagrange, estaban convencidos de que el movimiento de los cuerpos masivos —como las manzanas que caen y los planetas que orbitan— es óptimo en cierto sentido. Es decir, que la caída suavemente acelerada de una manzana desde el árbol hasta el suelo es, de algún modo, mejor que cualquier otro movimiento entre los mismos estados inicial y final. El gran logro de Lagrange fue formular esa idea en términos matemáticos precisos. Según su descripción, a cualquier movimiento concebible de la manzana entre unos estados inicial y final dados se le asigna una denominada «acción». El movimiento real que elige la manzana es el que minimiza o maximiza la acción. En cualquiera de los dos casos, el movimiento es el mejor de los posibles en un sentido matemático bien definido.
Para un discípulo de Newton, la formulación lagrangiana de la mecánica como un problema de optimización puede parecer una tontería. ¿Cómo va a elegir un objeto inanimado el trayecto óptimo entre muchas posibilidades? Lo que se supone que ocurre, según Newton, es que las cosas se mueven en línea recta hasta que una fuerza las empuja, y entonces cambian de dirección de acuerdo con F = ma. ¿Qué tiene eso de óptimo? El truco de magia es que, mediante una construcción muy cuidadosa de la «acción» de un cuerpo en movimiento, Lagrange pudo recobrar exactamente las leyes de Newton, ni más ni menos. Hay que reconocer que su elección de la «acción» fue poco intuitiva. Pero si adelantamos la película hasta la relatividad general, veremos el gran valor de la formulación de Lagrange. La acción de un objeto no es más que el tiempo transcurrido para un observador que se mueve con el objeto. El movimiento que ejecuta realmente un objeto optimiza el tiempo propiamente dicho que transcurre para ese objeto. En los casos que vamos a analizar, el tiempo propiamente dicho resulta maximizado.
Un ejemplo tomado de la relatividad especial nos ayudará a centrar el tratamiento. (Recuerda que relatividad especial implica que no incluimos aún la gravedad). Se llama la paradoja de los gemelos, y consiste en lo siguiente. Dos observadores, a los que llamaremos como de costumbre Alice y Bob, empiezan juntos con cronómetros idénticos. Le damos a Alice una nave espacial, y el plan es que vuele alejándose de Bob durante un día a velocidad constante (digamos a la mitad de la velocidad de la luz, para ser más concretos); luego da la vuelta y vuelve hasta Bob. Mientras, Bob se queda donde está y no hace nada. Si recordamos nuestra exposición en el capítulo 1 del tiempo propiamente dicho, podremos anticipar el resultado del experimento: la duración del viaje de Alice, según la mide Bob con su cronómetro, será mayor que los dos días que mide Alice con el suyo. De hecho, con los números que hemos dado, Bob medirá que el viaje ha durado unos 2,3 días.
La paradoja de los gemelos proviene del siguiente razonamiento defectuoso. Todo movimiento es relativo. Según Alice, es Bob quien se mueve alejándose de ella, y luego vuelve. ¿No debería esperar ella que fuera él quien mide el tiempo de viaje más corto?
Para percibir que este razonamiento es defectuoso, tenemos que identificar una clara diferencia entre Alice y Bob. La diferencia es que Alice aceleró cuando dio la vuelta para regresar. Bob nunca aceleró. Por ejemplo, podríamos dejarle flotar libremente en el espacio vacío durante todo el viaje de Alice. Desde el punto de vista lagrangiano, lo que ha hecho Bob es «lo mejor», porque es absolutamente natural y no requiere ninguna acción externa. Así que tiene sentido que sea él quien experimenta un tiempo propiamente dicho más largo.
Hay una variante fascinante de la paradoja de los gemelos que introduce efectos gravitatorios en el esquema (véase la figura 2.3). Digamos que Alice y Bob viven en las profundidades de un pozo gravitatorio, y ambos van allí a la escuela. Tienen unos dificultosos deberes para casa que tienen que entregar en 48 horas, digamos a las nueve de la mañana del lunes. Bob concluye, a partir de su experiencia con la paradoja de los gemelos, que él será quien tenga más tiempo para hacer los deberes si se mueve lo menos posible. De modo que se dirige a la escuela a paso muy lento y constante, haciendo los deberes por el camino, y llega allí a las nueve de la mañana del lunes. Alice, la eterna aventurera, piensa que lo mejor será montarse en su cohete y salir del pozo gravitatorio, pues así la ausencia de desplazamiento gravitatorio al rojo le dará más tiempo para hacer los deberes. Pero, por otro lado, le preocupa que la dilatación del tiempo que experimentará mientras se aleja y vuelve resulte más importante.
El principio del tiempo propio óptimo dice que, para maximizar su tiempo, Alice debería hacer lo que haría la materia inerte en las mismas circunstancias. ¿Qué hace la materia de forma natural? Bien, empecemos por admitir que le gusta estarse quieta. Así que parece que el plan de Bob de minimizar su movimiento yendo a la escuela muy despacio es el mejor. Pero la gravedad cambia las cosas. En un pozo gravitatorio, a la materia no le gusta estarse quieta. Le gusta caer. No es natural que Bob camine despacio a la escuela en presencia de gravedad; si lo puede hacer es solo porque está andando por encima de otro montón de materia que está aún más honda que él en el pozo gravitatorio. Si queremos que un trozo de materia inerte empiece en casa de Bob y Alice a las 9 de la mañana y acabe en la escuela 48 horas después, tenemos que lanzarlo de modo que viaje en un arco amplio hasta aterrizar en la escuela a las 9 de la mañana del lunes. Una vez que se ha imaginado eso, Alice se monta feliz en su cohete, despega con un gran empujón de sus propulsores y luego va en punto muerto durante el resto del fin de semana mientras hace los deberes frenéticamente[3]. El cohete está actuando ahora como un misil balístico, lo que significa que, salvo por el empujón inicial, se mueve bajo la influencia de la gravedad, sin ninguna otra fuerza. Dich o de otro modo, está en caída libre.
Los experimentos de Alice y Bob con el tiempo transcurrido ayudan a ilustrar el principio de equivalencia de Einstein. En su forma más simple, el principio de equivalencia dice que la aceleración es indistinguible de la gravedad. La propiedad esencial de la paradoja de los gemelos original, en su forma no gravitatoria, es que Alice tiene que acelerar para dar la vuelta y regresar hacia Bob. Si hacemos que esa aceleración sea lenta y continua en lugar de abrupta, tendremos el equivalente a que Alice pase todo el viaje en un campo gravitatorio. Por el contrario, la propiedad esencial de la variante gravitatoria de la paradoja de los gemelos es que Alice pasa el fin de semana en caída libre, mientras que Bob lo pasa en un campo gravitatorio.
De este modo, vemos que Atice y Bob realmente se intercambian los papeles en las dos versiones de la paradoja.
Un ejemplo más cotidiano del principio de equivalencia es que, cuando tomamos un ascensor, nos sentimos más pesados cuando el ascensor acelera hacia arriba, y más ligeros cuando acelera hacia abajo. Si el ascensor acelerara hacia arriba en el espacio vacío, sin ningún cuerpo gravitatorio cerca, nuestra experiencia como observadores dentro del ascensor sería idéntica a lo que experimentamos cuando el ascensor está quieto en el campo gravitatorio terrestre. Del mismo modo, si el ascensor estuviera en caída libre en el campo gravitatorio terrestre, sentiríamos la misma ingravidez dentro de él que si estuviéramos flotando libremente en el espacio vacío.
Para regresar a las ecuaciones de Einstein, seamos audaces y demos al ritmo al que fluye el tiempo su nombre matemático adecuado: función de lapso. En otras palabras, la función de lapso nos dice el ritmo al que el tiempo está pasando en cualquier punto dado del espacio. Una ecuación diferencial similar a una de las ecuaciones de Maxwell nos ofrece una regla para calcular la función de lapso en presencia de cualquier colección arbitraria de masas que se mueven despacio. Conociendo la función de lapso, podemos aplicar el principio del tiempo propiamente dicho óptimo para determinar la trayectoria de un cuerpo masivo que responde al campo gravitatorio.
La ecuación diferencial para calcular la función de lapso en presencia de masas que se mueven despacio es en realidad un caso especial de una de las ecuaciones de Einstein. Hay nueve funciones más, similares a la función de lapso, que especifican por completo la forma del espacio-tiempo curvado y, a grandes rasgos, hay una ecuación de campo de Einstein para cada una de ellas. En conjunto, esas diez funciones engloban lo que se denomina una métrica del espacio-tiempo. La métrica del espacio-tiempo es una regla para averiguar la distancia entre puntos cercanos y también el ritmo al que el tiempo fluye. Una vez que empezamos a hablar de métricas, entramos de verdad en el territorio de la geometría diferencial, que es el estudio de las superficies arbitrariamente curvadas, y de las geometrías curvadas de más dimensiones, incluidas las geometrías del espacio-tiempo curvo de la relatividad general.
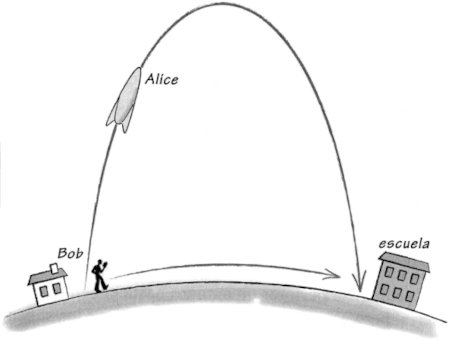
Figura 2.3. Bob hace los deberes mientras camina despacio a la escuela. Alice despega en un cohete y acaba sus deberes durante el vuelo. Si el cohete de Alice acelera de golpe y luego se desliza durante el resto del viaje, ella tendrá más tiempo que Bob para acabar los deberes antes de que el timbre de la escuela suene el lunes por la mañana.
Nuestro tratamiento de la gravedad «ordinaria» puede dejarte con la idea de que el espacio permanece perfectamente plano mientras que el tiempo transcurre a diferentes ritmos en distintos lugares. No es así. En realidad, el espacio se abre un poco en las regiones donde el tiempo corre más lento. Para entender qué significa esto, imagina que rodeamos la Tierra con una esfera perfecta y medimos con cuidado la superficie de esa esfera. A continuación, medimos el radio de la esfera. (Reconozcamos que esto requeriría perforar un agujero hasta el centro de la Tierra, pero estamos asumiendo que tenemos los superpoderes adecuados). Normalmente, encontraríamos que el área A y el radio r se relacionan por la fórmula A = 4πr2. Pero, debido a la presencia de la Tierra, r es un poquito mayor respecto a A de lo que debería ser para cumplir A = 4πr2. Otra forma de decirlo es que el volumen dentro de la esfera que rodea a la Tierra es un poco mayor que el volumen dentro de una esfera de idéntica superficie que rodee al espacio vacío. Como el desplazamiento gravitatorio al rojo, la expansión del espacio cerca de los cuerpos masivos es un efecto sutil, siempre que restrinjamos nuestra atención a la gravedad ordinaria, o de campo débil. De hecho, resulta que las longitudes espaciales (definidas de forma adecuada) se expanden en tanta cantidad como se ralentiza el tiempo. Ahora parece que todo nuestro tratamiento anterior de los cuerpos en caída fue engañoso, puesto que estábamos asumiendo que el desplazamiento gravitatorio al rojo era el único efecto de la gravedad. Lo que nos salva es que los observadores que se mueven despacio respecto a los cuerpos gravitatorios son mucho más sensibles a la ralentización del tiempo que a la expansión del espacio. Tenemos que asumir que estamos tratando con la gravedad ordinaria, lo que implica en esencia que no hay por ahí ningún cuerpo gravitatorio lo bastante denso como para formar un agujero negro. Ahora que estamos abandonando esa suposición simplificadora, tenemos que sumergirnos más hondo en la geometría diferencial para entender lo que ocurre.
La geometría diferencial (o al menos la parte de ella que necesitamos) se centra en tres conceptos: métricas, geodésicas y curvatura. Las tres se pueden ilustrar considerando las superficies curvas, como la superficie de la Tierra. La métrica es fácil, porque solo se refiere a la distancia. Bueno, al menos parece fácil al principio. De Washington DC a San Francisco hay 3930 kilómetros en línea recta. Lo que queremos decir con eso, en realidad, es que si viajas por la superficie de la Tierra (o poco más arriba) el camino más corto de Washington DC a San Francisco mide 3930 kilómetros. Como puntos en el espacio, sin embargo, las dos ciudades están un poquito más cerca, a unos 3860 kilómetros. La pequeña diferencia se debe a que, si pudiéramos viajar en línea recta por dentro de la Tierra, acortaríamos un poco la distancia respecto al viaje por la superficie. Cuando viajamos por la superficie, nuestro trayecto es forzosamente curvo; para calcular la distancia total, el enfoque natural es dividir el trayecto en trocitos pequeños, cada uno de ellos casi recto, y luego sumar las longitudes de todos los trocitos. La palabra «diferencial» se refiere a ese proceso de trocear las cosas y medir los trocitos. El objetivo de una métrica en geometría diferencial es decirnos las longitudes de los trocitos. Cuando queremos saber la longitud total de un trayecto, se asume en geometría diferencial que estamos a la altura de la tarea de sumar las longitudes de todos los trocitos, lo que al final es un ejercicio de cálculo integral.
Una geodésica por la superficie de la Tierra entre Washington DC y San Francisco es la trayectoria más corta disponible para quien viaja por la superficie. Una geodésica no es una línea recta, pero es lo más recta que puede ser una trayectoria por la superficie de la Tierra. Lo que queremos decir por «recta» es que, para viajar por una geodésica en la superficie de la Tierra desde Washington DC hasta San Francisco, tenemos que ir en línea recta sin hacer ninguna curva. Debido a la curvatura de la Tierra, esa trayectoria que es la más corta posible discurre un poco más al norte en latitud que cualquiera de las dos ciudades. Un ejemplo más acusado de este fenómeno es que los aviones trazan una ruta polar en los viajes largos, digamos de Atenas a San Francisco. Resulta que el camino más corto entre esas dos ciudades te lleva por Groenlandia, a una latitud mucho más alta que Atenas o San Francisco. (Por supuesto, los aviones no viajan por la superficie de la Tierra, sino por encima de ella; pero, en comparación con el radio de la Tierra, su altitud de crucero es insignificante así que, para lo que estamos debatiendo, podemos pensar que los aviones viajan por la superficie).
Parece que la curvatura debería ser fácil de entrada, pues todos estamos familiarizados con la forma en que se curva la superficie de la Tierra. Pero lo cierto es que hay algo muy sutil en la noción de curvatura que se suele utilizar en geometría diferencial (y que se usa en la relatividad). Para percibir esta sutileza, consideremos la diferencia entre un cono y una esfera. Ambos están curvados, pero están curvados de formas muy distintas. Un trozo plano de papel puede enrollarse como un cono sin estirarlo, pero si intentas cubrir una esfera con un papel plano, tendrás que arrugarlo o romperlo. Por eso decimos que la esfera está «curvada intrínsecamente», mientras que el cono es «intrínsecamente plano» (excepto justo en la punta). Tanto la esfera como el cono tienen «curvatura extrínseca», un término que se refiere a la idea usual de que están curvados como superficies en un mundo en tres dimensiones.
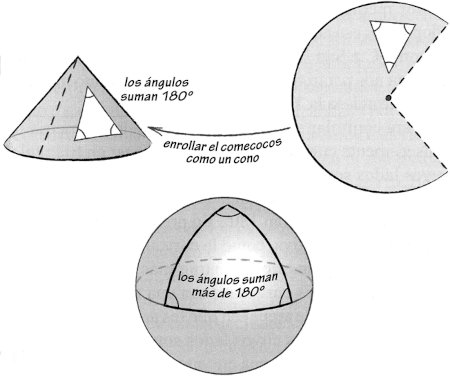
Figura 2.4. Un cono no tiene curvatura intrínseca, porque puede generarse enrollando un comecocos. Como resultado, cuando se dibuja un triángulo cuyos lados son segmentos de geodésicas, sus ángulos suman 180°. El mismo triángulo dibujado en el comecocos antes de enrollarlo tiene unos lados que son segmentos de recta ordinarios. Por el contrario, una esfera tiene una curvatura intrínseca positiva, de modo que un triángulo con lados geodésicos tiene unos ángulos que suman más de 180°.
Para la relatividad, lo único que importa es la curvatura intrínseca. Para centrarnos en la curvatura intrínseca, durante el tratamiento de las superficies curvadas, nos restringimos a preguntas que puedan responderse por mediciones realizadas solo en la superficie. Si adoptamos esa actitud, diremos que la distancia de Washington DC a San Francisco es de 3930 kilómetros, y ni siquiera nos pararemos a pensar sobre el camino más corto que atraviesa la Tierra.
Para controlar mejor lo que significa la geometría intrínsecamente curvada, tenemos que pensar en triángulos cuyos lados son geodésicas. En una geometría bidimensional plana, los ángulos en las esquinas de cualquiera de esos triángulos sumarán 180°. En presencia de una curvatura intrínseca positiva, como la curvatura de la superficie de la Tierra, los ángulos sumarán más de 180°. Resulta que hay superficies curvadas (con una forma parecida al cuello de un reloj de arena) en que los ángulos de los vértices de los triángulos cuyos lados son geodésicas suman menos de 180°. Esto es una curvatura intrínseca negativa.
Una vez que hemos presentado las principales ideas de la geometría diferencial, veamos cómo se generalizan al espacio-tiempo de cuatro dimensiones de la relatividad general.
Las métricas que se usan en relatividad general son un poco más complicadas que la métrica de la superficie de la Tierra, porque llevan a cabo dos tareas distintas. Una es determinar la distancia entre dos sucesos separados en el espacio, y la otra es determinar el tiempo transcurrido entre dos sucesos separados en el tiempo. El lapso entre dos sucesos separados en el tiempo es exactamente el tiempo que transcurriría para un observador en caída libre desde que observa un suceso hasta que observa el otro, asumiendo que los dos sucesos tienen lugar en el mismo sitio según su marco de referencia. Los sucesos separados en el espacio son más difíciles de conceptualizar, porque son por definición sucesos tan separados en el espacio que ningún observador que se mueva más despacio que la velocidad de la luz puede observar ambos en el mismo sitio en su marco de referencia. En un espaciotiempo estático (uno que no cambia con el tiempo), podemos definir la distancia entre sucesos separados en el espacio a partir de lo que tarda una señal enviada por uno en ser recibida en la posición del otro. Las métricas tienen una importancia absolutamente central en la relatividad general, porque las soluciones a las ecuaciones de Einstein son métricas del espacio-tiempo. Nuestra discusión de los agujeros negros en los capítulos 3 y 4 girará sobre unas métricas concretas del espacio-tiempo conocidas como las soluciones de Schwarzschild y Kerr.
Como ya hemos mencionado, una métrica en relatividad general engloba diez funciones, una de las cuales es esencialmente la función de lapso, que nos dice a qué ritmo transcurre el tiempo. Otra de esas diez funciones es la que nos dice cómo se abre el espacio en presencia de cuerpos masivos. Las otras ocho funciones describen diversas distorsiones del espacio-tiempo, algo similares a los espejos de los parques de atracciones que te muestran una imagen estirada en una dirección u otra. Podemos agrupar estas diez funciones en el llamado tensor métrico, que se suele escribir gμν, ¡que no se debe confundir con el tensor de Einstein Gμν!
Las geodésicas de la relatividad también son un poco más complicadas que las de las superficies curvas, en parte porque vienen en tres variedades.
Una geodésica de tipo espacial es el trayecto más corto entre dos puntos separados espacialmente, similar a una carretera recta por la superficie de la Tierra entre Washington DC y San Francisco. Pero una geodésica de tipo espacial en el espacio-tiempo es un trayecto que no puede seguir ningún observador, porque hacerlo implicaría superar la velocidad de la luz. Esto puede parecer una tontería. ¿Cómo va a ser imposible seguir el trayecto más corto entre dos puntos? La cuestión es que una geodésica en el espacio- tiempo no solo especifica adonde se supone que vas, sino también cuándo se supone que vas a llegar allí. Un buen ejemplo de geodésica de tipo espacial es un segmento de línea a tiempo constante entre dos puntos en el espacio de Minkowski. «Seguir» esta geodésica significaría que llegas en el mismo preciso instante en que sales, y ni que decir tiene que eso es imposible.
El segundo tipo de geodésica es una geodésica de tipo temporal, que es la clase de trayecto que siguen naturalmente los cuerpos masivos si no actúa sobre ellos más fuerza que la gravedad. El movimiento balístico de Alice en un campo gravitatorio es un ejemplo de geodésica de tipo temporal, y Bob flotando libremente en el espacio, lejos de todo campo gravitatorio, es otro ejemplo. Las geodésicas de tipo temporal maximizan el tiempo propiamente dicho, como vimos en relación con las varias versiones de la paradoja de los gemelos. De hecho, el principio de tiempo propiamente dicho óptimo alcanza su expresión completa en el requisito de que los cuerpos masivos en espacio-tiempos curvados arbitrariamente deben seguir geodésicas de tipo temporal.
Hay un tipo más de geodésica en la relatividad general, que es la geodésica nula. Es el trayecto natural de un rayo de luz en el espacio- tiempo curvo. A veces preferimos llamar «geodésicas espaciotemporales» a las geodésicas de la relatividad general, para subrayar que contienen información sobre el tiempo y no solo sobre el espacio. Pero la mayoría de los profesionales dicen simplemente «geodésica», y a partir de ahora adoptaremos esa terminología.
Cuando pasamos de las superficies bidimensionales a los espacio- tiempos de cuatro dimensiones, la curvatura se vuelve más complicada cuantitativamente, pero es similar conceptualmente: cuando nos planteamos preguntas sobre los ángulos a los que se encuentran las geodésicas, las respuestas pueden diferir de nuestras expectativas típicas del espacio plano, y difieren de la forma que capta el llamado tensor de curvatura de Riemann. El tensor de Einstein es una versión reducida del tensor de curvatura de Riemann que selecciona solo aquellos aspectos de la curvatura del espacio- tiempo que se ven afectados por la presencia de masa (o energía, o cantidad de movimiento, o presión, o tensión de cizalladura).
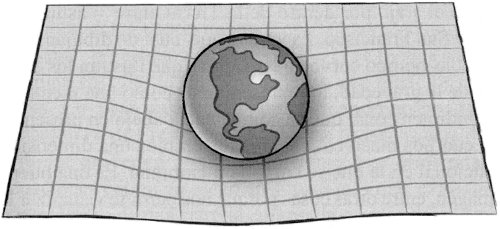
Figura 2.5. La Tierra causa un abultamiento en el espacio, que suele dibujarse mostrando el espacio combado hacia abajo. El espacio, en efecto, se curva en las cercanías de un cuerpo masivo, pero la curvatura es intrínseca, es decir, que tiene que ver con distorsiones del espacio dentro de sí mismo, y no con esa especie de abultamiento en una dimensión extra.
Al menos según nuestro conocimiento actual, no hay nada más allá de las cuatro dimensiones del espacio-tiempo en lo que este se pueda curvar. Las buenas preguntas sobre la curvatura en la relatividad general son las que pueden responderse mediante geodésicas en el espacio de cuatro dimensiones. Ni siquiera tenemos que pensar en «atajos» a través de alguna geometría ambiente mayor, como el atajo por dentro de la Tierra entre Washington DC y San Francisco. Es verdad que, cuando dibujamos el espacio-tiempo curvo en las figuras que ilustran los efectos de la gravedad, lo representamos como una membrana bidimensional que se comba hacia abajo en presencia de cuerpos masivos. Esa imagen emplea una dimensión adicional en la que se curva la membrana. Es una buena imagen, entre otras cosas porque nos permite visualizar la manera en que el espacio se abre un poco en la vecindad de un cuerpo masivo. Pero, por todo lo que sabemos, el mundo real solo es tetradimensional, y el espacio-tiempo tetradimensional se curva por sí mismo, sin necesidad de una quinta dimensión[4].
Las ecuaciones de campo de Einstein, Gμν = 8πGNTμν/c4, equivalen a diez ecuaciones diferenciales para las diez funciones del tensor métrico. Lo que las ecuaciones de Einstein dicen en conjunto es que masa, energía, cantidad de movimiento, presión y tensión de cizalladura (todas incluidas en Tμν) causan que el espacio-tiempo se curve. En las situaciones en que todos los cuerpos masivos se mueven despacio, y podemos ignorar la presión y la tensión de cizalladura, el componente más importante de las ecuaciones de campo de Einstein es el que solo tiene relación con el tiempo: G00 = 8πGNT00/c4. Ahora escribimos G00 en lugar de Gμνporque nos estamos centrando en la ecuación de Einstein que viene marcada por μ = 0 y ν = 0, y la convención es poner a un tensor el índice 0 cuando nos referimos a la dirección del tiempo, mientras que μ = 1, 2 o 3 se refieren a nuestras tres direcciones espaciales habituales. Cuando tratamos con la gravedad normal y corriente, la ecuación G00 = 8πGNT00/c4 se reduce a la regla para calcular la función de lapso que mencionamos antes. En otras palabras (y simplificando un poco), la ecuación 00 de Einstein es todo lo que necesitas para describir la gravedad normal y corriente. Las otras nueve ecuaciones entran en juego en situaciones más extremas, como dentro de una estrella colapsada o cerca de un agujero negro.
En resumidas cuentas, los dos cimientos esenciales de la relatividad general son las ecuaciones de campo de Einstein y el principio del tiempo propiamente dicho óptimo. Utilizando una formulación común, la materia le dice al espacio-tiempo cómo curvarse mediante las ecuaciones de Einstein, y el espacio-tiempo curvo le dice a su vez a la materia cómo moverse mediante el principio del tiempo propiamente dicho óptimo. De forma análoga, las cargas eléctricas le dicen al campo electromagnético lo que tiene que hacer mediante las ecuaciones de Maxwell, y el campo electromagnético genera a su vez fuerzas sobre las cargas eléctricas.
Hay un fenómeno más sobre el que la analogía del electromagnetismo nos recuerda que pensemos: la radiación. Exactamente igual que las ecuaciones de Maxwell, las ecuaciones de campo de Einstein tienen soluciones que describen una cascada autosostenida de perturbaciones del campo que se propagan por el espacio-tiempo. En el electromagnetismo, esas perturbaciones del campo son campos eléctricos y magnéticos. En la relatividad general, son distorsiones del espacio-tiempo que se describen más fácilmente como estirarse en una dirección espacial y encogerse en otra. Las ondas gravitatorias se generan por la materia en movimiento, al igual que la luz se puede generar por cargas eléctricas en movimiento. Una vez generadas, viajan por el espacio-tiempo a la velocidad de la luz. En efecto, son ondas en el espacio-tiempo, similares a las olas en el agua.
Igual que la luz, las ondas gravitatorias portan energía. Se han detectado de manera indirecta en unos sistemas estelares compactos denominados púlsares binarios. Esta detección, por Russell Hulse y Joseph Taylor, mereció el Premio Nobel de Física en 1993. Lo que observaron en realidad fue una lenta disminución del periodo orbital del sistema estelar binario: en efecto, las dos estrellas están cayendo en espiral lentamente una sobre la otra. La liberación de radiación gravitatoria dirige esa lenta caída en espiral, y la tasa observada de caída encaja con las predicciones de la relatividad general. La observación directa de ondas gravitatorias por el LIGO, en septiembre de 2015, tiene mucha relación con caídas en espiral similares, y promete ser una de las grandes claves de la física del siglo XXI.
Nos sumergiremos a más profundidad en los detalles de la radiación gravitatoria en el capítulo 6. Por ahora, resaltemos una diferencia esencial entre el electromagnetismo y la relatividad general: las ondas luminosas no interactúan entre sí, pero las ondas gravitatorias sí lo hacen. Por ejemplo, dos ondas de luz que se cruzan pasan una a través de la otra y siguen adelante sin desviarse. Por el contrario, dos ondas gravitatorias pueden colisionar, repelerse entre sí y salir del encuentro en nuevas direcciones. Esta tendencia a la dispersión es extremadamente débil a las energías que nos son accesibles. Es un efecto tan sutil que no parece probable que nadie que esté vivo hoy pueda llegar a verlo medido con éxito. Pero no cabe duda de que forma parte de la relatividad general. De hecho, esta es una de las principales razones por las que nos resulta tan difícil combinar la relatividad con la mecánica cuántica. El problema es que la autodispersión de las ondas gravitatorias se vuelve fuerte a energías muy altas, y no sabemos cómo formular la teoría cuántica en presencia de una autodispersión tan fuerte. La teoría de cuerdas resuelve este problema de manera hermosa, pero exponerlo nos desviaría muy lejos de nuestro objetivo principal. Así que, con la relatividad general en la mano, ¡vamos a aprender sobre los agujeros negros!
Capítulo 3
El agujero negro de Schwarzschild
Ahora que hemos aprendido los principios básicos de la relatividad especial y general, estamos listos para abordar los agujeros negros cara a cara. Empezaremos con el agujero de Schwarzschild. En términos muy breves, el agujero negro de Schwarzschild describe la respuesta del espacio-tiempo a una masa puntual. Con el término «respuesta» aludimos a la idea de que la materia le dice al espacio-tiempo cómo curvarse, y lo hace mediante las ecuaciones de campo de Einstein, Gμν = 8πGNTμν/c4. Un espacio-tiempo curvo se describe matemáticamente con las diez funciones del tensor métrico. Las ecuaciones de campo de Einstein dicen que no basta con cualquier conjunto prefabricado de diez funciones; lo que se requiere es unas funciones que varíen a través del espacio y el tiempo exactamente de la forma correcta, de manera que formen una solución a las ecuaciones de campo. El físico y astrónomo alemán Karl Schwarzschild publicó su famosa solución en 1916, aunque una carta que mandó a Einstein en diciembre de 1915 deja claro que ya entonces había encontrado la solución, muy poco después de que Einstein hubiera formulado la forma definitiva de sus ecuaciones de campo.
La solución de Schwarzschild es francamente difícil de entender. Ni siquiera Einstein pareció percibir algunos de sus argumentos esenciales, en especial la suavidad del horizonte. ¿Qué es esa perla negra de gravedad que cayó de modo tan fácil en las manos de Schwarzschild, pero que hasta Einstein tuvo problemas para comprender del todo?
Tuvieron que pasar cerca de 50 años tras el descubrimiento de Schwarzschild para que emergiera una imagen clara de su importancia física. Ya hemos explicado algunos rasgos de esa imagen: en especial, la idea de un horizonte de sucesos a partir del cual ninguna señal puede escapar, y la percepción de que en su interior el tiempo apunta radialmente hacia dentro. Para los astrofísicos, es muy importante entender las órbitas de los objetos masivos capturados por el tirón gravitatorio de un agujero negro de Schwarzschild, y vamos a dedicar buena parte de este capítulo a describir esas órbitas, y qué forma presentan para un observador distante. También explicaremos lo mejor que podamos (¡y en ausencia de la menor verificación experimental!) lo que, según pensamos, debe ocurrirle a un objeto que cae en un agujero negro de Schwarzschild. Por último, hablaremos de dos rasgos sorprendentes de los agujeros negros de Schwarzschild: los agujeros blancos y los agujeros de gusano, que no es probable que sean relevantes para los agujeros negros formados por el colapso gravitatorio de estrellas viejas, pero forman parte en cualquier caso del entendimiento actual de la solución de Schwarzschild. Antes de llegar a todo esto, vamos a intentar responder directamente la pregunta: ¿qué es la métrica de Schwarzschild en sí misma?
Lejos del horizonte, la métrica de Schwarzschild es casi, casi la métrica de Minkowski, que describimos en el capítulo 1. Dicho de otra forma, el espacio-tiempo muy lejano es casi plano, y los observadores de allí pueden describir correctamente su movimiento, y también los efectos del movimiento relativo como la dilatación del tiempo y la contracción de la longitud, usando solo la relatividad especial. A medida que nos acercamos al horizonte, el tiempo se ralentiza debido a la dilatación del tiempo que explicamos en el capítulo 2. Como indicamos en el prefacio, el tiempo cambia por completo de naturaleza en el horizonte, pero esa es una historia muy complicada, así que por ahora vamos a concentrar la atención en la región del espacio-tiempo que está fuera del horizonte. Allí, la ralentización del tiempo se puede describir perfectamente con una función de lapso, que es uno de los componentes de la métrica de Schwarzschild. El resto de la métrica de Schwarzschild describe el espacio tridimensional curvo que crea la gravedad alrededor de un agujero negro. Podemos pensar en las tres dimensiones del espacio como un radio y dos direcciones angulares. Moverse en la dirección radial significa ir directo hacia arriba, alejándose del agujero negro, o directamente hacia él. Moverse en una dirección angular significa rodear el agujero negro a un radio constante.
Uno se puede sentir confuso sobre lo que significa «radio» en la solución de Schwarzschild, ya que ese radio no se puede medir desde el centro del agujero negro, que es una singularidad más allá del horizonte de sucesos que destruye todo lo que la toque. La forma correcta de pensar en el radio es medir la circunferencia de un círculo centrado en la singularidad. Este círculo puede estar enteramente fuera del horizonte de sucesos, en el horizonte mismo o incluso dentro de él. Fuera del horizonte, podemos imaginar un experimento mental que nos permitiría medir la circunferencia. Habría que reclutar a muchos observadores, digamos Alice, Bob, Bill, Bruce, Barney y así hasta Burt. Cada uno de ellos utiliza una nave espacial para flotar en puntos alrededor del círculo. Equipamos con un láser a cada observador, y le damos a Alice un cronómetro. Pedimos a Alice que mande un pulso láser a uno de sus vecinos (digamos Bob) y que al mismo tiempo ponga en marcha su cronómetro. En cuanto Bob recibe el pulso de Alice, se gira de inmediato y manda un pulso láser similar a Bill. Luego Bill manda un pulso a Bruce, y así todo alrededor del círculo. Finalmente, Burt manda una señal a Alice y, cuando ella la recibe, para el cronómetro. Si ahora tomamos el tiempo total registrado por el cronómetro de Alice y lo multiplicamos por la velocidad de la luz, obtendremos una longitud que podemos definir, razonablemente, como la circunferencia del círculo. Después calculamos el radio dividiendo esa circunferencia por 2π.
Con esta definición esmerada de radio como una circunferencia dividida por 2π, podemos revisitar un fenómeno que describimos por primera vez en el capítulo 2: el espacio se abre un poco en las regiones donde el tiempo corre más lento. Imaginemos un agujero negro que contiene exactamente una masa solar, de modo que el horizonte está a un radio de 3 kilómetros. Ahora consideremos dos círculos centrados en la singularidad, uno de radio 10 kilómetros y otro de radio 10 kilómetros más un metro. Como vimos en el párrafo anterior, lo que queremos decir por «un radio de 10 kilómetros» es que el primer círculo tiene una circunferencia de 2π veces 10 kilómetros, y un poco más para el segundo círculo. En el espacio plano, esos dos círculos estarían exactamente a un metro uno de otro, es decir, que para viajar radialmente del primero al segundo, tendrías que viajar un metro. En la solución de Schwarzschild, tienes que viajar algo más de un metro: unos 1,2 metros en total, partiendo del círculo de 10 kilómetros.
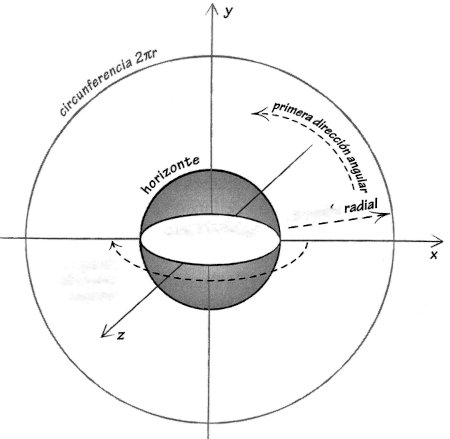
Figura 3.1. Las direcciones radial y angular de la solución de Schwarzschild. Fuera del horizonte, estas tres direcciones son las tres dimensiones del espacio. El radio se define de modo que un círculo centrado en el agujero negro tenga una circunferencia 2πr.
Bien, ahora tenemos un hecho claro. En la solución de Schwarzschild, el tiempo se ralentiza debido al desplazamiento gravitatorio al rojo por el mismo factor exacto que describe el estiramiento del radio. En otras palabras, la función de lapso, que describe cuán deprisa fluye el tiempo, se correlaciona a la perfección con otra función métrica que describe cuánta distancia adicional tienes que viajar radialmente hacia fuera respecto a la distancia que viajarías si el espacio fuera plano.
En los párrafos precedentes hemos explicado casi todos los aspectos de la solución original de Schwarzschild. Solo nos queda por describir una cosa, que es la forma precisa de la función de lapso. Lejos del horizonte, la función es exactamente 1, lo que significa que el tiempo pasa al ritmo habitual al que estamos acostumbrados en el espacio plano. La función de lapso es 0 en el horizonte, lo que significa que el tiempo ordinario deja de transcurrir allí: de hecho, esta es una manera de entender lo que es el horizonte. Entre medias, la función de lapso varía suavemente entre 0 y 1. ¿Cómo lo hace? La respuesta es que la función de lapso es la raíz cuadrada de 1 menos una constante dividida por el radio. Eso es un nombre kilométrico, así que mejor lo escribimos:
![]()
donde N es la función de lapso, r es el radio y rs es el radio del horizonte, llamado el radio de Schwarzschild. Con algunos factores, el radio de Schwarzschild equivale a la masa del agujero negro. Toda esta información detallada es lo que Schwarzschild pudo extraer resolviendo las ecuaciones de Einstein.
Una propiedad incómoda de la solución de Schwarzschild es que la función de lapso se hace 0 en el horizonte, y el estiramiento radial se hace infinito en correspondencia. Durante mucho tiempo se pensó que este comportamiento aparentemente singular indicaba una patología de la métrica de Schwarzschild. En realidad, la patología está en las coordinadas que hemos elegido para describir el tiempo y el radio. Estas coordenadas son las más adecuadas para describir a los observadores que flotan en una posición fija fuera del horizonte. La función de lapso que hemos debatido describe el desplazamiento gravitatorio al rojo, de nuevo para observadores que flotan en una posición fija. Que la función de lapso se haga 0 en el horizonte nos dice, en realidad, que es imposible flotar en el horizonte de un agujero negro. ¡No es extraño que la métrica parezca singular desde una perspectiva imposible! Si lo que describiéramos fuera la métrica de Schwarzschild desde la perspectiva de un observador que está cayendo libremente en el agujero negro, no habría nada singular ni inusual en la posición del horizonte. La diferencia entre un observador flotante y uno en caída libre se puede captar con un cambio de coordenadas similar en cierto modo a la transformación de Lorentz, aunque más sofisticado. Después de este cambio de coordenadas, que mezcla el tiempo y el radio, vemos que la solución de Schwarzschild es perfectamente suave en el horizonte. Solo persiste la singularidad en el centro del agujero negro.
La solución de Schwarzschild está entre nosotros. ¡Literalmente! El campo gravitatorio de la Tierra se puede describir con muy buena aproximación mediante la métrica espaciotemporal simple y curva de Schwarzschild. De hecho, la métrica del espacio-tiempo fuera de cualquier distribución de masa perfectamente esférica debe venir dada exactamente por la métrica de Schwarzschild. Las desviaciones de la métrica de Schwarzschild aquí en la Tierra (o, mejor dicho, justo por encima de la superficie de la Tierra) surgen porque la Tierra no es perfectamente esférica, porque está rotando y porque sentimos un poquito de tirón gravitatorio desde otros cuerpos masivos (sobre todo de la Luna).
Si estamos rodeados por una métrica de Schwarzschild, ¿quiere eso decir que en algún sitio bajo nosotros, cerca del centro de la Tierra, acecha el horizonte de un agujero negro? ¡No, por fortuna! La solución de Schwarzschild solo describe la geometría del espacio-tiempo fuera de la superficie de la Tierra. Dentro, hay que aplicar una solución diferente de las ecuaciones de campo de Einstein, y esta solución carece de singularidades (de hecho, en las cercanías del centro de la Tierra, la geometría del espacio- tiempo se vuelve casi plana). Como todos los planetas y estrellas conocidos en el tiempo del descubrimiento de Schwarzschild eran mucho mayores que sus correspondientes radios de Schwarzschild, resultaba tentador pensar que las propiedades de la materia realista nunca permitirían que una estrella se concentrara en un volumen tan pequeño que su radio se acercara lo más mínimo a su radio de Schwarzschild. Aunque, a lo largo de los años, se fueron acumulando argumentos que mostraban que ese postulado era erróneo, no fue hasta los años sesenta que la idea de los agujeros negros entró en la corriente principal de la física teórica.
Una característica paradójica de la solución de Schwarzschild es que, aunque pretende ser la respuesta del espacio-tiempo a una masa puntual, la masa puntual en cuestión no es parte de las ecuaciones que la métrica de Schwarzschild resuelve en realidad. Para ser exactos, la métrica de Schwarzschild resuelve las ecuaciones de campo de Einstein en el vacío, Gμν = 0, lo que quiere decir que no hay materia en ninguna parte. Al menos, no hay materia fuera del horizonte. Dentro del horizonte, las fórmulas de Schwarzschild aún se pueden usar, y sigue siendo cierto que resuelven las ecuaciones de campo de Einstein en el vacío, todo el camino hacia dentro hasta que el radio se hace cero. Justo cuando el radio es cero, la métrica de Schwarzschild se vuelve infinita de una forma muy fea. Y parece fea desde la perspectiva de cualquier observador, de modo que se trata de un problema mucho más grave que la singularidad aparente del horizonte que acabamos de describir. Podríamos pensar que la singularidad central es el lugar en que se concentra toda la masa del agujero negro. Pero debemos tener en mente que «lugar» ni siquiera es la palabra correcta; «tiempo» sería mejor, porque dentro del horizonte el radio es el tiempo, como explicaremos más abajo. Lo más probable es que la relatividad general, y hasta la propia geometría, no puedan aportar una buena descripción de la gravedad muy cerca de esa singularidad central, y que se necesite alguna otra teoría, por ejemplo una teoría cuántica de la gravedad (como la teoría de cuerdas).
Repasemos la descripción de los agujeros negros que hemos visto hasta ahora. La solución de Schwarzschild a las ecuaciones de campo de Einstein responde a la pregunta de cómo curva el espacio-tiempo una masa puntual, y el resultado es que el espacio-tiempo forma un agujero negro. Lejos del agujero negro, el espacio-tiempo está solo ligeramente curvado, y podemos entender lo que ocurre en términos de la función de lapso, regresando a la física gravitatoria newtoniana gracias a la manera en que el tiempo fluye ligeramente más deprisa cuanto más nos alejamos del agujero negro. Este enfoque se derrumba por completo en el radio de Schwarzschild, donde el tiempo, según lo mide un observador que flote allí, se detiene respecto al tiempo de un observador distante. La gente pensó al principio que esto era un fallo en la solución de Schwarzschild, o incluso en la propia teoría de Einstein, pero al final se percibió que este comportamiento solo nos dice que no tiene sentido tener un observador exactamente en el horizonte. Si seguimos hacia dentro, acabamos encontrando una singularidad de la curvatura que ni siquiera hoy entendemos por completo. En lo que sigue de este capítulo vamos a explorar más a fondo la física de los agujeros negros de Schwarzschild, preguntándonos qué les ocurre a los observadores y a los objetos que se mueven a su alrededor o caen en ellos. Incluso trataremos de la región destructiva cercana a la singularidad.
Empecemos por una pequeña historia que, en realidad, es anterior al descubrimiento de Schwarzschild. Einstein sabía que uno de los enigmas más notables de la astronomía era la precesión del perihelio de Mercurio. La órbita de Mercurio es ligeramente elíptica, como permiten las leyes de Kepler y la gravedad newtoniana. El perihelio de la órbita es el punto más próximo al Sol. Pero el eje mayor de la elipse, y por tanto también el perihelio, rota lentamente alrededor del Sol (movimiento de precesión), en la misma dirección en que órbita Mercurio. Este tipo de precesión se había estudiado de manera exhaustiva, y en tiempos de Einstein se creía que podía explicarse, en su mayor parte, por la influencia de otros planetas. El problema es que persistía una discrepancia muy pequeña incluso teniendo en cuenta todos los efectos de la gravedad newtoniana que se pudieron encontrar. Para subrayar lo pequeña que era esa discrepancia (¡y lo precisas que se habían vuelto las observaciones astronómicas del siglo XIX!), veamos los números. La precesión de la órbita de Mercurio es en realidad de solo 574 segundos de arco por siglo, y la mecánica newtoniana puede explicar unos 531 segundos de arco por siglo. La discrepancia consistía en los restantes 43 segundos de arco por siglo. Una discrepancia de 43 segundos de arco por siglo implica un cambio en el eje mayor de la elipse de Mercurio de más o menos 1/35000 de un grado por órbita. Antes de que Schwarzschild hallara su solución exacta de las ecuaciones de campo de Einstein, este pudo encontrar una aproximación lo bastante buena de la solución de Schwarzschild como para ofrecer una descripción precisa del movimiento planetario en el campo gravitatorio del Sol. Al aplicarlo a la órbita de Mercurio, sus cálculos revelaron un resultado coherente con la famosa precesión anómala de este planeta. Einstein tuvo muchas percepciones nuevas, así como algunas salidas en falso, en el camino hacia la forma final de las ecuaciones de campo en 1915, pero este resultado fue ciertamente un momento «¡eureka!», que le dio confianza en que había descubierto de verdad la teoría relativista correcta de la gravedad.
Con la métrica exacta de Schwarzschild en la mano, podemos calcular toda clase de órbitas de cuerpos masivos alrededor de agujeros negros, que difieren mucho más de las elipses de la gravedad newtoniana que la sutil precesión que hemos visto en la órbita de Mercurio. Y aun así, el cálculo pionero de Einstein contiene la semilla de la idea principal para caracterizar muchas de esas órbitas. Abandonemos por completo el sistema solar y tiremos para el centro de la Vía Láctea, donde acecha un agujero negro gigantesco. Este monstruo contiene unos 4 millones de masas solares. En realidad, no es un agujero negro de Schwarzschild, sino un agujero negro giratorio de Kerr, que es un objeto más complicado que describiremos en el capítulo 4. Para nuestra exposición actual, sin embargo, vamos a usar una licencia poética para fingir que el monstruo de la Vía Láctea es realmente un agujero negro de Schwarzschild; también vamos a ignorar cualquier otra materia que haya en la vecindad. Su radio de Schwarzschild es de unos 12 millones de kilómetros. Nuestros intrépidos observadores, Alice y Bob, deciden aparcar su nave espacial en una órbita circular con un radio de 150 millones de kilómetros desde el agujero negro. Ese es el radio de la órbita de la Tierra alrededor del Sol. Puesto que el tirón del agujero negro es mucho más fuerte que el del Sol (¡unos 4 millones de veces más fuerte!), la órbita circular que Alice y Bob ocupan es mucho más rápida que el circuito anual de la Tierra alrededor del Sol. De hecho, una vuelta entera solo les lleva unas 4 horas a Alice y Bob. En esta posición, la dilatación gravitatoria del tiempo hace que sus relojes vayan un 4 % más despacio que el de un observador muy distante.
Entonces, Alice se monta en un pequeño vehículo lanzadera. Tras soltar amarras con la nave principal, Alice se dispone a encender un pulso corto de sus motores para reducir su velocidad angular, y después apagarlos para disfrutar de una buena caída libre. Bob, por su parte, promete permanecer en su puesto de la nave principal y ver lo que le pasa a Alice. Para ayudarle a ello, Alice monta una luz intermitente en su lanzadera. Emite un destello amarillo una vez por segundo.
La gracia de este experimento mental es que, en cuanto sus motores se apagan, la trayectoria de Alice será una geodésica en la geometría del agujero negro de Schwarzschild. Como la velocidad inicial de Alice es menor que la velocidad necesaria para mantener una órbita circular, su órbita sin duda se va a sumergir de alguna manera hacia el agujero negro. De hecho, si Alice pusiera sus motores tan a tope que la lanzadera se detuviera por completo, su viaje subsiguiente consistiría en zambullirse radialmente hacia dentro, hasta ser tragada por el horizonte de sucesos. Alice es sin duda una temeraria, pero no tiene mucho interés en llegar a esa situación. Por eso preserva una parte de velocidad angular, confiando en caer en espiral hacia el agujero negro y luego volver en punto muerto hasta su radio original. Una vez allí, podrá navegar de vuelta hasta la nave principal, o podrá reducir su velocidad angular un poco más y darse otra vuelta.
Llegamos ahora al primer hecho importante sobre las órbitas de Alice: sufrirán una precesión de locura, y cuanto más profunda haga Alice su órbita, más precesión sufrirá. Incluso una órbita apenas elíptica sufrirá una precesión mucho mayor que la de Mercurio alrededor del Sol, ya que, en términos absolutos, la gravedad es mucho más fuerte donde se hallan Alice y Bob que en ninguna parte del sistema solar. Pese a ser más acusados, los efectos de precesión que pueden observar Alice y Bob se explican por unos cálculos similares a los que hizo Einstein para entender la órbita de Mercurio.
Tras haber experimentado con distintas órbitas, Alice descubre finalmente que puede hacer que su órbita tenga la precesión que ella quiera. He aquí cómo hacerlo.
Alice empieza en la nave principal, y ajusta con cuidado la velocidad inicial de modo que su órbita se hunda hasta un radio mínimo que sea un poco mayor que dos veces el radio de Schwarzschild. Luego para los motores.
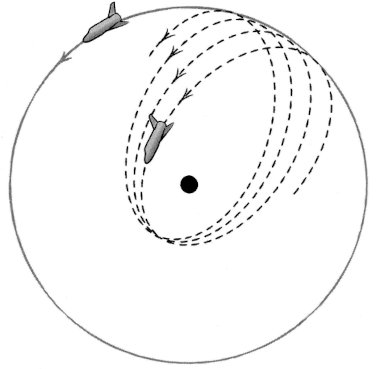
Figura 3.2. Una órbita circular (curva en línea continua), y un segmento de una órbita elíptica en precesión (curva discontinua). Una órbita elíptica newtoniana, o no relativista (que no se muestra), aparecería como una sola elipse; la precesión relativista puede considerarse, por tanto, la causa de que esa elipse, que de otra forma sería estática, rote continuamente con el tiempo, como se muestra.
Si elige bien la velocidad inicial, su lanzadera descenderá, revoloteará alrededor del agujero negro muchas, muchas veces y luego volverá a ascender hasta el radio en que empezó. El término científico para este tipo de movimiento es «órbita zoom-whirl». Alice considera que las órbitas zoom-whirl son la montaña rusa definitiva. Todo el camino es una caída libre, y en la fase de revoloteo (whirl) va muy deprisa, a unos dos tercios de la velocidad de la luz. El problema es que Alice está disfrutando de un juego peligroso. Si su velocidad inicial es un pelín demasiado pequeña, tal que su órbita se hunda por debajo de dos veces el radio de Schwarzschild, caerá en el agujero negro, a menos que le dé a los motores de la lanzadera una ráfaga de emergencia para acelerar hacia fuera y escapar. Esa ráfaga de emergencia debe aplicarse antes de que alcance el horizonte, o todo se habrá perdido.
Después de unos cuantos viajes en órbitas zoom-whirl desde altas elevaciones, Alice intenta persuadir a Bob de que baje a una órbita más cercana, de modo que él pueda sentir también el vértigo. Bob, sin embargo, es un tipo conservador, y las únicas órbitas que quiere probar con los motores apagados son órbitas circulares. Alice descubre una cosa muy extraña: cuanto más baja Bob, más lejos del agujero negro se tiene que poner ella en sus órbitas zoom-whirl sin empezar a caer (lo que requeriría una ráfaga de emergencia de sus cohetes para escapar). Por último, cuando Bob alcanza un radio igual a tres veces el radio de Schwarzschild, el juego de Alicia de precipitarse hacia abajo y volver arriba en punto muerto deja de funcionar por completo. Incluso si su velocidad inicial es solo un poquito menor que la de Bob al empezar la órbita, ella acabará atrapada en el pozo gravitatorio y se verá obligada a usar los cohetes para evitar ser tragada por el horizonte. Bob está ahora en la denominada órbita circular estable más interna (ISCO en sus siglas inglesas) del agujero negro. Existen órbitas circulares de menor radio, pero todas ellas son inestables, lo que significa que la menor perturbación puede enviar las órbitas a zambullirse en el agujero negro. Bob se niega a tomar esas órbitas menores. Son esencialmente las mismas órbitas que Alice describía durante la parte de revoloteo (whirl) de su juego zoom-whirl.
Preguntémonos ahora cómo ve Bob las señales de la luz amarilla intermitente de Alice mientras ella se entrega a sus acrobacias orbitales. Nos será de ayuda empezar dando un paso atrás y describir el denominado efecto Doppler, que ocurre incluso en ausencia de gravedad. De hecho, el efecto Doppler ni siquiera requiere la relatividad especial. Cuando oyes una ambulancia que se acerca con la sirena sonando, escucharás un perceptible descenso de la nota cuando la ambulancia te pasa. Para simplificar, imagina que, en vez de una sirena normal, la ambulancia emite un tono puro de frecuencia definida: digamos un la por encima del do medio del piano, es decir, una frecuencia de 440 hercios, o 440 vibraciones sonoras por segundo. Supongamos que la ambulancia viaja a un décimo de la velocidad del sonido. (Esto es bastante rápido para una ambulancia, pero no imposible: unos 124 kilómetros por hora). Lo que oirás mientras la ambulancia se acerca es una nota un 10 % más aguda que 440 hercios. Una vez que pasa, la nota que oirás es un 10 % más grave que 440 hercios. Este cambio de nota es el efecto Doppler. Surge porque, mientras la ambulancia se te acerca, cada vibración sonora sucesiva se genera un poquito más cerca de ti que la vibración previa. Por tanto, esas vibraciones sonoras están un poquito «apelotonadas» mientras se mueven hacia ti, y llegan a ti en una sucesión más rápida que si la ambulancia estuviera parada. Un fenómeno similar ocurre con la luz en la relatividad especial. Si, en ausencia de campos gravitatorios, Alice vuela directamente hacia Bob, las vibraciones electromagnéticas de la luz amarilla de la señal le parecerán a él más apelotonadas: más cortas en longitud de onda, y correspondientemente más altas en frecuencia. Eso significa que la luz amarilla parecerá un poco desplazada al azul. Por el contrario, si Alicia vuela alejándose de Bob, la señal de luz amarilla le parecerá a él un poco desplazada al rojo. Por la misma razón, los pulsos que Alice envía cada segundo (según el reloj de Alice) le parecerán a Bob más frecuentes de una vez por segundo si Alice se mueve hacia él, y menos frecuentes si se mueve alejándose de él. Da la impresión de que el efecto Doppler debería mezclarse con los efectos de la dilatación temporal de la relatividad especial, y esto ocurre en verdad; pero el resultado de un tratamiento relativista enteramente correcto es el que hemos descrito.
Cuando Alice describe órbitas zoom-whirl, la dilatación temporal gravitatoria tiene un efecto de desplazamiento al rojo sobre la luz que viaja desde la lanzadera hacia Bob, y este efecto se superpone al efecto Doppler.
Por el contrario, si Bob enviara un rayo de luz hacia Alicia, resultaría desplazado al azul gravitatoriamente.
Estos efectos gravitatorios se deben por entero a la tasa variable de flujo temporal en las diferentes profundidades de un pozo gravitatorio, y son variantes del fenómeno que subyace al experimento de Pound-Rebka que explicamos en el capítulo 2.
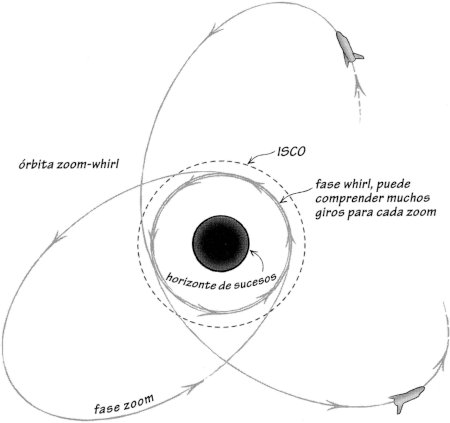
Figura 3.3. Una órbita zoom-whirl. ISCO son las siglas inglesas de órbita circular estable más interna.
Una complicación adicional es que los fotones de la señal luminosa de Alice pueden viajar en unas trayectorias más o menos complicadas en su camino hacia Bob. El escenario más simple es que Alice esté directamente debajo de Bob cuando su señal destella, justo cuando ella está en mitad de un revoloteo alrededor del agujero negro. Entonces los fotones que viajen más o menos directos hacia arriba alcanzarán a Bob, un poco desplazados al rojo debido a los efectos gravitatorios.[5] Sin embargo, si Alice está en el lado del agujero negro opuesto al de Bob cuando su señal luminosa destella, los fotones todavía pueden llegar a él, pero ¡tienen que hacer primero una finta alrededor del agujero negro! Increíblemente, esto puede suceder. Einstein incluso lo predijo. De hecho, otra confirmación temprana de la relatividad —la que otorgó a Einstein su fama mundial— fue la observación de la desviación de la luz estelar por el Sol durante un eclipse solar en 1919. Esta desviación es una versión débil de la forma en que los fotones emitidos por la lanzadera de Alice pueden serpentear desde la posición de ella, detrás del agujero negro, a medio camino alrededor del horizonte hasta alcanzar a Bob. ¡Pero eso no es todo lo que pueden hacer! Como la propia Alice, los fotones de su señal luminosa pueden encontrar órbitas especiales que les llevan todo alrededor del horizonte, incluso varias veces alrededor del horizonte, antes de encontrar su camino arriba hacia Bob. En principio, los fotones pueden incluso circular hasta la saciedad alrededor del agujero negro a un radio igual a una vez y media el radio de Schwarzschild.[6] Esta órbita circular, llamada el anillo de luz, es inestable; con todo, esta propiedad de un agujero negro es la responsable del brillante anillo de luz que bordea la «sombra» del agujero negro que los radiotelescopios están buscando actualmente, como veremos brevemente al final del capítulo 5.
En suma, Bob verá cada uno de los pulsos de Alice con alguna combinación de desplazamiento gravitatorio al rojo y efecto Doppler al rojo o al azul; más aún, Bob verá ecos débiles de cada pulso, correspondientes a la luz que viajó alrededor del agujero negro una vez, o incluso más veces, antes de escapar hacia fuera. El máximo desplazamiento al rojo será suficiente para empujar a los fotones fuera del espectro visible, bien dentro del infrarrojo, mientras que el máximo desplazamiento al azul solo bastará para poner los fotones en el extremo azul del espectro visible. En resumen, ¡Bob verá todos los colores del arco iris!
Ya hemos esquivado bastante tiempo el horizonte de un agujero negro. Es hora de cruzarlo. Alice y Bob ofrecen cada uno al otro cruzar el horizonte, pero ambos son lo bastante prudentes como para declinar la oferta, y deciden mandar una sonda satélite. Para simplificar las cosas, regresan al radio de 150 millones de kilómetros de su órbita circular original y se quedan allí mientras lanzan la sonda de manera que empieza parada y se zambulle radialmente hacia el agujero negro, sin ningún efecto zoomwhirl. Ponen la señal de luz amarilla intermitente en la sonda para poder ver lo que pasa. Debido a la combinación de los efectos gravitatorio y Doppler, los pulsos llegan con una frecuencia menor de una vez por segundo, y la luz está desplazada al rojo. La sonda en caída libre medirá un tiempo de 2638 segundos hasta alcanzar la ISCO desde su posición inicial de 150 millones de kilómetros, y luego otros 122 segundos adicionales hasta alcanzar el horizonte de sucesos. En ese momento, al menos según la relatividad general clásica, cruzará el horizonte sin ninguna fanfarria. De hecho, no hay nada especial allí que le diga a la sonda que ha cruzado. Alice y Bob, sin embargo, no la verán cruzar nunca, puesto que la dilatación gravitatoria del tiempo se hace infinita al acercarse al horizonte. Dicho de otro modo, cada pulso subsiguiente de la luz de navegación tarda cada vez más en alcanzarles y, en algún momento, un último pulso les llegará desde justo fuera del horizonte. Esto será así por muy corto que establezcan el intervalo entre los pulsos, pero quedémonos con el plan de un pulso por segundo según lo mide el cronómetro de la sonda. Supongamos que hemos organizado las cosas de modo que uno de los pulsos de la sonda se emite exactamente en el momento en que cruza el horizonte. Alice y Bob nunca verán ese pulso, aunque sí todos los anteriores. El último pulso que ven llega 3741 segundos después de que la sonda haya salido, mientras que el penúltimo llega a los 3686 segundos. Así, desde la perspectiva de Alice y Bob, el intervalo de un segundo entre pulsos se ha estirado hasta 55 segundos entre el penúltimo y el último pulso. Sus longitudes de onda estarán desplazadas al rojo por factores de 79 y 40 para el último y el penúltimo pulso, respectivamente. Si estos pulsos fueran emitidos por la sonda como una luz amarilla brillante de una longitud de onda de 570 nanómetros, Bob y Alice los detectarían como fotones infrarrojos con unas longitudes de onda de 45 y 23 micras, respectivamente.
La dilatación gravitacional del tiempo (a la que también hemos llamado desplazamiento gravitatorio al rojo) es proporcional a la inversa de la función lapso, que se hace cero en el horizonte; por tanto, la dilatación del tiempo se hace infinita allí. Esta es una forma de entender por qué el pulso que la sonda emite en el horizonte nunca llega a Alice y Bob, no hablemos ya de cualquiera de los pulsos que emite después: dentro del horizonte, la dilatación del tiempo se hace «más allá de infinito». Pero ¿qué puede significar una afirmación como esa? La sonda en caída libre no percibe nada extraño en el horizonte. Mas, si la sonda intenta acelerar de vuelta desde más allá del horizonte, fracasará en su intento. Por muy fuerte que sea el impulso que use para intentar salir de allí, no podrá siquiera alcanzar el horizonte. Ni siquiera podrá detener su movimiento hacia dentro. Esta es la propiedad fatídica del interior del agujero negro que subrayamos en el prefacio. Moverse hacia delante en el tiempo significa moverse hacia dentro en el radio. Ninguna fuerza puede tirar de un objeto para sacarlo del agujero negro, como ninguna fuerza puede tirar de nosotros para atrás en el tiempo. Los fotones de la sonda tampoco pueden hacer nada más que caer hacia dentro, una vez que la sonda ha cruzado el horizonte. La dilatación del tiempo realmente se ha hecho «más allá de infinito» en el sentido de que el tiempo dentro del agujero negro es por completo distinto que el tiempo fuera de él. El tiempo dentro del horizonte corre hacia dentro, y allí el futuro está limitado por la singularidad.
Un tiempo que apunta hacia dentro por dentro del horizonte es tan central a la física de los agujeros negros que vamos a regresar al lenguaje de la geometría diferencial para ofrecer una descripción más precisa de él. Recordemos que una métrica del espacio-tiempo tiene dos tareas: nos dice el tiempo propiamente dicho entre sucesos separados en el tiempo, y nos dice la distancia propiamente dicha entre sucesos que están separados en el espacio. Hay una forma bella de escribir una sola fórmula para la métrica del espacio-tiempo que ejecuta las dos tareas de una tacada. El truco es escribir una fórmula no para la distancia, sino para el cuadrado de la distancia entre dos sucesos cercanos. Si el cuadrado de la distancia es positivo, los dos sucesos están separados en el espacio. Si es negativo, están separados en el tiempo, y lo que habíamos pensado que era el cuadrado de la distancia es en realidad menos el cuadrado del tiempo propiamente dicho entre los sucesos. En la solución de Schwarzschild, como en cualquier solución de las ecuaciones de Einstein, la fórmula de la métrica (basada en la función lapso, el estiramiento radial y demás) es en realidad una de esas fórmulas del cuadrado de la distancia que pueden dar tanto valores positivos como negativos. Dos sucesos ligeramente separados en la dirección radial tienen una distancia al cuadrado entre ellos que es positiva fuera del horizonte, pero negativa dentro del horizonte. Este último punto es la clave: una distancia al cuadrado negativa significa que los sucesos están separados en el tiempo. En otras palabras, el radio se vuelve el eje del tiempo, mientras que el tiempo se vuelve un eje del espacio. Por extraño que suene todo esto, no hay nada raro en la curvatura de la geometría de Schwarzschild que está implicada ahí. Más bien, nuestras nociones habituales del tiempo y el radio se reconfiguran al cruzar el horizonte.
Independientemente de la manera en que el tiempo y el radio se confundan en el horizonte, nuestra idea original de radio en la solución de Schwarzschild sigue siendo válida: incluso dentro del agujero negro, el radio se puede entender aún como la circunferencia de un círculo centrado en el origen, dividida por 2π. Expresado de otra manera, el área de una esfera de cualquier radio dado en la solución de Schwarzschild es 4π veces el cuadrado del radio: la misma fórmula que aprendemos en la escuela. El verdadero significado de esta fórmula dentro del agujero negro es alarmante: el radio allí, como hemos sabido ahora, es también el tiempo, de modo que la esfera de la que estamos hablando es la extensión total de espacio en las dos direcciones angulares a un tiempo fijo. A medida que el tiempo se mueve hacia delante (lo que implica que el radio se mueve hacia dentro), la esfera se hace más pequeña. Cada vez más pequeña. Y entonces, ¡ay!, la singularidad.
Para explicar la clase de «¡ay!» que sentiríamos al acercarnos a la singularidad, tenemos que explicar las fuerzas de marea. Como Newton sabía muy bien, las mareas oceánicas que vemos aquí en la Tierra son una manifestación del tirón gravitatorio de la Luna sobre el planeta.[7] La Luna hace esto porque tira un poco más fuerte de la cara cercana de la Tierra que de la cara lejana. Este tirón desigual hace que la Tierra se elongue ligeramente en la dirección de la Luna. La Tierra entera siente ese tirón que la elonga, pero los océanos responden más a él porque el agua carece de rigidez. Las fuerzas de marea que ejerce la Luna actúan como si estuvieran tirando de la cara lejana de la Tierra en dirección opuesta a la Luna, mientras que al mismo tiempo tiran de la cara cercana de la Tierra en dirección a la Luna. Esto resulta al principio muy contrario a la intuición, puesto que sabemos que la gravedad es puramente atractiva. La clave es que las fuerzas de marea son el efecto residual después de que tengamos en cuenta el tirón medio de la Luna sobre la Tierra. Este tirón medio altera levemente el movimiento orbital de la Tierra, mientras que las fuerzas de marea solo estiran la Tierra un poquito.
Cuando la sonda cae a través del horizonte (véanse las figuras 3.4 y 3.5), en principio ya está experimentando algunas fuerzas de marea, pero no son muy fuertes, porque el agujero negro es enorme y la sonda es bastante pequeña. Pongamos que mide un metro de ancho. Pero las cosas cambian deprisa dentro del agujero negro. Como ya hemos visto, no hay ninguna cantidad de aceleración que pueda permitir a la sonda evitar la singularidad una vez que está dentro del horizonte. Resulta de hecho que, si queremos que la sonda maximice su tiempo propiamente dicho antes de su destino funesto, lo mejor que podemos hacer es no aplicarle ninguna aceleración en absoluto, sino dejarla estar en una geodésica. Entonces alcanzará la singularidad unos 27 segundos después de cruzar el horizonte. Las fuerzas de marea debidas al tirón gravitatorio del agujero negro crecerán deprisa a medida que la sonda se acerca a la singularidad, y de 10 a 100 microsegundos antes de chocar con la singularidad (el tiempo exacto dependerá de lo fuerte que sea el metal que hemos usado para construir la sonda) su casco se fracturará. Las cada vez más poderosas fuerzas de marea desharán las piezas de la sonda en trozos cada vez más pequeños, e incluso los trozos más pequeños acabarán desgarrándose en sus átomos componentes. Pero la cosa no acaba ahí. Pronto, las fuerzas de marea se hacen lo bastante fuertes para arrancar todos los electrones de los núcleos atómicos, luego romperán los núcleos en protones y neutrones libres, después en cuarks y gluones. Eso es un gran «¡ay!». No podemos decir lo que vendrá después, porque, hasta donde sabemos, los cuarks, los gluones y los electrones son partículas puntuales. Lo que sí podemos decir es que las dos direcciones angulares del espacio tridimensional están viéndose apretujadas en sí mismas, cada vez más pequeñas según nos acercamos a la singularidad, mientras que la tercera dirección espacial —que corresponde a lo que llamábamos tiempo fuera del agujero negro— experimenta un estiramiento cada vez más radical. Por tanto, todo, incluida nuestra sonda, se estruja y se estira hasta producir una línea infinitesimalmente fina.
Ahora parece que hemos explorado la solución de Schwarzschild desde el principio hasta su amargo final. Es en verdad una maravilla, que caracteriza de manera simple y precisa la geometría del espacio-tiempo curvo en la que vivimos, y al mismo tiempo nos ofrece una descripción aproximada de la geometría del espacio-tiempo que rodea al objeto más masivo de nuestra galaxia, es decir, el agujero negro colosal que ocupa su centro. Por sí mismo, un agujero negro de Schwarzschild es perfectamente estático, acechando como una araña en el centro de una red geométrica curvada. Como hemos visto, los objetos que vuelan demasiado cerca del horizonte tienen que luchar con todo su poder para escapar, y cualquier cosa que cruce el horizonte es (¡según pensamos!) enseguida digerida por las fuerzas de marea hasta producir el más minúsculo chorro de materia imaginable cayendo hacia la singularidad.
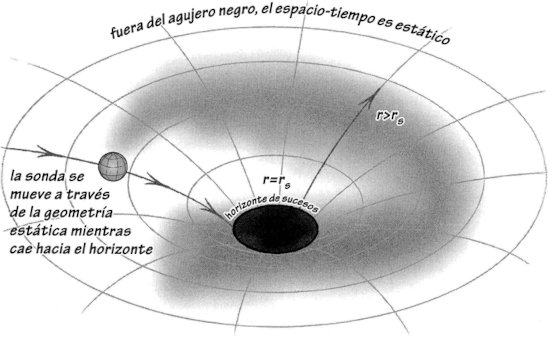
Figura 3.4. Una sonda que cae en un agujero negro: vista desde fuera del horizonte de sucesos.
En realidad, esto no es el fin de la historia de la solución de Schwarzschild. Hay otra cara de la métrica de Schwarzschild que es diametralmente opuesta a la parte del espacio-tiempo que forma el agujero negro. Se llama un agujero blanco. Aquí, empezando en una singularidad, el flujo del tiempo arrastra todo el espacio lejos de la singularidad, expulsándolo todo fuera de una frontera sin viaje de vuelta. Una vez expulsado, nunca puedes volver al agujero blanco. La razón por la que el agujero blanco debe ser parte de la solución de Schwarzschild puede intuirse a partir de la siguiente paradoja aparente. Las geodésicas, dejando aparte las singularidades, son lo que se llama técnicamente «completas»: como trayectorias de distancia óptima a través del espacio-tiempo, nunca empiezan o acaban; para la geodésica de una partícula o un fotón, siempre hay una trayectoria hacia delante o hacia atrás en el tiempo, partiendo de cualquier punto. El único sitio donde esta propiedad puede desintegrarse es cuando una geodésica acaba en una singularidad; entonces necesitamos una teoría de la gravedad cuántica para entender qué ocurre. Por supuesto, las fuerzas no gravitatorias pueden hacer que una partícula se mueva en una trayectoria que no es una geodésica, pero la geodésica está siempre allí como una trayectoria por el espacio-tiempo. Por ejemplo, si estás leyendo este libro sentado en una silla en tu café favorito, no estás siguiendo una geodésica: la presión que ejercen sobre ti la silla y el suelo lo evitan. Pero sigue habiendo una geodésica, que penetra en el suelo hacia el centro de la Tierra, y que alguna partícula u objeto no sometidos a esa presión, como un neutrino, seguirían.
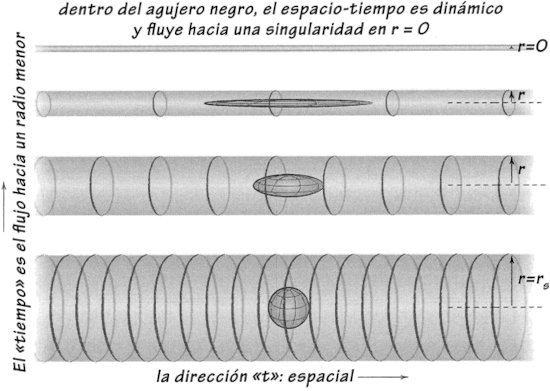
Figura 3.5. Una sonda que cae en un agujero negro: vista desde dentro del horizonte de sucesos. Dentro, la sonda resulta arrastrada por el colapso del espacio-tiempo. Según el «tiempo» avanza desde r = r en el horizonte de sucesos hacia r = 0 en la singularidad, la sonda se estira en una dirección espacial («t») hasta infinito, y se comprime en las dos direcciones espaciales esféricas hasta cero.
Con todo eso como telón de fondo, veamos ahora la paradoja aparente del espacio-tiempo de Schwarzschild. Un fotón que Alice y Bob hayan visto viajar radialmente hacia fuera desde la sonda que lanzaron hacia el agujero negro sigue una geodésica tras su emisión por la fuente de luz de la sonda. Pero la geodésica que sigue es completa, de modo que se extiende más debajo de su punto de emisión, todo seguido hasta el radio de Schwarzschild y más abajo hacia la singularidad. Piensa en ello de la manera siguiente. Supón que seguimos la trayectoria del fotón hacia atrás en el tiempo desde el punto en que Alice y Bob lo ven. Se está moviendo hacia radios cada vez más pequeños, y en algún momento del pasado alcanza la posición de la sonda. Aquí acaba la vida del fotón, pues es ahí donde la sonda lo creó. Pero la geodésica por la que se movía el fotón no acaba ahí: continúa hacia radios aún más pequeños viajando atrás en el tiempo, y en principio nada impide que un fotón real haya tomado ese camino. La trayectoria continúa así hasta el horizonte, y como el radio de Schwarzschild no es ninguna singularidad, incluso lo cruza y se prolonga hasta radios aún más pequeños que ese. Sabemos que nada puede escapar al agujero negro. Pero se diría que esa geodésica ofrece un camino para escapar, así que tenemos una contradicción.
La resolución de esta paradoja aparente es que esa geodésica no viene de la parte agujero negro de la métrica de Schwarzschild, sino de una parte por completo diferente del espacio-tiempo —el agujero blanco— donde el flujo dinámico del espacio-tiempo es exactamente el opuesto al del agujero negro. Dentro del agujero blanco, donde (o más bien «cuando») la coordenada radial es menor que el radio de Schwarzschild, ir hacia delante en el tiempo significa moverse hacia radios mayores. Así que, en vez de quedar atrapada en esta región, cualquier cosa que esté dentro se ve expulsada sin posibilidad de volver adentro. El radio cero dentro del agujero blanco es una singularidad, pero las fuerzas de marea son opuestas a las que vimos para el agujero negro: las líneas finas son ensanchadas y comprimidas hasta formar esferas.
¿Dónde está este agujero blanco? O más exactamente, ¿cuándo está? La respuesta es que el agujero blanco ocurrió en el pasado; de hecho, ocurrió arbitrariamente lejos en el pasado. En un sentido similar, el agujero negro es parte del futuro, y persistirá para siempre (si ignoramos los efectos cuánticos). Si esto resulta confuso, otra forma de pensar en todo este asunto del agujero blanco/ agujero negro es trazar una analogía con la cosmología del Big Bang. En la gravedad de Einstein, el Big Bang es una singularidad en la que nuestro universo «empezó». (Como ocurre con las singularidades de los agujeros negros, la relatividad general se deshace en la singularidad del Big Bang, así que lo que pasó realmente es un misterio). Aun cuando podemos ver los fotones que vinieron del Big Bang por todas partes, en forma del fondo cósmico de microondas, es evidente que no podemos viajar al Big Bang: no es un lugar, sino más bien un tiempo de nuestro pasado, y lo que nos queda de él es un universo en expansión. Del mismo modo, y con cierta licencia poética, podemos pensar que la solución de Schwarzschild describe un espacio-tiempo que empezó su vida como un agujero blanco, y lo que nos queda de él es un agujero negro. Desde fuera, los fotones que se produjeron en el agujero blanco parecerán venir de la región del espacio donde ahora está el agujero negro. Y es cierto, pero cuando estaban saliendo hacia el radio de Schwarzschild para al final cruzarlo, el agujero negro no estaba allí aún. Solo estaba el agujero blanco.
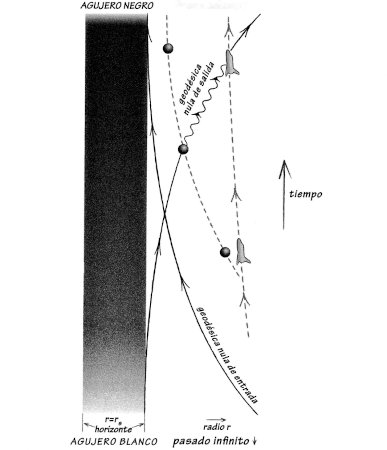
Figura 3.6. Una representación de la naturaleza completa agujero negro/agujero blanco de la solución de Schwarzschild. Desde la perspectiva de un observador externo (los observadores de la lanzadera, en este caso), todas las geodésicas nulas que salen radialmente se originan en el agujero blanco en el pasado; todas las geodésicas nulas que entran radialmente caen al agujero negro en el futuro. Sin embargo, ninguna de las dos clases de geodésicas es «vista» jamás cruzando el horizonte del agujero blanco ni el horizonte de sucesos, pues eso solo ocurre en el pasado infinito o el futuro infinito, según juzgue el observador. Un fotón saliente emitido por la sonda salta a una trayectoria geodésica nula de salida hasta que es absorbido (es decir, observado) por la lanzadera.
Para afilar nuestra comprensión del agujero negro de Schwarzschild, hemos explorado muchas posibles trayectorias para los objetos masivos (como la nave de Alice o la infortunada sonda) y para los fotones. En conjunto, todas esas trayectorias se denominan «trayectorias causales», porque es posible que un suceso espaciotemporal influya en un segundo suceso si ambos yacen en una trayectoria causal en la que el primero precede al segundo. Si ampliamos un poco nuestra visión del espacio-tiempo para incluir las trayectorias que no son causales, encontramos otra característica extraordinaria de la solución de Schwarzschild: el llamado agujero de gusano, o puente de Einstein-Rosen, que conecta el mundo en el que viven Alice y Bob a un segundo mundo con una estructura geométrica idéntica. En ese mundo, los no menos aventureros Alicia y Bradley pueden hacer los mismos experimentos en su agujero negro, y llegarían justo a las mismas conclusiones que Alice y Bob. Pero ninguna de las dos parejas sabría jamás de la existencia de la otra, porque las únicas conexiones entre sus mundos son trayectorias no causales, ya sean por el interior del agujero negro o por el del agujero blanco, que ninguna partícula, con o sin masa, puede seguir. En otras palabras, los dos mundos de fuera están desconectados causalmente, pero los de dentro se solapan. Se piensa que un agujero de gusano podría conectar dos partes del universo extremadamente alejadas, y esta noción ha hecho correr ríos de tinta en la ciencia ficción. El problema es que conectar regiones distantes del espacio-tiempo de una forma no causal no las conecta realmente en ningún sentido práctico. Que la conexión sea no causal significa precisamente que nada, literalmente, puede llegar de un lado al otro. El agujero de gusano no se puede atravesar. En la relatividad general hay soluciones de las ecuaciones de campo que describen agujeros de gusano que se puede atravesar, pero todas ellas requieren unas formas de materia «exóticas» que aún no han sido descubiertas, o que tal vez no existan en absoluto. Al final del capítulo 7 retomaremos la discusión de lo que pueden significar los agujeros de gusano «convencionales», es decir, los que no se pueden atravesar.
Pese a toda la confusión y violencia que ocurren dentro del horizonte (para no mencionar los mundos alternativos), desde fuera no se puede percibir ni un gemido. Este es un aspecto, de hecho, de una propiedad más general de los agujeros negros que se llama «teorema de no pelo» (del inglés no hair theorem). En este capítulo nos estamos centrando sobre todo en un tipo concreto de agujero negro, el agujero negro de Schwarzschild no rotatorio. En el siguiente examinaremos los agujeros negros rotatorios (llamados agujeros negros de Kerr) y los agujeros negros con carga eléctrica. Te estarás preguntando: ¿cuántos tipos de agujeros negros hay? La propuesta es que, si sabes la masa, la carga y el espín de un agujero negro, sabes exactamente su geometría completa. Esta propuesta impresionante es lo que se llama el teorema de no pelo, o a veces el teorema de la singularidad. Singular significa aquí que, si tomamos unos valores concretos para los parámetros de masa, espín y carga, habrá una y solo una forma que pueda adoptar el horizonte del agujero negro. El origen del término «teorema de no pelo» viene de una manera humorística de pensar sobre qué formas no únicas de horizonte pueden tener el aspecto de ser posibles. Quizá los agujeros negros puedan tener chichones, montañas, hoyuelos o valles. ¿Cuál sería el término general para esas características hipotéticas de los horizontes de los agujeros negros? «Pelo» es la opción favorita. Hay que reconocer que un término como «teorema de no características» está muy lejos del salero que posee la afirmación descarada «los agujeros negros no tienen pelo».
La forma de entender intuitivamente el teorema de no pelo es que los horizontes pueden tener algunas características temporales, pero estas vuelven a la nada en el tiempo que tarda la luz en dar una vuelta alrededor del anillo de luz. Demostrarlo con verdadero rigor matemático es difícil. El teorema de no pelo original, debido al físico canadiense Werner Israel, es menos ambicioso, pero es realmente un resultado demostrado con rigor. Israel probó que, si asumimos que el agujero negro se encuentra en estado estacionario (lo que implica que no hay características temporales que tuvieran que volver a la normalidad), se sigue que, en el horizonte y fuera de él, el agujero debe ser de Schwarzschild. En otras palabras, la de Schwarzschild es la única respuesta a la pregunta de qué geometrías espaciotemporales en estado estacionario y no rotatorias resuelven las ecuaciones de Einstein. Este resultado fue extendido después por otros científicos para incluir a los agujeros negros rotatorios, descritos por la solución de Kerr que examinaremos en el capítulo 4. Demostrar que las soluciones de estado estacionario son en efecto únicas (que es lo que hizo Israel) no llega a probar la afirmación más grandiosa de que todos los agujeros negros se estabilizan como soluciones de Schwarzschild o de Kerr, pero da un paso en esa dirección.
Todas las evidencias indican que las soluciones de Schwarzschild y de Kerr son en verdad los destinos estables del colapso gravitatorio. Cuando un agujero negro se forma a partir del colapso de una estrella masiva, o cuando dos agujeros negros chocan, el espacio-tiempo cercano al horizonte no está en absoluto en estado estacionario, y tiene mucha estructura interesante. Pero muy pronto toda la estructura se disipa en forma de ondas gravitatorias, y la geometría fuera del horizonte de sucesos se convierte en esa forma estacionaria perfecta y tersa descrita por una solución exacta de las ecuaciones de campo de Einstein. Lo que ocurre dentro del horizonte está mucho menos claro. La verdad es que, pese a nuestro conocimiento en principio del interior de las soluciones de Schwarzschild y de Kerr, lo que ocurre dentro del horizonte de un agujero negro formado dinámicamente es en gran parte un misterio que los científicos y los matemáticos siguen intentando descifrar.
Un agujero negro formado cuando colapsa una estrella masiva no tendrá un agujero blanco en el pasado: es la estrella lo que estaba ahí. Tampoco habrá ningún agujero de gusano hacia un segundo universo. En realidad, hay todavía un poco de misterio sobre la manera en que los agujeros negros supermasivos observados en el centro de las galaxias llegaron allí. No es inconcebible que pudieran tener algo similar a un agujero blanco en su pasado, ni que hubiera agujeros de gusano que los conectaran a otras partes del universo. Las regiones de agujero blanco en el pasado remoto de los agujeros negros supermasivos de nuestro universo tendrían que ser probablemente una modificación sustancial de los agujeros blancos de la métrica de Schwarzschild, puesto que nuestro pasado observable (el Big Bang) parece muy diferente de un agujero blanco de Schwarzschild. También es totalmente verosímil que los agujeros negros supermasivos se formaran por el colapso de estrellas masivas muy pronto en la evolución del universo y luego fueran creciendo a base de consumir materia y a otros agujeros negros hasta hacerse tan grandes como son hoy. De ser este el caso, no habría ningún agujero blanco, ni piezas de agujero de gusano pegadas a él. La conclusión es que hay un montón de evidencias observacionales de que existen regiones de agujero negro en nuestro universo, pero ninguna de agujeros blancos ni agujeros de gusano.
Hemos empezado a transmitir parte del carácter maravilloso de lo que verdaderamente es un agujero negro en la relatividad general. Y ojalá puedas apreciar ahora también por qué les llevó tanto tiempo a los científicos captar lo que en verdad representa la métrica de Schwarzschild, pese a que estuvo disponible para su exploración completa en todo su exacto detalle matemático desde poco después de que Einstein publicara sus ecuaciones de campo. Se necesitaron muchas matemáticas nuevas, incluida la solución de Kerr descubierta en 1963, antes de que la solución de Schwarzschild se pudiera tomar en serio. También fue esencial que los astrónomos empezaran a descubrir objetos en el universo que desafiaban las explicaciones convencionales, pero que podían entenderse si fueran agujeros negros. De otro modo, este dominio de la relatividad general se habría considerado una extravagancia matemática sin ninguna relevancia física (como de hecho ocurrió en los primeros tiempos de la teoría). La mayoría de nuestro entendimiento moderno de los agujeros negros cristalizó tras la muerte de Einstein, así que él no pudo apreciar por entero lo verdaderamente alucinantes que eran las consecuencias de su teoría.
Capítulo 4
Agujeros negros rotatorios
En el capítulo 3 hemos descrito todas las consecuencias gloriosas de la solución de Schwarzschild a las ecuaciones de campo de Einstein, que representa un agujero negro individual, estático y no rotatorio. Aquí examinaremos una extensión de la solución de Schwarzschild que describe los agujeros negros rotatorios. Esta extensión se llama agujero negro de Kerr en honor a Roy Kerr, el matemático que descubrió la solución. El agujero negro de Kerr es importante porque los agujeros negros del universo tienen casi siempre algo de rotación, o espín, y esto genera nuevos efectos interesantes. Uno de los principales efectos de su espín es que el espacio-tiempo es arrastrado alrededor del agujero negro a medida que gira, lo que recibe el nombre de «arrastre de marco» (del inglés frame dragging). Esto hace que las geodésicas exhiban una nueva clase de precesión. Recordemos que, en el caso de un agujero negro de Schwarzschild, la precesión es la rotación de la órbita elíptica, pero que esta rotación ocurre en el plano bidimensional y fijo de la órbita. En la solución de Kerr, el nuevo enfoque que añade el arrastre de marco es que ahora el propio plano orbital gira alrededor del eje de rotación del agujero negro, en el mismo sentido (a favor o en contra de las agujas del reloj respecto al eje) que la rotación del agujero negro. Cuanto más cerca del agujero negro está la partícula, más rápida se hace esa rotación inducida por el arrastre de marco. De hecho, en una zona llamada ergosfera, el arrastre de marco se hace tan extremo que todas las partículas —sean o no geodésicas, tengan o no masa (y por tanto incluso los fotones)— se ven forzadas a circular alrededor del agujero negro en el mismo sentido que su espín. La existencia de una ergosfera también permite que la energía rotatoria sea extraída del agujero negro; describiremos un método para hacerlo que se llama proceso de Penrose.
También presentaremos brevemente los agujeros negros con carga eléctrica, que son soluciones tanto para las ecuaciones de Maxwell del electromagnetismo como para las ecuaciones de campo de Einstein. Los agujeros negros cargados no son muy importantes para la astrofísica porque (según pensamos) la mayoría de los agujeros negros del universo son casi neutros eléctricamente. Ilustran, sin embargo, algunas ideas interesantes, en concreto la noción de que, si un agujero negro contiene demasiada carga, ¡el horizonte de sucesos deja de existir! Pero se cree que ningún proceso físico puede meter la suficiente carga en un agujero negro para erradicar su horizonte; entonces, una afirmación más correcta es que hay una carga eléctrica máxima que un agujero negro puede contener. De forma análoga, el espín de un agujero negro de Kerr no puede ser arbitrariamente grande. Los agujeros negros que tienen la carga o espín mayores posibles se llaman extremos. Aunque la carga y el espín no cambian mucho las propiedades generales del espacio-tiempo fuera del horizonte de sucesos, lo que pasa dentro es otra historia. Allí, pasado algún tiempo, el colapso del espacio- tiempo (que en un agujero negro de Schwarzschild progresa sin vacilar hasta una singularidad) se ralentiza y se revierte en el llamado horizonte interior. Aunque no es una singularidad, el horizonte interior posee algunas propiedades extrañas, por ejemplo que las ecuaciones de campo «se estropean» allí, y no pueden predecir con nitidez lo que le ocurre al espacio- tiempo más allá de allí. Si asumimos que la solución se puede extender tan suavemente como sea posible más allá de ese horizonte interior, el espacio- tiempo se expande a una nueva región con unas propiedades aún más extrañas: una singularidad de masa negativa y unas trayectorias por las que los observadores se pueden mover hacia atrás en el tiempo. En este capítulo exploramos en detalle todas estas propiedades.
Empecemos por justificar la búsqueda de un agujero negro rotatorio. En todo este capítulo, usaremos espín en el sentido clásico (la rotación sobre un eje dado), y no en el sentido mecanocuántico. El momento angular es una medida de cuánto rota un cuerpo. El espín es una medida del momento angular tanto en la mecánica clásica como en la cuántica, aunque en una y otra tiene unas características matemáticas y físicas muy distintas. El momento angular es una propiedad importante en física, entre otras cosas porque, en un sistema aislado, es una cantidad conservada. Una fuerza exterior (en forma de un par de torsión) puede cambiar el momento angular del sistema, pero, como consecuencia de la tercera ley de Newton, que es de aplicación en la mecánica cuántica y la relatividad, esto queda compensado por un cambio igual y opuesto en el momento angular del agente que ejerce la fuerza exterior. Casi cualquier planeta, estrella o agujero negro del universo tiene al menos algo de momento angular. Esto se debe a todas las dinámicas e interacciones con la materia circundante del universo que se despliega mientras el cuerpo se forma y evoluciona. No hay nada nuevo en esto que decimos: es todo mecánica clásica que se remonta a Newton y más allá. Pero implica que hay ciertas propiedades de los agujeros negros genéricos que esperamos encontrar en el universo que la solución de Schwarzschild, que describe un agujero negro cuyo momento angular es exactamente cero, deja escapar.
Lo que necesitamos entonces es una solución a las ecuaciones de campo que describa un agujero negro rotatorio. Queremos también poder recuperar la solución de Schwarzschild como el caso especial en que la rotación se hace tan pequeña que casi desaparece. Dado que la solución de Schwarzschild se publicó menos de un año después de la relatividad general, puede parecer extraño que no fuera hasta 1963 cuando Roy Kerr descubrió la largamente buscada solución rotatoria. Schwarzschild asumió una simetría esférica para derivar su solución, pero resulta que, cuando el agujero negro gira, distorsiona el espacio-tiempo vecino de tal forma que la geometría ya no puede ser simétrica esféricamente. Kerr buscó una clase menos restrictiva de soluciones, que se llaman axisimétricas. Estas soluciones tienen un solo eje de simetría alrededor del cual se puede rotar la geometría sin producir ningún cambio. Por ejemplo, un balón de rugby es axisimétrico (si ignoramos las costuras, la textura de la superficie y cualquier logotipo distintivo pintado en ella). El eje de simetría va de punta
a punta en la dirección más larga. Un balón de rugby bien lanzado girará alrededor de ese eje, y el espectador no notará el giro (aparte de que el logo se difuminará al girar). Si el lanzador es menos habilidoso, el mismo balón girará sobre cualquier otro eje y parecerá bambolearse o dar volteretas mientras vuela por el aire. Los discos y los cilindros son otros ejemplos de simetría axisimétrica, pero tienen una simetría adicional, en el sentido de que parecen axisimétricos alrededor de cualquier eje que pase por su centro.
Resulta que, si la geometría del espacio-tiempo es esféricamente simétrica, las ecuaciones de campo son drásticamente más simples que en la menos restrictiva situación axisimétrica, y esto es una de las razones de que llevara tanto tiempo descubrir la solución de Kerr. Eliminar la restricción de axisimetría complica las ecuaciones de campo todavía más, y es natural preguntarse si están por descubrir unas soluciones de agujero negro aún más intrincadas. Pero sabemos que no es así, gracias a la extraordinaria propiedad de no pelo que examinamos en el capítulo 3. Recordemos que este teorema establece que cualquier característica temporal (alias «pelo») que pueda tener un agujero negro se pierde muy deprisa, y el agujero negro se estabiliza en un estado estacionario único. En ausencia de materia o cargas eléctricas, este estado estacionario es la métrica de Kerr. Dicho de otro modo, cualquier característica no axisimétrica que pueda tener un agujero negro es necesariamente temporal. No existen soluciones de las ecuaciones de campo que den agujeros negros estacionarios más complicadas que la de Kerr.
Muchas propiedades de los agujeros negros no se ven afectadas cualitativamente por la rotación: por ejemplo, que la dilatación del tiempo ocurre entre observadores locales y distantes y se vuelve infinita al llegar al horizonte, que el horizonte es una frontera sin viaje de vuelta y el espacio- tiempo empieza a colapsarse sobre sí mismo al cruzarlo, y que las órbitas que pasan lo bastante cerca del agujero negro pueden exhibir dinámicas zoom-whirl. Sin embargo, los detalles de estos efectos pueden ser muy diferentes, y emergen fenómenos nuevos derivados de dos maneras importantes en que el espín cambia la geometría fuera del agujero negro. Primero, como acabamos de mencionar, la geometría ya no es esférica. En la métrica de Schwarzschild, las superficies de función lapso constante (lo que implica un desplazamiento gravitatorio al rojo constante) son esferas geométricas. En la métrica de Kerr, las superficies análogas se achatan alrededor de los polos, por donde pasa el eje de rotación, y se abomban en correspondencia en el ecuador. Esto es similar a la manera en que la forma de la Tierra, el Sol y otros cuerpos astronómicos masivos, que de otro modo serían esféricos, se deforman debido a su rotación. Cuanto más cerca del horizonte de sucesos del agujero negro, más perceptible es ese efecto de achatado/abombamiento, que también se hace más pronunciado cuanto más deprisa gira el agujero negro.
La segunda forma significativa en que la rotación cambia la geometría es que causa que el propio espacio-tiempo empiece a fluir alrededor del agujero negro, más deprisa cuanto más cerca del horizonte. Explicaremos más a fondo lo que queremos decir con que el espacio-tiempo «fluye», mediante la descripción de cómo esto afecta a las trayectorias geodésicas, pero una analogía adecuada sería pensar en cómo el aire fluye alrededor de un tornado. Aquí el aire representa el espacio-tiempo, y las geodésicas serían las partículas de polvo (o vacas desafortunadas) barridas por el tornado y arrastradas alrededor del ojo del huracán. En el contexto del espacio-tiempo, este efecto se llama arrastre de marco (del inglés frame dragging).
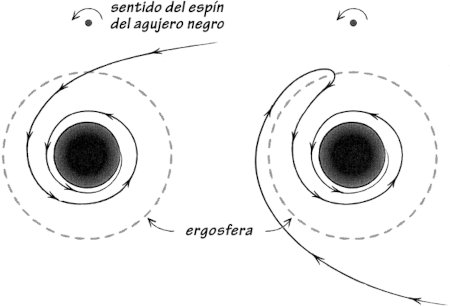
Figura 4.1. Efecto del arrastre de marco sobre las geodésicas que caen en un agujero negro de Kerr; a la izquierda (derecha), la partícula tiene un momento angular positivo (negativo) respecto al espín del agujero negro.
Esta propiedad no es exclusiva de los agujeros negros; de hecho, la rotación de la Tierra también causa un arrastre de marco, pero a unos niveles minúsculos en comparación con un agujero negro (tan pequeños que pueden ignorarse por los satélites del GPS, y que solo recientemente se han medido con los hipersensibles experimentos con satélites Gravity Probe B y LAGEOS).
Para empezar a estudiar todas las consecuencias del arrastre de marco, vamos a lanzar de nuevo a nuestras leales sondas satélites, soltándolas desde una situación de reposo a mucha distancia de un agujero negro de Kerr, para registrar su estructura geodésica. En el caso de un agujero negro de Schwarzschild, debido a que es simétrico esféricamente y no gira, no hay nada especial en identificar cualquier plano que lo seccione por el centro como su plano ecuatorial, y los dos puntos del horizonte que están directamente al norte y al sur del plano ecuatorial como sus polos: cualquier orientación de este plano sirve para ese propósito. Con un objeto rotatorio como un agujero negro de Kerr, lo más natural es definir los polos norte y sur como los puntos del horizonte conectados por el eje de rotación del agujero negro, con el plano ecuatorial yaciendo a un ángulo de 90° respecto a ese eje. Debido al arrastre de marco y a la simetría axial del agujero negro de Kerr, ahora sí importa a qué ángulo respecto al eje de rotación está la posición desde la que soltamos las sondas inicialmente. Examinemos los dos casos extremos: una sonda arrojada directamente por uno de los dos polos del agujero negro (no importa que sea el norte o el sur) y la otra por el ecuador. En un espacio-tiempo de Schwarzschild no habría diferencia: ambas sondas caerían radialmente, como vimos en el capítulo 3. Lo mismo ocurre en el espacio-tiempo de Kerr con la sonda arrojada por el polo, aunque la progresión exacta de la dilatación temporal y el desplazamiento gravitatorio al rojo, según las ve un observador distante mientras cae la sonda, será diferente. En el ecuador la historia cambia por completo. Al principio la sonda caerá radialmente, pero a medida que se acerca al horizonte, el giro del agujero negro empezará a arrastrarla alrededor de él. Vista desde la distancia, su trayectoria parecerá una espiral que se va encogiendo en el plano ecuatorial, empaquetándose en anillos cada vez más pegados entre sí alrededor del horizonte, pero sin cruzarlo nunca. La luz de la sonda sufrirá el desplazamiento al rojo y la dilatación temporal como en la solución de Schwarzschild, pero ahora parecerá venir de un punto del horizonte que está girando a una velocidad angular fija. Esta velocidad angular sería la misma para las sondas arrojadas desde cualquier ángulo, aunque cada una acabará en una posición de latitud correspondientemente distinta, y esas posiciones se extenderán por el horizonte. Observar el movimiento angular de las sondas que caen es una de las formas de medir la velocidad de rotación del agujero negro.
Desde la perspectiva de la sonda, que está cayendo desde fuera del horizonte, también ella se observaría a sí misma empezando a verse arrastrada alrededor del agujero negro. Como en el espacio-tiempo de Schwarzschild, alcanzará y cruzará el horizonte en un tiempo finito según su propio reloj. Así que hay todavía una disparidad infinita entre la tasa de flujo del tiempo de un observador que cruza el horizonte respecto a uno alejado. Más aún, en el momento en que la sonda cruza el horizonte, se habrá observado a sí misma rodeando el agujero negro solo un número finito de veces. Un observador externo nunca la verá cruzar. La sonda parecerá más bien abrazar el horizonte y rotar a su alrededor eternamente con una velocidad angular constante. Así que también hay una disparidad infinita entre las mediciones local y distante de la cantidad de vueltas que da la sonda alrededor del eje de rotación del agujero negro.
El efecto de arrastre de marco en una órbita más complicada que la caída libre ecuatorial o polar que acabamos de ver se puede entender mediante la noción de precesión del plano orbital. Junto a un agujero negro de Schwarzschild, cualquier geodésica que orbite alrededor del agujero negro se mueve en un plano bidimensional fijo que corta el origen de coordenadas del agujero negro. Lo llamamos el plano orbital. En este plano, la elipse de la órbita sufre una precesión, como describimos en el capítulo 3, pero nunca abandona el plano. Cerca de un agujero negro de Kerr, el arrastre de marco hace rotar (sufrir precesión) al plano orbital entero alrededor del eje de rotación. Lo deprisa que ocurra esta precesión depende de la velocidad de rotación del agujero negro, de lo inclinada que esté la órbita respecto al plano ecuatorial y de lo cerca del agujero negro que esté la sonda. Las órbitas ecuatoriales permanecen siempre en el plano ecuatorial, mientras que las órbitas alrededor de los polos del agujero negro experimentan la mayor precesión del plano. Una órbita que esté lejos del agujero negro mostrará muy poca precesión, independientemente de la inclinación de la órbita o de la velocidad de rotación del agujero negro. Así que, de nuevo como en los agujeros negros de Schwarzschild, muy lejos del agujero negro las dinámicas orbitales se describen bien con la física newtoniana. En el otro extremo del espectro, la precesión del plano orbital será especialmente pronunciada para las órbitas zoom-whirl, sobre todo si están ajustadas finamente. Aquí, en vez de orbitar en un círculo, la sonda trazará un patrón sobre una porción de una esfera entre una latitud fija por encima y por debajo del plano ecuatorial. Para una órbita ecuatorial esto es simplemente un círculo, pero una órbita polar llenará la superficie de la esfera con sus giros.
El arrastre de marco también influye en las no geodésicas (sondas con cohetes). Cerca del horizonte en la ergosfera, el arrastre de marco es tan fuerte que todas las trayectorias temporales y nulas son forzadas a rotar alrededor del agujero negro en la dirección de su rotación. Si uno está fuera del horizonte, pero dentro de la ergosfera, incluso si pone los cohetes a tope para moverse contra la dirección de rotación, y sin que importe lo muy intensa que sea esa fuerza, todavía se verá arrastrado alrededor del agujero negro en la dirección de su rotación. La forma de la frontera de la ergorregión, que es lo que llamamos ergosfera, es una versión achatada del horizonte, que toca el horizonte del agujero negro en los polos y se extiende hacia fuera a lo largo del ecuador (véase la figura 4.3). Cuanto más deprisa gira el agujero negro, mayor será el abombamiento ecuatorial de la ergosfera. De manera interesante, hay un límite a la velocidad de rotación que puede tener un agujero negro, y un agujero negro que gira a ese límite se llama extremo. En un agujero negro extremo de Kerr, la extensión ecuatorial de la ergosfera crece hasta dos veces el radio del horizonte. Dentro de la ergosfera, todas las partículas deben moverse en la misma dirección alrededor del agujero negro, aunque es posible que este movimiento sea más rápido o más lento en función de dónde esté la partícula en la ergosfera y de si actúan sobre ella otras fuerzas aparte de la gravedad. Si nos acercamos al horizonte, un observador externo verá que la dilatación del tiempo y el arrastre de marco trabajan juntos para hacer que todas las trayectorias de las partículas, geodésicas o no, giren con la misma velocidad angular que el horizonte.
¿Por qué un agujero negro no puede girar con una velocidad arbitrariamente alta? Matemáticamente, las soluciones de Kerr pueden tener más velocidad de rotación que la extrema, pero entonces el horizonte se desvanece (es decir, que el objeto ya no es un agujero negro). Estas soluciones son problemáticas en varios sentidos; uno es que, en ausencia de horizonte, la singularidad del espacio-tiempo queda expuesta al universo exterior. ¿Qué problema supone esto? Nada, en teoría, pero la relatividad general clásica no puede predecir lo que le pasa al futuro causal de una singularidad, y por tanto no sabemos ni lo que significa «quedar expuesto» en este caso. Usando cálculos modelo y simulaciones, los científicos han intentado hacer girar agujeros negros más que el extremo (o formar singularidades sin horizonte, para empezar), pero en sistemas que imitan lo que podría existir ahí fuera en el universo, ninguno ha tenido éxito. Este fracaso fue anticipado hace décadas por el físico y matemático británico sir Roger Penrose, que formuló la Conjetura de la Censura Cósmica, que propone que todas las singularidades que pueden formarse en la naturaleza están «vestidas» por horizontes de sucesos. Desde la perspectiva de un físico, esta es una regla desafortunada si la naturaleza la impone. La razón es que creemos que las singularidades del espacio-tiempo predichas por la relatividad general son lugares donde la teoría se deshace, y que lo que ocurre realmente debe describirse con una nueva teoría, llamémosla gravedad cuántica. Ver esos sucesos nos ofrecería una penetración sin precedentes en lo que realmente es la gravedad cuántica, pero si solo ocurren escondidos tras un horizonte de sucesos, se acabó nuestra suerte. Volveremos a este asunto cuando discutamos las colisiones de agujeros negros (capítulo 6).
Recapitulemos brevemente. La rotación complica la estructura geométrica de los agujeros negros de Kerr en comparación con el caso de Schwarzschild, y añade un nuevo giro a las trayectorias de partículas que están cerca del horizonte: el arrastre de marco. Imaginemos que arrojamos un conjunto de sondas con luces intermitentes hacia un agujero negro desde todas las direcciones. Un observador externo nunca las verá cruzar el horizonte; más bien le parecerán decelerar a medida que se aproximan a él, y congelarse en una pauta fija, con sus luces llegando cada vez más infrecuentes y más desplazadas al rojo. Con un agujero negro de Kerr observaremos un espectáculo similar, salvo que, debido al arrastre de marco, este patrón fijo rotará eternamente con el periodo de rotación del agujero negro. Lo que queremos describir a continuación es cómo la rotación de los agujeros negros de Kerr ofrece un mecanismo para permitir que se pueda dragar energía de ellos.
Recordemos que, en la relatividad, la masa equivale a la energía (E =mc2). Una forma común de energía es la energía cinética, y lo que la equivalencia E =mc2 implica es que la materia puede convertirse en otras formas de materia más energía cinética, y viceversa (por ejemplo, en una reacción nuclear). En un agujero negro, toda la materia equivalente a energía está atrapada, al menos si ignoramos los efectos cuánticos que expondremos en el capítulo 7. Sin embargo, la rotación es una forma de energía cinética, y esa sí puede extraerse de un agujero negro. Hay que darse cuenta de que nada en esa extracción vendría del interior del agujero negro; es la energía rotacional del espacio-tiempo que rodea al agujero negro lo que se puede explotar. Una forma de hacerlo es el llamado proceso de Penrose, en honor a su descubridor, el mismo Penrose que formuló la Conjetura de Censura Cósmica. Funciona de la siguiente forma (véase la figura 4.2). Una estación espacial que órbita alrededor del agujero negro, a cierta distancia, envía una nave de extracción de energía hacia el agujero negro a lo largo de una geodésica que entra en la ergorregión. Las geodésicas ecuatoriales son por tanto las mejores para este fin. Una vez en la ergorregión, la nave apunta cuidadosamente y lanza un proyectil pesado a muy alta velocidad en la dirección opuesta a la rotación del agujero negro. Por supuesto, debido al arrastre de marco, tanto el proyectil como la nave parecerán estarse moviendo alrededor del agujero negro en el mismo sentido; la nave simplemente estará moviéndose más deprisa. Es importante que el proyectil sea pesado, con una masa comparable a la de la nave por sí sola, porque así se impartirá a la nave un gran retroceso. El proyectil debe apuntarse de modo que ese retroceso desplace la nave a una órbita que la mande de vuelta a la estación espacial, mientras que el proyectil cae en el agujero negro. Si se le dispara con la suficiente velocidad, el proyectil tendrá un momento angular de signo opuesto al del agujero negro. Cuando el proyectil es absorbido por este, el giro del agujero negro decrecerá en la cantidad correspondiente. Pero el momento angular total se conserva, y por tanto (de nuevo la tercera ley de Newton) la nave debe haber ganado esa misma cantidad de momento angular. Y eso significa que la nave tiene que haber ganado energía cinética.
En realidad, nada de lo expuesto hasta ahora sobre el proceso de Penrose es inusual o extraordinario. De hecho, si repetimos este experimento mental sustituyendo el agujero negro por el Sol, se aplicarían los mismos argumentos de conservación. El Sol, al absorber al proyectil, vería reducido su momento angular, mientras que la nave gana una cantidad equivalente y por tanto gana energía cinética. En este caso, sin embargo, la nave nunca puede ganar la suficiente energía cinética para compensar el equivalente en energía de la masa perdida con el proyectil. En el agujero negro rotatorio ocurre algo inusual: si la órbita se modula con cuidado y el proyectil se apunta bien, la nave puede ganar tanta energía cinética que compense con creces la pérdida del proyectil. No resulta nada fácil dar con una explicación intuitiva de todo lo que pasa en el caso del agujero negro. En vez de eso, vamos a describir una pieza clave del cálculo que ilustra otra propiedad extravagante de la deformación extrema del espacio y el tiempo que ocurre cerca de los agujeros negros, y explica por qué es esencial para el proceso de Penrose que el proyectil se dispare desde dentro de la ergosfera.
En primer lugar, necesitamos hacer una breve digresión para hablar de la energía de un objeto en órbita. La energía puede adoptar distintas formas. La energía en reposo es la energía de la propia masa, y es a la que se refiere la ecuación E = mc2. También hay energía cinética, que es la energía del movimiento. Y, al menos en la gravedad newtoniana, está la energía potencial, que describe a qué profundidad de un pozo gravitatorio se sitúa un objeto. La energía potencial es negativa porque es la energía que tendríamos que añadir a un objeto inicialmente estacionario para levantarlo del pozo gravitatorio en el que lo habíamos encontrado. En la gravedad newtoniana, la energía mecánica total de un objeto en órbita (es decir, la suma de sus energías cinética y potencial) no cambia nunca, suponiendo que la única fuerza que actúa sobre el objeto es el tirón gravitatorio de una gran masa estacionaria como el Sol. Cualquier cambio en la energía cinética viene compensado por un cambio igual y opuesto en la energía potencial. En la relatividad general, es más complicado dar una definición de energía potencial que tenga sentido en todos los espacio-tiempos, pero, al menos para un objeto que se mueva en la geometría de Kerr, sí es posible hacerlo. El resultado es coherente con la definición de Newton lejos del agujero negro. Así que el resultado es que, alrededor de un agujero negro, es posible definir la energía mecánica total de un objeto en órbita (que ahora incluye su energía de masa en reposo) y, como el objeto en órbita sigue una geodésica, esta energía total no cambia nunca.
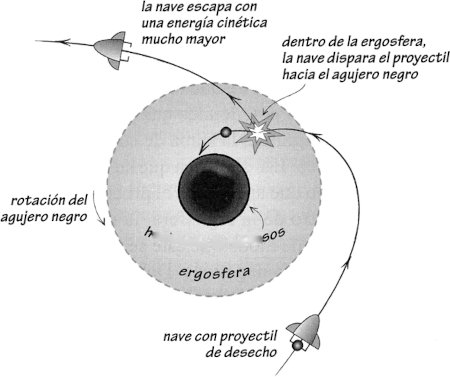
Figura 4.2. Ilustración del proceso de Penrose, visto en el sentido del eje de rotación del agujero negro hacia el plano ecuatorial, donde orbitan la nave extractora y el proyectil.
Ahora es cuando entra en escena la extraña propiedad del arrastre de marco. Hay órbitas geodésicas en la geometría de Kerr, enteramente confinadas dentro de la ergosfera, con la propiedad de que las partículas que las siguen tienen energías potenciales que son tan negativas que superan, en magnitud, la suma de su masa en reposo y su energía cinética. Eso significa que su energía total es negativa. Esto es lo que aprovecha el proceso de Penrose: mientras está dentro de la ergosfera, la nave extractora dispara el proyectil de modo que este se mueve en una de esas órbitas de energía negativas. Debido a la conservación de la energía, la nave extractora gana la suficiente energía cinética para compensar con creces el equivalente en energía de la masa en reposo que partió con el proyectil, más el equivalente positivo de la energía negativa neta del proyectil. Puesto que el proyectil se acabará perdiendo en el agujero negro, sería una buena idea fabricarlo con productos de desecho. El agujero negro no solo los engullirá enteros sin la menor queja, sino que nos devolverá más energía de la que pusimos. ¡Eso sí que es energía verde!
La cantidad máxima de energía que se puede extraer de un agujero negro de Kerr depende de lo rápido que gire. En el caso extremo (lo máximo que el agujero negro puede girar), cerca del 29 % de su energía está en la rotación del espacio-tiempo. Eso puede parecer poca cosa, pero recuerda que esto es energía equivalente a su masa en reposo: en comparación, los reactores de fisión nuclear cosechan menos de la décima parte de un 1 % de la energía equivalente a la masa en reposo.
La geometría del espacio-tiempo dentro del horizonte de un agujero negro en rotación es drásticamente diferente del espacio-tiempo de Schwarzschild. Sigamos a nuestra sonda que cruza el horizonte y veamos qué ocurre. Al principio las cosas parecerían similares al caso de Schwarzschild. Como entonces, el espacio-tiempo empieza a colapsarse, todo se ve arrastrado con él hacia radios más y más pequeños, y las fuerzas de marea empiezan a crecer. Pero en el agujero de Kerr, antes de que el radio se haga cero, el colapso se ralentiza y empieza a revertirse. En agujeros negros que giran deprisa, esto ocurrirá mucho antes de que las fuerzas de marea se hagan lo bastante intensas para amenazar a la sonda. Para intuir por qué ocurre esto, recuerda que, en la mecánica newtoniana, la rotación es responsable de lo que se llama fuerza centrífuga. Esto no es una fuerza fundamental, sino una consecuencia de la forma en que se mueven todos los constituyentes de la materia cuando están en una configuración rotatoria, y de la forma en que las fuerzas fundamentales dentro de la materia tienen que ajustarse para mantener el giro. El resultado se puede ver como algo que produce una fuerza efectiva hacia fuera. Si has tomado una curva cerrada en un coche rápido, has sentido esta fuerza. Del mismo modo, si has montado alguna vez en un tiovivo, sabrás que, cuanto más deprisa gire, más fuerte te tienes que agarrar a la barra de seguridad para aguantar, y si la sueltas saldrás despedido hacia fuera. La analogía no es perfecta para el espacio-tiempo, pero evoca la idea correcta. El momento angular del espacio-tiempo de un agujero negro de Kerr aporta una fuerza centrífuga efectiva que se opone a la pura atracción gravitatoria. Mientras el colapso dentro del horizonte canaliza el espacio-tiempo hacia radios más y más pequeños, la fuerza centrífuga se hace más y más intensa y llega a un punto en que es capaz de contrarrestar y revertir el colapso gravitatorio del espacio-tiempo.
En el momento en que el colapso llega a detenerse, la sonda alcanza el llamado horizonte interior del agujero negro. Las fuerzas de marea son suaves en ese punto, y a la sonda solo le supone una cantidad finita de tiempo llegar allí tras haber cruzado el horizonte de sucesos. Sin embargo, el mero hecho de que el colapso del espacio-tiempo se haya detenido no significa que se hayan acabado nuestros problemas y que la rotación haya curado de alguna manera la singularidad del interior de un agujero negro de Schwarzschild. Nada más lejos de la realidad. A mediados de los años sesenta, de hecho, Roger Penrose y Stephen Hawking demostraron un conjunto de teoremas de singularidad que establecen que, cuando quiera que ocurra un periodo de colapso gravitatorio, por muy breve que sea, debe haber algún tipo de singularidad que se forme a la postre. En el caso de Schwarzschild, se trata de una singularidad global y aplastante que se desarrolla a lo largo de todo el espacio interior al horizonte. En la solución de Kerr, la naturaleza de la singularidad es muy diferente y contraria a la intuición, dado lo que sabemos sobre el caso de Schwarzschild. Cuando la sonda alcanza el horizonte interior, la singularidad de Kerr se revela, pero aparece en el pasado causal de la vida de la sonda. Es como si la singularidad hubiera estado allí siempre, pero su influencia alcanzara solo ahora a la sonda. ¿Suena extraño? Lo es. Y hay varias cosas que fallan con la imagen del espacio-tiempo que nos indican que esta respuesta no es la definitiva.
El primer problema con que la singularidad se da a conocer al pasado de un observador que alcanza el horizonte interior es que, entonces, las ecuaciones de campo de Einstein fracasan en predecir de manera única y exclusiva lo que le ocurre al espacio-tiempo más allá de ese horizonte. El problema es que, en cierto sentido, de la singularidad puede salir cualquier cosa. Podemos suponer que una teoría de la gravedad cuántica podrá decirnos lo que realmente sale de allí, pero las ecuaciones de Einstein no se pronuncian en absoluto sobre esta cuestión. Por curiosidad, describiremos más abajo lo que pasa si exigimos que, al cruzar el horizonte, el espacio- tiempo sea tan suave como sea matemáticamente posible (si las funciones métricas son lo que los matemáticos llaman «analíticas»), pero no hay una buena justificación física para esta suposición. De hecho, el segundo problema con el horizonte interior indica justo lo contrario: que en un universo real, en el que hay materia y energía fuera del agujero negro, el espacio-tiempo se vuelve más bien no suave en el horizonte interior, y desarrolla allí una singularidad análoga a un pliegue o una arruga. Esto no es tan devastador como la singularidad de fuerza de marea infinita de la solución de Schwarzschild, pero como mínimo suscita dudas sobre la historia de la extensión suave y analítica. Quizá esto sea buena cosa, porque la extensión analítica cuenta una historia verdaderamente extraña.
Antes de meternos en esa extraña teoría, vamos a explicar por qué la materia exterior al agujero negro puede afectar de manera tan drástica al horizonte interior. El asunto se reduce a la disparidad del flujo del tiempo dentro y fuera, y a cómo la reversión del colapso por la rotación del espacio-tiempo afecta a esa disparidad. Recuerda que, en el espacio-tiempo de Schwarzschild, esta disparidad es responsable del desplazamiento al rojo y la dilatación temporal infinitos que perciben los observadores externos, y de por qué estos nunca pueden ver que nada cruce el horizonte. Esto sigue siendo cierto para Kerr, con el ángulo añadido que introduce el arrastre de marco. En cualquier caso, los observadores externos nunca pueden ver más allá del horizonte de sucesos, y por tanto no pueden ver el drama que se representa en el horizonte interior. La clave para entender lo que ocurre allí es hacerse la pregunta contraria: ¿qué ve la sonda cuando mira atrás hacia el universo exterior mientras cae hacia el horizonte interior? Primero, los efectos del flujo temporal son opuestos a los que ve un observador externo que mira hacia dentro. La sonda percibirá una contracción del tiempo (es decir, que los sucesos de fuera parecerán desarrollarse cada vez más rápido). También habrá un desplazamiento al azul gravitatorio, por el que la frecuencia de la luz proveniente de esos sucesos se desplazará hacia longitudes de onda más cortas, o hacia el extremo azul del espectro
electromagnético. Esto es similar a lo que la sonda habría visto al acercarse al horizonte de sucesos. Al alcanzar el horizonte de sucesos, cabría pensar que la contracción del tiempo y el desplazamiento al azul observados se hacen infinitos, como un reflejo exacto de la dilatación del tiempo y el desplazamiento al rojo infinitos que ve un observador externo. Esto es casi cierto para una sonda que pueda usar un poderoso cohete para flotar muy cerca del horizonte de sucesos, pero la experiencia de una sonda que atraviese el horizonte de sucesos en caída libre es muy diferente. Caer a través del horizonte de sucesos produce un gran efecto Doppler que, en parte, contrarresta la contracción temporal gravitatoria, y una sonda en trayectoria de caída libre que vuelva la vista atrás no verá, en realidad, nada que se salga mucho de lo ordinario mientras cruza el horizonte. Una vez dentro, sin embargo, la reversión del colapso del espacio-tiempo producida por el giro del agujero negro literalmente decelera la sonda. Cuando la sonda alcanza el horizonte interior, el efecto Doppler deja de contrarrestar los efectos gravitatorios sobre el flujo del tiempo, y la contracción del tiempo/desplazamiento al azul se vuelve en efecto infinita. En otras palabras, en una cantidad finita de su tiempo propiamente dicho, ¡la sonda podrá «ver» todo el tiempo infinito de la evolución del universo exterior! Bueno, no exactamente, que es por lo que hemos puesto ver entre comillas. El problema aquí es que los fotones de longitud de onda más corta tienen más energía y, antes de alcanzar el horizonte interior, los fotones resultarían desplazados al azul hasta unas energías tan altas que incinerarían una sonda hecha de cualquier material conocido. Este fenómeno se ha denominado singularidad de la hoja azul, y uno puede imaginar por qué esto pone en cuestión las hipótesis de que el horizonte interior es suave, salvo para el entorno esterilizado de un agujero negro de Kerr perfecto en el vacío, sin ningún fotón ni materia en el espacio-tiempo.
Con esta advertencia en mente, examinemos la extraña historia de hacer la extensión matemática lo más suave posible a través del horizonte interior. Al cruzar este horizonte, la sonda entra en una nueva rama del universo. En esta parte del universo la singularidad es siempre visible, y no hay horizonte de sucesos. La singularidad tiene la estructura de un anillo giratorio, con curvaturas y fuerzas de marea que se hacen infinitas al acercarse a él. Sin embargo, a diferencia de la singularidad de la solución de Schwarzschild, que ocurre en un momento del tiempo en el futuro de todas las trayectorias entrantes, la singularidad en anillo de Kerr está en una posición espacial concreta y puede ser esquivada por la sonda. La sonda puede hacer esto de un par de formas. Una es empezar a viajar hacia fuera, hacia radios mayores de nuevo, más allá de la posición radial donde estaba el horizonte interior. En este escenario, el espacio-tiempo canaliza la sonda hasta una región de agujero blanco del espacio-tiempo. La sonda resulta eyectada hacia fuera mientras esta parte del espacio-tiempo evoluciona como una nueva región de agujero negro de Kerr, con idénticas rotación y masa que aquel cuyo horizonte de sucesos cruzó la sonda inicialmente. La sonda no puede regresar nunca al agujero blanco, porque, al igual que en el caso de Schwarzschild, el agujero blanco está ahora en su pasado, y solo queda el nuevo agujero negro. Sin embargo, la sonda podría continuar en este tipo de movimiento para siempre, zambulléndose en el nuevo agujero negro, cruzando su horizonte interior, luego escapando de vuelta a través del siguiente agujero blanco hasta otra región más de agujero negro. La extensión analítica de Kerr da por tanto una secuencia infinita de universos de agujero negro conectados por agujeros blancos.
Una vez que cruza el horizonte interior, la otra opción que tiene la sonda es proseguir hacia dentro y pasar a través de la singularidad en anillo. Vale, ¿y qué?, simplemente ha pasado por el aro. ¿No podría haber rodeado el aro para acabar en el mismo sitio? Asombrosamente, la respuesta es no. La exigencia de suavidad máxima requiere que, tras atravesar el anillo, la sonda emerja en otra región distinta del universo. Esta región también se puede describir con la métrica de la solución de Kerr con la misma velocidad de rotación, pero ahora con la masa del agujero original de Kerr con signo menos. En otras palabras, el espacio-tiempo tiene una singularidad desnuda de masa negativa. Allí, la fuerza gravitatoria efectiva producida por la singularidad es en realidad repulsiva, y las geodésicas «caen» alejándose de ella. Y, lo que es aún más extravagante, hay una región del espacio-tiempo que tiene lo que se llaman curvas temporales cerradas. Un anillo es un ejemplo de curva cerrada: tiene una longitud finita y, empezando en cualquiera de sus puntos, viajar esa distancia le devuelve a uno al punto de partida. Pero las curvas cerradas «normales» son de tipo espacial, no temporal. Si viajas alrededor de un anillo, también te estás moviendo hacia delante en el tiempo, y así, cuando vuelves al punto de partida estás en la misma posición espacial, pero en el futuro respecto a cuando partiste. Esto es una curva de tipo temporal, pero no está cerrada. La cosa cambia con una curva temporal cerrada: cuando vuelves a la posición de partida, estás realmente en el mismo suceso espaciotemporal del que partiste.
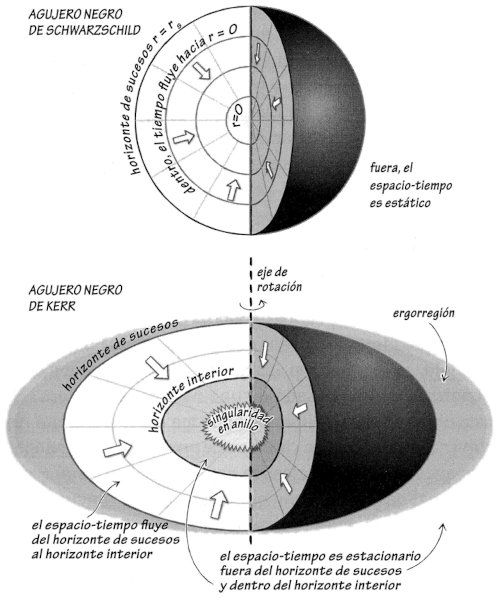
Figura 4.3. Imagen esquemática de la estructura interna de los agujeros negros.
Esencialmente, lo que tenemos en esta región de curvas temporales cerradas es una máquina del tiempo. Si estás lejos de la singularidad, no hay presente ninguna curva temporal cerrada y, aparte de la naturaleza repulsiva de la singularidad, el espacio-tiempo parecerá muy normal. Sin embargo, hay trayectorias que puedes seguir (no son geodésicas, así que necesitarás un cohete) que pueden llevarte a la región de curvas temporales cerradas. Una vez allí, puedes moverte en cualquier dirección de la coordenada t que mide el tiempo de los observadores distantes, pero tú siempre te estarías moviendo hacia delante según tu tiempo propiamente dicho. De modo que puedes viajar a cualquier t que desees y luego regresar a la parte distante del espacio-tiempo, incluso llegando antes de que salieras. Por supuesto, ahora se nos apelotonan todas las paradojas asociadas con el viaje en el tiempo: por ejemplo, ¿qué pasaría si acabaras tu pequeño viaje y convencieras a tu yo pasado de que no lo emprendiera? Si esta clase de espacio-tiempos pueden existir, y cómo resolver las paradojas en caso de que puedan, son cuestiones que quedan fuera del alcance de este libro. Sin embargo, y al igual que ocurría con el problema de la singularidad de la hoja azul en el horizonte interior, hay pistas en la relatividad general que indican que las regiones del espacio-tiempo con curvas temporales cerradas son inestables y pueden volverse singulares si uno intenta poner cualquier materia o energía en una de esas curvas. Más aún, en un agujero negro rotatorio formado en nuestro universo, la propia singularidad de la hoja azul puede evitar, ya de entrada, que se forme la región de masa negativa (y todos los demás universos de Kerr alcanzados a través de agujeros blancos). En cualquier caso, es bien curioso que la relatividad general exhiba unas soluciones tan extrañas. Lo más fácil es descartarlas como patológicas, pero recuerda que Einstein y muchos de sus contemporáneos hicieron lo mismo con los agujeros negros.
Acabaremos este capítulo con un breve tratamiento de los agujeros negros cargados. Hemos mencionado que los agujeros negros no tienen «pelo». En otras palabras, no dejan ninguna pista en la estructura del espacio-tiempo que te pueda indicar lo que ha entrado en ellos. En cierto sentido, tienen mala memoria y solo pueden recordar la masa total y el momento angular de las cosas que consumen. Pero ¿qué pasa si arrojas un electrón dentro del agujero negro? Si el agujero negro lo olvidara, ¿qué pasa con la carga eléctrica? ¿No violaría eso la conservación de la carga, una propiedad sagrada de la física de partículas? Sí que lo haría. Pero, por fortuna, los agujeros negros pueden tener pelo adicional para las fuerzas de largo alcance relacionadas con las cargas conservadas. El electromagnetismo describe esas fuerzas. Las soluciones a las ecuaciones de Maxwell del electromagnetismo combinadas con las de las ecuaciones de campo de Einstein, que describen los agujeros negros rotatorios y cargados, se llaman métrica de Kerr-Newman. Están caracterizadas solo por la masa, el espín y la carga eléctrica. En realidad, la solución que describe un agujero negro cargado no rotatorio se descubrió muchos años antes. Se llama agujero negro de Reissner-Nordström en honor de sus descubridores. La razón de que la solución de Reissner-Nordström se descubriera mucho antes es que, al igual que en la solución de Schwarzschild, el espacio- tiempo no rotatorio del agujero negro de Reissner-Nordström es esféricamente simétrico, y así las ecuaciones de campo son mucho más simples matemáticamente. Curiosamente, la carga, incluso por sí misma, otorga a la estructura interior de los agujeros negros unas propiedades similares a las que le otorga el momento angular. Hay horizontes interiores, singularidades de la hoja azul y múltiples universos conectados. Pero, sin rotación, la singularidad de anillo se contrae a un punto, y por tanto no hay regiones de masa negativa con curvas temporales cerradas en los espacio- tiempos de Reissner-Nordström.
Otra similitud con la rotación es que el campo eléctrico de un agujero negro cargado produce una presión efectiva hacia fuera similar a la fuerza centrífuga de la solución de Kerr. Esta presión efectiva tiene relación con la existencia de un horizonte interior en la solución de Reissner-Nordström. De modo que hay una cantidad máxima de carga para la que el agujero negro se vuelve extremo, y más allá de la cual el horizonte de sucesos deja de existir, revelando una singularidad desnuda. Como con la rotación, parece difícil o imposible sobrecargar un agujero negro. Hacerlo requeriría añadir más y más de la misma carga al agujero negro. Pero las cargas iguales se repelen, y al final la repulsión se volvería tan fuerte que no se podría meter allí una sola carga más. Se piensa que, en nuestro universo, todos los agujeros negros son eléctricamente neutros. Si de algún modo atraparan una gran cantidad de carga, enseguida atraerían iones de la carga opuesta del medio interestelar y quedarían neutralizados.
Capítulo 5
Agujeros negros en el universo
Los años sesenta y setenta, apodados la edad de oro de la relatividad general, presenciaron una revolución de nuestro entendimiento de los agujeros negros. El cuadro teórico moderno de un agujero negro que hemos visto en los capítulos anteriores se reveló en gran parte en esos años, usando unas matemáticas nuevas y unas percepciones brillantes de muchos investigadores, entre ellos John Wheeler, Kip Thorne, Werner Israel, Roger Penrose y Stephen Hawking. Al mismo tiempo, los astrónomos estaban escrutando cada vez con más profundidad en el universo con cada vez más sensibles telescopios ópticos y de radio, y obteniendo los primeros vislumbres del aspecto que ofrece el universo en la gama de los rayos X. Se descubrieron dos nuevas clases de objetos astronómicos por entonces completamente misteriosas —los cuásares y las binarias de rayos X— que hoy pensamos que son el hogar de agujeros negros.
Una binaria de rayos X es un sistema estelar compuesto por una estrella ordinaria que órbita muy cerca de una compañera invisible, que se piensa que es una enana blanca, una estrella de neutrones o un agujero negro. Se cree que la transferencia de materia desde la estrella observada hacia la compañera invisible explica la intensa emisión de fotones de rayos X que emiten estos sistemas.
Si no podemos ver a la compañera invisible, ¿cómo sabemos que está allí? La respuesta es por el desplazamiento Doppler de los fotones que se originan en la atmósfera de la estrella observada, causado por el movimiento orbital de la binaria. Los átomos y las moléculas absorben y emiten fotones solo a unas longitudes de onda concretas, llamadas líneas espectrales, y el conjunto de líneas es una propiedad única y distintiva de cada átomo o molécula particular. Por ejemplo, las luces callejeras de vapor de sodio son de un amarillo brillante, ya que la emisión predominante viene de dos líneas espectrales del sodio con 589,0 nanómetros y 589,6 nanómetros. Cuando los astrónomos miran a una estrella, pueden ver muchas líneas espectrales de absorción y emisión que provienen de los átomos y moléculas de la atmósfera de la estrella. Si la estrella es parte de un sistema binario, esas líneas alternarán un desplazamiento al rojo y otro al azul de forma periódica, debido al movimiento orbital de la estrella alrededor de su compañera. Este desplazamiento alterno al rojo y al azul es el mismo fenómeno que vimos en conexión con las órbitas zoom-whirl en el capítulo 3.
Vale, ahora sabemos que una binaria de rayos X es una binaria pese a que solo vemos una estrella. Pero ¿cómo sabemos que en algunos casos como Cyg X-l (una brillante binaria de rayos X en la constelación del Cisne, o Cygnus) la compañera es un agujero negro? Un escéptico podría decir, tal vez, que la compañera no es más que una estrella demasiado tenue para poder verla. La réplica a este escéptico es en realidad muy simple: la compañera invisible es demasiado masiva para ser una estrella tenue. Para desarrollar esta respuesta simple, tenemos que hilvanar algunas observaciones adicionales, las leyes de Kepler del movimiento orbital y la teoría de la evolución estelar. Vamos primero con las observaciones. A partir del desplazamiento Doppler, no solo podemos deducir que la estrella está en un sistema binario, sino también las propiedades detalladas de su órbita. El periodo de oscilación de las líneas espectrales es exactamente el periodo orbital de la binaria. La manera precisa en que el desplazamiento Doppler varía a lo largo de un solo periodo revela la elipticidad de la órbita. La amplitud del desplazamiento nos da un límite inferior para la velocidad máxima de la estrella (sería la verdadera velocidad máxima si estuviéramos viendo la órbita de canto, pero los astrónomos solo pueden deducir la inclinación de la órbita en raras circunstancias). Combinando estas observaciones con las leyes de Kepler del movimiento orbital obtenemos un límite inferior para la suma de las masas de las dos compañeras de la binaria. Podemos entonces deducir la masa de la compañera invisible si podemos calcular la masa de la estrella visible. Aquí es donde entra en escena la teoría de la evolución estelar. Resulta que, una vez que sabemos la temperatura superficial y la luminosidad de la estrella (que pueden establecerse por observación directa), nuestro conocimiento general de la evolución estelar basta para darnos una estimación bastante precisa de la masa.
La vida de una estrella está dirigida por una competición de fuerzas: la fuerza atractiva, hacia dentro, de la gravedad contra otras fuerzas que presionan hacia fuera. En realidad, esto también vale para un planeta como la Tierra, pero, a diferencia de los planetas, una estrella es demasiado masiva para que la presión generada por la materia fría equilibre a la gravedad, al menos al principio de su vida.[8] El progenitor de una estrella es una nube de gas, sobre todo hidrógeno. A medida que esa nube se colapsa, la presión y la temperatura de su núcleo crecen hasta que la temperatura se hace tan alta que empieza la fusión nuclear del hidrógeno. La fusión libera una cantidad tremenda de energía en forma de fotones y neutrinos, lo que a su vez calienta más el núcleo hasta el punto en que la presión térmica se vuelve suficiente para detener el colapso: ha nacido una estrella. Su apariencia externa indica que ha alcanzado el equilibrio, pero la composición química de su núcleo está evolucionando continuamente a medida que convierte el hidrógeno en helio. Lo que ocurra después de que la mayoría del hidrógeno se haya consumido depende de la masa de la estrella. No vamos a entrar en todos los detalles y posibilidades que surgen aquí, salvo subrayar que, en el caso de las estrellas más masivas (de 10 a 100 veces la masa del Sol), habrá múltiples fases de equilibrio, puntuadas por episodios de contracción que hacen que la temperatura y la presión del núcleo aumenten hasta disparar nuevas reacciones de fusión. Este proceso continúa hasta que se forma un núcleo de hierro.
Antes de meternos en lo que pasa en los estadios finales de la vida de una estrella, podemos ahora volver a la cuestión de cómo, conociendo la luminosidad y la temperatura de la superficie de una estrella, podemos determinar su masa. La verdad es que es más fácil pensar en esta pregunta desde el lado contrario: si sabemos la masa y la composición química de la estrella, podemos calcular su temperatura superficial y su luminosidad a partir de las ecuaciones de la estructura estelar. Aquí hay muchos detalles técnicos, pero los principios básicos son los siguientes. Cuanto más masiva sea una estrella, más presión térmica necesitará para contrarrestar su gravedad, y por tanto tendrá lugar más fusión nuclear, se liberarán más fotones y la estrella será más brillante. El centro de la estrella es lo más caliente, y la temperatura baja según te mueves hacia fuera, hasta alcanzar el mínimo en la superficie. La temperatura de la superficie depende de la estructura de la estrella, pero al menos durante la fase inicial de quemar hidrógeno, lo que los astrónomos llaman la secuencia principal, las estrellas más masivas son también las que tienen unas temperaturas superficies más altas. La temperatura superficial determina el color que percibimos de la estrella. Así, a partir de una observación del color y el brillo de una estrella, los astrónomos pueden hacer esos cálculos en el sentido inverso y obtener una estimación de la masa y la composición de una estrella.
Cyg X-l contiene una estrella con una temperatura superficial estimada de 30000 grados Kelvin y una masa de 20 masas solares. Una temperatura tan alta la hace aparecer azulada en el cielo nocturno (aunque está tan lejos de la Tierra que se necesita un buen par de prismáticos, o un telescopio, para verla), y el hecho de que tiene al menos 10 veces el tamaño del Sol la clasifica como una estrella supergigante azul. Usando esto y las observaciones del desplazamiento Doppler para modelar la órbita, los astrónomos han deducido que la compañera invisible tiene unas 15 masas solares. Entonces, ¿por qué tiene que ser esto un agujero negro? La respuesta viene de nuevo de la teoría de la estructura estelar. Como hemos explicado más arriba, a medida que una estrella masiva evoluciona, pasa por varios estadios de quemar combustible nuclear, y la energía que eso libera aporta la presión que contrarresta la gravedad. Las reacciones nucleares prosiguen hasta que se forman núcleos con unas masas próximas a la del hierro. La mayoría de ellos son estables, y cualquier proceso de fusión o fisión nuclear a partir de esta fase requiere energía.[9] En este punto los átomos están completamente ionizados, con todos los electrones flotando por ahí en un estado llamado un Fermi, o gas degenerado. Uno de los efectos de este estado degenerado de la materia es que puede ejercer una presión considerable (incluso a temperatura cero), llamada presión de degeneración. En una estrella de masa modesta como el Sol, la presión de degeneración es suficiente para soportar el núcleo cuando cesa la fusión nuclear (y, por cierto, en las estrellas de masa modesta esto ocurre antes de que se forme hierro), y termina su vida como una estrella enana blanca.
En las estrellas masivas, los estadios tardíos de su evolución son más espectaculares. Cuando el núcleo de hierro crece por encima del llamado límite de Chandrasekhar, que es de unas 1,4 veces la masa de nuestro Sol, la presión de degeneración de electrones se vuelve insuficiente para aguantar el núcleo, y entonces se colapsa. La temperatura y la densidad del núcleo crecen muy deprisa, y los fotones de alta energía empiezan a desintegrar el hierro. En este entorno extremadamente denso, los electrones y los protones libres se combinan deprisa para formar neutrones, y enseguida se forma un gas de neutrones. Los neutrones son fermiones, así que también ellos ejercen una presión de degeneración, y esta resulta ser significativamente mayor que la presión de degeneración de los electrones: tan alta que es capaz de detener el colapso del núcleo. Esto es en realidad un proceso bastante rápido y violento, que emite una poderosa onda de choque que se propaga hacia fuera a través de la estrella. Aunque los detalles son todavía un misterio, los astrónomos creen que eso es el comienzo de lo que después se observará como una supernova de tipo II. Durante el proceso, la mayoría de las capas externas de la estrella salen despedidas, pero parte del material llueve de vuelta sobre el núcleo, que ahora es una protoestrella de neutrones.
De manera análoga al límite de Chandrasekhar para las estrellas mantenidas por la presión de degeneración de electrones, hay un límite superior a la cantidad de masa que puede soportar la presión de degeneración de neutrones, que a veces se llama el límite de TolmanOppenheimer-Volkoff (TOV). La física de la materia del núcleo a las densidades extremas que se piensa que existen en las estrellas de neutrones no se comprende aún demasiado bien, y esto se traduce en una incertidumbre notable sobre el valor real del límite TOV. A partir de observaciones de las estrellas de neutrones que conocemos, ese límite es de al menos 3 masas solares. La teoría también nos dice que no puede ser más de unas 3 masas solares si hacemos lo que parece ser una suposición razonable: que las ondas sonoras de la estrella de neutrones no se pueden propagar más deprisa que la velocidad de la luz. Si la suficiente cantidad de material se acumula sobre el núcleo para elevar la masa por encima del límite TOV, la misma protoestrella de neutrones se colapsa. Puede haber algunas fases de la materia aún no descubiertas que vayan más allá de la densidad nuclear, pero mientras la velocidad del sonido en esas nuevas fases sea inferior a la de la luz, no se puede mantener ningún núcleo de más de 3 masas solares, y la relatividad general predice inequívocamente que se formará un agujero negro.
Volvamos a Cyg X-l. Sabemos que la compañera tiene unas 15 masas solares. Existen estrellas visibles que son más masivas (¡de hecho, la estrella visible de Cyg X-l es una de ellas!), pero, puesto que la compañera no es visible, no puede estar soportada por los procesos térmicos que mantienen a las estrellas ordinarias. Sin embargo, 15 masas solares está muy por encima del límite TOV. Así que razonamos que la compañera no puede ser una estrella convencional, una enana blanca, una estrella de neutrones ni otro objeto estelar compuesto de materia ordinaria (bariónica).
¿Podría ser una «estrella oscura» formada de materia oscura? La materia oscura es una partícula hipotética o familia de partículas hipotéticas que interactúa muy débilmente (o no interactúa en absoluto) con la materia ordinaria. Esta es la razón por la que no podemos «ver» la materia oscura, ya que interactúa de forma demasiado débil con el campo electromagnético como para producir los suficientes fotones para ser visible. La hipótesis de la materia oscura surgió hace varias décadas para explicar la siguiente observación: a escalas galácticas o mayores, los astrónomos ven que las estrellas y las galaxias se mueven como si sufrieran un tirón gravitatorio mucho mayor del que se puede justificar por todas las formas conocidas de materia en la zona: estrellas, polvo, gas, luz, neutrinos y demás. No tenemos ni idea de lo que causa esa fuerza anómala, pero, al menos de momento, muchos científicos apostarían a que es alguna forma de materia oscura. Desarrollando esta especulación, entonces, la materia oscura podría agregarse para formar objetos oscuros y compactos, y uno de ellos podría ser la compañera invisible de Cyg X-l. Sin embargo, la hipótesis de la materia oscura no excluye la existencia de agujeros negros (en realidad, hay quien ha propuesto que los agujeros negros son la materia oscura), así que habría que apilar más estratos de especulación para que las «estrellas negras» sean una respuesta probable y teóricamente viable a lo que se esconde en binarias como Cyg X-l.

Figura 5.1. Aspecto que puede tener un sistema binario de estrella y agujero negro, como Cyg X-l. La estrella puede tener un radio de millones de kilómetros, mientras que el agujero negro que acecha en el centro del disco de acreción tiene un radio de solo unos cientos de kilómetros, como mucho. Por tanto, la parte interior del disco alrededor de la órbita circular estable más interior (donde ocurre la mayor parte de la radiación de rayos X) no se puede resolver a la escala de esta figura. Un chorro de material puede también eyectarse desde las regiones interiores del disco, alimentado por la rotación del agujero negro.
Hay evidencias adicionales coherentes con que la compañera invisible en Cyg X-l sea un agujero negro. La más convincente es la emisión de rayos X que proviene de su vecindad. Aunque la estrella visible emite algunos fotones en el espectro de los rayos X, no emite ni mucho menos los suficientes para explicar la luminosidad de rayos X que se observa. Si la compañera es un agujero negro, está lo bastante cerca de la estrella para capturar una gran cantidad de gas y polvo procedente del viento estelar. Este material órbita alrededor del agujero negro en un disco hinchado, pero, debido a la viscosidad del material y a los efectos del campo magnético, migra lentamente hacia el agujero negro hasta que alcanza la órbita circular estable más interna (ISCO, por innermost stable circular orbit). Recordemos del capítulo 3 que la ISCO es lo más cerca que una partícula que siga una geodésica puede orbitar alrededor de un agujero negro sin caer en él. Para un agujero negro de Schwarzschild no rotatorio, la ISCO es tres veces el radio del horizonte de sucesos, pero en un agujero negro rotatorio se desplaza más adentro, y abraza al horizonte de sucesos en un agujero negro de Kerr de rotación máxima. Tras alcanzar la ISCO, el gas se zambulle deprisa en el agujero negro. El agujero negro, por tanto, está continuamente capturando material, y el disco de materia que rodea al agujero negro se denomina disco de acreción. Durante la larga migración hacia la ISCO, el gas se calienta. La fuente de energía para este calentamiento viene de la energía potencial gravitatoria liberada mientras el gas se acerca al agujero negro[10]. Cuanto más se acerca el gas al agujero negro, más se calienta, lo que significa que los fotones emitidos tienen una energía media más alta. Los fotones más energéticos, por tanto, vienen de la vecindad de la ISCO. El tamaño de la ISCO se relaciona con la masa del agujero negro, y por tanto los fotones más energéticos que emite un disco de acreción constituyen un indicador del tamaño del agujero negro. Para agujeros negros con varias veces la masa del Sol, como el que pensamos que existe en Cyg X-l, esa energía corresponde a la emisión de rayos X. Más aún, el flujo irregular de material del disco puede resultar en variaciones del brillo de los rayos X, llamadas oscilaciones cuasiperiódicas, y la escala de tiempo más corta de estas oscilaciones corresponde al periodo orbital de las partículas de la ISCO. Para los agujeros negros de masa estelar, esta variabilidad es del orden de unos pocos hercios (es decir, una escala de variación de varios milisegundos), que es lo que se observa en Cyg X-l y muchos otros candidatos a sistemas binarios con agujero negro que emiten rayos X.
Por muy simple que sea la respuesta a por qué la compañera es un agujero negro (es demasiado masiva para no serlo), como hemos explicado, lo cierto es que se basa en una larga cadena de argumentos teóricos. Algunos de esos argumentos están bastante bien apoyados por observaciones y experimentos (la evolución estelar por debajo de las densidades nucleares), y uno de ellos es muy verosímil pero enteramente especulativo (que no hay «estrellas» masivas y compactas de materia oscura que emiten rayos X). Por ello, una propuesta más conservadora sería que las propiedades observadas de las binarias de rayos X como Cyg X-l son coherentes con la interpretación del agujero negro, y que nadie ha ofrecido todavía una explicación alternativa dentro de las teorías convencionales y bien comprobadas. Hasta el 14 de septiembre de 2015, este era el mejor argumento que podíamos hacer sobre la realidad física de los agujeros negros. Ese día, la detección por el LIGO de la fusión de dos agujeros negros lo cambió todo. La ciencia nunca puede hacer una afirmación definitiva al cien por cien sobre algo de este tipo, pero observar una colisión mediante ondas gravitatorias descarta limpiamente todos los argumentos teóricos no gravitatorios que se necesitan para sustentar el caso de Cyg X-l (o el de los cuásares, que discutiremos a continuación), que se apoyan solo en las propiedades de la relatividad general en el vacío. En el capítulo 6 explicaremos más a fondo esta detección emocionante, que implica realmente la fundación de una nueva rama de la astronomía.
Hay en el universo una segunda población de agujeros negros para la que se han ido acumulando las evidencias desde finales de los años sesenta: los agujeros negros asociados inicialmente a los cuásares. El nombre «cuásar» se acuñó en los sesenta y deriva del término «objeto cuasiestelar», que en la época se podía traducir como: «No sabemos qué son estas cosas, pero desde luego son brillantes». Ahora pensamos que los cuásares son ejemplos de núcleos galácticos activos (AGN por sus siglas inglesas), donde una pequeña región del centro de una galaxia, que rodea a un enorme agujero negro, se llena de materia que emite una radiación copiosa mientras cae en espiral hacia el agujero negro. Los cuásares son extremadamente brillantes y extremadamente distantes, a muchos miles de millones de años luz de nosotros. Para comprender lo lejos que significa eso, recordemos que nuestra galaxia tiene un diámetro de ¡100000 años luz! (Un año luz es algo menos de 10 billones de kilómetros). Los cuásares son mucho más brillantes que una galaxia entera con miles de millones de estrellas. Se piensa que los agujeros negros que ocupan el corazón de los cuásares tienen unas masas entre varios millones y varios miles de millones de veces la masa del Sol, y nos referimos a ellos como agujeros negros supermasivos. Así, en cierto sentido, los cuásares son mucho más imponentes incluso que la primera fusión de agujeros negros detectada por el LIGO, que liberó una energía equivalente a tres meras masas solares, a partir de dos agujeros negros cuyas masas sumaban unas 65 masas solares. Sin embargo, esa energía equivalente a tres masas solares emergió en solo unas décimas de segundo. ¡Imagina lo que pasaría si se fusionaran dos agujeros negros supermasivos!
Como ocurría con las binarias de rayos X, debemos ser prudentes sobre la confianza con la que podemos afirmar que los cuásares son, en su centro, agujeros negros. Esta propuesta se remonta a 1969, cuando el astrofísico británico Donald Lynden Bell se dio cuenta de que una forma de explicar la luminosidad de los AGN era que estuviera alimentada por agujeros negros, aunque usó cómicamente el término «garganta de Schwarzschild» en lugar de «agujero negro», un nombre que John Wheeler había propuesto solo unos años antes. El mecanismo que propuso Lynden Bell para explicar la emisión de un cuásar es el mismo que el que hemos visto para la emisión de rayos X de Cyg X-l: un disco de acreción. La diferencia en los AGN es que, puesto que los agujeros negros son mucho mayores, la luminosidad del disco de acreción alcanza su máximo a unas longitudes de onda correspondientemente más largas, y por tanto brillan sobre todo en el espectro óptico y de radio. El mismo tamaño grande explica también la variabilidad en las escalas del orden de minutos a horas que se observa en la emisión de los cuásares: es el equivalente de las oscilaciones cuasiperiódicas del orden de milisegundos observadas en la emisión de CygX-l, solo que aumentadas a escala hasta los periodos más largos asociados a las grandes ISCO de los agujeros negros supermasivos. Lo que alimenta el disco de acreción de un agujero negro supermasivo es el gas y el polvo que le cae desde la galaxia circundante, así como alguna estrella ocasional que anda demasiado cerca del agujero negro y resulta desgarrada por las enormes fuerzas de marea cerca del horizonte del agujero negro. En conjunto, la materia consumida por el agujero negro proveniente del disco de acreción puede ascender a decenas, o incluso cientos, de masas solares cada año. Los discos de acreción, más que los agujeros negros en sí mismos, producen luz. Son faros brillantes de galaxias jóvenes, y la luz que hoy vemos de ellos se produjo hace miles de millones de años.
A primera vista puede parecer sorprendente que un disco de acreción sea una fuente de energía lo bastante poderosa para hacer que un cuásar brille más que la luz de todas las estrellas de una galaxia. La fuente de esa energía es la energía potencial gravitatoria del material que órbita alrededor del agujero negro. Esta es la misma energía potencial gravitatoria con la que bregamos diariamente aquí en la Tierra. Por ejemplo, la energía potencial gravitatoria es lo que explotamos en las centrales hidroeléctricas. El agua que corre desde la altura hacia elevaciones inferiores cede energía potencial gravitatoria, que la central hidroeléctrica convierte en electricidad que podemos usar para encender la luz en casa. Los cuásares son similares, pero producen algo así como un millón de trillones de veces tanta energía como una central hidroeléctrica de las grandes. Cuando tratamos con agujeros negros, una manera útil de caracterizar la cantidad de energía potencial que se puede convertir en otras formas de energía al caer desde muy lejos hasta la ISCO es verla como una fracción de la energía total en reposo (E = mc2) de la materia. Este número depende de la rotación del agujero negro, ya que la posición de la ISCO depende de ello. Ese porcentaje es el 6 % para un agujero negro no rotatorio, y asciende hasta el 42 % para un agujero negro de rotación máxima[11]. Estos son unos números enormes. En comparación, la cantidad de energía disponible a partir del agua que corre río abajo desde una colina a 100 metros de altitud es una billonésima de un 1 % de la energía de la masa en reposo[12]. La fuente de energía más eficiente que tenemos hoy a nuestra disposición es la energía nuclear de los reactores de fisión del uranio. Si todo el combustible de uranio se gasta en un reactor, se libera una energía equivalente a solo el 0,1 % de la masa en reposo. Eso es todavía una pequeña fracción en comparación con lo que es posible teóricamente en un disco de acreción alimentado por un agujero negro. Se piensa que la mayoría de los AGN operan a casi la máxima eficiencia posible, sin llegar a ella. La razón principal es que, a medida que el gas se calienta y empieza a emitir cantidades copiosas de energía, la presión térmica se hace lo bastante grande como para compensar el flujo del gas hacia el interior, y una parte de él resulta expelido por un análogo del viento.
A medida que fue prendiendo la noción de agujero negro, y los astrónomos empezaron a aceptar que los agujeros negros podían explicar la naturaleza de los cuásares, surgió la pregunta lógica de si las galaxias que no tienen núcleos galácticos activos podrían contener, de todos modos, agujeros negros supermasivos en su centro. De hecho, esta posibilidad ya fue insinuada por Lynden Bell en su artículo de 1969. Estos agujeros negros estarían latentes en el sentido de que no tienen mucho gas atrapado en un disco de acreción, y por tanto no serían tan luminosos. En las galaxias cercanas a nosotros se pueden tomar mediciones de los desplazamientos Doppler promedio de la colección de estrellas cercanas al núcleo de la galaxia. La dinámica orbital que se infiere de ello implica que hay realmente agujeros negros supermasivos en todas las galaxias grandes. Y esto es cierto, desde luego, en nuestra Vía Láctea, cuyo centro está lo bastante cerca de nosotros para que podamos resolver varias órbitas estelares individuales. Las estrellas orbitan lo que aparentemente es un agujero negro de unos 4 millones de veces la masa del Sol. En el palmarás de los agujeros negros supermasivos, este aparece hacia el final de la lista, pero no es incoherente con el tamaño de la Vía Láctea (las galaxias más grandes suelen tener agujeros negros mayores). La posición del agujero negro coincide con una brillante fuente de luz en la constelación Sagitario, llamada Sagitario A* (o simplemente Sgr A*). Se cree que la emisión de Sgr A* proviene de un disco de acreción que rodea al agujero negro, pero, comparado con un AGN, Sgr A* es extremadamente tenue, y está definitivamente en un estado latente.
A diferencia de lo que ocurre con sus homólogos de masa estelar, no hay una teoría universalmente aceptada sobre el origen de los agujeros negros supermasivos. Una posibilidad es que se originaran por el colapso de la primera generación de estrellas masivas que se formaron unos pocos cientos de millones de años después del Big Bang (que ocurrió hace casi 14000 millones de años). Estos agujeros negros habrían tenido inicialmente de decenas a cientos de veces la masa del Sol, pero, después de asentarse en el centro de las galaxias recién formadas, habrían crecido por acreción de gases y por fusión con otros agujeros negros. Un problema con esta hipótesis es explicar la observación de algunos cuásares muy distantes, de los que la luz que nos llega hoy viene de solo mil millones de años tras el Big Bang. Esto implica que un agujero negro supermasivo ya está allí, y el desafío para la hipótesis de acreción/fusión es explicar cómo pudo haber ocurrido tanto crecimiento en lo que, cosmológicamente, supone un tiempo corto de unos pocos cientos de millones de años. Otra hipótesis propone que las semillas de los agujeros negros supermasivos del presente vinieron de un tiempo mucho más temprano en el universo (o incluso de antes de lo que llamamos el Big Bang).
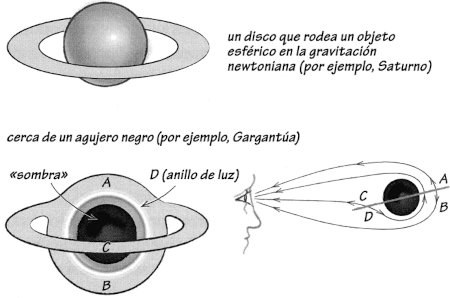
Figura 5.2. La «sombra» de un agujero negro. En la gravitación newtoniana (arriba), la luz que llega de un disco que órbita sobre un objeto masivo no se tuerce, y veríamos una imagen no distorsionada de la parte del disco que no está oscurecida. Alrededor de un agujero negro (abajo), la curvatura del espacio-tiempo es tan grande que las trayectorias de la luz resultan muy torcidas, tanto que todas las partes del disco son visibles. Las trayectorias de unos pocos de esos rayos de luz se ilustran abajo a la derecha, lo que da lugar a la imagen de abajo a la izquierda.
Los supuestos agujeros negros de esta clase se llaman agujeros negros primordiales. De momento no hay unos mecanismos teóricos enteramente convincentes para su formación, ni existen otras evidencias observacionales para ellos.
Vamos a concluir este capítulo mencionando brevemente un emocionante proyecto astronómico llamado Telescopio del Horizonte de Sucesos, que ya está empezando a suministrar imágenes de la llamada «sombra» de nuestro propio agujero negro galáctico, y del monstruo con más de mil millones de masas solares de la galaxia M87, que está relativamente cerca de nosotros, a solo un poco más de cincuenta millones de años luz. Lo peculiar de estos dos agujeros negros es que sus radios de Schwarzschild tienen unos tamaños angulares en el cielo mayores que los de ningún otro agujero negro conocido. En el caso de SgrA*, esto se debe a que está muy cerca de nosotros (en términos relativos), y en el de M87, a que es enorme. El Telescopio del Horizonte de Sucesos es en realidad una colección de radiotelescopios en posiciones muy separadas a lo largo del mundo, y que trabajan en tándem. Esto les permite explotar un efecto similar al del paralaje cuando miden simultáneamente las ondas de radio de la misma fuente —una técnica llamada interferometría— para alcanzar de hecho el poder de resolución angular que tendría un telescopio del tamaño de la Tierra. Como resultado, pueden resolver unas propiedades del cielo de muy pequeña escala, lo que es necesario para ver cosas cercanas al horizonte de esos agujeros negros. Por ejemplo, la extensión angular del horizonte de sucesos de Sgr A* es de solo 6 nanogrados. Intentar resolver esto es como tratar de distinguir los detalles de la cara de una moneda ¡tirada en la superficie de la Luna! Esta técnica de interferometría no puede dar a los telescopios el mismo poder de recolección de luz como un telescopio hipotético del tamaño de la Tierra (solo pueden recoger tanta luz como la suma de sus superficies), pero, al menos para el propósito de observar Sgr A* y M87, su poder de resolución es mucho más importante. Por supuesto, no podrán «ver» esos agujeros negros en sí mismos, pero sí la luz que viene de los discos de acreción que giran alrededor de ellos. La mayor parte de esta luz estará siguiendo las geodésicas del espacio-tiempo del agujero negro, pero, como vimos en los capítulos 3 y 4, muy cerca del horizonte, la deformación del espacio-tiempo es tan acusada que las trayectorias de los fotones estarán extremadamente curvadas, con algunas de ellas incluso viajando unas cuantas veces alrededor del agujero negro, cerca de su anillo de luz, antes de escapar hacia nosotros. El resultado es que el disco de acreción aparecerá bastante deformado. Una parte interior y con forma de círculo del disco de acreción, correspondiente a una región con unas pocas veces el tamaño del radio de Schwarzschild, aparecerá más oscura (la sombra), salvo por un anillo brillante que marca la posición del anillo de luz. Si estuviéramos viendo el disco de acreción de canto, la parte más próxima del disco de acreción pasaría por delante de la sombra. También podremos ver, por encima y por abajo del disco de acreción, una parte del disco que está detrás del agujero negro, de nuevo debido a la desviación de los fotones mientras pasan por allí.
Capítulo 6
Colisiones entre agujeros negros
Durante los capítulos 3, 4 y 5 nos hemos centrado en los agujeros negros aislados uno de otro. Estábamos muy interesados (¡y lo seguimos estando!) en la manera en que las estrellas orbitan alrededor de los agujeros negros supermasivos, y en cómo la materia forma discos de acreción alrededor de los agujeros negros, porque estos fenómenos aportan las mejores evidencias que tenemos para la existencia de los agujeros negros... es decir, las mejores hasta la observación por el LIGO de las ondas gravitatorias procedentes de la colisión de dos agujeros negros. Esa colisión tuvo lugar hace más de mil millones de años, y a un número comparable de años luz de distancia[13]. En este capítulo explicaremos algo de la teoría que está detrás de este suceso extraordinario: qué son las ondas gravitatorias, por qué colisionan los agujeros negros y al hacerlo producen ondas gravitatorias, y por qué han pasado 100 años desde que Einstein publicó la teoría de la relatividad general hasta que los científicos han podido medir directamente las ondas gravitatorias por primera vez.
Las colisiones de agujeros negros son los sucesos más violentos que permite la relatividad general. El Big Bang al principio del universo fue sin duda más espectacular, pero se requiere una teoría más abarcadora que la relatividad general para describir el origen del propio tiempo. Los físicos siguen buscando el marco teórico correcto para dar una explicación completa del Big Bang. Las colisiones de agujeros negros no requieren ninguna teoría mayor de ese tipo: por cualquier criterio, deberían bastar las ecuaciones de Einstein, Gμν = 8πGNTμν/c4. Para muchas colisiones de agujeros negros, de hecho, es probable que podamos ignorar el tensor de energía-impulso (Tμν, también llamado tensor de tensión-energía, que sería cero si no hay materia presente), porque la energía total de la materia exterior a los agujeros negros es pequeña comparada con la energía en reposo de los propios agujeros negros. Así, para describir las colisiones de agujeros negros, estamos llamados a resolver un conjunto de ecuaciones de aspecto supremamente simple: Gμν= 0. Una famosa foto de Einstein le muestra escribiendo en la pizarra un conjunto de ecuaciones: Rμν = 0. Aquí Rμνes el llamado tensor de Ricci, estrechamente relacionado con el tensor de Einstein y esencialmente equivalente a él en ausencia de materia. La elección por Einstein de los subíndices i y k no es más que una cuestión de gusto; lo mismo podría haber escrito Rμν = 0.
Ya hemos discutido antes las ecuaciones de campo de Einstein, pero, al lanzarnos a una explicación de las colisiones de agujeros negros, merece la pena revisar nuestra intuición de lo que describen las ecuaciones de campo. En breve, las ecuaciones de campo dan forma matemática a la idea de que la materia le dice al espacio cómo curvarse. ¿Qué permiten las ecuaciones de campo hacer al espacio-tiempo cuando no hay materia? Un ejemplo de espacio-tiempo permitido es no tener curvatura en absoluto. En otras palabras, un espacio-tiempo totalmente plano es una solución a las ecuaciones de Einstein en el vacío; pero no es la única. De hecho, otro ejemplo de espacio-tiempo permitido por las ecuaciones de campo en el vacío es un agujero negro aislado. Dentro del horizonte del agujero negro, como hemos visto, puede haber singularidades u otros rasgos peculiares que podemos asociar con un tensor no cero de energía-impulso. Pero fuera del horizonte es posible que no haya materia en absoluto. No deberíamos apostar demasiado por ninguna descripción del interior del agujero negro, porque ninguna señal de dentro nos puede alcanzar. Así que el punto de vista más económico es que un agujero negro aislado es un ejemplo de espacio-tiempo curvado incluso en la ausencia de materia.

Figura 6.1. Einstein dibujado con las ecuaciones de campo en el vacío de la relatividad general, que son un caso especial de las ecuaciones de Einstein en ausencia de materia.
Los agujeros negros que se mueven uno alrededor del otro ofrecen todavía otro ejemplo de solución a las ecuaciones de campo en el vacío.
Finalmente, un par de agujeros negros que orbitan uno sobre otro caerán en espiral y se fusionarán en un agujero negro de Kerr que gira muy deprisa. Esta es la clase de suceso que observó el LIGO el 14 de septiembre de 2015.
Una clase de soluciones más importante de las ecuaciones de campo en el vacío son las geometrías de ondas gravitatorias. Como explicamos en el capítulo 1, tenemos que entender las ondas gravitatorias en unos términos similares a la forma en que Maxwell describió la luz. Recordemos que la luz es una onda viajera (o de desplazamiento) de campos eléctricos y magnéticos, organizada de modo que la variación espacial del campo eléctrico causa la variación temporal del campo magnético, y viceversa, todo ello de acuerdo con las ecuaciones de Maxwell del electromagnetismo. Solemos pensar en los campos eléctricos como surgidos de la presencia de cargas eléctricas, mientras que los campos magnéticos resultan de la presencia de corrientes eléctricas; en la luz, sin embargo, los campos eléctricos y magnéticos, una vez creados, siguen propagándose indefinidamente, o al menos hasta que encuentran una materia que los absorba o los disperse. Las ondas gravitatorias son similares: una perturbación de la métrica del espacio-tiempo plano se propaga indefinidamente, con unas variaciones espaciales de la métrica que causan variaciones temporales según las ecuaciones de campo en el vacío.
Empujemos un poco más la analogía entre ondas gravitatorias y luz. Las ondas electromagnéticas se producen por cargas eléctricas en aceleración. Por ejemplo, una torre emisora de radio funciona enviando corrientes eléctricas alternas a un lado y a otro a lo largo de conductores. Estas corrientes —que no son ni más ni menos que cargas eléctricas que aceleran hacia un lado y el otro— son la causa última de los campos eléctricos y magnéticos que entonces se propagan hacia fuera hasta ser detectados por la radio que cualquiera de nosotros puede manejar. Las ondas de radio son realmente lo mismo que la luz, solo que con longitudes de onda más largas, y la luz visible puede producirse, en principio, mediante una aceleración similar de las cargas a un lado y a otro. Del mismo modo, las ondas gravitatorias son generadas por materia en aceleración. Una forma común de aceleración en los sistemas gravitatorios es la aceleración centrípeta de las órbitas circulares. Un ejemplo, que ya resumimos al final del capítulo 2, es que los sistemas estelares binarios generan radiación gravitatoria debido al movimiento orbital de cada estrella alrededor de la otra. La energía transportada por esta radiación conduce a una caída en espiral de las órbitas de las dos estrellas. Quizá no sea tan sorprendente, entonces, que los agujeros negros que se mueven en espiral cada uno sobre el otro deberían también emitir radiación. Desde una perspectiva filosófica, sin embargo, es muy sorprendente que la radiación gravitatoria pueda emerger de un sistema que no es más que espacio vacío (entendiendo por «vacío» el hecho de que resuelve las ecuaciones de campo). Esto trae a nuestra atención un asunto que ya hemos mencionado antes: que la propia gravedad gravita.
Las ondas gravitatorias detectadas por el LIGO se han comparado con el sonido; de manera particularmente célebre, los líderes del LIGO se han referido a los chirridos y aporreos que escuchan como «la música del cosmos». Esta analogía es tan inspiradora como útil, pero aquí queremos subrayar lo muy diferente que el sonido es de las ondas gravitatorias. El sonido es una onda de compresión en el aire. Eso quiere decir que una onda de sonido consiste en regiones alternantes de alta y baja presión que se propagan por un volumen de aire. Las moléculas individuales de aire están moviéndose constantemente en una danza térmica caótica, pero, por encima de ese movimiento complicado y azaroso, el sonido causa que las moléculas, en promedio, se deslicen un poco hacia el oyente porque una región de alta presión las empuja hacia delante, y luego se alejen un poco del oyente porque una región de baja presión las succiona hacia atrás. Este es un ejemplo de onda longitudinal, donde la palabra «longitudinal» se refiere al hecho de que el movimiento interno en que consiste la onda procede adelante y atrás en el mismo eje que define la dirección de propagación de la onda. En contraste, un ejemplo cotidiano de onda transversal es una onda en una cuerda tensa estirada en una dirección horizontal. Si sacudimos un extremo arriba y abajo, podemos ver la perturbación moverse a lo largo de la cuerda. «Transversal» se refiere a la forma en que el movimiento interno en que consiste la onda (arriba y abajo en el ejemplo que hemos descrito) forma un ángulo recto con el movimiento general de la onda (horizontal en este caso). Las ondas gravitatorias (y, por cierto, también la luz) son ondas transversales. Una implicación interesante es que una explosión en la que toda la materia acelere hacia fuera con una forma perfectamente esférica no produce radiación gravitatoria en absoluto[14]. Intentar producir ondas gravitatorias de esta manera sería como intentar crear una oscilación transversal arriba y abajo de una cuerda tensa sin más que tensar la cuerda más y más, sin moverla arriba y abajo en absoluto. El sonido se comporta de una forma muy diferente: una esfera de materia en explosión produciría un sonido increíblemente intenso, precisamente porque la explosión constituye un movimiento en la misma dirección (hacia fuera) en que el sonido se propaga naturalmente.
Una diferencia incluso más básica entre el sonido y las ondas gravitatorias es que el sonido requiere un medio para propagarse. Normalmente ese medio es aire, pero el sonido también puede viajar por el agua o por materiales sólidos. Sin embargo, el sonido no puede viajar por el vacío. La luz puede viajar por el vacío, y las ondas gravitatorias también.
Según el pensamiento moderno, el espacio-tiempo es el medio para las ondas gravitatorias de una manera estrechamente análoga a cómo la materia suministra el medio para las ondas sonoras. Desde este punto de vista, es realmente el carácter transversal de las ondas gravitatorias lo que las distingue del sonido, no la presencia o ausencia de un medio material.
El carácter transversal de las ondas gravitatorias tiene una importancia crucial para el diseño de los detectores de ondas gravitatorias. Consideremos con un poco más de cuidado, entonces, cómo es exactamente una onda gravitatoria. A efectos de visualización, imaginemos una onda gravitatoria que se propaga verticalmente hacia abajo, en dirección al detector LIGO de Livingston, Luisiana. Una onda gravitatoria no es más que una perturbación de la métrica del espacio-tiempo, así que lo único que puede hacer es cambiar las distancias. Para entender exactamente cómo lo hace, imaginemos que, en lugar del detector LIGO, montamos una rejilla cúbica tridimensional de instrumentos de medición, todos con relojes sincronizados, de modo que, intercambiando rayos de luz, puedan registrar cómo cambian en el tiempo las distancias espaciales entre ellos. (Tal vez esto es exactamente lo que habrían hecho los científicos del LIGO, ¡si su presupuesto lo hubiese permitido!). En ausencia de ondas gravitatorias, la configuración de instrumentos permanece estacionaria. ¿Qué pasa cuando llega la onda gravitatoria? El primer punto que hay que apreciar es que las distancias verticales no cambian en absoluto. Esto se debe a que las ondas gravitatorias son transversales, y la onda gravitatoria que tenemos en mente está llegando verticalmente hacia abajo. En la dirección horizontal norte- sur, sin embargo, las distancias entre los instrumentos aumentarán primero hasta una separación máxima, luego disminuirán hasta una separación mínima, y así sucesivamente mientras pasa cada ciclo de la onda. En la dirección este-oeste, se observarán esos mismos cambios de distancia, pero exactamente fuera de fase con las distancias norte-sur. Dicho de otro modo, la onda gravitatoria está simultáneamente «estirando» el espacio en la dirección norte-sur y «comprimiendo» el espacio en la dirección este-oeste, y luego al revés.
El detector LIGO de Livingston es mucho más simple que la rejilla cúbica de instrumentos de medición que imaginamos aquí. Tiene un brazo que se extiende 4 kilómetros a unos pocos grados sur-sureste desde la instalación central, y otro que se extiende 4 kilómetros en ángulo recto con el primero, a unos pocos grados oeste-suroeste. Las direcciones precisas de los brazos no importan para nuestros objetivos, así que supondremos en el resto de esta discusión que se extienden justo hacia el sur y justo hacia el oeste. No supone una idealización excesiva decir que el LIGO es de hecho como tres instrumentos de medición del tipo que hemos imaginado en el párrafo anterior: uno en la instalación central y uno en el extremo de cada brazo. Toda la lujosa interferometría láser que permite funcionar a LIGO se puede idealizar como la forma en que esos tres instrumentos de medición se intercambian rayos de luz para registrar cómo cambian con el tiempo las distancias entre ellos. En realidad, el LIGO no registra distancias absolutas, sino cómo cambian con el tiempo las diferencias entre distancias entre sus dos brazos. En breve, el LIGO registra mucho menos sobre el espacio- tiempo que nuestra rejilla cúbica imaginaria de instrumentos de medición, pero registra justo lo suficiente para detectar el patrón de estiramiento- compresión de una onda gravitatoria del tipo descrito en el párrafo anterior.
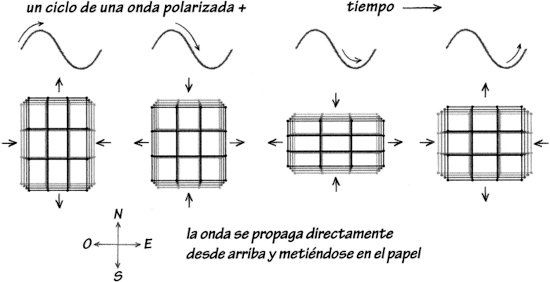
Figura 6.2. Efecto del paso de una onda gravitatoria por una rejilla cúbica. Podemos imaginar detectores en cada punto de la rejilla que miden cómo cambian con el tiempo las distancias a lo largo de la rejilla.
Supongamos ahora que llega una onda gravitatoria que estira el espacio- tiempo en el eje noroeste-sureste mientras lo comprime en el eje noreste- suroeste. Parece lógico que este tipo de onda gravitatoria deba ser tan común como el que hemos considerado antes. Podemos describir el patrón de estiramiento-compresión alineado en las direcciones norte-sur y este- oeste como la onda polarizada en más (+); y el patrón alineado en las direcciones noroeste-sureste y noreste-suroeste como el polarizado en cruz (×). Estos nombres vienen de la similitud de esos patrones de estiramiento- compresión con los símbolos + y ×, respectivamente. Dicho de otra forma, el patrón de una onda polarizada + es una versión rotada 45° de una onda polarizada ×.
Ahora viene el hecho escandaloso. ¡El LIGO de Livingston está ciego a las ondas polarizadas x! Esto se debe a que el patrón x no cambia la diferencia de distancia entre los dos brazos. Lo que ocurre más bien es que el ángulo entre los dos brazos crece y decrece; y solo en una cantidad imperceptiblemente pequeña. Por fortuna, la mayoría de la radiación no está puramente polarizada +, ni puramente polarizada x, sino en alguna mezcla de las dos. De modo que la sensibilidad del LIGO de Livingston a solo una de las dos polarizaciones posibles no es un estorbo tan grande como parece a primera vista. Recordemos también que solo hemos considerado ondas gravitatorias que vienen directamente de arriba; pero seguramente las ondas gravitatorias viajan en cualquier dirección de una manera más o menos democrática. La sensibilidad del LIGO de Livingston a las ondas gravitatorias varía de hecho tanto con la dirección como con la polarización, y lo mismo ocurre con el detector LIGO en Hanford, Washington. La situación no es muy diferente de las viejas antenas de televisión, que a veces requieren un ajuste delicado para recibir la mejor señal.
Al final, lo que registra cualquiera de los dos detectores LIGO es muy simple: la diferencia de distancia entre sus dos brazos. Pero esa medición tiene una exactitud asombrosa. Por ejemplo, cuando LIGO alcance la sensibilidad máxima para la que está diseñado (lo que se espera entre 2018 y 2020), será capaz de medir unos cambios de distancia tan pequeños como 10-19 metros. ¡Eso es una diezmilésima del tamaño de un protón! Se necesita una precisión tan increíble porque el estiramiento y la compresión del espacio-tiempo por las ondas gravitatorias es extremadamente pequeño. Por ejemplo, el movimiento orbital de Mercurio alrededor del Sol crea ondas gravitatorias, pero el LIGO no puede medirlas, porque son demasiado débiles y porque tienen una frecuencia mucho más baja de la que puede detectar el LIGO. Antes del 14 de septiembre de 2015, ningún instrumento de medición era lo bastante sensible para detectar ninguna onda gravitatoria en absoluto. El camino hacia la primera detección fue largo y arduo, con muchos científicos de todo el mundo empleando décadas para construir unos detectores de ondas gravitatorias cada vez más sensibles. Ahora, en el amanecer de la era de la astronomía de ondas gravitatorias, el LIGO solo puede detectar cataclismos como la fusión de agujeros negros. Cabe esperar que, a medida que mejore la sensibilidad de los detectores de ondas gravitatorias, podremos ver unas señales más sutiles, como las ondas gravitatorias generadas por las colisiones de estrellas de neutrones. La gravedad, por tanto, nos ofrece un estudio de las contradicciones: es la única fuerza lo bastante poderosa para abrumar a todas las demás y causar la formación de agujeros negros, pero al mismo tiempo es tan débil que los ecos gravitatorios de incluso los sucesos más terribles, como la colisión de estrellas de neutrones, siguen en el límite de lo perceptible para nuestros instrumentos de medición más sensibles.
Hagamos una pequeña pausa para repasar lo que hemos aprendido hasta ahora sobre las colisiones de agujeros negros y su detección. El asunto es simple en el sentido de que «todo» lo que estamos haciendo es estudiar soluciones a las ecuaciones de Einstein en el vacío, Gμν = 0. El problema, como explicaremos más adelante, es que esas ecuaciones son, en la práctica, extremadamente difíciles de resolver. Las soluciones en las que estamos interesados describen agujeros negros que caen en espiral uno sobre otro y emiten radiación gravitatoria en el proceso. Esta radiación gravitatoria se propaga por el espacio-tiempo y es detectada por el LIGO como una deformación del espacio-tiempo en la que las distancias son comprimidas brevemente en una dirección u otra, mientras que se estiran en la dirección ortogonal, y luego estiradas en la primera dirección mientras se comprimen en la segunda. Lo que queremos hacer a continuación es ofrecer una explicación más completa de lo que ocurre en las colisiones de agujeros negros, y de cómo su descripción en la relatividad general se traduce en los métodos prácticos que usa el LIGO para buscar sucesos que emiten ondas gravitatorias.
La primera vez que uno oye el término «colisión de agujeros negros», uno evoca de forma natural dos agujeros negros que zumban cada uno hacia el otro hasta colisionar de frente. Esto podría ocurrir, y generaría un montón de radiación gravitatoria, pero se piensa que es un suceso muy infrecuente. La razón es que los agujeros negros no son muy comunes en el universo (¡por fortuna para nosotros!), y hay mucho espacio entre ellos, en comparación con su tamaño. Incluso en un entorno abarrotado, como un cúmulo globular, cuyo núcleo puede contener cientos de agujeros negros con una separación hasta el vecino más próximo tan pequeña como un mes luz, una colisión semejante ocurriría solo una vez cada mil millones de años o más. Esto se debe, simplemente, a que es muy poco común que dos agujeros negros se encuentren por casualidad en rumbo de colisión.
Lo que ocurre más a menudo es que las dos estrellas de un sistema binario son lo bastante masivas para que, al final de su vida, se colapsen para formar agujeros negros, formando una binaria de agujeros negros. Estos agujeros negros no colisionarán de inmediato, pero están destinados a hacerlo tarde o temprano, porque ninguno tiene la suficiente velocidad para escapar del tirón del otro. Al principio, estarán simplemente orbitando el uno alrededor del otro. Supongamos, en aras de un tratamiento claro y concreto del tema, que los dos agujeros negros en cuestión sean similares a los que crearon la señal que observó el LIGO el 14 de septiembre de 2015. Vamos a simplificar la explicación un poco suponiendo que cada agujero negro tiene 32 masas solares, y pongamos que su separación inicial es de 384000 kilómetros, que es la distancia media entre la Tierra y la Luna. Asumamos también que ninguno de los dos agujeros negros tiene una rotación apreciable, de modo que, si estuvieran aislados, cada uno queda bien descrito por la solución de Schwarzschild. Cada uno tiene un horizonte de sucesos esférico con un radio de 95 kilómetros. En esa situación, la lenta espiral de sus órbitas, debida a la pérdida de energía en forma de radiación gravitatoria, llevará unos 210 años, acabando cuando se tocan sus horizontes de sucesos. Cuanto más lejos estuvieran los agujeros negros inicialmente, más tiempo llevará el proceso de caída en espiral. De hecho, el tiempo aumenta con la cuarta potencia de la separación inicial. Dicho de otro modo, si esos dos mismos agujeros negros hubieran estado inicialmente el doble de lejos uno del otro, completar su caída en espiral les habría llevado 16 veces más tiempo. Esta variación del tiempo con la cuarta potencia de la distancia hace precisa la afirmación de que la caída en espiral empieza despacio y se va haciendo más y más rápida cuanto más se acercan los dos agujeros negros. De hecho, las fases iniciales de la caída en espiral de agujeros negros que detectó por primera vez el LIGO puede haber tardado miles de millones de años. Como vamos a explicar pronto, la fase final a la que era sensible el LIGO duró solo unos pocos milisegundos.
La frecuencia de las ondas gravitatorias emitidas por el sistema binario de agujeros negros que estamos discutiendo es el doble de la frecuencia orbital. Esta frecuencia empieza siendo pequeña, y aumenta a medida que la caída en espiral progresa, lo que refleja el hecho de que los agujeros negros giran uno sobre otro cada vez más deprisa al acercarse entre sí. Parece contrario a la intuición que una pérdida de energía en forma de radiación gravitatoria tenga que causar un movimiento orbital cada vez más rápido. Ocurre de esa forma debido al balance entre energía potencial y cinética: a medida que los agujeros negros se acercan uno al otro, su energía potencial gravitatoria cae tan deprisa que pueden incrementar su energía cinética al mismo tiempo que emitir ondas gravitatorias.
La frecuencia que aumenta gradualmente es importante para la manera en que el LIGO busca colisiones de agujeros negros. El LIGO es sensible a frecuencias de ondas gravitatorias en el intervalo de 30-1000 hercios. Para las ondas sonoras, este es el intervalo de la audición humana, y por tanto, y pese a nuestra discusión de las ondas transversales y longitudinales, es adecuado que los científicos del LIGO se vean a sí mismos escuchando los sonidos de ondas gravitatorias que hace el universo. El sonido de la caída en espiral del sistema binario que hemos descrito antes alcanza los 30 hercios (un bajo profundo y atronador) a una separación de 990 kilómetros, y esto es solo 290 milisegundos antes de la fusión. En este estadio, los agujeros negros giran uno sobre otro a una velocidad de 47000 kilómetros por segundo, un poco más del 15 % de la velocidad de la luz. La frecuencia aumenta deprisa, y la fusión empieza a unos 190 hercios (cerca de un sol bajo el do medio del piano, en el intervalo de frecuencias de una voz hablada normal). En este momento, los dos agujeros negros vuelan a velocidades cercanas a 86000 kilómetros por segundo, casi un tercio de la velocidad de la luz. Los horizontes de sucesos se funden en una sola estructura, con una forma similar a una cáscara de cacahuete.
El lector podría pensar que las frecuencias que estamos considerando — de decenas a cientos de hercios— son solo ligeramente más pequeñas que las frecuencias de oscilación cuasiperiódica que mencionamos en relación con Cyg X-l. ¿Hay una conexión? ¡Desde luego que sí! Recordemos que el intervalo de frecuencias de unos pocos cientos de hercios, que corresponde a una escala de tiempo de unos pocos milisegundos, caracteriza la escala temporal más corta de variabilidad de las emisiones de rayos X procedentes del disco de acreción de Cyg X-l, y que la explicación era que esa escala temporal debería corresponder al periodo orbital de partículas en el ISCO del agujero negro que se forma en el corazón de Cyg X-l. De modo similar, un intervalo de frecuencias ligeramente más pequeño, que corresponde a unas escalas temporales ligeramente mayores, caracteriza el giro frenético de un par de agujeros negros de 32 masas solares en el momento de la fusión.
Una vez que los horizontes de sucesos se fusionan, sabemos intuitivamente qué esperar, según los teoremas de no pelo: el agujero negro en forma de cacahuete, muy irregular, debe asentarse hasta generar la forma de esfera ligeramente achatada de un agujero negro de Kerr. Este proceso se llama ringdown (bajar el telón), y es muy violento al principio. Durante el ringdown se generan ondas gravitatorias de muchas frecuencias diferentes, pero la dominante tiene una frecuencia de 300 hercios (un re por encima del do medio del piano). La onda de ringdown decae deprisa: su amplitud de vibración cae en un factor de 10 cada 8,6 milisegundos. Así que, 8,6 milisegundos tras la fusión, es 10 veces más pequeña que en la fusión; 17 milisegundos tras la fusión, es 100 veces más pequeña que en la fusión; 26 milisegundos tras la fusión, 1000 veces más pequeña, y así sucesivamente.
En una fracción de segundo, por tanto, el remanente de la fusión se asienta para formar un agujero negro de Kerr perfectamente inactivo.
Para recapitular: las ondas gravitatorias se producen todo a lo largo de la evolución de una binaria de agujeros negros a través de una caída en espiral larga y gradual, que acaba cuando los horizontes de los agujeros negros se funden y entran en ringdown hasta una solución de Kerr estacionaria. La radiación gravitatoria más poderosa, con mucho, se emite durante los pocos milisegundos que rodean el suceso de fusión propiamente dicho. La frecuencia de esta radiación está en el rango audible, aumentando desde un estruendo grave hasta un ruidoso alarido final. La forma de la onda en conjunto es lo que llamamos «chirrido» (chirp) de ondas gravitatorias, y en la región audible en la que el LIGO es más sensible, solo dura una fracción de segundo. Las colisiones de agujeros negros mayores darían un chirrido más grave; de hecho, las fusiones de agujeros negros con mucho más de 60 masas solares chirriarían a una frecuencia demasiado baja para que el LIGO las escuchara. Al revés, una fusión menos masiva chirriaría más tiempo en el intervalo de frecuencias de la sensibilidad del LIGO, y acabaría con un alarido más agudo. La nota del chirrido se relaciona con la masa total de los agujeros que se fusionan porque el chirrido proviene de las últimas pocas órbitas antes de la fusión, y la duración de esas órbitas es proporcional al radio del horizonte final, que a su vez es proporcional a la masa total.
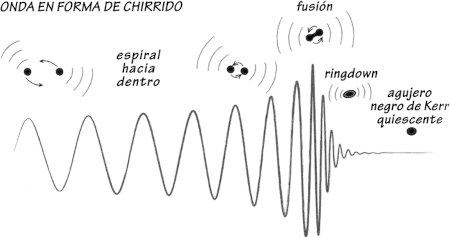
Figura 6.3. La onda gravitatoria en forma de «chirrido» que se forma al colisionar dos agujeros negros.
El primer suceso que escuchó el LIGO ocurrió hace más de mil millones de años. Eso es tan atrás en el tiempo que la onda entera resultó desplazada al rojo en casi un 10 % debido a la expansión cósmica: un efecto similar al desplazamiento al rojo de Doppler. En otras palabras, para el tiempo en que alcanzó la Tierra, el chirrido sonaba como el de unos agujeros negros un 10 % más pesados de lo que eran en realidad. El lector se podría preguntar: ¿cómo podemos distinguir entre un chirrido desplazado un 10 % al rojo que viene de agujeros negros distantes, y un chirrido no desplazado al rojo que viene de agujeros negros cercanos que son un 10 % más masivos? La respuesta es que la amplitud de la señal proveniente de agujeros negros cercanos sería mucho mayor. La amplitud decrece con el inverso de la distancia. Así que, si entendemos a partir de primeros principios (es decir, resolviendo las ecuaciones de campo en el vacío de Einstein) la fuerza y la frecuencia del chirrido producido por cualquier fusión dada de agujeros negros, podremos juzgar a partir de la fuerza y la frecuencia de un chirrido observado tanto la distancia con respecto a la fusión de agujeros negros que lo produjo como la masa total implicada.
A pesar de la tremenda pérdida de energía en forma de ondas gravitatorias, el remanente final de una fusión de agujeros negros acaba con mucha energía rotacional en forma de espín. Exactamente con cuánta rapidez gira el remanente depende también de cuáles eran los espines de los dos agujeros negros iniciales. En el ejemplo que hemos discutido, ambos eran inicialmente no rotatorios, y entonces el nuevo agujero negro de Kerr tiene un espín igual al 70 % del máximo permitido por la relatividad general. Su masa es de 61 masas solares, y las ondas gravitatorias se han llevado el equivalente a 3 masas solares de energía. La energía total se conserva cuando usamos E = mc2: empezamos con 32 + 32 = 64 masas solares, y hemos acabado con 61 masas solares en el remanente más 3 masas solares de radiación gravitatoria. Así, cerca del 5 % de la masa total de la binaria ha emergido en forma de radiación gravitatoria, con la vasta mayoría de la radiación surgiendo durante las pocas órbitas finales, la fusión y el ringdown. Como porcentaje, un 5 % de emisión de energía no suena demasiado impresionante. Sin embargo, la potencia (es decir, la velocidad de emisión de la energía) es casi inimaginable. Esa energía equivalente a 3 masas solares se irradia en una fracción de segundo, y alcanza una luminosidad máxima de 4×1049 vatios. Es difícil llegar a entender lo enorme que es ese número, pero consideremos lo siguiente. El Sol tiene una luminosidad de 4*1026 vatios, que es más o menos 20 billones de veces la velocidad de consumo energético de todas las actividades humanas sumadas. Hay unos 100000 millones de estrellas en nuestra galaxia, y unos 100000 millones de galaxias en el universo observable. Como burda aproximación, cada estrella es en promedio tan luminosa como el Sol, de modo que la luminosidad de luz estelar del universo entero es de 10000 millones de billones de veces la del Sol. En potencia, ¡eso solo representa una décima parte de la luminosidad de los últimos milisegundos de esta única colisión de agujeros negros! Esta es la clase de cataclismo que se requiere para generar rizos del espacio-tiempo lo bastante grandes para que los podamos medir aquí en la Tierra.
¿No debería semejante liberación de energía desgarrar el tejido del espacio-tiempo hasta hacerlo trizas? Aquí estamos siendo un poco frívolos con el lenguaje; una forma más seria de plantear la cuestión sería preguntarse si la excitación de semejantes vibraciones, extremadamente poderosas, en la geometría del espacio y el tiempo podría conducir a nuevas singularidades, ya sean vestidas o desnudas, además de las presentes en los agujeros negros que colisionaron. La respuesta es no: por muy fuertes que sean estas ondas gravitatorias, siguen sin serlo lo bastante para hacer eso. Si la luminosidad se hubiera aproximado a 4 × 1052 vatios —la llamada luminosidad de Planck, obtenida combinando la constante gravitatoria de Newton y la velocidad de la luz en una cantidad expresada en unidades de potencia—, la respuesta podría ser diferente.
Entonces, ¿cuánto de grandes son las vibraciones del espacio-tiempo causadas por esta fusión? Muy cerca de la binaria sería difícil caracterizar qué aspecto de la geometría podría atribuirse a la onda gravitatoria, respecto a lo que podría asociarse simplemente con el movimiento de los dos agujeros negros. A distancias mayores de unas 10 veces el radio de la órbita final, se hace posible discernir claramente las ondas gravitatorias polarizadas + y × que describimos antes, y ambas clases están en verdad presentes. Elijamos un punto a 5000 kilómetros de la fusión; eso es unas 50 veces el radio de la órbita final. La máxima cantidad fraccional de estiramiento y compresión a esa distancia será de un 0,3 %. Por ejemplo, supongamos que Alice, que mide 1,80 metros, estuviera allí observando el suceso. Alice sería estirada y comprimida en medio centímetro de cabeza a pies. Esa cantidad de estiramiento y compresión sería fácil de medir (aunque podría ser incómoda de experimentar). No así para el LIGO aquí en la Tierra, que está a unos mil millones de años luz de distancia. Debido a esta distancia enormemente mayor, la amplitud sería menor de la que Alice podría medir en un factor de 2 × 1018. Esta es la razón de que el LIGO fuera diseñado para tener la aparentemente ridícula sensibilidad de ser capaz de medir un cambio de una diezmilésima del tamaño de un protón a lo largo de una longitud de 4 kilómetros.
Como hemos sacado a relucir de nuevo la exquisita sensibilidad del LIGO, tenemos que matizar nuestra descripción de lo que realmente significa su sensibilidad, porque hay un detalle importante sobre la forma en que operan los detectores como el LIGO que no hemos mencionado aún. El ruido del LIGO —es decir, todas las otras cosas que causan que las distancias a lo largo de sus brazos vibren y por tanto se disfracen de ondas gravitatorias— es en realidad bastante grande, y la señal solo será audible por encima del mido en el caso de un suceso raro y muy poderoso como la colisión de agujeros negros detectada el 14 de septiembre de 2015. Aun así, el LIGO puede medir señales por debajo de lo audible mediante la aplicación de técnicas sofisticadas de análisis de datos, que usan las llamadas bibliotecas de moldes: grandes bibliotecas de predicciones teóricas para todas las posibles ondas gravitatorias que el LIGO podría detectar. Podemos ver un molde como la huella digital del suceso correspondiente, por ejemplo, la caída en espiral de dos agujeros negros no rotatorios con una masa de 32 masas solares cada uno. Las fuentes de ruido, como las vibraciones del suelo causadas por un camión que circula por una carretera cercana, o la actividad de talado de árboles que tiene lugar cerca del LIGO de Livingston, pero sus formas exactas son muy diferentes del chirrido de la fusión de agujeros negros. El LIGO se ve continuamente bombardeado por el ruido, y lo que mide, por tanto, es un revoltijo de todas esas huellas digitales del ruido impresas una encima de otra, a las que se suma de vez en cuando la huella digital de una onda gravitatoria. El molde puede servir entonces como una máscara que deja pasar la huella digital de la onda gravitatoria que casa con ella exactamente, mientras que al mismo tiempo bloquea las partes de las huellas digitales que no casan. Aunque esta técnica no puede eliminar el ruido por completo, es de una gran ayuda; suficiente para permitir al LIGO escuchar sucesos de ondas gravitatorias que ocurren mucho más lejos de la Tierra de lo que sería posible de otro modo.
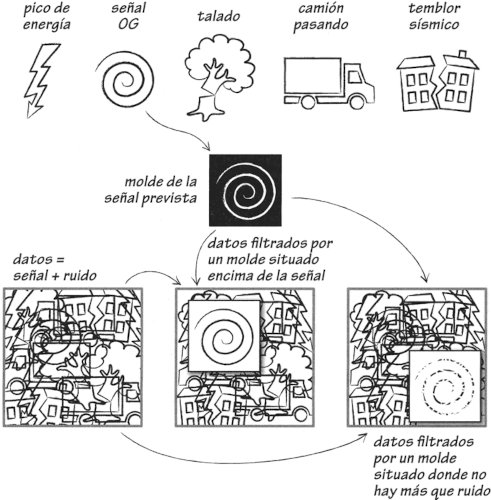
Figura 6.4. Así ayudan los moldes a descubrir una señal enterrada en el ruido. Cuando el molde se centra en la señal, emerge una representación limpia y sólida. Cuando se centra en el ruido, resulta una versión sucia e incompleta. OG significa «onda gravitatoria».
Hubo que superar un par de desafíos relacionados con los moldes para que el LIGO estuviera en condiciones de cumplir por completo su promesa de convertirse en un observatorio de ondas gravitatorias cuando alcanzara la sensibilidad para la que había sido diseñado. El primero es simplemente calcular todos los moldes para las colisiones de agujeros negros y otros sucesos verosímiles que puedan servir como fuentes de las ondas gravitatorias que puede ver el LIGO. Estas otras fuentes incluyen las colisiones entre agujeros negros y estrellas de neutrones; las fusiones de dos estrellas de neutrones; las explosiones de supernovas; estrellas de neutrones que giran rápidamente y tienen bultos en su superficie[15]; un océano cósmico de ondas gravitatorias creadas al principio de la evolución del universo; y una variedad de golpes, pliegues y sucesos de intersección en una red de cuerdas cósmicas con las que han especulado algunos cosmólogos[16]. Es un trabajo duro resolver las ecuaciones de campo de Einstein en todas esas situaciones diversas, pero hacerlo es necesario para construir los moldes que necesita el LIGO. Lo más desafiante en este sentido son las colisiones. Tras varias décadas de esfuerzos concertados de docenas de investigadores, el problema de la fusión de agujeros negros binarios se ha resuelto en lo esencial. Se ha logrado mediante una combinación de métodos analíticos (adecuados para las fases tempranas de la caída en espiral) y simulaciones numéricas con supercomputadores (necesarias para modelar la fase final de la caída en espiral y la colisión de los dos agujeros negros). Las estrellas de neutrones añaden más capas de complejidad al problema, porque las ecuaciones que gobiernan la dinámica de la materia que forma las estrellas de neutrones deben resolverse también. De hecho, y como expusimos en el capítulo 5, no tenemos un conocimiento detallado de las propiedades de la materia nuclear a las densidades extraordinariamente altas que, según se piensa, existen en las estrellas de neutrones. Se pueden construir moldes que cuantifiquen nuestras incertidumbres sobre la materia nuclear densa, y es razonable esperar que las observaciones de ondas gravitatorias procedentes de estrellas de neutrones en fusión, o de colisiones entre un agujero negro y una estrella de neutrones, nos enseñen mucho sobre las propiedades de la materia a unas densidades extremadamente altas.
El segundo problema con los moldes es más malvado. ¿Cómo podemos observar sucesos de ondas gravitatorias que no hemos previsto y para los que, por tanto, no hemos podido construir moldes? Una cuestión relacionada que resulta igual de preocupante es: ¿qué pasa si nuestros modelos teóricos de sucesos anticipados no son del todo correctos? A primera vista, entonces, parece como si LIGO fuera un instrumento de medición científica que está de alguna forma sesgado, y pudiera no ser capaz de descubrir nada que sea completamente nuevo o inesperado. Sin embargo, las cosas no son tan negras como pueden parecer: el LIGO emplea, de hecho, métodos de análisis libres de moldes que percibirían cualquier onda gravitatoria lo bastante potente, incluso si su forma no casa con nada que esté en la biblioteca de moldes. De modo similar, si una onda gravitatoria solo casa parcialmente con un molde porque hay algo en el molde que no es del todo correcto, el mismo análisis libre de moldes percibiría lo que se llama un residual: una señal remanente tras restar el molde que mejor encaja y que no es coherente con el ruido. Así que la conclusión es que los moldes nos permiten escuchar unos sucesos más distantes de los que sería posible detectar de otro modo y casar esas señales con las fuentes que predice la teoría, pero no impiden la posibilidad de que el LIGO descubra unas señales anómalas de ondas gravitatorias cuyo misterioso origen tendría entonces que entenderse.
Acabaremos este capítulo discutiendo las simulaciones numéricas de los agujeros negros en colisión. Estas simulaciones son un ingrediente esencial para crear los moldes que utiliza el LIGO. Tenemos que enfatizar que usar métodos numéricos para resolver ecuaciones suele ser un último recurso, al que apelamos solo cuando los cálculos de lápiz y papel se juzgan insuficientes para llegar a la física que queremos. También, restringimos la discusión a las colisiones de agujeros negros en ausencia de materia, de modo que las ecuaciones que debemos resolver son las ecuaciones de campo de Einstein en el vacío, Gμν = 0. ¿Cómo puede ser esto tan difícil?
La dificultad es que las ecuaciones de campo de Einstein son ecuaciones diferenciales, lo que significa que funcionan localmente en cuanto a la forma en que la métrica varía a través de una región infinitesimalmente pequeña de espacio y tiempo. Las ecuaciones diferenciales son casi siempre difíciles de resolver, y grandes sectores de investigación en matemática, física, química e ingeniería están dedicados a métodos de encontrar soluciones aproximadas a las ecuaciones diferenciales. Pensemos en ello como sigue. A un ordenador se le puede decir cómo sumar, restar, multiplicar y dividir, y hará esas operaciones aritméticas básicas con extrema velocidad. Pero una verdadera solución a una ecuación diferencial implica, en principio, un número infinito de operaciones básicas, porque la respuesta no es un simple número, sino algún tipo de curva continua —o de espacio-tiempo curvo, en el caso de las ecuaciones de Einstein— que requiere infinitos números para especificarla. Por supuesto, ningún ordenador puede hacer infinitos cálculos en un tiempo finito. Así que, en vez de eso, lo que necesitamos es una estrategia para hacer un número finito de cálculos que, pese a ello, se acerque mucho a la solución exacta de las ecuaciones diferenciales de interés. Más exactamente, queremos una estrategia para producir una secuencia de soluciones digitales aproximadas, con cada una de ellas dando una aproximación más cercana que la anterior a la solución exacta de las ecuaciones diferenciales. No consideramos que un problema numérico esté resuelto hasta que tenemos buenas evidencias de que nuestras soluciones digitales aproximadas se puedan hacer tan cercanas a una solución exacta como queramos, dado el suficiente tiempo de computación. Como analogía, piensa que estás viendo un vídeo con una conexión lenta a internet. Si tu software del buscador está bien configurado, obtendremos una versión borrosa y a saltos del vídeo que, pese a todo, corre a la velocidad correcta y tiene muchos colores correctos y algunas formas correctas. Si la conexión es más rápida, o si esperas un poco más a que el vídeo se descargue antes de empezar a verlo, el ordenador refinará los bloques de cada imagen como bloques más pequeños que muestran unos detalles más precisos y unos colores menos borrosos. Si esperas a que se descargue el vídeo completo, o si tienes una conexión rápida, verás el vídeo con la máxima resolución disponible. Las aproximaciones digitales sucesivas a las ecuaciones diferenciales son similares, con la diferencia de que, en principio, no hay ningún límite a cuánto puedes mejorar la aproximación. El único límite es cuánto tiempo de computación estás dispuesto a asignar a la tarea. La «simulación» numérica de las ecuaciones de Einstein es casi un nombre inapropiado, porque insinúa que el objetivo es imitar los rasgos esenciales del espacio-tiempo curvo a costa de ignorar algunos detalles. En realidad, el objetivo es dar con una estrategia para cartografiar todos los detalles del espacio-tiempo con una precisión cualquiera que hayamos predeterminado y en un tiempo finito. Un sello distintivo adicional de una simulación numérica exitosa de dos agujeros negros en colisión es que pueda llegar a la altura de las descripciones aproximadas de los regímenes de caída en espiral y de ringdown que estaban disponibles antes de que maduraran los métodos modernos de simulación numérica.
¿Qué tipo de estrategia deberíamos emplear para simular numéricamente las ecuaciones de campo de Einstein? Pensemos en el aspecto que debería tener la respuesta. Queremos una representación digital de la métrica que describa la geometría del espacio-tiempo. Recordemos que una métrica es una regla para decidir la distancia entre dos puntos cualesquiera. La geometría diferencial nos permite restringir la atención a los puntos que están muy juntos. El llamado tensor métrico nos dice la distancia de un punto dado a cualquier otro que esté lo bastante cerca. En la práctica, el tensor métrico es una matriz de cuatro por cuatro números. Tener una solución exacta de las ecuaciones de campo significa que conocemos exactamente el tensor métrico en todos los puntos del espacio- tiempo. Las soluciones de los agujeros negros de Schwarzschild y Kerr suministran esa información exacta en términos de unas fórmulas matemáticas muy inteligentes. En una simulación numérica, las fórmulas exactas no están disponibles, y por supuesto no podemos especificar el tensor métrico en los infinitos puntos del espacio-tiempo. Así que lo que hacemos es aislar una región del espacio-tiempo de gran interés (digamos, una región que rodee un par de agujeros negros que estén a punto de fusionarse) y llenarla con una rejilla de puntos. A cada uno de esos puntos finitos de la rejilla queremos asignarle un valor aproximado del tensor métrico. Al igual que en la analogía del vídeo de descarga lenta, nuestra intención es poder refinar la rejilla cada vez más, y con cada refinamiento queremos dar unos valores cada vez más precisos para todos los componentes de la métrica en cada punto de la rejilla. En breve, estamos discretizando el espacio-tiempo curvo para reducirlo a un constructo matemático tratable por un ordenador. Discretizar unas rejillas cada vez más finas es la clave de nuestra estrategia de simulación numérica. Una simulación grande actual puede tener hoy cientos de millones, o incluso de miles de millones de puntos en la rejilla.
Imponer las ecuaciones en el vacío de Einstein implica que el espacio- tiempo no se puede curvar de cualquier forma, sino solo de acuerdo con ciertas restricciones que nos dicen cómo la métrica tira y empuja de sus trocitos vecinos. Las verdaderas ecuaciones de Einstein son ecuaciones diferenciales, lo que significa que «vecino» se entiende como «arbitrariamente cerca». Cuando tratamos con un espacio-tiempo discretizado, tenemos que alterar un poquito las ecuaciones de Einstein de modo que se conviertan en reglas de cómo la métrica en un punto dado tira y empuja de la métrica en los puntos vecinos de la rejilla[17]. Al menos en principio, estas ecuaciones de Einstein discretizadas son manejables por un ordenador, porque solo implican un número finito de ecuaciones en un número finito de variables.
Quedan aún dos dificultades que son específicas de la relatividad general: las singularidades y las restricciones. El problema de las singularidades es en realidad familiar, y enteramente físico: los agujeros negros ocultan singularidades en las que las ecuaciones de campo de Einstein se vuelven absurdas. Si no tenemos cuidado, las simulaciones numéricas del espacio-tiempo tenderán a explorar el interior de los agujeros negros, y cuando el ordenador se choque con una singularidad tendremos un problema. Esto puede parecer un problema menor, puesto que la intuición física nos dice que los problemas que el ordenador encuentre dentro del horizonte de un agujero negro pueden ignorarse, porque ninguna señal puede salir de allí para «contaminar» el resto de la simulación. De hecho, la historia real es más sutil. Si se encuentra una singularidad en algún punto de la rejilla —lo que significa que el tensor métrico contiene algunos componentes infinitos—, el tirón/empujón codificado en las ecuaciones de Einstein discretizadas hará que los puntos vecinos de la rejilla se hagan singulares también. Luego los vecinos de estos se harán singulares, y así sucesivamente. Es difícil diseñar un código que impida a las singularidades propagarse de forma incontrolada. El enfoque correcto es identificar un horizonte poco después de que se forme, e instruir al ordenador para que no mire con demasiada profundidad dentro del horizonte. Manteniendo una pequeña capa de espaciotiempo dentro del horizonte, uno se puede asegurar de que toda la física de la relatividad clásica que ocurre cerca del horizonte queda capturada adecuadamente por la ecuación de Einstein discretizada; pero, excluyendo el interior profundo, impedimos que el ordenador encuentre una singularidad. Esta estrategia de exclusión hace un uso fuerte de la Conjetura de la Censura Cósmica de Penrose, según la cual las singularidades en las soluciones de las ecuaciones de Einstein solo pueden surgir dentro de los horizontes de sucesos. El hecho de que las simulaciones numéricas de las ecuaciones de Einstein funcionen cuando aplicamos una estrategia de exclusión como la recién descrita es, en realidad, una evidencia impresionante a favor de la Censura Cósmica.
El problema de las restricciones es de una naturaleza más técnica, pero merece la pena mencionarlo porque ocupa un lugar prominente en la manera real de hacer simulaciones numéricas de las ecuaciones de Einstein. Normalmente empezamos con alguna geometría inicial, como dos agujeros negros no rotatorios en órbita uno alrededor del otro, y nos preguntamos qué ocurre a medida que nos movemos hacia delante en el tiempo. Lo que esto significa en la práctica es que pensamos en nuestra gran rejilla, que discretiza el espacio-tiempo tetradimensional, como si estuviera dividida en rebanadas espaciales tridimensionales, y definimos el flujo del tiempo en términos de la función de lapso para conectar las rebanadas. El término común para cada rebanada espacial tridimensional es «rebanada de tiempo», porque la consideramos el conjunto de puntos en un tiempo definido. Lo que queremos es decirle a nuestro ordenador la métrica en solo unas pocas rebanadas de tiempo sucesivas (quizá solo dos), y luego pedirle que avance a la próxima rebanada usando las ecuaciones de Einstein discretizadas. Planeamos repetir el procedimiento, aumentado con una estrategia de exclusión para evitar singularidades, durante el tiempo necesario para ver que los agujeros negros se fusionan. Y esperamos que la geometría evolucione hasta que, en la última rebanada temporal de la simulación, vemos el agujero negro que resulta de la fusión, más una instantánea de todas las ondas gravitatorias producidas en la colisión radiando hacia fuera desde él.
Bien, ahora es cuando todo empieza a decaer. Una vez que se elige un patrón de rebanadas temporales, resulta que algunas de las ecuaciones de Einstein no nos ayudan a avanzar de una rebanada a la siguiente; solo nos valen como restricciones sobre qué tipo de geometrías se permiten en cada rebanada de tiempo. Incluso si organizamos todo con cuidado para satisfacer las restricciones a la perfección en una rebanada, encontramos en general que, usando las ecuaciones de Einstein discretizadas para progresar hacia delante en el tiempo, las restricciones solo se satisfacen imperfectamente en la siguiente rebanada. Peor aún, estas imperfecciones tienden a crecer con el tiempo, convirtiendo el resultado de nuestras simulaciones en ¡una basura! La solución es tan sutil como el problema. En vez de intentar satisfacer las restricciones a la perfección en cada rebanada, anticipamos que no serán satisfechas exactamente, pero alteramos las ecuaciones de Einstein discretizadas añadiendo lo que podríamos considerar, en sentido lato, una fuerza restauradora que empuja la solución hacia una que satisfaga las restricciones. Esta fuerza restauradora actúa en gran medida como la fuerza restauradora que puede ejercer un muelle: tira de un muelle hasta que esté fuera de equilibrio, y el muelle tirará de vuelta para intentar volver al equilibrio, con más fuerza cuanto más haya sido desplazado del equilibrio. Con las ecuaciones de Einstein, no estamos añadiendo ninguna fuerza física: es más bien un truco matemático que logra algo similar, donde el «equilibrio» es una solución que satisface las restricciones. Un tratamiento adecuado de las restricciones en la línea que acabamos de describir, junto con unas elecciones cuidadosamente seleccionadas sobre cómo representar las ecuaciones de Einstein en un espacio-tiempo discreto, conduce a unas simulaciones que realmente son capaces de capturar todos los detalles del espacio-tiempo en los sucesos de colisión de agujeros negros; por supuesto, siempre que solo hagamos preguntas sobre la geometría fuera del horizonte.
Resumiendo, la mayoría de las colisiones de agujeros negros en el universo son probablemente de la variedad «caída en espiral/fusión», que podemos describir simulando numéricamente las ecuaciones de campo de Einstein en el vacío, Gμν = 0. Hacer esto para una gran variedad de condiciones iniciales nos deja ver qué tipo de radiación gravitatoria se evapora de los agujeros negros mientras se fusionan. La liberación de energía en estos procesos es asombrosamente rápida: tan rápida que la luminosidad gravitatoria de los agujeros negros en fusión puede superar brevemente la suma de la luminosidad ordinaria de todas las estrellas del universo. La luminosidad ordinaria es la luz estelar. La luminosidad gravitatoria es la radiación gravitatoria, que se propaga desde los agujeros negros en fusión hacia fuera y se puede medir con detectores de ondas gravitatorias en forma de L como el LIGO. En el futuro, esperamos que las ondas gravitatorias revelen tanto sobre el universo como ha revelado la luz visible. Las ondas gravitatorias de las fusiones de estrellas de neutrones pueden ser el próximo gran descubrimiento[18]. Las ondas gravitatorias procedentes del universo muy joven, si se detectan, podrán ayudar a decirnos cómo era el universo en los primeros tiempos. ¡Y lo mejor de todo sería descubrir ondas gravitatorias de un tipo que nadie haya previsto! Entonces los teóricos se verían puestos a prueba para averiguar qué procesos físicos exóticos las han producido.
Capítulo 7
Termodinámica de los agujeros negros
Hasta ahora hemos pensado en los agujeros negros como objetos astrofísicos que se crean en supernovas o que residen en el centro de las galaxias. Vemos sus efectos de manera indirecta, observando la aceleración de las estrellas cercanas. La famosa observación de ondas gravitatorias por el LIGO el 14 de septiembre de 2015 es una observación más directa de una colisión de agujeros negros. Las herramientas que necesitamos para entender los agujeros negros en esos contextos son la geometría diferencial, las ecuaciones de Einstein y unos poderosos métodos analíticos y numéricos para resolver las ecuaciones de Einstein y describir las geometrías del espaciotiempo que crean los agujeros negros. Desde un punto de vista astrofísico, podríamos considerar cerrado el tema de los agujeros negros una vez que ya podemos dar una explicación enteramente cuantitativa de los espacio-tiempos relevantes. Desde una perspectiva teórica más amplia, sin embargo, hay mucho más que explorar. El propósito de este capítulo es alcanzar algunos de los puntos culminantes de los desarrollos teóricos modernos de la física de los agujeros negros, donde las ideas de la termodinámica y la teoría cuántica se intersecan con la relatividad general para producir unas revelaciones nuevas y sorprendentes. El resultado es que los agujeros negros son más que unos meros objetos geométricos. Tienen temperatura, tienen una entropía enorme y pueden ser manifestaciones del entrelazamiento cuántico. Nuestra descripción de los aspectos termodinámicos y cuánticos de los agujeros negros va a ser más incompleta que el tratamiento, en los capítulos previos, de los rasgos puramente geométricos de los espacio-tiempos de los agujeros negros. Pero los aspectos cuánticos, en particular, son una parte esencial y vital de la investigación teórica que está en marcha sobre los agujeros negros, y estamos impacientes por ofrecer al menos un boceto de ese trabajo.
En la relatividad general clásica —es decir, la geometría diferencial de las soluciones a las ecuaciones de Einstein— los agujeros negros son realmente negros, en el sentido de que nada puede escapar de ellos. Stephen Hawking mostró que esta situación cambia por completo cuando incluimos los efectos cuánticos: los agujeros negros, en realidad, emiten radiación de una temperatura concreta, conocida como la temperatura de Hawking. Para los agujeros negros de tamaño astrofísico (desde una masa estelar hasta los agujeros negros supermasivos), la temperatura de Hawking es tan pequeña que se puede ignorar en comparación con la temperatura del fondo cósmico de microondas, que es una forma de radiación que llena el universo y puede considerarse en sí misma una variante de la radiación de Hawking. El cálculo de Hawking sobre la temperatura de los agujeros negros es parte de un programa de investigación más amplio llamado termodinámica de los agujeros negros. Otra gran parte de ese programa es la entropía de los agujeros negros, que caracteriza la cantidad de información que se pierde dentro del agujero negro. Los objetos convencionales (como un vaso de agua, una barra de magnesio puro o una estrella) también tienen entropía, y uno de los puntos culminantes de la entropía de la termodinámica de los agujeros negros es que un agujero negro de un tamaño dado tiene más entropía que cualquier otra forma de materia que encaje en una región del mismo tamaño sin crear un agujero negro.
Antes de que nos sumerjamos a fondo en la radiación de Hawking y la entropía de los agujeros negros, vamos a hacer una rápida visita a la mecánica cuántica, la termodinámica y el entrelazamiento. La mecánica cuántica se desarrolló sobre todo en los años veinte, y su objetivo inicial era describir cosas muy pequeñas, como átomos. Unas nociones atesoradas durante mucho tiempo, como las posiciones exactas de las partículas individuales, se desenfocan en la mecánica cuántica, de modo que, por ejemplo, los electrones que rodean el núcleo atómico no se pueden localizar exactamente. En vez de eso, los electrones se mueven en los llamados orbitales, en los que la posición real de los electrones solo se puede determinar probabilísticamente. Para nuestros objetivos, sin embargo, es esencial que no saltemos a la probabilidad demasiado deprisa. Un átomo de hidrógeno (por poner un ejemplo simple) puede estar en un estado cuántico definido. El estado más simple de un átomo de hidrógeno es su estado basal, que es el estado de menor energía, y su energía se conoce exactamente. Más en general, la mecánica cuántica nos permite (en principio) estar absolutamente seguros del estado de cualquier sistema cuántico.
La probabilidad entra en escena cuando nos hacemos ciertas preguntas sobre un sistema mecanocuántico. Por ejemplo, si un átomo de hidrógeno está claramente en su estado basal, podemos preguntar: «¿Dónde se encontrará el electrón?», y las reglas de la mecánica cuántica nos darán solo una respuesta probabilística, que se reducirá más o menos a «el electrón está probablemente a menos de medio angstrom del núcleo del hidrógeno». (Un angstrom es 10-10 metros). Por otro lado es posible, mediante un proceso físico, averiguar la posición del electrón con una precisión mucho mayor de un angstrom. Un proceso típico es dispersar fuera del electrón un fotón con una longitud de onda muy corta, tras lo cual podemos reconstruir dónde estaba el electrón en el momento de la dispersión con una precisión de una vez la longitud de onda del fotón, más o menos. Este proceso físico cambia el estado del electrón, de modo que ya no está en el estado basal del átomo de hidrógeno, y ya no tiene una energía definida. Temporalmente, tiene casi una posición definida (es decir, en el radio de una vez la longitud de onda del fotón utilizado). La posición que tiene solo puede predecirse probabilísticamente con una precisión de un angstrom, pero, una vez que la midamos, sabremos lo que encontremos. En resumen, si medimos un sistema mecanocuántico de alguna manera, al menos según la visión convencional estamos forzándolo a un estado con un valor definido de la cantidad que estamos midiendo.
La mecánica cuántica no se aplica solo a sistemas pequeños, sino (según creemos) a todos los sistemas. Sin embargo, las reglas de la mecánica cuántica se vuelven enseguida complicadas en los sistemas grandes. Una propiedad esencial es la noción de entrelazamiento cuántico. Un ejemplo simple de entrelazamiento se puede ilustrar utilizando la noción de espín. Los electrones individuales tienen espín, así que, en la práctica, un electrón individual puede tener espín hacia arriba o hacia abajo respecto a un eje espacial que elijamos. El espín de un electrón es observable porque el electrón produce un pequeño campo magnético, similar al campo magnético de una barra imantada, y «espín arriba» significa que el polo norte del electrón apunta hacia abajo, mientras que «espín abajo» significa que el polo norte del electrón apunta hacia arriba. Se puede organizar que dos electrones estén en un estado cuántico conjunto en el que uno de ellos tiene espín arriba y el otro tiene espín abajo, pero es imposible decir qué electrón tiene qué espín[19]. De hecho, el estado basal de un átomo de helio incluye dos electrones en ese estado, precisamente, que se llama «estado singlete» porque el espín combinado de los dos electrones es cero. Si separamos los dos electrones sin perturbar sus espines, podemos afirmar que están, como conjunto, en un estado singlete de espín, pero no podemos decir qué espín tiene cada electrón por sí mismo. Si medimos un espín y encontramos que es arriba, podemos estar completamente seguros de que el otro espín es abajo. En esta situación, decimos que los espines están entrelazados, porque ninguno de ellos tiene un valor definido por sí mismo, pero los dos juntos están en un estado cuántico definido.
Einstein estuvo profundamente preocupado por el entrelazamiento, porque parece desafiar los principios de la relatividad. Consideremos el caso de dos electrones en un estado singlete de espín que están muy separados en el espacio. Para ser más precisos, demos un electrón a Alice y el otro a Bob. Digamos que Alice mide el espín de su electrón y encuentra que tiene espín arriba; pero Bob evita hacer ninguna medición en absoluto. Antes de que Alice haga su medición, es imposible decir cuál es el espín del electrón de Bob. Pero, en el mismo momento en que Alice completa su medición, ella puede decir con toda seguridad que el electrón de Bob tiene espín abajo (el contrario del que ella ha medido en su electrón). ¿Significa esto que la medición de ella fuerza instantáneamente al electrón de Bob a adoptar el estado de espín abajo? ¿Cómo podría ocurrir eso si los electrones están separados espacialmente? Einstein y sus colaboradores, Nathan Rosen y Boris Podolsky, sintieron que los problemas que rodeaban a la medición de sistemas entrelazados eran tan graves que ponían en peligro a la propia mecánica cuántica. La paradoja de Einstein-Podolsky-Rosen (EPR) utiliza un montaje como el que acabamos de describir para afirmar que la mecánica cuántica no puede ser una descripción completa de la realidad. El consenso moderno, basado en trabajos teóricos posteriores y muchas mediciones, es que la paradoja EPR es inválida, y la teoría cuántica es correcta. El entrelazamiento cuántico es real, y un síntoma de ello es que las mediciones en sistemas entrelazados estarán correlacionadas incluso si están muy separados en el espacio-tiempo.
Volvamos a la situación en que preparamos dos electrones en un singlete de espín y le damos uno a Alice y otro a Bob. Antes de que tenga lugar ninguna medición, ¿qué podemos decir sobre los electrones? Juntos, están en un estado cuántico definido (el estado de singlete de espín). El espín de Alice por sí mismo tiene la misma probabilidad de ser arriba o abajo. Más exactamente, su estado cuántico tiene la misma probabilidad de ser el estado cuántico espín arriba o el estado cuántico espín abajo. Ahora nos estamos apoyando en la probabilidad de una manera más profunda que antes. Previamente, habíamos considerado un estado cuántico definido (el estado basal del hidrógeno) y aprendimos que hay ciertas preguntas «malas», como: «¿Dónde encontraremos el electrón?», que tienen respuestas probabilísticas. Si hubiéramos hecho preguntas «buenas», como: «¿Cuál es la energía del electrón?», habríamos obtenido respuestas definidas. Ahora, en cambio, no hay preguntas «buenas» que hacer sobre el electrón de Alice sin referencia al electrón de Bob. (Estamos excluyendo las preguntas tontas como: «¿Tiene espín el electrón de Alice?», que están construidas para que solo tengan una respuesta posible). Así, cuando hablamos de la mitad de un estado entrelazado, tenemos que usar probabilidades para caracterizar cómo son las cosas. Las certezas emergen solo cuando consideramos cómo se relacionan las respuestas a las preguntas que Alice y Bob pueden preguntar.
Hemos empezado a propósito con uno de los sistemas mecanocuánticos más simples que conocemos: los espines de los electrones individuales. Los ordenadores cuánticos, según esperamos, se construirán con sistemas de una simplicidad similar. De hecho, los espines de los electrones individuales, u otros sistemas cuánticos equivalentes, se describen ahora como qubits (abreviatura de quantum bits, o bits cuánticos), anticipando así que su papel en los ordenadores cuánticos será análogo al de los bits en los ordenadores digitales.
Ahora supongamos que reemplazamos cada electrón por un sistema cuántico mucho más complicado, con muchos estados cuánticos en vez de solo dos. Tal vez, por ejemplo, les damos a Alice y Bob bloques de magnesio puro. Antes de que Alice y Bob empiecen a viajar por separado, dejamos que sus bloques interactúen, y les obligamos a que comiencen en un estado cuántico conjunto definido. Una vez que Alice y Bob se separan, sus bloques de magnesio dejan de interactuar. Al igual que ocurría con los electrones, cada bloque de magnesio está en un estado cuántico incierto, por más que, considerados en conjunto, los bloques estén en un estado cuántico definido. (Este tratamiento asume que Alice y Bob pueden mover sus bloques de magnesio sin perturbar de ningún modo el estado interno de cada bloque, al igual que antes supusimos que Alice y Bob podían separar los electrones entrelazados sin perturbar sus espines). Lo que es diferente ahora es que la incertidumbre sobre el estado cuántico de cada bloque por separado es enorme. No es difícil que cada bloque pueda tener más estados cuánticos que átomos hay en el universo. Aquí es donde la termodinámica entra en escena. Un sistema especificado de forma muy imprecisa puede, pese a todo, tener algunas propiedades macroscópicas que están bien definidas. La temperatura es una de esas propiedades. La temperatura es una medida de la probabilidad de que cualquier parte de un sistema tenga cierta energía media, donde una temperatura más alta corresponde a una mayor probabilidad de altas energías. La entropía es otra propiedad termodinámica, y es esencialmente el logaritmo del número de estados disponibles para un sistema. Aún otra propiedad termodinámica que puede ser interesante para un bloque de magnesio es la magnetización total, que equivale esencialmente a cuántos electrones más del bloque tienen espín arriba que espín abajo.
Hemos introducido la termodinámica como una forma de tratar un sistema cuyo estado cuántico no se conoce con precisión debido a algún entrelazamiento con otro sistema. Este es un punto de vista realmente poderoso, aunque está muy lejos de la forma de pensar de los creadores de la termodinámica. Esta gente, como Sadi Carnot, James Joule y Rudolf Clausius, trabajaron en plena revolución industrial del siglo XIX, y su interés se centraba en la más práctica de las cuestiones: ¿cómo funcionan las máquinas? La presión, el volumen, la temperatura y el calor eran el pan de cada día del diseño de máquinas. Carnot estableció que la energía suministrada en forma de calor no podía convertirse por entero en un trabajo útil, como levantar un objeto pesado. Siempre habrá algún desperdicio. Clausius hizo una contribución esencial al introducir el concepto de entropía, como una herramienta de contabilidad uniforme que mide cuánto desperdicio se genera en cualquier proceso relacionado con el calor. El descubrimiento clave fue que la entropía nunca puede disminuir, y de hecho se incrementa en casi todos los procesos. Los procesos en que se incrementa la entropía se llaman irreversibles, precisamente porque no pueden ocurrir al revés sin reducir la entropía. El desarrollo subsiguiente de la mecánica estadística por Clausius, Maxwell y Ludwig Boltzmann (entre otros) mostró que la entropía es una medida del desorden. Por lo común, cuanto más empujas algo, más desordenado se vuelve. Si diseñas un proceso para crear orden, será inevitable que genere más entropía de la que destruye, por ejemplo liberando calor. Por ejemplo, una grúa que apila barras de acero en perfecta alineación está creando orden en lo que concierne a la posición de las barras de acero, pero la acción de elevar las barras generará calor como subproducto, de manera que la entropía total se incrementa.
El punto de vista decimonónico sobre la termodinámica parece más alejado de la perspectiva del entrelazamiento cuántico de lo que realmente está. Cuando un sistema interactúa con un agente externo, su estado cuántico se entrelaza con el estado cuántico del agente externo. En general, ese entrelazamiento conducirá a una mayor incertidumbre sobre el estado cuántico del sistema, o, en otras palabras, a un incremento en el número de estados cuánticos disponibles para el sistema. Como resultado, la entropía del sistema —definida en términos del número de estados cuánticos disponibles— suele incrementarse como resultado de interacciones con otros sistemas.
En resumen, la mecánica cuántica aporta una nueva forma de caracterizar los estados de los sistemas físicos en que algunas cantidades (como la posición) se hacen borrosas, pero otras (por ejemplo, la energía) se conocen a menudo con precisión. En el entrelazamiento cuántico, dos sistemas en principio separados tienen un estado cuántico conjunto que es conocido, pero cada parte por sí misma tiene un estado cuántico incierto. El ejemplo estándar de entrelazamiento es un par de espines en estado de singlete, donde es imposible saber qué espín es arriba y cuál abajo. La incertidumbre en el estado cuántico de un sistema grande conduce al estudio de la termodinámica, donde propiedades macroscópicas como la temperatura y la entropía se conocen con buena precisión pese a que hay muchos posibles estados cuánticos microscópicos del sistema.
Una vez completada nuestra rápida visita a la mecánica cuántica, el entrelazamiento y la termodinámica, vamos a emprender el camino hacia la comprensión de cómo se utilizan para mostrar que los agujeros negros tienen temperatura. Bill Unruh dio un primer paso al mostrar que un observador en aceleración en un espacio plano percibiría una temperatura igual a su aceleración dividida por 2π. La clave para el cálculo de Unruh es que un observador que se mueve con aceleración constante en una dirección particular solo puede ver la mitad del espacio-tiempo plano. En efecto, la otra mitad está más allá de un horizonte que es similar al horizonte de un agujero negro. Esto suena imposible al principio. ¿Cómo puede el espacio plano exhibir un horizonte de agujero negro? Para captar la idea, reclutemos de nuevo a nuestro infalible grupo de observadores, Alice, Bob y Bill. A petición nuestra, los tres se alinean, con Alice entre Bob y Bill, y con 6 kilómetros de separación entre cada par adyacente de observadores. Se acuerda que, a tiempo cero, Alice se monta en un cohete y empieza a moverse hacia Bill (y por tanto alejándose de Bob) con aceleración constante. El cohete es muy bueno, capaz de imprimir una aceleración de 1,5 billones de veces la aceleración gravitatoria que experimenta un objeto cerca de la superficie de la Tierra. Esto es duro para Alice, obviamente; pero, como veremos, los números están elegidos con un objetivo concreto
en mente; y después de todo solo estamos tratando de posibilidades conceptuales. Justo en el momento en que Alice se monta en su cohete, Bob y Bill la saludan con la mano. (Podemos dar significado a la frase «justo en el momento» gracias a que, antes de que Alice se empiece a mover, ella está en el mismo marco de referencia que Bob y Bill, de modo que los tres pueden ponerse de acuerdo en una noción concreta del tiempo). Alice sin duda verá el saludo de Bill: de hecho, en su cohete lo verá antes de lo que lo habría visto de haberse quedado quieta, porque en el cohete se está moviendo hacia la posición de él. Por otro lado, ella se está alejando de Bob, así que podríamos concluir de manera razonable que Alice ve el saludo de Bob algo más tarde de lo que lo habría visto si se hubiera quedado quieta. Pero la verdad es más extraordinaria que eso: ¡Alice nunca verá el saludo de Bob! Para expresarlo de otra forma, los fotones que Bob transmite hacia Alice con su saludo nunca la alcanzarán, incluso aunque ella nunca llegue a moverse a la velocidad de la luz. Si Bob se hubiera situado algo más cerca de Alice, los fotones que mandara justo en el momento del arranque del cohete sí que la habrían alcanzado. Si se hubiera situado más lejos, no la habrían alcanzado. Es en este sentido en el que Alice solo puede ver la mitad del espacio-tiempo. En el momento en que Alice se empieza a mover, Bob está un poquito por detrás del horizonte que Alice observa.
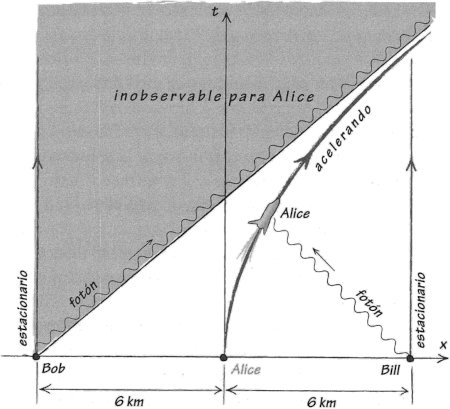
Figura 7.1. Alice acelera desde el reposo mientras Bob y Bill permanecen estacionarios. La aceleración de Alice es justo la suficiente para que nunca reciba los fotones que Bob manda hacia ella cuando la saluda a tiempo t = 0. Ella, sin embargo, sí recibe los fotones que le manda Bill a t = 0. La conclusión es que Alice solo puede observar la mitad del espacio-tiempo.
En nuestro tratamiento del entrelazamiento cuántico, nos hemos acostumbrado a la idea de que, incluso si un sistema mecanocuántico como un todo tiene un estado cuántico definido, sus partes pueden no tenerlo. De hecho, cuando hablamos de un sistema cuántico complicado, una parte de él puede caracterizarse mejor en términos termodinámicos, con una temperatura definida pese a su estado cuántico altamente incierto. Nuestro montaje actual con Alice, Bob y Bill es un poco como eso, pero el sistema cuántico en el que estamos pensando es espacio-tiempo vacío. Alice solo puede ver la mitad de él. Estipulemos que el espacio-tiempo como un todo está en su estado basal, lo que significa que no hay partículas presentes (aparte de Alice, Bob, Bill y el cohete). La parte del espacio-tiempo que Alice puede ver no estará en su estado basal; estará en un estado entrelazado con la parte que ella no puede ver. En sí mismo, el espacio- tiempo, tal y como Alice lo experimenta, está en un estado cuántico complicado e incierto caracterizado por una temperatura finita. El cálculo de Unruh muestra que esa temperatura es de unos 60 nanokelvin. En resumen, Alice ve un baño térmico de radiación a medida que acelera, y la temperatura de ese baño (en las unidades apropiadas) es su aceleración dividida por 2π.
La parte incómoda del cálculo de Unruh es que, aunque se refiere de principio a fin al espacio vacío, desafía el dictamen del rey Lear: «Nada vendrá de nada». ¿Cómo puede el espacio vacío ser tan complicado? El caso es que, en la teoría cuántica, el espacio vacío es un lugar muy ajetreado. Unas excitaciones efímeras llamadas partículas virtuales, con energía positiva y negativa, están todo el rato saltando a la existencia y fuera de ella. Una observadora que viva en el futuro lejano, llamémosla Carol, que pueda ver esencialmente todo el espacio vacío, podrá confirmar que ninguna partícula tiene una existencia duradera. La presencia de partículas de energía positiva en la parte del espacio-tiempo que Alice puede observar está ligada, a través del entrelazamiento cuántico, con excitaciones de energía igual y de signo opuesto en la región del espacio- tiempo que ella no puede observar. Carol percibe toda la verdad cuántica sobre el espacio-tiempo vacío, que es que no hay partículas. La experiencia de Alice, sin embargo, es que sí las hay.
La temperatura de Unruh parece una trampa porque no es tanto una propiedad del espacio plano como una propiedad de un observador en aceleración constante en el espacio plano. Sin embargo, la propia gravedad es una «fuerza trampa» en el sentido de que la «aceleración» que causa no es más que movimiento geodésico en una métrica curva. Como explicamos en el capítulo 2, el principio de equivalencia de Einstein afirma que la aceleración y la gravitación son esencialmente equivalentes. Desde este punto de vista, no es tan chocante que el horizonte de un agujero negro tenga una temperatura igual a la temperatura de Unruh de un observador en aceleración. Pero, podemos preguntarnos, ¿qué aceleración tenemos que usar? Si nos situamos lo bastante lejos de un agujero negro, su tirón gravitatorio sobre nosotros se hace tan pequeño como queramos. ¿Deberíamos entonces usar una aceleración correspondientemente pequeña para determinar la temperatura efectiva del agujero negro según la medimos nosotros? Eso sería una situación incómoda, porque se supone que la temperatura de un objeto no puede decrecer arbitrariamente; se supone que tiene algún valor fijo que incluso un observador muy distante podrá medir como finita.
Una perspectiva más cercana al espíritu de la explicación de Hawking sobre la temperatura de un agujero negro es que deberíamos usar la aceleración de un observador flotando muy cerca del horizonte del agujero negro, pero luego descontando la temperatura correspondiente por el factor de desplazamiento al rojo que experimenta ese observador. Este punto de vista es lo más cerca que estaremos del cálculo real de la temperatura de Hawking, así que caminemos por él sin prisa en el caso de un agujero negro de Schwarzschild. Cuando hablamos de un observador flotante, o estático, nos referimos a uno que permanece a un radio fijo del horizonte sin orbitar alrededor del agujero negro. Para hacer esto, el observador, digamos Anne, tiene que tirar de sí misma constantemente para alejarse del agujero negro, por ejemplo usando un cohete. Si Anne solo mira a su geometría local, el principio de equivalencia dice que ella no podrá distinguirla del espacio plano a través del cual está acelerando a una tasa constante. Cuanto más cerca esté Anne del horizonte real del agujero negro, mayor será esa aceleración aparente. Según los cálculos de Unruh, Anne percibirá una temperatura igual a su aceleración dividida por 2π. Parecemos estar cayendo en la misma trampa de antes: la temperatura percibida depende de la posición. Lo que nos salva es que Anne también está experimentando un considerable desplazamiento gravitatorio al rojo en comparación con otro observador, digamos Bart, que permanece lejos del agujero negro. (En este contexto, «lejos» significa muchas veces el radio de Schwarzschild). Cuanto más se acerque Anne al horizonte, mayor será la temperatura de Unruh que perciba. Pero su desplazamiento gravitatorio al rojo incrementado significa que, para cuando la radiación que ella ve se escapa del campo gravitatorio del agujero negro y alcanza a Bart, estará a una temperatura finita que no cambia mientras Anne se acerca más y más al horizonte. Esta temperatura finita es la temperatura de Hawking, y multiplicándola por 2π obtenemos una cantidad llamada la gravedad superficial del agujero negro. La gravedad superficial es la aceleración que Alice tendría que conseguir en el espacio plano para ver la misma temperatura de la radiación de Unruh que ve Bart como radiación de Hawking[20].
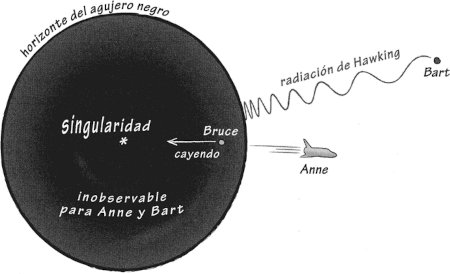
Figura 7.2. Esquema de la radiación de Hawking. Anne, que permanece a un radio fijo cerca del horizonte, es equivalente a un observador que acelera, debido a que siente el tirón gravitatorio. Ella ve la radiación por razones similares al efecto Unruh. Esa radiación se desplaza al rojo gravitatoriamente mientras se propaga hacia Bart, que también está estacionario, pero él está tan lejos del agujero negro que apenas siente su gravedad. El observador que cae, Bruce, no ve la radiación de Hawking mientras cruza el horizonte.
Dijimos antes que habíamos elegido los números para nuestro ejemplo del efecto Unruh por una razón concreta. De hecho, la aceleración de Alice, 1,5 billones de veces la aceleración gravitatoria de la Tierra, es casi igual a la gravedad de superficie en el horizonte de un agujero negro cuya masa
iguale la masa del Sol. Correspondientemente, la temperatura de Hawking de ese mismo agujero negro es la misma que la temperatura de Unruh que experimenta Alice, que es de 60 nanokelvin. Los agujeros negros mayores que ese tienen incluso unas temperaturas menores, inversamente proporcionales a su masa.
Nuestra descripción de la temperatura de Unruh ha enfatizado que un observador inercial en el futuro lejano (le llamamos Carol) observaría la verdad cuántica completa, es decir, que el estado cuántico de todo el espacio-tiempo es el vacío, sin ninguna excitación en absoluto. El estado térmico percibido de Alice comprende unas excitaciones de energía positiva que están entrelazadas mecanocuánticamente con excitaciones de energía negativa en la región del espacio-tiempo que ella no puede percibir. Resulta que hay análogos de estas afirmaciones en el caso de la radiación de Hawking, pero con algunas diferencias importantes. El observador estático al que hemos llamado Anne es el análogo más cercano al observador en aceleración Alice en nuestro tratamiento del efecto Unruh. Recuerda que, durante la mayor parte de esa discusión, Bob está más allá del horizonte que oculta a Alice la mitad del espacio-tiempo plano. Un análogo de Bob en el contexto del agujero negro sería un observador en caída libre, llamémosle Bruce, que cae dentro del horizonte del agujero negro. Bruce tiene un destino fatal, porque su futuro incluye con seguridad una colisión con la singularidad del agujero negro. Sin embargo, para un agujero negro grande, este destino infeliz puede retrasarse mucho tiempo, y es razonable preguntar qué observaciones hará Bruce durante ese lapso. La respuesta es que no observará ninguna temperatura en absoluto mientras cruza el horizonte, asumiendo que no esté llegando radiación al agujero negro desde ninguna otra fuente. Al menos localmente, cerca del horizonte del agujero negro, Bruce dirá que no hay excitaciones cuánticas en absoluto.
Las descripciones de Anne y Bart son diferentes de la de Bruce en que ellos sí ven partículas de energía positiva. Como ocurre en el caso del efecto Unruh, estas excitaciones de energía positiva deben estar ligadas mecanocuánticamente a excitaciones de energía negativa dentro del horizonte del agujero negro. Recuerda la naturaleza delicada de este tipo de argumentos: Bruce no ve realmente las excitaciones de energía negativa cuando cruza el horizonte hacia dentro; no ve ninguna excitación en absoluto. Las excitaciones de energía negativa dentro del horizonte se hacen necesarias solo para dar una explicación coherente de la teoría cuántica que incluya las perspectivas de Anne y Bart como observadores externos. Y, sin embargo, esas excitaciones peculiares tienen un papel físico importante. Sirven para reducir la masa total del agujero negro para compensar la energía que Anne y Bart dicen que está irradiando desde él.
Las excitaciones de energía positiva que salen y las excitaciones de energía negativa que entran están entrelazadas mecanocuánticamente, y al menos cerca del horizonte se puede argumentar que ese entrelazamiento sirve para mantener la teoría cuántica coherente entre un observador que cae adentro, como Bruce, y unos observadores estáticos como Anne y Bart. Es esta consistencia cuántica mediante el entrelazamiento lo que impulsa el efecto Hawking. Así, una sutileza tras otra acaban resultando en algo muy tangible: ¡una radiación de excitaciones de energía positiva desde el agujero negro!
Un contraste llamativo con el efecto Unruh es que resulta difícil organizar que un observador del futuro lejano pueda ver todo el espacio- tiempo, puesto que el interior del agujero negro no tiene ningún futuro lejano, y desde el exterior del agujero negro no podemos ver el interior. Tal vez, si el agujero negro se evapora por completo, un observador que observe el proceso entero pueda estar, de algún modo, en posesión de la verdad cuántica completa sobre el espacio-tiempo. O quizá ningún observador pueda ver la verdad completa sobre unos espacio-tiempos en que estén implicados agujeros negros, lo que significaría que la información sobre el estado cuántico se perdería literalmente. El enigma de cómo la evolución cuántica del pasado al futuro puede coexistir con los agujeros negros se conoce como la paradoja de la pérdida de información, y sigue debatiéndose hoy.
En suma, la imagen de la radiación de Hawking es que las excitaciones mecanocuánticas salen del agujero negro, desplazándose al rojo al hacerlo, y se perciben por un observador distante como un baño de radiación con una temperatura igual a la gravedad superficial del agujero negro dividida por 2π. En el proceso, la masa del agujero negro decrece lentamente o se evapora en correspondencia con la energía perdida por radiación. Hay cuestiones difíciles sobre la experiencia cuántica de los observadores que siguen distintas trayectorias en espacio-tiempos con agujeros negros que han dejado perplejas a generaciones de teóricos, pero, siempre que permanezcamos claramente fuera de un agujero negro, y siempre que el agujero negro en cuestión sea tan grande que no tenga tiempo de evaporarse por completo, lo que veremos será una radiación térmica a la temperatura de Hawking.
La radiación de Hawking es la propiedad termodinámica más celebrada de los agujeros negros. De igual importancia, sin embargo, es la entropía de Bekenstein-Hawking de los agujeros negros, llamada así por Jacob Bekenstein y Stephen Hawking. Recuerda que la entropía mide el número de estados cuánticos disponibles para un sistema. (Con más precisión, la entropía es el logaritmo del número de estados cuánticos disponibles). Su propiedad más importante es que, en procesos físicos, nunca decrece y normalmente aumenta. Otra propiedad importante es que la entropía de dos sistemas juntos no puede ser mayor que la suma de sus entropías separadas. En la materia ordinaria, lo más habitual es que la entropía de un todo sea la suma de las entropías de sus partes. Por ejemplo, la entropía de dos vasos de agua ordinarios a temperatura ambiente es el doble de la entropía de un solo vaso de agua. Si dos sistemas están entrelazados, su estado cuántico conjunto puede conocerse exactamente, en cuyo caso no tienen entropía en absoluto como un conjunto; y, sin embargo, ¡cada sistema por sí mismo puede tener una entropía considerable!
En el caso de los agujeros negros, la entropía resulta ser el área del horizonte dividida por una constante relacionada con la fuerza gravitatoria. La fórmula es S =A/4GN, donde GN es la constante de Newton, que también aparece en las ecuaciones de Einstein. Esta fórmula es tan central en las discusiones sobre los agujeros negros que habitualmente se la llama simplemente la ley del área. Los teoremas de la relatividad general clásica muestran que el área total de los horizontes de agujeros negros debe incrementarse en procesos como la colisión de agujeros negros. Este resultado se entiende como una versión para agujeros negros de la segunda ley de la termodinámica. Es importante subrayar que estos teoremas son de aplicación clásica, es decir, en ausencia de efectos cuánticos como la radiación de Hawking. En realidad, la radiación de Hawking hace que los agujeros negros pierdan masa lentamente, lo que implica que el área de su horizonte decrece; sin embargo, este proceso es extremadamente lento.
La ley del área muestra que los agujeros negros son muy diferentes de la materia termodinámica ordinaria. En efecto, la materia ordinaria suele tener una entropía que crece a escala con el volumen. Por ejemplo, recordemos que dos vasos de agua suelen tener el doble de la entropía que uno solo. También podemos decir que la entropía del agua crece a escala con la masa, puesto que dos vasos de agua tienen el doble de masa que uno solo. El hecho de que la entropía de los agujeros negros crezca con el área parece mostrar que los agujeros negros grandes tienen mucha menos entropía de la que podríamos haber esperado ingenuamente basándonos en su volumen, pero mucha más de la que esperaríamos basándonos en su masa. Para ver cómo funciona eso, supongamos que combinamos dos agujeros negros, cada uno con una masa solar, en un agujero negro mayor. Nuestra exposición solo va a ser aproximada, porque vamos a ignorar la explosión de ondas gravitatorias que saldría de la fusión, como vimos en el capítulo 6. Así que, ignorando eso, el agujero negro final tiene el doble de masa que los dos agujeros negros iniciales. La entropía real del agujero negro final es cuatro veces la entropía de cada agujero negro inicial. Eso es más de lo que esperaríamos según la masa, porque, si la entropía creciera con la masa, la entropía del agujero negro final sería solo del doble de la de uno de los agujeros negros iniciales. Pero es menos de lo que esperaríamos según el volumen, porque el agujero negro final tiene ocho veces el volumen de uno de los agujeros negros iniciales, pero solo tiene cuatro veces su entropía. La regla correcta de crecimiento emerge de pensar en la entropía como asociada al horizonte en sí mismo, como si un nuevo qubit de entropía se añadiera cada vez que el horizonte se incrementa en una cantidad proporcional a GN.
Una propuesta chocante, desarrollada originalmente por Bekenstein, es que los agujeros negros contienen más entropía que cualquier otra forma de materia que ocupe la misma región de espacio-tiempo. Una versión simple del argumento de Bekenstein es que, para que la materia ordinaria empaquetada en una región finita de espacio-tiempo tenga una gran cantidad de entropía, tiene que haber una gran cantidad de materia: tanta que estará amenazada por el colapso gravitatorio. Antes de que la materia ordinaria pueda exceder la entropía de un agujero negro, se colapsará, de hecho, para formar un agujero negro. En este sentido, el colapso de un agujero negro es el fenómeno más desordenado e irreversible posible.
La teoría de cuerdas aporta una justificación microscópica para la ley del área en ciertos contextos restringidos, pero en general no tenemos una derivación de la ley a partir de primeros principios. Ted Jacobson, sin embargo, ha argumentado que, asumiendo la termodinámica de los agujeros negros, en particular la ley del área, junto con unas nociones básicas de geometría diferencial, se pueden derivar las ecuaciones de Einstein que constituyen el corazón de la relatividad general. Más aún, se sabe que, si las ecuaciones de Einstein se modifican mientras se mantienen sus simetrías subyacentes, la ley del área cambia, pero el cálculo de Hawking permanece esencialmente igual. Así que se cree que la entropía de los agujeros negros es una herramienta muy refinada para describir la dinámica del espacio- tiempo. Aun así, ¿qué es exactamente la entropía de un agujero negro?
Juan Maldacena y Leonard Susskind han hecho una propuesta reciente para encajar mejor la entropía del entrelazamiento con la entropía de los agujeros negros. Se trata de lo siguiente. Recuerda la paradoja EPR, donde se entrelazan dos espines y luego se separan, y donde el punto confuso era que ninguno de los dos espines tiene un estado cuántico definido por sí mismo, aunque en conjunto sí lo tienen. Cada espín es un qubit, y cada uno por sí mismo tiene el equivalente a un qubit de entropía. ¿Podríamos imaginar, a algún nivel microscópico, que cada uno es un agujero negro, y que su entrelazamiento se manifiesta geométricamente como un agujero de gusano entre ellos? Hay dos objeciones obvias a esta idea. Primera, un agujero negro con solo un qubit de entropía es tan pequeño que la geometría puede no significar nada. Segunda, como vimos en el capítulo 3, los agujeros de gusano no se pueden atravesar. Para tratar de esquivar estas objeciones, empecemos por imaginar unos sistemas más grandes con más estados cuánticos disponibles, y por tanto mayores entropías. Pero insistamos en que dos de esos sistemas mayores, uno en posesión de Alice y otro de Bob, estén perfectamente entrelazados, de modo que su estado cuántico conjunto esté especificado con precisión. Previamente hemos ofrecido barras de magnesio puro como ejemplos de sistemas mayores, pero ahora queremos un estado de la materia más arcano, que después de un rato se colapsa en un agujero negro. Resumiendo, Alice y Bob acaban muy lejos uno de otro, cada uno en la vecindad de un agujero negro, y al menos una gran parte de la entropía de cada agujero negro se debe al entrelazamiento mecanocuántico entre los dos sistemas. Entonces, la propuesta es que un agujero de gusano conecta los agujeros negros, y que este agujero de gusano es una manifestación geométrica de su entrelazamiento.
¿Cómo podemos poner a prueba esta idea? Bien, hagamos un experimento mental en que Alice y Bob, cada uno por su cuenta, miden sus respectivos sistemas. Mirar de cerca un sistema en proceso de colapso gravitatorio es una tarea peligrosa, porque, con toda probabilidad, el observador será succionado al agujero negro en el proceso. Esto suena mal incluso desde el punto de vista conceptual, porque parece excluir la posibilidad de que Alice y Bob puedan hacer sus mediciones y luego compararlas para comprobar si sus sistemas están en verdad entrelazados. Pero ¡un momento! Hemos asumido que hay un agujero de gusano que conecta los dos agujeros negros. Alice y Bob pueden estar atrapados en sus respectivos agujeros negros, pero, debido al agujero de gusano, esos agujeros negros comparten el mismo interior. Es imposible para cada observador atravesar el agujero de gusano desde el exterior de uno al exterior del otro, pero realmente es posible que dos observadores que entran en el agujero de gusano desde los extremos opuestos se encuentren dentro de él. Así que Alice y Bob podrían, en efecto, comparar sus notas. Este es un buen punto a favor de la formación de un agujero de gusano, para empezar, porque, si tal agujero de gusano no se formara, Alice y Bob realmente no podrían comparar los resultados de sus mediciones, y la noción de entrelazamiento cuántico estaría en riesgo. Todo esto será un pobre consuelo para Alice y Bob, ya que, transcurrido un tiempo finito desde su entrada en sus respectivos agujeros negros, tendrán que colisionar contra la singularidad común que comparten. Pero, al menos, ¡podrán hacer un último test de la mecánica cuántica antes del final!
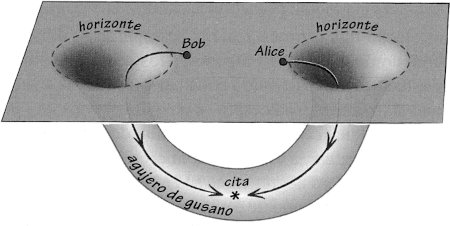
Figura 7.3. Un agujero de gusano que conecta regiones del espacio-tiempo cercanas a Alice y a Bob, respectivamente. Los agujeros de gusano que surgen de estados cuánticos entrelazados permiten a Alice y Bob encontrarse si ambos saltan dentro de agujeros negros. Entonces pueden verificar su entrelazamiento cuántico antes del impacto fatal con la singularidad del agujero negro.
Si damos un paso atrás desde esta discusión intensamente teórica, podemos preguntar razonablemente si hay algún interés práctico en los experimentos mentales del tipo que acabamos de ver, donde, como parte del experimento, los observadores tienen que zambullirse en un agujero negro. Los observadores que se queden fuera nunca podrán averiguar (al menos por métodos clásicos) si Alice y Bob llegaron o no a encontrarse. ¿Es todo esto una cuestión académica irrelevante? La sensación general entre los físicos teóricos es que no lo es. Debemos tener en mente que los horizontes de los agujeros negros son más una cuestión de destino futuro que de experiencia momentánea. Nosotros mismos podríamos estar en este momento cruzando hacia dentro de un agujero negro cósmico cuya futura singularidad está más allá en el futuro que la presente edad del universo. El colapso final puede ser un destino preferible a la interminable expansión del universo que imaginan muchos cosmólogos. ¿Puede algún tipo de destrucción creativa al final del espacio-tiempo mismo abrir nuestra percepción a unos paisajes con los que aún no hemos soñado?
No creemos en los viajes en el tiempo, y no nos dedicamos al misticismo. Pero ¿qué pasaría si pudiéramos escribir una carta a Albert Einstein para hablarle de la gravedad y los agujeros negros en unos cuantos párrafos? Que escribiríamos algo parecido a lo siguiente:
Julio de 2017
Querido Albert:
Lo primero, eres el más grande. La única ecuación de la física que conoce todo el mundo es E = mc2. La revista Time te nombró Persona del Siglo. Los chistes de Einstein ya no se cuentan mucho, porque cualquiera ve el final del chiste a kilómetros de distancia. Tenemos una millonada de armas nucleares, pero todavía no nos hemos hecho volar por los aires. De hecho, las bombas atómicas arrojadas al final de la segunda guerra mundial son las únicas que se han usado para matar gente intencionadamente.
Estamos, en nuestros días, verdaderamente interesados en la relatividad general y los agujeros negros porque un gran instrumento llamado LIGO ha detectado las ondas gravitatorias emitidas por una colisión de agujeros negros que ocurrió hace más de mil millones de años. Hemos escrito un libro sobre agujeros negros y, puesto que sabemos que estuviste profundamente interesado en la solución de Schwarzschild, y quizá a veces inseguro de su significación física, hemos pensado en hablarte de lo que ha pasado en los más de sesenta años que han transcurrido desde tu fallecimiento.
Primero, está esa cosa llamada horizonte de sucesos en la solución de Schwarzschild. Si lo atraviesas, no puedes volver atrás sin superar la velocidad de la luz. Si recuerdas la forma de la solución de Schwarzschild, había allí algunos rasgos extraños cuando el radio era igual a la masa hasta un factor de acoplamiento de Newton. En concreto, la parte temporal de la métrica se desvanece: es lo que ahora llamamos función de lapso. Ahí es donde está el horizonte de sucesos. La solución de Schwarzschild tiene también propiedades extrañas cuando el radio se hace cero, y nuestro mejor entendimiento es que esas propiedades extrañas marcan una singularidad espaciotemporal donde la propia geometría se deshace. Si entras en un agujero negro de Schwarzschild, estás destinado a encontrar la singularidad, pero no tenemos ni idea de lo que podría pasar a continuación... ni siquiera de si «a continuación» es la expresión correcta.
Ojalá pudieras haber visto todo el trabajo que se hizo en relatividad general en el par de décadas posteriores a tu muerte. John Wheeler estuvo en el ojo de ese huracán. (¡Y le conocimos! Vivió hasta 2008 y pasó un tiempo con nosotros en Princeton). Fue él quien popularizó el término «agujero negro» para describir la solución de Schwarzschild y las métricas relacionadas. Un neozelandés llamado Roy Kerr halló una generalización de la métrica de Schwarzschild que describe un agujero negro en rotación. ¡Es una métrica bastante complicada! Y es importante porque describe el estado final de las estrellas que colapsan, que siempre tienen algún momento angular distinto de cero.
Estamos muy seguros de que hay muchos agujeros negros en el universo. Tal y como Chandrasekhar, Tolman, Oppenheimer y Volkoff decían en los años treinta, si juntas demasiada masa, nada puede sujetarla. Es difícil calcular los números exactos, pero si, después de que una estrella consuma todo su combustible nuclear, quedan unas tres masas solares, se colapsará como un agujero negro. Lo que es más asombroso es que hay unos agujeros negros mucho mayores en el centro de las galaxias. La Vía Láctea tiene un agujero negro en su centro que contiene unos cuatro millones de masas solares. ¡No te tomamos el pelo! El consenso moderno es que muchas galaxias tienen unos agujeros negros mucho mayores en sus centros, tal vez con miles de millones de masas solares. No estamos seguros de cómo se formaron esos agujeros negros, pero en el caso de la Vía Láctea podemos estar seguros de su existencia trazando las órbitas de las estrellas individuales y viendo los efectos de la gravedad del agujero negro.
La detección de ondas gravitatorias por el LIGO fue maravillosa. LIGO es un gran interferómetro de Michelson, con cuatro kilómetros de lado. LIGO significa Observatorio de Ondas Gravitatorias por Interferometría Láser. Los láseres son esas increíbles fuentes de ondas monocromáticas, tan enfocadas y poderosas que podemos usarlas para soldar metales, pero tan baratas que las ponemos en los tocadiscos modernos en lugar de agujas. Aún no tenemos coches volantes, pero los láseres son muy chulos. Total, que el LIGO estaba justo preparándose para un experimento científico cuando llegó allí esa onda gravitatoria perfecta, que detectaron casi por accidente y pudieron casar con un molde que describe la fusión de dos agujeros negros, con unas treinta masas solares cada uno. Todo el mundo se impresiona una y otra vez con la relatividad general, porque tiene éxito al describir la región de campo fuerte cercana a los agujeros negros, donde el espacio-tiempo prácticamente se hace trizas, y también la región de campo lejano en que las ondas gravitatorias son susurros evanescentes que se deslizan por el espacio-tiempo.
Otra idea tuya que ha llegado muy lejos es la constante cosmológica. Aunque tú la llamaste tu mayor error, creemos ahora que está presente como una pequeña corrección a tus ecuaciones de campo. Lo cierto es que es importante a grandes escalas de longitud: los astrónomos no pueden explicar la evolución reciente del universo en expansión a menos que un gigantesco 70 % de toda la energía del universo provenga de la constante cosmológica, o al menos de algo que llamamos «energía oscura», y que se comporta de forma muy similar a ella. En vez de mantener el universo estático, como tú habías esperado cuando introdujiste por primera vez la constante cosmológica (agárrate a la silla), la energía oscura está empezando a acelerar el universo en un régimen de expansión exponencial. Caminando en otra dirección, la búsqueda de una teoría unificada ha conducido a un estudio intenso de los espacio-tiempos con una constante cosmológica negativa. La relatividad general en cinco dimensiones con una constante cosmológica negativa se conecta de manera natural con una teoría cuántica en la frontera tetradimensional del espacio-tiempo. ¡Es casi como si la teoría cuántica fuera una proyección de la relatividad general!
Estamos realmente seguros ahora de que la teoría cuántica es correcta (lo sentimos mucho). Un físico británico llamado Stephen Hawking demostró que la teoría cuántica implica que los agujeros negros emiten radiación, aunque a temperaturas muy bajas. Los agujeros negros también tienen una entropía tremendamente grande, pese a ser casi únicos como soluciones a tus ecuaciones de campo. Por si te hiciera sentir algo mejor, el artículo que escribiste con Podolsky y Rosen resultó ser importante. La gente está en nuestros días hasta intentando construir ordenadores mecanocuánticos utilizando ideas relacionadas con ese artículo.
Muchos profesores de Princeton ya no llevan corbata en el trabajo, pero la mayoría sí que llevamos calcetines. El lago Carnegie está tan bonito como siempre. No se ven muchos marineros allí, pero sí que ha habido un águila anidada justo en el borde del lago. Todavía no hemos encontrado una teoría unificada de campo, pero seguimos intentándolo. Lo mejor está aún por llegar.
Sinceramente tuyos:
Steve y Frans
Notas: