A Louise, Elizabeth y Gabrielle
En estas tres horas que hemos pasado caminando, dos sombras nos han acompañado, que nosotros mismos producimos; pero ahora que el Sol ha ascendido, estas dos sombras pisamos y a la espléndida claridad todo se ha reducido.
JOHN DONNE,
«Disertación sobre la sombra»
Cuando mis textos anteriores han tocado el tema de la historia, ha sido sobre todo la historia moderna de la física y la astronomía, más o menos desde finales del siglo XIX hasta la actualidad. Aunque en esta época hemos aprendido muchas cosas nuevas, las metas y criterios de la ciencia física no han cambiado desde el punto de vista material. Si a los físicos de 1900 se les pudiera enseñar el actual Modelo Estándar de la cosmología o de la física de las partículas elementales, una gran parte del modelo les llenaría de asombro, pero la idea de formular de manera matemática y validar experimentalmente unos principios impersonales que explican una amplia variedad de fenómenos les resultaría bastante familiar.
Hace tiempo decidí que necesitaba profundizar más, aprender más de una época anterior de la historia de la ciencia, cuando las metas y criterios de esta todavía no habían adquirido su forma actual. Como es natural en un profesor universitario, cada vez que quiero aprender algo me presento voluntario para impartir un curso sobre el tema. A lo largo de la década anterior, en la Universidad de Texas, de vez en cuando he impartido cursos sobre la historia de la física y la astronomía a alumnos que no tenían ninguna formación especial en el campo de la ciencia, la matemática o la historia. Este libro ha surgido de las notas de lectura para estos cursos.
Pero a medida que el libro evolucionaba, quizá he conseguido ofrecer algo que va un poco más allá de una simple narración: se trata de la perspectiva desde la que un científico actual en activo ve la ciencia del pasado. He aprovechado esta oportunidad para explicar mis opiniones acerca de la naturaleza de la física, y de su permanente vinculación con la tecnología, la filosofía, las matemáticas, la religión y la estética.
Antes de la historia existió la ciencia, más o menos. Si tomamos cualquier momento en el tiempo, la naturaleza nos presenta una amplia variedad de fenómenos desconcertantes: el fuego, las tormentas eléctricas, las plagas, el movimiento planetario, la luz, las mareas, etcétera. La observación del mundo condujo a generalizaciones útiles: el fuego quema, el trueno presagia la lluvia, las mareas son más altas cuando hay luna llena o luna nueva, etcétera. Todo ello acabó formando parte del sentido común de la humanidad. Pero de vez en cuando algunas personas deseaban algo más que una simple recopilación de hechos. Querían explicar el mundo.
No fue fácil. No es solo que nuestros predecesores no supieran lo que nosotros sabemos del mundo, sino, más importante aún, carecían de nuestra noción de qué hay que saber del mundo, y cómo aprenderlo. Una y otra vez, al preparar las clases de mi asignatura, me quedé impresionado al ver lo diferente que era la ciencia de los siglos anteriores a la de mi propia época. Tal como afirman las muy citadas líneas de una novela de L. P. Hartley: «El pasado es un país extraño; allí hacen las cosas de manera muy diferente a como las hacemos aquí». Espero que en este libro haya conseguido ofrecer al lector no solo una idea de lo que ocurrió en la historia de las ciencias exactas, sino también transmitir la sensación de lo difícil que ha resultado todo.
Por tanto, este libro no trata tan solo de cómo llegamos a aprender diversas cosas sobre el mundo, que es, naturalmente, el tema de cualquier historia de la ciencia. Lo que he pretendido en este libro es un poco distinto: se trata de cómo aprendimos a aprender lo que es el mundo.
No ignoro que la palabra «explicar» en el título de este libro puede suscitar algún problema para los filósofos de la ciencia, que ya han señalado la dificultad de distinguir de manera precisa entre la explicación y la descripción (algo que comentaré en el capítulo 8). Pero este libro trata más sobre la historia que sobre la filosofía de la ciencia. Lo que quiero dar a entender con la palabra «explicación» es algo impreciso, lo reconozco, lo mismo que queremos dar a entender en la vida cotidiana cuando intentamos explicar por qué un caballo ha ganado una carrera o por qué se ha estrellado un avión.
La palabra «descubrimiento» en el subtítulo también resulta problemática. Se me había ocurrido poner de subtítulo La invención de la ciencia moderna. Después de todo, la ciencia no existiría si los seres humanos no la practicaran. Elegí «descubrimiento» en lugar de «invención» para sugerir que la ciencia es como es no tanto a causa de diversas invenciones históricas y accidentales, sino porque la naturaleza es así. Con todas sus imperfecciones, la ciencia moderna es una técnica que se amolda lo suficiente a la naturaleza como para funcionar: una práctica que nos permite aprender cosas fiables acerca del mundo. En este sentido, se trata de una técnica que esperaba a que la gente la descubriera.
De este modo, podemos hablar del descubrimiento de la ciencia del mismo modo que un historiador puede hablar del descubrimiento de la agricultura. Con toda su variedad e imperfecciones, la agricultura es como es porque sus prácticas se amoldan lo suficiente a la realidad desde la biología como para que funcione: nos permite cultivar alimentos.
Con este subtítulo también pretendía distanciarme de los pocos constructivistas sociales que quedan: los sociólogos, filósofos e historiadores que intentan explicar no solo el proceso, sino incluso los resultados de la ciencia como productos de un entorno cultural específico.
Entre las ramas de la ciencia, este libro hará hincapié en la física y la astronomía. Fue en la física, sobre todo al aplicarla a la astronomía, donde la ciencia adquirió por primera vez una forma moderna. Naturalmente, algunas ciencias, como la biología, cuyos principios dependen en gran medida de accidentes históricos, solo pueden tomar como modelo la física hasta cierto punto. En los siglos XIX y XX, sin embargo, en cierto sentido el desarrollo de la biología científica, así como el de la química, siguió el modelo de la revolución de la física del siglo XVII.
La ciencia es ahora algo internacional, quizá el aspecto más internacional de nuestra civilización, pero el descubrimiento de la ciencia moderna ocurrió en lo que en términos generales podríamos denominar Occidente. La ciencia moderna aprendió sus métodos de la investigación llevada a cabo en Europa durante la revolución científica, que a su vez evolucionó de la labor realizada en Europa y en los países árabes durante la Edad Media, y en última instancia de la precoz ciencia de los griegos. Occidente tomó prestado gran parte del saber científico de otros lugares —la geometría de Egipto, los datos astronómicos de Babilonia, las técnicas aritméticas de Babilonia y la India, la brújula magnética de China, etcétera—, pero, que yo sepa, no importó los métodos de la ciencia moderna. Así que pondremos énfasis en Occidente (incluyendo el islam medieval) de la manera que tanto deploraban Oswald Spengler y Arnold Toynbee: no tengo gran cosa que decir de la ciencia fuera de Occidente, y nada en absoluto acerca del progreso interesante, pero completamente aislado, que tuvo lugar en la América precolombina.
Al relatar esta historia, me acercaré al pantanoso terreno que casi siempre evitan cuidadosamente nuestros historiadores contemporáneos: juzgar el pasado con los criterios del presente. Se trata de una historia irreverente; no soy reacio a criticar los métodos y teorías del pasado desde un punto de vista actual. Incluso me ha proporcionado cierta satisfacción descubrir unos cuantos errores cometidos por héroes científicos que nunca he visto mencionar a los historiadores.
Un historiador que dedica años a estudiar la obra de un gran hombre del pasado puede llegar a exagerar los logros de su héroe. Es algo que he visto en obras sobre Platón, Aristóteles, Avicena, Grosseteste y Descartes. Pero no es mi propósito acusar de estúpidos a los filósofos naturales del pasado. Más bien, al mostrar lo lejos que estaban esos inteligentísimos individuos de nuestra concepción actual de la ciencia, quiero mostrar lo difícil que fue descubrir la ciencia moderna, y lo poco obvias que eran sus prácticas y sus criterios. Esto también sirve como advertencia de que la ciencia quizá no ha adquirido todavía su forma definitiva. En diversos momentos de este libro sugiero que, por grande que sea el avance realizado en los métodos científicos, hoy en día podríamos estar repitiendo algunos de los errores del pasado.
Algunos historiadores de la ciencia han convertido en dogma el no referirse al conocimiento científico actual al estudiar la ciencia del pasado. Por el contrario, insistiré en utilizar el conocimiento actual para clarificar la ciencia anterior. Por ejemplo, aunque podría ser un interesante ejercicio intelectual intentar comprender cómo los astrónomos helenísticos Apolonio e Hiparco desarrollaron la teoría de que los planetas giran alrededor de la Tierra en órbitas circulares y epicíclicas utilizando tan solo los datos de que disponían, es algo que resulta imposible, pues muchos de los datos que utilizaron se han perdido. Pero sabemos que en la Antigüedad la Tierra y los planetas giraban alrededor del Sol en órbitas casi circulares, prácticamente igual que hoy, y, utilizando este conocimiento, seremos capaces de comprender cómo los datos de que disponían los antiguos astrónomos pudieron haberles sugerido su teoría de los epiciclos. En cualquier caso, ¿cómo es posible que hoy en día, al leer cualquier libro sobre astronomía antigua, olvidemos nuestros presentes conocimientos de lo que ocurre realmente en el sistema solar?
Para los lectores que deseen comprender en mayor detalle cómo las obras de los científicos anteriores encajan con lo que existe realmente en la naturaleza, he añadido unas «notas técnicas» al final del libro. No es necesario leer estas notas para seguir el texto principal, pero a algunos lectores podría servirles para aprender un poco de física y astronomía, tal como me ha pasado a mí al prepararlas.
La ciencia actual no es lo que era en sus comienzos. Sus resultados son impersonales. La inspiración y el juicio estético son importantes en el desarrollo de las teorías científicas, pero la verificación de estas teorías se basa en definitiva en pruebas experimentales e imparciales de sus predicciones. Aunque se utilizan las matemáticas a la hora de formular teorías físicas y calcular sus consecuencias, la ciencia no es una rama de las matemáticas, y las teorías científicas no se pueden deducir a partir de razonamientos puramente matemáticos. La ciencia y la tecnología se benefician mutuamente, pero en su nivel más básico, la ciencia no es una actividad que se emprenda por razones prácticas. Aunque la ciencia nada tiene que decir en un sentido o en otro de la existencia de Dios ni de la posibilidad de la vida después de la muerte, su meta es encontrar explicaciones a los fenómenos naturales que son puramente naturalistas. La ciencia es acumulativa; cada nueva teoría incorpora las teorías anteriores válidas como aproximaciones, e incluso explica por qué esas aproximaciones funcionan, caso de que así sea.
Todo esto de ningún modo les resultaba evidente a los científicos del mundo antiguo o de la Edad Media, y solo se aprendió con grandes dificultades en la revolución científica de los siglos XVI y XVII. Al principio, no había ninguna meta que se pareciera ni remotamente a la ciencia moderna. ¿Cómo es posible, entonces, que llegáramos a la revolución científica y a donde estamos ahora? Esto es lo que debemos intentar aprender mientras estudiamos el descubrimiento de la ciencia moderna.
Parte I
La física griega
Se podría argumentar hasta el infinito por qué fueron precisamente los griegos quienes lograron tantas cosas. Podría resultar significativo recalcar que la ciencia griega comenzó cuando los griegos vivían en pequeñas ciudades-estado independientes, muchas de ellas democracias. Pero como veremos, los griegos realizaron sus descubrimientos científicos más impresionantes después de que estos pequeños Estados quedaran integrados en grandes potencias: los reinos helenísticos y posteriormente el Imperio romano. En la época helenística y en la romana, los griegos llevaron a cabo contribuciones a la ciencia y las matemáticas que no se vieron significativamente superadas hasta la revolución científica europea de los siglos XVI y XVII.
Esta parte de mi relato de la ciencia griega trata de la física, y deja la astronomía griega para la segunda parte del libro. He dividido la primera parte en cinco capítulos, que tratan de manera más o menos cronológica sobre los cinco modos de pensamiento a los que la ciencia ha tenido que adaptarse: la poesía, las matemáticas, la filosofía, la tecnología y la religión. El tema de la relación de la ciencia con estos cinco ámbitos intelectuales será algo recurrente a lo largo de todo el libro. En primer lugar, dibujemos el marco. Allá por el siglo VI a. C., la costa oeste de lo que es hoy en día Turquía había estado colonizada durante una época por los griegos, que principalmente hablaban el dialecto jónico. La ciudad jónica más poderosa y rica era Mileto, fundada en un puerto natural cerca de donde el río Meandro desemboca en el mar Egeo. En Mileto, más de un siglo antes de la época de Sócrates, los griegos comenzaron a especular acerca de la sustancia fundamental de la que se componía el mundo.
Oí hablar por primera vez de los milesios cuando estudiaba en la Universidad de Cornell y seguía un curso de historia y filosofía de la ciencia. En ese curso oí que a los milesios se les llamaba «físicos». Al mismo tiempo también asistía a clases de física, en las que se nos hablaba de la teoría atómica moderna de la materia. Yo tenía la impresión de que la física milesia y la moderna tenían muy poco en común. No tanto por el hecho de que los milesios se equivocaran acerca de la naturaleza de la materia, sino más bien porque no alcanzaba a comprender cómo habían llegado a esas conclusiones. Los documentos históricos referentes al pensamiento griego antes de la época de Platón son fragmentarios, pero yo estaba bastante seguro de que durante la época arcaica y la clásica (aproximadamente desde el año 600 al 450 a. C., y del 450 al 300 a. C. respectivamente) ni los milesios ni ningún otro griego que estudiara la naturaleza razonaba de manera parecida a como lo hacían los científicos de nuestra época.
El primer milesio del que se tiene noticia es Tales, que vivió más o menos dos siglos antes de la época de Platón. Se cree que predijo un eclipse solar que sabemos que ocurrió en el año 585 a. C. y fue visible desde Mileto. Probablemente ni siquiera contando con los registros babilónicos de los eclipses podría haber llevado a cabo Tales esa predicción, pues cualquier eclipse solar es visible tan solo desde una región geográfica limitada, pero el hecho de que se le atribuyera esta predicción a Tales demuestra que la época de su madurez debió de transcurrir a principios del siglo VI a. C. No sabemos si Tales puso sus ideas por escrito. En cualquier caso, no ha sobrevivido ningún texto suyo, ni siquiera citado por un autor posterior. Se trata de una figura legendaria, una de esas figuras (como su contemporáneo Solón, que supuestamente redactó la Constitución ateniense) que de manera tradicional figuraba en la época de Platón como uno de los «siete sabios» de Grecia. Por ejemplo, Tales tiene fama de haber demostrado o importado de Egipto un famoso teorema de geometría (véase la Nota técnica 1). Lo que importa aquí es que, según se contaba, Tales sostenía la opinión de que toda la materia estaba compuesta de una sola sustancia fundamental. Según la Metafísica de Aristóteles: «La mayor parte de los primeros que filosofaron no consideraron los principios de todas las cosas sino desde el punto de vista de la materia […] Tales, fundador de esta filosofía, considera el agua como primer principio» [1]. Mucho después, Diógenes Laercio (fl. 230 d. C.), que escribió las biografías de los filósofos griegos, afirmó: «Su doctrina era que el agua era sustancia primordial y universal, y que el mundo es animado y lleno de divinidades» [2].
Al hablar de una «sustancia primordial y universal», ¿se refería Tales a que toda materia está compuesta de agua? Si es así, no tenemos ni idea de cómo llegó a esa conclusión, pero si alguien está convencido de que toda la materia está compuesta de una sustancia única y común, entonces el agua no es un mal candidato. El agua no solo se da en forma líquida, sino que también se puede convertir fácilmente en sólido congelándola, o en vapor hirviéndola. Es evidente que el agua también es esencial para la vida. Pero no sabemos si Tales consideraba que las piedras, por ejemplo, estaban realmente formadas de agua normal, o si solo existía algo profundo que la piedra y todos los demás sólidos poseían en común con el agua congelada.
Tales contaba con un alumno o compañero, Anaximandro, que llegó a una conclusión diferente. Él también opinaba que existía una sola sustancia fundamental, pero no la asociaba a ningún material corriente. Más bien la identificaba como una sustancia misteriosa que llamó lo ilimitado o infinito. Sobre este aspecto, contamos con la descripción que hace de sus opiniones Simplicio, un neoplatónico que vivió mil años después. Simplicio incluye lo que parece ser una cita directa de Anaximandro, que aquí indicamos en cursiva:
Entre aquellos que afirman que [el principio] es uno, está en movimiento y es ilimitado, Anaximandro, hijo de Praxíades, un milesio que se convirtió en sucesor y alumno de Tales, dijo que lo ilimitado es a la vez el principio y un elemento de las cosas que existen. Dice que no es ni el agua ni ningún otro de los así llamados elementos, sino algo de naturaleza ilimitada, de donde surgieron los cielos y los mundos que hay en ellos; y las cosas de las que surgen todo lo que existe son también aquellas adonde van a parar cuando se destruyen, conforme a cómo deben ser las cosas. Pues se otorgan mutuamente justicia y reparación por su ofensa conforme al orden del tiempo, hablando así de ellas en términos bastante poéticos. Y está claro que, tras haber observado cómo los cuatro elementos se transformaban el uno del otro, no le pareció adecuado elegir a ninguno como materia subyacente, sino otra cosa distinta de ellos.[3]
Un poco posteriormente, otro milesio, Anaxímenes, retomó la idea de que todo está compuesto de alguna materia común, aunque no consideraba que fuera el agua, sino el aire. Escribió un libro, del que solo nos ha llegado una frase: «El alma, al ser nuestro aire, nos controla, y el aliento y el aire circundan todo el mundo»[4].
Con Anaxímenes las aportaciones de los milesios tocaron a su fin. Mileto y otras ciudades jónicas de Asia Menor se vieron sometidas por la expansión del Imperio persa allá por el año 550 a. C. Mileto inició una revuelta en el 499 a. C. y fue asolada por los persas. Posteriormente revivió y se convirtió en una importante ciudad griega, pero nunca volvió a ser el centro de la ciencia griega.
La preocupación por la naturaleza de la materia pervivió fuera de Mileto, en otras ciudades jónicas. Existen indicios de que Jenófanes declaró que la tierra era la sustancia fundamental. Jenófanes había nacido en torno a 570 a. C. en Colofón, Jonia, y había emigrado al sur de Italia. En uno de sus poemas encontramos el verso siguiente: «Pues todas las cosas proceden de la tierra, y en la tierra acaban todas las cosas» [5]. Pero quizá esto no sea más que su versión del habitual sentimiento funerario: «Cenizas a las cenizas, polvo al polvo». Volveremos a encontrarnos con Jenófanes cuando abordemos la religión en el capítulo 5.
En Éfeso, no lejos de Mileto, en torno al 500 a. C. Heráclito enseñaba que la sustancia fundamental era el fuego. Escribió un libro, del que solo sobreviven algunos fragmentos. En uno de ellos leemos:
«Este ordenado kosmos[6], el mismo para todos, ninguno de los dioses y de los hombres lo ha creado, sino que existió siempre, existe y existirá en tanto que Fuego siempre vivo, encendiéndose hasta cierto punto y hasta cierto punto apagándose»[7].En otro fragmento Heráclito pone énfasis en los infinitos cambios de naturaleza, motivo por el cual le resultaba más natural tomar el parpadeante fuego —un agente de cambio— como elemento fundamental, antes que la tierra, el aire o el agua, que eran elementos más estables.
La opinión clásica de que toda la materia está compuesta no de uno, sino de los cuatro elementos —agua, aire, tierra y fuego— se debe probablemente a Empédocles, que vivió en Acragas (la moderna Agrigento), Sicilia, a principios del siglo V a. C., y que es el primero y casi el único griego en esta primera parte de nuestra historia que fue de origen dorio en lugar de jónico. Escribió sus poemas en hexámetros, de los que han sobrevivido muchos fragmentos. En De la naturaleza encontramos
«cómo de agua, tierra, éter y sol [fuego] al combinarse
surgieron formas y colores de los mortales seres»[8],
«de uno que era se disoció para ser múltiple:
fuego, agua, tierra y la enorme altura del aire
y, aparte de ellos, Odio pernicioso, por doquier igualado,
mas entre ellos la Amistad, igual en extensión y anchura que él» [9].
Estos presocráticos, desde Tales a Empédocles, al parecer consideraban los elementos como sustancias homogéneas e indiferenciadas. Una idea distinta que resulta más próxima a nuestra concepción actual se introdujo un poco posteriormente en Abdera, una población de la costa de Tracia fundada por refugiados de la revuelta de las ciudades jónicas en contra de Persia, que se inicia en el 499 a. C. El primer filósofo conocido de Abdera es Leucipo, del que solo sobrevive una frase, que sugiere una visión del mundo determinista: «Nada sucede en vano, sino que todo ocurre por una razón y una necesidad» [10]. Mucho más se sabe del sucesor de Leucipo, Demócrito. Nacido en Mileto, viajó por Babilonia, Egipto y Atenas antes de instalarse en Abdera a finales del siglo V a. C. Demócrito escribió libros sobre ética, ciencias naturales, matemáticas y música de los que sobreviven muchos fragmentos. Uno de ellos expresa la opinión de que toda la materia está formada por partículas diminutas e indivisibles llamadas átomos (que es la palabra griega que significa «indivisible») que se mueven en un espacio vacío: «Lo dulce existe por convención, al igual que lo amargo; [solo] los átomos y el Vacío existen en realidad»[11].
Al igual que los científicos modernos, esos primeros griegos estaban dispuestos a mirar debajo del aspecto superficial del mundo con la intención de encontrar un nivel más profundo de la realidad. A simple vista, no parece que la materia del mundo esté compuesta de agua, aire, tierra, fuego, ni de los cuatro elementos juntos, ni siquiera de átomos.
La aceptación de lo esotérico fue llevada al extremo por Parménides de Elea (la actual Velia), en el sur de Italia, que fue muy admirado por Platón. A principios del siglo V a. C., Parménides enseñaba, en contra de Heráclito, que el cambio aparente y la variedad de la naturaleza eran una ilusión. Sus ideas las defendió su pupilo Zenón de Elea (que no hay que confundir con otros Zenones, como por ejemplo Zenón el Estoico). En su libro Ataques, Zenón presentó diversas paradojas para demostrar la imposibilidad del movimiento. Por ejemplo, para cubrir todo el trayecto de una pista de carreras, primero es necesario cubrir la mitad de la distancia, y luego la mitad de la distancia que queda, y así hasta el infinito, de manera que es imposible cubrir la totalidad de la pista. Mediante el mismo razonamiento, por lo que podemos decir de los fragmentos que sobreviven, a Zenón le parecía imposible viajar a ninguna distancia, puesto que el movimiento es imposible.
Naturalmente, el razonamiento de Zenón era erróneo. Como luego señalaría Aristóteles [12], no existe ninguna razón por la que no podamos llevar a cabo un número infinito de pasos en un tiempo finito, siempre y cuando el tiempo necesario para cada paso sucesivo disminuya con la suficiente rapidez. Es cierto que una serie infinita como
1/2 + 1/3 + 1/4…
1/2 + 1/4 + 1/8…
posee una suma finita, que en este caso es igual a 1. Lo más sorprendente no es tanto que Parménides y Zenón se equivocaran como que no se molestaran en explicar por qué, si el movimiento es imposible, las cosas parecen moverse. De hecho, ninguno de los antiguos griegos, desde Tales a Platón, y tampoco los de Mileto, Abdera, Elea o Atenas, se molestaron en explicar en detalle de qué manera sus teorías acerca del componente primordial de la realidad justificaban el aspecto de las cosas.No se trata tan solo de pereza intelectual. Existía una veta de esnobismo intelectual entre los antiguos griegos que los llevó a considerar que no valía la pena comprender el aspecto de las cosas. Esto es tan solo un ejemplo de una actitud que ha ejercido una nefasta influencia en la historia de la ciencia. En diversas ocasiones se ha considerado que las órbitas circulares eran más perfectas que las elípticas, que el oro era más noble que el plomo y que el hombre es un ser superior a sus parientes simios.
¿Estamos cometiendo en la actualidad errores semejantes, estamos desperdiciando oportunidades para el progreso científico porque pasamos por alto fenómenos que parecen indignos de nuestra atención? No podemos estar seguros, aunque lo dudo. Naturalmente, no podemos examinarlo todo, sino que escogemos problemas que, de manera acertada o no, creemos que ofrecen la mejor perspectiva para la comprensión científica. Los biólogos que se interesan por los cromosomas o las células nerviosas estudian animales como la mosca de la fruta y los calamares, no las nobles águilas y los leones. A los físicos que estudian las partículas elementales a veces se les acusa de ocuparse de manera esnob de fenómenos que ocurren tan solo a los niveles de energía más altos alcanzables, pero ello se debe a que tan solo a esos altos niveles de energía podemos crear y estudiar de manera hipotética partículas de elevada masa, como las partículas de la materia oscura que, según los astrónomos, componen cinco sextas partes de la materia del universo. En cualquier caso, prestamos mucha atención a los fenómenos de baja energía, como la intrigante masa de los neutrinos, que es apenas una millonésima parte de la masa del electrón.
Al comentar los prejuicios de los presocráticos, no pretendo decir que en la ciencia no se den razonamientos apriorísticos. Por ejemplo, en la actualidad esperamos descubrir que nuestras leyes físicas más profundas satisfacen los principios de la simetría, que afirma que las leyes físicas no cambian cuando cambiamos nuestro punto de vista en ciertos aspectos concretos. Al igual que el principio de inmutabilidad de Parménides, algunos de estos principios de simetría no son inmediatamente aparentes en los fenómenos físicos: se habla de ruptura espontánea de la simetría. Es decir, las ecuaciones de nuestras teorías poseen cierta simplicidad; por ejemplo, tratan algunas especies de partículas de la misma manera, pero esta simplicidad no se aplica a las soluciones de las ecuaciones, que rigen los fenómenos reales. Sin embargo, contrariamente al compromiso de Parménides con lo inmutable, la presunción apriorística en favor de los principios de simetría surgió a partir de muchos años de experiencia en la búsqueda de principios físicos que describieran el mundo real, y tanto la simetría rota como la no rota quedan validadas por experimentos que confirman sus consecuencias. No implican los juicios de valor que aplicamos a los asuntos humanos.
Con Sócrates, a finales del siglo V a. C., y Platón, unos cuarenta años más tarde, el centro de la vida intelectual griega se trasladó a Atenas, una de las pocas ciudades de la Grecia jónica situada en la península Helénica. Casi todo lo que sabemos de Sócrates procede de su aparición en los diálogos de Platón, y de su presencia como personaje cómico en la obra de Aristófanes Las nubes. Parece ser que Sócrates no puso sus ideas por escrito, pero no parece que estuviera muy interesado en las ciencias naturales. En uno de los diálogos de Platón, Fedón, Sócrates recuerda lo decepcionado que quedó al leer un libro de Anaxágoras (hablaremos más de él en el capítulo 7), pues Anaxágoras describió la Tierra, el Sol, la Luna y las estrellas en términos puramente físicos, sin reparar en qué es lo mejor[13].
Platón, contrariamente a su héroe, Sócrates, era un aristócrata ateniense. Fue el primer filósofo griego del que conservamos muchas de sus obras en gran medida intactas. Platón, al igual que Sócrates, se interesó más por los asuntos humanos que por la naturaleza de la materia. Tenía la esperanza de llevar a cabo una carrera política que le permitiera poner en práctica sus ideas utópicas y antidemocráticas. En el año 367 a. C. Platón aceptó una invitación de Dionisio II para ir a Siracusa y ayudar a reformar su Gobierno, pero, por suerte para Siracusa, su proyecto de reforma acabó en nada.
En uno de sus diálogos, el Timeo, Platón combinó la idea de los cuatro elementos con el concepto abderitano de los átomos. Supuso que los cuatro elementos de Empédocles estaban formados por partículas cuya forma se correspondía a la de cuatro de los cinco cuerpos sólidos conocidos en matemáticas como poliedros regulares: cuerpos cuyas caras son todas polígonos idénticos, de aristas idénticas que se unen en vértices idénticos (véase la Nota técnica 2). Por ejemplo, uno de los poliedros regulares es el cubo, cuyas caras son todas cuadrados idénticos, y en cada vértice se unen tres cuadrados. Platón consideraba que los átomos de tierra tenían forma de cubo. Los otros poliedros regulares son el tetraedro (una pirámide con cuatro caras triangulares), el octaedro, de ocho caras, el icosaedro, de veinte caras, y el dodecaedro, de doce caras. Platón suponía que los átomos del fuego, el aire y el agua poseían, respectivamente, la forma del tetraedro, el octaedro y el icosaedro. Lo cual dejaba sin explicar el dodecaedro. Platón defendía que representaba el kosmos. Posteriormente Aristóteles introdujo un quinto elemento, o la quintaesencia, que, según él, llenaba el espacio por encima de la órbita de la Luna.
Al comentar estas primeras especulaciones es habitual considerar la naturaleza de la materia para recalcar hasta qué punto prefiguran los rasgos de la ciencia moderna. Demócrito es especialmente admirado; una de las principales universidades de la Grecia actual se denomina Universidad Demócrito. De hecho, el esfuerzo por identificar los constituyentes fundamentales de la materia prosiguió durante milenios, aunque el menú de elementos fue cambiando de época en época. Al comienzo de la era moderna los alquimistas habían identificado tres supuestos elementos: el mercurio, la sal y el azufre.
La moderna idea de los elementos químicos se remonta a la época de la revolución química instigada por Priestley, Lavoisier, Dalton y otros a finales del siglo XVIII, y en la actualidad incorpora 92 elementos que se dan de manera natural, desde el hidrógeno al uranio (incluyendo el mercurio y el azufre, pero no la sal), además de la lista cada vez más amplia de elementos más pesados que el uranio creados de manera artificial. En condiciones normales, un elemento químico puro está formado por átomos del mismo tipo, y los elementos se distinguen unos de otros por el tipo de átomo que los compone. Hoy en día no solo estudiamos los átomos, sino las partículas elementales que componen estos átomos aunque de una u otra manera seguimos indagando, en una empresa iniciada en Mileto, cuáles son los constituyentes fundamentales de la naturaleza.
Sin embargo, creo que no deberíamos insistir tanto en los aspectos modernos de la ciencia de la Grecia clásica o arcaica. Hay un importante rasgo de la ciencia moderna que no está presente de ninguna manera en los pensadores que he mencionado, desde Tales a Platón: ninguno de ellos intentó verificar y ni siquiera justificar (aparte quizá de Zenón) de manera fundamentada sus especulaciones. Al leer sus textos, uno se pregunta continuamente: «¿Cómo lo sabes?». Y esto se puede decir tanto de Demócrito como de los demás. En ninguno de los fragmentos de sus libros que sobreviven vemos el menor esfuerzo por demostrar que la materia realmente está compuesta de átomos.
Las ideas de Platón acerca de los cinco elementos son un buen ejemplo de su actitud despreocupada a la hora de justificar sus afirmaciones. En el Timeo, Platón comienza no con los poliedros regulares, sino con los triángulos, que propone unir para formar las caras de los poliedros.
¿Qué tipo de triángulos? Platón propone que debería ser el triángulo rectángulo isósceles, con ángulos de 45°, 45° y 90°; y el triángulo rectángulo escaleno con ángulos de 30°, 60° y 90°. Las caras cuadradas de los átomos cúbicos de tierra se pueden formar con dos triángulos rectángulos isósceles, y las caras triangulares de los átomos tetraédricos, octaédricos e icosaédricos del fuego, el aire y el agua (respectivamente) se pueden formar a partir de dos triángulos rectángulos escalenos. (El dodecaedro, que misteriosamente representa el cosmos, no se puede construir así).
Para explicar su elección, Platón, en el Timeo, afirma: «No obstante, si alguien pudiera descubrir y designar otro de esta misma clase que fuera aún más bello, que se lleve ese tal premio, veremos en él no un adversario sino un aliado […]. Por qué razón ello es así sería muy largo de demostrar. Pero no voy a discutir la recompensa a quien pueda descubrirlo y demostrarlo así»[14]. Me imagino hoy en día la reacción si yo sustentara una nueva conjetura acerca de la materia en un artículo de física afirmando que me llevaría demasiado tiempo explicar el razonamiento y desafiando a mis colegas a demostrar que la conjetura no es cierta.
Aristóteles llamó a los primeros filósofos griegos physiologi, palabra que a veces se traduce como «físicos» [15], aunque se trata de una interpretación errónea. La palabra physiologi significa simplemente «estudioso de la naturaleza» (physis), y los griegos de la Antigüedad tenían muy poco en común con los físicos de hoy en día. Sus teorías no nos dicen nada. Empédocles ya podía especular acerca de los elementos, y Demócrito acerca de los átomos, pero sus especulaciones no aportaban ninguna información nueva acerca de la naturaleza y, desde luego, no conducían a ningún método que permitiera poner a prueba sus teorías.
Me parece que para comprender a esos griegos de la Antigüedad es mejor considerarlos no como físicos o científicos, ni siquiera como filósofos, sino como poetas.
Debería aclarar lo que quiero dar a entender. Existe una concepción restringida de la poesía, en el sentido de que es un lenguaje que utiliza mecanismos verbales como el metro, la rima o la aliteración. Incluso ciñéndonos a esta concepción, Jenófanes, Parménides y Empédocles escribieron poesía. Después de las invasiones dóricas y la desintegración de la civilización micénica de la Edad del Bronce en el siglo XII a. C., los griegos pasaron a ser un pueblo en gran medida analfabeto. Sin escritura, la poesía es casi la única manera en que la gente se puede comunicar con las generaciones posteriores, pues es más fácil de recordar que la prosa. Los griegos volvieron a alfabetizarse allá por el 700 a. C., pero el nuevo alfabeto, que tomaron de los fenicios, fue utilizado por primera vez por Homero y Hesíodo para escribir poesía, parte de la cual consistía en los poemas recordados durante mucho tiempo procedentes de la Edad Oscura. La prosa vino después.
Incluso los primeros filósofos griegos que escribieron en prosa, como Anaximandro, Heráclito y Demócrito, adoptaron un estilo poético. Cicerón dijo de Demócrito que era más poético que muchos poetas. Platón, de joven, quiso ser poeta, y aunque escribía en prosa (y en su libro La República se mostró hostil a la poesía), su estilo literario siempre ha sido ampliamente admirado.
Pienso ahora en la poesía considerada en un sentido más amplio: en un lenguaje escogido por su efecto estético, más que para pretender decir claramente lo que uno cree que es cierto. Cuando Dylan Thomas escribe: «La fuerza que a través de la mecha verde impulsa la flor impulsa mis verdes años», no consideramos que se trate de una afirmación seria acerca de la unificación de las fuerzas de la botánica y la zoología, y no pretendemos verificarla; la consideramos (o al menos yo la considero) más bien una expresión de tristeza acerca de la edad y la muerte.
A veces parece claro que Platón no pretendía que lo interpretaran de manera literal. Un ejemplo mencionado con anterioridad consiste en su argumento, extraordinariamente pobre, a la hora de elegir dos triángulos como base de toda la materia. Y encontramos un ejemplo todavía más claro cuando, en el Timeo, Platón introduce la historia de la Atlántida, que supuestamente floreció miles de años antes de su época. Es imposible que Platón creyera en serio saber algo de lo que había ocurrido miles de años antes.
Con esto no pretendo decir que los primeros griegos decidieron escribir de manera poética para evitar que se corroboraran sus teorías. No sentían esa necesidad. Hoy en día ponemos a prueba nuestras especulaciones acerca de la naturaleza mediante teorías ya existentes para sacar conclusiones más o menos precisas que pueden ser puestas a prueba a través de la observación, algo que no ocurría con los griegos de la Antigüedad, ni con muchos de sus sucesores, por una razón muy sencilla: nunca habían visto que nadie lo hiciera.
A veces encontramos signos de que incluso cuando los griegos de la Antigüedad querían que se les tomara en serio, tenían dudas acerca de sus propias teorías, y consideraban que era imposible alcanzar un saber fidedigno. Utilicé un ejemplo en mi tratado de 1972 sobre la relatividad general. Como encabezamiento del capítulo sobre la especulación cosmológica, cité unas líneas de Jenófanes: «La verdad segura sobre los dioses y sobre todas las cosas de las que hablo/ no la conoce ningún humano y ninguno la conocerá./ Incluso aunque alguien anunciara alguna vez la verdad más acabada,/ él mismo no podría saberlo: todo está entreverado de conjetura»[16]. De modo parecido, en De las formas, Demócrito observó: «En realidad no sabemos nada con certeza», y: «Que en realidad no sabemos cómo es o no es cada cosa es algo que ha quedado demostrado en muchas maneras»[17].
En la física moderna sigue existiendo un elemento poético. No escribimos en verso, y gran parte de lo que escriben los físicos apenas alcanza el nivel de la prosa. Pero buscamos belleza en nuestras teorías, y utilizamos juicios estéticos como guía en nuestra investigación. Algunos consideramos que esto funciona porque siglos de éxitos y fracasos de la investigación física nos han acostumbrado a prever ciertos aspectos de las leyes de la naturaleza, y mediante esta experiencia hemos llegado a considerar que estos rasgos de las leyes naturales son hermosos [18]. Pero no consideramos la belleza de una teoría una prueba evidente de su verdad.
La teoría de cuerdas, por ejemplo, que describe los diferentes tipos de partículas elementales como modalidades distintas de vibración de diminutas cuerdas, es muy hermosa. Es una teoría coherente desde el punto de vista matemático, por lo que su estructura no es arbitraria, aunque en gran medida está fijada por el imperativo de la coherencia matemática. Así, posee la belleza de una forma artística rígida: un soneto o una sonata. Por desgracia, la teoría de cuerdas no conduce a ninguna predicción que pueda ser comprobada de manera experimental, y, como resultado, los teóricos (al menos casi todos ellos) todavía no tienen claro que la teoría de hecho pueda aplicarse al mundo real. Es esta insistencia en la verificación lo que más echamos de menos en todos los poetas estudiosos de la naturaleza, desde Tales a Platón.
Capítulo 2
Música y matemáticas
Es posible que el fenómeno que primero se estudiara mediante métodos aritméticos fuera la música, un estudio que fue obra de los seguidores de Pitágoras. Nativo de la isla jónica de Samos, Pitágoras emigró al sur de Italia en torno al 530 a. C. Allí, en la ciudad griega de Crotona, fundó una secta que perduró hasta el siglo IV a. C.
La palabra «secta» parece apropiada. Los primeros pitagóricos no dejaron textos escritos, pero según lo que nos relatan otros escritores [19], los pitagóricos creían en la transmigración de las almas. Al parecer llevaban túnicas blancas y tenían prohibido comer habas, porque esa legumbre se parecía al feto humano. Organizaron una especie de teocracia, y bajo su mandato el pueblo de Crotona destruyó la vecina ciudad de Síbari en el 510 a. C.
Lo que resulta relevante para la historia de la ciencia es que los pitagóricos también desarrollaron una gran pasión por las matemáticas. Según la Metafísica de Aristóteles[20], «los llamados pitagóricos se dedicaron por de pronto a las matemáticas, e hicieron progresar esta ciencia. Embebidos en este estudio, creyeron que los principios de las matemáticas eran los principios de todos los seres».
El énfasis que ponían en las matemáticas puede que surgiera de la observación de la música. Vieron que al tocar un instrumento de cuerda, si dos cuerdas de igual grosor, composición y tensión se pulsaban al mismo tiempo, el sonido era agradable si la razón entre la longitud de las cuerdas era un número entero pequeño. En el caso más simple, una cuerda es la mitad que la otra. En nuestra época, decimos que los sonidos de esas dos cuerdas están separados una octava, y catalogamos los sonidos que producen con la misma letra del alfabeto. Si una cuerda es dos tercios la longitud de la otra, las dos notas se dice que forman una «quinta», un acorde especialmente agradable. Si una cuerda es tres cuartas partes de longitud de la otra, entonces produce un acorde agradable llamado «cuarta». Por el contrario, si la razón entre dos cuerdas no corresponde a ningún número entero pequeño (por ejemplo, si la longitud de una cuerda es, pongamos, 100 000/314 159 la longitud de la otra), o la proporción ni siquiera es un número entero, entonces el sonido resulta discordante y desagradable. Ahora sabemos que ello obedece a dos razones que tienen que ver con la periodicidad del sonido producido por las dos cuerdas al sonar a la vez, y con la concordancia de los armónicos producidos por cada cuerda (véase Nota técnica 3). Los pitagóricos no sabían nada de todo esto, y de hecho no lo sabía nadie hasta que, en el siglo XVII, no se divulgó la obra del sacerdote francés Marin Mersenne. Por el contrario, los pitagóricos, según nos dice Aristóteles, consideraban que «el cielo en su conjunto es una armonía y un número»[21]. Esta idea pervivió durante mucho tiempo. Por ejemplo, Cicerón, en La República, nos cuenta una historia en la que el fantasma de Escipión el Africano, el gran general romano, introduce a su hijo en la música de las esferas.
Los pitagóricos hicieron sus mayores progresos en la matemática pura más que en la física. Todo el mundo ha oído hablar de el teorema de Pitágoras, según el cual, en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud) es igual a la suma de los cuadrados de los catetos (los dos lados menores, que conforman el ángulo recto). Nadie sabe si alguno de los pitagóricos demostró este teorema, ni cómo. Es posible ofrecer una demostración sencilla basándose en la teoría de las proporciones, una teoría debida al pitagórico Arquitas de Tarento, contemporáneo de Platón (véase la Nota técnica 4; la prueba[22] que aparece como Proposición 46 en el Libro I de los Elementos de Euclides es más complicada). Arquitas también resolvió un famoso problema: dado un cubo, construir otro cubo cuyo volumen sea exactamente el doble mediante métodos puramente geométricos.
El teorema de Pitágoras condujo directamente a otro gran descubrimiento: que en las construcciones geométricas pueden aparecer longitudes que no se pueden expresar como razones de números enteros. Si los dos catetos de un triángulo rectángulo poseen una longitud (en alguna unidad de medida) igual a 1, entonces el área total de los dos cuadrados con esas aristas es
12 + 12 = 2,
pues, según el teorema de Pitágoras, la longitud de la hipotenusa ha de ser un número cuyo cuadrado sea 2. Pero es fácil demostrar que un número cuyo cuadrado es 2 no se puede expresar en una razón de números enteros (véase Nota técnica 5). La prueba nos la ofrece el Libro X de los Elementos de Euclides, y la menciona anteriormente Aristóteles en su obra Primeros analíticos[23] como un ejemplo de reductio ad impossibile, pero sin darnos la fuente original. Existe la leyenda de que este descubrimiento se debe al pitagórico Hipaso, posiblemente nacido en Metaponto, en el sur de Italia, y que fue exiliado o asesinado por los pitagóricos por revelar su descubrimiento.Hoy en día podríamos describirlo como el descubrimiento de que los números como la raíz cuadrada de 2 son irracionales: no se pueden expresar como razones de números enteros. Según Platón[24], Teodoro de Cirene demostró que la raíz cuadrada de 3, 5, 6…, 15, 17, etcétera (es decir, aunque Platón no lo afirme, las raíces cuadradas de todos los números distintos a 1, 4, 9, 16, etcétera, que son los cuadrados de números enteros) son irracionales en el mismo sentido. Pero los griegos de la Antigüedad no lo habrían expresado así. Más bien, tal como aparece en la traducción de Platón, los lados de los cuadrados cuyas áreas son 2, 3, 5, etcétera pies cuadrados «no guardan proporción» con el pie entero. Los antiguos griegos solo concebían los números racionales, por lo que, para ellos, a la raíz cuadrada de 2 solo se le podía dar un significado geométrico, y esta limitación impidió que la aritmética siguiera desarrollándose.
Esta tradición de interesarse por la matemática pura prosiguió con la Academia de Platón. Al parecer había un cartel a la entrada que rezaba que no debía entrar nadie que no supiera nada de geometría. El propio Platón no era matemático, pero le entusiasmaban las matemáticas, quizá en parte porque, durante su viaje a Sicilia para hacer de preceptor de Dionisio el Joven de Siracusa, conoció al pitagórico Arquitas.
Uno de los matemáticos de la Academia que también tuvo una gran influencia sobre Platón fue Teeteto de Atenas, discípulo de Arquitas y personaje que da título a uno de los diálogos de Platón. Se atribuye a Teeteto el descubrimiento de los cinco sólidos regulares que, como hemos visto, proporcionaron una base a la teoría de los elementos de Platón. La prueba que aparece en los Elementos de Euclides, según la cual estos son los únicos sólidos regulares convexos posibles, podría deberse a Teeteto, que también realizó su aportación a la teoría de lo que denominamos números irracionales.
El matemático helénico más importante del siglo IV a. C. fue Eudoxo de Cnido, otro discípulo de Arquitas y contemporáneo de Platón. Aunque durante gran parte de su vida residió en la ciudad de Cnido, en la costa de Asia Menor, Eudoxo estudió en la Academia de Platón, a la que posteriormente regresó para dar clases. No nos ha llegado ningún texto de Eudoxo, pero se le atribuye la solución de un gran número de difíciles problemas matemáticos, como por ejemplo la demostración de que el volumen de un cono es un tercio del volumen del cilindro de la misma base y altura. (No tengo ni idea de cómo Eudoxo pudo hacerlo sin utilizar el cálculo matemático). Pero su mayor contribución a las matemáticas fue la introducción de un estilo riguroso en el que los teoremas se deducen de axiomas claramente expuestos. Es el estilo que posteriormente encontramos en los escritos de Euclides. De hecho, muchos detalles que aparecen en los Elementos de Euclides se han atribuido a Eudoxo.
Aunque el desarrollo de las matemáticas por parte de Eudoxo y los pitagóricos fue un gran logro intelectual en sí mismo, para las ciencias naturales fue un regalo envenenado. Para empezar, el estilo deductivo de la escritura matemática, consagrado por los Elementos de Euclides, fue imitado hasta la saciedad por aquellos que se dedicaban a las ciencias naturales, donde no resulta tan adecuado. Como veremos, en los escritos de Aristóteles sobre las ciencias naturales hay muy pocas matemáticas, aunque a veces suenan como una parodia del razonamiento matemático, como ocurre en su discusión del movimiento en la Física: «Así, el cuerpo A se desplazará a través del medio B en el tiempo C, y a través del medio D (que es menos denso) en el tiempo E; si las longitudes de B y D son iguales, los tiempos C y E serán proporcionales a la resistencia del medio. Sean entonces B agua y D aire» [25]. Quizá la obra capital de la física griega sea De los cuerpos flotantes, de Arquímedes, que comentaremos en el capítulo 4. Se trata de un libro escrito como un texto matemático, con postulados incuestionables seguidos de proposiciones deducidas de ellos. Arquímedes fue lo suficientemente inteligente como para elegir los postulados correctos, pero resulta más honesto presentar la investigación científica como una maraña de deducciones, inducciones y conjeturas.
Más importante que la cuestión del estilo, aunque relacionada con él, es la falsa meta inspirada por las matemáticas: alcanzar una verdad definitiva mediante el solo uso del intelecto. En su discusión de la educación de los reyes filósofos en La República, Platón hace argumentar a Sócrates que la astronomía debería practicarse del mismo modo que la geometría.
Según Sócrates, observar el cielo podría resultar un acicate para el intelecto, de la misma manera que mirar un diagrama geométrico podría ayudar en las matemáticas, pero en ambos casos el conocimiento real procede tan solo del pensamiento. Sócrates explica en La República que «para la práctica de la astronomía acudiremos a los problemas, lo mismo que cuando empleamos la geometría.
Dejaremos a un lado las cosas del cielo, si realmente queremos, ahondando en el estudio de la astronomía, obtener algún provecho de la parte inteligente que por naturaleza hay en el alma»[26].
Las matemáticas son el medio mediante el cual deducimos las consecuencias de los principios físicos. Más que eso: son el lenguaje indispensable en el que se expresan los principios de la física. A menudo inspiran nuevas ideas acerca de las ciencias naturales y, a su vez, las necesidades de la ciencia a menudo impulsan el desarrollo de las matemáticas. La obra del físico teórico Edward Witten ha arrojado tanta luz sobre las matemáticas que en 1990 se le concedió uno de los más altos galardones en esa materia, la Medalla Fields.
Pero las matemáticas no son una ciencia natural, pues en sí mismas, sin observación, no nos dicen nada del mundo. Y los teoremas matemáticos no se pueden verificar ni refutar mediante la observación de las cosas.
Eso no estaba del todo claro en la Antigüedad, y ni siquiera tampoco al principio de la era moderna. Hemos visto que Platón y los pitagóricos consideraban los objetos matemáticos, tales como los numerosos triángulos, componentes fundamentales de la naturaleza, y veremos que algunos filósofos consideraron la astronomía matemática como una rama de las matemáticas, y no de las ciencias naturales.
La distinción entre ciencia y matemáticas está ya bastante clara. Nos sigue resultando un misterio por qué las matemáticas, que se inventaron por razones que nada tienen que ver con la naturaleza, a menudo resultan ser útiles en las teorías físicas. En un famoso artículo [27], el físico Eugene Wigner se ha referido a «la irrazonable efectividad de las matemáticas». Pero por lo general no nos cuesta distinguir las ideas de las matemáticas de los principios de la ciencia, principios que en última instancia quedan justificados mediante la observación del mundo.
Los conflictos entre los matemáticos y los científicos surgen generalmente por la cuestión del rigor matemático. Desde principios del siglo XIX, los investigadores de las matemáticas puras han considerado el rigor como algo esencial; las definiciones y los postulados han de ser claros, y las deducciones han de seguirse con absoluta certeza. Los físicos son más oportunistas, y exigen tan solo una precisión y una certidumbre suficientes que les proporcionen una elevada probabilidad de evitar errores graves. En el prefacio a mi propio tratado sobre la teoría cuántica de campos, admito que «hay partes de este libro que harán llorar al lector con inclinaciones matemáticas».
Lo cual lleva a problemas de comunicación. Algunos matemáticos han dicho que los libros de física a menudo les parecen irritantemente imprecisos. Los físicos, como es mi caso, que necesitan herramientas matemáticas avanzadas, a menudo consideran que la búsqueda del rigor de los matemáticos complica sus textos de una manera que tiene poco interés para la física.
Se ha llevado a cabo un doble esfuerzo por parte de los físicos con más aptitudes para las matemáticas para formalizar la física de las modernas partículas elementales —la teoría cuántica de campos— sobre una base matemáticamente rigurosa, y se han llevado a cabo algunos progresos interesantes. Pero en el último medio siglo, el desarrollo del Modelo Estándar de ninguna manera se ha basado en alcanzar un mayor nivel de rigor matemático.
Las matemáticas de los antiguos griegos siguieron prosperando después de Euclides. En el capítulo 4 llegaremos a los grandes descubrimientos de matemáticos helenísticos posteriores, como Arquímedes y Apolonio.
Capítulo 3
Movimiento y filosofía
Macedonia acabó dominando el mundo griego después de que el ejército de Filipo derrocara a Atenas y Tebas en la batalla de Queronea, en el 338 a. C. Después de la muerte de Filipo, en el 336 a. C., Aristóteles regresó a Atenas, donde fundó su propia escuela, el Liceo. Fue una de las cuatro grandes escuelas de Atenas; las otras fueron la Academia de Platón, el Jardín de Epicuro y el Pórtico (o Stoa) de los estoicos. El Liceo prosiguió durante siglos, probablemente hasta que cerró después del saqueo de Atenas por parte de los soldados romanos a las órdenes de Sila en el 86 a. C. Mucho más sobrevivió la Academia de Platón, que bajo una forma u otra continuó hasta el año 529 de nuestra era, perdurando más que ninguna universidad europea hasta la fecha.
Las obras de Aristóteles que sobreviven parecen ser sobre todo notas para sus clases en el Liceo. Tratan de una asombrosa variedad de temas: astronomía, zoología, los sueños, la metafísica, la lógica, la ética, la retórica, la política, la estética, y lo que suele traducirse como «física». Según uno de sus traductores actuales[28], el libro de Aristóteles es « lacónico, compacto, abrupto, sus argumentos son condensados y su pensamiento denso», muy distinto del estilo poético de Platón. Confieso que Aristóteles me parece frecuentemente tedioso, algo que no ocurre con Platón, pero aunque a menudo Aristóteles está equivocado, no resulta estúpido, cosa que sí ocurre a veces con Platón.
Platón y Aristóteles son dos personas realistas, pero de una manera muy distinta. Platón era realista en el sentido medieval del término: creía en la realidad de las ideas abstractas, en particular de las formas ideales de las cosas. Lo que es real es la forma ideal de un pino, no los pinos individuales, que tan solo encarnan de manera imperfecta esa forma. Lo inmutable son las formas, tal como exigían Parménides y Zenón. Aristóteles era realista en el sentido moderno habitual: para él, aunque las categorías eran enormemente interesantes, lo real eran las cosas individuales, como por ejemplo cada uno de los pinos, y no las formas de Platón.
Aristóteles procuraba utilizar la razón y no la inspiración para justificar sus conclusiones. Podemos coincidir con el estudioso del mundo clásico R. J. Hankinson en que « no debemos perder de vista el hecho de que Aristóteles fue un hombre de su época, y para esa época fue extraordinariamente perspicaz, agudo y avanzado »[29]. No obstante, había principios que recorrían el pensamiento de Aristóteles que hubo que desaprender para poder descubrir la ciencia moderna.
Para empezar, la obra de Aristóteles está impregnada de teleología: las cosas son lo que son debido al propósito al que sirven. En la Física[30] leemos: « Pero la naturaleza es fin y aquello para lo cual; porque si en las cosas cuyo movimiento es continuo hay algún fin de ese movimiento, tal fin será su término extremo como aquello para lo cual ».
Este énfasis en la teleología era natural para alguien como Aristóteles, un hombre muy preocupado por la biología. En Asos y Lesbos Aristóteles estudió biología marina, y su padre, Nicómaco, había sido médico en la corte de Macedonia. Algunos amigos que saben más de biología que yo me dicen que los textos de Aristóteles sobre los animales resultan admirables. La teleología es algo natural para una persona que, como Aristóteles en su obra Partes de los animales, estudia el corazón o el estómago de un animal: es imposible que no se pregunte para qué sirve.
De hecho, hasta la obra de Darwin y Wallace en el siglo XIX, los naturalistas no llegaron a comprender que, aunque los órganos corporales tienen diversos propósitos, su evolución no tiene ningún propósito subyacente. Son lo que son porque han sufrido una selección natural a lo largo de millones de años de variaciones heredables no dirigidas. Y naturalmente, mucho antes de Darwin, los médicos habían aprendido a estudiar la materia y la fuerza sin pararse a preguntar cuál era su propósito.
El interés que al principio sintió Aristóteles por la zoología podría haber inspirado la importancia que le concedía a la taxonomía, a clasificar las cosas en categorías. Es algo que todavía utilizamos en parte; por ejemplo, la clasificación aristotélica de los gobiernos en democracias, aristocracias y tiranías. Pero en su mayor parte no tiene sentido. Me imagino cómo podría reclasificar Aristóteles los frutos: Todas las frutas vienen en tres variedades: hay manzanas, naranjas, y todas las frutas que no son ni manzanas y naranjas.
Hay una de las clasificaciones de Aristóteles que domina toda su obra, y que se convirtió en un obstáculo para el futuro de la ciencia. Él insistía en distinguir entre lo natural y lo artificial. Comienza el Libro II de la Física[31] afirmando: «Algunas cosas son por naturaleza, otras por otras causas». Solo lo natural era digno de su atención. Quizá fue esta distinción entre lo natural y lo artificial lo que impidió que Aristóteles y sus seguidores se interesaran por la experimentación. ¿De qué sirve crear una situación artificial cuando lo realmente interesante son los fenómenos naturales?
No es que Aristóteles descuidara la observación de los fenómenos naturales. A partir de la demora entre ver el rayo y escuchar el trueno, o entre ver los remos de una trirreme lejana y escuchar el sonido que producen al golpear el agua, concluyó que el sonido viajaba a una velocidad finita [32]. Veremos que también hizo uso de la observación para llegar a conclusiones acerca de la forma de la Tierra y de por qué se formaba el arcoíris. Pero todo esto eran observaciones fortuitas de los fenómenos naturales, no la creación de circunstancias artificiales con propósitos experimentales.
La distinción entre lo natural y lo artificial jugó un importante papel en el pensamiento de Aristóteles al abordar un problema de gran importancia en la historia de la ciencia: el movimiento de los cuerpos que caen. Aristóteles enseñaba que los cuerpos sólidos caen debido a que el lugar natural del elemento tierra es hacia abajo, hacia el centro del cosmos, y las chispas vuelan hacia arriba porque el lugar natural del fuego está en los cielos. La Tierra es prácticamente una esfera, con su centro en el centro del cosmos, porque eso permite que haya una mayor proporción de tierra que se acerque a ese centro. Además, si se le permite caer de manera natural, un cuerpo que cae posee una velocidad proporcional a su peso. Tal como leemos en De los cielos[33], según Aristóteles, «un peso dado se mueve a una distancia dada en un tiempo dado; un peso más grande se desplazará en la misma distancia en menos tiempo, pues el tiempo es inversamente proporcional al peso. Por ejemplo, si un peso es el doble de otro, tardará la mitad en recorrer el mismo espacio».
A Aristóteles no se le puede acusar de no observar los cuerpos que caen. Aunque no conocía la razón, la resistencia del aire o de cualquier otro medio que rodea a un cuerpo que cae hace que la velocidad acabe acercándose a un valor constante, la velocidad terminal, que no aumenta con el peso del cuerpo que cae (véase Nota técnica 6). Probablemente, para Aristóteles sea más importante el hecho de que la observación de que la velocidad de un cuerpo que cae aumenta con su peso encaja perfectamente con su idea de que el cuerpo cae porque el lugar natural de su materia se halla en dirección al centro del mundo.
Para Aristóteles, la presencia del aire o de algún otro medio era esencial para comprender el movimiento. Consideraba que, sin resistencia, los cuerpos se moverían a una velocidad infinita, un absurdo que lo condujo a rechazar la posibilidad de que existiera el espacio vacío. En la Física[34] argumenta: «Que no hay vacío separado, tal como algunos afirman, digámoslo de nuevo». Pero de hecho, es la velocidad terminal de un cuerpo que cae lo que resulta inversamente proporcional a la resistencia. La velocidad terminal sería de hecho infinita en ausencia de cualquier tipo de resistencia, pero en ese caso un cuerpo que cae nunca alcanzaría la velocidad terminal.
En el mismo capítulo, Aristóteles nos ofrece un argumento más sofisticado, que en el vacío no existiría nada a lo que el movimiento pudiera ser relativo: «así también en el vacío sería inevitable que un cuerpo estuviese en reposo, pues no habría un más o un menos hacia el cual se moviesen las cosas, ya que en el vacío como tal no hay diferencias»[35]. Pero este es un argumento que tan solo va en contra del vacío infinito; de otro modo, el movimiento en un vacío podría ser relativo a todo lo que estuviera fuera de ese vacío.
Como Aristóteles solo estaba familiarizado con el movimiento en presencia de una resistencia, creía que todo movimiento tiene una causa [36]. (Aristóteles distinguía cuatro tipos de causa: material, formal, eficiente y final, de las cuales la causa final es teleológica: es el propósito del cambio). Esta causa debe estar causada por otra cosa, y así sucesivamente, pero la secuencia de causas no puede ser infinita. Leemos en la Física[37]:
«Y puesto que todo lo que está en movimiento tiene que ser movido por algo, si una cosa es movida con movimiento local por otra que está en movimiento, y esta que mueve a su vez es movida por otra que está en movimiento, y esta última por otra, y así sucesivamente, tendrá que haber entonces un primer moviente ».La doctrina del primer motor (moviente) proporcionó posteriormente al cristianismo y al islam un argumento de la existencia de Dios. Pero como veremos, en la Edad Media la conclusión de que Dios no podía crear el vacío causó muchos problemas a los seguidores de Aristóteles tanto dentro del cristianismo como del islam.
A Aristóteles no le preocupaba el hecho de que las cosas no siempre se movieran hacia su lugar natural. Cuando uno tiene una piedra en la mano, esta no cae, pero para Aristóteles esto simplemente demostraba el efecto de la interferencia artificial en el orden natural. Pero le preocupaba seriamente el hecho de que una piedra arrojada hacia arriba siguiera subiendo durante un intervalo de tiempo, alejándose de la Tierra, después incluso de haber abandonado la mano. Su explicación, que en realidad no lo era, consistía en afirmar que la piedra sigue hacia arriba durante un intervalo por el movimiento que se le da mediante el aire. En el Libro III de De los cielos, explica que «la fuerza transmite el movimiento al cuerpo atándolo, por así decir, al aire. Por eso un cuerpo que se mueve mediante una restricción sigue moviéndose incluso cuando lo que le dio el impulso deja de acompañarlo» [38]. Como veremos, esta idea fue discutida a menudo y rechazada en la época antigua y la medieval.
El texto de Aristóteles sobre los cuerpos que caen es característico cuando menos de su física: un elaborado razonamiento basado en unos primeros principios asumidos, que a su vez se basan en observaciones fortuitas de la naturaleza, sin el menor interés en ponerlas a prueba.
Con ello no pretendo decir que la filosofía de Aristóteles fuera considerada por sus seguidores y sucesores una alternativa a la ciencia. En el mundo antiguo o medieval no existía ninguna concepción de la ciencia como algo distinto de la filosofía. Pensar en el mundo natural era filosofía. Incluso a finales del siglo XIX, cuando las universidades alemanas instituyeron el grado de doctor para estudiosos de las artes y las ciencias a fin de que tuvieran una categoría semejante a los doctores de teología, leyes y medicina, inventaron el título de «doctor en filosofía». Cuando anteriormente la filosofía se había comparado con alguna otra manera de reflexionar acerca de la naturaleza, no había sido con la ciencia, sino con las matemáticas.
Nadie en la historia de la filosofía ha tenido tanta influencia como Aristóteles. Como veremos en el capítulo 9, fue enormemente admirado por algunos filósofos árabes, e incluso de manera ciega por Averroes. En el capítulo 10 veremos cómo Aristóteles fue una gran influencia en la Europa cristiana del siglo XIII, cuando su pensamiento se reconcilió con el del cristianismo gracias a Tomás de Aquino. En plena Edad Media a Aristóteles se le conocía simplemente como «El Filósofo» y a Averroes como «El Comentarista». En el prólogo a Los cuentos de Canterbury, de Chaucer, se nos presenta a un estudioso de Oxford:
También había un clérigo de Oxenford […] pues prefería tener en el cabezal de su cama veinte libros de Aristóteles encuadernados en rojo y negro, y su filosofía, que ricas túnicas o un violín o un hermoso salterio.Naturalmente, ahora las cosas son diferentes. En la invención de la ciencia resultó fundamental separarla de lo que ahora se llama filosofía. Se sigue llevando a cabo una interesante labor en el campo de la filosofía de la ciencia, pero su influencia en la investigación científica es muy escasa.
La precoz revolución científica que comenzó en el siglo XIV, que relatamos en el capítulo 10, fue en gran medida una rebelión contra el aristotelismo. En los últimos años, los estudiosos de Aristóteles han comenzado una especie de contrarrevolución. El muy influyente historiador Thomas Kuhn narra cómo pasó de menospreciar a Aristóteles a admirarlo[39]:
Al hablar del movimiento, en concreto, sus escritos me parecían llenos de errores mayúsculos, pero también de lógica y observación. Estas conclusiones me parecían improbables. Después de todo, Aristóteles había sido el muy admirado codificador de la antigua lógica. Durante casi dos milenios después de su muerte, su obra jugó el mismo papel en la lógica que la de Euclides en la geometría […] ¿Cómo era posible que su singular talento le hubiera abandonado de manera tan sistemática al pasar estudiar el movimiento y la mecánica? Y del mismo modo, ¿por qué sus escritos sobre física se habían tomado tan en serio durante muchos siglos después de su muerte? […] De repente, los fragmentos que había en mi cabeza se ordenaron de una manera nueva y encajaron. La sorpresa me dejó boquiabierto, pues de repente Aristóteles parecía un físico realmente bueno, aunque de una clase que jamás había creído posible […] De repente había encontrado la manera de leer los textos de Aristóteles.Le oí estos comentarios a Kuhn cuando los dos recibimos un doctorado honoris causa de la Universidad de Padua, y posteriormente le pedí que me lo explicara. Su respuesta fue: «Lo que transformó mi primera lectura [de los textos de Aristóteles sobre física] fue mi comprensión, no mi evaluación, de lo que había conseguido». No lo comprendí: la frase «un físico realmente bueno» me parecía una evaluación.
Consideremos la falta de interés de Aristóteles por la experimentación: el historiador David Lindberg [40] observó: «La práctica científica de Aristóteles no se puede explicar, por tanto, como resultado de la estupidez ni de ninguna carencia por su parte —como ser incapaz de encontrar un procedimiento mejor—, sino como un método compatible con el mundo tal como él lo percibía y perfectamente adaptado a las cuestiones que le interesaban». Sobre la cuestión de más alcance de cómo juzgar el éxito de Aristóteles, Lindberg añadía: «Sería injusto y absurdo juzgar el éxito de Aristóteles por el grado en el que se adelantó a la ciencia moderna (como si su meta fuera responder a nuestras preguntas, y no a las suyas)». Y en la segunda edición de la misma obra escribió [41]: « Lo que mide el éxito de un sistema filosófico o de una teoría científica no es hasta qué punto se anticipa al pensamiento moderno, sino hasta qué punto consigue abordar los problemas científicos y filosóficos de su tiempo ».
No me lo tragué. Lo que es importante en la ciencia (dejo la filosofía a los demás) no es la solución de los problemas científicos más habituales de su tiempo, sino comprender el mundo. En el curso de esta obra, encontraremos qué tipo de explicaciones son posibles y qué tipo de problemas pueden conducir a esas explicaciones. El avance de la ciencia ha consistido en gran medida en descubrir qué preguntas se debían formular.
Naturalmente, hay que intentar comprender el contexto histórico de los descubrimientos científicos. Aparte de eso, la tarea del historiador depende de lo que intenta conseguir. Si su objetivo es tan solo recrear el pasado, comprender «cómo fue en realidad», entonces puede que no le resulte útil juzgar el éxito de un científico del pasado mediante criterios modernos. Pero este tipo de juicio es indispensable si lo que uno quiere es comprender cómo la ciencia progresó del pasado al presente.
Este progreso ha sido algo objetivo, no solamente una evolución de la moda. ¿Es posible poner en duda que Newton comprendió mejor el movimiento que Aristóteles, o que nosotros lo comprendemos mejor que Newton? Nunca ha sido muy fructífero preguntar qué movimientos son naturales, ni cuál es el propósito de este o del otro fenómeno físico.
Coincido con Lindberg en que sería injusto concluir que Aristóteles era estúpido. Mi propósito al juzgar el pasado mediante los criterios del presente es llegar a comprender lo difícil que resultaba, incluso para una persona tan inteligente como Aristóteles, aprender cómo estudiar la naturaleza. En la práctica de la ciencia moderna nada le parece evidente a alguien que nunca lo haya visto hacer.
Aristóteles abandonó Atenas a la muerte de Alejandro, en el 323 a. C., y murió poco después, en el 322. Según Michael Matthews
Capítulo 4
La física helenística y la tecnología
Esta época, desde Alejandro hasta Actium[42], se conoce normalmente como el periodo helenístico, un término (en alemán, Hellenismus) acuñado en la década de 1830 por Johann Gustav Droysen. No sé si esa fue la intención de Droysen, pero en mis oídos hay algo peyorativo en el sufijo inglés «istic». Al igual que la palabra inglesa «archaistic», por ejemplo, se usa para describir una imitación de lo arcaico, el sufijo parece dar a entender que la cultura helenística no era propiamente helénica, sino una mera imitación de los logros de la época clásica de los siglos V y IV a. C. Esos logros fueron muy importantes, sobre todo en geometría, teatro, historiografía, arquitectura y escultura, y quizá en las demás artes cuyas producciones clásicas no han sobrevivido, como por ejemplo la música y la pintura. Pero en la época helenística la ciencia alcanza unas cimas que no solo eclipsaron los logros científicos de la época clásica, sino que no tuvieron parangón hasta la revolución científica de los siglos XVI y XVII.
El centro vital de la ciencia helenística era Alejandría, la capital de los Ptolomeos, fundada por Alejandro en la desembocadura del Nilo. Alejandría se convirtió en la ciudad más importante del mundo griego; y posteriormente, durante el Imperio romano, solo fue superada por Roma en riqueza y tamaño.
Alrededor del 290 a. C., Ptolomeo I fundó el Museo de Alejandría, como parte de su palacio real. Originariamente tenía que ser un centro de estudios literarios y filológicos, dedicado a las nueve musas. Pero después de la ascensión al poder de Ptolomeo II, en el 285 a. C., el Museo se convirtió también en un centro de investigación científica. Los estudios literarios prosiguieron en el Museo y la Biblioteca de Alejandría, pero ahora, en el Museo, las ocho musas poéticas quedaron eclipsadas por su hermana científica, Urania, la musa de la astronomía. El Museo y la ciencia griega sobrevivieron al reinado de los Ptolomeos, y, como veremos, algunos de los más grandes logros de la ciencia de la Antigüedad ocurrieron en la mitad griega del Imperio romano, y en gran medida en Alejandría.
En la época helenística, las relaciones intelectuales entre Egipto y la patria griega se parecieron un poco a las relaciones entre Estados Unidos y Europa en el siglo XX[43]. La riqueza de Egipto y el generoso apoyo de al menos los tres primeros Ptolomeos consiguió llevar a Alejandría estudiosos que se habían labrado un nombre en Atenas, al igual que los sabios europeos acudieron a Estados Unidos a partir de la década de 1930. Alrededor del año 300 a. C., un antiguo miembro del Liceo, Demetrio de Falero (Demetrius Falerus), se convirtió en el primer director del Museo, y se trajo su biblioteca de Atenas. Más o menos en la misma época, Estratón de Lámpsaco, otro miembro del Liceo, fue llamado a Alejandría por Ptolomeo I para ser preceptor de su hijo, y es posible que fuera responsable del giro del Museo hacia la ciencia cuando ese hijo heredó el trono de Egipto.
Durante los periodos helenístico y romano, el tiempo que tardaba un barco de vela en ir de Atenas a Alejandría era parecido al tiempo que tardaba un vapor en ir de Liverpool hasta Nueva York en el siglo XX, y la gente viajaba a menudo entre Egipto y Grecia. Por ejemplo, Estratón no se quedó en Egipto; regresó a Atenas y se convirtió en el tercer director del Liceo.
Estratón era un observador muy agudo. Era capaz de concluir que los cuerpos que caían aceleraban en su descenso tras observar cómo las gotas de agua que caían de un tejado se iban separando al caer, cómo el continuo flujo de agua se dividía en gotas individuales. Ello se debe a que las gotas que han caído más lejos también son las que han caído durante más tiempo, y puesto que aceleran, esto significa que han viajado más deprisa que las gotas que las siguen, que llevan cayendo menos tiempo (véase Nota técnica 7). Estratón observó también que cuando un cuerpo cae desde muy poca distancia el impacto contra el suelo es insignificante, pero si cae desde más altura produce un impacto importante, lo que también demuestra que su velocidad aumenta en su caída [44].
Probablemente no sea ninguna coincidencia que los centros de la filosofía natural de Grecia, como Alejandría, Mileto y Atenas, fueran también los centros del comercio. Un mercado concurrido une a personas de diferentes culturas y alivia la monotonía de la agricultura. El comercio de Alejandría venía de lugares muy lejanos: cargamentos transportados en barco desde la India al mundo mediterráneo cruzaban el mar Arábigo, llegaban hasta el mar Rojo y desde ahí seguían por tierra hasta el Nilo, para luego bajar hasta Alejandría.
Pero el clima intelectual de Alejandría y Atenas era muy distinto. Para empezar, los estudiosos del Museo generalmente no aspiraban a elaborar teorías que lo abarcaran todo, como había ocurrido con los griegos desde Tales a Aristóteles. Como ha observado Floris Cohen [45]: «El pensamiento ateniense era global, y el alejandrino fragmentario». Los alejandrinos se concentraba en comprender fenómenos específicos, allí donde se podían hacer auténticos progresos. Estos temas incluían la óptica y la hidrostática, y por encima de todo la astronomía, el tema de la segunda parte de este libro.
No debemos echarles en cara a los griegos helenísticos que abandonaran el esfuerzo de formular una teoría general de todo. Una y otra vez se ha demostrado que un rasgo esencial del progreso científico ha sido comprender cuándo ha llegado el momento de abordar un problema y cuándo no. Por ejemplo, los principales físicos de principios del siglo XX, entre ellos Hendrik Lorentz y Max Abraham, se dedicaron a comprender la estructura del electrón, que se había descubierto recientemente. No sirvió de nada; nadie podía conseguir avanzar a la hora de comprender la naturaleza del electrón antes del advenimiento de la mecánica cuántica, ocurrido dos décadas después. El desarrollo de la teoría especial de la relatividad por parte de Albert Einstein fue posible porque este se negó a preocuparse de qué eran los electrones. En lugar de ello se preocupó por cómo la observación de cualquier cosa (incluidos los electrones) depende del movimiento del observador. El propio Einstein, en sus últimos años, abordó el problema de la unificación de las fuerzas de la naturaleza, y no llevó a cabo ningún progreso porque nadie en esa época sabía lo bastante de esas fuerzas.
Otra diferencia importante entre los científicos helenísticos y sus predecesores clásicos es que la época helenística adolecía menos de esa distinción esnob entre el saber en sí mismo y el saber utilitario: en griego, episteme comparado con techne (o en latín, scientia comparado con ars). A través de la historia, muchos filósofos han tenido a los inventores casi en la misma consideración que el chambelán de la corte, Filóstrato, tiene en El sueño de una noche de verano a Peter Quince y sus actores: «Ganapanes atenienses de manos callosas, que nunca han trabajado con la mente». Yo mismo, que trabajo en el campo de la física y mi investigación se centra en temas como las partículas elementales y la cosmología, sin ninguna aplicación práctica inmediata, desde luego no voy a decir nada en contra del saber en sí mismo, pero dedicarse a la investigación científica para satisfacer los anhelos humanos es una manera maravillosa de obligar a un científico a dejar de versificar y enfrentarse a la realidad [46].
Naturalmente, la gente se ha interesado por las mejoras tecnológicas desde que los primeros humanos aprendieron a utilizar el fuego para cocinar y a elaborar herramientas sencillas golpeando una piedra con otra. Pero el persistente esnobismo intelectual de los pensadores clásicos ha impedido que filósofos como Platón y Aristóteles intentaran dar una aplicación tecnológica a sus teorías.
Aunque este prejuicio no desapareció en la época helenística, perdió influencia. De hecho, las personas, incluso las que eran de origen humilde, podían hacerse famosas como inventores. Ctesibio de Alejandría, que era hijo de un barbero, inventó alrededor del 150 a. C. las bombas de succión y de fuerza, y un reloj de agua que daba la hora de manera más exacta que los anteriores relojes de agua manteniendo un nivel de agua constante en el recipiente del que fluía el agua. Ctesibio fue lo bastante famoso como para que el romano Vitruvio lo recordara dos siglos más tarde en su tratado De la arquitectura .
Es importante que parte de la tecnología de la época helenística la desarrollaran estudiosos que también se dedicaban a indagaciones científicas sistemáticas, que luego a veces se utilizaban en la tecnología. Por ejemplo, Filón de Bizancio, que pasó un tiempo en Alejandría alrededor del 250 a. C., fue ingeniero militar, y en la Mechanice syntaxism nos habla de puertos, fortificaciones, asedios y catapultas (un trabajo basado en parte en el de Ctesibio). Pero en la Neumática, Filón también ofreció argumentos experimentales que sustentaban las opiniones de Anaxímenes, Aristóteles y Estratón de que el aire es irreal. Por ejemplo, si una botella vacía se sumerge en el agua sin tapar y boca abajo, no entra agua, porque el aire que hay en el centro no puede ir a ninguna parte, pero si practicamos un agujero para que el aire pueda salir de la botella, entonces el agua entra y la llena [47].
Había un tema científico de importancia práctica al que los científicos griegos regresaban una y otra vez, incluso en el periodo romano: el comportamiento de la luz. Esta preocupación se remonta al comienzo de la era helenística, con la obra de Euclides.
Se sabe poco de la vida de Euclides. Se cree que vivió en la época de Ptolomeo I, y es posible que fuera el impulsor del estudio de las matemáticas en el museo de Alejandría. Su obra más conocida es Elementos[48], que comienza con algunas definiciones, axiomas y postulados geométricos y a continuación pasa a demostraciones más o menos rigurosas de teoremas cada vez más sofisticados. Pero Euclides también escribió la Óptica, que trata de la perspectiva, y su nombre también está asociado a la Catóptrica, que estudia el reflejo mediante espejos, aunque los historiadores modernos no creen que fuera el autor.
Cuando uno se para a pensarlo, hay algo peculiar en los reflejos. Cuando miras el reflejo de un objeto pequeño en un espejo plano, ves esa imagen en un punto definido, no desperdigada por todo el espejo. Sin embargo, hay muchas trayectorias que uno puede dibujar desde el objeto a diversos puntos del espejo y luego al ojo[49]. Pero al parecer, la luz solo sigue una trayectoria, de manera que la imagen aparece en el único punto en que esa trayectoria choca con el espejo. Pero ¿qué determina la localización de ese punto en el espejo? En la Catóptrica parece haber un principio fundamental que responde a esa cuestión: los ángulos que un rayo de luz forma con un espejo plano cuando llega al espejo y cuando se refleja son iguales. Solo una trayectoria puede satisfacer esa condición.
No sabemos quién descubrió ese principio en la época helenística. No obstante, sabemos que alrededor del año 60 de nuestra era, Herón de Alejandría, en su propia Catóptrica, proporciona una prueba matemática de la regla de los ángulos iguales, basada en su suposición de que la trayectoria que sigue un rayo de luz al ir del objeto al espejo y luego al ojo del observador es la trayectoria más corta (véase Nota técnica 8). Para justificar este principio, Herón se contentó con decir que «coincidimos en que la Naturaleza no hace nada en vano, ni obra sin necesidad» [50]. Quizá es una consecuencia de la teleología de Aristóteles: todo ocurre con un propósito. Pero Herón tenía razón; como veremos en el capítulo 14, en el siglo XVII Huygens fue capaz de deducir el principio de la distancia más corta (de hecho, el tiempo más corto) a partir de la naturaleza ondulatoria de la luz. El mismo Herón que exploró los fundamentos de la óptica utilizó sus conocimientos para inventar un instrumento de agrimensura práctica, el teodolito, y también explicó la acción de los sifones y diseñó catapultas militares y una primitiva máquina de vapor.
En Alejandría, el estudio de la óptica progresó en el año 150 de nuestra era gracias al gran astrónomo Claudio Ptolomeo (que no era pariente de los reyes). Su libro Óptica sobrevive en la traducción latina de una versión árabe perdida del también perdido original griego (o quizá hubo una versión siríaca intermedia). En su libro, Ptolomeo describió mediciones que verificaban la ley de los ángulos iguales de Euclides y Herón. También aplicó esa ley al reflejo de espejos curvos, como los que uno encuentra hoy en día en los parques de atracciones. Acertadamente comprendió que los reflejos en un espejo curvo son exactamente lo mismo que si el espejo fuera plano, tangentes al espejo en el punto de reflexión.
En el último libro de la Óptica, Ptolomeo también estudió la refracción, la curvatura de los rayos de luz cuando pasan de un medio transparente como el aire a otro transparente como el agua. Suspendió un disco, marcado con medidas de ángulo en los bordes, a mitad de camino de un recipiente de agua. Avistando un objeto sumergido a lo largo de un tubo montado sobre el disco, pudo medir los ángulos que formaban los rayos de incidencia y refracción con la normal, que es como se llama a la línea perpendicular a la superficie, con una exactitud que iba de una fracción de un grado a unos pocos grados [51]. Como veremos en el capítulo 13, la ley correcta relativa a esos ángulos la elaboró Fermat en el siglo XVII mediante una simple extensión del principio que Herón había aplicado a la reflexión: en la refracción, la trayectoria que sigue un rayo de luz que va del objeto al ojo no es la más corta, sino la que tarda menos tiempo. La distinción entre la distancia más corta y el menor tiempo es irrelevante para la reflexión, donde el rayo reflejado y el incidente pasan a través del mismo medio, y la distancia simplemente es proporcional al tiempo; pero importa para la refracción, pues la velocidad de la luz cambia a medida que el rayo pasa de un medio a otro. Eso era algo que Ptolomeo no comprendió; la ley correcta de la refracción, conocida como ley de Snell (o en Francia, ley de Descartes), no fue descubierta experimentalmente hasta principios del año 1600 de nuestra era.
El científico-tecnólogo más impresionante de la era helenística (o quizá de cualquier época) fue Arquímedes. Arquímedes vivió en el siglo III a. C. en la ciudad griega de Siracusa, Sicilia, pero se cree que al menos visitó Alejandría una vez. Se le atribuye la invención de diversas poleas y tornillos, y de diversas máquinas de guerra, como la «garra», basada en su comprensión de la palanca, con la que se podían capturar y volcar los barcos anclados cerca de la costa. Una invención utilizada en la agricultura durante siglos fue un gran tornillo, mediante el cual se podría subir el agua desde los arroyos para irrigar los campos. La historia de que Arquímedes, a la hora de defender Siracusa, utilizó espejos curvos para concentrar la luz del sol e incendiar los barcos romanos es casi con toda probabilidad una fábula, e ilustra su reputación de mago de la tecnología.
En Del equilibrio de los cuerpos, Arquímedes elaboró la ley que gobierna el equilibrio: una barra con pesos en ambos extremos se halla en equilibrio si la distancia a ambos extremos del fulcro sobre el que descansa la barra es inversamente proporcional a los pesos. Por ejemplo, una barra con cinco kilos en un extremo y un kilo en el otro está en equilibrio si la distancia del fulcro al peso de un kilo es cinco veces mayor que la distancia del fulcro al peso de cinco kilos.
El mayor logro de Arquímedes en el campo de la física se encuentra en su libro De los cuerpos flotantes[52]. Arquímedes razonó que si parte de un fluido sufre una presión mayor que otra mediante el peso del fluido o de algún cuerpo flotante sumergido, entonces el fluido se desplaza hasta que todas sus partes sientan la presión del mismo peso. Tal como él lo expresó:
Supongamos que un fluido es tal que sus partes son uniformes y continuas, y que la parte que sufre un empuje menor es desplazada por la que sufre un empuje mayor; y cada una de las partes es empujada por el fluido que está encima en una dirección perpendicular si el fluido está hundido en algo y comprimido por otra cosa.De aquí Arquímedes dedujo que un cuerpo flotante se hundía hasta un nivel tal que el peso del agua desplazada sería igual al de su propio peso. (Por eso el peso de un barco se llama su «desplazamiento»). Además, un cuerpo sólido que es demasiado pesado para flotar y está inmerso en el fluido, suspendido mediante una cuerda del brazo de una balanza, «será más ligero que su peso verdadero gracias al peso del fluido desplazado» (véase Nota técnica 9). La razón entre el auténtico peso del cuerpo y la disminución de su peso cuando está suspendido en el agua nos da la «gravedad específica» del cuerpo, la razón entre su peso y el peso del mismo volumen de agua. Cada material posee una gravedad específica característica: la del oro es 19,32, la del plomo 11,34, etcétera. Este método, deducido de un estudio teórico sistemático de la estática de fluidos, le permitió a Arquímedes saber si una corona estaba hecha de oro macizo o de oro al que le habían añadido metales más baratos. No está claro que Arquímedes pusiera alguna vez en práctica este método, pero fue utilizado durante siglos para juzgar la composición de los objetos.
Más impresionantes aún fueron los descubrimientos de Arquímedes en el campo de las matemáticas. Mediante una técnica que anticipó el cálculo integral, fue capaz de calcular las áreas y volúmenes de diversas figuras planas y cuerpos sólidos. Por ejemplo, el área de un círculo es el radio por cero coma cinco veces la circunferencia (véase Nota técnica 10). Utilizando métodos geométricos, fue capaz de demostrar que lo que llamamos pi (Arquímedes no utilizó ese término), la relación entre la circunferencia de un círculo y su diámetro está entre 31/7 y 310/17. Cicerón dijo que en la lápida de Arquímedes había visto una esfera circunscrita dentro de un cilindro, donde la superficie de la esfera tocaba los lados y las bases del cilindro, como una pelota de tenis que encaja perfectamente en su lata. Al parecer Arquímedes se mostraba orgulloso de haber demostrado que, en este caso, el volumen de la esfera es dos tercios el volumen del cilindro.
El historiador romano Tito Livio cuenta una anécdota de la muerte de Arquímedes, ocurrida en el 212 a. C., durante el saqueo de Siracusa por los soldados romanos a las órdenes de Marco Claudio Marcelo. (Siracusa había sido conquistada por una facción procartaginesa durante la Segunda Guerra Púnica). Mientras los soldados romanos se desperdigaban por la ciudad, se cuenta que Arquímedes fue asesinado por un soldado romano mientras intentaba resolver un problema de geometría.
Aparte del incomparable Arquímedes, el matemático helenístico más importante fue su joven contemporáneo Apolonio, que nació en el 262 a. C. en Perga, una ciudad de la costa sureste de Asia Menor, en aquel entonces bajo el control del reinado de Pérgamo, por entonces en pleno auge. Apolonio visitó Alejandría en la época de Ptolomeo III y Ptolomeo IV, que gobernaron desde el 247 al 203 a. C., y su obra más importante tiene que ver con las secciones cónicas: la elipse, la parábola y la hipérbole. Se trata de curvas que se pueden formar mediante un plano que atraviesa un cono en diversos ángulos. Mucho después, la teoría de las secciones cónicas fue crucial para Kepler y Newton, aunque en el mundo antiguo no encontró ninguna aplicación física.
A pesar de su brillante trabajo, sobre todo en la geometría, hay técnicas que echamos de menos en los matemáticos griegos y que resultan esenciales en la física moderna. Los griegos nunca aprendieron a escribir y manipular las fórmulas algebraicas. Fórmulas como E = mc2 y F = ma son parte indisoluble de la física moderna. (Las fórmulas las utilizó en obras puramente matemáticas Diofanto, que vivió en Alejandría allá por el año 250 de nuestra era, pero los símbolos de sus ecuaciones se limitaban a representar números enteros o racionales, algo muy distinto a los símbolos de las fórmulas de física). Incluso allí donde la geometría es importante, los físicos modernos suelen deducir lo que necesitan expresando los hechos geométricos de manera algebraica, con las técnicas de geometría analítica inventadas en el siglo XVII por René Descartes y otros, y descritas en el capítulo 13. Quizá por el merecido prestigio de los matemáticos griegos, el estilo geométrico persistió hasta bien entrada la revolución científica del siglo XVII. Cuando Galileo, en su libro de 1623 El ensayador, canta las alabanzas de los matemáticos, se refiere a la geometría [53]: «La filosofía está escrita en este libro omnipresente que se abre constantemente ante nuestros ojos, que es el universo; pero no se puede comprender a no ser que uno consiga comprender el lenguaje y conozca los caracteres en que está escrita. Está escrita en lenguaje matemático, y sus caracteres son triángulos, círculos y otras figuras geométricas; sin estos es humanamente imposible comprender ni una palabra, y uno acaba vagando en un laberinto oscuro». Galileo iba un poco por detrás de su tiempo al hacer más hincapié en la geometría que en el álgebra. En sus escritos utiliza el álgebra, pero es más geométrica que la de algunos de sus contemporáneos, y mucho más que la que se encuentra hoy en día en las publicaciones de física.
En la época moderna se le ha hecho un hueco a la ciencia pura, la que se investiga por sí misma, sin consideración a sus aplicaciones prácticas. En el mundo antiguo, antes de que los científicos aprendieran la necesidad de verificar sus teorías, la aplicación tecnológica de la ciencia tenía una especial importancia, pues cuando uno va a utilizar una teoría científica y no sólo a hablar de ella, la recompensa es muy grande si la teoría es acertada. Si Arquímedes, con sus mediciones de la gravedad específica, hubiera afirmado que una corona de plomo con un baño de oro estaba hecha de oro macizo, no habría sido muy popular en Siracusa.
No quiero exagerar hasta qué punto la tecnología basada en la ciencia era importante en la época helenística o en la romana. Muchos de los dispositivos de Ctesibio o de Herón parece ser que no eran más que juguetes o atrezo teatral. Los historiadores han especulado que en una economía basada en la esclavitud no había demanda de dispositivos que ahorraran mano de obra, como los que se podían haber desarrollado a partir de la máquina de vapor de juguete de Herón. La ingeniería civil y militar eran importantes en el mundo antiguo, y los reyes de Alejandría apoyaban el estudio de catapultas y otras armas de artillería, quizá en el Museo, pero no parece que se beneficiaran demasiado de la ciencia de su tiempo.
El campo en el que la ciencia griega tuvo un gran valor práctico fue aquel en el que había alcanzado un mayor desarrollo. Se trata de la astronomía, que abordaremos en la segunda parte.
Hay una importante excepción al comentario anterior de que la existencia de aplicaciones prácticas de la ciencia resulta un gran incentivo para que esta no sea errónea. Hasta la época actual, los médicos mejor considerados persistían en prácticas, como la sangría, cuyo valor nunca se había establecido experimentalmente, y que de hecho eran más perjudiciales que beneficiosas. Cuando en el siglo XIX se introdujo la técnica realmente útil de la antisepsis, una técnica para la que sí existía base científica, al principio muchos médicos se resistieron. Hasta bien entrado el siglo XX no se exigieron pruebas clínicas antes de aprobar el uso de un medicamento. Los médicos enseguida aprendieron a reconocer diversas enfermedades, y para ellas poseían remedios eficaces, como la corteza peruana —que contiene quinina— para la malaria. Sabían cómo preparar analgésicos, opiáceos, eméticos, laxantes, soporíferos y venenos. Pero a menudo se ha comentado que hasta más o menos el comienzo del siglo XX lo mejor que podía hacer cualquier persona enferma era evitar que se acercara ningún médico.
No es que no existiera ninguna teoría detrás de la práctica de la medicina. Existía la teoría humoral o de los cuatro humores: la sangre, la flema, la bilis negra y la bilis amarilla, que (respectivamente) nos convertían en sanguíneos, flemáticos, melancólicos o coléricos. La teoría humoral fue introducida en la época de la Grecia clásica por Hipócrates o por alguno de sus colegas cuyos textos se le han atribuido. Como afirmó muy posteriormente John Donne en «Los buenos días», la teoría sostenía que «cuando algo muere es que su mixtura no era proporcionada». La teoría humoral fue adoptada en la época romana por Galeno de Pérgamo, cuyos escritos fueron muy influyentes entre los árabes, y luego en Europa después del año 1000 de nuestra era. Aunque la teoría humoral fue generalmente aceptada, ignoro si se hizo un esfuerzo para poner a prueba su eficacia de manera experimental. (Hoy pervive la teoría en la Ayurveda, medicina tradicional india, pero solo con tres humores: aire, bilis y flema).
Además de la teoría de los humores, los médicos europeos, hasta la época moderna, debían comprender otra teoría de supuestas aplicaciones médicas: la astrología. Por irónico que parezca, el hecho de que los médicos pudieran estudiar estas teorías en la universidad hacía que los doctores en medicina disfrutaran de un prestigio mayor que los cirujanos, que sabían hacer cosas realmente útiles como reparar huesos rotos, pero que hasta la época moderna no estudiaron en la universidad.
Así pues, ¿por qué las doctrinas y prácticas de la medicina perduraron durante tanto tiempo sin que la ciencia empírica las corrigiera? Naturalmente, los avances son más difíciles en biología que en astronomía. Como comentaremos en el capítulo 8, los movimientos aparentes del Sol, la Luna y los planetas son tan regulares que era difícil no comprender cuándo una teoría no funcionaba; y esta percepción, al cabo de los siglos, llevaba a una teoría mejor. Pero si un paciente muere a pesar de todos los esfuerzos de un ilustre médico, ¿quién puede decir cuál es la causa? Quizá el paciente esperó demasiado para visitar al médico, o quizá no siguió sus órdenes con suficiente atención.
Al menos la teoría humoral y la astrología poseían un aire científico. ¿Cuál era la alternativa? ¿Volver a sacrificar animales a Asclepio?
Otro factor pudo haber sido la extrema importancia que tenía para los pacientes recuperarse de la enfermedad, lo que otorgaba a los médicos una autoridad sobre ellos, una autoridad que los médicos tenían que mantener para imponer sus supuestos remedios. Las personas que poseen autoridad siempre se resisten a cualquier investigación que pueda ponerla en entredicho, y no solo en el campo de la medicina.
Capítulo 5
Ciencia antigua y religión
Para el descubrimiento de la ciencia era esencial que las ideas religiosas se separaran del estudio de la naturaleza. Este divorcio llevó muchos siglos, y en la física no se acabó de completar hasta el siglo XVIII, e incluso entonces tampoco se aplicó a la biología.
No es que los científicos modernos decidieran desde el principio que no existía ningún ser sobrenatural. Eso es lo que yo creo, pero hay buenos científicos que son religiosos de verdad. Más bien, la idea es ver hasta dónde se puede llegar sin dar por supuesta una intervención sobrenatural. Solo así se puede practicar la ciencia, porque en cuanto uno invoca lo sobrenatural, se puede explicar cualquier cosa, y no se puede verificar ninguna explicación. Por eso la ideología del «diseño inteligente» que se promueve hoy en día no es ciencia, sino más bien la abdicación de la ciencia.
Las especulaciones de Platón están impregnadas de religión. En el Timeo describe cómo un dios colocó los planetas en sus órbitas, y es posible que incluso creyera que los propios planetas eran deidades. Incluso cuando los filósofos helénicos prescindieron de los dioses, algunos de ellos describieron la naturaleza en términos de valores y emociones humanos, algo que por lo general les interesaba más que el mundo inanimado. Como hemos visto al discutir los cambios en la materia, Anaximandro hablaba de justicia, y Empédocles de antagonismo. Platón pensaba que los elementos y otros aspectos de la naturaleza no eran dignos de estudio en sí mismos, sino porque para él ejemplificaban un tipo de bondad presente en el mundo natural y también en los asuntos humanos. Esta idea modelaba su religión, tal como encontramos en un pasaje del Timeo: «El Dios ha querido que todas las cosas fuesen buenas: ha dejado aparte, en la medida en que ello estaba en su mano, toda imperfección, y así ha tomado toda esa masa visible, desprovista de reposo y quietud, sometida a un proceso de cambio sin medida, y la ha llevado del desorden al orden, ya que estimaba que el orden vale infinitamente más que el desorden» [54].
Hoy en día, seguimos buscando el orden en la naturaleza, pero no creemos que sea un orden arraigado en valores humanos. Esta idea no ha satisfecho a todo el mundo. El gran físico del siglo XX Erwin Schrödinger habló en favor de un regreso al ejemplo de la Antigüedad [55] y a su fusión entre ciencia y valores humanos. En el mismo espíritu, el historiador Alexandre Koyré consideraba «desastroso»[56] el actual divorcio entre la ciencia y lo que ahora llamamos filosofía. Mi opinión es que este enfoque holístico a la hora de abordar la naturaleza es precisamente algo de lo que los científicos han tenido que desembarazarse, pues lo cierto es que en las leyes de la naturaleza no encontramos nada que se corresponda con las ideas de bondad, justicia, amor o antagonismo, y no podemos basarnos en la filosofía como vía fiable para el conocimiento científico.
No resulta fácil comprender exactamente de qué manera creían los paganos en su propia religión. Los griegos que habían viajado o leído mucho sabían que en los países de Europa, Asia y África se adoraba a una gran variedad de dioses y diosas, y algunos griegos intentaron verlos como las mismas deidades con diferentes nombres. Por ejemplo el devoto historiador Heródoto nos relata no que los egipcios nativos adoraran a una diosa llamada Bastet que se parecía a la diosa griega Artemisa, sino que adoraban a Artemisa con el nombre de Bastet. Otros suponían que estas deidades eran todas distintas y todas reales, e incluso adoraban a dioses extranjeros. Algunos de los dioses olímpicos, como Dionisio y Afrodita, habían sido importados de Asia.
Entre otros griegos, sin embargo, la multiplicidad de dioses y diosas llevaba al descreimiento. Es famoso el comentario del presocrático Jenófanes: «Los etíopes tienen dioses de nariz respingona y pelo negro, los tracios dioses de ojos grises y pelo rojo», y comentaba: «Pero si los bueyes (y los caballos) y los leones tuvieran manos o pudieran dibujar con las manos y crear obras de arte como las que crean los hombres, los caballos dibujarían a los dioses como caballos, y los bueyes como bueyes, y crearían los cuerpos [de sus dioses] de acuerdo con la forma que posee cada especie» [57]. En contraste con Heródoto, el historiador Tucídides no mostraba ningún signo de creencia religiosa. Criticó al general ateniense Nicias por la desastrosa decisión de suspender la evacuación de sus tropas de la campaña contra Siracusa por culpa de un eclipse lunar. Tucídides explicó que Nicias «tenía demasiada afición a la adivinación y cosas semejantes» [58].
El escepticismo se convirtió en algo muy corriente entre los griegos que se preocupaban por comprender la naturaleza. Como ya hemos visto, las especulaciones de Demócrito acerca de los átomos fueron completamente naturalistas, y sus ideas fueron adoptadas como un antídoto contra la religión, primero por Epicuro de Samos (341-271 a. C.), que se estableció en Atenas y al principio de la era helenística fundó la escuela ateniense conocida como el Jardín. A su vez, Epicuro inspiró al poeta romano Lucrecio, cuyo poema De la naturaleza de las cosas estuvo criando moho en las bibliotecas monásticas hasta su redescubrimiento en 1471, tras lo cual ejerció una gran influencia sobre el Renacimiento europeo. Stephen Greenblatt [59] ha rastreado el influjo de Lucrecio sobre Maquiavelo, Tomás Moro, Shakespeare, Montaigne, Gassendi[60], Newton y Jefferson. Incluso allí donde no se abandonó el paganismo, se observó una creciente tendencia entre los griegos a tomarlo de manera alegórica, como una clave para verdades ocultas. Tal como afirmó Gibbon: «La extravagancia de la mitología griega proclamaba, con una voz clara y audible, que el investigador devoto, en lugar de escandalizarse o quedar satisfecho con el sentido literal, debía explorar con perseverancia la sabiduría oculta que la prudencia de la Antigüedad había disfrazado con la máscara de la insensatez y la fábula»[61]. La búsqueda de sabiduría oculta condujo, en la época romana, a la aparición de la escuela que hoy en día conocemos como neoplatonismo, fundada en el siglo III de nuestra era por Plotino y su alumno Porfirio. Aunque no eran creativos desde el punto de vista científico, los neoplatónicos conservaron el interés de Platón por las matemáticas. Porfirio, por ejemplo, escribió una biografía de Pitágoras y un comentario a los Elementos de Euclides. Buscar significados ocultos debajo de la superficie es una de las grandes tareas de la ciencia, por lo que no parece sorprendente que los neoplatónicos conservaran al menos cierto interés por las cuestiones científicas.
A los paganos les interesaba más bien poco regular las creencias privadas de los demás. No existen fuentes escritas autorizadas de doctrinas religiosas paganas análogas a la Biblia o al Corán. La Ilíada y la Odisea, así como la Teogonía de Hesíodo, se tomaban como literatura, no como teología. El paganismo tenía muchos poetas y sacerdotes, pero no teólogos. No obstante, las expresiones abiertas de ateísmo eran peligrosas, al menos en Atenas, donde una acusación de ateísmo podía llegar a utilizarse como arma en un debate político, y los filósofos que expresaban incredulidad en el panteón pagano podían acabar sintiendo la cólera del Estado. El filósofo presocrático Anaxágoras fue obligado a abandonar Atenas por enseñar que el Sol no es un dios, sino una piedra caliente, más grande que el Peloponeso.
Platón, en concreto, se preocupó por preservar el papel de la religión en el estudio de la naturaleza. Le aterraban tanto las enseñanzas no teístas de Demócrito que decretó, en el Libro 10 de las Leyes, que en su sociedad ideal cualquiera que negara que los dioses eran reales e intervenían en los asuntos humanos sería condenado a cinco años de confinamiento solitario, a los que seguiría su muerte si el prisionero no se arrepentía.
En este punto, al igual que en muchos otros, el espíritu de Alejandría era muy distinto del de Atenas. No conozco ningún científico helenístico que manifieste en sus escritos ningún interés por la religión, ni tampoco ninguno que sufriera por su descreimiento.
La persecución religiosa no fue desconocida bajo el Imperio romano. Tampoco es que se pusiera ninguna objeción a los dioses extranjeros. El panteón de la etapa final del Imperio se amplió para incluir a la frigia Cibeles, a la egipcia Isis y al persa Mitra. Pero fueran cuales fueran las creencias que uno tuviera, había que jurar lealtad al Estado y también honrar públicamente la religión oficial. Según Gibbon, las religiones del Imperio romano «se consideraban igualmente ciertas por el pueblo, igualmente falsas por los filósofos e igualmente útiles por los magistrados» [62]. Los cristianos eran perseguidos no porque creyeran en Yahvé ni en Jesús, sino porque rechazaban en público la religión romana; generalmente se les exoneraba solo con que arrojaran una pizca de incienso en el altar de los dioses romanos.
Todo esto no interfirió con el trabajo de los científicos griegos bajo el Imperio romano. Hiparco y Ptolomeo nunca fueron perseguidos por sus teorías no teístas de los planetas. El devoto emperador Juliano criticó a los seguidores de Epicuro, pero no hizo nada para perseguirlos.
El cristianismo, aunque ilegal por su rechazo de la religión estatal, se extendió ampliamente por el Imperio en los siglos II y III. Lo legalizó en el año 313 Constantino I, y Teodosio I lo convirtió, en el año 380, en la única religión oficial del Imperio. Durante esos años, los grandes logros de la ciencia griega llegaron a su fin, por lo que, como es natural, los historiadores han acabado preguntándose si el ascenso del cristianismo tuvo algo que ver con el declive de aquella primitiva investigación científica.
En el pasado, la atención se había centrado en los posibles conflictos entre las enseñanzas de la religión y los descubrimientos de la ciencia. Por ejemplo, Copérnico dedicó su obra maestra De las revoluciones de las esferas celestes al papa Paulo III, y en su dedicatoria advirtió en contra de utilizar pasajes de las Sagradas Escrituras para contradecir la labor de los científicos. Citó como ejemplo execrable las opiniones de Lactancio, el tutor cristiano del hijo mayor de Constantino:
Pero si por casualidad hay algún «charlatán» que se arroga el derecho a emitir opiniones, aunque no sepa nada de matemáticas, y si de una manera desvergonzada distorsiona el sentido de algún pasaje de las Sagradas Escrituras para hacerlo venir bien a su propósito, y se atreve a censurar y atacar mi obra, me preocupa tan poco que tacharé sus opiniones de necias. Pues es sabido que Lactancio, que por lo demás es un escritor distinguido, pero de ningún modo un matemático, habla de una manera completamente infantil al referirse a la forma de la Tierra, y se ríe de aquellos que afirman que la Tierra tiene forma de globo[63].
Eso no era del todo justo. Lo que decía Lactancio es que era imposible que el cielo estuviera debajo de la Tierra [64]. Aducía que si el mundo fuera una esfera, entonces tendría que haber personas y animales que vivieran en las antípodas, lo cual es absurdo, pues no hay razón por la que la gente y los animales tengan que habitar todas las partes de una Tierra esférica. ¿Y acaso habría algo malo en que la gente y los animales vivieran en las antípodas? Lactancio sugiere que caerían hacia «la parte inferior del cielo». A continuación reconoce la opinión contraria de Aristóteles (al que no cita por su nombre), al afirmar que «está en la naturaleza de las cosas, a causa de su peso, verse atraídas hacia el centro de la Tierra», solo para acusar a aquellos que mantienen esta opinión de «defender un absurdo con otro absurdo». Naturalmente, es Lactancio quien dice cosas absurdas, pero al contrario de lo que sugería Copérnico, Lactancio no se basaba en las Escrituras, sino tan solo en un razonamiento extremadamente superficial acerca de los fenómenos naturales. Con todo, no creo que el conflicto directo entre las Escrituras y el conocimiento científico fuera una importante fuente de tensión entre el cristianismo y la ciencia.
Me parece que resultó mucho más importante el extendido parecer, entre los primeros cristianos, de que la ciencia pagana nos distraía de las cosas del espíritu, que deberían preocuparnos más, idea que se remonta al principio del cristianismo, a san Pablo, que advirtió: «Mirad que nadie os esclavice mediante la vana falacia de una filosofía, fundada en tradiciones humanas, según los elementos del mundo y no según Cristo» [65]. En este sentido, la más famosa afirmación se debe al padre de la Iglesia Tertuliano, que alrededor del año 200 preguntó: «¿Qué tiene que ver Atenas con Jerusalén, o la Academia con la Iglesia?». (Tertuliano escogió Atenas y la Academia para simbolizar la filosofía helénica, con la que, suponemos, estaba más familiarizado que con la ciencia de Alejandría). Encontramos una cierta desilusión con el saber pagano en el padre de la Iglesia más importante, Agustín de Hipona. Agustín estudió filosofía griega cuando era joven (aunque solo en traducciones latinas) y presumía de comprender a Aristóteles, aunque posteriormente se preguntaba: «¿Y de qué me servía tampoco que leyese y entendiese por mí mismo, y sin necesidad de maestro que me los explicasen, todos los libros de las artes que llaman liberales, cuantos pude haber a las manos, si me hallaba entonces delincuente esclavo de mis desordenados apetitos?»[66]. A Agustín también le preocupaban los conflictos entre el cristianismo y la filosofía pagana. Al final de su vida, en el 426, volvió la mirada hacia sus escritos anteriores y comentó: «Me han desagradado, además, los elogios que prodigué a Platón y a los platónicos, y a los filósofos de la Academia, mucho más de lo que era decoroso con hombres tan irreligiosos, sobre todo con aquellos contra cuyos errores la doctrina cristiana debe defenderse» [67].
Otro factor: el cristianismo ofrecía oportunidades de prosperar en la Iglesia a los jóvenes inteligentes, algunos de los cuales podrían haberse convertido en matemáticos o científicos. Los obispos y presbíteros generalmente estaban exentos de la jurisdicción de los tribunales civiles ordinarios, y de pagar impuestos. Un obispo como Cirilo de Alejandría o Ambrosio de Milán podía ejercer un considerable poder político, mucho más que un estudioso del Museo de Alejandría o de la Academia de Atenas. Eso era algo nuevo. Bajo el paganismo, los cargos religiosos habían ido a parar a hombres ricos o con poder político, en lugar de ir a parar la riqueza y el poder a los religiosos. Por ejemplo, Julio César y sus sucesores alcanzaron la dignidad de supremo pontífice, no como reconocimiento a su devoción o saber, sino a consecuencia de su poder político.
La ciencia griega sobrevivió durante un tiempo tras la adopción del cristianismo, aunque casi toda ella en forma de comentarios a trabajos anteriores. El filósofo Proclo, un neoplatónico del siglo V que trabajó en la Academia de Platón de Atenas, escribió un comentario sobre los Elementos de Euclides, con algunas aportaciones originales. En el capítulo 8 tendré ocasión de citar a un miembro posterior de la Academia, Simplicio, por sus observaciones, en un comentario a Aristóteles, acerca de las opiniones de Platón en relación con las órbitas planetarias. A finales del siglo IV encontramos a Teón de Alejandría, que escribió un comentario sobre la gran obra astronómica de Ptolomeo, el Almagesto, y preparó una edición mejorada de Euclides. Su famosa hija Hipatia se convirtió en líder de la escuela neoplatónica de la ciudad. Un siglo más tarde, en Alejandría, el cristiano Juan Filópono escribió comentarios sobre Aristóteles en los que disentía de las doctrinas de este referentes al movimiento. Juan afirmaba que si los cuerpos lanzados hacia arriba no caían de inmediato no se debía a que fueran transportados por el aire, como había creído Aristóteles, sino a que cuando eran lanzados se les aportaba alguna cualidad que los mantenía en movimiento, una idea que avanzaba la del impulso o el momento. Pero no hubo más científicos ni matemáticos creativos del calibre de Eudoxo, Aristarco, Hiparco, Euclides, Eratóstenes, Arquímedes, Apolonio, Herón o Ptolomeo.
Fuera debido o no al auge del cristianismo, incluso los comentaristas acabaron desapareciendo. En el 415 Hipatia fue asesinada por una turba instigada por el obispo Cirilo de Alejandría, aunque es difícil decir si fue por razones políticas o religiosas. En el 529, el emperador Justiniano (que lideró la reconquista de Italia y África, la codificación de la ley romana y la construcción de la basílica de Santa Sofía de Constantinopla) ordenó el cierre de la Academia neoplatónica de Atenas. Sobre este suceso, aunque Gibbon muestra predisposición contra el cristianismo, habla con tanta elocuencia que debemos citarlo:
Las armas góticas fueron menos fatales para las escuelas atenienses que la instauración de una nueva religión, cuyos ministros reemplazaron el ejercicio de la razón, resolvieron todas las cuestiones mediante un artículo de fe y condenaron a los infieles escépticos a las llamas eternas. En muchos volúmenes de laboriosa controversia defendieron la flaqueza del entendimiento y la corrupción del corazón, insultaron la naturaleza humana en los sabios de la Antigüedad y proscribieron el espíritu de la investigación filosófica, tan repugnante para la doctrina, o al menos para el temperamento, de un humilde creyente[68].La mitad griega del Imperio romano sobrevivió hasta el año 1453 de nuestra era, pero, como veremos en el capítulo 9, el centro vital de la investigación científica se había desplazado mucho antes hacia oriente, a Bagdad.
Parte II
La astronomía griega
El otro rasgo especial de la astronomía antigua es que resultaba útil, algo que no ocurría con la física de la Antigüedad. Los usos de la astronomía se comentan en el capítulo 6.
El capítulo 7 analiza lo que, a pesar de sus imperfecciones, se puede considerar como un triunfo de la ciencia helenística: la medida del tamaño del Sol, la Luna y la Tierra, y la distancia al Sol y a la Luna. El capítulo 8 aborda el problema planteado por el movimiento de los planetas, un problema que siguió preocupando a los astrónomos durante la Edad Media y que, con el tiempo, condujo al nacimiento de la ciencia moderna.
Capítulo 6
La utilidad de la astronomía[69]
Sabemos que las estrellas se utilizaron con un propósito similar muy al principio de la historia. Alrededor del año 3000 a. C. los egipcios sabían que el acontecimiento crucial de su agricultura, el desbordamiento del Nilo en junio, coincidía con la salida heliacal de la estrella Sirio. (Es el día del año en el que Sirio se hace visible por primera vez justo antes del amanecer; durante el año, antes de ese día no es visible por la noche, y posteriormente es visible mucho antes del amanecer). Homero, que escribió alrededor del 700 a. C., compara a Aquiles con Sirio, que se halla en lo alto al final del verano: «El astro que en el otoño se distingue por sus vivos rayos entre muchas estrellas durante la noche obscura y recibe el nombre de perro de Orión, el cual, con ser brillantísimo, constituye una señal funesta, porque trae excesivo calor a los míseros mortales»[70]. Un poco posteriormente, el poeta Hesíodo, en su obra Los trabajos y los días, les decía a los agricultores que el mejor momento para cosechar la viña era durante la salida heliacal de Arturo, y que había que arar en la puesta cósmica de la constelación de las Pléyades. (Es el día del año en el que esas estrellas se ven ponerse por primera vez justo antes del amanecer; en la época anterior del año, no se ponen antes de que el Sol aparezca, y luego se ponen bastante antes del amanecer). Siguiendo a Hesíodo, los calendarios conocidos como paramegmata, que marcaban la salida y el ocaso de las estrellas visibles cada día, fueron ampliamente utilizados por los griegos, cuyas ciudades-estado no compartían ninguna otra manera de identificar las fechas.
Al observar las estrellas por la noche, no oscurecidas por la luz de las ciudades modernas, los observadores de muchas de las primeras civilizaciones podían ver claramente que, con pocas excepciones (de las que hablaremos después), la posición relativa de las estrellas entre sí es siempre la misma. Por eso las constelaciones no cambian de una noche a otra, ni de un año a otro. Pero todo el firmamento de esas estrellas «fijas» parece girar cada noche de este a oeste alrededor de un punto del cielo que está siempre justo al norte, y de ahí que se conozca como polo norte celeste. En términos modernos, es el punto hacia el cual se extiende el eje de la Tierra si lo prolongamos del Polo Norte hacia el cielo.
Esta observación hizo posible que desde muy pronto los marineros utilizaran las estrellas para orientarse por la noche. Homero nos cuenta cómo Odiseo, en su regreso a Ítaca, se ve atrapado por la ninfa Calipso en su isla, situada en el Mediterráneo occidental, hasta que Zeus ordena a Calipso que deje proseguir su camino a Odiseo. La ninfa le dice a Odiseo que siga «la Osa, llamada el Carro por sobrenombre […] que tuviera la Osa a mano izquierda durante la travesía»[71]. La Osa, naturalmente, es la Osa Mayor, la constelación también conocida como el Carro, y en los tiempos modernos como el Cazo. La Osa Mayor está cerca del polo norte celeste. Así, en la latitud del Mediterráneo la Osa Mayor nunca se pone («nunca se bañaría ni se sumergiría en el océano», tal como lo expresa Homero), y está siempre más o menos al norte. Con la Osa a la izquierda, Odiseo sigue navegando hacia el este, rumbo a Ítaca.
Algunos griegos aprendieron a orientarse mejor con otras constelaciones. Según la biografía de Alejandro Magno escrita por Arriano, aunque casi todos los marineros de su época utilizaban la Osa Mayor para saber dónde estaba el norte, los fenicios, los mejores marinos del mundo antiguo, utilizaban la Osa Menor, una constelación no tan visible como la Osa Mayor, pero mucho más cercana al polo norte celeste. El poeta Calímaco, tal como lo cita Diógenes Laercio[72], afirmaba que el uso de la Osa Menor se remontaba a Tales.
Durante el día, también da la impresión de que el Sol gira de este a oeste en torno al polo norte celeste. Naturalmente, durante el día por lo general no podemos ver las estrellas, pero Heráclito[73], y quizá otros antes que él, parecen haber comprendido que las estrellas siempre están allí, aunque durante el día su luz quede apagada por la del Sol. Algunas estrellas se pueden ver justo antes del alba o poco después del ocaso, cuando la posición del Sol en el cielo es conocida, con lo que parece claro que el Sol no se mantiene en una posición fija en relación con las estrellas. Más bien, como se sabía perfectamente en Babilonia y la India desde mucho tiempo atrás, además de parecer que gira de este a oeste cada día junto con las estrellas, el Sol se mueve cada año alrededor del cielo de oeste a este, siguiendo un camino conocido como el zodíaco, cuyo orden señalan las constelaciones tradicionales de Aries, Tauro, Géminis, Cáncer, Leo, Virgo, Libra, Escorpio, Sagitario, Capricornio, Acuario y Piscis. Como veremos, la Luna y los planetas también se desplazan a través del zodíaco, aunque no precisamente siguiendo los mismos caminos. El trayecto concreto que sigue el Sol a través de estas constelaciones se conoce como la «eclíptica».
Una vez se comprendió el zodíaco, resultó fácil localizar el Sol en medio de las estrellas. Bastaba con fijarse en qué constelación del zodíaco estaba más alta en el cielo a medianoche; el Sol estaba en la constelación del zodíaco directamente opuesta. Se supone que fue Tales quien dio la cifra de 365 días como el tiempo que tarda el Sol en recorrer un circuito completo en el zodíaco.
Podríamos concebir el firmamento de las estrellas como una esfera que gira rodeando la Tierra, en la que el polo norte celestial queda encima del Polo Norte terrestre. Pero el zodíaco no es el ecuador de esta esfera. Más bien, como supuestamente descubrió Anaximandro, el zodíaco está inclinado 23,5° con relación al ecuador celeste, donde Cáncer y Géminis son los que están más cerca del polo norte celeste, y Capricornio y Sagitario los que están más lejos. En la época moderna, esta inclinación, que es responsable de las estaciones, se debe al hecho de que el eje de rotación de la Tierra no es perpendicular al plano de su órbita, que se halla bastante próximo al plano en el que se mueven casi todos los objetos del sistema solar, sino que está inclinado de la perpendicular en un ángulo de 23,5° ; en el verano septentrional, el Sol se halla en la dirección hacia la que se inclina el Polo Norte, y en el invierno septentrional se aleja de esa dirección.
La astronomía comenzó a ser una ciencia precisa con la introducción del dispositivo conocido como gnomon, que permitía una medida exacta de los movimientos aparentes del Sol. El gnomon, que el obispo del siglo IV Eusebio de Cesarea atribuye a Anaximandro, y Heródoto a los babilonios, no es más que un objeto vertical alargado que se coloca en un terreno horizontal al que llegan los rayos del sol. Con el gnomon uno puede saber con exactitud cuándo es mediodía; es el momento en el que el Sol está más alto, de manera que la sombra que proyecta es la más corta. A mediodía, en cualquier lugar que esté al norte de los trópicos, el Sol se halla justo al sur, y la sombra del gnomon apunta justo al norte, con lo que uno puede señalar de manera permanente en el terreno los puntos de la brújula. El gnomon también proporciona un calendario. Durante la primavera y el verano el Sol sale un poco al norte del este, mientras que en otoño e invierno sale al sur del este. Cuando, al amanecer, la sombra del gnomon apunta justo al oeste, el Sol sale justo al este, con lo que la fecha tiene que ser o bien el equinoccio vernal, cuando el invierno da lugar a la primavera, o el equinoccio de otoño, cuando acaba el verano y comienza el otoño. Los solsticios de verano e invierno son los días del año en los que la sombra del gnomon a mediodía es respectivamente la más corta o la más larga. (Un reloj de sol es diferente de un gnomon; el objeto vertical es paralelo al eje de la Tierra, no a la dirección vertical, de manera que su sombra, a una hora dada, queda cada día en la misma dirección, lo que hace que sea más útil como reloj, pero inservible como calendario).
El gnomon resulta un magnífico ejemplo del importante vínculo entre la ciencia y la tecnología: un artilugio tecnológico inventado para un propósito práctico puede abrir el camino a los descubrimientos científicos. Con el gnomon fue posible llevar un cómputo preciso de los días de cada estación, como por ejemplo el periodo que va de un equinoccio al solsticio siguiente, o desde ahí al siguiente equinoccio. Así fue como Euctemón, un contemporáneo ateniense de Sócrates, descubrió que la duración de las estaciones no era exactamente igual. Eso era lo que uno esperaría si el Sol girara alrededor de la Tierra (o la Tierra alrededor del Sol) en una órbita circular y a velocidad constante, con la Tierra (o el Sol) en el centro, en cuyo caso las estaciones serían de igual duración. Durante siglos los astrónomos intentaron comprender por qué las estaciones no eran todas iguales, pero la explicación correcta de esta y otras anomalías no llegó hasta el siglo XVII, cuando Johannes Kepler comprendió que la Tierra se mueve alrededor el Sol en una órbita elíptica y no circular, y que el Sol no se halla en el centro de la órbita, sino un poco desplazado a un lado, en un punto llamado foco, y se mueve a una velocidad que aumenta y disminuye a medida que la Tierra se acerca y se aparta del Sol.
Cada noche, la Luna también parece girar como las estrellas, de este a oeste en torno al polo norte celeste; y a la larga se desplaza, al igual que el Sol, a través del zodíaco de oeste a este, aunque tarda un poco más de 27 días, en lugar de un año, en completar un círculo sobre ese fondo de estrellas. Como el Sol parece moverse a través del zodíaco en la misma dirección, aunque más lentamente, la Luna tarda 29 días y medio en regresar a la misma posición relativa del Sol. (De hecho son 29 días, 12 horas, 44 minutos y 3 segundos). Puesto que las fases de la Luna dependen de la posición relativa de esta y del Sol, el intervalo de 29 días y medio es el mes lunar[74], el intervalo que hay entre dos lunas nuevas. Desde muy pronto se observó que los eclipses de luna ocurren durante la luna llena más o menos cada 18 años, cuando el trayecto de la Luna sobre el fondo de las estrellas se cruza con el del Sol[75].
En algunos aspectos, la Luna ofrece un calendario más práctico que el Sol. Al observar la fases de la Luna durante cualquier noche, uno puede saber con facilidad y de manera aproximada cuántos días han transcurrido desde la última luna nueva, mucho más fácilmente de lo que uno puede saber en qué época del año se encuentra simplemente mirando el Sol. Por ello, los calendarios lunares fueron corrientes en el mundo antiguo, y todavía sobreviven, por ejemplo, en el islam para fines religiosos. Pero, naturalmente, cuando se trata de la agricultura, la navegación o la guerra, uno tiene que prever los cambios de estación, y estos están gobernados por el Sol. Por desgracia, el año no posee un número entero de meses lunares —el año es aproximadamente 11 días más largo que los 12 meses lunares—, por lo que la fecha de los solsticios o los equinoccios no permanecería fija en un calendario basado en las fases de la Luna.
Otra complicación habitual es que el año mismo no es un número entero de días, lo que, en la época de Julio César, llevó a introducir un año bisiesto cada cuatro. Pero esto creó nuevos problemas, pues el año no posee exactamente 365 días y cuarto, sino que es 11 minutos más largo.
A lo largo de la historia se han producido incontables esfuerzos, demasiados para relatar aquí, para construir calendarios que tengan en cuenta exactamente estas complicaciones. Una aportación fundamental la llevó a cabo alrededor del 432 a. C. Metón de Atenas, que probablemente colaboraba con Euctemón. Quizá mediante el uso de los registros babilónicos, Metón observó que 19 años son exactamente 235 meses lunares, y solo difieren en dos horas. De manera que se podía crear un calendario que cubriera 19 años en lugar de uno, en el que la época del año y la fase de la Luna quedarían correctamente identificadas para cada día. El calendario se repetiría entonces para cada periodo sucesivo de 19 años. Pero aunque 19 años son exactamente 235 meses lunares, es más o menos un tercio del día menos que 6940 días, así que Metón tuvo que recomendar que, después de transcurridos un par de ciclos de 19 años, habría que descontar un día del calendario.
El esfuerzo de los astrónomos para reconciliar los calendarios basados en el Sol y la Luna queda ilustrado por la definición de la Pascua de Resurrección. El concilio de Nicea, celebrado en el año 325 de nuestra era, decretó que la Pascua se celebraría el primer domingo después de la primera luna llena posterior al equinoccio vernal. Durante el reinado de Teodosio I se declaró delito capital celebrar la Pascua el día equivocado. Por desgracia, la fecha exacta en la que se observa el equinoccio vernal varía de un lugar a otro en la superficie de la Tierra [76]. Para evitar el horror de que la Pascua se celebrara en días distintos en lugares distintos, fue necesario prescribir una fecha definida para el equinoccio vernal, y también para la primera luna llena posterior. La Iglesia romana de finales de la Antigüedad adoptó el ciclo metónico para este propósito, pero las comunidades monásticas de Irlanda adoptaron un ciclo judío más antiguo de 84 años. En el siglo VII, la pugna entre los misioneros romanos y los monjes irlandeses para controlar la Iglesia de Inglaterra fue sobre todo un conflicto por la fecha de la Pascua.
Hasta la época moderna, la construcción de calendarios ha sido una de las tareas más importantes de los astrónomos, lo que llevó a la adopción de nuestro moderno calendario del año 1582 bajo los auspicios del papa Gregorio XIII. Para calcular la fecha de la Pascua, el equinoccio vernal está fijado ahora en el 21 de marzo, pero es el 21 de marzo tal como lo da el calendario gregoriano en Occidente y el calendario juliano en las iglesias ortodoxas de Oriente. Así que la Pascua se sigue celebrando en días distintos en diferentes partes del mundo.
Aunque la astronomía científica encontró útiles aplicaciones en la era helenística, eso no impresionó a Platón. Encontramos un diálogo revelador entre Sócrates y su interlocutor Glaucón en La República[77]. Sócrates sugiere que la astronomía debería incluirse en la educación de los reyes filósofos, y Glaucón enseguida está de acuerdo: «Pues tanto para la labranza como para la navegación es conveniente conocer las estaciones, los meses y los años; y no digamos para la eficacia de la estrategia». Sócrates lo llama cándido. Para él, el sentido de la astronomía es que «con estas ciencias se purifica y reaviva el órgano del alma de cada uno […] Y es este órgano el que merece una atención mayor que diez mil ojos, pues solo por él puede contemplarse la verdad». Este esnobismo intelectual era menos corriente en Alejandría que en Atenas, pero aparece, por ejemplo, en el siglo I de nuestra era en los escritos del filósofo Filón de Alejandría, que observa que «lo que es apreciable por el intelecto es siempre superior a lo que es visible por los sentidos externos» [78]. Por suerte, quizá por la presión de las necesidades prácticas, los astrónomos aprendieron a no fiarse tan solo del intelecto.
Capítulo 7
La medición del sol, la luna y la tierra
En dicha labor fue esencial, en primer lugar, comprender la naturaleza de los eclipses de sol y de luna, y descubrir que la Tierra es una esfera. Tanto el mártir cristiano Hipólito como el filósofo Aecio, que vivió en el siglo I o el II de nuestra era, afirman que el primero que comprendió los eclipses fue Anaxágoras, un griego jónico nacido en torno al 500 a. C. en Clazómenas (cerca de Esmirna), que enseñaba en Atenas [79]. Quizá basándose en la observación de Parménides de que la Luna siempre está de cara al Sol, Anaxágoras concluyó que «es el Sol quien hace brillar la Luna»[80]. A partir de ello, resultaba natural inferir que los eclipses de luna ocurrían cuando esta cruzaba la sombra de la Tierra. También se cree que comprendió que los eclipses de sol ocurrían cuando la sombra de la Luna caía sobre la Tierra.
Sobre la forma de la Tierra, la combinación de razón y observación le resultó muy útil a Aristóteles. Diógenes Laercio y el geógrafo griego Estrabón atribuyen a Parménides el saber, antes que Aristóteles, que la Tierra es una esfera, pero no tenemos ni idea de cómo Parménides llegó a esta conclusión, si es que lo hizo. En De los cielos, Aristóteles aportó argumentos empíricos y teóricos para explicar la forma esférica de la Tierra. Como hemos visto en el capítulo 3, según la teoría deductiva de la materia de Aristóteles, los elementos pesados, la tierra y el agua (aunque esta no tanto) parecen acercarse al centro del cosmos, mientras que el aire y (más aún) el fuego tienden a alejarse de él. La Tierra es una esfera cuyo centro coincide con el centro del cosmos, porque ello permite que la mayor cantidad del elemento tierra se acerque a este centro. Aristóteles no se basó tan solo en este argumento teórico, sino que añadió pruebas empíricas para demostrar la forma esférica de la Tierra. La sombra que la Tierra proyecta sobre la Luna durante un eclipse lunar es curva[81], y la posición de las estrellas en el cielo parece cambiar a medida que viajamos al norte o al sur:
En los eclipses el perfil es siempre curvo, y puesto que es la interposición de la Tierra lo que provoca el eclipse, la forma de esa línea vendrá provocada por la forma de la superficie de la Tierra, que por tanto es esférica. Además, nuestra observación de las estrellas deja claro no solo que la Tierra es circular, sino también que es un círculo de no gran tamaño. Pues un pequeño cambio de posición por nuestra parte hacia el norte o hacia el sur provoca una manifiesta alteración del horizonte. Lo que quiero decir es que se da un gran cambio en las estrellas que están sobre nuestras cabezas, y las estrellas que vemos son diferentes a medida que vamos hacia el norte o hacia el sur. De hecho, hay algunas estrellas que se ven en Egipto y en la vecindad de Chipre que no se observan en las regiones septentrionales; y de igual modo, estrellas que en el norte se observan de manera permanente, en esas regiones salen y se ponen[82].Es característico de la actitud de Aristóteles hacia las matemáticas que no intente utilizar estas observaciones de las estrellas para llevar a cabo una estimación cuantitativa del tamaño de la Tierra. Aparte de ello, me parece desconcertante que Aristóteles no citara un fenómeno que debía de resultarle familiar a todo marinero. Cuando en un día claro se ve por primera vez en el mar un barco a gran distancia se dice «casco en el horizonte» —la curva de la Tierra oculta toda la nave menos la parte superior de sus mástiles—, pero, al acercarse, el resto del barco se hace visible [83].
El hecho de que Aristóteles comprendiera que la Tierra era redonda no era un logro despreciable. Anaximandro había creído que la Tierra era un cilindro, y que vivíamos sobre su cara plana. Según Anaxímenes, la Tierra es plana, mientras que el Sol, la Luna y las estrellas flotan en el aire, y quedan ocultos cuando se hallan detrás de las partes elevadas de la Tierra. Jenófanes había escrito: «Lo que tenemos a nuestros pies es el límite superior de la Tierra; pero la parte que hay abajo se extiende hasta el infinito»[84]. Posteriormente, tanto Demócrito como Anaxágoras creyeron, con Anaxímenes, que la Tierra era plana.
Sospecho que la creencia persistente de que la Tierra era plana quizá se debiera al problema evidente que plantea una Tierra esférica: si la Tierra es una esfera, ¿por qué entonces los viajeros no se caen? Esta cuestión quedaba perfectamente contestada con la teoría de la materia de Aristóteles, que comprendió que no existe una dirección universal «hacia abajo» que sigan al caer los objetos colocados en cualquier parte. Más bien, en todas las partes de la Tierra los objetos compuestos por los elementos pesados, la tierra y el agua, tienden a caer hacia el centro del mundo, de acuerdo con la observación.
A este respecto, la teoría de Aristóteles de que el lugar natural de los elementos más pesados es el centro del cosmos funcionaba como la moderna teoría de la gravitación, con la importante diferencia de que para Aristóteles había tan solo un centro del cosmos, mientras que ahora comprendemos que cualquier masa grande tiende a contraerse hasta formar una esfera bajo la influencia de su propia gravitación, y que entonces atrae a otros cuerpos hacia su centro. La teoría de Aristóteles no explicaba por qué cualquier cuerpo distinto de la Tierra debería ser una esfera, y sin embargo sabía que la Luna, cuando menos, era una esfera, algo que podía deducir del cambio gradual de sus fases, de llena a nueva y vuelta a empezar [85].
Después de Aristóteles, los astrónomos y filósofos (aparte de unos pocos como Lactancio) coincidieron de manera casi unánime en que la Tierra era una esfera. En su imaginación, Arquímedes incluso vio la forma esférica de la Tierra en un vaso de agua; en la Proposición 2 deDe los cuerpos flotantes demuestra que: «La superficie de cualquier fluido en reposo es la superficie de una esfera cuyo centro es la Tierra» [86]. (Tal cosa sería cierta solo en ausencia de la tensión superficial, que Arquímedes no tuvo en cuenta).
Ahora pretendo abordar lo que, en algunos aspectos, es el ejemplo más impresionante de la aplicación de las matemáticas a las ciencias naturales en el mundo antiguo: la obra de Aristarco de Samos. Aristarco nació alrededor del 310 a. C. en la isla jónica de Samos; estudió como alumno de Estratón de Lámpsaco, el tercer director del Liceo de Atenas, y posteriormente trabajó en Alejandría hasta su muerte, en torno al 230 a. C. Por fortuna, su obra maestra, De los tamaños y distancias del Sol y la Luna, ha sobrevivido[87]. En ella, Aristarco adopta cuatro observaciones astronómicas como postulados:
- «En la época de la media luna, la distancia del Sol a la Luna es menos de un cuadrante por un trigésimo de cuadrante». (Es decir, cuando la Luna está justo medio llena, el ángulo entre las líneas de visión a la Luna y el Sol es 3° menor que 90°, es decir, 87°).
- La Luna apenas cubre el disco visible del Sol durante un eclipse solar.
- «La anchura de la sombra de la Tierra es de dos Lunas». (La interpretación más simple es que, en la posición de la Luna, una esfera que fuera dos veces el diámetro de la Luna llenaría la sombra de la Tierra durante un eclipse solar. Es de presumir que esto lo averiguó midiendo el tiempo que transcurre desde el momento en que un borde de la Luna comenzaba a quedar oscurecido por la sombra de la Tierra hasta cuando quedaba oscurecida del todo, y desde el tiempo en que estaba totalmente a oscuras hasta que el eclipse terminaba).
- «La Luna subtiende una quinceava parte del zodíaco». (El zodíaco completo es un círculo de 360°, pero es evidente que Aristarco se refiere aquí a un signo del zodíaco; el zodíaco está formado por 12 constelaciones, de manera que un signo ocupa un ángulo de 360°/12 = 30°, y una quinceava parte son 2°).
- La distancia de la Tierra al Sol es entre 19 y 20 veces más grande que la distancia de la Tierra a la Luna.
- El diámetro del Sol es entre 19 y 20 veces más grande que el diámetro de la Luna.
- El diámetro de la Tierra es entre 108/43 y 60/19 veces más grande que el diámetro de la Luna.
- La distancia de la Tierra a la Luna es entre 30 y 45/2 veces más grande que el diámetro de la Luna.
A partir de estas conclusiones, Aristarco calculó el tamaño del Sol y la Luna y su distancia de la Tierra, todo ello en términos del diámetro de la Tierra. En concreto, al combinar los puntos 2 y 3, Aristarco pudo concluir que el diámetro del Sol es entre 361/60 y 215/ 27 veces más grande que el diámetro de la Tierra.
El razonamiento de Aristarco era matemáticamente impecable, pero sus resultados se desviaban bastante de la realidad, porque en los puntos 1 y 4 los datos que utilizaba como punto de partida eran completamente erróneos. Cuando la Luna está medio llena, el ángulo que se forma entre las líneas de visión al Sol y la Luna no es de 87°, sino de 89,853°, con lo que el Sol está 390 veces más lejos de la Tierra que la Luna, y por tanto es mucho más grande de lo que Aristarco pensaba. Era imposible que esta medida la llevara a cabo un astrónomo a simple vista, aunque Aristarco explicó de manera totalmente correcta que cuando la Luna está medio llena el ángulo entre las líneas de visión al Sol y la Luna no es inferior a 87°. Además, el disco visible de la Luna subtiende un ángulo de 0,519°, no de 2°, con lo que la distancia de la Tierra a la Luna es más de 111 veces el diámetro de esta. Sin duda, Aristarco podría haber realizado cálculos mejores, y en El calculador de arena Arquímedes insinúa que así lo hizo en su obra posterior. [88]
La diferencia fundamental entre la ciencia de Aristarco y la nuestra no son los errores de sus observaciones. Algunos errores esporádicos graves siguen afectando a la observación astronómica y la física experimental. Por ejemplo, en la década de 1930 se creía que la velocidad a la que se expande el universo era siete veces más rápida de lo que ahora sabemos. La verdadera diferencia entre Aristarco y los astrónomos y físicos de la actualidad no es que los datos de sus observaciones fueran erróneos, sino que jamás los puso en duda, y ni siquiera reconoció que pudieran ser imperfectos.
Hoy en día, los físicos y los astrónomos aprenden a tomarse la incertidumbre experimental muy en serio. Aun cuando, de estudiante universitario, yo sabía que quería ser físico teórico y que nunca haría experimentos, era obligatorio seguir, con todos los demás físicos de Cornell, un curso de laboratorio. Casi todo el tiempo lo pasábamos calculando la incertidumbre de nuestras mediciones, aunque, desde el punto de vista histórico, esta atención a la incertidumbre tardaría mucho en aparecer. Que yo sepa, nadie en la época antigua o medieval intentó jamás calcular en serio la incertidumbre de una medida, y como veremos en el capítulo 14, incluso Newton se mostraba displicente con las incertidumbres experimentales.
Vemos en Aristarco el pernicioso efecto del prestigio de las matemáticas. Su libro se lee como los Elementos de Euclides: los datos de los puntos 1 al 4 se toman como postulados, y los resultados se deducen con rigor matemático. El error de observación de sus resultados fue mucho mayor que los estrechos límites que rigurosamente demostró para los diversos tamaños y distancias. Quizá Aristarco no pretendía decir que el ángulo entre las líneas de visión del Sol y la Luna, cuando la Luna estaba medio llena, era realmente de 87°, sino que solo lo tomaba como ejemplo para ilustrar lo que se podía deducir. No en vano Aristarco fue conocido entre sus contemporáneos como «el Matemático», en contraste con su maestro Estratón, a quien se conocía como «el Físico».
Pero Aristarco acertó en un punto cualitativo importante: el Sol es mucho mayor que la Tierra. Para recalcar este punto, Aristarco observó que el volumen del Sol es al menos (361/60)3 (más o menos 218) veces más grande que el volumen de la Tierra. Naturalmente, ahora sabemos que es mucho más grande.
Tanto Arquímedes como Plutarco afirmaron que Aristarco había deducido del gran tamaño del Sol que no es este el que da vueltas alrededor de la Tierra, sino que es la Tierra la que da vueltas alrededor del Sol. Según afirma Arquímedes en El calculador de arena[89], Aristarco había deducido no solo que la Tierra gira alrededor del Sol, sino también que la órbita del Sol es ínfima comparada con la distancia a las estrellas fijas. Es probable que Aristarco abordara un problema planteado por alguna teoría del movimiento de la Tierra. Al igual que los objetos que hay en el suelo parecen moverse adelante y atrás cuando los vemos desde un tiovivo, debería parecer también que las estrellas se mueven adelante y atrás durante el año al verlas desde la Tierra en movimiento. Es algo que Aristóteles pareció comprender cuando comentó[90] que si la Tierra se moviera, entonces «las estrellas fijas nos rebasarían y darían la vuelta. Pero eso es algo que no se observa. Las mismas estrellas parecen salir y ponerse en las mismas partes de la Tierra». En concreto, si la Tierra gira alrededor del Sol, entonces cada estrella debería parecer que traza en el cielo una curva cerrada, cuyo tamaño dependería de la relación entre el diámetro de la órbita de la Tierra alrededor del Sol y la distancia a la estrella.
Pero si la Tierra gira alrededor del Sol, ¿por qué los antiguos astrónomos no veían ese movimiento aparente anual de las estrellas, conocido como paralaje anual? Para que el paralaje resultara lo bastante pequeño como para escapar a la observación, era necesario asumir que las estrellas se hallaban al menos a cierta distancia. Por desgracia, Arquímedes, en El calculador de arena no menciona el paralaje de manera explícita, y no sabemos si en el mundo antiguo se utilizó ese argumento para calcular un límite inferior a la distancia a las estrellas.
Aristóteles había proporcionado otros argumentos en contra del movimiento de la Tierra, algunos basados en su teoría del movimiento natural hacia el centro del universo mencionada en el capítulo 3, aunque había otro argumento basado en la observación. Aristóteles razonó que si la Tierra se moviera, entonces los cuerpos lanzados directamente hacia arriba quedarían atrás a causa del movimiento de la Tierra, por lo que caerían en un lugar diferente a donde fueron arrojados. Por el contrario, observa[91], «los cuerpos pesados arrojados enérgicamente hacia arriba en línea recta regresan al punto del que arrancaron, aun cuando se los lance a una distancia ilimitada». Este argumento fue repetido muchas veces, sobre todo por Claudio Ptolomeo (al que conocimos en el capítulo 4) en torno al año 150 de nuestra era, y por Jean Buridan en la Edad Media, hasta que (como veremos en el capítulo 10), Nicolás Oresme dio una respuesta a este argumento.
Sería posible juzgar hasta qué punto la idea de una Tierra en movimiento estaba extendida en el mundo antiguo si poseyéramos una buena descripción de un planetario antiguo, un modelo mecánico del sistema solar[92]. Cicerón, en La República, nos relata una conversación acerca de un planetario en el año 129 a. C., veintitrés años antes de su nacimiento. En esa conversación, un tal Lucio Furio Filón supuestamente se refería a un planetario construido por Arquímedes y que le habían arrebatado después de la conquista de Siracusa por parte de Marcelo, y que posteriormente fue visto en la casa del nieto de Marcelo. No es fácil adivinar por este relato de tercera mano cómo funcionaba el planetario (y además, faltan algunas páginas de esta parte de De Re Publica), pero en un punto del relato Cicerón cita unas palabras de Filón, según las cuales en este planetario «se dibujaba el movimiento del Sol y la Luna, y de las cinco estrellas que llamamos errantes [planetas]», lo que sin duda sugiere que en el planetario lo que se movía era el Sol y no la Tierra [93].
Como veremos en el capítulo 8, mucho antes de Aristarco, los pitagóricos creían que tanto la Tierra como el Sol se movían en torno a un fuego central. No tenían ninguna prueba de ello, pero de algún modo sus especulaciones quedaron en el recuerdo, mientras que las de Aristarco prácticamente se olvidaron. Solo se conoce a un astrónomo antiguo que adoptara las ideas heliocéntricas de Aristarco: el olvidado Seleuco de Seleucia, que vivió en el 150 a. C. En la época de Copérnico y Galileo, cuando los astrónomos y los clérigos querían referirse a la idea de que la Tierra se mueve, la llamaban pitagórica, no aristarquea. Cuando visité la isla de Samos en el año 2005, encontré muchos bares y restaurantes que se llamaban Pitágoras, pero ninguno que se llamara Aristarco de Samos.
Es fácil entender por qué la idea del movimiento de la Tierra no arraigó en el mundo antiguo. Es un movimiento que no percibimos, y antes del siglo XIV nadie comprendía que existiera alguna razón por la que debiéramos percibirlo. Además, ni Arquímedes ni ningún otro nos legó el menor indicio de que Aristarco hubiera explicado cómo veríamos el movimiento de los planetas desde una Tierra en movimiento.
La medición de la distancia de la Tierra a la Luna ganó mucha exactitud con Hiparco, generalmente considerado el mayor observador astronómico del mundo antiguo[94]. Hiparco llevó a cabo observaciones astronómicas en Alejandría desde el 161 hasta el 146 a. C., y luego las continuó hasta el 127 a. C., quizá en la isla de Rodas. Casi todas sus obras se han perdido; sabemos de su labor astronómica principalmente por el testimonio de Claudio Ptolomeo, tres siglos más tarde. Uno de sus cálculos se basó en la observación de un eclipse de sol, que ahora sabemos que ocurrió el 14 de marzo del 189 a. C. En este eclipse el disco del Sol quedó totalmente oculto en Alejandría, pero solo cuatro quintos dejaron de verse en el Helesponto (en la actualidad los Dardanelos, entre Asia y Europa). Puesto que el diámetro aparente de la Luna y el Sol son casi iguales, y según la medición de Hiparco eran de unos 33' (minutos de arco) o 0,55°, Hiparco fue capaz de concluir que la dirección de la Luna, tal como se veía desde el Helesponto y desde Alejandría, difería en una quinta parte de 0,55°, es decir, 0,11°. A partir de las observaciones del Sol, Hiparco averiguó la latitud del Helesponto y de Alejandría, así como el emplazamiento de la Luna en el cielo en el momento del eclipse, con lo que fue capaz de calcular la distancia a la Luna como un múltiplo del radio de la Tierra. Considerando los cambios de tamaño aparente de la Luna durante un mes lunar, Hiparco concluyó que la distancia de la Tierra a la Luna varía entre 71 y 83 radios de la Tierra. En realidad, la distancia media es de unos 60 radios de la Tierra.
Ahora debería comentar otro de los grandes descubrimientos de Hiparco, aunque no directamente relevante para la medida de tamaños y distancias. Hiparco preparó un catálogo de estrellas, una lista de unas 800 estrellas, dando la posición celeste de cada una. Es un reconocimiento a su labor que nuestro mejor catálogo actual de estrellas, que nos da la posición de 118 000, se elaborara mediante observaciones de un satélite artificial que recibe el nombre de Hiparco.
La medida de las posiciones de las estrellas por parte de Hiparco lo condujo al descubrimiento de un fenómeno extraordinario, que no fue comprendido hasta la obra de Newton. Para explicar este descubrimiento, hay que decir algo acerca de cómo se describen las posiciones celestes. El catálogo de Hiparco no ha sobrevivido, y no sabemos cómo describía esas posiciones. A partir de la época romana, comúnmente se utilizaban dos opciones. Un método, utilizado posteriormente en el catálogo de estrellas de Ptolomeo[95], representa las estrellas fijas como puntos en una esfera, cuyo ecuador es la eclíptica (la trayectoria a través de las estrellas que dibuja el Sol en un año). La latitud y la longitud celestes ubican las estrellas en esta esfera del mismo modo que la latitud y la longitud ordinarias nos dan el emplazamiento de puntos sobre la superficie terrestre[96]. En un método diferente, que puede que fuera utilizado por Hiparco[97], las estrellas se consideran de nuevo puntos de una esfera, pero esta se orienta con el eje de la Tierra y no con la eclíptica; el polo norte de esta esfera es el polo norte celeste, en torno al cual las estrellas parecen girar cada noche, y en lugar de latitud y longitud, las coordenadas de esta esfera se conocen como declinación y ascensión recta.
Según Ptolomeo[98], las medidas de Hiparco fueron lo bastante exactas como para que observara que la longitud celeste (o ascensión recta) de la estrella Espiga había cambiado 2° desde que la observara en Alejandría, mucho tiempo atrás, el astrónomo Timocares. No es que la estrella Espiga hubiera cambiado su posición en relación con las otras estrellas, sino que lo que había cambiado era el emplazamiento del Sol en la esfera celeste en el equinoccio de otoño, el punto desde el cual se vería entonces la longitud celeste.
Resulta difícil precisar cuánto tiempo llevó este cambio. Timocares nació alrededor del 320 a. C., unos 130 años antes de Hiparco; pero se cree que murió joven, alrededor del 280 a. C., unos 160 antes de Hiparco. Si suponemos que las observaciones de ambos de la Espiga están separadas unos 150 años, entonces estas observaciones indican que la posición del Sol en el equinoccio de otoño cambia más o menos 1° cada 75 años [99]. A esa velocidad, este punto equinoccial llevaría a cabo una precesión a través de la totalidad del círculo de 360° del zodíaco en 360 veces 75 años, es decir, 27 000 años.
Hoy en día comprendemos que la precesión de los equinoccios está causada por un cambio de orientación en el eje de rotación de la Tierra (igual que ocurre con el eje de una peonza) en torno a una dirección perpendicular al plano de su órbita, con un ángulo entre esta dirección y el eje de la Tierra que permanece casi fijo a 23,5°. Los equinoccios son las fechas en las que la línea que separa la Tierra del Sol queda perpendicular al eje de la Tierra, de manera que un cambio en la dirección del eje provoca la precesión de los equinoccios. Veremos en el capítulo 14 que el primero en explicar este cambio de dirección fue Isaac Newton, como efecto de la atracción gravitatoria del Sol y la Luna que provoca la protuberancia ecuatorial. En realidad, el eje de la Tierra tarda 25 727 años en recorrer una circunferencia completa. Resulta extraordinaria la exactitud con la que la obra de Hiparco predijo una extensión de tiempo tan grande. (Por cierto, es la precesión de los equinoccios lo que explica por qué los navegantes antiguos tenían que buscar dónde estaba el norte a partir de la posición en el cielo de las constelaciones que estaban cerca del polo norte celeste, y no a partir de la posición de la Estrella del Norte, Polaris. Polaris no se ha desplazado en relación con las otras estrellas, pero en la Antigüedad el eje de la Tierra no apuntaba a Polaris, como hace ahora, y en el futuro Polaris ya no estará en el polo norte celeste).
Regresando ahora a las medidas celestes, todas las estimaciones de Aristarco e Hiparco expresaban el tamaño de las distancias de la Luna y el Sol como múltiplos del tamaño de la Tierra. El tamaño de la Tierra lo midió Eratóstenes unas décadas después de la obra de Aristarco. Eratóstenes nació en el 273 a. C. en Cirene, una ciudad griega en la costa del Mediterráneo de lo que hoy es Libia, fundada más o menos en el 630 a. C., que había pasado a formar parte del reino de los Ptolomeos. Se educó en Atenas y asistió al Liceo, y en torno al 245 a. C. fue llamado por Ptolomeo III para ir a Alejandría, donde se convirtió en miembro del Museo y en preceptor del futuro Ptolomeo IV. Más adelante fue el quinto director de la Biblioteca, más o menos en el 234 a. C. Sus principales obras —De la medición de la Tierra, Memorias geográficas y Hermes— por desgracia han desaparecido, aunque fueron ampliamente citadas en la Antigüedad.
La medición del tamaño de la Tierra por parte de Eratóstenes la describió el filósofo estoico Cleómedes en De los cielos[100], en alguna fecha posterior al 50 a. C. Eratóstenes comenzó con las observaciones de que a mediodía, durante el solsticio de verano, el Sol queda directamente sobre nuestras cabezas en Syene, una antigua ciudad egipcia que Eratóstenes suponía que debía quedar justo al sur de Alejandría, mientras que las mediciones con un gnomon en Alejandría mostraban que el Sol, durante el solsticio y a mediodía, estaba desplazado de la vertical una quincuagésima parte de un círculo completo, o sea 7,2°. De ella concluyó que la circunferencia de la Tierra es 50 veces la distancia de Alejandría a Syene (véase Nota técnica 12). Se había calculado (probablemente gracias a los marchadores, entrenados para que cada paso tuviera la misma longitud) que la distancia de Alejandría a Syene era de 5000 estadios, de manera que la circunferencia de la Tierra debía de ser de 250 000 estadios.
¿Hasta qué punto era exacto este cálculo? No conocemos la longitud de los estadios tal como la utilizaba Eratóstenes, y Cleómedes probablemente tampoco la conocía, puesto que (contrariamente a nuestras millas o kilómetros) nunca se le dio una definición oficial. Pero sin conocer la longitud de un estadio, sí podemos juzgar la exactitud del uso de la astronomía por parte de Eratóstenes. La circunferencia de la Tierra es en realidad 47,9 veces la distancia de Alejandría a Syene (la moderna Asuán), de manera que la conclusión de Eratóstenes de que la Tierra era 50 veces la distancia de Alejandría a Syene era en realidad bastante exacta, fuera cual fuera la longitud de un estadio[101]. En su faceta de astrónomo, si no de geógrafo, Eratóstenes lo había hecho bastante bien.
Capítulo 8
El problema de los planetas
Los planetas se desplazan a través del cielo a diferentes velocidades: Mercurio y Venus tardan un año en completar un circuito del zodíaco; Marte tarda un año y 322 días; Júpiter 11 años y 315 días, y Saturno 29 años y 166 días. Todo esto son periodos medios, pues los planetas no se mueven a velocidad constante a través del zodíaco, e incluso a veces invierten la dirección de su movimiento durante un tiempo, antes de reemprender el movimiento hacia el este. Gran parte de la historia de la aparición de la ciencia moderna tiene que ver con el esfuerzo, prolongado durante dos milenios, de explicar los peculiares movimientos de los planetas.
Los pitagóricos fueron los primeros que pretendieron esbozar una teoría de los planetas y del Sol y la Luna. Imaginaron que los cinco planetas, junto con el Sol y la Luna, y también la Tierra giraban en torno a un fuego central. Para explicar por qué en la Tierra no vemos este fuego central, los pitagóricos supusieron que vivimos en el lado de la Tierra que queda hacia fuera, lejos del fuego. (Como casi todos los presocráticos, los pitagóricos creían que la Tierra era plana; la veían como un disco que siempre presentaba el mismo lado al fuego central, y en el que nosotros estábamos al otro lado. El movimiento diario de la Tierra alrededor del fuego central supuestamente explicaba el movimiento diario aparente de los objetos que se movían más lentamente en torno a la Tierra: el Sol, la Luna, los planetas y las estrellas)[104]. Según Aristóteles y Aecio, el pitagórico Filolao del siglo V a. C. inventó una contra-Tierra, que describía una órbita que no podíamos ver desde nuestro lado de la Tierra, porque o bien quedaba entre la Tierra y el fuego central o, desde la Tierra, al otro lado del fuego central. Aristóteles explicó la introducción de la contra-Tierra como resultado de la obsesión pitagórica con los números. La Tierra, el Sol, la Luna y los cinco planetas, junto con la esfera de las cinco estrellas fijas, componían los nueve objetos que giraban en torno al fuego central, pero los pitagóricos suponían que el número de estos objetos debía de ser 10, un número perfecto en el sentido de que
10 = 1 + 2 + 3 + 4.
Tal como lo describe con cierta sorna Aristóteles[105], los pitagóricossuponían que los elementos de los números eran los elementos de todas las cosas, y que todo el cielo era una escala musical y un número. Y todas las propiedades de los números y las escalas que podían demostrar que concordaban con los atributos y partes y la totalidad de la disposición de los cielos, las recogían y las hacían encajar en su esquema, y si algo no encajaba en alguna parte, enseguida llevaban a cabo alguna adición para que toda su teoría resultara coherente. Por ejemplo, como se cree que el número 10 es perfecto y comprende toda la naturaleza de los números, afirmaban que los cuerpos que se desplazan a través de los cielos eran diez, pero como los cuerpos visibles son solo nueve, para solucionarlo inventaron un décimo: la «contra-Tierra».Al parecer, los pitagóricos nunca intentaron demostrar que su teoría explicaba en detalle los movimientos aparentes del Sol, la Luna y los planetas en el cielo, sobre el fondo de las estrellas fijas. La explicación de estos movimientos aparentes sería una tarea para los siglos posteriores, y no se completaría hasta la época de Kepler.
Para esta labor resultó de gran ayuda la introducción de mecanismos como el gnomon, que permitía estudiar los movimientos del Sol, y otros instrumentos que permitirían medir los ángulos entre las líneas de visión hacia diversos planetas y estrellas, o entre dichos objetos astronómicos y el horizonte. Naturalmente, toda esta astronomía se llevaba a cabo a simple vista. Resulta irónico que Claudio Ptolomeo, que había estudiado en profundidad el fenómeno de la refracción y la reflexión (incluyendo los fenómenos de la refracción en la atmósfera sobre la posición aparente de las estrellas) y que, como veremos, jugó un papel crucial en la historia de la astronomía, nunca comprendiera que las lentes y los espejos curvos podían utilizarse para ampliar las imágenes de los cuerpos astronómicos, como en el telescopio refractor de Galileo Galilei y en el telescopio reflector inventado por Isaac Newton.
No fueron solo los instrumentos físicos los que promovieron los grandes avances de la astronomía científica entre los griegos. Estos avances fueron posibles también por el progreso en las matemáticas. A medida que se iban solucionando los problemas, el gran debate de la astronomía antigua y medieval ya no era entre aquellos que creían que la Tierra y el Sol estaban en movimiento, sino entre dos concepciones diferentes de cómo el Sol, la Luna y los planetas giraban alrededor de una Tierra estacionaria. Como veremos, gran parte de este debate tenía que ver con dos concepciones distintas del papel de las matemáticas en las ciencias naturales.
La historia comienza con lo que yo llamo los deberes de Platón. Según el neoplatónico Simplicio, que alrededor del 530 de nuestra era escribió su comentario sobre De los cielos de Aristóteles,
Platón establece el principio de que el movimiento de los cuerpos celestes es circular, uniforme y constantemente regular. Por tanto, les plantea a los matemáticos el siguiente problema: ¿Qué movimientos circulares, uniformes y perfectamente regulares deben admitirse como hipótesis para poder salvar las apariencias presentadas por los planetas?[106]«Salvar (o guardar) las apariencias» es la traducción tradicional; Platón se pregunta qué combinaciones de movimientos de los planetas (e incluyo el Sol y la Luna) en círculos a velocidad constante, y siempre en la misma dirección, presentarían un aspecto exactamente igual que el que de hecho observamos.
Esta cuestión la abordó por primera vez un contemporáneo de Platón, el matemático Eudoxo de Cnido[107]. Elaboró un modelo matemático descrito en un libro perdido,De las velocidades, cuyo contenido nos ha llegado a partir de descripciones de Aristóteles [108] y Simplicio[109]. Según este modelo, las estrellas son transportadas alrededor la Tierra por una esfera que gira una vez al día de este a oeste mientras que el Sol, la Luna y los planetas son transportados alrededor de la Tierra sobre esferas que a su vez son transportadas por otras esferas. El modelo más simple tendría dos esferas para el Sol. La esfera exterior gira alrededor de la Tierra una vez al día de este a oeste, con el mismo eje y velocidad de rotación que la esfera de las estrellas; pero el Sol está sobre el ecuador de una esfera interior, que comparte la rotación de la esfera exterior como si estuviera pegada a ella, pero también gira en torno a su propio eje de oeste a este una vez al año. El eje de la esfera interior está inclinado 23,5° con relación al eje de la esfera exterior. Esto explicaría tanto el movimiento aparente diario del Sol y su aparente movimiento anual a través del zodíaco. De manera semejante, se podría suponer que la Luna es transportada en torno a la Tierra por otras dos esferas contragiratorias, con la diferencia de que la esfera interior sobre la cual da vueltas la Luna lleva a cabo una rotación completa de oeste a este una vez al mes en lugar de una vez al año. Por razones que no están claras, se supone que Eudoxo añadió una tercera esfera tanto para el Sol como para la Luna. Dichas teorías se denominan «homocéntricas», porque las esferas asociadas con los planetas, así como el Sol y la Luna, poseen todas el mismo centro, el centro de la Tierra.
El movimiento irregular de los planetas planteaba un problema más difícil. Eudoxo le daba a cada planeta cuatro esferas: una esfera exterior que gira una vez al día en torno a la Tierra de este a oeste, con el mismo eje de rotación que la esfera de las estrellas fijas y las esferas exteriores del Sol y la Luna; la siguiente esfera, al igual que las esferas interiores del Sol y la Luna, giraba más lentamente a diversas velocidades de oeste a este en torno a un eje inclinado unos 23,5° con respecto al eje de la esfera exterior; y las dos esferas más interiores giraban, exactamente a la misma velocidad, en direcciones opuestas en torno a dos ejes casi paralelos inclinados en un gran ángulo con respecto al eje de las dos esferas exteriores. El planeta va adosado a la esfera interior. Las dos esferas exteriores le dan a cada planeta su revolución diaria siguiendo a las estrellas en torno a la Tierra, y su movimiento medio en periodos más largos a lo largo del zodíaco. Los efectos de las dos esferas interiores que giran en direcciones opuestas quedaría anulado si sus ejes fueran exactamente paralelos, pero como se supone que sus ejes no son paralelos del todo, superponen un movimiento en forma de ocho sobre el movimiento medio de cada planeta a través del zodíaco, explicando la esporádica inversión de la dirección de los planetas. Los griegos llamaban a esta trayectoria hipopede, porque se parecía a las correas que se utilizaban para atar los caballos.
El modelo de Eudoxo no concordaba del todo con las observaciones del Sol, la Luna y los planetas. Por ejemplo, su imagen del movimiento del Sol no explicaba las diferencias de duración entre las estaciones, que, como vimos en el capítulo 6, Euctemón descubrió gracias a la ayuda del gnomon. No funcionaba con Mercurio, y tampoco con Venus y Marte. Para mejorar las cosas, Calipo de Cícico propuso un nuevo modelo. Añadió dos esferas más al Sol y la Luna, y una más a Mercurio, Venus y Marte. El modelo de Calipo por lo general funcionaba mejor que el de Eudoxo, aunque introdujo unas nuevas peculiaridades ficticias al movimiento aparente de los planetas.
En los modelos homocéntricos de Eudoxo y Calipo, el Sol, la Luna y los planetas poseían cada uno un grupo diferente de esferas, en el que había unas esferas exteriores que giraban al unísono con una esfera diferente que transportaba las estrellas fijas. Todo esto es un primer ejemplo de lo que los físicos modernos denominan «ajuste fino». Criticamos una teoría llamándola de ajuste fino cuando sus rasgos se manipulan para que algunas cosas sean iguales sin comprender por qué deberían ser iguales. El aspecto del ajuste fino en la teoría científica es como un grito de angustia procedente de la naturaleza, que se queja de que a veces necesita que la expliquemos de manera mejor.
La aversión al ajuste fino condujo a los físicos modernos a llevar a cabo un descubrimiento de una importancia fundamental. A finales de la década de 1950, se identificó que dos tipos de partículas inestables llamadas tau y theta se descomponían de maneras distintas: la theta en dos partículas más ligeras llamadas piones, y la tau en tres piones. Las partículas tau y theta no solo tenían la misma masa, sino que tenían la misma vida media, ¡aun cuando se descompusieran de manera totalmente distinta! Los físicos supusieron que la tau y la theta no podían ser la misma partícula, pues por razones complicadas la simetría de naturaleza entre derecha e izquierda (que dicta que las leyes de la naturaleza deben parecer las mismas cuando el mundo se ve a través de un espejo que cuando se ve directamente) debería impedir que la misma partícula se descompusiera a veces en dos piones y a veces en tres. Con lo que sabíamos en aquella época, habría sido posible ajustar las constantes de nuestras teorías para conseguir que las masas y las vidas medias de tau y theta fueran iguales, aunque habría sido difícil digerir esa teoría: parecía un ajuste fino desesperado. Al final se descubrió que no hacía falta ningún ajuste fino, pues las dos partículas eran en realidad la misma. La simetría entre derecha e izquierda, aunque seguida por las fuerzas que mantenían juntos los átomos y sus núcleos, no se mantiene en diversos procesos de la desintegración, incluyendo la desintegración de las partículas tau y theta [110]. Los físicos que comprendieron este fenómeno tuvieron razón al desconfiar de la idea de que, por casualidad, las partículas tau y theta tuvieran la misma masa y la misma vida media: eso habría sido demasiado ajuste fino.
Hoy en día nos encontramos con un tipo de ajuste fino aún más inquietante. En 1998 los astrónomos descubrieron que la expansión del universo no se estaba frenando, como se esperaría de la atracción gravitatoria de las galaxias entre sí, sino que se aceleraba. Esta aceleración se atribuyó a una energía asociada al propio espacio, conocida como energía oscura. La teoría indica que hay diferentes aportaciones a la energía oscura. Algunas se pueden calcular, otras no. Las aportaciones a la energía oscura que podemos calcular resultan ser más grandes que el valor de la energía oscura observada por los astrónomos más o menos en 120 órdenes de magnitud, es decir, un 1 seguido por 120 ceros. No es una paradoja, porque podemos suponer que estas aportaciones calculables a la energía oscura quedan anuladas por aportaciones que no podemos calcular, pero esa anulación tendría que ser precisa hasta 120 decimales. Este nivel de ajuste fino es intolerable, y los teóricos han estado trabajando con denuedo para encontrar una manera mejor de explicar por qué la cantidad de energía oscura es mucho más pequeña que lo que sugieren nuestros cálculos. Una posible explicación se menciona en el capítulo 11.
Al mismo tiempo, hay que reconocer que algunos ejemplos aparentes de ajuste fino son simples accidentes. Por ejemplo, las distancias de la Tierra al Sol y a la Luna están más o menos en la misma proporción que sus diámetros, de manera que, vistos desde la Tierra, el Sol y la Luna parecen más o menos del mismo tamaño, como lo demuestra el hecho de que la Luna cubra el Sol durante un eclipse solar total. No hay razón para suponer que esto sea otra cosa que una coincidencia.
Aristóteles se propuso reducir el ajuste fino de los modelos de Eudoxo y Calipo. En la Metafísica[111] propuso unir todas las esferas en un solo sistema conectado. En lugar de darle al planeta más exterior, Saturno, cuatro esferas, como habían hecho Eudoxo y Calipo, le dio solo sus tres esferas interiores; el movimiento diario de Saturno de este a oeste se explicaba al unir esas tres esferas a la esfera de las estrellas fijas. Aristóteles también añadió, dentro de las tres de Saturno, tres esferas extras que giraban en direcciones opuestas a fin de anular el efecto del movimiento de las tres esferas de Saturno sobre las esferas del siguiente planeta, Júpiter, cuyas esferas exteriores estaban adosadas a la parte más interior de las tres esferas extras situadas entre Júpiter y Saturno.
A costa de añadir esas tres esferas contragiratorias extras, y al unir las tres esferas exteriores de Saturno a la esfera de las estrellas fijas, Aristóteles consiguió algo bastante hábil. Ya no era necesario preguntarse por qué el movimiento diario de Saturno debería seguir precisamente el de las estrellas, pues Saturno estaba físicamente unido a la esfera de las estrellas. Pero entonces Aristóteles lo estropeó todo: le dio a Júpiter las cuatro esferas que le habían dado Eudoxo y Calipo. El problema que eso planteaba era que Júpiter tendría un movimiento diario procedente de Saturno y también de la más exterior de las cuatro esferas, de manera que cada día daría dos vueltas alrededor de la Tierra. ¿Acaso se le olvidó que las tres esferas contragiratorias que había dentro de las esferas de Saturno anularían solo los movimientos especiales de Saturno, y no su rotación diaria en torno a la Tierra?
Peor aún, Aristóteles añadió solo tres esferas contragiratorias dentro de las cuatro esferas de Júpiter, a fin de anular sus movimientos especiales, pero no su movimiento diario, y a continuación le dio a Marte, el siguiente planeta, las cinco esferas que le había dado Calipo, por lo que Marte giraría alrededor de la Tierra tres veces al día. Siguiendo de esta guisa, en el esquema de Aristóteles, Venus, Mercurio, el Sol y la Luna girarían alrededor de la Tierra respectivamente cuatro, cinco, seis y siete veces.
Me quedé atónito por este aparente fallo cuando leí la Metafísica de Aristóteles, y luego me enteré de que varios autores ya lo habían observado, entre ellos J. L. E. Dreyer, Thomas Heath y W. D. Ross[112]. Algunos afirmaban que el texto era corrupto. Pero si Aristóteles realmente presentó el esquema descrito en la versión que conocemos de la Metafísica, esto no se puede explicar afirmando que pensaba en términos diferentes a los nuestros, o que le interesaban problemas diferentes a los nuestros. Tendríamos que concluir que, en sus propios términos, al trabajar en un problema que le interesaba, había sido descuidado o estúpido.
Aun cuando Aristóteles hubiera colocado el número correcto de esferas contragiratorias, a fin de que cada planeta siguiera a las estrellas en torno a la Tierra tan solo una vez al día, su esquema seguiría dependiendo en gran medida del ajuste fino. Las esferas contragiratorias introducidas en el interior de las esferas de Saturno para anular el efecto de sus movimientos especiales sobre los movimientos de Júpiter tendrían que girar exactamente a la misma velocidad que las tres esferas de Saturno para que la anulación funcionara, y lo mismo ocurriría con los planetas más cercanos a la Tierra. Y, al igual que ocurría con Eudoxo y Calipo, en el esquema de Aristóteles las segundas esferas de Mercurio y Venus tendrían que girar exactamente a la misma velocidad que la segunda esfera del Sol, a fin de explicar el hecho de que Mercurio, Venus y el Sol se movieran juntos a través del zodíaco, de manera que los planetas interiores nunca se vean lejos del Sol en el cielo. Venus, por ejemplo, es siempre el lucero de la tarde o el de la mañana, y nunca se ve alto en el cielo a medianoche.
Al menos un astrónomo antiguo parece haberse tomado muy en serio el problema del ajuste fino: Heráclides Póntico. Fue alumno de la Academia de Platón en el siglo IV a. C., y es posible que estuviera al frente de ella cuando Platón se marchó a Sicilia. Tanto Simplicio[113] como Aecio afirman que Heráclides enseñaba que la Tierra gira en torno a su eje [114], eliminando de un golpe el supuesto giro simultáneo diario de las estrellas, los planetas, el Sol y la Luna alrededor de la Tierra. La propuesta de Heráclides fue esporádicamente mencionada por algunos escritores del final de la Antigüedad y en la Edad Media, pero no fue ampliamente conocida hasta la época de Copérnico, de nuevo, probablemente, porque no percibimos la rotación de la Tierra. Nada indica que Aristarco, que escribió un siglo después de Heráclides, sospechara que la Tierra no solo se mueve alrededor del Sol, sino que gira en torno a su eje.
Según Calcidio, un cristiano que tradujo el Timeo del griego al latín en el siglo IV, Heráclides también propuso que, puesto que Mercurio y Venus nunca se ven lejos del Sol en el cielo, giran alrededor del Sol y no alrededor de la Tierra, eliminando así otro poco de ajuste fino de los esquemas de Eudoxo, Calipo y Aristóteles: la coordinación artificial de las revoluciones de las segundas esferas del Sol y los planetas interiores. Pero aún se supone que el Sol, la Luna y otros tres planetas exteriores giran en torno a una Tierra estacionaria, aunque rotatoria. Esta teoría funciona muy bien para los planetas interiores, porque les da precisamente los mismos movimientos aparentes que en la versión más simple de la teoría copernicana, en la que Mercurio, Venus y la Tierra describen círculos a velocidad constante en torno al Sol. Por lo que se refiere a los planetas interiores, la única diferencia entre Heráclides y Copérnico es el punto de vista: o bien se basa en la Tierra o bien se basa en el Sol.
Además del ajuste fino inherente a los esquemas de Eudoxo, Calipo y Aristóteles, había otro problema: estos esquemas homocéntricos no concuerdan muy bien con las observaciones. Entonces se creía que los planetas brillaban con luz propia, y puesto que en estos esquemas las esferas sobre las que van los planetas siempre permanecen a la misma distancia de la superficie de la Tierra, el brillo de los planetas no debería cambiar nunca. Sin embargo, era evidente que su brillo cambiaba enormemente. Tal como lo cita Simplicio[115], en torno al año 200 de nuestra era el filósofo Sosígenes el Peripatético había comentado que
sin embargo, las [hipótesis] de Eudoxo y los suyos no preservan los fenómenos, y solo aquellos que ellos mismos han conocido previamente y aceptado. ¿Y qué necesidad hay de referirnos a otras cosas, algunas de las cuales Calipo de Cícico también intentó preservar cuando Eudoxo no fue capaz de hacerlo, si es que Calipo las conservó? […] Lo que quiero decir es que hay veces en que los planetas parecen estar cerca, y otras en que parecen estar lejos de nosotros. Y en el caso de algunos, eso es aparente a simple vista. Pues la estrella que llamamos Venus y también la que llamamos Marte parecen muchas veces más grandes cuando están en mitad de su retrogradación, de manera que en las noches sin luna Venus provoca que los cuerpos proyecten sombras.Allí donde Simplicio o Sosígenes mencionan el tamaño de los planetas, probablemente deberíamos comprender que se refieren a su luminosidad; a simple vista no podemos ver el disco de ningún planeta, pero cuanto más luminoso es un punto de luz, más grande parece.
De hecho, este argumento no es tan concluyente como pensaba Simplicio. Los planetas (al igual que la Luna) brillan por la luz reflejada del Sol, de manera que su luminosidad cambiaría incluso en los esquemas de Eudoxo et ál. al pasar por diferentes fases (al igual que las fases de la Luna). Esto no se comprendió hasta la obra de Galileo. Pero aun cuando las fases de los planetas se tuvieran en cuenta, los cambios de luminosidad que se esperarían en las teorías homocéntricas no habría concordado con lo que se ve en realidad.
Para los astrónomos profesionales (si no para los filósofos), la teoría homocéntrica de Eudoxo, Calipo y Aristóteles fue suplantada, en las eras helenística y romana, por una teoría que explicaba mucho mejor el movimiento aparente del Sol y los planetas. Esta teoría se basaba en tres mecanismos matemáticos —el epiciclo, el excéntrico y el ecuante— que se describirán más adelante. No sabemos quién inventó el epiciclo y el excéntrico, pero sin duda fueron conocidos por el matemático helenístico Apolonio de Perga y por el astrónomo Hiparco de Nicea, a quien hemos conocido en los capítulos 6 y 7 [116]. Sabemos de la teoría de los epiciclos y los excéntricos a través de los escritos de Claudio Ptolomeo, que inventó el ecuante, y con cuyo nombre la teoría se ha visto asociada desde entonces.
Ptolomeo vivió allá por el año 150 de nuestra era, en la época de los emperadores antoninos, en el auge del Imperio romano. Trabajó en el Museo de Alejandría, y murió después del año 161 de nuestra era. Ya hemos comentado su estudio de la reflexión y la refracción en el capítulo 4. Su obra astronómica se describe en Hè Megalè Syntaxis, un título que los árabes transformaron en Almagesto, y por el cual se ha conocido en Europa. El Almagesto tuvo tanto éxito que los escribas dejaron de copiar las obras de astrónomos anteriores como Hiparco; como resultado, ahora resulta difícil distinguir la propia obra de Ptolomeo de las de ellos.
El Almagesto mejoró el catálogo de estrellas de Hiparco, incluyendo 1028, cientos más que Hiparco, y ofreciendo alguna indicación de su luminosidad así como de su posición en el cielo[117]. La teoría de Ptolomeo de los planetas, el Sol y la Luna fue mucho más importante para el futuro de la ciencia. En un aspecto, la elaboración de la teoría que se describe en el Almagesto es sorprendentemente moderna en sus métodos. Para los movimientos planetarios se proponen modelos matemáticos que contienen diversos parámetros numéricos libres, que luego se calculan limitando las predicciones de los modelos para que concuerden con la observación. Más adelante veremos un ejemplo de ello, en relación con el excéntrico y el ecuante.
En su versión más simple, la teoría ptolemaica afirma que cada planeta gira en un círculo conocido como «epiciclo», no alrededor de la Tierra, sino alrededor de un punto en movimiento que gira alrededor de la Tierra en otro círculo conocido como «deferente». Los planetas interiores, Mercurio y Venus, completan su epiciclo en 88 y 225 días respectivamente, mientras que el modelo sufre un ajuste fino para que el centro de epiciclo gire alrededor de la Tierra en el deferente exactamente en un año, permaneciendo siempre en la línea entre la Tierra y el Sol.
Podemos ver por qué esto funciona. No hay nada en el movimiento aparente de los planetas que nos indique lo lejos que están. De ahí que, en la teoría de Ptolomeo, el movimiento aparente de cualquier planeta en el cielo no dependa del tamaño absoluto del epiciclo y el deferente, sino que depende tan solo de la razón de sus tamaños. Si Ptolomeo hubiera querido, podría haber ajustado los tamaños del epiciclo y el deferente de Venus, mantener la razón fija, y lo mismo con Mercurio, a fin de que ambos planetas tuvieran el mismo deferente, a saber, la órbita del Sol. Entonces, el Sol había sido el punto de la deferente en torno al cual los planetas interiores se desplazan en sus epiciclos. Esta no es la teoría propuesta por Hiparco ni Ptolomeo, pero proporciona al movimiento de los planetas el mismo aspecto, pues difiere solamente en la escala global de las órbitas, la cual no afecta a los movimientos aparentes. Este caso especial de la teoría del epiciclo es exactamente lo mismo que la teoría atribuida a Heráclides que hemos comentado antes, en la que Mercurio y Venus giran alrededor del Sol mientras este da vueltas en torno a la Tierra. Como ya hemos mencionado, la teoría de Heráclides funciona porque es equivalente a aquella en la que la Tierra y los planetas interiores giran alrededor del Sol, y las dos teorías difieren tan solo en el punto de vista del astrónomo. Así pues, no es accidental que la teoría del epiciclo de Ptolomeo, según la cual Mercurio y Venus tienen los mismos movimientos aparentes que en la teoría de Heráclides, además funcione bastante bien en comparación con la observación.
Ptolomeo podría haber aplicado la misma teoría de los epiciclos y deferentes a los planetas exteriores —Marte, Júpiter y Saturno—, pero para que la teoría funcionara habría sido necesario que el movimiento de los planetas en torno a los epiciclos fuera mucho más lento que el movimiento del centro de los epiciclos alrededor de los deferentes. No sé qué habría tenido de malo esta variante, pero por alguna razón Ptolomeo escogió un camino distinto. En la versión más simple de este esquema, cada planeta exterior pasa sobre su epiciclo en torno a un punto de la deferente una vez al año, y ese punto de la deferente gira alrededor de la Tierra en un periodo más largo: 1,88 años para Marte, 11,9 años para Júpiter, y 29,5 años para Saturno. Aquí encontramos un tipo distinto de ajuste fino: la línea que va del centro del epiciclo al planeta es siempre paralela a la línea que va de la Tierra al Sol. Este esquema concuerda bastante bien con los movimientos aparentes observados de los planetas exteriores, porque aquí, al igual que ocurre con los planetas interiores, los diferentes casos especiales de esta teoría que difieren solo en la escala del epiciclo y la deferente (manteniendo fija su razón) dan los mismos movimientos aparentes, y hay un valor especial de esta escala que hace que este modelo sea el mismo que el de la teoría copernicana más simple, diferenciándose tan solo en el punto de vista: la Tierra o el Sol. Para los planetas exteriores, el valor especial de esta escala es aquel en el que el radio del epiciclo es igual a la distancia del Sol a la Tierra (véase Nota técnica 13).
La teoría de Ptolomeo explicaba perfectamente la inversión aparente de la dirección de los movimientos planetarios. Por ejemplo, Marte parece retroceder en su movimiento a través del zodíaco cuando se halla en el punto de su epiciclo más cercano a la Tierra, porque se supone que entonces el movimiento en torno al epiciclo se halla en dirección opuesta al supuesto movimiento del epiciclo en torno a la deferente, y es más rápido. Esto no es más que la transcripción, dentro de un marco de referencia basado en la Tierra, de la moderna afirmación de que Marte parece retroceder en el zodíaco cuando la Tierra pasa a su lado mientras ambos giran alrededor del Sol. Es también el momento en que es más luminoso (como se ha observado en la cita anterior de Simplicio), porque en ese momento está más cerca de la Tierra, y el lado de Marte que vemos está encarado al Sol.
La teoría desarrollada por Hiparco, Apolonio y Ptolomeo no fue una fantasía que, por pura suerte, resultó concordar bastante bien con la observación pero que no tenía relación con la realidad. Por lo que se refiere al movimiento aparente del Sol y los planetas, en su versión más simple, con un solo epiciclo para cada planeta y sin más complicaciones, esta teoría nos ofrece exactamente las mismas predicciones que la versión más simple de la teoría de Copérnico; es decir, una teoría en la que la Tierra y los demás planetas dan vueltas en círculos a velocidad constante con el Sol en el centro. Como ya se ha explicado en relación con Mercurio y Venus (y cuya explicación se ha ampliado en la Nota técnica 13), ello se debe a que la teoría ptolemaica se halla en esa categoría de teorías que dan los mismos movimientos aparentes del Sol y los planetas, y un miembro de esa categoría (aunque no el adoptado por Ptolomeo) nos da exactamente los mismos movimientos del Sol y los planetas en relación unos con otros que la versión más simple de la teoría copernicana.
Sería hermoso acabar aquí la historia de la astronomía griega. Por desgracia, tal como comprendió perfectamente el propio Copérnico, las predicciones de la versión más simple de la teoría copernicana para los movimientos aparentes de los planetas no concuerdan del todo con la observación, y tampoco las predicciones de la versión más simple de la teoría ptolemaica, que son idénticas. Sabemos, desde la época de Kepler y Newton, que las órbitas de la Tierra y de los demás planetas no son exactamente circulares, que el Sol no está exactamente en el centro de esas órbitas, y que la Tierra y los demás planetas no se desplazan en sus órbitas a una velocidad exactamente constante. Naturalmente, todo esto los astrónomos griegos no lo comprendían en términos modernos. Gran parte de la historia de la astronomía hasta Kepler se dedicó a intentar ajustar las pequeñas inexactitudes de las versiones simples tanto de la teoría ptolemaica como de la copernicana.
Platón había hablado de círculos y de movimiento uniforme, y que nosotros sepamos, nadie en la Antigüedad concebía que los cuerpos astronómicos pudieran tener ningún movimiento que no estuviera compuesto de movimientos circulares, aunque Ptolomeo estaba dispuesto a transigir en la cuestión del movimiento uniforme. Ptolomeo y sus precursores, trabajando con la limitación de que las órbitas estuvieran compuestas de círculos, inventó diversas complicaciones para que sus teorías concordaran más exactamente con la observación, tanto para el Sol y la Luna como para los planetas [118].
Una complicación consistió simplemente en añadir más epiciclos. El único planeta que lo necesitaba, según Ptolomeo, era Mercurio, cuya órbita se aleja más del círculo que la de ningún otro planeta. Otra complicación era el excéntrico; la Tierra se consideraba no el centro del deferente de cada planeta, sino situada a cierta distancia de ese centro. Por ejemplo, en la teoría de Ptolomeo, el centro del deferente de Venus estaba desplazado de la Tierra en un 2 por ciento del radio del deferente[119].
El excéntrico se podía combinar con otro recurso matemático introducido por Ptolomeo, el ecuante, que prescribe que cada planeta posee una velocidad variable en su órbita, aparte de la variación debida al epiciclo del planeta. Podríamos imaginar que, sentados en la Tierra, veríamos cada planeta, o para ser más exactos, el centro del epiciclo de cada planeta, girando en torno a nosotros a una velocidad constante (digamos, en grados de arco por día), pero Ptolomeo sabía que esto no concordaba del todo con la observación. Una vez introducido un excéntrico, uno podía imaginar que deberíamos ver los centros de los epiciclos de los planetas moverse a una velocidad constante, no alrededor de la Tierra, sino alrededor de los deferentes de los planetas. Pero ¡ah!, eso tampoco funcionaba. En lugar de eso, para cada planeta Ptolomeo introdujo lo que vino a conocerse como un ecuante, un punto situado sobre el lado opuesto del centro del deferente de la Tierra, pero a igual distancia de este centro; y supuso que los centros de los epiciclos de los planetas giran a una velocidad constante en torno al ecuante. El hecho de que la Tierra y el ecuante se hallan a la misma distancia del centro del deferente no se dedujo basándose en ideas filosóficas preconcebidas, sino que se calculó dejando esas distancias como parámetros libres y hallando los valores de las distancias para las cuales las predicciones de la teoría coincidían con la observación.
Existían discrepancias considerables entre el modelo de Ptolomeo y la observación. Como veremos al llegar a Kepler en el capítulo 11, si se utilizaba de manera sistemática, la combinación de un solo epiciclo para cada planeta y un excéntrico y un ecuante [120] para el Sol y para cada planeta podía indicar perfectamente el movimiento real de los planetas, incluida la Tierra, en órbitas elípticas, lo bastante como para concordar con casi todas las observaciones realizadas sin telescopio. Pero Ptolomeo no era sistemático. No utilizó el ecuante al describir el supuesto movimiento del Sol en torno a la Tierra; y esta omisión —puesto que la localización de los planetas se refiere a la posición del Sol— también desbarató las predicciones de los movimientos planetarios. Tal como ha recalcado George Smith[121], que nadie después de Ptolomeo parezca haber considerado seriamente esas discrepancias como guía para una teoría mejor es algo que denota la distancia existente entre la astronomía antigua y medieval y la ciencia moderna.
La Luna presentaba dificultades especiales: el tipo de teoría que funciona bastante bien con el movimiento aparente del Sol y los planetas no funcionaba en el caso de la Luna. No se comprendió hasta la obra de Isaac Newton que ello se debía a que el movimiento de la Luna se ve significativamente afectado por la gravitación de dos cuerpos —el Sol y la Tierra—, mientras que el movimiento de los planetas está casi exclusivamente gobernado por la gravitación de un solo cuerpo: el Sol. Hiparco había propuesto una teoría del movimiento de la Luna con un solo epiciclo, ajustado para explicar el tiempo que transcurría entre los eclipses; pero tal como reconoció Ptolomeo, este modelo no sirvió para predecir la localización de la Luna en el zodíaco entre eclipse y eclipse. Ptolomeo fue capaz de solucionar este error con un modelo más complicado, pero esta teoría también tenía sus problemas: la distancia entre la Luna y la Tierra variaría mucho, y conduciría a un cambio mucho mayor en el tamaño aparente de la Luna del que podemos observar.
Como ya se ha mencionado, en el sistema de Ptolomeo y sus predecesores no hay manera de que la observación de los planetas pudiera indicar los cambios de tamaño de sus deferentes y epiciclos; la observación solo podría haber fijado la razón de esos tamaños para cada planeta [122]. Ptolomeo llenó ese vacío en Las hipótesis de los planetas, una secuela del Almagesto. En esa obra invocó el principio a priori, quizá sacado de Aristóteles, de que en el sistema del mundo no hay huecos. Se supone que cada planeta, así como el Sol y la Luna, ocupa una cáscara, que se extiende desde la mínima a la máxima distancia del planeta, el Sol o la Luna hasta la Tierra, y que estas cáscaras encajaban perfectamente sin dejar ningún hueco. En este esquema, los tamaños relativos de las órbitas de los planetas, y del Sol y la Luna eran todos fijos, una vez uno decidía su orden hacia fuera desde la Tierra. Además, la Luna está bastante cerca de la Tierra como para que su distancia absoluta (en unidades del radio de la Tierra) se pueda calcular de diversas maneras, incluyendo el método de Hiparco comentado en el capítulo 7. El propio Ptolomeo desarrolló el método del paralaje: la razón entre la distancia a la Luna y el radio de la Tierra se puede calcular a partir del ángulo observado entre el cenit y la dirección de la Luna y el valor calculado que tendría ese ángulo si la Luna se observara desde el centro de la Tierra[123] (véase Nota técnica 14). De aquí que, según los supuestos de Ptolomeo, lo único necesario para calcular la distancia del Sol y los planetas era conocer el orden de sus órbitas alrededor de la Tierra.
Se consideraba que la órbita más interior es siempre la de la Luna, debido a que el Sol y los planetas de vez en cuando quedaban eclipsados por esta. Además, era natural suponer que los planetas más alejados eran aquellos que parecen tardar más tiempo en dar la vuelta a la Tierra, por lo que Marte, Júpiter y Saturno se tomaban en este orden desde la Tierra. Pero el Sol, Venus y Mercurio parecían tardar, de media, un año en dar la vuelta a la Tierra, por lo que su orden seguía siendo un tema polémico. Ptolomeo suponía que el orden desde la Tierra en el siguiente: la Luna, Mercurio, Venus, el Sol, y luego Marte, Júpiter y Saturno. Los resultados de Ptolomeo al calcular las distancias del Sol, la Luna y los planetas como múltiplos del diámetro de la Tierra resultaron mucho más pequeños que sus valores reales, y la distancia del Sol y la Luna fue similar (quizá de manera no casual) a los resultados de Aristarco comentados en el capítulo 7.
Las complicaciones de los epiciclos, ecuantes y excéntricos le han dado mala reputación a la astronomía ptolemaica, aunque no deberíamos creer que Ptolomeo se empecinó en introducir estas complicaciones para compensar el error de considerar la Tierra como el centro inmóvil del sistema solar. Las complicaciones, aparte de asignar un solo epiciclo para cada planeta (y ninguno para el Sol), no tenían nada que ver con el hecho de si la Tierra giraba alrededor del Sol o el Sol alrededor de la Tierra. Eran necesarias por el hecho, no comprendido hasta la época de Kepler, de que las órbitas no son círculos, el Sol no se halla en el centro de las órbitas y las velocidades no son constantes. Las mismas complicaciones también afectaban la teoría original de Copérnico, que supuso que las órbitas de los planetas y la Tierra tenían que ser circulares y sus velocidades constantes. Por suerte, se trata de una aproximación bastante buena, y la versión más simple de la teoría del epiciclo, asignándole tan solo uno a cada planeta y ninguno al Sol, funciona mucho mejor que las esferas homocéntricas de Eudoxo, Calipo y Aristóteles. Si Ptolomeo hubiera incluido un ecuante junto con un excéntrico para el Sol, y también para cada planeta, las discrepancias entre la teoría y la observación habrían sido demasiado pequeñas para ser detectadas con los métodos entonces disponibles.
Pero esto zanjó la disputa entre las teorías ptolemaica y aristotélica de los movimientos planetarios. La teoría ptolemaica concordaba mejor con la observación, pero chocaba con el supuesto de la física aristotélica de que todos los movimientos celestes deben ser círculos cuyo centro es el centro de la Tierra. De hecho, los extraños movimientos en epiciclos habrían sido difíciles de tragar incluso para alguien a quien tanto le diera una teoría como otra.
Durante mil quinientos años continuó el debate entre los defensores de Aristóteles, a menudo denominados físicos o filósofos, y los partidarios de Ptolomeo, a los que se referían como astrónomos o matemáticos. Los aristotélicos a menudo reconocían que el modelo de Ptolomeo encajaba mejor con los datos, pero consideraban este hecho algo que simplemente era de interés para los matemáticos, y no relevante para comprender la realidad. Su actitud quedó expresada en una afirmación de Gémino de Rodas, que vivió allá por el año 70 a. C., y que fue citado tres siglos más tarde por Alejandro de Afrodisia, que a su vez fue citado por Simplicio[124], en un comentario a la Física de Aristóteles. Sus palabras plantean el gran debate entre los científicos naturales (palabra que a veces se traduce como «físicos») y los astrónomos:
Una de las preocupaciones de la investigación física es indagar en la sustancia de los cielos y de los cuerpos celestes, sus poderes y la naturaleza de su nacimiento y defunción; por Zeus, puede revelar la verdad de su tamaño, forma y posición. La astronomía no pretende pronunciarse sobre ninguna de estas cuestiones, sino que revela la naturaleza ordenada de los fenómenos celestes, mostrando que los cielos son de hecho un cosmos ordenado, y también discute el tamaño, forma y distancia relativa de la Tierra, el Sol y la Luna, así como los eclipses, las conjunciones de cuerpos celestes y las cualidades y cantidades inherentes en sus trayectorias. Puesto que dentro de la astronomía encontramos el estudio de la cantidad, la magnitud y cualidad de sus formas, es comprensible que recurra a la aritmética y la geometría a este respecto. Y acerca de estas cuestiones, que son las únicas que ha prometido explicar, posee la capacidad de llegar a resultados mediante el uso de la aritmética y la geometría. El astrónomo y el científico natural, por consiguiente, en muchas ocasiones pretenden alcanzar el mismo objetivo, por ejemplo, que el Sol es un cuerpo de tamaño considerable, que la Tierra es esférica, pero no utilizan la misma metodología. Pues el científico natural demostrará cada uno de sus puntos a partir de la sustancia de los cuerpos celestes, o de sus poderes, o del hecho de que son de la mejor manera posible, o de su nacimiento y transformación, mientras que el astrónomo acude a las propiedades de sus formas y tamaños, o a la cantidad de movimiento y el tiempo que corresponde a este […] En general, al astrónomo no le interesa conocer lo que por naturaleza está en reposo y lo que por naturaleza está en movimiento; más bien debe hacer suposiciones acerca de lo que está en reposo y lo que se mueve, y considerar con qué suposiciones concuerda lo que vemos en los cielos. Debe extraer sus principios básicos del científico natural, a saber, que la danza de los cuerpos celestes es simple, regular y ordenada; a partir de esos principios conseguirá demostrar que el movimiento de todos los cuerpos celestes es circular, tanto los de aquellos que describen trayectorias paralelas, como los que siguen círculos oblicuos.Los «científicos naturales» de Gémino comparten algunas características de los físicos teóricos de la actualidad, pero con enormes diferencias. Siguiendo a Aristóteles, Gémino considera que los científicos naturales se basan en primeros principios, incluyendo principios teleológicos: el científico natural supone que los cuerpos celestes «son de la mejor manera posible». Para Gémino, es solo el astrónomo quien utiliza las matemáticas, como un complemento a sus observaciones. Lo que Gémino no imagina es ese toma y daca que se ha desarrollado entre teoría y observación. La física teórica moderna lleva a cabo deducciones a partir de principios básicos, pero se sirve de las matemáticas en su labor, y los principios, en sí mismos, se expresan de manera matemática y se aprenden de la observación, y desde luego no considerando lo que es «mejor».
En la referencia de Gémino a los movimientos de los planetas «que describen trayectorias paralelas, como los que siguen círculos oblicuos», podemos reconocer las esferas homocéntricas que giran sobre ejes inclinados en los esquemas de Eudoxo, Calipo y Aristóteles, a los que Gémino, como buen aristotélico, naturalmente sería fiel. Por otro lado, Adrasto de Afrodisia, que alrededor del año 100 de nuestra era escribió un comentario sobre el Timeo, y una generación más tarde el matemático Teón de Esmirna, estaban tan convencidos de la teoría de Apolonio e Hiparco que intentaron convertirla en respetable, interpretando los epiciclos y deferentes como esferas sólidas transparentes, al igual que las esferas homocéntricas de Aristóteles, aunque ahora ya no eran homocéntricas.
Algunos autores, al enfrentarse a las teorías rivales de los planetas, se dieron por vencidos y declararon que los humanos no estaban destinados a comprender los fenómenos celestes. Así, a mitad del siglo V de nuestra era, en su comentario al Timeo, el pagano neoplatónico Proclo proclamó [125]:
Cuando nos enfrentamos a objetos sublunares, nos basta, debido a la inestabilidad del material que los constituye, con comprender lo que ocurre en la mayoría de casos. Pero cuando queremos saber cosas celestes, utilizamos la sensibilidad y apelamos a todo tipo de invenciones de lo más inverosímiles […] Que así son las cosas lo demuestran claramente los descubrimientos llevados a cabo acerca de estas cosas celestes: a partir de hipótesis diferentes extraemos las mismas conclusiones relativas a los mismos objetos. Entre estas hipótesis hay algunas que explican los fenómenos mediante epiciclos, otras que lo hacen mediante excéntricos, y aun otras que explican los fenómenos mediante esferas contragiratorias que carecen de planetas. Seguramente el criterio de Dios es más certero. Pero por lo que respecta a nosotros, debemos satisfacernos con «aproximarnos» a estas cosas, pues somos hombres, que solo pueden hablar de lo que es probable, y cuyas enseñanzas parecen fábulas.Proclo se equivocaba en tres aspectos. Pasaba por alto la cuestión de que las teorías ptolemaicas que utilizaban los epiciclos y los excéntricos funcionaban mucho mejor a la hora de «explicar los fenómenos» que las teorías aristotélicas, que utilizaban la hipótesis de las «esferas contragiratorias» homocéntricas. También existe un punto técnico de poca importancia: al referirse a las hipótesis «que explican los fenómenos mediante epiciclos, otras que lo hacen mediante excéntricos», Proclo parece no comprender que en el caso en el que un epiciclo puede desempeñar el papel de un excéntrico no se trata de hipótesis diferentes, sino de maneras distintas de describir lo que es matemáticamente la misma hipótesis. Pero sobre todo, Proclo se equivocaba al suponer que es más difícil comprender los movimientos celestes que los de la Tierra, por debajo de la órbita de la Luna. Lo que es cierto es lo contrario. Sabemos cómo calcular los movimientos de los cuerpos del sistema solar con exquisita precisión, pero somos incapaces de predecir los terremotos o los huracanes. Pero Proclo no era el único. Siglos más tarde, en el caso de Maimónides, veremos repetirse este injustificado pesimismo acerca de la posibilidad de comprender los movimientos de los planetas.
El físico convertido en filósofo Pierre Duhem[126], que escribió durante la primera década del siglo XX, tomó partido por los ptolemaicos porque su modelo encajaba mejor con los datos, pero rechazaba a Teón y Adrasto por intentar darle realidad al modelo. Quizá porque era profundamente religioso, Duhem pretendía restringir el papel de la ciencia simplemente a la construcción de teorías matemáticas que coincidieran con la observación, más que a esfuerzos globales para explicarlo todo. No comparto esa opinión, pues lo que pretende la labor de mi generación de físicos es una explicación en el mismo sentido en que utilizamos habitualmente la palabra, no como una simple descripción [127]. Cierto, no es fácil distinguir de manera precisa entre descripción y explicación. Yo diría que explicamos una generalización sobre el mundo mostrando cómo se deduce de una generalización más fundamental, pero ¿qué queremos decir con fundamental? No obstante, creo que sabemos lo que queremos decir cuando afirmamos que las leyes de la gravitación y el movimiento de Newton son más fundamentales que las tres leyes del movimiento planetario de Kepler. El gran éxito de Newton consistió en explicar los movimientos de los planetas, no simplemente en describirlos. Newton no explicó la gravitación, y sabía que no lo había hecho, pero es lo que ocurre siempre con las explicaciones, que siempre queda algo para una futura explicación.
Por culpa de sus extraños movimientos, los planetas no servían como relojes, ni calendarios ni brújulas. En la época helenística y posteriormente se les dio un uso distinto en la astrología, una falsa ciencia aprendida de los babilonios[128] . La nítida distinción actual entre astronomía y astrología era mucho menos clara en la época antigua y medieval, porque todavía no habíamos aprendido que los asuntos humanos son irrelevantes para las leyes que gobiernan las estrellas y los planetas. A partir de la época de los Ptolomeos, los gobernantes apoyaron el estudio de la astronomía, sobre todo con la esperanza de que les revelara el futuro, con lo que los astrónomos dedicaron gran parte de su tiempo a la astrología. De hecho, Claudio Ptolomeo no fue solo el autor del libro astronómico más importante de la Antigüedad, el Almagesto, sino también de un libro de texto de astrología, el Tetrabiblos.
Pero no puedo despedirme de la astronomía griega con un comentario tan amargo. Para acabar felizmente la segunda parte de este libro incluyo una cita de Ptolomeo en la que nos habla del placer que le proporciona la astronomía[129]:
Sé que soy mortal, una criatura de un día; pero cuando estudio los círculos giratorios de las estrellas, mis pies ya no tocan la Tierra, sino que, sentado al lado del propio Zeus, me harto de ambrosía, el alimento de los dioses.
Parte III
La Edad Media
Durante la Edad Media, ni en el mundo islámico ni en la Europa cristiana encontramos nada comparable. El milenio transcurrido entre la caída de Roma y la revolución científica tampoco fue un desierto intelectual. Los logros de la ciencia griega se conservaron, y en algunos casos se mejoraron en las instituciones del islam y en las universidades de Europa, lo que preparó el terreno para la revolución científica.
Lo que se conservó en la Edad Media no fueron tan solo los logros de la ciencia griega. En el islam y el cristianismo medieval veremos una prolongación de los antiguos debates acerca del papel de la filosofía, las matemáticas y la religión en la ciencia. Después del hundimiento del Imperio romano occidental, en el siglo V, la mitad oriental de habla griega pervivió como el Imperio bizantino, e incluso aumentó su extensión. El Imperio bizantino alcanzó la culminación de su éxito militar durante el reinado del emperador Heraclio, cuyo ejército, en el año 627 de nuestra era, destruyó el ejército del Imperio persa, el antiguo enemigo de Roma, en la batalla de Nínive. Pero al cabo de una década los bizantinos tuvieron que enfrentarse a un adversario más formidable.
En la Antigüedad los árabes eran considerados un pueblo bárbaro que vivía en las fronteras de los imperios romano y persa, «que separan el desierto de los sembrados». Eran paganos, y su religión se centraba en la ciudad de La Meca, en la porción colonizada de Arabia occidental conocida como el Hiyaz. A partir de finales del siglo VI, Mahoma, un habitante de La Meca, se propuso convertir a sus conciudadanos al monoteísmo. Al encontrar oposición, él y sus acólitos huyeron en el 622 a Medina, que entonces utilizaron como base militar para la conquista de La Meca y casi toda la península Arábiga.
Después de la muerte de Mahoma, en el 632, una mayoría de musulmanes siguió la autoridad de cuatro líderes sucesivos con sede primero en Medina: sus compañeros y parientes Abu Bakr, Omar, Uthman y Alí. Hoy en día los musulmanes suníes los reconocen como los «cuatro califas bien guiados». Los musulmanes conquistaron la provincia bizantina de Siria en el 634, apenas siete años después de la batalla de Nínive, y a continuación pasaron a Persia, Mesopotamia y Egipto.
Estas conquistas introdujeron a los árabes en un mundo más cosmopolita. Por ejemplo, el general Amrou, que conquistó Alejandría, le relató al califa Omar: «He tomado una ciudad de la que lo único que puedo decir es que contiene 6000 palacios, 4000 baños, 400 teatros, 12 000 verduleros y 40 000 judíos» [130].
Una minoría, los predecesores de los chiítas de la actualidad, aceptaron tan solo la autoridad de Alí, el cuarto califa y marido de la hija de Mahoma, Fátima. La escisión del mundo islámico se hizo permanente después de una revuelta contra Alí, en la que este y su hijo Husain fueron asesinados. Una nueva dinastía, el califato omeya, se estableció en Damasco en el 661.
Bajo el dominio de los Omeyas, las conquistas árabes se expandieron hacia los territorios de lo que es hoy Afganistán, Pakistán, Libia, Túnez, Argelia y Marruecos, casi toda España y gran parte de Asia central, más allá del río Oxus. Desde las antiguas tierras de Bizancio, que ahora gobernaban, comenzaron a asimilar la ciencia griega. Parte del saber griego procedía de Persia, cuyos gobernantes habían dado la bienvenida a los eruditos griegos (entre ellos Simplicio) antes del apogeo del islam, cuando la Academia neoplatónica se cerró por orden del emperador Justiniano. Lo que se perdió con el cristianismo se ganó con el islam.
Fue en la época de la siguiente dinastía suní, el califato abásida, cuando la ciencia árabe entró en su edad de oro. Bagdad, la capital de los Abásidas, se construyó a ambas orillas del río Tigris, en Mesopotamia, bajo el gobierno de Al-Mansur, califa entre el 754 y el 775. Se convirtió en la ciudad más grande del mundo, o al menos en la más grande fuera de China. Su gobernante más conocido fue Harum Al-Rashid, califa entre el 786 y el 809, famoso por Las mil y una noches. Fue bajo el califato de Al-Rashid y su hijo Mamun, califa entre el 813 y el 833, cuando la traducción del griego, el persa y el hindi alcanzó su mayor esplendor. Mamun envió una misión a Constantinopla para traer manuscritos en griego. Entre la delegación probablemente se encontraba el físico Hunain ibn Ishaq, el más importante traductor del siglo IX, que fundó una dinastía de traductores, preparando a su hijo y a su sobrino para que continuaran su labor. Hunain tradujo obras de Platón y Aristóteles, así como textos médicos de Dioscórides, Galeno e Hipócrates. Obras matemáticas de Euclides, Ptolomeo y otros fueron traducidas al árabe en Bagdad, algunas a través del siríaco como lengua intermedia. El historiador Philip Hitti ha definido perfectamente el contraste entre el saber en esa época en Bagdad y el analfabetismo de Europa a principios de la Edad Media: «Pues mientras en oriente Al-Rashid y Mamun ahondaban en la filosofía griega y persa, sus contemporáneos occidentales, Carlomagno y sus nobles apenas eran capaces de escribir su nombre»[131].
A veces se ha dicho que la mayor contribución a la ciencia del califato abásida fue la fundación de un instituto de traducción e investigación, la Bayt al-Hikmah, la Casa de la Sabiduría. Este instituto supuestamente tenía que tener para los árabes la misma función que el Museo y la Biblioteca de Alejandría para los griegos. Esta opinión la ha puesto en duda un estudioso de la lengua y la literatura árabes, Dimitri Gutas [132]. Señala que Bayt al-Hikmah es una traducción de un término persa que había sido utilizado durante mucho tiempo en la Persia preislámica para designar los almacenes de libros, casi todos de historia y poesía persa más que de ciencia griega. Se conocen pocas obras traducidas en la Bayt al-Hikmah durante el califato de Mamun, y estas se tradujeron del persa más que del griego. Veremos que en la Bayt al-Hikmah se llevó a cabo cierta investigación astronómica, pero sabemos poco de su alcance. Lo que no admite disputa es que, ya fuera en la Bayt al-Hikmah o no, la propia ciudad de Bagdad, en la época de Mamun y Al-Rashid, fue un gran centro de traducción e investigación.
La ciencia árabe no se limitó a Bagdad, sino que se extendió por el oeste hasta Egipto, España y Marruecos, y por el este hasta Persia y Asia central. No solo participaban en ella árabes, sino también persas, judíos y turcos. Formaban parte de la civilización árabe y escribían en árabe (o al menos en el alfabeto árabe). En aquella época, en el campo de la ciencia, el árabe poseía un prestigio parecido al que hoy en día posee el inglés. En algunos casos resulta difícil saber cuál es el origen étnico de estos personajes. Por lo general les aplicamos la etiqueta de «árabes».
De manera bastante aproximada, podemos identificar dos tradiciones científicas distintas que dividieron a los eruditos árabes. Por un lado, había auténticos matemáticos y astrónomos no muy preocupados con lo que hoy denominaríamos filosofía. Luego estaban los filósofos y físicos, no muy activos en matemáticas, y poderosamente influidos por Aristóteles. Su interés por la astronomía era sobre todo astrológico. Cuando lo que les preocupaba era la teoría de los planetas, los filósofos/físicos preferían la teoría aristotélica de las esferas centradas en la Tierra, mientras que los astrónomos/matemáticos por lo general seguían la teoría ptolemaica de los epiciclos y deferentes comentada en el capítulo 8. Aquello fue un auténtico cisma intelectual que, como veremos, persistió en Europa hasta la época de Copérnico.
Los descubrimientos de la ciencia árabe fueron obra de muchos individuos, aunque ninguno de ellos destaca claramente del resto, como ocurre, por ejemplo con Galileo y Newton en la revolución científica europea. Lo que sigue es una breve galería de científicos musulmanes medievales que espero sirva para hacerse una idea de sus logros y variedad.
El primero de los astrónomos/matemáticos importantes de Bagdad fue Al-Juarismi, un persa nacido alrededor de 780 en lo que es ahora Uzbekistán. Al-Juarismi trabajó en la Bayt al-Hikmah y preparó unas tablas astronómicas muy utilizadas, basadas en parte en observaciones indias. Su libro más famoso de matemáticas fue Hisāb al-ŷabr w'al-muqābala, dedicado al califa Mamun (que era medio persa). De este título se deriva la palabra «álgebra». Pero en realidad no era un libro de lo que hoy se denomina álgebra. Fórmulas como la que da la solución a las ecuaciones de segundo grado se expresaban en palabras, no en los símbolos que son un elemento esencial del álgebra. (A este respecto, las matemáticas de Al-Juarismi estaban menos avanzadas que las de Diofanto). De Al-Juarismi también procede el nombre que le damos a la regla para solventar problemas, «algoritmo». El texto de Hisāb al-ŷabr w'al-muqābala contiene una confusa mezcla de números romanos; los números babilonios tenían como base aritmética el 60; y un nuevo sistema de números aprendidos de la India tomaba como base el 10. Quizá la aportación matemática más importante de Al-Juarismi fue su explicación a los árabes de estos números indios, que a su vez se conocieron en Europa como números arábigos.
Además de la importante figura de Al-Juarismi, se reunió en Bagdad un productivo grupo de astrónomos del siglo IX, entre ellos Al-Farghani (Alfraganus) [133], que escribió un popular resumen del Almagesto de Ptolomeo y desarrolló su propia versión del esquema planetario descrito en Las hipótesis de los planetas de Ptolomeo.
Una de las ocupaciones más importantes de este grupo de Bagdad fue mejorar la medición del tamaño de la Tierra llevada a cabo por Eratóstenes. Al-Farghani, en concreto, afirmó que su circunferencia era más pequeña, cosa que, siglos más tarde, animó a Colón (como ya he mencionado en la nota al pie de la página 81) a pensar que podría sobrevivir a un viaje oceánico hacia el oeste desde España a Japón, quizá el error de cálculo más afortunado de la historia.
El árabe más influyente entre los astrónomos europeos fue Al-Battani (Albatenius), nacido alrededor del año 858 a. C. en la parte septentrional de Mesopotamia. Utilizó y corrigió el Almagesto de Ptolomeo, llevando a cabo mediciones más exactas del ángulo de 23,5° entre el trayecto del Sol a través del zodíaco y el ecuador celeste, de la duración del año y de las estaciones, de la precesión de los equinoccios y de la posición de las estrellas. Introdujo una cantidad trigonométrica, el seno, procedente de la India, en lugar de la cuerda, su pariente más próximo, utilizada y calculada por Hiparco (véase Nota técnica 15). Su trabajo fue frecuentemente citado por Copérnico y Tycho Brahe.
El astrónomo persa Al-Sufi (Azophi) llevó a cabo un descubrimiento cuya importancia cosmológica no se reconoció hasta el siglo XX. En el año 964, en su Libro de las estrellas fijas, describió una «pequeña nube» siempre presente en la constelación de Andrómeda. Se trata de la primera observación conocida de lo que ahora se denominan galaxias, en este caso la gran galaxia espiral M31. Al-Sufi trabajó en Isfahán, y también participó en la traducción de obras de astronomía griega al árabe.
Quizá el astrónomo más impresionante de la era abásida fue Al-Biruni, cuya obra fue desconocida en la Europa medieval, por lo que no existe ninguna versión latinizada de su nombre. Al-Biruni vivía en Asia central, y en 1017 visitó la India, donde dio conferencias sobre filosofía griega. Consideró la posibilidad de que la Tierra girara sobre su eje, proporcionó valores exactos a la latitud y longitud de diversas ciudades, preparó una tabla de la cantidad trigonométrica conocida como tangente y midió la gravedad específica de diversos sólidos y líquidos. Se burló de las pretensiones de la astrología. En la India, Al-Biruni inventó un nuevo método para medir la circunferencia de la Tierra. Tal como lo describe [134]:
Cuando estuve viviendo en el fuerte de Nandana, en la tierra de la India, observé, desde una montaña elevada situada al oeste del fuerte, una gran llanura que quedaba al sur de la montaña. Se me ocurrió que quería poner a prueba ese método [un método descrito anteriormente]. Así pues, desde lo alto de la montaña, llevé a cabo una medida empírica del contacto entre la Tierra y el cielo azul. Descubrí que la línea de visión [hacia el horizonte] se había hundido por debajo de la línea de referencia [es decir, de la dirección horizontal] en 34 minutos de arco. A continuación medí la perpendicular de la montaña [es decir, su altura] y descubrí que era de 652,055 codos, siendo el codo la medida habitual utilizada en esa región para medir la tela[135].A partir de esos datos, Al-Biruni concluyó que el radio de la Tierra es 12 803 337,0358 codos. Algo no funcionaba con ese cálculo; a partir de los datos que citaba, el radio debería haberle salido con una longitud de 13,3 millones de codos (véase Nota técnica 16). Naturalmente, es imposible que conociera la altura de la montaña con la exactitud que afirmaba, de manera que no había ninguna diferencia práctica entre 12,8 millones de codos y 13,3 millones. Al dar el radio de la Tierra con una precisión de doce cifras significativas, Al-Biruni fue culpable de una precisión fuera de lugar, el mismo error que vimos en Aristarco: realizar cálculos y dar los resultados con un grado de precisión mucho mayor que el justificado por la exactitud de las medidas en que se basaba el cálculo.
En una ocasión tuve el mismo problema. Hace mucho, había conseguido un trabajo veraniego, y me dedicaba a calcular la trayectoria de átomos a través de una serie de imanes en un aparato de partículas atómicas, antes de los ordenadores portátiles o de las calculadoras electrónicas de bolsillo. Pero yo tenía una calculadora electromecánica que era capaz de sumar, restar, multiplicar y dividir hasta ocho cifras significativas. Por pereza, en mi informe di los resultados de los cálculos con hasta ocho cifras significativas, tal como salían de la calculadora, sin molestarme en redondearlas con una precisión más realista. Mi jefe se quejó de que las medidas del campo magnético en el que se basaban mis cálculos eran exactas solo en unos decimales, y que pretender más precisión resultaba absurdo.
En cualquier caso, no podemos juzgar la exactitud del resultado de Al-Biruni, según el cual el radio de la Tierra es de unos 13 millones de codos, porque nadie sabe cuál es la lógica exacta de su codo. Al-Biruni afirmó que había 4000 codos en una milla, pero ¿qué era para él una milla entonces?
Omar Jayam, el poeta y astrónomo, nació en el año 1048 en Nishapur, Persia, y murió allí alrededor de 1131. Dirigió el observatorio de Isfahán, donde compiló tablas astronómicas y planeó una reforma del calendario. En Samarcanda, en el Asia central, escribió sobre temas de álgebra, como la solución de las ecuaciones de tercer grado. Los lectores de habla inglesa lo conocen mejor como poeta, a través de la magnífica traducción del siglo XIX llevada a cabo por Edward Fitzgerald de una selección de 75 entre la gran cantidad de escritos por Omar Jayam en persa y conocidos como las Rubaiyat. No ha de sorprendernos que la persona práctica y realista que escribió esos versos se opusiera con toda contundencia a la astrología.
La mayor contribución árabe a la física tuvo lugar en el campo de la óptica, primero a final del siglo X gracias a la labor de Ibn Sahl, que quizá calculara la regla que da la dirección de los rayos refractados de luz (tema que ampliaremos en el capítulo 13), y luego por el gran Al-Haitam (Alhacén), que nació en Basra, al sur de Mesopotamia, allá por el 965, pero que trabajó en El Cairo. Entre los libros que nos han llegado encontramos la Óptica, La luz de la luna, El halo y el arcoíris, De los espejos paraboloides comburentes, La formación de la sombra, La luz de las estrellas, Discurso sobre la luz, La esfera ardiente y La forma del eclipse. Correctamente atribuyó la curvatura de la luz de la refracción al cambio de velocidad de esta cuando pasa de un medio a otro, y descubrió de manera experimental que el ángulo de refracción es proporcional al ángulo de incidencia solo para ángulos pequeños. Pero no dio la fórmula general correcta. En astronomía, siguió a Adrasto y Teón al intentar ofrecer una explicación física a los epiciclos y deferentes de Ptolomeo.
Jabir ibn Hayyan fue un pionero de la química que se cree que vivió a finales del siglo VIII o principios del IX. Se sabe poco de su vida, y no está claro si las muchas obras en árabe que se le atribuyen son realmente producto de una sola persona. También hay un gran corpus de obras en latín que aparecieron en Europa en los siglos XIII y XIV atribuidas a un tal «Geber», pero ahora se cree que el autor de estas obras no es el mismo que el autor de las obras en árabe atribuidas a Jabir ibn Hayyan. Jabir desarrolló técnicas de evaporación, sublimación, fundido y cristalización. Se interesó por la transmutación de metales inferiores en oro, y de ahí que a menudo se le domine alquimista, aunque la distinción entre química y alquimia tal como se practicaba en su época es artificial, pues no existía ninguna teoría científica fundamental que explicara que dichas transmutaciones eran imposibles. En mi opinión, para el futuro de la ciencia es más importante la distinción entre los químicos o alquimistas que siguieron a Demócrito y consideraron el funcionamiento de la materia desde una perspectiva puramente naturalista —ya fueran sus teorías equivocadas o no—, y aquellos que, al igual que Platón —y, a menos que hablaran de manera metafórica, Anaximandro y Empédocles—, introdujeron valores humanos o religiosos en estudio de la materia. Jabir probablemente pertenece a estos últimos, pues, por ejemplo, le daba gran importancia al significado químico del 28, el número de letras del alfabeto árabe, el idioma del Corán. De algún modo resultaba importante que 28 fuera el producto de 7, supuestamente el número de metales, por 4, el número de cualidades: frío, caliente, húmedo y seco.
La primera figura importante de la tradición médico-filosófica árabe fue Al-Kindi (Alkindus), que nació en Basra de familia noble pero trabajó en Bagdad en el siglo IX. Fue seguidor de Aristóteles e intentó reconciliar las doctrinas de este con las de Platón y el islam. Al-Kindi fue un erudito, muy interesado en las matemáticas, pero al igual que Jabir siguió a los pitagóricos al utilizarlas como una especie de magia numérica. Escribió sobre óptica y medicina, y atacó la alquimia, aunque defendió la astrología. Al-Kindi también supervisó parte de las traducciones del griego al árabe.
Más impresionante fue Al-Razi (Rhazes o Rasis), un persa de habla árabe de la generación posterior a Al-Kindi. Entre sus obras encontramos Tratado sobre la viruela y el sarampión. En sus Dudas referentes a Galeno desafió la autoridad del influyente médico romano y cuestionó la teoría, que se remontaba a Hipócrates, de que la salud es una cuestión de equilibrio entre los cuatro humores (tal como hemos explicado en el capítulo 4). Manifestó: «La medicina es una filosofía, y ello no es compatible con renunciar a la crítica en relación con los principales autores». En una excepción a las clásicas opiniones de los médicos árabes, Al-Razi también se enfrentó a las enseñanzas aristotélicas, como la de que el espacio debe ser finito.
El más famoso de los médicos islámicos fue Ibn Sina (Avicena), otro persa de habla árabe. Nació en el 980 cerca de Bujará, en el Asia central; fue médico de la corte del sultán de Bujará, y se le nombró gobernador de la provincia. Avicena fue aristotélico, y, al igual que Al-Kindi, intentó reconciliar a Aristóteles con el islam. Su obra Al Qanun, también conocida como el Canon de Avicena, fue el texto médico más influyente de la Edad Media.
Al mismo tiempo, la medicina comenzó a florecer en la España árabe. Al Zahrawi (Abulcasis) nació en el 936 cerca de Córdoba, la metrópolis de Andalucía, y trabajó allí hasta su muerte, en 1013. Fue el cirujano más importante de la Edad Media, y tremendamente influyente en la Europa cristiana. Quizá porque la cirugía no llevaba una carga tan grande de teoría infundada como otras ramas de la medicina, Al Zahrawi procuró mantener la medicina separada de la filosofía y la teología.
El divorcio entre la medicina y la filosofía no duró. En el siglo siguiente el médico Ibn Bayyah (Avempace) nació en Zaragoza, y trabajo allí y en Fez, Sevilla y Granada. Fue aristotélico y criticó a Ptolomeo, cuya astronomía rechazó, aunque desaprobaba la teoría del movimiento de Aristóteles.
Ibn Bayyah fue sucedido por su alumno Ibn Tufail (Abubacer), también nacido en la España musulmana. Practicó la medicina en Granada, Ceuta y Tánger, y fue visir y médico del sultán de la dinastía almohade. Arguyó que no existe contradicción entre Aristóteles y el islam, y al igual que su maestro rechazó los epiciclos y excéntricos de la astronomía ptolemaica.
A su vez Ibn Tufail tuvo un alumno distinguido, Al-Bitruji (Alpetragio), que fue astrónomo, pero heredó la filiación aristotélica de su maestro y su rechazo de Ptolomeo. Al-Bitruji intentó sin éxito reinterpretar el movimiento de los planetas en epiciclos en términos de esferas homocéntricas.
Un médico de la España musulmana que acabó siendo más famoso como filósofo fue Ibn Rushd (Averroes). Nacido en 1126 en Córdoba, fue nieto del imán de la ciudad. Llegó a ser cadí (juez) de Sevilla en 1169 y de Córdoba en 1171, y por recomendación de Ibn Tufali pasó a ser médico de la corte en 1182. Como científico de la medicina, Averroes fue conocido sobre todo por identificar la función de la retina del ojo, y su fama se basa principalmente en su obra como comentarista de Aristóteles. Casi da un poco de bochorno leer su elogio de Aristóteles:
[Aristóteles] fundó y completó la lógica, la física y la metafísica. Digo que fundó estas disciplinas porque las obras escritas antes que él sobre esas ciencias no son ni dignas de mención y quedan totalmente eclipsadas por sus propios escritos. Indico que las completó porque nadie, desde su época hasta ahora, es decir, a lo largo de mil quinientos años, ha sido capaz de añadir nada a sus escritos ni de encontrar en ellos ningún error de importancia[136].El padre del escritor contemporáneo Salman Rushdie escogió el apellido de Rushdie en honor al racionalismo laico de Ibn Rushd.
Naturalmente, Ibn Rushd rechazó la astronomía ptolemaica por ser contraria a la física, es decir, a la física de Aristóteles. Era consciente de que las esferas homocéntricas de Aristóteles no «salvaban las apariencias», e intentó reconciliar a Aristóteles con la observación, aunque concluyó que esta era una tarea para el futuro:
En mi juventud esperaba que me fuera posible llevar esta investigación [astronómica] a una conclusión satisfactoria. Ahora, en mi vejez, he perdido toda esperanza, pues diversos obstáculos se han interpuesto en mi camino. Pero lo que voy a decir quizá llame la atención de futuros investigadores. La ciencia astronómica de nuestra época seguramente no ofrece nada de lo que se pueda derivar una realidad existente. El modelo que se ha desarrollado en la época en que vivimos concuerda con los cálculos, no con lo que existe [137].Naturalmente, las esperanzas que Ibn Rushd depositó en los futuros investigadores fueron infundadas; nadie fue capaz de conseguir que la teoría aristotélica de los planetas funcionara.
En la España musulmana se practicó también una astronomía seria. En Toledo, Al-Zarqali (Azarquiel), en el siglo XI, fue el primero en medir la precesión de la órbita aparente del Sol en torno a la Tierra (en realidad, sería la precesión de la órbita de la Tierra alrededor del Sol) que ahora sabemos se debe sobre todo a la atracción gravitatoria entre la Tierra y otros planetas. A esta precesión le dio un valor de 12,9'' (segundos de arco) por año, un valor que coincide bastante con el actual de 11,6'' por año[138]. Un grupo de astrónomos, entre ellos Al-Zarqali, utilizó la obra anterior de Al-Juarismi y Al-Battani para construir las Tablas de Toledo, que sucedieron a las Tablas fáciles. Estas tablas astronómicas y sus sucesoras describieron en detalle los movimientos aparentes del Sol, la Luna y los planetas a través del zodíaco, y supusieron un hito en la historia de la astronomía.
Bajo el califato omeya y su sucesora, la dinastía almorávide bereber, España fue un centro cosmopolita de aprendizaje, tan hospitalario con los judíos como con los musulmanes. Musa ben Maimón (Maimónides) era judío y nació en 1135 en Córdoba durante esta época feliz. Bajo el islam, los judíos y cristianos nunca fueron más que ciudadanos de segunda clase, pero durante la Edad Media la situación de los judíos fue por lo general mucho mejor bajo dominio árabe que en la Europa cristiana. Por desgracia para Maimónides, durante su juventud España estuvo dominada por el califato de los fanáticos islamistas almohades, y tuvo que huir. Primero intentó encontrar refugio en Almería, Marrakech, Cesarea y El Cairo, y por fin consiguió instalarse en Fustat, un barrio de las afueras de El Cairo. Allí trabajó hasta su muerte, en 1204, como rabino, cuya influencia se extendió por todo el mundo judío medieval, y como médico enormemente valorado por los árabes y los judíos. Su obra más conocida es la Guía de perplejos, escrita en forma de cartas a un joven perplejo. En ella expresaba su rechazo de la astronomía ptolemaica por ser contraria a Aristóteles [139]:
Ya conoces, en materia astronómica, lo que, bajo mi dirección, has estudiado y aprendiste en el Almagesto; pero no disponíamos de tiempo para iniciarte en ulteriores elucubraciones.
Lo que ya sabes es que tocante a la regularidad de los movimientos y conformidad del curso de los astros con lo perceptible, todo depende de dos principios (o hipótesis): o un epiciclo, o una esfera excéntrica, o ambos a la vez. Pero quiero llamar tu atención sobre el hecho de que una y otra hipótesis se salen de toda regla, y, en definitiva, se oponen a todo cuanto enseña la Física.A continuación pasa a reconocer que el esquema de Ptolomeo concuerda con la observación, y el de Aristóteles no, y al igual que hizo Proclo anteriormente, Maimónides se desespera ante la dificultad de comprender los cielos.
Respecto al mundo celeste, el hombre nada alcanza, salvo esa exigua dosis matemática que ves. Diré en términos poéticos [140]: «Los cielos son cielos para Yhwh, pero la tierra se la dio a los hijos de los hombres»; es decir, que solo Dios conoce la verdadera naturaleza del cielo, su sustancia, forma, movimiento y causas; y en cuanto a lo que hay bajo el cielo, otorgó al hombre la facultad de conocerlo. Lo que resultó ser cierto fue todo lo contrario; el movimiento de los cuerpos celestes fue lo primero que se comprendió en el amanecer de la ciencia moderna.
Dan fe de la influencia de la ciencia árabe en Europa la larga lista de palabras derivadas de sus originales árabes: no solo álgebra y algoritmo, sino también nombres de estrellas como Aldebarán, Algol, Alphecca, Altair, Betelgeuse, Mizar, Rigel, Vega, etcétera, y de términos químicos como alcalino, alambique, alcohol, alizarina, y, por supuesto, alquimia.
Este breve repaso nos deja una pregunta: ¿por qué fueron aquellos que en concreto practicaban la medicina, como Ibn Bayyah, Ibn Tufail, Ibn Rushd y Maimónides, quienes tanto se aferraron a las enseñanzas de Aristóteles? Se me ocurren tres razones posibles. Primero, es natural que los médicos fueran los más interesados en los escritos de Aristóteles sobre biología, y en esto Aristóteles sobresalía. Además, los médicos árabes estaban muy influidos por los escritos de Galeno, que admiraba enormemente a Aristóteles. Finalmente, la medicina era un campo en el que la confrontación precisa de teoría y observación era muy difícil (y todavía lo es), de manera que el hecho de que la física y la astronomía aristotélica no coincidieran en detalle con la observación puede que no les pareciera tan importante a los médicos. En contraste, el trabajo de los astrónomos se utilizaba para finalidades en las que eran esenciales unos resultados correctos y precisos, como por ejemplo la elaboración de calendarios, la medición de la distancia de la Tierra, el conocimiento de la hora exacta para las oraciones diarias y la determinación de la quibla, o dirección de La Meca, ya que hay que orientarse hacia ella durante la oración. Incluso los astrónomos que aplicaban su ciencia a la astrología tenían que ser capaces de detallar con precisión en qué signo del zodíaco se encontraban el Sol y los planetas en cualquier fecha determinada; y no es probable que toleraran una teoría como la de Aristóteles, que daba respuestas erróneas.
El califato abásida llegó a su fin a finales de 1258, cuando los mongoles, a las órdenes de Hulegu Kan, saquearon Bagdad y mataron al califa. El Gobierno abásida se había desintegrado mucho antes. El poder político y militar había pasado de los califas a los sultanes turcos, e incluso la autoridad religiosa del califa se había visto debilitada por la fundación de Gobiernos islámicos independientes: el califato omeya, que se había trasladado a España, el califato fatimí de Egipto y la dinastía almorávide de Marruecos y España, a la que sucedió el califato almohade del norte de África y España. Partes de Siria y Palestina habían sido temporalmente reconquistadas por los cristianos, primero por los bizantinos y luego por los cruzados francos.
La ciencia árabe ya había comenzado a declinar antes del final del califato abásida, quizá a comienzos del año 1100 de nuestra era. Después de eso, no hubo más científicos de la estatura de Al-Battani, Al-Biruni, Ibn Sina y Al-Haitam. Se trata de un punto controvertido, y el encono de la polémica se ve agudizado por la política actual. Algunos estudiosos rechazan que ese declive existiera [141].
Sin duda es cierto que la ciencia prosiguió incluso después del final de la era abásida, bajo los mongoles en Persia y luego en la India, y después bajo los turcos otomanos. Por ejemplo, la construcción del observatorio de Maraghe, en Persia, se llevó a cabo por orden de Hulegu en 1259, justo un año después del saqueo de Bagdad, en gratitud por lo mucho que, según él, los astrónomos lo habían ayudado en sus conquistas. Su director y fundador, el astrónomo Al-Tusi, escribió acerca de la geometría esférica (la geometría a que obedecen los grandes círculos sobre una superficie esférica, como la esfera imaginaria de las estrellas fijas), compiló tablas astronómicas y sugirió modificaciones a los epiciclos ptolemaicos. Al-Tusi fundó una dinastía científica: su alumno Al-Shirazi fue astrónomo y matemático, y el alumno de este, Al-Farisi, llevó a cabo un trabajo pionero en el campo de la óptica, explicando el arcoíris y sus colores como resultado de la refracción de la luz del Sol en las gotas de lluvia.
Más impresionante me parece Ibn Al-Shatir, un astrónomo del siglo XIV de Damasco, que, prosiguiendo el trabajo de los astrónomos de Maraghe, desarrolló una teoría de los movimientos planetarios en la que el ecuante de Ptolomeo quedaba reemplazado por un par de epiciclos, satisfaciendo así la exigencia de Platón de que el movimiento de los planetas debería estar compuesto de movimientos a velocidad constante en torno a círculos. Ibn Al-Shatir también presentó una teoría del movimiento de la Luna basada en los epiciclos: evitaba la excesiva variación en la distancia de la Luna a la Tierra que había afectado a la teoría lunar de Ptolomeo. Los primeros trabajos de Copérnico, de los que nos habla en su Commentariolus, presentan una teoría lunar que es idéntica a la de Ibn Al-Shatir, y una teoría planetaria que nos da los mismos movimientos aparentes que la de este [142]. Ahora se cree que Copérnico averiguó estos resultados (si no su fuente) cuando de joven estudió en Italia.
Algunos autores han dado gran importancia al hecho de que una construcción geométrica, la «pareja de Tusi», que había sido inventada por Al-Tusi en su trabajo sobre el movimiento planetario, fuera utilizada posteriormente por Copérnico. (Se trata de un método para convertir matemáticamente el movimiento giratorio de dos esferas que se tocan en una oscilación en línea recta). Todavía es objeto de debate si Copérnico supo de la existencia de la pareja de Tusi por fuentes árabes o si la inventó él mismo[143]. No es que se mostrara reacio a atribuirla a los árabes, y citó a cinco, entre ellos Al-Battani, Al-Bitruji e Ibn Rushd, pero no mencionó a Al-Tusi.
Resulta revelador que, fuera cual fuera la influencia de Al-Tusi e Ibn Al-Shatir en Copérnico, su obra no haya sido seguida por los astrónomos islámicos. En cualquier caso, la pareja de Tusi y los epiciclos planetarios de Ibn Al-Shatir fueron medios para abordar las complicaciones (aunque ni Al-Tusi, ni Ibn Al-Shatir ni Copérnico lo supieran) debidas en realidad a las órbitas elípticas de los planetas y al emplazamiento descentrado del Sol. Se trata de complicaciones que (tal como se ha comentado en los capítulos 8 y 11) afectaron de igual modo a las teorías ptolemaica y copernicana, y nada tuvieron que ver con si el Sol gira alrededor de la Tierra o la Tierra alrededor del Sol. Ningún astrónomo árabe anterior a la época moderna propuso seriamente ninguna teoría heliocéntrica.
Se siguieron construyendo observatorios en los países islámicos. Es posible que el de mayor tamaño fuera el de Samarcanda, construido en la década de 1420 por el monarca Ulugh Beg de la dinastía timúrida, fundada por Timur Lenk (Tamerlán). Allí se calcularon valores más exactos para el año sideral (365 días, 5 horas, 49 minutos y 15 segundos) y la precesión de los equinoccios (70 en lugar de 75 años por grado de precesión, en comparación con el valor moderno de 71,46 años por grado).
Justo antes del final del periodo abásida tuvo lugar un importante avance de la medicina: el descubrimiento por parte del médico árabe Ibn Al-Nafis de la circulación pulmonar, la circulación de la sangre desde el lado derecho del corazón a través de los pulmones, donde se mezcla con el aire, para luego regresar al lado izquierdo del corazón. Ibn Al-Nafis trabajó en hospitales de Damasco y El Cairo, y también escribió sobre oftalmología.
Pero a pesar de estos ejemplos, es difícil evitar la impresión de que, en el mundo islámico, la ciencia comenzó a perder impulso hacia el final de la era abásida, y luego siguió decayendo. Cuando llegó la revolución científica, esta tuvo lugar en Europa, no en las tierras del islam, y tampoco participaron científicos islámicos. Incluso cuando ya se podía disponer de telescopios, en el siglo XVII, los observatorios astronómicos de los países islámicos siguieron limitándose a la astronomía a simple vista[144] (aunque ayudada por complejos instrumentos), y casi siempre con fines religiosos y para elaborar calendarios más que con un propósito científico.
La imagen de este declive inevitablemente suscita la misma pregunta planteada por el declive de la ciencia hacia el final del Imperio romano: ¿tuvieron que ver estos declives con el avance de la religión? En el caso del islam, y también del cristianismo, el conflicto entre la ciencia y la religión es un asunto complicado, y no intentaré dar una respuesta definitiva. Aquí se plantean al menos dos preguntas. En primer lugar: ¿cuál es la actitud general de los científicos islámicos hacia la religión? Es decir, ¿los únicos científicos creativos fueron aquellos que dejaron de lado la influencia de la religión? Y en segundo lugar: ¿cuál era la actitud hacia la ciencia de la sociedad musulmana?
El escepticismo religioso estaba extendido entre los científicos de la era abásida. El ejemplo más claro nos lo proporciona el astrónomo Omar Jayam, que generalmente se considera ateo. Nos revela su escepticismo en varias estrofas de las Rubaiyat[145]:
Hay quien suspira por el esplendor del mundo,otros por el paraíso del profeta;coge las monedas, olvídate del crédito,¡y no atiendas el rumor del lejano tambor!¿Por qué todos los santos y sabiosque tanto discutieron de los dos mundos,se nos presentan ahora como necios profetas? Sus palabrasreciben ahora desdén, y sus bocas las calla el polvo.De joven yo mismo frecuenté con avideza santos y doctores, y grandes argumentos escuchésobre esto y lo otro: pero una y otra vezsalí por la misma puerta que la que entré. (La traducción literal es por supuesto menos poética, pero expresa esencialmente la misma actitud). No es de extrañar que después de su muerte a Jayam se le calificara de «serpiente venenosa para la sharía». Hoy en día, en Irán, la censura gubernamental exige que las versiones publicadas de la poesía de Jayam se editen para eliminar o revisar sus sentimientos ateos.
El aristotélico Ibn Rush fue desterrado alrededor de 1195 por sospechoso de herejía. Otro médico, Al-Razi, fue abiertamente escéptico. En su libro Los trucos de los profetas arguyó que los milagros son simples trucos, que la gente no necesita líderes religiosos y que Euclides e Hipócrates son más útiles para la humanidad que los que enseñan religión. Su contemporáneo, el astrónomo Al-Biruni, simpatizó lo bastante con estas opiniones como para escribir una biografía llena de admiración hacia Al-Razi.
Por otro lado, el médico Ibn Sina mantuvo una desagradable correspondencia con Al-Biruni, y le dijo que Al-Razi debería haberse limitado a las cosas que comprendía, como los forúnculos y los excrementos. El astrónomo Al-Tusi fue un chiíta devoto, y escribió de teología. El nombre del astrónomo Al-Sufi sugiere que fue un místico sufí.
Es difícil hacer una valoración de estos ejemplos individuales. Muy pocos científicos árabes han dejado constancia de sus inclinaciones religiosas. Mi propia intuición es que el silencio indica más escepticismo, y quizá miedo, que devoción.
Luego está la cuestión de la actitud de los musulmanes en general hacia la ciencia. El califa Mamun, que fundó la Casa de la Sabiduría, sin duda fue un gran sostén de la ciencia, y quizá resulte significativa su pertenencia a una secta musulmana, los mutazilíes, que buscaban una interpretación más racional del Corán, y que posteriormente fueron atacados por ello. Pero no hay que considerar a los mutazilíes unos escépticos religiosos. No dudaban que el Corán era la palabra de Dios; tan solo defendían que había sido creado por Dios, y que no había existido siempre. Tampoco hay que confundirlos con los modernos libertarios civiles; perseguían a los musulmanes que creían que no había necesidad de que Dios creara el Corán eterno.
Allá por el siglo XI había signos en el islam de abierta hostilidad a la ciencia. El astrónomo Al-Biruni se quejaba de las actitudes anticientíficas que exhibían los extremistas islámicos[146]:
Los extremistas que hay entre ellos tachan las ciencias de ateas y proclaman que hacen descarriar a la gente, con la única intención de convertirlos en ignorantes que, como ellos, odien las ciencias. Pues esto los ayudará a ocultar su ignorancia y a abrir la puerta a la completa destrucción de la ciencia y los científicos.Existe una conocida anécdota, según la cual Al-Biruni fue criticado por un legalista religioso porque el astrónomo utilizó un instrumento que enumeraba los meses según sus nombres en griego, el idioma de los cristianos bizantinos. Al-Biruni replicó: «Los bizantinos también comen».
La figura clave en el crecimiento de la tensión entre ciencia e islam se dice a menudo que fue Al-Ghazali (Algazael). Nacido en 1058 en Persia, se trasladó a Siria y luego a Bagdad. También dio bastantes bandazos intelectuales, pasando del islam ortodoxo al escepticismo y de vuelta a la ortodoxia, pero combinada con el misticismo sufí. Tras empaparse de las obras de Aristóteles y resumirlas en Las intenciones de los filósofos, posteriormente atacó al racionalismo en su obra más conocida: La incoherencia de los filósofos[147] (Ibn Rushd, partidario de Aristóteles, escribió una réplica: La incoherencia de la incoherencia). He aquí como Al-Ghazali expresa su opinión de la filosofía griega:
Los herejes de nuestra época han escuchado los nombres, que tanto respeto inspiran, de Sócrates, Hipócrates, Platón, Aristóteles, etcétera. Se han dejado engañar por las exageraciones pronunciadas por los seguidores de estos filósofos, exageraciones que pretenden hacernos creer que los antiguos maestros poseían una extraordinaria capacidad intelectual; que la matemática, la lógica, la física y la metafísica desarrolladas por ellos eran las más profundas; que su magnífica inteligencia justifica sus osados intentos de descubrir las Cosas Ocultas mediante métodos deductivos; y que con toda la sutileza de su inteligencia y la originalidad de sus logros repudiaron la autoridad de las leyes religiosas: negaron la validez del contenido positivo de las religiones históricas, y creen que todo eso no son más que mentiras y trivialidades mojigatas.El ataque de Al-Ghazali contra la ciencia tomó la forma del «ocasionalismo», la doctrina que afirma que todo lo que ocurre es una ocasión singular, no gobernada por las leyes de la naturaleza sino directamente por la voluntad de Dios. (Esta doctrina no era nueva en el islam: la había propuesto un siglo antes Al-Ash'ari, adversario de los mutazilíes). En el Problema XVII de Al-Ghazali, «Refutación de su creencia en la imposibilidad de desviarse del curso natural de los hechos», leemos:
En nuestra opinión, la relación entre lo que se cree que es la causa y el efecto no [es] necesaria […] [Dios] posee el poder de crear la satisfacción del hambre sin comer, o la muerte sin cortar la cabeza, o incluso la supervivencia cuando la cabeza ya ha sido cortada, o cualquier otra cosa entre lo que está relacionado (independientemente de lo que se supone que es su causa). Los filósofos rechazan esta posibilidad; de hecho, afirman que es imposible. Puesto que la investigación de estas cosas (que son innumerables) puede llevar un tiempo indefinido, consideremos solo un ejemplo; a saber, el hecho de que un trozo de algodón se queme cuando entra en contacto con el fuego. Admitimos la posibilidad de un contacto entre ambos que no resulte en que la tela se queme, y también admitimos la posibilidad de una transformación del algodón en cenizas sin que entre en contacto con el fuego. Y ellos rechazan esta posibilidad […] Nosotros afirmamos que es Dios —por mediación de los ángeles, o directamente— el agente que provocará la negrura del algodón; o la desintegración de sus partes y su transformación en un montón de cenizas humeantes. El fuego, que es algo inanimado, carece de acción.
Otras religiones, como el judaísmo y el cristianismo, también admiten la posibilidad de milagros, desviaciones del orden natural, pero hemos visto que aquí Al-Ghazali negaba la importancia de cualquier orden natural.
Es algo difícil de comprender, porque sin duda observamos ciertas regularidades en la naturaleza. Dudo que Al-Ghazali ignorara que no es seguro poner la mano en el fuego. Podría haber dejado un lugar para la ciencia en el mundo del islam, como un estudio de lo que Dios generalmente desea que ocurra, una postura adoptada en el siglo XVII por Nicolas Malebranche. Pero Al-Ghazali no siguió ese camino. Su motivo lo expresa en otra obra, El principio de las ciencias[148], en la que compara la ciencia al vino. El vino refuerza el cuerpo, pero sin embargo está prohibido a los musulmanes. Del mismo modo, la astronomía y las matemáticas refuerzan la mente, pero «sin embargo tememos que, por culpa de ellas, uno pueda haberse atraído hacia doctrinas que son peligrosas».
No son solo los textos de Al-Ghazali los que dan fe de una creciente hostilidad islámica hacia la ciencia en la Edad Media. En 1194, en la Córdoba almohade, en el otro extremo del mundo islámico, los ulemas (eruditos religiosos locales) quemaban todos los libros médicos y científicos. Y en 1449 los fanáticos religiosos destruyeron el observatorio de Ulugh Beg en Samarcanda.
En el islam actual vemos signos de las mismas preocupaciones que inquietaban a Al-Ghazali. Mi amigo el difunto Abdus Salam, un físico paquistaní que ganó el primer Premio Nobel concedido a un musulmán (por su labor llevada a cabo en Inglaterra e Italia), me dijo en una ocasión que había intentado convencer a los gobernantes de los Estados del golfo Pérsico, ricos en petróleo, para que invirtieran en investigación científica. Y aunque se mostraban entusiastas a la hora de apoyar la tecnología, temían que la ciencia pura pudiera ser culturalmente corrosiva. (El propio Salam era un musulmán devoto. Era leal a una secta musulmana, el movimiento ahmadía, que ha sido considerado herético en Pakistán, y durante años no pudo regresar a su país natal).
Resulta irónico que en el siglo XX, Sayyid Qutb, el guía espiritual del actual islamismo radical, reclamara la sustitución del cristianismo, el judaísmo y el islamismo de su época por un islamismo universal purificado, en parte porque albergaba la esperanza de crear así una ciencia islámica que cerrara la brecha entre ciencia y religión. Pero los científicos árabes de su edad de oro no practicaban la ciencia islámica. Practicaban la ciencia a secas.
A medida que el Imperio romano entraba en decadencia en Occidente, la Europa que quedaba fuera del ámbito bizantino se convirtió en pobre, rural y en gran parte analfabeta. Y allí donde sobrevivía el alfabetismo, se concentraba en la Iglesia y era solo en latín. A principios de la Edad Media, en la Europa occidental prácticamente nadie sabía leer griego.
Algunos fragmentos del saber griego habían sobrevivido en las bibliotecas de los monasterios en forma de traducciones al latín, incluidas partes del Timeo de Platón y traducciones llevadas a cabo, allá por el año 500 de nuestra era, por el aristócrata romano Boecio de la obra de Aristóteles que trataba de lógica y de un libro de texto de aritmética. También había obras escritas en latín por los romanos en las que explicaban la ciencia griega. La más notable era una enciclopedia del siglo V extrañamente titulada Las nupcias de Mercurio con Filología, de Marciano Capella, que abordaba (como siervas de la filología) las siete artes liberales: gramática, lógica, retórica, geografía, aritmética, astronomía y música. En su discusión de la astronomía, Marciano describió la antigua teoría de Heráclides, según la cual Mercurio y Venus dan vueltas alrededor del Sol mientras el Sol da vueltas alrededor de la Tierra, una descripción elogiada un milenio más tarde por Copérnico. Pero incluso con estos fragmentos de saber antiguo, los europeos de principios de la Edad Media no sabían casi nada de los grandes logros científicos de los griegos. Sometidos a las repetidas invasiones de los godos, los vándalos, los hunos, los ávaros, los árabes, los magiares y los pueblos nórdicos, la gente de Europa occidental tenía otras preocupaciones.
Europa comenzó a revivir en los siglos X y XI. Las invasiones se fueron reduciendo, y nuevas técnicas mejoraron la productividad de la agricultura [149]. No fue hasta finales del siglo XIII cuando comenzó de nuevo una labor científica importante, aunque no se conseguirían grandes resultados hasta el siglo XVI. En el intervalo, sin embargo, se pusieron los cimientos institucionales e intelectuales para el renacimiento de la ciencia.
En los siglos X y XI —una época religiosa—, gran parte de la nueva riqueza de Europa no fue a parar a los campesinos, sino a la Iglesia. Tal como describió maravillosamente el cronista francés Raoul (o Radulfo) Glaber alrededor de 1030: «Fue como si el mundo, sacudiéndose y desembarazándose de lo antiguo, se vistiera con los ropajes blancos de la Iglesia». Para el futuro del aprendizaje, más importantes fueron las escuelas adjuntas a las catedrales, como las de Orleans, Reims, Colonia, Utrecht, Sens, Toledo, Chartres y París.
Estas escuelas enseñaban al clero no solo la religión, sino un programa de artes liberales laicas legado de la época romana, basado en parte en los textos de Boecio y Marciano: el trivium de gramática, lógica y retórica; y, sobre todo, en Chartres, el quadrivium de aritmética, geometría, astronomía y música. Algunas de estas escuelas se remontaban a la época de Carlomagno, pero en el siglo XI comenzaron a atraer a profesores de categoría intelectual, y en algunas de ellas se apreció un renovado interés por reconciliar el cristianismo con el conocimiento del mundo natural. Tal como observó el historiador Peter Dear[150], «aprender acerca de Dios aprendiendo lo que ha hecho, y comprender los motivos y propósitos de su creación, fue considerado por muchos como una empresa eminentemente devota». Por ejemplo, Thierry de Chartres, que daba clases en París y en Chartres, y que se convirtió en rector de esta última escuela en 1142, explicó el origen del mundo tal como se describe en el Génesis en términos de la teoría de los cuatro elementos que aprendió en el Timeo.
Otro hecho aún más importante que el florecimiento de las escuelas catedralicias, aunque no desvinculado de él, fue la nueva oleada de traducciones de las obras de científicos anteriores. Al principio las traducciones eran no tanto directamente del griego como del árabe: o bien las obras de científicos árabes, o bien obras que habían sido traducidas anteriormente del griego al árabe o del griego al siríaco y luego al árabe.
La empresa de traducción comenzó muy pronto, a mitad del siglo X, a instancias del monasterio de Santa María de Ripoll, en los Pirineos, cerca de la frontera entre la Europa cristiana y la España omeya. Para ilustrar cómo este nuevo saber se pudo propagar por la Europa medieval, y su influencia en las escuelas catedralicias, consideremos la carrera de Gerbert d'Aurillac. Nacido en el 945 en Aquitania de padres desconocidos, aprendió algo de matemáticas y astronomía en Cataluña; pasó algún tiempo en Roma; de allí pasó a Reims, donde dio clases de números árabes y ábaco y reorganizó la escuela catedralicia; se convirtió en abad y posteriormente arzobispo de Reims; asistió a la coronación del fundador de una nueva dinastía de reyes franceses, Hugo Capeto; siguió al emperador alemán Otto III a Italia y Magdeburgo; se convirtió en arzobispo de Rávena; y en el 999 fue elegido papa con el nombre de Silvestre II. Su alumno Fulbert de Chartres estudió en la escuela catedralicia de Reims y se convirtió en obispo de Chartres en 1006, siendo responsable de la reconstrucción de su magnífica catedral.
El ritmo de traducciones se aceleró en el siglo XII. A comienzos del siglo, un inglés, Adelard de Bath, viajó a lo largo y ancho de los países árabes; tradujo obras de Al-Juarismi, y en sus Cuestiones naturales divulgó el saber de los árabes. De algún modo, Thierry de Chartres supo del uso del cero en la matemática árabe y lo introdujo en Europa. Probablemente el traductor más importante del siglo XII fue Gerardo de Cremona, que trabajó en Toledo, la capital de la España cristiana antes de las conquistas árabes, y aunque fue reconquistada por los castellanos en 1085, siguió siendo un centro de cultura árabe y judía. Su traducción del árabe al latín del Almagesto de Ptolomeo divulgó la astronomía griega en la Europa medieval. Gerardo también tradujo los Elementos de Euclides, y obras de Arquímedes, Al-Razi, Al-Farghani, Galeno, Ibn Sina y Al-Juarismi. Después de la caída de la Sicilia árabe a manos de los normandos en 1091, las traducciones pasaron a hacerse directamente del griego al latín sin intermediarios árabes, y las que tuvieron una influencia más inmediata fueron las de Aristóteles. Fue en Toledo donde se tradujo la mayor parte de la obra de Aristóteles procedente de fuentes árabes; allí, por ejemplo, Gerardo tradujo De los cielos, la Física y la Meteorología.
En la Iglesia, no todo el mundo dio la bienvenida a las obras de Aristóteles. El cristianismo medieval había estado mucho más influido por el platonismo y el neoplatonismo, en parte a través del ejemplo de san Agustín. Los escritos de Aristóteles eran naturalistas de un modo que no lo eran los de Platón, y su visión de un cosmos gobernado por leyes, incluso leyes tan mal desarrolladas como las suyas, presentaba la imagen de un Dios con las manos atadas, la misma imagen que tanto había incomodado a Al-Ghazali. El conflicto que presentaba Aristóteles era, al menos en parte, un conflicto entre dos órdenes mendicantes: los franciscanos, o frailes grises, orden fundada en 1209, que se oponía a las enseñanzas de Aristóteles; y los dominicos, o frailes negros, orden fundada en 1216 y que abrazó las enseñanzas de «El Filósofo».
Este conflicto fue palpable en las nuevas instituciones europeas de enseñanza superior, las universidades. La escuela catedralicia de París recibió un fuero real por el que se convertía en universidad en 1200. (Un poco anterior era la Universidad de Bolonia, pero esta estaba especializada en leyes y medicina, y no jugó un papel importante en la física medieval). Casi de inmediato, en 1210, a los eruditos de la Universidad de París se les prohibió enseñar los libros de Aristóteles sobre filosofía natural. En 1213, el papa Gregorio IX solicitó que las obras de Aristóteles se expurgaran para poder enseñar sin peligro las partes útiles.
La prohibición de enseñar a Aristóteles no fue universal. Sus obras se impartían en la Universidad de Toulouse desde su fundación en 1229. En París, la prohibición total de enseñar a Aristóteles se levantó en 1234, y en décadas subsiguientes el estudio de Aristóteles se convirtió en el centro de la educación. Eso fue en gran medida la labor de los clérigos del siglo XIII, Alberto Magno y Tomás de Aquino. Al estilo de la época, se les concedieron pomposos títulos doctorales: Alberto era «doctor universal», y Tomás «doctor angélico».
Alberto Magno estudió en Padua y en Colonia, se hizo fraile dominico y en 1241 fue a París, donde entre 1245 y 1248 ocupó una cátedra de profesor para eruditos extranjeros. Posteriormente se trasladó a Colonia, donde fundó la Universidad. Alberto era un aristotélico moderado más partidario del sistema ptolemaico que de las esferas homocéntricas de Aristóteles, aunque le preocupaba que esto entrara en conflicto con la física de este último. Según él, la Vía Láctea estaba formada por muchas estrellas y (contrariamente a lo que afirmaba Aristóteles) las manchas de la Luna eran imperfecciones intrínsecas. El ejemplo de Alberto fue seguido un poco más tarde por otro dominico alemán, Dietrich de Friburgo, que de manera independiente repitió parte de los estudios de Al-Farisi sobre el arcoíris. En 1941 el Vaticano declaró a Alberto santo patrón de todos los científicos.
Tomás de Aquino pertenecía a la baja nobleza del sur de Italia. Después de educarse en el monasterio de Monte Cassino y en la Universidad de Nápoles, frustró las esperanzas familiares de verlo convertido en abad de un rico monasterio; como Alberto Magno, se hizo fraile dominico. Tomás estuvo en París y en Colonia, donde estudió con Alberto. Posteriormente regresó a París y fue profesor en la universidad en los periodos comprendidos entre 1256-1259 y 1269 y 1272.
La gran obra de Aquino fue la Summa Theologica, una fusión global de filosofía aristotélica y teología cristiana. En ella, siguió un camino intermedio entre los aristotélicos extremistas, conocidos como averroístas por Ibn Rushd, y los extremistas antiaristotélicos, como los miembros de la recién fundada orden de frailes agustinos. Aquino se opuso de manera enérgica a una doctrina que casi todo el mundo (quizá de manera injusta) atribuía a averroístas del siglo XIII como Sigerio de Brabante y Boecio de Dacia. Según esta doctrina, es posible mantener opiniones filosóficamente ciertas, como la doctrina de la materia o la imposibilidad de la resurrección de los muertos, al tiempo que se reconoce que son falsas desde el punto de vista religioso. Para Aquino solo podía haber una verdad. En astronomía, se inclinó hacia la teoría homocéntrica de los planetas de Aristóteles, arguyendo que esa teoría se fundaba sobre la razón, mientras que la teoría ptolemaica simplemente coincidía con la observación, y otras hipótesis también podrían encajar con los datos. Por otro lado, Aquino disentía de Aristóteles acerca de la teoría del movimiento, pues argüía que incluso en el vacío cualquier movimiento llevaría un tiempo finito. Se cree que Aquino alentó la traducción latina de Aristóteles, Arquímedes y otros autores directamente del griego por parte de su contemporáneo, el dominico inglés William de Moerbeke. En 1255, a los estudiantes de París se les examinaba de sus conocimientos de las obras de Aquino.
Pero los problemas que planteaba Aristóteles no habían terminado. A partir de la década de 1250, la oposición a Aristóteles en París fue liderada apasionadamente por el franciscano san Buenaventura. Las obras de Aristóteles fueron prohibidas en Toulouse en 1245 por el papa Inocencio IV. En 1270 el arzobispo de París, Étienne Tempier, prohibió la enseñanza de 13 proposiciones aristotélicas. El papa Juan XXI ordenó a Tempier que analizara la cuestión más detenidamente, y en 1277 Tempier condenó 219 doctrinas de Aristóteles o de Aquino [151]. Robert Kilwardy, arzobispo de Canterbury, extendió esta condena a Inglaterra, y en 1284 la renovó su sucesor, John Pecham.
Las proposiciones condenadas en 1277 se pueden dividir según las razones de su condena. Algunas presentaban un conflicto con las escrituras; por ejemplo, las que afirman la eternidad del mundo:
9. Que no hubo ningún primer hombre ni habrá un último; por el contrario, siempre hubo y habrá una generación de hombres a partir de otros.Algunas de las doctrinas condenadas describían métodos de aprender la verdad que desafiaban la autoridad religiosa; por ejemplo:
87. Que el mundo es eterno para todas las especies que contiene; y que el tiempo es eterno, al igual que el movimiento, la materia, el agente y el recipiente.
38. Que no hay que creer nada a menos que sea evidente o se pueda afirmar a partir de cosas que son evidentes.Finalmente, algunas de las proposiciones condenadas habían suscitado la misma cuestión que había preocupado a Al-Ghazali: que el razonamiento filosófico y científico parecen limitar la libertad de Dios; por ejemplo:
150. Que sobre cualquier cuestión, el hombre no debe quedar satisfecho con la certeza basada en la autoridad.
153. Que nada se conoce mejor porque se sepa teología.
34. Que la primera causa no pudo crear varios mundos.La condena de las proposiciones de Aristóteles y Aquino no duró. Bajo la autoridad del nuevo papa, que había sido educado por los dominicos, Juan XXII, Tomás de Aquino fue canonizado en 1323. El obispo de París abolió la condena en 1325, decretando: «Anulamos por completo la mencionada condena de artículos y declaraciones de excomunión por lo que tocan, o se dice que tocan, a las enseñanzas del bienaventurado Tomás, mencionado anteriormente, y a causa de ello ni aprobamos ni desaprobamos estos artículos, sino que los dejamos para la libre discusión escolástica» [152]. En 1341, a los maestros en letras de la Universidad de París se les exigía que juraran que enseñarían «el sistema de Aristóteles y su comentarista Averroes, y los otros comentaristas y expositores antiguos del susodicho Aristóteles, excepto en aquellos casos contrarios a la fe»[153].
49. Que Dios no pudo dotar a los cielos de un movimiento rectilíneo, y la razón es que quedaría un vacío.
141. Que Dios no puede hacer que exista un accidente sin un sujeto, ni conseguir que existan más [de tres] dimensiones de manera simultánea.
Los historiadores disienten acerca de la importancia de este episodio de condena y rehabilitación para el futuro de la ciencia. Aquí se plantean dos cuestiones: si no se hubiera anulado la condena, ¿qué efecto habría tenido sobre la ciencia? Y si nunca se hubieran condenado las enseñanzas de Aristóteles ni de Aquino, ¿cuál habría sido su efecto sobre la ciencia?
Me parece que por lo que concierne a la condena de la ciencia, de no haberse anulado el efecto habría resultado desastroso, y no por la importancia de las conclusiones de Aristóteles sobre la naturaleza, erróneas casi todas ellas. Contrariamente a lo que pensaba Aristóteles, existió una época en que no había hombres; sin duda existían muchos sistemas planetarios, y puede que hubiera muchos big bangs; las cosas del cielo pueden moverse, y a menudo se mueven, en línea recta; el vacío es posible; y en la moderna teoría de cuerdas hay más de tres dimensiones, y las otras dimensiones no se pueden observar porque están tremendamente compactadas. El peligro de la condena procedía de las razones por las que estas proposiciones se habían condenado, y no por el rechazo de las proposiciones en sí mismas.
Aun cuando Aristóteles se equivocaba en lo referente a las leyes de la naturaleza, era importante creer que existían leyes de la naturaleza. Si se hubiera permitido que se mantuviera la condena de las generalizaciones acerca la naturaleza, como las proposiciones 34, 49 y 141, sobre la base de que Dios podía hacer cualquier cosa, entonces la Europa cristiana podría haber caído en ese mismo ocasionalismo que alentaba en el islam Al-Ghazali.
Además, la condena de los artículos que cuestionaban la autoridad religiosa (como el 38, el 150 y el 153 mencionados anteriormente) fueron parte un episodio relacionado con el conflicto entre las facultades de artes liberales y de teología en las universidades medievales. La teología poseía una categoría claramente superior; con su estudio se obtenía un grado de doctor en teología, mientras que las facultades de artes liberales no podían conceder un grado mayor que el de maestro en letras. (Las profesiones académicas iban encabezadas por los doctores en teología, leyes y medicina en este orden, seguidos por los maestros en letras). Levantar la condena no solo concedió la misma categoría a las artes liberales que a la teología, sino que ayudó a liberar las facultades de artes liberales del control intelectual de sus colegas teológicos.
Más complicado es juzgar cuál habría sido el efecto si la condena no hubiera ocurrido nunca. Como veremos, en el siglo XIV la autoridad de Aristóteles sobre las cuestiones de física y astronomía se ponía cada vez más en entredicho en París y Oxford, aunque a veces había que camuflar las nuevas ideas como si fueran simplemente secundum imagionationem, es decir, algo imaginado más que afirmado. ¿Habría sido posible poner en entredicho a Aristóteles si su autoridad no hubiera quedado debilitada por las condenas del siglo XIII? David Lindberg [154] cita el ejemplo de Nicolás Oresme (del que hablaremos más adelante), que en 1377 afirmó que es permisible imaginar que la Tierra se mueve en línea recta a través de un espacio infinito, pues «decir lo contrario es mantener un artículo condenado en París»[155]. Quizá el curso de los acontecimientos del siglo XIII se puede resumir afirmando que la condena salvó a la ciencia del aristotelismo dogmático, y que el levantamiento de la condena salvó a la ciencia del cristianismo dogmático.
Después de la era de la traducción y el conflicto por la recepción de Aristóteles, la labor científica creativa comenzó por fin en Europa en el siglo XIV. La figura señera fue Jean Buridan, un francés nacido en 1296 cerca de Arras, que pasó gran parte de su vida en París. Buridan era clérigo, pero seglar; es decir, no era miembro de ninguna orden religiosa. En filosofía era nominalista, y creía en la realidad de las cosas individuales, y no en las clases de cosas. Por dos veces Buridan recibió el honor de ser elegido rector de la Universidad de París, en 1328 y 1340.
Buridan era empirista, y rechazaba la necesidad lógica de los principios científicos: «Estos principios no son inmediatamente evidentes; de hecho, es posible que dudemos de ellos durante mucho tiempo. Pero se les llama principios porque son indemostrables, y no se pueden deducir de otras premisas ni demostrarse mediante ningún procedimiento formal, pero se aceptan porque se ha observado que son ciertos en muchos ejemplos y falsos en ninguno» [156].
Comprenderlo resultó esencial para el futuro de la ciencia, y no fue tan fácil. La vieja e imposible meta platónica de una ciencia natural puramente educativa se interponía en el camino de un progreso que solo se podía alcanzar basándose en una observación y un análisis meticulosos. Incluso hoy encontramos cierta confusión respecto a este punto. Por ejemplo, el psicólogo Jean Piaget [157] creía que había detectado signos de que los niños poseían una comprensión innata de la relatividad, que perdían posteriormente, como si la relatividad fuera en cierto modo lógica o filosóficamente necesaria, más que una conclusión en última instancia basada en observaciones de cosas que viajan a la velocidad de la luz o casi.
Aunque empirista, Buridan no era experimentalista. Al igual que en el caso de Aristóteles, su razonamiento se basaba en la observación cotidiana, pero era más cauto que Aristóteles a la hora de llegar a conclusiones generales. Por ejemplo, Buridan se enfrentó a un viejo problema de Aristóteles: por qué un proyectil lanzado horizontalmente o hacia arriba no comienza de inmediato lo que se supone que es su movimiento natural, a saber, bajar en línea recta cuando abandona la mano. Por diversos motivos, Buridan rechazó la explicación de Aristóteles de que el proyectil es transportado por el aire durante un cierto tiempo. En primer lugar, el aire resiste más que asiste al movimiento, pues, para poder avanzar, un cuerpo sólido debe separarlo. Además, ¿por qué se mueve el aire, cuando la mano que arroja el proyectil deja de moverse? Y por otra parte, una lanza, cuando es puntiaguda en la parte de atrás, se desplaza a través del aire igual o mejor que una chata en la parte posterior, que es desde donde el aire la puede empujar.
Más que suponer que el aire ayuda a que se muevan los proyectiles, Buridan supuso que se trata de un efecto de algo llamado «ímpetu» que la mano le aporta al proyectil. Como hemos visto, una idea un tanto parecida la propuso Juan Filópono, y el ímpetu de Buridan prefiguró a su vez lo que Newton llamaría «cantidad de movimiento», o en términos modernos, momento, aunque no sea exactamente lo mismo. Buridan compartía con Aristóteles la suposición de que algo ha de mantener las cosas en movimiento, y este fue el papel que le concedió al impulso, que, por lo tanto, no era tan solo una propiedad del movimiento, como el momento. Jamás identificó el ímpetu que transporta un cuerpo como su masa por su velocidad, que es como se define el momento en la física newtoniana. Sin embargo, había dado con algo. La cantidad de fuerza que se requiere para parar un cuerpo en movimiento en un tiempo dado es proporcional a su momento, y en este sentido el momento juega el mismo papel que el ímpetu de Buridan.
Buridan amplió la idea del ímpetu al movimiento circular, suponiendo que los planetas se mantienen en movimiento gracias a su ímpetu, que les ha proporcionado Dios. De este modo, Buridan buscaba ese tipo de compromiso entre la ciencia y la religión que se haría popular siglos más tarde: Dios pone en marcha la maquinaria del cosmos, después de la cual este es gobernado por las leyes de la naturaleza. Pero aunque la conservación del momento mantiene a los planetas en movimiento, en sí mismo no puede mantenerlos en movimiento en órbitas curvas, tal como Buridan creía que provocaba el ímpetu; eso requería una fuerza adicional, que con el tiempo sería reconocida como la fuerza de la gravitación.
Buridan también contempló una idea debida originariamente a Heráclides: que la Tierra gira una vez al día de oeste a este. Reconoció que con eso veríamos lo mismo que si los cielos giraran alrededor de una Tierra estacionaria una vez al día de este a oeste. También reconoció que esta era una teoría más natural, puesto que la Tierra es mucho más pequeña que el firmamento del Sol, la Luna, los planetas y las estrellas. Pero rechazó la rotación de la Tierra, razonando que si la Tierra gira, entonces una flecha disparada en línea recta hacia arriba caería al oeste del arquero, pues la Tierra se habría movido debajo de la flecha mientras esta volaba. Resulta irónico pensar que Buridan se podría haber ahorrado este error de haber comprendido que la rotación de la Tierra le daría a la flecha un ímpetu que la impulsaría hacia el este junto con la Tierra en su giro. Por el contrario, lo condujo a error la noción del ímpetu, el considerar tan solo el ímpetu vertical que el arco le da a la flecha, sin tener en cuenta el horizontal que adquiere de la rotación de la Tierra.
La idea del ímpetu de Buridan mantuvo su influencia durante siglos. Se enseñaba en la Universidad de Padua cuando Copérnico estudió medicina allí a principios del siglo XVI. En ese mismo siglo, Galileo la aprendió como estudiante en la Universidad de Pisa.
Buridan tomó partido por Aristóteles en otra cuestión: la imposibilidad del vacío. Pero, como era habitual, basa su conclusión en observaciones: cuando el aire se sorbe de una pajita de beber, el líquido que entra en ella impide que se cree el vacío; y cuando se separan las asas de un fuelle, el aire que entra impide el vacío, por lo que era natural concluir que la naturaleza aborrece el vacío. Como veremos en el capítulo 12, la explicación correcta de estos fenómenos en términos de presión del aire no fue comprendida hasta el siglo XVII.
La obra de Buridan fue ampliada por dos de sus alumnos: Alberto de Sajonia y Nicolás Oresme. Los escritos de Alberto sobre filosofía obtuvieron una gran resonancia, pero fue Oresme quien llevó a cabo la mayor contribución a la ciencia.
Oresme nació en 1325 en Normandía, y llegó a París para estudiar con Buridan en la década de 1340. Se oponía con contundencia a estudiar el futuro por medio de «la astrología, la geomancia, la necromancia o artes parecidas, como si se las pudiera llamar artes». En 1377 Oresme fue nombrado obispo de la ciudad de Lisieux, en Normandía, donde murió en 1382.
El libro de Oresme De los cielos y la Tierra[158] (escrito en lengua vernácula para comodidad del rey de Francia) posee la forma de un extenso comentario sobre Aristóteles, en el que una y otra vez discrepa del Filósofo. En ese libro Oresme reconsideró la idea de que los cielos no giran alrededor de la Tierra de este a oeste, sino que es más bien la Tierra la que gira sobre su eje de oeste a este. Tanto Buridan como Oresme reconocieron que observamos solamente el movimiento relativo, con lo que ver moverse los cielos deja abierta la posibilidad de que en realidad sea la Tierra la que se mueva. Oresme expuso varias objeciones a esta idea y las rebatió. En el Almagesto, Ptolomeo había argumentado que si la Tierra giraba, entonces las nubes y los objetos arrojados quedarían atrás; y como hemos visto, Buridan había argumentado en contra de la rotación de la Tierra afirmando que si esta girara de oeste a este, entonces una flecha lanzada en línea recta hacia arriba caería hacia la izquierda debido a la rotación de la Tierra, contrariamente a la observación, que nos dicta que la flecha cae en línea recta en el mismo lugar de la superficie de la Tierra desde el que se ha lanzado. Oresme replicó que la rotación de la Tierra se lleva con ella la flecha, junto con el arquero y el aire y todo lo demás que hay en la superficie, aplicando así la teoría del ímpetu de Buridan de una manera que su autor no había comprendido.
Oresme respondió a otra objeción sobre la rotación de la Tierra, una objeción de tipo muy distinto: en las Sagradas Escrituras (por ejemplo en el Libro de Josué) hay pasajes que nos dicen que el Sol gira a diario alrededor de la Tierra. Oresme replicó que eso era simplemente una concesión a las costumbres del habla popular, como cuando se escribe que Dios se enfadó o se arrepintió, cosas que no hay que tomar de manera literal. En esta argumentación, Oresme seguía a Tomás de Aquino, que había lidiado con el pasaje del Génesis en el que supuestamente Dios proclama: «Haya un firmamento por en medio de las aguas, que las aparte unas de otras». Aquino había explicado que Moisés estaba adaptando su manera de hablar a la capacidad de su público y que no había que tomarlo de manera literal. El literalismo bíblico podría haber sido un lastre en el progreso de la ciencia de no haber abundado dentro de la Iglesia personajes como Aquino y Oresme, que adoptaron una perspectiva más ilustrada.
A pesar de todos sus argumentos, Oresme finalmente se rindió a la idea más extendida de una tierra estacionaria, afirmando:
Posteriormente se vio que no se puede mostrar de manera concluyente mediante ningún argumento que los cielos se mueven […] No obstante, todo el mundo mantiene, y yo mismo lo creo, que son los cielos los que se mueven, y no la Tierra: pues Dios ha decretado que el mundo no se moverá, a pesar de las razones contrarias porque está claro que no hay pruebas concluyentes. Sin embargo, después de considerar todo lo que se ha dicho, se podría creer que lo que se mueve es la Tierra, y no los cielos, pues lo opuesto tampoco es evidente. Empero, a primera vista parece que esto se opone más a la razón natural que todos o muchos de los artículos de nuestra fe. Lo que he dicho por pura diversión o ejercicio intelectual puede servir, de esta manera, como un medio útil para refutar y contener a aquellos que intentan impugnar nuestra fe a base de argumentos [159].No sabemos si Oresme realmente se mostraba reacio a dar el paso final a la hora de reconocer que la Tierra gira o si simplemente quería aparentar fidelidad a la ortodoxia religiosa.
Oresme también se anticipó a un aspecto de la teoría newtoniana de la gravitación. Afirmó que los objetos pesados no tienen necesariamente que caer hacia el centro de nuestra Tierra si están cerca de otro mundo. La idea de que pudiera haber otros mundos, más o menos como la Tierra, resultaba teológicamente muy atrevida. ¿Dios había creado a seres humanos en esos otros mundos? ¿Cristo había ido a esos otros mundos para redimir a esos humanos? Las cuestiones eran infinitas y subversivas.
Contrariamente a Buridan, Oresme era matemático. Su mayor aportación matemática condujo a una mejora en el trabajo que se había llevado a cabo anteriormente en Oxford, de manera que ahora debemos desplazar nuestro foco de Francia a Inglaterra, y retroceder un poco en el tiempo, aunque pronto volveremos con Oresme.
Allá por el siglo XII, Oxford se había convertido en una próspera población con plaza de abastos en la cuenca alta del Támesis, y comenzó a atraer a estudiantes y profesores. La aglomeración informal de escuelas de Oxford se reorganizó como universidad a principios del siglo XIII. Tradicionalmente, la línea de rectores de Oxford comienza en 1224 con Robert Grosseteste, posteriormente obispo de Lincoln, que dio origen al interés del Oxford medieval por la filosofía natural. Grosseteste leyó a Aristóteles en griego y escribió sobre óptica y el calendario, y también sobre Aristóteles. Los estudiosos que le sucedieron en Oxford le citaban a menudo.
En Robert Grosseteste and the Origins of Experimental Science[160] , A. C. Crombie fue más allá, y le asignó a Grosseteste un papel fundamental en el desarrollo de los métodos experimentales que condujeron al advenimiento de la física moderna, aunque esto me parece exagerar la importancia de Grosseteste. Como queda claro en el libro de Crombie, para Grosseteste un «experimento» consistía en la observación pasiva de la naturaleza, un método no muy distinto del de Aristóteles. Ni Grosseteste ni ninguno de sus sucesores medievales pretendían aprender principios generales a base de experimentar en el sentido moderno, es decir, manipulando de manera agresiva los fenómenos naturales. Las teorizaciones de Grosseteste también han recibido elogios[161], pero en su obra no hay nada que sea comparable con el desarrollo de las teorías cuantitativamente acertadas de Herón, Ptolomeo y Al-Haitam, o las del movimiento planetario de Hiparco, Ptolomeo y Al-Biruni, entre otros.
Grosseteste ejerció una gran influencia sobre Roger Bacon, quien en su energía intelectual e inocencia científica fue un auténtico representante del espíritu de su tiempo. Tras estudiar en Oxford, Bacon enseñó a Aristóteles en París en la década de 1240, iba y venía entre París y Oxford, y se hizo fraile franciscano alrededor de 1257. Al igual que Platón, fue un entusiasta de las matemáticas, pero no las utilizó mucho. Escribió de manera abundante sobre óptica y geografía, pero no añadió nada importante a la obra anterior de los griegos y los árabes. Hasta un punto que resultaba extraordinario en su época, Bacon se mostraba también optimista con la tecnología:
También se podrán hacer coches sin animales que se moverán con increíble rapidez […] También se podrán construir máquinas voladoras en las que un hombre se sentará en medio de la máquina haciendo girar algún motor, mediante el cual unas alas artificiales batirán como un pájaro volador [162].No es de extrañar que a Bacon se le conociera como el «Doctor Mirabilis».
En 1264, la primera facultad residencial en Oxford fue fundada por Walter de Merton, en aquella época canciller de Inglaterra y posteriormente obispo de Rochester. Fue en el Merton College donde comenzaron los estudios serios de matemáticas en Oxford, allá por el siglo XIV. Las figuras clave fueron cuatro fellows de la facultad: Thomas Bradwardine (c. 1295-1349), William Heytesbury (fl. 1335), Richard Swineshead (fl. 1340-1355) y John de Dumbleton (fl. 1338-1348). Su logro notable, conocido como el teorema de la velocidad media de Merton College, por primera vez ofrece una descripción matemática del movimiento no uniforme; es decir, el movimiento a una velocidad que no permanece constante.
El primero en dejar constancia por escrito de este teorema fue William Heytesbury (rector de la Universidad de Oxford en 1371), en su Regulae solvendi sophismata. Definió la velocidad en cualquier instante de un movimiento no uniforme como la razón entre la distancia recorrida y el tiempo que habría transcurrido si el movimiento hubiese sido uniforme a esa velocidad. De hecho, esta definición es circular, y de ahí que no sirva. Una definición más moderna, posiblemente lo que Heytesbury pretendía decir, es que, en un movimiento no uniforme, la velocidad en cualquier instante es la razón entre la distancia recorrida y el tiempo transcurrido si la velocidad fue la misma en cada breve intervalo de tiempo en torno a ese instante, tan breve que durante ese intervalo el efecto de la aceleración es despreciable. Heytesbury definió entonces la aceleración uniforme como un movimiento no uniforme en el que la velocidad aumenta en la misma cantidad en cada intervalo de tiempo idéntico. A continuación expuso el teorema [163]:
Cuando cualquier cuerpo móvil sufre una aceleración uniforme desde el reposo a cualquier grado [de velocidad], en ese tiempo recorrerá la mitad de la distancia que recorrería si en ese mismo tiempo se hubiera movido de manera uniforme al grado de velocidad que termina ese incremento de velocidad. Pues este movimiento, en su conjunto, corresponderá al grado medio de ese incremento de velocidad, que es precisamente la mitad de ese grado de velocidad que es su velocidad terminal.Es decir, la distancia recorrida durante un intervalo de tiempo, cuando un cuerpo se acelera de manera uniforme, es la distancia que había recorrido en el movimiento uniforme si su velocidad en ese intervalo fuera igual a la media de la velocidad real. Si algo se hace de manera uniforme desde el reposo a una velocidad final, entonces su velocidad media durante ese intervalo es la mitad de su velocidad final, de manera que la distancia recorrida es la mitad de la velocidad final por el tiempo transcurrido.
Diversos autores probaron este teorema: Heytesbury, John de Dumbleton y posteriormente Nicolás Oresme. La prueba de este último es la más interesante, porque introdujo una técnica para representar las relaciones algebraicas mediante gráficos. Así, fue capaz de reducir el problema de calcular la distancia recorrida cuando un cuerpo acelera de manera uniforme del reposo a una velocidad final al problema de calcular el área de un triángulo rectángulo, en el que los lados que convergen en ángulo recto poseen una longitud igual respectivamente al tiempo transcurrido y a la velocidad final (véase Nota técnica 17). De este modo, el teorema de la velocidad media se deduce de un hecho elemental de la geometría: que el área de un triángulo rectángulo es la mitad del producto de los catetos.
Ni los profesores de Merton College ni tampoco Nicolás Oresme parecen haber aplicado el teorema de la velocidad media al caso más importante en el que es relevante: el movimiento de los cuerpos que caen libremente. Para los profesores de Oxford y para Oresme, el teorema era un ejercicio intelectual con el que pretendían demostrar que eran capaces de abordar el movimiento no uniforme de manera matemática. Si el teorema de la velocidad media da fe de una creciente habilidad en el uso de las matemáticas, también demuestra lo difícil que era todavía el encaje entre las matemáticas y la ciencia natural.
Hay que reconocer que, aunque resulte evidente (como había demostrado Estratón) que los cuerpos que caen aceleran, no es evidente que la velocidad de un cuerpo que cae aumente en proporción al tiempo, la característica de la aceleración uniforme, más que en proporción a la distancia recorrida. Si el ritmo del cambio de la distancia recorrida (es decir, la velocidad) fuera proporcional a dicha distancia, entonces esta, una vez que el cuerpo comienza a caer, aumentaría exponencialmente con el tiempo, al igual que una cuenta bancaria que recibe un interés proporcional a la cantidad que hay en la cuenta aumenta exponencialmente con el tiempo (aunque si el interés es bajo, se tarda mucho tiempo en verlo). La primera persona en conjeturar que el aumento de la velocidad de un cuerpo que cae es proporcional al tiempo transcurrido parece haber sido el fraile dominico del siglo XVI Domingo de Soto[164], unos dos siglos después de Oresme.
Desde mediados del siglo XIV a mediados del XV, Europa fue asolada por una catástrofe. La Guerra de los Cien Años entre Inglaterra y Francia desangró Inglaterra y devastó Francia. La Iglesia sufrió un cisma, con un papa en Roma y otro en Aviñón. La peste negra diezmó una gran parte de la población en todas partes.
Quizá como resultado de la Guerra de los Cien Años, en ese periodo el centro del trabajo científico se desplazó hacia el este, desde Francia e Inglaterra a Alemania e Italia. La carrera de Nicolás de Cusa abarcó ambas regiones. Nacido en 1401 en la población de Cusa, en las cercanías del río Mosela, murió en 1464 en la provincia de Umbría, Italia. Nicolás se educó en Heidelberg y Padua, y se convirtió en abogado canónigo, diplomático, y a partir de 1448 en cardenal. Sus escritos muestran la constante dificultad medieval de separar la ciencia natural de la teología y la filosofía. Nicolás escribió en términos vagos acerca de una Tierra que se mueve y de un mundo sin límites, pero sin utilizar las matemáticas. Aunque posteriormente fue citado por Kepler y Descartes, es difícil entender que pudieran aprender nada de él.
En la Baja Edad Media encontramos de nuevo la separación que habíamos visto en el mundo árabe entre los astrónomos matemáticos profesionales (que utilizaban el sistema ptolemaico) y los filósofos físicos, seguidores de Aristóteles. Entre los astrónomos del siglo XV, sobre todo en Alemania, encontramos a Georg von Peurbach y a su discípulo Johann Müller de Königsberg (Regiomontanus), que juntos prosiguieron y ampliaron la teoría ptolemaica de los epiciclos[165]. Copérnico posteriormente hizo un uso abundante del Epítome del Almagesto de Regiomontanus. Entre los médicos encontramos a Alessandro Achillini (1463-1512) de Bolonia y a Girolamo Fracastoro de Verona (1478-1553), ambos educados en Padua, en aquella época un baluarte del aristotelismo.
Fracastoro nos ofrece una versión sesgada (aunque interesante) del conflicto[166]:
Eres perfectamente consciente de que aquellos que eligen la profesión de la astronomía siempre han encontrado una extrema dificultad en explicar el aspecto que presentan los planetas. Pues hay dos maneras de explicarlo: uno por medio de las esferas llamadas homocéntricas, el otro por medio de las así llamadas esferas excéntricas [epiciclos]. Cada uno de estos métodos tiene sus peligros, cada uno sus escollos. Aquellos que utilizan las esferas homocéntricas nunca consiguen llegar a una explicación de los fenómenos. Y los que usan las esferas excéntricas es cierto que parecen explicar los fenómenos de manera más adecuada, pero su concepción de esos cuerpos divinos es errónea, casi se podría decir que impía, pues les atribuyen posiciones y formas que no concuerdan con los cielos. Sabemos que, entre los antiguos, Eudoxo y Calipo muchas veces se vieron inducidos a error por estas dificultades. Hiparco se contó entre los primeros que prefirió admitir las esferas excéntricas a ser incapaz de explicar los fenómenos. Ptolomeo le siguió, y pronto prácticamente todos los astrónomos le dieron la razón a Ptolomeo. Pero contra estos astrónomos, o al menos contra la hipótesis de los excéntricos, toda la filosofía ha levantado una protesta continuada. ¿Qué estoy diciendo? ¿La filosofía? La naturaleza y las esferas celestes protestan cada vez más. Hasta ahora, no se ha encontrado a ningún filósofo que reconozca que estas escenas monstruosas existen entre los cuerpos divinos y perfectos.Para ser justo, las observaciones no estaban todas del lado de Ptolomeo y en contra de Aristóteles. Uno de los fallos del sistema aristotélico de las esferas homocéntricas, tal como, según hemos visto, había observado Sosígenes allá por el año 200 a. C., es que coloca los planetas siempre a la misma distancia de la Tierra, en contradicción con el hecho de que la luminosidad de los planetas aumenta y disminuye a medida que parecen girar en torno a la Tierra. Pero la teoría de Ptolomeo parece ir demasiado lejos en la otra dirección. Por ejemplo, en ella la distancia máxima de Venus a la Tierra es 6,5 veces su distancia mínima, de manera que si Venus brilla con luz propia, entonces (puesto que su brillo aparente es inverso al cuadrado de la distancia) su brillo máximo debería ser 6,52 = 42 veces más grande que su brillo mínimo, cosa que desde luego no es el caso. La teoría de Ptolomeo había sido criticada por este motivo en la Universidad de Viena por Henry de Hesse (1325-1397). La resolución del problema consiste, naturalmente, en que los planetas no brillan con luz propia, sino con la luz reflejada del Sol, por lo que su brillo aparente depende no solo de su distancia a la Tierra, sino también, al igual que ocurre con el brillo de la Luna, de su fase. En el momento en que Venus está más lejos de la Tierra, se halla en el lado del Sol más lejano a la Tierra, de manera que su cara queda totalmente iluminada; cuando está más cerca de la Tierra queda más o menos entre la Tierra y el Sol, y lo que vemos, sobre todo, es su cara oscura. Por consiguiente, para Venus los efectos de la fase y la distancia se anulan en parte, moderando la variación de su brillo. Pero todo esto no se comprendía hasta que Galileo descubrió las fases de Venus.
Pronto la polémica entre la astronomía ptolemaica y la aristotélica quedó barrida por un conflicto más profundo, la de aquellos que seguían a Ptolomeo o Aristóteles y que aceptaban que los cielos giraban alrededor de una Tierra estacionaria, y el resurgimiento de la idea de Aristarco, que afirmaba que quien estaba en reposo era el Sol.
Parte IV
La revolución científica
Hay algo en este tipo de consenso que siempre atrae la atención de los escépticos de la siguiente generación de historiadores. En décadas anteriores algunos han expresado dudas acerca de la importancia o incluso la existencia de la revolución científica [169]. Por ejemplo, Steven Shapin empezó de manera memorable un libro con la frase: «La revolución científica no existe, y este libro trata de ello»[170].
Las críticas a la idea de la revolución científica adquieren dos formas opuestas. Por un lado, algunos historiadores arguyen que los descubrimientos de los siglos XVI y XVII no fueron más que una continuación natural del progreso científico que ya había ocurrido en Europa o en las tierras del islam (o en ambos lugares) durante la Edad Media. En concreto, esta es la opinión de Pierre Duhem[171]. Otros historiadores señalan los vestigios del pensamiento precientífico que prosiguió durante la revolución científica; por ejemplo, el hecho de que en algunos momentos Copérnico y Kepler suenen como Platón, que Galileo hiciera horóscopos cuando nadie pagaba por ellos, y que Newton considerara el sistema solar y la Biblia como pistas para adentrarnos en la mente de Dios.
Hay elementos de verdad en ambas críticas. Sin embargo, estoy convencido de que la revolución científica significó una auténtica ruptura en la historia intelectual, y lo considero desde la perspectiva de un científico contemporáneo. Con las pocas y brillantes excepciones griegas, la ciencia anterior al siglo XVI me parece muy distinta de la que yo mismo practico o veo en el trabajo de mis colegas. Antes de la revolución científica, la ciencia estaba impregnada de religión y de lo que llamamos filosofía, y todavía no había resuelto su relación con las matemáticas. En física y astronomía, después del siglo XVII ya me siento cómodo. Reconozco algo muy semejante a la ciencia de mi propia época: la búsqueda de leyes impersonales expresadas matemáticamente y que permiten predicciones precisas de un amplio espectro de fenómenos, leyes corroboradas por la comparación de estas predicciones con la observación y experimentación. La revolución científica existió, y el resto de este libro trata sobre ella.
Capítulo 11
El sistema solar solucionado
Poco después de llegar a Frombork, Copérnico escribió una breve obra anónima, posteriormente tituladaDe hypothesibus motuum coelestium a se constitutis commentariolus, generalmente conocida como el Commentariolus o Breve comentario[172]. El Commentariolus no se publicó hasta mucho después de la muerte de su autor, y no tuvo tanta influencia como su obra posterior, pero es una buena aproximación a las ideas que guiaron su obra.
Tras una breve crítica de las teorías anteriores de los planetas, en el Commentariolus Copérnico postula los siete principios de su nueva teoría. He aquí una paráfrasis, con algunos comentarios añadidos:
- Las órbitas de los cuerpos celestes no tienen ningún centro. (Los historiadores no se ponen de acuerdo acerca de si Copérnico consideraba que estos cuerpos se transportaban sobre esferas materiales[173], como suponía Aristóteles).
- El centro de la Tierra no es el centro del universo, sino solo el centro de la órbita de la Luna, y el centro de gravedad hacia el que se ven atraídos los cuerpos de la Tierra.
- Todos los cuerpos celestes excepto la Luna giran alrededor del Sol, que es, por tanto, el centro del universo. (Pero como comentaremos más adelante, Copérnico consideraba que el centro de las órbitas de la Tierra y de los demás planetas no era el Sol, sino un punto cerca del Sol).
- La distancia entre la Tierra y el Sol es despreciable en comparación con la distancia de las estrellas fijas. (Imagino que Copérnico planteó este supuesto para explicar por qué no vemos el paralaje anual: el movimiento anual aparente de las estrellas causado por el movimiento de la Tierra alrededor del Sol. Pero el problema del paralaje no aparece en ningún lugar del Commentariolus).
- La causa del movimiento diario aparente de las estrellas alrededor de la Tierra no es más que la rotación de la Tierra sobre su eje.
- La causa del movimiento aparente del Sol es la rotación de la Tierra sobre su eje y la revolución de la Tierra (al igual que los demás planetas) alrededor del Sol.
- El movimiento retrógrado aparente de los planetas viene causado por el movimiento de la Tierra, y se da cuando la Tierra pasa junto a Marte, Júpiter y Saturno, o en su órbita es rebasada por Mercurio o Venus.
Una de las ventajas era que el movimiento de la Tierra explicaba una amplia variedad de movimientos aparentes del Sol, las estrellas y los demás planetas. Así, Copérnico consiguió eliminar el «ajuste fino» adoptado por la teoría ptolemaica, según el cual el centro de los epiciclos de Mercurio y Venus tenía que permanecer siempre sobre la línea que unía la Tierra y el Sol, y que las líneas entre Marte, Júpiter y Saturno y los centros de sus respectivos epiciclos tenían que permanecer siempre paralelas a la línea entre la Tierra y el Sol. En consecuencia, la revolución del centro del epiciclo de cada planeta interior alrededor de la Tierra y la revolución de cada planeta exterior mediante un giro completo de su epiciclo tenía que someterse al ajuste fino para que durara exactamente un año. Copérnico comprendió que estos requisitos antinaturales simplemente reflejaban el hecho de que vemos el sistema solar desde una plataforma que gira alrededor del Sol.
Otra ventaja estética de la teoría copernicana tenía que ver con su mayor concreción en relación con el tamaño de las órbitas de los planetas. Recordemos que el movimiento aparente de los planetas en la astronomía ptolemaica dependía no de los tamaños de los epiciclos y deferentes, sino solo de la proporción de la razón entre el epiciclo y el deferente de cada planeta. Si a uno se le antojaba, incluso podía considerar que el deferente de Mercurio era más grande que el de Saturno, siempre y cuando el tamaño del epiciclo de Mercurio quedara debidamente ajustado. Siguiendo el ejemplo de las Hipótesis de los planetas de Ptolomeo, los astrónomos habitualmente asignaban tamaños a las órbitas basándose en el supuesto de que la distancia máxima de un planeta a la Tierra es igual a la distancia mínima de la Tierra al siguiente planeta exterior, lo que fijaba los tamaños relativos de las órbitas planetarias para cualquier orden de los planetas que se eligiera, empezando por la Tierra, pero esa elección era bastante arbitraria. En cualquier caso, los supuestos de las Hipótesis de los planetas no se basaban en la observación ni habían sido confirmados por esta.
Por el contrario, para que el esquema de Copérnico coincidiera con la observación, el radio de cada órbita planetaria tenía que mantener una razón fija con la órbita de la Tierra[175]. En concreto, debido a la diferencia en la manera en que Ptolomeo había introducido los epiciclos para los planetas interiores y exteriores (y dejando aparte las complicaciones relacionadas con la forma elíptica de las órbitas), la razón de los radios de los epiciclos y los deferentes debe ser igual a la razón entre las distancias del Sol a la Tierra y los planetas para los planetas interiores, e igual a esta razón inversa para los planetas exteriores (véase Nota técnica 13). Copérnico no presentó así sus resultados; los ofreció en términos de un complicado «esquema de triangulación», que transmitía la falsa impresión de que estaba llevando a cabo nuevas predicciones confirmadas por la observación. Pero, de hecho, calculó con exactitud los radios de las órbitas planetarias. Descubrió que, desde el Sol, el orden de los planetas era: Mercurio, Venus, Tierra, Marte, Júpiter y Saturno; este es precisamente el mismo orden de sus periodos, que Copérnico estimuló respectivamente en 3 meses, 9 meses, 1 año, 2 años y medio, 12 años y 30 años. Aunque todavía no existía ninguna teoría que dictara las velocidades de los planetas en sus órbitas, a Copérnico le debió de parecer una prueba del orden cósmico el que cuanto más grande era la órbita de un planeta más lentamente giraba alrededor del Sol[176].
La teoría de Copérnico proporciona un ejemplo clásico de cómo se puede escoger una teoría basándose en criterios estéticos sin ninguna prueba experimental que la favorezca sobre las otras. El argumento en favor de la teoría copernicana en el Commentariolus era simplemente que gran parte de lo que resultaba peculiar de la teoría copernicana quedó automáticamente explicado por la revolución y rotación de la Tierra, y que la teoría copernicana era mucho más concreta que la ptolemaica en lo referente al orden de los planetas y los tamaños de sus órbitas. Copérnico reconoció que la idea de una Tierra en movimiento la habían propuesto mucho antes los pitagóricos, pero también observó (con acierto) que era una idea que habían «afirmado de manera gratuita», sin los argumentos que él pudo proponer.
Había algo más en la teoría ptolemaica que a Copérnico no le gustaba, aparte del ajuste fino y la incertidumbre con relación al tamaño y orden de las órbitas planetarias. Fiel al dictamen de Platón de que los planetas se mueven en círculos a velocidad constante, Copérnico rechazó el uso que hacía Ptolomeo de mecanismos como el ecuante a la hora de abordar el hecho de que los planetas no se movieran en un movimiento circular ni a una velocidad fija. Como ya había hecho Ibn Al-Shatir, Copérnico introdujo más epiciclos: seis para Mercurio, tres para la Luna, y cuatro para cada uno de los otros planetas: Venus, Marte, Júpiter y Saturno. Aquí no mejoró el Almagesto bajo ningún concepto.
Esta obra de Copérnico ilustra otro tema recurrente en la historia de la física: una teoría sencilla y hermosa que concuerda bastante bien con la observación a menudo está más cerca de la verdad que una teoría fea y complicada que concuerda mejor con la observación. La aplicación más sencilla de las ideas generales de Copérnico habría sido darle a cada planeta, la Tierra incluida, una órbita circular a velocidad constante, con el Sol en el centro de todas las órbitas, prescindiendo completamente de los epiciclos. Eso habría concordado con la versión más simple de la astronomía ptolemaica, que proponía un solo epiciclo para cada planeta, ninguno para el Sol y la Luna, y ausencia de excéntricos y ecuantes. Tampoco habría concordado exactamente con todas las observaciones, pues los planetas no se mueven en círculos, sino sobre elipses casi circulares; sus velocidades son aproximadamente constantes; y el Sol no se halla en el centro de cada elipse, sino en un punto un poco descentrado, conocido como foco (véase Nota técnica 18). A Copérnico le habría convenido aún más seguir a Ptolomeo e introducir un excéntrico y un ecuante para cada órbita planetaria, pero incluyendo también la órbita de la Tierra; la discrepancia con la observación habría sido entonces demasiado pequeña para que los astrónomos de la época pudieran medirla.
Existe un episodio en el desarrollo de la mecánica cuántica que muestra la importancia de no preocuparse demasiado acerca de los pequeños conflictos con la observación. En 1925 Erwin Schrödinger elaboró un método para calcular las energías de los estados del átomo más simple, el de hidrógeno. Sus resultados coincidían bastante con el patrón básico de esas energías, pero los detalles finos de sus resultados, que tenían en cuenta cómo la mecánica de la relatividad especial se apartaba de la mecánica newtoniana, no coincidían con los detalles finos de las energías medidas. Schrödinger al principio no divulgó sus resultados, hasta que sabiamente comprendió que obtener el patrón básico de los niveles de energía era ya un logro importante y que valía la pena publicarlo, y que el tratamiento correcto de los efectos de la relatividad podía esperar. Años más tarde lo proporcionó Paul Dirac.
Además de los numerosos epiciclos, hubo otra complicación adoptada por Copérnico, parecida al excéntrico de la astronomía ptolemaica. Se consideraba que el centro de la órbita de la Tierra no era el Sol, sino un punto que quedaba a relativamente poca distancia del Sol. Estas complicaciones explicaban de manera aproximada diversos fenómenos, como la duración desigual de las estaciones descubierta por Euctemón, que en realidad son consecuencias del hecho de que el Sol es el foco y no el centro de la órbita elíptica de la Tierra, y que la velocidad de la Tierra en su órbita no es constante.
Otra de las complicaciones introducidas por Copérnico fue necesaria solo por culpa de un malentendido. Al parecer Copérnico consideraba que la revolución de la Tierra alrededor del Sol le daría al eje de rotación de la Tierra un giro anual de 360° alrededor de la dirección perpendicular al plano de la órbita de la Tierra, de manera parecida a como un dedo situado al final del brazo extendido de un bailarín que ejecuta una pirueta sufriría un giro de 360° alrededor de la dirección vertical a cada rotación del bailarín. (Quizá se vio influido por la antigua idea de que los planetas están montados sobre esferas sólidas transparentes). Naturalmente, la dirección del eje de la Tierra no cambia de manera apreciable en el curso de un año, por lo que Copérnico se vio obligado a darle a la Tierra un tercer movimiento, aparte de su revolución alrededor del Sol y su rotación en torno a su eje, que prácticamente anularía el giro de este. Copérnico supuso que esta anulación no sería perfecta, de manera que el eje de la Tierra seguiría girando durante muchos años y produciendo la lenta precesión de los equinoccios que había descubierto Hiparco. Después del trabajo de Newton, quedó claro que la revolución de la Tierra en torno al Sol de hecho no influía en la dirección del eje de la Tierra, aparte de algún efecto insignificante debido a la acción de la gravedad del Sol y la Luna sobre el abultamiento ecuatorial de la Tierra, y así (tal como afirmó Kepler) no era necesario que Copérnico llevara a cabo ninguna anulación.
Con todas estas complicaciones, la teoría de Copérnico seguía siendo más sencilla que la de Ptolomeo, aunque no demasiado. Si bien Copérnico quizá no lo supiera, su teoría habría estado más cerca de la verdad de no haberse preocupado por los epiciclos y dejado que los científicos del futuro abordaran las pequeñas inexactitudes de su teoría.
Los Commentariolus no aportaban demasiados detalles técnicos. Estos los presentó en su gran obraDe Revolutionibus Orbium Coelestium[177], más conocida como De Revolutionibus, acabada en 1543, cuando Copérnico estaba en su lecho de muerte. El libro comienza con una dedicatoria a Alessandro Farnese, el papa Paulo III. En ella, Copérnico planteaba de nuevo la antigua discusión entre las esferas homocéntricas de Aristóteles y los excéntricos y epiciclos de Ptolomeo, señalando que las primeras no explican las observaciones, y que las últimas «contradicen los primeros principios de la regularidad del movimiento». En apoyo de su atrevimiento al sugerir una Tierra en movimiento, Copérnico citaba un pasaje de Plutarco:
Algunos creen que la Tierra permanece en reposo. Pero Filolao el Pitagórico considera que, al igual que el Sol y la Luna, gira alrededor del fuego en un círculo oblicuo. Heráclides de Ponto y Ecfanto el Pitagórico afirman que la Tierra se mueve, no en un movimiento progresivo, sino como una nueva derrota de oeste a este en torno a su centro.(En la edición habitual de De Revolutionibus Copérnico no menciona a Aristarco, pero su nombre había aparecido originalmente y había sido eliminado). Copérnico seguía explicando que, mientras que otros habían considerado que la Tierra se movía, a él también se le debería permitir poner a prueba esa idea. A continuación exponía su conclusión:
Dando por supuestos los movimientos que le atribuyo a la Tierra en este mismo volumen, mediante un prolongado e intenso estudio por fin he averiguado que si los movimientos de los demás planetas están correlacionados con la órbita de la Tierra, y se calculan para la revolución de cada planeta, no solo se deducen de ellos sus fenómenos, sino también el orden y tamaño de todos los planetas y esferas, y el cielo mismo está conectado hasta tal punto que no se puede desplazar ninguna de sus partes sin trastocar las demás y el universo en su totalidad.Al igual que en el Commentariolus, Copérnico apelaba al hecho de que su teoría hacía más predicciones que la de Ptolomeo; dictaba un orden único para los planetas y los tamaños de sus órbitas necesarias para explicar la observación, mientras que la teoría de Ptolomeo dejaba todo eso sin determinar. Naturalmente, Copérnico no tenía manera alguna de confirmar que sus radios orbitales eran correctos sin asumir la verdad de su teoría; hubo que esperar a que Galileo observara las fases planetarias.
Casi todo el texto de De Revolutionibus es extremadamente técnico, y desarrolla las ideas generales del Commentariolus. Un punto digno de mención es que en el Libro 1 Copérnico afirma un compromiso a priori con el movimiento compuesto de círculos. Así, el Capítulo 1 del libro comienza:
En primer lugar, hemos de observar que el universo es esférico. La razón es que, de todas las formas, la esfera es la más perfecta, no precisa articulación y es una totalidad completa, que no puede aumentar ni disminuir [aquí Copérnico parece Platón]; o que es la más espaciosa de las figuras, la mejor adaptada para encerrar y conservar todas las cosas [es decir, la que tiene más volumen dada una superficie]; o incluso que todas las partes que forman el universo, es decir el Sol, la Luna, los planetas y las estrellas, se ha visto que tienen esta forma [¿qué podía saber de la forma de las estrellas?]; o que la totalidad siempre busca quedar circunscrita por este límite, como se puede ver en las gotas de agua y otros cuerpos fluidos cuando buscan quedar contenidos en sí mismos [esto es efecto de la tensión superficial, irrelevante a escala planetaria]. Por lo tanto, nadie pondrá en entredicho que esta forma sea propia de los cuerpos divinos.
A continuación explica en el Capítulo 4 que, en consecuencia, el movimiento de los cuerpos celestes es «uniforme, eterno y circular, o compuesto de movimientos circulares».
En el Libro 1, Copérnico señaló uno de los aspectos más hermosos del sistema heliocéntrico: explicaba por qué Mercurio y Venus nunca se ven lejos del Sol en el cielo. Por ejemplo, el hecho de que Venus nunca se vea a más de 45° del Sol se explica por el hecho de que su órbita alrededor de este es más o menos el 70 por ciento del tamaño de la órbita de la Tierra (véase Nota técnica 19). Como vimos en el Capítulo 11, en la teoría de Ptolomeo esto precisaba un ajuste fino del movimiento de Mercurio y Venus, a fin de que los centros de sus epiciclos estén siempre sobre la línea que une la Tierra y el Sol. El sistema de Copérnico hacía innecesario el ajuste fino de Ptolomeo para el movimiento de los planetas exteriores, que mantenían la línea entre cada planeta y el centro de su epiciclo paralela a la línea entre la Tierra y el Sol.
El sistema copernicano encontró la oposición de los líderes religiosos, antes incluso de la publicación de De Revolutionibus. El conflicto se exageró en una famosa polémica del siglo XIX, A History of the Warfare of Science with Theology in Christendom, del primer rector de Cornell, Andrew Dickson White[178], que presenta diversas citas poco fiables de Lutero, Melanchthon, Calvino y Wesley. Pero el conflicto existía. Tenemos el registro escrito de las conversaciones de Martín Lutero con sus discípulos en Wittenberg, conocidas como Tischreden (Discursos en la mesa)[179]. En la entrada del 4 de junio de 1539 leemos:
Se mencionó a un nuevo astrólogo que quería demostrar que la Tierra se mueve, y no el cielo, el Sol y la Luna […] [comentó Lutero]: «Así van las cosas ahora. Todo aquel que quiere ser inteligente ha de estar en desacuerdo con lo que opinan los demás. Ha de hacer algo por su cuenta. Es lo que hace este necio que quiere poner toda la astronomía patas arriba. Incluso en lo referente a estas cosas que la gente quiere trastocar creo en las Sagradas Escrituras, pues Josué ordenó que el Sol permaneciera inmóvil, y no la Tierra» [180].Unos años después de la publicación de De Revolutionibus, Philipp Melanchthon (1497-1569), colega de Lutero, se unió al ataque contra Copérnico, citando ahora el Eclesiastés 1:5: «Sale el Sol y el Sol se pone; corre hacia su lugar y allí vuelve a salir».
Los conflictos con el texto literal de la Biblia naturalmente presentaban problemas para el protestantismo, que había sustituido la autoridad del papa por la de las Escrituras. Aparte de eso, había un problema latente para todas las religiones: el lugar del hombre, la Tierra, había quedado degradado a un simple planeta más entre los otros cinco.
Los problemas surgieron ya con la impresión de De Revolutionibus. Copérnico había mandado su manuscrito a un editor de Núremberg, y el editor designó como corrector a un clérigo luterano, Andreas Osiander, cuya afición era la astronomía. Probablemente expresando sus propias opiniones, Osiander añadió un prefacio que se creyó que era de Copérnico, hasta que la sustitución quedó desenmascarada en el siglo siguiente por Kepler. En este prefacio Osiander hace que Copérnico rechace cualquier intención de presentar la verdadera naturaleza de las órbitas planetarias con las siguientes palabras [181]:
Pues es el deber de un astrónomo presentar la historia de los movimientos celestes [aparentes] mediante un estudio meticuloso y experto. A continuación debe concebir y proponer las causas de estos movimientos o hipótesis acerca de ellos. Puesto que de ningún modo puede atinar la verdadera causa, adoptará las suposiciones que permitan calcular de manera correcta los movimientos a partir de los principios de la geometría para el futuro y también para el pasado.El prefacio de Osiander concluye:
Por lo que se refiere a las hipótesis, que nadie espere certezas de la astronomía, pues esta no las puede aportar, a no ser que uno acepte como verdaderas ideas concebidas para otro propósito, y finalice su estudio siendo más necio que cuando lo comenzó.Este concordaba con las opiniones de Gémino allá por el 70 a. C. (al que hemos citado en el capítulo 8), pero era bastante contrario a la evidente intención de Copérnico, tanto en el Commentariolus como en De Revolutionibus, de describir la auténtica composición de lo que ahora se denomina el sistema solar.
A pesar de lo que los clérigos, considerados de manera individual, pudieran haber pensado acerca de la teoría heliocéntrica, los protestantes, en general, no hicieron ningún esfuerzo para prohibir las obras de Copérnico. La oposición católica a Copérnico tampoco se organizó hasta el siglo XVII. La famosa ejecución de Giordano Bruno por parte de la Inquisición romana en 1600 no fue por su defensa de Copérnico, sino por herejía, de la cual (según el criterio de la época) seguramente era culpable. Pero, como veremos, en el siglo XVII la Iglesia católica puso todo su ahínco en eliminar las ideas copernicanas.
Lo que fue realmente importante para el futuro de la ciencia fue la recepción de Copérnico entre sus colegas astrónomos. El primero que quedó convencido por las ideas de Copérnico fue su único discípulo, Rheticus, que en 1540 publicó una explicación de la teoría copernicana, y que en 1543 ayudó a queDe Revolutionibus llegara a manos del editor de Núremberg. (Inicialmente era Rheticus quien tenía que escribir el prefacio a De Revolutionibus, pero cuando se marchó para ocupar un cargo docente en Leipzig, la tarea recayó, por desgracia, en Osiander). Rheticus anteriormente había ayudado a Melanchthon a convertir la Universidad de Wittenberg en un centro de estudios matemáticos y astronómicos.
La teoría de Copérnico adquirió prestigio cuando, en 1551, Erasmus Reinhold, bajo el patronato del duque de Prusia, la utilizó para compilar una nueva serie de tablas astronómicas, las Tablas Prusianas, que permiten calcular el emplazamiento de los planetas en el zodíaco en cualquier día concreto. Suponían una mejora evidente sobre las anteriormente utilizadas, las Tablas Alfonsinas, elaboradas en 1275 en Castilla, en la corte de Alfonso X. La mejora se debía no a la superioridad de la teoría de Copérnico, sino más bien a la acumulación de nuevas observaciones en los siglos transcurridos entre 1275 y 1551, y quizá también al hecho de que la mayor simplicidad de las teorías heliocéntricas facilitaba los cálculos. Naturalmente, los partidarios de una Tierra estacionaria podrían argüir que De Revolutionibus proporcionaba tan solo un esquema de cálculo práctico, no una auténtica imagen del mundo. De hecho, las Tablas Prusianas fueron utilizadas por el astrónomo y matemático jesuita Christoph Clavius en la reforma del calendario de 1582, bajo el papa Gregorio XIII, que nos proporcionó nuestro moderno calendario gregoriano, aunque Clavius jamás abandonó su creencia en una Tierra estacionaria.
Hubo un matemático que intentó reconciliar esta creencia con la teoría copernicana. En 1568, el yerno de Melanchthon, Caspar Peucer, profesor de matemáticas en Wittenberg, razonó en Hypotyposes orbium coelestium que debería ser posible, mediante una transformación matemática, reescribir la teoría de Copérnico de forma que la Tierra, y no el Sol, permaneciera estacionaria. Ese fue precisamente el resultado alcanzado por uno de los alumnos de Peucer, Tycho Brahe.
Tycho Brahe fue el observador astronómico más competente de la historia antes de la introducción del telescopio, y autor de la teoría más plausible alternativa a la de Copérnico. Nacido en 1546 en la provincia de Skåne, ahora al sur de Suecia, pero hasta 1658 parte de Dinamarca, Tycho fue hijo de un noble danés. Se educó en la Universidad de Copenhague, donde en 1560 se entusiasmó con la acertada predicción de un eclipse de sol parcial. Se trasladó a universidades de Alemania y Suiza, a Leipzig, Wittenberg, Rostock, Basilea y Augsburgo. Durante esos años estudió las Tablas Prusianas y quedó impresionado por el hecho de que las tablas predijeran la fecha de la conjunción de 1563 de Saturno y Júpiter con pocos días de diferencia, mientras las antiguas Tablas Alfonsinas se habían desviado en muchos meses.
De nuevo en Dinamarca, Tycho se instaló durante una temporada en la casa de su tío en Herrevad, Skåne, donde en 1572 observó en la constelación de Casiopea lo que llamó una «nueva estrella». (Ahora se sabe que fue la explosión termonuclear, conocida como supernova de tipo Ia, de una estrella preexistente. Los restos de esa explosión fueron descubiertos por radioastrónomos en 1952 a una distancia de unos 9000 años luz, demasiado lejos para que la estrella pudiera verse sin telescopio antes de la explosión). Tycho se pasó meses observando la nueva estrella, utilizando un sextante de construcción propia, y descubrió que no mostraba ningún paralaje diurno, el desplazamiento posicional diario entre las estrellas que sería de esperar a causa de la rotación de la Tierra (o la revolución diaria alrededor de la Tierra de todo lo demás) si la nueva estrella estuviera tan cerca como la Luna, o más (véase Nota técnica 20). Concluyó: «Esta nueva estrella no se localiza en las regiones superiores del aire, justo debajo de la esfera lunar, ni en ningún lugar cercano a la Tierra […] sino muy por encima de la Luna, en los mismísimos cielos»[182]. Cosa que entraba en directa contradicción con el principio de Aristóteles, según el cual los cielos, más allá de la órbita de la Luna, no pueden sufrir ningún cambio. La observación hizo famoso a Tycho.
En 1576 el rey danés Federico II le concedió a Tycho el señorío de la pequeña isla de Hven, en el estrecho entre Skåne y la extensa isla danesa de Selandia, junto con una pensión para mantener el edificio y un centro de investigación científica. Allí Tycho construyó Uraniborg, que incluía un observatorio, una biblioteca, un laboratorio químico y una imprenta. El edificio estaba decorado con retratos de astrónomos del pasado —Hiparco, Ptolomeo, Al-Battani y Copérnico— y de un patrón de las ciencias, Guillermo IV, landgrave de Hesse-Cassel. En Hven, Tycho adiestró a algunos ayudantes y de inmediato comenzó sus observaciones.
Ya en 1577 Tycho observó un cometa y descubrió que no presentaba ningún paralaje diurno observable, cosa que demostraba, de nuevo en contra de la opinión de Aristóteles, que en los cielos, más allá de la órbita de la Luna, ocurrían cambios. Ahora Tycho también pudo concluir que la trayectoria del cometa habría atravesado o bien las supuestas esferas homocéntricas de Aristóteles o las esferas de la teoría ptolemaica. (Lo que, naturalmente, supondría un problema solo si las esferas se concebían como sólidos duros. Esta era la doctrina de Aristóteles, que, como hemos visto en el capítulo 8, los astrónomos helenísticos Adrasto y Teón habían trasladado a la teoría ptolemaica. La idea de las esferas duras había revivido en la época moderna [183], no mucho antes de que Tycho la descartara). Los cometas aparecen con más frecuencia que las supernovas, y Tycho consiguió repetir esas observaciones con otros cometas en años posteriores.
A partir de 1538 Tycho trabajó en una nueva teoría de los planetas, basada en la idea de que la Tierra está en reposo, el Sol y la Luna giran alrededor de la Tierra, y los cinco planetas dan vueltas alrededor del Sol. Se publicó en 1588 como Capítulo 8 del libro de Tycho sobre el cometa, de 1577. En esta teoría se supone que la Tierra no se mueve ni da vueltas, por lo que, además de poseer un movimiento más lento, el Sol, la Luna, los planetas y las estrellas todos giran alrededor de la Tierra de este a oeste una vez al día. Algunos astrónomos adoptaron, por el contrario, una teoría «semitychoniana», en la que los planetas giran alrededor del Sol, el Sol gira alrededor de la Tierra, pero la Tierra gira y las estrellas están en reposo. (El primer defensor de una teoría semitychoniana fue Nicolaus Reimers Baer, aunque él no utilizaría esa descripción, pues afirmaba que Tycho le había robado el sistema tychoniano original)[184].
Tal como se ha mencionado varias veces anteriormente, la teoría tychoniana es idéntica a la versión de la teoría de Ptolomeo (jamás considerada por este) en la que los deferentes de los planetas interiores se hacen coincidir con la órbita del Sol alrededor de la Tierra, y los epiciclos de los planetas exteriores poseen el mismo radio que la órbita del Sol alrededor de la Tierra. Por lo que se refiere a las separaciones y las velocidades relativas de los cuerpos celestes, también es equivalente a la teoría de Copérnico, y solo difiere en el punto de vista: Copérnico postulaba un Sol estacionario, y Tycho una Tierra estacionaria y no rotatoria. Por lo que se refiere a las observaciones, la teoría de Tycho posee la ventaja de que de manera automática no predecía ningún paralaje estelar, y no tenía que asumir que las estrellas están mucho más lejos de la Tierra que el Sol o los planetas (cosa que, naturalmente, ahora sabemos que es así). También resultaba innecesaria la respuesta de Oresme al problema clásico que había desconcertado a Ptolomeo y Buridan: que los objetos arrojados hacia arriba al parecer quedarían atrás si la Tierra girara o se moviera.
Para el futuro de la astronomía, la aportación más importante de Tycho no fue su teoría, sino la exactitud sin precedentes de sus observaciones. Cuando visité Hven, en la década de 1970, no encontré señal alguna de los edificios de Tycho, pero allí, todavía en el suelo, se encontraban los inmensos cimientos de piedra sobre los que Tycho había asegurado sus instrumentos. (Desde mi visita, han instalado un museo y unos jardines en su honor). Con esos instrumentos, Tycho consiguió localizar objetos en el cielo con una desviación de tan solo 1/15°. También en Uraniborg se alza una estatua de granito, tallada por Ivar Johnson en 1936, en la que se ve a Tycho en una postura muy adecuada para un astrónomo: de cara al cielo [185].
El patrono de Tycho, Federico II, murió en 1588. Lo sucedió Christian IV, al que los daneses hoy en día consideran como uno de sus más grandes reyes, pero que por desgracia sintió muy poco interés por apoyar la astronomía. Las últimas observaciones de Tycho desde el observatorio de Hven se llevaron a cabo en 1597; posteriormente emprendió un viaje que lo llevó a Hamburgo, Dresde, Wittenberg y Praga, donde se convirtió en el matemático imperial del emperador del Sacro Imperio Romano Rodolfo II y comenzó a trabajar en una nueva serie de tablas astronómicas, las Tablas Rudolfinas. Después de la muerte de Tycho en 1601, su labor fue continuada por Kepler.
Johannes Kepler fue el primero en comprender la naturaleza de las desviaciones del movimiento circular uniforme que habían desconcertado a los astrónomos desde la época de Platón. Cuando tenía cinco años, le inspiró la visión del cometa de 1577, el primero que Tycho estudió en su nuevo observatorio de Hven. Kepler asistió a la Universidad de Tubinga, donde, bajo la dirección de Melanchthon, adquirió eminencia en teología y matemáticas. En Tubinga Kepler estudió estas dos disciplinas, pero le interesaron más las matemáticas. Aprendió la teoría de Copérnico de Michael Mästlin, un profesor de matemáticas que le dio clases en Tubinga, y quedó convencido de su verdad.
En 1594 Kepler fue contratado para dar clases de matemáticas en una escuela luterana de Graz, al sur de Austria. Fue allí donde publicó su primera obra original, el Mysterium Cosmographicum (El misterio cosmográfico). Como hemos visto, una de las ventajas de la teoría de Copérnico era que permitía que las observaciones astronómicas se utilizaran para encontrar resultados únicos para el orden de los planetas, comenzando a contar desde el Sol y por los tamaños de sus órbitas. Como era todavía corriente en la época, en su obra Kepler concibió estas órbitas como círculos trazados por los planetas al ser transportados en esferas transparentes, girando en la teoría copernicana alrededor del Sol. Estas esferas no eran estrictamente superficies tridimensionales, sino diminutas conchas cuyo radio interior y exterior era la distancia mínima y máxima del planeta al Sol. Kepler conjeturó que los radios de estas esferas se ven limitados por una condición a priori: que cada esfera (aparte de la esfera más exterior, la de Saturno) encaje de manera precisa dentro de uno de los cinco poliedros regulares, y que cada esfera (aparte de la esfera más interior, la de Mercurio) encaje exactamente fuera de uno de estos poliedros regulares. En concreto, en su ordenación hacia fuera a partir del Sol, Kepler colocó (1) la esfera de Mercurio, (2) a continuación un octaedro, (3) la esfera de Venus, (4) un icosaedro, (5) la esfera de la Tierra, (6) un dodecaedro, (7) la esfera de Marte, (8) un tetraedro, (9) la esfera de Júpiter, (10) un cubo, y finalmente (11) la esfera de Saturno, todos encajados de manera ajustada.
Este esquema dictaba los tamaños de las órbitas de todos los planetas, sin libertad para ajustar los resultados, como no fuera eligiendo el orden de los cinco poliedros regulares que encajaban en los espacios entre los planetas. Hay 30 maneras diferentes de escoger el orden de los poliedros regulares [186], de manera que no resulta sorprendente que Kepler pudiera encontrar una manera de elegir el orden de forma que los tamaños pronosticados de las órbitas planetarias encajaran más o menos con los resultados de Copérnico.
De hecho, el esquema original de Kepler funcionaba mal para Mercurio, con el que Kepler tuvo que hacer un apaño, y solo moderadamente bien para los otros planetas[187].
Pero al igual que otros muchos personajes del Renacimiento, Kepler estaba profundamente influido por la filosofía platónica, y al igual que Platón, le intrigaba el teorema según el cual los poliedros regulares existen solo en cinco formas distintas, lo que solo nos da seis planetas posibles, incluyendo la Tierra. Kepler proclamó orgulloso: «¡Ya has dado con la razón que explica el número de planetas!».
Hoy en día nadie se toma en serio un esquema como el de Kepler, aun cuando hubiera funcionado mejor. Ello no se debe a que hayamos superado la antigua fascinación platónica por las listas de objetos matemáticamente posibles, como los poliedros regulares. Hay otras listas que continúan intrigando a los físicos. Por ejemplo, se sabe que hay solo cuatro tipos de «números» para los que es posible una versión de la aritmética que incluye la división: los números reales, los números complejos (entre ellos la raíz cuadrada de –1), y cantidades más exóticas conocidas como cuaterniones y octoniones. Algunos físicos han dedicado mucho esfuerzo a intentar incorporar los cuaterniones y los octoniones, así como los números reales y complejos, a las leyes fundamentales de la física. Lo que hace que el esquema de Kepler nos resulte ya tan ajeno no es su intento de encontrar algún significado físico fundamental a los poliedros regulares, sino que lo hiciera en el contexto de las órbitas planetarias, que no son más que accidentes históricos. Sean cuales sean las leyes fundamentales de la naturaleza, podemos estar bastante seguros de que no se refieren a los radios de las órbitas planetarias.
Eso no fue simplemente una estupidez por parte de Kepler. En su época nadie sabía (y Kepler tampoco lo creía) que las estrellas eran soles con su propio sistema planetario, y no simplemente luces sobre una esfera en algún lugar exterior a la esfera de Saturno. Por lo general se consideraba que el sistema solar era prácticamente la totalidad del universo, y que había sido creado al principio de los tiempos. Era perfectamente natural, por tanto, suponer que la detallada estructura del sistema solar es tan fundamental en la naturaleza como cualquier otra cosa.
Hoy en día podríamos encontrarnos en una posición parecida en la física teórica. Por lo general se supone que lo que llamamos el universo en expansión, la enorme nube de galaxias que observamos separándose velozmente y de manera uniforme en todas direcciones, es la totalidad del universo. Consideramos que las constantes de la naturaleza que medimos, como las masas de las diversas partículas elementales, con el tiempo se deducirán de las leyes fundamentales de la naturaleza todavía desconocidas. Pero también es posible que lo que llamamos el universo en expansión no sea más que una pequeña parte de un «multiverso» mucho más grande que contenga muchas partes en expansión como la que nosotros observamos, y que las constantes de naturaleza adquieran valores distintos en partes distintas del multiverso. En este caso, esas constantes son parámetros ambientales que nunca se deducirán de principios fundamentales, del mismo modo que no podemos deducir las distancias de los planetas al Sol de principios fundamentales. A lo más que podemos aspirar es a una estimación antrópica. De los miles de millones de planetas de nuestra galaxia, solo una ínfima minoría posee la temperatura y la composición química adecuadas para poder albergar vida, pero es evidente que cuando la vida comienza y evoluciona hasta dar lugar a los astrónomos, estos se encuentran en un planeta perteneciente a esta minoría. Por ello, no resulta sorprendente que el planeta en el que vivimos no esté a una distancia del Sol ni el doble ni la mitad de a la que nos encontramos. Del mismo modo, parece probable que tan solo una pequeña minoría de los subuniversos del multiverso poseyeran constantes físicas que permitieran la evolución de la vida, aunque, naturalmente, cualquier científico se encontrará en un subuniverso perteneciente a esa minoría. Esta había sido una de las explicaciones del orden de magnitud de la energía oscura mencionada en el capítulo 8, antes de que la energía oscura se descubriera [188]. Todo esto, por supuesto, es enormemente especulativo, pero sirve como advertencia de que, al intentar comprender las constantes de naturaleza, puede que nos encontremos con la misma decepción que Kepler se encontró al intentar explicar las dimensiones del sistema solar.
Algunos distinguidos físicos deploran la idea del multiverso, porque son incapaces de aceptar la posibilidad de que en la naturaleza haya constantes que no se puedan calcular nunca. Es cierto que la idea del multiverso podría ser un completo error, por lo que resultaría prematuro renunciar al esfuerzo de calcular todas las constantes físicas que conocemos. Pero el hecho de que nos haga desdichados no ser capaces de llevar a cabo esos cálculos no es ningún argumento contra la idea del multiverso. Sean cuales sean las leyes finales de la naturaleza, no hay razón para suponer que estén diseñadas para que los físicos se sientan felices.
En Graz, Kepler inició una correspondencia con Tycho Brahe, que había leído el Mysterium Cosmographicum. Tycho invitó a Kepler a visitarlo en Uraniborg, pero Kepler consideró que estaba demasiado lejos. En febrero de 1600 Kepler aceptó la invitación de Tycho para ir a visitarlo a Praga, capital del Sacro Imperio Romano desde 1583. Allí Kepler comenzó a estudiar los datos de Tycho, especialmente los relacionados con los movimientos de Marte, y encontró discrepancia de 0,13° entre esos datos y la teoría de Ptolomeo[189].
Kepler y Tycho no hicieron buenas migas y Kepler regresó a Graz. Justo en esa época los protestantes eran expulsados de esa ciudad, y en agosto de 1600 Kepler y su familia fueron obligados a marcharse. De nuevo en Praga, Kepler comenzó una colaboración con Tycho, y se pusieron a trabajar en las Tablas Rudolfinas, la nueva serie de tablas astronómicas que iba a reemplazar a las Tablas Prusianas de Reinhold. Después de la muerte de Tycho en 1601, los problemas económicos de Kepler se solucionaron por una temporada al ser nombrado sucesor de Tycho como matemático de la corte del emperador Rodolfo II.
El emperador era un entusiasta de la astrología, por lo que uno de los deberes de Kepler como matemático de la corte era hacer horóscopos, una actividad a la que se había dedicado desde su época de estudiante en Tubinga, a pesar de su escepticismo acerca de las predicciones astrológicas. Afortunadamente, también tuvo tiempo para dedicarse a la verdadera ciencia. En 1604 observó una nueva estrella en la constelación Ofiuco, la última supernova en la galaxia o cerca de ella hasta 1987. En el mismo año publicó Astronomaiae Pars Optica (La parte óptica de la astronomía), una obra sobre la teoría óptica y sus aplicaciones a la astronomía, que incluía cómo la refracción en la atmósfera afectaba a las observaciones de los planetas.
Kepler siguió estudiando los movimientos de los planetas, e intentando sin éxito hacer cuadrar los precisos datos de Tycho con la teoría copernicana añadiendo excéntricos, epiciclos y ecuantes. Kepler acabó su obra en 1605, pero su publicación se retrasó por una disputa con los herederos de Tycho. Finalmente, en 1609 Kepler publicó sus resultados en Astronomia Nova ( Nueva astronomía fundada en causas, o física celeste, expuesta en comentarios sobre los movimientos de la estrella Marte, a partir de las observaciones de Tycho Brahe ).
La Parte III de la Astronomia Nova llevó a cabo una mejora importante en la teoría copernicana introduciendo un ecuante y un excéntrico para la Tierra, de manera que existe un punto al otro lado del centro de su órbita en torno al cual la línea de la Tierra gira a una velocidad constante. Eso eliminaba casi todas las discrepancias que habían entorpecido las teorías planetarias desde la época de Ptolomeo, pero los datos de Tycho eran tan buenos que Kepler se dio cuenta de que todavía existían algunos conflictos entre la teoría y la observación.
En algún momento Kepler quedó convencido de que la tarea era inútil, y tuvo que abandonar el supuesto, común a Platón, Aristóteles, Ptolomeo, Copérnico y Tycho, de que los planetas se mueven en órbitas compuestas de círculos, y concluyó que las órbitas planetarias poseían forma ovalada. Finalmente, en el Capítulo 58 de los 70 de que constaba su Astronomia Nova, Kepler precisó la cuestión. En lo que posteriormente se conocería como la primera ley de Kepler, concluyó que los planetas (incluyendo la Tierra) se mueven en elipses, y que el Sol es un foco de la elipse, no el centro. Al igual que un círculo se describe completamente (aparte de su localización) mediante un solo número, su radio, la elipse se puede describir completamente (aparte de su localización y su orientación) mediante dos números, que se pueden tomar como la longitud del eje más largo y del más corto, o equivalentes a la longitud del eje más largo y a un número conocido como «excentricidad», que muestra la diferencia entre el eje mayor y el menor (véase Nota técnica 18). Los dos focos de una elipse son dos puntos del eje más largo, a la misma distancia del centro, con una separación entre ellos igual a la excentricidad por la longitud del eje más largo de la elipse. Para una excentricidad cero, los dos ejes de la elipse tienen la misma longitud, los dos focos se fusionan en un solo punto y la elipse degenera en un círculo.
De hecho, las órbitas de todos los planetas que Kepler conocía tienen excentricidades pequeñas, como se puede ver en la siguiente tabla de valores actuales (proyectada para el año 1900):
| Planeta | Excentricidad |
| Mercurio | 0,205615 |
| Venus | 0,006820 |
| Tierra | 0,016750 |
| Marte | 0,093312 |
| Júpiter | 0,048332 |
| Saturno | 0,055890 |
Por este motivo, las versiones simplificadas de las teorías copernicanas y ptolemaica (sin epiciclos en la teoría copernicana y con solo un epiciclo para cada uno de los cinco planetas en la teoría ptolemaica) habría funcionado bastante bien [190].
La sustitución de los círculos por elipsis tuvo otra implicación trascendental. Los círculos se pueden generar mediante la rotación de las esferas, pero no existe ningún cuerpo sólido cuya rotación pueda producir una elipse, lo cual, unido a las conclusiones de Tycho extraídas de su observación del cometa en 1577, tuvo una gran influencia a la hora de acabar con la antigua idea de que los planetas eran transportados en esferas giratorias, una idea que el propio Kepler había asumido en el Mysterium Cosmographicum. Kepler y sus sucesores ahora concebían los planetas como objetos que viajaban en órbitas independientes en el espacio exterior.
Los cálculos que aparecen en Astronomia Nova también utilizaron lo que posteriormente fue conocido como segunda ley de Kepler, aunque esta ley no se estableció claramente hasta 1621, en su Epítome de astronomía copernicana. La segunda ley nos dice que la velocidad de un planeta cambia a medida que el planeta se mueve en torno a su órbita, y que a medida que el planeta se desplaza, la línea entre el Sol y el planeta abarca áreas iguales en tiempos iguales. Para abarcar un área dada, cuando un planeta está cerca del Sol tiene que moverse más lejos en su órbita que cuando está lejos del Sol, por lo que la segunda ley de Kepler tiene la consecuencia de que cada planeta ha de moverse más deprisa cuanto más se acerca al Sol. Aparte de insignificantes correcciones proporcionales al cuadrado de la excentricidad, la segunda ley de Kepler equivale a afirmar que la línea que va del planeta al otro foco (el que no es el Sol) gira a una velocidad constante; es decir, gira el mismo ángulo cada segundo (véase Nota técnica 21). Así, para una buena aproximación, la segunda ley de Kepler da las mismas velocidades planetarias que las del antiguo ecuante, un punto en el lado opuesto del centro del círculo desde el Sol (o para Ptolomeo, desde la Tierra), y a la misma distancia desde el centro, en torno al cual la línea hasta el planeta gira a velocidad constante. Así pues, el ecuante no es más que el foco vacío de la elipse. Solo los espléndidos datos obtenidos por Tycho para Marte le permitieron a Kepler concluir que los excéntricos y los ecuantes no son suficientes; las órbitas circulares han de ser sustituidas por elipses [191].
La segunda ley también tuvo aplicaciones profundas, al menos para Kepler. En Mysterium Cosmographicum, Kepler había concebido que los planetas se movían mediante un «alma motora». Pero ahora que se había descubierto que la velocidad de cada planeta disminuía a medida que aumentaba la distancia desde el Sol, Kepler concluyó que los planetas se ven impelidos en sus órbitas por el mismo tipo de fuerza que emana del Sol:
Si sustituimos la palabra «fuerza» [vis] por la palabra «alma» (anima), tenemos el mismísimo principio en el que se basa la física celeste en el Comentario sobre Marte [Astronomia Nova].Pues yo antes creía que la causa que movía los planetas era un alma, pues estaba imbuido de las enseñanzas de J. C. Scaliger [192] sobre las inteligencias motoras. Pero cuando comprendí que esa causa motora se debilita a medida que aumenta la distancia al Sol, al igual que se atenúa la luz del Sol, concluí que esa fuerza debía de ser corpórea[193]. Naturalmente, los planetas prosiguen su movimiento no a causa de una fuerza que irradia desde el Sol, sino más bien porque no hay nada que agote su impulso. Pero se mantienen en sus órbitas y no vagan en medio del espacio interestelar gracias a una fuerza que emana del Sol, la fuerza gravitatoria, de manera que Kepler no se equivocaba del todo. La idea de una fuerza ejercida a distancia iba ganando popularidad en la época, debido en parte a la investigación del magnetismo por parte del presidente del Real Colegio de Cirujanos y médico de la corte de Isabel I, William Gilbert, al que Kepler se remitió. Si por «alma» Kepler había pretendido darle su significado habitual, entonces la transición de una «física» basada en las almas a otra basada en las fuerzas era un paso esencial a la hora de acabar con esa antigua mezcla de religión y ciencia natural.
La Astronomia Nova no se escribió con el ánimo de evitar la polémica. Al utilizar la palabra «física» en el título completo, Kepler lanzaba un reto a la antigua idea, popular entre los seguidores de Aristóteles, de que la astronomía debía preocuparse tan solo de la descripción matemática de las apariencias, mientras que para comprender las cosas de verdad había que volverse hacia la física, es decir, hacia la física de Aristóteles. Kepler estaba afirmando sin ambages que eran los astrónomos como él quienes practicaban la verdadera física. De hecho, gran parte del pensamiento de Kepler estaba inspirado por una idea errónea de la física, la de que el Sol impulsa los planetas en sus órbitas mediante una fuerza similar al magnetismo.
Kepler también desafió a todos los que se oponían a Copérnico. La introducción a la Astronomia Nova contiene el siguiente párrafo:
Advertencia para idiotas. Pero a todo aquel que sea demasiado estúpido para comprender la ciencia astronómica, o demasiado pusilánime para creer a Copérnico sin que afecte a su fe, le aconsejaría que, una vez renunciado a los estudios astronómicos, y tras haber condenado todos aquellos estudios filosóficos que le plazca, se preocupe de sus asuntos y se vaya a su casa a escarbar su terruño [194].
Las primeras leyes de Kepler no tenían nada que decir acerca de la comparación de las órbitas de distintos planetas. Ese hueco se llenó en 1619 en su libro Harmonices mundi, que se conoció como la tercera ley de Kepler[195]: «La razón que existe entre los periodos de dos planetas es exactamente las distancias medias elevadas a 3/2» [196]. Es decir, el cuadrado del periodo sideral de cada planeta (el tiempo que tarda en completar un circuito completo de su órbita) es proporcional al cubo del eje más largo de la elipse. Es decir, que si T es el periodo sideral en años, y a es la mitad de la longitud del eje más largo de la elipse en unidades astronómicas (UA), donde 1 UA se define como la mitad del eje más largo de la órbita de la Tierra, entonces la tercera ley de Kepler afirma que T2/a3 es el mismo para todos los planetas. Puesto que por definición la Tierra tiene un T igual a 1 año y un a igual a 1 UA, en estas unidades T2/a3 sería igual a uno, por lo que, según la ley de Kepler, para todo planeta se ha de cumplir que T2/a3 = 1. La exactitud con la que los valores modernos siguen esta regla aparece en la siguiente tabla:
| Planeta | a (AU) | T (años) | T2/a3 |
| Mercurio | 0,38710 | 0,24085 | 1,0001 |
| Venus | 0,72333 | 0,61521 | 0,9999 |
| Tierra | 1,00000 | 1,00000 | 1,00000 |
| Marte | 1,52369 | 1,88809 | 1,0079 |
| Júpiter | 5,2028 | 11,8622 | 1,001 |
| Saturno | 9,540 | 29,4577 | 1,001 |
(Las desviaciones de la perfecta igualdad de T2/a3 obedecen a los minúsculos efectos de los campos gravitatorios de los propios planetas al actuar entre sí).
Todavía no del todo emancipado del platonismo, Kepler intentó comprender los tamaños de las órbitas, resucitando su anterior uso de los poliedros regulares en Mysterium Cosmographicum. También le dio vueltas a la idea pitagórica de que los distintos periodos planetarios forman una especie de escala musical. Al igual que los demás científicos de su época, Kepler pertenecía solo en parte al nuevo mundo de la ciencia que se estaba gestando, y en parte a la más antigua tradición poética y filosófica.
Las Tablas Rudolfinas se concretaron por fin en 1672. Basadas en la primera y la segunda ley de Kepler, eran mucho más exactas que las Tablas Prusianas anteriores. Las nuevas tablas predecían que habría un tránsito de Mercurio (es decir, que se vería pasar Mercurio por delante del Sol) en 1631. Kepler no lo vio. Al ser protestante, se vio obligado a abandonar la católica Austria, y murió en 1630 en Ratisbona.
La obra de Copérnico y Kepler presentó argumentos en favor de un sistema solar heliocéntrico basado en la simplicidad y la coherencia de las matemáticas más que en una concordancia con la observación. Como hemos visto, las versiones más sencillas de las teorías copernicana y ptolemaica llevaban a cabo las mismas predicciones para los movimientos aparentes del Sol y los planetas, coincidiendo bastante con la observación, mientras que las mejoras de la teoría copernicana introducidas por Kepler podría haberlas introducido Ptolomeo de haber utilizado un ecuante y un excéntrico para el Sol, así como para los planetas, y de haber añadido unos cuantos epiciclos más. La primera observación que favoreció de manera decisiva el heliocentrismo por encima del antiguo sistema ptolemaico la proporcionó Galileo Galilei.
Con Galileo llegamos a uno de los más grandes científicos de la historia, a una categoría que comparte con Newton, Darwin y Einstein. Revolucionó la observación astronómica al introducir y utilizar el telescopio, y su estudio del movimiento proporcionó un paradigma para la moderna física experimental. Además, en un grado único, su carrera científica fue acompañada de gran dramatismo, del que solo tenemos un relato condensado.
Galileo fue un patricio toscano, aunque no rico, nacido en Pisa en 1564, e hijo del teórico musical Vincenzo Galilei. Tras estudiar en un monasterio florentino, se matricula en medicina en la Universidad de Pisa en 1581. Para un estudiante de medicina no es sorprendente que en esa época fuera seguidor de Aristóteles. Galileo pasó de interesarse por la medicina a interesarse por la matemática, y durante una época dio clases de matemáticas en Florencia, la capital de la Toscana. En 1589 Galileo fue llamado de vuelta a Pisa para ocupar la cátedra de matemáticas.
Mientras se encontraba en la Universidad de Pisa, Galileo comenzó a estudiar los cuerpos que caen, y parte de su trabajo lo describió en un libro titulado De Motu (Del movimiento), que nunca publicó. Galileo concluyó, contrariamente a Aristóteles, que la velocidad de un cuerpo que cae no depende de manera apreciable de su peso. Se cuenta que llegó a esa conclusión dejando caer varios pesos desde la torre inclinada de Pisa, aunque no existe ninguna prueba de que fuera así. Mientras estaba en Pisa, Galileo no publicó nada acerca de su trabajo sobre los cuerpos que caen.
En 1591 Galileo se trasladó a Padua para ocupar la cátedra de matemáticas en la universidad, que por entonces era la universidad de la República de Venecia y la más distinguida intelectualmente de Europa. A partir de 1597 consiguió complementar su salario universitario fabricando y vendiendo instrumentos matemáticos utilizados en los negocios y en la guerra.
En 1597 Galileo recibió dos ejemplares del Mysterium Cosmographicum de Kepler, a consecuencia de lo cual le escribió, reconociendo que, al igual que él, era copernicano, aunque todavía no había hecho pública esa opinión. Kepler contestó que Galileo debería salir en defensa de Copérnico, instándole con la frase: «¡Da un paso al frente, oh Galileo!»[197].
Galileo no tardó en entrar en conflicto con los aristotélicos que dominaban la enseñanza de filosofía en Padua, al igual que en el resto de Italia. En 1604 impartió una conferencia sobre la «nueva estrella» observada ese año por Kepler. Al igual que Tycho y Kepler, llegó a la conclusión de que existen cambios en los cielos por encima de la órbita de la Luna. Por ello lo atacó su amigo Cesare Cremonini, profesor de filosofía en Padua. Galileo replicó con un ataque a Cremonini en una obra escrita en un rústico dialecto de Padua, en forma de diálogo entre dos campesinos. El campesino que representa a Cremonini arguye que las reglas habituales de medida no se aplican en los cielos; y el campesino que expresa las opiniones de Galileo replica que los filósofos no saben nada de medidas, y que para ello hay que confiar en los matemáticos, ya sea para medir los cielos o la polenta.
En 1609 comenzó una revolución en el campo de la astronomía, cuando Galileo oyó hablar por primera vez de un nuevo dispositivo holandés conocido como catalejo. Las propiedades de aumento de las esferas de cristal llenas de agua se conocía en la Antigüedad, y por ejemplo las había mencionado el estadista y filósofo romano Séneca. La ampliación había sido estudiada por Al-Haitam, y en 1267 Roger Bacon había escrito acerca de las lentes de aumento en Opus Maius. Con las mejoras en la fabricación del cristal, las lentes de lectura se habían convertido en algo corriente en el siglo XIV. Pero para aumentar de tamaño objetos lejanos es necesario combinar un par de lentes, una para enfocar los rayos paralelos de luz procedentes de cualquier punto sobre el objeto para que converjan, y el segundo para reunir esos rayos de luz, ya sea con una lente cóncava mientras todavía convergen o con una lente convexa en cuanto empiezan a divergir otra vez, y en cualquier caso, enviándolos en direcciones paralelas al ojo. (Cuando el ojo está relajado, el cristalino enfoca rayos paralelos de luz hasta un solo punto en la retina, y la localización de ese punto depende de la dirección de los rayos paralelos). En los Países Bajos, a principios del siglo XVII, se producían catalejos con lentes así dispuestas, y en 1608 varios fabricantes de gafas holandeses solicitaron patentes para sus catalejos. Sus solicitudes fueron rechazadas con el argumento de que el dispositivo ya era ampliamente conocido. Los catalejos pronto se pudieron comprar en Francia e Italia, aunque su capacidad de aumento era solo de tres o cuatro veces el tamaño natural. (Es decir, si las líneas de visión a dos puntos lejanos están separadas por un ángulo pequeño, entonces con esos catalejos parecen estar separadas tres o cuatro veces ese ángulo).
En algún momento de 1609, Galileo oyó hablar del catalejo, y pronto fabricó una versión mejorada, en la que la primera lente era convexa en el lado que daba hacia delante y plana en la parte de atrás, y tenía una larga distancia focal[198], mientras que la segunda era cóncava en el lado encarado a la primera lente y plana en la parte de atrás, y su distancia focal era menor. Con esta disposición, para enviar la luz desde un origen a muy largas distancias en rayos paralelos al ojo, la distancia entre las lentes debe considerarse como la diferencia de las distancias focales, y la ampliación alcanzada es la distancia focal de la primera lente dividida por la distancia focal de la segunda (véase Nota técnica 23). Galileo pronto fue capaz de alcanzar una ampliación de ocho o nueve veces. El 23 de agosto de 1609 enseñó su catalejo al dogo y a los notables de Venecia y les demostró que con él podrían ver los barcos en el mar dos horas antes de que la imagen fuera visible para el ojo humano. El valor de dicho dispositivo para una potencia marítima como Venecia fue evidente. Después de que Galileo donara su catalejo a la República veneciana, su salario como profesor se triplicó y se le garantizó una plaza de por vida. En noviembre Galileo había mejorado la ampliación de su catalejo hasta veinte veces y comenzó a utilizarlo para ver las estrellas.
Con ese catalejo, posteriormente conocido como telescopio, Galileo llevó a cabo seis descubrimientos astronómicos de importancia histórica. El primero lo describió en Siderius Nuncius (El mensajero de las estrellas)[199], publicado en Venecia en marzo de 1610.
1. El 20 de noviembre de 1609, Galileo enfocó su telescopio por primera vez a la luna creciente. En el lado luminoso vio que la superficie era rugosa:
Gracias a ello, cualquiera puede saber con la certeza de los sentidos que la Luna no se halla cubierta por una superficie lisa y pulida, sino áspera y desigual, y que, a la manera de la faz de la Tierra, hállase recubierta por doquier de ingentes prominencias, profundas oquedades y anfractuosidades.En la cara oscura, cerca del terminador, el límite con el lado luminoso, pudo ver manchas de luz, que interpretó como cumbres montañosas iluminadas por el Sol cuando estaba a punto de rebasar el horizonte lunar. A partir de la distancia al terminador de estos puntos luminosos fue capaz de calcular que algunas de estas montañas tenían al menos seis kilómetros de altura (véase Nota técnica 24). Galileo también interpretó la tenue iluminación observada del lado oscuro de la Luna. Rechazó diversas sugerencias de Erasmus Reinhold y de Tycho Brahe en el sentido de que la luz procedía de la Luna misma o de Venus, o de las estrellas, y afirmó con acierto que «esta maravillosa luminosidad» se debe al reflejo del Sol en la Tierra, al igual que la Tierra, de noche, se ve tenuemente iluminada por el Sol que se refleja en la Luna. Así, un cuerpo celeste como la Luna no se vería que era tan diferente desde la Tierra.
2. El catalejo permitió a Galileo observar «una multitud casi inconcebible» de estrellas mucho más tenues que las estrellas de sexta magnitud, demasiado como para que pudieran verse a simple vista. Se comprobó que las seis estrellas visibles de las Pléyades iban acompañadas de más de 40 estrellas distintas, y en la constelación de Orión se distinguieron más de 500 estrellas nunca vistas. Cuando volvió el telescopio hacia la Vía Láctea, comprobó que estaba compuesta de muchas estrellas, tal como había intuido Alberto Magno.
3. Galileo relató que los planetas que había visto con ayuda de su telescopio eran «globos exactamente circulares que parecían pequeñas lunas», pero fue incapaz de discernir que las estrellas fueran así. Por el contrario, descubrió que, aunque las estrellas parecían mucho más brillantes cuando se veían con el telescopio, no parecían sensiblemente más grandes. Su explicación fue confusa. Galileo sabía que el tamaño aparente de las estrellas viene provocado por la curvatura de los rayos de luz en diversas direcciones, debida a fluctuaciones al azar en la atmósfera de la Tierra más que por nada intrínseco a las inmediaciones de las estrellas. Son estas fluctuaciones las que provocan el aparente titilar de las estrellas [200]. Galileo concluyó que, puesto que no era posible discernir la forma de las estrellas con su telescopio, debían de estar mucho más lejos de nosotros que los planetas. Tal como observó posteriormente, esto ayuda a explicar por qué, si la Tierra gira alrededor del Sol, no observamos un paralaje estelar anual.
4. El descubrimiento más espectacular e importante que nos relata en Siderius Nuncius lo llevó a cabo el 7 de enero de 1610. Al enfocar su telescopio sobre Júpiter, Galileo vio «tres pequeñas estrellas colocadas junto al planeta, pequeñas pero muy luminosas». Al principio Galileo pensó que no eran más que tres estrellas fijas más, demasiado tenues para haberse visto antes, aunque le sorprendió que parecieran estar alineadas siguiendo la eclíptica, dos al este de Júpiter y una al oeste. Pero a la noche siguiente estas tres «estrellas» se encontraban al oeste de Júpiter, y el 10 de enero solo pudo ver dos, ambas al este. Finalmente, el 13 de enero vio que eran visibles cuatro de esas «estrellas», más o menos alineadas a lo largo de la eclíptica. Galileo concluyó que Júpiter va acompañado en su órbita de cuatro satélites, similares a la Luna, y que al igual que nuestra Luna, giran más o menos en el mismo plano en forma de órbitas planetarias, que están cerca de la eclíptica, el plano de la órbita de la Tierra alrededor del Sol. (Se las conoce como las cuatro grandes lunas de Júpiter: Ganímedes, Io, Calisto y Europa, llamada así por ser una de las numerosas conquistas amorosas de Zeus (Júpiter en la mitología romana)[201].
Este descubrimiento supuso un gran espaldarazo a la teoría copernicana. Para empezar, el sistema de Júpiter y sus lunas proporciona un ejemplo en miniatura de lo que Copérnico había concebido como el sistema del Sol y sus planetas: cuerpos celestes moviéndose en torno a un cuerpo que no era la Tierra. Además, el ejemplo de las lunas de Júpiter enterró la objeción de Copérnico según la cual, si la Tierra se movía, ¿por qué la Luna no quedaba rezagada? Todo el mundo estaba de acuerdo en que Júpiter se movía, y sin embargo era evidente que las lunas no quedaban rezagadas.
Aunque los resultados llegaron demasiado tarde para quedar incluidos en Siderius Nuncius, a finales de 1611 Galileo había medido los periodos orbitales de los cuatro satélites de Júpiter que había descubierto, y en 1612 publicó sus resultados en la primera página de una obra sobre otros asuntos [202]. Presentamos los resultados de Galileo junto a los valores actuales en días (d), horas (h) y minutos (m) en la tabla inferior:
| Satélite jupiteriano | Período (Galileo) | Período (moderno) |
| Io | 1d 18h 30m | 1d 18h 29m |
| Europa | 3d 13h 20m | 3d 13h 18m |
| Ganímides | 7d 4h | 7d 4h 0m |
| Calisto | 16d 18h | 16d 18h 5m |
La exactitud de las medidas de Galileo da fe de sus concienzudas observaciones y su preciso cronometraje [203].
Galileo dedicó Siderius Nuncius a su antiguo alumno Cosme II de Médici, que ahora era el gran duque de Toscana, y a los cuatro acompañantes de Júpiter los llamó las «estrellas mediceas». Fue un cumplido calculado. Galileo cobraba un buen salario en Padua, pero le habían dicho que no se lo volverían a aumentar. Además, para ganarse ese salario tenía que dar clases, lo que le robaba tiempo para sus investigaciones. Llegó a un acuerdo con Cosme, que le nombró matemático y filósofo de la corte, y le asignó una cátedra en Pisa sin ninguna responsabilidad docente. Galileo insistió en el título de «filósofo de la corte», pues, a pesar de los apasionantes avances llevados a cabo en la astronomía por matemáticos como Kepler, y a pesar de los argumentos de profesores como Clavius, los matemáticos seguían teniendo una posición inferior a la de los filósofos. Además, Galileo deseaba que su trabajo se tomara en serio, como parte de esa disciplina que los filósofos llamaban «física», una explicación de la naturaleza del Sol, la Luna y los planetas, no solo una explicación matemática de las apariencias.
En el verano de 1610, Galileo abandonó Padua rumbo a Florencia, una decisión que con el tiempo resultó ser desastrosa. Padua se hallaba en el territorio de la República de Venecia, donde en aquella época la influencia vaticana era mucho menor que en cualquier otro estado de Italia, pues había resistido con éxito un interdicto papal años antes de la marcha de Galileo. El traslado a Florencia provocó que Galileo fuera mucho más vulnerable al control de la Iglesia. Cualquier decano de la universidad de entonces podría considerar que ese peligro no era más que un justo castigo a Galileo por eludir sus deberes docentes. Pero de momento, la llegada del castigo quedó postergada.
5. En septiembre de 1610, Galileo llevó a cabo el quinto de sus grandes descubrimientos astronómicos. Enfocó su telescopio hacia Venus y descubrió que tenía fases, como las de la Luna. Le mandó a Kepler un mensaje en clave: «La Madre del Amor [Venus] emula las formas de Cynthia [la Luna]». La existencia de fases sería de esperar tanto en la teoría ptolemaica como en la copernicana, pero las fases serían distintas. En la teoría ptolemaica, Venus se encuentra siempre más o menos entre la Tierra y el Sol, por lo que nunca podemos ver su fase llena. En la teoría copernicana, por otro lado, Venus está completamente iluminado cuando se halla al otro lado de su órbita desde la Tierra.
Esa fue la primera prueba directa de que la teoría ptolemaica era errónea. Recordemos que, según la teoría ptolemaica, el movimiento solar y el planetario, observado desde la Tierra, se ve igual que en la teoría copernicana, sea cual sea el deferente que escojamos para cada planeta. Pero no se ve igual si lo observamos desde cada planeta. Naturalmente, Galileo no podía ir a los planetas para ver qué aspecto tenían desde allí los movimientos del Sol y de los demás planetas. Pero las fases de Venus le revelaron la dirección del Sol visto desde ese planeta: la cara iluminada es la que da al Sol. Solo un caso especial de la teoría ptolemaica nos revelaría ese dato correctamente: que los deferentes de Venus y Mercurio fueran idénticos a la órbita del Sol, que, como ya se ha observado, es exactamente la teoría de Tycho. Esta versión nunca fue adoptada por Ptolomeo ni por ninguno de sus seguidores.
6. Después de regresar a Florencia, Galileo descubrió una ingeniosa manera de estudiar la cara del Sol: a través de un telescopio para proyectar su imagen sobre una pantalla. Gracias a ello consiguió su sexto descubrimiento: ver unas manchas oscuras que se movían a través del Sol. Sus resultados se publicaron en 1613 en Cartas sobre las manchas solares.
Hay momentos en la historia en los que una nueva tecnología abre enormes posibilidades para la ciencia pura. En el siglo XIX, la mejora de las bombas de vacío posibilitó experimentos sobre las descargas eléctricas en tubos en los que se había hecho el vacío que condujeron al descubrimiento del electrón. El perfeccionamiento de las emulsiones fotográficas por parte de la Ilford Corporation permitió el descubrimiento de gran cantidad de nuevas partículas elementales en la década posterior a la Segunda Guerra Mundial. El desarrollo del radar de microondas durante esa misma guerra permitió que las microondas se utilizaran para investigar los átomos, lo que en 1947 permitió poner a prueba de manera decisiva la electrodinámica cuántica. Y no deberíamos olvidarnos del gnomon. Pero ninguna de estas nuevas tecnologías condujo a resultados científicos tan impresionantes como los que se obtuvieron a partir del uso del telescopio por parte de Galileo.
Las reacciones ante los descubrimientos de Galileo oscilaron entre la cautela y el entusiasmo. El antiguo adversario de Galileo en Padua, Cesare Cremonini, se negó a mirar por el telescopio, al igual que Giulio Libri, profesor de filosofía en Pisa. Por otro lado, Galileo fue elegido miembro de la Academia Linceana, fundada unos años antes y que fue la primera academia científica europea. Kepler utilizó un telescopio que le mandó Galileo y confirmó los descubrimientos de este. (Kepler elaboró la teoría del telescopio y pronto inventó su propia versión, con dos lentes convexas).
Al principio Galileo no tuvo problemas con la Iglesia, quizá porque su apoyo a Copérnico todavía no era explícito. En Siderius Nuncius apenas lo menciona una vez, y ya hacia el final, en relación con la cuestión de por qué, si la Tierra se mueve, no deja a la Luna rezagada. En aquella época no era Galileo, sino los aristotélicos como Cremonini. quienes tenían problemas con la Inquisición de Roma, en gran parte por los mismos motivos que condujeron a la condena de varios principios aristotélicos en 1277. Pero Galileo consiguió enfrentarse tanto a los jesuitas como a los filósofos aristotélicos, lo que a la larga no le hizo ningún bien.
En julio de 1611, poco después de ocupar su nuevo puesto en Florencia, Galileo entabló un debate con los filósofos que, siguiendo lo que imaginaban era una doctrina de Aristóteles, argumentaban que el hielo sólido tenía un densidad (peso por volumen) mayor que el agua líquida. El cardenal jesuita Roberto Bellarmine, que había formado parte del tribunal de la Inquisición que había condenado a muerte a Giordano Bruno, se puso de parte de Galileo, con el argumento de que, puesto que el hielo flota, ha de ser menos denso que el agua. En 1612, Galileo publicó sus conclusiones acerca de los cuerpos que flotan en su Discurso sobre los cuerpos flotantes[204].
En 1613 Galileo se enfrentó a los jesuitas, entre los que se contaba Christoph Scheiner, en una discusión sobre el tema de la astronomía periférica: las manchas solares, ¿tienen que ver con el Sol mismo? ¿Se trata, como pensaba Galileo, de nubes que están justo encima de su superficie, lo que proporcionaría un ejemplo (como las montañas de la Luna) de la imperfección de los cuerpos celestes? ¿O son pequeños planetas que dan vueltas alrededor del Sol más cercanos que Mercurio? Si se pudiera determinar que son nubes, entonces aquellos que afirmaban que el Sol gira alrededor de la Tierra no podrían afirmar que las nubes de la Tierra quedarían atrás si esta girara alrededor del Sol. En sus Cartas sobre las manchas solares de 1613, Galileo argumentó que las manchas solares parecen estrecharse a medida que se acercan al borde del disco solar, y cerca de este borde se ven oblicuas, de lo que se deducía que al girar eran arrastradas por la superficie del Sol. También despertó polémica quién fue el primero en descubrir las manchas solares, aunque ese no fue más que otro episodio del conflicto cada vez más acusado con los jesuitas, en el que la injusticia no estuvo siempre del mismo bando[205]. Lo más importante para el futuro fue que Galileo, en sus Cartas sobre las manchas solares, por fin defendió públicamente a Copérnico.
El conflicto de Galileo con los jesuitas se intensificó con la publicación en 1623 de El ensayador, un ataque contra el matemático jesuita Orazio Grassi por la conclusión perfectamente correcta de este, en concordancia con Tycho, de que la falta de paralaje diurno demuestra que los cometas están más allá de la órbita de la Luna. Por el contrario, Galileo presentó una peculiar teoría: la de que los cometas son reflejos de la luz del Sol procedente de perturbaciones lineales de la atmósfera, y que no muestran paralaje diurno porque las perturbaciones se mueven con la Tierra a medida que esta gira. Quizá el auténtico enemigo de Galileo no era Orazio Gras, sino Tycho Brahe, que había presentado una teoría geocéntrica de los planetas que entonces la observación no podía refutar.
En aquellos años todavía era posible que la Iglesia tolerara el sistema copernicano como un mecanismo puramente matemático para calcular los movimientos aparentes de los planetas, aunque no como una teoría de la verdadera naturaleza de los planetas y sus movimientos. Por ejemplo, en 1615 Bellarmine le escribió al monje napolitano Paolo Antonio Foscarini para tranquilizarlo y advertirle acerca de su defensa del sistema copernicano:
Tengo la impresión de que Su Reverencia y el Signor Galileo obrarían con prudencia si se contentaran con hablar de manera hipotética y no absoluta, como siempre he creído que había hablado Copérnico. [¿Acaso el prefacio de Osiander había engañado a Bellarmine? A Galileo desde luego que no]. Decir que al asumir que la Tierra se movía y el Sol permanecía inmóvil salvaba las apariencias mejor que los excéntricos y los epiciclos era algo sin duda acertado. [Bellarmine al parecer no comprendía que Copérnico, al igual que Ptolomeo, había utilizado epiciclos, solo que no tantos]. Esto no entraña ningún peligro y es suficiente para el matemático. Pero pretender afirmar que el Sol de verdad permanece inmóvil en el centro del mundo, que gira solo sobre sí mismo sin ir de este a oeste, y que la Tierra está situada en el tercer cielo y gira muy rápidamente en torno al Sol, eso es algo muy peligroso. No solo podría irritar a todos los filósofos y teólogos escolásticos, también podría perjudicar la fe y pretender que las Sagradas Escrituras son falsas[206].Al ver el debate que se estaba generando sobre el copernicanismo, en 1615 Galileo escribió una celebrada carta acerca de la relación entre ciencia y religión a Cristina de Lorena, gran duquesa de Toscana, a cuyo matrimonio con el difunto gran duque Fernando I había asistido Galileo [207]. Tal como Copérnico había afirmado en De Revolutionibus, Galileo mencionó el rechazo de la forma esférica de la tierra por parte de Lactancio como un terrible ejemplo del uso de las Sagradas Escrituras para contradecir los descubrimientos de la ciencia. También criticó la interpretación literal del texto del Libro de Josué que Lutero había invocado contra Copérnico para demostrar el movimiento del Sol. Galileo razonó que la Biblia nunca pretendió ser un texto de astronomía, puesto que de los cinco planetas solo menciona Venus, y apenas un par de veces. El fragmento más famoso de la carta a Cristina dice así: «Me gustaría afirmar aquí lo que le escuché decir a un eclesiástico de la más alta jerarquía: "Que la intención del Espíritu Santo es enseñarnos a ir al cielo, no cómo va el cielo"». (Una nota marginal de Galileo indicaba que ese eminente eclesiástico era el erudito cardenal César Baronio, director de la biblioteca vaticana). Galileo también ofreció la interpretación de la afirmación de Josué, según la cual el Sol se había detenido: fue la rotación del Sol, revelada a Galileo por el movimiento de las manchas solares, lo que se había detenido, deteniendo a su vez el movimiento orbital y la rotación de la Tierra y los demás planetas, lo que, como se describe en la Biblia, prolongó el día de la batalla. No está claro si Galileo realmente creía este absurdo o simplemente buscaba protección política.
En contra del consejo de sus amigos, en 1615 Galileo fue a Roma para declarar en contra de la supresión del copernicanismo. El papa Paulo V no deseaba de ninguna manera alimentar la controversia y, siguiendo el consejo de Bellarmine, decidió someter la teoría copernicana a un comité de teólogos. El veredicto fue que el sistema copernicano es «necio y absurdo en Filosofía, y formalmente herético en la medida en que contradice la postura expresa de las Sagradas Escrituras en muchos fragmentos»[208].
En febrero de 1616 Galileo tuvo que presentarse ante la Inquisición, donde recibió dos órdenes confidenciales. Un documento firmado le ordenaba no sostener y defender el copernicanismo. Un documento sin firmar iba más allá, y le ordenaba no sostener, defender ni enseñar el copernicanismo de ninguna manera. En marzo de 1616 la Inquisición publicó un edicto público en el que no se mencionaba a Galileo, pero se prohibía el libro de Foscarini, y se exigía que las obras de Copérnico se expurgaran. De Revolutionibus se incluyó en el Índice de libros prohibidos a los católicos. En lugar de regresar a Ptolomeo o a Aristóteles, algunos astrónomos católicos, como el jesuita Giovanni Battista Riccioli, en su Almagestum Novum de 1651, se pronunció en favor del sistema de Tycho, que por entonces no se podía refutar mediante la observación. De Revolutionibus permaneció en el Índice hasta 1835, malogrando la enseñanza de la ciencia en algunos países católicos, como por ejemplo España.
Galileo pensó que las cosas mejorarían a partir de 1624, cuando Maffeo Barberini se convirtió en el papa Urbano VIII. Barberini fue un florentino admirador de Galileo, al que recibió en Roma y le concedió media docena de audiencias. En esas conversaciones Galileo le explicó su teoría de las mareas, en la que había estado trabajando antes de 1616.
La teoría de Galileo se basaba sobre todo en el movimiento de la Tierra. De hecho, la idea era que las aguas de los océanos se agitan adelante y atrás con la rotación de la Tierra mientras esta da vueltas alrededor del Sol. Durante este movimiento, la velocidad neta de cualquier punto sobre la superficie de la Tierra en la dirección del movimiento de esta en su órbita aumenta y disminuye continuamente. Esto pone en marcha una onda oceánica periódica cuyo periodo es de un día y, como ocurre con cualquier otra oscilación, hay armónicos, con periodos de medio día, un tercio de día, etcétera. De este modo, se excluía cualquier influencia de la Luna, pero desde la Antigüedad era sabido que la marea más alta o pleamar tiene lugar en la luna llena y nueva, mientras que la marea más baja o bajamar se da a veces en cuarto creciente o decreciente. Galileo intentó explicar la influencia de la Luna suponiendo que, por alguna razón, la velocidad orbital de la Tierra aumenta durante la luna nueva, cuando esta se halla entre el Sol y la Tierra, y disminuye en la luna llena, cuando esta se halla al otro lado de la Tierra desde el punto de vista del Sol.
No fue la afirmación más acertada de Galileo. Tampoco es que su teoría fuera errónea. Sin una teoría de la gravitación no había manera de que Galileo comprendiera correctamente las mareas, aunque debería haber sabido que una teoría especulativa de las mareas que no contara con un sostén empírico importante no podía tenerse en cuenta como verificación del movimiento de la Tierra.
El Papa dijo que permitiría la publicación de su teoría de las mareas si Galileo consideraba el movimiento de la Tierra como una hipótesis matemática, no como algo que tuviera que ser cierto. Urbano explicó que no aprobaba el edicto público de la Inquisición de 1616, pero que tampoco estaba dispuesto a derogarlo. En estas conversaciones Galileo no le mencionó al Papa las órdenes que la Inquisición le había impartido en privado.
En 1632 Galileo estaba a punto de publicar su teoría de las mareas, que se había acabado convirtiendo en una defensa global del copernicanismo. De momento, la Iglesia no había hecho pública ninguna crítica a Galileo, de manera que cuando solicitó al obispo local permiso para publicar un nuevo libro, le fue concedido. Se trataba de sus Diálogos (Diálogos sobre los dos sistemas principales del mundo: el ptolemaico y el copernicano).
El título del libro de Galileo es peculiar. En aquella época no había dos, sino cuatro sistemas principales del mundo: además del ptolemaico y el copernicano, estaban el aristotélico, basado en esferas homocéntricas que giraban alrededor de la Tierra, y el de Tycho, en el que el Sol y la Luna giraban en torno a una Tierra estacionaria, aunque todos los demás planetas giraban alrededor del Sol. ¿Por qué Galileo ni siquiera tuvo en cuenta el sistema aristotélico y el de Tycho?
En relación con el sistema aristotélico, podemos decir que no coincidía con la observación, aunque eso se había sabido durante dos mil años, lo que no le había hecho perder partidarios. No hay más que recordar el argumento de Fracastoro a comienzos del siglo XVI, citado en el capítulo 10. Un siglo más tarde, era evidente que Galileo consideraba que no merecía la pena contestar a esos argumentos, aunque no está claro cómo llegó a esa conclusión.
Por otra parte, el sistema de Tycho funcionaba demasiado bien para descartarlo de un plumazo, y no hay duda de que Galileo lo conocía. Es posible que pensara que su propia teoría de las mareas demostraba que la Tierra se mueve, aunque no hubiera datos cuantitativos que la sustentaran. O quizá Galileo simplemente no quería que Copérnico compitiera con el formidable Tycho.
Los Diálogos consistían en una conversación entre tres personajes: Salviati, que representaba a Galileo y se llama así por un amigo de este, el noble florentino Filippo Salviati; Simplicio, un aristotélico al que se llama así quizá por Simplicio (y quizá porque se pretendía que representara a un simplón); y Sagredo, llamado así por Francesco Sagredo, el matemático veneciano y amigo de Galileo, para que con su sabiduría juzgara quién tenía razón. En los primeros tres días de la conversación Salviati desmonta los argumentos de Simplicio, y las mareas no aparecen hasta el cuarto día. Aquello sin duda violaba el edicto sin firmar que la Inquisición había entregado a Galileo, y posiblemente también el edicto firmado menos estricto (que no sostuviera ni defendiera el copernicanismo). Para empeorar aún más las cosas, los Diálogos estaban en italiano y no en latín, de manera que cualquier italiano instruido, y no solo los eruditos, podía leerlos.
Fue en ese momento cuando al papa Urbano le enseñaron el edicto sin firmar de la Inquisición de 1616 (quizá fueron los enemigos que Galileo había acumulado en las anteriores polémicas sobre las manchas solares y los cometas). La cólera de Urbano puede que se viera incrementada por la sospecha de que el personaje de Simplicio se basaba en él. Tampoco ayudó que algunas de las palabras del Papa cuando era cardenal aparecieran en boca de Simplicio. La Inquisición prohibió la venta de los Diálogos, pero era demasiado tarde: el libro ya se había agotado.
Galileo fue juzgado en abril de 1633. La acusación se centraba en su violación de los delitos de la Inquisición de 1616. A Galileo le enseñaron los instrumentos de tortura e intentó llegar a un acuerdo, admitiendo que su vanidad personal lo había llevado demasiado lejos, aunque de todos modos fue condenado a prisión perpetua bajo «vehemente sospecha de herejía», y obligado a abjurar de su opinión de que la Tierra se movía alrededor del Sol. (Según una historia apócrifa, cuando Galileo abandonó el tribunal, murmuró en voz baja: «Eppur si muove», es decir: «Y sin embargo, se mueve»).
Por suerte, a Galileo no se le trató con toda la dureza que podría haber recibido. Se le permitió iniciar su periodo de cárcel como invitado del arzobispo de Siena, y luego proseguirlo en su propia villa de Arcetri, cerca de Florencia y en la proximidad de la residencia-convento de sus hijas, la hermana Maria Celeste y la hermana Arcángela[209]. Como veremos en el capítulo 12, durante esos años Galileo pudo seguir trabajando en el problema del movimiento, iniciado medio siglo antes en Pisa.
Galileo murió en 1642 mientras todavía estaba bajo arresto domiciliario en Arcetri. No fue hasta 1835 cuando los libros que, como el de Galileo, defendían el sistema copernicano, fueron eliminados del Índice de libros prohibidos por la Iglesia católica, aunque mucho antes la astronomía copernicana había sido ampliamente aceptada en casi todos los países católicos, y también en los protestantes. En el siglo XX Galileo fue rehabilitado por la Iglesia [210]. En 1979 el papa Juan Pablo II se refirió a la Carta a Cristina de Galileo, afirmando que había «formulado importantes normas de carácter epistemológico que resultan indispensables para reconciliar las Sagradas Escrituras y la ciencia»[211]. Se convocó una comisión para estudiar el caso de Galileo, que concluyó que, en su época, la Iglesia se había equivocado. El Papa contestó: «El error de los teólogos de su tiempo, mientras mantenían la centralidad de la Tierra, fue considerar que nuestra comprensión de la estructura del mundo físico quedaba impuesta, en cierta manera, por el sentido literal de las Sagradas Escrituras»[212].
Mi opinión es que esto es del todo insuficiente. La Iglesia por supuesto no puede eludir un conocimiento (que ahora es vox populi) ni dejar de reconocer que se equivocó sobre el movimiento de la Tierra. Pero supongamos que las opiniones astronómicas de la Iglesia hubieran sido correctas y las de Galileo equivocadas. Aun así, la Iglesia obró mal condenando a Galileo a prisión y negándole el derecho a publicar, al igual que había obrado mal al quemar a Giordano Bruno, aunque fuera un hereje[213]. Por suerte, aunque no sé si esto ha sido explícitamente reconocido por la Iglesia, hoy no son concebibles este tipo de acciones. Con la excepción de aquellos países islámicos que castigan la blasfemia o la apostasía, el mundo en general ha aprendido la lección de que los gobiernos y las autoridades religiosas no pueden imponer castigos penales por opiniones religiosas, sean ciertas o falsas.
A partir de los cálculos y observaciones de Copérnico, Tycho Brahe, Kepler y Galileo, se había esgrimido una descripción correcta del sistema solar, codificada en las tres leyes de Kepler. La explicación de por qué los planetas obedecen estas leyes tuvo que esperar una generación, hasta la llegada de Newton.
Capítulo 12
Comienzan los experimentos
En cierto sentido, la gente siempre ha experimentado, utilizando la prueba y error a fin de descubrir maneras de hacer cosas, desde fundir la mena a cocer pasteles. Cuando hablamos del inicio de la experimentación, me refiero tan solo a experimentos llevados a cabo para descubrir o poner a prueba teorías generales acerca de la naturaleza.
En este sentido, no es posible ser muy preciso acerca del comienzo de la experimentación [214]. Es posible que Arquímedes hubiera puesto a prueba su teoría hidrostática de manera experimental, pero su tratado De los cuerpos flotantes seguía el estilo puramente deductivo de las matemáticas, y no hay ningún indicio de que utilizara la experimentación. Herón y Ptolomeo llevaron a cabo experimentos para poner a prueba sus teorías de la reflexión y la refracción, pero su ejemplo no fue seguido hasta siglos más tarde.
En el siglo XVII, apareció una novedad en la experimentación: el deseo de utilizar públicamente los resultados para juzgar la validez de las teorías físicas. Esto lo encontramos a principios de dicho siglo en los estudios de hidrostática, como se ve en el Discurso sobre los cuerpos flotantes de 1612. Más importante fue el estudio cuantitativo del movimiento de los cuerpos que caen, requisito esencial del trabajo de Newton. Fue su trabajo sobre este problema, y también sobre la naturaleza de la presión del aire, lo que marcó el verdadero comienzo de la física experimental moderna.
Como muchas otras cosas, el estudio experimental del movimiento comienza con Galileo. Sus conclusiones acerca del movimiento aparecieron en los Diálogos sobre dos nuevas ciencias, acabado en 1635, cuando estaba bajo arresto domiciliario en Arcetri. La publicación fue prohibida por la Congregación del Índice de la Iglesia, pero algunos ejemplares salieron clandestinamente de Italia. En 1638 el libro se publicó en la ciudad universitaria protestante de Leiden, con la firma de Louis Elzevir. Los protagonistas de Dos nuevas ciencias vuelven a ser Salviati, Simplicio y Sagredo, que interpretan los mismos papeles que antes.
Entre muchas otras cosas, el «Primer día» de Dos nuevas ciencias afirma que los cuerpos pesados y ligeros caen a la misma velocidad, contradiciendo la doctrina de Aristóteles de que los cuerpos pesados caen más deprisa que los ligeros. Naturalmente, por culpa de la resistencia del aire, los cuerpos ligeros caen un poco más despacio que los pesados. Al enfrentarse a este problema, Galileo demuestra que comprende la necesidad de los científicos de conformarse con aproximaciones, oponiéndose a las afirmaciones exactas basadas en una matemática rigurosa tan del gusto de los griegos. Tal como Salviati le explica a Simplicio[215]:
Aristóteles dice: «Una bola de hierro de cien libras que cae de la altura de cien codos llega antes que una de una libra que haya descendido un solo codo». Yo digo que llegan al mismo tiempo. Vos encontraréis, al hacer la experiencia, que la mayor se anticipa en dos dedos a la menor, es decir, que cuando la mayor choca en tierra la otra está alejada dos dedos. Ahora bien, quisierais esconder tras estos dos dedos los noventa y nueve codos de Aristóteles y hablando de mi error mínimo pasar en silencio ese otro tan enorme.Galileo también demuestra que el aire posee un peso positivo; calcula su densidad; comenta el movimiento a través de la resistencia del medio; explica la armonía musical; y nos informa del hecho de que las oscilaciones de un péndulo poseen la misma duración, sea cual sea la amplitud de las oscilaciones [216]. Este es el principio que décadas más tarde conduciría a la invención de los relojes de péndulo y a la medida exacta de la velocidad de aceleración de los cuerpos que caen.
El «Segundo día» de Dos nuevas ciencias aborda la fuerza de los cuerpos de diversas formas. Hasta el «Tercer día» Galileo no regresa al problema del movimiento y lleva a cabo su contribución más importante. Inicia el «Tercer día» considerando algunas propiedades triviales del movimiento uniforme, y a continuación pasa a definir la aceleración uniforme siguiendo más o menos las mismas directrices que la definición del Merton College del siglo XIV: la velocidad aumenta en cantidades iguales a cada intervalo igual de tiempo. Galileo también prueba el teorema de la velocidad media, más o menos siguiendo la prueba de Oresme, aunque en ningún momento se refiere a este ni a los profesores de Merton. Contrariamente a sus predecesores medievales, Galileo va más allá del teorema matemático y aduce que los cuerpos que caen libremente sufren una aceleración uniforme, pero se niega a investigar la causa de esta aceleración.
Como ya se han mencionado en el capítulo 10, en la época había una alternativa a la teoría de que los cuerpos caen con una aceleración uniforme que contaba con un amplio respaldo. Según esta otra opinión, la velocidad que adquieren los cuerpos que caen libremente en cualquier intervalo de tiempo es proporcional a la distancia recorrida en ese intervalo, no al tiempo[217]. Galileo presenta varios argumentos en contra de esta teoría[218], pero el veredicto en relación a estas diferentes teorías de la aceleración de los cuerpos que caen tenía que proceder de la experimentación.
Si la distancia recorrida desde la posición de reposo es igual (según el teorema de la velocidad media) a la mitad de la velocidad alcanzada por el tiempo transcurrido, y si esa velocidad es proporcional a ese tiempo transcurrido, la distancia recorrida en caída libre debería ser proporcional al cuadrado del tiempo (véase Nota técnica 25). Esto es lo que Galileo se proponía verificar.
Los cuerpos que caen se mueven demasiado rápidamente para que Galileo pudiera alcanzar esa conclusión viendo lo lejos que llega un cuerpo que cae en un intervalo determinado de tiempo, por lo que se le ocurrió ralentizar la caída estudiando unas bolas que rodaban por un plano inclinado. Para que los resultados fueran relevantes tuvo que demostrar que el movimiento de una bola que rueda por un plano inclinado guarda relación con el de un cuerpo que cae libremente. Lo hizo observando que la velocidad que alcanza una bola después de rodar por un plano inclinado depende tan solo de la distancia vertical que la bola ha recorrido, no del ángulo de inclinación del plano[219]. Una bola que cae libremente se puede considerar como una que rueda por un plano vertical, y así, si la velocidad con la que rueda una bola por un plano inclinado es proporcional al tiempo transcurrido, entonces lo mismo debería ser cierto de una bola que cae libremente. En el caso de un plano inclinado en un ángulo pequeño, la velocidad es, naturalmente, mucho menor que la velocidad de un cuerpo que cae libremente (esta es la gracia de utilizar un plano inclinado), pero las dos velocidades son proporcionales, y también la distancia recorrida a lo largo del plano es proporcional a la distancia que habría recorrido en el mismo tiempo un cuerpo que cayera libremente.
En Dos nuevas ciencias Galileo nos dice que la distancia a recorrida es proporcional al cuadrado del tiempo. Galileo había llevado a cabo estos experimentos en Padua en 1603 con un plano de menos de 2° de ángulo con la horizontal, en el que había trazado líneas que señalaban intervalos de más o menos un milímetro[220]. Calculó el tiempo mediante la igualdad de los intervalos entre unos sonidos emitidos cuando la bola alcanzaba las señales en su trayectoria, cuyas distancias desde el punto de partida estaban en la proporción de
12 = 1
22 = 4
32 = 9…
Galileo ya había considerado la aceleración de los cuerpos que caen en la obra comentada en el capítulo 11, Diálogos sobre los dos sistemas principales del mundo: el ptolemaico y el copernicano. En el «Segundo día» de este Diálogo anterior, Salviati afirma que la distancia recorrida es proporcional al cuadrado del tiempo, aunque la explicación resulta confusa. También menciona que una bola de cañón que se dejara caer desde una altura de 100 codos alcanzaría el suelo en 5 segundos. Está bastante claro que Galileo no lleva a cabo la medición del tiempo de este experimento[222], sino que lo presenta tan solo como un ejemplo ilustrativo. Si tomamos la longitud de un codo como 53,75 centímetros, entonces, utilizando el valor moderno de aceleración debida a la gravedad, el tiempo necesario para que un cuerpo pesado caiga cien codos es de 3,3 segundos, no de 5. Pero al parecer, Galileo nunca intentó en serio medir la aceleración debida a la gravedad.
El «Cuarto día» de los Diálogos sobre dos nuevas ciencias aborda la trayectoria de los proyectiles. Las ideas de Galileo se basaban en gran medida en un experimento que realizó en 1608[223] (comentado en detalle en la Nota técnica 26). A una bola se le permite rodar por un plano inclinado desde diversas alturas iniciales, a continuación rueda por la mesa horizontal sobre la que se ha colocado el plano inclinado y finalmente es lanzada al vacío desde el borde de la mesa. Al medir la distancia recorrida cuando la bola toca el suelo, y mediante la observación de la trayectoria de la bola en el aire, Galileo concluyó que la trayectoria es una parábola. No describe este experimento en Dos nuevas ciencias, sino que nos explica de manera teórica por qué es una parábola. El punto crucial, que resultaría esencial en la mecánica de Newton, es que cada componente del movimiento del proyectil se ve sometido por separado al componente correspondiente de la fuerza que actúa sobre el proyectil en su totalidad. En cuanto el proyectil cae del borde de la mesa o sale disparado de un cañón, ya no existe nada más que la resistencia del aire para cambiar su movimiento horizontal, por lo que la distancia recorrida es prácticamente proporcional al tiempo transcurrido. Por otro lado, en el mismo periodo de tiempo, como cualquier cuerpo que cae libremente, el proyectil sufre una aceleración hacia abajo, de manera que la distancia vertical que recorre al caer es proporcional al cuadrado del tiempo transcurrido. De ello se sigue que la distancia vertical al caer es proporcional al cuadrado de la distancia horizontal recorrida. ¿Qué tipo de curva posee esta propiedad? Galileo nos muestra que el recorrido del proyectil es una parábola, utilizando la definición de Apolonio de que la parábola es la intersección de un cono con un plano paralelo a la superficie del cono (véase Nota técnica 26).
Los experimentos descritos en Dos nuevas ciencias suponen una ruptura histórica con el pasado. En lugar de limitarse al estudio de la caída libre, que Aristóteles había considerado como un movimiento natural, Galileo dirigió su atención a los movimientos artificiales de bolas constreñidas a rodar por un plano inclinado o proyectiles lanzados hacia arriba. En este sentido, el plano inclinado de Galileo es un antepasado lejano del acelerador de partículas actual, con el que de manera artificial creamos partículas que no se encuentran en la naturaleza.
El trabajo sobre el movimiento llevado a cabo por Galileo lo continuó Christiaan Huygens, quizá la figura más impresionante de la brillante generación situada entre la de Galileo y la de Newton. Huygens nació en 1629 en una familia de funcionarios de alto rango que habían trabajado en la administración de la República holandesa bajo la Casa de Orange. Entre 1645 y 1647 estudió leyes y matemáticas en la Universidad de Leiden, pero luego se dedicó a tiempo completo a las matemáticas y posteriormente a las ciencias naturales. Al igual que Descartes, Pascal o Boyle, Huygens fue un erudito y se interesó por una amplia variedad de problemas matemáticos, astronómicos, estadísticos, hidrostáticos, dinámicos y ópticos.
La obra astronómica más importante de Huygens fue su estudio telescópico del planeta Saturno. En 1655 descubrió su luna más grande, Titán, revelando así que no solo la Tierra y Júpiter tenían satélites. También explicó que el peculiar aspecto no circular de Saturno, ya observado por Galileo, se debe a los anillos que rodean el planeta.
En 1656-1657 Huygens inventó el reloj de péndulo. Se basaba en la observación de Galileo de que, en un péndulo, el tiempo de cada oscilación es independiente de la amplitud de esta. Huygens reconoció que ello es cierto solo en el límite de oscilaciones muy pequeñas, y encontró una manera ingeniosa de procurar que el tiempo fuera independiente de la amplitud incluso en el caso de oscilaciones de amplitud apreciable. Mientras que los relojes mecánicos anteriores adelantaban o atrasaban unos cinco minutos al día, el reloj del péndulo de Huygens por lo general no adelantaba ni atrasaba más de diez segundos al día, y uno de ellos tan solo atrasaba medio segundo por día[224].
A partir del periodo del reloj de un péndulo de una amplitud determinada, al año siguiente Huygens fue capaz de inferir el valor de la aceleración de los cuerpos que caen libremente cerca de la superficie de la Tierra. En el Horologium oscillatorium —publicado posteriormente, en 1673—, Huygens fue capaz de demostrar que «el tiempo de una pequeña oscilación está relacionado con el tiempo de la caída perpendicular de la mitad de la altura del péndulo, al igual que la circunferencia de un círculo está relacionada con su diámetro»[225]. Es decir, el tiempo que tarda un péndulo en recorrer un pequeño ángulo de un lado al otro es igual a π por el tiempo que tarda un cuerpo en caer a una distancia igual a la mitad de la longitud del péndulo. (No es un resultado fácil de obtener tal como lo hizo Huygens, sin cálculo matemático). Utilizando este principio, y midiendo los periodos del péndulo de diversas longitudes, fue capaz de calcular la aceleración debida a la gravedad, algo que Galileo no pudo medir con exactitud con los medios de que disponía. Tal como lo expresó Huygens, un cuerpo que cae libremente recorre 151/12 «pies de París» en el primer segundo. La variación estimada del pie de París con el moderno pie inglés oscila entre 1,06 y 1,08; si consideramos que un pie de París es igual a 1,07 pies ingleses, entonces el resultado de Huygens es que un cuerpo que cae libremente cae 16,1 pies en el primer segundo, lo que implica una aceleración de 32,2 pies por segundo al cuadrado, lo que concuerda perfectamente con el moderno valor estándar de 32,17 pies por segundo al cuadrado. (Como buen experimentador, Huygens comprobó que la aceleración de los cuerpos que caen queda dentro del error experimental de la aceleración que había inferido a partir de sus observaciones de los péndulos). Como veremos, esta medición, repetida posteriormente por Newton, resultó esencial a la hora de relacionar la fuerza de la gravedad sobre la Tierra con la fuerza que mantiene la Luna en su órbita.
La aceleración debida a la gravedad podría haberse inferido de las mediciones anteriores del tiempo que tarda un peso en recorrer diversas distancias en caída libre llevadas a cabo por Riccioli[226]. Para medir el tiempo con exactitud, Riccioli utilizó un péndulo que había sido minuciosamente calibrado contando sus oscilaciones en un día solar o sideral. Para su sorpresa, sus mediciones confirmaron la conclusión de Galileo de que la distancia recorrida es proporcional al cuadrado del tiempo. Partiendo de estas mediciones, publicadas en 1651, podría haber calculado (aunque Riccioli no lo hizo) que la aceleración debida a la gravedad es 30 pies romanos por segundo al cuadrado. Es una suerte que Riccioli dejara constancia de que la altura de la torre Asinelli de Bolonia, de la que se dejaron caer muchos de los pesos, era de 312 pies romanos. La torre todavía sigue en pie, y su altura actual es de 323 pies ingleses actuales, con lo que el pie de Riccioli debiera ser 323/312 = 1,035 pies ingleses, con lo que 30 pies romanos por segundo al cuadrado corresponden a 31 pies ingleses por segundo al cuadrado, en exacta concordancia con el valor actual. De hecho, si Riccioli hubiera conocido la relación de Huygens entre el periodo de un péndulo y el tiempo necesario para que un cuerpo recorra la mitad de su altura, podría haber utilizado su calibración de los péndulos para calcular la aceleración debida a la gravedad, sin tener que dejar caer nada desde las torres de Bolonia.
En 1664 Huygens fue elegido para la nueva Académie Royale des Sciences, cargo que iba acompañado de un estipendio, y se trasladó a París, donde pasó las dos décadas siguientes. Su gran trabajo sobre óptica, el Tratado sobre la luz, fue escrito en París en 1678 y expuso la teoría ondulatoria de la luz. No se publicó hasta 1690, quizá porque Huygens había albergado la esperanza de traducirlo del francés al latín, pero murió en 1695 sin haber encontrado tiempo para llevar la tarea a cabo. En el capítulo 14 volveremos a la teoría ondulatoria de Huygens.
En un artículo de 1669 del Journal des Sçavans, Huygens expuso de manera correcta las reglas que rigen las colisiones de los cuerpos rígidos (que Descartes había comprendido de manera errónea): es la conservación de lo que ahora denominamos momento y energía cinética [227]. Huygens sostenía haber confirmado sus resultados de manera experimental, supuestamente estudiando el impacto de pesas de péndulo al colisionar, cuya velocidad final e inicial se podía calcular de manera precisa. Como veremos en el capítulo 14, en su obra Horologium oscillatorium Huygens calculó la aceleración asociada al movimiento en una trayectoria curva, un resultado de gran importancia para la obra de Newton.
El ejemplo de Huygens nos muestra hasta qué punto la ciencia había dejado de imitar a las matemáticas: ya no se basaba en la deducción ni pretendía esa certidumbre característica de las matemáticas. En el prefacio a su Tratado sobre la luz, Huygens explica: [228]
[En este libro] se encontrarán demostraciones que se alejan de la certeza de la Geometría, y que incluso difieren mucho de ella, pues mientras los Geómetras demuestran sus Proposiciones mediante Principios fijos e irrefutables, nuestros Principios se verifican mediante las conclusiones que se extraen de ellos; y la naturaleza de estas cosas no permite que se pueda hacer de otra manera.Se trata de una descripción de los métodos de la física moderna tan buena como cualquier otra. En la obra de Galileo y Huygens sobre el movimiento, la experimentación se utilizó para refutar la física de Aristóteles. Lo mismo se puede decir del estudio contemporáneo de la presión del aire. La imposibilidad del vacío fue una de las doctrinas de Aristóteles que se puso en entredicho en el siglo XVII. Con el tiempo se acabó comprendiendo que fenómenos como la succión, que parecía surgir del principio de que la naturaleza aborrece el vacío, de hecho representaba el efecto de la presión del aire. En Italia, Francia e Inglaterra hubo tres figuras que desempeñaron un papel clave en este descubrimiento.
Los poceros de Florencia hacía tiempo que sabían que las bombas de succión no podían subir el agua a más de 18 codos, o 32 pies ingleses (o 9,75 metros). El valor real del nivel del mar está más cerca de 33,5 pies (10,21 metros). Galileo y otros creían que esto mostraba una limitación al horror al vacío de la naturaleza. Una interpretación diferente la ofreció Evangelista Torricelli, un florentino que estudiaba geometría, el movimiento de los proyectiles, mecánica de fluidos y óptica, y fue un pionero en el cálculo matemático. Torricelli afirmó que la limitación de las bombas de succión surge porque el peso del aire sobre el agua del pozo podía sustentar tan solo una columna de agua no mayor de 18 codos de altura. Este peso se difunde a través del aire, de manera que cualquier superficie, ya sea horizontal o no, se ve sometida por el aire a una fuerza proporcional a su área; la fuerza por el área, o presión, ejercida por el aire en reposo es igual al peso de una columna vertical de aire, que subiera hasta lo alto de la atmósfera, dividida por el área transversal de la columna. Esta presión actúa sobre la superficie del agua en el pozo, y se suma a la presión del agua, de manera que cuando la presión del aire en lo alto de un tubo vertical inmerso en el agua se ve reducida por el bombeo, el agua asciende por el tubo, pero solo mediante una cantidad limitada por la presión finita del aire.
En la década de 1640 Torricelli emprendió una serie de experimentos para demostrar esta idea. Razonó que, puesto que el peso de un volumen de mercurio es 13,6 veces el peso del mismo volumen de agua, la altura máxima de una columna de mercurio en un tubo de cristal vertical cerrado en la parte superior que puede ser soportada por el aire —ya sea por el aire presionando sobre la superficie de la cubeta de mercurio en el que el tubo se encuentra, o en la parte inferior abierta del tubo cuando se expone al aire— debería ser de 18 codos dividido entre 13,6 (utilizando valores modernos más exactos 33,5 pies/13,6 = 30 pulgadas = 760 milímetros). En 1646 observó que si un tubo de cristal vertical más largo que este y cerrado en la parte superior se llena de mercurio, entonces parte del mercurio bajará hasta que la altura de este en el tubo sea de unas 30 pulgadas, lo cual deja un espacio vacío en lo alto, conocido ahora como el «vacío de Torricelli». Dicho tubo puede servir de barómetro para medir los cambios en la presión del aire ambiental; cuanto más alta sea la presión del aire, más alta será la columna de mercurio que puede soportar.
El erudito francés Blaise Pascal es conocido por su obra de teología cristiana, los Pensamientos, y por su defensa de la secta jansenista en contra de la orden de los jesuitas, aunque también llevó a cabo su aportación a la geometría y la teoría de la probabilidad, y examinó los fenómenos neumáticos estudiados por Torricelli. Pascal razonó que si la columna de mercurio en un tubo de cristal abierto en la parte inferior mantiene su altura por la presión del aire, entonces la altura de la columna debería disminuir cuando el tubo se traslada a una montaña, donde hay más altitud, y donde hay menos aire encima, con lo que la presión de este es menor. Después de que esta predicción quedara verificada en una serie de expediciones entre 1648 y 1651, Pascal concluyó: «Todos los efectos atribuidos a [el horror al vacío] se deben al peso y presión del aire, que es la única causa verdadera» [229].
Pascal y Torricelli han recibido el honor de que se utilizara su nombre para designar modernas unidades de presión. Un pascal es la presión que produce una fuerza de un newton (la fuerza que da a una masa de un kilogramo una aceleración de un metro por segundo al cuadrado) cuando se ejerce en un área de 1 metro cuadrado. Un Torr es la presión que soportará una columna de un milímetro de mercurio. La presión normal es de 760 Torr, que equivale a poco más de 100 000 pascales.
La obra de Torricelli y Pascal fue ampliada por Robert Boyle, hijo del conde de Cork, y miembro de la absentista élite protestante que dominaba Irlanda en la época. Se educó en Eton College, hizo un largo viaje por el continente y se puso de parte del Parlamento en las guerras civiles que asolaron Inglaterra en la década de 1640. Y algo insólito para un miembro de su clase, estaba fascinado por la ciencia. En 1642 se familiarizó con las nuevas ideas que revolucionaron la astronomía, cuando leyó los Diálogos sobre los dos sistemas principales del mundo de Galileo. Boyle fue partidario de las explicaciones naturalistas de los fenómenos naturales, y declaró que «Nadie está más dispuesto [que yo] a reconocer y venerar la Divina Omnipotencia, [pero] lo que se discute no es lo que Dios puede hacer, sino lo que pueden hacer los agentes naturales, sin elevarse por encima de la esfera de la naturaleza»[230]. Pero también adujo que las maravillosas capacidades de los animales y los hombres demostraban que tenían que haber sido concebidos por un creador benevolente.
Los estudios de Boyle sobre la presión del aire se publicaron en 1660 en Nuevos experimentos físico-mecánicos referentes a la elasticidad del aire . En sus experimentos utilizó una bomba de aire mejorada, inventada por su ayudante Robert Hooke, al que volveremos a referirnos en el capítulo 14. Extrayendo el aire de diversos recipientes, Boyle fue capaz de establecer que el aire es imprescindible para la propagación del sonido, para el fuego y para la vida. Descubrió que el nivel de mercurio de un barómetro cae cuando se extrae el aire de su entorno, lo que resultó un poderoso argumento a favor de la conclusión de Torricelli de que la presión del aire es responsable de fenómenos anteriormente atribuidos al horror de la naturaleza al vacío. Utilizando una columna de mercurio para variar la presión y el volumen del aire en un tubo de cristal, impidiendo que entrara o saliera aire y manteniendo la temperatura constante, Boyle fue capaz de estudiar la relación entre presión y volumen. En 1662, en una segunda edición de Nuevos experimentos, señaló que la presión varía con el volumen de manera que el producto de la presión por el volumen es un número fijo, regla conocida como la ley de Boyle.
Ni siquiera los experimentos de Galileo con los planos inclinados ilustran tan bien el nuevo estilo agresivo de física experimental como estos experimentos relacionados con la presión del aire. Ya no se trataba de filósofos naturales que esperaban que la naturaleza revelara sus principios a un observador casual. Por el contrario, a la madre naturaleza se la trataba como a un astuto adversario, a la que había que arrancar sus secretos mediante la ingeniosa construcción de circunstancias artificiales.
Capítulo 13
El método reconsiderado
Francis Bacon nació en 1561, hijo de Nicholas Bacon, lord custodio del Sello Privado de Inglaterra. Tras educarse en el Trinity College, Cambridge, obtuvo el título de abogado, y se dedicó a las leyes, la diplomacia y la política. Se convirtió en barón de Verulam y lord canciller de Inglaterra en 1618, y posteriormente recibió el título de vizconde de St. Albans, pero en 1621 fue encontrado culpable de corrupción y el Parlamento lo inhabilitó para la función pública.
La reputación de Bacon en la historia de la ciencia se basa sobre todo en su libro Novum Organum (Nuevo instrumento, o Auténticas directrices para la interpretación de la naturaleza), publicado en 1620. En este libro, Bacon, que no era científico ni matemático, expresaba una visión extremadamente empírica de la ciencia, y rechazaba no solo a Aristóteles, sino también a Ptolomeo y Copérnico. Los descubrimientos habrían de surgir directamente de la observación de la naturaleza meticulosa y sin prejuicios, no mediante una reducción de los primeros principios. También menospreció cualquier investigación que no tuviera una inmediata utilidad práctica. En La Nueva Atlantis imaginó un instituto de investigación cooperativa, la «Casa de Salomón», cuyos miembros se dedicaban a recoger datos útiles de la naturaleza. Se suponía que así el hombre volvería a adquirir el dominio de la naturaleza que perdió tras la expulsión del edén. Bacon murió en 1626. Se cuenta que, fiel a sus principios empíricos, sucumbió a una neumonía tras un estudio experimental de la congelación de la carne.
Bacon y Platón son dos extremos opuestos. Naturalmente, ambos extremos son erróneos. El progreso se basa en una mezcla de observación o experimentación, que puede sugerir principios generales, y deducciones de estos principios que se pueden poner a prueba con nuevas observaciones o experimentos. La búsqueda de conocimiento de valor práctico puede servir como correctivo para la especulación descontrolada, pero comprender el mundo posee un valor en sí mismo, conduzca o no a algo útil. Los científicos de los siglos XVII y XVIII invocaban a Bacon como contrapeso a Platón y Aristóteles, de manera parecida a como un político estadounidense podía invocar a Jefferson sin haberse visto influido por nada de lo que Jefferson hizo o dijo. No tengo nada claro que los escritos de Bacon mejoraran los estudios de ningún científico. Galileo no necesitó que Bacon le dijera que llevara a cabo experimentos, y tampoco lo necesitaron Boyle ni Newton. Un siglo antes de Galileo, otro florentino, Leonardo da Vinci, experimentaba con cuerpos que caían, con líquidos y muchas otras cosas[231]. Solo conocemos su obra a partir de un par de tratados sobre pintura y el movimiento de fluidos compilados tras su muerte, y a partir de cuadernos que desde entonces se han ido descubriendo esporádicamente, pero si los experimentos de Leonardo no influyeron en el progreso de la ciencia, al menos demuestran que la experimentación flotaba en el aire mucho antes de la existencia de Bacon.
René Descartes fue, en general, una figura más digna de atención que Bacon. Nacido en 1596 en la nobleza jurídica de Francia, la noblesse de robe, se educó en el colegio jesuita de La Flèche, estudió leyes en la Universidad de Poitiers y sirvió en el Ejército de Maurice de Nassau en la Guerra de la Independencia holandesa. En 1619 Descartes decidió dedicarse a la filosofía y a las matemáticas, una labor a la que se aplicó de manera concienzuda después de 1628, cuando se instaló en Holanda de manera permanente.
Descartes expresó sus opiniones sobre la mecánica en Le Monde, escrito a principios de la década de 1630, pero no publicado hasta 1664, después de su muerte. En 1637 publicó una obra filosófica, Discours de la méthode por bien conduire sa raison, et chercher la vérité dans les sciences (Discurso del método para conducir bien la propia razón y buscar la verdad en las ciencias) . Estas ideas las desarrolló aún más en su obra más extensa, los Principios de filosofía, publicada en latín en 1644 y luego en traducción francesa en 1647. En estas obras Descartes expresa su escepticismo acerca del conocimiento derivado de la autoridad o de los sentidos. Para Descartes, el único hecho cierto es que él existe, deducido de la observación de que está pensando en ello. De ahí concluye que el mundo existe, pues lo percibe sin ejercer ningún esfuerzo de voluntad. Rechaza la teleología aristotélica: las cosas son como son, no por el propósito al que sirven. Ofrece varios argumentos (ninguno de ellos convincente) de la existencia de Dios, pero rechaza la autoridad de la religión organizada. También rechaza las fuerzas ocultas que actúan a distancia: las cosas interactúan una con otra a través del empuje o la tracción directa.
Descartes fue el primero en introducir las matemáticas en la física, pero al igual que Platón, sentía demasiada admiración por la certidumbre del razonamiento matemático. En la Parte I de los Principios de la filosofía, titulada «De los principios del conocimiento humano», Descartes escribía cómo los principios científicos fundamentales se podían deducir con certeza mediante el pensamiento. Podemos confiar en la «iluminación natural o facultad de conocimiento que nos concede Dios», pues «sería algo completamente contradictorio que Él nos engañara» [232]. Resulta extraño que Descartes considerara que un dios que permite los terremotos y la peste no permita que un filósofo se engañe.
Descartes aceptó la aplicación de principios físicos fundamentales a sistemas específicos que pudieran implicar incertidumbre, y reclamó la necesidad de experimentación si uno no conocía todos los detalles de lo que el sistema contiene. En su discusión de la astronomía en la Parte III de los Principios de la filosofía, considera diversas hipótesis acerca de la naturaleza del sistema planetario, y cita las observaciones de Galileo acerca de las fases de Venus como motivo para preferir las hipótesis de Copérnico y Tycho a las de Ptolomeo.
Este breve resumen apenas nos ofrece una idea de las opiniones de Descartes. Su filosofía fue y es muy admirada, sobre todo en Francia y entre los especialistas en filosofía, cosa que me resulta desconcertante. Para alguien que afirmaba haber encontrado el auténtico método para obtener un conocimiento fiable, resulta extraordinario lo equivocado que estaba acerca de tantos aspectos de la naturaleza. Se equivocó al afirmar que la Tierra es prolata (es decir, que, en la Tierra, la distancia de polo a polo es mayor que la del plano ecuatorial). Al igual que Aristóteles, se equivocó al afirmar que el vacío es imposible. Se equivocó al afirmar que la luz se transmite de manera instantánea[233]. Se equivocó al afirmar que el espacio está lleno de vórtices materiales que transportan los planetas en sus trayectorias. Se equivocó al afirmar que la glándula pineal es el asiento del alma responsable para la conciencia humana. Se equivocó al calcular la cantidad de movimiento que se conserva en las colisiones. Se equivocó al afirmar que la velocidad de un cuerpo que cae libremente es proporcional a la distancia recorrida. Finalmente, después de haber observado a varios adorables gatos, estoy convencido de que también se equivocaba al afirmar que los animales son máquinas sin verdadera conciencia. Al hablar de Descartes, Voltaire expresaba unas reservas parecidas[234]:
Se engañó sobre la naturaleza del alma, sobre las pruebas de la existencia de Dios, sobre la materia, sobre las leyes del movimiento, sobre la naturaleza de la luz; admitió ideas preconcebidas, inventó nuevos elementos, creó un mundo, hizo al hombre a su modo; y se dijo con razón que el hombre de Descartes no es en efecto más que el hombre de Descartes, muy alejado del hombre verdadero.Los errores científicos de Descartes no tendrían importancia al valorar la obra de alguien que hubiera escrito acerca de ética o de filosofía política, o incluso de metafísica; pero como Descartes escribió acerca del «método para conducir bien la propia razón y buscar la verdad en las ciencias», sus repetidos fracasos a la hora de comprender las cosas deben de proyectar una sombra sobre su criterio filosófico. Lo cierto es que la deducción no tiene tanto peso como Descartes le atribuyó.
Incluso los más grandes científicos cometen errores. Hemos visto que Galileo se equivocó con las mareas y los cometas, y veremos que Newton se equivocó con la difracción. A pesar de todos sus errores, Descartes, contrariamente a Bacon, llevó a cabo aportaciones importantes a la ciencia. Estas se publicaron como suplemento al Discurso del método, bajo tres encabezamientos: geometría, óptica y meteorología [235]. Estos escritos, más que los filosóficos, representan en mi opinión aportaciones positivas a la ciencia.
La mayor contribución de Descartes fue la invención de un nuevo método matemático, ahora conocido como geometría analítica, en el que las curvas o la superficie se representaban mediante ecuaciones que las coordenadas de puntos de la curva o de la superficie debían satisfacer. En general, las «coordenadas» pueden ser cualquier número que nos dé la localización de un punto, como la longitud, la latitud y la altitud, pero las que se conocen como «coordenadas cartesianas» utilizan como referencia ejes ortogonales que se cortan en un punto de origen, y son la distancia al origen de las proyecciones ortogonales desde un punto sobre cada uno de los ejes. Por ejemplo, en la geometría analítica un círculo de radio R es una curva en la que las coordenadas x e y son las distancias medidas desde el centro del círculo a lo largo de dos direcciones perpendiculares cualesquiera que satisfacen la ecuación
x2 + y2 = R2
(la Nota técnica 18 ofrece una descripción parecida de una elipse). El uso de las letras del alfabeto para representar distancias u otros números desconocidos lo comenzó a utilizar en el siglo XVI el matemático, cortesano y criptoanalista François Viète, aunque este todavía escribía las ecuaciones en palabras. El formalismo actual del álgebra y su aplicación a la geometría analítica son obra de Descartes.Mediante la geometría analítica, podemos encontrar las coordenadas de los puntos de intersección de dos curvas, o la ecuación de la curva en la que se cruzan dos superficies, solventando el par de ecuaciones que definen las curvas o las superficies. Hoy en día casi todos los físicos solucionan los problemas geométricos de esta manera, utilizando la geometría analítica, más que los métodos clásicos de Euclides.
Las aportaciones más importantes de Descartes en el campo de la física se vieron en el estudio de la luz. Primero, en su Óptica, Descartes presentó la relación entre los ángulos de incidencia y de refracción cuando la luz pasa de un medio A a un medio B (por ejemplo, del aire al agua): si el ángulo entre el rayo incidente y la perpendicular a la superficie que separa los dos medios es i, y el ángulo entre el rayo refractado y esta perpendicular es r, entonces el seno[236] de i dividido entre el seno de r es una constante independiente del ángulo n:
seno de i / seno de r = n
En el caso más común en el que el medio A es el aire (o, en sentido estricto, el espacio vacío), n es la constante conocida como «índice de refracción» del medio B. Por ejemplo, si A es aire y B es agua, entonces n es el índice de refracción del agua, más o menos 1,33. En cualquier caso como este, en el que n es mayor que 1, el ángulo de refracción r es más pequeño que el ángulo de incidencia i, y el rayo de luz que entra en el medio más denso se inclina hacia la dirección perpendicular a la superficie.Desconocida para Descartes, esta relación ya la había obtenido empíricamente en 1621 el danés Willebrord Snell, e incluso antes el inglés Thomas Harriot; y una figura en un manuscrito del físico árabe del siglo X Ibn Sahl sugiere que era algo que no le resultaba desconocido. Pero Descartes fue el primero en publicarla. Hoy en día la relación se conoce generalmente como la ley de Snell, excepto en Francia, donde es más común que se atribuya a Descartes.
La manera en que Descartes dedujo la ley de refracción es difícil de seguir, en parte porque ni en su deducción ni en la exposición del resultado hizo uso del concepto trigonométrico del seno de un ángulo. Por el contrario, la escribió en términos puramente geométricos, aunque como hemos visto, el concepto de seno lo trajo de la India siete siglos antes Al-Battani, cuya obra era muy conocida en la Europa medieval. La deducción de Descartes se basaba en una analogía con lo que este imaginaba que ocurría cuando una pelota de tenis atraviesa una red delgada; la pelota perderá algo de velocidad, pero la red no puede tener ningún efecto en el componente de la velocidad de la pelota a lo largo de la red. Este supuesto conduce (como se ve en la Nota técnica 27) al resultado citado anteriormente: la razón de los senos de los ángulos que la pelota de tenis forma con la perpendicular a la red antes y después de golpearla es una constante independiente del ángulo n. Aunque resulta difícil ver este resultado en la exposición de Descartes, debió de comprenderlo, porque con un valor apropiado para n consigue más o menos las respuestas numéricas acertadas en su teoría del arcoíris, que comentaremos más adelante.
En la deducción de Descartes hay dos cosas claramente erróneas. Es evidente que la luz no es una pelota de tenis, y la superficie que separa el aire y el agua o el cristal no es una fina red, de modo que se trata de una analogía de dudosa pertinencia, sobre todo para Descartes, que consideraba que la luz, contrariamente a una pelota de tenis, siempre viaja a velocidad infinita[237]. Además, la analogía de Descartes también conduce a un valor erróneo para n. En el caso de las pelotas de tenis (como se ve la Nota técnica 27), su supuesto implica que n es igual a la razón de la velocidad de la pelota vB en el medio B después de atravesar la red y su velocidad vA en el medio A antes de golpear la red. Naturalmente, la pelota se frenaría al atravesar la red, de manera que vB sería menor que vA, y su razón n sería menor a 1. Si esto se aplicara a la luz, significaría que el ángulo que forman el rayo refractado y la perpendicular a la superficie sería mayor que el ángulo entre el rayo incidente y su perpendicular. Descartes lo sabía, e incluso aportó un diagrama que mostraba la trayectoria de la pelota de tenis al desviarse de la perpendicular. Descartes también sabía que esto no funcionaba en el caso de la luz, pues al menos desde la época de Ptolomeo se había observado que un rayo de luz, al entrar en el agua procedente del aire, se dobla hacia la perpendicular a la superficie del agua, de manera que el seno de i es mayor que el seno de r, por lo que n es mayor que 1. En una exposición bastante embarullada que soy incapaz de comprender, Descartes en cierto modo arguye que la luz viaja más fácilmente en el agua que en el aire, por lo que para la luz n es más grande que 1. Para el propósito de Descartes, su fracaso a la hora de explicar el valor de n en realidad no tenía importancia, porque podía, como así hizo, obtener el valor de n de la experimentación (quizá de los datos que aparecen en la Óptica de Ptolomeo), que naturalmente da una n mayor que 1.
Una deducción más convincente de la ley de refracción la presentó el matemático Pierre de Fermat (1601-1665), siguiendo la deducción que había llevado a cabo Herón de Alejandría de la regla de los ángulos iguales que gobiernan la reflexión, aunque suponiendo ahora que los rayos de luz siguen la trayectoria del menor tiempo, en lugar de seguir la trayectoria de la distancia más corta. Este supuesto (como se ve en la Nota técnica 28) conduce a la fórmula correcta: que n es la razón entre la velocidad de la luz en el medio A y la velocidad en el medio B, y por lo tanto mayor que 1 cuando A es el aire y B es el agua o el cristal. Descartes nunca hubiera podido deducir esta fórmula para n, pues para él la luz viajaba de manera instantánea. (Como veremos en el capítulo 14, Christiaan Huygens llega a otra deducción del resultado correcto, basándose en su teoría de la luz como una perturbación que se desplaza, algo que no se basaba en la suposición a priori de Fermat de que el rayo de luz escoge la trayectoria en la que el tiempo es menor).
Descartes llevó a cabo una brillante aplicación de la ley de refracción: en su Meteorología utilizó su relación entre los ángulos de incidencia y de refracción para explicar el arcoíris. Es uno de los momentos en que más brilló como científico. Aristóteles había afirmado que los colores del arcoíris se producían cuando diminutas partículas de agua suspendidas en el aire reflejaban la luz [238]. Además, tal como hemos visto en los capítulos 9 y 10, en la Edad Media tanto Al-Farisi como Dietrich de Friburgo habían reconocido que el arcoíris se debe a la refracción de los rayos de luz cuando entran y salen de las gotas de lluvia suspendidas en el aire. Pero Descartes fue el primero en presentar una descripción cuantitativa detallada de cómo funciona este fenómeno.
Primero Descartes lleva a cabo un experimento, utilizando un delgado globo esférico de cristal lleno de agua como modelo de una gota de lluvia. Observó que cuando los rayos del sol entraban en el globo en diversas direcciones, la luz que emergía a un ángulo de unos 42° con respecto a la dirección de incidencia era «completamente roja e incomparablemente más brillante que el resto». Concluyó que un arcoíris (o al menos su borde rojo) traza en el cielo un arco en el que el ángulo que forman la línea de visión hacia el arcoíris y la dirección del arcoíris al sol es de unos 42°. Descartes supuso que los rayos de luz se desvían mediante la refracción cuando entran en una gota, se reflejan en la superficie posterior de la gota, y luego vuelven a desviarse mediante refracción cuando salen de la gota y vuelven al aire. Pero ¿qué explica la propiedad de las gotas de lluvia de devolver la luz en un ángulo, preferentemente, de unos 42° con la dirección de incidencia?
Para responder a esta pregunta, Descartes consideró los rayos de luz que entran en una gota esférica de agua siguiendo diez líneas paralelas distintas. Clasificó estos rayos mediante lo que hoy se conoce como su parámetro de impacto b, la distancia más cercana al centro de la gota que alcanzaría el rayo si atravesara la gota sin refracción. El primer rayo lo escogió de manera que, si no se refractaba, pasaría por el centro de la gota a una distancia igual al 10 por ciento del radio R de la gota (es decir, siendo b = 0,1 R) mientras que el décimo rayo se escogió para que rozara la superficie de la gota (por lo que b = R), y los rayos intermedios quedaban separados a la misma distancia entre estos dos. Descartes calculó la trayectoria de cada rayo al refractarse mientras entraban en la gota, al reflejarse en la superficie posterior de la gota, y luego al volver a retractarse al abandonarla, utilizando la ley de reflexión de ángulos iguales de Euclides y Herón, así como su propia ley de refracción, y considerando que el índice de refracción n del agua era 4/3. La siguiente tabla proporciona los valores encontrados por Descartes para el ángulo Φ (phi) entre el rayo emergente y la dirección incidente para cada rayo, junto con los resultados de mis propios cálculos utilizando el mismo índice de refracción:
| b/R | Φ (Descartes) | Φ (Recalculación) |
| 0,1 | 5°40' | 5°44' |
| 0,2 | 11°19' | 11°20' |
| 0,3 | 17°56' | 17°6' |
| 0,4 | 22°30' | 22°41' |
| 0,5 | 27°52' | 28°6' |
| 0,6 | 32°56' | 33°14' |
| 0,7 | 37°26' | 37°49' |
| 0,8 | 40°44' | 41°13' |
| 0,9 | 40°57' | 41°30' |
| 1,0 | 13°40' | 14°22' |
La inexactitud de algunos de los resultados de Descartes se puede achacar a las limitadas herramientas matemáticas disponibles en su época. No sé si tuvo acceso a una tabla de senos, y desde luego no disponía de nada parecido a una calculadora de bolsillo moderna. Sin embargo, Descartes habría demostrado mejor criterio si hubiera presentado sus resultados con una aproximación de grados en lugar de querer precisar los minutos de arco.
Tal como observó Descartes, existe una variedad relativamente amplia de valores del parámetro de impacto b y del ángulo de incidencia para los cuales el ángulo Φ se acerca a 40°. A continuación repitió el cálculo para otros 18 rayos más estrechamente espaciados con valores de b que oscilaban entre el 80 y el 100 por ciento del radio de la gota, en los que Φ estaba alrededor de 40°. Descubrió que el ángulo Φ para 14 de esos 18 rayos oscilaba entre 40° y un máximo de 41° 30'. De manera que esos cálculos teóricos explicaban su observación experimental mencionada anteriormente de un ángulo preferente de más o menos 42°.
La Nota técnica 29 nos ofrece una versión moderna de los cálculos de Descartes. En lugar de calcular el valor numérico del ángulo Φ entre los rayos que entran y los que salen para cada uno de los rayos de un conjunto, como hizo Descartes, deducimos una fórmula simple que nos da Φ para cada rayo, con un parámetro de impacto b, y para cada valor de la razón n entre la velocidad de la luz en el aire y la velocidad de la luz en el agua. Esta fórmula se usa entonces para encontrar el valor de Φ allí donde se concentran los rayos emergentes [239].
Cuando n es igual a 4/3 del valor más abundante de Φ, allí donde la luz emergente está un tanto concentrada, resulta ser de 42,0°, tal como descubrió Descartes, que incluso calculó el ángulo correspondiente para el arcoíris secundario, producido por la luz que se refleja dos veces dentro de una gota de lluvia antes de salir.
Descartes vio una relación entre la separación de colores que es característica del arcoíris y los colores que mostraba la refracción de la luz en un prisma, pero fue incapaz de abordar el fenómeno cuantitativamente, pues no sabía que la luz blanca del sol se compone de luz de todos los colores, ni que el índice de refracción de la luz depende ligeramente de su color. De hecho, mientras Descartes había considerado que el índice para el agua era de 4/3 = 1,333…, de hecho está más cerca de 1,330 para longitudes de onda características de la luz roja y más cerca de 1,343 para la luz azul. Descubrimos (utilizando la fórmula general derivada de la Nota técnica 29) que el valor máximo para el ángulo Φ entre el rayo de incidencia y el de salida es de 42,8° para la luz roja y de 40,7° para la luz azul. Por eso Descartes veía una brillante luz roja cuando miraba su globo de agua a un ángulo de 42° en dirección a los rayos del sol. El valor del ángulo Φ está por encima del valor máximo de 40,7° del ángulo al que puede salir la luz azul del globo de agua, por lo que ninguna luz del extremo azul del espectro podía ser vista por Descartes; pero está solo por debajo del valor máximo de 42,8° de Φ para la luz roja, de manera que ello provocaría que la luz roja fuera especialmente brillante.
La obra de Descartes sobre óptica sintonizaba mucho más con la física moderna. Descartes supuso sin ningún fundamento que la luz que cruza el límite entre dos medios diferentes se comporta como una pelota de tenis que penetra en una fina red, y utilizó esa suposición para deducir una relación entre los ángulos de incidencia y refracción que (con la apropiada elección del índice de refracción n) coincidía con la observación. Luego, utilizando un globo lleno de agua como modelo de una gota de lluvia, llevó a cabo observaciones que sugerían el posible origen del arcoíris, y a continuación demostró matemáticamente que esas observaciones eran consecuencia de su teoría de la refracción. No comprendía los colores del arcoíris, de manera que pasó por alto la cuestión, y publicó lo que comprendía. Eso es exactamente lo que haría un físico en la actualidad, pero aparte de su aplicación de las matemáticas a la física, ¿qué tiene que ver con el Discurso del método de Descartes? No veo ningún indicio de que siguiera su propia fórmula «para conducir bien la propia razón y buscar la verdad en las ciencias».
Debería añadir que en sus Principios de la filosofía Descartes ofreció una mejora cualitativa importante a la idea del ímpetu de Buridan [240]. Afirmó que «todo movimiento, por sí mismo, sigue una línea recta», de manera que (contrariamente a Aristóteles y Galileo) se necesita una fuerza para que los cuerpos planetarios se mantengan en sus órbitas curvas. Pero Descartes no intentó calcular esa fuerza. Como veremos en el capítulo 14, sería Huygens quien calcularía la fuerza necesaria para mantener un cuerpo en movimiento a una velocidad dada en un círculo de un radio dado, y Newton explicaría esa fuerza, así como la fuerza de la gravitación.
En 1649 Descartes viajó a Estocolmo para dar clases a la reina Cristina. Quizá como resultado del frío clima sueco, y por tener que levantarse para dar clases a la reina a una hora intempestivamente temprana, al año siguiente, al igual que Bacon, murió de neumonía. Catorce años después sus obras se unieron a las de Copérnico y Galileo en el índice de libros prohibidos para los católicos.
Los escritos de Descartes sobre el método científico han merecido una gran atención entre los filósofos, pero no creo que hayan tenido una influencia positiva en la práctica de la investigación científica (ni siquiera, como he comentado antes, sobre las obras científicas más logradas del propio Descartes). Sus textos tuvieron un efecto negativo: retrasaron la recepción de la física newtoniana en Francia. El programa expuesto en el Discurso del método, consistente en deducir los principios científicos mediante la razón pura, no funcionó, y no podía haber funcionado. Huygens se consideraba de joven un seguidor de Descartes, pero acabó comprendiendo que los principios científicos eran solo hipótesis que había que poner a prueba comparando sus consecuencias con la observación[241].
Por otro lado, la obra de Descartes sobre óptica demuestra que también él comprendía que ese tipo de hipótesis científica es a veces necesaria. Laurens Laudan ha encontrado pruebas de lo mismo en sus escritos sobre química de los Principios de filosofía[242]. Esto suscita la cuestión de si realmente algún científico aprendió de Descartes la práctica de llevar a cabo hipótesis y luego comprobarlas de manera experimental, cosa que según Laudan sí ocurría con Boyle. Mi opinión es que esta práctica hipotética fue ampliamente comprendida antes de Descartes. ¿Cómo se podría describir, si no, lo que hizo Galileo al utilizar la hipótesis de que los cuerpos que caen aceleran de manera uniforme, y deducir de ella la consecuencia de que los proyectiles siguen una trayectoria parabólica, poniéndolo luego experimentalmente a prueba?
Según la biografía de Descartes escrita por Richard Watson[243]: «Sin el método cartesiano de analizar cosas materiales en sus elementos primarios, nunca habríamos obtenido la bomba atómica. La aparición de la ciencia moderna en el siglo XVII, la Ilustración en el XVIII, la Revolución Industrial del XIX, el ordenador personal del XX, y el desciframiento del cerebro en el siglo XXI: todo es cartesiano». Descartes realizó una gran aportación a las matemáticas, pero es absurdo suponer que son sus páginas sobre el método científico lo que ha producido todos estos afortunados avances.
Descartes y Bacon son solo dos de los filósofos que a lo largo de los siglos intentaron formular reglas para la investigación científica, algo que nunca funciona. Aprendemos a practicar la ciencia no imponiendo reglas acerca de cómo practicarla, sino a partir de la experiencia de trabajar en ella, impulsados por la satisfacción que obtenemos cuando nuestros métodos consiguen explicar algo.
Capítulo 14
La síntesis newtoniana
Quienes escriben acerca de Newton a veces ponen énfasis en que no se trataba de un científico moderno. En este sentido, la afirmación más conocida es la de John Maynard Keynes (que había comprado algunos de los documentos de Newton en la subasta de 1936 de Sotheby's): «Newton no fue el primero de la Edad de la Razón. Fue el último de los magos, el último de los babilonios y sumerios, la última gran mente que se asomó al mundo visible e intelectual con los mismos ojos de aquellos que comenzaron a construir nuestro mundo intelectual hace bastante menos de 10 000 años» [245]. Pero Newton no era un vestigio con talento de un pasado mágico. Tampoco un mago ni un científico totalmente moderno, sino que cruzó la frontera entre la filosofía natural del pasado y lo que acabó siendo la ciencia moderna. Los logros de Newton, si no su punto de vista o comportamiento personal, proporcionaron el paradigma que toda la ciencia posterior ha seguido al volverse moderna.
Isaac Newton nació el día de Navidad de 1642 en la granja de su familia, Woolsthorpe Manor, Lincolnshire. Su padre, un pequeño propietario analfabeto, murió poco antes de su nacimiento. Su madre ocupaba una categoría social superior, pues era miembro de la pequeña nobleza, y tenía un hermano que se había graduado en la Universidad de Cambridge y era clérigo. Cuando Newton tenía tres años su madre volvió a casarse y abandonó Woolsthorpe, dejándolo con su abuela. A los diez años, Newton asistió a la escuela unitaria pública de Grantham, a casi trece kilómetros de Woolsthorpe, donde vivía en la casa de un farmacéutico. En Grantham aprendió latín y teología, aritmética y geometría y un poco de griego y hebreo.
A los 17 años Newton volvió a casa para asumir sus deberes de granjero, pero descubrió que era un trabajo que no se le daba muy bien. Dos años más tarde lo mandaron al Trinity College, Cambridge, como becario (sizar), lo que significaba que pagaría el importe de las tasas, el alojamiento y la manutención atendiendo a los profesores y a aquellos estudiantes que habían podido pagar sus matrículas. Al igual que Galileo en Pisa, comenzó su vocación universitaria con Aristóteles, pero no tardó en interesarse por otras cuestiones. En su segundo año empezó a escribir una serie de notas, Questiones quandam philosophicae, en un cuaderno donde anteriormente había tomado notas sobre Aristóteles, y que por suerte todavía se conserva.
En diciembre de 1663, la Universidad de Cambridge recibió una donación de un miembro del Parlamento, Henry Lucas, mediante la cual se fundaba una cátedra de matemáticas, la cátedra Lucasiana, con un estipendio de 100 libras al año. La cátedra se inauguró en 1664 y fue ocupada por Isaac Barrow, el primer catedrático de matemáticas de Cambridge, doce años mayor que Newton. Más o menos en esa época Newton empezó a estudiar matemáticas, en parte con Barrow y en parte solo, y recibió su título de licenciado en Filosofía y Letras. En 1665 la peste asoló Cambridge, casi toda la Universidad cerró y Newton volvió a su casa. A partir de 1664 Newton comenzó sus investigaciones científicas, que describiremos más adelante.
A su regreso a Cambridge, en 1667, Newton fue elegido profesor permanente del Trinity College, un cargo que le reportó dos libras al año y libre acceso a la biblioteca de la facultad. Trabajó estrechamente con Barrow, ayudándole a preparar versiones escritas de sus conferencias. Cuando en 1669 Barrow dimitió de su cátedra Lucasiana para dedicarse por completo a la teología, sugirió que el cargo fuera a parar a Newton. Con la ayuda financiera de su madre, Newton comenzó a vivir con cierto desahogo: compró ropa y muebles nuevos y empezó a jugar un poco [246].
Un poco antes, inmediatamente después de la restauración de la monarquía de los Estuardo en 1660, unos cuantos londinenses —entre ellos Boyle, Hooke y el astrónomo y arquitecto Christopher Wren— habían formado una sociedad que se reunía para debatir sobre filosofía natural y observar experimentos. Al principio, solo tenía un miembro extranjero, Christiaan Huygens. La sociedad recibió un acta real en 1662 y pasó a llamarse la Royal Society of London, y ha seguido siendo la academia nacional de ciencias de Gran Bretaña. En 1672 Newton fue elegido miembro de la Royal Society, de la que posteriormente se convirtió en presidente.
En 1675 Newton se enfrentó a una crisis. Ocho años después de ser elegido profesor permanente del Trinity College, llegó un momento en que los profesores permanentes de cualquier facultad de Cambridge tenían que tomar las sagradas órdenes en la Iglesia de Inglaterra. Para ello tenían que jurar su fe en la doctrina de la Trinidad, algo imposible para Newton, que rechazaba la decisión del Concilio de Nicea de que el Padre y el Hijo estuvieran hechos de la misma sustancia. Por suerte, el acta de fundación de la cátedra Lucasiana estipulaba que quien la detentara no tenía por qué desempeñar ningún papel activo en la Iglesia, y sobre esa base el rey Carlos II emitió un decreto mediante el cual quien detentara la cátedra Lucasiana no se vería obligado a tomar las sagradas órdenes, por lo que Newton pudo seguir en Cambridge.
Veamos ahora la gran obra que Newton comenzó en Cambridge en 1664. Esta investigación se centraba en la óptica, las matemáticas y lo que posteriormente se denominaría dinámica. Su labor en cualquiera de estas tres áreas lo cualificaría como uno de los científicos más grandes de la historia.
Los principales logros experimentales de Newton tuvieron que ver con la óptica[247]. Sus notas de estudiante, las Questiones quandam philosophicae, nos muestran ya su interés por la naturaleza de la luz. Newton concluyó, contrariamente a Descartes, que la luz no es una presión en los ojos, pues si lo fuera el cielo nos parecería más brillante cuando corremos. En 1665, en Woolsthorpe, llevó a cabo su mayor aportación a la óptica, su teoría del color. Desde la Antigüedad se sabía que aparecen colores cuando la luz atraviesa un trozo curvo de cristal, pero se consideraba que esos colores, de algún modo, los producía el cristal. Newton conjeturó que la luz blanca está formada por todos los colores, y que el ángulo de refracción del cristal o el agua depende levemente del color, y que la luz roja se curva un poco menos que la luz azul, de manera que los colores se separan cuando la luz atraviesa un prisma o una gota de lluvia [248]. Eso explicaría lo que Descartes no había entendido: la aparición de colores en el arcoíris. Para poner a prueba su idea, Newton llevó a cabo dos experimentos decisivos. En el primero, tras utilizar un prisma para crear rayos separados de luz azul y roja, dirigió esos rayos de manera separada a otros prismas, y descubrió que no había más dispersión en colores distintos. A continuación, con una inteligente disposición de prismas, consiguió combinar todos los colores distintos producidos por la refracción de la luz blanca, descubriendo que esta se producía al combinarse todos los colores.
El hecho de que el ángulo de refracción depende del color posee la desdichada consecuencia de que las lentes de cristal de los telescopios, como los de Galileo, Kepler y Huygens, enfocan los distintos colores de la luz blanca de manera distinta, con lo que las imágenes de objetos lejanos quedan borrosas. Para evitar esta aberración cromática, en 1669 Newton inventó un telescopio en el que la luz inicialmente la concentra un espejo curvo en lugar de una lente de cristal. (Entonces un espejo plano desvía los rayos de luz desde el telescopio a un ocular de cristal, de manera que no toda la aberración cromática se consigue eliminar). Con un telescopio reflectante de apenas quince centímetros de largo, consiguió ampliar la imagen 40 veces. Todos los telescopios astronómicos importantes que enfocan la luz son ahora telescopios reflectantes, descendientes del invento de Newton. En mi primera visita a la sede actual de la Royal Society, en la Carlton House Terrace, me agasajaron llevándome al sótano para que pudiera contemplar el pequeño telescopio de Newton, el segundo que construyó.
En 1671, Henry Oldenburg, secretario y alma de la Royal Society, invitó a Newton a publicar una descripción de su telescopio. Este envió una carta con la descripción solicitada y su trabajo sobre el color para Philosophical Transactions of the Royal Society a principios de 1672, lo que dio pie a una polémica sobre la originalidad e importancia del trabajo de Newton, de la que participó sobre todo Hooke, que había sido supervisor de los experimentos de la Royal Society desde 1662, y que detentaba un puesto de profesor subvencionado por sir John Cutler desde 1664. Hooke no era un oponente de poca monta, pues había hecho importantes aportaciones a la astronomía, la microscopia, la relojería, la mecánica y la planificación urbana. Afirmaba haber llevado a cabo los mismos experimentos con la luz que Newton, y decía que estos no habían demostrado nada: los colores simplemente se añadían a la luz blanca gracias al prisma.
En 1635, en Londres, Newton dio una conferencia sobre su teoría de la luz. Conjeturó que la luz, al igual que la materia, se compone de muchas partículas diminutas, en contra de la opinión, propuesta más o menos en la misma época por Hooke y Huygens, de que la luz es una onda. Fue esa una ocasión en la que a Newton le falló su criterio científico. Existen muchas observaciones, algunas incluso de la época de Newton, que demuestran la naturaleza ondulatoria de la luz. Es cierto que la moderna mecánica cuántica describe la luz como un conjunto de partículas sin más, llamadas fotones, pero en la luz con que nos encontramos en la experiencia cotidiana el número de fotones es enorme, y en consecuencia la luz se comporta como una onda.
En su Tratado sobre la luz de 1678, Huygens describe la luz como una onda de perturbación en un medio, el éter, que consiste en un gran número de diminutas partículas materiales muy juntas. Al igual que en una onda oceánica en alta mar no es el agua lo que se mueve a lo largo de la superficie del océano, sino la perturbación del agua, del mismo modo, según la teoría de Huygens, es la onda de perturbación de las partículas del éter lo que se mueve en un rayo de luz, no las propias partículas. Cada partícula sometida a perturbación actúa como una nueva fuente de perturbación, lo que se va sumando a la amplitud total de la onda. Naturalmente, desde el trabajo de James Clerk Maxwell en el siglo XIX sabemos que (incluso dejando aparte los efectos cuánticos) Huygens solo tenía razón a medias: la luz es una onda, pero una onda de perturbaciones en campos eléctricos y magnéticos, no una onda de perturbaciones de partículas materiales.
Utilizando esta teoría ondulatoria de la luz, Huygens fue capaz de deducir el resultado de que la luz en un medio homogéneo (o en un espacio vacío) se comporta como si viajara en línea recta, pues solo siguiendo estas líneas las ondas producidas por todas las partículas sometidas a perturbación se suman de manera constructiva. Aportó una nueva deducción de la ley de los ángulos iguales para la reflexión, y de la ley de Snell para la refracción, sin el supuesto a priori de Fermat de que los rayos de luz siguen la trayectoria que les lleva menos tiempo (véase Nota técnica 30). En la teoría de la refracción de Huygens, un rayo de luz se curva al pasar en un ángulo oblicuo a través de la línea divisoria entre dos medios con velocidades de la luz distintas, de manera muy parecida a cómo cambia de dirección la marcha de una columna de soldados cuando la vanguardia de la columna entra en terreno pantanoso, en el que se reduce la velocidad de marcha.
Si se me permite la digresión, era esencial en la teoría ondulatoria de Huygens que la luz viajara a velocidad finita, contrariamente a lo que había considerado Descartes. Huygens arguye que los efectos de esta velocidad finita son difíciles de observar, simplemente porque la luz viaja muy deprisa. Si, por ejemplo, la luz tarda una hora en recorrer la distancia de la Luna a la Tierra, entonces en el momento de un eclipse de luna esta no se vería directamente delante del Sol, sino rezagada unos 33°. Del hecho de que no la veamos rezagada Huygens concluyó que la velocidad de la luz debe ser al menos 100 000 veces más rápida que la del sonido. Y es correcto; de hecho es más o menos un millón de veces más rápida.
Huygens pasó a describir observaciones recientes de las lunas de Júpiter llevadas a cabo por el astrónomo danés Ole Rømer. Estas observaciones demostraban que el periodo de revolución de Io parece más corto cuando la Tierra y Júpiter se acercan uno u otro y más largo cuando se separan. (La atención se centró en Io porque, de las lunas de Júpiter de Galileo, era la que tenía el periodo orbital más corto: solo 1,77 días). Huygens lo interpretó como lo que posteriormente se conocería como «efecto Doppler»: cuando Júpiter y la Tierra se acercan o se apartan, su separación, cada vez que se completa un periodo de separación de Io, aumenta o disminuye respectivamente, y si la luz viaja a una velocidad finita, el intervalo de tiempo entre observaciones de periodos completos de Io debería ser respectivamente menor o mayor que si Júpiter y la Tierra estuvieran en reposo. En concreto, el desplazamiento fraccionario del periodo aparente de Io debería ser la razón entre la velocidad relativa de Júpiter y la Tierra siguiendo la dirección que los separa y la velocidad de la luz, donde la velocidad relativa se toma como positiva o negativa si Júpiter o la Tierra se separan o se acercan, respectivamente (véase Nota técnica 31). Midiendo los cambios aparentes en el periodo de Io y sabiendo la velocidad relativa de la Tierra y Júpiter, se podía calcular la velocidad de la luz. Como la Tierra se mueve mucho más deprisa que Júpiter, es principalmente la velocidad de la Tierra la que domina la velocidad relativa. En aquel entonces no se conocía muy bien la escala del sistema solar, y tampoco el valor numérico de la velocidad relativa de separación de la Tierra y Júpiter, pero utilizando los datos de Rømer, Huygens fue capaz de calcular que la luz tarda 11 minutos en recorrer una distancia igual al radio de la órbita de la Tierra, resultado para el que no había que conocer el tamaño de la órbita. Dicho de otra manera, puesto que la unidad astronómica (UA) de distancia se define como el radio medio de la órbita de la Tierra, la velocidad de la luz calculada por Huygens era de 1 UA por 11 minutos. El valor actual es de 1 UA por 8,32 minutos.
Tanto Newton como Huygens ya habrían dispuesto de pruebas experimentales de la naturaleza ondulatoria de la luz, gracias al descubrimiento de la difracción por parte del jesuita boloñés Francesco Maria Grimaldi (alumno de Riccioli), publicado póstumamente en 1665. Grimaldi descubrió que la sombra de una varilla estrecha y opaca a la luz del Sol no es perfectamente nítida, sino que muestra unos bordes recortados, que se deben al hecho de que la longitud de onda de la luz no es despreciable en comparación con el grosor de la varilla, aunque Newton afirmó que en realidad eran el resultado de algún tipo de refracción en la superficie de aquella. La polémica de la naturaleza corpuscular u ondulatoria de la luz quedó zanjada cuando, a principios del siglo XIX, Thomas Young descubrió la interferencia: el efecto de refuerzo o cancelación de las ondas de luz que llegan a puntos concretos siguiendo trayectorias distintas. Como ya se ha mencionado, en el siglo XX se descubrió que ambas teorías no son incompatibles. En 1905, Einstein comprendió que aunque la luz, a casi todos los efectos, se comporta como una onda, su energía llega en pequeños paquetes, posteriormente llamados fotones, y cada uno posee una energía y un momento minúsculos proporcionales a la frecuencia de la luz.
Finalmente Newton presentó su trabajo sobre la luz en su libro Opticks, escrito (en inglés) a principios de la década de 1690. Se publicó en 1704, cuando su autor ya era famoso.
Newton no fue solo un gran físico, sino también un matemático creativo. En 1664 comenzó a leer obras de matemáticas, entre ellas los Elementos de Euclides y la Geometrie de Descartes. Pronto comenzó a encontrar soluciones a una variedad de problemas, muchas de ellas con infinitos. Por ejemplo, consideró las series infinitas, como
x – x2/ 2 + x3/3 – x4/4 +…,
y demostró que la suma es el logaritmo[249] de 1 + x.En 1665 Newton comenzó a pensar en infinitesimales. Se planteó un problema: supongamos que conocemos la distancia D(t) recorrida en un tiempo t; ¿cómo averiguamos la velocidad en cada momento? Razonó que en el movimiento no uniforme, la velocidad en cualquier instante es la proporción entre la distancia recorrida y el tiempo transcurrido en un intervalo infinitesimal de tiempo en ese instante. Introduciendo el símboloo para un intervalo infinitesimal de tiempo, definió la velocidad del tiempo t como la razón entre la distancia recorrida entre el tiempot y el tiempo t + o, y el intervalo de tiempo o; es decir, la velocidad es [D(t + o) – D(t)]/o. Por ejemplo, si D(t) = t3, entonces D(t + o) = 3 + t3 +3to2 + o3. Para un o infinitesimal, podemos despreciar los términos proporcionales a o2 y o3, y tomar D(t + o) = t3 + 3t2o, de manera que D(t + o) – D(t) = 3t2o, y la velocidad es simplemente 3t2. Newton lo llamó la «fluxión» de D(t), pero acabó conociéndose como la «derivada», la herramienta fundamental del cálculo diferencial moderno [250].
Newton había inventado el cálculo diferencial e integral, aunque este trabajo tardó mucho tiempo en ser ampliamente conocido. A finales de 1671 decidió publicarlo junto con una explicación de su trabajo sobre óptica, pero al parecer ningún librero londinense estaba dispuesto a emprender la edición sin un generoso subsidio[251].
En 1669, Barrow le pasó el manuscrito de Newton, De analysi per aequationes numero terminorum infinitas, al matemático John Collins. En 1676, en una visita a Londres, el filósofo y matemático Gottfried Wilhelm Leibniz, antiguo alumno de Huygens y unos años mayor que Newton, y que de manera independiente había descubierto el año anterior los puntos fundamentales del cálculo, vio una copia que había hecho Collins del libro de Newton. En 1676 Newton reveló algunos resultados en unas cartas con la intención de que las viera Leibniz. Este publicó su obra sobre el cálculo en artículos aparecidos en 1684 y 1685, sin reconocer el trabajo de Newton. En estas publicaciones Leibniz introdujo la palabra «cálculo», y presentó su notación moderna, incluyendo el signo de integración ∫.
Para reivindicar su descubrimiento del cálculo, Newton describió su propio método en dos artículos incluidos en la edición de 1704 de Opticks. En enero de 1705 una reseña anónima de Opticks insinuaba que había tomado sus métodos de Leibniz. Tal como intuyó Newton, era el propio Leibniz quien había escrito esa reseña. En 1709, en Philosophical Transactions of the Royal Society se publicó un artículo de John Keill defendiendo que había sido Newton el primero en descubrir el cálculo, a lo que Leibniz replicó en 1711 con una airada queja a la Royal Society. En 1712 la Royal Society convocó un comité anónimo para que analizara la polémica. Dos siglos más tarde se hicieron públicos los miembros de este comité, y resultó que estaba formado casi en su totalidad por partidarios de Newton. En 1715 el comité informó que había que atribuirle a Newton el mérito de la invención del cálculo. El informe había sido redactado para el comité por el propio Newton. Sus conclusiones fueron apoyadas por una reseña anónima del informe, también escrita por él.
La opinión de los eruditos contemporáneos[252] es que Leibniz y Newton descubrieron el cálculo de manera independiente. Newton lo llevó a cabo una década antes que Leibniz, pero hay que concederle a este un gran mérito por publicar su trabajo. Por el contrario, Newton, después de su primer intento de encontrar un editor para su tratado sobre el cálculo en 1671, permitió que su trabajo permaneciera inédito hasta que se vio obligado a divulgarlo por la polémica con Leibniz. En el proceso del descubrimiento científico [253], la decisión de publicarlo es generalmente un elemento crítico. Indica que el autor considera que la obra es correcta y que la pueden utilizar otros científicos. Por esta razón, en la actualidad la atribución de un descubrimiento científico recae en el primero que lo publica. Pero aunque Leibniz fue el primero en publicar su trabajo sobre el cálculo, como veremos, fue Newton quien aplicó el cálculo a los problemas científicos. Aunque, al igual que Descartes, Leibniz fue un gran matemático cuya obra filosófica es muy admirada, no llevó a cabo ninguna aportación importante a las ciencias naturales.
Fueron las teorías de Newton sobre el movimiento y la gravitación lo que históricamente tuvo más influencia. Desde tiempo atrás se sabía que la fuerza de la gravedad que provoca la caída de los objetos a la Tierra disminuye con la distancia a la superficie de la Tierra. Esta idea la había sugerido en el siglo IX un monje irlandés que había viajado mucho, Duns Scoto (Johannes Scotus Erigena, o John el Escocés), pero no se había sugerido que esa fuerza tuviera ninguna relación con el movimiento de los planetas. La idea de que la fuerza que mantienen los planetas en sus órbitas disminuye de manera inversamente proporcional al cuadrado de la distancia del Sol puede que la propusiera por primera vez en 1645 un sacerdote francés, Ismael Bullialdus, posteriormente citado por Newton y elegido miembro de la Royal Society. Pero fue Newton quien consiguió que la idea resultase convincente y relacionó esa fuerza con la gravedad.
Cincuenta años más tarde, Newton relató cómo comenzó a estudiar la gravitación. Aunque esta afirmación precisa una abundante explicación, considero que debo citarla, pues describe en las propias palabras de Newton lo que parece ser un momento crucial en la historia de la civilización. Según Newton, fue en 1666 cuando:
Comencé a pensar que la gravedad se extendía a la órbita de la Luna y (tras haber descubierto cómo calcular la fuerza con la que un globo que gira dentro de una esfera presiona la superficie de la esfera), a partir de la regla de Kepler de que los periodos de los Planetas estaban en proporción sesquiáltera a sus distancias del centro de sus Órbitas, deduje que las fuerzas que mantienen a los Planetas en sus Órbitas deben de ser inversamente proporcionales a los cuadrados de sus distancias del centro en torno al cual giran, y así comparé la Luna en su Órbita con la fuerza de la gravedad en la superficie de la Tierra, y descubrí que se correspondían de manera bastante aproximada. Todo ello [incluyendo su obra sobre las series infinitas y el cálculo] ocurrió en los dos años de la peste de 1665 y 1666. Pues esa fue mi época más creativa y en la que más me dediqué a las Matemáticas y la Filosofía[254].Como ya he dicho, esto requiere cierta explicación.
En primer lugar, el paréntesis de Newton: «tras haber descubierto cómo calcular la fuerza con la que un globo que gira dentro de una esfera presiona la superficie de la esfera», se refiere al cálculo de la fuerza centrífuga, un cálculo que ya había llevado a cabo Huygens (probablemente sin que Newton tuviera conocimiento) en torno a 1659. Para Huygens y Newton (al igual que para nosotros), la aceleración poseía una definición más amplia que un simple número que daba el cambio de velocidad por tiempo transcurrido; es una cantidad dirigida, que nos da el cambio por tiempo transcurrido en la dirección así como en la magnitud de velocidad. Existe una aceleración en el movimiento circular incluso a velocidad constante: se trata de la «aceleración centrípeta», que consiste en un giro continuo hacia el centro del círculo. Huygens y Newton concluyeron que un cuerpo que se mueve a una velocidad constante v en torno a un círculo de radio r acelera hacia el centro del círculo con una velocidad v2/r, de manera que la fuerza necesaria para mantenerlo en movimiento sobre el círculo y que no se escape en línea recta hacia el espacio es proporcional a v2/r (véase Nota técnica 32). La resistencia a esta aceleración centrípeta se experimenta como lo que Huygens denominó fuerza centrífuga, como cuando hacemos girar en círculo un peso al extremo de una cuerda. En el caso del peso, lo que resiste la fuerza centrífuga es la tensión de la cuerda. Pero no hay ninguna cuerda que una los planetas al Sol. ¿Qué es entonces lo que resiste la fuerza centrífuga producida por el movimiento casi circular de un planeta en torno al Sol? Como veremos, la respuesta a esta pregunta condujo al descubrimiento de Newton de la ley de la gravitación de la inversa del cuadrado.
A continuación, al hablar de «la regla de Kepler de que los periodos de los Planetas estaban en proporción sesquiáltera a sus distancias al centro de sus Órbitas», Newton se refería a lo que ahora llamamos la tercera ley de Kepler: que el cuadrado de los periodos de los planetas en sus órbitas es proporcional al cubo del radio medio de sus órbitas; o, en otras palabras, que los periodos son proporcionales a la potencia 3/2 («la proporción sesquiáltera») del radio medio[255]. El periodo de un cuerpo que se mueve con una velocidad v en torno a un círculo de radio r es la circunferencia 2πr dividida por la velocidad v, de manera que, para órbitas circulares, la tercera ley de Kepler nos dice que r2/v2 es proporcional a r3, y que por tanto sus inversas son proporcionales: v2/r2 es proporcional a 1/r3. De ahí se sigue que la fuerza que mantiene a los planetas en sus órbitas, que es proporcional a v2/r, debe ser proporcional a 1/r2. Esa es la ley de la gravedad del inverso del cuadrado.
En sí misma, se podría considerar una reformulación de la tercera ley de Kepler. En la consideración de los planetas que hace Newton no encontramos nada que relacione la fuerza que mantiene a los planetas en sus órbitas y los fenómenos habitualmente experimentados asociados con la gravedad en la superficie de la Tierra. Esta relación la proporcionó Newton al tener en cuenta la Luna. La afirmación que hace Newton de que «comparé la Luna en su Órbita con la fuerza de la gravedad en la superficie de la Tierra, y descubrí que se correspondían de manera bastante aproximada» indica que había calculado la aceleración centrípeta de la Luna, y descubierto que era menor que la aceleración de los cuerpos que caen sobre la superficie de la Tierra justo en la proporción que uno esperaría si esas aceleraciones fueran inversamente proporcionales al cuadrado de la distancia al centro de la Tierra.
Para ser más concretos, Newton consideró que el radio de la órbita de la Luna (conocido a partir de las observaciones del paralaje diurno de la Luna) era 60 veces el radio de la Tierra; de hecho, es 60,2 el radio de la Tierra. Utilizó un tosco cálculo del radio de la Tierra [256], que dio un tosco valor para el radio de la órbita de la Luna, y sabiendo que el periodo sideral de la revolución de la Luna en torno a la Tierra es 27,3 días, pudo calcular la velocidad de la Luna, y de ahí su aceleración centrípeta. Esta aceleración resultó ser menor que la aceleración de los cuerpos que caen sobre la superficie de la Tierra por un factor aproximado (muy aproximado) de 1/(60)2, tal como sería de esperar si la fuerza que mantiene a la Luna en su órbita es la misma que atrae a los cuerpos hacia la superficie terrestre, aunque reducida de acuerdo con la ley de la inversa del cuadrado (véase Nota técnica 33). A eso se refería Newton al afirmar que había descubierto que las fuerzas «se correspondían de manera bastante aproximada».
Este fue el paso culminante en la unificación de lo celeste y lo terrestre en las ciencias. Copérnico había ubicado la Tierra entre los planetas, Tycho había mostrado que hay cambios en los cielos y Galileo había visto que la superficie de la Luna era desigual, semejante a la de la Tierra, pero nada de ello relacionaba el movimiento de los planetas con fuerzas que pudieran observarse en la Tierra. Descartes había intentado comprender los movimientos del sistema solar como el resultado de vórtices no muy distintos de los vórtices en una charca de agua sobre la Tierra, pero su teoría no tuvo éxito. Ahora Newton había demostrado que la fuerza que mantiene la Luna en su órbita en torno a la Tierra y a los planetas en sus órbitas en torno al Sol es la misma fuerza de la gravedad que hace que una manzana caiga al suelo en Lincolnshire, todo gobernado por las mismas leyes cuantitativas. A partir de entonces, la distinción entre lo celeste y lo terrestre, que había constreñido la especulación física desde Aristóteles, tuvo que abandonarse para siempre. Pero todo esto aún estaba muy lejos de constituir un principio de gravitación universal, que afirmaría que cada cuerpo del universo, no solo la Tierra y el Sol, atrae a los demás cuerpos con una fuerza que disminuye en proporción inversa al cuadrado de la distancia entre ellos.
Todavía había cuatro grandes agujeros en los argumentos de Newton:
1. Al comparar la aceleración centrípeta de la Luna con la aceleración de los cuerpos que caen sobre la superficie de la Tierra, Newton había asumido que la fuerza que produce esas aceleraciones disminuye de manera inversamente proporcional al cuadrado de la distancia, pero la distancia ¿desde dónde? Este detalle tiene poca importancia en el caso del movimiento de la Luna, que está tan lejos de la Tierra que esta se puede considerar casi como un punto particular por lo que se refiere al movimiento de la Luna. Pero para una manzana que cae al suelo en Lincolnshire, la Tierra se extiende desde el fondo del árbol, a menos de un metro, hasta un punto de las antípodas, a casi 12 756 kilómetros de distancia. Newton había supuesto que la distancia relevante para la caída de cualquier objeto cerca de la superficie de la Tierra es su distancia al centro de esta, pero eso no era tan evidente.
2. La explicación que daba Newton de la tercera ley de Kepler hacía caso omiso de las evidentes diferencias entre los planetas. En cierto modo importa poco que Júpiter sea mucho más grande que Mercurio; la diferencia de sus aceleraciones centrípetas tiene que ver simplemente con su distancia al Sol. Y de manera más sorprendente, la comparación de Newton de la aceleración centrípeta de la Luna y la aceleración de los cuerpos que caen sobre la superficie terrestre ignoraba la evidente diferencia entre la Luna y un cuerpo que cae al suelo, como es una manzana. ¿Por qué no importan estas diferencias?
3. En la obra fechada entre 1665 y 1666, Newton interpretaba la tercera ley de Kepler como la afirmación de que los productos de las aceleraciones centrípetas de los diversos planetas y los cuadrados de sus distancias al Sol son iguales para todos los planetas. Pero el valor habitual de este producto no es en absoluto igual al producto de la aceleración centrípeta de la Luna y el cuadrado de su distancia de la Tierra; es mucho más grande. ¿Qué explica esta diferencia?
4. Finalmente, en esta obra Newton había considerado que las órbitas de los planetas alrededor del Sol, y de la Luna alrededor de la Tierra, eran circulares y a velocidad constante, aun cuando Kepler ya había demostrado que no eran precisamente circulares, sino elípticas, que el Sol y la Tierra no estaban en el centro de las elipsis, y que las velocidades de los planetas son solo aproximadamente constantes.
En los años posteriores a 1666 Newton lidió con estos problemas. Mientras tanto, hubo otros que llegaron a las mismas conclusiones que Newton había alcanzado. En 1679, el antiguo adversario de Newton, Hooke, publicó sus conferencias Cutlerianas, que contenían algunas ideas sugerentes, aunque no matemáticas, acerca del movimiento y la gravitación:
En primer lugar, todo Cuerpo Celeste posee un poder gravitatorio o de atracción hacia su propio Centro, mediante el cual no solo atrae a sus propias partes, y evita que se alejen volando de él, como podemos observar que hace la Tierra, sino que también atrae a otros Cuerpos Celestes que quedan dentro de la esfera de su actividad. La segunda suposición es la siguiente: que todos los cuerpos que adquieren un movimiento directo y sencillo seguirán avanzando en línea recta hasta que alguna otra fuerza los desvíe y los haga describir un Círculo, una Elipsis o cualquier otra Línea Curva compuesta. La tercera suposición es que todas las fuerzas de atracción actúan de manera mucho más poderosa cuanto más cerca está de su propio Centro el cuerpo sobre el que actúan[257].Hooke le escribió a Newton comentándole sus especulaciones, entre ellas la ley de la inversa del cuadrado. Newton no le hizo caso, y le contestó que no había oído hablar del trabajo de Hooke, y que el «método de los indivisibles»[258] (es decir, el cálculo) era necesario para comprender los movimientos planetarios.
En agosto de 1684 Newton recibió en Cambridge la decisiva visita del astrónomo Edmund Halley. Al igual que Newton y Hooke, y también Wren, Halley había visto la relación entre la ley de la inversa del cuadrado de la gravitación y la tercera ley de Kepler para órbitas circulares. Halley le preguntó a Newton cuál sería la forma de la órbita de un cuerpo que se desplazara bajo la influencia de una fuerza que disminuye con la inversa del cuadrado de la distancia. Newton le contestó que la órbita sería una elipsis, y le prometió enseñarle una prueba. Ese mismo año Newton le presentó un documento de diez páginas, Sobre el movimiento de los cuerpos en órbita, que enseñaba cómo abordar el movimiento general de los cuerpos bajo la influencia de la fuerza dirigida hacia un cuerpo central.
Tres años más tarde la Royal Society publicó los Philosophiae Naturalis Principia Mathematica (Principios matemáticos de la filosofía natural), sin duda el libro más importante en la historia de la física.
Un físico actual que hojeara los Principia se quedaría sorprendido al ver lo poco que se parece a los tratados modernos de física. Hay muchos diagramas geométricos, pero pocas ecuaciones. Casi parece que Newton hubiera olvidado su propio desarrollo del cálculo. Pero tampoco es exactamente así. En muchos de sus diagramas se ven elementos que supuestamente se vuelven infinitesimales o infinitamente numerosos. Por ejemplo, al demostrar que la regla de áreas iguales de Kepler se aplica a cualquier fuerza dirigida hacia un centro fijo, Newton imagina que el planeta recibe de manera infinita muchos impulsos hacia el centro, cada uno de ellos separado del siguiente por un intervalo de tiempo infinitesimal. Este es exactamente el tipo de operación que se convierte no solo en respetable, sino también en fácil y rápida, gracias a las fórmulas generales de cálculo, pero estas fórmulas generales no aparecen por ninguna parte en sus Principia. En este volumen las matemáticas de Newton no son muy distintas de las que Arquímedes había utilizado al calcular las áreas del círculo, ni de las que Kepler había utilizado al calcular los volúmenes de toneles de vino.
El estilo de los Principia le recuerda al lector los Elementos de Euclides. Comienza con definiciones [259]:
Definición I
La cantidad de materia es una medida de la misma que resulta de su densidad y volumen conjuntamente.
Lo que en la traducción inglesa leemos como «cantidad de materia» se denomina massa en el latín de Newton, y hoy en día también se le llama «masa». Aquí Newton la define como el producto de la densidad por el volumen. Aunque Newton no define la densidad, su definición de la masa sigue siendo útil porque sus lectores podían dar por sentado que los cuerpos compuestos por las mismas sustancias, como el hierro a una temperatura dada, tendrán la misma densidad. Tal como había mostrado Arquímedes, las medidas de la gravedad específica proporcionan valores para la densidad relativa a la del agua. Newton observa que medimos la masa de un cuerpo a partir de su peso, pero confunde masa y peso.
Definición II
La cantidad de movimiento es una medida del mismo que resulta de la velocidad y la cantidad de materia conjuntamente.
Lo que Newton llama «cantidad de movimiento» es lo que hoy denominamos «momento», y Newton lo define como el producto de la velocidad por la masa.
Definición III
La fuerza inherente de la materia [vis insita] es la fuerza de resistencia mediante la que todo cuerpo, en la medida en que es capaz, persevera en su estado, ya sea de reposo o de movimiento uniformemente rectilíneo y hacia delante.
A continuación Newton explica que esta fuerza resulta de la masa del cuerpo, y que «no difiere en ningún aspecto de la inercia de la masa». Ahora a veces distinguimos la masa, en cuanto que cantidad que se resiste a un cambio en el movimiento, como «masa inerte».
Definición IV
La fuerza impresa es la acción ejercida sobre un cuerpo para hacerlo cambiar de estado, ya sea desde el reposo o de un movimiento uniformemente rectilíneo y hacia delante.
Esto define el concepto general de fuerza, pero no nos ayuda a definir ningún valor numérico para una fuerza dada. Las definiciones V, VI, VII y VIII definen la aceleración centrípeta y sus propiedades.
Después de las definiciones viene un escolio, o anotación, en el que Newton se niega a definir el espacio y el tiempo, pero ofrece una descripción:
I. El tiempo absoluto, el verdadero y el matemático, en sí o de sí mismo, y por su propia naturaleza, sin relación con ninguna fuerza externa, fluye de manera uniforme […]
II. El espacio absoluto, de su propia naturaleza sin relación a nada externo, siempre permanece homogéneo e inamovible.
Tanto Leibniz como el obispo George Berkeley criticaron su visión del tiempo y el espacio, arguyendo que solo las posiciones relativas en el tiempo y el espacio tienen algún sentido. Newton había reconocido en su escolio que normalmente solo encontramos posiciones y velocidades relativas, pero que ahora comprendía de manera nueva el espacio absoluto: en la mecánica de Newton, la aceleración (contrariamente a la posición o la velocidad) posee un significado absoluto. ¿Cómo podría ser de otro modo? La experiencia corriente nos dicta que la aceleración tiene un efecto; no hace falta preguntar: «Aceleración ¿con respecto a qué?». A partir de la fuerza que nos presiona hacia atrás en nuestro asiento, sabemos que estamos ganando velocidad porque el coche en el que nos encontramos ha acelerado de repente, miremos o no por la ventanilla del vehículo. Como veremos, en el siglo XX las ideas del espacio y el tiempo de Leibniz y Newton se reconciliaron con la teoría general de la relatividad.
Veamos por fin las famosas tres leyes del movimiento de Newton:
Primera ley
Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que se vea obligado a cambiar de estado por fuerzas impresas sobre él.
Esto ya lo sabían Gassendi y Huygens. No está claro por qué Newton se molestó en incluirlo como una ley aparte, puesto que la primera ley es una consecuencia trivial (aunque importante) de la segunda.
Segunda ley
El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.
Al hablar aquí de «cambio de movimiento» Newton se refiere al cambio en el momento, lo que llamaba «cantidad de movimiento» en la Definición II. De hecho es la velocidad del cambio del momento lo que es proporcional a la fuerza. Convencionalmente definimos las unidades en las que se mide la fuerza para que la velocidad del cambio de momento sea de hecho igual a la fuerza. Puesto que el momento es la masa por la velocidad, su velocidad de cambio es la masa por la aceleración. La segunda ley de Newton afirma, por tanto, que la masa por la aceleración es igual a la fuerza que produce la aceleración. Pero la famosa ecuación F = ma no aparece en los Principia; en el siglo XVIII los matemáticos del continente europeo reformularán así esa segunda ley.
Tercera ley
A cualquier acción le corresponde siempre una reacción igual y contraria; en otras palabras, las acciones mutuas de los cuerpos son siempre iguales y se dirigen en sentidos opuestos.
En un auténtico estilo geométrico, Newton sigue presentando una serie de corolarios deducidos de estas leyes. Entre ellos es notable el Corolario III, que nos da la ley de conservación del momento (véase Nota técnica 34).
Tras completar sus definiciones, leyes y corolarios, Newton comienza en el Libro I a deducir consecuencias. Demuestra que las fuerzas centrales (las fuerzas dirigidas hacia un solo punto central) y solo las fuerzas centrales imparten a un cuerpo un movimiento que abarca áreas iguales en tiempos iguales; que las fuerzas centrales inversamente proporcionales al cuadrado de la distancia y solo esas fuerzas centrales producen movimiento en una sección cónica, es decir, un círculo, una elipse, una parábola o una hipérbole; y que para el movimiento sobre una elipse dicha fuerza nos da periodos proporcionales al eje mayor de la elipse elevado a 3/2 (que, como se ha mencionado en el capítulo 11, es la distancia media del planeta al Sol a lo largo de su trayectoria). Así pues, una fuerza central que sea el inverso del cuadrado de la distancia puede explicar todas las leyes de Kepler. Newton también llena un vacío en su comparación de la aceleración centrípeta lunar y la aceleración de los cuerpos que caen, demostrando en la Sección XII del Libro I que un cuerpo esférico compuesto por partículas donde cada una de ellas produce una fuerza inversamente proporcional al cuadrado de la distancia de esa partícula produce una fuerza total que es inversamente proporcional al cuadrado de la distancia al centro de la esfera.
Al final de la Sección I del Libro I encontramos un extraordinario escolio en el que Newton comenta que ya no se basaba en la idea de los infinitesimales. Explica que «fluxiones» como las velocidades no son una razón entre infinitesimales, como había escrito antes; por el contrario, «estas razones últimas con las que las cantidades desaparecen no son en realidad razones de cantidades últimas, sino límites a los que se aproximan de manera continua las razones de cantidades que decrecen sin límite, y que pueden acercarse tanto que su diferencia es menor que cualquier cantidad dada». Esto resulta fundamental para la idea moderna de límite, sobre la que se basa en la actualidad el cálculo. Lo que no es moderno en los Principia es la idea de Newton de que los límites han de estudiarse utilizando los métodos de la geometría.
El Libro II presenta un largo tratamiento del movimiento de los cuerpos a través de fluidos; el objetivo primordial de esta discusión era deducir las leyes que gobiernan las fuerzas de resistencia en tales cuerpos[260]. Este libro desmonta la teoría de los vórtices de Descartes. A continuación calcula la velocidad de las ondas sonoras. Su resultado en la Proposición 49 (que la velocidad es la raíz cuadrada de la razón de la presión y la densidad) es correcta tan solo en cuanto a la magnitud, porque entonces nadie sabía cómo tener en cuenta los cambios de temperatura durante la expansión y la compresión. Pero (junto con su cálculo de la velocidad de las ondas oceánicas) fue un logro asombroso: era la primera vez que alguien había utilizado los principios de la física para ofrecer un cálculo más o menos realista de la velocidad de cualquier tipo de onda.
Al final, en el Libro III, El sistema del mundo, Newton llega a los datos procedentes de la astronomía. En la época de la primera edición de los Principia todo el mundo estaba de acuerdo con lo que se denomina la primera ley de Kepler: que los planetas se mueven en órbitas elípticas; pero la segunda y la tercera suscitaban considerables dudas: que la línea que va del Sol a cada planeta abarca áreas iguales en tiempos iguales, y que los cuadrados de los periodos de los diversos movimientos planetarios son proporcionales al cubo del eje principal de estas órbitas. Newton parece haberse aferrado a las leyes de Kepler no porque estuvieran perfectamente fundamentadas, sino porque encajaban también con su teoría. En el Libro III observa que las lunas de Júpiter y Saturno obedecen a la segunda y la tercera ley de Kepler, que las fases observadas de los cinco planetas, aparte de la Tierra, demostraban que giraban alrededor del Sol, que los seis planetas obedecen las leyes de Kepler y que la Luna satisface la segunda ley de este [261]. Sus concienzudas observaciones del cometa de 1680 demostraron que también se había movido en una sección cónica: una elipse o una hipérbole; en cualquier caso, muy próximo a una parábola. A partir de todo esto (y de su anterior comparación de la aceleración centrípeta de la Luna y la aceleración de los cuerpos que caen sobre la superficie terrestre), llegó a la conclusión de que existe una fuerza central que obedece una ley de la inversa del cuadrado, mediante la cual las lunas de Júpiter, Saturno y la Tierra se ven atraídas hacia sus planetas, y todos los planetas y cometas son atraídos por el Sol. Del hecho de que las aceleraciones producidas por la gravitación sean independientes de la naturaleza del cuerpo que se acelera, ya sea un planeta, una luna o una manzana, dependiendo tan solo de la naturaleza del cuerpo que produce la fuerza y la distancia entre ellos, junto con el hecho de que la aceleración producida por cualquier fuerza es inversamente proporcional a la masa del cuerpo sobre el que actúa, concluye que la fuerza de la gravedad sobre cualquier cuerpo ha de ser proporcional a la masa de ese cuerpo, de manera que cuando calculamos la aceleración se anula la dependencia de la masa del cuerpo. Esto traza una clara distinción entre la gravitación y el magnetismo, que actúan de manera muy distinta sobre cuerpos de composición distinta, aun cuando posean la misma masa.
Así pues, Newton, en su Proposición 7, utiliza su tercera ley del movimiento para descubrir que la fuerza de la gravedad depende de la naturaleza del cuerpo que produce la fuerza. Consideremos los cuerpos, 1 y 2, cuya masa sea m1 y m2. Newton había demostrado que la fuerza gravitatoria ejercida por el cuerpo 1 sobre el cuerpo 2 es proporcional a m2, y que la fuerza que el cuerpo 2 ejerce sobre el cuerpo 1 es proporcional a m1. Pero según la tercera ley, estas fuerzas son de igual magnitud, de manera que ambas han de ser proporcionales a m1 y m2. Newton consiguió confirmar la tercera ley en las colisiones, pero no en las interacciones gravitatorias. Tal como había recalcado George Smith, pasaron muchos años hasta que se pudo confirmar la proporcionalidad de la fuerza gravitatoria con la masa inercial de los cuerpos que atraían y de los que eran atraídos. Sin embargo, concluyó Newton, «la gravedad existe de manera universal en todos los cuerpos y es proporcional a la cantidad de materia de cada uno». Por eso el producto de las aceleraciones centrípetas de los diversos planetas y los cuadrados de sus distancias al Sol son mucho más grandes que el producto de la aceleración centrípeta de la Luna y el cuadrado de su distancia de la Tierra: es solo que el Sol, que provoca la fuerza gravitatoria sobre los planetas, es mucho más grande que la Tierra.
Estos resultados de Newton habitualmente se resumen en una fórmula para la fuerza gravitatoria F entre los cuerpos de masas m1 y m2 separados por una distancia r:
F = G × m1 × m2/ r2
donde G es una constante universal conocida hoy en día como la constante de Newton. Ni esta fórmula ni la constante G aparecen en los Principia, y aunque Newton hubiera introducido esta constante no podría haber descubierto su valor, porque desconocía la masa del Sol o de la Tierra. Al calcular el movimiento de la Luna o de los planetas, G aparece tan solo como un factor multiplicador de la masa de la Tierra o del Sol, respectivamente.
Incluso desconociendo el valor de G, Newton consiguió utilizar su teoría de la gravitación para calcular las razones de las masas de diversos cuerpos del sistema solar (véase Nota técnica 35). Por ejemplo, conociendo la razón de las distancias de Júpiter y Saturno hasta sus lunas y hasta el Sol, y conociendo la razón entre los periodos orbitales de Júpiter y Saturno y sus lunas, consiguió calcular la razón entre las alteraciones centrípetas de las lunas de Júpiter y Saturno y sus planetas, y entre la aceleración centrípeta de estos planetas y el Sol, a partir de lo cual pudo calcular la razón de las masas de Júpiter, Saturno y el Sol. Puesto que la Tierra tiene también una luna, en principio se pudo utilizar la misma técnica para calcular la razón de las masas de la Tierra y el Sol. Por desgracia, aunque la distancia de la Tierra a la Luna era perfectamente conocida a partir del paralaje diurno de la Luna, el paralaje diurno del Sol era demasiado pequeño para medirlo, por lo que la razón de las distancias de la Tierra al Sol y la Luna era desconocida. (Como vimos en el capítulo 7, los datos utilizados por Aristarco y las distancias que infirió de esos datos eran totalmente inexactos). De todos modos Newton siguió adelante y calculó la razón de las masas, utilizando un valor para la distancia entre la Tierra y el Sol que era apenas un límite inferior de esa distancia, y de hecho más o menos la mitad de su auténtico valor. He aquí los resultados de Newton para las razones de las masas, que da como corolario al Teorema VIII del Libro III de los Principia, junto con los valores modernos [262]:
| Razón | Valor de Newton | Valor actual |
| m (Sol)/ m(Júpiter) | 1,067 | 1,048 |
| m (Sol)/ m(Saturno) | 3,021 | 3,497 |
| m (Sol)/ m(Tierra) | 169,282 | 332,950 |
Como se puede ver a partir de esta tabla, los resultados de Newton eran bastante buenos para Júpiter, no malos para Saturno, pero totalmente erróneos para la Tierra, porque se desconocía su distancia al Sol. Newton era plenamente consciente de los problemas que planteaban las desviaciones de la observación, pero, al igual que casi todos los científicos hasta el siglo XX, era muy despreocupado a la hora de dar la horquilla resultante de desviación en sus resultados calculados. Además, como hemos visto en los casos de Aristarco y Al-Biruni, incluía el resultado de sus cálculos con una precisión mucho mayor que la que le garantizaba la exactitud de los datos sobre los que basaba los cálculos.
Por cierto, la primera estimación seria del tamaño del sistema solar la llevaron a cabo en 1672 Jean Richer y Giovanni Domenico Cassini. Midieron la distancia a Marte observando a diferencia en la dirección a Marte tal como se veía desde París y desde Cayena; puesto que la razón de las distancias de los planetas desde el Sol ya se conocía desde la teoría copernicana, eso les daba la distancia entre la Tierra y el Sol. En unidades modernas, su resultado fue de una distancia de 140 millones de kilómetros, razonablemente aproximada al valor moderno de 149,5985 millones de kilómetros como distancia media. Posteriormente se llevó a cabo una medida más exacta comparando observaciones en diferentes emplazamientos de la Tierra del tránsito de Venus sobre la cara del Sol en 1761 y en 1769, que nos dio una distancia entre la Tierra y el Sol de 153 millones de kilómetros [263].
En 1797-1798, Henry Cavendish consiguió por fin medir la fuerza gravitatoria entre masas de laboratorio, de lo cual se pudo inferir un valor para G. Pero Cavendish no se refería así a su medición, sino que, utilizando la conocida aceleración de 9,8 metros por segundo cuadrado debida al campo gravitatorio de la Tierra en su superficie y el volumen conocido de la Tierra, calculó que la densidad media de la Tierra era 5,48 veces la densidad del agua.
El resultado concordaba con una práctica de la física que ya venía de antiguo: comunicar los resultados como razones de proporciones en lugar de como magnitudes definidas. Por ejemplo, como hemos visto, Galileo demostró que la distancia que recorre un cuerpo al caer sobre la superficie de la Tierra es proporcional al cuadrado del tiempo, pero en ningún momento dijo que la constante que multiplicaba el cuadrado del tiempo que da la distancia recorrida fuera la mitad de 9,8 metros por segundo cuadrado. Ello se debía, al menos en parte, a la falta de cualquier unidad de longitud universalmente reconocida. Galileo podría haber dado la aceleración debida a la gravedad como braccia por segundo cuadrado, pero ¿qué hubiera significado eso para un inglés, o incluso para los italianos que vivían fuera de la Toscana? La estandarización internacional de unidades de longitud y peso [264] comenzó en 1742, cuando la Royal Society mandó dos reglas marcadas con las pulgadas estándar inglesas a la Académie des Sciences francesa; los franceses las marcaron con sus propias medidas de longitud y las mandaron de vuelta a Londres. Pero no fue hasta la adopción gradual internacional del sistema métrico, iniciada en 1799, cuando los científicos tuvieron un sistema de unidades universalmente comprendido. Hoy citamos un valor para G de 66,724 billones de metros por segundo al cuadrado y kilogramo: es decir, un pequeño cuerpo cuya masa sea un kilogramo a una distancia de un metro produce una aceleración gravitatoria de 66,724 billones de metros por segundo al cuadrado.
Tras exponer las teorías del movimiento y la gravitación de Newton, los Principia pasan a analizar algunas de sus consecuencias, que van mucho más allá de las tres leyes de Kepler. Por ejemplo, en la Proposición 14 Newton explica la precesión de las órbitas planetarias medidas (para la Tierra) por Al-Zarqali, aunque Newton no intenta un cálculo cuantitativo.
En la Proposición 19 Newton observa que los planetas deben de ser todos achatados, pues su rotación produce fuerzas centrífugas que son más grandes en el ecuador y se desvanecen en los polos. Por ejemplo, la rotación de la Tierra produce una aceleración centrípeta en su ecuador igual a 0,33528 metros por segundo al cuadrado, en comparación con los 9,8 metros por segundo al cuadrado de los cuerpos que caen, con lo que la fuerza centrífuga producida por la rotación de la Tierra es mucho menor que su atracción gravitatoria, aunque no enteramente despreciable, y por tanto la Tierra es casi esférica, aunque un tanto achatada. Las observaciones de la década de 1740 demostraron finalmente que el mismo péndulo oscila más lentamente cerca del ecuador que en latitudes más altas, tal como se esperaría si en el ecuador el péndulo estuviera más alejado del centro de la Tierra, pues la Tierra es achatada.
En la Proposición 39 Newton demuestra que el efecto de la gravedad sobre la Tierra achatada causa una precesión de su eje de rotación, la «precesión de los equinoccios», observada por primera vez por Hiparco. (Newton sentía un interés extraacadémico por esta precesión; utilizó sus valores junto con antiguas observaciones de las estrellas en un intento de fechar sucesos supuestamente históricos, como la expedición de Jasón y los Argonautas) [265]. En la primera edición de los Principia, Newton calcula, de hecho, que la precesión anual debida al Sol es de 6,82° (grados de arco) y que el efecto de la Luna es más grande en un factor de 61/3, lo que da un total de 50,0'' (segundos de arco) por año, una medida que coincide perfectamente con la precesión de 50'' por año entonces medida, y que se acerca al valor actual de 50,375'' por año.
Muy impresionante, pero Newton comprendió posteriormente que su resultado para la precesión debida al Sol (y de ahí para la precesión total) era 1,6 veces demasiado pequeña. En la segunda edición corrigió el resultado para el efecto del Sol, y también corrigió la razón de los efectos del Sol y la Luna, de manera que el total se acercaba de nuevo a 50'' por año, todavía en perfecta coincidencia con lo que se había observado [266]. Newton contaba con la correcta explicación cualitativa de la precesión de los equinoccios, y su cálculo proporcionó el orden de magnitud correcto para ese efecto, aunque para obtener una respuesta que concordara exactamente con la observación tuvo que hacer muchos ingeniosos ajustes.
Esto no es más que un ejemplo de cómo Newton manipulaba sus cálculos para que coincidieran perfectamente con las observaciones. Aparte de este ejemplo, R. S. Westfall[267] ha dado otros, como los cálculos de la velocidad del sonido de Newton, y su comparación de la aceleración centrípeta de la Luna con la aceleración de los cuerpos que caen sobre la superficie de la Tierra, mencionada anteriormente. A lo mejor Newton consideraba que sus adversarios, reales e imaginarios, nunca quedarían convencidos de nada que no coincidiera casi a la perfección con las observaciones.
En la Proposición 24 presenta su teoría de las mareas. Gramo a gramo, la Luna atrae al océano con más fuerza de lo que atrae a la Tierra sólida, cuyo centro está más alejado, y atrae a la Tierra sólida con más fuerza de lo que atrae al océano que se encuentra al lado de la Tierra alejado de la Luna. Así, se da un abultamiento provocado por la marea en el océano que queda debajo de la Luna, donde la gravedad de esta aleja el agua de la Tierra, y en el lado opuesto de la Tierra, donde la gravedad de la Luna aleja la Tierra del agua. Esto explicaba por qué en algunos lugares las mareas altas están separadas por 12 horas en lugar de 24. Pero el efecto es demasiado complicado para que esta teoría de las mareas pudiera verificarse en la época de Newton. Las mareas más altas y más bajas, conocidas como mareas vivas, tienen lugar cuando hay luna nueva o llena, de manera que el Sol, la Luna y la Tierra están en línea, lo que intensifica el efecto de la gravitación. Pero las peores complicaciones proceden del hecho de que las fuerzas gravitatorias en los océanos se ven enormemente influidas por la forma de los continentes y la topografía del fondo del océano, algo que Newton no pudo tener en cuenta.
Es un tema común en la historia de la física. La teoría de la gravitación de Newton llevó a cabo acertadas previsiones para fenómenos simples como el movimiento planetario, pero fue incapaz de dar una explicación cuantitativa de fenómenos más complicados, como las mareas. Hoy en día nos hallamos en una posición parecida con relación a la teoría de las poderosas fuerzas que mantienen unidos los quarks dentro de los protones y los neutrones dentro de los núcleos atómicos, una teoría conocida como la cromodinámica cuántica. Esta teoría ha conseguido explicar ciertos procesos de alta energía, como la producción de diversas partículas que interactúan poderosamente en la aniquilación de electrones energéticos y sus antipartículas, y su explicación nos convence de que la teoría es correcta. No podemos utilizar la teoría para calcular valores exactos para otras cosas que nos gustaría explicar, como las masas de los protones y los neutrones, porque el cálculo es demasiado complicado. De ahí que, como ocurre con la teoría de las mareas de Newton, la actitud adecuada sea la paciencia. Las teorías físicas quedan confirmadas cuando nos permiten calcular suficientes cosas que son lo bastante simples como para permitir cálculos fiables, aun cuando no podamos calcular todo lo que nos gustaría.
El Libro III de los Principia presenta cálculos de cosas ya medidas, y nuevas predicciones de otras cosas que todavía no se habían medido, pero incluso en la tercera y última edición de los Principia, Newton no pudo señalar ninguna predicción que se hubiera verificado en los cuarenta años transcurridos desde la primera edición. Sin embargo, en conjunto las pruebas a favor de la teoría del movimiento y la gravitación de Newton eran abrumadoras. Newton no tenía por qué seguir a Aristóteles ni explicar por qué existe la gravedad, y no lo intentó. En su «Escolio general» concluyó que:
Hasta ahora he explicado los fenómenos de los cielos y de nuestros mares por la fuerza de la gravedad, pero todavía no he asignado a esta ninguna causa. De hecho, esta fuerza surge por alguna causa que llega hasta el centro del Sol y de los planetas sin disminuir su capacidad para actuar, y que no actúa en proporción a la cantidad de superficies de las partículas sobre las que actúa (como suelen hacer las causas mecánicas), sino en proporción a la cantidad de materia sólida , y cuya acción se extiende por todas partes hasta inmensas distancias, y disminuye siempre de manera inversamente proporcional al cuadrado de la distancia […]Hasta ahora no he podido deducir de los fenómenos las razones de estas propiedades de la gravedad, y no voy a «inventarme» ninguna hipótesis.El libro de Newton apareció con una apropiada oda de Halley. Esta es la estrofa final:
Vosotros que os alimentáis del néctar celeste,venid a celebrar y cantar conmigoel nombre de Newton, a las musas tan querido;pues descubrió los ocultos tesoros de la verdad:y, a través de su mente, Febo con tal esplendor proyectóel radio de su propia divinidadque ningún mortala los dioses más se acercó. Los Principia establecieron las leyes del movimiento y el principio de la gravitación universal, pero eso es subestimar su importancia. Newton había legado al futuro un modelo de lo que podía ser la física teórica: una serie de principios matemáticos simples que gobiernan con precisión un vasto ámbito de fenómenos diferentes. Aunque Newton sabía perfectamente que la gravitación no era la única fuerza física, en la práctica su teoría era universal: cada partícula del universo atrae a todas las demás partículas con una fuerza proporcional al producto de su masa e inversamente proporcional al cuadrado de su distancia. Los Principia no solo deducían las reglas del movimiento planetario de Kepler como solución exacta de un problema simplificado, el movimiento de masas puntuales en respuesta a la gravitación de una sola esfera grande; también explicaban (aunque en algunos casos solo de manera cualitativa) una amplia variedad de fenómenos distintos: la precesión de los equinoccios, la precesión del perihelio, las trayectorias de los cometas, los movimientos de las lunas, la subida y bajada de las mareas y la caída de las manzanas [268]. En comparación, todos los éxitos anteriores de la teoría física eran limitados.
Tras la publicación de los Principia en 1686-1687, Newton se hizo famoso. Fue elegido miembro del parlamento por la Universidad de Cambridge en 1689 y de nuevo en 1701. En 1694 fue nombrado intendente de la Casa de la Moneda, donde encabezó una reforma de la acuñación de la moneda al tiempo que conservaba su cátedra Lucasiana. Cuando el zar Pedro el Grande fue a Inglaterra en 1698, insistió en visitar la Casa de la Moneda con la esperanza de charlar con Newton, pero no he encontrado ningún relato de su encuentro. En 1699, Newton fue nombrado director de la Casa de la Moneda, un puesto mucho mejor pagado. Renunció a su cátedra y se hizo rico. En 1703, tras la muerte de su antiguo enemigo Hooke, Newton se convirtió en presidente de la Royal Society. Fue nombrado caballero en 1705. Cuando en 1727 murió a causa de una piedra en el riñón, se le hizo un funeral de Estado en la abadía de Westminster, a pesar de que se había negado a aceptar los últimos sacramentos de la Iglesia de Inglaterra. Voltaire informó que Newton «ha sido enterrado como un rey que hubiera hecho el bien a sus súbditos»[269].
La teoría de Newton no encontró una aceptación universal[270]. A pesar del compromiso de Newton con el Cristianismo Unitariano, en Inglaterra hubo quien, como el teólogo John Hutchinson y el obispo Berkeley, estaban horrorizados por el naturalismo impersonal de la teoría de Newton, algo que resultaba injusto con su devoción personal. Newton incluso afirmó que solo la intervención divina podía explicar por qué la atracción gravitatoria mutua de los planetas no desestabilizaba el sistema solar [271], y por qué algunos cuerpos como el Sol y las estrellas brillaban con luz propia, mientras que otros, como los planetas y sus satélites, permanecían a oscuras. Hoy en día comprendemos la luz del Sol y las estrellas de una manera naturalista: brillan porque se calientan a causa de las reacciones nucleares de sus núcleos.
Aunque injustos con Newton, Hutchinson y Berkeley no se equivocaban del todo con el newtonianismo. Siguiendo el ejemplo de la obra de Newton, cuando no sus opiniones personales, a finales del siglo XVIII la física se había divorciado del todo de la religión.
Otro obstáculo para la aceptación de la obra de Newton era la antigua y falsa oposición entre matemáticas y física que hemos visto en un comentario de Gémino de Rodas citado en el capítulo 8. Newton no hablaba el lenguaje aristotélico de sustancias y cualidades, y no intentaba explicar la causa de la gravitación. El sacerdote Nicolás de Malebranche (1638-1715), al reseñar los Principia, dijo que era la obra de un geómetra, no de un físico. Sin duda Malebranche estaba pensando en la física al estilo de Aristóteles. Lo que no comprendía era que el ejemplo de Newton había modificado la definición de la física.
La crítica más contundente de la teoría de la gravitación de Newton procedió de Christiaan Huygens [272]. Admiraba enormemente los Principia, y no dudaba que los movimientos de los planetas estaban gobernados por una fuerza que disminuía de manera inversamente proporcional al cuadrado de la distancia, pero mantenía ciertas reservas acerca de si era verdad que toda partícula de materia atrae a otra partícula con una fuerza proporcional al producto de sus masas. Acerca de este punto, parece ser que Huygens se vio inducido a error por unas medidas inexactas de las velocidades de los péndulos a diversas latitudes, lo que pareció demostrar que la disminución de la velocidad del péndulo cerca del ecuador podría explicarse completamente como efecto de la fuerza centrífuga debida a la rotación de la Tierra. Si era cierto, eso implicaría que la Tierra no era achatada, como sería en el caso de que las partículas de la Tierra se atrajeran unas a otras, como había escrito Newton.
Ya en vida de Newton, su teoría de la gravitación encontró la oposición de Descartes en Francia y de su antiguo adversario, Leibniz, en Alemania. Ambos argumentaron que una atracción que actuara sobre millones de miles de espacios vacíos sería un elemento oculto de la filosofía natural, e insistieron en que a la acción de la gravedad se le debía dar una explicación racional, y no asumirla sin más.
En este punto, los filósofos naturales del continente europeo se aferraban al viejo ideal científico, que se remontaba a la época helénica: que las teorías científicas en última instancia debían fundarse solamente en la razón. Hemos aprendido a renunciar a ello. Aun cuando nuestra muy convincente teoría de los electrones y la luz se puede deducir del modelo estándar actual de las partículas elementales, que a su vez podría (esperemos) deducirse de una teoría más profunda, por muy lejos que vayamos nunca llegaremos a un fundamento que se base sobre la razón pura. Al igual que yo, casi todos los físicos de la actualidad se resignan al hecho de que siempre tendremos que preguntarnos por qué nuestras teorías más profundas no son de otra manera.
La oposición al newtonianismo halló su expresión en un famoso intercambio de cartas que tuvo lugar durante 1715 y 1716 entre Leibniz y un discípulo de Newton, el reverendo Samuel Clarke, que había traducido su Opticks al latín. Gran parte de su discusión se centraba en la naturaleza de Dios: ¿intervenía en el funcionamiento del mundo, tal como pensaba Newton, o lo había puesto en marcha para que funcionara por sí mismo desde el principio? [273] La polémica me parece tremendamente fútil, pues aunque trataran de algo real, es algo acerca de lo cual ni Clarke ni Leibniz podían saber absolutamente nada.
En última instancia, la oposición a las teorías de Newton no tuvo la menor importancia, pues la física newtoniana fue de éxito en éxito. Halley consiguió que las observaciones de los cometas de 1531, 1607 y 1682 encajaran en una sola órbita elíptica casi parabólica, demostrando que todo eran apariciones recurrentes del mismo comenta. Utilizando la teoría de Newton a la hora de tener en cuenta las perturbaciones gravitatorias debidas a la masa de Júpiter y Saturno, el matemático francés Alexis-Claude Clairaut y sus colaboradores predijeron, en noviembre de 1758, que este cometa regresaría al perihelio a mediados de abril de 1759. El cometa se observó el día de Navidad de 1758, quince años después de la muerte de Halley, y alcanzó el perihelio el 13 de marzo de 1759. A mediados del siglo XVIII la teoría de Newton se propagó gracias a las traducciones francesas de los Principia por parte de Clairaut y Émilie du Châtelet, y a través de la influencia de Voltaire, amante de Du Châtelet. Fue otro francés, Jean d'Alambert (1717-1783), quien en 1749 publicó el primer cálculo correcto y exacto de la precesión de los equinoccios basado en las ideas de Newton. Con el tiempo el newtonianismo triunfo en todas partes.
Eso no ocurrió porque la teoría de Newton satisficiera un criterio metafísico preexistente de la teoría científica. Tampoco respondía a las ideas de finalidad, centrales en la física de la Aristóteles, sino que proporcionaba principios universales que permitían el cálculo preciso de muchas cosas que antes habían parecido misteriosas. De este modo, ofreció un modelo irresistible para lo que debería ser, y podría ser, una teoría física.
Es un buen ejemplo de cómo la selección darwiniana actúa en la historia de la ciencia. Nos proporciona un intenso placer conseguir explicar algo con éxito, al igual que cuando Newton explicó las leyes del movimiento planetario de Kepler, junto con otras muchas cosas. Las teorías y los métodos científicos que sobreviven son aquellos que proporcionan esa satisfacción, encajen o no con ningún modelo preexistente sobre cómo habría que practicar la ciencia.
El rechazo de las teorías de Newton por parte de los seguidores de Descartes y Leibniz sugiere una moraleja para la práctica de la ciencia: nunca es seguro rechazar sin más una teoría que ha conseguido tantos éxitos impresionantes a la hora de explicar la observación como la de Newton. Las teorías convincentes puede que funcionen por razones que sus creadores no comprenden, y al final no son más que aproximaciones a otras teorías aún más convincentes, pero nunca simplemente errores.
En el siglo XX no siempre fue necesaria esta lección. La década de 1920 vio el advenimiento de la mecánica cuántica, un marco radicalmente nuevo para la teoría física. En lugar de calcular las trayectorias de un planeta o una partícula, se calcula la evolución de ondas de probabilidad, cuya intensidad en cualquier posición y tiempo nos dice la probabilidad de encontrar el planeta o partícula allí y entonces. El abandono del determinismo horrorizó tanto a los fundadores de la mecánica cuántica, entre ellos Max Planck, Erwin Schrödinger, Louis de Broglie y Albert Einstein, que ya no siguieron trabajando en las teóricas de la mecánica cuántica, como no fuera para señalar las consecuencias inaceptables de esas teorías. Algunas de las críticas de la mecánica cuántica llevadas a cabo por Schrödinger y Einstein son preocupantes, y siguen inquietándonos hoy en día, pero al final de la década de 1920 la mecánica cuántica había triunfado hasta tal punto a la hora de explicar las propiedades de los átomos, las moléculas y los fotones que había que tomarla en serio. El rechazo de las teorías de la mecánica cuántica por parte de estos físicos significaba que eran incapaces de participar en el gran avance de la física de los sólidos, los núcleos atómicos y las partículas elementales de las décadas de 1930 y 1940.
Al igual que la mecánica cuántica, la teoría del sistema solar de Newton había proporcionado lo que posteriormente se conocería como el Modelo Estándar. Introduje ese terminó en 1971[274] para describir la teoría de la estructura y evolución del universo en expansión tal como se había desarrollado hasta ese momento, explicando que:
Naturalmente, el modelo estándar podría estar equivocado en parte o en su conjunto. Sin embargo, su importancia reside no en su verdad indiscutible, sino en el punto de coincidencia que ofrece a una enorme variedad de datos cosmológicos. Al comentar estos datos en el contexto de una modalidad cosmológica estándar, podemos comenzar a apreciar su relevancia cosmológica, sea cual sea el modelo que al final resulte correcto.Poco más tarde, otros físicos y yo comenzamos a utilizar el término Modelo Estándar para referirnos a nuestra teoría incipiente de partículas elementales y sus diversas interacciones. Naturalmente, los sucesores de Newton no utilizaron ese término para referirse a la teoría newtoniana del sistema solar, pero podrían haberlo hecho. La teoría newtoniana sin duda proporcionaba un punto de encuentro para los astrónomos que intentaban explicar las observaciones que iban más allá de las leyes de Kepler.
Fueron muchos los autores que en el siglo XVIII y a principios del XIX desarrollaron los métodos para aplicar la teoría de Newton a los problemas en los que participaban más de dos cuerpos. Una innovación de gran importancia futura la examinó sobre todo Pierre-Simon Laplace a principios del siglo XIX. En lugar de sumar las fuerzas gravitatorias ejercidas por todos los cuerpos en un conjunto parecido al sistema solar, se calculó un «campo», una condición espacial que, en cada punto, da la magnitud y dirección de la aceleración producida por todas las masas del conjunto. Para calcular el campo, hay que solventar las ecuaciones diferenciales a las que obedece. (Estas ecuaciones imponen condiciones a la forma en la que el campo varía cuando el punto en el que se mide se mueve en alguna de las tres direcciones perpendiculares). Este enfoque provoca que sea casi trivial demostrar el teorema de Newton de que las fuerzas gravitatorias ejercidas fuera de una masa esférica son inversamente proporcionales al cuadrado de la distancia al centro de la esfera. Como veremos en el capítulo 15, más importante fue el papel fundamental que iba a jugar el concepto de campo a la hora de comprender la electricidad, el magnetismo y la luz.
En 1846, estas herramientas matemáticas fueron utilizadas de manera independiente por John Couch Adams y Jean-Joseph Leverrier para predecir la existencia y ubicación del planeta Neptuno a partir de las irregularidades en la órbita del planeta Urano. Neptuno fue descubierto poco después, en el lugar esperado.
Siguieron dándose pequeñas discrepancias entre la teoría y la observación, tanto en el movimiento de la Luna y de los cometas Halley y Encke, como en la precesión del perihelio de la órbita de Mercurio, que, según se observó, era 43'' (segundos de arco) por siglo mayor de lo que podían explicar las fuerzas gravitatorias producidas por los demás planetas. Finalmente se descubrió que las discrepancias en el movimiento de la Luna y los cometas se debían a fuerzas no gravitatorias, pero el hecho de que la precesión de Mercurio fuera mayor de lo esperado no se explicó hasta la aparición en 1915 de la teoría general de la relatividad de Albert Einstein.
En la teoría de Newton, las fuerzas gravitatorias en un punto y en un momento dados dependen de la posición de todas las masas al mismo tiempo, de manera que un cambio repentino de cualquiera de estas posiciones (como por ejemplo una erupción solar) produce un cambio instantáneo en todas las fuerzas gravitatorias, algo que entraba en conflicto con el principio de la teoría de la relatividad especial de 1905 de Einstein, según la cual ninguna influencia puede viajar más rápido que la luz, lo que apuntaba a una clara necesidad de modificar la teoría de la gravitación. En la teoría general de Einstein, un cambio repentino en la posición de una masa producirá un cambio en el campo gravitatorio que se halla en la vecindad inmediata de la masa, que entonces se propaga a la velocidad de la luz a distancias mayores.
La relatividad general rechaza la idea de Newton de un espacio y un tiempo absolutos. Las ecuaciones subyacentes son las mismas en todos los marcos de referencia, sea cual sea su aceleración o rotación. Hasta aquí Leibniz habría quedado satisfecho, pero de hecho la relatividad general justifica la mecánica newtoniana. Su formulación matemática se basa en una propiedad que comparte con la teoría de Newton: que todos los cuerpos, en un momento dado, sufren la misma aceleración debida a la gravedad. Esto significa que podemos eliminar los efectos de la gravitación en cualquier punto utilizando un marco de referencia, conocido como marco inercial, que comparte esta aceleración. Por ejemplo, uno no siente los efectos de la gravedad de la Tierra en un ascensor que cae libremente. Es en estos marcos inerciales de referencia donde se aplican las leyes de Newton, al menos para cuerpos cuya velocidad no se acerca a la de la luz.
El éxito del tratamiento del movimiento de los planetas y los cometas por parte de Newton demuestra que los marcos inerciales en la vecindad del sistema solar son aquellos en los que el Sol, y no la Tierra, está en reposo (o se mueve a velocidad constante). Según la relatividad general, ello obedece a que se trata del marco de referencia en el que la materia de galaxias lejanas no gira alrededor del sistema solar. En este sentido, la teoría de Newton proporciona una sólida base para preferir la teoría copernicana a la de Tycho. Pero en la relatividad general podemos utilizar cualquier marco de referencia que se nos antoje, no solo marcos inerciales. Si fuéramos a adoptar un marco de referencia como el de Tycho, en el que la Tierra está en reposo, entonces las galaxias lejanas parecerían llevar a cabo giros circulares una vez al año, y en la relatividad general este enorme movimiento crearía fuerzas afines a las de la gravitación, que actuarían sobre el Sol y los planetas y les impartirían los movimientos de la teoría de Tycho. Al parecer, es algo que Newton entrevió. En su Proposición 43, inédita, que no formó parte de los Principia, Newton reconoció que la teoría de Tycho podía ser cierta si alguna otra fuerza, aparte de la gravitación habitual, actuara sobre el Sol y los planetas [275].
Cuando en 1919 se confirmó la teoría de Einstein, gracias a la observación (ya vaticinada) de cómo se desviaban los rayos de luz a causa del campo gravitatorio del Sol, el Times declaró que se había demostrado que Newton se equivocaba. Eso fue un error. La teoría de Newton se puede considerar una aproximación a la de Einstein, una teoría que se vuelve más válida para objetos que se mueven a velocidades mucho menores a la de la luz. La teoría de Einstein no solo no desmiente la de Newton, sino que explica por qué la de este funciona, y cuándo funciona. La propia teoría de la relatividad general es sin duda una aproximación a una teoría más satisfactoria.
En la relatividad general, un campo gravitatorio se puede describir plenamente especificando, en cada punto del espacio y el tiempo, los marcos inerciales en los que los efectos de la gravitación no se hacen sentir. Esto se parece matemáticamente al hecho de poder trazar un mapa de una pequeña región en torno a cualquier punto de una superficie curva en la que la superficie parece plana, como el mapa de una ciudad sobre la superficie de la Tierra; la curvatura de toda la superficie se puede describir compilando un atlas de mapas locales que se solapen. De hecho, esta similitud matemática nos permite describir cualquier campo gravitatorio como una curvatura del espacio y el tiempo.
La base conceptual de la relatividad general es aquí distinta de la de Newton. En la teoría de la relatividad general, la idea de la fuerza gravitatoria queda reemplazada en gran medida por el concepto de curvatura del espacio-tiempo. Fue una píldora difícil de tragar para algunos. En 1730 Alexander Pope escribió un memorable epitafio para Newton:
La naturaleza y las leyes naturales en la noche se escondían;Dios dijo: «¡Creemos a Newton!». Y se hizo de día. En el siglo XX, el poeta satírico inglés J. C. Squire[276] añadió dos versos más:
Pero aquello no duró, pues el Demonio gritó:«¡A Einstein creemos!», y se restauró el statu quo .
No se lo crean. La teoría de la relatividad general tiene muchísimo que ver con el estilo de las teorías del movimiento y la gravitación de Newton: se basa en principios generales que se pueden expresar como ecuaciones matemáticas, de los que se pueden deducir matemáticamente consecuencias para una amplia variedad de fenómenos, que cuando se comparan con las observaciones permiten que se verifique la teoría. La diferencia entre las teorías de Einstein y las de Newton es mucho menor que las diferencias entre las teorías de Newton y las de cualquiera de sus predecesores.
Pero sigue planteándose una cuestión: ¿por qué la revolución científica de los siglos XVI y XVII se da en ese momento y en ese lugar? No faltan explicaciones posibles. En el siglo XV ocurrieron en Europa muchos cambios que contribuyeron a poner los cimientos de la revolución científica. Se consolidaron Gobiernos nacionales en Francia con Carlos VII y Luis XI y en Inglaterra con Enrique VII. La caída de Constantinopla en 1453 provocó que muchos estudiosos griegos huyeran hacia Italia e incluso más al oeste. El Renacimiento en las humanidades impuso unos criterios más rigurosos para la exactitud de los textos antiguos y sus traducciones. La invención de la imprenta y el tipo móvil consiguieron que la comunicación entre los estudiosos fuera más rápida y barata. El descubrimiento y exploración de América reforzó la idea de que había muchas cosas que los antiguos no sabían. Además, según las «tesis de Merton», la reforma protestante de principios del siglo XVI creó las condiciones para los grandes avances científicos de la Inglaterra del siglo XVII. El sociólogo Robert Merton sostenía la tesis de que el protestantismo creó una actitud social favorable a la ciencia y promovió una combinación de racionalismo y empirismo, así como la creencia de que se podía comprender el orden de la naturaleza, unas actitudes y creencias que encontró en el comportamiento de los científicos protestantes[277].
No resulta fácil juzgar lo importante que fueron estas influencias externas en la revolución científica. Pero aunque soy incapaz de decir por qué fue precisamente Isaac Newton quien descubrió las leyes clásicas del movimiento de la gravitación, ni por qué eso ocurrió en la Inglaterra de finales del siglo XVII, creo saber por qué esas leyes adquirieron su forma definitiva. Y la razón es muy simple: porque el mundo obedece las leyes de Newton de una manera muy aproximada.
Tras haber repasado la historia de la física desde Tales a Newton, ahora me gustaría presentar algunas reflexiones acerca de qué nos ha llevado a la moderna concepción de la ciencia representada por los logros de Newton y sus sucesores. Ni en el mundo antiguo ni en el medieval se concebía como una meta nada parecido a la ciencia moderna. De hecho, si nuestros predecesores pudieran haber imaginado la ciencia como es en la actualidad, no les habría gustado mucho. La ciencia moderna es impersonal, no deja espacio a la intervención sobrenatural ni (fuera de las ciencias del comportamiento) a los valores humanos; no tiene ningún propósito, y tampoco ofrece esperanzas de certezas. ¿Cómo hemos llegado aquí, entonces?
«Al enfrentarse a un mundo desconcertante, la gente de todas las culturas ha buscado explicaciones. Incluso cuando abandonaron la mitología, la mayoría de intentos de explicarlo no llevaron a nada satisfactorio». Tales intentó explicar la materia suponiendo que todo es agua, pero ¿adónde podía llegar con esa idea? ¿Qué nueva información le proporcionaba? Ni en Mileto ni en ninguna otra parte se podía construir nada sobre la idea de que todo es agua.
Pero de vez en cuando alguien encuentra una manera de explicar algunos fenómenos que encaja perfectamente y resulta tan clarificadora que proporciona una intensa satisfacción a su descubridor, sobre todo cuando se trata de un hallazgo cuantitativo y la observación lo corrobora en detalle. Imaginemos cómo se debió de sentir Ptolomeo cuando comprendió que, añadiendo un ecuante a los epiciclos y excéntricos de Apolonio e Hiparco, acababa de descubrir una teoría de los movimientos planetarios que le permitía predecir con bastante exactitud dónde estaba cada planeta en el cielo en un momento dado. Podemos hacernos una idea de su dicha a partir de las líneas que cité anteriormente: «Cuando estudio los círculos giratorios de las estrellas, mis pies ya no tocan la Tierra, sino que, sentado al lado del propio Zeus, me harto de ambrosía, el alimento de los dioses».
Su alegría tenía un fallo… pero siempre hay alguno. No hace falta ser un seguidor de Aristóteles para sentirse repelido por el peculiar movimiento en forma de lazo de los planetas siguiendo los epiciclos de la teoría de Ptolomeo. También estaba ese incómodo ajuste fino: los centros de los epiciclos de Mercurio y Venus tenían que tardar exactamente un año en dar una vuelta alrededor de la Tierra, el mismo tiempo que Marte, Júpiter y Saturno necesitaban para dar una vuelta en torno a su epiciclo. Durante más de mil años los filósofos discutieron cuál era el papel que correspondía a astrónomos como Ptolomeo: si comprender los cielos o simplemente que encajaran los datos.
Qué gran satisfacción debió de sentir Copérnico cuando comprendió que el ajuste fino y las órbitas en forma de lazo del esquema de Ptolomeo surgían simplemente porque vemos el sistema solar desde una Tierra que se mueve. Aun defectuosa, la teoría copernicana no acabó de encajar los datos sin algunas serias complicaciones. Hasta qué punto debió de disfrutar entonces Kepler, un hombre de gran talento matemático, al reemplazar el caos copernicano con movimientos sobre elipsis que obedecían a sus tres leyes.
Así pues, el mundo actúa sobre nosotros como una máquina que no para de darnos lecciones, reforzando nuestras buenas ideas con momentos de satisfacción. Después de siglos aprendemos de qué manera es posible comprender el mundo y cómo lograrlo. Aprendemos a no preocuparnos por el propósito del mundo, porque eso nunca lleva a la dicha que buscamos. Aprendemos a abandonar la búsqueda de certezas, porque las explicaciones que nos hacen felices nunca son definitivas. Aprendemos a hacer experimentos, a no preocuparnos por la artificialidad de nuestros planteamientos. Desarrollamos un sentido estético que nos aporta pistas de qué teorías funcionan, y eso aumenta nuestra satisfacción cuando funcionan. Cada vez comprendemos más cosas. Todo es impredecible y no obedece a ningún plan, pero conduce a un conocimiento fiable, y disfrutamos al andar el camino.
El gran descubrimiento de Newton dejó muchas cosas sin comprender. Siguen siendo un misterio la naturaleza de la materia, las propiedades de fuerzas que no eran la gravitación y que actúan sobre la materia, y las extraordinarias capacidades de la vida. En los años posteriores a Newton [278] se llevó a cabo un enorme progreso que supera con mucho el alcance de este libro, por no hablar de un solo capítulo. Este epílogo no tiene más objeto que recalcar un solo punto, que a medida que la ciencia progresaba después de Newton, comenzaba a formarse una imagen sorprendente: resultaba que el mundo está gobernado por leyes naturales mucho más simples y más unificadas que lo que habían imaginado en la época de Newton.
El propio Newton, en el Libro III de la Opticks, esboza una teoría de la materia que al menos abarca la óptica y la química:
Ahora las partículas de materia más pequeñas podrían cohesionarse mediante una atracción muy fuerte y componer partículas mayores de fuerza más débil; y muchas de estas podrían unirse y componer partículas aún mayores cuya fuerza es aún más débil, y así sucesivamente, hasta que el progreso acaba en las partículas mayores en las que se basan las operaciones de la química y los colores de los cuerpos naturales, y que al unirse componen cuerpos de considerable magnitud[279].También centró su atención en las fuerzas que actúan sobre estas partículas:
Pues de los fenómenos de la naturaleza debemos aprender qué cuerpos se atraen mutuamente, y cuáles son las propiedades y leyes de la atracción, antes de investigar la causa mediante la cual tiene lugar la atracción. La atracción de la gravedad, el magnetismo y la electricidad llegan a distancias muy considerables, por lo que han sido observadas a simple vista; y es posible que haya otros tipos de atracción que alcancen solo pequeñas distancias y escapen a la observación[280].Esto nos muestra que Newton era perfectamente consciente de que existen otras fuerzas de la naturaleza distintas de la gravitación. La electricidad estática se conocía de antiguo. Platón había mencionado en el Timeo que cuando se frota un trozo de ámbar (en griego electron), puede atraer pequeños fragmentos de materia. El magnetismo era conocido a partir de las propiedades de la magnetita, utilizadas por los chinos en la quiromancia y estudiadas en detalle por el médico de la reina Isabel, William Gilbert. Newton insinúa la existencia de fuerzas todavía no conocidas a causa de su cortísimo alcance, una premonición de las fuerzas nucleares débil y fuerte descubiertas en el siglo XX.
A principios del siglo XIX la invención de la pila eléctrica por parte de Alessandro Volta posibilitó llevar a cabo detallados experimentos cuantitativos en los campos de la electricidad y el magnetismo, y pronto se vio que no eran fenómenos completamente separados. Primero, en 1820 Hans Christian Ørsted, en Copenhague, descubrió que un imán y un alambre por el que discurre una corriente eléctrica ejercen entre ellos una fuerza mutua. Tras enterarse de ese resultado, André-Marie Ampère descubrió en París que los alambres que transportan una corriente eléctrica también ejercen una fuerza el uno sobre el otro. Ampère conjeturó que esos diversos fenómenos son todos el mismo: las fuerzas ejercidas por y sobre un trozo de hierro magnetizado se deben a corrientes eléctricas que circulan dentro del hierro.
Al igual que había ocurrido con la gravitación, la idea de que las corrientes y los imanes ejercieran fuerzas el uno sobre el otro se sustituyó por la idea de campo, en este caso un campo magnético. Cada imán y alambre que transporta una corriente contribuye al campo magnético total en cualquier punto de su vecindad, y este campo magnético ejerce una fuerza sobre cualquier imán o corriente eléctrica en ese punto. Michael Faraday atribuyó esos campos magnéticos producidos por una corriente eléctrica a las líneas de un campo magnético que rodeaba el alambre. También afirmó que las fuerzas eléctricas producidas por un trozo de ámbar frotado se debían a un campo eléctrico, representado por líneas que emanan radialmente a partir de las cargas eléctricas del ámbar. Y lo más importante, en la década de 1830 Faraday demostró la relación entre los campos eléctrico y magnético: un campo magnético cambiante, como el producido por una corriente eléctrica en un rollo de alambre que gira, produce un campo eléctrico, que puede inducir corrientes eléctricas en otro alambre. Es este fenómeno el que se utiliza para generar electricidad en las actuales centrales eléctricas.
La unificación definitiva de electricidad y magnetismo llegó unas décadas más tarde, de la mano de James Clerk Maxwell. Este consideraba los campos eléctrico y magnético como tensiones en un medio que todo lo ocupa, el éter, y expresó lo que se conocía acerca de la electricidad y el magnetismo en ecuaciones que relacionaban los campos y la velocidad a que se transformaban uno en otro. La novedad que añadió Maxwell fue que, al igual que un campo magnético cambiante genera un campo eléctrico, también un campo eléctrico cambiante genera un campo magnético. Como ocurre a menudo en la física, la base conceptual de las ecuaciones de Maxwell en términos de ese supuesto éter se ha abandonado, pero las ecuaciones sobreviven, incluso en las camisetas que llevan los estudiantes de física[281].
La teoría de Maxwell tuvo una consecuencia espectacular. Puesto que los campos eléctricos oscilantes producen campos magnéticos oscilantes, y estos producen campos eléctricos oscilantes, es posible obtener una oscilación autosostenida de campos magnéticos y eléctricos en el éter, o, como diríamos hoy día, en el espacio vacío. Allá por 1862 Maxwell descubrió que esta oscilación electromagnética se propagaba a una velocidad que, según sus ecuaciones, tenía más o menos el mismo valor numérico que la velocidad de la luz que se había obtenido. Es natural que Maxwell enseguida sacara la conclusión de que la luz no es más que una oscilación mutuamente autosostenida de campos eléctricos y magnéticos. La luz visible posee una frecuencia demasiado alta para ser producida por corrientes de circuitos eléctricos ordinarios, pero en la década de 1880 Heinrich Hertz fue capaz de generar ondas según las ecuaciones de Maxwell: ondas de radio que diferían de la luz visible solo porque tenían una frecuencia muy inferior. Así pues, la electricidad y el magnetismo se habían unificado no solo entre ellos, sino con la óptica.
Al igual que con la electricidad y el magnetismo, los avances a la hora de comprender la naturaleza de la materia comenzaron con la medida cuantitativa, es decir, las medidas de los pesos de las sustancias que participaban en las reacciones químicas. La figura clave en la revolución química fue un acaudalado francés, Antoine Lavoisier. A finales del siglo XVIII identificó el hidrógeno y el oxígeno como elementos, y demostró que el agua se compone de hidrógeno y oxígeno, que el aire es una mezcla de elementos y que el fuego se debe a la combinación de otros elementos con el oxígeno. Además, basándose en tales medidas, poco después John Dalton descubrió que el peso con que se combinan los elementos en las reacciones químicas se puede comprender basándose en la hipótesis de que los compuestos químicos puros, como el agua o la sal, están formados por un gran número de partículas (posteriormente llamadas moléculas) que a su vez están formadas por un número concreto de átomos de elementos puros. La molécula del agua, por ejemplo, está formada por dos átomos de hidrógeno y uno de oxígeno. En las décadas siguientes los químicos identificaron muchos elementos: algunos conocidos, como el carbono, el azufre y los metales corrientes; y otros aislados por primera vez, como el cloro, el calcio y el sodio. La tierra, el aire, el fuego y el agua no formaban parte de la lista. En la primera mitad del siglo XIX se calcularon las fórmulas químicas correctas de moléculas como el agua y la sal, lo que permitió calcular la proporción entre las masas de los átomos de los diferentes elementos y los pesos de las sustancias que participaban en las reacciones químicas.
La teoría atómica de la materia alcanzó un gran éxito cuando Maxwell y Ludwig Boltzman demostraron que el calor se podía comprender como energía distribuida entre enormes números de átomos o moléculas. Este paso hacia la unificación encontró la resistencia de algunos físicos, entre ellos Pierre Duhem, que dudaba de la existencia de los átomos y sostenía que la teoría del calor, la termodinámica, era al menos tan fundamental como la mecánica de Newton y la electrodinámica de Maxwell. Pero poco después de comienzos del siglo XX, varios experimentos nuevos convencieron a casi todo el mundo de que los átomos eran reales. Una serie de experimentos llevados a cabo por J. J. Thomson, Robert Millikan y otros demostraron que las cargas eléctricas se ganan y se pierden solo como múltiplos de una carga fundamental: la carga del electrón, una partícula descubierta por Thomson en 1897. El movimiento «browniano» azaroso de pequeñas partículas en la superficie de líquidos fue interpretada por Albert Einstein en 1905 como fruto de las colisiones de las moléculas individuales del líquido, una interpretación confirmada por los experimentos de Jean Perrin. Como respuesta a los experimentos de Thomson y Perrin, el químico Wilhelm Ostwald, que anteriormente había expresado su escepticismo acerca de los átomos, dejó en 1908 constancia de su cambio de opinión, en una declaración que de manera implícita volvía la mirada hasta Demócrito y Leucipo: «Ahora estoy convencido de que desde hace poco poseemos pruebas experimentales de la naturaleza discreta o granular de la materia, que las hipótesis atómicas buscaron en vano durante centenares y miles de años» [282].
Pero ¿qué son los átomos? Un gran paso hacia la respuesta tuvo lugar en 1911, cuando unos experimentos llevados a cabo en el laboratorio de Manchester de Ernest Rutherford mostraron que la masa de átomos de oro se concentra en un pequeño núcleo de fuerte carga positiva, alrededor del cual giran electrones más ligeros cargados negativamente. Los electrones son los responsables de los fenómenos de la química ordinaria, mientras que cualquier cambio en el núcleo libera las grandes cantidades de energía encontradas en la radiactividad.
Lo cual suscitó una nueva pregunta: ¿qué impide que los electrones atómicos en sus órbitas pierdan energía a través de la emisión de radiación y caigan en espiral hacia el núcleo? Eso no solo descartaría la existencia de átomos estables, sino que las frecuencias de la radiación emitida en esas pequeñas catástrofes atómicas formaría un continuo, lo cual contradecía la observación de que los átomos pueden emitir y absorber radiación solo a ciertas frecuencias discretas, que se pueden ver como líneas luminosas u oscuras en el espectro de los gases. ¿Qué determina esas frecuencias especiales?
Las respuestas se encontraron en las primeras tres décadas del siglo XX con el desarrollo de la mecánica cuántica, la innovación más radical de la física teórica desde la obra de Newton. Como su nombre sugiere, la mecánica cuántica requiere una cuantización (discreción) de las energías de varios sistemas. En 1913 Niels Bohr propuso que un átomo puede existir solo en ciertos estados de energía definida, y ofreció algunas reglas para calcular estas energías de los átomos más simples. Siguiendo el trabajo anterior de Max Planck, en 1905 Einstein ya había sugerido que la energía de la luz se da en forma de cuantos, partículas posteriormente llamadas fotones, y que cada fotón posee una energía proporcional a la frecuencia de la luz. Tal como explicó Bohr, cuando un átomo pierde energía al emitir un solo fotón, la energía de este fotón ha de ser igual a la diferencia entre las energías del estado atómico inicial y final, una exigencia que fija su frecuencia. Siempre hay un estado atómico de menor energía, que no puede emitir radiación y que por tanto es estable.
En la década de 1920, a estos primeros pasos les siguió el desarrollo de reglas generales de la mecánica cuántica, reglas que se pueden aplicar a cualquier sistema físico, y que principalmente fueron obra de Louis de Broglie, Werner Heisenberg, Wolfgang Pauli, Pascual Jordan, Erwin Schrödinger, Paul Dirac y Max Born. Las energías de los estados atómicos permitidos se calculan solucionando una ecuación, la ecuación de Schrödinger, de un tipo matemático general que ya era conocida a partir del estudio de las ondas sonoras y luminosas. La cuerda de un instrumento musical solo es capaz de producir los tonos para los que un número entero de medias longitudes de onda encaja en la cuerda; de manera análoga, Schrödinger descubrió que los niveles de energía permitidos de un átomo son aquellos para los que la onda gobernada por la ecuación de Schrödinger encaja perfectamente en torno a los átomos sin discontinuidades. Pero como reconoció por primera vez Born, estas ondas no son de presión ni de campos electromagnéticos, sino ondas de probabilidad: es más probable que haya cerca una partícula cuando la función de onda es más grande.
La mecánica cuántica no solo solucionó el problema de la estabilidad de los átomos y la naturaleza de las líneas espectrales; también introdujo la química en el marco de la física. Conociendo ya las fuerzas eléctricas existentes entre los electrones y los núcleos atómicos, la ecuación de Schrödinger pudo aplicarse a las moléculas y a los átomos, y permitió calcular la energía en sus diversos estados. Así fue posible decidir en principio qué moléculas son estables y qué reacciones químicas se permiten desde el punto de vista energético. En 1929 Dirac anunció triunfante que «las leyes físicas subyacentes necesarias para la teoría matemática de una gran parte de la física y de toda la química ya son completamente conocidas» [283].
Lo cual no significaba que los químicos les hubieran endosado sus problemas a los físicos y se hubieran retirado. Tal como Dirac comprendió perfectamente, para todas las moléculas, excepto para las más pequeñas, la ecuación de Schrödinger es demasiado complicada para resolverse, de manera que siguen siendo indispensables las herramientas y los conocimientos especiales de la química. Pero a partir de la década de 1920 se comprendió que cualquier principio general de la química, como la regla de que los metales forman compuestos estables con elementos halógenos como el cloro, obedece a que la mecánica cuántica del grupo de los electrones está sometida a fuerzas electromagnéticas.
A pesar de que este fundamento explicaba muchas cosas, estaba muy lejos de quedar satisfactoriamente unificado. Había partículas: los electrones, los protones y los neutrones que componen el núcleo atómico. Y había campos: el campo electromagnético, y cualquier otro campo de corto alcance y desconocido por entonces, supuestamente responsable de las poderosas fuerzas que mantienen unido el núcleo atómico y de las fuerzas débiles que convierten los neutrones en protones o los protones en neutrones en la radiactividad. Esta distinción entre partículas y campos fue desechada en la década de 1930 con el advenimiento de la teoría cuántica de campos. Al igual que existe un campo electromagnético, cuya energía y momento vienen en paquetes conocidos como fotones, también existe un campo de electrones, cuya energía y momento vienen en paquetes de electrones, y lo mismo ocurre con otros tipos de partículas elementales.
Todo esto estaba lejos de ser evidente. Podemos sentir directamente los efectos de los campos gravitatorio y electromagnético porque los cuantos de estos campos poseen una masa cero, y existen partículas tales (conocidas como bosones) que en gran número pueden ocupar el mismo estado. Estas propiedades permiten que los fotones se unan para formar campos eléctricos y magnéticos que parecen obedecer a las reglas de la física clásica (es decir, no cuántica). Los electrones, por el contrario, poseen masa, por lo que dos partículas (conocidas como fermiones) no pueden ocupar el mismo estado, de manera que los campos de electrones nunca se pueden ver en observaciones macroscópicas.
A finales de la década de 1940, la electrodinámica cuántica, la teoría cuántica de campos de fotones, electrones y antielectrones, alcanzó un éxito asombroso, calculando cantidades, como la fuerza del campo magnético del electrón, que coincidían con los experimentos hasta muchos decimales [284]. Después de este logro, resultaba natural intentar desarrollar una teoría cuántica de campos que abarcara no solo los fotones, los electrones y los antielectrones, sino también las demás partículas descubiertas en los rayos cósmicos y aceleradores, y las fuerzas fuertes y débiles que actúan sobre ellos.
Ahora tenemos una teoría cuántica de campos conocida como Modelo Estándar, que es una versión ampliada de la electrodinámica cuántica. Junto con el campo de electrones hay un campo de neutrinos, cuyos cuantos son fermiones parecidos a electrones pero con carga eléctrica cero y masa casi cero. Hay un par de campos de quarks, cuyos cuantos son los componentes de los protones y neutrones que forman el núcleo atómico. Por razones que nadie entiende, este menú se repite dos veces, con quarks mucho más pesados y partículas parecidas a electrones mucho más pesadas, y con sus neutrinos asociados. El campo electromagnético aparece en una imagen unificada «electrodébil», junto con otros campos responsables de las interacciones nucleares débiles, que permiten que los protones se conviertan en neutrones y viceversa en la descomposición radiactiva. Los cuantos de estos campos son bosones pesados: el W+ y el W-, con carga eléctrica, y el eléctricamente neutro Z0. Hay también ocho campos de «gluones» matemáticamente parecidos y responsables de las interacciones nucleares fuertes, que mantienen unidos los quarks dentro de los protones y neutrones. En 2012 se descubrió la última pieza que faltaba del Modelo Estándar: un bosón pesado eléctricamente neutro que había sido predicho por la parte electrodébil del Modelo Estándar.
El Modelo Estándar no es el final de la historia. Deja fuera la gravitación; no explica la «materia oscura», que según los astrónomos supone cinco sextas partes de la masa del universo; y deja demasiadas cantidades numéricas sin explicar, como las proporciones de las masas de los diversos quarks y partículas parecidas a los electrones. Pero aun así, el Modelo Estándar ofrece una visión extraordinariamente unificada de todos los tipos de materia y fuerza (excepto la gravitación) que encontramos en nuestros laboratorios, en una serie de ecuaciones que caben en una sola hoja de papel. Podemos estar seguros de que el Modelo Estándar será al menos una parte aproximada de cualquier teoría futura mejor.
El Modelo Estándar les habría parecido insatisfactorio a muchos filósofos naturales, desde Tales a Newton. Es impersonal; no hay el menor atisbo de preocupación humana, ni por el amor ni por la justicia. No ayudará a nadie que lo estudie a ser mejor persona, como esperaba que ocurriera Platón con el estudio de la astronomía. Además, contrariamente a lo que Aristóteles esperaba de una teoría física, el Modelo Estándar no tiene ningún propósito. Naturalmente, vivimos en un universo gobernado por el Modelo Estándar, y podemos imaginar que los electrones y los dos quarks ligeros son lo que son para que nosotros podamos existir, pero entonces, ¿qué pensar de sus homólogos más pesados, que son irrelevantes para nuestras vidas?
El Modelo Estándar se expresa en ecuaciones que gobiernan los diversos campos, pero no se puede deducir tan solo de las matemáticas. Tampoco se infiere directamente de la observación de la naturaleza. De hecho, los quarks y los gluones se atraen por fuerzas que aumentan con la distancia, por lo que estas partículas nunca se pueden observar de manera aislada. El Modelo Estándar tampoco se puede deducir de ninguna idea filosófica. Se trata más bien de un producto de la intuición, guiado por el juicio estético, y validado por el éxito de muchas de sus predicciones. Aunque el Modelo Estándar no es el final de la historia, pensamos que muchos de sus aspectos reaparecerán en cualquier teoría que lo suceda.
La intimidad que existió antaño entre la física y la astronomía ha continuado. Ahora comprendemos las reacciones nucleares lo bastante bien no solo para calcular cómo brillan y evolucionan el Sol y la estrellas, sino también para comprender cómo se produjeron los elementos más ligeros en los primeros minutos de la presente expansión del universo. Y al igual que en el pasado, la astronomía le presenta ahora a la física un reto formidable: la expansión del universo se acelera, supuestamente debido a la energía oscura contenida no en la masa ni en los movimientos de las partículas, sino en el espacio mismo.
Hay un aspecto de la experiencia que a primera vista parece desafiar la comprensión si nos basamos en una teoría física carente de propósito como el Modelo Estándar. No podemos evitar la teleología al hablar de las cosas vivas. Describimos corazones, pulmones, raíces y flores en términos del propósito que tienen, una tendencia que solo se incrementó con la gran expansión, posterior a Newton, de la información acerca de las plantas y los animales debida a naturalistas como Carl Linneo y Georges Cuvier. No solo los teólogos, sino también los científicos, entre ellos Robert Boyle e Isaac Newton, han visto las maravillosas aptitudes de las plantas y los animales como prueba de un Creador benévolo. Aun cuando podamos evitar una explicación sobrenatural de las actitudes de las plantas y los animales, desde siempre parece inevitable que para comprender la vida hubiéramos de basarnos en principios teleológicos muy distintos a los que sustentaban teorías físicas como la de Newton.
La unificación de la biología con el resto de la ciencia comenzó a ser posible a mediados del siglo XIX, con las propuestas independientes de Charles Darwin y Alfred Russel Wallace de la teoría de la evolución a través de la selección natural. La evolución era ya una idea conocida, sugerida por los fósiles. Muchos de los que aceptaron la realidad de la evolución la explicaban como resultado de un principio fundamental de la biología, una tendencia inherente de las cosas vivas a mejorar, un principio que habría excluido cualquier unificación de la biología con la física. Darwin y Wallace, por el contrario, propusieron que la evolución actúa a través de variaciones heredables, y que las variaciones favorables no son más probables que las desfavorables, aunque las variaciones que mejoran las posibilidades de sobrevivir y reproducirse son las que tienen más probabilidades de propagarse. [285]
Se tardó mucho en aceptar la selección natural como el mecanismo de la evolución. En la época de Darwin nadie conocía el mecanismo de la herencia, ni de la aparición de variaciones heredables, por lo que los biólogos aún albergaban la esperanza de encontrar una teoría que explicara su propósito. Resultaba especialmente desagradable imaginar que los humanos son el resultado de millones de años de selección natural actuando sobre variaciones heredables al azar. Con el tiempo, el descubrimiento de las reglas de la genética y la incidencia de las mutaciones condujo, en el siglo XX, a una «síntesis neodarwiniana» que le dio una base más firme a la teoría de la evolución a través de la selección natural. Finalmente la teoría se cimentó sobre la química, y por tanto sobre la física, al comprender que la información genética se transmite mediante las moléculas de doble hélice del ADN.
Así fue como la biología se unió a la química en una visión unificada de la naturaleza basada en la física. Pero es importante reconocer las limitaciones de esta unificación. Nadie va a reemplazar el lenguaje y los métodos de la biología con una descripción de los seres vivos en términos de moléculas individuales, por no hablar de quarks y electrones. Para empezar, los seres vivos, más aún que las grandes moléculas de la química orgánica, son demasiado complicados para una descripción así. Y más importante todavía, aun cuando pudiéramos seguir el movimiento de cada átomo de una planta o animal, en esa inmensa masa de datos perderíamos lo que nos interesa: un león que caza un antílope o una flor que atrae a las abejas.
Para la biología, al igual que para la geología —pero no para la química— hay otro problema. Los seres vivos son lo que son no solo por los principios de la física, sino también por un gran número de accidentes históricos, incluido aquel en que un cometa o meteoro impactó contra la Tierra hace 65 millones de años con la fuerza suficiente como para exterminar a los dinosaurios, y retrocediendo aún más hasta el hecho de que la Tierra se formó a una cierta distancia del Sol y con una cierta composición química inicial. Podemos comprender algunos de estos accidentes de manera estadística, pero no individual. Kepler se equivocaba; nadie será capaz de calcular jamás la distancia de la Tierra al Sol basándose tan solo en los principios de la física. Lo que queremos dar a entender por unificación de la biología con el resto de la ciencia es solo que no puede haber principios de biología independientes, y tampoco de geología. Cualquier principio general de biología es lo que es debido a los principios fundamentales de la física unidos a los accidentes históricos, que por definición no se pueden explicar nunca.
El punto de vista aquí descrito se denomina (a menudo con desaprobación) «reduccionismo». Hay quienes se oponen al reduccionismo incluso dentro de la física. Los físicos que estudian los fluidos o los sólidos a menudo citan ejemplos de «emergencia»: la aparición, en la descripción de fenómenos macroscópicos, de conceptos como la transición de calor o de fase, que no poseen analogía alguna en la física de las partículas elementales, y que no dependen de los detalles de las partículas elementales. Por ejemplo, la termodinámica, la ciencia del calor, se aplica a una amplia variedad de sistemas: no solo a aquellos considerados por Maxwell y Boltzmann, que contienen gran número de moléculas, sino también a las superficies de grandes agujeros negros. Pero no se aplica a todo, y cuando preguntamos si se aplica un sistema dado y por qué, hemos de referirnos a principios más profundos y más fundamentales de la física. En este sentido, el reduccionismo no es un programa para la reforma de la práctica científica, sino una concepción de por qué el mundo es como es.
No sabemos durante cuánto tiempo la ciencia seguirá por este camino reduccionista. Quizá lleguemos a un punto en el que, con los recursos de nuestra especie, ya no podamos seguir avanzando. En este momento, parece que existe una escala de masa más o menos un trillón de veces más grande que la masa del átomo de oxígeno en la que la gravedad y otras fuerzas todavía no detectadas se unifican con las fuerzas del Modelo Estándar. (Se conoce como la «masa de Planck»; es la masa que tendrían que poseer las partículas para que su atracción gravitatoria fuera tan fuerte como la repulsión eléctrica entre dos electrones con la misma separación). Aun cuando los físicos dispusiéramos de todos los recursos económicos de la raza humana, no se nos ocurre ninguna manera de crear partículas con una masa tan grande en nuestros laboratorios.
A lo mejor se nos agotan los recursos intelectuales: quizá los humanos no seamos lo bastante inteligentes para comprender las leyes realmente fundamentales de la física. O quizá encontremos fenómenos que en principio no se acomoden a la estructura unificada para todas las ciencias. Por ejemplo, aunque quizá lleguemos a comprender los procesos cerebrales responsables de la conciencia, resulta difícil entender cómo podremos describir alguna vez los sentimientos conscientes en términos físicos.
Sin embargo, hemos recorrido un largo camino, y todavía no hemos llegado al fin[286]. Se trata de una historia extraordinaria: cómo Newton unificó la física celeste y la terrestre, cómo se desarrolló una teoría unificada de la electricidad y el magnetismo que acabó explicando la luz, cómo la teoría cuántica del electromagnetismo se amplió para incluir las fuerzas nucleares fuertes y débiles, y cómo la química e incluso la biología acabaron formando parte de una concepción de la naturaleza, unificada aunque incompleta, basada en la física. Los amplios principios científicos que descubrimos se han reducido, y se siguen reduciendo, para alcanzar una teoría física más fundamental.
He tenido la suerte de contar con la ayuda de varios doctos eruditos: el experto en el mundo clásico Jim Hankinson, y los historiadores Bruce Hunt y George Smith. Han leído casi todo el libro, y he llevado a cabo numerosas correcciones basadas en sus sugerencias. Les agradezco profundamente su ayuda. También estoy en deuda con Louise Weinberg por sus inapreciables comentarios críticos, y por sugerir los versos de John Donne que ahora adornan las páginas iniciales de este libro. Gracias también a Peter Dear, Owen Gingerich, Alberto Martínez, Sam Schweber y Paul Woodruff por su consejo en temas específicos. Finalmente, por su aliento y buenos consejos, le estoy muy agradecido a mi sabio agente, Morton Janklow; y a mis estupendos editores en HarperCollins, Tim Duggan y Emily Cunningham.
Las siguientes notas describen los antecedentes científicos y matemáticos de muchos de los descubrimientos históricos comentados en este libro. Los lectores que hayan aprendido algo de álgebra y geometría en la educación secundaria y no se hayan olvidado del todo de lo que aprendieron no deberían tener ningún problema con el nivel de matemáticas de estas notas. De todos modos, he intentado organizar el libro de manera que los lectores que no estén interesados en los detalles técnicos puedan saltarse esas notas y seguir comprendiendo el texto principal.
Una advertencia: el razonamiento de estas notas no es necesariamente idéntico al que se ha seguido históricamente. Desde Tales a Newton, el estilo de las matemáticas que se aplicó a los problemas físicos fue mucho más geométrico y menos algebraico de lo que es común hoy en día. Pero analizar estos problemas en ese estilo geométrico sería difícil para mí y tedioso para el lector. En estas notas demostraré que los resultados obtenidos por los filósofos naturales del pasado siguen (o en algunos casos, no siguen) las observaciones y supuestos en los que se basaron, pero sin intentar reproducir fielmente los detalles de su razonamiento.
§1. Teorema de Tales
El teorema de Tales utiliza un razonamiento geométrico simple para derivar un resultado acerca de los círculos y los triángulos que no es inmediatamente obvio. Fuera o no Tales quien demostró este resultado, resulta útil observar el teorema como un ejemplo del alcance del conocimiento geométrico de los griegos antes de la época de Euclides.
Consideremos cualquier círculo, de cualquier diámetro. Sean A y B los puntos de intersección de diámetro y el círculo. Tracemos una línea desde A y B a cualquier otro punto P del círculo. El diámetro y las líneas que van de A a P y de B a P forman un triángulo, ABP (identificamos los triángulos enumerando sus tres vértices). El teorema de Tales nos dice que se trata de un triángulo rectángulo: el ángulo del triángulo ABP en el punto P es un ángulo recto, o dicho de otro modo, tiene 90°.
El truco a la hora de demostrar este teorema consiste en trazar una línea desde el centro C del círculo hasta el punto P, lo que divide el triángulo ABP en dos triángulos, ACP y BCP (véase figura 1). Estos dos triángulos son isósceles, es decir, triángulos con dos lados iguales. En el triángulo ACP, los lados CA y CP son ambos radios del círculo, por lo que, según la definición de círculo, poseen la misma longitud.(identificamos los lados del triángulo por los vértices que conectan). De manera parecida, en el triángulo BCP, los ladosCB y CP son iguales. En un triángulo isósceles, los ángulos adyacentes a los dos ángulos iguales son iguales, por lo que el ángulo α (alfa) en la intersección de los lados AP y AC es igual al ángulo de la intersección de los lados AP y CP, mientras que el ángulo β (beta) en la intersección de los lados BP y BC es igual al ángulo en la intersección de los lados BP y CP.
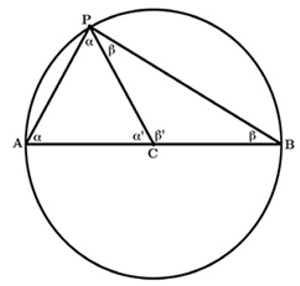
Figura 1. Demostración del teorema de Tales. El teorema afirma que, dado cualquier punto P del círculo, el ángulo entre las líneas de los extremos del diámetro a Pes un ángulo recto.
2α + α' = 180°
2β + β' = 180°
2(α + β) + (α' + β') = 360°
Ahora bien, α' + β' es el ángulo entre AC y BC, que se unirán en una línea recta, que por tanto es medio giro, es decir, 180°, por lo que2(α + β) = 360° − 180° = 180°
y por tanto, α + β = 90°. Pero con solo echar un vistazo a la figura 1 ya veremos que α + β es el ángulo entre los lados AP y BP del triángulo ABP, con el que comenzamos, de manera que vemos ahora que se trata, de hecho, de un triángulo rectángulo, que es lo que se quería demostrar.§2. Sólidos platónicos
En las especulaciones de Platón acerca de la naturaleza de la materia, jugaron un papel fundamental una clase de formas sólidas conocidas como poliedros regulares, que hemos acabado conociendo con el nombre de sólidos platónicos. Los poliedros regulares se pueden considerar generalizaciones tridimensionales de los polígonos regulares de la geometría plana, y en cierto sentido se componen de polígonos regulares. Un polígono regular es una figura plana limitada por un número n de líneas rectas; todas ellas son de la misma longitud y se encuentran en los vértices n con los mismos ángulos. Ejemplos son el triángulo equilátero (un triángulo en el que todos los lados son iguales) y el cuadrado. Un poliedro regular es una figura sólida limitada por polígonos regulares, todos ellos idénticos, y posee el mismo número N de polígonos que se encuentran con los mismos ángulos en cada vértice.
El ejemplo más familiar de un poliedro regular es el cubo. Un cubo está limitado por seis cuadrados iguales, y en cada uno de sus ocho vértices se encuentran tres cuadrados. Hay un ejemplo incluso más simple de poliedro regular, el tetraedro, una pirámide triangular limitada por cuatro triángulos equiláteros iguales, donde en cada uno de esos cuatro vértices se encuentran tres triángulos. (Aquí solo nos ocuparemos de los poliedros que son convexos, o sea, donde cada vértice apunta hacia fuera, como es el caso del cubo y el tetraedro). Como hemos leído en el Timeo, de alguna manera Platón sabía que estos poliedros regulares solo podían tener cinco formas posibles, que él consideraba las formas de los átomos de los que se componía toda materia. Son el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro, que poseen 4, 6, 8, 12 y 20 caras respectivamente.
El primer intento de demostrar que existen solo cinco poliedros regulares que ha sobrevivido de la Antigüedad es el último y culminante párrafo de los Elementos de Euclides. Desde la Proposición 13 a la 17 del Libro XIII, Euclides había presentado las construcciones geométricas del tetraedro, el octaedro, el cubo, el icosaedro y el dodecaedro. Entonces afirma: «Digo ahora que no se puede construir ninguna otra figura, aparte de las cinco mencionadas, que contenga figuras equiláteras y equiangulares iguales entre sí»[288]. De hecho, lo que Euclides demuestra en realidad después de esa afirmación es algo menos convincente: que para un polígono regular solo existen cinco combinaciones del número n de lados de cada cara poligonal, y del número N de polígonos que se encuentran en cada vértice. La prueba que vamos a ofrecer es esencialmente la misma que la de Euclides, expresada en términos modernos.
El primer paso consiste en calcular el ángulo interior θ (theta) en cada uno de los n vértices de un polígono regular de n lados. Trazamos una línea desde el centro del polígono a cada uno de los vértices del perímetro, lo que divide el interior del polígono en n triángulos. Puesto que la suma de los ángulos de cualquier triángulo es 180°, y cada uno de estos triángulos posee dos vértices de ángulos θ/2, el ángulo del tercer vértice de cada triángulo (el que está en el centro del polígono) ha de ser 180° – θ. Pero estos n ángulos deben sumar 360°, con lo que n (180° – θ) = 360°. La solución es:
θ = 180º -360º/n
Por ejemplo, para un triángulo equilátero tenemos n = 3, por lo que θ = 180° – 120° = 60°, mientras que para un cuadrado n = 4, de manera queθ = 180° – 90 = 90°.
El siguiente paso consiste en imaginar que recortamos todas las aristas y los vértices de un polígono regular excepto un vértice, y empujamos el poliedro hasta que forme un solo plano en ese vértice. Los N polígonos que se encuentran en ese vértice se hallan en el mismo plano, pero ha de sobrar espacio, o los N polígonos habrían formado una sola cara. De manera que tenemos que N θ < 360°. Utilizando la fórmula anterior para θ y dividiendo ambos lados de la desigualdad por 360°, entonces tenemosN (½ - 1/n) < 1
o de manera equivalente (dividiendo ambos lados por N),½ < 1/n + 1/N ≥ 3
Ahora bien, es imprescindible que n ≥ 3, pues de lo contrario no existiría área entre los lados de los polígonos, y también ha de darse que N ≥ 3, pues de lo contrario no habría espacio entre las caras que se unen en un vértice. (Por ejemplo, para un cubo n = 4, porque los lados son cuadrados, y N = 3). Así, la desigualdad anterior no permite que 1/n o 1/N sea tan pequeño como 1/2 – 1/3 = 1/6, y en consecuencia ni n ni N pueden ser tan grandes como 6. Podemos comprobar fácilmente cada par de valores de números enteros 5 ≥ N ≥ 3 y 5 ≥ n ≥ 3 para ver si satisfacen la desigualdad, y encontrar que solo hay cinco pares que lo cumplen:| (a) | N = 3, | n = 3 |
| (b) | N = 4, | n = 3 |
| (c) | N = 5, | n = 3 |
| (d) | N = 3, | n = 4 |
| (e) | N = 3, | n = 5 |
(En los casos n = 3, n = 4 y n = 5, los lados del poliedro regular son respectivamente triángulos equiláteros, cuadrados y pentágonos regulares). Estos son los valores de N y n que encontramos en el tetraedro, el octaedro, el icosaedro, el cubo y el dodecaedro.
Todo esto lo demostró Euclides. Pero no demostró que solo existe un polígono regular para cada par de n y N. Ahora vamos a ir más allá de Euclides, y demostraremos que para cada valor de N y n podemos encontrar resultados únicos para las demás propiedades del polígono: el número C de caras, el número A de aristas y el número V de vértices. Aquí tenemos tres incógnitas, de manera que para este propósito necesitamos tres ecuaciones. Para deducir la primera, observemos que el número total de aristas de todos los polígonos de la superficie del poliedro es nC, pero cada una de las A aristas linda con dos polígonos, de manera que
2A = nC
Además, hay N aristas que se unen en cada uno de los V vértices, y cada uno de las A aristas unen dos vértices, de manera que2A = NV
Finalmente, existe una relación más útil entre C, A y V. Al deducir esta relación, debemos llevar a cabo una suposición adicional: que el poliedro está conectado de una manera simple, en el sentido de que cualquier trayecto entre dos puntos de la superficie se puede deformar de manera continua hasta componer otro trayecto entre sus puntos. Este es el caso, por ejemplo, del cubo de tetraedro, pero no del poliedro (regular o no) construido al dibujar caras y aristas sobre la superficie de un donut. Un teorema profundo afirma que cualquier poliedro conectado de manera simple se puede construir añadiendo aristas, caras y/o vértices a un tetraedro, y luego, si es necesario, apretando el polímero resultante hasta conseguir la forma deseada. Utilizando este dato, ahora demostraremos que cualquier poliedro (regular o no) conectado de manera simple satisface esta relación:C − A + V = 2
Resulta fácil comprobar que el tetraedro la satisface: en ese caso tenemos C = 4, A = 6 y V = 4, de manera que el lado izquierdo de la ecuación es 4 – 6 + 4 = 2. Ahora bien, si añadimos una arista a cualquier poliedro, recorriendo una cara de una arista a otra, añadimos una nueva cara y dos nuevos vértices, de manera que C y V aumentan en una unidad y dos unidades respectivamente. Pero esto divide cada antigua arista en los extremos de la nueva arista en dos fragmentos, de manera que A aumenta 1 + 2 = 3, y la cantidad C – A + V por tanto no cambia. De manera parecida, si añadimos una arista que vaya de un vértice hasta una de las antiguas aristas, entonces aumentamos C y V en una unidad cada uno, y B en dos unidades, de manera que la cantidad C – A + V permanece inmutable.Finalmente, si añadimos una arista que vaya de un vértice a otro vértice, entonces aumentamos tanto C como A en una unidad cada uno y V no cambia, de manera que la cantidad C – A + V tampoco cambia. Puesto que cualquier poliedro conectado de manera simple se puede construir de esta manera, todos los poliedros poseen el mismo valor para esta cantidad, que por tanto tiene que ser C – A + V = 2, al igual que para un tetraedro. (Este es un ejemplo simple de una rama de las matemáticas conocidas como topología; la cantidad C – A + V se conoce en topología como «característica de Euler» del poliedro).
Ahora podemos solucionar estas tres ecuaciones para C, A y V. Resulta más sencillo utilizar las primeras dos ecuaciones para sustituir C y V en la tercera ecuación por 2A/n y 2A/N, respectivamente, de manera que la tercera ecuación se convierte en 2A/n – A+2A/N = 2, lo que nos da
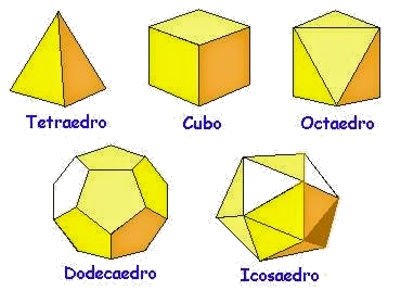
Estos son los sólidos platónicos.
Los pitagóricos descubrieron que dos cuerdas de un instrumento musical de la misma tensión, grosor y composición producen un sonido agradable cuando se pulsan al mismo tiempo si la proporción de las longitudes de las cuerdas es la de números enteros pequeños, como por ejemplo 1/2, 2/3, 1/4, 3/4, etcétera. Para comprender por qué es así, primero tenemos que calcular la relación general entre la frecuencia, la longitud de onda y la velocidad de cualquier onda.
Cualquier onda viene caracterizada por algún tipo de amplitud oscilatoria. La amplitud de una onda sonora es la presión del aire que transporta la onda; la amplitud de una ola oceánica es la altura del agua; la amplitud de una onda luminosa con una dirección concreta de polarización es el campo eléctrico en esa dirección; y la amplitud de una onda que se mueve a lo largo de la cuerda de un instrumento musical es el desplazamiento de la cuerda desde su posición normal en una dirección en ángulo recto a la cuerda.
Existe un tipo especialmente simple de onda conocido como sinusoide. Si tomamos una instantánea de una sinusoide en cualquier momento, vemos que la amplitud desaparece en diversos puntos en la dirección en que se desplaza la onda. Si nos concentramos un momento en ese punto, y observamos en la dirección en que se desplaza la onda, veremos que la amplitud sube y vuelve a caer a cero; a continuación cae hasta un valor negativo y vuelve a cero, y se repite todo el ciclo una y otra vez a medida que nos alejamos en la dirección de la onda. La distancia entre los puntos del principio y del final de cualquier ciclo completo es la longitud característica de la onda, conocida como longitud de onda, y representa de manera convencional por el símbolo λ (lambda). Será importante para lo que vamos a explicar a continuación observar que, como la longitud de onda no solo desaparece al principio y al final de un ciclo, sino también en medio, la distancia entre sucesivos puntos en que desaparece es la mitad de una longitud de onda λ/2. La separación entre dos puntos en los que la amplitud desaparece debe ser un número entero de medias longitudes de onda.
Existe un teorema matemático fundamental (que no se hizo explícito hasta principios del siglo XIX) según el cual prácticamente cualquier perturbación (es decir, cualquier perturbación que posee una dependencia lo bastante regular de la distancia en la onda) se puede expresar como la suma de ondas sinusoides de diversas longitudes de onda (lo que se conoce como «análisis de Fourier»).
Cada sinusoide individual exhibe una oscilación característica en el tiempo, así como en la distancia siguiendo la dirección del movimiento de la onda. Si la onda viaja con una velocidad v, entonces en un tiempo t recorre una distancia vt. El número de longitudes de onda que pasan a través de un punto fijo en un tiempo t será, por tanto, vt/λ, de manera que, en un punto dado en el que la amplitud y la velocidad del cambio se repiten una y otra vez, el número de ciclos por segundo es v/λ, y se conoce como la frecuencia, y se suele representar por la letra f, de manera que f = v/λ. La velocidad de la onda de vibración de una cuerda se aproxima a una constante que depende de la tensión y la masa de la cuerda, pero que es casi independiente de su longitud de onda o de su amplitud, de manera que para esas ondas (al igual que para la luz) la frecuencia es simplemente inversamente proporcional a la longitud de onda.
Consideremos ahora la cuerda de algún instrumento musical, de longitud L. La amplitud de la onda debe desaparecer al extremo de la cuerda, donde esta se mantiene fija. Esta condición limita las condiciones de onda de cada sinusoide que pueden contribuir a la amplitud total de la vibración de la cuerda. Hemos observado que la distancia entre dos puntos en los que la amplitud de cualquier sinusoide se desvanece solo puede ser un número entero de medias longitudes de onda. Así, la onda de una cuerda que está fija en ambos extremos debe contener un número entero N de medias longitudes de onda, de manera que L = Nλ/2. Es decir, que las únicas longitudes de onda posible son λ = 2L/N, donde N = 1, 2, 3, etcétera, de manera que las únicas frecuencias posibles son[289]:
v = vN /2L
La frecuencia más baja, en el caso de que N = 1, es v/2L; todas las frecuencias superiores, para N = 2, N = 3, etcétera, se conocen como «armónicos». Por ejemplo, la frecuencia más baja en la cuerda del do medio de cualquier instrumento es 261,63 ciclos por segundo, aunque también vibra a 523,25 ciclos por segundo, a 784,89 ciclos por segundo, etcétera. La intensidad de los diferentes armónicos es lo que diferencia la cualidad de los sonidos de los distintos instrumentos musicales.Supongamos ahora que se preparan dos cuerdas para que vibren a diferentes longitudes de onda L1 y L2, pero que por lo demás son idénticas, y, en particular, poseen la misma velocidad de onda v. En el tiempo t, los modos de vibración de la frecuencia más baja en la primera y segunda cuerda serán n1 = v1t = vt/2L1, y n2 = v2t = vt/2L2 ciclos o fracciones de ciclos respectivamente. La proporción es:
n1 /n2 = L2/L1
Así, a fin de que las vibraciones más bajas de ambas cuerdas recorran números enteros de ciclos en el mismo tiempo, la cantidad L2/ L1 ha de ser una proporción de números enteros, es decir, un número racional. (En este caso, en el mismo tiempo cada armónico de cada cuerda recorrerá también un número entero de ciclos). El sonido producido por las dos cuerdas se repetirá, al igual que si se hubiera pulsado una sola cuerda, lo que parece ayudar a que el sonido sea agradable. Por ejemplo, si L2/L1 = 1/2, entonces la vibración de la cuerda 2 de frecuencia más baja recorrerá dos ciclos completos para cada ciclo completo de la correspondiente vibración de la cuerda 1. En este caso, decimos que las notas producidas por las dos cuerdas están separadas por una octava. Todas las teclas distintas del do del piano producen frecuencias que están separadas una octava. Si L2/ L1 = 2/3, las dos cuerdas producen un acorde llamado una quinta. Por ejemplo, si una cuerda produce un do medio, a 261,63 ciclos por segundo, entonces otra cuerda cuya longitud sea 2/3 producirá un sol medio, a una frecuencia de 3/2 × 261,63 = 392,45 ciclos por segundo [290]. Si L2/L1 = 3/4, el acorde se llama una cuarta.La otra razón que explica que estos acordes nos resulten agradables tiene que ver con los armónicos. A fin de que el armónico N1 de la cuerda 1 posea la misma frecuencia que el armónico N2 de la cuerda 2, se ha de cumplir que vN1/2L1 = vN2/2L2, de manera que
L2 /L1 = N2/N1
De nuevo, la proporción de las longitudes es un número racional, aunque por una razón diferente. Pero si esta proporción es un número irracional, como π es la raíz cuadrada de 2, entonces los armónicos de las dos cuerdas puede que nunca coincidan, aunque las frecuencias de los armónicos superiores estén arbitrariamente cerca. Al parecer, esto suena horrible.§4. Teorema de Pitágoras
El teorema conocido como de Pitágoras es el resultado más famoso de la geometría plana. Aunque se cree que su descubridor es un miembro de la escuela de Pitágoras, posiblemente Arquitas, los detalles de su origen son desconocidos. Lo que presentamos aquí es la demostración más simple, la que utiliza la idea de proporcionalidad comúnmente utilizada en las matemáticas griegas.
Consideremos un triángulo en cuyos vértices sean A, B y P, y cuyo ángulo en P sea recto. El teorema afirma que el área de un cuadrado cuyo lado es AB (la hipotenusa del triángulo) es igual a la suma de las áreas de los cuadrados cuyos lados son los otros dos del triángulo, AP y BP.
Figura 2. Demostración del teorema de Pitágoras. Este teorema afirma que la suma de las áreas de los cuadrados cuyos lados son AP y BP es igual al área de un cuadrado cuyos lados son la hipotenusa AB. Para demostrar ese teorema, hay que trazar una línea desde P a un punto C en el que la recta es perpendicular a la línea que va desde A a B.
AB2 = AP2 + BP2
El truco de la demostración consiste en trazar una línea desde P hasta la hipotenusa AB que forma con esta un ángulo recto, es decir, en el punto C (véase figura 2). Esto divide el triángulo ABP en dos triángulos rectángulos más pequeños, APC y BPC. Es fácil comprender que estos triángulos más pequeños son parecidos al triángulo ABP, es decir, todos sus ángulos correspondientes son iguales. Si consideramos que los ángulos en los vértices A y B son α (alfa) y β (beta), entonces el triángulo ABP posee tres ángulos, α, β y 90°, por lo que α + β + 90° = 180°. El triángulo APC posee un ángulo que es α y otro que es de 90°, por lo que para que la suma de los ángulos sea 180°, el tercer ángulo ha de ser β. De manera parecida, el triángulo BPC tiene un ángulo que es β y el otro 90°, por lo que el tercer ángulo deben ser α.Como estos triángulos son similares, sus lados correspondientes son proporcionales. Es decir, AC debe guardar la misma proporción con la hipotenusa AP del triángulo ACP que posee AP con la hipotenusa AB del triángulo original ABP, y BC debe guardar la misma proporción con BP que BP tiene con AB. Podemos expresarlo en términos algebraicos más convenientes como proporciones de las longitudes AC, AP, etcétera:
AP2 = AC × AB, y BP2 = BC × AB.
Si sumamos estas dos ecuaciones obtenemos:AP2 + BP2 = (AC + BC) × AB
Pero AC + BC = AB, que es el resultado que había que demostrar.§5. Números irracionales
Los únicos números que les resultaban conocidos a los primeros matemáticos griegos fueron los racionales. Estos son números o bien enteros, como 1, 2, 3, etcétera, o fracciones de números enteros, como 1/2, 2/3, etcétera. Si la proporción de las longitudes de dos líneas es un número racional, se dice que las líneas son «conmensurables»: por ejemplo, si la proporción es 3/5, entonces cinco veces una línea tiene la misma proporción que tres veces la otra. Así pues, resulta terrible descubrir que no todas las líneas son inconmensurables. En particular, en un triángulo rectángulo isósceles, la hipotenusa es inconmensurable con ninguno de los dos lados iguales. En términos modernos, puesto que según el teorema de Pitágoras el cuadrado de la hipotenusa de dicho triángulo es igual al doble del cuadrado de cualquiera de los dos lados iguales, la longitud de la hipotenusa es igual a la longitud de cualquiera de los otros dos lados por la raíz cuadrada de 2, lo que nos lleva a afirmar que la raíz cuadrada de 2 no es un número racional. La prueba que nos ofrece Euclides en el Libro X de los Elementos consiste en suponer lo contrario: en términos modernos, existe un número racional cuya raíz cuadrada es 2, y de ahí se deduce un absurdo.
Supongamos que un número racional p/q (en el que p y q son números enteros) posee una raíz cuadrada que es igual a 2:
(p/q)2 = 2
Existirá un número infinito de dichos pares de números, que encontraremos multiplicando cualquier p y q dados por números enteros iguales cualesquiera. Pero consideremos que p y q son los números enteros más pequeños para los que (p/q)2 = 2. De esta ecuación se sigue quep2 = 2q2
Esto demuestra que p2 es un número par, pero el producto de dos números impares es impar, de manera que p tiene que ser par. Es decir, podemos escribir p = 2p', donde p' es un número entero. Pero entoncesq2 = 2p2
De manera que, por el mismo razonamiento que antes, q es par, y por tanto se puede escribir como q = 2q', donde q' es un número entero. Pero entonces p/q = p'/q', de manera que(p'/q')2 = 2
donde p' y q' son números enteros, respectivamente la mitad que p y q, lo que contradice la definición de p y q como los números enteros más pequeños para los que(p/q)2 = 2. De este modo, el supuesto original, que existen números enteros p y q para los que (p/q)2 = 2, conduce a una contradicción, y por tanto es imposible.Este teorema posee una extensión evidente: cualquier número como 3, 5, 6, etcétera que no sea el cuadrado de un número entero no puede ser cuadrado de ningún número racional.
Por ejemplo, si 3 = (p/q)2, donde p y q son los números enteros más pequeños para los que tal cosa es cierta, entonces p2 = 3q2, pero esto es imposible a no ser que p = 3p' para algún número entero p', pero entonces q2 = 3p'2, de manera que q = 3q' para algún número entero q, por lo que 3 = (p'/q')2, lo que contradice la afirmación de que p y q son los números enteros más pequeños para los que p2 = 3q2. Así pues, la raíces cuadradas de 3, 5, 6… son siempre números irracionales.
En las matemáticas modernas aceptamos la existencia de los números irracionales, como el número que representamos como √2 cuyo cuadrado es 2. Los decimales de esos números son infinitos, y no terminan y se repiten; por ejemplo, √2 = 1,414215562… El número de números racionales e irracionales es infinito, pero en cierto sentido hay muchos más números irracionales que racionales, pues los números racionales se pueden enumerar en una secuencia infinita que incluye cualquier número racional dado:
1, 2, 1/2, 1/3, 2/3, 3/2, 4, 1/4, 3/4, 4/3…
mientras que una lista como esta de números irracionales no es posible.§6. Velocidad terminal
Para comprender cómo las observaciones de los cuerpos que caen podrían haber engendrado en Aristóteles sus ideas del movimiento, podemos utilizar un principio físico que él desconocía, la segunda ley del movimiento de Newton. Ese principio nos dice que la aceleración de un cuerpo (el ritmo a que aumenta su velocidad) es igual a la fuerza total F que actúa sobre un cuerpo dividido entro la masa del cuerpo m:
a = F/m
Hay dos fuerzas principales que actúan sobre un cuerpo que cae a través del aire. Una es la fuerza de la gravedad, que es proporcional a la masa del cuerpo:Fgrav = mg
Aquí g es una constante independiente de la naturaleza del cuerpo que cae. Es igual a la aceleración del cuerpo que cae sometido tan solo a la gravedad, y su valor es de 9,8 metros por segundo al cuadrado en y cerca de la superficie de la Tierra. La otra fuerza es la resistencia del aire. Se trata de una cantidad f(v) proporcional a la densidad del aire, que aumenta con la velocidad y también depende de la forma y el tamaño del cuerpo, aunque no de su masa:Faire = −f(v)
El signo menos se coloca en esta fórmula para la fuerza de resistencia del aire porque pensamos en la aceleración como una fuerza hacia abajo, y para un cuerpo que cae la fuerza de la resistencia del aire actúa hacia arriba, de manera que con este signo menos en la fórmula, f(v) es positiva. Por ejemplo, cuando un cuerpo cae a través de un fluido lo bastante viscoso, la resistencia del aire es proporcional a la velocidadf (v) = kv
donde k es una constante positiva que depende del tamaño y la forma del cuerpo. En el caso de un meteoro o un misil que entra en el aire enrarecido de la zona superior de la atmósfera, tenemosf (v) = Kv2
donde K es otra constante positiva.Utilizando las fórmulas para estas fuerzas en la fuerza total
F = Fgrav + Faire,
y utilizando el resultado de la ley de Newton, tenemosa = g − f (v)/m
Cuando un cuerpo se libera, su velocidad desaparece, de manera que no hay resistencia del aire y su aceleración hacia abajo es simplemente g. A medida que transcurre el tiempo, su velocidad aumenta, y la resistencia del aire comienza a reducir su aceleración. Con el tiempo, la velocidad se acerca a un valor en el que el término −f(v)/m simplemente anula el término g de la fórmula para la aceleración, y esta se vuelve despreciable. Se trata de la velocidad terminal, definida como la solución a la ecuación:F (vterminal) = gm
Aristóteles nunca mencionó la velocidad terminal, pero la velocidad dada por esta fórmula posee algunas de las mismas propiedades que atribuyó a la velocidad de los cuerpos que caen. Puesto que f(v) es una función creciente de v, la velocidad terminal aumenta con la masa m. En el caso especial en que f(v) = kv, la velocidad terminal es simplemente proporcional a la masa e inversamente proporcional a la resistencia del aire:vterminal = gm/k
Pero estas no son propiedades generales de la velocidad de los cuerpos que caen; los cuerpos pesados no alcanzan una velocidad terminal hasta que no llevan mucho tiempo cayendo.§7. Gotas que caen
Estratón observó que las gotas que caen se alejan cada vez más a medida que van cayendo, y concluyó de ello que las gotas se aceleran hacia abajo. Si una gota ha caído más lejos que otra, entonces ha estado cayendo más tiempo, y si las gotas se están separando, entonces la que lleva cayendo más tiempo debe de estar cayendo más deprisa, lo que demuestra que la caída se acelera. Aunque Estratón no lo sabía, la aceleración es constante, y, como veremos, ello produce una separación entre las gotas proporcional al tiempo transcurrido.
Como se ha mencionado en la Nota técnica 6, si despreciamos la resistencia del aire, entonces la aceleración hacia abajo de cualquier cuerpo que cae es una constante g, que en las inmediaciones de la superficie de la Tierra posee un valor de 9,8 metros por segundo al cuadrado. Si un cuerpo cae desde la posición de reposo, entonces al cabo de un intervalo de tiempo τ (tau) su velocidad hacia abajo será gτ. De aquí que si las gotas 1 y 2 caen desde la posición de reposo y desde el mismo origen en un tiempo t1 y t2, entonces en un momento posterior t la velocidad hacia abajo de estas gotas será
v1 = g(t−t1) y v2 = g(t−t2),
respectivamente. Por tanto, la diferencia de sus velocidades será:v1 − v2 = g(t − t1) − g(t − t2) = g(t2 − t1)
Aunque tanto v1 como v2 aumentan con el tiempo, su diferencia es independiente del tiempo t, de manera que la separación entre las gotas simplemente aumenta en proporción al tiempo:s = (v1 − v2)t = gt(t1 − t2)
Por ejemplo, si la segunda gota abandona el origen una décima de segundo después de la primera, entonces después de medio segundo las gotas estarán separadas 32 × 1/2 × 1/10 = 48 centímetros.§8. Reflexión
La deducción de la ley de reflexión por parte de Herón de Alejandría fue uno de los primeros ejemplos de la deducción matemática de un principio físico a partir de un principio más general y profundo. Supongamos que un observador en el punto A ve el reflejo en un espejo de un objeto situado en el punto B.
Si el observador ve la imagen del objeto en el punto P del espejo, el rayo de luz debería haber viajado desde B a P y luego hasta A. (Herón probablemente habría dicho que la luz había viajado desde el observador situado en A hasta el espejo y luego hasta el objeto situado en B, como si el ojo se hubiera prolongado para tocar el objeto, aunque esto tanto da en el razonamiento que vamos a exponer). El problema de la reflexión es: ¿dónde está en el espejo el punto P?
Para responder esta pregunta, Herón supuso que la luz recorre siempre la menor trayectoria posible. En el caso de la reflexión, esto implica que P debe estar situado en un sitio tal que la longitud total del trayecto desde B a P y luego hasta A sea el trayecto más corto posible desde B hasta cualquier lugar del espejo y luego hasta A. A partir de este concluyó que el ángulo θi (theta) entre el espejo y el rayo incidente (la línea que va desde B hasta el espejo) es igual al ángulo θr que forman el espejo y el rayo reflejado (la línea que va del espejo hasta A).
Figura 3. Demostración del teorema de Herón. Este teorema afirma que el trayecto más corto de un objeto en B hasta el espejo y luego hasta el ojo en A es aquel para el que los ángulos θi y θr son iguales. Las líneas continuas marcadas con flecha representan el trayecto de un rayo de luz; la línea horizontal es el espejo; y la línea de puntos es una línea perpendicular al espejo que va desde B hasta B', un punto al otro lado del espejo a una distancia igual a B.
§9. Cuerpos que flotan y cuerpos sumergidos
En su gran obra De los cuerpos flotantes, Arquímedes supuso que si los cuerpos flotan o quedan suspendidos en el agua, de manera que áreas iguales a profundidades iguales en el agua se ven presionadas hacia abajo por pesos distintos, entonces el agua y los cuerpos se desplazarán hasta que todas las áreas iguales en cualquier profundidad dada sufran una presión hacia abajo del mismo peso. A partir de este supuesto, dedujo consecuencias generales tanto para los cuerpos que flotan como para los sumergidos, algunas de las cuales fueron incluso de importancia práctica.
En primer lugar, consideremos un cuerpo, por ejemplo un barco, cuyo peso es menor que el peso de un volumen de agua idéntico. El cuerpo flotará sobre la superficie del agua y desplazará cierta cantidad de esta. Si señalamos una zona horizontal en el agua, a cierta profundidad justo por debajo del cuerpo que flota, con un área igual al área del cuerpo en su línea de flotación, entonces la presión hacia abajo en esta superficie será el peso del cuerpo que flota además del peso del agua por encima de esa línea, pero no incluirá el agua desplazada por el cuerpo, pues esta ya no queda por encima de esa zona. Podemos compararlo con la presión sobre un área igual a una profundidad igual, lejos de la localización del cuerpo flotante. Naturalmente, esto no incluye el peso del cuerpo flotante, pero incluye todo el agua desde esta línea hasta la superficie, sin agua desplazada. A fin de que ambas líneas sufran una presión que obedezca al mismo peso, el peso del agua desplazada por el cuerpo que flota ha de ser igual al peso del cuerpo que flota. Por eso al hablar del peso de un barco nos referimos a su «desplazamiento».
A continuación consideremos un cuerpo cuyo peso sea mayor que el peso de un volumen igual de agua. Dicho cuerpo no flotará, pero se puede suspender en el agua desde un cable. Si el cable está unido al brazo de una balanza, entonces podremos medir así el peso Paparente del cuerpo cuando está sumergido en el agua. El peso que presiona sobre una zona horizontal en el agua a cierta profundidad justo debajo del cuerpo suspendido será igual al peso real Preal del cuerpo suspendido menos el peso aparente Paparente, que se anula por la tensión del cable, más el peso del agua por encima de la línea, que naturalmente no incluye el agua desplazada por el cuerpo. Podemos compararlo con el peso ejercido sobre un área igual a una profundidad igual, un peso que no incluye Preal ni − Paparente, pero que sí incluye el peso de todo el agua desde esta zona hasta la superficie sin agua desplazada. Para que ambas líneas sufran la presión del mismo peso, ha de ocurrir que
Preal − Paparente = Pdesplazado
donde Pdesplazado es el peso del agua desplazada por el cuerpo suspendido. De manera que al pesar el cuerpo cuando está suspendido en el agua y luego cuando está fuera del agua, podamos averiguar Paparente, Preal y, por tanto, Pdesplazado. Si el cuerpo tiene un volumen V, entoncesPdesplazado = ρaguaV
donde ρagua (rhoagua) es la densidad (peso por volumen) del agua, aproximadamente un gramo por centímetro cúbico. (Naturalmente, en el caso de un cuerpo que tenga una forma simple como un cubo podemos averiguar V simplemente midiendo las dimensiones del cuerpo, aunque es algo difícil en el caso de un cuerpo de forma irregular, como una corona). Además, el peso real del cuerpo es:Preal = ρcuerpoV
donde ρcuerpo es la densidad del cuerpo. El volumen se anula en la proporción de Preal y Pdesplazado, de manera que a partir de la medida tanto del Paparente como del Preal podemos averiguar la proporción de las densidades del cuerpo y del agua:
Preal − Paparente = 0,20 × Preal,
de manera que su densidad ha de ser 1/0,2 = 5 veces la densidad del agua. O sea, que su gravedad específica es 5.En este análisis el agua no tiene nada de especial; si las mismas medidas se tomaran para un cuerpo suspendido en algún otro líquido, entonces la proporción del peso real del cuerpo con el decremento de su peso al estar suspendido en el líquido nos daría la proporción de la densidad del cuerpo con la densidad de ese líquido. Esta relación a veces se utiliza con un cuerpo de peso y volumen conocidos para medir las densidades de diversos líquidos en los que se puede suspender el cuerpo.
§10. Áreas de círculos
Para calcular el área de un círculo, Arquímedes imaginó que un polígono con un gran número de grados quedaba circunscrito fuera del círculo. Para simplificar, consideremos un polígono regular, cuyos lados y ángulos sean todos iguales.
El área del polígono es la suma de las áreas de todos los triángulos rectángulos formados al dibujar una línea desde el centro hasta cada vértice del polígono, y por las líneas que van del centro al punto medio de los lados del polígono (véase la figura 4, en la que como polígono tomamos un octágono regular). El área de un triángulo rectángulo es el producto de los dos catetos partido entre dos, porque en su hipotenusa se pueden apilar dos triángulos para formar un rectángulo, cuya área es el producto de los dos lados. En nuestro caso, esto significa que el área de cada triángulo es la mitad del producto de la distancia r al punto medio del lado (que es el radio del círculo) y la distancia s desde el punto medio del lado hasta el vértice más cerca del polígono, que naturalmente es la mitad de la longitud de ese lado del polígono.
Cuando sumamos todas estas áreas, descubrimos que el área de todo el polígono es igual a r veces la circunferencia total del polígono partido entre dos.
Figura 4. Cálculo del área de un círculo . En este cálculo se circunscribe un polígono de muchos lados alrededor de un círculo. Aquí el polígono tiene ocho lados, y su área ya se acerca mucho a la del círculo. A medida que añadimos más lados al polígono, su área se va acercando más y más a la del círculo.
En la época moderna, definimos un número π = 3,14159… como aquel para el que se cumple que la circunferencia de un círculo de radio r es 2 πr. El área del círculo es, por tanto
1/2 × r × 2πr = πr2
El mismo argumento funciona si inscribimos polígonos dentro del círculo, en lugar de circunscribirlos fuera del círculo como en la figura 4. Puesto que el círculo está siempre entre un polígono exterior circunscrito a su alrededor y un polígono interior inscrito dentro, utilizar ambos tipos de polígonos le permitió a Arquímedes calcular los límites superior e inferior de la proporción de la circunferencia de un círculo con su radio; en otras palabras, para 2 π.§11. Tamaños y distancias del Sol y la Luna
Aristarco utilizó cuatro observaciones para determinar la distancia de la Tierra al Sol y a la Luna y los diámetros del Sol y la Luna, todo ello en términos del diámetro de la Tierra. Echemos un vistazo a cada observación y veamos lo que se puede aprender de ellas. Vemos en los gráficos queds y dl son las instancias de la Tierra al Sol y a la Luna respectivamente; y Ds, Dl y Dt son los diámetros del Sol, la Luna y la Tierra. Supondremos que los diámetros son despreciables comparados con las distancias, de manera que al referirnos a la distancia de la Tierra a la Luna o al Sol, no hace falta especificar desde qué puntos de la Tierra, la Luna o el Sol se miden las distancias.
Observación 1
Cuando la Luna está medio llena, el ángulo entre las líneas de visión de la Tierra a la Luna y el Sol es de 87°.
Cuando la Luna está medio llena, el ángulo que forman las líneas de visión de la Luna a la Tierra y de la Luna al Sol ha de ser exactamente 90° (véase figura 5a), de manera que el triángulo formado por las líneas Luna-Sol, Luna-Tierra y Tierra-Sol es un triángulo rectángulo, donde la línea Tierra-Sol es la hipotenusa. La proporción entre el lado adyacente al ángulo θ (theta) de un triángulo rectángulo y la hipotenusa es una cantidad trigonométrica conocida como coseno de θ, abreviado cos θ, que podemos buscar en unas tablas o en cualquier calculadora científica. De manera que tenemos
dt/ds = cos 87° = 0,05234 = 1/19,11
y esta observación indica que el Sol se encuentra 19,11 veces más lejos de la Tierra que la Luna. Sin saber trigonometría, Aristarco solo podía concluir que este número se encuentra entre 19 y 20. (En realidad el ángulo no es 87°, sino 89,853°, y el Sol en realidad se encuentra 389,77 veces más lejos de la Tierra que la Luna).Observación 2
La Luna cubre completamente el disco visible del Sol durante un eclipse solar.
Esto nos muestra que el Sol y la Luna poseen en esencia el mismo tamaño aparente, en el sentido de que el ángulo entre las líneas de visión desde la Tierra a los lados opuestos del disco del Sol es el mismo para la Luna (véase figura 5b).
Figura 5. Las cuatro observaciones utilizadas por Aristarco para calcular los tamaños y distancias al Sol y la Luna . (a) El triángulo formado por la Tierra, el Sol y la Luna cuando la Luna está medio llena. (b) La Luna cuando tapa el disco del Sol durante un eclipse total de sol. (c) La Luna cuando se adentra en la sombra de la Tierra durante un eclipse de luna. La esfera que encaja perfectamente en esta sombra posee un diámetro dos veces el de la Luna, y P es el punto terminal de la sombra proyectada por la Tierra. (d) Las líneas de visión a la Luna abarcan un ángulo de 2°; el ángulo real se acerca más a 0,5°.
Ds/Dl = ds/dl
Utilizando el resultado de la observación 1, esto nos da Ds/Dl = 19,11, mientras que la proporción actual de los diámetros se acerca más a 390.Observación 3
La sombra de la Tierra en la posición de la Luna durante un eclipse de luna tiene exactamente la amplitud suficiente para encajar una esfera cuyo diámetro es el doble que el de la Luna.
Sea P el punto en el que termina el cono de la sombra proyectada por la Tierra. Entonces tenemos tres triángulos similares: el formado por el diámetro del Sol y las líneas desde los bordes del disco de la Tierra hasta P; el formado por el diámetro de la Tierra y las líneas que van de los bordes del disco de la Tierra hasta P; y el formado por el doble del diámetro de la Luna y las líneas que van de una esfera con ese diámetro a la posición de la Luna durante un eclipse solar hasta P (véase figura 5c). De ahí se sigue que las proporciones de los lados correspondientes a estos triángulos son todas iguales. Supongamos que el punto P se encuentra una distancia d0 de la Luna. Entonces el Sol se halla a la distancia ds + dl + d0 de P y la Tierra se halla a la distancia dl + d0 de P, por lo que
DtDs (Dt – 2Dl)
nos da(ds + dl)Dt(Dt − 2Dl) = dlDs ( Dt − 2Dl) + 2Dldl (Ds − Dt)
Los términosdlDs × (−2Dl) y 2DldlDs
de la derecha se anulan. El resto de la ecuación de la derecha tiene un factor Dt, que anula el factor Dt del lado izquierdo, dejándonos con una fórmula para Dt:
De mucha mayor importancia histórica es el hecho de que si combinamos Ds/Dl = 19,1 y Dt/Dl = 2,85, descubrimos que Ds/Dt = 19,1/2,85 = 6,70. El valor real es Ds/Dt = 109,1, pero lo importante es que el Sol es considerablemente mayor que la Tierra. Aristarco recalcó ese punto al comparar los volúmenes en lugar de los diámetros; si la proporción de los diámetros es 6,7, entonces la proporción de los volúmenes es 6,73 = 301. Si hemos de creer a Arquímedes, es esta comparación la que condujo a Aristarco a concluir que la Tierra gira alrededor del Sol, y no el Sol alrededor de la Tierra.
Los resultados de Aristarco descritos hasta ahora ofrecen unos valores para todas las proporciones de diámetros del Sol, la Luna y la Tierra, y la proporción de las distancias al Sol y a la Luna, pero no nos ofrece la proporción de ninguna distancia con ningún diámetro. Esto nos lo dará la cuarta observación:
Observación 4
La Luna subtiende un ángulo de 2°. (Véase figura 5d). Puesto que en un círculo completo tenemos 360°, y un círculo de radio dl tiene una circunferencia de 2 πdl, el diámetro de la Luna es:
Con los resultados de las observaciones 2 y 3 para la razón Dt/Dl entre de los diámetros de la Tierra y la Luna, y ahora con el resultado de la observación 4 para la razón Dl/dl del diámetro y la distancia de la Luna, Aristarco fue capaz de averiguar la razón entre la distancia a la Luna y el diámetro de la Tierra. Por ejemplo, si consideramos que Dt/dl = 2,85 y Dl/dl = 0,035, eso nos daría un valor de
§12. El tamaño de la Tierra
Eratóstenes utilizó la observación de que a mediodía, durante el solsticio de verano, en Alejandría el Sol se aleja de la vertical 1/50 de un círculo completo (es decir, 360°/50 = 7,2°), mientras que en Syene, una ciudad que supuestamente se encontraba exactamente al sur de Alejandría, durante el solsticio de verano, a mediodía, el Sol quedaba justo encima.
Al estar el Sol tan lejos, los rayos que caen sobre la Tierra en Alejandría y Syene son esencialmente paralelos. La dirección vertical hasta cualquier ciudad es simplemente la continuación de una línea desde el centro de la Tierra a esa ciudad, de manera que el ángulo entre las líneas que van del centro de la Tierra a Syene y Alejandría debe de ser 7,2°, o 1/50 de un círculo completo (véase figura 6). De aquí que, basándonos en los supuestos de Eratóstenes, la circunferencia de la Tierra deba ser 50 veces la distancia entre Alejandría y Syene.
Syene no se encuentra en el ecuador de la Tierra, tal como podría sugerir el dibujo de la figura, sino más bien cerca del Trópico de Cáncer, en la línea de altitud 231/2°. (Es decir, el ángulo entre las líneas que van del centro de la Tierra a cualquier punto del Trópico de Cáncer y a un punto que quede exactamente al sur del ecuador es de 231/2°).
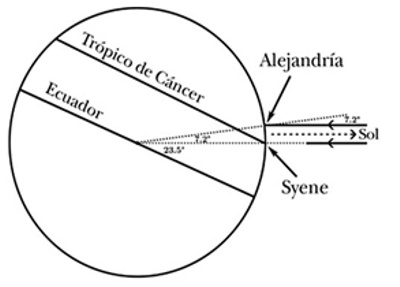
Figura 6. La observación utilizada por Eratóstenes para calcular el tamaño de la Tierra . Las líneas horizontales marcadas con flechas indican los rayos del Sol en el solsticio de verano. Las líneas de puntos van del centro de la Tierra a Alejandría y Syene, y marcan la dirección vertical en cada lugar.
§13. Epiciclos para los planetas interiores y exteriores
En el Almagesto, Ptolomeo presentó una teoría de los planetas según la cual, en su versión más simple, cada planeta describe un círculo llamado epiciclo en torno a un punto del espacio que a su vez gira sobre la Tierra en un círculo conocido como deferente del planeta. La cuestión que se plantea es por qué esta teoría funciona tan bien a la hora de explicar los movimientos aparentes de los planetas tal como se ven desde la Tierra. La respuesta para los planetas interiores, Mercurio y Venus, es diferente que para los planetas exteriores, Marte, Júpiter y Saturno.
En primer lugar consideremos los planetas interiores, Mercurio y Venus. Tal como lo entendemos hoy en día, la Tierra y cada planeta giran alrededor del Sol a distancias más o menos constantes de este y más o menos a velocidades constantes. Si no nos preocupamos por las leyes de la física, podemos cambiar perfectamente nuestro punto de vista y adoptar uno centrado en la Tierra. Desde esta perspectiva, el Sol gira alrededor de la Tierra, y cada planeta gira alrededor del Sol, todos a velocidades y a distancias constantes. Es una versión simplificada de la teoría debida a Tycho Brahe, que quizá también fue propuesta por Heráclides. Nos da los movimientos aparentes correctos de los planetas, dejando aparte pequeñas correcciones debidas al hecho de que los planetas en realidad se mueven en órbitas elípticas casi circulares y no en círculos; y el Sol no se halla en el centro de estas elipses, sino a una distancia relativamente pequeña de los centros, y la velocidad de cada planeta varía un tanto a medida que el planeta gira en torno a su órbita. Es también un caso especial de la teoría de Ptolomeo (aunque este nunca la considerara), según la cual el deferente no es sino la órbita del Sol alrededor de la Tierra, y el epiciclo es la órbita de Mercurio o Venus en torno al Sol.
Ahora bien, por lo que se refiere a la posición aparente en el cielo del Sol y los planetas, podemos multiplicar la distancia cambiante de cada planeta desde la Tierra por una constante sin cambiar las apariencias. Se puede hacer, por ejemplo, multiplicando el radio del epiciclo y el deferente por un factor constante, elegido de manera independiente para Mercurio y Venus. Por ejemplo, podemos considerar que el radio del deferente de Venus es la mitad de la distancia de la Tierra al Sol, y que el radio de este epiciclo es la mitad del radio de la órbita de Venus alrededor del Sol. Esto no cambia el hecho de que los centros de los epiciclos de los planetas siempre permanecen en línea entre la Tierra y el Sol (véase figura 7a, que muestra el epiciclo y el deferente para uno de los planetas interiores, no dibujado a escala). El movimiento aparente de Venus y Mercurio en el cielo no cambiará por esta transformación, siempre y cuando no cambiemos la proporción entre el radio del deferente y el epiciclo de cada planeta. Es la versión simplificada de la teoría propuesta por Ptolomeo para los planetas interiores, según la cual el planeta gira en torno a su epiciclo en el mismo tiempo que tarda en dar la vuelta al Sol, 88 días para Mercurio y 225 para Venus, mientras que el centro del epiciclo al Sol en torno a la Tierra, y el circuito del deferente tarda un año en completarse.
En concreto, puesto que no cambiamos la razón entre los radios del deferente y el epiciclo, hemos de tener que
rEPI /rDEF = rp/rT
donde rEPI y rDEF son los radios del epiciclo y el deferente en el esquema de Ptolomeo, y rP y rT son los radios de las órbitas del planeta y de la Tierra en la teoría de Copérnico (o de manera equivalente, los radios de las órbitas del planeta alrededor del Sol y del Sol alrededor de la Tierra en la teoría de Tycho). Naturalmente, Ptolomeo no sabía nada de las teorías de Tycho ni de Copérnico, y no llevó a su teoría por este camino. Esta discusión sirve para mostrar tan solo por qué la teoría de Ptolomeo funciona tan bien, no cómo llegó ella.Consideremos los planetas exteriores, Marte, Júpiter y Saturno. En la versión más simple de la teoría de Copérnico (o de Tycho) cada planeta mantiene una distancia fija no solo respecto al Sol, sino también respecto a un punto en movimiento C' en el espacio, que se mantiene a una distancia fija de la Tierra. Para hallar este punto, dibujamos un paralelogramo (figura 7b), cuyos primeros tres vértices son, en este orden, la posición T de la Tierra, la posición S del Sol y la posición P' de uno de los planetas. El punto en movimiento C' es el cuarto vértice del paralelogramo. Puesto que la línea entre T y S tiene una longitud fija, y la línea entre P' y C' es el lado opuesto del paralelogramo, también posee una longitud igual y fija, de manera que el planeta permanece una distancia fija de C', que es igual a la distancia entre la Tierra y el Sol. De manera parecida, puesto que la línea entre S y P' posee una longitud fija, y la línea entre T y C' es el lado opuesto del paralelogramo, también posee una longitud igual y fija, de manera que el punto C' permanece a una distancia fija de la Tierra, igual a la distancia del planeta al Sol. Este es un caso especial de la teoría de Ptolomeo, aunque un caso que nunca consideró, en el que el deferente no es sino la órbita del punto C' alrededor de la Tierra, y el epiciclo es la órbita de Marte, Júpiter o Saturno alrededor de C'.
De nuevo, por lo que se refiere a la posición aparente en el cielo del Sol y los planetas, podemos multiplicar la distancia cambiante de cualquier planeta a la Tierra por una constante sin cambiar las apariencias, multiplicando el radio del epiciclo y el deferente por un factor constante, escogido de manera independiente para cada planeta exterior. Aunque ya no tenemos un paralelogramo, la línea entre el planeta y C sigue siendo paralela a la línea entre la Tierra y el Sol. El movimiento aparente de cada planeta exterior en el cielo no sufrirá ningún cambio mediante esta transformación, siempre y cuando no cambiemos la proporción del radio del deferente y el epiciclo de cada planeta.
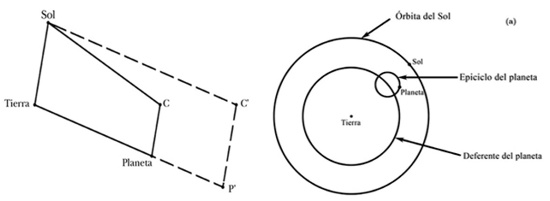
Figura 7. Una versión sencilla de la teoría del epiciclo descrita por Ptolomeo . (a) El supuesto movimiento de uno de los planetas interiores, Mercurio o Venus. (b) El supuesto movimiento de uno de los planetas exteriores, Marte, Júpiter y Saturno. El planeta P recorre un epiciclo en torno al punto C en un año, con la línea de C a P siempre paralela a la línea que va de la Tierra al Sol, mientras que el punto C gira en torno a la Tierra en el deferente en un tiempo más prolongado. (Las líneas de puntos indican un caso especial de la teoría ptolemaica, para el cual es equivalente a la de Copérnico).
En concreto, puesto que no cambiamos la razón entre los radios del deferente y el epiciclo, se debe cumplir que
rEPI /rDEF = rT/rp
donde rEPI y rDEF son de nuevo el radio del epiciclo y el deferente en el esquema de Ptolomeo, y rT y rP son los radios de las órbitas del planeta y la Tierra en la teoría de Copérnico (o de manera equivalente, los radios de las órbitas del planeta en torno al Sol y del Sol en torno a la Tierra en la teoría de Tycho). De nuevo, esta discusión describe no de dónde sacó Ptolomeo su teoría, sino solo por qué esta funcionaba tan bien.§14. Paralaje lunar
Supongamos que la dirección a la Luna se observa desde el punto O en la superficie de la Tierra en un ángulo ζ' (zeta prima) hasta el cenit en O. La Luna se mueve de una manera fluida y regular alrededor del centro de la Tierra, por lo que, utilizando los resultados de repetidas observaciones de la Luna, es posible calcular la dirección del centro C de la Tierra a la Luna L en el mismo momento, y en particular calcular el ángulo ζ entre la dirección desde C a la Luna y la dirección del cénit en O, que es la misma dirección de la línea del centro de la Tierra a O. Los ángulos ζ y ζ' difieren ligeramente porque el radio rt de la Tierra no es del todo despreciable comparado con la distancia d de la Luna al centro de la Tierra, y a partir de esta diferencia Ptolomeo pudo calcular la razón entre d/rt.
Los puntos C, O y L forman un triángulo, en el que el ángulo en C es ζ, el ángulo en O es 180° −ζ' y (puesto que la suma de los ángulos de cualquier triángulo es 180°) el ángulo en L es 180° − ζ − (180° − ζ') = ζ' − ζ (véase figura 8). Podemos calcular la razón d/rt a partir de estos ángulos mucho más fácilmente de lo que lo hizo Ptolomeo, mediante un teorema de la trigonometría moderna: que en cualquier ángulo la longitud de los lados es proporcional a los senos de los ángulos opuestos. (Los senos se discuten en la Nota técnica 15). El ángulo opuesto a la línea de longitud rt desde C a O es ζ' − ζ, y el ángulo opuesto la línea de longitud d desde C a L es 180° − ζ', de manera que
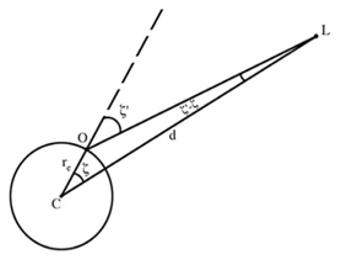
Figura 8. Uso del paralaje para medir la distancia a la Luna. Aquí ζ' es el ángulo observado entre la línea de visión hasta la Luna y la dirección vertical, y ζ es el valor que tendría este ángulo si la Luna se observara desde el centro de la Tierra.
sen ζ' = 0,776
sen (ζ' − ζ) = 0,0195
En cualquier caso, los cálculos de Ptolomeo fueron más precisos que los de Aristarco, de cuyos valores para la proporción de los diámetros de la Tierra y la Luna y de la distancia y el diámetro de la Luna podía haber inferido que d/rt se halla entre 215/9 = 23,9 y 57/4 = 14,3. Pero si Aristarco hubiera utilizado un valor correcto de más o menos 1/2° para el diámetro angular del disco de la Luna en lugar del valor de 2° que utilizó, se había encontrado con que d/rt era cuatro veces más grande, entre 57,2 y 95,6. Entre esa horquilla se encuentra el valor real.
§15. Senos y cuerdas
Los matemáticos y astrónomos de la Antigüedad posiblemente utilizaron una rama de las matemáticas conocida como trigonometría, que hoy en día se enseña en las escuelas secundarias. Dado cualquier ángulo de un triángulo rectángulo (aparte del propio ángulo recto), la trigonometría nos explica cómo calcular las proporciones de las longitudes de todos los lados. En particular, el cateto opuesto al ángulo dividido entre la hipotenusa es una cantidad conocida como el «seno» de ese ángulo, que se puede encontrar buscando en tablas matemáticas o tecleando el ángulo en una calculadora manual y apretando «sen». (El lado del triángulo adyacente a un ángulo dividido entre la hipotenusa es el «coseno» de ese ángulo, y el lado opuesto dividido entre el lado adyacente es la «tangente» del ángulo, pero nosotros tendremos suficiente con los senos). Aunque en la matemática helenística no aparece en ninguna parte la idea de seno, el Almagesto de Ptolomeo hace uso de una cantidad relacionada, conocida como la «cuerda» de un ángulo.
Para definir la cuerda de un ángulo θ (theta), trazamos un círculo de radio 1 (en cualquier unidad de longitud que nos parezca conveniente) y dibujamos dos líneas radiales desde el centro a la circunferencia, separadas por ese ángulo. La cuerda del ángulo es la longitud de la línea recta, o cuerda, que conecta los puntos donde las dos líneas radiales se cruzan con la circunferencia (véase figura 9). El Almagesto nos ofrece una tabla de cuerdas[291] en una notación sexagesimal babilónica, con los ángulos expresados en grados de arco, que van de 1/2° a 180°. Por ejemplo, la cuerda de 45° se da como 45 15 19, o en notación moderna
La cuerda tiene una aplicación natural para la astronomía. Si imaginamos que las estrellas se encuentran en una esfera de radio igual a 1, cuyo centro es el de la Tierra, entonces, si las líneas de visión a dos estrellas están separadas por un ángulo θ, la distancia aparente en línea recta entre las estrellas será la cuerda de θ.
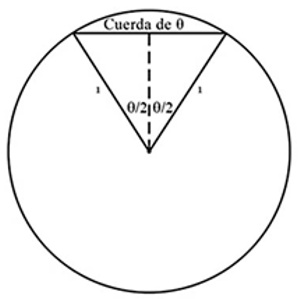
Figura 9. La cuerda de un ángulo θ. El círculo que tenemos aquí posee un radio igual a 1. Las líneas radiales del sólido componen un ángulo θ en el centro de este círculo; la línea horizontal discurre entre las intersecciones de estas líneas con el círculo, y su longitud es la cuerda de este ángulo.
cuerda de θ = 2 sen (θ/2)
De aquí que cualquier cálculo que se pueda hacer con los senos también se puede llevar a cabo con las cuerdas, aunque en casi todos los casos resulta menos conveniente.§16. Horizontes
Normalmente, nuestra visión del exterior se ve obstruida por los árboles cercanos, las casas u otros obstáculos. Desde lo alto de una colina, en un día despejado, podemos ver mucho más lejos, pero nuestro campo de visión sigue restringido por un horizonte, más allá del cual las líneas de visión quedan bloqueadas por la propia Tierra. El astrónomo árabe Al-Biruni describió un inteligente método para utilizar este fenómeno familiar a la hora de medir el radio de la Tierra, sin tener que conocer ninguna otra distancia aparte de la altura de la montaña.
Un observador O en lo alto de una colina puede ver un punto H en la superficie de la Tierra en el que la línea de visión es tangente a la superficie (véase figura 10). Esta línea de visión forma un ángulo recto con la línea que une H con el centro de la Tierra C, con lo que el triángulo OCH es un triángulo rectángulo. La línea de visión no se halla en la dirección horizontal, sino debajo, formando un ángulo θ , que es pequeño, porque la Tierra es grande y el horizonte está lejos. Por lo tanto, el ángulo entre la línea de visión y la dirección vertical de la colina es 90° − θ, y como la suma de los ángulos de cualquier triángulo tiene que ser 180°, el ángulo agudo del triángulo en el centro de la Tierra es 180° − 90° − (90° − θ) = θ.
El cateto adyacente a este ángulo es la línea desde C a H, cuya longitud es el radio r de la Tierra, mientras que la hipotenusa del triángulo es la distancia de C a O, que es r + h, donde h es la altura de la montaña.
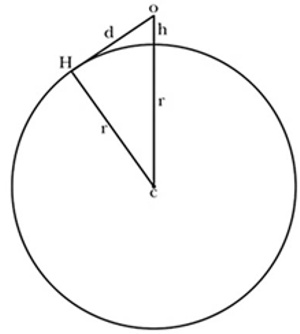
Figura 10. El uso del horizonte por parte de Al-Biruni para medir el tamaño de la Tierra. O es un observador sobre una colina de altura h; H es el horizonte visto por este observador; la línea que va de H a O es tangente a la superficie de la Tierra en H, y por tanto forma un ángulo recto con la línea que va desde el centro C de la Tierra a H.
r = h /0,0000489 = 20 450h
Al-Biruni señaló que la altura de la montaña era de 652,055 codos (una precisión mucho mayor de la que podría haber alcanzado), lo que nos da que r = 13,3 millones de codos, mientras que el resultado que él nos dio fue 12,8 millones de codos. Desconozco el origen del error de Al-Biruni.§17. Prueba geométrica del teorema de la velocidad media
Supongamos que trazamos un gráfico de la velocidad comparada con el tiempo durante la aceleración uniforme, y colocamos la velocidad en el eje vertical y el tiempo en el horizontal.
La gráfica será una línea recta, que ascenderá desde una velocidad cero en un tiempo cero hasta la velocidad final en el tiempo final. A cada ínfimo intervalo de tiempo, la distancia recorrida es el producto de la velocidad en ese tiempo (esta velocidad cambia en una cantidad despreciable durante el intervalo si este es lo bastante breve) multiplicada por el intervalo de tiempo. Es decir, la distancia recorrida es igual al área de un pequeño rectángulo cuya altura es la altura de la gráfica en ese tiempo y cuya anchura es el ínfimo intervalo de tiempo (véase figura 11a). Podemos rellenar el área de debajo de la gráfica, desde el tiempo inicial al final, con esos pequeños rectángulos, y la distancia total recorrida será entonces el área total de todos estos rectángulos, es decir, el área que hay debajo de la gráfica (véase figura 11b).
Naturalmente, por muy delgados que hagamos los rectángulos, decir que el área que hay debajo de la gráfica es igual al área total de los rectángulos es solo una aproximación. Pero podemos hacer los rectángulos todo lo delgados que queramos, con lo que la aproximación será todo lo buena que deseemos. Al imaginar el límite de un número infinito de rectángulos infinitamente delicados, podemos concluir que la distancia recorrida es igual al área que hay debajo del gráfico de la velocidad en relación con el tiempo.
Figura 11. Prueba geométrica del teorema de la velocidad media . La línea inclinada es el gráfico de la velocidad en relación con el tiempo para un cuerpo uniformemente acelerado desde la posición de reposo. (a) La anchura del pequeño rectángulo es un breve intervalo de tiempo; su área se acerca a la distancia recorrida en ese intervalo. (b) El tiempo durante un periodo de aceleración uniforme, dividido en breves intervalos; como el número de rectángulos se ha incrementado, la suma de las áreas de los rectángulos se convierte en arbitrariamente próxima al área que hay debajo de la línea inclinada. (c) El área que hay debajo de la línea inclinada es el producto del tiempo transcurrido y la velocidad final dividido entre dos.
El teorema afirma que el área de un triángulo rectángulo es el producto de los dos catetos dividido entre dos. Ello se sigue directamente del hecho de que podemos unir dos de sus triángulos para formar un rectángulo, cuya área es el producto de los lados (véase figura 11c). En nuestro caso, los dos catetos son la velocidad final y el tiempo total transcurrido. La distancia recorrida es el área de un triángulo rectángulo con esas dimensiones, o el producto de la velocidad final del tiempo total transcurrido dividido entre dos. Pero puesto que la velocidad aumenta desde cero a un ritmo constante, su valor medio es la mitad de su valor final, de manera que la distancia recorrida es la velocidad media multiplicada por el tiempo transcurrido. Y este es el teorema de la velocidad media.
§18. Elipses
Una elipse es un tipo especial de curva cerrada sobre una superficie plana. Hay al menos tres maneras distintas de dar una descripción precisa de esta curva.
Figura 12. Los elementos de una elipse. Los puntos marcados dentro de la elipse son sus dos focos; a y b son la mitad del semieje menor y el semieje mayor de la elipse; y la distancia de cada foco al centro de la elipse es ea. La suma de las longitudes r+ y r- de las dos líneas de puntos desde el foco hasta un punto P es igual a 2a siempre que P esté sobre la elipse. La elipse muestra una elipticidad de e ≈ 0,8.
Una elipse es una serie de puntos de un plano que satisfacen la ecuación
b ≤ r ≤ a
Observemos que en la intersección de la elipse con el eje horizontal tenemos que y = 0, con lo que x2 = a2 , y por tanto x = + a; así la Ec. (1) describe una elipse cuyo diámetro largo va de −a hasta +a en la dirección horizontal. Además, en la intersección de la elipse con el eje vertical tenemos x = 0, por lo que y2 = b2, y por tanto y = + b, por lo que la Ec. (1) describe una elipse cuyo diámetro corto discurre paralelo a la dirección vertical, desde − b hasta +b (véase figura 12). El parámetro a se denomina «semieje mayor» de la elipse. Convencionalmente se define la excentricidad de una elipse como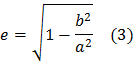
Segunda definición
Otra definición clásica de una elipse es que se trata de una serie de puntos en un plano para los que la suma de las distancias a dos puntos fijos (los focos de la elipse) es una constante. Para la elipse definida por la Ec. (1), estos dos puntos están en x = + ea, y = 0, donde e es la excentricidad tal como se define en la Ec. (3). Las distancias de estos dos puntos a un punto de la elipse, donde x e y satisfagan la Ec. (1), son:
r+ + r− = 2a (5)
Esto se puede considerar como una generalización de la definición clásica de círculo: una serie de puntos que están en la misma distancia de un solo punto.Puesto que existe una completa asimetría entre los dos focos de la elipse, las distancias medias r+' y r−' de los puntos de la elipse (donde cada segmento lineal de una longitud dada en una elipse dada tiene igual peso en la media) desde los dos focos han de ser iguales: r+' = r−', y por tanto Ec. (5) nos da
La definición original de una elipse dada por Apolonio de Perga es que se trata de una sección cónica: la intersección de un cono con un plano con cierta inclinación respecto al eje del cono. En la época actual, un cono con su eje en la dirección vertical es una serie de puntos en tres dimensiones que satisface la condición de que el radio de las secciones transversales circulares del cono son proporcionales a la distancia en la dirección vertical:
z = βu + γ (9)
donde β (beta) y γ (gamma) son dos números más que respectivamente especifican la inclinación y la altura del plano. (Estamos definiendo las coordenadas para que el plano sea paralelo al eje y). Al combinar la Ec. (9) con el cuadrado de la Ec. (8) obtenemosu2 + y2 = α (βu + γ)2
o de manera equivalente
§19. Elongaciones y órbitas de los planetas interiores
Uno de los grandes logros de Copérnico fue calcular valores definidos para los tamaños relativos de las órbitas planetarias. Un ejemplo especialmente simple es el cálculo de los radios de las órbitas de los planetas interiores a partir de la distancia máxima aparente de estos planetas del Sol.
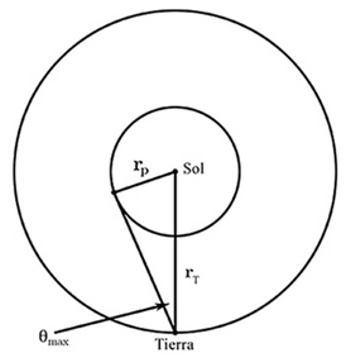
Figura 13 . Las posiciones de la Tierra y un planeta interior (Mercurio o Venus) cuando el planeta está en su máxima distancia aparente del Sol. Los círculos son las órbitas de la Tierra y el planeta.
| Elongación máxima θmax | Seno de θmax | rP/rT | |
| Mercurio | 24° | 0,41 | 0,39 |
| Venus | 45° | 0,71 | 0,72 |
Las pequeñas discrepancias entre el seno de θmax y las razones observadas rP/rT de los radios orbitales de los planetas interiores y la Tierra se deben a que estas órbitas no forman un círculo perfecto con el Sol en el centro, y al hecho de que las órbitas no están exactamente en el mismo plano.
§20. Paralaje diurno
Consideremos una «nueva estrella» o cualquier otro objeto que o bien esté en reposo con respecto a las estrellas fijas o se mueva muy poco en relación con las estrellas en el curso del día. Supongamos que está mucho más cerca de la Tierra que las estrellas. Podemos suponer que la Tierra gira una vez al día sobre su eje de este a oeste, o que este objeto y las estrellas giran alrededor de la Tierra una vez al día de oeste a este; en cualquier caso, como vemos el objeto en diferentes direcciones a diferentes horas de la noche, su posición parece desplazarse durante cada noche en relación con las estrellas. Esto es lo que se denomina «paralaje diurno» del objeto. Una medida del paralaje diurno permite determinar la distancia del objeto, y si se descubre que el paralaje diurno es demasiado pequeño para medirse, esto nos da el límite inferior de la distancia.
Para calcular la cantidad de este desplazamiento angular consideremos la posición aparente del objeto en relación con las estrellas vista desde un observatorio fijo de la Tierra, justo cuando el objeto asoma por el horizonte, y cuando está en el punto más alto del cielo. Para facilitar el cálculo consideraremos el caso geométricamente más simple: el observatorio está en el ecuador, y el objeto está en el mismo plano que el ecuador. Naturalmente, esto no es exactamente el paralaje diurno de la nueva estrella observada por Tycho, pero indicará el orden de magnitud de ese paralaje.
La línea que va del observatorio al objeto cuando este empieza a asomar por el horizonte es tangente a la superficie de la Tierra, de manera que el ángulo entre esta línea y la línea del observatorio al centro de la Tierra es un ángulo recto. Estas dos líneas, junto con la línea del objeto al centro de la Tierra, forman un triángulo rectángulo (véase figura 14). El ángulo θ (theta) de este triángulo en ese objeto posee un seno igual a la razón del lado opuesto, el radio rT de la Tierra, con la hipotenusa, la distancia d del objeto al centro de la Tierra. Tal como se ve en la figura, el ángulo es también el desplazamiento aparente de la posición del objeto en relación con las estrellas entre el momento en que asoma por el horizonte y cuando está en el punto más alto del cielo. El desplazamiento total en su posición desde que asoma por el horizonte hasta que se pone por debajo del horizonte es 2θ.
Por ejemplo, si consideramos que el objeto está a la misma distancia que la Luna, entonces d ≈ 402 340 km, mientras que rT ≈ 6437,4 km, de manera que sen θ ≈ 4/250, y por tanto θ ≈ 0,9°, y el paralaje diurno es 1,8°. Desde un punto concreto de la Tierra, como Hven, hasta un objeto en una ubicación concreta del cielo, como el de la nueva estrella de 1572, el paralaje diurno es más pequeño, pero todavía es del mismo orden de magnitud, alrededor de 1°. Este tamaño es lo bastante grande como para haber sido detectado a simple vista por un astrónomo tan experto como Tycho Brahe, pero este no pudo detectar ningún paralaje diurno, así que fue capaz de concluir que la nueva estrella de 1572 estaba más lejos que la Luna. Por otro lado, no hubo ninguna dificultad en medir el paralaje diurno de la propia Luna, y averiguar de esta manera la distancia entre la Luna y la Tierra.
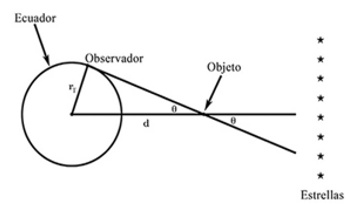
Figura 14. Uso del paralaje diurno para medir la distancia de la Tierra a algún objeto . Aquí la visión es desde un punto por encima del Polo Norte de la Tierra. Para simplificar, se supone que el observador está en el ecuador, y el objeto se halla en el mismo plano que el ecuador. Las dos líneas separadas por un ángulo θ son las líneas de visión del objeto cuando surge por el horizonte y, seis horas más tarde, cuando está directamente por encima del observador.
Según la primera ley de Kepler, los planetas, incluida la Tierra, giran alrededor del Sol en una órbita elíptica, pero eso no es el centro de la elipse; es un punto descentrado del semieje mayor, uno de los dos focos de la elipse (véase Nota técnica 18). La excentricidad e de la elipse se define de tal modo que la distancia de cada foco al centro de la elipse es ea, donde a es la longitud del semieje mayor de la elipse partido entre dos. Además, según la segunda ley de Kepler, la velocidad de cada planeta en su órbita no es constante, sino que varía de tal modo que la línea del Sol al planeta barre áreas iguales en tiempos iguales.
Hay una manera aproximada distinta de expresar la segunda ley, estrechamente relacionada con la antigua línea del ecuante utilizada en la astronomía ptolemaica. En lugar de considerar la línea que va del Sol al planeta, consideremos la línea que va del planeta al otro foco de la elipse, el foco vacío. La excentricidad e de algunas órbitas planetarias no es despreciable, pero e2 es muy pequeño para todos los planetas. (La órbita más excéntrica es la de Mercurio, para la cual e = 0,206 y e2 = 0,042; para la Tierra e2 = 0,00028). De manera que al calcular los movimientos de los planetas resulta una buena aproximación mantener solo términos que son independientes de la excentricidad e o proporcionales a e, despreciando todos los términos proporcionales a e2 o potencias superiores dee. En esta aproximación, la segunda ley de Kepler es equivalente a afirmar que la línea que va desde el foco vacío hasta el planeta barre ángulos iguales en tiempos iguales. Es decir, que la línea entre el foco vacío de la elipse y el planeta gira alrededor de ese foco a una velocidad constante.
En concreto, vamos a ver que si A es la velocidad a la que el área es barrida por la línea que va del Sol al planeta, y ώ (omega con un punto encima) es la velocidad del cambio del ángulo φ entre el eje mayor de la elipse y la línea desde el foco vacío hasta el planeta, entonces
ώ = 2 RA/a2 + O(e2) (1)
donde O(e2) denota términos proporcionales a e2 o potencias superiores de e, y R es un número cuyo valor depende de las unidades que utilicemos para medir los ángulos. Si medimos los ángulos en grados, entonces R = 360°/2π = 57,293…°, un ángulo conocido como «radián». O podemos medir el ángulo en radianes, en cuyo caso tomaremos R = 1. La segunda ley de Kepler nos dice que, en un intervalo de tiempo dado, el área barrida por la línea que va del Sol al planeta es siempre la misma; esto significa que A es constante, de manera que ώ es constante, hasta términos proporcionales a e2. De manera que para una buena aproximación, en un intervalo de tiempo dado, el ángulo barrido desde el foco vacío de la elipse hasta el planeta es siempre el mismo.Ahora bien, en la teoría descrita por Ptolomeo, el centro del epiciclo de cada planeta gira alrededor de la Tierra en una órbita circular, el deferente, pero la Tierra no está en el centro del deferente, sino que la órbita es excéntrica: la Tierra se encuentra en un punto a pequeña distancia del centro. Además, la velocidad a la que el centro del epiciclo gira alrededor de la Tierra no es constante, y la velocidad a la que la línea que va de la Tierra a su centro gira tampoco es constante. A fin de explicar correctamente el movimiento aparente de los planetas se introdujo el dispositivo del ecuante. Se trata de un punto al otro lado del centro del deferente desde la Tierra, y a una distancia igual desde el centro. La línea que va del ecuante (más que de la Tierra) al centro del epiciclo se suponía que tenía que ser barrida por ángulos iguales en tiempos iguales.
El lector no habrá dejado de observar que esto es muy parecido a lo que ocurre según las leyes de Kepler. Naturalmente, el papel del Sol y la Tierra se invierte en la astronomía ptolemaica y copernicana, pero en la teoría de Kepler el foco vacío de la elipse desempeña el mismo papel que el ecuante en la astronomía ptolemaica, y la segunda ley de Kepler explica por qué la introducción del ecuante funcionó bien a la hora de explicar el movimiento aparente de los planetas.
Por alguna razón, aunque Ptolomeo introdujo un excéntrico para explicar el movimiento del Sol en torno a la Tierra, en este caso no utilizó ningún ecuante. Si hubiera incluido este ecuante final (además de algunos epiciclos introducidos para explicar por qué Mercurio se apartaba tanto de una órbita circular), la teoría ptolemaica podría haber explicado perfectamente el movimiento aparente de los planetas.
He aquí la prueba de la Ec. (1). Definimos θ como el ángulo entre el semieje mayor de la elipse y la línea que va del Sol al planeta, y recordamos que Φ se define como el ángulo entre el semieje mayor y la línea que va del foco vacío al planeta. Al igual que en la Nota técnica 18, definimos r+ y r− como las longitudes de estas líneas; es decir, las distancias del Sol al planeta y del foco vacío al planeta, respectivamente, dadas (según esa nota) por
r± = a ± ex (2)
donde x es la coordinada horizontal del punto de la elipse; es decir, es la distancia desde ese punto a una línea que corta la elipse en su eje menor. El coseno de un ángulo (simbolizado cos) se define en trigonometría al considerar un triángulo rectángulo con ese ángulo como uno de los vértices; el coseno de un ángulo es la razón entre el cateto adyacente a ese ángulo y la hipotenusa del triángulo. De aquí que, al referirnos a la figura 15,
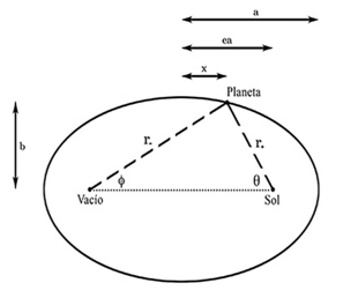
Figura 15. Movimiento elíptico de los planetas . La forma de la órbita es aquí una elipse, la cual (como en la figura 12) posee una elipticidad de 0,8, mucho más grande que la de cualquier órbita planetaria del sistema solar. Las líneas marcadas como r+ y r− respectivamente son la distancia entre el planeta y el Sol y el foco vacío de la elipse.
(Se ha insertado un signo menos porque queremos que dA sea positivo cuando Φ aumenta, a fin de que δΦ sea positivo cuando δθ es negativo). Así, la Ec. (8) se puede escribir:
Si tomamos δA y δΦ como el área y el ángulo barridos en un intervalo de tiempo infinitesimal δt y dividimos la Ec. (10) entre δt, encontramos la relación correspondiente entre las velocidades de barrido de las áreas y los ángulos:
(1 − e cos θ)2 = 1 − 2e cos θ + e2 cos2θ,
de manera que los términos de orden cero y primer orden en el numerador y denominador de esta fracción son los mismos, y la diferencia entre numerador y denominador aparece solo en términos proporcionales a e2. Así, la ecuación (11) inmediatamente ofrece el resultado deseado, la Ec. (1). Para ser un poco más concretos, podemos mantener los términos en la Ec. (11) de orden e2:
§22. Distancia focal
Consideremos una lente de cristal vertical, de superficie curvada convexa delante y superficie plana detrás, como la lente que Galileo y Kepler utilizaron en el extremo frontal de sus telescopios. Las superficies curvadas que son más fáciles de pulir son segmentos de esferas, y asumiremos que la parte frontal convexa de la lente es un segmento de una esfera de radio r. También supondremos todo el tiempo que la lente es delgada, con un grosor máximo mucho menor que r.
Supongamos que un rayo de luz viaja en dirección horizontal, paralelo al eje de la lente, e incide en esta en el punto P, y que la línea que va del centro de curvatura C (detrás de la lente) hasta P forma un ángulo θ (theta) con el eje de la lente. La lente curvará el rayo de luz, de manera que cuando salga de la parte posterior de la lente formará un ángulo distinto Φ con el eje de la lente. Entonces el rayo incidirá en el eje de la lente en algún punto F (véase figura 16a). Vamos a calcular la distancia f de este punto a la lente, y demostrar que es independiente de θ, de manera que todos los rayos horizontales de luz que inciden en la lente alcanzan el eje en el mismo punto F. Así, podemos decir que la luz que incide en la lente se enfoca en el punto F; la distancia f de ese punto de la lente se conoce como «distancia focal» de la lente.
En primer lugar, observemos que el arco de la parte frontal de la lente que va desde la línea central hasta P es una fracción de θ/360° de la circunferencia total 2 πr de un círculo de radio r. Por otro lado, el mismo arco es una fracción Φ/360° de toda la circunferencia 2 πf de un círculo de radio f. Puesto que estos arcos son iguales, tenemos que
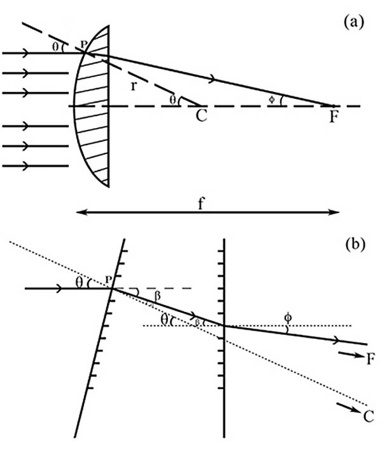
Figura 16. Distancia focal. (a) Definición de distancia focal. La distancia horizontal β punto P, donde el rayo forma un pequeño ángulo θ con una línea que sale del centro de curvatura C y es perpendicular a la superficie esférica convexa en P; este rayo se desvía por culpa de la lente y forma un ángulo Φ con el eje de la lente e incide en ese eje en un punto focal F a una distancia f de la lente. Se trata de la distancia focal. Con un Φ proporcional a θ , todos los rayos horizontales se enfocan hacia ese punto. (b) Cálculo de la distancia focal. Lo que mostramos aquí es una pequeña parte de la lente, y la línea continua con tramos e inclinada de la izquierda indica un breve segmento de la superficie convexa de la lente. La línea continua marcada con una flecha señala el trayecto de un rayo de luz que entra en la lente en P, donde forma un pequeño ángulo θ con la normal a la superficie convexa. Esta normal se muestra como una línea inclinada de puntos, un segmento de la línea que va desde P hasta el centro de curvatura de la lente, que queda fuera de los límites de esta figura. Dentro de la lente, este rayo se refracta, por lo que forma un ángulo α con esta normal, y se refracta de nuevo cuando deja la lente, formando un ángulo Φ con la normal a la superficie posterior plana de la lente. Esta normal se muestra como una línea de puntos paralela al eje de la lente.
α = θ/n
donde n > 1 es una constante conocida como el «índice de refracción», que depende de las propiedades del cristal y del medio que lo rodea, normalmente el aire. (Fermat demostró que n es la velocidad de la luz del aire dividida por la velocidad de la luz del cristal, pero esta información no nos hace falta). El ángulo β (beta) entre el rayo de luz dentro del cristal y la línea central de la lente es por tanto:β = θ − α = (1 − 1/n)θ
Esto es el ángulo que forman el rayo de luz y la normal a la superficie posterior plana de la lente cuando el rayo de luz llega a su superficie. Por otro lado, cuando el rayo de luz sale de la parte posterior de la lente forma un ángulo distinto Φ (phi) con la normal a la superficie. La relación entre Φ y β es la misma que si la luz fuera en dirección contraria, en cuyo caso Φ sería el ángulo de incidencia y β el ángulo de refracción, de manera que β = Φ/n, y por tantoΦ = nβ = (n − 1)θ
Así que vemos que Φ es simplemente proporcional a θ, y por tanto, utilizando la fórmula anterior para f/r, tenemos que
Si el radio de curvatura r es muy grande, entonces la curvatura de la superficie frontal de la lente es muy pequeña, de manera que la lente es prácticamente igual a la superficie plana del cristal, y la curvatura de la luz al entrar en la lente queda prácticamente anulada por su curvatura al salir de ella. De manera parecida, sea cual sea la forma de la lente, si el índice de refracción n se acerca a 1, entonces la lente desvía muy poco el rayo de luz. En los casos en que la distancia focal es muy grande, decimos que la lente es débil. Una lente fuerte es aquella que tiene un radio de curvatura moderado y un índice de refracción sensiblemente distinto de 1, como por ejemplo una lente hecha de cristal, para la que n ~ 1,5.
Un resultado parecido se obtiene si la superficie posterior de la lente no es plana, sino un segmento de una esfera de radio r'. En este caso la distancia focal es:
El concepto de distancia focal también se puede ampliar a las lentes cóncavas, como las lentes que Galileo utilizó como ocular de su telescopio. Una lente cóncava puede captar rayos de luz que convergen y desplegarlos de manera que queden paralelos o incluso diverjan. Podemos definir la distancia focal de dicha lente considerando los rayos de luz convergentes que la lente convierte en paralelos; la longitud focal es la distancia que hay detrás de la lente hasta el punto en que dichos rayos convergerían si la lente no los convirtiera en paralelos. Aunque el significado es diferente, la distancia focal de una lente cóncava la da una fórmula parecida a la que hemos obtenido para una lente convexa.
§23. Telescopios
Como hemos visto en la Nota técnica 22, una lente convexa delgada concentrará los rayos de luz que inciden en paralelo hasta un eje central en un punto F de ese eje, a una distancia que está detrás de la lente conocida como distancia focal f de la lente. Los rayos de luz paralelos que inciden en la lente formando un pequeño ángulo γ (gamma) con el eje central también serán enfocados por la lente, pero a un punto un poco desplazado del eje central. Para ver cuál es ese desplazamiento, podemos imaginar que rotamos el dibujo de la trayectoria del rayo de la figura 16a alrededor de la lente formando un ángulo γ. La distancia d del punto focal del eje central de la lente dividida por la circunferencia de un círculo de radio f será igual al ángulo γ dividido entre 360°:
No podemos ver esta imagen virtual simplemente observándola, pues tras alcanzar esta imagen los rayos de luz divergen de nuevo. Para enfocarse en un punto de la retina de un ojo humano relajado, los rayos de luz deben entrar en la lente del ojo en dirección más o menos paralela. El telescopio de Kepler incluía una segunda lente convexa, conocida como el ocular, que enfocaba los rayos divergentes de luz de la imagen virtual para que salieran del telescopio en direcciones paralelas. Al repetir el análisis mencionado, pero invirtiendo la dirección de los rayos de luz, vemos que para que los rayos que salen de un punto de la fuente de luz abandonen el telescopio en direcciones paralelas, el ocular debe colocarse una distancia f' de la imagen virtual, en la que f' es la distancia focal del ocular (véase figura 17b). Es decir, la longitud L del telescopio ha de ser la suma de las distancias focales
L = f + f '
El intervalo de direcciones Δγ' de los rayos de luz procedentes de diferentes puntos de la fuente luminosa al entrar en el ojo mantiene una relación con el tamaño de la imagen virtual de
Para obtener una ampliación significativa, necesitamos que la lente que hay en la parte anterior del telescopio sea mucho más débil que el ocular, con f >> f'.
Esto no es fácil. Según la fórmula de la longitud focal que hemos dado en la Nota técnica 22, para obtener un ocular de cristal fuerte cuya distancia focal f' sea corta, es necesario que tenga un radio de curvatura pequeño, lo que significa que o bien ha de ser muy pequeño, o no debe de ser fino (es decir, el grosor ha de ser mucho menor que el radio de curvatura), en cuyo caso no enfoca bien la luz. También podemos hacer que la lente de la parte frontal sea débil, con una distancia focal f grande, pero en este caso la longitud L = f + f' ≈ f del telescopio ha de ser grande, lo cual es incómodo. Galileo tardó cierto tiempo en refinar su telescopio para que le diera una ampliación suficiente para poder usarlo con fines astronómicos.
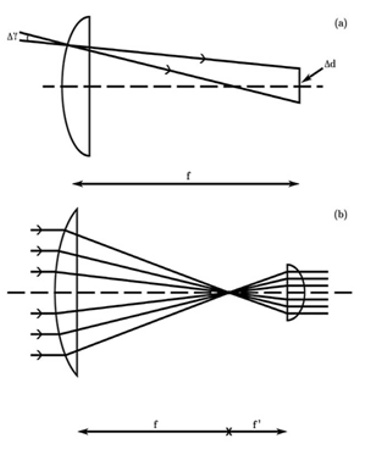
Figura 17. Telescopios . (a) Formación de una imagen virtual. Las dos líneas continuas marcadas con flechas son los rayos de luz que entran en la lente en líneas separadas por un ángulo Δγ. Estas líneas (y otras paralelas a ellas) se enfocan en puntos a una distancia f de la lente, con una separación vertical Δd proporcional a Δγ . (b) Las lentes del telescopio de Kepler. Las líneas marcadas con flechas indican la trayectoria de los rayos de luz que entran en una lente convexa débil procedentes de un objeto lejano, en direcciones esencialmente paralelas; la lente las enfoca en un punto a una distancia f de la lente; divergen de este punto; y se desvían gracias a una lente convexa fuerte, de manera que entran en el ojo en direcciones paralelas.
§24. Montañas en la Luna
Los lados luminoso y oscuro de la Luna están divididos por una línea conocida como el «terminador», en la que los rayos del Sol llegan perfectamente tangentes a la superficie de la Luna. Cuando Galileo volvió su telescopio hacia la Luna observó manchas luminosas en el lado oscuro de la Luna, cerca del terminador, y las interpretó como reflejos de montañas lo bastante altas como para interceptar los rayos del Sol que llegaban desde el otro lado del terminador. Era capaz de inferir la altura de estas montañas mediante una construcción geométrica parecida a la utilizada por Al-Biruni para medir el tamaño de la Tierra. Dibujemos un triángulo cuyos vértices sean el centro C de la Luna, la cima de una montaña M del lado oscuro de la Luna que intercepta un rayo de Sol, y el punto T sobre el terminador donde ese rayo roza la superficie de la Luna (véase figura 18). Tenemos un triángulo rectángulo; la línea TM es tangente a la superficie de la Luna en T, de manera que esta línea ha de ser perpendicular a la línea CT. La longitud de CT es justo el radio r de la Luna, mientras que la longitud de TM es la distancia d de la montaña al terminador. Si la montaña posee una altura h, entonces la longitud de CM (la hipotenusa del triángulo) es r + h. Según el teorema de Pitágoras, tenemos entonces que
(r + h)2 = r2 + d2
y por tantod2 = (r + h)2 − r2 = 2rh + h2
Puesto que el tamaño de cualquier montaña de la Luna es mucho menor que el tamaño de esta, podemos despreciar h2 en comparación con 2 rh. Al dividir ambas ecuaciones entre 2r2 obtenemos
Galileo, en Siderius Nuncius, afirmó que a veces veía manchas luminosas en el lado oscuro de la Luna a una distancia aparente del terminador mayor de una vigésima parte (1/20) del diámetro aparente de la Luna, por lo que para estas montañas
d/r > 1/10,
y por tanto, según la fórmula anteriorh/r > (1/10)2/2 = 1/200
Galileo estimó que el radio de la Luna era de 1000 millas[292], por lo que estas montañas tendrían al menos cinco millas de altura. (Por razones que no están claras, Galileo dio una cifra de cuatro millas, pero puesto que él intentaba tan solo establecer un límite inferior a la altura de la montaña, quizá tan solo se estaba mostrando conservador). Galileo creía que esa altura era mayor que cualquier montaña de la Tierra, pero ahora sabemos que en la Tierra hay montañas que tienen casi seis millas de altura (9654 m), de manera que las observaciones de Galileo indicaban que las alturas de las montañas de la Luna no son muy distintas de las alturas de las montañas terrestres.
Figura 18. Medida de la altura de las montañas de la Luna por parte de Galileo. La línea horizontal marcada con una flecha indica un rayo de luz que roza la Luna en el terminador T, señalando el límite entre el lado oscuro y el luminoso de la Luna, y luego llega a la cima M de una montaña de altura h a una distancia d del terminador.
§25. Aceleración gravitatoria
Galileo demostró que un cuerpo que cae sufre una aceleración uniforme; es decir, su velocidad aumenta en la misma cantidad a cada intervalo igual de tiempo. En términos modernos, un cuerpo que cae desde la posición de reposo, al cabo de un tiempo t tendrá una velocidad v dada por una cantidad proporcional a t:
v = gt
donde g es una constante que caracteriza el campo gravitatorio de la superficie de la Tierra. Aunque g varía de un lugar a otro en la superficie terrestre, nunca es muy diferente de 9,8 metros por segundo al cuadrado.Según el teorema de la velocidad media, la distancia que recorrerá ese cuerpo en un tiempo t es vmediat, donde vmedia es la media de gt y cero; en otras palabras, vmedia = gt/2. De ahí que la distancia recorrida sea
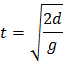
Epotencial = mgh = mg(h0 − d)
De ahí que si tenemos d = gt2/2, la energía total sea una constante:E = Ecinética + Epotencial = mgh0
Podemos darle la vuelta y deducir la relación entre la velocidad y la distancia recorrida suponiendo que se da la conservación de la energía. Si establecemos una E igual al valor mgh0 que tiene en t = 0, cuando v = 0 y h = h0, entonces la conservación de la energía nos da que en cualquier momento
Este es un ejemplo elemental de la conservación de la energía, que convierte el concepto de energía en algo útil en una amplia variedad de contextos. En concreto, la conservación de la energía muestra la relevancia de los experimentos de Galileo en los que utilizaba bolas que rodaban por un plano inclinado para el problema de la caída libre, aunque este no sea un argumento utilizado por Galileo. Para una bola de masa m que rueda por un plano, la energía cinética es mv2/2, donde v es la velocidad a lo largo del plano, y la energía potencial es mgh, donde h es de nuevo la altura. Además aparece la energía de rotación de la bola, que toma la forma de
Mediante un razonamiento complicado, Huygens fue capaz de demostrar que el tiempo que tarda un péndulo de longitud L en oscilar un pequeño ángulo de un lado a otro es:
§26. Trayectorias parabólicas
Supongamos que se dispara un proyectil horizontal con una velocidad v. Si despreciamos la resistencia del aire, proseguirá con su componente horizontal de velocidad, pero acelerará hacia abajo. De ahí que al cabo de un tiempo t se haya desplazado a una distancia horizontalx = vt y a una distancia hacia abajo z proporcional al cuadrado del tiempo, convencionalmente definida como z = gt2/2, donde g = 9,8 metros por segundo al cuadrado, una constante que el primero en medir fue Huygens, tras la muerte de Galileo. Teniendo en cuenta que t =x/v, tenemos que
z = gx2 /2v2
Esta ecuación, que nos da que una coordenada es proporcional al cuadrado de la otra, define una parábola.Observemos que si el proyectil se dispara desde un cañón a una altura h sobre el suelo, entonces la distancia x recorrida cuando el proyectil ha caído una distancia z = h y ha alcanzado el suelo es
Aun sin conocer v ni g, Galileo podría haber verificado que la trayectoria del proyectil es una parábola midiendo la distancia recorrida d para diversas alturas de caída h, y comprobando que d es proporcional a la raíz cuadrada de h. No está claro que Galileo lo supiera, pero hay pruebas de que en 1608 llevó a cabo un experimento que tenía mucho que ver con ello, mencionado brevemente en el capítulo 12. Una bola rueda por un plano inclinado desde diversas alturas iniciales H, a continuación rueda por la mesa horizontal sobre el que está colocado el plano inclinado, y finalmente se dispara hacia el aire desde el borde de la mesa. Tal como se muestra en la Nota técnica 25, la velocidad de la bola cuando llega al final del plan inclinado es:
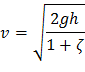
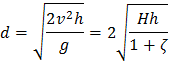
En muchos casos de la astronomía y las matemáticas, resulta conveniente definir una parábola como el caso límite de una elipse, cuando un foco se aleja mucho del otro. La ecuación para una elipse cuyo semieje mayor es 2a y cuyo semieje menor es 2b viene dada en la Nota técnica 18 como
donde, porque nos será más cómodo más adelante, hemos reemplazado las coordenadas x e y utilizadas en la nota 18 por z −z0, y x, donde z0 es una constante que se puede escoger como queramos. El centro de esta elipse está enz = z0 y x = 0. Como hemos visto en la nota 18, hay un foco en z − z0 = −ae, x = 0, donde e es la excentricidad, con
e2 = 1 − b2/a2,
y el punto donde la curva más se acerca a este foco es en z − z0 = −a y x = 0. Nos convendrá darle este punto de máxima proximidad a las coordenadas z = 0 y x = 0, escogiendo z0 = a, en cuyo caso el foco cercano se halla en z = z0 − ea = (1 − e)a. Queremos que a y b se hagan infinitamente grandes, para que el otro foco llegue al infinito y la curva no tenga una coordinada x máxima, pero queremos que la distancia (1 − e) a de máxima aproximación al foco más cercano permanezca finita, de manera que establecemos1 − e = ℓ/a
donde ℓ se mantiene fija mientras a tiende al infinito. Puesto que en el límite e se acerca a la unidad, el semieje menor nos lo da la fórmulab2 = a2(1 − e2) = a2(1 − e)(1 + e) → 2a2(1 − e) = ℓ a
Utilizando z0 = a y esta fórmula para b2, la ecuación para la elipse se convierte en
Figura 19. La trayectoria parabólica de un proyectil disparado desde una colina en dirección horizontal. El punto F es el foco de esta parábola.
√(x2 + y2) = α(z + z0),
y la ecuación de un plano paralelo al cono como simplementey = α (z − z0)
donde z0 es arbitrario, la intersección del cono y el plano satisface la ecuaciónx2 + α2 (z2 − 2zz0 + z02) = α2 + 2zz0 + z02
Tras anular los términos α2z2 y α2z02, la ecuación queda como
z0 = ℓ/α2
Observemos que una parábola de una forma dada se puede obtener a partir de cualquier cono, con un valor cualquiera del parámetro angular α (alpha), porque la forma de cualquier parábola (contrariamente a su localización y orientación) viene determinada completamente por un parámetro ℓ con las unidades de longitud; no necesitamos saber de manera separada ningún parámetro sin unidades como α ni la excentricidad de la elipse.§27. Deducción de la ley de refracción de la pelota de tenis
Descartes intentó deducir la ley de refracción basándose en el supuesto de que un rayo de luz se desvía al pasar de un medio a otro del mismo modo que la trayectoria de una pelota de tenis se desvía al penetrar en una fina tela. Supongamos que una pelota de tenis con una velocidad vA impacta en una pantalla de tela de manera oblicua. Perderá cierta velocidad, de manera que tras penetrar en la pantalla su velocidad será vB < vA, pero no esperamos que el paso de la pelota a través de la pantalla produzca ningún cambio en el componente de la velocidad de la pelota a lo largo de la pantalla. Podemos dibujar un triángulo cuyos lados son el componente de la velocidad inicial de la pelota perpendicular a la pantalla y el componente paralelo a esta, y cuya hipotenusa es vA. Si la trayectoria original de la pelota forma un ángulo i con la perpendicular a la pantalla, entonces el componente de su velocidad en la dirección paralela a la pantalla es vA sen i. (véase figura 20). De manera parecida, si tras penetrar en la pantalla la trayectoria de la pelota forma un ángulo r con la perpendicular a la pantalla, entonces el componente de su velocidad en la dirección paralela a la pantalla es vB sen r. Utilizando el supuesto de Descartes de que el paso de la pelota través de la pantalla podría cambiar solamente el componente de la velocidad perpendicular a la interfase, y no el componente paralelo, tenemos
vA sen i = vB sen r
y por tanto
Figura 20. Velocidad de la pelota de tenis. La línea horizontal señala una pantalla en la que penetra una pelota de tenis con una velocidad inicial vA y final vB . Las líneas continuas marcadas con flechas indican la magnitud y dirección de las velocidades de la pelota antes y después de penetrar en la pantalla. Las líneas horizontales de puntos muestran los componentes vA sen i y vB sen r de estas velocidades paralelas a la pantalla, donde los ángulos i y r se miden entre la dirección de la pelota y la línea vertical de puntos perpendicular al punto de contacto.
Tal como demostró Fermat, cuando la luz pasa de un medio donde la velocidad es vA a otro en el que la velocidad es vB, el índice de refracción n de hecho es igual a vA/vB y no a vB/vA. Descartes no sabía que la luz viaja a una velocidad finita, y presentó un argumento insustancial para explicar por qué n es mayor que la unidad cuando A es el aire y B es el agua. Para las aplicaciones del siglo XVII, como la teoría del arcoíris de Descartes, no tuvo importancia, porque n se tomaba como independiente del ángulo, cosa que es correcta para la luz pero no para las pelotas de tenis, y su valor se obtuvo observando la refracción, no midiendo la velocidad de la luz en diversos medios.
§28. Deducción de la ley de refracción del principio del menor tiempo
Herón de Alejandría presentó una deducción de la ley de reflexión, según la cual el ángulo de reflexión es igual al ángulo de incidencia, a partir del supuesto de que el trayecto del rayo de luz de un objeto al espejo y luego al ojo es el más corto posible. También podría haber supuesto que el tiempo es el más breve posible, puesto que el tiempo que tarda la luz en recorrer cualquier distancia es esta distancia dividida por la velocidad de la luz, y en el reflejo la velocidad de la luz no cambia. Por otro lado, en la refracción tenemos que un rayo de luz atraviesa la separación entre dos medios distintos (como el aire y el cristal) en los que la velocidad de la luz es diferente, y hemos de distinguir entre un principio de menor distancia y otro de menor tiempo. Simplemente del hecho de que un rayo de luz se desvíe al pasar de un medio a otro sabemos que la luz, al refractarse, no sigue la menor distancia, que sería una línea recta. Más bien, como demostró Fermat, la correcta ley de refracción se puede derivar suponiendo que la luz sigue el trayecto de menor tiempo.
Para llevar a cabo esta deducción, supongamos que un rayo de luz viaja desde el punto PA en un medio A en el que la velocidad de la luz es vA hasta el punto PB en un medio B en el que la velocidad de la luz es vB . Para que esto resulte fácil de describir, supongamos que la superficie que separa los dos medios es horizontal. Llamemos a los ángulos que forman los rayos de luz en los medios A y B con la dirección vertical i y r respectivamente. Si los puntos PA y PB son las distancias verticales dA y dB desde la superficie de separación, entonces la distancia horizontal de estos puntos desde el punto donde los rayos que cruzan esta superficie son dA tan i y dB tan r, respectivamente, donde tan indica la tangente del ángulo, la razón entre el cateto opuesto y el adyacente en un triángulo rectángulo (véase figura 21). Aunque estas distancias no se fijan de antemano, su suma es la distancia horizontal fija L entre los puntos PA y PB:
L = dA tan i + dB tan r
Para calcular el tiempo t transcurrido cuando la luz va de PA a PB, observamos que las distancias recorridas en los medios A y B son dA/cos i y dB/cos r, respectivamente, donde cos es el coseno de un ángulo, la razón entre el cateto adyacente y la hipotenusa en un triángulo rectángulo. El tiempo transcurrido es la distancia dividida por la velocidad, de manera que el tiempo transcurrido total aquí es:
Necesitamos encontrar una relación general entre los ángulos i y r (independiente de L, dA y dB) que satisfaga ese ángulo i y que haga que el tiempo t sea mínimo, cuando r depende de i de manera queL permanece fijo. Para este propósito, consideremos δi, una variación infinitesimal δ (delta) del ángulo de incidenciai. La distancia horizontal entre PA y PB es fija, de manera que cuando i cambia en una cantidad δi, el ángulo de refracción r también tiene que cambiar, pongamos en una cantidad δr, puesto que hemos impuesto la condición de que L ha de permanecer fijo. Además, en el mínimo de t, la gráfica de t e i debe ser plana, pues si t aumenta o disminuye en algún i, el mínimo debe estar en otro valor de i donde t sea más pequeño. Lo que significa que el cambio en t provocado por un diminuto cambio δi debe desaparecer, al menos para el primer orden en δi. De manera que para encontrar la trayectoria de tiempo menor podemos imponer la condición que cuando variamos tanto i como r, los cambios δL y δt deben desaparecer al menos para el primer orden en δi y δr.
Figura 21. Trayectoria de un rayo de luz durante la refracción. La línea horizontal marca la interfase entre dos medios transparentes A y B, en los que la luz tiene velocidades diferentes vA y vB y forma unos ángulos i y r entre el rayo de luz y la línea vertical de puntos perpendicular a la interfase. La línea continua marcada con flechas representa la trayectoria de un rayo de luz que viaja desde el punto PA en el medio A hasta el punto P de la interfase entre los medios y luego hasta el punto PB en el medio B.
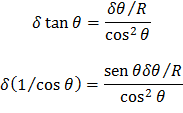
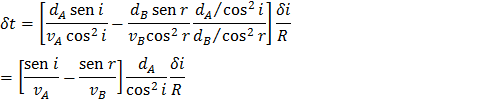
n = vA /vB
Esta es la ley correcta de la refracción, con la fórmula correcta para n.§29. La teoría del arcoíris
Supongamos que un rayo de luz llega a una gota de lluvia esférica en un punto P, donde forma un ángulo i con la normal a la superficie de la gota. Si no hubiera refracción, el rayo de luz cruzaría la gota en línea recta. En este caso, la línea desde el centro C de la gota hasta el punto Q de máxima proximidad del rayo al centro formaría un ángulo recto con el rayo de luz, de manera que el triángulo PCQ sería un triángulo rectángulo cuya hipotenusa sería igual al radio R del círculo, y el ángulo en P igual a i (véase figura 22a). El parámetro de impacto b se define como la distancia de máxima proximidad del rayo no refractado al centro, de manera que es la longitud del lado CQ del triángulo, que la trigonometría elemental nos da como
b = R sen i De igual modo podemos caracterizar perfectamente los rayos de luz individuales mediante su valor de b/R, como hizo Descartes, o por el valor del ángulo de incidencia i.
Por culpa de la refracción, el rayo en realidad entra en la gota formando un ángulo r con la normal, dado por la ley de refracción:
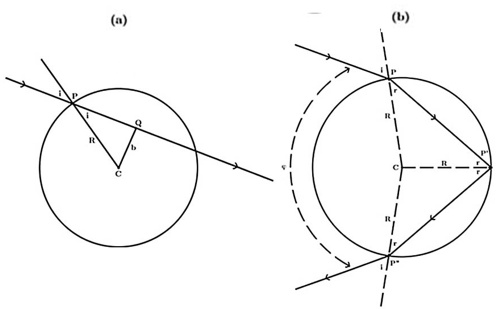
Figura 22. El trayecto de un rayo de luz solar en una gota esférica de agua. El rayo está indicado por líneas continuas con flechas, y entra en la gota en el punto P, donde forma un ángulo i con la normal a la superficie. (a) Trayectoria del rayo si no hay refracción, donde Q es el punto de mayor proximidad del rayo al centro C en este caso. (b) El rayo refractado al entrar en la gota en P, reflejado por la superficie posterior de la gota en P', y a continuación refractado de nuevo al dejar la gota en P'. Las líneas de puntos van del centro C de la gota hasta los puntos en los que el rayo se encuentra con la superficie de la gota.
2(i − r) + 180° − 2r = 180° − 4r + 2i
Si el rayo de luz rebota directamente en la gota (como ocurre en el caso de que i = 0 y r = 0), este ángulo sería de 180° y los rayos de luz inicial y final estarían en la misma línea, de manera que el ángulo real Φ (phi) entre los rayos de luz inicial y final es:Φ = 4r − 2i
Podemos expresar r en términos de i, como
Si observamos un cielo neblinoso con el sol detrás de nosotros, vemos que la luz se refleja sobre todo desde las direcciones del cielo en las que el ángulo entre nuestra línea de visión y los rayos de sol está más cerca de 42°. Estas direcciones forman un arco, que generalmente va desde la superficie de la Tierra hacia el cielo y luego baja de nuevo hasta la superficie. Como n depende ligeramente del color de la luz, lo mismo ocurre con el valor máximo del ángulo de desviación Φ, de manera que este arco se extiende en colores distintos. Y es el arcoíris.
No es difícil deducir una fórmula analítica que nos dé el valor máximo de Φ para cualquier valor del índice de refracción n. Para averiguar el máximo de Φ, utilizamos el hecho de que este máximo se da en un ángulo de incidencia i en el que la gráfica de Φ comparada con i es plana, de manera que la variación δΦ (delta phi) en Φ, producida por una pequeña variación δ en i, desaparece para el primer orden en δi. Para utilizar esta condición, hacemos uso de una fórmula de cálculo estándar, que nos dice que cuando realizamos un pequeño cambio δx en x, el cambio en el arcsen x es:
donde si el arcsen x se mide en grados, entonces tenemos R = 360°/2π. Así, cuando el ángulo de incidencia varía una cantidad δi, el ángulo de desviación cambia en
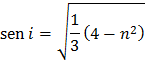
i = 59,4°, donde r = 40,2°, y Φmax = 42,0°.
§30. Deducción de la teoría ondulatoria de la ley de refracciónLa ley de refracción, que tal como se ha descrito en la Nota técnica 28 se puede deducir del supuesto de que los rayos de luz refractada siguen la trayectoria de menor tiempo, también se puede deducir basándonos en la teoría ondulatoria de la luz. Según Huygens, la luz es una perturbación en un medio, que puede ser un material transparente o el espacio, que aparentemente es vacío. El frente de la perturbación es una línea que avanza en dirección perpendicular a ese frente y a una velocidad característica del medio.
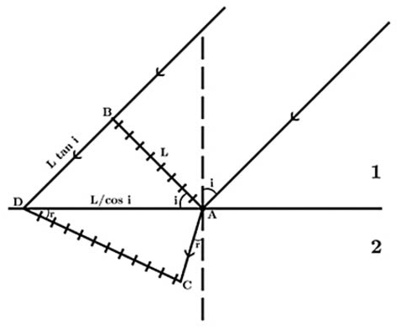
Figura 23. Refracción de una onda de luz . La línea horizontal marca de nuevo la interfase entre los medios transparentes, en los que la luz tiene velocidades distintas. Las líneas con tramos muestran el segmento del frente de una onda en dos momentos diferentes: cuando el borde anterior de la onda alcanza la interfase, y cuando la alcanza el borde posterior. Las líneas continuas marcadas con flechas muestran la trayectoria de los bordes anterior y posterior del frente de la onda.
sen r = v2 sen i/v1
o en otras palabras
No es ningún accidente que la teoría ondulatoria, tal como fue elaborada por Huygens, dé los mismos resultados para la refracción que el principio de Fermat del menor tiempo. Se puede demostrar que, incluso para ondas que atraviesan un medio heterogéneo en el que la velocidad de la luz cambia gradualmente en diversas direcciones, y no solo repentinamente en una interfase plana, la teoría ondulatoria de Huygens siempre nos dará una trayectoria para la luz que tarde el menor tiempo a la hora de viajar entre dos puntos.
§31. Medición de la velocidad de la luz
Supongamos que observamos un proceso periódico que ocurre a cierta distancia de nosotros. Para ser más concretos consideremos una luna que gira alrededor de un planeta lejano, aunque los análisis que vamos a llevar a cabo se aplicarían a cualquier proceso que se repite de manera periódica. Supongamos que la luna alcanza la misma fase en su órbita en dos momentos consecutivos t1 y t2; por ejemplo, podrían ser los momentos en que la luna aparece consecutivamente por detrás del planeta. Si el periodo orbital intrínseco de la luna es T, entonces t2 − t1 = T. Este es el periodo que observamos, suponiendo que la distancia entre nosotros y el planeta sea fija. Pero si esta distancia cambia, entonces el periodo que observamos se desplazará de T en una cantidad que depende de la velocidad de la luz.
Supongamos que las distancias entre nosotros y el planeta en dos momentos sucesivos, cuando la luna se halla en la misma fase en su órbita, son d1 y d2. Entonces observamos estas fases en la órbita en los momentos
t '1 = t1 + d1/c
t '2 = t2 + d2/c
donde c es la velocidad de la luz. (Estamos suponiendo que la distancia entre el planeta y su luna es despreciable). Si la distancia entre nosotros y este planeta cambia a una velocidad v, bien porque el planeta se mueve, bien porque nos movemos nosotros, o porque nos movemos los dos, entonces d2 − d1 = vT, con lo que el periodo observado es:
A partir de ello Huygens determinó la velocidad de la luz, basándose en la observación de Rømer del cambio del periodo orbital aparente de la luna de Júpiter, Io. Pero conociendo la velocidad de la luz, el mismo cálculo nos puede dar la velocidad relativa v de un objeto lejano. En particular, las ondas luminosas de una línea específica del espectro de frecuencias de una galaxia lejana oscilarán con un periodo característico T, relacionado con su frecuencia ν (nu) y la longitud de onda λ (lambda), en T = 1 − ν = λ/c. Este periodo intrínseco se conoce a partir de las observaciones de los espectros en los laboratorios de la Tierra. Y a principios del siglo XX se descubrió que las líneas espectrales observadas en galaxias muy lejanas tienen longitudes de onda más largas, y por ello periodos más largos, de lo que podemos inferir que estas galaxias se están alejando de nosotros.
§32. Aceleración centrípeta
La aceleración es una magnitud que nos indica el cambio de velocidad por unidad de tiempo, pero la velocidad de cualquier cuerpo, además de una magnitud, posee una dirección. La velocidad de cualquier cuerpo que se mueve en círculo cambia continuamente de dirección, girando hacia el centro del círculo, por lo que incluso a velocidad constante sufre una aceleración continua hacia el centro, conocida como aceleración centrípeta.
Calculemos la aceleración centrípeta de un cuerpo que recorre un círculo de radio r a velocidad constante v. Durante un breve intervalo entre t1 y t2, el cuerpo recorrerá el círculo en una pequeña distancia v Δt, donde Δt (delta t) = t2 − t1, y el vector radial (la flecha que va del centro del círculo al cuerpo) girará un pequeño ángulo Δθ (delta theta). El vector velocidad (una flecha de magnitud v en la dirección del movimiento del cuerpo) es siempre tangente al círculo, y de ahí que forme un ángulo recto con el vector radial, por lo que, mientras la dirección del vector radial cambia en un ángulo Δθ, la dirección del vector velocidad cambiará con el mismo ángulo. Así pues, tenemos dos triángulos: uno cuyos lados son los vectores radiales en los momentos t1 y t2 y la cuerda que conecta las posiciones del cuerpo en estos dos momentos; y otro cuyos lados son los vectores velocidad en los momentos t1 y t2, y el cambio Δv en la velocidad entre esos dos momentos (véase figura 24). Para ángulos pequeños Δθ, la diferencia de longitud entre la cuerda y el arco que conecta las posiciones de los cuerpos en los momentos t1 y t2 es despreciable, de manera que podemos considerar que la longitud de la cuerda es vΔt.
Ahora bien, estos triángulos son semejantes (es decir, difieren en tamaño, pero no en su forma) porque son ambos triángulos isósceles (cada uno tiene dos lados iguales) con el mismo ángulo Δθ entre los dos lados iguales. De manera que la razón entre el lado corto y el largo de cada triángulo debería ser la misma. Es decir:
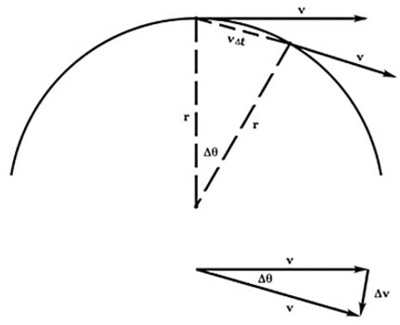
Figura 24. Cálculo de la aceleración centrípeta. Arriba: velocidades de una partícula que se mueve en un círculo en dos momentos separados por un breve intervalo de tiempo Δt. Abajo: estas dos velocidades, unidas en un triángulo cuyo lado más corto es el cambio de velocidad en este intervalo de tiempo.
La supuesta distinción de los antiguos entre los fenómenos de los cielos y los de la Tierra fue puesta seriamente en entredicho por la comparación de Newton entre la aceleración centrípeta de la Luna en su órbita y la aceleración hacia abajo de un cuerpo que cae cerca de la superficie de la Tierra.
A partir de las medidas del paralaje diurno de la Luna, en la época de Newton se sabía de manera exacta que la distancia media desde la Tierra era 60 veces el radio de la Tierra. (La proporción real es 60,27). Para calcular el radio de la Tierra, Newton consideró que 1' (minuto de arco) en el ecuador era una milla de 5000 pies, de manera que siendo 360° un círculo completo y 60' igual a 1°, el radio de la Tierra era:
Lo que nos da una aceleración centrípeta de
§34. Conservación del momento
Supongamos que dos objetos que se mueven, de masas m1 y m2, colisionan de frente. Si en un breve intervalo de tiempo δt (delta t) el objeto 1 ejerce una fuerza F sobre el objeto 2, entonces, en este intervalo de tiempo, el objeto 2 experimentará una aceleración a2, que según la segunda ley de Newton, obedece a la relación m2a2 = F. Entonces su velocidad v cambiará según la cantidad
δv2 = a2δt = Fδt/m2
Según la tercera ley de Newton, la partícula 2 ejercerá sobre la partícula 1 una fuerza −F que es igual en magnitud, pero (como indica el signo menos) de dirección opuesta, de manera que en el mismo intervalo la velocidad v1 del objeto 1 sufrirá un cambio en la dirección opuesta a δv2, dado porδv1 = a1δt = −Fδt/m1
El cambio final en el momento total m1v1 + m2v2 es, por tanto,m1δv1 + m2δv2 = 0
Naturalmente, es posible que los dos objetos estén en contacto durante un periodo prolongado de tiempo, durante el cual puede que la fuerza no sea constante, pero puesto que el momento se conserva para cada breve intervalo de tiempo, se conserva durante todo el periodo.§35. Masas planetarias
En la época de Newton se sabía que había cuatro cuerpos del sistema solar que tenían satélites: se sabía que Júpiter y Saturno, además de la Tierra, tenían lunas, y que todos los planetas eran satélites del Sol. Según la ley de la gravitación de Newton, un cuerpo de masa M ejerce una fuerza
F = GMm/r2
sobre un satélite de masa m a una distancia r (donde G es una constante de la naturaleza), por lo que según la segunda ley del movimiento de Newton, la aceleración centrípeta del satélite seráa = F/m = GM/r2.
El valor de la constante G y la escala global del sistema solar no se conocían en época de Newton, pero estas cantidades desconocidas no aparecen en las razones de las masas calculadas a partir de las razones de las distancias y las razones de las aceleraciones centrípetas. Si dos satélites de dos cuerpos cuya masa es M1 y M2 se encuentran a una distancia de esos cuerpos cuya razón r1 /r2 es conocida, y poseen aceleraciones centrípetas cuya razón a1/a2 es conocida, entonces la razón de las masas se puede extraer de la fórmula
a1/a2 = (r1/r2)/(T1/T2)2
y la razón de las masas inferida de los periodos orbitales y las razones de las distancias es:
Esta bibliografía enumera las modernas fuentes secundarias de la historia de la ciencia en las que me he basado, y también las obras originales de científicos del pasado que he consultado, desde fragmentos de los presocráticos hasta los Principia de Newton, y de manera más básica hasta la época actual. Las obras enumeradas están todas en inglés o son traducciones al inglés; por desgracia, no sé latín ni griego, y mucho menos árabe. No pretende ser una lista de las fuentes más autorizadas, ni de las mejores ediciones de cada fuente. Son simplemente los libros que he consultado al escribir Explicar el mundo en las mejores ediciones que he podido conseguir.
Fuentes originales
- Arquímedes, The Works of Archimedes, trad. T. L. Heath (Cambridge University Press, Cambridge, 1897).
- Aristarco, Aristarchus of Samos, trad. T. L. Heath (Clarendon, Oxford, 1923).
- Aristóteles, The Complete Works of Aristotle-The Revised Oxford Translation, ed. J. Barnes (Princeton University Press, Princeton, Nueva Jersey, 1984). [Ed. esp.: Metafísica, trad. de Patricio de Azcárate (Espasa-Calpe, Madrid, 1990); Física, trad. de Guillermo R. de Echandía (Gredos, Madrid, 1995)].
- Agustín, san, Confessions, trad. Albert Cook Outler (Westminster, Philadelphia, Pensilvania, 1955). [Ed. esp.: Confesiones, trad. de Eugenio Ceballos, Espasa-Calpe, Madrid, 1983); Retractions, trad. M. I. Bogan (Catholic University of America Press, Washington, D.C., 1968).
- Cicerón, On the Republic y On the Laws, trad. Clinton W. Keys (Loeb Classical Library, Harvard University Press, Cambridge, Massachusetts, 1928). [Ed. esp.: Sobre la república; Sobre las leyes, trad. de José Guillén (Tecnos, Madrid, 1986)].
- Cleómedes, Lectures on Astronomy, ed. y trad. A. C. Bowen y R. B. Todd (University of California Press, Berkeley y Los Ángeles, 2004).
- Copérnico, Nicolas Copernicus On the Revolutions, trad. Edward Rosen (Polish Scientific Publishers, Varsovia, 1978; reimp., Johns Hopkins University Press, Baltimore, Maryland, 1978); Copernicus-On the Revolutions of the Heavenly Spheres, trad. A. M. Duncan (Barnes y Noble, Nueva York, 1976). [Ed. esp.: Sobre las revoluciones de los orbes celestes, trad. de Carlos Mínguez Pérez (Tecnos, Madrid, 1987)];Three Copernican Treatises, trad. E. Rosen (Farrar, Straus, and Giroux, Nueva York, 1939). Lo componen Commentariolus, Letter Against Werner, y Narratio prima of Rheticus.
- DARWIN, Charles, On the Origin of Species by Means of Natural Selection, 6.ª ed. (John Murray, Londres, 1885). [Ed. esp.: El origen de las especies, trad. de Antonio de Zulueta (Espasa-Calpe, Madrid, 1988)].
- DESCARTES, René, Discourse on Method, Optics, Geometry, and Meteorology, trad. Paul J. Olscamp (Bobbs-Merrill, Indianapolis, Indiana, 1965). [Ed. esp.: Discurso del método; Dióptricas; Meteoros; y Geometría, trad. de Guillermo Quintás Alonso (Alfaguara, Madrid, 1991)]; Principles of Philosophy, trad. V. R. Miller y R. P. Miller (D. Reidel, Dordrecht, 1983). [Ed. esp.: Los principios de la filosofía, trad. de Guillermo Quintás (Alianza, Madrid, 1995)].
- Euclides, The Thirteen Books of the Elements, 2.ª ed., trad. Thomas L. Heath (Cambridge University Press, Cambridge, 1925). [Ed. esp.: Elementos, trad. de María Luisa Puertas Castaños (Gredos, Madrid, 2000)].
- Filón, The Works of Philo, trad. C. D. Yonge (Hendrickson, Peabody, Massachusetts, 1993).
- GALILEI, Galileo, Dialogue Concerning the Two Chief World Systems: Ptolemaic and Copernican, trad. Stillman Drake (Modern Library, Nueva York, 2001). [Ed. esp.: Galileo, ed. de Víctor Navarro (Península, Barcelona, 1991)]; Discourse on Bodies in Water, trad. Thomas Salusbury (University of Illinois Press, Urbana, 1960); Discoveries and Opinions of Galileo, trad. Stillman Drake (Anchor, Nueva York, 1957). ContieneThe Starry Messenger, Letter to Christina y fragmentos de Letters on Sunspots y The Assayer.;The Essential Galileo, trad. de Maurice A. Finocchiaro (Hackett, Indianapolis, Indiana, 2008). Incluye The Sidereal Messenger,Letter to Castelli, Letter to Christina, Reply to Cardinal Bellarmine, etcétera;Siderius Nuncius, or The Sidereal Messenger, trad. de Albert van Helden (University of Chicago Press, Chicago, Illinois, 1989); Two New Sciences, Including Centers of Gravity and Force of Percussion, trad. Stillman Drake (University of Wisconsin Press, Madison, 1974).
- GALILEI, Galileo y Christoph SCHEINER, On Sunspots, trad. y ed. Albert van Helden y Eileen Reeves (University of Chicago Press, Chicago, Illinois, 2010).
- HAMID AL-GHAZALI, Abu, The Beginnings of Sciences, trad. I. Goldheizer, en Studies on Islam, ed. Merlin L. Swartz (Oxford University Press, Oxford, 1981); The Incoherence of the Philosophers, trad. de Sabih Ahmad Kamali (Pakistan Philosophical Congress, Lahore, 1958).
- Heródoto, The Histories, trad. Aubery de Selincourt, ed. rev. (Penguin Classics, Londres, 2003). [Ed. esp.: Los nueve libros de la historia, trad. de María Rosa Lida de Malkiel (Orbis, Barcelona, 1987)].
- Homero, The Iliad, trad. Richmond Lattimore (University of Chicago Press, Chicago, Illinois, 1951). [Ed. esp.: Ilíada, trad. de Luis Segalá y Estalella (Espasa- Calpe, Madrid, 1962)]; The Odyssey, trad. Robert Fitzgerald (Farrar, Straus, and Giroux, Nueva York, 1961). [Ed. esp.: Odisea, trad. de Luis Segalá y Estalella (Espasa-Calpe, Madrid, 1973)].
- Horacio, Odes and Epodes, trad. Niall Rudd (Loeb Classical Library, Harvard University Press, Cambridge, Massachusetts, 2004). [Ed. esp.: Odas y Epodos, trad. de Manuel Fernández Galiano (Cátedra, Madrid, 1997)].
- HUYGENS, Christiaan, The Pendulum Clock or Geometrical Demonstrations Concerning the Motion of Pendula as Applied to Clocks, trad. Richard J. Blackwell (Iowa State University Press, Ames, 1986); Treatise on Light, trad. Silvanus P. Thompson (University of Chicago Press, Chicago, Illinois, 1945).
- KEPLER, Johannes, Epitome of Copernican Astronomy and Harmonies of the World, trad. de C. G. Wallis (Prometheus, Amherst, Nueva York, 1995); New Astronomy (Astronomia Nova), trad. de W. H. Donahue (Cambridge University Press, Cambridge, 1992).
- JAYAM, Omar, The Rubáiyát, the Five Authorized Editions, trad. Edward Fitzgerald (Walter J. Black, Nueva York, 1942). [Ed. esp.:Rubaiyat, trad. de Esteve Serra i Arús (José J. Olañeta, Palma de Mallorca, 2008)]; The Rubáiyát, a Paraphrase from Several Literal Translations, de Richard Le Gallienne (John Lan, Londres, 1928).
- LACTANCIO, Divine Institutes, trad. A. Bowen y P. Garnsey (Liverpool University Press, Liverpool, 2003). [Ed. esp.: Instituciones divinas, trad. de E. Sánchez Salor (Gredos, Madrid, 1990)].
- LAERCIO, Diógenes, Lives of the Eminent Philosophers, trad. R. D. Hicks (Loeb Classical Library, Harvard University Press, Cambridge, Massachusetts, 1972). [Ed. esp.: Vidas, opiniones y sentencias de los filósofos más ilustres, trad. de José Ortiz Sanz (Luis Navarro, Madrid, 1885)].
- LEIBNIZ, Gottfried Wilhelm, The Leibniz-Clarke Correspondence, ed. H. G. Alexander (Manchester University Press, Manchester, 1956).
- LUTERO, Martín, Table Talk, trad. W. Hazlitt (H. G. Bohn, Londres, 1857).
- MAIMÓNIDES, Guide to the Perplexed, trad. M. Friedländer, 2.ª ed. (Routledge, Londres, 1919). [Ed. esp.: Guía de perplejos, trad. de David González Maeso (Editora Nacional, Madrid, 1983)].
- NEWTON, Isaac, The Mathematical Papers of Isaac Newton, ed. D. Thomas Whiteside (Cambridge University Press, Cambridge, 1968); Mathematical Principles of Natural Philosophy, trad. de Florian Cajori, rev. trad. Andrew Motte (University of California Press, Berkeley y Los Ángeles, 1962); Opticks, or a Treatise of the Reflections, Refractions, Inflections, and Colours of Light (Dover, Nueva York, 1952, basado en la 4.ª ed., Londres, 1730). [Ed. esp.: Óptica o tratado de las reflexiones, refracciones, inflexiones y colores de la luz, trad. de Carlos Solís (Alfaguara, Madrid, 1977)]; The Principia-Mathematical Principles of Natural Philosophy, trad. de I. Bernard Cohen y Anne Whitman, con «A Guide to Newton's Principia» de I. Bernard Cohen (University of California Press, Berkeley y Los Ángeles, 1999). [Ed. esp.: Principios matemáticos de la filosofía natural, ed. de Antonio Escohotado (Editoria Nacional, Madrid, 1982)].
- ORESME, Nicole, The Book of the Heavens and the Earth, trad. de A. D. Menut y A. J. Denomy (University of Wisconsin Press, Madison, 1968).
- Platón, Phaedo, trad. de Alexander Nehamas y Paul Woodruff (Hackett, Indianapolis, Indiana, 1995); Plato, vol. 9 (Loeb Classical Library, Harvard University Press, Cambridge, Massachusetts, 1929). Incluye Phaedo, etcétera; Republic, trad. de Robin Wakefield (Oxford University Press, Oxford, 1993); Timaeus and Critias, trad. de Desmond Lee (Penguin, Nueva York, 1965); The Works of Plato, trad. de Benjamin Jowett (Modern Library, Nueva York, 1928). Incluye Phaedo, Republic, Theaetetus, etcétera [Ed. esp.: Obras Completas, varios traductores (Aguilar, Madrid, 1974)].
- Ptolomeo, Almagest, trad. de G. J. Toomer (Duckworth, Londres, 1984); Optics, trad. de A. Mark Smith, en «Ptolemy's Theory of Visual Perception-An English Translation of the Optics with Commentary», Transactions of the American Philosophical Society 86, Parte 2 (1996).
- Simplicio, On Aristotle's «On the Heavens 2.10-14», trad. de I. Mueller (Cornell University Press, Ithaca, Nueva York, 2005);On Aristotle's «On the Heavens 3.1-7», trad. de I. Mueller (Cornell University Press, Ithaca, Nueva York, 2005); On Aristotle's «Physics 2», trad. de Barrie Fleet (Duckworth, Londres, 1997).
- Tucídides, History of the Peloponnesian War, trad. de Rex Warner (Penguin, Nueva York, 1954, 1972). [Ed. esp.: Historia de la guerra del Peloponeso, trad. de Francisco Rodríguez Adrados (Hernando, Madrid, 1969)].
Recopilaciones de fuentes originales
- BARNES, J., Early Greek Philosophy (Penguin, Londres, 1987); The Presocratic Philosophers, ed. rev. (Routledge and Kegan Paul, Londres, 1982).
- BERGGREN, J. Lennart, «Mathematics in Medieval Islam», en The Mathematics of Egypt, Mesopotamia, China, India, and Islam, ed. de Victor Katz (Princeton University Press, Princeton, Nueva Jersey, 2007).
- CLAGETT, Marshall, The Science of Mechanics in the Middle Ages (University of Wisconsin Press, Madison, 1959).
- COHEN, M. R. y I. E. DRABKIN, A Source Book in Greek Science (Harvard University Press, Cambridge, Massachusetts, 1948).
- DRAKE, Stillman y I. E. DRABKIN, Mechanics in Sixteenth Century Italy (University of Wisconsin Press, Madison, 1969).
- DRAKE, Stillman y C. D. O'MALLEY, The Controversy on the Comets of 1618 (University of Pennsylvania Press, Filadelfia, 1960). Traducciones de obras de Galileo, Grassi, y Kepler.
- FREEMAN, K., The Ancilla to the Pre-Socratic Philosophers (Harvard University Press, Cambridge, Massachusetts, 1966).
- GRAHAM, D. W., The Texts of Early Greek Philosophy-The Complete Fragments and Selected Testimonies of the Major Presocratics (Cambridge University Press, Nueva York, 2010).
- GRANT, E., ed., A Source Book in Medieval Science (Harvard University Press, Cambridge, Massachusetts, 1974).
- HEATH, T. L., Greek Astronomy, (J. M. Dent & Sons, Londres, 1932).
- IBRY-MASSIE, G. L. y P. T. KEYSER, Greek Science of the Hellenistic Era (Routledge, Londres, 2002).
- MAGIE, William Francis, A Source Book in Physics (McGraw-Hill, Nueva York, 1935).
- MATTHEWS, Michael, The Scientific Background to Modern Philosophy (Hackett, Indianapolis, Indiana, 1989).
- SWARTZ, Merlin L., Studies in Islam (Oxford University Press, Oxford, 1981).
Fuentes secundarias
- L'Anno Galileiano, International Symposium a cura dell'Universita di Padova , 2-6 dicembere 1992, vol. 1 (Edizioni LINT, Trieste, 1995). Ponencias en inglés de T. Kuhn y S. Weinberg; véase también Tribute to Galileo.
- BARNES, J., ed., The Cambridge Companion to Aristotle (Cambridge University Press, Cambridge, 1995). Artículos de J. Barnes, R. J. Hankinson, y otros.
- BUTTERFIELD, Herbert, The Origins of Modern Science, ed. rev (Free Press, Nueva York, 1957).
- CHANDRASEKHAR, S., Newton's Principia for the Common Reader (Clarendon, Oxford, 1995).
- CHRISTIANSON, R., Tycho's Island (Cambridge University Press, Cambridge, 2000).
- CIPOLLA, Carlo M., Clocks and Culture 1300-1700 (W. W. Norton, Nueva York, 1978). [Ed. esp.: Las máquinas del tiempo, trad. de Antoni Martínez Riu (Crítica, Barcelona, 2010)].
- CLAGETT, Marshall, ed., Critical Studies in the History of Science (University of Wisconsin Press, Madison, 1959). Artículos de I. B. Cohen y otros.
- COHEN, H. Floris, How Modern Science Came into the World-Four Civilizations, One 17th-Century Breakthrough (Amsterdam University Press, Amsterdam, 2010).
- CRAIG, John, Newton at the Mint (Cambridge University Press, Cambridge, 1946).
- CREASE, Robert P., World in the Balance-The Historic Quest for an Absolute System of Measurement (W. W. Norton, Nueva York, 2011).
- CROMBIE, A. C., Medieval and Early Modern Science (Doubleday Anchor, Garden City, Nueva York, 1959); Robert Grosseteste and the Origins of Experimental Science-1100-1700, (Clarendon, Oxford, 1953).
- DARRIGOL, Olivier, A History of Optics from Greek Antiquity to the Nineteenth Century (Oxford University Press, Oxford, 2012).
- DEARM, Peter, Revolutionizing the Sciences-European Knowledge and Its Ambitions, 1500-1700, 2.ª ed. (Princeton University Press, Princeton, Nueva Jersey, y Oxford, 2009).
- Dicks, D. R., Early Greek Astronomy to Aristotle (Cornell University Press, Ithaca, Nueva York, 1970).
- Dictionary of Scientific Biography, The , ed. de Charles Coulston Gillespie (Scribner, Nueva York, 1970).
- DRAKE, Stillman, Galileo at Work-His Scientific Biography (University of Chicago Press, Chicago, Illinois, 1978).
- DUHEM, Pierre, The Aim and Structure of Physical Theory, trad. Philip K. Weiner (Athenaeum, Nueva York, 1982). [Ed. esp.:La teoría física: su objeto y estructura, trad. de Antoni Martínez Riu (Herder, Barcelona, 2003)]; Medieval Cosmology-Theories of Infinity, Place, Time, Void, and the Plurality of Worlds, trad. Roger Ariew (University of Chicago Press, Chicago, Illinois, 1985); To Save the Phenomena-An Essay on the Idea of Physical Theory from Plato to Galileo, trad. E. Dolan y C. Machler (University of Chicago Press, Chicago, Illinois, 1969).
- EVANS, James, The History and Practice of Ancient Astronomy (Oxford University Press, Oxford, 1998).
- FANTOLI, Annibale, Galileo-For Copernicanism and for the Church, 2.ª ed., trad. G. V. Coyne (University of Notre Dame Press, South Bend, Indiana, 1996).
- FINOCCHIARO, Maurice A., Retrying Galileo, 1633-1992 (University of California Press, Berkeley y Los Ángeles, 2005).
- FORSTER, E. M., Pharos and Pharillon (Knopf, Nueva York, 1962).
- FREEMAN, Kathleen, The Pre-Socratic Philosophers, 3.ª ed. (Basil Blackwell, Oxford, 1953).
- GALISON, Peter, How Experiments End (University of Chicago Press, Chicago, Illinois, 1987).
- GIBBON, Edward, The Decline and Fall of the Roman Empire (Everyman's Library, Nueva York, 1991). [Ed. esp.: Decadencia y caída del Imperio romano, trad. de José Sánchez de León Medina (Atalanta, Madrid, 2012)].
- GLEICK, James, Isaac Newton (Pantheon, Nueva York, 2003).
- GRAHAM, Daniel W., Science Before Socrates-Parmenides, Anaxagoras, and the New Astronomy (Oxford University Press, Oxford, 2013).
- GRANT, Edward, The Foundations of Modern Science in the Middle Ages (Cambridge University Press, Cambridge, 1996); Planets, Stars, and Orbs-The Medieval Cosmos, 1200-1687 (Cambridge University Press, Cambridge, 1994).
- GRAUKROGER, Stephen, ed., Descartes-Philosophy, Mathematics, and Physics (Harvester, Brighton, 1980).
- GRAUKROGER, Stephen, John SCHUSTER y John SUTTON, eds., Descartes' Natural Philosophy (Routledge, Londres y Nueva York, 2000).
- GREEN, Peter, Alexander to Actium (University of California Press, Berkeley, 1990).
- GUTAS, Dimitri, Greek Thought, Arabic Culture-The Graeco-Arabic Translation Movement in Baghdad and Early 'Abba¯sid Society (Routledge, Londres, 1998).
- HALL, Rupert, Philosophers at War: The Quarrel Between Newton and Leibniz (Cambridge University Press, Cambridge, 1980).
- HASKINS, Charles Homer, The Rise of Universities (Cornell University Press, Ithaca, Nueva York, 1957).
- HEILBRON, J. L., Galileo (Oxford University Press, Oxford, 2010).
- HELDEN, Albert VAN, Measuring the Universe-Cosmic Dimensions from Aristarchus to Halley (University of Chicago Press, Chicago, Illinois, 1983).
- HITTI, P. K., History of the Arabs (Macmillan, Londres, 1937).
- HOGENDIJK, J. P. y A. I. SABRA, eds., The Enterprise of Science in Islam = New Perspectives (MIT Press, Cambridge, Massachusetts, 2003).
- HUFF, Toby E., Intellectual Curiosity and the Scientific Revolution (Cambridge University Press, Cambridge, 2011).
- KHALIFI, Jim AL-, The House of Wisdom (Penguin, Nueva York, 2011).
- KING, Henry C., The History of the Telescope (Charles Griffin, Toronto, 1955; reed. Dover, Nueva York, 1979).
- KING-HELE, D. G. y A. R. HALE, eds., «Newton's Principia and His Legacy», Notes and Records of the Royal Society of London 42, 1-122 (1988).
- KOYRÉ, Alexandre, From the Closed World to the Infinite Universe (Johns Hopkins University Press, Baltimore, Maryland, 1957). [Ed. esp.: Del mundo cerrado al universo finito, trad. de Carlos Solís (Siglo XXI, México, 1989)].
- KUHN, Thomas S., The Copernican Revolution (Harvard University Press, Cambridge, Massachusetts, 1957). [Ed. esp.: La revolución copernicana, trad. de Domènec Bergadà (Ariel, Barcelona, 1985)]; The Structure of Scientific Revolutions (University of Chicago Press, Chicago, Illinois, 1962, 2.ª ed. 1970). [Ed. esp.: La estructura de las revoluciones científicas, trad. de Agustín Contín (Fondo de Cultura Económica, Madrid, 1971)].
- LINDBERG, David C., The Beginnings of Western Science (University of Chicago Press, Chicago, Illinois, 1992; 2.ª ed. 2007). [Ed. esp.: Los inicios de la ciencia occidental (Paidós, Barcelona, 2002)].
- LINDBERG, D. C. y R. S. WESTFALL, eds., Reappraisals of the Scientific Revolution (Cambridge University Press, Cambridge, 2000).
- LLOYD, G. E. R., Methods and Problems in Greek Science (Cambridge University Press, Cambridge, 1991).
- MACHAMER, Peter, ed., The Cambridge Companion to Galileo (Cambridge University Press, Cambridge, 1998).
- MARTÍNEZ, Alberto A., The Cult of Pythagoras-Man and Myth (University of Pittsburgh Press, Pittsburgh, Pensilvania, 2012).
- MASOOD, E., Science and Islam (Icon, Londres, 2009).
- MERTON, Robert K., «Motive Forces of the New Science», Osiris, 4, Parte 2 (1938); reeditado en Science, Technology, and Society in Seventeenth Century England (Howard Fertig, Nueva York, 1970), y On Social Structure and Science, ed. Piotry Sztompka (University of Chicago Press, Chicago, Illinois, 1996), pp. 223-240.
- NEUGEBAUER, Otto, Astronomy and History-Selected Essays (Springer Verlag, Nueva York, 1983); A History of Ancient Mathematical Astronomy (Springer Verlag, Nueva York, 1975).
- OSLER, M. J., ed., Rethinking the Scientific Revolution (Cambridge University Press, Cambridge, 2000). Artículos de M. J. Osler, B. J. T. Dobbs, R. S. Westfall y otros.
- ROWLAND, Ingrid D., Giordano Bruno-Philosopher and Heretic (Farrar, Straus, and Giroux, Nueva York, 2008).
- SARTON, George, Introduction to the History of Science, Volume 1, From Homer to Omar Khayyam (Carnegie Institution of Washington, Washington, D.C., 1927).
- SCHRÖDINGER, Erwin, Nature and the Greeks (Cambridge University Press, Cambridge, 1954). [Ed. esp.: La naturaleza y los griegos, trad. de Víctor Gómez Pin (Tusquets, Barcelona 1997)].
- SHAPIN, Steven, The Scientific Revolution (University of Chicago Press, Chicago, Illinois, 1996).
- SOBEL, Dava, Galileo's Daughter (Walker, Nueva York, 1999).
- SWARTZ, Merlin L., Studies in Islam (Oxford University Press, Oxford, 1981).
- SWERDLOW, N. M. y O. NEUGEBAUER, Mathematical Astronomy in Copernicus's De Revolutionibus (Springer Verlag, Nueva York, 1984).
- TATON, R. y C. WILSON, eds., Planetary Astronomy from the Renaissance to the Rise of Astrophysics-Part A: Tycho Brahe to Newton (Cambridge University Press, Cambridge, 1989).
- Tribute to Galileo in Padua, International Symposium a cura dell'Universita di Padova, 2-6 dicembere 1992 , vol. 4 (Edizioni LINT, Trieste, 1995). Artículos en inglés de J. MacLachlan, I. B. Cohen, O. Gingerich, G. A. Tammann, L. M. Lederman, C. Rubbia y Steven Weinberg; véase también L'Anno Galileiano.
- VLASTOS, Gregory, Plato's Universe (University of Washington Press, Seattle, 1975).
- Voltaire, Philosophical Letters, trad. E. Dilworth (Bobbs-Merrill Educational Publishing, Indianapolis, Indiana, 1961). [Ed. esp.: Cartas filosóficas, trad. de Fernando Savater (Editora Nacional, Madrid, 1983)].
- WATSON, Richard, Cogito Ergo Sum-The Life of René Descartes (David R. Godine, Boston, Massachusetts, 2002).
- WEINBERG, Steven, Discovery of Subatomic Particles, rev. ed. (Cambridge University Press, Cambridge, 2003); Dreams of a Final Theory (Pantheon, Nueva York, 1992; reeditado con un nuevo epílogo, Vintage, Nueva York, 1994). [Ed. esp.: El sueño de una teoría final, trad. de José Javier García Sanz (Crítica, Barcelona, 1994)]; Facing Up-Science and Its Cultural Adversaries (Harvard University Press, Cambridge, Massachusetts, 2001); Lake Views-This World and the Universe (Harvard University Press, Cambridge, Massachusetts, 2009).
- WESTFALL, Richard S., The Construction of Modern Science-Mechanism and Mechanics (Cambridge University Press, Cambridge, 1977); Never at Rest-A Biography of Isaac Newton (Cambridge University Press, Cambridge, 1980).
- WHITE, Andrew Dickson, A History of the Warfare of Science with Theology in Christendom (Appleton, Nueva York, 1895).
- WHITE, Lynn, Medieval Technology and Social Change (Oxford University Press, Oxford, 1962). [Ed. esp.: Tecnología medieval y cambio social, trad. de Ernesto Córdoba Palacios (Paidós, Barcelona, 1990)].
Notas:
[1] Aristóteles, Metafísica, Libro I, Capítulo 3, 938b 6, p. 43, trad. de Patricio de Azcárate (Espasa Calpe, Madrid, 1990).
[2] Diógenes Laercio, Vida, opiniones y sentencias de los filósofos más ilustres, Libro I, trad. de José Ortiz y Sanz (Navarro, Madrid, 1887), p. 31.
[3] De J. Barnes, The Presocratic Philosophers, ed. rev. (Routledge and Kegan Paul, Londres, 1982), p. 29. Las citas de esta obra, a partir de aquí citada como Presocratic Philosophers, son traducciones al inglés [y del inglés al español] de citas de fragmentos del libro clásico de consulta de Hermann Diels y Walter Kranz, Die Fragmente der Vorsokratiker (10.ª ed., Berlín, 1952).
[4] Presocratic Philosophers, p. 53
[5] De J. Barnes, Early Greek Philosophy (Penguin, Londres, 1987), p. 97. A partir de aquí citado como Early Greek Philosophy. Al igual que en el caso de Presocratic Philosophers, las citas están tomadas de Diels y Kranz, 10.ª ed.
[6] Tal como ha señalado Gregory Vlastos en Plato’s Universe (University of Washington Press, Seattle, 1975), existió una forma adverbial de la palabra kosmos que Homero utilizaba para denotar «socialmente aceptable» y «moralmente adecuado». Este uso sobrevive en inglés [y en castellano] en la palabra cosmetic [«cosmético»]. Su uso por parte de Heráclito refleja el parecer helénico de que el mundo no dista mucho de como debería ser. La palabra también aparece en inglés [y en castellano] en los cognados equivalentes a «cosmos» y «cosmología».
[7] De K. Freeman, The Ancilla to the Pre-Socratic Philosophers (Harvard University Press, Cambridge, Massachusetts, 1966), p. 26. A partir de aquí citado como Ancilla. Se trata de una traducción al inglés de Diels, Fragmente der Vorsokratiker, 5.ª ed.
[8] Empédocles, Acerca de la naturaleza, trad. de Alberto Bernabé (Alianza, Madrid, 1988), p. 222.
[9] Ibíd., p. 213.
[10] Early Greek Philosophy, p. 243.
[11] Ancilla, p. 93.
[12] Aristóteles, Física, Libro IV, Capítulo 9, 239b.
[13] Platón, Fedón, 97c-98c. Cito aquí de las Obras completas de Platón (Aguilar, Madrid, 1969, VV. TT.)
[14] Platón, Obras completas. Timeo, 54 a-b, p. 1150, trad. de Francisco de P. Samaranch.
[15] Por ejemplo, en la traducción al castellano de la Física de Aristóteles de Guillermo R. de Echandía (Gredos, Madrid, 1995).
[16] Trad. de José Sánchez-Cerezo de la Fuente. www.webdianoia.com/presocrat/jenofa_text.htm.
[17] Early Greek Philosophy, p. 253.
[18] He escrito más extensamente acerca de este punto en el capítulo «Beautiful Theories», en Dreams of a Final Theory (Pantheon, Nueva York, 1992; reeditado con un nuevo prefacio, Vintage, Nueva York, 1994).
[19] Para el origen de estas historias, véase Alberto A. Martínez, The Cult of Pythagoras–Man and Mith (University of Pittsburg Press, Pennsylvania, 2012).
[20] Aristóteles, Metafísica, Libro I, Capítulo 5, 985b 23-26, p. 49, trad. de Patricio de Azcárate.
[21] Ibíd., 986a 2, p. 49.
[22] De hecho (tal como se ha comentado en la nota técnica 2), fuera lo que fuera lo que demostró Teeteto, los Elementos no demuestran lo que el libro afirma probar, que solo hay cinco sólidos regulares conversos posibles. Los Elementos demuestran que, en el caso de los poliedros regulares, solo hay cinco combinaciones del número de lados de cada cara y del número de caras que convergen en cada vértice, pero no demuestran que para cada combinación de esos números solo exista un poliedro regular convexo posible.
[23] Aristóteles, Prior Analytics, Libro I, Capítulo 23, 41a 23-30. [Cuando no existe traducción española, traducimos de la edición inglesa: The Complete Works of Aristotle–The Revised Oxford Translation, ed. de J. Barnes (Princeton University Press, Princeton, Nueva Jersey, 1984)].
[24] Platón¸ Obras completas, Teeteto, 529e, trad. de José Antonio Míguez.
[25] Aristóteles, Física, 215, pp. 1-5, trad. de Guillermo R. de Echandía (Gredos, Madrid, 1995), p. 140.
[26] Platón, Obras completas, La República, 529e, p. 788, trad. de José Antonio Míguez.
[27] E. P. Wigner, «The Unreasonable Effectiveness of Mathematics», Communications in Pure and Applied Mathematics, 1-14.
[28] J. Barnes, en The Complete Works of Aristotle—The Revised Oxford Translation (Princeton University Press, Princeton, Nueva Jersey, 1984).
[29] R. J. Hankinson, en The Cambridge Companion to Aristotle, ed. de J. Barnes (Cambridge University Press, Cambridge, 1995), p. 165.
[30] Aristóteles, Física, Libro II, Capítulo 2, 194a 29-31, trad. de Guillermo R. de Echandía (Gredos, Madrid, 1995), p. 52.
[31] Ibíd., Capítulo 1, 192a 9, p. 45.
[32] Aristóteles, Meteorology, Libro II, Capítulo 9, 396b 7-11 (trad. al castellano de la trad. de Oxford, p. 596).
[33] Aristóteles, On the Heavens, Libro I, Capítulo 6, 273b 30-31, 274a, 1 (de la trad. de Oxford, p. 455).
[34] Aristóteles, Física, Libro IV, Capítulo 8, 214b 12-13, trad. de Guillermo R. de Echandía (Gredos, Madrid, 1995), p. 138.
[35] Ibíd., 214b 32-34, p. 139.
[36] La palabra griega kineson, que generalmente se traduce como «movimiento», de hecho posee un significado mucho más general, y se refiere a cualquier tipo de cambio. Así, la clasificación de Aristóteles de los tipos de causas se aplicaba no solo a un cambio de posición, sino también a cualquier tipo de cambio. La palabra griega fora se refiere de manera específica a un cambio de emplazamiento, y generalmente se traduce como «locomoción».
[37] Ibíd., Libro VII, Capítulo 1, 242a 50-54, p. 244.
[38] Aristóteles, On the Heavens, Libro III, Capítulo 3, 301b 25-26 (de la trad. de Oxford, p. 494).
[39] Thomas Kuhn, «Remarks on receiving the Laurea», en L’Anno Galileiano (Edizioni LINT, Trieste, 1995).
[40] David C. Lindberg, en The Beginnings of Western Science (University of Chicago Press, Chicago, Illinois, 1992), pp. 53-54.
[41] David C. Lindberg, en The Beginnings of Western Science, 2.ª ed. (University of Chicago Press, Chicago, Illinois, 2007), p. 65.
[42] Michael R. Matthews, en la Introducción de The Scientific Background to Modern Philosophy (Hackett, Indianápolis, Indiana, 1989).
[43] Tomo prestado el título del tratado actual más importante sobre esta época: Peter Green, Alexander to Actium (University of California Press, Berkeley, 1990).
[44] Creo que esta observación pertenece originariamente a George Sarton.
[45] La descripción de la obra de Estratón por parte de Simplicio se presenta en una traducción inglesa de M. R. Cohen y I. E. Drabkin, A Source Book in Greek Science (Harvard University Press, Cambridge, Massachusetts, 1948), pp. 211-212.
[46] H. Floris Cohen, How Modern Science Came into the World (Amsterdam University Press, Ámsterdam, 2010), p. 17.
[47] Para la interacción entre la tecnología y la investigación física en los tiempos actuales, véase Bruce J. Hunt, Pursuing Power and Light: Technology and Physics from James Watt to Albert Einstein (Johns Hopkins University Press, Baltimore, Maryland, 2010).
[48] Los experimentos de Filón se describen en una carta citada por G. I. Ibry-Massie y P. T. Keysser, Greek Science of the Hellenistic Era (Routledge, Londres, 2002), pp. 216-219.
[49] La traducción clásica en inglés es Euclides, The Thirteen Books of the Elements, 2.ª ed., trad. de Thomas L. Heath (Cambridge University Press, Cambridge, 1925). [En castellano, Euclides, Elementos, Gredos, Madrid, trad. de María Luisa Puertas Castaños, 2000].
[50] En el mundo antiguo generalmente se suponía que cuando vemos algo la luz viaja del ojo al objeto, como si la visión fuera una especie de tacto que exige que lo proyectemos a lo que vemos. En la siguiente discusión daré por sentada nuestra idea actual, que en la visión la luz viaja del objeto al ojo. Por suerte, al analizar la reflexión y la refracción, tanto da en qué dirección vaya la luz.
[51] Es una cita de un manuscrito griego del siglo VI, que aparece en traducción inglesa en Ibry-Massie y Keyser, Greek Science of the Hellenistic Era.
[52] Véase Tabla V. 1, p. 233, de la traducción de la Óptica de Ptolomeo, de A. Mark Smith, en «Ptolemy’s Theory of Visual Perception», Transactions of the American Philosophical Society 86, 2.ª Parte (1996).
[53] Las citas proceden de la traducción de T. L. Heath, The Works of Archimedes (Cambridge University Press, Cambridge, 1897).
[54] El ensayador es una polémica contra los adversarios jesuitas de Galileo en forma de carta al chambelán papal Virginio Cesarini. Como veremos en el capítulo 11, en dicha obra Galileo ataca la acertada idea de Tycho Brahe y los jesuitas de que los cometas se encuentran más lejos de la Tierra que la Luna. (La cita que aparece está basada en una traducción al inglés de Maurice A. Finochiaro, en The Essential Galileo, Hackett, Indianápolis, Indiana, 2008, p. 183).
[55] Platón, Obras completas, Timeo, 30a, p. 1134, trad. de Francisco de P. Samaranch.
[56] Erwin Schrödinger, Shearman Lectures en el University College de Londres, mayo de 1948, publicadas como Nature and the Greeks (Cambridge University Press, 1954).
[57] Alexandre Koyré, From the Closed World to the Infinite Universe (Johns University Hopkins Press, Baltimore, Maryland, 1957), p. 159.
[58] Ancilla, p. 22.
[59] Tucídides, Historia de la guerra del Peloponeso, p. 212, vol. 2, trad. de Francisco Rodríguez Adrados (Hernando, Madrid, 1969)
[60] S. Greenblatt, «The Answer Man: An Ancient Poem Was Rediscovered and the World Swerved», The New Yorker, 8 de agosto de 2011, pp. 28-33.
[61] Pierre Gassendi fue un sacerdote y filósofo francés que intentó reconciliar el atomismo de Epicuro y Lucrecio con el cristianismo.
[62] Edward Gibbon, The Decline and Fall of the Roman Empire, Capítulo XXIII (Everyman’s Library, Nueva York, 1991), p. 412. [Decadencia y caída del Imperio Romano, Atalanta, Madrid, trad. de José Sánchez de León Meduiña, 2012]. A partir de ahora citado como Gibbon, Decline and Fall.
[63] Ibíd., Capítulo II, p. 34.
[64] Nicolaus Copernicus, On the Revolutions of Heavenly Spheres, trad. de Charles Glenn Wallis (Prometheus, Amherst, Nueva York, 1995), p. 7.
[65] Lactancio, Divine Institutes, Libro 3, Sección 24, trad. de A. Bowen y P. Garnsey (Liverpool University Press, 2003).
[66] San Pablo, Epístola a los Colosenses 2:8 (Biblia de Jerusalén).
[67] San Agustín, Las confesiones, Libro IV. Espasa-Calpe, Madrid, trad. de Eugenio Cevallos, 1954, p. 87.
[68] San Agustín, Retractions, Libro I, Capítulo 1, trad. de M. I. Bogan (Catholic University of America Press, Washington, D.C., 1968), p. 10.
[69] Gibbon, Decline and Fall, Capítulo XL, p. 231.
[70] Este capítulo se basa en parte en mi artículo «The Missions of Astronomy», New York Review of Books, 56, núm. 16 (22 de octubre de 2009), pp. 19-22; reeditado en The Best American Science and Nature Writing, ed. de Freeman Dyson (Houghton Mifflin Harcourt, Boston, Massachusetts, 2010), pp. 23-31, y en The Best American Science Writing, ed. de Jerome Groopman (HarperCollins, Nueva York, 2010), pp. 272-281.
[71] Homero, Ilíada, Libro 22, 26-29, p. 230. Las citas son de la traducción de Luis Segalá y Estalella. Espasa Calpe, Madrid, 1962.
[72] Homero, Odisea, Libro V, p. 58. Las citas son de la traducción de Luis Segalá y Estalella. Espasa Calpe, Madrid, 1973.
[73] Diógenes Laercio, Vidas, opiniones y sentencias de los filósofos más ilustres, Libro 1, 23, trad. de José Ortiz y Sanz (Navarro, Madrid, 1887).
[74] Se trata de la interpretación de algunas líneas de Heráclito propuesta por D. R. Dicks, Early Greek Astronomy to Aristotle (Cornell University Press, Ithaca, Nueva York, 1970).
[75] Para ser más exactos, es algo que se conoce como el mes lunar sinódico. El periodo de 27 días para que la Luna regrese a la misma posición relativa respecto a las estrellas fijas se conoce como el mes lunar sideral.
[76] Esto no ocurre cada mes, pues el plano de la órbita de la Luna alrededor del Sol está ligeramente inclinado con respecto al plano de la órbita de la Tierra alrededor del Sol. La Luna cruza el plano de la órbita de la Tierra dos veces cada mes sideral, pero esto ocurre solo durante la luna llena, cuando la Tierra se halla entre el Sol y la Luna, y solo una vez más o menos cada 18 años.
[77] El equinoccio es el momento en el que el Sol, en su movimiento sobre el fondo de las estrellas, cruza el ecuador celeste. (En la época moderna, es el momento en el que la línea situada entre la Tierra y el Sol queda perpendicular al eje de la Tierra). En puntos de la Tierra con diferente longitud, este momento sucede a diferentes horas del día, con lo que podría haber una diferencia de un día en la fecha en que diferentes observadores observan el equinoccio. Lo mismo se puede aplicar a las fases de la Luna.
[78] Platón, Obras completas, La República, 527 d-e, p. 786, trad. de José Antonio Míguez.
[79] Filón, On the Eternity of the World, I (1), trad. al inglés de la cita de C. D. Yonge, The Works of Philo (Hendrikson Peabody, Massachusetts, 1993), p. 707.
[80] La importancia de Parménides y Anaxágoras como fundadores de la astronomía científica griega la recalca Daniel W. Graham, Science Before Socrates-Parmenides, Anaxagoras, and the New Astronomy (Oxford University Press, Oxford, 2013).
[81] Ancilla, p. 18
[82] Se ha sostenido (en O. Neugebauer, A History of Ancient Mathematicanl Astronomy, Springer-Verlag, Nueva York, 1975) que el razonamiento de Aristóteles acerca de la forma de la sombra de la Tierra sobre la Luna no es concluyente, puesto que existe una infinita variedad de formas terrestres y lunares que darían la misma forma curva.
[83] Aristóteles, On the Heavens, Libro II, Capítulo 14, 297b 26-298a 5 (trad. de Oxford, pp. 488-489).
[84] Samuel Eliot Morison citaba este argumento en su biografía de Colón (Admiral of the Ocean Sea, Little Brown, Boston, Massachusetts, 1942) para demostrar que, contrariamente a una extendida suposición, mucho antes de que Colón zarpara ya se sabía con seguridad que la Tierra era una esfera. El debate en la corte de Castilla acerca de si apoyar la propuesta de expedición de Colón no se refería a la forma de la Tierra, sino a su tamaño. Colón pensaba que la Tierra era lo bastante pequeña como para poder zarpar desde España y llegar a la costa este de Asia sin que se le agotara la comida ni el agua. Se equivocaba acerca del tamaño de la Tierra, aunque, por supuesto, lo salvó la inesperada aparición de América entre Europa y Asia.
[85] Ancilla, p. 23.
[86] Aristóteles, On the Heavens, Libro II, Capítulo 11.
[87] Arquímedes, On Floating Bodies, en la trad. inglesa de T. L. Heath, The Works of Archimedes (Cambridge University Press, Cambridge, 1897), p. 254. A partir de aquí citado como Arquímedes, trad. de Heath.
[88] Una traducción al inglés la da Thomas Heath en Aristarchus of Samos (Clarendon, Oxford, 1923).
[89] En El calculador de arena encontramos un comentario fascinante de Arquímedes, según el cual Aristarco había descubierto que «el Sol parece ser más o menos 1/720 parte del zodíaco». (The Works of Archimedes, trad. de T. L. Heath, Cambridge University Press, Cambridge, 1897, p. 223). Es decir, el ángulo subtendido en la Tierra por el disco del Sol es 1/720 veces 360°, o sea, 0,5°, no muy lejos del valor correcto de 0,519°. Arquímedes incluso afirmó que lo había verificado mediante sus propias observaciones. Pero como hemos visto en las obras que han sobrevivido, Aristarco había afirmado que el ángulo subtendido por el disco de la Luna era de 2°, y había observado que los discos del Sol y la Luna tienen el mismo tamaño aparente. ¿Quizá aquí citaba una medida posterior tomada por Aristarco que no figura en las obras que nos han llegado? ¿O estaba citando su propia medida y atribuyéndola a Aristarco? He oído sugerir a algunos estudiosos que el origen de la discrepancia es un error al copiar el texto o una mala interpretación, pero esto me parece muy improbable. Como ya he observado, Aristarco había concluido de su medición del diámetro angular de la Luna que su distancia a la Tierra debía ser entre 30 y 45/2 veces más grande que el diámetro de la Luna, un resultado bastante incompatible con un tamaño aparente de alrededor de 0,5°. La trigonometría moderna nos dice, por otro lado, que si el tamaño aparente de la Luna fuera 2°, entonces su distancia de la Tierra sería 28,6 veces su diámetro, un número que de hecho se halla entre 30 y 45/2. (El calculador de arena no es una obra seria de astronomía, sino una demostración por parte de Arquímedes de que podía calcular números muy grandes, tales como el número de granos de arena necesarios para llenar la esfera de las estrellas fijas).
[90] Arquímedes, The Sand reckoner, trad. de Heath, p. 222.
[91] Aristóteles, On the Heavens, Libro II, 296b 4-6 (trad. de Oxford).
[92] Aristóteles, On the Heavens, Libro II, 14, 296b 23-24 (trad. de Oxford).
[93] Existe un famoso mecanismo antiguo conocido como el Mecanismo de Anticitera, descubierto en 1901 por unos recolectores de esponjas en las costas de la isla mediterránea de Anticitera, entre Creta y la península griega. Se cree que se perdió durante un naufragio entre el 150 y el 100 a. C. Aunque el Mecanismo de Anticitera ahora no es más que una corroída masa de bronce, los estudiosos han conseguido deducir su funcionamiento estudiando su interior con rayos X. Al parecer, no es un planetario, sino un dispositivo calendárico que nos indica la posición aparente del Sol y los planetas en el zodíaco en cualquier fecha. Lo más importante es que su intrincado mecanismo da fe de la extraordinaria competencia de la tecnología helenística.
[94] Cicerón, De Re Publica, 1. xiv § 21-22, en Cicero, On the Republic and On the Laws, trad. de Clinton W. Keys (Loeb Classical Library, Harvard University Press, Cambridge, Massachusetts, 1928), pp. 41-43.
[95] Esta obra la han reconstruido estudiosos contemporáneos; véase Albert van Helden, Measuring the Universe, Cosmic Dimensions from Aristarchus to Halley (University of Chicago Press, Chicago, Illinois, 1983), pp. 10-13.
[96] Ptolemy’s Almagest, trad. y anotado por G. J. Toomer (Duckworth, Londres, 1984). El catálogo de estrellas de Ptolomeo está en las páginas 341-399.
[97] La latitud celeste es la separación angular entre la estrella y la eclíptica. Mientras en la Tierra medimos la longitud a partir del meridiano de Greenwich, la longitud celeste es la separación angular, sobre un círculo de latitud celeste fija, entre la estrella y el meridiano celeste sobre el que encontramos la posición del Sol en el equinoccio vernal.
[98] Para una visión contraria, véase O. Neugebauer, A History of Ancient Mathematical Astronomy (Springer-Verlag, Nueva York, 1975), pp. 288, 577.
[99] Ptolomeo, Almagest, Libro VII, Capítulo 2
[100] Sobre la base de sus propias observaciones de la estrella Regulus, Ptolomeo, en su Almagesto, da una cifra de 1° aproximadamente en 100 años.
[101] Cleómedes, Lectures on Astronomy, ed. y trad. de A. C. Bowen y R. B. Todd (University of California Press, Berkeley y Los Ángeles, 2004).
[102] Eratóstenes tuvo suerte. Syene no queda exactamente al sur de Alejandría (su longitud es de 32,9° E, mientras que la de Alejandría es 29,9° E), y durante el solsticio de verano, a mediodía, en Syene el Sol no queda precisamente sobre nuestras cabezas, sino que forma más o menos un ángulo de 0,4° con la vertical. Los dos errores se anularon parcialmente. Lo que Eratóstenes había medido en realidad era la proporción entre la circunferencia de la Tierra y la distancia de Alejandría al Trópico de Cáncer (denominado el círculo tropical de verano por Cleómedes), el círculo de la superficie de la Tierra donde a mediodía, durante el solsticio de verano, el Sol queda directamente sobre nuestras cabezas. Alejandría se halla a una latitud de 31,2°, mientras que la latitud del Trópico de Cáncer es 23,5°, 7,7° menor que la latitud de Alejandría, de manera que la circunferencia de la Tierra es, de hecho, 360/7,7° = 46,75 veces más grande que la distancia entre Alejandría y el Trópico de Cáncer, que es un poco menos que la proporción de 50 dada por Eratóstenes.
[103] Para mayor claridad, cuando en este capitulo me refiera a los planetas me referiré solo a los cinco: Mercurio, Venus, Marte, Júpiter y Saturno.
[104] En inglés también podemos ver la correspondencia de los días de la semana con los planetas y los dioses asociados a los nombres de cada día. Saturday (sábado), Sunday (domingo) y Monday (lunes) se asocian evidentemente con Saturno, el Sol y la Luna; Tuesday (martes), Wednesday (miércoles), Thursday (jueves) y Friday (viernes) se basan en el asociación de los dioses germánicos con sus supuestos equivalentes latinos: Tyr con Marte, Wotan con Mercurio, Thor con Júpiter y Frigga con Venus.
[105] G. W. Burch, «The Counter-Earth», Osiris, 11, 267, (1954).
[106] Aristóteles, Metafísica, Libro I, Parte 5, 986a 1. Pero en el Libro II de On the Heavens, 293b, 23-25, Aristóteles afirma que la contra-Tierra supuestamente tenía que explicar por qué los eclipses de luna son más comunes que los solares.
[107] El pasaje citado nos lo ofrece Pierre Duhem en To Save the Phenomena–An Essay on the Idea of Phyisical Theory from Plato to Galileo, trad. de E. Dolan y C. Machler (University of Chicago Press, Chicago, Illinois, 1969), p. 5, a partir de ahora citado como Duhem, To Save the Phenomena. Una traducción más reciente de este pasaje de Simplicio nos la ofrece I. Mueller: véase Simplicio, On Aristotle’s «On the Heavens» 2, 10-14 (Cornell University Press, Ithaca, Nueva York, 2005), 492.31-493.4, p. 33. No sabemos si Platón llegó a plantear este problema. Simplicio citaba a Sosígenes el Peripatético, un filósofo del siglo II de nuestra era.
[108] Para unas clarísimas ilustraciones del modelo de Eudoxo, véase James Evans, The History and Practice of Ancient Astronomy (Oxford University Press, Oxford, 1998), pp. 307-309.
[109] Aristóteles, Metafísica, Libro XII, Capítulo 8, 1073b 1-1074a 1.
[110] Para una traducción de I. Mueller, véase Simplicio, On Aristotle «On the Heavens 3.1-7» (Cornell University Press, Ithaca, Nueva York, 2005), 493.1-497.8, pp. 33-36.
[111] Este fue el trabajo, en 1956, de los físicos Tsung-Dao Lee y Chen Ning-Yang.
[112] Aristóteles, Metafísica, Libro XII, Sección 8, 1073b 18-1074a 14.
[113] Estas referencias las da D. R. Dicks, Early Astronomy to Aristotle (Cornell University Press, Ithaca, Nueva York, 1970), p. 202. Dicks tiene una idea distinta de lo que Aristóteles pretendía conseguir.
[114] Mueller, Simplicius, On Aristotle’s «On the Heavens 2.10-14», 519.9-11, p. 59.
[115] En un año de 3651/4 días, la Tierra en realidad gira sobre su eje 3661/4 veces. El Sol parece girar alrededor de la Tierra 3651/4 veces en este periodo, porque al mismo tiempo que la Tierra gira 3661/4 veces sobre su eje, gira alrededor del Sol una vez en la misma dirección, lo que da 3651/4 revoluciones aparentes del Sol alrededor de la Tierra. Puesto que la Tierra tarda 365,25 días de 24 horas en girar 366, 25 veces en relación con las estrellas, el tiempo que tarda la Tierra en girar una vez es (365,25 × 24 horas)/366,25, o sea, 23 horas, 56 minutos y 4 segundos. Es lo que se conoce como el día sideral.
[116] Ibíd., 504.19-30, p. 43
[117] Véase Libro I de Otto Neugebauer, A History of Ancient Mathematical Astronomy (Springer-Verlag, Nueva York, 1975).
[118] En los catálogos, desde la época de Ptolomeo hasta el presente, la aparente luminosidad de las estrellas se describe en términos de su «magnitud». La magnitud aumenta al decrecer la luminosidad. La estrella más brillante, Sirio, tiene una magnitud de –1,4; Vega, otra estrella brillante, tiene una magnitud de cero, y las estrellas que son apenas visibles a simple vista son de sexta magnitud. En 1856, el astrónomo Norman Pogson comparó la luminosidad aparente medida de un número de estrellas con las magnitudes que se les habían atribuido históricamente, y sobre esa base proclamó que si una estrella tiene una magnitud 5 unidades más grande que otra, es 100 veces más tenue.
[119] En uno de los pocos atisbos del origen del uso de los epiciclos, Ptolomeo, al comienzo del Libro XII del Almagesto, atribuye a Apolonio de Perga el haber demostrado un teorema relativo al uso de los epiciclos y excéntricos para explicar el movimiento aparente del Sol.
[120] En la teoría del movimiento del Sol, un excéntrico se puede considerar como una especie de epiciclo, sobre el cual la línea que va del centro del epiciclo al Sol discurre siempre paralela a la línea entre la Tierra y el centro del deferente del Sol, desplazando así el centro de la órbita del Sol de la Tierra. Algo parecido se observa en relación con la Luna y los planetas.
[121] El término «ecuante» no fue utilizado por Ptolomeo. Él se refería, por el contrario, a un «excéntrico bisecado», indicando que el centro del deferente se considera que está en medio de la línea que conecta el ecuante y la Tierra.
[122] G. Smith, comunicación privada.
[123] Lo mismo se puede decir cuando se añaden los excéntricos y los ecuantes; la observación podría haber fijado solamente las razones entre las distancias de la Tierra y el ecuante y el centro del deferente, y los radios del deferente y el epiciclo, de manera separada para cada planeta.
[124] Ptolomeo, Almagest, trad. ingl. de G. T. Toomer (Duckworth, Londres, 1984), Libro V, Capítulo 13, pp. 247-251. Véase también O. Neugebauer, A History of Ancient Mathematical Astronomy, Part One (Springer-Verlag, Berlín, 1975), pp. 100-103.
[125] Barrie Flete, trad. de Simplicius on Aristotle «Physics 2» (Duckworth, Londres, 1997), 291.23-292-29, pp. 47-48.
[126] Citado por Duhem, To Save the Phenomena, pp. 20-21.
[127] Ibid.
[128] Para un comentario sobre el significado de explicación en la ciencia, y las referencias a otros artículos sobre el tema, véase S. Weinberg, «Can Science Explain Everything? Anything?», en New York Review of Books, 48, núm. 9: 47-50 (31 de mayo de 2001). Reproducido en Australian Review (2001); en portugués, Folha da S. Paolo (2001); en francés, La Recherche (2001); The Best American Science Writing, ed. M. Ridley y A. Lightman (HarperCollins, 2002); The Norton Reader (W. W. Norton, Nueva York, diciembre 2003); Explanations—Styles of Explanation in Science, ed. de John Cornwell, Oxford University Press, 2004), 23-28; en húngaro, Akadeemia 176, núm. 8: 1734-49 (2005); S. Weinberg, Lake Views-This World and The Universe (Harvard University Press, Cambridge, Massachusetts, 2009).
[129] La asociación de la astrología con los babilonios viene ilustrada en la Oda XI del Libro 1 de Horacio: «No investigues, pues no es lícito, Leucónoe, el fin que ni a mí/ ni a ti los dioses destinen; a cálculos babilonios/ no te entregues. ¡Más vale sufrir lo que hay que ser!». Suena mejor en latín: «Tu ne quaesieris —scire nefas— quem mihi, quem tibi, finem di dederint, Leuconoë, nec Babylonios temptaris numeros, ut melius, quidquid erit, pati». Horacio, Odas y Epodos, trad. de Manuel Fernández Galiano (Cátedra, Madrid, 1997).
[130] Esta cita no procede del Almagesto, sino de la Greek Anthology, estrofas compiladas en el Imperio bizantino alrededor del 900 de nuestra era. La traducción inglesa es de Thomas L. Heath, Greek Astronomy (Dover, Mineola, Nueva York, 1991), p. lvii.
[131] Esta carta la cita Eutiquio, entonces patriarca de Alejandría. La traducción inglesa es de E. M. Forster, Pharos and Pharillon (Knopf, Nueva York, 1962), pp. 21-22. Una traducción menos concisa la da Gibbon en Decline and Fall, capítulo 51
[132] P. K. Hitti, History of the Arabs (Macmillan, Londres, 1937), p. 315.
[133] D. Gutas, Greek Thought, Arabic Culture-The Graeco-Arabic Translation Movement in Baghdad and Early ‘Abba¯sid Society (Routledge, Londres, 1998), pp. 53-60.
[134] Alfraganus es el nombre latinizado por el que Al-Farghani llegó a ser conocido en la Europa medieval. A partir de ahora también daré los nombres latinizados de otros árabes, como en este caso, entre paréntesis.
[135] Al-Biruni, Book of the Determination at Coordinates of Localities, Capítulo 5, seleccionado y traducido por J. Lennart Berggren en The Mathematics of Egypt, Mesopotamia, China, India, and Islam, ed. Voctor Katz (Princeton University Press, Princeton, Nueva Jersey, 2007).
[136] Al-Biruni de hecho utilizó una mezcla de los sistemas numérico decimal y sexagesimal. Dio la altura de la montaña en codos, y eran 652;3;18, es decir, 652 más 3/60 más 18/3,600, que equivale a 652,055 en la moderna notación decimal.
[137] Citado por P. Duhem en To Save the Phenomena, p. 29.
[138] Citado por R. Arnaldez y A. Z. Iskandar en The Dictionary of Scientific Biography (Scribner, Nueva York, 1975), vol. 12, p. 3.
[139] G. J. Toomer, Centaurus 14, 306 (1969).
[140] Maimónides, Guía de perplejos, Parte 2, Capítulo 24. p. 308, trad. de David Gonzalo Maeso (Editora Nacional, Madrid, 1983).
[141] Ibíd., p. 311. Aquí Maimónides cita los Salmos 115:16.
[142] Véase G. J. Toomer, Centaurus 14, 306 (1969).
[143] N. M. Swerdlow, Proceedings of the American Philosophical Society, 117, 423 (1973).
[144] Que Copérnico lo aprendió de fuentes árabes lo defiende F. J. Ragep, History of Science, 14, 65 (2007).
[145] Esto lo documenta Toby E. Huff, Intellectual Curiosity and the Scientific Revolution (Cambridge University Press, Cambridge, 2011), Capítulo 5.
[146] Se trata de las estrofas 13, 29 y 30 de la segunda versión de Fitzgerald [de donde se han traducido al castellano].
[147] Citado por Jim Al-Khalili, The House of Wisdom (Penguin, Nueva York, 2011), p. 188.
[148] Al-Ghazali’s Tahafut al-Falasifah, trad. de Sabih Ahmad Kamali (Pakistan Philosophical Congress, Lahore, 1958).
[149] Al-Ghazali, Fatihat al-‘Ulum, trad. de I. Goldheizer, en Studies on Islam, ed. de Merlin L. Swartz (Oxford University Press, 1981), cita, p. 195
[150] Véase, por ejemplo, Lynn White, Jr., Medieval Technology and Social Change (Oxford University Press, Oxford, 1962), Capítulo 2.
[151] Peter Dear, Revolutionizing the Sciences-European Knowledge and Its Ambitions 1500-1700, 2.ª ed. (Princeton University Press, Princeton, Nueva Jersey y Oxford, 2009), p. 15.
[152] Los artículos de la condena los encontramos en la traducción de Edward Grant (Harvard University Press, Cambridge, Massachusetts, 1974), pp. 48-50.
[153] Ibíd., p. 47.
[154] Citado en David C. Lindberg, The Beginnings of Western Science (University of Chicago Press, Chicago, Illinois, 1992), p. 241
[155] Ibíd.
[156] Nicole Oresme, Le livre du ciel et du monde, en francés, y trad. A. D. Menut y A. J. Denomy (University of Wisconsin Press, Madison, 1968), p. 369.
[157] Citado en «Buridan», en Dictionary of Scientific Biography, ed. de Charles Coulston Gillespie (Scribner, Nueva York, 1973), vol. 2, pp. 604-605.
[158] Véase el artículo de Piaget en The Voices of Time, ed. de J. T. Fraser (Braziller, Nueva York, 1966).
[159] Oresme, Le Livre.
[160] Ibíd., pp. 537-539.
[161] A. C. Crombie, Robert Grosseteste and the Origins of Experimentation–1100-1700 (Clarendon, Oxford, 1953).
[162] Por ejemplo, véase C. R. McLeish, Nature, 507, 161-63 (13 de marzo de 2014).
[163] Citado en A. C. Crombie, Medieval and Early Modern Science (Doubleday Anchor, Garden City, Nueva York, 1959), vol. 1, p. 53.
[164] Trad. de Ernest A. Moody, en A Source Book in Medieval Science, ed. E. Grant, p. 239. Me he tomado la libertad de cambiar la palabra «latitud» de la traducción de Moody por «incremento de velocidad», que creo que indica con más exactitud el significado de Heytesbury
[165] De Soto se cita en una traducción inglesa de W. A, Wallace, Isis, 59, 384 (1968).
[166] Un escritor posterior, Georg Hartman (1489-1564), afirmaba que había visto una carta de Regiomontanus en la que se leía lo siguiente: «El movimiento de las estrellas debe variar una fracción muy pequeña debido al movimiento de la Tierra» (Dictionary of Scientific Biography, Scribner, Nueva York, 1975, volumen II, p. 351). Si ello es cierto, entonces Regiomontanus puede que se anticipara a Copérnico, aunque la frase también es coherente con la doctrina pitagórica de que la Tierra y el Sol deben girar en torno al centro del mundo.
[167] Citado en Duhem, To Save the Phenomena, pp. 49-50.
[168] Butterfield acuñó la expresión: «la interpretación progresista de la historia», que utilizó para criticar a los historiadores que juzgan el pasado según su aportación a nuestras actuales prácticas ilustradas. Pero cuando le llegó el momento de abordar la revolución científica, Butterfield fue completamente progresista, como yo.
[169] Herbert Butterfield, The Origins of Modern Science, ed. rev. (Free Press, Nueva York, 1957), p. 7.
[170] Para recopilaciones de ensayos sobre el tema, véase Reappraisals of the Scientific Revolution, ed. de D. C. Lindberg y R. S. Westfall (Cambridge University Press, Cambridge, 1990), y Rethinking the Scientific Revolution, ed. de M. J. Osler (Cambridge University Press, Cambridge, 2000).
[171] Steven Shapin, The Scientific Revolution (University of Chicago Press, Chicago, Illinois, 1996), p. 1.
[172] Pierre Duhem, The System of World: A History of Cosmological Doctrines from Plato to Copernicus (Hermann, París, 1913).
[173] Para una traducción inglesa, véase Edward Rossen, Three Copernican Treatises (Farrar, Strauss, and Giroux, Nueva York, 1939), o Noel M. Swerdlow, «The Derivation and First Draft of Copernicus’ Planetary Theory: A Translations of the Commentarilous with Commnentary», Proceedings of the American Philosophical Society 117, 423 (1973).
[174] Para un resumen, véase N. Jardine, Journal of the History of Astronomy 13, 168 (1982).
[175] O. Neugebauer, Astronomy and History-Selected Essays (Springer-Verlag, Nueva York, 1983), ensayo 40.
[176] Como se ha mencionado en el capítulo 8, solo un caso especial en la versión más sencilla de la teoría de Ptolomeo (un epiciclo para cada planeta, y ninguno para el Sol) es equivalente a la versión más sencilla de la teoría copernicana, que difiere tan solo en el punto de vista: es el caso especial en el que se procura que los deferentes de los planetas interiores coincidan con la órbita del Sol en torno a la Tierra, mientras los radios de los epiciclos de los planetas exteriores son todos iguales a la distancia al Sol desde la Tierra. En este caso especial de la teoría ptolemaica, los radios de los epiciclos de los planetas interiores y los radios de los deferentes de los planetas exteriores coinciden con los radios de las órbitas planetarias de la teoría copernicana.
[177] La importancia de esta correlación la recalca Bernard R. Goldstein, Journal of the History of Astronomy, 33, 219 (2002).
[178] Para una traducción inglesa, véase Nicolas Copernicus On the Revolutions, trad. de Edward Rosen (Polish Scientific Publishers, Varsovia, 1978); reimpresión Johns Hopkins University Press, Baltimore, Maryland, 1978); o Copernicus-On the Revolutions of the Heavenly Spheres, trad. de A. M. Duncan (Barnes and Noble, Nueva York, 1967). Las citas aquí son de Rosen.
[179] A. D. White, A History of the Warfare of Science with Theology in Christendom (Appleton, Nueva York, 1895), vol. 1, pp. 126-128. Para una deflación de White, véase D. C. Lindberg y R. L. Numbers, «Beyond War and Peace: A Reappraisal of the Encounter Between Christianity and Science», Church History, 58, núm. 3 (septiembre de 1986): 338.
[180] Este párrafo ha sido citado por Lindberg y Numbers, «Beyond War and Peace», y por T. Kuhn, The Copernican Revolution (Harvard University Press, Cambridge, Massachusetts, 1957), p. 191. La fuente de Kuhn es White, A History of the Warfare of Science with Theology. El original alemán es Sämtliche Schriften, ed. de J. G. Walch (J. J. Gebauer, Halle, 1743), vol. 22, p. 2260.
[181] Josué, 10:12.
[182] Esta traducción inglesa del prefacio de Osiander está sacada de la trad. de Rosen, Nicolas Copernicus On the Revolutions.
[183] Citado en R. Christianson, Tycho’s Island (Cambridge University Press, Cambridge, 2000), p. 17.
[184] Sobre la idea de las esferas celestes duras, véase Edward Rosen, «The Dissolution of the Solid Celestial Spheres», Journal of the History of Ideas 46, 13 (1985). Rosen defiende que Tycho exageró al afirmar que esta idea había sido ampliamente aceptada antes de su época.
[185] Para la reivindicación de la autoría del sistema de Tycho y sus variaciones, véase C. Schofield, «The Tychonic and Semi-Tychonic World Systems», in Planetary Astronomy from the Rise of Astrophysics–Part A: Tycho Brahe to Newton, ed. R. Taton y C. Wilson (Cambridge University Press, Cambridge, 1989).
[186] Para una fotografía de esta estatua, tomada por Owen Gingerich, véase el frontispicio de mi recopilación de ensayos Facing Up-Science and Its Cultural Adversaries (Harvard University Press, Cambridge, Massachusetts, 2001).
[187] Dadas cinco cosas distintas, hay 120 maneras de escoger el orden; cualquiera de las cinco puede ser la primera, cualquiera de las restantes puede ser la segunda, cualquiera de las restantes puede ser la tercera, y cualquiera de las restantes puede ser la cuarta, lo que solo deja una posibilidad para la quinta. Así pues, el número de posibilidades de ordenar cinco cosas es 5 × 4 × 3 × 2 × 1 = 120. Pero por lo que se refiere a la razón de las esferas circunscritas e inscritas, los cinco poliedros regulares no son todos diferentes; esta razón es la misma para el cubo y para el octaedro, y también para el icosaedro y el dodecaedro. De ahí que dos disposiciones de los cinco poliedros en las que tan solo intercambiamos un cubo por un octaedro, o un icosaedro por un dodecaedro, den el mismo modelo de sistema solar. El número de modelos distintos es, por tanto: 120/(2 × 2) = 30.
[188] Por ejemplo, si un cubo está inscrito dentro del radio interior de la esfera de Saturno, y circunscrito por el radio exterior de la esfera de Júpiter, entonces la razón de la mínima distancia de Saturno al Sol y la máxima instancia de Saturno al Sol, que según Copérnico era 1,586, debería ser igual a la distancia del centro de un cubo a cualquiera de sus vértices dividida por la distancia del centro del mismo cubo al centro de cualquiera de sus caras, o √3 = 1,732, que es un 9 por ciento demasiado grande.
[189] S. Weinberg, «Anthropic Bound on the Cosmological Constant», Physical Review Letters, 59, 2067 (1987); H. Martel, P. Shapiro, y S. Weinberg, «Likely Values of the Cosmological Constant», Astrophysical Journal 492, 29 (1998).
[190] El movimiento de Marte es el caso de prueba ideal de las teorías planetarias. Contrariamente a Mercurio o Venus, Marte se puede ver en lo alto del cielo nocturno, donde las observaciones son más fáciles. En una serie dada de años, da muchas más revoluciones en su órbita que Júpiter o Saturno, y su órbita se separa del círculo más que en el caso de ninguno de los otros planetas importantes, excepto Mercurio (que nunca se ve lejos del Sol, y por lo tanto es difícil de observar), de modo que las desviaciones del movimiento circular a velocidad constante son mucho más evidentes en el caso de Marte que en el de ningún otro planeta.
[191] El efecto principal de eliminar la forma elíptica de las órbitas planetarias no es tanto el propio hecho de que sea una elipse, sino que el Sol sea un foco en lugar del centro de la elipse. Para ser precisos, la distancia entre cualquier foco en el centro de una elipse es proporcional a la excentricidad, mientras que la variación de la distancia de los puntos de la elipse al foco es proporcional al cuadrado de la excentricidad, lo cual, en caso de que sea pequeña, hace que la distancia sea mucho más pequeña. Por ejemplo, para una excentricidad de 0,1 (parecida a la de la órbita de Marte) la distancia más pequeña del planeta al Sol es tan solo 0,5 por ciento más pequeña que la distancia más grande. Por otro lado, la distancia al Sol desde el centro de esta órbita es un 10 por ciento el radio medio de la órbita.
[192] J. R. Voelkel y O. Gingerich, «Giovanni Antonio Magini’s “Keplerian” Tables of 1614 and Their Implications for the Reception of Keplerian Astronomy in the Seventeenth Century», Journal for the History of Astronomy 32, 237 (2001).
[193] Se trata de Julius Caesar Scaliger, un apasionado defensor de Aristóteles y oponente de Copérnico.
[194] Citado en Robert S. Westfall, The Construction of Modern Science-Mechanism and Mechanics (Cambridge University Press, Cambridge, 1977), p. 10.
[195] Esta es la traducción de William H. Donahue, en Johannes Kepler-New Astronomy (Cambridge University Press, Cambridge, 1992), p. 65.
[196] Johannes Kepler, Epitome of Copernican Astronomy and Harmonies of the World, trad. de Charles Glenn Wallis (Prometheus, Amherst, Nueva York, 1995), p. 180.
[197] Una discusión posterior muestra que, al hablar de distancia media, Kepler se refería no a la distancia media a lo largo del tiempo, sino más bien a la media de las distancias mínimas y máximas del planeta al Sol. Tal como se ve en la nota técnica 18, las distancias mínimas y máximas de un planeta al Sol son (1 – e)a y (1 + e)a, donde e es la excentricidad y a es la mitad del semieje mayor de la elipse, de manera que la distancia media es simplemente a. Asimismo se muestra en la nota técnica 18 que se trata también de la distancia del planeta al Sol, promediado a lo largo de la distancia recorrida por el planeta en su órbita.
[198] Citado por Owen Gingerich en Tribute to Galileo in Padua, International Symposium a cura dell’Universita di Padova 2-6 dicembere 1992, vol. 4 (Edizioni LINT, Trieste, 1995).
[199] La distancia focal es una longitud que caracteriza las propiedades ópticas de una lente. En el caso de las lentes convexas, es la distancia, detrás de la lente, a la que convergen los rayos que entran en ella en paralelo. En el caso de la lente cóncava, que separa a los rayos que convergen en direcciones paralelas, la distancia focal es aquella a la que, detrás de la lente, convergerían los rayos si no fuera por ella. La distancia focal depende del radio de curvatura de la lente y de la razón de las velocidades de la luz en el aire y en el cristal (véase nota técnica 22).
[200] Citas de Galileo Galilei, El mensaje y el mensajero sideral, p. 37, trad. de Carlos Solís Santos (Alianza, Madrid, 1984).
[201] El tamaño angular de los planetas es lo bastante grande como para que las líneas de visión desde los puntos individuales de un disco planetario estén más separadas al atravesar la atmósfera de la Tierra que el tamaño de las fluctuaciones atmosféricas típicas; como resultado, los efectos de las fluctuaciones sobre la luz procedente de diferentes líneas de visión no están correlacionados, por lo que tienden a anularse más que a sumarse de manera coherente. Por eso no vemos titilar a los planetas.
[202] A Galileo le habría apenado saber que estos son los nombres que sobreviven en la actualidad. Se los dio a los satélites de Júpiter, en 1614, Simon Marius, un astrónomo alemán que disputó con Galileo sobre quién había descubierto antes los satélites.
[203] Galileo Galilei, Discorse e Dimostrazione Matematiche. Para un facsímil de la traducción de 1663 de Thomas Salusbury, véase Galileo Galilei, Discourse on Bodies in Water, con introducción y notas de Stillman Drake (University of Illinois Press, Urbana, 1960). [En castellano se puede encontrar en Galileo, ed. de Víctor Navarro (Península, Barcelona, 1991)].
[204] Hemos de suponer que Galileo no utilizó un reloj, sino que más bien observó el movimiento aparente de las estrellas. Puesto que estas parecen girar 360° en torno a la Tierra en 24 horas, un cambio de 1° en la posición de una estrella indica el transcurso de un intervalo de tiempo igual a 24 horas dividido entre 360, es decir, 4 minutos.
[205] Para una edición moderna de la traducción del siglo XVII, véase Galileo, Discourse on Bodies in Water, trad. de Thomas Salusbury, introducción y notas de Stillman Drake.
[206] Para los detalles de este conflicto, véase, L. Heilbron, Galileo (Oxford University Press, Oxford, 2010).
[207] Esta carta ha sido ampliamente citada. La traducción que citamos aquí es de Duhem, To Save the Phenomena, p. 107. Una traducción más completa aparece en Stillman Drake, Discoveries and Opinions of Galileo (Anchor, Nueva York, 1957), pp. 162-164.
[208] Una traducción de la carta completa la encontramos en Drake, Discoveries and Opinions of Galileo, pp. 175-216.
[209] Citado en Stillman Drake, Galileo (Oxford University Press, Oxford, 1980), p. 64.
[210] La cartas de Maria Celeste a su padre por fortuna han llegado hasta nosotros. Muchas aparecen citadas en Dava Sobel, Galileo’s Daughter (Walker, Nueva York, 1999). Pero, por desgracia, las cartas de Galileo a su hija se han perdido.
[211] Véase Annibale Fantoli, Galileo-For Copernicanism and for the Church, 2.ª ed., trad. de G. V. Coyne (University of Notre Dame Press, South Bend, Indiana, 1996); Maurice A. Finocchiaro, Retrying Galileo, 1633-1992 (University of California Press, Berkeley, Los Ángeles, 2005).
[212] Citado en Drake, Galileo, p. 90.
[213] Citado por Gingerich, Tribute to Galileo, p. 343.
[214] Hice una afirmación muy parecida en el mismo congreso de Padua en el que Kuhn expresó los comentarios sobre Aristóteles citados en el capítulo 4, y donde Gingerich impartió su charla sobre Galileo que he citado aquí. Véase S. Weinberg, L’Anno Galileiano (Edizioni LINT, Trieste, 1995), p. 129.
[215] Véase See G. E. R. Lloyd, Proceedings of the Cambridge Philosophical Society, N.S. 10, 50 (1972), reproducido en Methods and Problems in Greek Science (Cambridge University Press, Cambridge, 1991).
[216] Galileo Galilei, «Discursos y demostraciones matemáticas sorbe dos nuevas ciencias», en Galileo, p. 240, ed. de Víctor Navarro (Península, Barcelona, 1991).
[217] En realidad, esto solo es cierto para oscilaciones del péndulo en ángulos pequeños, aunque Galileo no observó esa salvedad. De hecho, menciona que oscilaciones de 50° o 60° (grados de arco) tienen la misma duración que oscilaciones mucho más pequeñas, lo que sugiere que en realidad no experimentó tanto con el péndulo como afirmaba.
[218] De manera literal, esto significaría que un cuerpo arrojado desde la posición de reposo nunca caería, puesto que al ser la velocidad inicial cero al final del primer instante infinitesimal, no se habría movido, por lo que la velocidad proporcional a la distancia seguiría siendo una velocidad cero. Quizá la doctrina de que la velocidad es proporcional a la distancia recorrida se pretendía aplicar tan solo después de un breve periodo inicial de aceleración.
[219] Uno de los argumentos de Galileo es falaz, porque se aplica tan solo a la velocidad media durante un intervalo de tiempo, no a la velocidad adquirida al final de ese intervalo.
[220] Esto se demuestra en la nota técnica 25. Tal como se explica allí, aunque Galileo no lo sabía, la velocidad de la bola que rueda por un plano no es igual a la velocidad de un cuerpo que hubiera recorrido la misma diferencia en vertical, porque parte de la energía liberada por el descenso vertical se transmite a la rotación de la bola. Pero las velocidades son proporcionales, de manera que la conclusión cualitativa de Galileo de que la velocidad de un cuerpo que cae es proporcional al tiempo transcurrido no cambia cuando tenemos en cuenta la rotación de la bola.
[221] Stillman Drake, Galileo (Oxford University Press, Oxford, 1980), p. 33.
[222] T. B. Settle, «An Experiment in the History of Science», Science, 133, 19 (1961).
[223] Esta es la conclusión de Drake en la nota al final a la p. 259 de Galileo Galilei, Dialogue Concerning the Two Chief World Systems: Ptolemaic and Copernican, trad. de Stillman Drake (Modern Library, Nueva York, 2001).
[224] Conocemos este experimento gracias a un documento inédito, folio 116v, en la Biblioteca Nazionale Centrale, Florencia. Véase Stillman Drake, Galileo at Work-His Scientific Biography (University of Chicago Press, Chicago, Illinois, 1978), pp. 128-132; A. J. Hahn, «The Pendulum Swings Again: A Mathematical Reassessment of Galileo’s Experiments with Inclined Planes», Archive for the History of the Exact Sciences 56, 339 (2002), con una reproducción del folio en la p. 344.
[225] Carlo M. Cipolla, Clocks and Culture 1300–1700 (W. W. Norton, Nueva York, 1978), pp. 59, 138.
[226] Christiaan Huygens, The Pendulum Clock or Geometrical Demonstrations Concerning the Motion of Pendula as Applied to Clocks, trad. de Richard J. Blackwell (Iowa State University , Ames, 1986), p. 171.
[227] Esta medición la describe en detalle Alexandre Koyré en Proceedings of the American Philosophical Society 97, 222 (1953) y 45, 329 (1955). Véase también Christopher M. Graney, «Anatomy of a Fall: Giovanni Battista Riccioli and the Story of g», Physics Today, septiembre de 2012, pp. 36-40.
[228] Sobre la polémica acerca de estas leyes de conservación, véase G. E. Smith, «The Vis-Viva Dispute: A Controversy at the Dawn of Mathematics», Physics Today, octubre de 2006, p. 31.
[229] Christiaan Huygens, Treatise on Light, trad. de Silvanus P. Thompson (University of Chicago Press, Chicago, Illinois, 1945), p. vi.
[230] Citado por Steven Shapin en The Scientific Revolution (University of Chicago Press, Chicago, Illinois, 1996), p. 105.
[231] Ibíd., p. 185.
[232] Véanse los artículos sobre Leonardo en Dictionary of Scientific Biography, ed. de Charles Coulston Gillespie (Scribner, Nueva York, 1970), vol. 8, pp. 192-245.
[233] Las citas son de René Descartes, Los principios de la filosofía, p. 19, trad. de Guillermo Quintás (Alianza, Madrid, 1995).
[234] Descartes comparó la luz con un palo rígido, que cuando se empuja por un extremo al instante se mueve hacia el otro. También se equivocaba con los palos, aunque por razones que ni siquiera podía conocer. Cuando un palo se empuja por un extremo, nada ocurre en el otro hasta que una onda de compresión (esencialmente una onda de sonido) ha viajado de un extremo del palo al otro. La velocidad de esta onda aumenta con la rigidez del palo, pero la teoría de la relatividad especial de Einstein no permite que nada sea perfectamente rígido; ninguna onda puede tener una velocidad que supere la de la luz. El uso que hace Descartes de ese tipo de comparación lo comenta Peter Galison en «Descartes Comparisons: From the Invisible to the Visible», Isis, 75, 311 (1984).
[235] Voltaire, Cartas filosóficas, p. 121, trad. de Fernando Savater (Editora Nacional, Madrid, 1983).
[236] Es extraño que muchas traducciones modernas inglesas del Discurso del método no incluyan estos suplementos, como si carecieran de interés para los filósofos. Para una edición inglesa que los incluya, véase René Descartes, Discourse on Method, Optics, Geometry, and Meteorolgy, trad. de Paul J. Olscamp (Bobbs-Merrill, Indianápolis, Indiana, 1965).
[237] Recordemos que el seno de un ángulo, en un triángulo rectángulo, es el lado opuesto a ese ángulo dividido entre la hipotenusa del triángulo. Aumenta a medida que el ángulo pasa de cero a 90°, en proporción al ángulo para ángulos pequeños, y luego más lentamente.
[238] Se ha defendido que la analogía de la pelota de tenis encaja con la teoría de la luz de Descartes, que la ve como algo que surge de la dinámica de los diminutos corpúsculos que llenan el espacio; véase John A. Schuster, «Descartes Opticien-The Construction of the Law of Refraction and the Manufacture of Its Physical Rationales, 1618-29», en Descartes’ Natural Philosophy, ed. de S. Graukroger, J. Schuster, y J. Sutton (Routledge, Londres y Nueva York, 2000), pp. 258-312.
[239] Aristóteles, Meteorology, Libro III, Capítulo 4, 374a, 30–31 (trad. de Oxford, p. 603).
[240] Esto se hace averiguando el valor de b/R donde un cambio infinitesimal de b no produce ningún cambio en Φ, de manera que, para ese valor de Φ, el gráfico de Φ en relación con b/R es plano. Este es el valor de b/R cuando Φ alcanza su valor máximo. (Cualquier curva suave como la gráfica de Φ en relación con b/R que alcanza un máximo y luego cae de nuevo debe de ser plana en el máximo. Un punto en el que la curva no es plana no puede ser el máximo, pues si en algún punto la curva asciende a derecha o izquierda, habrá puntos a la derecha o izquierda donde la curva sea más alta). Los valores de Φ en la horquilla donde la curva de Φ en relación con b/R es casi plana varían solo lentamente cuando variamos b/R, de manera que hay relativamente muchos rayos con valores de Φ en esa horquilla.
[241] Descartes, Los principios de la filosofía, pp. 72, 122, trad. de Guillermo Quintás (Alianza, Madrid, 1995).
[242] Sobre este punto, véase Peter Dear, Revolutionizing the Sciences-European Knowledge and Its Ambitions, 1500-1700, 2.ª ed. (Princeton University Press, Princeton, Nueva Jersey y Oxford, 2009), Capítulo 8.
[243] L. Laudan, «The Clock Metaphor and Probabilism: The Impact of Descartes on English Methodological Thought», Annals of Science, 22, 73 (1966). A las conclusiones contrarias llegó G. A. J. Rogers, «Descartes and the Method of English Science», Annals of Science, 29, 237 (1972).
[244] Richard Watson, Cogito Ergo Sum—The Life of René Descartes (David R. Godine, Boston, Massachusetts, 2002).
[245] Siendo cincuentón, Newton contrató a la hermosa hija de su hermanastra, Catherine Barton, como ama de llaves, y aunque fueron buenos amigos no parece que mantuvieran ningún vínculo romántico. Voltaire, que se encontraba en Inglaterra en la época de la muerte de Newton, informó que el médico de este y el «cirujano en cuyos brazos murió» le confirmaron que Newton jamás había tenido intimidad con una mujer (véase Voltaire, Philosophical Letters, Bobbs-Merrill Educational Publishing, Indianápolis, Ind., 1961, p. 63). Voltaire no explica cómo podían saberlo el médico y el cirujano.
[246] Estas palabras proceden de un discurso, «Newton, el hombre», que Keynes tenía que pronunciar en un encuentro de la Royal Society en 1946. Keynes murió tres meses antes del encuentro y el discurso lo pronunció su hermano.
[247] Esto se describe en D. T. Whiteside, ed., Introducción General al Volumen 20, The Mathematical Papers of Isaac Newton (Cambridge University Press, Cambridge, 1968), pp. xi–xii.
[248] Newton dedicó un esfuerzo comparable a los experimentos de alquimia. También se la podría denominar química, pues entre ambas no había ninguna distinción importante. Tal como se ha comentado en relación con Jabir ibn Hayyan en el capítulo 9, hasta finales del siglo XVIII no existió ninguna teoría química asentada que descartara los objetivos de la alquimia, como la transmutación de los metales de baja ley en oro. Aunque los estudios de Newton sobre alquimia no representaron un abandono de la ciencia, tampoco condujeron a nada importante.
[249] Un fragmento plano de cristal no separa los colores, pues aunque cada color se curva en un ángulo ligeramente distinto al entrar en el cristal, todos retornan a su dirección original al salir. Como los lados de un prisma no son paralelos, los rayos de luz de distintos colores que se refractan de manera distinta al entrar en el cristal alcanzan, al salir, la superficie del prisma en ángulos que no son iguales a los ángulos de refracción al entrar, de manera que, cuando esos rayos se curvan para salir del prisma, los diferentes colores siguen separados en los mismos ángulos.
[250] Se trata del «logaritmo natural» de 1 + x, la potencia a la que hay que elevar la constante e = 2,71828… para obtener el resultado de 1 + x. La razón de esta peculiar definición es que el logaritmo natural posee algunas propiedades que son mucho más simples que las del «logaritmo común», en el que 10 ocupa el lugar de e. Por ejemplo, la fórmula de Newton demuestra que el logaritmo natural de 2 nos lo da la serie 1 - 1/2 + 1/3 - 1/4 +…, mientras que la fórmula del logaritmo común de 2 es más complicada.
[251] El hecho de despreciar los términos 3to2 y o3 en este cálculo puede llevar a pensar que el cálculo es solo aproximado, pero esto es engañoso. En el siglo XIX las matemáticas aprendieron a prescindir de la idea bastante vaga de un infinitesimal o, y a hablar de límites precisamente definidos: la velocidad es el número al que [D(t + o) – D(t)]/o se puede acercar todo lo que queramos siempre que tomemos una o lo bastante pequeña. Como veremos, Newton posteriormente se alejó de los infinitesimales y se acercó a la idea moderna de los límites.
[252] Ibíd., vol. 2, nota al pie, pp. 206-207; y vol. 3, pp. 6-7.
[253] Véase, por ejemplo, Richard S. Westfall, Never at Rest-A Biography of Isaac Newton (Cambridge University Press, Cambridge, 1980), capítulo 14.
[254] Peter Galison, How Experiments End (University of Chicago Press, Chicago, Illinois, 1987).
[255] Citado en Westfall, Never at Rest, p. 143.
[256] Las tres leyes de Kepler del movimiento planetario no habían quedado confirmadas del todo antes de Newton, aunque la primera ley —que cada órbita planetaria es una elipse con el Sol en un foco— era ampliamente aceptada. Fue la deducción de Newton de las tres leyes en los Principia la que condujo a la aceptación general de las tres.
[257] La primera medida razonablemente precisa de la circunferencia de la Tierra la calculó alrededor de 1669 Jean-Félix Picard (1620-1682), y Newton la utilizó para mejorar sus cálculos.
[258] Citado en Dictionary of Scientific Biography, ed. de Charles Coulson Gillespie (Scribner, Nueva York, 1970), vol. 6, p. 485.
[259] Citado en James Gleick, Isaac Newton (Pantheon, Nueva York, 2003), p. 120.
[260] Citas de I. Bernard Cohen y Anne Whitman, trads., Isaac Newton-The Principia, 3.ª ed. (University of California Press, Berkeley y Los Ángeles, 1999). Antes de esta versión, la clásica era The Principia-Mathematical Principles of Natural Philosophy (University of Califonia Press, Berkeley y Los Ángeles, 1962), trad. de Florian Cajori (1792), trad. rev. por Andrew Motte.
[261] G. E. Smith, «Newton’s Study of Fluid Mechanics», International Journal of Engineering Science, 36, 1377 (1998).
[262] Newton fue incapaz de solventar el problema de los tres cuerpos —la Tierra, el Sol y la Luna— con la suficiente exactitud como para calcular las peculiaridades del movimiento de la Luna que habían preocupado a Ptolomeo, Ibn Al-Shatir y Copérnico. Lo consiguió finalmente en 1752 Alexis-Claude Clairaut, que utilizó las teorías del movimiento y la gravitación de Newton.
[263] Los datos astronómicos actuales de este capítulo proceden de C. W. Allen, Astrophysical Quantities, 2.ª ed. (Athlone, Londres, 1963).
[264] La obra clásica sobre la historia de la medición del tamaño del sistema solar es la de Albert van Helden, Measuring the Universe-Cosmic Dimensions from Aristarchus to Halley (University of Chicago Press, Chicago, Illinois, 1985).
[265] Véase Robert P. Crease, World in the Balance-The Historic Quest for an Absolute System of Measurement (W. W. Norton, Nueva York, 2011).
[266] Véase J. Z. Buchwald y M. Feingold, Newton and the Origin of Civilization (Princeton University Press, Princeton, Nueva Jersey, 2014).
[267] Véase S. Chandrasekhar, Newton’s Principia for the Common Reader (Clarendon, Oxford, 1995), pp. 472-476; Richard S. Westfall, Never at Rest (Cambridge University Press, Cambridge, 1980), pp. 736-739.
[268] R. S. Westfall, «Newton and the Fudge Factor», Science, 179, 751 (1973).
[269] Véase G. E. Smith, «How Newton’s Principia Changed Physics», en Interpreting Newton: Critical Essays, ed. de A. Janiak y E. Schliesser (Cambridge University Press, Cambridge, 2012), pp. 360-395.
[270] Voltaire, Cartas filosóficas, p. 118, trad. de Fernando Savater (Editora Nacional, Madrid, 1983).
[271] La oposición al newtonianismo se describe en artículos de A. B. Hall, E. A. Fellmann y P. Casini en «Newton’s Principia: A Discussion Organized and Edited by D. G. King-Hele y A. R. Hall», Monthly Notices of the Royal Astronomical Society, 42, 1 (1988).
[272] En el Libro III de Opticks, Newton expresó la opinión de que el sistema solar es inestable, y que requiere algún esporádico reajuste. La cuestión de la estabilidad del sistema solar siguió envuelta en la polémica durante siglos. A finales de la década de 1980, Jacques Laskar mostró que el sistema solar es caótico; resulta imposible predecir los movimientos de Mercurio, Venus, la Tierra y Marte a más de cinco millones de años vista. Algunas condiciones iniciales causan que los planetas colisionen o sean expulsados del sistema solar después de unos cuantos miles de millones de años, cosa que no ocurre con otros que son casi indistinguibles. Véase J. Laskar, «Is the Solar System Stable?», www.arxiv.org/1209.5996 (2012).
[273] Christiaan Huygens, Discours de la Cause de la Pesanteur (1690), trad. de Karen Bailey y anotaciones de Karen Nailey y G. E. Smith, disponible gracias a Smith, de la Tuft University (1997).
[274] Shapin ha observado que este conflicto tuvo incluso implicaciones políticas: Steven Shapin, «Of Gods and Kings: Natural Philosophy and Politics in the Leibniz-Clarke Disputes», Isis, 72, 187 (1981).
[275] S. Weinberg, Gravitation and Cosmology (Wiley, Nueva York, 1972), Capítulo 15.
[276] G. E. Smith, inédito.
[277] Citado en A Random Walk in Science, ed. R. L. Weber y E. Mendoza (Taylor and Francis, Londres, 2000).
[278] Robert K. Merton, «Motive Forces of the New Science», Osiris, 4, Parte 2 (1938); reproducido en Science, Technology, and Society in Seventeenth Century England (Howard Fertig, Nueva York, 1970), y en On Social Structure and Science, ed. Piotry Sztompka (University of Chicago Press, Chicago, Illinois, 1996), pp. 223-240.
[279] Presento un relato más detallado de este progreso en The Discovery of Subatomic Particles, ed. rev., (Cambridge University Press, Cambridge, 2003).
[280] Isaac Newton, Opticks, or A Treatise of the Reflections, Refractions, Inflections and Colours of Light (Dover, Nueva York, 1952, basado en la 4.ª ed., Londres, 1730), p. 394.
[281] Ibíd., p. 376.
[282] El propio Maxwell no escribió las leyes que gobiernan los campos magnético y eléctrico en la forma conocida hoy en día como «ecuaciones de Maxwell». En sus ecuaciones encontramos campos conocidos como potenciales, cuyas velocidades de cambio con el tiempo y la posición son los campos eléctrico y magnético. La versión moderna más familiar de las ecuaciones de Maxwell es obra de Oliver Heaviside, que las presentó allá por 1881.
[283] Esto procede de Outlines of General Chemistry, de Ostwald, y lo cita G. Holton en Historical Studies in the Physical Sciences, 9, 161 (1979), y I. B. Cohen, en Critical Problems in the History of Science, ed. de M. Clagett (University of Wisconsin Press, Madison, 1959).
[284] P. A. M. Dirac, «Quantum Mechanics of Many-Electron Systems», Proceedings of the Royal Society, A123, 713 (1929).
[285] A partir de aquí no citaré el nombre de ningún físico, pues fueron tantos los que participaron en las investigaciones que ocuparían demasiado espacio, y muchos siguen vivos, por lo que me arriesgaría a ofender a algunos si no los citara.
[286] Agrupo aquí la selección sexual y la selección natural, y el equilibrio que se da de vez en cuando en medio de la evolución constante; y no distingo entre mutaciones y desviación genética como fuente de las variaciones heredables. Estas distinciones son muy importantes para los biólogos, pero no afectan a lo que quiero constatar aquí: que no hay ninguna ley de la biología independiente que diga que las variaciones heredables tienen más posibilidades de suponer una mejoría.
[287] Para adelantarme a las acusaciones de plagio, reconozco que este último párrafo es una variación sobre el último párrafo de El origen de las especies de Darwin.
[288] Puede que esto no se supiera en la época de Tales, en cuyo caso la demostración ha de fecharse en una época posterior.
[289] De la traducción habitual de T. L. Heath (Euclides’ Elements, Green Lion Press, Santa Fe, Nuevo México, 2002, p. 480).
[290] En una cuerda de piano existen pequeñas correcciones debidas a la rigidez de la cuerda; estas correcciones producen términos en v proporcionales a 1/L3. Aquí haremos caso omiso.
[291] En algunas escalas musicales, el sol medio se da a una frecuencia un tanto distinta, a fin de que sea posible crear otros acordes agradables en los que intervenga el sol medio. El ajuste de frecuencias para llevar a cabo todos los acordes agradables posibles se denomina «temperado» de la escala.
[292] Esta tabla aparece en la traducción del Almagesto de G. J. Toomer (Ptolemy’s Almagest, Duckworth, Londres, 1984, pp. 57-60).
[293] La definición que utilizó Galileo de «milla» no es muy distinta de la moderna milla inglesa. En unidades modernas, el radio de la Luna es de hecho de 1080 millas (1737 km).