Historia de las matemáticas
Ian Stewart
Las matemáticas no nacieron plenamente formadas. Fueron haciéndose gracias a los esfuerzos acumulativos de muchas personas que procedían de muchas culturas y hablaban diferentes lenguas. Ideas matemáticas que se siguen utilizando hoy datan de hace más de 4.000 años.
Muchos descubrimientos humanos son efímeros; el diseño de las ruedas de carro fue muy importante para el Reino Nuevo Egipcio, pero hoy día no es exactamente tecnología de vanguardia. Las matemáticas, por el contrario, suelen ser permanentes. Una vez que se ha hecho un descubrimiento matemático está a disposición de cualquiera, y con ello adquiere una vida propia. Las buenas ideas matemáticas difícilmente pasan de moda, aunque la forma de implementarlas puede sufrir cambios espectaculares. Hoy seguimos utilizando métodos para resolver ecuaciones que fueron descubiertas por los antiguos babilonios. Ya no utilizamos su notación, pero el vínculo histórico es innegable.
De hecho, la mayoría de las matemáticas que se enseñan hoy en la escuela tienen más de 200 años.
La inclusión de las matemáticas modernas en los programas de estudio en los años sesenta del siglo pasado llevó la asignatura al siglo XIX. Pero, contra lo que pueda parecer, las matemáticas no se han quedado quietas. Hoy día, se crean más matemáticas nuevas cada semana que las que los babilonios pudieron manejar en dos mil años.
El progreso de la civilización humana y el progreso de las matemáticas han ido de la mano. Sin los descubrimientos griegos, árabes e hindúes en trigonometría, la navegación en océanos abiertos hubiera sido una tarea aún más aventurada de lo que fue cuando los grandes marinos abrieron los seis continentes. Las rutas comerciales de China a Europa, o de Indonesia a las Américas, se mantenían unidas por un invisible hilo matemático.
La sociedad de hoy no podría funcionar sin matemáticas. Prácticamente todo lo que hoy nos parece natural, desde la televisión hasta los teléfonos móviles, desde los grandes aviones de pasajeros hasta los sistemas de navegación por satélite en los automóviles, desde los programas de los trenes hasta los escáneres médicos, se basa en ideas y métodos matemáticos. A veces son matemáticas de mil años de edad; otras veces son matemáticas descubiertas la semana pasada. La mayoría de nosotros nunca nos damos cuenta de que están presentes, trabajando entre bastidores para facilitar esos milagros de la tecnología moderna.
Esto no es bueno: nos hace creer que la tecnología funciona por magia, y nos lleva a esperar nuevos milagros cada día. Por otra parte, es también completamente natural: queremos utilizar estos milagros con tanta facilidad y tan poco esfuerzo mental como sea posible. El usuario no debería cargarse con información innecesaria sobre la maquinaria subyacente que hace posible los milagros. Si todos los pasajeros de un avión tuvieran que superar un examen de trigonometría antes de embarcar en el avión, pocos de nosotros dejaríamos la tierra alguna vez. Y aunque eso podría reducir nuestra pisada de carbono, también haría nuestro mundo muy pequeño y provinciano.
Escribir una historia de las matemáticas verdaderamente completa es virtualmente imposible. La disciplina es ahora tan amplia, tan compleja y tan técnica, que ni siquiera un experto podría entender por completo un libro semejante; dejando aparte el hecho de que nadie podría escribirlo. Morris Kline se acercó con su épico Pensamiento matemático desde la antigüedad hasta los tiempos modernos. Tiene más de 1.200 páginas de letra pequeña, y deja fuera casi todo lo que ha sucedido en los últimos cien años.
Este libro es mucho más corto, lo que quiere decir que he tenido que ser selectivo, especialmente en lo que se refiere a los siglos XX y XXI. Soy plenamente consciente de todos los temas importantes que he tenido que omitir. No hay geometría algebraica, ni teoría de cohomología, ni análisis de elementos finitos, ni ondeletes.
La lista de lo que falta es mucho más larga que la lista de lo que se ha incluido.
Mis elecciones se han guiado por lo que probablemente es la formación básica de los lectores y por la concisión con que pueden explicarse las nuevas ideas.
La historia sigue aproximadamente un orden cronológico dentro de cada capítulo, pero los capítulos están ordenados por temas. Esto es necesario para darle una coherencia narrativa, si lo pusiera todo en orden cronológico, la discusión saltaría de forma aleatoria de un tema a otro, sin ningún sentido de dirección.
Esto podría estar más cerca de la historia real, pero haría el libro ilegible. Por eso, cada nuevo capítulo empieza con una vuelta al pasado, y luego toca algunos de los hitos históricos por los que pasó la disciplina en su desarrollo. Los primeros capítulos se detienen a mucha distancia en el pasado; los últimos capítulos recorren a veces todo el camino hasta el presente.
He tratado de dar una idea de las matemáticas modernas, por lo que entiendo cualquier cosa hecha en los últimos 100 años más o menos, seleccionando temas de los que los lectores pueden haber oído hablar y relacionándolos con las tendencias históricas generales. La omisión de un tema no implica que carezca de importancia, pero creo que tiene más sentido dedicar algunas páginas a hablar de la demostración de Andrew Wiles del Último Teorema de Fermat -de lo que la mayoría de los lectores han oído hablar- que, por ejemplo, a la geometría no-conmutativa, de la que tan sólo el fundamento ocuparía varios capítulos.
En definitiva, ésta es una historia, no la historia. Y es historia en el sentido en que cuenta un relato sobre el pasado. No se dirige a historiadores profesionales, no hace las finas distinciones que ellos creen necesarias, y a veces describe ideas del pasado a través de los ojos del presente. Esto último es el pecado capital para un historiador, porque hace que parezca que los antiguos estaban luchando por llegar a nuestro modo de pensamiento actual. Pero creo que es defendible y esencial si el objetivo principal es partir de lo que ahora sabemos y preguntar de dónde proceden dichas ideas. Los griegos no estudiaron la elipse para hacer posible la teoría de las órbitas planetarias de Kepler, ni Kepler formuló sus tres leyes del movimiento planetario para que Newton las convirtiera en su ley de la gravedad. Sin embargo, la historia de la ley de Newton se basa firmemente en el trabajo griego sobre la elipse y el análisis de Kepler de los datos observacionales.
Un subtema del libro son los usos prácticos de las matemáticas. Aquí he ofrecido una muestra muy ecléctica de aplicaciones, pasadas y presentes. Una vez más, la omisión de un tema no indica que carezca de importancia.
Las matemáticas tienen una historia larga y gloriosa aunque algo olvidada, y la influencia de la disciplina sobre el desarrollo de la cultura humana ha sido inmensa. Si este libro transmite una minúscula parte de la historia, habrá alcanzado lo que yo me propuse.
Coventry
Mayo de 2007
Capítulo 1
Fichas, cuentas y tablillas
El nacimiento de los números
Las matemáticas empezaron con los números, y los números siguen siendo fundamentales, incluso si la disciplina ya no se limita a los cálculos numéricos. Sobre la base de los números, las matemáticas han construido conceptos más sofisticados y se han desarrollado hasta constituir un área muy amplia y variada del pensamiento humano, que va mucho más allá de lo que encontramos en un típico temario escolar. Las matemáticas de hoy tratan más de estructuras, pautas y formas que de los propios números. Sus métodos son muy generales, y a menudo muy abstractos. Tienen aplicaciones en la ciencia, la industria, el comercio..., incluso las artes. Las matemáticas son universales y ubicuas.
§. Empezó con números
Durante muchos miles de años, matemáticos de muchas y diferentes culturas han creado una enorme superestructura cimentada en los números: geometría, cálculo infinitesimal, dinámica, probabilidad, topología, caos, complejidad, etc. La revista Mathematical Reviews, que registra cada nueva publicación matemática, clasifica la disciplina en casi un centenar de áreas mayores, subdivididas en varios miles de especialidades.
Hay más de 50.000 matemáticos investigadores en el mundo, que publican más de un millón de páginas de matemáticas nuevas cada año. Matemáticas genuinamente nuevas, no sólo pequeñas variaciones sobre resultados ya existentes.
“Los números parecen muy simples y directos, pero las apariencias engañan.”
Los matemáticos también han investigado en los fundamentos lógicos de su disciplina, y han descubierto conceptos aún más fundamentales que los números: lógica matemática, teoría de conjuntos. Pero, una vez más, la motivación principal, el punto de partida del que fluye todo lo demás, es el concepto de número.
Los cálculos con números pueden ser duros; obtener el número correcto puede ser difícil. Incluso así, es mucho más fácil utilizar números que especificar qué son realmente. Los números cuentan cosas, pero no son cosas: podemos coger dos tazas, pero no podemos coger el número «dos».
Los números se denotan por símbolos, pero no son símbolos: diferentes culturas utilizan diferentes símbolos para el mismo número. Los números son abstractos, y sin embargo nuestra sociedad se basa en ellos y no funcionaría sin ellos. Los números son una construcción mental, y sin embargo tenemos la sensación de que seguirían teniendo significado incluso si la humanidad fuera barrida por una catástrofe mundial y no quedara ninguna mente para contemplarlos.
§. Las primeras marcas
La historia de las matemáticas empieza con la invención de símbolos escritos para denotar números. Nuestro familiar sistema de «dígitos» 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, para representar todos los números imaginables, por grandes que sean, es una invención relativamente reciente; nació hace unos 1.500 años, y su extensión a los «decimales», que nos permite representar números con alta precisión, no tiene más de 450 años. Los computadores, que han introducido los cálculos matemáticos en nuestra cultura de forma tan profunda que ya no notamos su presencia, llevan con nosotros tan sólo unos 50 años.
Y sólo hace 20 años que disponemos de computadores suficientemente potentes y rápidos para servirnos en nuestros hogares.
Sin números, la civilización tal como ahora la conocemos no podría existir. Los números están por todas partes, como sirvientes ocultos que corren de un lado a otro entre bastidores: llevan mensajes, corrigen nuestra ortografía cuando escribimos a máquina, programan nuestros vuelos de vacaciones al Caribe, llevan el registro de nuestros bienes, garantizan que nuestros medicamentos sean seguros y efectivos. Y, en contrapartida, hacen posibles las armas nucleares y guían bombas y misiles hacia sus objetivos.
No todas las aplicaciones de las matemáticas han mejorado la condición humana.
¿Cómo surgió esta industria numérica verdaderamente enorme?
Incluso entonces, los contables ya estaban registrando quién era el propietario de qué, y de cuánto; incluso si todavía no se había inventado la escritura y no había símbolos para los números.
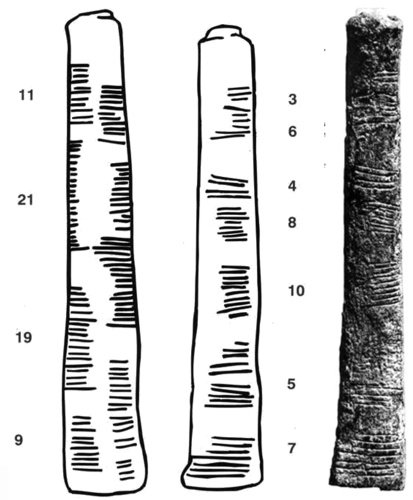
El hueso de Ishango, con las pautas de marcas y los números que pueden representar
En lugar de símbolos numerales, aquellos contables antiguos utilizaban pequeñas fichas de arcilla. Unas eran conos, otras eran esferas y otras tenían forma de huevos.
“Todo empezó con pequeñas fichas de arcilla, hace 10.000 años en el Próximo Oriente.”
Había cilindros, discos y pirámides. La arqueóloga Denise Schhmandt-Besserat dedujo que estas fichas representaban productos básicos de la época. Las esferas de arcilla representaban fanegas de grano, los cilindros representaban animales, los huevos jarras de aceite. Las fichas más antiguas datan del 8.000 a.C. y fueron de uso común durante 5.000 años.
Izquierda. Las marcas de cuenta tienen la ventaja de que pueden ir añadiéndose de una en una, durante largos periodos, sin alterar o borrar marcas anteriores. Se siguen utilizando hoy, a menudo en grupos de cinco con el quinto trazo cruzando diagonalmente los cuatro anteriores. Derecha. La presencia de marcas de cuenta aún puede verse en los numerales modernos. Nuestros símbolos 1,2, 3 se derivan, respectivamente, de un solo trazo, dos trazos horizontales unidos por una línea inclinada, y tres trazos horizontales unidos por una línea inclinada
Con el paso del tiempo, las fichas se hicieron más elaboradas y más especializadas. Había conos decorados para representar barras de pan, y tabletas en forma de diamante para representar cerveza. Schmandt-Besserat se dio cuenta de que estas fichas eran mucho más que un artificio de contabilidad.
Eran un primer paso vital en el camino hacia los símbolos numerales, la aritmética y las matemáticas. Pero ese paso inicial fue bastante extraño, y parece dado por accidente.
Se dio porque las fichas se utilizaban para llevar registros, quizá con fines impositivos o financieros, o como prueba legal de propiedad. Las fichas tenían la ventaja de que los contables podían ordenarlas rápidamente para calcular cuántos animales o cuánto grano poseía o debía alguien. El inconveniente era que las fichas podían ser falsificadas. Así que para asegurar que nadie interfería en las cuentas, los contables guardaban las fichas en recipientes de arcilla, como si estuvieran precintadas. Podían descubrir rápidamente cuántas fichas, y de qué tipo, había dentro de un recipiente dado rompiéndolo. Siempre podían hacer un nuevo recipiente para un almacenamiento posterior.
Sin embargo, romper repetidamente un recipiente y renovarlo era una forma muy poco eficaz de descubrir lo que había dentro, y los burócratas de la antigua Mesopotamia pensaron algo mejor. Inscribieron símbolos en el recipiente que hacían una lista de las fichas que contenía. Si había dentro siete esferas, los contables dibujaban siete esferas en la arcilla húmeda de la vasija.
En algún momento los burócratas mesopotámicos se dieron cuenta de que, una vez que habían dibujado los símbolos en el exterior del recipiente, ya no necesitaban los contenidos, y ya no tenían que romper el recipiente para ver qué fichas había dentro.
Este paso obvio pero crucial dio lugar a un conjunto de símbolos numerales escritos, con diferentes formas para diferentes clases de bienes. Todos los demás símbolos numerales, incluidos los que hoy utilizamos, son los descendientes intelectuales de este antiguo artificio burocrático. De hecho, es posible que la sustitución de fichas por símbolos haya constituido también el nacimiento de la propia escritura.
§. Marcas de cuenta
Estas marcas de arcilla no eran ni mucho menos los más antiguos ejemplos de escritura numeral, pero todos los ejemplos anteriores son poco más que rayas, «marcas de cuenta», que registran números como una serie de trazos, tales como
| | | | | | | | | | | | |
para representar el número 13. Las marcas más viejas conocidas de este tipo, 29 muescas grabadas en un hueso de pata de babuino, tienen unos 37.000 años. El hueso se encontró en una cueva en las montañas Lebombo, en la frontera entre Swazilandia y Sudáfrica, por lo que la cueva se conoce como la Cueva de la Frontera, y el hueso es el hueso de Lebombo. A falta de una máquina del tiempo, no hay modo de estar seguros de lo que representan las marcas, pero podemos hacer conjeturas informadas. Un mes lunar tiene 28 días, de modo es posible que las muescas estén relacionadas con las fases de la Luna.
Hay reliquias similares de la Europa antigua. Un hueso de lobo encontrado en la antigua Checoslovaquia tiene 57 marcas dispuestas en once grupos de cinco con dos sueltas, y tiene unos 30.000 años. Dos veces 28 es 56, de modo que esto podría ser un registro lunar de dos meses. Una vez más, parece que no hay modo de comprobar esta sugerencia. Pero las marcas parecen deliberadas, y debieron hacerse por alguna razón.
Otra antigua inscripción matemática, el hueso de Ishango en Zaire, tiene 25.000 años (estimaciones previas de 6.000-9.000 años fueron revisadas en 1995). A primera vista las marcas a lo largo del borde del hueso parecen hechas casi al azar, pero quizá haya pautas ocultas. Una fila contiene los números primos entre 10 y 20, a saber, 11, 13, 17 y 19, cuya suma es 60. Otra hilera contiene 9, 11, 19 y 21, que también suman 60. La tercera hilera recuerda un método utilizado a veces para multiplicar dos números por duplicación y por división por dos repetida. Sin embargo, las pautas aparentes pueden ser una simple coincidencia, y también se ha sugerido que el hueso de Ishango es un calendario lunar.
Las marcas de cuenta tienen la ventaja de que pueden irse añadiendo de una en una, durante largos periodos, sin alterar o borrar marcas anteriores. Se siguen utilizando hoy, a menudo en grupos de cinco con el quinto trazo cruzando diagonalmente los cuatro anteriores.
La presencia de marcas de cuenta es profunda, y aún puede verse en los numerales modernos. Nuestros símbolos 1, 2, 3 se derivan, respectivamente, de un solo trazo, dos trazos horizontales unidos por una línea inclinada, y tres trazos horizontales unidos por una línea inclinada.
§. Las marcas se convierten en numerales
El camino histórico desde las fichas de los contables a los numerales modernos es largo e indirecto. Con el paso de los milenios, los pueblos de Mesopotamia desarrollaron la agricultura, y su forma de vida nómada dio paso a un asentamiento permanente en una serie de ciudades-estado: Babilonia, Erido, Lagash, Sumer, Ur. Los primitivos símbolos inscritos en tablillas de arcilla húmeda se transformaron en pictogramas -símbolos que representan palabras mediante imágenes simplificadas de lo que las palabras significan- y posteriormente los pictogramas se simplificaron y quedaron reducidos a un pequeño número de marcas con forma de cuña, que se imprimían en la arcilla utilizando un estilete seco con un extremo plano y afilado. Podían hacerse diferentes tipos de cuñas manejando el estilete de diferentes maneras. Hacia el 3.000 a.C. los sumerios habían desarrollado una elaborada forma de escritura, ahora llamada cuneiforme: «en forma de cuña».
La historia de este periodo es complicada; diferentes ciudades se hicieron dominantes en tiempos diferentes. La ciudad de Babilonia, en particular, alcanzó gran importancia, y aproximadamente un millón de tablillas de arcilla babilónicas han sido extraídas de las arenas mesopotámicas. Unos pocos cientos de ellas tratan de matemáticas y astronomía, y muestran que los babilonios tenían un amplio conocimiento de ambas disciplinas. En particular, eran astrónomos expertos y desarrollaron un simbolismo sistemático y sofisticado para los números con el que podían representar datos astronómicos con alta precisión.
Los símbolos numerales babilónicos van mucho más allá de un simple sistema de recuento, y son los más antiguos símbolos conocidos en hacerlo.
Se utilizan dos tipos diferentes de cuña: una cuña delgada y vertical para representar el numero 1, y una cuña gruesa horizontal para el número 10.
Estas cuñas se disponían en grupos para indicar los números 2-9 y 20-50.
Sin embargo, esta pauta se detiene en 59, y la cuña delgada toma entonces un segundo significado, el número 60.
Se dice por ello que el sistema de numeración babilónico es de «base 60», o sexagesimal. Es decir, el valor de un símbolo puede ser un número, o 60 veces dicho número, o 60 veces 60 veces dicho número, dependiendo de la posición del símbolo. En esto es similar a nuestro familiar sistema decimal, en el que el valor de un símbolo se multiplica por 10, o por 100, o por 1.000, dependiendo de su posición. En el número 777, por ejemplo, el primer 7 significa «siete cientos», el segundo significa «setenta» y el tercero significa «siete».
Para un babilonio, una serie de tres repeticiones 
del símbolo para «7» tendría un significado diferente, aunque basado en un principio similar. El primer símbolo significaría 7 × 60 × 60, o 25.200; el segundo significaría 7 × 60 = 420; el tercero significaría 7. Por lo tanto, el grupo de tres significaría 25.200 + 420 + 7, que es 25.627 en nuestra notación. Aún pueden encontrarse hoy reliquias de los números babilonios de base 60.
Los 60 segundos en un minuto, 60 minutos en una hora y 360 grados en un círculo completo se remontan a la antigua Babilonia.
Símbolos babilónicos para los números 1-59
Puesto que es difícil escribir a máquina en cuneiforme, los estudiosos escriben los numerales babilónicos utilizando una mezcla de nuestra notación de base 10 y su notación de base 60. Así, las tres repeticiones del símbolo cuneiforme para 7 se escribirán como 7, 7, 7. Y algo como 23, 11, 14 indicará los símbolos babilónicos para 23, 11 y 14 escritos en orden, con el valor numérico (23 × 60 × 60) + (11 × 60) + 14, lo que da 83.474 en nuestra notación.
§. Los babilonios
Nosotros no sólo utilizamos diez símbolos para representar números arbitrariamente grandes: también utilizamos los mismos símbolos para representar números arbitrariamente pequeños. Para hacerlo empleamos la «coma decimal». Los dígitos a la izquierda de la coma representan números enteros; los que están a la derecha de la coma representan fracciones. Fracciones especiales son los múltiplos de una décima, una centésima y así sucesivamente. Por lo tanto 25,47, pongamos por caso, significa 2 decenas + 5 unidades + 4 décimas + 7 centésimas.
Los babilonios conocían este truco y lo utilizaron con un efecto extraordinario en sus observaciones astronómicas. Los estudiosos denotan al equivalente babilónico de la coma decimal por un punto y coma (;), pero ésta es una «coma sexagesimal» y los múltiplos a su derecha son múltiplos de 1/60, (1/60 × 1/60) = 1/3600 y así sucesivamente. Como ejemplo, la lista de números 12, 59; 57, 17 significa
12 × 60 + 59 + 57/60 + 17/3600
que es aproximadamente 779,955.
Se conocen casi 2.000 tablillas babilónicas con información astronómica, aunque muchas de éstas son pura rutina, consistentes en descripciones de maneras de predecir eclipses, tablas de sucesos astronómicos regulares y breves extractos. Unas 300 tablillas son más ambiciosas y más excitantes; tabulan observaciones del movimiento de Mercurio, Marte, Júpiter y Saturno, por ejemplo.
Por fascinante que pueda ser, la astronomía babilónica es algo tangencial a nuestra historia principal, que es la de las matemáticas «puras» babilónicas. Pero parece probable que la aplicación a la astronomía fuera un acicate para la búsqueda de las áreas más cerebrales de dicha disciplina. Por ello es justo reconocer cuán precisos eran los astrónomos babilonios cuando se trataba de observar sucesos celestes. Por ejemplo, encontraron que el periodo orbital de Marte (estrictamente, el tiempo transcurrido entre apariciones sucesivas en la misma posición en el cielo) era 12, 59; 57, 17 días en su notación, aproximadamente 779,955 días, como ya se ha señalado.
La cifra moderna es 779,936 días.
Para qué les servían los númerosLa tabla babilónica de Júpiter: Los babilonios utilizaban su sistema de numeración para el comercio y la contabilidad cotidiana, pero también lo utilizaban para un fin más sofisticado: la astronomía.
Tabla babilónica de JúpiterPara esto, la capacidad de su sistema para representar números fraccionarios con gran precisión era esencial. Varios centenares de tablillas registran datos planetarios. Entre ellas hay una única tablilla, muy dañada, que detalla el movimiento diario del planeta Júpiter durante un periodo de unos 400 días. Fue escrita en la misma Babilonia, alrededor del 163 a.C. Una entrada típica de la tablilla lista los números
126 8 16;
6, 46, 58
-0;0,45,18
-0;0,11,42
+0;0,0,10,
que corresponden a varias cantidades empleadas para calcular la posición del planeta en el cielo. Nótese que los números se escriben con tres lugares sexagesimales, ligeramente mejor que cinco cifras decimales.
§. Los antiguos egipcios
Quizá la más grande de las civilizaciones antiguas fue la de Egipto, que floreció en las orillas del Nilo y en el Delta del Nilo entre el 3150 a.C. y el 31 a.C., con un extenso periodo «predinástico» anterior que se extiende hacia atrás hasta el 6000 a.C. y un declive gradual bajo el dominio romano del 3 1 a.C. en adelante. Los egipcios eran constructores consumados, tenían un sistema muy desarrollado de creencias y ceremonias religiosas y eran registradores obsesivos. Pero sus logros matemáticos eran modestos comparados con las alturas alcanzadas por los babilonios.
El antiguo sistema egipcio para escribir números naturales es muy simple y directo. Hay símbolos para los números 1, 10, 100, 1.000, y así sucesivamente. Repitiendo estos símbolos hasta nueve veces, y combinando luego los resultados, se puede representar cualquier número natural. Por ejemplo, para escribir el número 5.724 los egipcios agruparían cinco de sus símbolos para 1.000, siete símbolos para 100, dos símbolos para 10 y cuatro símbolos para 1.
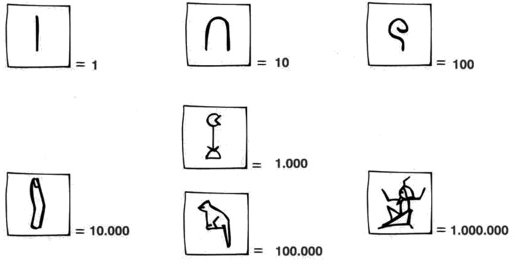
Símbolos numerales egipcios
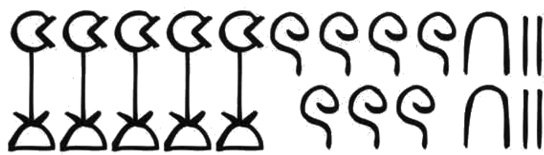
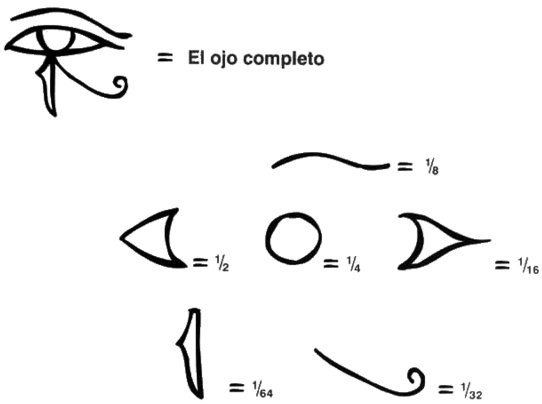
Las fracciones provocaban graves dolores de cabeza a los egipcios. En diversos períodos utilizaron varias notaciones diferentes para fracciones. En el Reino Antiguo (2.700-2.200 a.C.), una notación especial para nuestras fracciones ½, ¼, ⅛, 1/16, 1/32 y 1/64 se obtenía por división por dos repetida. Estos símbolos utilizaban partes del jeroglífico «ojo de Horus» u «ojo de la cobra».
El sistema egipcio más conocido para las fracciones fue ideado durante el Reino Medio (2.200-1.700 a.C.). Empieza con una notación para cualquier fracción de la forma 1 /n, donde n es un entero positivo. El símbolo 
(el jeroglífico para la letra R) se escribe sobre los símbolos egipcios estándar para n. Por ejemplo, 1/n se escribe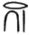
. Las demás fracciones se expresan entonces añadiendo varias de estas «fracciones unidad». Por ejemplo,
5/6 = ½ + 1/3.
Es interesante que los egipcios no escribían 2/5 como 1/5 + 1/5. Parece que su regla era: utilizar fracciones unidad distintos. Había también notaciones diferentes para algunas de las fracciones más simples, tales como ½, ⅔ y ¾.
La notación egipcia para las fracciones era engorrosa y muy poco adecuada para el cálculo. Les servía bastante bien en los registros oficiales, pero fue casi completamente ignorada por las culturas posteriores.
El número 5724 en jeroglíficos egipcios
Fracciones especiales formadas con partes del ojo de la cobra
Símbolos especiales para fracciones especiales
§. Números y personas
Guste o no la aritmética, no se pueden negar los profundos efectos que han tenido los números en el desarrollo de la civilización humana. La evolución de la cultura y la de las matemáticas han ido de la mano durante los últimos cuatro milenios. Sería difícil desenredar causa y efecto; yo dudaría en argumentar que la innovación matemática impulsa el cambio cultural, o que las necesidades culturales determinan la dirección del progreso matemático. Pero ambas afirmaciones contienen algo de verdad, porque matemáticas y cultura evolucionan conjuntamente.
Hay, no obstante, una diferencia significativa. Los cambios culturales están muy «en la superficie». Los nuevos tipos de vivienda, las nuevas formas de transporte, incluso los nuevos modos de organizar las burocracias gubernamentales, son relativamente obvios para todo ciudadano. Las matemáticas, sin embargo, tienen lugar fundamentalmente entre bastidores. Cuando los babilonios utilizaban sus observaciones astronómicas para predecir eclipses solares, por ejemplo, el ciudadano medio quedaba impresionado por la precisión con que los sacerdotes predecían estos sucesos sorprendentes, incluso si la mayoría de los sacerdotes tenían poca o ninguna idea de los métodos empleados. Ellos sabían cómo leer tablillas que listaban datos de eclipses, pero lo que importaba era cómo utilizarlos. Cómo se habían construido era un arte arcano, que quedaba para los especialistas.
Algunos sacerdotes pueden haber tenido una buena educación matemática -todos los escribas instruidos la tenían, y los sacerdotes instruidos tomaban, en sus primeros años, prácticamente las mismas lecciones que los escribas-, pero una apreciación de las matemáticas no era realmente necesaria para disfrutar de los beneficios que surgían de los nuevos descubrimientos en la disciplina. Así ha sido siempre y, sin duda, así seguirá siendo. Los matemáticos apenas reciben crédito por cambiar nuestro mundo. ¿Cuántas veces vemos todo tipo de milagros modernos atribuidos a los «computadores», sin la más mínima apreciación de que los computadores sólo trabajan eficazmente si son programados para utilizar sofisticados «algoritmos» -procedimientos para resolver problemas- y que la base de todos los algoritmos está en las matemáticas?
Las matemáticas más visibles son las relacionadas con la aritmética, pero la invención de las calculadoras de bolsillo, las cajas registradoras que suman cuánto hay que pagar, y los programas de pago de impuestos que nos hacen las cuentas, están ocultando cada vez más a la aritmética entre bastidores. Pese a todo, la mayoría de nosotros somos conscientes de que la aritmética está allí. Dependemos por completo de los números, ya sea para seguir las obligaciones legales, recaudar impuestos, comunicar instantáneamente con el otro lado del planeta, explorar la superficie de Marte o evaluar el último medicamento maravilloso. Todas estas cosas se remontan a la antigua Babilonia y a los escribas y maestros que descubrieron maneras eficaces de registrar números y calcular con ellos. Aquéllos utilizaban sus habilidades aritméticas con dos fines principales: asuntos cotidianos y mundanos de los seres humanos ordinarios, tales como la contabilidad y la medida de tierras, y actividades intelectuales como predecir eclipses o registrar los movimientos del planeta Júpiter a través del cielo nocturno.
La evolución de la cultura y la de las matemáticas han ido de la mano durante los últimos cuatro milenios.
Hoy hacemos lo mismo. Utilizamos matemáticas sencillas, poco más que aritmética, para centenares de tareas minúsculas: cuánto tratamiento antiparásitos poner en el estanque de un jardín, cuántos rollos de papel de pared tenemos que comprar para empapelar el dormitorio o si ahorraremos dinero yendo un poco más lejos en busca de gasolina más barata. Y nuestra cultura utiliza matemáticas sofisticadas para la ciencia, la tecnología y, cada vez más, también para el comercio. La invención de la notación numeral y la aritmética figuran, junto a las del lenguaje y la escritura, como unas de las innovaciones que nos transformaron de monos adiestrables en seres humanos genuinos.
Para qué nos sirven los númerosLa mayoría de los modernos automóviles de gama alta están ahora equipados con navegación por satélite, y sistemas individuales de navegación por satélite pueden comprarse a un precio relativamente barato. Un pequeño dispositivo, acoplado a nuestro automóvil, nos dice dónde estamos exactamente en cualquier momento y nos presenta un mapa -a menudo con espectaculares gráficos en colores y con perspectivas- que muestra las carreteras vecinas. Un sistema de voz puede incluso decirnos por dónde ir para llegar a un destino especificado. Si esto suena como algo sacado de la ciencia ficción, lo es. Un componente esencial, que no es parte de la pequeña caja acoplada al automóvil, es el sistema de posicionamiento global (GPS), que comprende 24 satélites que orbitan alrededor de la Tierra (a veces más, cuando se lanzan los satélites de reemplazo). Estos satélites envían señales, y estas señales pueden utilizarse para deducir la posición del automóvil con un margen de unos pocos metros.
Las matemáticas entran en juego en muchos aspectos de la red GPS, pero aquí mencionamos sólo uno: cómo se utilizan las señales para calcular la posición del automóvil.
Las señales de radio viajan a la velocidad de la luz, que es aproximadamente 300.000 kilómetros por segundo. Un computador a bordo del automóvil -un chip en la caja que compramos- puede calcular la distancia del automóvil a cualquier satélite dado si conoce cuánto ha tardado la señal en viajar desde el satélite al automóvil.
Este tiempo es normalmente del orden de una décima de segundo, pero ahora es fácil medirlo de forma precisa. El truco consiste en estructurar la señal de modo que contenga información sobre el tiempo.
En efecto, el satélite y el receptor en el automóvil cantan una misma canción, y comparan su compás. Las «notas» procedentes del satélite irán ligeramente retrasadas respecto a las producidas en el automóvil. En esta analogía, las letras podrían ir así:
Automóvil… una paloma, trátala con cariño que es...
Satélite…si a tu ventana llega una paloma...
Aquí la canción del satélite va unas tres palabras detrás de la misma canción en el automóvil. Satélite y receptor deben generar la misma «canción», y «notas» sucesivas deben ser identificables, de modo que la diferencia de tiempo es fácil de observar.
Por supuesto, el sistema de navegación por satélite no utiliza realmente una canción. La señal consiste en una serie de pulsos breves cuya duración está determinada por un «código pseudo- aleatorio». Éste consiste en una secuencia de números que parece aleatoria pero que realmente está basada en una regla matemática. Tanto el satélite como el receptor conocen la regla, de modo que pueden generar la misma secuencia de pulsos.
Capítulo 2
La lógica de la forma
Los primeros pasos en geometría
En matemáticas hay dos tipos principales de razonamiento: el simbólico y el visual. El razonamiento simbólico tuvo su origen en la notación numeral, y pronto veremos cómo llevó a la invención del álgebra, en cuyos símbolos pueden representarse números abstractos («la incógnita») antes que concretos («7»).
A partir de la Edad Media las matemáticas se basaron cada vez más en el uso de símbolos, como confirmará una ojeada a cualquier libro de texto moderno de matemáticas.
Los comienzos de la geometría
Además de símbolos, los matemáticos usan diagramas, lo que abre varios tipos de razonamiento visual. Las imágenes son menos formales que los símbolos, y por esta razón su uso ha sido mal visto a veces. Hay una sensación ampliamente extendida de que una imagen es de algún modo menos rigurosa, lógicamente hablando, que un cálculo simbólico. Es cierto que las imágenes dejan más lugar para diferencias de interpretación que los símbolos. Además, las imágenes pueden contener hipótesis ocultas: no podemos dibujar un triángulo «general»; cualquier triángulo que dibujemos tendrá un tamaño y una forma particulares, que quizá no sean representativos de un triángulo arbitrario. Sin embargo, la intuición visual es una característica tan poderosa del cerebro humano que las imágenes desempeñan un papel destacado en matemáticas. De hecho, después del número, introducen un segundo concepto importante en la disciplina: la forma.
La fascinación de los matemáticos por las formas se remonta a muy atrás. Existen diagramas en las tablillas de arcilla babilónicas. Por ejemplo, la tablilla catalogada como YBC 7289 muestra un cuadrado y dos diagonales. Los lados del cuadrado están marcados con numerales cuneiformes para 30.
Sobre una diagonal está marcado 1;24,51,10 y debajo de ella 42;25,35, que es su producto por 30 y, por lo tanto, la longitud de dicha diagonal. De modo que 1; 24,5 1,10 es la longitud de la diagonal de un cuadrado más pequeño, con lados unidad. El teorema de Pitágoras nos dice que esta diagonal es la raíz cuadrada de 2, que escribimos √2. La aproximación 1; 24, 51, 10 para √2 es muy buena.
Tablilla YBC 7269 y sus numerales cuneiformes
El primer uso sistemático de diagramas, junto con un uso limitado de símbolos y una fuerte dosis de lógica, se da en los escritos geométricos de Euclides de Alejandría. La obra de Euclides seguía una tradición que se remontaba al menos al culto pitagórico, que floreció alrededor del 500 a.C., pero Euclides insistía en que cualquier enunciado matemático debe tener una demostración lógica antes de que pueda asumirse como verdadero. Por ello los escritos de Euclides combinan dos innovaciones distintas: el uso de figuras y la estructura lógica de las demostraciones. Durante siglos la palabra «geometría» estuvo estrechamente asociada con ambas.
En este capítulo vamos a seguir la historia de la geometría desde Pitágoras, pasando por Euclides y su precursor Eudoxo, hasta el periodo final de la Grecia clásica y los sucesores de Euclides, Arquímedes y Apolonio. Estos primeros geómetras prepararon el camino para todo el trabajo posterior sobre pensamiento visual en matemáticas. También fijaron cánones de demostración lógica que no fueron superados durante milenios.
§. Pitágoras
Hoy casi damos por supuesto que las matemáticas ofrecen una clave para las leyes subyacentes en la Naturaleza. La primera reflexión sistemática en esta línea de la que hay noticia procede de los pitagóricos, un culto más bien místico que data aproximadamente del 600 a.C. al 400 a.C. Su fundador, Pitágoras, nació en Samos alrededor del 569 a.C. Cuándo y dónde murió es un misterio, pero en el 460 a.C. el culto que él fundó fue atacado y destruido, y sus lugares de reunión asaltados y quemados. En uno de ellos, la casa de Milón de Crotona, fueron masacrados más de cincuenta pitagóricos.
Muchos supervivientes huyeron a Tebas en el Alto Egipto. Posiblemente Pitágoras era uno de ellos, pero incluso esto es una conjetura pues, leyendas aparte, no sabemos prácticamente nada sobre Pitágoras. Su nombre es bien conocido, básicamente debido a su famoso teorema sobre triángulos rectángulos, pero ni siquiera sabemos si Pitágoras lo demostró.
Sabemos mucho más sobre la filosofía y las creencias de los pitagóricos. Entendían que las matemáticas tratan con conceptos abstractos, no con la realidad. Sin embargo, creían también que estas abstracciones estaban encarnadas de algún modo en conceptos «ideales», que existían en algún reino extraño de la imaginación, de modo que, por ejemplo, un círculo dibujado en la arena con un palo es un intento fallido de un círculo ideal, perfectamente redondo e infinitamente fino.
El aspecto más influyente de la filosofía del culto pitagórico es la creencia en que el universo se funda en los números.
Expresaban esta creencia en simbolismo mitológico y la apoyaban con observaciones empíricas. Por el lado místico, consideraban que el número I es la fuente primaria de todas las cosas en el universo.
La armonía del mundoEl principal apoyo empírico para el concepto pitagórico del universo numérico procedía de la música, en donde habían advertido algunas notables relaciones entre sonidos armónicos y razones numéricas simples. Utilizando experimentos sencillos, ellos descubrieron que si una cuerda pulsada produce una nota de un tono particular, entonces una cuerda de longitud mitad produce una nota extraordinariamente armoniosa, ahora llamada la octava. Una cuerda de una longitud dos tercios produce la siguiente nota más armoniosa, y una de tres cuartos de longitud también produce una nota armoniosa.
Hoy estos aspectos numéricos de la música se remiten a la física de las cuerdas vibrantes, que se mueven en pautas ondulatorias. El número de ondas que pueden encajar en una longitud dada de cuerda es un número entero, y estos números enteros determinan las razones numéricas simples. Si los números no forman una razón simple, entonces las ilotas correspondientes interfieren, produciendo «batidos» discordantes que son desagradables al oído. La historia completa es más compleja, e incluye aquello a lo que el cerebro está acostumbrado, pero hay un argumento físico preciso tras el descubrimiento pitagórico.
Los números 2 y 3 simbolizaban los principios femenino y masculino. El número 4 simbolizaba la armonía, y también los cuatro elementos (Tierra, Aire, Fuego, Agua) a partir de los cuales está hecho todo. Los pitagóricos creían que el número 10 tenía profunda trascendencia mística, porque 10 = 1 + 2 + 3 + 4, que combina la unidad primaria, el principio femenino, el principio masculino y los cuatro elementos. Además, estos números formaban un triángulo, y la totalidad de la geometría griega se basaba en propiedades de los triángulos.
Los pitagóricos reconocían la existencia de nueve cuerpos celestes: el Sol, la Luna, Mercurio, Venus, la Tierra, Marte, Júpiter y Saturno, más el Fuego Central, que era diferente del Sol. Tan importante era el número 10 en su visión de la cosmología que creían que había un décimo cuerpo, la Anti-Tierra, perpetuamente oculto a nosotros tras el Sol.
El número diez forma un triángulo
Como hemos visto, los números 1, 2, 3,..., llevaban de manera natural a un segundo tipo de número, las «fracciones», que los matemáticos llaman números racionales. Un número racional es una fracción a/b donde a, b son números naturales (y b es distinto de 0; de lo contrario, la fracción no tiene sentido). Las fracciones subdividen a los números naturales en partes arbitrariamente finas, de modo que en particular la longitud de una línea en una figura geométrica puede aproximarse tanto como queramos por un número racional. Parece natural imaginar que con suficientes subdivisiones se llegaría al número exactamente; si fuera así, todas las longitudes serían racionales.
Si esto fuera cierto, haría la geometría mucho más sencilla, porque dos longitudes cualesquiera serían múltiplos enteros de una longitud común (quizá pequeña), y por ello podrían obtenerse empalmando montones de copias de esta longitud común. Esto quizá no suena muy importante, pero con ello toda la teoría de longitudes, áreas y especialmente figuras «semejantes» -figuras con la misma forma pero diferentes tamaños- sería mucho más sencilla. Todo podría demostrarse utilizando diagramas formados a partir de muchos montones de copias de una forma básica.
Por desgracia, este sueño no puede realizarse. Según la leyenda, uno de los seguidores de Pitágoras, Hipaso de Metaponto, descubrió que este enunciado es falso. En concreto, demostró que la diagonal de un cuadrado unidad es irracional: no es una fracción exacta. Se dice (con base dudosa, pero es una buena historia) que cometió el error de anunciar este hecho cuando los pitagóricos estaban cruzando el Mediterráneo en barco, y sus compañeros de culto quedaron tan irritados que le arrojaron por la borda y se ahogó.
Lo más probable es que simplemente fuera expulsado del culto. Cualquiera que fuera su castigo, parece que a los pitagóricos no les gustó su descubrimiento.
La interpretación moderna de la observación de Hipaso es que √2 es irracional. Para los pitagóricos, este hecho brutal era un duro golpe para su creencia casi religiosa en que el universo estaba enraizado en los números (por lo que ellos entendían los números naturales). Las fracciones -razones de números enteros- encajaban muy bien en esta visión del mundo, pero los números que demostrablemente no eran fracciones no lo hacían. Y por ello, ya fuera ahogado o expulsado, el pobre Hipaso se convirtió en una de las primeras víctimas de la irracionalidad, por así decir, de las creencias religiosas.
Estas dos formas son semejantes
§. Irracionales
Finalmente los griegos encontraron una manera de manejar los irracionales. Funciona porque cualquier número irracional puede ser aproximado por un número racional. Cuanto mejor es la aproximación, más complicado se hace dicho racional, y siempre hay algún error. Pero haciendo el error cada vez menor, hay una posibilidad de aproximar las propiedades de los irracionales explotando propiedades análogas a las de los números racionales que los aproximan. El problema está en establecer esta idea de una forma que sea compatible con la aproximación griega a la geometría y la demostración. Esto resulta ser factible, pero complicado.
¿Es la razón a:b igual a la razón c:d?
La teoría griega de los irracionales fue concebida por Eudoxo alrededor del 370 a.C. Su idea consiste en representar cualquier magnitud, racional o irracional, como la razón de dos longitudes; es decir, en términos de un par de longitudes. Así, dos-tercios se representa por dos líneas, una de longitud dos y otra de longitud tres (una razón 2:3). Análogamente, √2 se representa por el par formado por la diagonal de un cuadrado unidad y su lado (una razón √2:1). Nótese que ambos pares de líneas pueden construirse geométricamente.
El punto clave consiste en definir cuándo dos de estas razones son iguales.
La teoría griega de los irracionales fue concebida por Eudoxo alrededor del 370 a.C.
¿Cuándo es a:b = c:d? A falta de un sistema de números apropiado, los griegos no podían hacerlo dividiendo una longitud por otra y comparando a + b con c + d. En su lugar, Eudoxo encontró un engorroso pero preciso método de comparación que podía realizarse dentro de las convenciones de la geometría griega. La idea consiste en tratar de comparar a y c formando múltiplos enteros ma y nc. Esto puede hacerse empalmando m copias de a extremo con extremo, y lo mismo con n copias de b. Utilizamos los mismos dos múltiplos m y n para comparar mb y nd. Si las razones a:b y c:d no son iguales, dice Eudoxo, entonces podemos encontrar m y n para exagerar la diferencia a tal extremo que ma > nc pero mb < nd. De hecho, podemos definir la igualdad de razones de esta manera.
Esta definición requiere acostumbrarse. Está hecha muy cuidadosamente a medida de las limitadas operaciones permitidas en la geometría griega.
Sin embargo funciona; permitió a los geómetras griegos tomar teoremas que podían ser demostrados fácilmente para razones racionales y extenderlos a razones irracionales.
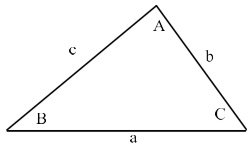
Teorema de Pitágoras: si el triángulo tiene un ángulo recto, entonces el área del cuadrado más grande, A, es la misma que la de los otros dos, B y C. juntos
A menudo utilizaban un método llamado «exhaustion», que les permitía demostrar teoremas que nosotros demostraríamos actualmente utilizando la idea de «límite» y el cálculo infinitesimal. De esta manera demostraron que el área de un círculo es proporcional al cuadrado de su radio. La demostración parte de un hecho más simple, que se encuentra en Euclides: las áreas de dos polígonos semejantes están en la misma proporción que los cuadrados de los lados correspondientes.
El círculo plantea nuevos problemas porque no es un polígono. Por ello, los griegos consideraron dos secuencias de polígonos: una dentro del círculo, y la otra fuera. Ambas secuencias se acercan cada vez más al círculo, y la definición de Eudoxo implica que la razón de las áreas de los polígonos aproximantes es la misma que la razón de las áreas de los círculos.
§. Euclides
El geómetra griego más conocido, aunque probablemente no el matemático más original, es Euclides de Alejandría. Euclides fue un gran sintetizador, y su texto de geometría, los Elementos, se convirtió en un éxito de ventas perenne. Euclides escribió al menos diez textos sobre matemáticas, pero sólo cinco de ellos sobreviven; todos a través de copias posteriores, y diez sólo en parte. No tenemos documentos originales de la antigua Grecia. Los cinco supervivientes euclidianos son los Elementos, la División de figuras, los Datos, los Fenómenos y la Óptica.
Los Elementos es la obra maestra geométrica de Euclides, y ofrece un tratamiento definitivo de la geometría de dos dimensiones (el plano) y tres dimensiones (el espacio). La División de figuras y los Datos contienen varios complementos y comentarios sobre geometría. Los Fenómenos están dirigidos a los astrónomos, y tratan de la «geometría esférica», la geometría de figuras dibujadas en la superficie de una esfera. La Óptica es también geométrica, y podría considerarse mejor como una incipiente investigación de la geometría de la perspectiva: cómo transforma el ojo humano una escena tridimensional en una imagen bidimensional.
Quizá la mejor manera de pensar en la obra de Euclides es como un examen de la lógica de las relaciones espaciales. Si una forma tiene ciertas propiedades, éstas pueden implicar lógicamente otras propiedades. Por ejemplo, si un triángulo tiene los tres lados iguales -un «triángulo equilátero»-, entonces los tres ángulos deben ser iguales. Este tipo de enunciado, que lista algunas hipótesis y luego afirma sus consecuencias lógicas, se denomina un «teorema». Este teorema concreto relaciona una propiedad de los lados de un triángulo con una propiedad de sus ángulos. Un ejemplo menos intuitivo y más famoso es el teorema de Pitágoras.
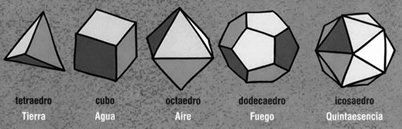
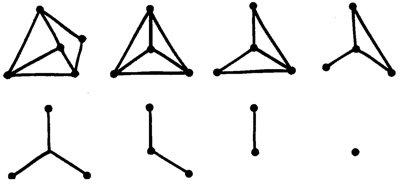
Poliedros regularesUn sólido es regular (o platónico) si está formado por caras idénticas. Los pitagóricos conocían cinco sólidos de este tipo
El tetraedro, formado a partir de cuatro triángulos equiláteros.
El cubo (o hexaedro), formado a partir de seis cuadrados.
El octaedro, formado a partir de ocho triángulos equiláteros.
El dodecaedro, formado a partir de 12 pentágonos regulares.
El icosaedro, formado a partir de 20 triángulos equiláteros.
Los Elementos se dividen en 13 libros, que se siguen unos a otros en una secuencia lógica. Analizan la geometría del plano y algunos aspectos de la geometría del espacio. El punto culminante es la demostración de que hay exactamente cinco sólidos regulares: el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro. Las formas básicas permitidas en geometría plana son líneas rectas y círculos, a veces en combinación; por ejemplo, un triángulo está formado por tres líneas rectas. En geometría espacial encontramos también planos, cilindros y esferas.
Ellos los asociaron con los cuatro «elementos» de la antigüedad -tierra, aire, fuego y agua- y con un «quinto elemento», la quintaesencia.
Para los matemáticos modernos lo más interesante en la geometría de Euclides no es su contenido, sino su estructura lógica. A diferencia de sus predecesores, Euclides no se limita a afirmar que un teorema es verdadero.
El ofrece una demostración.
¿Qué es una demostración? Es una especie de historia matemática, en la que cada paso es una consecuencia lógica de algunos de los pasos previos. Cada enunciado que se afirma tiene que justificarse haciendo referencia a enunciados previos y demostrando que es una consecuencia lógica de ellos. Euclides comprendió que este proceso no puede llevarse hacia atrás indefinidamente: tiene que empezar en alguna parte, y estos enunciados iniciales no pueden ser demostrados, o de lo contrario el proceso de demostración empieza realmente en algún lugar diferente.
Para empezar a rodar, Euclides hizo una lista de varias definiciones: enunciados claros y precisos de lo que significan ciertos términos técnicos, tales como «línea» o «círculo».
Euclides de Alejandría
325 - 265 a. C.Euclides es famoso por su libro de geometría, Los Elementos, que fue un importante, de hecho el principal, texto de enseñanza de la geometría durante dos milenios.
Sabemos muy poco de la vida de Euclides. Enseñó en Alejandría. Alrededor del 450 a.C. el filósofo griego Proclo escribió:
«Euclides... vivió en la época del primer Ptolomeo, pues Arquímedes, que siguió de cerca al primer Ptolomeo, menciona a Euclides... Ptolomeo preguntó en cierta ocasión [a Euclides] si había un camino más corto para estudiar geometría que los Elementos, a lo que éste contestó que no había ningún camino real a la geometría. Por lo tanto era más Joven que el circulo de Platón, pero más viejo que Eratóstenes y Arquímedes... era un platónico, pues simpatizaba con su filosofía, e hizo de la construcción de las denominadas figuras platónicas ¡sólidos regulares] el objetivo de los Elementos».
Una definición típica es «un ángulo obtuso es un ángulo mayor que un ángulo recto». La definición le proporcionaba la terminología que necesitaba para enunciar sus hipótesis indemostradas, que clasificaba en dos tipos: nociones comunes y postulados. Una típica noción común es «cosas que son iguales a la misma cosa son iguales entre sí». Un postulado típico es «todos los ángulos rectos son iguales entre sí».
Hoy día agrupamos ambos tipos y les llamamos axiomas. Los axiomas de un sistema matemático son las hipótesis subyacentes que hacemos sobre el mismo. Consideramos los axiomas como las reglas del juego, e insistimos en que se juegue de acuerdo con las reglas. Ya no preguntamos si las reglas son «verdaderas», ya no pensamos que sólo pueda jugarse a un juego. Alguien que quiera jugar a este juego concreto debe aceptar las reglas; si no lo hace, es libre de jugar a un juego diferente, pero no será el juego determinado por estas reglas concretas.
En los días de Euclides, y durante los casi los 2.000 años siguientes, los matemáticos no pensaban así ni mucho menos. En general veían los axiomas como «verdades autoevidentes», tan obvias que nadie podía cuestionarlas seriamente. Por ello Euclides hizo todo lo que pudo para hacer todos sus axiomas obvios... y estuvo muy cerca de conseguirlo. Pero un axioma, el «axioma de las paralelas», es inusualmente complicado y poco intuitivo, y muchos trataron de deducirlo de hipótesis más sencillas. Más tarde veremos a qué notables descubrimientos llevó esto.
Paso a paso, a partir de estos comienzos simples, los Elementos continúan ofreciendo demostraciones de teoremas geométricos cada vez más sofisticados. Por ejemplo, la Proposición 5 del Libro I demuestra que los ángulos en la base de un triángulo isósceles (un triángulo con dos lados iguales) son iguales.
Este teorema fue conocido por generaciones de escolares Victorianos como el «pons asinorum» o puente para asnos: el diagrama se parece a un puente, y era el primer obstáculo serio para los estudiantes que trataban de aprender la asignatura de memoria en lugar de entenderla. La Proposición 32 del Libro I demuestra que los ángulos de un triángulo suman 180º. La Proposición 47 del Libro I es el Teorema de Pitágoras.
Euclides deducía cada teorema de teoremas previos y varios axiomas. Construyó una torre lógica, que subía cada vez más hacia el cielo, con los axiomas como cimientos y la deducción lógica como el mortero que unía los ladrillos.
Hoy nos sentimos menos satisfechos con la lógica de Euclides porque tiene muchas lagunas. Euclides da muchas cosas por supuestas; su lista de axiomas está lejos de ser completa. Por ejemplo, puede parecer obvio que si una recta pasa por un punto dentro de un círculo, entonces debe cortar al círculo en alguna parte, al menos si se prolonga lo suficiente. Ciertamente parece obvio si se dibuja una imagen, pero hay ejemplos que demuestran que no se sigue de los axiomas de Euclides. Euclides lo hizo bastante bien, pero supuso que propiedades aparentemente obvias de los diagramas no necesitaban una demostración ni una base axiomática.
Esta omisión es más seria de lo que podría parecer. Hay algunos ejemplos famosos de razonamiento falaz que surgen de errores sutiles en las figuras.
Uno de ellos «demuestra» que todo triángulo tiene dos lados iguales.
§. ¿Jerigonza?
El Libro V de los Elementos va en una dirección muy diferente, y más bien oscura, de la de los Libros I-IY No parece geometría convencional. De hecho, a primera vista se lee básicamente como una jerigonza. ¿Qué tenemos que hacer, por ejemplo, con la Proposición I del Libro V? Dice: si ciertas magnitudes son equimúltiplos de otras magnitudes, entonces si cualquier múltiplo de una de las magnitudes lo es una de las otras, dicho múltiplo también lo será de todas.
El lenguaje (que he simplificado un poco) no ayuda, pero la demostración aclara lo que Euclides pretendía. El matemático inglés del siglo XIX Augustus de Morgan explicaba la idea en lenguaje simple en su libro de texto de geometría: «Diez pies y diez pulgadas son diez veces tanto como un pie y una pulgada».
¿Qué quiere Euclides aquí? ¿Son trivialidades vestidas como teoremas?
“¿Son trivialidades vestidas como teoremas? En absoluto.”
¿Son sinsentidos místicos? En absoluto. Este material puede parecer oscuro, pero nos lleva a la parte más profunda de los Elementos: las técnicas de Eudoxo para tratar razones irracionales. Hoy día los matemáticos prefieren trabajar con números, y puesto que éstos son más familiares, interpretaré a menudo las ideas griegas en dicho lenguaje.
Euclides no podía evitar enfrentarse a las dificultades de los números irracionales, porque el clímax de los Elementos -y para muchos su principal objetivo- era la demostración de que existen exactamente cinco sólidos regulares: el tetraedro, el cubo (o hexaedro), el octaedro, el dodecaedro y el icosaedro. Euclides demostró dos cosas: no hay otros sólidos regulares, y estos cinco existen realmente, pueden construirse geométricamente y sus caras encajan perfectamente, sin el más mínimo error.
Dos de los sólidos regulares, el dodecaedro y el icosaedro, incluyen al pentágono regular: el dodecaedro tiene caras pentagonales, y las cinco caras del icosaedro que rodean a cualquier vértice determinan un pentágono.
Los pentágonos regulares están directamente relacionados con lo que Euclides llamaba «razón extrema y media».
La razón entre las diagonales y los lados es áurea
Sobre una línea recta AB, se construye un punto C de modo que la razón AB : AC es igual a AC : BC. Es decir, la línea entera guarda la misma proporción con el segmento más grande que el segmento más grande guarda con el más pequeño. Si dibujamos un pentágono e inscribimos una estrella de cinco puntas, los lados de la estrella están relacionados con los lados del pentágono por esta razón particular.
Hoy día llamamos a esta razón el número áureo. Es igual a 1 + (√5/2), y este número es irracional. Su valor numérico es aproximadamente 1,618. Los griegos pudieron demostrar que era irracional explotando la geometría del pentágono. Por ello Euclides y sus predecesores eran conscientes de que, para tener una comprensión adecuada del dodecaedro y el icosaedro, debían entender los irracionales.
Esta es, al menos, la visión convencional de los Elementos.
David Fowler argumenta en su libro Las matemáticas de la Academia de Platón que hay una visión alternativa: en esencia, la inversa. Tal vez el objetivo principal de Euclides era la teoría de los irracionales, y los sólidos regulares eran tan sólo una aplicación.
Razón extrema y media (ahora llamada razón áurea). La razón entre la línea superior y la del centro es igual a la razón entre la línea central y la inferior
La evidencia puede interpretarse de una forma u otra, pero una característica de los elementos encaja mejor en esta teoría alternativa. Buena parte del material sobre «teoría de números» no es necesario para la clasificación de los sólidos regulares; entonces, ¿por qué Euclides incluyó este material?
Pi con enorme precisiónEl valor de π ha sido calculado ahora con varios miles de millones de cifras decimales, utilizando métodos más sofisticados. Tales cálculos son de interés por sus métodos, para poner a prueba sistemas de computación, y por pura curiosidad, pero el resultado mismo tiene poca importancia. Las aplicaciones prácticas de n no requieren, en general, más de cinco o seis cifras. El récord actual es 51.539.600.000 cifras decimales, calculadas por Yasumasa Kanada y Daisuke Takahashi. Ellos realizaron dos cálculos independientes utilizando dos métodos diferentes, para obtener 51.539.607.552 cifras de n. Los resultados coincidían en los primeros 51.539.607.510 cifras, por lo que redujeron la proclamación de su récord a 51.539.600.000 cifras exactas.
Sin embargo, el mismo material está estrechamente relacionado con los números irracionales, lo que podría explicar por qué fue incluido.
§. Arquímedes
El más grande de los matemáticos antiguos fue Arquímedes. Hizo importantes contribuciones a la geometría, estuvo en la vanguardia de las aplicaciones de las matemáticas al mundo natural y fue un ingeniero consumado.
Arquímedes de Siracusa
287 - 212 a.C.Arquímedes nació en Siracusa, en la Magna Grecia (la actual Sicilia), hijo del astrónomo Fidias. Visitó Egipto, donde supuestamente inventó el tornillo de Arquímedes, que hasta hace muy poco era ampliamente utilizado para elevar agua del Nilo para irrigación. Es probable que visitara a Euclides en Alejandría, y seguro que mantuvo correspondencia con matemáticos alejandrinos.
Sus habilidades matemáticas fueron insuperables y de amplio alcance. Les dio un uso práctico y construyó enormes máquinas de guerra basadas en su ley de la palanca, capaces de lanzar rocas enormes contra el enemigo. Sus máquinas fueron utilizadas con gran efecto en el sitio romano de Alejandría en el 212 a.C. Utilizó incluso la geometría de la reflexión óptica para concentrar los rayos solares sobre una flota romana invasora e incendiar las naves.
Sus libros conservados (sólo en copias posteriores) son Sobre equilibrios en el plano, la Cuadratura de la parábola, Sobre la esfera y el cilindro, Sobre los cuerpos flotantes, Medida del círculo y El arenario, junto con El método, descubierto en 1906 por Johan Heiberg.
Pero para los matemáticos, Arquímedes será siempre recordado por su obra sobre círculos, esferas y cilindros, que ahora asociamos con el número π («pi»), que es aproximadamente 3,14159. Por supuesto, los griegos no trabajaban directamente con n: ellos lo veían geométricamente como la razón entre la circunferencia de un círculo y su diámetro.
Culturas anteriores habían advertido que la circunferencia de un círculo es siempre el mismo múltiplo de su diámetro, y sabían que este múltiplo era aproximadamente 3 1/7, quizá un poco mayor. Los babilonios utilizaban 3 ⅛. Pero Arquímedes fue mucho más lejos; sus resultados iban acompañados de demostraciones rigurosas, en el espíritu de Eudoxo. Hasta donde sabían los griegos, la razón entre la circunferencia de un círculo y su diámetro podría ser irracional. Ahora sabemos que realmente es así, pero la demostración tuvo que esperar hasta 1770, cuando Johann Heinrich ideó una. (El valor que se da a veces en la escuela, 3 1/7, es conveniente aunque sólo aproximado.) Sea como fuere, puesto que Arquímedes no pudo demostrar que π es racional, tuvo que suponer que podría no serlo.
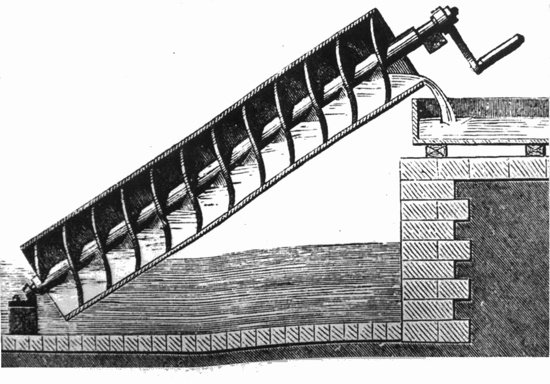
Tornillo de Arquímedes
La geometría griega trabajaba mejor con polígonos: formas hechas de líneas rectas. Pero un círculo es curvo, de modo que Arquímedes se acercó al mismo aproximándolo por polígonos. Para estimar π él comparó la circunferencia de un círculo con los perímetros de dos series de polígonos: una serie situada en el interior del círculo, y la otra a su alrededor.
Los perímetros de los polígonos dentro del círculo deben ser más cortos que el círculo, mientras que los de fuera del círculo deben ser más largos que el círculo.
El palimpsesto de Arquímedes
Para hacer el cálculo más fácil, Arquímedes construía sus polígonos bisecando repetidamente los lados de un hexágono regular (un polígono de seis lados) para obtener polígonos regulares con 12 lados, 24, 48 y así sucesivamente. Se detuvo en 96. Sus cálculos demostraban que
3 10/71 < π < 3 1/7
es decir, π está en algún lugar entre 3,1408 y 3,1429 en notación decimal actual.
La obra de Arquímedes sobre la esfera es de especial interés, porque no sólo conocemos su demostración rigurosa sino la forma en que la encontró -que decididamente no era rigurosa-. La demostración se da en su libro Sobre la esfera y el cilindro.
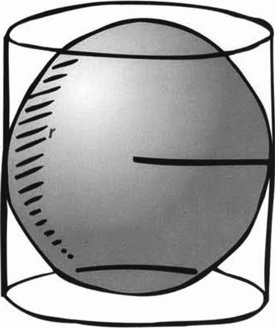
Una esfera y su cilindro circunscrito
Él demuestra que el volumen de una esfera es dos-tercios del de un cilindro circunscrito, y que las áreas de aquellas partes de la esfera y del cilindro que yacen entre dos planos paralelos cualesquiera son iguales. En lenguaje moderno, Arquímedes demostró que el volumen de una esfera es 4πr3/3, donde r es el radio, y el área de su superficie es 4πr2 Estos hechos básicos se siguen utilizando hoy.
La demostración hace un uso consumado de la exhaustion. Este método tiene una limitación importante: hay que saber cuál es la respuesta antes de tener muchas posibilidades de demostrarla. Durante siglos los estudiosos no tenían ninguna idea de cómo Arquímedes conjeturó la respuesta.
Pero en 1906 el estudioso danés Heiberg estaba estudiando un pergamino del siglo XIII en el que había escritas unas oraciones. Él advirtió líneas tenues de una inscripción anterior que había sido borrada para dejar lugar para las oraciones. Descubrió que el documento original era una copia de varias obras de Arquímedes, algunas de ellas previamente desconocidas.
(Y lo que es más sorprendente, ahora se sabe que el mismo manuscrito contiene fragmentos de obras perdidas de otros dos autores antiguos.)
Una obra de Arquímedes, el Método de los teoremas mecánicos, explica cómo conjeturar el volumen de una esfera. La idea consiste en hacer rebanadas infinitamente delgadas de la esfera y colocar las rebanadas en un plato de una balanza; en el otro plato se cuelgan rebanadas similares de un cilindro y un cono, cuyos volúmenes Arquímedes ya conocía. La ley de la palanca da el valor buscado para el volumen.
El pergamino fue vendido por dos millones de dólares en 1998 a un comprador privado.
§. Problemas para los griegos
La geometría griega tenía limitaciones, algunas de las cuales superó introduciendo nuevos métodos y conceptos. Euclides sólo admitía las construcciones geométricas que podían realizarse usando una vara no marcada («regla») y un par de compases (en lo sucesivo «compás»; la palabra «par» es técnicamente necesaria, por la misma razón por la que cortamos papel con un par de tijeras, pero no seamos pedantes). A veces se dice que él hizo de esto un requisito, pero no está explicitado como una regla sino que está implícito en sus construcciones. Con instrumentos extra -idealizados de la misma manera que la curva trazada por un compás está idealizada como un círculo perfecto- son posibles nuevas construcciones.
Por ejemplo, Arquímedes sabía que se puede trisecar un ángulo utilizando una vara recta en la que hay dos marcas fijas. Los griegos llamaban a tales procesos «construcciones neusis».
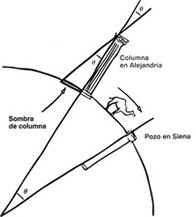
Para qué les servía la geometríaAlrededor del 250 a.C. Eratóstenes de Cirene utilizó la geometría para estimar el tamaño de la Tierra.
Él advirtió que a mediodía en el solsticio de verano, el Sol estaba casi exactamente encima de Siena (actualmente Asuán), porque se reflejaba en el fondo de un pozo vertical.
El mismo día del año, la sombra de una alta columna indicaba que la posición del Sol en Alejandría estaba a un cincuentavo de un círculo completo (unos 7,2º) respecto a la vertical. Los griegos sabían que la Tierra era esférica, y Alejandría estaba casi en dirección norte desde Siena, de modo que la geometría de una sección circular de la esfera implicaba que la distancia de Alejandría a Siena es la cincuentava parte de la circunferencia de la Tierra.
Cómo midió Eratóstenes el tamaño de la TierraEratóstenes sabía que una caravana de camellos tardaba 50 días en ir de Alejandría a Siena, y recorría una distancia de 100 estadios cada día; luego la distancia de Alejandría a Siena son 5.000 estadios, lo que hace la circunferencia de la Tierra de 250.000 estadios. Por desgracia no sabemos con seguridad qué longitud tenía un estadio, pero se estima en 157 metros, lo que lleva a una circunferencia de 39.250 km. La cifra moderna es 39.840 km.
Ahora sabemos (como los griegos debieron haber sospechado) que una trisección exacta del ángulo con regla y compás es imposible, de modo que la contribución de Arquímedes se extiende a lo que realmente es posible. Otros dos problemas famosos de la época son la duplicación del cubo (construir un cubo cuyo volumen sea el doble del de un cubo dado) y la cuadratura del círculo (construir un cuadrado con la misma área de un círculo dado).
Secciones cónicas
Se sabe también que ambos son imposibles utilizando regla y compás.
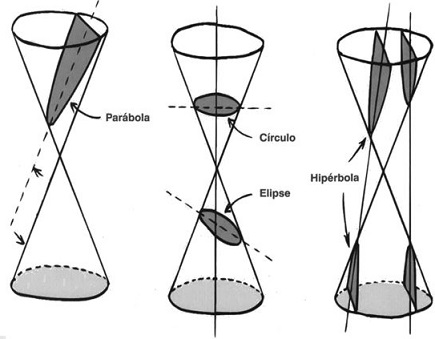
Una ampliación trascendental de las operaciones permitidas en geometría, que dio fruto en el trabajo árabe sobre la ecuación cúbica alrededor del año 800 y tuvo aplicaciones importantes en mecánica y astronomía, fue la introducción de una nueva clase de curvas, las secciones cónicas.
Estas curvas, que son extraordinariamente importantes en la historia de las matemáticas, se obtienen seccionando un cono doble con un plano. Hoy abreviamos el nombre en cónicas. Se dan en tres tipos principales:
- La elipse, una curva ovalada cerrada que se obtiene cuando el plano corta sólo a una mitad del cono. Los círculos son elipses especiales.
- La hipérbola, una curva con dos ramas infinitas, que se obtiene cuando el plano corta las dos mitades del cono.
- La parábola, una curva transicional «entre» elipses e hipérbolas, en el sentido en que es paralela a una recta que pasa por el vértice del cono y yace en el cono.
Una parábola sólo tiene una rama, pero se extiende hasta el infinito.
Las secciones cónicas fueron estudiadas con detalle por Apolonio de Perga, quien viajó desde Perga, en Asia Menor, a Alejandría para estudiar con Euclides. Su obra maestra, las Secciones cónicas de aproximadamente el 230 a.C., contiene 487 teoremas. Euclides y Arquímedes habían estudiado algunas propiedades de los conos, pero se necesitaría todo un libro para resumir los teoremas de Apolonio. Una idea importante merece mención aquí. Es la noción de los focos de una elipse (o de una hipérbola). Los focos son dos puntos especiales asociados con estos dos tipos de cónica. Entre sus principales propiedades distinguimos una: la suma de las distancias de un punto cualquiera de la elipse a sus dos focos es constante (igual al diámetro mayor de la elipse). Los focos de una hipérbola tienen una propiedad similar, pero ahora tomamos la diferencia de las dos longitudes.
“Los griegos sabían cómo trisecar ángulos y cómo duplicar el cubo utilizando cónicas... también podían cuadrar el círculo.”
Los griegos sabían cómo trisecar ángulos y cómo duplicar el cubo utilizando cónicas. Con la ayuda de otra; curvas especiales, especialmente la cuadratriz, también podían cuadrar el círculo.
Las matemáticas griegas aportaron dos ideas cruciales al desarrollo humano. La más obvia fue una comprensión sistemática de la geometría. Utilizando la geometría como una herramienta, los griegos entendieron el tamaño y la forma de nuestro planeta, su relación con el Sol y la Luna, incluso los movimientos complicados del resto del Sistema Solar. Utilizaron la geometría para excavar largos túneles partiendo de ambos extremos para encontrarse en el centro, lo que reducía el tiempo de construcción a la mitad. Construían máquinas gigantescas y poderosas, basadas en principios simples como la ley de la palanca, con fines tanto pacíficos como bélicos. Explotaron la geometría en la construcción de buques y en la arquitectura, donde edificios como el Partenón nos muestran que matemáticas y belleza no están tan alejadas. La elegancia visual del Partenón deriva de muchos trucos matemáticos astutos, utilizados por el arquitecto para superar las limitaciones del sistema visual humano y las irregularidades en el propio terreno en el que descansaba el edificio.
La segunda aportación griega fue el uso sistemático de la deducción lógica para asegurar que lo que se estaba afirmando también podía justificarse.
El argumento lógico nadó de su filosofía, pero encontró su forma más desarrollada y explícita en la geometría de Euclides y sus sucesores. Sin sólidos fundamentos lógicos no podrían haber aparecido las matemáticas posteriores.
El nuevo estadio de Wembley. En su construcción se han utilizado principios básicos descubiertos en la Antigua Grecia y desarrollados durante los siglos siguientes por muchas culturas.
Ambas influencias siguen siendo hoy vitales. La ingeniería moderna -la fabricación y el diseño asistido por computador, por ejemplo- descansa firmemente sobre los principios geométricos descubiertos por los griegos. Todo gran edificio que se levanta está diseñado de modo que no se venga abajo; muchos están diseñados para resistir terremotos. Cualquier torre, cualquier puente colgante, cualquier estadio de fútbol es un tributo a los geómetras de la antigua Grecia.
El pensamiento racional, la argumentación lógica, son igualmente vitales. Nuestro mundo es demasiado complejo, y potencialmente demasiado peligroso, para que basemos nuestras decisiones en lo que queremos creer y no en lo que es realmente.
Hiparía de Alejandría
370 - 475Hiparía es la primera mujer matemática de la que hay noticia. Era hija de Teón de Alejandría, también un matemático. Probablemente fue de su padre de quien aprendió las matemáticas. Hacia el año 400 ella se había convertido en la directora de la Escuela Platónica de Alejandría, donde daba clases de filosofía y matemáticas.
No sabemos si Hiparía hizo contribuciones originales a las matemáticas, pero ayudó a Teón a escribir un comentario sobre el Almagesto de Ptolomeo, y quizá también le haya ayudado a preparar una nueva edición de los Elementos en la que se basaron todas las ediciones posteriores. Ella escribió comentarios sobre la Aritmética de Diofanto y las Cónicas de Apolonio.
Entre los estudiantes de Hiparía había varias figuras destacadas en la religión en auge de la cristiandad, entre ellas Silesio de Cirene. Hay registro de algunas de las cartas que éste le escribió, donde alaba sus capacidades. Por desgracia, muchos de los primeros cristianos consideraban que la filosofía y la ciencia de Hiparía estaban enraizadas en el paganismo, lo que llevó a algunos a rechazar su influencia. En el 412, Cirilo, el nuevo patriarca de Alejandría, entró en rivalidad política con Orestes, el prefecto romano. Hiparía era buena amiga de Orestes y sus capacidades como maestra y oradora fueron vistas como una amenaza por los cristianos. Ella se convirtió en un blanco de los disturbios políticos y fue descuartizada por una turba. Una fuente culpa a una secta fundamentalista, los monjes de Nitria, que apoyaban a Cirilo. Otra, culpa a la plebe alejandrina. Una tercera fuente afirma que ella formó parte de una rebelión política, y su muerte era inevitable.
Su muerte fue brutal, desmembrada por una multitud con tejas cortantes (algunos dicen que con conchas de ostras). Su cuerpo mutilado fue entonces quemado. Este castigo puede ser prueba de que Hiparía fue condenada por brujería -la primera bruja importante en ser asesinada por los primeros cristianos- porque el castigo para la brujería prescrito por Constantino II era que «sus carnes sean desgarradas hasta los huesos con ganchos de hierro».
El método científico está construido deliberadamente para superar un deseo humano profundamente asentado que consiste en suponer que lo que queremos que sea cierto -lo que afirmamos «conocer»- es realmente cierto.
"... cualquier estadio de fútbol es mi tributo a los geómetras de la Antigua Grecia."
En ciencia se pone el acento en tratar de demostrar que aquello de lo que uno está profundamente convencido es falso. Las ideas con más probabilidad de ser correctas son las que sobreviven a los intentos rigurosos de refutarlas.
Para qué nos sirve la geometríaLa expresión de Arquímedes para el volumen de una esfera se sigue utilizando hoy. Una aplicación, que requiere conocer π con gran precisión, es la unidad patrón de masa para el conjunto de la ciencia. Durante muchos años, por ejemplo, un metro se definía como la longitud de una barra metálica concreta cuando se medía a una temperatura concreta.
Muchas unidades básicas se definen ahora en términos de cosas tales como cuánto tarda un átomo de un elemento específico en vibrar un enorme número de veces. Pero otras aún se basan en objetos físicos, y la masa es uno de estos casos. Un kilogramo se define actualmente como la masa de un cilindro concreto, hecho de platino e iridio y conservado en París. El cilindro se ha construido con una precisión extraordinariamente alta. La densidad del metal también ha sido medida con mucha precisión. La fórmula es necesaria para calcular el volumen del cilindro, que relaciona densidad con masa.
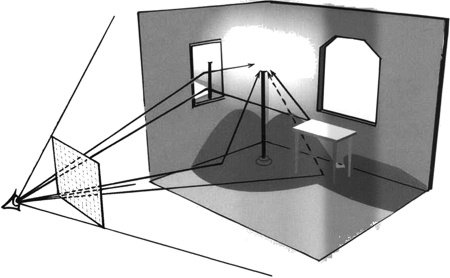
Principio de trazado de rayos y una imagen de muestraOtro uso moderno de la geometría se da en los gráficos por computador. Las películas hacen un amplio uso de imágenes generadas por computador (CGI), y a menudo es necesario generar imágenes que incluyen reflexiones -en un espejo, en un vaso de vino, algo que atrape la luz.
Sin tales reflexiones la imagen no parecería realista. Una manera eficaz de hacerlo consiste en «rastrear rayos». Cuando miramos una escena desde una dirección particular, nuestro ojo detecta un rayo de luz que ha rebotado en los objetos de la escena y entra en el ojo procedente de dicha dirección. Podemos seguir la trayectoria de este rayo trabajando hacia atrás. En cualquier superficie reflectante rebota de modo que el rayo original y el rayo reflejado forman ángulos iguales en la superficie. La traducción de este hecho geométrico en cálculos numéricos permite al computador rastrear el rayo hacia atrás por muchos rebotes que pudieran ser necesarios antes de que choque con algo opaco. (Pueden ser necesarios varios rebotes; por ejemplo, si el vaso de vino está colocado delante de un espejo.)
Capítulo 3
Notaciones y números
El origen de nuestros símbolos numerales
Estamos tan acostumbradosal sistema de números actual, con su uso de los diez dígitos decimales 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 (en los países de Occidente), que puede producir sorpresa el advertir que hay modos completamente diferentes de escribir números. Incluso hoy, diversas culturas -la arábiga, la china, la coreana- usan diferentes símbolos para los diez dígitos, aunque todas ellas combinan estos símbolos para formar números mayores utilizando el mismo método «posicional» (centenas, decenas, unidades).
Pero las diferencias en notación pueden ser más radicales que eso.
No hay nada especial en el número 10. Resulta que es el número de dedos de las manos en el ser humano, que son ideales para contar, pero si en su lugar hubiéramos desarrollado siete dedos, o doce, sistemas muy similares hubiesen funcionado igual de bien, quizá mejor en algunos casos.
§. Numerales romanos
La mayoría de los occidentales conocen al menos un sistema alternativo, los números romanos, en el que, por ejemplo, el año 2007 se escribe MMVII.
La mayoría de nosotros también somos conscientes, al menos si se nos lo recuerda, de que empleamos dos métodos distintos para escribir números que no son enteros: fracciones como 3/4 y decimales 0,75. Pero otra notación numeral, que encontramos en las calculadoras, es la notación «científica» para números muy grandes o muy pequeños, tales como 5 × 109 para cinco mil millones (que se suele presentar como 5E9 en la pantalla de una calculadora) o 5 × 10-6 para cinco millonésimas.
Estos sistemas simbólicos se desarrollaron durante miles de años, y muchos sistemas alternativos florecieron en diversas culturas. Ya hemos encontrado el sistema sexagesimal babilónico (que surgiría de modo natural para cualquier criatura que tuviera 60 dedos), y los más simples y más limitados símbolos numerales egipcios, con su extraño tratamiento de las fracciones. Posteriormente, sistemas de base 20 fueron utilizados en América Central por la civilización maya.
Sólo en tiempos relativamente recientes se decidió la Humanidad por los métodos actuales para escribir números, y su uso llegó a establecerse por una mezcla de tradición y conveniencia. Las matemáticas tratan de conceptos, no de símbolos, pero una buena elección de símbolos puede ser muy útil.
§. Numerales griegos
Empezamos la historia de los símbolos numerales con los griegos. La geometría griega supuso una gran mejora sobre la geometría babilónica, pero no así la aritmética griega, hasta donde podemos decir a partir de las fuentes que nos han llegado. Los griegos dieron un gran paso atrás; no utilizaban la notación posicional. En su lugar utilizaban símbolos específicos para múltiplos de 10 o 100, de modo que, por ejemplo, el símbolo para 50 no guardaba ninguna relación particular con los símbolos para 5 o 500.
La prueba más antigua que tenemos de los numerales griegos data de alrededor del 1100 a.C. Hacia el 600 a.C. el simbolismo había cambiado, y para el 400 a.C. había cambiado de nuevo, con la adopción del sistema ático, que recuerda a los numerales romanos. Utilizaba |, ||, |||, |||| para los números 1,2, 3 y 4. Para 5 se utilizaba la letra mayúscula griega «pi» (Π), probablemente porque es la primera letra de «penta». Análogamente, 10 se escribía Δ, la primera letra de «deka»; 100 se escribía H, la primera letra de «hekaton»; 1.000 se escribía Ξ, la primera letra de «chilloi»; y 10.000 se escribía M, la primera letra de «myrioi». Más tarde Π se cambió por Τ. Así, el número 2.178, por ejemplo, se escribía
Ξ ΞH Δ Δ Δ Δ Δ Δ Δ Τ| | |
Aunque los pitagóricos hicieron de los números la base de su filosofía, no sabemos cómo los escribían. Su interés en los números cuadrados y triangulares sugiere que quizá representaran los números mediante pautas de puntos. Para el periodo clásico, 600-300 a.C., el sistema griego había cambiado de nuevo, y se utilizaban 27 letras diferentes del alfabeto para denotar números de 1 a 900, de esta forma:
Estas son las letras griegas minúsculas, aumentadas por tres letras extra derivadas del alfabeto fenicio: s (stigma), p (copa), T (sampi).
Utilizar letras para representar números podría haber producido ambigüedad, de modo que se colocaba una línea horizontal encima de los símbolos numerales. Para escribir números mayores que 999 el valor de un símbolo podía multiplicarse por 1.000 colocando un trazo delante del mismo.
Los diversos sistemas griegos eran razonables como método para registrar los resultados de cálculos, pero no para realizar los propios cálculos. (Imaginémonos intentando multiplicar σμλ por ωλδ, por ejemplo.) Los cálculos propiamente dichos se llevaban a cabo probablemente utilizando un ábaco, quizá representado por guijarros en la arena, especialmente al principio.
Los griegos escribían las fracciones de varias maneras. Una de ellas consistía en escribir el numerador, seguido por una prima, y luego el denominador, seguido por una doble prima. A veces el denominador se escribía dos veces.
Así 21/47 se escribiría
κα' μζ''
donde κα es 21 y μζ es 47. También utilizaban fracciones al estilo egipcio, y había un símbolo especial para ½. Algunos astrónomos griegos, en especial Ptolomeo, empleaban el sistema sexagesimal babilónico por precisión, aunque utilizando símbolos griegos para los «dígitos» componentes. Todo era muy diferente de lo que utilizamos hoy. De hecho, era un revoltijo.
§. Matemáticos indios
Los 10 símbolos que se utilizan actualmente para denotar dígitos decimales suelen conocerse como numerales indoarábigos, porque tuvieron su origen en la India y fueron asumidos y desarrollados por los árabes.
Los más antiguos numerales indios eran más parecidos al sistema egipcio. Por ejemplo, los numerales Kharosthi, utilizados del 400 a.C. al 100 d.C., representaban los números 1 a 8 como
| || ||| X |X ||X |||X XX
con un símbolo especial para 10. Las primeras huellas de lo que con el tiempo llegaría a ser el moderno sistema simbólico aparecieron alrededor del 300 a.C., en los numerales Brahmi. Inscripciones budistas de la época incluyen precursores de los posteriores símbolos hindúes para 1, 4 y 6. Sin embargo, el sistema Brahmi utilizaba símbolos diferentes para múltiplos de 10 o múltiplos de 100, de modo que era similar al simbolismo de los números griegos, excepto que utilizaba símbolos especiales en lugar de letras del alfabeto.
El sistema Brahmi no era un sistema posicional. Ya en el año 100 hay registros del sistema Brahmi completo. Inscripciones en cuevas y en monedas muestran que siguió en uso hasta el siglo IV.
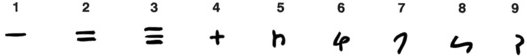
Numerales Brahmi 1-9
Entre los siglos IV y VI el Imperio Gupta alcanzó el control de una gran parte de la India, y los numerales Brahmi se transformaron en los numerales Gupta. De éstos se transformaron en los numerales Nagari. La idea era la misma, pero los símbolos eran diferentes.
Es probable que los indios desarrollaran la notación posicional hacia el siglo i, pero las más antiguas pruebas documentales datables de la notación posicional la sitúan en el año 594. La prueba es un documento legal que lleva la fecha 346 en el calendario Chedii, pero algunos estudiosos creen que esta fecha puede ser una falsificación. De todas formas, hay acuerdo general en que la notación posicional estaba en uso en la India desde aproximadamente el 400 en adelante.
Hay un problema al utilizar únicamente los símbolos 1-9: la notación es ambigua. Por ejemplo, ¿qué significa 25? Podría significar (en nuestra notación) 25, o 205, o 2005, o 250, etc. En notación posicional, donde el significado de un símbolo depende de su posición, es importante especificar dicha posición sin ambigüedad. Hoy lo hacemos utilizando un décimo símbolo, el cero (0). Pero las primeras civilizaciones necesitaron un tiempo sorprendentemente largo para reconocer el problema y resolverlo de esa manera. Una razón era filosófica: ¿cómo puede 0 ser un «número» cuando un número es una cantidad de cosas? ¿Es «nada» una cantidad? Otra razón era práctica: habitualmente quedaba claro por el contexto si 25 significaba 25 o 250 o lo que fuera.
En algún momento antes del 400 a.C. -se desconoce la fecha exacta- los babilonios introdujeron un símbolo especial para indicar una posición «ausente» en su notación numeral. Esto ahorraba a los escribas el esfuerzo de dejar un espacio cuidadosamente medido, y hacía posible calcular lo que significaba un número incluso si estaba escrito descuidadamente. Esta invención fue olvidada, o no fue transmitida a otras culturas, y con el tiempo fue redescubierta por los hindúes. El manuscrito Bhakshali, cuya fecha es discutida pero se encuentra en algún lugar entre 200 y 1100, utiliza un punto grueso •. El texto jaino Lokavibhaaga del 458 utiliza el concepto de 0, pero no un símbolo. Un sistema posicional que carecía del numeral «cero» fue introducido por Aryabhata alrededor del 500. Los matemáticos indios posteriores tenían nombres para cero, pero no utilizaban un símbolo.
El primer uso indiscutido de cero en notación posicional aparece en una tablilla de piedra en Gwailior datada en el 876.
§. Brahmagupta, Mahavira y Bhaskara
Los matemáticos indios más importantes fueron Aryabhata (nacido en el 476), Bramagupta (nacido en el 598), Mahavira (siglo IX) y Bhaskara (nacido en el 1114). Realmente deberían ser descritos como astrónomos, porque las matemáticas eran entonces consideradas una técnica astronómica. Las matemáticas existentes estaban escritas como capítulos en textos de astronomía; no se veían como una disciplina independiente.
Aryabhata nos dice que escribió su libro Aryabahiya cuando tenía 23 años. Aunque la sección matemática de su libro es breve, contiene un material muy rico: un sistema alfabético de numerales, reglas aritméticas, métodos de solución para ecuaciones lineales y cuadráticas, trigonometría (incluyendo la función seno y el «seno verso» 1-cos θ). Hay una aproximación excelente, 3,1416, a π.
El antiguo observatorio Jantar Mantar cerca de Jaipur. Hoy resulta evidente que el diseñador era un matemático consumado
Brahmagupta fue el autor de dos libros: Brahmasphutasiddhanta y Khanda Khadyaka. El primero es el más importante; es un texto de astronomía con varias secciones sobre matemáticas, con aritmética y un equivalente verbal del álgebra simple. El segundo libro incluye un método notable para interpolar tablas de senos; es decir, encontrar el seno de un ángulo a partir de los senos de un ángulo más grande y otro más pequeño.
Para qué les servía la aritméticaEl texto chino de matemáticas más antiguo que se conserva es el Chiu Chang, que data de aproximadamente el año 100.
Un problema típico es: Dos piculs y medio de arroz se compran por 3/7 de un tael. ¿Cuántos piculs pueden comprarse por 9 taels? La solución propuesta utiliza lo que los matemáticos medievales llamaban la «regla de tres».
En notación moderna, sea x la cantidad buscada.
Entonces
x/9 = (5/2)/(3/7)
de modo que x = 52 ½ piculs. Un picul son aproximadamente 65 kilogramos.
Mahavira era un jaino, e incluyó muchas matemáticas jainas en su Ganita Sara Sangraha. Este libro incluía la mayoría de los contenidos de los libros de Aryabhata y Brahmagupta, pero iba mucho más allá y era en general más sofisticado. Incluía fracciones, permutaciones y combinaciones, la solución de ecuaciones cuadráticas, triángulos pitagóricos y un intento de encontrar el área y el perímetro de una elipse.
Bhaskara (conocido como «el maestro»), escribió tres obras importantes: Lilavati, Bijaganita y Siddhanta Siromani. Según Fyzi, poeta de la corte del emperador mogul Akhar, Lilavati era el nombre de la hija de Bhaskara.
Su padre realizó el horóscopo de su hija y determinó la época más propicia para su boda. Para dramatizar su predicción, puso dentro de un cuenco de agua una copa con un agujero, construida de modo que se hundiera cuando llegara el momento propicio. Pero Lilavati se inclinó sobre el cuenco y una perla de su vestido cayó en la copa y bloqueó el agujero. La copa no se hundió, lo que significaba que Lilavati nunca podría casarse. Para consolarla, Bhaskara escribió un libro de texto de matemáticas para ella. La leyenda no registra lo que ella pensaba de esto.
Lilavati contiene ideas sofisticadas en aritmética, incluyendo «sacar los nueves», en donde los números son reemplazados por la suma de sus cifras para comprobar cálculos. Contiene reglas similares para la divisibilidad por 3, 5, 7 y 11. El papel del 0 como un número por sí mismo queda claro. Bijaganita trata de la solución de ecuaciones. Siddhanta Siromani trata de geometría: tablas de senos, diversas relaciones trigonométricas. Tan grande era la reputación de Bhaskara que sus obras todavía se copiaban alrededor de 1800.
§. El sistema hindú
El sistema hindú empezó a difundirse en el mundo árabe antes de que estuviera plenamente desarrollado en su país de origen. El estudioso Severus Sebokht escribe de su uso en Siria en el 662: «Omitiré toda discusión de la ciencia de los indios... de sus sutiles descubrimientos en astronomía... y de sus valiosos métodos de cálculo... Sólo quiero decir que su cálculo se hace por medio de nueve signos».
“... Lilavati nunca podría casarse. Para consolarla, Bhaskara escribió un libro de texto de matemáticas para ella.”
En el 776 apareció en la corte del califa un viajero procedente de la India y mostró sus habilidades en el método de cálculo «siddhanta», además de trigonometría y astronomía. Parece que la base para los métodos computacionales era el Brahmasphutasiddhanta de Brahmagupta, escrito en el 628; pero cualquiera que fuera el libro, fue inmediatamente traducido al árabe.
Inicialmente los numerales hindúes eran utilizados principalmente por estudiosos; los métodos más antiguos siguieron siendo ampliamente utilizados en la comunidad de negocios y en la vida cotidiana arábiga, hasta aproximadamente el año 1000. Pero Sobre el cálculo con numerales hindúes de Al-Khwarizmi en el 825 dio a conocer el sistema hindú en todo el mundo árabe. El tratado en cuatro volúmenes Sobre el uso de los numerales indios (Ketab fi Isti’mal al-‘Adad al-Hindi) de Al-Kindi en el 830 aumentó la conciencia de que era posible realizar todos los cálculos numéricos utilizando sólo los 10 dígitos.
§. ¿La Edad Oscura?
Mientras Arabia e India estaban haciendo avances importantes en matemáticas y ciencia, Europa estaba relativamente estancada, aunque el periodo medieval no fue exactamente la «Edad Oscura» de la concepción popular. Se hicieron algunos avances, pero éstos fueron lentos y no especialmente radicales. El ritmo del cambio empezó a acelerarse cuando la noticia de los descubrimientos orientales llegó a Europa. Italia está más cerca del mundo árabe que la mayoría de las regiones de Europa, de modo que era probablemente inevitable que los avances árabes en matemáticas llegaran a Europa a través de Italia. Venecia, Génova y Pisa eran centros comerciales importantes, y los mercaderes partían de estos puertos hacia el Norte de África y el extremo oriental del Mediterráneo. Intercambiaban lana y madera europeas por seda y especias.
Hubo un comercio metafórico en ideas tanto como el comercio literal en mercancías. Los descubrimientos árabes en ciencia y matemáticas llegaron a lo largo de las rutas comerciales, a menudo de boca a oreja. A medida que el comercio hacía a Europa más próspera, el trueque dio paso al dinero, y la contabilidad y el pago de impuestos se hicieron más complejos.
Evolución de los símbolos numerales occidentales
Una figura influyente fue Leonardo de Pisa, cuyo libro Liber Abbaci se publicó en 1202. (La palabra italiana «ábaco» significa normalmente «cálculo», y no implica necesariamente el uso del ábaco, un término latino.) En este libro, Leonardo introdujo los símbolos numerales indoarábigos en Europa.
Leonardo de Pisa (Fibonacci)
1170 - 1250Leonardo, nacido en Italia, creció en África del Norte, donde su padre Guilielmo trabajaba como diplomático en nombre de los mercaderes que comerciaban en Bugia (en la actual Argelia). Acompañó a su padre en muchos viajes, descubrió el sistema árabe para escribir núme┐│ros y comprendió su importancia. En su Líber Abbaci de 1202 escribe: «Cuando mi padre, a quien su país había nombrado notario público en las aduanas de Bugia en representación de los mercaderes de Pisa que allí iban, estaba en su cargo, me llevó con él mientras yo era todavía un niño, y pensando en la utilidad y la conveniencia futura, deseó que yo permaneciera allí y recibiera instrucción en la escuela de contabilidad. Allí, cuando yo había sido introducido en el arte de los nueve símbolos indios gracias a una notable enseñanza, el conocimiento del arte pronto me gustó más que todo lo demás».
El libro introdujo la notación indo- arábiga en Europa, y constituía un texto general de aritmética que contenía rico material relacionado con el comercio y la conversión de moneda. Aunque se necesitaron varios siglos para que la notación indoarábiga desplazara al ábaco tradicional, pronto se hicieron patentes las ventajas de un sistema de cálculo con una notación clara.
Leonardo, a veces conocido por su apodo «Fibonacci», que significa «hijo de Bonaccio», pero no hay registro de este nombre antes del siglo XVIII, y probablemente fue inventado entonces por Guillaume Libri.
El Liber Abbaci incluye, y promociona, otro artificio notacional que sigue hoy en uso: la barra horizontal en una fracción, tal como en «tres cuartos».
Los hindúes empleaban una notación similar, pero sin barra; parece que la barra fue introducida por los árabes. Fibonacci la empleó ampliamente, pero su uso difería del actual en algunos aspectos. Por ejemplo, él utilizaba la misma barra como parte de varias fracciones diferentes.
Puesto que las fracciones son muy importantes en nuestra historia, vale la pena añadir algunos comentarios sobre la notación. En una fracción como 3/4, el 4 «abajo» nos dice que dividamos la unidad en cuatro partes iguales, y el 3 «arriba» nos dice entonces que seleccionemos tres de dichas partes. De manera más formal, 4 es el denominador y 3 es el numerador. Por conveniencia tipográfica las fracciones se suelen escribir en una única línea en la forma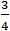 
, o a veces en la forma de compromiso 3/4. La barra horizontal se transforma entonces en una barra diagonal.
En general, no obstante, apenas utilizamos notación fraccionaria en el trabajo práctico. Básicamente utilizamos «decimales», escribiendo π como 3,14159, digamos, lo que no es exacto pero es suficientemente próximo para la mayoría de los cálculos. Históricamente tenemos que dar un pequeño salto para llegar a los decimales, pero aquí estamos siguiendo cadenas de ideas, no cronología, de modo que será mucho más sencillo dar el salto. Por lo tanto, saltamos hasta 1585, cuando Guillermo el Silencioso escogió al holandés Simón Stevin como tutor privado para su hijo Mauricio de Nassau.
A partir de este reconocimiento, Stevin se labró una carrera, llegando a ser inspector de Diques, contramaestre general de la Armada y, finalmente, ministro de Finanzas. Rápidamente comprendió la necesidad de procedimientos contables precisos, y estudió a los aritméticos italianos del periodo renacentista y la notación indoarábiga transmitida a Europa por Leonardo de Pisa. Encontró engorrosos los cálculos con fracciones, y hubiera preferido la precisión y el orden de los sexagesimales babilónicos si no fuera por el uso de la base 60. Trató de encontrar un sistema que combinara lo mejor de ambos, e inventó uno similar al sistema babilónico pero con base 10: los decimales.
Publicó su nuevo sistema notacional, dejando claro que había sido ensayado y comprobado, y que hombres muy prácticos lo habían encontrado muy práctico. Además, señaló su eficacia como herramienta para los negocios: «todos los cálculos que se encuentran en los negocios pueden realizarse sólo con enteros sin la ayuda de fracciones».
Su notación no incluía la familiar «coma decimal», pero condujo rápidamente a la notación decimal actual. Donde nosotros escribimos 5,7731, pongamos por caso, Stevin escribía 5⓪7①7②3③1④. El símbolo ⓪indicaba un número entero, ①indicaba una décima, ② una centésima, y así sucesivamente.
A medida que la gente se acostumbraba al sistema se prescindió de ①, ② y sucesivos, y se retuvo sólo ⓪ que, contraída y simplificada, se convirtió en la habitual coma decimal.
§. Números naturales
Los matemáticos llaman números naturales al sistema de los números enteros positivos.
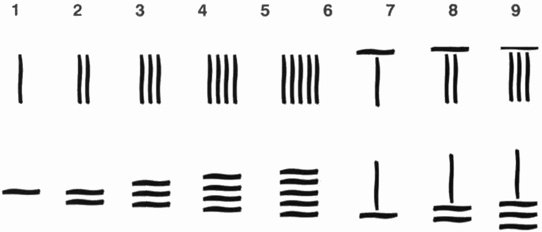
Antiguas barras de recuento chinas
Si incluimos también los números negativos tenemos los enteros. Los números racionales (o simplemente los «racionales») son las fracciones positivas y negativas, los números reales (o simplemente los «reales») son los decimales positivos y negativos, que se prolongan indefinidamente si es necesario.
¿Cómo entraron en la historia los números negativos?
En los comienzos del primer milenio los chinos empleaban un sistema de «varas de recuento» en lugar de un ábaco. Disponían las varas en pautas para representar números.
La hilera superior de la figura muestra varas heng, que representaban unidades, centenas, decenas de millar y así sucesivamente, según su posición en una hilera de tales símbolos.
Planteando ecuaciones al estilo chino. Las barras sombreadas son rojas
La hilera inferior muestra varas tsung, que representaban decenas, millares y así sucesivamente. De modo que los dos tipos de varas se alternaban. Los cálculos se realizaban mediante manipulaciones sistemáticas de las varas.
“En los comienzos del primer milenio los chinos empleaban un sistema de «varas de recuento» en lugar de un ábaco.”
Cuando resolvían un sistema de ecuaciones lineales, los calculadores chinos disponían las varas en una mesa. Utilizaban varas rojas para términos que se suponía que había que sumar y varas negras para términos que se suponía que había que restar. Así, para resolver ecuaciones que nosotros escribiríamos
3x - 2y = 4
x + 5y = 7
ellos ordenaban las dos ecuaciones como dos columnas de una tabla: una con los números 3 (rojo), 2 (negro), 4 (rojo), y la otra con 1 (rojo), 5 (rojo), 7 (rojo).
La «notación» rojo/negro no trataba realmente con números negativos sino con la operación de restar. Sin embargo, fijó el escenario para un concepto de números negativos, cheng fu shu. Ahora un número negativo se representaba utilizando la misma disposición de varas que la del correspondiente número positivo, pero colocando encima otra vara en diagonal.
Numerales mayasUn notable sistema de números, que utilizaba notación de base 20, en lugar de base 10, fue desarrollado por los mayas que vivían en América Central alrededor del año 1000. En el sistema de base 20. los símbolos equivalentes a nuestro 347 significarían 3 × 400 + 4 × 20 + 7 × 1, (pues 202 = 400) que es 1.287 en nuestra notación. Los símbolos reales se muestran aquí.
Las primeras civilizaciones que usaron base 10 lo hicieron probablemente porque los seres humanos tienen diez dedos en las manos. Se ha sugerido que los mayas contaban también con los dedos de los pies, y por eso utilizaban base 20.
Para Diofanto todos los números tenían que ser positivos, y por ello rechazaba las soluciones negativas a las ecuaciones.
Los matemáticos hindúes encontraron que los números negativos eran útiles para representar deudas en los cálculos financieros; deber a alguien una suma de dinero era peor, desde el punto de vista financiero, que no tener dinero, de modo que una deuda debería ser claramente «menos que cero». Si uno tiene tres libras y paga 2, entonces le quedan 3 - 2 = 1. Por la misma razón, si debe 2 libras y gana 3, su valor neto es -2 + 3 = 1. Bhaskara comenta que un problema particular tenía dos soluciones, 50 y -5, pero le ponía nervioso la segunda solución, y decía que «no debe tomarse; la gente no aprueba las soluciones negativas».
Pese a estos recelos, los números negativos fueron siendo aceptados gradualmente. Su interpretación, en un cálculo real, requería cierto cuidado.
A veces no tenían sentido, a veces podían ser deudas, a veces podían significar un movimiento descendente en lugar de uno ascendente. Pero al margen de la interpretación, su aritmética funcionaba perfectamente, y eran tan útiles como ayuda computacional que hubiera sido estúpido no utilizarlos.
§. La aritmética perdura
Nuestro sistema numeral es tan familiar que tendemos a suponer que es el único posible, o al menos el único razonable. En realidad, evolucionó, de forma laboriosa y con numerosas vías muertas, durante miles de años.
Hay muchas alternativas; algunas fueron utilizadas por culturas anteriores, como los mayas. Notaciones diferentes para los numerales 0-9 se utilizan hoy en diferentes países. Y nuestros computadores representan números internamente en forma binaria, no decimal: sus programadores aseguran que los números se conviertan de nuevo a forma decimal antes de que aparezcan en la pantalla o en una impresora.
“... la civilización moderna se vendría abajo rápidamente si dejáramos de enseñar aritmética...”
Dado que los computadores son ahora ubicuos, ¿tiene sentido seguir enseñando aritmética? Sí, y por varias razones. Alguien tiene que ser capaz de diseñar y construir calculadoras y computadores, y hacer que realicen la tarea correcta; esto requiere entender la aritmética, cómo y por qué funciona, no solo cómo hacerla. Y si su única habilidad aritmética es leer lo que hay en una calculadora, probablemente usted no advertirá que el supermercado se ha equivocado en su factura.
Para qué nos sirve la aritméticaNosotros utilizamos la aritmética continuamente en nuestra vida diaria, en el comercio y en la ciencia. Hasta el desarrollo de las calculadoras electrónicas y los computadores hacíamos los cálculos a mano, con papel y lápiz, o utilizábamos ayudas tales como el ábaco o un calculador rápido (un libro impreso con tablas de múltiplos de cantidades de dinero). Hoy la mayor parte de la aritmética se hace electrónicamente entre bastidores: las cajas del supermercado dicen ahora a las cajeras cuánto dinero deben devolver, por ejemplo, y los bancos nos dicen el total de nuestra cuenta automáticamente, en lugar de tener un contable que lo haga. La cantidad de aritmética «consumida» por una persona normal durante un solo día es sustancial.
La aritmética por computador no se realiza realmente en formato decimal. Los computadores utilizan un sistema de base 2, o binario, y no de base 10. En lugar de unidades, decenas, centenas, millares y demás, los computadores utilizan 1, 2, 4, 8,16, 32, 64, 128, 256 y así sucesivamente: las potencias de dos, cada una de ellas doble de su predecesora. (Por esto la tarjeta de memoria de su cámara digital viene en tamaños curiosos como 256 megabytes.)
En un computador, el número 100 se descompone como 64 + 32 + 4 y se almacena en la forma 1100100
Sin «internalizar» las operaciones básicas de la aritmética, el conjunto de las matemáticas le será inaccesible. Quizá usted no se preocupe por eso, pero la civilización moderna se vendría abajo rápidamente si dejáramos de enseñar aritmética, porque no se pueden detectar los futuros ingenieros y científicos cuando tienen cinco años. O incluso los futuros banqueros y contables.
Por supuesto, una vez que se tiene «a mano» una idea básica de la aritmética, utilizar una calculadora es una buena manera de ahorrar tiempo y esfuerzo. Pero, igual que no se aprende a caminar utilizando siempre una muleta, tampoco se aprende a pensar razonablemente sobre números fiándose solamente de una calculadora.
Capítulo 4
La atracción de lo desconocido
X marca el lugar
El uso de símbolos en matemáticas va mucho más allá de su aparición en notaciones para números, como dejará claro una ojeada informal a cualquier texto de matemáticas. El primer paso importante hacia el razonamiento simbólico-frente a la mera representación simbólica- se dio en el contexto de la solución de problemas. Numerosos textos antiguos, que se remontan a la época de la antigua Babilonia, presentan a sus lectores información sobre una cantidad desconocida y luego preguntan por su valor.
Una fórmula estándar (en el sentido literario) en las tablillas babilónicas dice: «Yo encontré una piedra pero no la pesé». Después de alguna información adicional -«cuando yo añadí una segunda piedra de la mitad de peso, el peso total era de 15 gin»- al estudiante se le pide calcular el peso de la piedra original.
§. Álgebra
Problemas de este tipo dieron lugar con el tiempo a lo que ahora llamamos álgebra, en donde los números se representan por letras. La cantidad desconocida se denota tradicionalmente por la letra x, las condiciones que se aplican a x se enuncian como fórmulas matemáticas, y al estudiante se le enseñan métodos estándar para extraer el valor de x a partir de dichas fórmulas. Por ejemplo, el problema babilónico anterior se escribiría como
x + ½x = 15,
y aprenderíamos la forma de deducir que
x = 10
En el nivel escolar, el álgebra es una rama de las matemáticas en la que números desconocidos se representan por letras, las operaciones de la aritmética se representan por símbolos y la tarea principal consiste en deducir los valores de las cantidades desconocidas a partir de las ecuaciones. Un problema típico en el álgebra de la escuela consiste en encontrar un número desconocido x dada la ecuación
x2 + 2x = 120.
Esta «ecuación cuadrática» tiene una solución positiva, x = 10. Aquí
x2 + 2x = 102 + 2 × 10 = 100 + 20 = 120.
También tiene una solución negativa,
x = -12
En este caso
x2 + 2x = (-12)2 + 2 × (-12) = 144 - 24 = 120.
Los antiguos habrían aceptado la solución positiva, pero no la negativa. Hoy admitimos ambas, porque en muchos problemas los números negativos tienen un significado razonable y corresponden a respuestas físicamente factibles, y porque realmente las matemáticas se hacen más sencillas si se admiten los números negativos.
“¿Cómo surgió el álgebra?”
En matemáticas avanzadas, el uso de símbolos para representar números es sólo un aspecto minúsculo de la disciplina, el contexto en el que empezó.
El álgebra trata de las propiedades de expresiones simbólicas por sí mismas; trata de estructura y forma, no sólo de números. Esta visión más general del álgebra se desarrolló cuando los matemáticos empezaron a plantear preguntas generales sobre álgebra de nivel escolar. En lugar de tratar de resolver ecuaciones concretas, examinaron la estructura más profunda del propio proceso de solución.
Una tablilla cuneiforme del periodo Babilonio Antiguo muestra un problema geométrico algebraico
¿Cómo surgió el álgebra? Lo que vino primero fueron los problemas y los métodos. Sólo más adelante fue inventada la notación simbólica, lo que ahora consideramos que es la esencia del tema. Había muchos sistemas notacionales, pero finalmente uno de ellos eliminó a todos sus competidores. El nombre «álgebra» apareció en medio de este proceso, y es de origen árabe. (La inicial «al», el término árabe para «el», lo delata.)
§. Ecuaciones
Lo que ahora llamamos la «solución de ecuaciones», en la que hay que encontrar una incógnita a partir de información apropiada, es casi tan vieja como la aritmética. Hay evidencia indirecta de que los babilonios ya resolvían ecuaciones bastante complicadas en el 2000 a.C., y evidencia directa de soluciones de problemas más sencillos, en forma de tablillas cuneiformes, que se remonta hasta alrededor del 1 700 a.C.
La porción que sobrevive de la Tablilla YBC 4652 del periodo babilónico Antiguo (1800-1600 a.C.), contiene once problemas para resolver; el texto de la tablilla indica que originalmente había 22 problemas. Una pregunta típica es:
«Encontré una piedra, pero no la pesé. Después pesé 6 veces su peso, añadí 2 gin y añadí un tercio de un séptimo multiplicado por 24. Lo pesé. El resultado era 1 ma-na. ¿Cuál era el peso original de la piedra?».
Un peso de 1 ma-na son 60 gin.
En notación moderna, llamaríamos x al peso buscado en gin. Entonces la pregunta nos dice que
(6x + 2) + ⅓ × 1/7 × 24(6x + 2) = 60
y métodos algebraicos estándar llevan a la respuesta x = 4 ⅓ gin.
La tablilla da esta respuesta pero no da una indicación clara de cómo se obtiene. Podemos estar seguros de que no había sido encontrada utilizando métodos simbólicos como los que ahora utilizamos, porque tablillas posteriores prescriben métodos de solución en términos de ejemplos típicos: «tomar la mitad de este número, sumar el producto de estos dos, tomar la raíz cuadrada...» y así sucesivamente.
Este problema, como los otros en YBC 4652, es lo que ahora llamamos una ecuación lineal, lo que indica que la incógnita x entra sólo en su primera potencia. Todas estas ecuaciones pueden reescribirse en la forma
ax + b = 0
con solución
x = -b/a
Pero en los tiempos antiguos, sin el concepto de números negativos y sin manipulación simbólica, encontrar una solución no era tan simple. Incluso hoy, muchos estudiantes tendrían dificultades con los problemas de YBC 4652.
Más interesantes son las ecuaciones cuadráticas, en las que la incógnita puede aparecer también elevada a la segunda potencia: al cuadrado. La formulación moderna toma la forma
ax2 + bx + c = 0
y hay una fórmula estándar para encontrar x. El enfoque babilónico se ejemplifica en un problema en la Tablilla BM 13901:
«He sumado siete veces el lado de mi cuadrado y once veces el área, [obteniendo] 6; 15».
(Aquí 6; 15 es la forma simplificada de la notación sexagesimal babilónica, y significa 6 más 15/60, ó 6¼ en notación moderna.) La solución enunciada dice:
«Escribe 7 y 11. Multiplica 6; 15 por 11 [obteniendo] 1,8;45. Divide 7 por la mitad, [obteniendo] 3;30 y 3;30. Multiplica, [obteniendo] 12;15. Suma [esto] a 1,8;45 [obteniendo] resultado 1,21. Esto es el cuadrado de 9. Resta 3;30, que multiplicaste, de 9. Resultado 5;30. El recíproco de 11 no puede encontrarse. Pero ¿qué debo multiplicar por 11 para obtener 5;30? [La respuesta es] 0;30, el lado del cuadrado es 0;30».
Nótese que la tablilla le dice al lector lo que tiene que hacer, pero no por qué. Es una receta.
“... la tablilla le dice al lector lo que tiene que hacer, pero no por qué.”
Para poder escribirla alguien tiene que haber entendido por qué funcionaba, pero una vez descubierta podía ser utilizada por cualquiera que tuviera la formación adecuada. No sabemos si las escuelas de Babilonia enseñaban meramente la receta o explicaban por qué funcionaba.
La receta tal como está parece muy oscura, pero interpretarla es más fácil de lo que cabría esperar. Los números complicados ayudan realmente; aclaran qué reglas se están utilizando. Para encontrarlas, simplemente tenemos que ser sistemáticos. En notación moderna escribimos
a = 11. b = 7, c = 6;15 = 6¼
Entonces la ecuación toma la forma
ax2 + bx = c
con aquellos valores concretos para a, b, c. Tenemos que deducir x. La solución babilónica nos dice:
- Multiplicar c por a, lo que da ac.
- Dividir b por 2, que es b/2.
- Elevar b/2 al cuadrado para obtener b2/4.
- Sumar esto a ac, que es ac + b2/4.
- Tomar su raíz cuadrada √ac + b2/4.
- Restar b/2, lo que hace √ac + b2/4 -b/2.
- Dividir esto por a, y la respuesta es
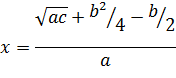
Esto es equivalente a la fórmula que se enseña hoy
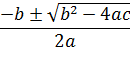
Está muy claro que los babilonios sabían que su procedimiento era general. El ejemplo citado es demasiado complejo para que la solución sea especial, diseñada para abordar este problema solamente.
¿Qué pensaban los babilonios de su método, y cómo llegaron a él? Tuvo que haber alguna idea relativamente sencilla tras un proceso tan complicado. Parece plausible, aunque no hay prueba directa, que tuvieran una idea geométrica, «completar el cuadrado». Una versión algebraica de esto también se enseña hoy. Podemos representar la pregunta, que por claridad decidimos escribir en la forma x2 + ax = b, como una imagen:
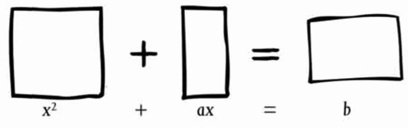
Aquí el cuadrado y el primer rectángulo tienen altura x; sus anchuras son x y a, respectivamente. El rectángulo más pequeño tiene área b. La receta babilónica divide efectivamente el primer rectángulo en dos piezas.
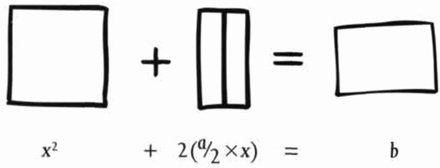
Podemos entonces reordenar las dos piezas y pegarlas en los bordes del cuadrado:
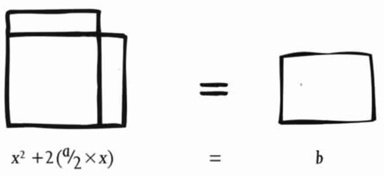
El diagrama de la izquierda pide a gritos ser completado para dar un cuadrado más grande, añadiendo el cuadrado sombreado:
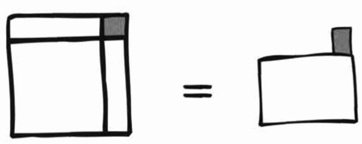
Para que la ecuación siga siendo válida, el mismo cuadrado sombreado extra se añade también al otro diagrama. Pero ahora reconocemos el diagrama de la izquierda como el cuadrado de lado (x + a/2), y la imagen geométrica es equivalente al enunciado algebraico
x2 + 2(a/2 × x) + (a/2)2 = b + (a/2)2.
Puesto que el primer miembro es un cuadrado, podemos reescribirlo como
(x + a/2)2 = b + (a/2)2
y entonces es natural tomar una raíz cuadrada
x + a/2 = √b+(a/2)2
y finalmente reordenarlo para deducir que
x = √b+(a/2)2 - a/2
que es exactamente la forma en que procede la receta babilónica.
No hay evidencia en ninguna tablilla que apoye la idea de que esta imagen geométrica llevó a los babilonios a su receta. Sin embargo, esta sugerencia es plausible, y está apoyada indirectamente por varios diagramas que aparecen en tablillas de arcilla.
§. Al-jabr
La palabra «álgebra» procede del árabe al-jabr, un término empleado por Muhammad ibn Musa al-Khwarizmi, que floreció alrededor del 820. Su obra Al-Kitab al-jbr w’al-mugabala (Libro de compendio de cálculo por el método de completado y balanceado) explicaba métodos generales para resolver ecuaciones manipulando cantidades desconocidas.
“La palabra «álgebra» procede del árabe al-jabr,..”
Al-Khwarizmi utilizaba palabras, no símbolos, pero sus métodos son similares a los que se enseñan hoy. Al-jabr significa «sumar cantidades iguales a ambos miembros de una ecuación», que es lo que hacemos cuando partimos de
x - 3 = 5
y deducimos que
x = 8.
En efecto, hacemos esta deducción sumando 3 a ambos miembros. Al-muqabala tiene dos significados. Hay un significado especial: «restar cantidades iguales de ambos miembros de una ecuación», que es lo que hacemos para pasar de
x + 3 = 5
a la respuesta
x = 2
Pero también tiene un significado general: «comparación». Al-Khwarizmi da reglas generales para resolver seis tipos de ecuaciones, que pueden ser utilizadas para resolver todas las ecuaciones lineales y cuadráticas. En su obra encontramos así las ideas del álgebra elemental, pero no el uso de símbolos.
§. Ecuaciones cúbicas
Los babilonios podían resolver ecuaciones cuadráticas, y su método era esencialmente el mismo que el que se enseña hoy. Desde el punto de vista algebraico no implica nada más complicado que una raíz cuadrada, aparte de las operaciones estándar de la aritmética (sumar, restar, multiplicar, dividir).
El siguiente paso obvio son las ecuaciones cúbicas, que incluyen el cubo de la incógnita. Nosotros escribimos tales ecuaciones como
ax3 + bx2 + cx + d = 0
donde x es la incógnita y los coeficientes a, b, c, d son números conocidos. Pero hasta el desarrollo de los números negativos los matemáticos clasificaban las ecuaciones cúbicas en muchos tipos distintos, de modo que, por ejemplo,
x3 + 3x = 7
y
x3 - 3x = 7
eran consideradas completamente diferentes, y requerían métodos diferentes para su solución.
Los griegos descubrieron cómo utilizar secciones cónicas para resolver algunas ecuaciones cúbicas. El álgebra moderna demuestra que si una cónica interseca a otra cónica, los puntos de intersección están determinados por una ecuación de tercer o cuarto grado (dependiendo de las cónicas).
Los griegos no lo sabían como un hecho general, sino que explotaban sus consecuencias en casos concretos, utilizando las cónicas como un nuevo tipo de «instrumento geométrico».
La serie de FibonacciLa sección tercera del Líber Abluid contiene un problema cuyo origen parece estar en Leonardo: «Un hombre pone un pareja de conejos en un lugar rodeado por todos lados de una pared. ¿Cuántos pares de conejos pueden crearse a partir de esta primera pareja en un año si cada mes cada pareja engendra una nueva pareja, que se hace fértil a partir del segundo mes?
Este problema más bien extravagante lleva a una curiosa, y famosa, serie de números:
1, 2, 3, 5, 8, 13, 21, 34, 55
y así sucesivamente. Cada número es la suma de los dos que le preceden. Esto se conoce como la Serie de Fibonacci, y aparece repetidamente en matemáticas y en el mundo natural. En particular, muchas flores tienen un número de Fibonacci de pétalos. Esto no es una coincidencia sino una consecuencia de la pauta de crecimiento de la planta y la geometría de los «primordia» -minúsculos grupos de células en la punta del brote en crecimiento que dan lugar a estructuras importantes, pétalos incluidos.
Aunque la regla de crecimiento de Fibonacci para la población de conejos es poco realista, reglas más generales de tipo similar (llamadas modelos de Leslie) se utilizan hoy para ciertos problemas en dinámica de poblaciones, el estudio de cómo cambian de tamaño las poblaciones animales conforme los animales crían y mueren.
Esta línea de ataque fue completada y codificada por el persa Omar Khayyam, más conocido por su poema Rubaiyat. Alrededor de 1075 él clasificó las ecuaciones cúbicas en 14 tipos, y demostró cómo resolver cada tipo utilizando cónicas en su obra Sobre las demostraciones de los problemas de álgebra y comparación. El tratado era un tour de forcé geométrico, y depuró el problema geométrico casi por completo. Un matemático moderno plantearía algunos reparos: algunos de los casos de Ornar no están completamente resueltos porque él supone que existen ciertos puntos construidos geométricamente cuando a veces no es así.
Para qué les servía el álgebraVarios capítulos del Líber Abbaci contienen problemas algebraicos relevantes para las necesidades de los mercaderes. Uno de ellos, no muy práctico, dice así: «Un hombre compra 30 pájaros: periquitos, milanos y gorriones. Un periquito cuesta 3 monedas de plata, un milano 2, y un gorrión ½. Él paga 30 monedas de plata. ¿Cuántos pájaros de cada tipo compra?».
En notación moderna, si llamamos x al número de periquitos, y al número de milanos, y z al número de gorriones, debemos resolver dos ecuaciones
x + y + z = 30
3x + 2y + ½z = 30
En números reales o racionales, estas ecuaciones tendrían infinitas soluciones, pero hay una condición extra implícita en la pregunta: los números x, y, z son enteros. Resulta que sólo existe una solución: 3 periquitos, 5 milanos y 22 gorriones.
Leonardo también menciona una serie de problemas sobre la compra de un caballo. Un hombre dice a otro: «Si tú me das una tercera parte de tu dinero, yo puedo comprar el caballo».
El otro dice, «Si tú me das una cuarta parte de tu dinero, yo puedo comprar el caballo». ¿Cuál es el precio del caballo? Esta vez hay muchas soluciones; la más pequeña en números enteros fija el precio del caballo en 11 monedas de plata.
Es decir, él supone que sus cónicas se cortan cuando pueden no hacerlo. Pero estos son defectos menores.
Las soluciones geométricas de la cúbica estaban muy bien, pero ¿podían existir soluciones algebraicas que incluyeran cosas tales como raíces cúbicas pero nada más complicado?
“Por lo tanto, el combate matemático público era una cosa seria.”
Los matemáticos de la Italia del Renacimiento hicieron uno de los más trascendentales avances en álgebra cuando descubrieron que la repuesta es «sí». En aquellos días los matemáticos se ganaban su reputación tomando parte en competiciones públicas. Cada competidor planteaba problemas a su oponente, y quien más resolviera se consideraba el ganador. Los miembros de la audiencia podían hacer apuestas sobre quién ganaría. Los competidores a menudo apostaban grandes sumas de dinero; en un caso del que hay noticia, el perdedor tuvo que pagar al ganador (y sus amigos) treinta banquetes. Además, era muy probable que aumentara la capacidad del ganador para atraer a estudiantes de pago, fundamentalmente procedentes de la nobleza. Por tanto, el combate matemático público era una cosa seria.
En 1535 tuvo lugar una de estas competiciones entre Antonio Fiore y Niccolo Fontana, apodado Tartaglia, el «tartamudo». Tartaglia barrió a Fiore, y la noticia de su éxito se difundió, llegando a oídos de Girolamo Cardano. Y Cardano aguzó el oído. El estaba escribiendo un texto de álgebra general, y las preguntas que Fiore y Tartaglia se habían planteado se referían a las ecuaciones cúbicas. En aquella época las ecuaciones cúbicas estaban clasificadas en tres tipos diferentes, una vez más debido a que no se reconocían los números negativos. Fiore sólo sabía resolver un tipo. Inicialmente Tartaglia sabía resolver un tipo diferente. En símbolos modernos, su solución de una ecuación cúbica del tipo x3 + ax = b es
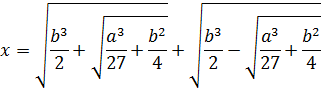
Aproximadamente una semana antes de la competición, en un brote de desesperación inspirada, Tartaglia descubrió cómo resolver también los otros tipos. Entonces planteó a Fiore sólo los tipos que sabía que Fiore no podría resolver.
Cardano, al saber de la competición, se dio cuenta de que los dos combatientes habían concebido métodos para resolver ecuaciones cúbicas. Queriendo añadirlos a su libro, se dirigió a Tartaglia y le pidió que le revelara sus métodos. Naturalmente Tartaglia era reacio, porque su modo de vida dependía de ellos, pero finalmente fue convencido para divulgar el secreto. Según Tartaglia, Cardano prometió que nunca publicaría el método. Por ello, es comprensible que Tartaglia se enfadara cuando su método apareció en el Ars Magna -el Gran Arte del Algebra- de Cardano. Se quejó amargamente y acusó a Cardano de plagio.
Omar Kayyham fue más conocido por su poesía pero también fue un matemático notable
Pero Cardano estaba lejos de amedrentarse. Era un jugador inveterado, que había ganado y perdido sumas considerables de dinero a las cartas, los dados e incluso al ajedrez. Perdió de esta manera toda la fortuna de la familia y se vio reducido a la penuria.
Se necesitaron cientos de años para desarrollar el simbolismo algebraico actual.
También era un genio, un médico competente, un matemático brillante y un autopublicista consumado, aunque sus atributos positivos estaban mitigados por una franqueza que a veces se hacía ofensivamente directa e insultante. Por ello se le puede perdonar a Tartaglia que supusiera que Cardano le había mentido y había robado su descubrimiento. El hecho de que Cardano hubiera dado todo el crédito a Tartaglia en su libro sólo empeoró las cosas; Tartaglia sabía que quien sería recordado era el autor del libro, y no una oscura figura de la que se hiciese una simple mención.
Sin embargo, Cardano tenía una excusa, y muy buena. Y también tenía una buena razón para romper su promesa a Tartaglia. La razón era que un estudiante de Cardano, Ludovico Ferrari, había encontrado un método para resolver ecuaciones cuárticas, que incluyen la cuarta potencia de la incógnita. Esto era algo completamente nuevo y de enorme importancia. Por supuesto, Cardano también quería incluir las ecuaciones cuárticas en su libro. Puesto que era su estudiante quien había hecho el descubrimiento, esto habría sido legítimo. Pero el método de Ferrari reducía la solución de cualquier cuártica a la de una cúbica asociada, de modo que se basaba en la solución de Tartaglia de las ecuaciones cúbicas. Cardano no podía publicar el trabajo de Ferrari sin publicar también el de Tartaglia.
Entonces le llegaron nuevas noticias que ofrecían una salida. Fiore, que había perdido con Tartaglia en combate público, era un estudiante de Scipio Del Ferro. Cardano oyó que Del Ferro había resuelto los tres tipos de cúbica, no sólo el que había pasado a Fiore. Y se rumoreaba que un tal Annibale del Nave poseía papeles inéditos de Del Ferro. Por ello, Cardano y Ferrari fueron a Bolonia en 1543 a consultar con Del Nave, vieron los papeles, y allí, delante de sus narices, había soluciones de los tres tipos de cúbica. Así que Cardano podía decir honestamente que no estaba publicando el método de Tartaglia, sino el de Del Ferro.
Tartaglia no veía las cosas así. Pero no tenía una respuesta real a la afirmación de Cardano de que la solución no era descubrimiento de Tartaglia en absoluto, sino de Del Ferro. Tartaglia publicó una larga y amarga diatriba sobre el asunto, y fue desafiado a un debate público por Ferrari, que defendía a su maestro. Ferrari ganó de calle, y Tartaglia nunca se recuperó realmente del revés.
§. Símbolos algebraicos
Los matemáticos de la Italia del Renacimiento habían desarrollado muchos métodos algebraicos pero su notación era todavía rudimentaria. Se necesitaron cientos de años para desarrollar el simbolismo algebraico actual.
Girolamo CardanoGirolamo Cardano (también conocido como Hieronymus Cardanus, Jerónimo Cardano) fue el hijo ilegitimo del abogado milanés Fazio Cardano y una viuda joven llamada Chiara Micheria que estaba tratando de criar a tres niños. Los niños murieron a causa de la peste en Milán mientras Chiara estaba dando a luz a Girolamo en la cercana Pavía. Fazio era un matemático capaz y transmitió su pasión por la disciplina a Girolamo. Contra los deseos de su padre, Girolamo estudió medicina en la Universidad de Pavía.
Fazio hubiera querido que estudiara derecho.
Siendo todavía un estudiante, Cardano fue elegido rector de la Universidad de Padua, a la que se había trasladado, por un solo voto. Tras malgastar una pequeña herencia de su padre muerto recientemente, Cardano se dedicó al juego -cartas, dados y ajedrez- para aumentar sus finanzas. Siempre llevaba una navaja y en cierta ocasión cortó el rostro de un rival de quien creía que estaba haciendo trampas.
En 1525 Cardano obtuvo el título de medicina, pero su solicitud para entrar en el Colegio de Médicos de Milán fue rechazada, probablemente debido a su reputación de persona difícil. Practicó la medicina en la villa de Sacca, y se casó con Lucia Bandarini, hija de un capitán de la milicia. La práctica no prosperó, y en 1533 Girolamo se dedicó de nuevo al juego, pero ahora sufrió fuertes pérdidas y tuvo que empeñar las joyas de su mujer y parte de las pertenencias de la familia.
Cardano tuvo un golpe de fortuna y se le ofreció el antiguo puesto de su padre como profesor de matemáticas en la Fundación Piatti. Paralelamente siguió practicando la medicina, y algunas curaciones milagrosas aumentaron su reputación como médico. En 1539, tras varios intentos, fue admitido finalmente en el Colegio de Médicos. Empezó a publicar textos eruditos sobre varios temas, incluidas las matemáticas.
Cardano escribió una notable autobiografía, El libro de mi vida, una miscelánea de capítulos sobre temas diversos. Alcanzó la cima de su fama y visitó Edimburgo para tratar al arzobispo de Saint Andrews, John Hamilton. Hamilton padecía un asma severa. Bajo los cuidados de Cardano su salud mejoró espectacularmente, y Cardano dejó Escocia 2.000 coronas de oro más rico.
Llegó a ser profesor en la Universidad de Pavía, y las cosas iban muy bien hasta que su hijo mayor Giambatista se casó en secreto con Brandonia di Seroni, «una mujer indigna y desvergonzada» en estimación de Cardano. Ella y su familia humillaron y amedrentaron públicamente a Giambatista, que la envenenó. Pese a los esfuerzos de Cardano. Giambatista fue ejecutado. En 1570 Cardano fue procesado por herejía por haber hecho el horóscopo de Jesús. Fue encarcelado, y luego liberado, pero privado del empleo de la universidad. Fue a Roma, donde inesperadamente el Papa le concedió una pensión y fue admitido en el Colegio de Médicos.
Predijo la fecha de su propia muerte, y supuestamente se aseguró de acertar cometiendo suicidio. Pese a sus muchas tribulaciones, siguió optimista hasta el final.
Uno de los primeros en utilizar símbolos en lugar de números desconocidos fue Diofanto de Alejandría. Su aritmética, escrita alrededor del 250, constaba originalmente de 13 libros, seis de los cuales se han conservado como copias posteriores. Se centran en la solución de ecuaciones algebraicas, ya sea en números enteros o en números racionales -fracciones p/q donde p y q son enteros. La notación de Diofanto difiere considerablemente de la que utilizamos hoy.
Aunque la aritmética es el único documento conservado sobre este tema, hay evidencia fragmentaria de que Diofanto formaba parte de una tradición más amplia y no era una figura aislada. La notación de Diofanto no es muy adecuada para los cálculos, pero los resume en una forma compacta.
Los matemáticos árabes del período medieval desarrollaron métodos sofisticados para resolver ecuaciones, pero los expresaban en palabras, no en símbolos.
El paso a la notación simbólica se aceleró en el periodo renacentista.
El primero de los grandes algebristas en empezar a utilizar símbolos fue François Viète, que enunció muchos de sus resultados en forma simbólica, pero su notación difería considerablemente de la moderna. No obstante, él utilizaba letras del alfabeto para representar cantidades conocidas tanto como incógnitas. Para distinguirlas adoptó el convenio de que las consonantes B, C, D, F, G... representaban cantidades conocidas, mientras que las vocales A, E, I... representaban incógnitas.
En el siglo XV lucieron su aparición algunos símbolos rudimentarios, en particular las letras p y m para suma y resta: más y menos. Éstas eran abreviaturas antes que verdaderos símbolos. Los símbolos + y - también aparecieron en esta época. Surgieron en el comercio, donde eran utilizados por los mercaderes alemanes para distinguir artículos por exceso y por defecto. Los matemáticos también empezaron a utilizarlos rápidamente; los primeros ejemplos escritos son de 1481. William Oughtred introdujo el símbolo x para la multiplicación, y fue rotundamente (y correctamente) criticado por Leibniz sobre la base de que esto se confundía demasiado fácilmente con la letra x.
En 1557, en su The Whetstone of Witte, el matemático inglés Robert Recordé inventó el símbolo = para la igualdad, en uso desde entonces. Decía que él no podía pensar en dos cosas que fueran más iguales que dos líneas paralelas de la misma longitud. Sin embargo, él utilizaba líneas mucho más largas que lo que hacemos hoy, algo así como =======. Viète escribía inicialmente la palabra «æqualis» para igualdad, pero más tarde la reemplazó por el símbolo ~. René Descartes utilizaba un símbolo diferente "µ"
Los símbolos actuales > y < para «mayor que» y «menor que» se deben a Thomas Harriot. Los paréntesis redondos ( ) aparecen en 1544, y los paréntesis cuadrados [ ] y los corchetes { } eran utilizados por Viète hacia 1593. Descartes utilizaba el símbolo de raíz cuadrada √, que es una elaboración de la letra r para radix, o raíz; pero escribía √c para la raíz cúbica.
Para ver lo diferente que era la notación algebraica renacentista de la nuestra, he aquí un breve extracto del Ars Magna de Cardano:
5p: R m: 15
5m: R m: 15
25m:m: 15 qd. est 40.
En notación moderna esto sería
(5 + √-15)(5- √-15) = 25- (-15) = 40.
De modo que aquí vemos p: y m: para más y menos, R para «raíz cuadrada», y «qd. est» que abrevia la frase latina «que es». El escribía
qdratu aeqtur 4 rebus p:32
donde nosotros escribiríamos
x2 = 4x + 32
y por lo tanto utilizaba abreviaturas independientes «rebus» y «qdratu» para la incógnita («cosa») y su cuadrado. En otro lugar utilizaría R para la incógnita, z para su cuadrado y C para su cubo.
Una figura influyente pero poco conocida fue el francés Nicolás Chuquet, cuyo libro Triparty en la Science de Nombres de 1484 discutía tres temas matemáticos principales: aritmética, raíces e incógnitas. Su notación para las raíces era muy parecida a la de Cardano, pero él empezó a sistematizar el tratamiento de potencias de la incógnita, utilizando superíndices. Se refería a las cuatro primeras potencias de la incógnita como premier, champs, cubiez y champs de champs. Para lo que ahora escribimos 6x, 4x2 y 5x3, él utilizaba .6.1, .4.2 y .5.3.
También utilizaba potencias cero y negativas, escribiendo .2.0 y .3.1 donde nosotros escribiríamos 2 y 3x-1. En resumen, utilizaba notación exponencial (superíndices) para potencias de la incógnita, pero no tenía un símbolo explícito para la propia incógnita.
La omisión fue reparada por Descartes. Su notación era muy parecida a la que utilizamos hoy, con una excepción. Donde nosotros escribiríamos
5 + x + 6x2 + 11x3 + 3x4
Descartes escribía
5 + 4x + 6xx +11x3 + 3x4.
Es decir, él utilizaba xx para el cuadrado. En ocasiones, sin embargo, utilizaba x2. Newton escribía las potencias de la incógnita exactamente como hacemos ahora, incluyendo exponentes fraccionarios y negativos, tales como x3/2 para la raíz cuadrada de x3. Fue Gauss quien finalmente abolió xx en favor de x2; una vez que lo había hecho el Gran Maestro, todos los demás le siguieron.
§. La lógica de las especies
El álgebra empezó como una forma de sistematizar problemas en aritmética, pero para la época de Viète había adquirido una vida propia. Antes de Viète, la manipulación y el simbolismo algebraicos eran vistos como maneras de enunciar y llevar a cabo procedimientos aritméticos, pero los números seguían siendo el punto principal. Viète hizo una distinción crucial entre lo que él llamaba «la lógica de las especies» y «la lógica de los números».
En su visión, una expresión algebraica representaba toda una clase («especie») de expresiones aritméticas. Era un concepto diferente. En su In Artem Analyticam Isagoge (Introducción al arte analítico) de 1591 explicaba que el álgebra es un método para operar sobre formas generales, mientras que la aritmética es un método para operar sobre números concretos.
Para qué nos sirve el álgebraLos principales consumidores de álgebra en el mundo moderno son los científicos, que representan las regularidades de la naturaleza en términos de ecuaciones algebraicas. Estas ecuaciones pueden resolverse para representar magnitudes desconocidas en términos de otras conocidas. La técnica se ha hecho tan rutinaria que nadie advierte que está utilizando álgebra.
El álgebra se aplicaba a la arqueología en un episodio del Time Team, cuando los intrépidos arqueólogos de la televisión querían calcular la profundidad de un pozo medieval. La primera idea era dejar caer algo dentro del pozo y cronometrar cuánto tiempo tardaba en llegar al fondo. Tardaba 6 segundos. La fórmula algebraica relevante aquí es
s = ½ gt2
donde s es la profundidad, t es el tiempo que tarda en dar contra el fondo y g es la aceleración debida a la gravedad, aproximadamente 10 metros por segundo cada segundo. Tomando t = 6, la fórmula nos dice que el pozo tiene una profundidad aproximada de 180 metros.
Debido a ciertas dudas sobre si habían recordado la fórmula correctamente, el Time Team utilizó 3 largas cintas métricas unidas.
La profundidad medida era de hecho muy cercana a 180 metros.
El álgebra interviene de forma más obvia si sabemos la profundidad y queremos calcular el tiempo. Ahora tenemos que resolver la ecuación para escribir t en función de s, lo que lleva a la respuesta
t= √(2s/t)
Sabiendo que s = 180 metros, por ejemplo, predecimos que t es la raíz cuadrada de 360/10, es decir, la raíz cuadrada de 36.
Esto quizá suene como una sutileza lógica, pero la diferencia en el punto de vista era importante. Para Viète, un cálculo algebraico como (en nuestra notación)
(2x + 3y) - (x + y) = x + 2y
expresa una manera de manipular expresiones simbólicas. Los términos individuales 2x + 3y y demás son objetos matemáticos en sí mismos. Pueden ser sumados, restados, multiplicados y divididos sin considerarlos nunca como representaciones de números específicos. Para los predecesores de Viète, sin embargo, esa misma ecuación era simplemente una relación numérica que era válida cuando quiera que números concretos sustituían a los símbolos x e y. Así, el álgebra adquiriría una vida propia, como las matemáticas de expresiones simbólicas. Fue el primer paso para liberar al álgebra de las ataduras de la interpretación aritmética.
Capítulo 5
Triángulos eternos
Trigonometría y logaritmos
La geometría euclidiana se basa en triángulos, principalmente porque todo polígono puede construirse a partir de triángulos, y muchas formas interesantes, tales como círculos o elipses, pueden aproximarse por polígonos.
Las propiedades métricas de los triángulos -las que pueden medirse, tales como las longitudes de los lados, los tamaños de los ángulos o el área total- están relacionadas por una variedad de fórmulas, algunas de ellas muy elegantes. El uso práctico de dichas fórmulas, que son extraordinariamente útiles en navegación y topografía, requería el desarrollo de la trigonometría, que básicamente significa «medir triángulos».
§. Trigonometría
La trigonometría generó varias «funciones especiales»: reglas matemáticas para calcular una magnitud a partir de otra. Estas funciones llevan nombres como «seno», «coseno» y «tangente». Las funciones trigonométricas resultaron ser de vital importancia para el conjunto de las matemáticas, y no sólo para medir triángulos.
La trigonometría es una de las técnicas matemáticas más ampliamente utilizadas: está implicada en todo lo que va de la topografía a la navegación y a los sistemas de navegación GPS en los automóviles. Su uso en ciencia y tecnología es tan común que normalmente pasa desapercibido, como corresponde a cualquier herramienta universal. Desde el punto de vista histórico estuvo íntimamente asociada a los logaritmos, un método ingenioso para convertir multiplicaciones (que son difíciles) en sumas (que son mucho más simples). Las ideas principales surgieron aproximadamente entre el 1400 y el 1600, aunque tuvieron una larga «prehistoria» y muchos embellecimientos posteriores. La notación todavía sigue hoy en plena evolución.
En este capítulo echaremos una ojeada a los temas básicos: las funciones trigonométricas, la función exponencial y los logaritmos.
“La humanidad debe mucho a estos pioneros dedicados y obstinados”
También consideraremos algunas aplicaciones, antiguas y modernas. Muchas de las aplicaciones más antiguas son técnicas computacionales que en su mayoría se han vuelto obsoletas ahora que los computadores están ampliamente extendidos. Por ejemplo, difícilmente alguien utiliza tablas de logaritmos para hacer sumas.
Nadie utiliza tablas en absoluto, pues los computadores pueden calcular los valores de las funciones con gran rapidez y alta precisión.
Trigonometría. Ideas básicasLa trigonometría se basa en varias funciones especiales, de las que las más básicas son el seno, el coseno y la tangente. Estas funciones se aplican a un ángulo, tradicionalmente representado por la letra griega θ («theta»). Pueden definirse en términos de un triángulo rectángulo, cuyos tres lados a, b, c se denominan el lado adyacente, el lado opuesto y la hipotenusa.
Entonces:
El seno de theta es sen θ = b/c
El coseno de theta es cos θ = a/c
La tangente de theta es tan θ = b/a
Así definidos, los valores de estas tres funciones, para cualquier ángulo dado θ, están determinados por la geometría del triángulo. (El mismo ángulo puede aparecer en triángulos de tamaños diferentes, pero la geometría de los triángulos semejantes implica que las razones establecidas son independientes del tamaño.) Sin embargo, una vez que estas funciones han sido calculadas y tabuladas, pueden ser utilizadas para «reconstruir» el triángulo a partir del ángulo θ.
Las tres funciones están relacionadas por varias fórmulas bellas. En particular, el Teorema de Pitágoras implica que
sen2 θ + cos2 θ = 1
Pero cuando los logaritmos fueron inventados, eran las tablas numéricas las que los hacían útiles, especialmente en áreas como la astronomía en donde eran necesarios largos y complicados cálculos numéricos. Y los inventores tuvieron que pasar años -décadas- de su vida haciendo las sumas. La humanidad debe mucho a estos pioneros dedicados y obstinados.
§. Triángulos
El problema básico que aborda la trigonometría es el cálculo de propiedades de un triángulo -longitud de los lados, tamaño de los ángulos- a partir de otras de dichas propiedades. Es mucho más fácil describir la historia temprana de la trigonometría si primero resumimos las características principales de la trigonometría «moderna», que es básicamente una reelaboración en notación del siglo XVIII de temas que se remontan a los griegos, si no antes. Este resumen proporciona un marco dentro del cual podemos describir las ideas de los antiguos sin enredarnos en conceptos oscuros y eventualmente obsoletos.
Relación entre el Sol, la Luna y la Tierra cuando la Luna está en cuarto
La trigonometría parece haberse originado en la astronomía, donde las distancias son inaccesibles pero es relativamente fácil medir ángulos. El astrónomo griego Aristarco, en una obra de aproximadamente el 260 a.C., Sobre las estrellas y las distancias al Sol y la Luna, dedujo que el Sol está entre 18 y 20 veces más lejos de la Tierra que la Luna. (La cifra correcta está más cerca de 400, pero Eudoxo y Fidias habían sugerido 10.)
Su razonamiento era que cuando la Luna estaba en cuarto, el ángulo que formaban las direcciones del observador al Sol y a la Luna era de aproximadamente 87º (en unidades modernas).
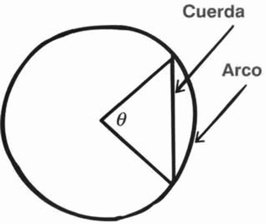
Arco y cuerda correspondientes a un ángulo θ
Utilizando propiedades de triángulos que equivalen a estimaciones trigonométricas, dedujo (en notación moderna) que sen 30º está entre 1/18 y 1/20, lo que lleva a su estimación para la razón de las distancias a la Luna y al Sol. El método era correcto, pero las observaciones eran muy poco aproximadas; el ángulo correcto es 89,8º.
Las primeras tablas trigonométricas fueron derivadas por Hiparco en torno al 150 a.C. En lugar de la moderna función seno, él utilizaba una cantidad íntimamente relacionada, que desde el punto de vista geométrico era igualmente natural. Imaginemos un círculo con dos radios que forman un ángulo θ. Los puntos en donde estos radios cortan al círculo pueden unirse por una línea recta, llamada cuerda. También pueden considerarse como los puntos extremos de un arco de círculo.
Hiparco hizo una tabla que relaciona arcos y longitudes de cuerda para un rango de ángulos. Si el círculo tiene radio 1, entonces la longitud del arco es igual a θ cuando este ángulo se mide en unidades conocidas como radianes. Un poco de geometría elemental muestra que la longitud de la cuerda en notación moderna es 2 sen θ/2. Por ello, el cálculo de Hiparco está muy estrechamente relacionado con una tabla de senos, incluso si no estaba presentado de esta manera.
§. Astronomía
Curiosamente, el trabajo inicial en trigonometría era más complicado que la mayor parte de lo que se enseña hoy en las escuelas, debido una vez más a las necesidades de la astronomía (y, más tarde, la navegación). El espacio natural con el que trabajar no era el plano, sino la esfera. En efecto, el cielo parece el interior de una gigantesca superficie esférica que rodea completamente al observador, y los cuerpos celestes son tan lejanos que parecen estar situados en dicha superficie esférica.
Como consecuencia, los cálculos astronómicos remiten a la geometría de una esfera, no de un plano. Los requisitos no son geometría plana y trigonometría, sino geometría esférica y trigonometría.
Una de las primeras obras en esta área es la Sphærica de Menelao escrita hacia el año 100. Sirva como muestra un teorema que no tiene análogo en geometría euclidiana: si dos triángulos tienen los mismos ángulos, entonces son congruentes: tienen los mismos tamaño y forma. (En el caso euclidiano los triángulos son semejantes: misma forma pero posiblemente diferentes tamaños.) En geometría esférica los ángulos de un triángulo no suman 180º, como suman en el plano. Por ejemplo, es obvio que un triángulo cuyos vértices yacen en el Polo Norte y en dos puntos del ecuador separados 90º tienen los tres ángulos iguales a un ángulo recto, de modo que su suma es 270º. En general, cuanto más grande se hace el triángulo, más grande se hace la suma de sus ángulos. De hecho, esta suma, menos 180º, es proporcional al área total del triángulo.
Estos ejemplos dejan claro que la geometría esférica tiene sus propias características y aspectos nuevos. Lo mismo ocurre con la trigonometría esférica, pero las cantidades básicas siguen siendo las funciones trigonométricas estándar. Sólo cambian las fórmulas.
§. Ptolomeo
Con mucho, el texto más importante de trigonometría de la Antigüedad fue la Sintaxis matemática de Ptolomeo de Alejandría, que data de aproximadamente el año 150. Es más conocido como el Almagesto, un término árabe que significa «el más grande». Incluía tablas trigonométricas, una vez más establecidas en términos de cuerdas, junto con los métodos utilizados para calcularlas, y un catálogo de posiciones de estrellas en la esfera celeste.
Un aspecto esencial del método computacional era el teorema de Ptolomeo: si ABCD es un cuadrilátero cíclico (un cuadrilátero cuyos vértices yacen en un círculo) entonces
AB × CD + BC × DA = AC × BD
(la suma de los productos de pares de lados opuestos es igual al producto de las diagonales).
Una interpretación moderna de este hecho es el notable par de fórmulas
Lo importante en estas fórmulas es que si se conocen los senos y cosenos de dos ángulos, entonces se puede calcular también la suma de dichos ángulos. Por lo tanto, partiendo de (digamos) sen 1º y cos 1º, se puede deducir sen 2º y cos 2º tomando θ = φ = 1º. Luego se puede deducir sen 3º y cos 3º tomando θ = 1º y φ = 2º, y así sucesivamente. Había que saber cómo empezar, pero después de eso todo lo que se necesitaba era aritmética; bastante de ella, pero nada más complicado.
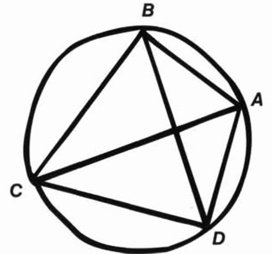
Cuadrilátero cíclico y sus diagonales
Empezar era más fácil de lo que podría parecer, y ello requería aritmética y raíces cuadradas. Utilizando el hecho obvio de que θ/2 + θ/2 = θ, el teorema de Ptolomeo implica que
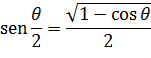
Partiendo de cos 90º = 0, se puede dividir el ángulo repetidamente por 2, y obtener el seno y el coseno de un ángulo tan pequeño como se quiera. (Ptolomeo utilizaba ¼º). Luego se puede ir hacia atrás pasando por todos los múltiplos enteros de dicho ángulo pequeño. En resumen: unas pocas fórmulas trigonométricas generales, aplicadas de la forma adecuada, «extraen» de unos pocos valores simples para ángulos específicos, valores para prácticamente todos los ángulos que uno quiera. Era un extraordinario tour de forcé, y sirvió a los astrónomos durante más de mil años.
§. Movimiento planetario
Un aspecto final digno de mención del Almagesto es el tratamiento que hacía de las órbitas de los planetas. Cualquiera que observe con regularidad el cielo nocturno descubre rápidamente que los planetas vagan en el fondo de estrellas «fijas», y que sus trayectorias parecen bastante complicadas, moviéndose a veces hacia atrás o viajando en lazos alargados.
Eudoxo, respondiendo a una petición de Platón, había encontrado un modo de representar estos movimientos complejos en términos de esferas que giraban montadas sobre otras esferas. Esta idea fue simplificada por Apolonio e Hiparco, que utilizaban epiciclos: círculos cuyos centros se mueven a lo largo de otros círculos, y así sucesivamente. Ptolomeo refinó el sistema de epiciclos, que llegó a proporcionar un modelo muy aproximado de los movimientos planetarios.
§. Los comienzos de la trigonometría
Los primeros conceptos trigonométricos aparecen en los escritos de los matemáticos y astrónomos hindúes: Pancha Siddhanta de Varahamihira en el año 500, Brama Sputa Siddhanta de Brahmagupta en el 628 y el más detallado Siddhanta Siromani de Bhaskaracharya en 1150.
Los matemáticos indios utilizaban generalmente la semi-cuerda, o jya-ardha, que de hecho es el seno moderno. Varahamihira calculó esta función para 24 múltiplos enteros de 3º 45’, hasta 90º. Alrededor del 600, en el Maha Bhaskariya, Bhaskara dio una útil fórmula aproximada para el seno de un ángulo agudo, que él atribuía a Aryabhata. Estos autores dedujeron varias fórmulas trigonométricas básicas.
“Los primeros conceptos trigonométricos aparecen en los escritos de los matemáticos y astrónomos hindúes.”
El Tratado sobre el cuadrilátero del matemático árabe Nasir-Eddin combinaba la geometría plana y la esférica en un desarrollo unificado, y daba varias fórmulas básicas para triángulos esféricos. Trataba el tema de forma matemática y no como una parte de la astronomía. Pero su obra pasó desapercibida en Occidente hasta aproximadamente el año 1450.
Debido al vínculo con la astronomía, casi toda la trigonometría era esférica hasta 1450. En particular, la topografía -hoy día una usuaria importante de trigonometría- se realizaba utilizando métodos empíricos, codificados por los romanos. Pero a mediados del siglo XV la trigonometría plana empezó a independizarse, inicialmente en la Liga Hanseática alemana. La Liga controlaba la mayor parte del comercio, y en consecuencia era rica e influyente. Y necesitaba mejorar los métodos de navegación, junto con mejoras en el calendario y en los usos prácticos de las observaciones astronómicas.
Movimiento de Marte visto desde la Tierra
Una figura clave fue Johannes Müller, normalmente conocido como Regiomontano. Era un pupilo de George Peurbach, quien empezó a trabajar en una nueva versión corregida del Almagesto. En 1471, financiado por su patrón Bernard Walther, calculó una nueva tabla de senos y una tabla de tangentes.
Otros matemáticos destacados de los siglos XV y XVI calcularon sus propias tablas trigonométricas, con frecuencia de una extraordinaria precisión. George Joachim Rhaeticus calculó senos para un círculo de radio 1015 -en la práctica, tablas precisas hasta 15 cifras decimales, pero multiplicando todos los números por 1015 para obtener enteros- para todos los múltiplos de un segundo de arco. Enunció la ley de los senos para triángulos esféricos,
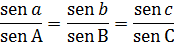
y la ley de los cosenos
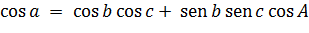
en su De Triangulis, escrito en 1462-1463 pero no publicado hasta 1533.
Aquí A, B, C son los ángulos del triángulo, y a, b, c son sus lados, medidos por los ángulos que determinan en el centro de la esfera.
Viète escribió ampliamente sobre trigonometría, siendo su primer libro sobre el tema el Canon Mathematicus de 1579. Recogió y sistematizó varios métodos para «resolver triángulos»: calcular todos los lados y ángulos a partir de un subconjunto de información. Inventó nuevas identidades trigonométricas, entre ellas algunas interesantes expresiones para senos y cosenos de múltiplos enteros de θ en términos del seno y el coseno de θ.
§. Logaritmos
El segundo tema de este capítulo es una de las funciones más importantes en matemáticas: el logaritmo, log x. Inicialmente, el logaritmo era importante porque satisface la ecuación
log xy = log x + log y
y por consiguiente puede utilizarse para convertir multiplicaciones (cuyo cálculo es engorroso) en sumas (que son más sencillas y más rápidas).
Para multiplicar dos números x e y, se forman primero sus logaritmos, se suman, y luego se encuentra el número que tiene dicha suma como logaritmo (su anti-logaritmo). Este número es el producto xy. Una vez que los matemáticos hubieran calculado tablas de logaritmos, éstas podían ser utilizadas por cualquiera que comprendiera el método. Desde el siglo XVII hasta mediados del siglo XX, prácticamente todos los cálculos científicos, especialmente los astronómicos, utilizaban logaritmos.
A partir de los años sesenta del siglo XX, las calculadoras y los computadores electrónicos hicieron a los logaritmos obsoletos para fines de cálculo.
No obstante, el concepto siguió siendo vital para las matemáticas, porque los logaritmos habían encontrado papeles fundamentales en muchas partes de las matemáticas, incluidos el cálculo infinitesimal y el análisis complejo. Muchos procesos físicos y biológicos incluyen un comportamiento logarítmico.
Hoy día nos acercamos a los logaritmos considerándolos como el inverso de las exponenciales. Utilizando «logaritmos de base 10», que son una elección natural para la notación decimal, decimos que x es el logaritmo de y si y = 10x. Por ejemplo, puesto que 103 = 1.000, el logaritmo de 1.000 (en base 10) es 3. La propiedad básica de los logaritmos se sigue de la ley exponencial
10a + b = 10a × 10b.
Sin embargo, para que los logaritmos sean útiles tenemos que ser capaces de encontrar un x para cualquier y real positivo. Siguiendo el ejemplo de Newton y otros autores de su período, la idea principal es que cualquier potencia racional 10p/q puede definirse como la raíz q-ésima de 10p. Puesto que cualquier número real x puede ser aproximado con precisión arbitraria por un número racional p/q, podemos aproximar 10x por 10p/q. Ésta no es la manera más eficaz de calcular el logaritmo, pero es la manera más simple de demostrar que existe.
Históricamente, el descubrimiento de los logaritmos fue menos directo. Empezó con John Napier, barón de Murchiston en Escocia. Él tuvo un permanente interés en los métodos eficaces de cálculo, e inventó las varas de Napier (o huesos de Napier), un conjunto de palos marcados que podían utilizarse para hacer multiplicaciones de forma rápida y fiable simulando métodos de papel y lápiz. Alrededor de 1594 empezó a trabajar en un método más teórico, y sus escritos nos dicen que le llevó veinte años perfeccionarlo y publicarlo. Parece probable que su punto de partida fueran las «progresiones geométricas», secuencias de números en las que cada término se obtiene del precedente multiplicándolo por un número fijo, tales como las potencias de 2
1 → 2 → 4 → 8 → 16 → 32 →...
o las potencias de 10
1 → 10 → 100 → 1.000 → 10.000 → 100.000 → ...
Se había advertido hacía tiempo que sumar los exponentes era equivalente a multiplicar las potencias. Esto estaba bien si uno quería multiplicar dos potencias de 2, digamos, o dos potencias enteras de 10. Pero había grandes huecos entre estos números, y las potencias de 2 o 10 no parecían servir de mucho cuando se trataba de problemas como 57.681 × 29.443, pongamos por caso.
Trigonometría planaHoy día la trigonometría se desarrolla primero en el plano, donde la geometría es más simple y los principios básicos son más fáciles de captar. (Es curioso cuan a menudo nuevas ideas matemáticas se desarrollan inicialmente en un contexto complicado, y las simplicidades subyacentes emergen mucho después.) Existe una ley de los senos, y una ley de los cosenos, para triángulos planos, y vale la pena hacer una pequeña digresión para explicarlas. Consideremos un triángulo plano con ángulos A, B, C y lados a, b, c.
Lados y ángulos de un triánguloAhora la ley de los senos toma la forma
y la ley de los cosenos es
a2 = b2 + c2 - 2bc cos A,
con fórmulas similares que incluyen los otros ángulos. Podemos utilizar la ley de los cosenos para encontrar los ángulos de un triángulo a partir de sus lados.
§. Logaritmos neperianos
Mientras el buen barón estaba tratando de llenar de algún modo los huecos en las progresiones geométricas, el médico del rey Jacobo VI de Escocia, James Craig, contó a Napier el descubrimiento que era de amplio uso en Dinamarca, con el extraño nombre de prostaferesis. Este se refería a cualquier proceso que convertía productos en sumas. El método principal en uso práctico se basaba en una fórmula descubierta por Viète:
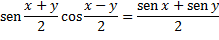
Si se disponía de tablas de senos y cosenos, se podía utilizar esta fórmula para convertir un producto en una suma. Era lioso, pero seguía siendo más rápido que multiplicar los números directamente.
Napier captó la idea, y encontró una mejora importante.
“Napier captó la idea, y encontró una mejora importante.”
Formó una serie geométrica con una razón común muy próxima a 1. Es decir, en lugar de potencias de 2 o potencias de 10, habría que utilizar potencias de, digamos, 1,0000000001. El espaciado entre las potencias sucesivas de dicho número es muy pequeño, lo que acaba con estos molestos «huecos». Por algún motivo, Napier escogió una razón ligeramente menor que 1, a saber 0,9999999. Por eso su serie geométrica va hacia atrás desde un número grande a otros cada vez más pequeños. De hecho, él empezaba con 10.000.000 y luego lo multiplicaba por potencias sucesivas de 0,9999999. Si escribimos Naplog x para el logaritmo neperiano de x, éste tiene la curiosa característica de que
Naplog 10.000.000 = 0
Naplog 9.999.999 = 1
y así sucesivamente. El logaritmo neperiano, Naplog x, satisface la ecuación
Naplog(107xy) = Naplog(x) + Naplog(y).
Esto puede utilizarse para el cálculo, porque es fácil multiplicar o dividir por una potencia de 10, pero no es elegante. No obstante, es mucho mejor que la fórmula trigonométrica de Viète.
§. Logaritmos de base 10
La siguiente mejora llegó cuando Henry Briggs, el primer catedrático saviliano de geometría de la Universidad de Oxford, visitó a Napier.
Briggs sugirió reemplazar el concepto de Napier por uno más simple: el logaritmo (en base 10), L = log10x, que satisface la condición x = 10L. Ahora
log10xy = log10 x + log10y
y todo es fácil. Para encontrar xy se suman sus logaritmos y luego se encuentra el antilogaritmo del resultado.
Para qué les servía la trigonometríaEl Almagesto de Ptolomeo fue la base de todos los estudios del movimiento planetario anteriores al descubrimiento de Johannes Kepler de que las órbitas son elípticas.
Un epiciclo. El planeta P gira uniformemente alrededor del punto D. que a su vez gira uniformemente alrededor del punto CLos movimientos observados de un planeta son complicados debido al movimiento relativo de la Tierra, que no se había reconocido en la época de Ptolomeo. Incluso si los planetas se movieran a velocidad uniforme en círculos, el movimiento de la Tierra alrededor del Sol requeriría una combinación de dos movimientos circulares diferentes, y un modelo preciso tiene que ser decididamente más complicado. El esquema de epiciclos de Ptolomeo combina movimientos circulares haciendo que el centro de un círculo de vueltas en otro círculo. Este círculo puede a su vez moverse alrededor de un tercer círculo, y así sucesivamente. La geometría del movimiento circular uniforme implica de forma natural funciones trigonométricas, y los astrónomos posteriores las utilizaron para los cálculos de órbitas.
Napier murió antes de que estas ideas pudieran difundirse; era el año 1617, y su descripción de sus varas de cálculo, Rhabdología, acababa de publicarse. Su método original para calcular, el Mirifici Logarithmorum Canonis Constructio, apareció dos años después. Briggs asumió la tarea de calcular una tabla de logaritmos «briggsianos» (de base 10, o comunes). Lo hizo partiendo de log10 10 = 1 y tomando raíces cuadradas sucesivas. En 1617 publicó Logarithmorum Chilias Prima, los logaritmos de los enteros de 1 a 1.000, establecidos hasta 14 cifras decimales.
Su Arithmetic Logarithmica de 1624 tabulaba logaritmos comunes de números de 1 a 20.000 y de 90.000 a 100.000, también con 14 cifras.
La idea creció como una bola de nieve. John Speidell calculó logaritmos de funciones trigonométricas -tales como log sen x - publicados como Nuevos Logaritmos en 1619. El relojero suizo Jobst Bürgi publicó su propia obra sobre logaritmos en 1610, y es muy posible que tuviera la idea básica en 1588, mucho antes que Napier. Pero el desarrollo histórico de las matemáticas depende de lo que la gente publica -en el sentido original de «hacer público»-, y las ideas que permanecen en privado no tienen influencia en nadie más. Por ello, el crédito, probablemente con razón, tiene que ir a esas personas que ponen sus ideas en prensa, o al menos en cartas de amplia circulación. (La excepción es la persona que pone las ideas de otros en prensa sin darles el crédito debido. Esto es inaceptable.)
§. La letra «e»
Asociado con la versión de Napier de los logaritmos está uno de los números más importantes en matemáticas, ahora denotado por la letra e. Su valor es aproximadamente 2,7182. Aparece si tratamos de formar logaritmos partiendo de una serie geométrica cuya razón común es ligeramente mayor que 1. Esto lleva a la expresión (1 + 1 /n)n donde n es un entero muy grande; y cuanto mayor se hace n, más se acerca la expresión a un número especial, que denotamos por e.
Esta fórmula sugiere que hay una base «natural» para los logaritmos, que no es 10 ni 2, sino e. El logaritmo natural de x es un número y que satisface la condición x = loge y. En las matemáticas actuales, el logaritmo natural se escribe y = log x. A veces la base e se hace explícita como y = logex, pero esta notación está restringida básicamente a las matemáticas escolares, porque en ciencias y en matemáticas avanzadas los únicos logaritmos de importancia son los logaritmos naturales. Los logaritmos en base 10 son mejores para los cálculos en notación decimal, pero los logaritmos naturales son fundamentales desde el punto de vista matemático.
La expresión ex se llama exponencial de x, y es uno de los conceptos más importantes en todas las matemáticas. El número e es uno de esos extraños números especiales que aparecen en matemáticas y tienen una gran trascendencia. El más familiar de tales números es π. Estos dos son la punta de un iceberg; hay muchos otros. Presumiblemente son también los números especiales más importantes en las matemáticas actuales, porque afloran por todo el paisaje matemático.
§. ¿Dónde estaríamos sin ellos?
Sería difícil subestimar la deuda que tenemos con aquellos individuos previsores que inventaron los logaritmos y la trigonometría y pasaron años de su vida calculando tediosamente las primeras tablas numéricas de tales cantidades. Sus esfuerzos prepararon el camino para una comprensión científica cuantitativa del mundo natural, y permitieron la generalización de los viajes y el comercio al mejorar la navegación y la cartografía.
Las técnicas básicas de topografía se basan en cálculos trigonométricos. Incluso hoy, cuando los equipos utilizan láseres y los cálculos se hacen en un chip construido a medida, los conceptos que el láser y el chip incorporan son descendientes directos de la trigonometría que intrigaba a los matemáticos de la India y Arabia antiguas.
Los logaritmos hicieron posible que los matemáticos hicieran cálculos de forma rápida y exacta. Veinte años de esfuerzo, por parte de un matemático, en un libro de tablas ahorraron decenas de miles hombre-años de trabajo posterior. Entonces se hizo posible realizar análisis científicos que de otra forma hubieran llevado demasiado tiempo; incluso sin computadores, utilizando sólo papel y lápiz y el cerebro humano. La ciencia no podría haber avanzado sin algunos de esos métodos. Los beneficios de una idea tan simple han sido verdaderamente incalculables.
Para qué nos sirve la trigonometríaLa trigonometría es fundamental para la topografía, en escalas que van desde emplazamientos de construcciones hasta continentes.
Es relativamente fácil medir ángulos con alta precisión, pero las distancias son mucho más difíciles, especialmente en un terreno abrupto.
Por eso los topógrafos empiezan haciendo una medida cuidadosa de una longitud, la línea de base, es decir, la distancia entre dos puntos concretos. Luego forman una red de triángulos y utilizan los ángulos medidos, más trigonometría, para calcular los lados de estos triángulos. De este modo puede construirse un mapa, preciso de toda el área de interés.
El proceso se conoce como triangulación. Para comprobar su precisión, puede hacerse una segunda medida de distancia una vez que la triangulación se ha completado.
Triangulación de África del Sur por LaCailleLa figura muestra un ejemplo primitivo, una famosa exploración realizada en Sudáfrica en 1751 por el gran astrónomo Abbé Nicolas-Louis de Lacaille. Su objetivo principal era catalogar las estrellas de los cielos australes, pero para hacerlo con precisión tenía que medir primero el arco de un meridiano adecuado. Para ello, desarrolló una triangulación al norte de Ciudad del Cabo.
Su resultado sugería que la curvatura de la Tierra es menor en las latitudes australes que en las septentrionales, una deducción sorprendente que fue verificada por medidas posteriores.
La Tierra tiene una forma ligeramente de pera. Sus actividades de catalogación tuvieron tanto éxito que él dio nombre a 15 de las 88 constelaciones ahora reconocidas, tras observar más de 10.000 estrellas utilizando un pequeño telescopio refractor.
Capítulo 6
Curvas y coordenadas
Geometría es álgebra, es geometría
Aunque es habitual clasificar las matemáticas en áreas independientes, tales como aritmética, álgebra, geometría y demás, esta clasificación debe más a la conveniencia humana que a la verdadera estructura de la disciplina. En matemáticas no hay fronteras rígidas y claras entre áreas aparentemente distintas, y problemas que parecen pertenecer a un área pueden ser resueltos utilizando métodos de otra. De hecho, los mayores avances se suelen producir cuando se establece alguna conexión inesperada entre temas que antes parecían distintos.
§. Pierre Fermat
Las matemáticas griegas tienen huellas de tales conexiones, como son los vínculos entre el Teorema de Pitágoras y los números irracionales o el uso de Arquímedes de analogías mecánicas para encontrar el volumen de la esfera.
La verdadera extensión e influencia de tal fertilización cruzada se hizo innegable en un corto periodo de tiempo en torno a 1630. Durante ese breve periodo, dos de los más grandes matemáticos del mundo descubrieron una notable conexión entre álgebra y geometría. De hecho, ellos demostraron que cada una de estas áreas puede convertirse en la otra utilizando «coordenadas».
Toda la obra de Euclides, y la obra de sus sucesores, puede reducirse a cálculos algebraicos. Recíprocamente, todo en álgebra puede interpretarse en términos de la geometría de curvas y superficies.
Podría parecer que tales conexiones hacen superflua una de las dos áreas.
Si toda la geometría puede reemplazarse por álgebra, ¿por qué necesitamos la geometría? La respuesta es que cada área tiene su punto de vista característico, que en ocasiones puede ser muy penetrante y poderoso. A veces es mejor pensar geométricamente, y a veces es superior el pensamiento algebraico.
La primera persona que describió las coordenadas fue Pierre Fermat.
Fermat es más conocido por su trabajo sobre teoría de números, pero también estudió muchas otras áreas de las matemáticas, incluidas la probabilidad, la geometría y las aplicaciones a la óptica. Alrededor de 1620, Fermat estaba tratando de entender la geometría de curvas, y empezó por reconstruir, a partir de la poca información de que disponía, un libro perdido de Apolonio llamado Sobre los loci en
el plano. Hecho esto, Fermat se embarcó en sus propias investigaciones, que escribió en 1629 pero no publicó hasta cincuenta años más tarde, como Introducción a los locis planos y sólidos.
Al hacerlo descubrió las ventajas de reformular conceptos geométricos en términos algebraicos.
Propiedad focal de la elipse
Locus, en plural loci, es hoy un término obsoleto, pero era común incluso en 1960. En castellano se traduce como lugar geométrico. Aparece cuando buscamos todos los puntos en el plano o en el espacio que satisfacen unas condiciones geométricas concretas.
“Fermat introdujo ejes oblicuos en el plano.”
Por ejemplo, podríamos preguntar por el lugar geométrico de todos los puntos del plano tales que la suma de sus distancias a dos puntos dados es la misma. Este lugar geométrico resulta ser una elipse con los dos pinitos como focos.
Esta propiedad de la elipse ya era conocida por los griegos. Fermat advirtió un principio general: si las condiciones impuestas sobre los puntos pueden expresarse como una única ecuación que incluye dos incógnitas, el lugar geométrico correspondiente es una curva, o una línea recta, que consideramos un tipo especial de curva para evitar distinciones innecesarias. El ilustró este principio mediante un diagrama en el que dos cantidades desconocidas A y E se representan como distancias en dos direcciones distintas.
Luego hizo una lista de algunos tipos especiales de ecuaciones que conectan A y E, y explicó qué curvas representan. Por ejemplo, si A2 = 1 + E2, entonces el lugar geométrico en cuestión es una hipérbola.
En términos modernos, Fermat introdujo ejes oblicuos en el plano (oblicuos significa que no se cortan necesariamente en ángulos rectos). Las variables A y E son las dos coordenadas de cualquier punto dado con respecto a estos ejes, que nosotros llamaríamos x e y.
Aproximación de Fermat a las coordenadas
Por lo tanto, el principio de Fermat establece que cualquier ecuación en dos variables define una curva; y sus ejemplos nos dicen qué tipo de ecuaciones corresponden a qué tipo de curva, basándose en las curvas estándar conocidas por los griegos.
§. Descartes
La notación moderna de coordenadas dio fruto en la obra de Descartes.
En la vida cotidiana estamos familiarizados con espacios de dos y tres dimensiones, y se necesita un gran esfuerzo de imaginación para contemplar otras posibilidades. Nuestro sistema visual presenta a cada ojo el mundo exterior como una imagen bidimensional -como la imagen de una pantalla de televisor-. Imágenes ligeramente diferentes procedentes de cada ojo se combinan en el cerebro para dar una sensación de profundidad, gracias a la cual percibimos el mundo circundante como si tuviera tres dimensiones.
La clave para los espacios multidimensionales es la idea de un sistema de coordenadas, que fue introducido por Descartes en un apéndice, La geometría, a su Discurso del método. Su idea es que la geometría del plano puede reinterpretarse en términos algebraicos.
Su enfoque es esencialmente el que ya se ha señalado. Escogemos un punto en el plano y le llamamos el origen. Trazamos dos ejes: líneas que pasan por el origen y se cortan a ángulos rectos.
Etiquetamos un eje con el símbolo x y el otro con el símbolo y. Entonces cualquier punto P en el plano está determinado por el par de distancias (x, y), que nos dice lo lejos que está el punto del origen cuando se mide paralelamente a los ejes x e y, respectivamente.
Rene DescartesDescartes empezó a estudiar matemáticas en 1616 como alumno del científico holandés Isaac Beeckman. Dejó Holanda para recorrer Europa y se unió al ejército bávaro en 1619. Continuó viajando entre 1620 y 1628, y visitó Bohemia, Hungría, Alemania, Holanda, Francia e Italia. Conoció a Mersenne en París en 1622, y desde entonces mantuvo correspondencia regular con él, lo que le puso en contacto con la mayoría de los eruditos destacados del periodo.
En 1628 Descartes se estableció en Holanda, y comenzó su primer libro, Le Monde ou Traite de la Lumiére, sobre la física de la luz. La publicación fue retrasada cuando Descartes se enteró del arresto domiciliario de Galileo Galilei y sintió miedo. El libro se publicó, de forma incompleta, después de su muerte. Sin embargo, él desarrolló sus ideas sobre el pensamiento lógico en una obra importante publicada en 1637: Discours de la Méthode. El libro tenía tres apéndices: La Dioptrique, Les Météores y La Géometrie.
Su libro más ambicioso, Principia Philosophiae, se publicó en 1644. Estaba dividido en cuatro partes: Principios de conocimiento humano, Principios de las cosas materiales, El mundo visible y La Tierra. Era un intento de ofrecer un fundamento matemático unificado para todo el universo físico, que reducía a mecánica todo lo que hay en la naturaleza.
En 1649 Descartes fue a Suecia para ser tutor de la reina Cristina. La reina era muy madrugadora mientras que Descartes se levantaba normalmente a las once. Enseñar matemáticas a la reina a las cinco cada mañana, en un clima frío, supuso una gran tensión para la salud de Descartes. Al cabo de unos meses murió de neumonía.
Por ejemplo, en un mapa, x podría ser la distancia al este del origen (los valores negativos representan distancias al oeste), mientras que y podría ser la distancia al norte del origen (los valores negativos representan las distancias al sur). Las coordenadas funcionan también en un espacio tridimensional, pero ahora dos números no son suficientes para localizar un punto. Sin embargo, tres números sí lo son. Además de las distancias este-oeste y norte-sur, necesitamos saber lo lejos que está un punto por encima o por debajo del origen. Normalmente utilizamos un número positivo para distancias hacia arriba, y un número negativo para distancias hacia abajo. Las coordenadas en el espacio toman la forma (x, y, z).
Las coordenadas tal como se utilizan hoyEl desarrollo inicial de la geometría de coordenadas tendrá más sentido si explicamos primero cómo trabaja la versión moderna. Existen diversas variantes, pero las más comunes empiezan trazando dos rectas perpendiculares en el plano, llamadas ejes. Su punto de encuentro común es el origen. Los ejes se disponen convencionalmente de modo que uno de ellos es horizontal y el otro vertical.
A lo largo de ambos ejes escribimos los números enteros, con los números positivos en una dirección y los negativos en la otra. Convencionalmente, se denomina eje x al eje horizontal y eje y al vertical. Los símbolos x e y se utilizan para representar puntos en estos ejes respectivos -distancia al origen-.
Un punto general en el plano, a distancia x del eje horizontal y distancia y a lo largo d se etiqueta con un par de números (x, y). E números son las coordenadas de dicho punto.
Cualquier ecuación que relaciona x e y restringe los puntos posibles. Por ejemplo si x2 + y2 = 1, entonces (x, y) debe estar a distancia 1 del origen, por el Teorema de Pitágoras. Tales puntos forman un círculo. Decimos que x2 + y2 = 1 es la ecuación de dicho círculo
Toda ecuación corresponde a una curva en el plano; recíprocamente, toda curva corresponde a una ecuación.
Por esto se dice que el plano es bidimensional, mientras que el espacio es tridimensional. El número de dimensiones viene dado por cuántos números necesitamos para especificar un punto.
En el espacio tridimensional, una única ecuación que incluye x, y y z define normalmente una superficie. Por ejemplo, x2 + y2 + z2= 1, afirma que el punto (x, y, z) está siempre a una distancia 1 del origen, lo que implica que yace en la superficie de la esfera unidad cuyo centro es el origen.
Nótese que la palabra «dimensión» no está definida aquí por sí misma. No encontramos el número de dimensiones de un espacio encontrando algunas cosas llamadas dimensiones y contándolas luego. En su lugar, calculamos cuántos números se necesitan para especificar una posición en el espacio, y ése es el número de dimensiones.
§. Coordenadas cartesianas
La geometría de coordenadas cartesianas revela una unidad algebraica tras las secciones cónicas: curvas que los griegos habían construido como secciones de un cono doble. Desde el punto de vista algebraico resulta que las secciones cónicas son las curvas más simples después de las líneas rectas. Una línea recta corresponde a una ecuación lineal
ax + by + c = 0
con constantes a, b, c. Una sección cónica corresponde a una ecuación cuadrática
ax2 + bxy + cy2 + dx + ey + f = 0
con constantes a, b, c, d, e, f. Descartes estableció este hecho, pero no dio una demostración. Sin embargo, estudió un caso especial, basado en un teorema debido a Pappus que caracterizaba las secciones cónicas, y demostró que en este caso la ecuación resultante es cuadrática.
El folium de Descartes
Luego pasó a considerar ecuaciones de orden más alto, que definen curvas más complejas que la mayoría de las que aparecen en la geometría clásica griega. Un ejemplo típico es el folium de Descartes, con ecuación
x3 + y3 - 3axy = 0
que forma un lazo con dos extremos que tienden al infinito Quizá se dio aquí la contribución más importante hecha por el concepto de coordenadas: Descartes se apartó de la visión griega de los objetos que estaban construidos por medios geométricos específicos y las vio como el aspecto visual de una fórmula algebraica.
Como comentó Isaac Newton en 1707, «Los modernos que van mucho más allá [que los griegos] han recibido en geometría todas las líneas que pueden expresarse por ecuaciones».
Coordenadas polares
Estudiosos posteriores inventaron numerosas variantes sobre el sistema de coordenadas cartesianas. En una carta de 1643 Fermat asumió las ideas de Descartes y las extendió a tres dimensiones. Aquí menciona superficies tales como elipsoides y paraboloides, que están determinadas por ecuaciones cuadráticas en las tres variables x, y, z. Una contribución influyente fue la introducción de coordenadas polares por Jakob Bernoulli en 1691. El utilizó un ángulo θ y una distancia r para determinar puntos en el plano en lugar de un par de ejes.
Espiral de Arquímedes
Ahora las coordenadas son (r, θ).
De nuevo, las ecuaciones en estas variables especifican curvas. Pero ahora, ecuaciones simples pueden especificar curvas que resultarían muy complicadas en coordenadas cartesianas. Por ejemplo la ecuación r = θ corresponde a una espiral, del tipo conocido como una espiral arquimediana.
¿Qué Bernoulli hizo qué?
Una lista de control de los BernoulliLa familia Bernoulli tuvo una enorme influencia en el desarrollo de las matemáticas. Eran suizos, y durante cuatro generaciones produjeron matemáticas importantes, tanto puras como aplicadas. A veces descritos como una «mafia matemática», los Bernoulli típicamente iniciaban una carrera tal como derecho, medicina o la eclesiástica, pero con el tiempo volvían a lo suyo y se convertían en matemáticos, ya fueran profesionales o aficionados.
Muchos conceptos matemáticos diferentes llevan el nombre Bernoulli, pero no siempre se trata del mismo Bernoulli. Más que ofrecer detalles biográficos sobre ellos, he aquí un resumen de quién hizo qué.
Jacob (1654-1705)
Coordenadas polares, fórmula parael radio de curvatura de una curva plana. Curvas especiales, tales como la catenaria y la lemniscata. Demostró que una isócrona (una curva a lo largo de la cual un cuerpo caería con velocidad vertical uniforme) es una cicloide invertida. Discutió figuras isoperimétricas, que tienen la longitud más corta bajo diferentes condiciones, un tema que más tarde llevó al cálculo de variaciones. Estudiante temprano de la probabilidad y autor del primer libro sobre el tema, Ars Conjectandi. Pidió que en su tumba se grabara una espiral logarítmica, junto con la inscripción Eadem mutata resurgo (Me levantaré igual aunque cambiado).
Johann I (1667-1748)
Desarrolló el cálculo infinitesimal y lo promocionó en Europa. El Marquis de L’Hôpital puso la obra de Johann en el primer libro de texto de cálculo infinitesimal. La «regla de L’Hôpital» para evaluar límites que se reducen a 0/0 se debe a Johann.
Escribió sobre óptica (reflexión y refracción), trayectorias ortogonales de familias de curvas, longitudes de curvas y evaluación de áreas por series, trigonometría analítica y la función exponencial.
La braquistócrona (curva de descenso más rápido), longitud de la cicloide.
Nicolaus I (1687-1759)
Ocupó la cátedra de matemáticas de Galileo en Padua. Escribió sobre geometría y ecuaciones diferenciales.
Más tarde enseñó lógica y derecho. Matemático dotado aunque no muy productivo. Mantuvo correspondencia con Leibniz, Euler y otros (sus logros principales están diseminados entre 560 piezas de correspondencia). Formuló la Paradoja de San Petersburgo en probabilidad. Criticó el uso indiscriminado de series divergentes por parte de Euler. Ayudó en la publicación del Ars Conjectandi de Jakob Bernoulli. Apoyó a Leibniz en su controversia con Newton.
Nicolaus II (1695-1726)
Llamado a la Academia de San Petersburgo, murió ahogado ocho meses después. Discutió la Paradoja de San Petersburgo con Daniel.
Daniel (1700-1782)
El más famoso de los tres hijos de Johann. Trabajó en probabilidad, astronomía, física e hidrodinámica.
Su Hydrodynamica de 1738 contiene el «principio de Bernoulli» sobre la relación entre presión y velocidad. Escribió sobre mareas, teoría cinética de los gases y cuerdas vibrantes. Pionero en ecuaciones en derivadas parciales.
Johann II (1710-1790)
El más joven de los tres hijos de Johann. Estudió derecho pero se convirtió en profesor de matemáticas en Basilea. Trabajó en la teoría matemática del calor y la luz.
Johann III (1744-1807)
Como su padre, estudió derecho pero luego se volvió a las matemáticas. Llamado a la Academia de Berlín cuando tenía 19 anos. Escribió sobre astronomía, azar y decimales recurrentes.
Jacob II (1759-1789)
Importantes trabajos en elasticidad, hidrostática y balística.
§. Funciones
Una aplicación importante de las coordenadas en matemáticas es un método de representar funciones gráficamente.
Una función no es un número sino una receta que parte de un número y calcula un número asociado. La receta en cuestión se suele enunciar como una fórmula que asigna a cada número x (posiblemente en un intervalo limitado) otro número f(x).
Gráfica de una función f
Por ejemplo, la función «raíz cuadrada» está definida por la regla f(x) = √x, es decir, «tomar la raíz cuadrada del número dado».
Esta receta requiere que x sea positivo. Análogamente la función «cuadrado» se define por f(x) = x2, y esta vez no hay restricciones sobre x.
Podemos representar una función geométricamente definiendo la coordenada y, para un valor dado de x, por y = f(x). Esta ecuación establece una relación entre las dos coordenadas, y por consiguiente determina una curva. Esta curva se denomina gráfica de la función f.
La gráfica de la función f(x) = x2 resulta ser una parábola. La de la raíz cuadrada f(x) =√x es media parábola, pero acostada. Funciones más complicadas llevan a curvas más complicadas. La gráfica de la función y = sen x es una curva ondulada.
El mensaje más profundo de la geometría de coordenadas trata de las conexiones cruzadas en matemáticas. Conceptos cuyas realizaciones físicas parecen totalmente diferentes pueden ser aspectos diferentes de lo mismo.
Gráficas del cuadrado y de la raíz cuadrada
§. Coordenadas geométricas hoy
Las coordenadas son una de esas ideas simples que pueden cambiar la historia. Las utilizamos en todas partes, normalmente sin advertir que lo estamos haciendo. Prácticamente todas las gráficas por computador emplean un sistema de coordenadas interno, y la geometría que aparece en la pantalla se trata de manera algebraica. Una operación tan simple como rotar una fotografía digital unos pocos grados, para poner el horizonte horizontal, se basa en la geometría de coordenadas.
Gráfica de la función seno
Las apariencias superficiales pueden ser engañosas. Buena parte de la efectividad de las matemáticas como forma de entender el universo deriva de su capacidad para adaptar ideas y transferirlas de un área de la ciencia a otra.
Para qué les servían las coordenadasLa geometría de coordenadas puede ser utilizada en superficies más complicadas que el plano, tales como la esfera. Las coordenadas más comunes en la esfera son la longitud y la latitud. Por ello la cartografía, y el uso de mapas en navegación, puede verse como una aplicación de la geometría de coordenadas.
El principal problema de navegación para un capitán consistía en determinar la latitud y la longitud de su barco. La latitud es relativamente fácil, porque el ángulo del Sol por encima del horizonte varía con la latitud y puede ser tabulado.
Longitud y latitud como coordenadasDesde 1730, el instrumento estándar para encontrar la latitud fue el sextante (ahora casi obsoleto por el GPS). Fue inventado por Newton, pero él no lo publicó.
Fue redescubierto de forma independiente por el matemático inglés John Hadley y el inventor americano Thomas Godfrey. Los navegantes anteriores habían utilizado el astrolabio, que se remonta a la Arabia medieval.
La longitud es más complicada. El problema fue finalmente resuelto construyendo un reloj de alta precisión que se ponía en marcha con la hora local en el punto de partida del viaje. La hora de la salida y la puesta del Sol, y los movimientos de la Luna y las estrellas, dependen de la longitud, lo que hace posible determinar la longitud comparando la hora local con la hora del reloj. La historia de la invención del cronómetro por John Harrison, que resolvió el problema, ha sido muy bien narrada por Dava Sobel en Longitud.
Las matemáticas son lo último en transferencia de tecnología. Y son estas conexiones cruzadas, que se nos han revelado durante los últimos 4.000 años, las que hacen de las matemáticas una disciplina unificada.
Para qué nos sirven las coordenadasNosotros seguimos usando coordenadas en los mapas, pero otro uso común de la geometría de coordenadas se da en la Bolsa, donde las fluctuaciones de algunos precios se registran como una curva.
Aquí la coordenada x es el tiempo, y la coordenada y es el precio. Cantidades enormes de datos financieros y científicos se registran de la misma manera.
Datos de la Bolsa representados en coordenadas
Capítulo 7
Pautas en los números
Los orígenes de la teoría de los números
Pese a estar cada vez más fascinados por la geometría, los matemáticos no perdieron su interés por los números.
Pero empezaron a plantearse preguntas más profundas, y respondieron a muchas de ellas. Algunas tuvieron (pie esperar a técnicas más poderosas. Otras permanecen sin respuesta hasta hoy.
§. Teoría de números
Hay algo absolutamente fascinante en los números. Números naturales puros, sin adornos: 1, 2, 3, 4, 5. ¿Qué podría ser más simple? Pero ese exterior simple encierra profundidades ocultas, y muchas de las preguntas más sorprendentes en matemáticas se refieren a propiedades aparentemente directas de los números naturales. El área se conoce como teoría de números, y resulta difícil precisamente porque sus ingredientes son muy básicos y simples. La misma simplicidad de los números naturales deja muy pocos «recovecos» para técnicas ingeniosas.
Las primeras contribuciones serias a la teoría de números -es decir, una teoría completa con demostraciones, no sólo afirmaciones- se encuentran en las obras de Euclides, donde las ideas están sutilmente enmascaradas como geometría. La disciplina fue desarrollada como una nueva área de las matemáticas por el griego Diofanto, algunos de cuyos escritos se conservan en copias posteriores. Recibió un gran impulso en el siglo XVII por parte de Fermat, y fue desarrollada por Leonhard Euler, Joseph-Louis Lagrange y Cari Friedrich Gauss como una rama profunda y extensa de las matemáticas que afectaba a muchas otras áreas, a veces aparentemente inconexas. A finales del siglo XX estas conexiones han sido utilizadas para responder a algunos -aunque no todos- de los antiguos enigmas, incluida una conjetura muy famosa hecha por Fermat alrededor de 1650, conocida como su «último teorema».
Durante la mayor parte de su historia, la teoría de números ha tratado del funcionamiento interno de las propias matemáticas, con pocas conexiones con el mundo real. Si alguna vez hubo una rama del pensamiento matemático que vivía confinada en torres de marfil, ésa era la teoría de números, pero la llegada del computador digital lo ha cambiado todo. Los computadores trabajan con representaciones electrónicas de números naturales, y los problemas y oportunidades planteados por los computadores llevan frecuentemente a la teoría de números. Tras 2.500 años como ejercicio puramente intelectual, la teoría de números ha tenido finalmente un impacto en la vida cotidiana.
§. Primos
Cualquiera que contemple la multiplicación de números naturales llega a advertir una distinción fundamental. Muchos números pueden ser «descompuestos» en piezas más pequeñas, en el sentido de que los números más grandes aparecen al multiplicar las piezas. Por ejemplo, 10 es 2 × 5, y 12 es 3 × 4.
“Los primos forman los «bloques constituyentes» básicos para todos los números.”
Algunos números, sin embargo, no se descomponen de esta manera. No hay modo de expresar 11 como producto de dos números naturales más pequeños; lo mismo sucede con 2, 3, 5, 7 y muchos otros.
De los números que pueden expresarse como producto de dos números más pequeños se dice que son compuestos. Los que no pueden expresarse así son primos. Según esta definición, el número 1 debería considerarse primo, pero por buenas razones se coloca en una clase especial por sí mismo y se llama una unidad. Por lo tanto, los primeros primos son los números
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41
Como esta lista sugiere, no hay pauta obvia para los primos (excepto que todos salvo el primero son impares). De hecho, parecen ocurrir de manera irregular y no hay una forma simple de predecir el siguiente número en la lista. Incluso así, no hay duda de que este número está de algún modo determinado: basta con ensayar números sucesivos hasta encontrar el siguiente primo.
A pesar, o quizá a causa, de su distribución irregular, los primos son de vital importancia para las matemáticas. Forman los «bloques constituyentes» básicos para todos los números, en el sentido de que números mayores se crean multiplicando números más pequeños. La química nos dice que cualquier molécula, por complicada que sea, está formada por átomos: partículas «indivisibles» de materia. Análogamente, las matemáticas nos dicen que cualquier número, por grande que pueda ser, está formado por primos: números «indivisibles». Por ello los primos son los átomos de la teoría de números.
Esta característica de los primos es útil porque muchas cuestiones en matemáticas pueden resolverse para todos los números naturales con tal de que puedan resolverse para los primos, y los primos tienen propiedades especiales que a veces hacen más fácil la solución de la cuestión. Este aspecto dual de los primos -importante pero de mal comportamiento- excita la curiosidad del matemático.
Euclides introdujo los primos en el Libro VII de los Elementos, y dio demostraciones de tres propiedades clave. En terminología moderna, éstas son:
- todo número puede expresarse como producto de primos;
- dicha expresión es única excepto en el orden en que aparecen los primos, y
- hay infinitos primos.
Lo que Euclides estableció y demostró en realidad es ligeramente diferente.
La Proposición 31 del Libro VII nos dice que cualquier número compuesto está «medido por» algún primo, es decir, es dividido exactamente por dicho primo. Por ejemplo, 30 es compuesto, y es exactamente divisible por varios primos, entre ellos 5; de hecho 30 = 6 × 5. Repitiendo este proceso de «extraer» un divisor, o factor, primo podemos descomponer cualquier número en un producto de primos. Así, partiendo de 30 = 5 × 6, observamos que 6 es también compuesto, con 6 = 2 × 3. Ahora 30 = 2 × 3 × 5, y los tres factores son primos.
Si en su lugar hubiéramos partido de 30 = 10 × 3, entonces descompondríamos 10 como 10 = 2 × 5, lo que lleva a 30 = 2 × 5 × 3. Aparecen los mismos tres primos, pero multiplicados en un orden diferente, lo que por supuesto no afecta al resultado. Puede parecer obvio que descompongamos como descompongamos un número en primos, siempre obtenemos el mismo resultado excepto en el orden, pero esto resulta ser difícil de demostrar. De hecho, enunciados similares en algunos sistemas de números relacionados resultan ser falsos, pero para números naturales ordinarios el enunciado es verdadero.
¿Por qué no es obvia la unicidad de los números primos?Puesto que los primos son los átomos de la teoría de números, podría parecer obvio que siempre aparezcan los mismos átomos cuando se descompone un número en primos. Después de todo, los átomos son las piezas indivisibles. Si se pudiera descomponer un número de dos formas distintas, ¿no implicaría ello dividir un átomo? Pero aquí la analogía con la química es algo equívoca.
Para ver que la unicidad de la factorización prima no es obvia, podemos trabajar con un conjunto restringido de números: 1 5 9 13 17 21 25 29, y así sucesivamente. Estos son los números que exceden en 1 a un múltiplo de 4. Los productos de tales números también tienen la misma propiedad, de modo que podemos construir tales números multiplicando números más pequeños del mismo tipo. Definamos un «cuasiprimo» como cualquier número en esta lista que no es el producto de dos números más pequeños de la lista. Por ejemplo, 9 es cuasiprimo: los únicos números más pequeños en la lista son 1 y 5, y su producto no es 9. (Sigue siendo cierto que 9 = 3 × 3, por supuesto, pero el número 3 no está en la lista.)
Es obvio -y cierto- que todo número en la lista es un producto de cuasiprimos.
Sin embargo, aunque estos cuasiprimos son los «átomos» del conjunto, sucede algo bastante extraño. El número 693 se descompone en dos maneras diferentes:
693 = 9 × 77 = 21 × 33,
y los cuatro factores
9, 21, 13 y 77
son cuasiprimos.
Por lo tanto, la unicidad de la factorización falla para este tipo de número.
La factorización prima es única. Euclides demuestra el hecho clave necesario para establecer la unicidad en la Proposición 30 del Libro VII de los Elementos: si un primo divide al producto de dos números, entonces debe dividir al menos a alguno de dichos números. Una vez que conocemos la Proposición 30, la unicidad de la factorización prima es una consecuencia directa.
“En términos modernos, la lista de primos es infinita.”
La proposición 20 del Libro IX afirma que: «Los números primos son más que cualquier multitud asignada de números primos». En términos modernos, la lista de primos es infinita. La demostración se da para un caso representativo: supongamos que hay sólo tres números primos, a, b, y c. Multipliquémoslos y sumemos 1 al producto, para obtener a × b × c + 1. Este número debe ser divisible por algún primo, pero este primo no puede ser ninguno de los tres originales; en efecto, éstos dividen a abe exactamente, luego no pueden dividir también a a × b × c + 1, pues entonces dividirían a la diferencia, que es 1.
Por consiguiente, hemos encontrado un nuevo primo, lo que contradice la hipótesis de que a, b, c son todos los primos que existen.
El mayor número primo conocidoNo hay un primo máximo, pero el mayor número primo conocido hasta septiembre de 2006 es
232.582.657 - 1
que tiene 9.808.358 cifras decimales. Los números de la forma 2p - 1, con p primo, se llaman primos de Mersenne, porque Mersenne conjeturó en su Cogitata Physica-Mathematica de 1644 que dichos números son primos para
p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 y 257,
y compuestos para todos los demás números naturales hasta 257.
Existen métodos especiales de alta velocidad para comprobar si tales números son primos, y ahora sabemos que Mersenne cometió cinco errores. Sus números son compuestos cuando p = 67 y 257, y hay tres primos más con p = 61, 89, 107. Actualmente se conocen 44 primos de Mersenne. Encontrar otros nuevos es una buena manera de poner a prueba nuevos supercomputadores, pero no tiene ninguna trascendencia práctica.
Aunque la demostración de Euclides utiliza tres primos, la misma idea funciona con una lista mayor. Multipliquemos todos los primos en la lista, sumemos 1 y luego tomemos algún factor primo del resultado: esto genera siempre un primo que no está en la lista. Por consiguiente ninguna lista finita de primos puede ser completa.
§. Diofanto
Hemos mencionado a Diofanto de Alejandría en relación con la notación algebraica, pero su mayor influencia se manifestó en la teoría de números. Diofanto estudió cuestiones generales, antes que cuestiones numéricas concretas, aunque sus respuestas eran números concretos. Por ejemplo: «encontrar tres números tales que su suma, y la suma de dos cualesquiera de ellos, es un cuadrado perfecto». Su respuesta es 41, 80 y 320. Comprobación: la suma de los tres es 441 = 212. Las sumas de los pares son 41 + 80 = 112; 41 + 320 = 192 y 80 + 320 = 202.
Una de las ecuaciones más conocidas resuelta por Diofanto es una curiosa versión del Teorema de Pitágoras. Podemos enunciar el teorema de forma algebraica: si un triángulo rectángulo tiene lados a, b, c, siendo c el más largo, entonces a2 + b2 = c2. Hay algunos triángulos rectángulos especiales para los que los lados son números enteros. El más simple y más conocido es aquel en que a, b, c son 3, 4, 5, respectivamente; aquí 32 + 42 = 9 + 16 = 52.
Otro ejemplo, el siguiente más simple, es 52 + 122 = 132.
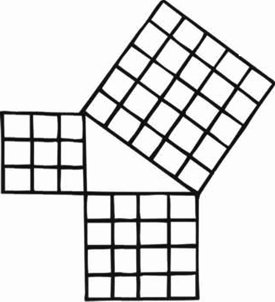
El triángulo rectángulo 3-4-5
De hecho, hay infinitas de estas tripletas pitagóricas. Diofanto encontró todas las posibles soluciones en números enteros de lo que ahora escribimos como la ecuación
a2 + b2 = c2.
Su receta consiste en tomar dos números enteros cualesquiera y formar la diferencia entre sus cuadrados, el doble de su producto y la suma de sus cuadrados. Estos tres números forman siempre una tripleta pitagórica, y todos estos triángulos aparecen de esta manera con tal de que admitamos también que los tres números estén multiplicados por una constante. Por ejemplo, si los números son 1 y 2 obtenemos el famoso triángulo 3-4-5. En particular, puesto que hay infinitas maneras de escoger los dos números, existen infinitas tripletas pitagóricas.
Lo que no sabemos de los números primosIncluso hoy, los números primos siguen guardando secretos. Dos famosos problemas no resueltos son la Conjetura de Goldbach y la Conjetura de los Primos Gemelos.
Christian Goldbach era un matemático aficionado que mantenía correspondencia regular con Euler. En una carta de 1742, él mostraba que todo número entero mayor que 2 parecía ser suma de tres primos. Goldbach veía 1 como un primo, lo que ya no hacemos; como consecuencia, ahora excluiríamos los números 3 = 1 + 1 +1 y 4 = 2+ 1 + 1. Euler propuso una conjetura más fuerte: que todo número par mayor que 2 es suma de dos primos. Por ejemplo, 4 = 2 + 2, 6 = 3 + 3, 8 = 5 + 3, 10 = 5 + 5, y así sucesivamente. Esta conjetura implica la de Goldbach. Euler confiaba en que su conjetura era cierta, pero no pudo encontrar una demostración y la conjetura sigue abierta. Experimentos con computador han demostrado que es cierta para todo número par hasta 1018. El resultado más conocido fue obtenido por Chen Jing-Run en 1973 utilizando complicadas técnicas tomadas del análisis. El demostró que todo número par suficientemente grande es suma de dos primos, o un primo y un cuasiprimo (un producto de dos primos).
La conjetura de los primos gemelos es mucho más antigua y se remonta a Euclides. Afirma que hay infinitos primos gemelos p y p + 2. Ejemplos de números primos son 5, 7 y 11, 13. Tampoco en este caso se conoce ninguna demostración o refutación. En 1966, Chen demostró que hay infinitos primos p, tales que p + 2 es o primo o cuasiprimo. Actualmente los mayores primos gemelos conocidos son 2,003,663,613 × 2195,000 ± 1, encontrados por Eric Vautier, Patrick McKibbon y Dmitri Gribenko en 2007.
§. Fermat
Después de Diofanto la teoría de números quedó estancada durante más de mil años hasta que fue retomada por Fermat, quien hizo muchos descubrimientos importantes. Uno de sus teoremas más elegantes nos dice exactamente cuándo un entero dado n es una suma de dos cuadrados perfectos: n = a2 + b2. La solución es más simple cuando n es primo. Fermat observó que hay tres tipos básicos de primos:
(i) El número 2, el único primo par.
(ii) Primos que son iguales a un múltiplo de 4 más 1, tales como 5,13, 17 y así sucesivamente -estos primos son todos impares.
(iii) Primos que son iguales a un múltiplo de 4 menos 1, tales como 3,7, 11 y así sucesivamente -estos primos son también impares.
Él demostró que un primo es una suma de dos cuadrados si pertenece a las categorías (I) o (II), y no es una suma de dos cuadrados si pertenece a la categoría (III).
Por ejemplo, 37 está en la categoría (II), pues es 4 × 9 + 1, y 37 = 62 + 12, una suma de dos cuadrados. En cambio, 31 = 4 × 8 - 1 está en la categoría (III), y por mucho que tratemos de escribir 31 como una suma de dos cuadrados encontraremos que nada funciona. (Por ejemplo, 31 = 25 + 6, donde 25 es un cuadrado pero 6 no lo es.)
El resultado es que un número es una suma de dos cuadrados si y sólo si todo divisor primo de la forma 4k - 1 aparece elevado a una potencia par.
Utilizando métodos similares, Joseph-Louis Lagrange demostró en 1770 que todo entero positivo es una suma de cuatro cuadrados perfectos (incluidos uno o más ceros). Fermat había enunciado previamente este resultado, pero no hay registro de ninguna demostración.
Uno de los descubrimientos más influyentes de Fermat es también uno de los más simples. Se conoce como el Pequeño Teorema de Fermat, para evitar la confusión con su Último Teorema (a veces llamado «Gran Teorema»), y afirma que si p es un primo cualquiera y a es un número natural cualquiera, entonces ap - a es un múltiplo de p. Cuando p es compuesto, la propiedad correspondiente es normalmente falsa, pero no siempre. El resultado más celebrado de Fermat necesitó 350 años para ser demostrado.
Él lo enunció alrededor de 1640 y afirmó que tenía una demostración, pero todo lo que conocemos de su trabajo es una corta nota. Fermat poseía una copia de la Arithmetica de Diofanto que inspiró muchas de sus investigaciones, y con frecuencia escribía sus propias ideas en el margen. En algún momento debió haber estado pensando en la ecuación pitagórica: sumar dos cuadrados para obtener un cuadrado. Se preguntó qué sucedería si en lugar de con cuadrados se ensayaba con cubos, pero no encontró ninguna solución.
Pierre Fermat
1601-1665Pierre Fermat nació en Beaumont-de-Lomagne, Francia, en 1601, hijo del mercader de cuero Dominique Fermat y de Claire de Long, la hija de una familia de abogados. Para 1629 había hecho importantes descubrimientos en geometría y en la teoría precursora del cálculo infinitesimal, pero escogió el derecho como carrera y llegó a ser consejero en el Parlamento de Toulouse en 1631. Esto le tituló para añadir el «de» a su nombre.
Sus superiores murieron a causa de un brote de peste y él progresó rápidamente. En 1648 se convirtió en consejero del rey en el Parlamento local de Toulouse, donde sirvió el resto de su vida, y alcanzó el máximo nivel en la Corte Criminal en 1652.
Nunca mantuvo una posición académica, pero las matemáticas eran su pasión. En 1653 contrajo la peste y se rumoreó que había muerto, pero sobrevivió. Mantuvo una extensa correspondencia con otros intelectuales, en particular el matemático Pierre de Carcavi y el monje Marin Mersenne. Trabajó en mecánica, óptica, probabilidad y geometría, y su método para encontrar los valores máximo y mínimo de una función preparó el camino para el cálculo infinitesimal. Se convirtió en uno de los matemáticos más destacados del mundo, pero sólo publicó una pequeña parte de su trabajo, principalmente porque no estaba dispuesto a perder el tiempo necesario para ponerlo en forma publicable.
Su influencia más duradera se manifestó en la teoría de números, en donde desafió a otros matemáticos a demostrar una serie de teoremas y a resolver varios problemas. Entre ellos estaba la (mal llamada) «ecuación de Pell» nx2 + 1 = y2, y la afirmación de que la suma de dos cubos perfectos no nulos no puede ser un cubo perfecto. Éste es un caso especial de una conjetura más general, el «Último Teorema de Fermat» en el que los cubos son reemplazados por potencias n-ésimas para cualquier n ≥ 3.
Murió en 1665, sólo dos días después de concluir un caso legal.
El mismo problema aparece con las potencias cuarta, quinta o mayores.
En 1670, Samuel, hijo de Fermat, publicó una edición de la traducción de Bachet de la Arithmetica, que incluía las notas al margen de Fermat. Una de esas notas llegó a hacerse famosa: la afirmación de que si n ≥ 3, la suma de dos potencias n-ésimas no es nunca un potencia n-ésima. La nota al margen afirma:
«Resolver un cubo en la suma de dos cubos, una cuarta potencia en dos cuartas potencias o, en general, cualquier potencia mayor que la segunda en dos del mismo tipo es imposible; de lo que he encontrado una notable demostración. Este margen es demasiado pequeño para contenerla».
No parece probable que su demostración, si existía, fuera correcta. La primera, y actualmente única, demostración fue obtenida por Andrew Wiles en 1994; utiliza métodos abstractos avanzados que no existieron hasta finales del siglo XX.
Después de Fermat, varios matemáticos importantes trabajaron en teoría de números, en especial Euler y Lagrange. La mayoría de los teoremas que Fermat había enunciado pero no demostrado fueron pulidos durante este periodo.
§. Gauss
El siguiente gran avance en teoría de números lo hizo Gauss, quien publicó su obra maestra, Disquisitiones Arithmeticæ (Investigaciones en Aritmética), en 1801. Este libro llevó la teoría de números al centro de la escena matemática. Desde entonces la teoría de números fue un componente nuclear de la corriente principal matemática. Gauss se centró principalmente en su propia y nueva obra, pero también estableció las bases de la teoría de números y sistematizó las ideas de sus predecesores.
El más importante de estos cambios fundacionales fue una idea muy simple pero muy poderosa: la aritmética modular. Gauss descubrió un nuevo tipo de sistema de números, análogo a los enteros pero que difiere en un aspecto clave: un número particular, conocido como el módulo, se identifica con el número 0. Esta curiosa idea, ahora denominada aritmética modular, resultó ser fundamental para nuestra comprensión de las propiedades de divisibilidad de los enteros ordinarios.
Esta es la idea de Gauss. Dado un entero m, se dice que a y b son congruentes con el módulo m, denotado
a ≡ b(mod m)
si la diferencia a - b es exactamente divisible por m. Entonces la aritmética módulo m trabaja exactamente igual que la aritmética ordinaria, salvo que podemos reemplazar m por 0 en cualquier lugar del cálculo. Por lo tanto, puede ignorarse cualquier múltiplo de m.
A veces se utiliza la expresión «aritmética de reloj» para captar el espíritu de la idea de Gauss. En un reloj el número 12 es en la práctica el mismo que 0 porque las horas se repiten después de doce pasos (24 en la Europa continental y en actividades militares). Siete horas después de las 6 en punto no son las 1 ≡ 3 en punto, sino la 1 en punto, y en el sistema de Gauss. Por ello, la aritmética modular es como un reloj que necesita m horas para completar el círculo. No es sorprendente que la aritmética modular aparezca siempre que los matemáticos consideran cosas que cambian en círculos repetitivos.
Carl Friedrich Gauss
1777-1855Gauss fue muy precoz; se dice que cuando tenía tres años corregía los errores aritméticos de su padre.
En 1792, con la ayuda financiera del duque de Brunswick-Wolfenbüttel, Gauss fue al Collegium Carolinum de Brunswick.
Allí hizo varios descubrimientos matemáticos importantes, incluida la ley de reciprocidad cuadrática y el teorema de los números primos, pero no los demostró. Durante los años 1795-1798 estudió en Gotinga, donde descubrió cómo construir un polígono regular de 17 lados con regla y compás. Sus Disquisitiones Arithmeticæ, la obra más importante en teoría de números hasta la fecha, fue publicada en 1801.
La reputación pública de Gauss se basó, no obstante, en una predicción astronómica. En 1801 Giuseppe Piazzi descubrió el primer asteroide: Ceres.
Las observaciones eran tan escasas que los astrónomos temían no poder encontrarlo de nuevo cuando reapareciera de detrás del Sol. Varios astrónomos predijeron dónde reaparecería; también lo hizo Gauss. Sólo Gauss estaba en lo cierto. De hecho, Gauss había utilizado un método de su propia invención, ahora denominado el «método de mínimos cuadrados», para obtener resultados precisos a partir de observaciones limitadas. No reveló esta técnica en ese momento, pero desde entonces ha sido fundamental en estadística y en ciencia observacional.
En 1805 Gauss se casó con Johanna Ostoff, a quien amaba profundamente, y en 1807 dejó Brunswick para convertirse en director del Observatorio de Gotinga. En 1808 murió su padre, y Johanna murió en 1809 tras dar a luz a su segundo hijo. Poco después el hijo también murió.
Pese a estas tragedias personales, Gauss continuó su investigación, y en 1809 publicó su Teoría Motus Corporum Cœlestium in Sectionibus Conicis Solem Ambientium, una contribución importante a la mecánica celeste.
Se casó de nuevo, con Minna, una íntima amiga de Johanna, pero fue más un matrimonio de conveniencia que por amor.
Alrededor de 1816 Gauss escribió una revisión de las deducciones del axioma de las paralelas a partir de los otros axiomas de Euclides, en donde presentaba una opinión que probablemente había mantenido desde 1800: la posibilidad de una geometría lógicamente consistente que difería de la de Euclides.
En 1818 se le encargó un examen geodésico de Hanover, e hizo importantes contribuciones a los métodos empleados en topografía. En 1831, tras la muerte de Minna, Gauss empezó a trabajar con el físico Wilhelm Weber sobre el campo magnético de la Tierra.
Ellos descubrieron lo que ahora se denominan leyes de Kirchhoff para los circuitos eléctricos, y construyeron un telégrafo rudimentario pero efectivo. Cuando Weber fue obligado a dejar Gotinga en 1837, la obra científica de Gauss entró en declive, aunque siguió interesado en el trabajo de otros, en particular Ferdinand Eisenstein y Georg Bernhard Riemann. Murió en paz mientras dormía.
Las Disquisitiones Arithmeticæ utilizaban aritmética modular como base para ideas más profundas, y aquí mencionamos tres.
El grueso del libro es una extensión de gran alcance de las observaciones de Fermat de que primos de la forma 4k + 1 son una suma de dos cuadrados, mientras que los de la forma 4k - 1 no lo son. Gauss re-enunció este resultado como una caracterización de enteros que pueden escribirse en la forma x2 + y2 con x e y enteros. Entonces preguntó qué sucede si en lugar de esta fórmula utilizamos una forma cuadrática general, ax2 + bxy + cy2.
Sus teoremas son demasiado técnicos para discutir aquí pero obtuvo una comprensión casi completa de esta cuestión.
Para qué les servía la teoría de númerosUna de las primeras aplicaciones prácticas de la teoría de números se da en los engranajes. Si se colocan juntas dos ruedas dentadas de modo que sus dientes engranen, y una rueda dentada tiene m dientes y la otra n dientes, entonces el movimiento de las ruedas está relacionado con estos números. Por ejemplo, supongamos que una rueda tiene 30 dientes y la otra tiene 7. Si giramos la rueda grande exactamente una vez, ¿qué hace la rueda más pequeña? Vuelve a la posición inicial después de 7, 14, 21 y 28 vueltas. Así, las 2 vueltas finales, para completar 30, la adelantan sólo dos vueltas. Este número resulta porque es el resto de dividir 30 por 7. Por lo tanto, el movimiento de las ruedas dentadas es una representación mecánica de la división con resto, y ésta es la base de la aritmética modular.
El mecanismo de AntikiteraLas ruedas dentadas fueron usadas por los artesanos de la antigua Grecia para diseñar un aparato notable, el mecanismo de Antikitera.
En 1900 un buzo buscador de esponjas, Elias Stadiati, encontró una masa informe de roca corroída en los restos de un naufragio del año 65 a.C., cerca de la isla de Antikitera a unos 40 metros de profundidad. En 1902 el arqueólogo Valerios Stais advirtió que la roca contenía un engranaje, que era en realidad el resto de un complicado mecanismo de bronce. Tenía una inscripción con palabras en el alfabeto griego. La función del mecanismo ha sido deducida a partir de su estructura y sus inscripciones, y resulta ser una calculadora astronómica. Hay más de 30 engranajes -la última reconstrucción en 2006, sugiere que originalmente había 37-.
Los números de dientes corresponden a razones astronómicas importantes. En particular, dos ruedas tienen 53 dientes -un número difícil de fabricar- y este número procede del ritmo al que rota el punto de la Luna más alejado de la Tierra. Todos los factores primos de los números de dientes están basados en dos ciclos astronómicos clásicos, los ciclos metónico y de Saros. Análisis mediante rayos x han revelado nuevas inscripciones y las han hecho legibles, y ahora es seguro que el aparato se utilizaba para predecir las posiciones del Sol, la Luna y probablemente los planetas entonces conocidos. Las inscripciones datan de aproximadamente 150-100 a.C.
El mecanismo de Antikitera tiene un diseño sofisticado, que parece incorporar la teoría de Hiparco del movimiento de la Luna. Muy bien puede haber sido construido por uno de sus estudiantes, o al menos con su ayuda. Probablemente era un «juguete de ejecutivo» para un personaje real, antes que un instrumento práctico, lo que puede explicar su exquisito diseño y manufactura.
Otro tema es la ley de reciprocidad cuadrática, que intrigó y desconcertó a Gauss durante muchos años. El punto de partida es una pregunta sencilla: ¿cómo son los cuadrados perfectos respecto a un módulo dado? Por ejemplo, supongamos que el módulo es 11. Entonces los posibles cuadrados perfectos (de los números menores que 11) son
0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100
que, cuando se reducen (mod 11), dan
0, 1, 4, 9, 5, 3, 3, 5, 9, 4, 1
donde cada número distinto de 0 aparece dos veces. Estos números son los residuos cuadráticos, mod 11.
La clave para esta pregunta está en examinar los números primos. Si p y q son primos, ¿cuándo es q un cuadrado (mod p)? Gauss descubrió que aunque no hay una manera simple de responder a esta pregunta directamente, guarda una notable relación con otra pregunta: ¿cuándo es p un cuadrado (mod q)? Por ejemplo, la lista anterior muestra que q = 5 es un cuadrado módulo p ≡ 11. También es cierto que 11 es un cuadrado módulo 5, porque 11 ≡ 1 (mod 5) y 1 ≡ 12. De modo que aquí ambas preguntas tienen la misma respuesta.
Gauss demostró que esta «ley de reciprocidad» es válida para cualquier par de primos impares, salvo cuando ambos primos son de la forma 4k - 1, en cuyo caso las dos preguntas tienen siempre respuestas opuestas. Es decir: para dos primos impares p y q cualesquiera
q es un cuadrado (mod p) si y sólo si p es un cuadrado (mod q)
a menos que ambos p y q sean de la forma 4k - 1, en cuyo caso
q es un cuadrado (mod p) si y sólo si p no es un cuadrado (mod q).
Inicialmente Gauss no era consciente de que ésta no era una observación nueva: Euler había advertido la misma pauta. Pero a diferencia de Euler, Gauss consiguió demostrar que siempre es verdadera. La demostración era muy difícil, y Gauss necesitó varios años para llenar una laguna pequeña pero crucial.
Un tercer tema en las Disquisitiones es el descubrimiento que había convencido a Gauss para hacerse matemático cuando tenía 19 años: una construcción geométrica para el 17-gono regular. Euclides proporcionó construcciones, utilizando regla y compás, para polígonos regulares con 3, 5 y 15 lados; también sabía que estos números podían duplicarse repetidamente bisecando ángulos, lo que daba polígonos regulares con 4, 6, 8 y 10 lados, y así sucesivamente. Pero Euclides no dio construcciones para polígonos de 7 lados, de 9 lados o de cualquier otro número distinto de los recién listados. Durante aproximadamente dos mil años el mundo matemático supuso que Euclides había dicho la última palabra y no se podía construir ningún otro polígono regular. Gauss demostró que no era así.
Marie-Sophie Germain
1776-1831Sophie Germain era hija del mercader de seda Ambroise-François Germain y de Marie-Madelaine Gruguelin. A los 13 años leyó sobre la muerte de Arquímedes, a quien mató un soldado romano mientras contemplaba un diagrama geométrico en la arena, y ello le inspiró para hacerse matemática.
A pesar de los esfuerzos bien intencionados de sus padres por disuadirla -las matemáticas no se consideraban entonces una vocación adecuada para una joven-, ella leyó las obras de Newton y Euler envuelta en una manta mientras su madre y su padre dormían. Cuando sus padres se convencieron de su compromiso con las matemáticas, cedieron y empezaron a ayudarla, dándole soporte financiero a lo largo de su vida.
Ella obtuvo apuntes de clase de la École Polytechnique y escribió a Lagrange adjuntándole algún trabajo original propio bajo el nombre «Monsieur LeBlanc. Lagrange, impresionado, descubrió finalmente que el autor era una mujer, y tuvo el buen sentido de animarla y convertirse en su patrocinador. Los dos trabajaron juntos, y algunos de los resultados de ella fueron incluidos en una edición posterior del Ensayo sobre la Teoría de los Números de Legendre en 1798. Su corresponsal más famoso fue Gauss. Sophie estudió las Disquisitiones Aríthmeticæ, y de 1804 a 1809 escribió varias cartas a su autor, ocultando de nuevo su sexo y utilizando el nombre LeBlanc. Gauss alabó el trabajo de LeBlanc en cartas a otros matemáticos. En 1806 descubrió que LeBlanc era realmente una mujer, con ocasión de la ocupación de Braunschweig por los franceses. Preocupada porque Gauss pudiera sufrir la misma suerte que Arquímedes, Sophie entró en contacto con un amigo de la familia que era un alto mando del ejército francés, el general Pernety. Gauss se enteró y descubrió que LeBlanc era realmente Sophie.
Sophie no tenía por qué haberse preocupado. Gauss estaba aún más impresionado y le escribió: «Pero cómo describirle mi admiración y asombro al ver que mi estimado corresponsal Monsieur LeBlanc se metamorfoseaba en este ilustre personaje ... Cuando una persona del sexo que, según nuestras costumbres y prejuicios, debe encontrar infinitamente más dificultades que los hombres para familiarizarse con estas investigaciones espinosas, consigue pese a todo superar estos obstáculos y penetrar en las partes más oscuras de ellos, entonces sin duda ella debe tener el valor más noble, talento absolutamente extraordinario y un genio superior».
Sophie obtuvo algunos resultados sobre el Último Teorema de Fermat, los mejores disponibles hasta 1840. Entre 1810 y 1820 trabajó en las vibraciones de superficies, un problema planteado por el Instituto de Francia. En particular, se buscaba una explicación para las «figuras de Chladni»: figuras simétricas que aparecen cuando se espolvorea arena sobre una placa metálica a la que luego se hace vibrar utilizando un arco de violín. En su tercer intento fue premiada con una medalla de oro, aunque por razones desconocidas, posiblemente una protesta por el tratamiento injusto a las mujeres científicas, ella no apareció en la ceremonia del premio.
En 1829 se le detectó un cáncer de pulmón, pero siguió trabajando en teoría de números y en la curvatura de superficies hasta que murió dos años más tarde.
Es fácil ver que el problema principal está en construir p-gonos regulares cuando p es primo. Gauss señaló que tal construcción es equivalente a resolver la ecuación algebraica
xp - 1 + xp - 2 + xp - 3 +...+x2 + x + 1 = 0
Ahora bien, una construcción con regla y compás puede verse, gracias a la geometría de coordenadas, como una secuencia de ecuaciones cuadráticas.
“Euclides había elidió la última palabra y no se podía construir ningún otro polígono regular. Gauss demostró que no era así”
Si existe una construcción de este tipo, se sigue (de manera no totalmente trivial) que p - 1 debe ser una potencia de 2.
Los casos griegos p = 3 y 5 satisfacen esta condición: aquí p - 1 = 2 y 4, respectivamente. Pero no son los únicos primos semejantes. Por ejemplo 17 - 1 = 16 es una potencia de 2.
Para que nos sirve la teoría de númerosLa teoría de números constituye la base de muchos códigos de seguridad importantes utilizados en el comercio por internet. El más conocido de dichos códigos es el criptosistema RSA (Ronald Rivest, Adi Shamir y Leonard Adelman), que tiene la sorprendente característica de que el método para encriptar mensajes puede hacerse público sin revelar el procedimiento inverso para desencriptar el mensaje.
Supongamos que Alicia quiere enviar un mensaje secreto a Bob. Antes de hacerlo, ambos se ponen de acuerdo en dos números primos grandes p y q (que tengan al menos un centenar de dígitos) y los multiplican para obtener M = pq. Pueden hacer público este número si lo desean. Ellos calculan también K = (p - 1)(q - 1), pero mantienen este número en secreto.
Ahora Alicia representa su mensaje como un número x en el intervalo de 0 a M (o una serie de tales números si es un mensaje largo). Para encriptar el mensaje ella escoge un número a, que no tiene factores en común con K y calcula y = -xa(mod M). El número a debe ser conocido para Bob, y también puede hacerse público.
Para desencriptar mensajes, Bob tiene que conocer un número b tal que ab ≡ 1 mod K. Este número (que existe y es único) se mantiene en secreto. Para desencriptar y, Bob calcula yb(mod M).
¿Por qué esto desencripta?
Porque
yb ≡ ((x)a)b ≡ xab ≡ x1 ≡ x(mod M)
utilizando una generalización del Pequeño Teorema de Fermat debida a Euler.
Este método es práctico porque existen testes eficientes para encontrar primos grandes. Sin embargo, no hay ningún método conocido para encontrar eficientemente los factores primos de un número grande. Por eso, decir públicamente cuál es el producto pq no ayuda a encontrar p y q, y sin éstos, no se puede calcular el valor de b necesario para desencriptar el mensaje.
Esto todavía no demuestra que el 17-gono se puede construir, pero ofrece un fuerte indicio, y Gauss consiguió encontrar una reducción explícita de esta ecuación de grado 16 a una serie de cuadráticas. Él afirmó, pero no demostró, que una construcción es posible cuando p - 1 es una potencia de 2 (requiriendo todavía que p sea primo), y que es imposible para todos los demás primos. La demostración fue pronto completada por otros.
Estos primos especiales se denominan primos de Fermat, porque fueron estudiados por Fermat. Éste observó que si p es un primo y p - 1 = 2k entonces k debe ser también una potencia de 2. Él anotó los primeros primos de Fermat:
2, 3, 5, 17, 257, 65.537
Conjeturó que los números de esta forma son siempre primos, pero esto era falso. Euler descubrió que cuando m = 5 hay un factor 641.
Se sigue de esto que deben existir también construcciones de regla y compás para el 257-gono regular y el 65.537-gono regular. F. J. Richelot construyó el 257-gono regular en 1832, y su trabajo es correcto. J. Hermes pasó 10 años trabajando en el 65.537-gono, y completó su construcción en 1894. Estudios recientes sugieren que contiene errores.
La teoría de números empezó a hacerse matemáticamente interesante con la obra de Fermat, quien detectó muchas de las pautas importantes ocultas en el extraño y enigmático comportamiento de los números naturales. Su enojosa tendencia a no dar demostraciones fue corregida por Euler, Lagrange y algunas figuras menores, con la única excepción de su «Último Teorema», pero el área siguió consistiendo en teoremas aislados, con frecuencia profundos y difíciles, pero no muy estrechamente relacionados entre sí.
Todo eso cambió cuando Gauss entró en escena y concibió fundamentos conceptuales generales para la teoría de números, tales como la aritmética modular. Él relacionó también la teoría de números con la geometría en su trabajo sobre polígonos regulares. Desde ese momento, la teoría de números se hizo una parte principal del tapiz de las matemáticas.
Las intuiciones de Gauss llevaron al reconocimiento de nuevos tipos de estructuras en matemáticas: nuevos sistemas de números, tales como los enteros mod m, y nuevas operaciones, tales como la composición de formas cuadráticas. Visto en retrospectiva, la teoría de números de finales del siglo XVIII y principios del XIX llevó al álgebra abstracta de finales de los siglos XIX y XX. Los matemáticos empezaban a ampliar la gama de conceptos y estructuras que eran objetos de estudio aceptables. Pese a su tema especializado, las Disquisitiones Muthematicæ son un hito importante en el desarrollo de la aproximación moderna al conjunto de las matemáticas. Ésta es una de las razones por la que Gauss es tan respetado por los matemáticos.
“Con frecuencia se necesita tiempo -a veces cientos de años- para que una buena idea matemática adquiera importancia práctica”
Hasta finales del siglo XX la teoría de números siguió siendo una rama de las matemáticas puras, interesante por sí misma, y por sus numerosas aplicaciones dentro de las propias matemáticas, pero de poca importancia real para el mundo exterior. Todo eso cambió con la invención de las comunicaciones digitales a finales del siglo XX. Puesto que la comunicación dependía entonces de los números, apenas sorprende que la teoría de números llegase a estar en la vanguardia de tales áreas de aplicación.
Con frecuencia se necesita tiempo -a veces cientos de años- para que una buena idea matemática adquiera importancia práctica, pero finalmente la mayoría de los temas que los matemáticos encuentran importantes por sí mismos resultan ser valiosos también en el mundo real.
Capítulo 8
El sistema del mundo
La invención del cálculo infinitesimal
El avance más importante en la historia de las matemáticas fue el cálculo infinitesimal. Fue inventado alrededor de 1680 por Isaac Newton y Gottfried Leibniz de forma independiente. Leibniz lo publicó primero, pero Newton -incitado por amigos ultrapatriotas- reclamó la prioridad y describió a Leibniz como un plagiario. La disputa agrió las relaciones entre los matemáticos ingleses y los de la Europa continental durante un siglo, y los ingleses fueron los que más perdieron con ello.
§. El sistema del mundo
Incluso si es probable que Leibniz merezca la prioridad, Newton hizo del cálculo infinitesimal una técnica capital de la disciplina en ciernes de la física matemática, la ruta más efectiva que conoce la humanidad hacia la comprensión del mundo natural. Newton llamó a su teoría «el sistema del mundo». Quizá esto no parezca muy modesto, pero es una descripción muy justa. Antes de Newton, la comprensión que se tenía de las pautas en la naturaleza consistía básicamente en las ideas de Galileo sobre los cuerpos en movimiento, en particular la trayectoria parabólica de un objeto tal como una bala de cañón, y el descubrimiento de Kepler de que Marte sigue una elipse a través de los cielos. Después de Newton, las pautas matemáticas gobernaban casi todo en el mundo físico: los movimientos de los cuerpos terrestres y celestes, el flujo del aire y del agua, la transmisión del calor, la luz y el sonido, y la fuerza de la gravedad.
Resulta curioso, no obstante, que la publicación más importante de Newton sobre las leyes matemáticas de la naturaleza, sus Principia Mathematica, apenas mencionan el cálculo infinitesimal; en su lugar, se basa en una inteligente aplicación de la geometría al estilo de los antiguos griegos. Pero las apariencias engañan: documentos inéditos conocidos como los «papeles de Portsmouth» muestran que cuando estaba trabajando en los Principia, Newton ya tenía las ideas principales del cálculo infinitesimal. Es probable que Newton utilizase los métodos del cálculo infinitesimal para hacer muchos de sus descubrimientos, pero decidió no presentarlos de esta forma.
Su versión del cálculo infinitesimal fue publicada después de su muerte en el Método de fluxiones de 1732.
Cálculo infinitesimal
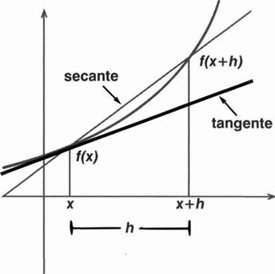
Aproximaciones geométricas a la derivada
¿Qué es el cálculo infinitesimal? Los métodos de Newton y Leibniz son más fáciles de entender si presentamos previamente las ideas principales. El cálculo infinitesimal es la matemática de las tasas de cambio instantáneas: ¿con qué rapidez está cambiando una magnitud concreta en este preciso instante? Un ejemplo físico: un tren se mueve por una vía: ¿con qué rapidez se mueve precisamente ahora?
El cálculo infinitesimal tiene dos ramas principales. El cálculo diferencial proporciona métodos para calcular tasas de cambio, y tiene muchas aplicaciones geométricas, en particular encontrar tangentes a curvas. El cálculo integral hace lo contrario: dada la tasa de cambio de una magnitud, determina la propia magnitud. Las aplicaciones geométricas del cálculo integral incluyen los cálculos de áreas y volúmenes. Quizá el descubrimiento más importante es esta conexión inesperada entre dos preguntas geométricas «clásicas» aparentemente no relacionadas: encontrar tangentes a una curva y encontrar áreas.
El cálculo infinitesimal trata de funciones: procedimientos que toman un número general y calculan un número asociado. El procedimiento se especifica normalmente por una fórmula, que asigna a un número dado x (posiblemente en un rango específico) un número asociado f(x). Ejemplos son la función raíz cuadrada f(x) = √x (que requiere que x sea positivo) y la función cuadrado f(x) = x2 (donde no hay ninguna restricción para x).
La primera idea clave del cálculo infinitesimal es la diferenciación, que obtiene la derivada de una función. La derivada es la tasa a la que está cambiando f(x), comparada con cómo está cambiando x: la tasa de cambio de f(x) con respecto a x.
Desde el punto de vista geométrico, la tasa de cambio es la pendiente de la tangente a la gráfica de f en el valor x. Puede aproximarse encontrando la pendiente de la secante: una línea que corta a la gráfica de f en dos puntos próximos, correspondientes a x y x + h, respectivamente, donde h es pequeño. La pendiente de la secante es
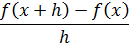
Supongamos ahora que h se hace muy pequeño. Entonces la secante se aproxima a la tangente a la gráfica en x. De modo que, en cierto sentido, la pendiente requerida -la derivada de f en x- es el «límite» de esta expresión cuando h se hace arbitrariamente pequeño.
Ensayemos este cálculo con un ejemplo sencillo, f(x) = x2. En este caso
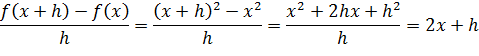
A medida que h se hace muy, muy pequeño, la pendiente 2x + h se aproxima cada vez más a 2x. Por ello, la derivada de f es la función g para la que g(x) = 2x.
La principal cuestión conceptual aquí es definir lo que se entiende por «límite». Se necesitó más de un siglo para encontrar una definición lógica.
La otra idea clave en el cálculo infinitesimal es la de integración. Esto se ve más fácilmente como el proceso inverso de la diferenciación. Así, la integral de g, escrita
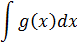
es cualquier función f(x) cuya derivada es g(x). Por ejemplo, puesto que la derivada de es g(x) = 2x, la integral de g(x) = 2x es, en símbolos
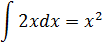
La necesidad del cálculo infinitesimal
La inspiración para la creación del cálculo infinitesimal llegó de dos direcciones. Dentro de las matemáticas puras, el cálculo diferencial se desarrolló a partir de métodos para encontrar tangentes a curvas, y el cálculo integral se desarrolló a partir de métodos para calcular las áreas de figuras planas y los volúmenes de sólidos. Pero el estímulo vino de la física: una comprensión creciente de que la naturaleza tiene pautas. Por razones que aún no entendemos realmente, muchas de las pautas fundamentales en la naturaleza implican tasas de cambio. Por ello sólo tienen sentido, y sólo pueden descubrirse, gracias al cálculo infinitesimal.
“El modelo de Hiparco no era muy preciso...”
Antes del Renacimiento, el modelo más preciso del movimiento del Sol, la Luna y los planetas era el de Ptolomeo. En su sistema la Tierra estaba fija, y todo lo demás -en particular el Sol- giraba a su alrededor en una serie de círculos (reales o imaginarios, dependiendo del gusto). Los círculos tenían su origen como esferas, en la obra del astrónomo griego Hiparco; sus esferas giraban en torno a ejes gigantescos, algunos de los cuales estaban unidos a otras esferas y se movían con ellas. Este tipo de movimiento compuesto parecía necesario para modelar los movimientos complejos de los planetas. Recordemos que algunos planetas, tales como Mercurio, Venus y Marte, parecían viajar a lo largo de trayectorias complicadas que incluían lazos. Otros -Júpiter y Saturno eran los únicos otros planetas conocidos en aquella época- se comportaban de manera más suave, pero incluso estos cuerpos mostraban irregularidades extrañas, conocidas desde los tiempos de los babilonios.
Ya hemos descrito el sistema de Ptolomeo, conocido como epiciclos, que reemplazaba las esferas por círculos, pero retenía el movimiento compuesto.
El modelo de Hiparco no era muy preciso, comparado con las observaciones, pero el modelo de Ptolomeo encajaba muy bien con las observaciones y durante más de mil años se vio como la última palabra sobre el tema.
Sus escritos, traducidos al árabe como el Almagesto, fueron utilizados por astrónomos de muchas culturas.
§. Dios frente a ciencia
No obstante, ni siquiera el Almagesto estaba de acuerdo con todos los movimientos planetarios. Además, era bastante complicado. Alrededor del año 1000, algunos pensadores árabes y europeos empezaron a preguntarse si el movimiento diario del Sol podría explicarse por una Tierra en rotación, y algunos de ellos también jugaron con la idea de que la Tierra da vueltas alrededor del Sol. Pero poco salió de esas especulaciones en aquella época.
Johannes Kepler
1571-1530Kepler era hijo de un mercenario y de la hija de una posadera. Su padre murió, probablemente en la guerra entre los Países Bajos y el Sacro Imperio Romano, cuando Kepler era niño, y desde entonces vivió con su madre en la posada de su abuelo.
Fue precoz en matemáticas, y en 1589 estudió astronomía con Michael Maestlin en la Universidad de Tubinga. Allí entró en contacto con el sistema ptolemaico.
La mayoría de los astrónomos de la época estaban más interesados en calcular órbitas que en preguntarse cómo se movían realmente los planetas, pero Kepler se interesó desde el principio en las trayectorias precisas seguidas por los planetas, antes que en el sistema de epiciclos propuesto. Se familiarizó con el sistema copernicano, y rápidamente se convenció de que era literalmente verdadero y no sólo un truco matemático.
Eli 1596 hizo su primer intento por encontrar pautas en los movimientos de los planetas, vía su Mysterium Cosmographicum (Misterio del cosmos) con su extraño modelo basado en los sólidos regulares. Este modelo no estaba de acuerdo con las observaciones, de modo que Kepler escribió a un destacado astrónomo observacional, Tycho Brahe. Kepler se convirtió en el asistente matemático de Brahe, quien le puso a trabajar en la órbita de Marte. Tras la muerte de Brahe, Kepler siguió trabajando en el problema. Brahe había dejado una gran riqueza de datos y Kepler se esforzó en encajarlos en una órbita razonable. Los cálculos que sobreviven ocupan más de 1.000 páginas, que Kepler califica como «mi guerra con Marte». Su órbita final era tan precisa que la única diferencia con los datos modernos se debe a una mínima deriva de la órbita durante los siglos transcurridos.
1611 fue un mal año. El hijo de Kepler murió a los siete años de edad. A continuación murió su mujer. Luego, el emperador Rodolfo, que toleraba a los protestantes, abdicó y Kepler se vio obligado a dejar Praga. En 1613 Kepler se volvió a casar, y un problema que le ocurrió durante la celebración de su boda le llevó a escribir su Nueva estereometría de las barricas de vino, de 1615.
En 1619 publicó Harmonices Mundi (La armonía del mundo) una secuela de su Misterio del cosmos. El libro contenía muchas matemáticas nuevas, incluidas pautas de teselación y poliedros. También formuló la tercera ley del movimiento planetario. Mientras estaba escribiendo el libro, su madre fue acusada de brujería. Con ayuda de la Facultad de Derecho de Tubinga, ella fue finalmente liberada, en parte porque los acusadores no habían seguido el procedimiento legal correcto para la tortura.
Sin embargo, en la Europa del Renacimiento la actitud científica empezó a arraigar, y una de las primeras víctimas fueron los dogmas religiosos.
En esa época la Iglesia católica romana ejercía un control sustancial sobre la visión del universo de sus seguidores. No se trataba sólo de que la existencia del universo, y su despliegue diario, fueran atribuidos al Dios cristiano.
Lo importante, era que se creyera que la naturaleza correspondía a una lectura muy literal de la Biblia. Por consiguiente se veía la Tierra como el centro de todas las cosas, la base sólida alrededor de la cual giraban los cielos. Y los seres humanos eran el pináculo de la creación, la razón de la existencia del universo.
Ninguna observación científica puede refutar la existencia de un creador desconocido e invisible. Pero las observaciones pueden -y lo hicieron- desacreditar la visión de la Tierra como centro del universo. Y esto causó un enorme revuelo, y llevó a la muerte a muchas personas inocentes, a veces de una forma terriblemente cruel.
§. Copérnico
Lo peor llegó en 1543, cuando el estudioso polaco Nicholas Copérnico publicó un libro sorprendente, original y algo herético: Sobre las revoluciones de las esferas celestes. Como Ptolomeo, él utilizaba epiciclos para alcanzar precisión. A diferencia de Ptolomeo, él colocaba al Sol en el centro, mientras todo lo demás, incluida la Tierra, pero excluida la Luna, giraba alrededor del Sol. Sólo la Luna giraba alrededor de la Tierra.
La razón principal de Copérnico para esta propuesta radical era pragmática: en lugar de los 77 epiciclos de Ptolomeo sólo necesitaba 34. Entre los epiciclos ideados por Ptolomeo había muchas repeticiones de un mismo círculo: círculos de tamaño y velocidad de rotación concretos aparecían asociados con muchos cuerpos distintos. Copérnico comprendió que si todos estos epiciclos se transferían a la Tierra, sólo uno de ellos sería necesario. Ahora interpretamos esto en términos del movimiento de los planetas con respecto a la Tierra.
Si suponemos erróneamente que la Tierra está fija, como parece estarlo para un observador ingenuo, entonces el movimiento de la Tierra alrededor del Sol se transfiere a todos los planetas como un epiciclo adicional.
Otra ventaja de la teoría de Copérnico era que trataba a todos los planetas exactamente de la misma manera. Ptolomeo necesitaba mecanismos diferentes para explicar los planetas internos y los planetas externos. Ahora, la única diferencia era que los planetas internos estaban más cerca del Sol que la Tierra, mientras que los planetas externos estaban más lejos. Todo tenía un sentido perfecto. Pero en conjunto fue rechazado, y por varias razones, no todas ellas religiosas.
La teoría de Copérnico era complicada, poco familiar y su libro era difícil de leer. Tycho Brahe, uno de los mejores observadores astronómicos de la época, encontró sutiles discrepancias entre la teoría heliocéntrica de Copérnico y algunas observaciones, que también discrepaban de la teoría de Ptolomeo; y trató de encontrar un compromiso mejor.
§. Kepler
Cuando Brahe murió, sus papeles fueron heredados por Kepler, quien pasó años analizando las observaciones en busca de pautas. Kepler era una especie de místico, en la tradición pitagórica, y tendía a imponer pautas artificiales en los datos observacionales. El más famoso de estos intentos abortados por encontrar regularidades en los cielos fue su bella, pero completamente equivocada, explicación del espaciado de los planetas en términos de los sólidos regulares. En su época, los planetas conocidos era seis: Mercurio, Venus, la Tierra, Marte, Júpiter y Saturno. Kepler se preguntó si sus distancias al Sol seguían una pauta geométrica.
Teoría de Kepler del espaciado de las órbitas planetarias
También se preguntó por qué había seis planetas. Se dio cuenta de que seis planetas dejan lugar para cinco formas interpuestas, y puesto que había exactamente cinco sólidos regulares, esto explicaría el límite de seis planetas. Dio con una serie de seis esferas, cada una de las cuales llevaba en su ecuador la órbita de un planeta. Entre las esferas, firmemente anidados entre una esfera y la siguiente, colocó los cinco sólidos, en el orden
Mercurio
Octaedro
Venus
Icosaedro
La tierra
Dodecaedro
Marte
Tetraedro
Júpiter
Cubo
Saturno
Los números encajaban razonablemente bien, especialmente dada la precisión limitada de las observaciones en aquella época. Pero hay 120 maneras diferentes de reordenar los cinco sólidos, que dan un número enorme de espaciados diferentes entre ellos.
“Kepler se preguntó por qué había seis planetas.”
Apenas sorprende que uno de éstos estuviera razonablemente de acuerdo con la realidad. El descubrimiento posterior de más planetas fue un golpe definitivo para este tipo particular de búsqueda de pautas y lo envió al cubo de basura de la historia.
En este proceso, sin embargo, Kepler descubrió algunas pautas que aún reconocemos como genuinas, ahora llamadas «Leyes de Kepler del Movimiento Planetario». Las extrajo, tras unos veinte años de cálculos, de las observaciones de Tycho Brahe de Marte. Las leyes afirman:
i. Los planetas se mueven alrededor del Sol en órbitas elípticas.
ii. Los planetas barren áreas iguales en tiempos iguales.
iii. El cuadrado del periodo de revolución de un planeta es proporcional al cubo de su distancia media al Sol
La característica más heterodoxa de la obra de Kepler es que descartaba el círculo clásico (supuestamente la forma más perfecta posible) en favor de la elipse. Lo hizo con alguna renuencia, diciendo que sólo se fijó en la elipse cuando todo lo demás había quedado descartado.
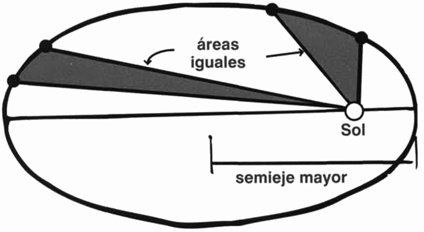
El planeta se mueve durante un intervalo de tiempo dado
No hay ninguna razón especial para esperar que estas tres leyes guarden alguna relación más estrecha con la realidad que la hipotética ordenación de sólidos regulares, pero resultó que las tres leyes tenían una importancia física real.
§. Galileo
Otra figura importante del periodo fue Galileo Galilei, quien descubrió regularidades matemáticas en el movimiento de un péndulo y en los cuerpos que caen. En 1S89, como profesor de matemáticas en la Universidad de Pisa, realizó experimentos con cuerpos que caían rodando por un plano inclinado, pero no publicó sus resultados. Fue en esta época cuando se dio cuenta de la importancia de los experimentos controlados en el estudio de los fenómenos naturales, una idea que es ahora fundamental para toda la ciencia. Se dedicó a la astronomía e hizo una serie de descubrimientos fundamentales que finalmente le llevaron a adoptar la teoría copernicana del Sol como el centro del sistema solar. Esto le encaminó hacia una confrontación con la Iglesia, y finalmente fue juzgado por herejía y puesto bajo arresto domiciliario.
Durante los últimos años de su vida, con su salud en declive, escribió los Discursos y Demostraciones matemáticas sobre dos nuevas ciencias, donde explicaba su trabajo sobre el movimiento de cuerpos en planos inclinados. Estableció que la distancia que recorre un cuerpo inicialmente en reposo que se mueve con aceleración uniforme es proporcional al cuadrado del tiempo. Esta ley es la base de su primer descubrimiento de que un proyectil sigue una trayectoria parabólica. Junto con las leyes de Kepler del movimiento planetario, dio nacimiento a una nueva disciplina: la mecánica, el estudio matemático de cuerpos en movimiento.
Galileo Galilei
1784-1842Galileo era hijo de Vincenzo Galilei, un profesor de música que había realizado experimentos con cuerdas para validar sus teorías musicales. Cuando tenía diez años Galileo fue al Monasterio de Vallombrosa para ser educado con vistas a hacerse médico.
Pero Galileo no estaba realmente interesado en la medicina, y pasó el tiempo estudiando matemáticas y «filosofía natural» -lo que ahora llamamos ciencia.
En 1589 Galileo se convirtió en profesor de matemáticas en la Universidad de Pisa. En 1591 asumió un puesto mejor pagado en Padua, donde enseñó geometría euclidiana y astronomía a los estudiantes de medicina. En aquella época los médicos hacían uso de la astrología para tratar a sus pacientes, por lo que estos temas eran una parte obligada del currículum.
Al tener noticia del invento del telescopio, Galileo construyó uno por su cuenta y se hizo tan bueno en ello que ofreció sus métodos al Senado de Venecia, garantizándole los derechos de su uso a cambio de un aumento de salario. En 1609 Galileo observó los cielos e hizo un descubrimiento tras otro: cuatro de las lunas de Júpiter, estrellas individuales en la Vía Láctea, montañas en la Luna.
Descubrió la existencia de manchas solares y publicó esta observación en 1612. Para entonces sus descubrimientos astronómicos le habían convencido de la verdad de la teoría heliocéntrica de Copérnico, y en 1616 hizo explícitas sus ideas en una carta a la gran duquesa Cristina, donde afirmaba que la teoría copernicana representa la realidad física y no es solamente una manera conveniente de simplificar los cálculos.
En este momento el papa Pablo V ordenó a la Inquisición que decidiera sobre la verdad o falsedad de la teoría heliocéntrica, y ésta fue declarada falsa. Galileo recibió instrucciones de no defender la teoría, pero entonces fue elegido un nuevo papa, Urbano VIII, que parecía menos estricto sobre la cuestión, de modo que Galileo no se tomó la prohibición muy en serio.
En 1623 publicó Il Saggiatore (El Ensayador), y se lo dedicó a Urbano. En él incluía la famosa frase «el universo está escrito en el lenguaje de las matemáticas, y sus caracteres son triángulos, círculos y otras figuras geométricas, sin los que es humanamente imposible entender una sola palabra de él».
En 1630 Galileo pidió permiso para publicar otro libro, Dialogo sobre los dos sistemas máximos del mundo, sobre las teorías geocéntrica y heliocéntrica. En 1632, cuando llegó el permiso de Florencia (no de Roma), siguió adelante. El libro pretendía demostrar que la Tierra se mueve: la prueba principal eran las mareas. En realidad, la teoría de las mareas de Galileo era completamente falsa, pero las autoridades de la Iglesia vieron el libro como dinamita teológica y la Inquisición lo prohibió, convocando a Galileo a Roma para ser juzgado por herejía. Fue declarado culpable, aunque escapó con una sentencia de prisión en forma de arresto domiciliario. En esto tuvo más suerte que muchos otros herejes, para quienes ser quemados en la hoguera era un castigo común. Mientras estaba bajo arresto domiciliario escribió sus Discursos, en los que explicaba su trabajo sobre cuerpos en movimiento al mundo exterior. Fue sacado clandestinamente de Italia y publicado en Holanda.
Éste era el contexto astronómico y físico que llevó al cálculo infinitesimal. A continuación, examinaremos el contexto matemático.
§. La invención del cálculo
La invención del cálculo infinitesimal fue el resultado de una serie de investigaciones anteriores de lo que parecen ser problemas no relacionados pero con una unidad oculta. Entre éstos estaban: calcular la velocidad instantánea de un objeto en movimiento a partir de la distancia que ha recorrido en cualquier instante dado, encontrar la tangente a una curva, encontrar la longitud de una curva, encontrar los valores máximo y mínimo de una magnitud variable, encontrar el área de una forma en el plano y el volumen de un sólido en el espacio. Algunas ideas y ejemplos importantes fueron desarrollados por Fermat, Descartes y, menos famoso, el inglés Isaac Barrow, pero los métodos seguían siendo especiales.
§. Leibniz
El primer progreso real importante fue obra de Gottfried Wilhelm Leibniz, un abogado de profesión que dedicó buena parte de su vida a las matemáticas, la lógica, la filosofía, la historia y muchas ramas de la ciencia. Alrededor de 1673 empezó a trabajar en el problema clásico de encontrar la tangente a una curva, y advirtió que éste era en efecto el «problema inverso» al de encontrar áreas y volúmenes. El último se reducía a encontrar una curva dadas sus tangentes; el primer problema era exactamente el inverso.
Leibniz utilizó esta relación para definir lo que, de hecho, eran integrales, utilizando la abreviatura omn. Así, en sus manuscritos encontramos fórmulas tales como
omn x2 = x3/3.
En 1675 había sustituido omn por el símbolo ∫ aún utilizado hoy, una letra s alargada al viejo estilo, que representa «sum». El trabajaba en términos de incrementos pequeños dx y dy de las cantidades x e y, y utilizaba su razón para determinar el tasa de cambio de y como función de x. En esencia, si f es una función, Leibniz escribía
dy = f(x + dx) - f(x)
de modo que
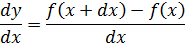
que es la habitual aproximación «secante» a la pendiente de la tangente.
Leibniz reconoció que esta notación tiene sus problemas. Si dy y dx son distintos de cero, entonces dy/dx no es la tasa de cambio instantánea de y, sino una aproximación. Trató de evitar este problema suponiendo que dx y dy eran «infinitesimalmente pequeños». Un infinitesimal es un número distinto de cero que es más pequeño que cualquier otro número diferente de cero. Por desgracia, es fácil ver que no puede existir tal número (medio infinitesimal es también distinto de cero, pero más pequeño), de modo que esta aproximación hace poco más que desplazar el problema a otro lugar.
En 1676 Leibniz sabía cómo integrar y diferenciar cualquier potencia de x, y escribió la fórmula
dxn = nxn-1dx
que ahora escribimos como
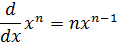
En 1677 dedujo reglas para diferenciar la suma, el producto y el cociente de dos funciones, y en 1680 había obtenido la fórmula para la longitud de un arco de curva, y el volumen de un sólido de revolución, como integrales de varias cantidades relacionadas.
Aunque conocemos estos hechos, y las fechas asociadas, por sus notas no publicadas, él no publicó sus ideas sobre el cálculo infinitesimal hasta bastante más tarde, en 1684. Jakob y Johann Bernoulli encontraron este artículo bastante oscuro y lo describieron como «un enigma antes que una explicación». En retrospectiva, vemos que para esa fecha Leibniz había descubierto una parte importante del cálculo infinitesimal básico, con aplicaciones a curvas complicadas como la cicloide, y tenía una correcta comprensión de conceptos tales como el de curvatura. Por desgracia, sus escritos eran fragmentarios y prácticamente ilegibles.
§. Newton
El otro creador del cálculo infinitesimal fue Isaac Newton. Dos de sus amigos, Barrow y Edmond Halley, llegaron a reconocer su extraordinaria capacidad y le animaron a publicar su trabajo. A Newton le disgustaba ser criticado, y cuando en 1672 publicó sus ideas sobre la luz, su trabajo provocó una tormenta de críticas, que reforzaron su renuencia a llevar sus ideas a la imprenta. De todas formas, continuó publicando esporádicamente y escribió dos libros. En privado continuó desarrollando sus ideas sobre la gravedad, y en 1684 Halley trató de convencer a Newton para que publicara su trabajo. Pero aparte de los recelos generales de Newton por las críticas, había un obstáculo técnico. El se había visto obligado a modelar los planetas como partículas puntuales, con masa no nula pero tamaño nulo, lo que le parecía poco realista e invitaba a la crítica. Quería reemplazar estos puntos poco realistas por esferas sólidas, pero no podía demostrar que la atracción gravitatoria de una esfera es la misma que la de una partícula puntual de la misma masa.
“Los Principia vieron la luz en 1687”
En 1686 consiguió salvar esta dificultad, y los Principia vieron la luz del día en 1687. Contenían más ideas nuevas. Las más importantes eran las leyes matemáticas del movimiento, que extendían la obra de Galileo, y la gravedad, basada en las leyes encontradas por Kepler.
La ley del movimiento de Newton más importante (hay otras secundarias) afirma que la aceleración de un cuerpo en movimiento, multiplicada por su masa, es igual a la fuerza que actúa sobre el cuerpo. Ahora bien, la velocidad es la derivada de la posición, y la aceleración es la derivada de la velocidad.
Isaac Newton
1642-1727Newton vivió en una granja en la minúscula villa de Woolsthorpe, en Lincolnshire. Su padre había muerto dos meses antes de que él naciera, y su madre llevaba la granja. Fue educado en escuelas locales
muy corrientes, y no mostró ningún talento especial, salvo una habilidad con los juguetes mecánicos. En una ocasión hizo un globo de aire caliente y lo lanzó con el gato de la familia como piloto; ni el globo ni el gato volvieron a verse. Fue al Trinity College, en la Universidad de Cambridge, gracias a que había obtenido notas razonables en la mayoría de los exámenes -excepto en geometría-. Como estudiante de licenciatura no causó gran impacto.
Luego, en 1665, la gran plaga comenzó a devastar Londres y sus alrededores, y los estudiantes fueron enviados a casa antes de que Cambridge corriera la misma suerte. De vuelta a la granja familiar, Newton empezó a pensar mucho más profundamente en cuestiones científicas y matemáticas.
Durante 1665-1666 concibió su ley de la gravedad para explicar el movimiento planetario, desarrolló las leyes de la mecánica para explicar y analizar cualquier tipo de cuerpo o partícula en movimiento, inventó el cálculo diferencial y el integral, e hizo avances importantes en óptica. Como era propio de él, no publicó nada de su trabajo, y volvió tranquilamente a Cambridge donde obtuvo su grado de maestro y fue elegido miembro del college. Luego se aseguró la posición de la Cátedra Lucasiana de Matemáticas, cuando quien la ocupaba, Barrow, renunció en 1669. Impartió lecciones muy corrientes, más bien malas, a las que asistían muy pocos estudiantes.
Así que incluso para establecer la ley de Newton necesitamos la segunda derivada de la posición con respecto al tiempo, que actualmente se escribe
Newton escribía, en su lugar, dos puntos sobre la x.
La ley de la gravedad afirma que todas las partículas de la naturaleza se atraen unas a otras con una fuerza que es directamente proporcional a sus masas e inversamente proporcional al cuadrado de la distancia entre ellas.
Para qué les servía el cálculo infinitesimalUno de los primeros usos del cálculo infinitesimal para entender fenómenos naturales fue en el problema de la forma de un puente colgante. La cuestión era controvertida: algunos matemáticos pensaban que la respuesta era una parábola, pero otros discrepaban. En 1691 Leibniz, Christiaan Huygens y Johann Bernoulli publicaron propuestas de soluciones. La más clara era la de Bernoulli. Él escribió una ecuación diferencial para describir la posición de la cadena, basada en la mecánica newtoniana y las leyes de movimiento de Newton.
Resultó que la solución no era una parábola, sino una curva conocida como una catenaria, con ecuación
y = k(ex + e-x)
para k constante.
Una cadena que cuelga forma una catenariaLos cables de suspensión de los puentes, sin embargo, son parabólicos.
El puente colgante Clifton-una parábolaLa diferencia aparece porque estos cables soportan, además de su propio peso, el peso del puente. Una vez más, esto puede demostrarse utilizando el cálculo infinitesimal.
Así, por ejemplo, la fuerza con que se atraen la Tierra y la Luna se reduciría a la cuarta parte si la Luna se llevara a una distancia doble, o a una novena parte si su distancia se triplicase. Una vez más, debido a que esta ley trata de fuerzas, implica a la segunda derivada de las posiciones.
La integral definida
Newton dedujo esta ley a partir de las tres leyes de Kepler del movimiento planetario. La deducción publicada era una obra maestra de geometría euclidiana clásica. Newton escogió este estilo de presentación porque utilizaba matemáticas familiares, y por ello no podría ser criticado fácilmente. Pero muchos aspectos de los Principia debían su génesis a la invención no publicada del cálculo infinitesimal de Newton.
Entre su obra anterior sobre el tema había un artículo titulado Sobre el análisis por medio de ecuaciones con un número infinito de términos, que hizo circular entre algunos amigos en 1669. En terminología moderna, preguntaba cuál es la ecuación de una función f(x) si el área bajo su gráfica es de la forma xm. (En realidad preguntaba algo ligeramente más general, pero dejémoslo así.) El dedujo, para su satisfacción, que la respuesta es
f(x) = mxm-1.
Para qué nos sirve el cálculo infinitesimalLas ecuaciones diferenciales abundan en la ciencia: son de lejos la manera más común de modelar sistemas naturales. Por escoger una aplicación al azar, se utilizan rutinariamente para calcular las trayectorias de las sondas espaciales, tales como la misión Mariner a Marte, las dos naves Pioneer que exploraron el sistema solar y nos dieron imágenes maravillosas de Júpiter, Saturno, Urano y Neptuno, y los recientes vehículos robóticos de seis ruedas Mars Rovers Spirit y Opportunity que exploraron el Planeta Rojo.
La misión Cassini, que actualmente explora Saturno y sus lunas, es otro ejemplo. Entre sus descubrimientos está la existencia de lagos de metano y etano líquido en Titán, una luna de Saturno. Por supuesto, el cálculo infinitesimal no es la única técnica utilizada por misiones espaciales; pero sin él, estas misiones nunca habrían despegado literalmente del suelo.
De forma más práctica, toda aeronave que vuela, todo automóvil que viaja por carretera y todo puente colgante y edificio a prueba de terremotos debe su diseño en parte al cálculo infinitesimal. Incluso nuestra comprensión de cómo cambia el tamaño de las poblaciones animales con el tiempo deriva de ecuaciones diferenciales.
La Mars Rover Spirit (impresión artística, NASA)Lo mismo sucede con la difusión de las epidemias, donde modelos basados en el cálculo infinitesimal se utilizan para planificar la forma más eficaz de intervenir y prevenir la expansión de la enfermedad. Un modelo reciente de la «enfermedad de las vacas locas» en UK ha mostrado que la estrategia adoptada en su día no era la mejor disponible.
El enfoque de Newton para calcular derivadas era muy similar al de Leibniz, salvo que él utilizaba º en lugar de dx, y por ello su método adolece del mismo problema lógico: parece ser sólo aproximado. Pero Newton pudo demostrar que suponiendo que º es muy pequeño, la aproximación sería cada vez mejor. «En el límite» cuando o se hace tan pequeño como queramos, el error desaparece. Por ello, mantenía Newton, su resultado final era exacto. Introdujo una nueva palabra, fluxión, para recoger la idea principal: la de una cantidad «que fluye hacia» cero pero sin llegar realmente a ello.
En 1671 escribió un tratamiento más extenso, el Método de fluxiones y series infinitas. El primer libro sobre cálculo infinitesimal no se publicó hasta 1711; el segundo apareció en 1736. Es evidente que en 1671 Newton poseía la mayor parte de las ideas básicas del cálculo infinitesimal.
Los objetores a este procedimiento, en particular el obispo George Berkeley en su libro de 1734, El analista, un discurso dirigido a un matemático infiel, señaló que es ilógico dividir numerador y denominador por o si más tarde º se hace 0. En efecto, el procedimiento oculta el hecho de que la fracción es en realidad 0/0 que, como es bien conocido, carece de sentido. Newton respondió que él no estaba haciendo realmente º igual a 0; él estaba calculando lo que sucedía cuando o se acercaba tanto como quisiéramos a 0 sin llegar a ello realmente. El método trataba de fluxiones, no de números.
Los matemáticos buscaron refugio en analogías físicas -Leibniz se refería al «espíritu de finura» frente al «espíritu de la lógica»- pero Berkeley tenía toda la razón. Se necesitó más de un siglo para encontrar una buena respuesta a sus objeciones, definiendo la noción intuitiva de «paso al límite» de una forma rigurosa. El cálculo infinitesimal se convirtió entonces en una disciplina más sutil, el análisis. Pero durante un siglo después de la invención del cálculo infinitesimal, nadie excepto Berkeley se preocupó mucho por sus fundamentos lógicos, y el cálculo infinitesimal floreció a pesar de este defecto.
Floreció porque Newton tenía razón, pero tuvieron que pasar casi 200 años antes de que su concepto de una fluxión fuera formulado de una manera lógicamente aceptable, en términos de límites. Por fortuna para las matemáticas, el progreso no quedó detenido hasta que se descubriera una fundamentación lógica decente. El cálculo infinitesimal era demasiado útil, y demasiado importante, para quedar en suspenso por unos pocos reparos lógicos. Berkeley estaba indignado, y mantenía que el método sólo parecía funcionar debido a que varios errores se cancelaban mutuamente. Tenía razón; pero no se preguntó por qué siempre se cancelaban. Porque si fuera así, ¡no serían realmente errores en absoluto!
Asociado con la diferenciación está el proceso inverso, la integración.
La integral de f(x), escrita ∫f(x)dx, es cualquier función que da f(x) cuando es diferenciada. Geométricamente representa el área bajo la gráfica de la función f. La integral definida ∫abf(x)dx es el área bajo la gráfica entre los valores x = a y x = b.
Derivadas e integrales resolvían problemas que habían puesto a prueba el ingenio de matemáticos anteriores. Velocidades, tangentes, máximos y mínimos podían encontrarse utilizando diferenciación. Longitudes, áreas y volúmenes podían calcularse por integración. Pero había más. Sorprendentemente, parecía que las pautas de la naturaleza estaban escritas en el lenguaje del cálculo infinitesimal.
§. Los ingleses se quedan rezagados
Conforme la importancia del cálculo infinitesimal se hacía cada vez más patente, mayor prestigio se atribuía a su creador. Pero ¿quién era el creador?
Hemos visto que Newton empezó a pensar en el cálculo infinitesimal en 1665, pero no publicó nada sobre el tema hasta 1687. Leibniz, cuyas ideas seguían líneas bastante similares a las de Newton, había empezado a trabajar en el cálculo infinitesimal en 1673, y publicó sus primeros artículos sobre el tema en 1684. Los dos trabajaban independientemente, pero Leibniz podía haber aprendido algo del trabajo de Newton cuando visitó París en 1672 y Londres en 1673; Newton había enviado una copia de Sobre el análisis a Barrow en 1669, y Leibniz habló con varias personas que también conocían a Barrow, de modo que podría haber conocido este trabajo.
Cuando Leibniz publicó su trabajo en 1684, algunos de los amigos de Newton se sintieron agraviados -probablemente porque a Newton se le habían adelantado en la publicación y todos ellos se dieron cuenta con retraso de lo que había en juego- y acusaron a Leibniz de robar las ideas de Newton. Los matemáticos continentales, especialmente los Bernoulli, saltaron en defensa de Leibniz, sugiriendo que era Newton, y no Leibniz, el culpable de plagio. En realidad, los dos habían hecho sus descubrimientos de forma casi totalmente independiente, como muestran sus manuscritos inéditos; para enturbiar las cosas, ambos habían tomado mucho del trabajo previo de Barrow, quien probablemente tenía más motivos de queja que cualquiera de ellos.
Trayectoria parabólica de un proyectil
Las acusaciones podrían haber sido retiradas fácilmente, pero en su lugar la disputa se enconó; Johann Bernoulli extendió su disgusto con Newton a toda la nación inglesa. El resultado final fue un desastre para las matemáticas inglesas, porque los ingleses se apegaron obstinadamente al estilo geométrico de pensamiento de Newton, que era difícil de usar, mientras que el análisis continental empleaba los métodos algebraicos más formales de Leibniz e hizo avanzar la disciplina con rapidez. Por consiguiente, quienes mayor provecho sacaron en física matemática fueron franceses, alemanes, suizos y holandeses, mientras que las matemáticas inglesas languidecían en un remanso.
§. La ecuación diferencial
La idea más importante que emergió del aluvión de trabajo sobre el cálculo infinitesimal era la existencia, y la utilidad, de un nuevo tipo de ecuación: la ecuación diferencial. Las ecuaciones algebraicas relacionan varias potencias de un número desconocido. Las ecuaciones diferenciales son mucho más grandes: relacionan varias derivadas de una función desconocida.
Las leyes de movimiento de Newton nos dicen que si y(t) es la altura de una partícula que se mueve bajo la acción de la gravedad cerca de la superficie de la Tierra, entonces la segunda derivada es proporcional a la fuerza g que actúa; en concreto,
donde m es la masa. Esta ecuación no especifica directamente la función y.
En su lugar, especifica una propiedad de su segunda derivada. Debemos «resolver» la ecuación diferencial para encontrar y. Dos integraciones sucesivas dan la solución
donde b es la altura inicial de la partícula y a es su velocidad inicial. La fórmula nos dice que la gráfica de la altura y frente al tiempo t es una parábola vertical. Esta es la observación de Galileo.
Los esfuerzos pioneros de Copérnico, Kepler, Galileo y otros científicos del Renacimiento llevaron al descubrimiento de pautas matemáticas en el mundo natural. Algunas pautas aparentes resultaron ser espurias, y fueron descartadas; otras ofrecieron modelos muy precisos de la naturaleza, que fueron conservados y desarrollados. De estos primeros inicios emergió la noción de que vivimos en un «universo mecánico», que marcha según reglas rígidas e inquebrantables, a pesar de la seria oposición religiosa, principalmente de la Iglesia de Roma.
El gran descubrimiento de Newton fue que las pautas de la naturaleza parecen manifestarse no como regularidades en ciertas magnitudes sino como relaciones entre sus derivadas. Las leyes de la naturaleza están escritas en el lenguaje del cálculo infinitesimal; lo que importa no son los valores de variables físicas, sino los ritmos con que cambian. Fue una intuición profunda, y creó una revolución que llevó, más o menos directamente, a la ciencia moderna y cambió nuestro planeta para siempre.
Capítulo 9
Pautas en la naturaleza
Formulando las leyes de la física
El mensaje principal de los Principia de Newton no eran las «leyes» de la naturaleza específicas que él descubrió y utilizó, sino la idea de que tales leyes existen, junto con la prueba de que la manera de modelar matemáticamente las leyes de la naturaleza es con ecuaciones diferenciales. Mientras en Inglaterra los matemáticos se enzarzaban en polémicas estériles acerca del supuesto (y totalmente ficticio) robo por parte de Leibniz de las ideas de Newton sobre el cálculo infinitesimal, los matemáticos del continente estaban recogiendo los beneficios de la gran intuición de Newton, haciendo importantes incursiones en mecánica celeste, elasticidad, dinámica de fluidos, calor, luz y sonido: los temas centrales de la física matemática. Muchas de las ecuaciones que dedujeron siguen utilizándose hoy, pese a -o quizá a causa de- los muchos avances en las ciencias físicas.
§. Ecuaciones diferenciales
Para empezar, los matemáticos se concentraron en encontrar fórmulas explícitas para soluciones de tipos particulares de ecuaciones diferenciales ordinarias. En cierto modo esto fue desafortunado porque la atención se centró en las escasas ecuaciones que podían resolverse por una fórmula de este tipo antes que en ecuaciones que describían genuinamente la naturaleza.
“...la atención se centró en las escasas ecuaciones que podían resolverse por una fórmula...”
Un buen ejemplo es la ecuación diferencial para un péndulo, que toma la fórmula
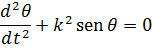
para una constante adecuada k, donde t es el tiempo y θ es el ángulo en que cuelga el péndulo, siendo θ = 0 la posición vertical hacia abajo. No hay solución de esta ecuación en términos de funciones clásicas (polinómicas, exponenciales, logarítmicas, trigonométricas y demás). Existe una solución que utiliza «funciones elípticas», inventadas más de un siglo más tarde.
Sin embargo, si suponemos que el ángulo es pequeño, de modo que consideramos un péndulo que hace «pequeñas oscilaciones», entonces sen θ es aproximadamente igual a θ, y cuanto más pequeño se hace θ mejor es esta aproximación. Así, la ecuación diferencial puede reemplazarse por
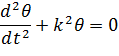
y ahora hay una fórmula para la solución, en general,
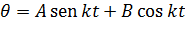
con constantes A y B determinadas por la posición y la velocidad angular iniciales del péndulo.
Este enfoque tiene algunas ventajas: por ejemplo, podemos deducir rápidamente que el periodo del péndulo -el tiempo que tarda en completar una oscilación- es 2π/k. El mayor inconveniente es que la solución falla cuando θ se hace suficientemente grande (y aquí incluso 20º es «grande» si buscamos una respuesta precisa). Hay también una cuestión de rigor: ¿podemos asegurar que una solución exacta de una ecuación aproximada da una solución aproximada de una ecuación exacta? Aquí la respuesta es «sí», pero esto no se demostró hasta alrededor de 1900.
La segunda ecuación puede resolverse explícitamente porque es lineal: incluye sólo la primera potencia de la incógnita θ y de su derivada, y los coeficientes son constantes. La función prototipo para todas las ecuaciones diferenciales lineales es la exponencial y = ex. Ésta satisface la ecuación
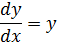
Es decir, ex es su propia derivada. Esta propiedad es una razón por la que el número e es «natural». Una consecuencia es que la derivada del logaritmo natural log x es 1/x, de modo que la integral de 1/x es log x. Cualquier ecuación diferencial lineal con coeficientes constantes puede resolverse utilizando funciones exponenciales y trigonométricas (que, como veremos, son realmente exponenciales disfrazadas).
§. Ordinarias y parciales
Hay dos tipos de ecuaciones diferenciales. Una ecuación diferencial ordinaria (EDO) se refiere a una función desconocida y de una sola variable x, y relaciona varias derivadas de y, tales como dy/dx y d2y/dx2. Las ecuaciones diferenciales descritas hasta ahora han sido ordinarias. Mucho más difícil, pero fundamental para la física matemática, es el concepto de ecuación en derivadas parciales (EDP). Una ecuación semejante se refiere a una función desconocida y de dos o más variables, tal como y(x,t) donde x e y son coordenadas espaciales y t es el tiempo. La EDP relaciona esta función con expresiones en sus «derivadas parciales» con respecto a cada una de las variables. Se utiliza una nueva notación para representar derivadas de unas variables con respecto a otras mientras las restantes se mantienen fijas. Así, ∂x/∂t indica la tasa de cambio de f con respecto al tiempo, mientras x e y se mantienen constantes. Esto se denomina una derivada parcial, de ahí el término «ecuación en derivadas parciales».
Euler introdujo las EDP en 1734 y D'Alembert hizo algún trabajo sobre ellas en 1743, pero estas primeras investigaciones fueron aisladas y especiales. El primer gran avance llegó en 1746, cuando D'Alembert volvió a un viejo problema, la cuerda de violín vibrante. Johann Bernoulli había discutido una versión «elemento finito» de esta cuestión en 1727, considerando la vibración de un número finito de masas puntuales igualmente espaciadas a lo largo de una cuerda sin masa. D’Alembert trató una cuerda continua, de densidad uniforme, aplicando los cálculos de Bernoulli a n masas y haciendo luego tender n a infinito. Así, una cuerda continua se consideraba como infinitos segmentos infinitesimales de cuerda conectados.
Partiendo de los resultados de Bernoulli, que se basaban en la ley de movimiento de Newton, y haciendo algunas simplificaciones (por ejemplo, que el tamaño de la vibración es pequeño), D'Alembert se vio llevado a la EDP
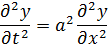
donde y = y(x,t) es la forma de la cuerda en el instante t, como función de la coordenada horizontal x. Aquí a es una constante relacionada con la tensión en la cuerda y su densidad. Por un argumento ingenioso, D'Alembert demostró que la solución general de su EDP tenía la forma
y(x, t) = f(x + at) + f(x - at),
donde f es periódica, con un periodo doble de la longitud de la cuerda, y f es también una función impar -es decir, f(-x) = -f(x). Esta forma satisface la «condición de contorno» natural de que los extremos de la cuerda no se muevan.
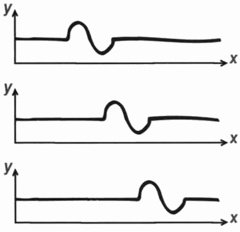
Instantáneas sucesivas de una onda que viaja de izquierda a derecha
§. Ecuación de ondas
Hoy llamamos ecuación de ondas a la EDP de D'Alembert, e interpretamos su solución como una superposición de ondas colocadas de forma simétrica, una moviéndose con velocidad a y otra con velocidad -a (es decir, viajando en direcciones opuestas). Se ha convertido en una de las ecuaciones más importantes en física matemática, porque las ondas aparecen en muchas circunstancias diferentes.
Euler examinó el artículo de D'Alembert, e inmediatamente trató de mejorarlo. En 1753 demostró que sin la condición de contorno la solución general es
y(x, t) = f(x + at) + g(x - at)
donde f y g son periódicas, pero no satisfacen otras condiciones. En particular, estas funciones pueden tener diferentes fórmulas en diferentes rangos de x, una característica que Euler calificaba como funciones «discontinuas», aunque en la terminología actual son continuas pero tienen derivadas primeras discontinuas.
En un artículo anterior publicado en 1749 él señaló que (por simplicidad tomaremos la longitud de la cuerda igual a 1) las funciones periódicas impares más simples son funciones trigonométricas
f(x) = sen x, sen 2x, sen 3x, sen 4x, ...
y así sucesivamente. Estas funciones representan vibraciones sinusoidales puras de frecuencias 1/π, 2/π, 3/π, 4/π, etc.
Modos de vibración de una cuerda
La solución «general», decía Euler, es una superposición de tales curvas. La curva seno básica sen (πx) es el «modo fundamental» de vibración, y las otras son modos superiores, que ahora llamamos «armónicos».
La comparación de la solución de Euler de la ecuación de ondas con la solución de D'Alembert llevó a una crisis fundacional. D'Alembert no reconocía la posibilidad de funciones discontinuas en el sentido de Euler. Además, parecía haber un defecto fundamental en el trabajo de Euler, porque las funciones trigonométricas son continuas, y así lo son todas las superposiciones (finitas) de ellas. Euler no se había comprometido con la cuestión de superposiciones finitas versus infinitas -en aquellos días nadie era realmente muy riguroso sobre tales materias, y aún quedaba un duro camino para aprender que eso importa-. Ahora el fallo en hacer tal distinción estaba causando serios problemas. La controversia se mantuvo a fuego lento hasta que el trabajo posterior de Fourier la reavivó.
§. Música, luz, sonido y electromagnetismo
Los antiguos griegos sabían que una cuerda vibrante puede producir muchas notas musicales diferentes, dependiendo de la posición de los «nodos», o puntos en reposo. En el caso de la «frecuencia fundamental» sólo los puntos extremos están en reposo. Si la cuerda tiene un nodo en su centro, entonces produce una nota una octava más alta; y cuantos más nodos haya, mayor será la frecuencia de la nota. Las vibraciones más altas se denominan armónicos.
Las vibraciones de una cuerda de violín son ondas estacionarias: la forma de la cuerda en cualquier instante es la misma, excepto que está estirada o comprimida en una dirección perpendicular a su longitud. La máxima cantidad de estiramiento es la amplitud de la onda, que físicamente determina el tono de la nota. Las formas de onda mostradas son de tipo sinusoidal; y sus amplitudes varían sinusoidalmente con el tiempo.
“Los antiguos griegos sabían que la cuerda vibrante puede producir muchas notas musicales.”
En 1759 Euler extendió estas ideas de cuerdas a tambores. De nuevo dedujo una ecuación de ondas que describe cómo varía con el tiempo el desplazamiento de la membrana en la dirección vertical. Su interpretación física es que la aceleración de una parte pequeña de la membrana es proporcional a la tensión media ejercida sobre ella por las partes vecinas de la membrana. Los tambores difieren de las cuerdas de violín no sólo en su dimensionalidad -un tambor es una membrana bidimensional plana-, sino en que tiene un contorno mucho más interesante. En esta disciplina, los contornos son absolutamente cruciales. El contorno de un tambor puede ser cualquier curva cerrada, y la condición clave es que el contorno del tambor está fijo.
Vibraciones de una guitarra real
El resto de la membrana puede moverse, pero su borde está firmemente sujeto.
Los matemáticos del siglo XVIII fueron capaces de resolver las ecuaciones para el movimiento de tambores de varias formas. Una vez más encontraron que todas las vibraciones pueden construirse a partir de unas más simples, y que éstas daban una lista específica de frecuencias. El caso más simple es el tambor rectangular, cuyas vibraciones más simples son combinaciones de ondulaciones sinusoidales en las dos direcciones perpendiculares. Un caso más difícil es el tambor circular, que lleva a unas nuevas funciones llamadas funciones de Bessel. Las amplitudes de estas ondas siguen variando sinusoidalmente con el tiempo, pero su estructura espacial es más complicada.
Vibraciones de una membrana de tambor circular
La ecuación de ondas es extraordinariamente importante. Las ondas aparecen no sólo en instrumentos musicales sino también en la física de la luz y el sonido. Euler encontró una versión tridimensional de la ecuación de ondas, que aplicó a las ondas sonoras. Aproximadamente un siglo después. James Clerk Maxwell extrajo las mismas expresiones matemáticas de sus ecuaciones para el electromagnetismo, y predijo la existencia de ondas de radio.
§. Atracción gravitatoria
Otra aplicación importante de las EDP apareció en la teoría de la atracción gravitatoria, de otro modo conocida como teoría del potencial. El problema motivador fue la atracción gravitatoria de la Tierra, o de cualquier otro planeta. Newton había modelado los planetas como esferas perfectas, pero su forma verdadera está más cercana a un elipsoide. Y mientras la atracción gravitatoria de una esfera es la misma que la de una partícula puntual (para distancias fuera de la esfera), esto ya no es cierto para los elipsoides.
Colin Maclaurin hizo avances significativos en estas cuestiones en una memoria que ganó un premio en 1740 y en un libro posterior, el Tratado de fluxiones, publicado en 1742. Su primer paso consistió en demostrar que si un fluido de densidad uniforme gira con una velocidad uniforme, bajo la influencia de su propia gravedad, entonces la forma de equilibrio es un esferoide oblato, un elipsoide de revolución. Luego estudió las fuerzas atractivas generadas por tal esferoide, con éxito limitado. Su resultado principal era que si dos esferoides tienen los mismos focos, y si una partícula yace en el plano ecuatorial o en el eje de revolución, entonces la fuerza ejercida sobre ella por uno u otro esferoide es proporcional a sus masas.
En 1743 Clairaut continuó trabajando en este problema en su Théorie de la figure de la Terre. Pero el gran avance fue obra de Legendre. Éste demostró una propiedad básica no sólo de los esferoides, sino de cualquier sólido de revolución: si se conoce su atracción gravitatoria en todo punto a lo largo de su eje, entonces se puede deducir la atracción en cualquier otro punto.
Su método consistía en expresar la atracción como una integral en coordenadas polares esféricas. Manipulando esta integral, él expresó su valor como una superposición de «armónicos esféricos». Éstos están determinados por funciones especiales ahora denominadas polinomios de Legendre. En 1784 siguió trabajando en este tema, y demostró muchas propiedades básicas de estos polinomios.
La EDP fundamental para la teoría del potencial es la ecuación de Laplace, que aparece en el Traité de mecanique celeste, en cinco volúmenes, que se empezó a publicar en 1799. Era conocida por investigadores anteriores, pero el tratamiento de Laplace fue definitivo. La ecuación toma la forma
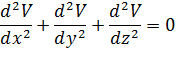
donde V(x,y,z) es el potencial en un punto (x,y,z) del espacio.
Intuitivamente, dice que el valor del potencial en cualquier punto dado es el promedio de sus valores en una esfera minúscula que rodea a dicho punto.
Un elipsoide
La ecuación es válida fuera del cuerpo; dentro, debe ser modificada para dar la que ahora se conoce como ecuación de Poisson.
§. Calor y temperatura
Los éxitos con el sonido y la gravitación animaron a los matemáticos a dirigir su atención hacia otros fenómenos físicos. Uno de los más importantes era el calor. A comienzos del siglo XIX la ciencia del flujo de calor se estaba convirtiendo en un tema de gran interés práctico, principalmente a causa de las necesidades de la industria metalúrgica, pero también debido a un creciente interés en la estructura del interior de la Tierra, y en particular en la temperatura en el interior del planeta. No hay ninguna forma directa de medir la temperatura a mil kilómetros o más bajo la superficie de la Tierra, de modo que las únicas medidas disponibles eran indirectas y era esencial entender cómo fluía el calor a través de cuerpos de composiciones diferentes.
En 1807 Joseph Fourier envió un artículo sobre el flujo de calor a la Academia Francesa de Ciencias, pero los recensores lo rechazaron porque no estaba suficientemente desarrollado. Para animar a Fourier a continuar el trabajo, la Academia hizo del flujo de calor el tema de su gran premio de 1812. El tema fue anunciado con mucha antelación, y en 1811 Fourier había revisado sus ideas, las presentó al premio y lo ganó. Sin embargo, su trabajo fue muy criticado por su falta de rigor lógico y la Academia se negó a publicarlo como una memoria. Fourier, irritado por esta falta de apreciación, escribió su propio libro, Théorie analytique du chaleur, publicado en 1822. Buena parte del artículo de 1811 estaba incluido sin modificaciones, pero también había material extra. En 1824 Fourier se desquitó: fue nombrado secretario de la Academia e inmediatamente publicó su artículo de 1811 como una memoria.
“En 1824 Fourier se desquitó: fue nombrado secretario de la Academia”
El primer paso de Fourier consistió en derivar una EDP para el flujo de calor. Con varias hipótesis simplificadoras: el cuerpo debe ser homogéneo (tiene las mismas propiedades en todas partes) e isótropo (se comporta de la misma manera en todas direcciones), y demás. Llegó a lo que ahora llamamos la ecuación del calor, que describe cómo cambia con el tiempo la temperatura en cualquier punto de un cuerpo tridimensional. La ecuación del calor tiene una forma muy similar a la ecuación de Laplace y la ecuación de ondas, pero la derivada parcial con respecto al tiempo es de primer orden, no de segundo. Este minúsculo cambio supone una profunda diferencia para las matemáticas de las EDP.
Había ecuaciones similares para cuerpos en una y dos dimensiones (barras y láminas) obtenidas eliminando los términos en z (para dos dimensiones) y luego en y (para una). Fourier resolvió la ecuación del calor para una barra (cuya longitud tomamos como π), y cuyos límites se mantienen a temperaturas fijas, suponiendo que en el instante t = 0 (condición inicial) la temperatura de un punto x de la barra es de la forma
b1 sen x + b2 sen2x + b3 sen3x +...
(una expresión sugerida por cálculos preliminares) y dedujo que la temperatura debía venir dada entonces por una expresión similar pero más complicada en la que cada término está multiplicado por una función exponencial apropiada. La analogía con los armónicos en la ecuación de ondas es sorprendente. Pero allí cada «modo» dado por una pura función seno oscila indefinidamente sin perder amplitud, mientras que aquí cada «modo» sinusoidal de la distribución de temperatura decae exponencialmente con el tiempo, y los modos más altos decaen con mayor rapidez.
La razón física para la diferencia es que en la ecuación de ondas la energía se conserva, de modo que las vibraciones no pueden desaparecer. Pero en la ecuación del calor la temperatura se difunde a lo largo de la barra, y se pierde en los extremos porque éstos se mantienen fríos.
El resultado del trabajo de Fourier es que cuandoquiera que desarrollamos la distribución inicial de temperatura en serie de Fourier -una serie de funciones senos y cosenos como la anterior-, entonces podemos leer inmediatamente cómo fluye el calor a través del cuerpo conforme pasa el tiempo. Fourier consideraba obvio que cualquier distribución inicial de temperatura podría expresarse de esta forma, y es aquí donde empezaban las dificultades; algunos de sus contemporáneos se habían preocupado precisamente por esta cuestión durante algún tiempo, en relación con las ondas, y se habían convencido de que era mucho más difícil de lo que parecía.
El argumento de Fourier para la existencia de un desarrollo en senos y cosenos era complicado, confuso y muy poco riguroso. Se paseó por todas las matemáticas para deducir, finalmente, una simple expresión para los coeficientes b1,. b2, b3, ...
Si llamamos f(x) a la distribución inicial de temperatura, su resultado era
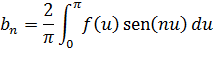
Euler ya había escrito esta fórmula en 1777, en el contexto de la ecuación de ondas para el sonido, y la demostró utilizando la ingeniosa observación de que modos distintos, sen nθx y sen mθx son ortogonales, lo que significa que
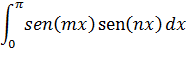
es cero siempre que m y n sean enteros distintos, pero no nulos; de hecho, es igual a π/2 cuando m = n. Si suponemos que f(x) tiene un desarrollo de Fourier, multiplicamos ambos miembros por sen x e integramos, entonces todos los términos excepto uno, desaparecen, y el término restante da la fórmula de Fourier para bn.
§. Dinámica de fluidos
Ninguna discusión de las EDP de la física matemática estaría completa sin mencionar la dinámica de fluidos. De hecho, ésta es un área de enorme importancia práctica porque estas ecuaciones describen el flujo del agua alrededor de los submarinos, del aire alrededor de los aviones e incluso el flujo del aire alrededor de los coches de Fórmula 1.
Cómo funcionan las series de FourierUna función «discontinua» típica es la onda cuadrada S(x), que toma los valores 1 cuando -π < x ≤ 0 y -1 cuando 0 < x ≤ π, y tiene periodo 2π. Aplicando la fórmula de Fourier a la onda cuadrada obtenemos la serie
S(x) = sen x + 1/3 sen 3x + 1/5 sen 5x +...
El desarrollo de Fourier de una onda cuadrada: arriba las curvas seno componentes y abajo, su sumaLos términos se suman, como se muestra en el diagrama de abajo.
Aunque la onda cuadrada es discontinua, cada aproximación es continua.
Sin embargo, las esquinas se acentúan a medida que se suman más términos, lo que hace que la gráfica de la serie de Fourier se haga cada vez más escalonada cerca de las discontinuidades.
Así es como una serie infinita de funciones continuas puede desarrollar una discontinuidad.
Euler inició la disciplina en 1757 deduciendo una EDP para el flujo de un fluido de viscosidad nula -«adherencia» cero-. Esta ecuación sigue siendo realista para algunos fluidos, pero es demasiado simple para muchos usos prácticos. Las ecuaciones para un flujo viscoso fueron obtenidas por Claude Navier en 1821, y de nuevo por Poisson en 1829. Incluían varias derivadas parciales de la velocidad del fluido. En 1845 George Gabriel Stokes dedujo las mismas ecuaciones a partir de principios físicos más básicos, y ahora se conocen con las ecuaciones de Navier-Stokes.
§. Ecuaciones diferenciales ordinarias
Cerramos esta sección con dos contribuciones de gran alcance al uso de las EDO en mecánica. En 1788 Lagrange publicó su Mécanique analytique, donde afirmaba orgullosamente que «no se encontrarán figuras en esta obra. Los métodos que expongo no requieren construcciones, ni argumentos geométricos o mecánicos, sino sólo operaciones algebraicas, sujetas a un curso regular y uniforme».
Para qué les servían las ecuaciones diferencialesEl modelo de Kepler de las órbitas elípticas no es exacto. Lo sería si sólo hubiera dos cuerpos en el sistema solar, pero cuando hay presente un tercer cuerpo, éste cambia («perturba») la órbita elíptica. Puesto que los planetas están muy espaciados, el problema sólo afecta a pequeños detalles del movimiento, y la mayoría de las órbitas siguen siendo casi elipses. Sin embargo, Júpiter y Saturno se comportan de forma muy extraña, a veces retrasándose respecto a donde «deberían estar» y a veces adelantándose.
El efecto es debido a su gravitación mutua, junto con la del Sol.
La ley de gravitación de Newton se aplica a cualquier número de cuerpos, pero los cálculos se hacen muy difíciles cuando hay tres cuerpos o más. En 1748, 1750 y 1752 la Academia Francesa de Ciencias ofreció premios para cálculos precisos de los movimientos de Júpiter y Saturno.
Júpiter y Saturno en una imagen compuestaEn 1748 Euler utilizó ecuaciones diferenciales para estudiar cómo la gravedad de Júpiter perturba la órbita de Saturno, y ganó el premio. Lo intentó de nuevo en 1752, pero su trabajo contenía errores importantes. Sin embargo, las ideas subyacentes resultaron ser útiles posteriormente.
En esa época, las trampas de los argumentos visuales se habían hecho evidentes y Lagrange estaba decidido a evitarlas. Las figuras vuelven a estar de moda ahora, aunque apoyadas por lógica sólida, pero la insistencia de Lagrange en el tratamiento formal de la mecánica inspiró una nueva unificación de la disciplina, en términos de «coordenadas generalizadas». Cualquier sistema puede describirse utilizando muchas variables diferentes. En el caso de un péndulo, por ejemplo, la coordenada usual es el ángulo en que cuelga el péndulo, pero la distancia horizontal entre la lenteja y la vertical serviría igualmente.
Las ecuaciones de movimiento se presentan de forma muy diferente en sistemas de coordenadas diferentes, y Lagrange pensaba que esto era poco elegante. Encontró una manera de reescribir las ecuaciones de movimiento en una forma que parece la misma en todos los sistemas de coordenadas. La primera innovación consiste en emparejar las coordenadas: con cada coordenada de posición q (tal como el ángulo del péndulo) hay asociada la correspondiente coordenada de velocidad q (la velocidad del movimiento angular del péndulo). Si hay k coordenadas de posición, hay también k coordenadas de velocidad.
En lugar de una ecuación diferencial de segundo orden en las posiciones, Lagrange obtuvo una ecuación diferencial de primer orden en las posiciones y las velocidades.
Sofia Vasilyevna Kovalevskaya
1850-1891Sofia Kovalevskaya era hija de un general de artillería y miembro de la nobleza rusa. Sucedió que las paredes de su habitación de niña habían sido empapeladas con páginas de notas de clase sobre análisis. A los 11 años ella estudió el papel de la pared y aprendió por sí sola el cálculo infinitesimal. Se sintió atraída hacia las matemáticas, que prefería a cualquier otra área de estudio. Su padre trató de disuadirla, pero ella persistió contra viento y marea, leyendo libros de álgebra mientras sus padres estaban durmiendo.
Se dice que Sofia Vasilyevna Kovalevskaya trabajó en matemáticas para aliviar sus sentimientos de culpa; su marido, de quien se había separado, se suicidó.
Para viajar y conseguir una educación se vio obligada a casarse, pero el matrimonio nunca funcionó. En 1869 estudió matemáticas en Heidelberg pero, debido a que no se admitían mujeres como estudiantes, tuvo que convencer a la universidad para que la dejara asistir a clases de forma oficiosa. Manifestó un impresionante talento matemático y en 1871 fue a Berlín, donde estudió con el gran analista Karl Weierstrass. Tampoco ahora se la admitió como estudiante oficial, pero Weierstrass le dio lecciones particulares.
Realizó una investigación original, y en 1874 Weierstrass dijo que su trabajo era adecuado para un doctorado. Ella había escrito tres artículos, sobre EDP, funciones elípticas y los anillos de Saturno. Ese mismo año la Universidad de Gotinga le concedió un grado de doctor. El artículo sobre EDP fue publicado en 1875.
En 1878 tuvo una hija, pero volvió a las matemáticas en 1880 y trabajó sobre la refracción de la luz. En 1883 su marido, de quien se había separado, se suicidó, y ella dedicó cada vez más tiempo a las matemáticas para aliviar sus sentimientos de culpa. Consiguió un puesto en la Universidad en Estocolmo, donde dio clases en 1884. En 1889 se convirtió en la tercera mujer catedrática en una universidad europea, tras Marie Agnesi (quien nunca asumió el puesto) y la física Laura Bassí. Allí hizo una investigación sobre el movimiento de un cuerpo rígido, la presentó a un premio ofrecido por la Academia de Ciencias en 1886 y lo ganó. El jurado encontró el trabajo tan brillante que aumentó el importe del premio. Un trabajo posterior sobre el mismo tema fue recompensado con un premio por la Academia de Ciencias Sueca, y le llevó a ser elegida para la Academia Imperial de Ciencias.
Formuló esto en términos de una magnitud ahora conocida como el lagrangiano.
Hamilton mejoró la idea de Lagrange, haciéndola incluso más elegante. Desde el punto de vista físico, él utilizaba el momento en lugar de la velocidad para definir las coordenadas extra. Desde el punto de vista físico matemático, él definía una magnitud ahora denominada el hamiltoniano, que puede interpretarse -en muchos sistemas- como energía. El trabajo teórico en mecánica utiliza en general el formalismo hamiltoniano, que ha sido extendido también a la mecánica cuántica.
Velocidad del viento y temperatura del globo terrestre computadas a partir de una versión ampliada de las ecuaciones de Navier-Stokes
§. Los físicos se hacen matemáticos
Los Principia de Newton eran impresionantes, con su revelación de profundas leyes matemáticas subyacentes a los fenómenos naturales. Pero lo que sucedió luego fue todavía más impresionante. Los matemáticos abordaron toda la panoplia de la física: sonido, luz, calor, flujo de los fluidos, gravitación, electricidad, magnetismo. En cada caso dieron con ecuaciones diferenciales que describían la física, a menudo de forma muy precisa.
“... la radio, la televisión y los aviones comerciales dependen de las matemáticas de las ecuaciones diferenciales.”
Las consecuencias a largo plazo han sido extraordinarias. Muchos de los más importantes avances tecnológicos, tales como la radio, la televisión y los aviones comerciales dependen, de muchas maneras, de las matemáticas de las ecuaciones diferenciales.
El tema es aún objeto de intensa actividad investigadora y cada día surgen nuevas aplicaciones. Es justo decir que la invención por parte de Newton de las ecuaciones diferenciales, desarrolladas por sus sucesores en los siglos XVIII y XIX, es en muchos aspectos responsable de la sociedad en que vivimos. Esto sólo alcanza a mostrar lo que está sucediendo entre bastidores, si uno se molesta en mirar.
Para qué nos sirven las ecuaciones diferencialesHay un vínculo directo entre la ecuación de ondas y la radio y la televisión.
Alrededor de 1830 Michael Faraday realizó experimentos sobre electricidad y magnetismo, investigando la creación de un campo magnético por una corriente eléctrica y de un campo eléctrico por un imán en movimiento. Las dinamos y los motores eléctricos actuales son descendientes directos de su aparato. En 1864 James Clerk Maxwell reformuló las teorías de Faraday como ecuaciones matemáticas para el electromagnetismo: las ecuaciones de Maxwell. Son EDP que incluyen los campos eléctrico y magnético.
Una simple deducción a partir de las ecuaciones de Maxwell lleva a la ecuación de ondas. Este cálculo muestra que la electricidad y el magnetismo pueden viajar juntos como una onda, a la velocidad de la luz. ¿Qué viaja a la velocidad de la luz? La luz. Por lo tanto, la luz es una onda electromagnética. La ecuación no ponía limitaciones a la frecuencia de la onda, y las ondas de luz ocupan un rango de frecuencias relativamente pequeño, de modo que los físicos dedujeron que debería haber ondas electromagnéticas con otras frecuencias. Heinrich Hertz demostró la existencia física de tales ondas, y Guglielmo Marconi las convirtió en un dispositivo práctico: la radio. La tecnología creció como una bola de nieve.
Ondas de radioLa televisión y el radar se basan también en ondas electromagnéticas. También lo hacen la navegación por satélite GPS, los teléfonos móviles y las comunicaciones por computador «inalámbricas».
Capítulo 10
Cantidades imposibles
¿Pueden tener raíces cuadradas los números negativos?
Los matemáticos distinguen varios tipos de números diferentes, con propiedades diferentes. Lo que realmente importa no son los números individuales, sino el sistema al que pertenecen: la compañía en la que están.
Cuatro de estos sistemas de números son familiares: los números naturales, 0, 1, 2, 3,...; los enteros, que incluyen también los números naturales negativos; los números racionales, compuestos de fracciones p/q, donde p y q son enteros y q es distinto de cero; y los números reales, que generalmente se presentan como decimales que «se prolongan indefinidamente» -cualquier cosa que esto signifique-y representan tanto a los números racionales, con cifras decimales que se repiten, como a los números irracionales como √2, e y π cuya expansión decimal no repite indefinidamente el mismo bloque de dígitos.
§. Enteros
El nombre «entero» simplemente significa «completo»; los otros nombres dan la impresión de que los sistemas en cuestión son cosas sensibles y razonables: naturales, racionales y por supuesto reales. Los nombres reflejan, y animan, una visión muy arraigada de que los números son características del mundo que nos rodea.
Mucha gente piensa que la única manera de hacer investigación matemática consiste en inventar números nuevos. Esta idea es casi siempre errónea; muchas matemáticas no tratan con números en absoluto, y en cualquier caso el objetivo habitual es inventar nuevos teoremas, no nuevos números.
En ocasiones, sin embargo, inventar «números nuevos» es necesario. Y una de estas invenciones, un denominado número «imposible» o «imaginario», cambió por completo la faz de las matemáticas y aumentó enormemente su potencia. Ese número era la raíz cuadrada de menos uno. Para los primeros matemáticos una descripción semejante parecía ridícula, porque el cuadrado de cualquier número es siempre positivo. Por lo tanto, los números negativos no pueden tener raíces cuadradas.
“...los números negativos no pueden tener raíces cuadradas. Pero supongamos que...”
Pero supongamos que las tuvieran. ¿Qué sucedería?
Los matemáticos necesitaron mucho tiempo para apreciar que los números son invenciones artificiales hechas por seres humanos; invenciones muy eficaces para captar muchos aspectos de la naturaleza, por supuesto, pero que no eran más parte de la naturaleza que uno de los triángulos de Euclides o una fórmula del cálculo infinitesimal. Desde un punto de vista histórico vemos que los matemáticos empezaron a luchar con esta pregunta filosófica cuando empezaron a entender que los números «imaginarios» eran inevitables, útiles y de algún modo estaban al mismo nivel que los más familiares números reales.
§. Los problemas con las ecuaciones cúbicas
Las ideas matemáticas revolucionarias rara vez se descubren en los contextos más simples y (vistos con perspectiva) más obvios. Casi siempre surgen de algo mucho más complicado. Así sucedió con la raíz cuadrada de menos uno. Hoy día, lo habitual es introducir este número en términos de la ecuación cuadrática x2 + 1 =0, cuya solución es la raíz cuadrada de menos uno, cualquier cosa que esto signifique. Entre los primeros matemáticos en preguntarse si esto tenía un sentido razonable estaban los algebristas del Renacimiento, que tropezaron con las raíces cuadradas de números negativos de una manera sorprendentemente indirecta: la solución de ecuaciones cúbicas.
Recordemos que Del Ferro y Tartaglia descubrieron soluciones algebraicas a las ecuaciones cúbicas, posteriormente expuestas por Cardano en su Ars Magna. En símbolos modernos, la solución de una ecuación cúbica x3 + ax = b es
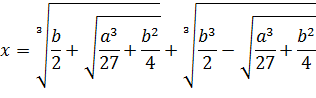
Los matemáticos del Renacimiento expresaban esta solución en palabras, pero el procedimiento era el mismo.
A veces esta fórmula funcionaba muy bien, pero otras veces tropezaba con problemas. Cardano advirtió que cuando la fórmula se aplica a la ecuación, que tiene la solución obvia x = 4, el resultado se expresa como
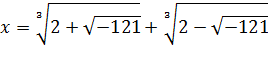
Sin embargo, esta expresión no parecía tener un significado razonable, porque -121 no tiene raíz cuadrada. Un Cardano intrigado escribió a Tartaglia pidiéndole una aclaración, pero Tartaglia pasó por alto el punto y, como era de esperar, su respuesta fue inútil.
Una respuesta, si así se le puede llamar, fue ofrecida por Rafael Bombelli en su libro en tres volúmenes L’Algebra, impreso en Venecia en 1572 y en Bolonia en 1579. A Bombelli le preocupaba que el Ars Magna de Cardano era bastante oscura, y se propuso escribir algo más claro. El operaba sobre la molesta raíz cuadrada como si fuera un número ordinario, y advirtió que
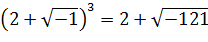
de donde dedujo la curiosa fórmula
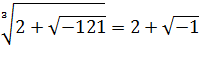
Del mismo modo, Bombelli obtuvo la fórmula
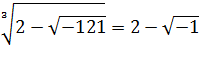
Ahora podía reescribir la suma de las dos raíces cúbicas como
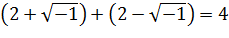
Así, este extraño método daba la respuesta correcta, un entero perfectamente normal, pero llegaba a ello manipulando cantidades «imposibles».
Todo esto era muy interesante, pero ¿por qué funcionaba?
§. Los números imaginarios
Para responder a esta pregunta los matemáticos tuvieron que desarrollar buenas maneras de pensar en raíces cuadradas de cantidades negativas y hacer cálculos con ellas.
Los autores anteriores, entre ellos Descartes y Newton, interpretaban estos números «imaginarios» como una señal de que un problema no tenía solución.
Si uno quería encontrar un número cuya raíz cuadrada era menos uno, la solución formal «raíz cuadrada de menos uno» era imaginaria, de modo que no existía solución.
La recta de números reales
Pero el cálculo de Bombelli implicaba que en los números imaginarios había algo más que eso. Podían utilizarse para encontrar soluciones; podían ocurrir cuando las soluciones sí existían.
En 1673 John Wallis inventó una manera sencilla de representar números imaginarios como puntos en un plano. Partió de la representación familiar de los números reales como una recta, con los números positivos a la derecha y los negativos a la izquierda.
Luego introdujo otra recta, que formaba un ángulo recto con la primera, y colocó los imaginarios a lo largo de esta nueva recta.
Esto es similar a la aproximación algebraica de Descartes a la geometría plana, utilizando ejes de coordenadas.
Los números reales forman un eje en la figura, y los imaginarios otro.
Wallis no enunció la idea exactamente así -su versión era más próxima a la aproximación de Fermat a las coordenadas que a la de Descartes-, pero la idea subyacente es la misma.
Dos copias de la recta de números reales que forman un ángulo recto
El resto del plano corresponde a números «complejos» que constan de dos partes: una real y una imaginaria.
En coordenadas cartesianas medimos la parte real a lo largo de la recta real y medimos la parte imaginaria paralela a la recta imaginaria. Así, 3 + 2i yace tres unidades a la derecha del origen y dos unidades arriba.
La idea de Wallis resolvía el problema de dar sentido a los números imaginarios, pero nadie le prestó la más mínima atención. No obstante, su idea ganó terreno lentamente en el subconsciente de los matemáticos.
El plano complejo según Wessel
La mayoría de ellos dejaron de preocuparse porque la raíz cuadrada de menos uno no pudiera ocupar una posición en la recta real, y se dieron cuenta de que podía vivir en algún lugar en el mundo más amplio del plano complejo. Algunos no apreciaron la idea: en 1758 François Daviet de Foncenex, en un artículo sobre números imaginarios, afirmaba que era absurdo pensar que los imaginarios formaban una recta a un ángulo recto con la recta real.
Pero otros la tomaron en serio y entendieron su importancia.
La idea de que un plano complejo podía ampliar la confortable recta real y dar hogar a los imaginarios estaba implícita en la obra de Wallis, aunque ligeramente oscurecida por la forma en que la presentaba. Fue explicitada por el noruego Caspar Wessel en 1797. Wessel era topógrafo, y lo que le interesaba principalmente era representar la geometría del plano en términos de números. En retrospectiva, sus ideas podían verse como un método de representar números complejos en términos de geometría plana. Pero él publicaba en danés, y su trabajo pasó desapercibido hasta un siglo más tarde, cuando fue traducido al francés. El matemático francés Jean-Robert Argand publicó independientemente la misma representación de los números complejos en 1806, y Gauss la descubrió independientemente de ambos en 1811.
§. Análisis complejo
Si los números complejos hubieran sido útiles sólo para el álgebra, podrían haber seguido siendo una curiosidad intelectual, de poco interés fuera de las matemáticas puras. Pero a medida que crecía el interés por el cálculo infinitesimal, y éste adoptaba una forma más rigurosa como análisis, la gente empezó a advertir que una fusión realmente interesante del análisis real con los números complejos -el análisis complejo- era no sólo posible sino deseable. En realidad, para muchos problemas, esencial.
Este descubrimiento derivaba de los intentos iniciales de pensar en funciones complejas. Las funciones más simples, tales como el cuadrado o el cubo, dependían sólo de manipulaciones algebraicas, de modo que era fácil definir estas funciones para números complejos. Para elevar al cuadrado un número complejo simplemente se le multiplica por sí mismo, el mismo proceso que se aplicaría a un número real. Las raíces cuadradas de números complejos son algo más complicadas, pero hay una recompensa agradable por hacer el esfuerzo: todo número complejo tiene una raíz cuadrada.
En realidad, todo número complejo no nulo tiene precisamente dos raíces cuadradas, una igual a menos la otra. Por ello, aumentar los números reales con un nuevo número, i, no sólo proporcionaba a -1 una raíz cuadrada, sino que proporcionaba raíces para cualquier cosa en el sistema ampliado de los números complejos.
¿Qué pasaba con senos, cosenos, la función exponencial y el logaritmo? Ahora las cosas empezaban a hacerse muy interesantes, pero también muy intrigantes, especialmente cuando se llegaba a los logaritmos.
“Las raíces cuadradas de números complejos son algo más complicadas.”
Como sucedió con el propio i, los logaritmos de números complejos se convirtieron en problemas puramente «reales». En 1702 Johann Bernoulli estaba investigando el proceso de integración aplicado a recíprocas de cuadráticas. El conocía una técnica ingeniosa para realizar esta tarea siempre que la ecuación cuadrática en cuestión tuviera dos soluciones reales r y s. Entonces podemos reescribir la expresión a integrar en términos de «fracciones parciales»
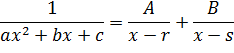
lo que lleva a la integral
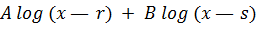
Pero ¿qué pasa si la cuadrática no tiene raíces reales? ¿Cómo se puede integrar, por ejemplo, la recíproca de x2 + 1? Bernoulli se dio cuenta que una vez definida el álgebra compleja, el truco de la fracción parcial sigue funcionando, pero ahora r y s son números complejos. Así, por ejemplo,
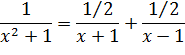
y la integral de esta función toma la forma
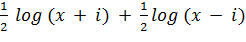
Este paso final no era plenamente satisfactorio, porque pedía una definición del logaritmo de un número complejo. ¿Era posible dar sentido a tal enunciado?
Bernoulli pensaba que lo era, y procedió a utilizar su nueva idea con un excelente resultado. Leibniz también explotó ideas de este tipo, pero los detalles matemáticos no eran simples. En 1712 ambos estaban discutiendo sobre un aspecto muy básico de esta aproximación. Olvidemos los números complejos; ¿qué era el logaritmo de un número real negativo? Bernoulli pensaba que el logaritmo de un número real negativo debería ser real; Leibniz insistía en que era complejo. Bernoulli tenía algo parecido a una demostración de su afirmación: suponiendo el formalismo habitual del cálculo infinitesimal, la ecuación
puede integrarse para dar
log (-x) = log(x)
Sin embargo, Leibniz no estaba convencido, y creía que la integración sólo era correcta para x real positivo.
Esta controversia particular fue resuelta por Euler en 1749, y dio la razón a Leibniz. Bernoulli, decía Euler, había olvidado que cualquier integración incluye una constante arbitraria. Lo que Bernoulli debería haber deducido era que
para alguna constante c. ¿Cuál era esta constante? Si los logaritmos de números negativos (y complejos) deben comportarse como los logaritmos de números reales, que es la clave de toda la cuestión, entonces debería ser cierto que
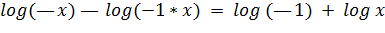
de modo que c = log (-1). Entonces Euler se embarcó en una serie de bellos cálculos que daban una forma más explícita para c. En primer lugar encontró una manera de manipular varias fórmulas que incluían números complejos, suponiendo que se comportaban como números reales, y dedujo una relación entre funciones trigonométricas y la exponencial:
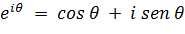
una fórmula que había sido anticipada en 1714 por Roger Cotes. Haciendo θ = n, Euler obtuvo el precioso resultado
eiπ = -1
que relaciona las dos constantes matemáticas fundamentales e y π.
Es extraordinario que exista una relación semejante, y todavía más extraordinario que sea tan simple. Esta fórmula encabeza regularmente las listas de «las fórmulas más bellas de todos los tiempos».
Tomando el logaritmo, deducimos inmediatamente que
log (-1) = iπ
lo que revela el secreto de la constante enigmática c: es iπ. Como tal, es imaginaria, de modo que Leibniz tenía razón y Bernouilli estaba equivocado.
Para qué les servían los números complejosLas partes real e imaginaria de una función compleja satisfacen las ecuaciones de Cauchy-Riemann, que están íntimamente relacionadas con las EDP para la gravitación, la electricidad, el magnetismo y algunos tipos de flujo de fluidos en el plano.
Campo magnético de un imán, puesto de manifiesto por limaduras de hierro: puede utilizarse el análisis complejo para calcular dichos camposEsta relación hizo posible resolver muchas ecuaciones de la física matemática pero sólo para sistemas en dos dimensiones.
Hay más, sin embargo, y esto abre una caja de Pandora. Si hacemos θ = 2π, entonces
e2iπ = 1.
Así, log (1) = 2iπ. Entonces la ecuación x = x * 1 implica que
log x = log x + 2iπ
de lo que concluimos que si n es un entero cualquiera,
log x = log x + 2niπ
A primera vista esto no tiene sentido; parece implicar que 2niπ = 0 para todo n. Pero hay una manera de interpretarlo que sí tiene sentido. Sobre los números complejos, la función logarítmica es «multivaluada». De hecho, a menos que el número complejo z sea cero, la función log z puede tomar infinitos valores distintos. (Cuando z = 0, el valor log 0 no está definido.)
Los matemáticos estaban acostumbrados a funciones que podían tomar varios valores distintos, siendo la raíz cuadrada el ejemplo más obvio: aquí, incluso un número real poseía dos raíces cuadradas distintas, una positiva y la otra negativa. Pero ¿infinitos valores? Esto era muy extraño.
Augustin-Louis Cauchy
1789-1857Augustin-Louis Cauchy nació en París durante una época de turbulencia política. Laplace y Lagrange eran amigos de la familia, de modo que Cauchy estuvo en contacto con a las matemáticas superiores a una edad temprana.
Fue a l’École Polytechnique, donde se graduó en 1807. En 1810 realizó trabajos de ingeniería en Cherburgo, incluido en los preparativos de la invasión de Inglaterra que planeaba Napoleón, pero siguió pensando sobre matemáticas, leyendo la Mecanique céleste de Laplace y la Théorie des functions de Lagrange.
Buscó incesantemente puestos académicos, con poco éxito, pero siguió trabajando en matemáticas Su famoso artículo sobre integrales complejas, que marca de hecho la fundación del análisis complejo, apareció en 1814, y finalmente logró su objetivo de un puesto académico, pues un año más tarde se convirtió en profesor ayudante de análisis en la École Polytechnique. Ahora sus matemáticas avanzaron y un artículo sobre ondas le valió el premio de 1816 de la Academia de Ciencias. Siguió desarrollando el análisis complejo, y en sus Leçons sur le calcul differentiel de 1829 dio la primera definición explícita de una función compleja.
Tras la revolución de 1830 Cauchy fue a Suiza por un breve periodo y en 1831 se convirtió en profesor de física teórica en Turín. Hay informes de que sus cursos eran muy desorganizados. En 1833 estaba en Praga, como tutor del nieto de Carlos X, pero al príncipe no le gustaban las matemáticas ni la física y Cauchy solía perder los nervios. Volvió a París en 1838 y recuperó su puesto en la Academia, pero no recuperó sus puestos docentes hasta que Louis Philippe fue depuesto en 1848. En conjunto publicó la sorprendente cantidad de 789 artículos de investigación en matemáticas.
§. ¿Teorema de Cauchy?
Lo que realmente provocó un revuelo fue el descubrimiento de que se podía hacer cálculo infinitesimal -análisis- con funciones complejas, y que la teoría resultante era elegante y útil. Tan útil, de hecho, que la base lógica de la idea dejó de ser una cuestión importante. Cuando algo funciona, y uno siente que lo necesita, deja generalmente de preguntarse si tiene sentido. La introducción del análisis complejo parece haber sido una decisión consciente de la comunidad matemática, una generalización tan obvia y convincente que cualquier matemático con sensibilidad querría ver lo que sucedía. En 1811 Gauss escribió una carta a un amigo, el astrónomo Friedrich Bessel, en la que revelaba su representación de los números complejos como puntos en un plano; también mencionaba algunos resultados más profundos. Entre ellos hay un teorema básico del que cuelga el conjunto del análisis complejo. Hoy le llamamos Teorema le Cauchy, porque fue publicado por Cauchy, pero Gauss tuvo la idea mucho antes en sus escritos no publicados.
Este teorema concierne a las integrales definidas de funciones complejas: es decir, expresiones
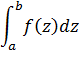
donde a y b son números complejos. En análisis real esta expresión puede ser evaluada encontrando una «antiderivada» F(z) de f(z), es decir, una función F(z) tal que su derivada dF(z)/dz = f(z).
Dos caminos distintos P y Q de -1 a 1 en el plano complejo
Entonces la integral definida es igual a F(b) - F(a). En particular, su valor depende sólo de los puntos extremos a y b, no de cómo se va de uno a otro.
El análisis complejo, decía Gauss, es diferente. Ahora el valor de la integral puede depender del camino que toma la variable z cuando se mueve de a a b. Puesto que los números complejos forman un plano, su geometría es más rica que la de la recta real, y aquí es donde cuenta la riqueza extra.
Por ejemplo, supongamos que se integra f(z) = 1/z de a = -1 a b = 1.
Si el camino en cuestión es un semicírculo P situado por encima del eje real, entonces la integral resulta ser -πi. Pero si el camino es un semicírculo Q por debajo del eje real, entonces la integral resulta ser πi. Los dos valores son diferentes, y la diferencia es 2πi.
Esta diferencia, decía Gauss, ocurre porque la función 1/z tiene mal comportamiento. Se hace infinita dentro de la región encerrada por los dos caminos. Lo hace en z = 0, que aquí es el centro del círculo formado por los dos caminos. «Pero si esto no sucede... yo afirmo», escribía Gauss a Bessel, «que la integral tiene sólo un valor incluso si se toma sobre caminos diferentes con tal de que [la función] no se haga infinita en el espacio encerrado por los dos caminos. Este es un teorema muy bello, cuya demostración daré en una ocasión conveniente». Pero nunca lo hizo.
En su lugar, el teorema fue redescubierto y publicado por Augustin-Louis Cauchy, el verdadero fundador del análisis complejo. Quizá Gauss haya tenido la idea, pero las ideas son inútiles si nadie llega a verlas. Cauchy publicó su trabajo. De hecho, Cauchy rara vez dejaba de publicar. Se dice que la regla, todavía hoy en uso, según la cual la revista Comptes Rendus de l’Academie Française no acepta artículos de más de cuatro páginas, fue introducida explícitamente para impedir que Cauchy la llenase con su enorme producción. Pero la introducción de la regla sólo sirvió para que Cauchy escribiera montones de artículos cortos. De su prolífica pluma salieron rápidamente las principales líneas del análisis complejo. Y es una teoría más simple, más elegante y en muchos aspectos más completa que el análisis real, de donde partió la idea general.
Por ejemplo, en análisis real una función puede ser diferenciable, pero su derivada puede no serlo. Puede ser diferenciable 23 veces, pero no 24.
Puede ser diferenciable tantas veces como uno quiera, pero no poseer una representación en serie de potencias. Ninguna de estas cosas desagradables puede suceder en análisis complejo. Si una función es diferenciable, entonces puede ser diferenciada tantas veces como uno quiera; además, tiene una representación en serie de potencias. La razón -íntimamente relacionada por el Teorema de Cauchy y probablemente un hecho utilizado por Gauss en su demostración desconocida- es que, para ser diferenciable, una función compleja debe satisfacer unas condiciones muy restrictivas, conocidas como condiciones de Cauchy-Riemann. Estas ecuaciones llevan directamente al resultado de Gauss de que la integral entre dos puntos puede depender del camino escogido. De forma equivalente, como advirtió Cauchy, la integral alrededor de un camino cerrado no tiene por qué ser cero. Es cero con tal de que la función en cuestión sea diferenciable (de modo que en particular no es infinita) en todos los puntos dentro del camino.
Para qué nos sirven los números complejosHoy, los números complejos son ampliamente utilizados en física e ingeniería. Un ejemplo simple se da en el estudio de las oscilaciones, movimientos que se repiten periódicamente. Los ejemplos incluyen la vibración de un edificio en un terremoto, las vibraciones en los automóviles y la transmisión de corrientes eléctricas alternas.
El tipo de oscilación más simple y fundamental toma la forma a cos ωt, donde t es el tiempo, a es la amplitud de la oscilación y tu es su frecuencia. Resulta conveniente reescribir esta fórmula como la parte real de la función compleja eiωt. El uso de números complejos simplifica los cálculos porque la función exponencial es más sencilla que el coseno. Por eso los ingenieros que estudian oscilaciones prefieren trabajar con exponenciales complejas, y volver a la parte real sólo al final del cálculo.
Los números complejos determinan también las estabilidades de los estados estacionarios de los sistemas dinámicos, y son ampliamente utilizados en la teoría del control. Esta disciplina trata de los métodos de estabilizar sistemas que de otro modo serían inestables. Un ejemplo es el uso de superficies de control en el movimiento controlado por ordenador para estabilizar la lanzadera espacial en vuelo. Sin esta aplicación del análisis complejo, la lanzadera espacial volaría como un ladrillo.
Existía incluso un teorema -el «teorema del residuo»- que daba el valor de una integral alrededor de un camino cerrado, y éste dependía sólo de la localización de los puntos en donde la función se hacía infinita y de su comportamiento cerca de dichos puntos. En resumen, la estructura general de una función compleja está determinada por sus singularidades: los puntos en los que tiene mal comportamiento. Y las singularidades más importantes son sus polos, los lugares en donde se hace infinita.
La raíz cuadrada de menos uno intrigó a los matemáticos durante siglos. Aunque parecía no haber tal número, seguía apareciendo en los cálculos. Y había indicios de que el concepto podía tener algún sentido, porque podía ser utilizado para obtener resultados perfectamente válidos que en sí mismos no implicaban tomar la raíz cuadrada de un número negativo.
Conforme siguieron aumentando los usos satisfactorios de esta cantidad «imposible», los matemáticos empezaron a aceptarla como un artificio útil. Su estatus siguió siendo incierto hasta que se entendió que hay una extensión lógicamente consistente del sistema tradicional de los números reales en donde la raíz cuadrada de menos uno es un nuevo tipo de cantidad; aunque un tipo que obedece a todas las leyes estándar de la aritmética.
Desde el punto de vista geométrico, los números reales forman una recta y los números complejos forman un plano; la recta real es uno de los dos ejes de este plano. Desde el punto de vista algebraico, los números complejos son simplemente pares de números reales con formulas especiales para sumar o multiplicar los pares.
Aceptados ahora como cantidades razonables, los números complejos se difundieron rápidamente por todas las matemáticas porque simplificaban los cálculos al evitar la necesidad de considerar por separado números positivos y negativos. En este aspecto pueden considerarse análogos a la invención anterior de los números negativos, que evitaban la necesidad de considerar la suma y la resta por separado. Hoy, los números complejos, y el cálculo infinitesimal con funciones complejas, se utilizan de forma rutinaria como una técnica indispensable en prácticamente todas las ramas de la ciencia, la ingeniería y las matemáticas.
Capítulo 11
Fundamentos firmes
Dando sentido al cálculo
En 1800 matemáticos y físicos habían desarrollado el cálculo infinitesimal como una herramienta indispensable para el estudio del mundo natural, y los problemas que surgieron de esta relación llevaron a una riqueza de nuevos conceptos y métodos -por ejemplo, maneras de resolver ecuaciones diferenciales- que hicieron del cálculo infinitesimal una de las áreas de investigación más ricas y más candentes en el conjunto de las matemáticas.
La belleza y potencia del cálculo infinitesimal se habían hecho innegables. Sin embargo, las críticas del obispo Berkeley a su base lógica seguían sin respuesta, y a medida que la gente empezó a abordar temas más sofisticados, todo el edificio empezó a mostrarse decididamente tambaleante. El inicial uso displicente de series infinitas, sin considerar su significado, producía absurdos tanto como buenas ideas. Los fundamentos del análisis de Fourier eran inexistentes y diferentes matemáticos proclamaban demostraciones de teoremas contradictorios. Palabras como «infinitesimal» eran discutidas sin estar definidas; abundaban las paradojas lógicas; incluso se cuestionaba el significado de la palabra «función». Evidentemente estas circunstancias insatisfactorias no podían continuar indefinidamente.
Ordenarlo todo requería una cabeza clara y una disposición a reemplazar intuición por precisión, incluso si se perdía generalidad. Los actores principales fueron Bernhard Bolzano, Cauchy, Niels Abel, Peter Dirichlet y, sobre todo, Weierstrass. Gracias a sus esfuerzos, hacia 1900 incluso las manipulaciones más complicadas de series, límites, derivadas e integrales podían realizarse con seguridad, precisión y sin paradojas. Se había creado una nueva disciplina: el análisis. El cálculo infinitesimal se convirtió en un aspecto central del análisis, pero conceptos más sutiles y más básicos, tales como continuidad y límites, tomaron la prioridad lógica para soportar las ideas del cálculo infinitesimal. Los infinitesimales fueron eliminados por completo.
§. Fourier
Antes de que se entrometiera Fourier, los matemáticos eran felices creyendo saber lo que era una función. Era una especie de proceso, f, que tomaba un número, x, y generaba otro número, f(x).Qué números x tienen sentido depende de cuál es f. Si f(x) = 1/x, por ejemplo, entonces x tiene que ser diferente de cero. Si f(x) = √x estamos trabajando con números reales, entonces x debe ser positivo. Pero cuando se les pedía una definición, los matemáticos solían ser algo vagos.
Ahora entendemos que la fuente de sus dificultades era que estaban tratando de entender varios aspectos diferentes del concepto de función; no sólo que es una «regla» que asocia a un número x otro número f(x), sino qué propiedades posee dicha regla: continuidad, diferenciabilidad, capacidad de ser representada por algún tipo de fórmula y demás.
En particular, no sabían muy bien cómo manejar funciones «discontinuas», tales como
f(x) = 0 si x < 0
f(x) = 1 si x > 0
Esta función salta repentinamente de 0 a 1 cuando x pasa por 0. Había una sensación dominante de que la razón obvia para el salto era el cambio en la fórmula: de f(x) = 0 a f(x) = 1. Junto a ello existía la sensación de que ésta es la única manera en que pueden aparecer los saltos; que cualquier fórmula simple evitaba automáticamente tales saltos, de modo que un cambio pequeño en x siempre causaba un cambio pequeño en f(x).
Otra fuente de dificultades eran las funciones complejas, donde -como hemos visto- funciones naturales como la raíz cuadrada son bivaluadas, y los logaritmos son infinitamente multivaluados. Evidentemente el logaritmo debe ser una función; pero cuando hay infinitos valores, ¿cuál es la regla para obtener f(t) a partir de t? Parece haber infinitas reglas diferentes, todas igualmente válidas. Para que estas dificultades conceptuales fueran resueltas había que restregárselas a los matemáticos en sus narices para que experimentaran hasta qué punto era confusa la situación. Y fue Fourier quien realmente les provocó, con su sorprendente idea de escribir cualquier función como una serie infinita de senos y cosenos, desarrollada en su estudio del flujo de calor.
“Y fue Fourier quien realmente les provocó...”
La intuición física de Fourier le decía que su método debería ser muy general. Podemos imaginar que en un experimento se mantiene la temperatura de una barra metálica a 0 grados a lo largo de la mitad de su longitud, y a 10 grados, o 50, o lo que sea, a lo largo de la otra mitad. La física no parece molestarse por funciones «discontinuas», cuyas fórmulas cambian repentinamente. La física no trabajaba con fórmulas. Nosotros utilizamos fórmulas para modelar la realidad física, pero eso es sólo técnica, es como nos gusta pensar. Por supuesto, la temperatura se difuminará un poco en la unión de estas dos regiones, pero los modelos matemáticos son siempre aproximaciones a la realidad física. El método de Fourier de las series trigonométricas, aplicado a una función «discontinua» de este tipo, parecía dar resultados perfectamente razonables. Las barras de acero suavizaban realmente la distribución de temperatura tal como especificaba la solución de la ecuación del calor, obtenida utilizando series trigonométricas. En La teoría analítica del calor dejó clara su postura:
«En general, la función f(x) representa una sucesión de valores u ordenadas cada uno de los cuales es arbitrario. No suponemos que dichas ordenadas estén sujetas a una ley común. Se suceden unas a otras de cualquier manera».
Palabras fuertes; por desgracia, las pruebas en su apoyo no equivalían a una demostración matemática.
Si acaso, eran aún más resbaladizas que los razonamientos utilizados por personas como Euler y Bernoulli.
Además, si Fourier tenía razón, entonces su serie se derivaba en efecto de una «ley común» para funciones discontinuas. La función anterior, con valores 0 y 1, tiene una pariente periódica, la onda cuadrada.
Y la onda cuadrada tiene una única serie de Fourier, muy bonita, que funciona igualmente bien en aquellas regiones donde la función es 0 y en aquellas regiones donde la función es 1. De modo que esta función que parece estar representada por dos leyes diferentes puede reescribirse en términos de una sola ley.
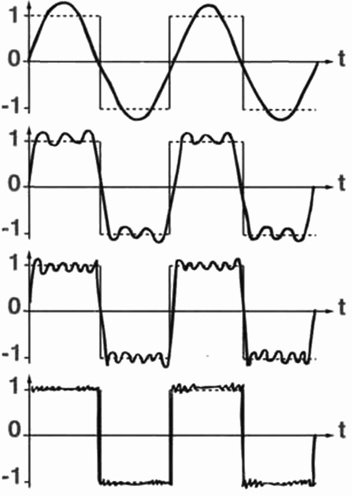
La onda cuadrada y algunas de sus aproximaciones de Fourier
Poco a poco, los matemáticos del siglo XIX empezaron a separar las diferentes cuestiones conceptuales en esta difícil área. Una era el significado del término «función». Otra eran las diversas maneras de representar una función: una fórmula, una serie de potencias, una serie de Fourier o lo que sea. Una tercera era qué propiedades poseía la función. Una cuarta era qué representaciones garantizaban qué propiedades. Un único polinomio, por ejemplo, define una función continua. Pero parecía que una única serie de Fourier podía no hacerlo.
El análisis de Fourier se convirtió rápidamente en el test para las ideas sobre el concepto de función. Aquí los problemas cobraban su máximo relieve; aquí las distinciones técnicas esotéricas resultaban importantes. Y fue en un artículo sobre series de Fourier, en 1837, donde Dirichlet introdujo la definición moderna de una función. De hecho, él coincidía con Fourier: una variable y es una función de otra variable x si para cada valor de x (en un rango particular) hay especificado un único valor de y. El afirmaba explícitamente que no se requería ninguna «ley» o fórmula particular: basta con que y esté especificada por una secuencia bien definida de operaciones matemáticas aplicadas a x.
Lo que en la época debió de haber parecido un ejemplo extremo es «uno que él puso antes», en 1829: una función f(x) que toma un valor cuando x es racional, y un valor diferente cuando x es irracional. Esta función es «discontinua en todo punto». (Hoy día, funciones como ésta se consideran bastante leves; es posible un comportamiento mucho peor.)
Para Dirichlet, la raíz cuadrada no era una función bivaluada. Eran dos funciones univaluadas. Para x real, es natural -pero no esencial- tomar la raíz cuadrada positiva como uno de los valores, y la raíz cuadrada negativa como el otro. En el caso de los números complejos no hay elecciones naturales obvias, aunque puede hacerse algo para hacer la vida más fácil.
§. Funciones continuas
Ahora los matemáticos estaban cayendo en la cuenta de que aunque a veces enunciaban definiciones del término «función», tenían el hábito de suponer propiedades extra que no se seguían de la definición. Por ejemplo, suponían que cualquier fórmula razonable, tal como un polinomio, definía automáticamente una función «continua». Pero nunca lo habían demostrado. De hecho, no podían demostrarlo, porque no habían definido «continua». Toda el área estaba plagada de vagas intuiciones, la mayoría de ellas erróneas.
La persona que hizo el primer intento serio de ordenar este revoltijo fue un sacerdote, filósofo y matemático bohemio. Su nombre era Bernhard Bolzano. El dio una base lógica a la mayoría de los conceptos básicos del cálculo infinitesimal. Había una excepción importante, y es que él daba por hecha la existencia de los números reales. Insistía en que los números infinitesimales y los números infinitamente grandes no existían, y que por ello no podían utilizarse por muy sugerentes que puedan ser. Y dio la primera definición efectiva de una función continua: f es continua si la diferencia f(x + a) - f(x) puede hacerse tan pequeña como queramos escogiendo a suficientemente pequeño. Los autores anteriores solían decir cosas como «si a es infinitesimal entonces f(x + a) - f(x) es infinitesimal». Pero para Bolzano, a era sólo un número como cualquier otro. Para él, lo importante era que cada vez que se especifica cuán pequeño queremos que sea f(x + a) - f(x), debe especificarse un valor adecuado para a. No era necesario que el mismo valor funcionara en todos los casos.
Así, por ejemplo, f(x) = 2x es continua, porque 2(x + a) - 2x = 2a. Si queremos que 2a sea más pequeño que un número específico, digamos 1010, entonces tenemos que hacer a más pequeño que 1010/2. Si ensayamos una función más complicada, como f(x) = x2, entonces los detalles exactos son un poco complicados porque el a correcto depende de x tanto como del tamaño escogido 1010, pero cualquier matemático competente puede calcularlo en pocos minutos. Utilizando esta definición, Bolzano demostró -por primera vez- que una función polinómica es continua. Pero durante cincuenta años nadie lo advirtió. Bolzano había publicado su trabajo en una revista que los matemáticos apenas leían ni tenían acceso ella. En estos días de internet es difícil darse cuenta de cuán pobres eran las comunicaciones hace tan sólo 50 años, y ya no digamos 180.
“...y poco a poco emergió orden a partir del caos.”
En 1821 Cauchy dijo prácticamente lo mismo, pero utilizando una terminología ligeramente confusa. Su definición de continuidad de una función f era que f(x) y f(x+a) difieren en una cantidad infinitesimal cuando a es infinitesimal, lo que a primera vista se parece a la vieja y pobremente definida aproximación. Pero «infinitesimal» para Cauchy no se refería a un único número que era infinitamente pequeño, sino a una secuencia de números siempre decreciente. Por ejemplo, la secuencia 0,1, 0,01, 0,001, 0,0001 y así sucesivamente, es infinitesimal en el sentido de Cauchy, pero cada uno de los números individuales, tales como 0,001, es sólo un número real convencional, «pequeño», quizá, pero no infinitamente pequeño. Teniendo en cuenta esta terminología, vemos que el concepto de Cauchy de continuidad equivale a exactamente lo mismo que el de Bolzano.
Para qué les servía el análisisLa física matemática del siglo XIX llevó al descubrimiento de varias ecuaciones diferenciales importantes. En ausencia de computadores de alta velocidad, capaces de encontrar soluciones numéricas, los matemáticos de la época inventaron nuevas «funciones especiales» para resolver estas ecuaciones. Estas funciones se siguen utilizando hoy. Un ejemplo es la ecuación de Bessel, obtenida por primera vez por Daniel Bernouilli y generalizada por Bessel. Toma la forma
y las funciones estándar, tales como exponenciales, senos, cosenos y logaritmos, no proporcionan una solución.
Sin embargo, es posible utilizar el análisis para encontrar soluciones en forma de series de potencias. Las series de potencias determinan nuevas funciones, las funciones de Bessel.
El tipo más simple de función de Bessel se denota por Jk(x); hay varios más. Las series de potencias permiten el cálculo de Jk(x) con cualquier precisión deseada.
Intensidad de un rayo láser descrita por la función de Bessel Jk(x)Las funciones de Bessel aparecen de forma natural en muchos problemas sobre círculos y cilindros, tales como la vibración de un tambor circular, la propagación de ondas electromagnéticas en una guía de ondas cilíndrica, la conducción del calor en una barra metálica cilíndrica y la física de láseres.
Otro crítico del pensamiento resbaladizo sobre procesos infinitos fue Abel, quien se quejaba de que la gente estaba utilizando series infinitas sin investigar si las sumas tenían sentido. Sus críticas calaron, y poco a poco emergió orden a partir del caos.
§. Límites
Las ideas de Bolzano dieron impulso a estas mejoras. El hizo posible definir el límite de una secuencia infinita de números, y a partir de ello la suma de una serie infinita. En particular, su formalismo implicaba que la suma
1 + ½ + ¼ + ⅛ + 1/16 +...
continuada indefinidamente es una suma infinita, y su valor es exactamente 2. No un poco menos; no una cantidad infinitesimal menos; es pura y simplemente 2.
Para ver cómo es esto, supongamos que tenemos una secuencia de números
a0, a1, a2, a3,...
que continúa indefinidamente. Decimos que an tiende a un límite a cuando n tiende a infinito si, dado cualquier número ε > 0, existe un número N tal que la diferencia entre an y a es menor que ε cuando n > N. (El símbolo ε, que es tradicional, es la «épsilon» griega.) Nótese que todos los números en esta definición son finitos, no hay infinitesimales ni infinitos.
Para sumar la serie infinita anterior, examinamos las sumas finitas
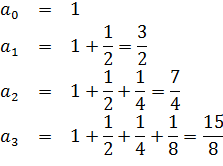
y así sucesivamente. La diferencia entre an y 2 es 1/2n. Para hacer esto menor que ε hacemos n > N = log2 (1/ε).
De una secuencia que tiene un límite finito se dice que es convergente.
Una suma infinita se define como el límite de la secuencia de sumas finitas obtenida añadiendo cada vez más términos. Si dicho límite existe, la serie es convergente. Derivadas e integrales son tan sólo límites de varios tipos. Existen -es decir, tienen sentido matemático- con tal de que dichos límites converjan. Los límites, precisamente como mantenía Newton, tratan de a qué se aproximan ciertas cantidades cuando otro número se aproxima a infinito o a 0. El número no tiene que llegar a infinito o a 0.
Todo el cálculo infinitesimal descansaba ahora en un fundamento sólido.
El inconveniente era que cuando se utilizaba un proceso de paso a límite, había que asegurarse de que convergía. La mejor forma de hacerlo era demostrar teoremas cada vez más generales sobre qué tipo de funciones son continuas, o diferenciables, o integrables, y qué secuencias o series convergen. Esto es lo que el análisis procedió a hacer, y es la razón por la que ya no nos preocupamos por las dificultades apuntadas por el obispo Berkeley. Es también la razón por la que ya no discutimos sobre series de Fourier: tenemos una idea sólida de cuándo convergen, cuándo no lo hacen y, de hecho, en qué sentido convergen. Existen variaciones sobre el tema básico, y para las series de Fourier hay que elegir las correctas.
§. Series de potencias
Weierstrass se dio cuenta de que las mismas ideas funcionaban tanto para números complejos como para números reales. Todo número complejo z = x + iy tiene un valor absoluto |z| = √(x2 + y2), que por el Teorema de Pitágoras es la distancia de 0 a z en el plano complejo. Si medimos el tamaño de una expresión compleja utilizando su valor absoluto, entonces los conceptos de límites, series y demás, para números reales, tales como los formuló Bolzano, pueden ser transferidos inmediatamente al análisis complejo.
Weierstrass advirtió que un tipo particular de serie infinita parecía ser especialmente útil. Se conoce como una serie de potencias, y se parece a un polinomio de grado infinito:
f(z) = a0 + a1z + a2z2 + a3z3 + ...
donde los coeficientes an son números concretos. Weierstrass se embarcó en un enorme programa de investigación, dirigido a fundamentar la totalidad del análisis complejo sobre series de potencias. Funcionó de forma brillante.
Por ejemplo, se puede definir la función exponencial
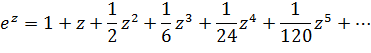
donde los números 2, 3, 4 y demás son factoriales: productos de enteros consecutivos (como 6! = 1 × 2 × 3 × 4 × 5 × 6 = 120).
La hipótesis de RiemannEl problema más famoso no resuelto en el conjunto de las matemáticas es la Hipótesis de Riemann, un problema en análisis complejo que surgió en relación con los números primos pero que tiene repercusiones en todas las matemáticas.
Alrededor de 1793 Gauss conjeturó que el número de primos menores que x es aproximadamente x/log x. De hecho sugirió una aproximación más precisa llamada la integral logarítmica. En 1737 Euler había advertido una conexión intrigante entre la teoría de números y el análisis: la serie infinita
1 + 2-s + 3-s + 4-s +...
es igual al producto, sobre todos los primos p, de la serie
1 + p – s + p - 2s + p - 3s... = 1/(1-p)
Aquí debemos tomar s > 1 para que la serie converja.
En 1848 Pafnuty Chebyshev hizo algún avance hacia una demostración, utilizando una función compleja relacionada con la serie de Euler, más tarde denominada la función zeta ζ(t). El papel de esta función fue aclarado por Riemann en su artículo de 1859 Sobre los números primos menores que una cantidad dada. El demostró que las propiedades estadísticas de los primos están estrechamente relacionadas con los ceros de la función zeta, es decir, las soluciones de la ecuación ζ(t)=0.
En 1896 Jacques Hadamard y Charles de la Vallée Poussin utilizaron la función zeta para demostrar el Teorema de los Números Primos. El paso principal consiste en demostrar que ζ(t) es diferente de cero para todo z de la forma 1 + it. Cuanto más control podamos obtener sobre la localización de los ceros de la función zeta, más aprendemos sobre los primos. Riemann conjeturó que todos los ceros, distintos de algunos ceros obvios en enteros negativos pares, yacen en la línea crítica z = ½ + it.
En 1914 Hardy demostró que un número infinito de ceros yacen sobre esta recta. Pruebas extensas por computador también apoyan la conjetura. Entre 2001 y 2005 el programa ZetaGrid de Sebastian Wedeniwski verificó que los primeros 100.000 millones de ceros yacen sobre la línea crítica.
La Hipótesis de Riemann era parte del Problema 8 en la famosa lista de Hilbert de 23 grandes problemas matemáticos no resueltos, y es uno de los problemas del milenio propuestos para el premio del Instituto Clay de Matemáticas.
Euler ya había obtenido esta fórmula de modo heurístico; ahora Weierstrass podía darle un sentido riguroso. Inspirándose una vez más en el libro de Euler, pudo relacionar las funciones trigonométricas con la función exponencial, definiendo
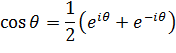
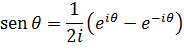
Todas las propiedades estándar de estas funciones se seguían de su expresión en serie de potencias. Se podía incluso definir π, y demostrar que eiπ = -1, como había mantenido Euler. Y eso a su vez significaba que los logaritmos complejos eran lo que Euler había afirmado. Todo tenía sentido. El análisis complejo no era tan sólo una extensión mística del análisis real: era una disciplina razonable por sí misma. De hecho, a veces era más sencillo trabajar en el dominio complejo y leer el resultado real al final.
Para Weierstrass todo esto era sólo un comienzo, la primera fase de un vasto programa. Pero lo que importaba era obtener el fundamento correcto. Si se hacía, el material más sofisticado se seguiría inmediatamente.
“Incluso Euler hizo algunas afirmaciones cosas completamente estúpidas.”
Weierstrass era inusualmente lúcido, y podía ver su camino a través de una complicada combinación de límites y derivadas e integrales sin confundirse. También podía detectar las potenciales dificultades. Uno de sus teoremas más sorprendentes demuestra que existe una función f(x) de una variable real x, que es continua en todo punto, pero no es diferenciable en ninguno. La gráfica de f es una curva única y no quebrada, pero es una curva tan ondulada que no tiene una tangente bien definida en ningún punto. Sus predecesores no lo hubieran creído; sus contemporáneos se preguntaban para que servía.
Sus sucesores la desarrollaron en una de las teorías más excitantes del siglo XX, los fractales.
Pero sabremos más de esa historia más adelante.
§. Una base firme
Los primeros inventores del cálculo infinitesimal habían adoptado una aproximación bastante displicente respecto a las operaciones infinitas. Euler había supuesto que las series de potencias eran igual que polinomios, y utilizó esta hipótesis con efecto devastador. Pero en las manos de los mortales corrientes este tipo de hipótesis puede llevar fácilmente a absurdos.
Valor absoluto de la función zeta de Riemann
Incluso Euler hizo algunas afirmaciones completamente estúpidas. Por ejemplo, él empezó por formar la serie de potencias
1 + x + x2 + x3 + x4+...
que suma 1/(1-x), hizo x = -1 y dedujo que 1 - 1 + 1 - 1 + 1 - 1 + ... = -½, lo que no tiene sentido. La serie de potencias no converge a menos que x se encuentre estrictamente entre - 1 y 1, como deja claro la teoría de Weierstrass.
Tomar en serio las críticas como las que hizo el obispo Berkeley enriqueció a la larga a las matemáticas, y las colocó sobre una base firme. Cuanto más complicadas se hacían las teorías, más importante era asegurarse de que se estaba en terreno firme.
Hoy día, la mayoría de los usuarios de las matemáticas ignoran una vez más tales sutilezas, con la seguridad de que han «sido ordenadas» y de que algo que parece razonable es muy probable que tenga una justificación rigurosa. Tienen que estar agradecidos a Bolzano, Cauchy y Weierstrass por esta confianza. Mientras, los matemáticos profesionales siguen desarrollando conceptos rigurosos acerca de procesos infinitos. Hay incluso un movimiento por reavivar el concepto de un infinitesimal, conocido como análisis no estándar, y es perfectamente riguroso y técnicamente útil en algunos problemas que de otro modo resultan intratables. Evita las contradicciones lógicas haciendo de los infinitesimales un nuevo tipo de número, no un número real convencional. En espíritu está próximo a la manera en que pensaba Cauchy. Sigue siendo una especialidad minoritaria, pero observemos este espacio.
Lo que el análisis hace por nosotrosEl análisis se utiliza en biología para estudiar el crecimiento de poblaciones de organismos. Un ejemplo sencillo es el modelo logístico o de Verhulst-Pearl. Aquí el cambio en la población x como función del tiempo t se modela por una ecuación diferencial
donde la constante M es la «capacidad de sustentación», la máxima población que puede sostener el entorno.
Métodos estándar en análisis dan la solución explícita
que se llama curva logística. La pauta de crecimiento correspondiente empieza con un crecimiento rápido (exponencial), pero cuando la población alcanza la mitad de la capacidad de sustentación, el crecimiento empieza a frenarse y con el tiempo la población se estabiliza en la capacidad de sustentación.
Consumo mundial de petróleo 1900-2000: curva suave, ecuación logística; curva sinuosa, datos realesLa curva no es totalmente realista, aunque se ajusta bastante bien a muchas poblaciones reales. Modelos más complicados del mismo tipo proporcionan mejores ajustes a los datos reales.
El consumo humano de recursos naturales también puede seguir una pauta similar a la curva logística, lo que hace posible estimar la demanda futura y cuánto tiempo pueden durar los recursos.
Capítulo 12
Triángulos imposibles
¿Es la geometría de Euclides la única posible?
El cálculo infinitesimal se basaba en principios geométricos, pero la geometría se reducía a cálculos simbólicos, que luego se formalizaron como análisis. Sin embargo, el papel del pensamiento visual en matemáticas también se estaba desarrollando en una dirección nueva o inicialmente bastante chocante. Durante más de 2.000 años el nombre do Euclides había sido sinónimo de geometría. Sus sucesores desarrollaron sus ideas, especialmente en su trabajo sobre secciones cónicas, pero no lucieron cambios radicales en el propio concepto do geometría. En esencia, se suponía que sólo puedo haber una geometría, y que ésta os una descripción matemática exacta de la verdadera geometría del espacio físico. La gente encontraba difícil concebir siquiera una alternativa.
Esto no podía durar.
§. Geometría esférica y proyectiva
La primera desviación importante de la geometría euclidiana surgió del problema muy práctico que planteaba la navegación. Sobre distancias cortas, la Tierra es casi plana, y sus accidentes geográficos pueden representarse en un plano. Pero a medida que los barcos hacían viajes cada vez más largos, había que tener en cuenta la forma verdadera del planeta. Varias civilizaciones antiguas sabían que la Tierra es redonda: hay una amplia evidencia, desde la forma en que los barcos desaparecen en el horizonte hasta la sombra del planeta sobre la Luna durante los eclipses lunares. Se suponía en general que la Tierra es una esfera perfecta.
En realidad, la esfera está ligeramente achatada: el diámetro en el ecuador es de 12.756 km, mientras que de polo a polo es de 12.714 km. La diferencia es relativamente pequeña: una parte en 300. En épocas en que los navegantes cometían rutinariamente errores de varios centenares de kilómetros, una Tierra esférica proporcionaba un modelo matemático perfectamente aceptable. En esa época, no obstante, el acento estaba en la trigonometría esférica antes que en la geometría; las bases de los cálculos de navegación, no el análisis lógico de la esfera como un tipo de espacio. Puesto que la esfera entra de forma natural dentro del espacio euclidiano tridimensional, nadie consideraba que la geometría esférica fuera diferente de la euclidiana. Cualquier diferencia era resultado de la curvatura de la Tierra. La geometría del propio espacio seguía siendo euclidiana.
“... la geometría estuvo estancada entre los años 300 y 1000.”
Una desviación más importante de Euclides fue la introducción, desde principios del siglo XVII en adelante, de la geometría proyectiva. El tema no surgió de la ciencia sino del arte: las investigaciones teóricas y prácticas de la perspectiva por parte de los artistas del Renacimiento en Italia. El objetivo era hacer cuadros que parecieran realistas; el resultado fue una nueva manera de pensar en geometría. Pero, una vez más, este desarrollo podía verse como una innovación dentro del marco euclidiano clásico. Se trataba de cómo vemos el espacio, no del propio espacio.
El descubrimiento de que Euclides no estaba solo, de que pueden existir tipos de geometría lógicamente consistentes en los que muchos de los teoremas de Euclides no son válidos, surgió de un renovado interés por los fundamentos lógicos de la geometría, discutidos y desarrollados desde mediados del siglo XVIII hasta mediados del XIX. La gran cuestión era el Quinto Postulado de Euclides, que -dicho en forma algo tosca- afirmaba la existencia de rectas paralelas. Los intentos de deducir el Quinto Postulado a partir de los restantes axiomas de Euclides llevaron finalmente al convencimiento de que no es posible tal deducción. Existen tipos consistentes de geometría distintos de la euclidiana. Hoy, estas geometrías «no euclidianas» se han convertido en herramientas indispensables en matemáticas puras y en física matemática.
§. Geometría y arte
En lo que concernía a Europa, la geometría estuvo estancada entre los años 300 y 1600. La resurrección de la geometría como un tema vivo llegó de la cuestión de la perspectiva en el arte: cómo plasmar de forma realista un mundo tridimensional en un lienzo bidimensional.
Los artistas del Renacimiento no sólo creaban cuadros. Muchos se empleaban en hacer obras de ingeniería, ya fuera con fines pacíficos o guerreros. Su arte tenía un lado práctico, y la geometría de la perspectiva era una búsqueda práctica que se aplicaba a la arquitectura tanto como a las artes visuales. Había también un interés creciente en óptica, las matemáticas de la luz, que floreció una vez que se hubieran inventado el telescopio y el microscopio. El primer artista importante en pensar sobre las matemáticas de la perspectiva fue Filippo Brunelleschi. De hecho, su arte fue principalmente un vehículo para sus matemáticas. Un libro seminal es Dell a Pintura de Leone Battista Alberti escrito en 1435 e impreso en 1511.
Proyectando una imagen, Alberto Durero
Alberti empezaba haciendo algunas simplificaciones importantes y relativamente inocuas: la marca de un verdadero matemático. La visión humana es un tema complejo. Por ejemplo, utilizamos dos ojos ligeramente separados para generar imágenes estereoscópicas que dan una sensación de profundidad. Alberti simplificaba la realidad suponiendo un único ojo con una pequeña pupila que funcionaba como el orificio de una cámara. Imaginaba a un artista pintando una escena, fijando su caballete y tratando de hacer que la imagen en el lienzo encajara con la percibida por su (único) ojo. Lienzo y realidad proyectan sus imágenes en la retina, en el fondo del ojo. La forma (conceptual) más simple de asegurar un encaje perfecto es hacer el lienzo transparente, mirar a través del mismo desde una posición fija y dibujar en el lienzo exactamente lo que el ojo ve.
Así, la escena tridimensional es proyectada en el lienzo. Se une cada rasgo de la escena al ojo por una línea recta y se marca el lugar donde esta línea corta al lienzo: allí es donde se pinta ese rasgo.
Esta idea no es muy práctica si se toma al pie de la letra, aunque algunos artistas así lo hacían, utilizando materiales translúcidos, o vidrio, en lugar de un lienzo. A veces lo hacían como un paso preliminar, y luego trasladaban el esbozo resultante a un lienzo para el cuadro propiamente dicho. Un enfoque más práctico consiste en utilizar esta formulación conceptual para relacionar la geometría de la escena tridimensional con la de la imagen tridimensional.
La geometría euclidiana ordinaria trata de características que permanecen invariables bajo movimientos rígidos: longitudes, ángulos. Euclides no la formulaba así, pero su uso de «triángulos congruentes» como herramienta básica tiene el mismo efecto. (Estos son triángulos del mismo tamaño y forma, pero en posiciones diferentes.) De modo similar, la geometría de la perspectiva se reduce a las características que permanecen invariables bajo proyección. Es fácil ver que longitudes y ángulos no se comportan así. Podemos tapar la Luna con nuestro pulgar, de modo que las longitudes pueden cambiar. Los ángulos no lo hacen mejor; cuando miramos la esquina de un edificio, que forma un ángulo recto, sólo parece realmente un ángulo recto si la vemos de frente.
¿Qué propiedades de las figuras geométricas se conservan bajo proyección? Las más importantes son tan simples que es fácil pasar por alto su importancia. Los puntos siguen siendo puntos. Las líneas rectas siguen siendo rectas.
La imagen de un punto situado sobre una línea recta está situada sobre la imagen de dicha línea. Por consiguiente, si dos líneas se cortan en un punto, sus imágenes se cortan en el punto correspondiente. Las «relaciones de incidencia» de puntos y líneas se conservan bajo proyección.
Una característica importante que no se conserva completamente es la relación «paralela». Imaginémonos de pie en medio de una carretera larga y estrecha y miremos al frente. Los dos lados de la carretera, que en la realidad tridimensional son paralelos -y por lo tanto nunca se encuentran- no parecen paralelos. En su lugar convergen hacia un único punto en el horizonte lejano. Se comportan así en un plano ideal infinito, no sólo en una tierra ligeramente redondeada. De hecho, sólo se comportan exactamente así en un plano. En una esfera habría un hueco minúsculo, demasiado pequeño para verse, allí donde las líneas cruzan el horizonte. Y la cuestión general de las líneas paralelas en una esfera es en cualquier caso complicada.
Esta propiedad de las líneas paralelas es muy útil en el dibujo en perspectiva. Está detrás de la manera habitual de dibujar en perspectiva cajas rectangulares, utilizando una línea de horizonte y dos «puntos de fuga», que están allí donde los bordes paralelos de la caja cruzan el horizonte en perspectiva. El De Prospectiva Pingendi (1482-1487) de Piero della Francesca desarrollaba los métodos de Alberti como técnicas prácticas para los artistas, y los utilizó con gran efecto en sus pinturas espectaculares y muy realistas.
Teorema de Desargues
Los escritos de los pintores del Renacimiento resolvieron muchos problemas en la geometría de la perspectiva, pero eran semiempíricos, carentes del fundamento lógico que Euclides había proporcionado a la geometría ordinaria. Estas cuestiones de fundamentos fueron finalmente resueltas por Brook Taylor y Johann Heinrich en el siglo XVIII. Pero para entonces estaban sucediendo cosas más excitantes en geometría.
§. Desargues
El primer teorema no trivial en geometría proyectiva fue descubierto por el ingeniero/arquitecto Girad Desargues y publicado en 1648 en un libro de Abraham Bosse. Desargues demostró el notable teorema siguiente. Supongamos que los triángulos ABC y A’B’C’ están «en perspectiva», lo que significa que las tres líneas AA, BB y CC pasan por el mismo punto. Entonces los tres puntos P, Q y R en donde se cortan los lados correspondientes de los dos triángulos yacen en la misma línea. Este resultado se denomina hasta hoy Teorema de Desargues. No hace mención a longitudes ni ángulos: trata puramente sobre relaciones de incidencia entre líneas y puntos. Por lo tanto, es un teorema proyectivo.
Hay un truco que hace obvio el teorema: imaginémoslo como mi dibujo de una figura tridimensional en la que los dos triángulos yacen en dos planos. Entonces la línea a lo largo de la cual se intersecan dichos planos es la línea que contiene los tres puntos de Desargues P, Q y R. Con un poco de cuidado, los teoremas pueden incluso demostrarse de esta manera, construyendo una figura tridimensional adecuada cuya proyección se parece a los dos triángulos. Podemos así utilizar métodos euclidianos para demostrar teoremas proyectivos.
§. Los axiomas de Euclides
La geometría proyectiva difiere de la geometría euclidiana en su punto de vista (esto pretende ser un chiste), pero sigue estando relacionada con la geometría euclidiana. Es el estudio de nuevos tipos de transformación, las proyecciones, pero el modelo subyacente del espacio que está siendo transformado es euclidiano. De todas formas, la geometría proyectiva hizo a los matemáticos más receptivos a la posibilidad de nuevos tipos de pensamiento geométrico.
Y una vieja pregunta, que había estado latente durante siglos, salió a la luz una vez más.
Casi todos los axiomas de Euclides para la geometría eran tan obvios que ninguna persona en su sano juicio podía cuestionarlos seriamente.
Por ejemplo, «todos los ángulos rectos son iguales». Si ese axioma fallaba, tenía que haber algo erróneo en la definición de un ángulo recto. Pero el Quinto Postulado, el que trataba realmente de líneas paralelas, tenía un sabor característicamente diferente. Era complicado. Euclides lo enuncia así:
«Si una línea recta que corta a dos líneas rectas hace los ángulos interiores en un mismo lado menores que dos ángulos rectos, las dos líneas rectas, si se prolongan indefinidamente, se cortan en ese lado en el que los ángulos son menores que dos ángulos rectos».
Sonaba más como un teorema que como un axioma. ¿Era un teorema? ¿Podía haber alguna manera de demostrarlo, partiendo quizá de algo más simple y más intuitivo?
John Playfair introdujo una mejora en 1795. Él lo sustituyó por el enunciado de que dada una recta, y un punto no situado en dicha recta, existe una y sólo una recta que pasa por el punto y es paralela a la recta dada. Este enunciado es lógicamente equivalente al Quinto Postulado de Euclides, es decir, cada uno es consecuencia del otro, dados los axiomas restantes.
§. Legendre
En 1794 Adrien-Marie Legendre descubrió otro enunciado equivalente, la existencia de triángulos semejantes: triángulos que tienen los mismos ángulos pero con lados de tamaños diferentes. Pero él, y la mayoría de los demás matemáticos, querían algo aún más intuitivo.
“... y la mayoría de los demás matemáticos querían algo aún más intuitivo.”
De hecho, existía la sensación de que el Quinto Postulado era sencillamente superfluo, una consecuencia de los otros axiomas. Todo lo que faltaba era una demostración. Por ello Legendre ensayó todo tipo de cosas. Utilizando sólo los otros axiomas, demostró -al menos para su satisfacción- que los ángulos de un triángulo suman 180º o menos. (El debía saber que en geometría esférica la suma es mayor, pero ésa es la geometría de la esfera, no del plano.) Si la suma es siempre 180º, se sigue el Quinto Postulado. Por ello supuso que la suma podía ser menor que 180º, y desarrolló las consecuencias de dicha hipótesis.
Una consecuencia sorprendente era una relación entre el área del triángulo y la suma de sus ángulos. En concreto, el área es proporcional a la cantidad en que la suma de los ángulos difiere de 180º. Esto parecía prometedor: si pudiera construir un triángulo cuyos lados fueran el doble que los de un triángulo dado, pero con los mismos ángulos, entonces obtendría una contradicción, porque el triángulo mayor tendría la misma área que el menor. Pero por mucho que tratara de construir el triángulo mayor, siempre se encontró apelando al Quinto Postulado.
El consiguió salvar un resultado positivo de su trabajo. Sin suponer el Quinto Postulado, demostró que era imposible que irnos triángulos tengan ángulos que sumen más de 180º, mientras otros triángulos tienen ángulos que sumen menos de 180º. Si un triángulo tuviera ángulos que sumaran más de 180º, lo mismo sucedería con todos los triángulos; y algo similar si la suma fuera menor que 180º. De modo que había tres casos posibles:
- Los ángulos de todo triángulo suman exactamente 180º (geometría euclidiana).
- Los ángulos de todo triángulo suman menos de 180º.
- Los ángulos de todo triángulo suman más de 180º (un caso que Legendre pensaba que había excluido; más tarde se vio que había hecho otras hipótesis implícitas para conseguirlo).
§. Saccheri
En 1733 Gerolamo Saccheri, un sacerdote jesuita de Pavía, publicó un esfuerzo heroico, Euclides ab ovni naevo vindicatus (Euclides vindicado de todo error). Consideraba también tres casos, el primero de los cuales era la geometría euclidiana, pero él utilizaba un cuadrilátero para hacer la distinción.
Cuadrilátero de Saccheri: la recta CD se ha dibujado curvada para evitar hipótesis euclidianas sobre los ángulos C y D
Supongamos que el cuadrilátero es ABCD, con A y B ángulos rectos y AC = BD. Entonces, decía Saccheri, la geometría euclidiana implica que los ángulos C y D son ángulos rectos. Y lo que es menos obvio: si C y D son ángulos rectos en cualquier cuadrilátero de este tipo, entonces se sigue el Quinto Postulado.
Sin utilizar el Quinto Postulado, Saccheri demostró que los ángulos C y D son iguales. Por lo tanto, quedaban dos posibilidades distintas:
• Hipótesis del ángulo obtuso: C y D son mayores que un ángulo recto.
• Hipótesis del ángulo agudo: C y D son menores que un ángulo recto.
La idea de Saccheri consistía en suponer estas hipótesis de una en una, y deducir una contradicción lógica. Eso dejaría la geometría euclidiana como la única posibilidad lógica.
Para qué les servía la geometría no euclidianaEn 1813 Gauss estaba llegando al convencimiento de que lo que él llamó inicialmente geometría anti-euclidiana, luego astral y finalmente no euclidiana, era una posibilidad lógica. Empezó a preguntarse cuál era la verdadera geometría del espacio, y midió los ángulos de un triángulo formado por tres montañas: Brocken, Hohehagen e Inselberg. Para que la curvatura de la Tierra no influyera, él utilizó medidas de líneas visuales. La suma de los ángulos que midió era 15 segundos de arco mayor que 180º. Si acaso, éste sería el caso del ángulo obtuso, pero la probabilidad de errores observacionales hacía cuestionable todo el ejercicio. Gauss necesitaba un triángulo mucho más grande e instrumentos mucho más precisos para medir sus ángulos.
Empezó con la hipótesis del ángulo obtuso, y en una serie de teoremas dedujo -o eso pensaba- que los ángulos C y D debían ser ángulos rectos después de todo. Esto era una contradicción, de modo que la hipótesis del ángulo obtuso tenía que ser falsa. A continuación, supuso la hipótesis del ángulo agudo, que llevaba a otra serie de teoremas, todos correctos, y bastante interesantes en sí mismos. Finalmente demostró un teorema bastante complicado sobre una familia de rectas que pasaban por un punto, que implicaba que dos de estas rectas tendrían una perpendicular común en el infinito. Esto no es realmente una contradicción, pero Saccheri pensaba que lo era, y declaró que la hipótesis del ángulo agudo estaba también refutada.
Eso dejaba sólo la geometría euclidiana, por lo que Saccheri pensó que su programa estaba vindicado, junto con el de Euclides. Pero otros advirtieron que él no había obtenido realmente una contradicción de la hipótesis del ángulo agudo; sólo un teorema bastante sorprendente. En 1759 D'Alembert calificó el estatus del Quinto Postulado como «el escándalo de los elementos de geometría».
§. Lambert
Un matemático alemán, Georg Klügel, leyó el libro de Saccheri y presentó la opinión heterodoxa y bastante chocante de que la creencia en la verdad del Quinto Postulado era una cuestión de experiencia antes que de lógica. Básicamente, lo que estaba diciendo era que hay algo en nuestra manera de pensar acerca del espacio que nos hace creer en la existencia de líneas paralelas del tipo concebido por Euclides.
En 1766, Lambert, siguiendo la sugerencia de Klügel, se embarcó en una investigación que era similar a la de Saccheri, pero él partía de un cuadrilátero con tres ángulos rectos. El ángulo restante debía ser un ángulo recto (geometría euclidiana), agudo u obtuso. Como Saccheri, él pensaba que el caso del ángulo obtuso llevaba a una contradicción.
Más exactamente, él decidió que llevaba a la geometría esférica, donde hacía tiempo que se sabía que los ángulos de un cuadrilátero sumaban más de 360º, porque los ángulos de un triángulo suman más de 180º. Puesto que la esfera no es el plano, el caso obtuso está descartado.
Sin embargo, él no afirmaba lo mismo para el caso del ángulo agudo.
En su lugar, demostró algunos teoremas curiosos, de los que el más sorprendente era una fórmula para el área de un polígono de n lados. Sumemos todos los ángulos, y restemos esta suma de 2n - 4 ángulos rectos: el resultado es proporcional al área del polígono. Esta fórmula recordaba una fórmula similar de Lambert para la geometría esférica: sumemos todos los ángulos, y restemos de esta suma 2n - 4 ángulos rectos: de nuevo el resultado es proporcional al área del polígono. Hay una diferencia menor: la resta se realiza en el orden opuesto. Klügel se vio llevado a una predicción notablemente profética aunque oscura: la geometría del caso del ángulo agudo es la misma que la de una esfera con radio imaginario.
Entonces escribió un artículo corto sobre funciones trigonométricas de ángulos imaginarios, donde obtenía algunas fórmulas bellas y perfectamente consistentes. Ahora reconocemos estas funciones como las denominadas funciones hiperbólicas, que pueden definirse sin utilizar números imaginarios y satisfacen todas las fórmulas de Lambert. Evidentemente debía haber algo interesante tras esta curiosa y enigmática sugerencia. Pero ¿qué?
§. El dilema de Gauss
Ahora los geómetras mejor informados empezaban a tener una sensación definida de que el Quinto Postulado de Euclides no podía ser demostrado a partir de los otros axiomas.
“Kant había defendido que la geometría del espacio debía ser euclidiana.”
El caso del ángulo agudo parecía demasiado autoconsistente para llevar siempre a una contradicción. Por otra parte, una esfera de radio imaginario no era el tipo de objeto que podía proponerse para justificar dicha creencia.
Uno de estos geómetras era Gauss, quien ya a una temprana edad se convenció de que era posible una geometría no euclidiana lógicamente consistente y demostró muchos teoremas en una geometría semejante. Pero, como dejó claro en 1829 en una carta a Bessel, él no tenía intención de publicar nada de este trabajo porque temía despertar «la ira de los beodos». La gente poco imaginativa no lo entendería, y en su ignorancia y adhesión sin límites a la tradición ridiculizarían el trabajo. En esto puede haber estado influido por el estatus jerárquico de la ampliamente aclamada obra de Kant en filosofía; Kant había defendido que la geometría del espacio debía ser euclidiana.
En 1799 Gauss escribía al húngaro Wolfgang Bolyai, diciéndole que la investigación:
«parece más bien obligarme a dudar de la verdad de la propia geometría. Es cierto que he dado con muchas cosas que para muchas personas constituirían una demostración [del Quinto Postulado a partir de los otros axiomas]; pero a mis ojos no valen nada».
Otros matemáticos eran menos circunspectos. En 1826 Nikolai Ivanovich Lobachevski, en la Universidad de Kazan en Rusia, impartió lecciones sobre geometría no euclidiana. El no sabía nada del trabajo de Gauss, pero había demostrado teoremas similares usando sus propios métodos. Dos artículos sobre el tema aparecieron en 1829 y 1835. Más que desencadenar revueltas, como Gauss había temido, estos artículos pasaron al olvido sin dejar mucha huella. En 1840 Lobachevski publicó un libro sobre el tema, en el que se quejaba de la falta de interés. En 1855 publicó un segundo libro sobre el tema.
De forma independiente, el hijo de Wolfgang Bolyai, Janos, un oficial del ejército, dio con ideas similares en torno a 1825, y las presentó en un artículo de 26 páginas que fue publicado como apéndice al texto de geometría de su padre Tentamen juventud studiosam in elementa mathesos (Ensayo sobre los elementos de matemáticas para jóvenes estudiosos) de 1832.
El modelo de Poincaré para la geometría hiperbólica deja claro que hay infinitas rectas «paralelas» que pasan por un punto y no cortan a una recta dada
«He hecho descubrimientos tan maravillosos que yo mismo estoy lleno de asombro», escribió a su padre.
Gauss leyó el trabajo, pero explicó a Wolfgang que le era imposible alabar los esfuerzos del joven porque se estaría alabando a sí mismo. Esto era quizá algo injusto, pero así era como Gauss solía actuar.
§. Geometría no euclidiana
La historia de la geometría no euclidiana es demasiado complicada para describir con todo detalle, pero podemos resumir lo que siguió a estos esfuerzos pioneros.
Hay una profunda unidad tras los tres casos advertidos por Saccheri, por Lambert y por Gauss, Bolyai y Lobachevski. Lo que los une es el concepto de curvatura. La geometría no euclidiana es realmente la geometría natural de una superficie curva.
Si la superficie está curvada positivamente como una esfera, entonces tenemos el caso del ángulo obtuso. Éste fue rechazado porque la geometría esférica difiere de la euclidiana en aspectos obvios; por ejemplo, dos «líneas» cualesquiera, es decir, círculos máximos, se cortan en dos puntos, y no en el único punto que esperaríamos de las líneas rectas euclidianas.
En realidad, ahora entendemos que esta objeción es infundada. Si «identificamos» puntos diametralmente opuestos de la esfera -es decir, suponemos que son idénticos-, entonces las líneas (círculos máximos) seguirán teniendo sentido, porque si un punto yace en un círculo máximo, también lo hace el punto diametralmente opuesto. Con esta identificación, casi todas las propiedades geométricas siguen sin cambios, pero ahora las líneas se cortan en un «punto». Desde el punto de vista topológico, la superficie que resulta es el plano proyectivo, aunque la geometría en cuestión no es la geometría proyectiva ortodoxa. Ahora la llamamos geometría elíptica, y se considera tan razonable como la geometría euclidiana.
Si la superficie está curvada negativamente, con forma de una silla de montar, entonces tenemos el caso del ángulo agudo. La geometría resultante se llama hiperbólica. Tiene muchas características intrigantes que la distinguen de la geometría euclidiana.
Si la superficie tiene curvatura nula, como un plano euclidiano, entonces es el plano euclidiano, y obtenemos la geometría euclidiana.
Las tres geometrías satisfacen todos los axiomas de Euclides distintos del Quinto Postulado. La decisión de Euclides de incluir su postulado está vindicada.
Estas diversas geometrías pueden modelarse de varias maneras diferentes.
"... hay varias alternativas a la geometría de Euclides."
La geometría hiperbólica es especialmente versátil a este respecto. En un modelo el espacio en cuestión es la mitad superior del plano complejo, omitiendo el eje real y todo lo que hay debajo del mismo. Una «recta» es un semicírculo que corta al eje real a ángulos rectos. Desde el punto de vista topológico, este espacio es el mismo que un plano y las rectas son idénticas a rectas ordinarias. La curvatura de las líneas refleja la curvatura negativa del espacio subyacente.
En un segundo modelo de geometría hiperbólica, introducido por Poincaré, el espacio se representa como el interior de un círculo, sin incluir su frontera, y las líneas rectas son círculos que cortan a la frontera a ángulos rectos. Una vez más, la geometría distorsionada refleja la curvatura del espacio subyacente. El artista Maurits Escher produjo muchas figuras basadas en este modelo de geometría hiperbólica, que él aprendió del geómetra canadiense Coxeter.
Estos dos modelos indican una profunda relación con ciertos grupos de transformaciones del plano complejo: la geometría hiperbólica es la geometría de sus invariantes, según el Programa de Erlangen de Félix Klein. Otra clase de transformaciones, llamadas transformaciones de Möbius, traen a juego también la geometría elíptica.
§. La geometría del espacio
¿Qué pasa con la geometría del espacio? Ahora estamos de acuerdo con Klügel, y desdeñamos a Kant. Ésta es una cuestión de experiencia, no algo que pueda deducirse por el puro pensamiento. La relatividad general de Einstein nos dice que el espacio (y el tiempo) puede estar curvado; la curvatura es el efecto gravitatorio de la materia. La curvatura puede variar de un lugar a otro, dependiendo de cómo está distribuida la materia. Por ello, «la» geometría del espacio no es realmente la cuestión. El espacio puede tener diferentes geometrías en diferentes lugares. La geometría de Euclides funciona bien en escalas humanas, en el mundo humano, porque la curvatura gravitatoria es tan pequeña que no la observamos en nuestra vida diaria.
Pero ahí fuera, en el universo mayor, dominan las geometrías no euclidianas.
Para los antiguos y hasta bien entrado el siglo XIX, las matemáticas y el mundo real estaban desesperantemente confundidos. Existía la creencia general de que las matemáticas eran una representación de características básicas e inevitables del mundo real, y que la verdad matemática era absoluta. En ningún lugar estaba esta hipótesis más profundamente arraigada que en la geometría clásica. Para prácticamente todos los que importantes en este asunto, el espacio era euclidiano. ¿Qué otra cosa podía ser?
Esta pregunta dejó de ser retórica cuando empezaron a aparecer alternativas lógicamente consistentes con la geometría de Euclides. Se necesitó tiempo para reconocer que eran lógicamente consistentes -tan consistentes, al menos, como la geometría de Euclides- e incluso más tiempo para comprender que nuestro propio espacio físico podría no ser perfectamente euclidiano. Como siempre, la culpa iba a ser del provincialismo humano: estábamos proyectando nuestras experiencias limitadas a un minúsculo rincón del universo sobre el universo en conjunto. Nuestra imaginación parece estar sesgada a favor de un modelo euclidiano, probablemente porque en las pequeñas escalas de nuestra experiencia es un modelo excelente, y también el más sencillo disponible.
Gracias a un pensamiento imaginativo y heterodoxo, a menudo ferozmente contestado por una mayoría menos imaginativa, ahora se entiende -al menos por parte de matemáticos y físicos- que hay muchas alternativas a la geometría de Euclides, y que la naturaleza del espacio físico es una cuestión de observación, no de pensamiento puro. Hoy día distinguimos claramente entre modelos matemáticos de la realidad y la propia realidad. En la práctica, buena parte de las matemáticas no guarda ninguna relación obvia con la realidad -pero es útil, de todas formas.
Para qué nos sirve la geometría no euclidiana¿Qué forma tiene el universo? La pregunta puede parecer simple pero responderla es difícil; en parte porque el universo es muy grande, pero sobre todo porque estamos dentro de él y no podemos «apartarnos» y verlo en conjunto. En una analogía que se remonta a Gauss, una hormiga que vive en una superficie y la observa sólo desde dentro de dicha superficie, no podría decir fácilmente si la superficie es un plano, una esfera, un toro o algo más complicado.
La relatividad general nos dice que cerca de un cuerpo material, tal como una estrella, el espacio es curvo. Las ecuaciones de Einstein, que relacionan la curvatura con la densidad de materia, tienen muchas soluciones diferentes. En las más simples, el universo en conjunto tiene curvatura positiva, y su topología es la de una esfera.
Espacio con curvatura positiva, negativa o nula
Un universo cerrado se curva «sobre sí mismo». Líneas que divergían vuelven a juntarse. Densidad > densidad crítica.
Un universo abierto se curva «hacia fuera de sí mismo». Líneas que divergen se curvan para formar ángulos cada vez mayores entre sí. Densidad < densidad crítica.
Un universo plano no tiene curvatura. Las líneas que divergen mantienen un ángulo constante entre ellas. Densidad = densidad críticaPero, hasta donde podemos decir, la curvatura global del universo real podría ser negativa. Ni siquiera podemos saber si el universo es infinito, como el espacio euclidiano, o si es de extensión finita, como una esfera. Algunos físicos mantienen que el universo es infinito, pero la base experimental para esta afirmación es altamente cuestionable. La mayoría piensa que es finito.
Lo sorprendente es que un universo finito puede existir sin tener una frontera.
La esfera es así en dos dimensiones, y también lo es un toro. Al toro se le puede dar una geometría plana, heredada de un cuadrado al identificar lados opuestos. Los topólogos también han descubierto que el espacio puede ser finito pero curvado negativamente: una manera de construir tales espacios es tomar un poliedro finito en un espacio hiperbólico e «identificar» varias caras, de modo que una línea que sale del poliedro a través de una cara vuelve a entrar inmediatamente por otra cara. Esta construcción es similar a la forma en que se «enrollan» los bordes de la pantalla en muchos juegos de ordenador.
Si el espacio es finito, entonces debería ser posible observar la misma estrella en direcciones diferentes, aunque podría parecer mucho más lejana en unas direcciones que en otras, y la región observable del universo podría ser demasiado pequeña en cualquier caso. Si un espacio finito tiene geometría hiperbólica, estas ocurrencias múltiples de las mismas estrellas en diferentes direcciones determinan un sistema de círculos gigantes en los cielos, y la geometría de estos círculos determina qué espacio hiperbólico se está observando. Pero los círculos podrían estar en cualquier lugar entre los miles de millones de estrellas que se pueden ver, y hasta ahora los intentos de observarlos, basados en correlaciones estadísticas entre las posiciones aparentes de las estrellas, no han dado ningún resultado.
Para obtener el espacio dodecaédrico de Poincaré se identifican las caras opuestasEn 2003 datos de la Wilkinson Microwave Anisotropy Probe llevaron a Jean-Pierre Luminet y sus colaboradores a proponer que el espacio es finito pero con curvatura positiva. Encontraron que el «espacio dodecaédrico» de Poincaré -obtenido identificando caras opuestas de un dodecaedro curvo- da el mejor acuerdo con las observaciones. Esta sugerencia recibió amplia publicidad como la afirmación de que el universo tiene la forma de un balón de fútbol. Esta sugerencia no ha sido confirmada, y actualmente no tenemos idea de la verdadera forma del espacio. Sin embargo, tenemos una comprensión mucho mejor de lo que hay que hacer para descubrirlo.
Capítulo 13
La emergencia de la simetría
Cómo no resolver una ecuación
Alrededor de 1850 las matemáticas sufrieron uno de los cambios más trascendentales de su historia, aunque ello no se hizo entonces evidente. Antes de 1800, los principales objetos de estudio matemático eran relativamente concretos: números, triángulos, esferas. El álgebra utilizaba fórmulas para representar manipulaciones con números, pero las propias fórmulas se veían como representaciones simbólicas de procesos, no como cosas en sí mismas. Pero hacia 1900 fórmulas y transformaciones se veían como cosas, no como procesos, y los objetos del álgebra eran mucho más abstractos y más generales. De hecho, casi todo valía en lo concerniente al álgebra. Incluso «leyes» básicas, tales como la ley conmutativa de la multiplicación, ab = ba, habían sido abandonadas en algunas áreas importantes.
§. Teoría de grupos
Estos cambios llegaron fundamentalmente porque los matemáticos descubrieron la «teoría de grupos», una rama del álgebra que surgió de intentos infructuosos por resolver ecuaciones algebraicas, en especial la ecuación «química», o de quinto grado. Pero menos de 50 años después de su descubrimiento, la teoría de grupos ya había sido reconocida como el marco correcto para estudiar el concepto de simetría.
“Hoy, la teoría de grupos se ha convertido en una herramienta indispensable...”
A medida que los nuevos métodos entraban en la conciencia colectiva, se hizo claro que la simetría es una idea profunda y central, con innumerables aplicaciones en las ciencias físicas y también en las biológicas. Hoy, la teoría de grupos se ha convertido en una herramienta indispensable en todas las áreas de las matemáticas y de la ciencia, y sus relaciones con la simetría se destacan en la mayoría de los textos introductorios. Pero se necesitaron varias décadas para llegar a este punto de vista. Alrededor de 1900 Henri Poincaré decía que la teoría de grupos era efectivamente el conjunto de las matemáticas reducidas a su esencia, lo que era algo exagerado, aunque una exageración defendible.
“Sin duda las fórmulas serían muy complicadas...”
El punto crucial en la evolución de la teoría de grupos fue la obra de un joven matemático, Évariste Galois. Hubo una prehistoria larga y complicada: las ideas de Galois no surgieron de la nada. Y hubo una post-historia igualmente complicada y a veces algo embarullada, mientras los matemáticos experimentaban con el nuevo concepto y trataban de ver lo que era importante y lo que no lo era. Pero fue Galois, más que cualquier otro, quien entendió claramente la necesidad de los grupos, estudió algunas de sus propiedades fundamentales y mostró su valor en las matemáticas. No es del todo sorprendente que su obra pasara casi inadvertida durante su vida. Era demasiado original, quizá, pero también hay que decir que la personalidad de Galois y su fuerte implicación en la política revolucionaria no ayudaron mucho.
Fue una figura trágica, en una época de muchas tragedias personales, y su vida fue una de las más dramáticas, y quizá románticas, entre las de los matemáticos importantes.
§. Resolviendo ecuaciones
La historia de la teoría de grupos se remonta al antiguo trabajo babilónico sobre ecuaciones cuadráticas. Por lo que concierne a los babilonios, su método pretendía un uso práctico; era una técnica computacional, y parece que ellos no se hacían preguntas profundas sobre la misma. Si uno sabía cómo encontrar raíces cuadradas, y había dominado la aritmética básica, podía resolver cuadráticas.
Hay algunos indicios, en las tablillas de arcilla que nos han llegado, de que los babilonios también pensaron en ecuaciones cúbicas, e incluso en algunas ecuaciones cuárticas. Los griegos, y después de ellos los árabes, descubrieron métodos geométricos para resolver ecuaciones cúbicas basados en secciones cónicas. (Ahora sabemos que las tradicionales rectas y círculos euclidianos no pueden resolver tales problemas exactamente. Se necesitaba algo más sofisticado; y resultó que las cónicas servían para ello.) Una de las figuras destacadas fue el persa Omar Khayyam, más conocido por su poema Rubaiyat. Ornar resolvió todos los tipos posibles de cúbicas mediante métodos geométricos sistemáticos. Pero, como hemos visto, una solución algebraica de las ecuaciones cúbicas y cuárticas tuvo que esperar hasta el Renacimiento, con la obra de Del Ferro, Tartaglia, Fiore, Cardano y su pupilo Ferrari.
La pauta que parecía emerger de todo este trabajo era simple, incluso si los detalles eran confusos. Se puede resolver cualquier cúbica utilizando operaciones aritméticas, más raíces cuadradas y más raíces cúbicas. Se puede resolver cualquier cuártica utilizando operaciones aritméticas, más raíces cuadradas, más raíces cúbicas y más raíces cuartas: aunque las últimas pueden reducirse a dos raíces cuadradas tomadas una detrás de otra. Parecía plausible que esta pauta continuara, de modo que se pudiera resolver cualquier química utilizando operaciones aritméticas, más raíces cuadradas, raíces cúbicas, raíces cuartas y raíces químicas. Y así sucesivamente para ecuaciones de cualquier grado. Sin duda las fórmulas serían muy complicadas, y encontrarlas sería aún más complicado, pero pocos parecían dudar de que existieran.
Pasaron siglos sin signos de que se hubiera encontrado ninguna fórmula semejante. Entonces, algunos de los grandes matemáticos decidieron examinar con más detalle el área en conjunto, ver lo que estaba sucediendo realmente entre bastidores, unificar los métodos conocidos y simplificarlos de modo que se hiciera obvio por qué funcionaban. Luego, pensaban, sería simplemente cuestión de aplicar los mismos principios generales y la quíntica cedería su secreto.
El trabajo más satisfactorio y más sistemático en esta línea fue realizado por Lagrange. El reinterpretó las fórmulas clásicas en términos de las soluciones que se estaban buscando.
Las simetrías de una cuadráticaConsideremos una ecuación cuadrática, en la forma ligeramente simplificada
x2 + px + q = 0
Supongamos que las dos soluciones son x = a y x = b
x2 + px + q = (x - a) (x - b)
y esto nos dice que
a + b=-p
ab = q
Por lo tanto, aunque no sabemos aún las soluciones, sabemos su suma y su producto sin mucho esfuerzo.
¿Por qué es así? La suma a + b es la misma que b + a; no cambia-cuando se permutan las soluciones. Lo mismo sucede con ab = ba. Resulta así que toda función simétrica de las soluciones puede expresarse en términos de los coeficientes p y q. Recíprocamente, cualquier expresión en p y q es siempre una función simétrica de a y b. En una visión general, la conexión entre las soluciones y los coeficientes está determinada por una propiedad de simetría.
Las funciones asimétricas no se comportan de este modo.
Un buen ejemplo es la diferencia entre las raíces. Cuando intercambiamos a y b, la diferencia a - b se convierte en b - a, que no es lo mismo. Sin embargo -y esto es crucial- no es muy diferente: simplemente equivale a cambiar el signo de a - b. Por lo tanto, el cuadrado es completamente simétrico: (a - b)2 = (b - a)2. Pero cualquier función completamente simétrica de las soluciones debe tener una expresión en los coeficientes. Tomemos la raíz cuadrada y habremos expresado a - b en términos de los coeficientes sin utilizar nada más esotérico que una raíz cuadrada. Ya conocemos a + b: es igual a - p. Puesto que también conocemos a - b, la suma de estos dos números es 2a y la diferencia es 2b.
Dividiendo por 2, obtenemos fórmulas para a y para b.
Lo que hemos hecho es demostrar que debe existir una fórmula para las soluciones a y b que no incluye nada más esotérico que una raíz cuadrada, basada en características generales de las simetrías de expresiones algebraicas. Esto es impresionante: hemos demostrado que el problema posee una solución sin tener que molestarnos en calcular todos los detalles liosos que nos dicen cuál es. En cierto sentido, hemos descubierto por qué los babilonios fueron capaces de encontrar un método. Esta pequeña historia arroja nueva luz sobre la palabra «entender». Podemos entender la solución que da el método babilónico siguiendo los pasos y comprobando la lógica. Pero ahora hemos comprendido por qué tenía que haber un método semejante: no mostrando una solución, sino examinando propiedades generales de las presuntas soluciones. Aquí, la propiedad clave resulta ser la simetría.
Con algo más de trabajo, que lleva a una expresión explícita para (a - b)2, este método da una fórmula para las soluciones. Es equivalente a la fórmula que aprendemos en la escuela y al método utilizado por los babilonios.
Lo que importaba, decía él, era cómo se comportaban ciertas expresiones algebraicas especiales formadas a partir de dichas soluciones cuando las propias soluciones eran «permutadas»: reordenadas. El sabía que cualquier expresión completamente simétrica -una expresión que permaneciera exactamente igual independientemente de cómo se intercambiaran las soluciones- podía expresarse en términos de los coeficientes de la ecuación, haciéndola una cantidad «conocida». Más interesantes eran las expresiones que sólo tomaban unos pocos valores diferentes cuando las soluciones eran permutadas. Estas parecían tener la clave para resolver la ecuación.
“Pero ahora Lagrange sabía por qué ésas eran las respuestas y, mejor aún, sabía por qué había respuestas que encontrar.”
El sentido bien desarrollado que tenía Laplace de la forma y la belleza le decía que ésta era una idea importante. Si pudiera obtener algo similar para las ecuaciones cúbica y cuártica, entonces podría descubrir cómo resolver la química.
Utilizando la misma idea básica encontró que funciones «parcialmente» simétricas de las soluciones le permitían reducir una ecuación cúbica a una cuadrática. La cuadrática introducía una raíz cuadrada, y el proceso de reducción podía ordenarse utilizando una raíz cúbica. Análogamente, cualquier ecuación cuártica podía reducirse a una cúbica, a la que él llamó la cúbica resolvente. Por lo tanto se podía resolver una cuártica utilizando raíces cuadradas y cúbicas para tratar la cúbica resolvente y raíces cuartas para relacionar la respuesta con las soluciones buscadas.
En ambos casos las respuestas eran idénticas a las fórmulas clásicas del Renacimiento. Tenían que serlo, pues ésas eran las respuestas. Pero ahora Lagrange sabía por qué ésas eran las respuestas y, mejor aún, sabía por qué había respuestas que encontrar.
El debió sentirse muy excitado en esta etapa de su investigación. Pasando a la química, y aplicando las mismas técnicas, uno espera obtener una cuártica resolvente: trabajo hecho. Pero, seguramente para su disgusto, él no obtuvo un cuártica resolvente. Obtuvo una séxtica resolvente: una ecuación de sexto grado.
En lugar de hacer las cosas más sencillas, su método hacía la química más complicada.
¿Era esto un defecto del método? ¿Podría algo más ingenioso todavía resolver la química? Parece que Lagrange lo creía. Escribió que confiaba en que su nuevo punto de vista sería útil para cualquiera que tratara de desarrollar una manera de resolver químicas. Parece que no se le ocurrió que no pudiera existir tal método; que su aproximación fallaba porque en general las químicas no tienen soluciones en «radicales», que son expresiones que incluyen operaciones aritméticas y raíces diversas, tales como raíces quintas. Para complicar las cosas, algunas químicas tienen tales soluciones; por ejemplo, x5 - 2 = 0 tiene la solución x = 5√2. Pero éste es un caso bastante simple, y no realmente típico.
Dicho sea de paso, todas las ecuaciones quínticas tienen soluciones; en general son números complejos, y pueden encontrarse mediante cálculo numérico con la precisión que se quiera. El problema estaba en las fórmulas algebraicas para las soluciones.
§. En busca de una solución
Conforme las ideas de Lagrange empezaron a calar, creció la sensación de que quizá el problema no podía resolverse. Quizá la ecuación química general no puede resolverse por radicales. Parece que Gauss lo pensaba, en privado, pero expresó la opinión de que éste no era un problema que mereciera ser abordado. Es quizá uno de los pocos ejemplos donde le falló su intuición sobre lo que es importante; otro fue el Último Teorema de Fermat, pero aquí los métodos necesarios estaban más allá incluso de Gauss, y tardaron un par de siglos en surgir. Lo irónico, no obstante, es que Gauss ya había iniciado parte del álgebra necesaria para demostrar la insolubilidad de la química. La había introducido en su trabajo sobre la construcción de polígonos regulares con regla y compás. Y en este trabajo también había establecido un precedente, al demostrar (al menos para su propia satisfacción) que algunos polígonos no podían construirse de esta manera. El 9-gono regular era un ejemplo. Gauss lo «sabía», pero nunca escribió una demostración; una fue ofrecida un poco más tarde por Pierre Wantzel.
Por lo tanto, Gauss había establecido un precedente para la proposición de que algunos problemas no podrían ser solubles por métodos particulares.
La primera persona en intentar una demostración de la imposibilidad fue Paolo Ruffini, quien llegó a ser profesor de matemáticas en la Universidad de Módena en 1789. Siguiendo las ideas de Lagrange sobre funciones simétricas, Ruffini llegó a convencerse de que no existe ninguna fórmula que no incluya nada más esotérico que raíces n-ésimas para resolver la quíntica. En su Teoría general de ecuaciones de 1799 presentaba una demostración de que «la solución algebraica de ecuaciones generales de grado mayor que 4 es siempre imposible». Pero su demostración era tan enorme -500 páginas de longitud- que nadie estaba dispuesto a comprobarla, especialmente porque había rumores de que contenía errores. En 1803 Ruffini publicó una demostración nueva y simplificada, pero no tuvo mejor suerte. Durante su vida, Ruffini nunca consiguió asegurarse el crédito por demostrar que la quíntica es insoluble.
La contribución más importante de Ruffini consistió en darse cuenta que las permutaciones pueden ser combinadas unas con otras. Hasta entonces, una permutación era una reordenación de una colección de símbolos. Por ejemplo, si numeramos las raíces de una quíntica como 1, 2, 3, 4, 5, entonces estos símbolos pueden ser reordenados como 5, 4, 3, 2, 1, ó 4, 2, 1, 5, 3, ó 2, 3, 1, 5, 4 ó cualquier otra cosa. Hay 120 ordenaciones posibles. Ruffini comprendió que había otra manera de ver una reordenación semejante: como una receta para reordenar cualquier otro conjunto de cinco símbolos.
El truco consistía en comparar el orden «estándar» 1, 2, 3, 4, 5 con el orden reordenado. A modo de ejemplo sencillo, supongamos que el orden reordenado era 5, 4, 3, 2, 1. Entonces la regla para pasar del orden estándar inicial al orden nuevo era simple: «invertir el orden». Pero se puede invertir el orden de cualquier secuencia de cinco símbolos. Si los símbolos son a, b, c, d, e, el inverso es e, d, c, b, a. Si los símbolos de partida son 2, 3, 4, 5, 1, entonces su inverso es 1, 5, 4, 3, 2. Esta nueva manera de ver una permutación significaba que se podían realizar dos permutaciones una detrás de otra -una especie de «multiplicación» de permutaciones. El álgebra de permutaciones, multiplicadas de esta forma, tenía la clave de los secretos de la quíntica.
§. Abel
Ahora sabemos que había un error técnico en la demostración de Ruffini, pero las ideas principales eran válidas y la laguna podía llenarse. Él consiguió algo: su libro llevó a una sensación vaga pero generalizada de que la quíntica no es soluble por radicales. Casi nadie pensaba que Ruffini lo hubiera demostrado, pero los matemáticos empezaron a dudar de que pudiera existir una solución. Por desgracia, el efecto principal de esta creencia fue el de disuadir a todos de trabajar en el problema.
Una excepción fue Abel, un joven noruego con un talento precoz para las matemáticas, que pensaba que había resuelto la quíntica cuando aún estaba en la escuela. Con el tiempo descubrió un error, pero siguió intrigado por el problema y siguió trabajando en él esporádicamente. En 1823 encontró una demostración de la imposibilidad de resolver la quíntica, y esta demostración era totalmente correcta. Abel utilizó una estrategia similar a la de Ruffini, pero su táctica era mejor. Al principio no conocía la investigación de Ruffini; más tarde seguro que la conocía, pero afirmaba que era incompleta. Sin embargo, él no menciona ningún problema específico con la demostración de Ruffini. Lo irónico es que un paso en la demostración de Abel es exactamente lo que se necesita para llenar la laguna de la de Ruffini.
Podemos hacernos una idea general de los métodos de Abel sin entrar en muchos tecnicismos. Él plantea el problema distinguiendo dos tipos de operaciones algebraicas. Supongamos que empezamos con varias cantidades; pueden ser números concretos o expresiones algebraicas con varias incógnitas. A partir de ellas podemos construir muchas otras cantidades.
“Cuando funciona, este truco es espectacular, y aquí funcionaba maravillosamente.”
La manera «fácil» de hacerlo es combinar las cantidades existentes sumándolas, restándolas, multiplicándolas o dividiéndolas. Así, a partir de una simple incógnita, x, podemos crear expresiones como
x2, 3x + 4 ó (x + 7)/(2x - 3).
Desde el punto de vista algebraico todas estas expresiones están en pie de igualdad con la propia x.
La segunda manera de obtener nuevas cantidades a partir de las existentes es utilizar radicales. Tomamos una de las modificaciones «inocuas» de las cantidades existentes y extraemos una raíz. Llamamos a tal paso «añadir un radical». Si es una raíz cuadrada, decimos que el grado del radical es 2; si es una raíz cúbica, entonces el grado es 3, y así sucesivamente.
En estos términos, la fórmula de Cardano para la cúbica puede resumirse como el resultado de un procedimiento de dos pasos. Se empieza con los coeficientes de la cúbica (y cualquier combinación inocua de ellos). Se añade un radical de grado 2. Luego se añade otro radical de grado 3. Ya está. Esta descripción nos dice qué tipo de fórmula aparece, pero no cuál es exactamente.
A veces la clave para responder a un enigma matemático no es centrarse en los detalles finos, sino considerar los aspectos generales. Menos puede significar más. Cuando funciona, este truco es espectacular, y aquí funcionaba maravillosamente. Permitía a Abel reducir cualquier fórmula hipotética para resolver la química a sus pasos esenciales: extraer una secuencia de radicales, en algún orden, con varios grados. Siempre es posible hacer que los grados sean primos; por ejemplo, una raíz sexta es la raíz cúbica de una raíz cuadrada.
Llamamos a tal secuencia una torre radical. Una ecuación es soluble por radicales si al menos una de sus soluciones puede expresarse por una torre radical. Pero en lugar de tratar de encontrar una torre radical, Abel simplemente supuso que existía una torre radical, y se preguntó qué aspecto debía tener la ecuación original.
Sin advertirlo, Abel llenó la laguna en la demostración de Ruffini.
Demostró que cuandoquiera que una ecuación puede resolverse por radicales, debe existir una torre radical que lleva a dicha solución y que incluye sólo los coeficientes de la ecuación original. Esto se denomina el «teorema sobre irracionalidades naturales», y afirma que no puede ganarse nada incluyendo toda una pila de nuevas cantidades que no estén relacionadas con los coeficientes originales. Esto debería ser obvio, pero Abel comprendió que en muchos aspectos es el paso crucial en la demostración.
La clave de la demostración de imposibilidad de Abel es un ingenioso resultado preliminar. Supongamos que tomamos mía expresión en las soluciones, x1, x2, x3, x4, x5 de la ecuación, y extraemos su raíz p-ésima para algún número primo p. Además, suponemos que la expresión original no varía cuando aplicamos dos permutaciones especiales
S: x1, x2, x3, x4, x5 → x2, x3, x1, x4, x5
y
T: x1, x2, x3, x4, x5 → x1, x2, x4, x5, x3
Luego, Abel demostró que la raíz p-ésima de dicha expresión tampoco varía cuando aplicamos S y T. Este resultado preliminar lleva directamente a la demostración del teorema de imposibilidad, «escalando la torre» paso a paso. Suponemos que la quíntica puede resolverse por radicales, de modo que hay una torre radical que empieza con los coeficientes y recorre todo el camino de subida hasta una solución.
Évariste Galois
1811-1832Évariste Galois era hijo de Nicholas Gabriel Galois y Adelaida Marie Demante. Creció en la Francia revolucionaria, y tuvo una ideología política típicamente izquierdista.
Su gran contribución a las matemáticas no fue reconocida hasta 14 años después de su muerte.
La Revolución Francesa había empezado con la toma de la Bastilla en 1789 y la ejecución de Luis XVI en 1793. En 1804 Napoleón Bonaparte se proclamó emperador, pero después de una serie de derrotas militares fue obligado a abdicar y la monarquía fue restaurada en 1814 bajo Luis XVIII. En 1824 Luis había muerto y el rey era ahora Carlos X.
En 1827, Galois empezó a mostrar un talento inusual -y una obsesión- para las matemáticas.
Trató de ingresar en la prestigiosa École Polytechnique, pero no aprobó el examen. En 1829 su padre, entonces alcalde de la ciudad, se suicidó ahorcándose cuando sus enemigos políticos inventaron un falso escándalo. Poco después, Galois intentó una vez más ingresar en la École Polytechnique, y fue suspendido de nuevo. Entonces entró en la École Nórmale.
En 1830 Galois presentó sus investigaciones sobre la solución de ecuaciones algebraicas a un premio que ofrecía la Academia de Ciencias. El recensor, Fourier, murió al poco tiempo y el artículo se perdió. El premio fue para Abel (quien para entonces había muerto de tuberculosis) y para Cari Jacobi. El mismo año Carlos X fue depuesto y huyó para salvar la vida. El director de la École Nórmale encerró a sus estudiantes para impedir que se uniesen al movimiento. Galois, furioso, escribió una carta sarcástica atacando al director por su cobardía, lo que le supuso su expulsión inmediata.
Como compromiso, Louis-Philipe fue proclamado rey. Galois se unió a una milicia republicana, la Artillería de la Guardia Nacional, pero el nuevo rey la abolió. Diecinueve de los oficiales de la Guardia fueron arrestados y juzgados por sedición, pero el jurado retiró los cargos. El Día de la Bastilla Galois fue detenido de nuevo por llevar el uniforme ahora ilegal de la Guardia.
En prisión supo lo que había sucedido con su artículo. Poisson lo había rechazado por no ser suficientemente claro. Galois intentó suicidarse pero los otros prisioneros se lo impidieron. Su odio por la oficialidad se hizo ahora extremo y manifestó síntomas de paranoia. Pero cuando se desencadenó una epidemia de cólera, los prisioneros fueron liberados, entonces Galois se enamoró de Stephanie du Motel, la hija del médico de los alojamientos de Galois. La relación no prosperó y Stephanie le puso fin Uno de los camaradas revolucionarios de Galois le retó entonces a un duelo. Una teoría plausible dice que el adversario era Ernest Duchátelet, que había estado en prisión con Galois. Parece que el duelo fue una especie de ruleta rusa: los duelistas eligieron al azar entre dos pistolas, sólo una de las cuales estaba cargada, y se dispararon a quemarropa. Galois escogió la pistola equivocada, recibió un tiro en el estómago y murió al día siguiente.
Fragmento de un manuscrito de Évariste GaloisLa noche anterior al duelo escribió un largo resumen de sus ideas matemáticas, incluida una descripción de su demostración de que todas las ecuaciones de grado 5 o superior no pueden resolverse por radicales. En este trabajo desarrolló el concepto de grupo de permutaciones y dio los primeros pasos importantes hacia la teoría de grupos. Su manuscrito estuvo a punto de perderse, pero finalmente llegó a Joseph Liouville. un miembro de la Academia. En 1843 Liouville se dirigió a la Academia afirmando que en los papeles de Galois había encontrado una solución «tan correcta como profunda de este bonito problema: dada una ecuación irreducible de grado primo, decidir si es o no soluble por radicales». Liouville publicó los papeles de Galois en 1846, haciéndolos fácilmente accesibles a la comunidad matemática.
El «primer piso» de la torre -la expresión inocua en los coeficientes- no varía cuando aplicamos las permutaciones S y T, porque éstas permutan las soluciones, no los coeficientes. Por consiguiente, por el resultado preliminar de Abel, el segundo piso de la torre tampoco varía cuando aplicamos S y T, porque se alcanza añadiendo una raíz p-ésima de algo que hay en el primer piso, para algún primo p. Por el mismo razonamiento, el tercer piso de la torre no varía cuando aplicamos S y T. Lo mismo sucede con el cuarto piso, el quinto piso... hasta el último piso.
Para qué les servía la teoría de gruposUna de las primeras aplicaciones serias de la teoría de grupos a la ciencia fue la clasificación de todas las posibles estructuras cristalinas. Los átomos en un cristal forman una red tridimensional regular, y el punto matemático importante consiste en listar todos los posibles grupos de simetría de tales redes, porque éstos dan efectivamente las simetrías del cristal.
En 1891 Evgraf Fedorov y Arthur Schönflies demostraron que existen exactamente 230 «grupos espaciales» cristalográficos diferentes. William Barlow obtuvo una lista similar pero incompleta.
Las técnicas modernas para encontrar la estructura de moléculas biológicas, tales como proteínas, se basan en hacer pasar rayos X a través de un cristal formado por dichas moléculas y observar las figuras de difracción resultantes. Las simetrías del cristal son importantes para deducir la forma de la molécula en cuestión. También lo es el análisis de Fourier.
Sin embargo, el último piso contiene una solución de la ecuación. ¿Podría ser x1? Si lo es, entonces x, no debe variar cuando aplicamos S. Pero S aplicado a x1 da x2, no x1, de modo que no vale. Por razones similares, a veces utilizando T, la solución definida por la torre tampoco puede ser x2, x3, x4 ni x5.
Las cinco soluciones están excluidas de cualquier torre semejante; de modo que la hipotética torre no puede contener de hecho una solución.
No hay escape de esta trampa lógica. La química es insoluble porque cualquier solución (por radicales) debe tener propiedades autocontradictorias, y por consiguiente no puede existir.
§. Galois
La búsqueda no sólo de la química, sino de todas las ecuaciones algebraicas, fue ahora asumida por Évariste Galois, una de las figuras más trágicas en la historia de las matemáticas. El propio Galois se propuso la tarea de determinar qué ecuaciones podían resolverse por radicales y cuáles no podían. Como varios de sus predecesores, él comprendió que la clave para la solución algebraica de ecuaciones estaba en cómo se comportaban las soluciones cuando se permutaban. El problema estaba en la simetría.
Ruffini y Abel habían comprendido que una expresión en las soluciones no tenía necesariamente que ser simétrica o no serlo. Podía ser parcialmente simétrica: invariable frente a unas permutaciones pero no frente a otras. Galois advirtió que las permutaciones que determinan alguna expresión en las raíces no forman ninguna colección vieja. Tienen un rasgo característico simple. Si se toman dos permutaciones cualesquiera que determinan la expresión, y se multiplican, el resultado también determina la permutación. Él llamó grupo a un sistema tal de permutaciones. Una vez que hemos comprendido que esto es cierto, es muy fácil demostrarlo. El truco consiste en advertirlo y reconocer su importancia.
El resultado de las ideas de Galois es que la quíntica no puede resolverse por radicales porque tiene el tipo equivocado de simetrías. El grupo de una ecuación quíntica «general» consiste en todas las permutaciones de las cinco soluciones. La estructura algebraica de este grupo es incompatible con una solución por radicales.
Galois trabajó en otras áreas de las matemáticas, e hizo descubrimientos igualmente profundos. En particular, generalizó la aritmética modular para clasificar lo que ahora llamamos campos de Galois. Éstos son sistemas finitos en los que pueden definirse las operaciones aritméticas de suma, resta, multiplicación y división, y se aplican todas las leyes habituales. El tamaño de un campo de Galois es siempre una potencia de un primo, y hay exactamente un campo tal para cada potencia prima.
§. Jordán
El concepto de grupo apareció por primera vez de una forma clara en la obra de Galois, aunque con indicios anteriores en los voluminosos escritos de Ruffini y en las elegantes investigaciones de Lagrange. Menos de una década después de que las ideas de Galois estuvieran ampliamente disponibles, gracias a Liouville, las matemáticas estaban en posesión de una teoría de grupos bien desarrollada.
El principal arquitecto de esta teoría fue Camille Jordán, cuyo obra Traite deSubstitutions et des Equations Algébriques, de 667 páginas, fue publicada en 1870. Jordán desarrolló toda la disciplina de una forma sistemática y global.
La implicación de Jordán en la teoría de grupos empezó en 1887, cuando él mostró el vínculo profundo con la geometría de una manera muy explícita, clasificando los tipos básicos de movimiento de un cuerpo rígido en el espacio euclidiano. Y lo que es más importante, hizo un intento muy bueno por clasificar cómo estos movimientos podían combinarse en grupos. Su motivación principal era la investigación cristalográfica de Auguste Bravais, quien inició el estudio matemático de las simetrías cristalinas, especialmente la red de átomos subyacente. Los artículos de Jordán generalizaban la obra de Bravais. Él anunció su clasificación en 1887, y publicó los detalles en 1888-1889.
“Pero su trabajo fue un paso importante hacia la comprensión de los movimientos rígidos euclidianos...”
Técnicamente, Jordán trataba sólo con grupos cerrados, en los que el límite de cualquier secuencia de movimientos en el grupo es también un movimiento en el mismo grupo. Éstos incluyen todos los grupos finitos, por razones triviales, y también grupos como «todas las rotaciones de un círculo en torno a su centro». Un ejemplo típico de grupo no cerrado, no considerado por Jordán, podrían ser «todas las rotaciones de un círculo en torno a su centro en múltiplos racionales de 360º». Este grupo existe, pero no satisface la propiedad límite (porque no incluye, por ejemplo, la rotación de 360√2 grados, que es el límite de aproximaciones de ángulo racional). Los grupos de movimientos no cerrados son enormemente variados, y casi con certeza están más allá de cualquier clasificación razonable. Los cerrados son tratables, pero difíciles.
Los principales movimientos rígidos en el plano son traslaciones, rotaciones, reflexiones y reflexiones con deslizamiento. En el espacio tridimensional encontramos también movimientos de torsión, como el movimiento de un sacacorchos: el objeto se traslada a lo largo de un eje fijo y simultáneamente rota alrededor del mismo eje.
Jordán empezó con grupos de traslaciones e hizo una lista de diez tipos, todos ellos mezclas de traslaciones continuas (de cualquier distancia) en unas direcciones y traslaciones discretas (en múltiplos enteros de una distancia fija) en otras direcciones. También listó los principales grupos finitos de rotaciones y reflexiones: cíclicos, diédricos, tetraédricos, octaédricos e icosaédricos. Distinguió el grupo O(2) de todas las rotaciones y reflexiones que dejan fija una línea en el espacio, el eje, y el grupo O(3) de todas las rotaciones y reflexiones que dejan fijo un punto en el espacio, el centro.
Más tarde se hizo patente que esta lista era incompleta. Por ejemplo, había pasado por alto algunos de los más sutiles grupos cristalográficos en el espacio tridimensional. Pero su trabajo fue un paso importante hacia la comprensión de los movimientos rígidos euclidianos, que son importantes en mecánica, así como en el cuerpo principal de las matemáticas puras.
El libro de Jordán tenía un alcance verdaderamente enorme. Empezaba con aritmética modular y campos de Galois, que además de proporcionar ejemplos de grupos constituyen también el fondo esencial para el resto del libro. El tercio central trabaja con grupos de permutaciones, que Jordán llama «sustituciones». El plantea las ideas básicas de los «subgrupos normales», que son los que utilizaba Galois para demostrar que el grupo de simetría de la química es incompatible con una solución por radicales, y demuestra que dichos subgrupos pueden utilizarse para descomponer un grupo general en fragmentos más simples. Demuestra que los tamaños de dichos fragmentos no dependen de cómo se descomponga el grupo. En 1889 Otto Hölder mejoró este resultado, interpretando los fragmentos como grupos en sí mismos, y demostró que su estructura de grupo, y no sólo su tamaño, es independiente de cómo se descomponga el grupo. Hoy este resultado se llama Teorema de Jordan-Hölder.
Un grupo es simple si no se descompone de esta manera. El Teorema de Jordan-Hölder nos dice en efecto que los grupos simples se relacionan con los grupos generales de la misma manera que los átomos se relacionan con las moléculas en química. Los grupos simples son los «constituyentes atómicos» de todos los grupos. Jordán demostró que el grupo alternante An que comprende todas las permutaciones de n símbolos que cambian un número par de pares de símbolos, es simple siempre que n ≥ 5. Ésta es la razón principal de teoría de grupos por la que la química es insoluble por radicales.
Para qué nos sirve la teoría de gruposLa teoría de grupos es ahora indispensable en las matemáticas, y su uso en ciencia es generalizado. En particular, aparece en teorías de formación de pautas en muchos contextos científicos diferentes.
Un ejemplo es la teoría de las ecuaciones de reacción- difusión, introducidas por Alan Turing en 1952 como una posible explicación de
las pautas simétricas en la piel de los animales. En estas ecuaciones, un sistema de sustancias químicas puede difundirse a través de una región del espacio, y las sustancias químicas también pueden reaccionar para producir nuevas sustancias. Turing sugirió que algunos de estos procesos podrían fijar una «pre-pauta» en un embrión animal en desarrollo, que posteriormente podría convertirse en pigmentos que manifestarían la pauta en el adulto.
Supongamos por simplicidad que la región es un plano. Entonces las ecuaciones son simétricas bajo movimientos rígidos. La única solución de las ecuaciones que es simétrica bajo todos los movimientos rígidos es un estado uniforme, el mismo en todas partes. Esto se traduciría en un animal sin ningunas marcas específicas, del mismo color en todas partes. Sin embargo, el estado uniforme puede ser inestable, en cuyo caso la solución real observada será simétrica bajo algunos movimientos rígidos pero no bajo otros. Este proceso se denomina ruptura de simetría.
Una pauta típica con ruptura de simetría en el plano consiste en franjas paralelas. Otra es un conjunto de manchas regulares. También son posibles pautas más complicadas. Es interesante que manchas y franjas estén entre las pautas más comunes en las pieles animales, y muchas de las más complicadas pautas matemáticas se encuentran también en animales.
Pautas de Turing en un modelo matemático y en un pezEl proceso biológico real, que incluye efectos genéticos, debe ser más complicado que lo que supuso Turing, pero el mecanismo de ruptura de simetría subyacente debe ser matemáticamente muy similar.
Un nuevo desarrollo importante fue la teoría de Jordán de las «sustituciones lineales». Aquí las transformaciones que constituyen el grupo no son permutaciones de un conjunto finito, sino cambios lineales en una lista finita de variables. Por ejemplo, tres variables x, y, z podrían transformarse en nuevas variables X, Y, Z por medio de ecuaciones lineales
X = a1x + a2y + a3z
Y = b1x + b2y + b3z
Z = c1x + c2y + c3z,
donde las a, b y c son constantes. Para hacer el grupo finito, Jordán tomaba normalmente dichas constantes como elementos de los enteros módulo un primo, o más generalmente un campo de Galois.
También en 1889, Jordán desarrolló su propia versión de la teoría de Galois y la incluyó en el Traite. Demostró que una ecuación es soluble si y sólo si su grupo es soluble, lo que significa que todos los componentes simples tienen orden primo. El aplicó la teoría de Galois a problemas geométricos.
§. Simetría
Los 4.000 años de búsqueda para resolver las ecuaciones químicas habían llegado a un parón abrupto cuando Ruffini, Abel y Galois demostraron que no es posible una solución por radicales. Aunque era un resultado negativo, tuvo una enorme influencia en el desarrollo posterior de las matemáticas y de la ciencia. Esto sucedió porque el método introducido para demostrar la imposibilidad resultó ser fundamental para la comprensión matemática de la simetría, y la simetría resultó ser vital tanto en matemáticas como en ciencia.
Los efectos fueron profundos. La teoría de grupos llevó a una visión más abstracta del álgebra, y con ello a una visión más abstracta de las matemáticas. Aunque muchos científicos «prácticos» eran inicialmente reacios a moverse hacia la abstracción, con el tiempo se hizo evidente que los métodos abstractos son con frecuencia más potentes que los concretos, y la mayor parte de la oposición ha desaparecido. La teoría de grupos también dejó claro que los resultados negativos pueden seguir siendo importantes, y que una insistencia en la demostración puede a veces llevar a descubrimientos trascendentales. Supongamos que los matemáticos hubieran dado por hecho sin demostración que las químicas no pueden resolverse, simplemente sobre la base plausible de que nadie podía encontrar una solución. Entonces nadie hubiera inventado la teoría de grupos para explicar por qué no pueden resolverse. Si los matemáticos hubieran tomado el camino fácil, y hubieran supuesto que la solución es imposible, las matemáticas y la ciencia habrían sido una pálida sombra de lo que son hoy.
Por eso es por lo que los matemáticos insisten en las demostraciones.
Capítulo 14
El álgebra se hace adulta
Los números dan paso a las estructuras
Hacia 1860 la teoría de los grupos de permutaciones estaba bien desarrollada. La teoría de invariantes -expresiones algebraicas que no cambian cuando se realizan ciertos cambios de variable- había llamado la atención sobre diversos conjuntos infinitos de transformaciones, tales como el grupo proyectivo de todas las proyecciones del espacio. En 1808 Camille Jordán había estudiado grupos de movimientos en el espacio tridimensional, y las dos corrientes empezaron a fusionarse.
§. Conceptos sofisticados
Empezaba a emerger un nuevo tipo de álgebra en la que los objetos de estudio no eran números desconocidos sino conceptos más sofisticados: permutaciones, transformaciones, matrices. Los procesos de ayer se habían convertido en las cosas de hoy. Las tradicionales «reglas del álgebra» tuvieron que ser modificadas con frecuencia para adaptarlas a las necesidades de estas nuevas estructuras. Junto con los grupos, los matemáticos empezaron a estudiar estructuras llamadas «anillos», «campos» y «álgebras» diversas.
Un estímulo para esta nueva visión del álgebra procedía de las ecuaciones en derivadas parciales, la mecánica y la geometría: el desarrollo de los grupos de Lie y las álgebras de Lie. Otra fuente de inspiración era la teoría de números: aquí podían utilizarse «números algebraicos» para resolver ecuaciones diofánticas, entender las leyes de reciprocidad e incluso atacar el Último Teorema de Fermat. De hecho, la culminación de tales esfuerzos fue la demostración del Último Teorema de Fermat por Andrew Wiles en 1995.
§. Lie y Klein
En 1869 el matemático noruego Sophus Lie entabló amistad con el matemático prusiano Félix Klein. Ambos tenían un interés común en la geometría lineal, un vástago de la geometría proyectiva introducida por Julius Plücker. Lie concibió una idea muy original: debería haber para las ecuaciones diferenciales algo análogo a la teoría de Galois de las ecuaciones algebraicas.
Una ecuación algebraica puede resolverse por radicales sólo si tiene el tipo correcto de simetrías; es decir, si tiene un grupo de Galois soluble.
Análogamente, sugería Lie, una ecuación diferencial puede resolverse por métodos clásicos sólo cuando la ecuación queda inalterada por una familia continua de transformaciones. Lie y Klein trabajaron en variaciones sobre esta idea durante 1869-1870; este trabajo culminó en 1872 en la caracterización que hizo Klein de la geometría como los invariantes de un grupo, establecida en su programa de Erlangen.
Este programa surgió de una nueva manera de pensar acerca de la geometría euclidiana, en términos de sus simetrías. Jordán ya había señalado que las simetrías del plano euclidiano son movimientos rígidos de varios tipos: traslaciones, que deslizan el plano en alguna dirección; rotaciones, que lo giran alrededor de un punto fijo; reflexiones, que le dan la vuelta respecto a una recta fija; y, lo que es menos obvio, reflexiones con deslizamiento, que lo reflejan y luego lo trasladan en una dirección paralela a la línea especular.
Estas transformaciones forman un grupo, el grupo euclidiano, y son rígidas en el sentido de que no cambian las distancias. Por consiguiente, tampoco cambian ángulos.
Así, Klein comprendió que estos conceptos son los «invariantes» del grupo euclidiano: las cantidades que no cambian cuando se aplica una transformación del grupo.
De hecho, si se «conoce» el grupo euclidiano se pueden deducir sus invariantes, y a partir de éstos se obtiene la geometría euclidiana.
Ahora longitudes y ángulos son los conceptos básicos de la geometría de Euclides.
Lo mismo sucede con otros tipos de geometría. La geometría elíptica es el estudio de los invariantes del grupo de movimientos rígidos en un espacio con curvatura positiva, la geometría hiperbólica es el estudio de los invariantes del grupo de movimientos rígidos en un espacio con curvatura negativa, la geometría proyectiva es el estudio de los invariantes del grupo de proyecciones, y así sucesivamente.
Félix Klein
1849-1925Klein nació en Dusseldorf en una familia de clase alta: su padre era secretario del jefe de gobierno prusiano. Fue a la Universidad de Bonn con intención de hacerse físico, pero se convirtió en ayudante de laboratorio de Julius Plücker.
Se suponía que Plücker estaba trabajando en matemáticas y física experimental, pero sus intereses se habían centrado en la geometría, y Klein cayó bajo su influencia.
La tesis de Klein en 1868 era sobre geometría aplicada a la mecánica. En 1870 estaba trabajando con Lie en teoría de grupos y geometría diferencial.
En 1871 descubrió que la geometría no euclidiana es la geometría de una superficie proyectiva con una sección cónica distinguida. Este hecho demostraba, de forma muy obvia y directa, que la geometría no euclidiana es lógicamente consistente si lo es la geometría euclidiana. Esto acabó prácticamente con la controversia sobre el estatus de la geometría no euclidiana.
En 1872 Klein se convirtió en profesor en Erlangen. y en su «Programa de Erlangen» de 1872 unificó casi todos los tipos de geometría conocidos, y clarificó los vínculos entre ellos, considerando la geometría como los invariantes de un grupo de transformaciones. Con ello la geometría se convertía en una rama de la teoría de grupos. Escribió este articulo para su lección inaugural, pero no lo presentó en realidad en tal ocasión. Al encontrar Erlangen poco propicia, se trasladó a Münich en 1875. Se casó con Anne Hegel, nieta del famoso filósofo. Cinco años más tarde fue a Leipzig, donde prosperó matemáticamente.
Klein creía que su mejor trabajo era en teoría de funciones complejas, donde hizo profundos estudios de funciones invariantes bajo varios grupos de transformaciones del plano complejo. En particular, desarrolló la teoría del grupo simple de orden 168 en este contexto. Entró en rivalidad con Poincaré para resolver el «problema de uniformización» para funciones complejas, pero su salud se resintió probablemente debido al tremendo esfuerzo implicado.
En 1886 fue nombrado profesor en la Universidad de Gotinga, y se centró en la administración, formando una de las mejores escuelas de matemáticas del mundo. Permaneció allí hasta su retiro en 1913.
Del mismo modo que las coordenadas relacionan el álgebra con la geometría, los invariantes relacionan la teoría de grupos con la geometría. Cada geometría define un grupo correspondiente, el grupo de todas las transformaciones que conservan los conceptos geométricos relevantes. Recíprocamente, cada grupo de transformaciones define una geometría correspondiente, la de los invariantes.
Klein utilizó esta correspondencia para demostrar que ciertas geometrías eran esencialmente iguales a otras, porque sus grupos eran idénticos excepto en su interpretación. El mensaje más profundo es que cualquier geometría está definida por sus simetrías. Hay una excepción: la geometría de superficies de Riemann, cuya curvatura puede cambiar de un punto a otro. Esta no encaja en el programa de Klein.
§. Los grupos de Lie
La investigación conjunta de Lie y Klein llevó a Lie a introducir una de las ideas más importantes de la matemática moderna, la de un grupo de transformaciones continuo, ahora conocido como un grupo de Lie.
Es un concepto que ha revolucionado las matemáticas y la física, porque los grupos de Lie recogen muchas de las simetrías más importantes del universo físico y la simetría es un poderoso principio organizador; tanto para la filosofía subyacente a nuestra representación matemática de la naturaleza como para los cálculos técnicos.
Sophus Lie creó la teoría de los grupos de Lie en una oleada de actividad que empezó en el otoño de 1873. El concepto de grupo de Lie ha evolucionado considerablemente desde el trabajo inicial de Lie. En términos modernos, un grupo de Lie es una estructura con propiedades tanto algebraicas como topológicas, y ambas están relacionadas. En concreto, es un grupo (un conjunto con una operación de composición que satisface varias identidades algebraicas, muy en particular la ley asociativa) y una variedad topológica (un espacio que localmente se parece al espacio euclidiano de una dimensión dada pero que puede estar curvado o distorsionado de alguna otra manera a nivel global), tal que la ley de composición es continua (cambios pequeños en los elementos que se componen producen cambios pequeños en el resultado).
“...la motivación original de Lie no es la aplicación más importante.”
El concepto de Lie era más concreto: un grupo de transformaciones continuas en varias variables. El se vio llevado a estudiar tales grupos de transformaciones mientras buscaba una teoría de la solubilidad o insolubilidad de ecuaciones diferenciales análoga a la de Evariste Galois para ecuaciones algebraicas, pero hoy aparecen en una enorme variedad de contextos matemáticos, y la motivación original de Lie no es la aplicación más importante.
Quizá el ejemplo más simple de un grupo de Lie es el conjunto de todas las rotaciones de un círculo. Cada rotación está unívocamente determinada por un ángulo entre 0º y 360º. El conjunto es un grupo porque la composición de dos rotaciones es una rotación --de la suma de los dos ángulos correspondientes a las primeras-. Es una variedad de dimensión uno, porque hay una correspondencia uno-a-uno entre ángulos y puntos en un círculo; los arcos de círculo pequeños son simplemente segmentos de recta ligeramente curvados, y una recta es un espacio euclidiano de dimensión uno. Finalmente, la ley de composición es continua porque cambios pequeños en los ángulos sumados producen cambios pequeños en su suma.
Un ejemplo más difícil es el grupo de todas las rotaciones del espacio tridimensional que conservan un origen dado. Cada rotación está determinada por un eje -una recta que pasa por el origen en una dirección arbitraria- y un ángulo de rotación alrededor de dicho eje. Se necesitan dos variables para determinar un eje (por ejemplo, la longitud y latitud del punto en que el eje corta a una esfera de referencia centrada en el origen) y una tercera para determinar el ángulo de rotación; por consiguiente, este grupo tiene dimensión tres. A diferencia del grupo de rotaciones de un círculo, el grupo de rotaciones del espacio es no conmutativo; el resultado de componer dos transformaciones depende del orden en que se realizan.
En 1873, después de una breve dedicación a las EDP, Lie volvió a los grupos de transformaciones e investigó las propiedades de las transformaciones «infinitesimales». Demostró que las transformaciones infinitesimales derivadas de un grupo continuo no son cerradas bajo composición, pero sí son cerradas bajo una nueva operación conocida como el paréntesis, escrita [x,y].
En notación matricial esto es el «conmutador» xy-yx. La estructura algebraica resultante se conoce como un álgebra de Lie. Hasta aproximadamente 1930 los términos «grupo de Lie» y «álgebra de Lie» no se utilizaban: en su lugar, estos conceptos eran conocidos como «grupo continuo» y «grupo infinitesimal», respectivamente.
Hay fuertes interrelaciones entre la estructura de un grupo de Lie y la de su álgebra de Lie, que Lie expuso en una obra en tres volúmenes, Theorie der Transformationsgruppen (Teoría de los grupos de transformaciones) escrita conjuntamente con Friedrich Engel. Ellos discutían en detalle cuatro «familias clásicas» de grupos, dos de las cuales son los grupos de rotaciones en un espacio n-dimensional para n par y n impar. Los dos casos son bastante diferentes, y ésa es la razón por la que se distinguen. Por ejemplo, en dimensión impar una rotación posee siempre un eje fijo; en dimensión par no lo hace.
§. Killing
El siguiente desarrollo realmente sustancial fue obra de Wilhelm Killing.
“El resultado del trabajo de Killing es notable.”
En 1888 Killing sentó las bases de una teoría de estructuras para álgebras de Lie, y en particular clasificó todas las álgebras de Lie simples, los bloques constituyentes básicos de los que se componen todas las demás álgebras de Lie. Killing partió de la estructura conocida de las álgebras de Lie más directas, las álgebras de Lie lineales especiales sl(n) para n ≥ 2,5 empieza con todas las matrices n × n con coeficientes complejos, y sea AB-BA el paréntesis de Lie de dos matrices A y B. Esta álgebra de Lie no es simple, pero la sub-álgebra sl(n) de todas las matrices cuyos términos diagonales suman cero es simple. Tiene dimensión n2-1.
Lie conocía la estructura de esta álgebra, y demostró que cualquier álgebra de Lie simple tenía un tipo de estructura similar. Es notable que pudiera demostrar algo tan específico partiendo sólo del conocimiento de que el álgebra de Lie es simple. Su método consistía en asociar a cada álgebra de Lie simple una estructura geométrica conocida como un sistema raíz. Utilizó métodos de álgebra lineal para estudiar y clasificar sistemas raíz, y luego dedujo la estructura del álgebra de Lie correspondiente a partir de la del sistema raíz. Así, clasificar las posibles geometrías del sistema raíz equivale a clasificar las álgebras de Lie simples.
El resultado del trabajo de Killing es notable. Él demostró que las álgebras de Lie simples caen en cuatro familias infinitas, ahora llamadas An, Bn, Cn y Dn. Había cinco excepciones: G2, F4, E6, E2 y E8. Killing pensaba en realidad que había seis excepciones, pero dos de ellas resultaron ser la misma álgebra con dos apariencias diferentes. Las dimensiones de las álgebras de Lie excepcionales son 12, 56, 78, 133 y 248. Siguen siendo un poco misteriosas, aunque ahora entendemos bastante bien por qué existen.
§. Grupos de Lie simples
Debido a las estrechas relaciones entre un grupo de Lie y su álgebra, la clasificación de las álgebras de Lie simples llevó también a una clasificación de los grupos de Lie simples. En particular, las cuatro familias An, Bn, Cn y Dn son las álgebras de Lie de las cuatro familias clásicas de grupos de transformaciones. Éstos son, respectivamente, los grupos de todas las transformaciones lineales en el espacio n + 1 -dimensional, el grupo de rotaciones en un espacio 2n + 1 -dimensional, el grupo simpléctico en 2n dimensiones, que es importante en mecánica clásica y cuántica y en óptica, y el grupo de rotaciones en el espacio 2n-dimensional. Más tarde se añadieron algunos toques finales a esta historia: en particular la introducción por Harold Scott MacDonald Coxeter y Eugene (Evgenii) Dynkin de una aproximación gráfica al análisis combinatorio de sistemas raíz, ahora conocida como diagramas de Coxeter o diagramas de Dynkin.
Los grupos de Lie son importantes en las matemáticas modernas por muchas razones. En mecánica, por ejemplo, muchos sistemas tienen simetrías y dichas simetrías hacen posible encontrar soluciones de las ecuaciones dinámicas. Las simetrías forman generalmente un grupo de Lie. En física matemática, el estudio de las partículas elementales se basa fuertemente en el aparato de los grupos de Lie, una vez más debido a ciertas propiedades de simetría. El grupo excepcional de Killing E8 desempeña un papel importante en teoría de supercuerdas, una importante aproximación actual a la unificación de la mecánica cuántica y la relatividad general. El descubrimiento épico de Simon Donaldson en 1983 de que el espacio euclidiano tetradimensional posee estructuras diferenciables no estándar se basa, fundamentalmente, en una característica inusual del grupo de Lie de todas las rotaciones en el espacio tetradimensional. La teoría de los grupos de Lie es vital para el conjunto de las matemáticas modernas.
§. Grupos abstractos
En el programa de Erlangen de Klein es esencial que los grupos en cuestión consistan en transformaciones; es decir, los elementos del grupo «actúan sobre» un espacio. Buena parte del trabajo anterior sobre grupos suponía esta estructura. Pero la investigación posterior requería un elemento de abstracción extra: retener la propiedad de grupo pero desechar el espacio. Un grupo consistía en entidades matemáticas que podían combinarse para dar entidades similares, pero dichas entidades no tenían por qué ser transformaciones.
Los números son un ejemplo. Dos números (enteros, racionales, reales, complejos) pueden ser sumados, y el resultado es un número del mismo tipo. Los números forman un grupo bajo la operación de suma, pero los números no son transformaciones. Por ello, incluso si el papel de los grupos como transformaciones había unificado la geometría, la hipótesis de un espacio subyacente tenía que ser desechada para unificar la teoría de grupos.
Entre los primeros en acercarse a dar este paso estaba Arthur Cayley, en tres artículos de 1849 y 1854. En ellos Cayley decía que un grupo comprende un conjunto de operadores, 1, a, b, c y así sucesivamente. El «compuesto» ab de dos operadores cualesquiera debía ser otro operador; el operador especial 1 satisface 1a = a y a1 = a para todos los operadores a; finalmente, la ley asociativa (ab)c = a (be) debía ser válida. Pero sus operadores seguían operando sobre algo (un conjunto de variables). Además, él había omitido una propiedad crucial: que todo a debe tener un inverso a' tal que a'a = aa' = 1. Así, Cayley estuvo cerca de alcanzar el premio, pero falló por poco.
“Gauss inició el proceso cuando introdujo lo que ahora llamamos enteros Gaussianos.”
En 1858 Richard Dedekind permitió que los elementos del grupo fueran entidades arbitrarias, no sólo transformaciones u operadores, pero incluyó la ley conmutativa ab = ba en su definición. Su idea estaba bien para lo que el pretendía, la teoría de números, pero excluía a la mayoría de los grupos interesantes en la teoría de Galois, por no hablar del mundo matemático más general. El concepto moderno de un grupo abstracto fue introducido por Walther van Dyck en 1882-1883. El incluía la existencia de un inverso, pero rechazaba la necesidad de la ley conmutativa. Tratamientos puramente axiomáticos de los grupos fueron proporcionados poco después, por Edward Huntington y Eliakin Moore en 1902, y por Leonard Dickson en 1905.
Una vez separada la estructura abstracta de los grupos de cualquier interpretación específica, la disciplina se desarrolló rápidamente. La investigación inicial consistía básicamente en «coleccionar mariposas»: la gente estudiaba ejemplos individuales de grupos, o tipos especiales, buscando pautas comunes. Pronto aparecieron los conceptos y técnicas principales, y la disciplina floreció.
§. Teoría de números
Otra fuente importante de nuevos conceptos algebraicos fue la teoría de números. Gauss inició el proceso cuando introdujo lo que ahora llamamos enteros gaussianos. Estos son números complejos a + bi, donde a y b son enteros. Sumas y productos de tales números tienen también la misma forma. Gauss descubrió que el concepto de un número primo se generaliza a los enteros gaussianos. Un entero gaussiano es primo si no puede expresarse como un producto de otros enteros gaussianos de una manera no trivial. La factorización prima para enteros gaussianos es única. Algunos primos ordinarios, tales como 3 y 7, siguen siendo primos cuando los consideramos como enteros gaussianos, pero otros no: por ejemplo 5 = (2 + i) (2 - i). Este hecho está íntimamente relacionado con el teorema de Fermat sobre números primos y sumas de dos cuadrados, y los enteros gaussianos ilustran dicho teorema y sus afines.
Si dividimos un entero gaussiano por otro, el resultado no tiene por qué ser un entero gaussiano, pero está cerca: es de la forma a + bi, donde a y b son racionales. Estos son los números gaussianos. Con más generalidad, los teóricos de números descubrieron que algo similar es válido si tomamos cualquier polinomio p(x) con coeficientes enteros y luego consideramos todas las combinaciones lineales a1x1 +...+ anxn de sus soluciones x1... xn. Tomando a1an racionales, obtenemos un sistema de números complejos que es cerrado bajo suma, resta, multiplicación y división; lo que significa que cuando se aplican estas operaciones a un número semejante, el resultado es un número del mismo tipo. Este sistema constituye un campo de números algebraico. Si en su lugar exigimos que a1... an sean enteros, el sistema es cerrado bajo suma, resta y multiplicación, pero no bajo división: es un anillo de números algebraico.
“En 1847 Gabriel Lame afirmó que tenía una demostración para todas las potencias, pero Eduard Kummer señaló un error”
La aplicación más ambiciosa de estos nuevos sistemas de números fue el Último Teorema de Fermat: el enunciado de que «la ecuación de Fermat» xn + yn = zn no tiene soluciones enteras cuando la potencia n es 3 o más. Nadie pudo reconstruir la supuesta «notable demostración» de Fermat, y parecía cada vez más dudoso que él hubiese poseído una. Pese a todo se hicieron algunos progresos. Fermat encontró demostraciones para cubos y potencias cuartas, Peter Lejeune-Dirichlet trabajó con potencias quintas en 1828 y Henri Lebesgue encontró una demostración para las potencias séptimas en 1840.
En 1847 Gabriel Lamé afirmó que tenía una demostración para todas las potencias, pero Eduard Kummer señaló un error. Lamé había supuesto sin demostración que la unicidad de la factorización prima es válida para los números algebraicos, pero esto es falso para algunos (de hecho la mayoría) campos de números algebraicos.
Kummer demostró que la unicidad falla para los campos de números algebraicos que aparecen en el estudio del Último Teorema de Fermat para potencias 23-ésimas. Pero Kummer no abandonó fácilmente, y encontró una manera de evitar este obstáculo inventando un nuevo artilugio matemático, la teoría de los «números ideales». En 1847 él había demostrado el Último Teorema de Fermat para todas las potencias hasta 100, excepto para 37, 59 y 67.
Emmy Amalie Noether
1882-1925Emmy Amalie Noether del matemático Max Noether y de Ida Kaufman, ambos de origen judío. En 1900 se cualificó para enseñar idiomas pero en su lugar decidió que su futuro estaba en las matemáticas. En esa época las universidades alemanas permitían que las mujeres siguieran cursos de forma oficiosa si el profesor daba permiso, y ella lo hizo así de 1900 a 1902. Luego fue a Gotinga, donde asistió a las clases de Hilbert, Klein y Minkowski en 1903 y 1904.
Obtuvo un doctorado en 1907 con el teórico de invariantes Paul Goordan. Su tesis calculaba un sistema de invariantes muy complicado. Para los hombres, el paso siguiente sería la Habilitación, pero esto no estaba permitido a las mujeres. Ella se quedó en casa en Erlangen, ayudando a su padre discapacitado, pero continuó su investigación, y su reputación creció rápidamente.
En 1915 fue invitada de nuevo a Gotinga por Klein y Hilbert, quienes lucharon por cambiar las reglas para permitir que ella fuera miembro del claustro. Finalmente lo consiguieron en 1919.
Poco después de su llegada, ella demostró un teorema fundamental, a veces llamado Teorema de Noether, que relaciona las simetrías de un sistema físico con leyes de conservación. Su trabajo fue utilizado por Einstein para formular partes de la relatividad general. En 1921 escribió un artículo sobre teoría de anillos e ideales, donde adoptaba una visión axiomática abstracta. Este trabajo formó una parte importante del clásico texto Álgebra moderna de Bartel Leendert van der Waerden.
Cuando Alemania cayó bajo el régimen nazi, ella fue despedida por ser judía, y dejó Alemania para ocupar un puesto en Estados Unidos. Van der Waerden decía que para ella, «las relaciones entre números, funciones y operadores se hacían transparentes, susceptibles de generalización y productivas sólo después de que habían sido ... reducidas a relaciones conceptuales generales».
Desarrollando maquinaria extra, Kummer y Dimitri Mirimanoff demostraron también dichos casos en 1857. Para los años ochenta del siglo xx métodos similares habían demostrado todos los casos hasta la potencia 150.000, pero el método estaba perdiendo fuerza.
§. Anillos, campos y álgebras
La noción de Kummer de un número ideal era engorrosa, y Dedekind la reformuló en términos de «ideales», subsistemas especiales de enteros algebraicos. En las manos de la escuela de Hilbert en Gotinga, y en particular de Emmy Noether, toda el área fue colocada sobre una base axiomática.
Andrew Wiles
1953Andrew Wiles nació en 1953 en Cambridge, Inglaterra. A los 10 años leyó acerca del Último Teorema de Fermat y decidió hacerse matemático y demostrarlo. Para cuando obtuvo su doctorado había abandonado esta idea, porque el teorema parecía intratable, y trabajó en teoría de números de «curvas elípticas», un área en apariencia diferente. Se trasladó a los Estados Unidos y fue profesor en Princeton.
En los años ochenta del siglo XX se estaba haciendo claro que podría haber un vínculo inesperado entre el Último Teorema de Fermat y una cuestión profunda y difícil sobre curvas elípticas. Gerhard Frey hizo explícito este vínculo por medio de la denominada conjetura de Taniyama-Shimura. Cuando Wiles supo de la idea de Frey dejó cualquier otro trabajo para concentrarse en el Último Teorema de Fermat, y al cabo de siete años de investigación en solitario se convenció de que había encontrado una demostración, basada en un caso concreto de la conjetura de Taniyama-Shimura. Esta demostración resultó tener una laguna, pero Wiles y Richard Taylor llenaron la laguna y una demostración completa fue publicada en 1995.
Otros matemáticos pronto extendieron las ideas para demostrar la conjetura de Taniyama-Shimura completa, perfeccionando los nuevos métodos. Wiles recibió muchos reconocimientos por su demostración, incluido el Premio Wolf. En 1998, y dado que superaba ligeramente la edad para una medalla Fields, tradicionalmente limitada a personas de menos de 40 años, le fue concedida una placa de plata especial por la Unión Matemática Internacional. Fue nombrado Caballero de la Orden del Imperio Británico en 2000.
Mediante listas de axiomas adecuadas se definieron, junto con los grupos, otros tres tipos de sistemas algebraicos: anillos, campos y álgebras.
En un anillo, las operaciones de suma, resta y multiplicación están definidas, y satisfacen todas las leyes habituales del álgebra excepto la ley conmutativa de la multiplicación. Si esta ley también es válida, tenemos un anillo conmutativo.
En un campo, las operaciones de suma, resta, multiplicación y división están definidas, y satisfacen todas las leyes habituales del álgebra incluida la ley conmutativa de la multiplicación. Si esta ley falla, tenemos un anillo de división.
Un álgebra es como un anillo, pero sus elementos también pueden multiplicarse por varias constantes, los números reales, los números complejos o -en el escenario más general- un campo. Las leyes de la suma son las habituales, pero la multiplicación puede satisfacer una variedad de axiomas diferentes. Si es asociativa tenemos un álgebra asociativa. Si satisface algunas leyes relacionadas con el conmutador xy - yx, es un álgebra de Lie.
Para qué les servía el álgebra abstractaEn su libro de 1854, Las leyes del pensamiento, George Boole demostró que el álgebra puede aplicarse a la lógica, inventando lo que ahora se conoce como álgebra booleana.
Aquí no podemos hacer otra cosa que transmitir un sabor de las ideas de Boole. Los operadores lógicos más importantes son no, y y o. Si un enunciado S es verdadero, entonces no-S es falso, y a la inversa. S y T es verdadero si y sólo si S y T son ambos verdaderos. S o T es verdadero con tal de que al menos uno de los dos, S o T, sea verdadero. Boole advirtió que si reescribimos T como 1 y S como 0, entonces el álgebra de estos operadores lógicos es muy similar al álgebra ordinaria, con tal de que pensemos en 0 y 1 como enteros módulo 2, de modo que 1 + 1 = 0 y -S es lo mismo que S. Por lo tanto, no-S es 1 + S, S y T es ST, y S o T es S + T + ST. La suma S + T corresponde al o excluyente (escrito xor por los científicos de la computación).
S xor T es verdadero si T es verdadero o S es verdadero, pero no ambos. Boole descubrió que su curiosa «álgebra de la lógica» es completamente autoconsistente si se tienen en cuenta estas reglas algo extrañas y se utilizan de forma sistemática. Éste fue uno de los primeros pasos hacia una teoría formal de la lógica matemática.
Hay docenas, quizá centenares de tipos diferentes de estructuras algebraicas, cada una de ellas con su propia lista de axiomas. Algunas han sido inventadas precisamente para explorar las consecuencias de axiomas interesantes, pero la mayoría surgieron porque eran necesarias en algún problema específico.
§. Grupos finitos simples
El punto culminante de la investigación en el siglo xx de grupos finitos fue la clasificación satisfactoria de todos los grupos finitos simples. Esto consiguió para los grupos finitos lo que Killing había conseguido para los grupos de Lie y sus álgebras de Lie. Es decir, llevó a una descripción completa de todos los posibles bloques constituyentes básicos para los grupos finitos, los grupos «simples». Si los grupos son moléculas, los grupos simples son sus átomos constituyentes.
La clasificación de Killing de los grupos de Lie simples demostró que éstos deben pertenecer a una de cuatro familias infinitas An, Bn, Cn y Dn, con exactamente cinco excepciones G2, F4, E6, E7yE8. La clasificación final de todos los grupos finitos simples fue obra de muchos matemáticos, demasiados para ser mencionados uno por uno, pero el programa general para resolver este problema se debía a Daniel Gorenstein. La respuesta, publicada en 1888-1890, tiene una curiosa similaridad: hay una lista de familias infinitas y una lista de excepciones. Pero ahora hay muchas más familias, y las excepciones son 26.
Las familias comprenden los grupos alternantes (conocidos para Galois) y un montón de grupos «tipo Lie», que son como los grupos de Lie simples pero sobre varios campos finitos y no sobre los números complejos. También hay algunas curiosas variaciones sobre este tema. Las excepciones son 26 grupos individuales, con indicios de algunas pautas comunes pero ninguna estructura unificada. La primera demostración de que la clasificación está completa llegó gracias al trabajo combinado de cientos de matemáticos, y su longitud total ocupaba unas 10.000 páginas. Además, algunas partes cruciales de la demostración no fueron publicadas. Trabajo reciente por parte de quienes siguen en esta área de investigación ha permitido recalcular la clasificación de una manera más directa, una aproximación que se hace posible una vez que se sabe la respuesta. Los resultados están apareciendo como una serie de libros de texto, que totalizan unas 2.000 páginas.
El más misterioso de los grupos simples excepcionales, y el más grande, es el monstruo. Su orden es
246 × 320 × 59 × 76 × 112 × 133 × 17 × 19 × 23 × 29 × 31 × 41 × 47 × 59 × 71
que es igual a
808017424794512875886459904961710757005754368000000000
aproximadamente 8×1053. Su existencia fue conjeturada en 1973 por Bernd Fischer y Robert Griess. En 1980 Griess demostró que existía, y dio una construcción algebraica como el grupo de simetría de un álgebra 196.884-dimensional. El monstruo parece tener algunos vínculos inesperados con la teoría de números y el análisis complejo, enunciados por John Conway como la «conjetura del brillo de luna monstruoso». Esta conjetura fue demostrada por Richard Borcherds en 1992, quien fue premiado con una medalla Fields -el premio más prestigioso en matemáticas.
§. El Último Teorema de Fermat
Las aplicaciones de los campos de números algebraicos a la teoría de números se desarrollaron en la segunda mitad del siglo xx, y tomaron contacto con muchas otras áreas de las matemáticas, incluidas la teoría de Galois y la topología algebraica. La culminación de este trabajo fue una demostración del Último Teorema de Fermat, unos 350 años después de que fuera enunciado por primera vez.
La idea realmente decisiva procedía de una bella área que yace en el corazón del trabajo moderno sobre ecuaciones diofánticas: la teoría de las «curvas elípticas». Estas son ecuaciones en las que un cuadrado perfecto es igual a un polinomio cúbico, y representan el área de las ecuaciones diofánticas que los matemáticos entienden muy bien. Sin embargo, la disciplina tiene sus propios grandes problemas no resueltos. El mayor de todos es la conjetura deTaniyama-Weil, nombre debido a Yutaka Taniyama y André Weil. Esta dice que toda curva elíptica puede representarse en términos de funciones modulares, que son generalizaciones de funciones trigonométricas estudiadas en particular por Klein.
A principios de la década de los ochenta del siglo XX Gerhard Frey encontró un vínculo entre el Ultimo Teorema de Fermat y las curvas elípticas. Supongamos que existe una solución a la ecuación de Fermat; entonces se puede construir una curva elíptica con propiedades muy inusuales -tan inusuales que la existencia de la curva parece altamente improbable-. En 1986 Keneth Ribet precisó esta idea al demostrar que si la conjetura de Taniyama-Weil es verdadera, entonces la curva de Frey no puede existir. Por consiguiente, tampoco puede existir la presunta solución de la ecuación de Fermat, lo que demostraría el Último Teorema de Fermat. La aproximación dependía de la conjetura de Taniyama-Weil, pero demostraba que el Último Teorema de Fermat no es simplemente una curiosidad histórica aislada. Más bien yace en el corazón de la moderna teoría de números.
“Andrew Wiles había soñado de niño con demostrar el Ultimo Teorema de Fermat.”
Andrew Wiles había soñado de niño con demostrar el Último Teorema de Fermat, pero cuando se convirtió en un profesional decidió que era tan sólo un problema aislado; no resuelto, pero no realmente importante.
Para qué nos sirve el álgebra abstractaLos campos de Galois forman la base de un sistema de codificación que es ampliamente utilizado en varias aplicaciones comerciales, especialmente CD y DVD.
Cada vez que oímos música o miramos un video, estamos utilizando álgebra abstracta.
Estos métodos se conocen como códigos de Reed- Solomon, por los nombres de Irving Reed y Gustave Solomon, quienes los introdujeron en 1960. Son códigos de corrección de errores basados en un polinomio, con coeficientes en un campo finito, construido a partir de los datos a codificar, tales como señales musicales o de video. Es sabido que un polinomio de grado n está unívocamente determinado por sus valores en n puntos distintos. La idea consiste en calcular el polinomio en más de n puntos. Si no hay errores, cualquier subconjunto de n datos reconstruirá el mismo polinomio. Si los hay, y siempre que el número de errores no sea demasiado grande, sigue siendo posible deducir el polinomio.
En la práctica los datos se representan como bloques codificados, con 2m-1 símbolos de m-bits por bloque, donde un bit es un dígito binario 0 ó 1. Una elección bastante común es m = 8, porque muchos de los ordenadores más antiguos trabajan en «bytes», secuencias de ocho bits. Aquí el número de símbolos en un bloque es 255. Un código de Reed-Solomon común pone 223 bytes de datos codificados en cada bloque de 255 bytes, y utiliza los 32 bytes restantes para «símbolos de paridad» que establecen si ciertas combinaciones de dígitos en los datos deberían ser pares o impares. Este código puede corregir hasta 16 errores por bloque.
El trabajo de Ribet le hizo cambiar de opinión. En 1993 él anunció una demostración de la conjetura de Taniyama-Weil para una clase especial de curvas elípticas, suficientemente general para demostrar el Último Teorema de Fermat. Pero cuando el artículo fue enviado para publicación, apareció una seria laguna. Wiles estaba a punto de abandonar cuando «de repente, de forma totalmente inesperada, tuve esta increíble revelación... era indescriptiblemente bella, era tan simple y elegante que no podía creerlo». Con la ayuda de Richard Taylor, él revisó la demostración y cubrió la laguna. Su artículo fue publicado en 1995.
Podemos estar seguros de que cualesquiera que fueran las ideas que Fermat tenía en mente cuando afirmó poseer una demostración de su Último Teorema, éstas debían ser muy diferentes de los métodos utilizados por Wiles.
¿Realmente tenía Fermat una demostración simple e ingeniosa, o se estaba engañando? Es un enigma que, a diferencia de su Último Teorema, nunca podrá resolverse.
§. La matemática abstracta
El paso hacia una visión más abstracta de las matemáticas fue una consecuencia natural de la creciente diversidad de su material. Cuando las matemáticas trataban fundamentalmente de números, los símbolos del álgebra eran simplemente lugares donde colocar números. Pero a medida que crecían las matemáticas, los símbolos empezaron a cobrar vida propia. El significado de los símbolos se hizo menos importante que las reglas de acuerdo con las que podían manipularse dichos símbolos. Ni siquiera las reglas eran sagradas: las leyes tradicionales de la aritmética, tales como la ley conmutativa, no siempre eran adecuadas en nuevos contextos.
No fue sólo el álgebra la que se hizo abstracta. El análisis y la geometría se centraron también en cuestiones más generales, por razones similares.
“No fue sólo el álgebra la que se hizo abstracta.”
El cambio principal en el punto de vista tuvo lugar desde mediados del siglo XIX a mediados del XX. Después de ello se inició un periodo de consolidación, a medida que los matemáticos trataban de encontrar un compromiso entre las necesidades de formalismo abstracto, por un lado, y aplicación a la ciencia, por otro. Abstracción y generalidad van de la mano, aunque la abstracción también puede oscurecer el significado de las matemáticas. Pero ahora ya no se trata de si la abstracción es útil o necesaria: los métodos abstractos han mostrado su valor al hacer posible resolver muchos problemas ancestrales tales como el Último Teorema de Fermat. Y lo que ayer parecía poco más que un juego formal, resulta ser mañana una herramienta vital para la ciencia o el comercio.
Capítulo 15
Geometría de la lámina elástica
Lo cualitativo vence a lo cuantitativo
Todos los ingredientes principales de la geometría de Elídales -rectas, ángulos, círculos, cuadrados y demás- están relacionados con la medida. Los segmentos de recta tienen longitudes, los ángulos tienen un tamaño definido y un ángulo de 90º difiere esencialmente de uno de 89º o 91º, los círculos están definidos en términos de sus radios, los cuadrados tienen lados de una longitud dada. El ingrediente oculto que conforma toda la obra de Elididos es la longitud, una magnitud «métrica» que no cambia por movimientos rígidos y que define el concepto euclidiano equivalente al movimiento, la congruencia.
§. Medida
Cuando los matemáticos tropezaron por primera vez con otros tipos de geometría, también eran geometrías métricas. En geometría no euclidiana, longitudes y ángulos están bien definidos; sencillamente tienen propiedades diferentes de las longitudes y los ángulos en el plano euclidiano. La llegada de la geometría proyectiva cambió esto: las transformaciones proyectivas pueden cambiar longitudes y pueden cambiar ángulos. La geometría euclidiana y los dos tipos principales de geometrías no euclidianas son rígidas. La geometría proyectiva es más flexible, pero incluso aquí existen invariantes más sutiles, y en la imagen de Klein lo que define una geometría es un grupo de transformaciones y los correspondientes invariantes.
Cuando el siglo XIX se acercaba a su fin, los matemáticos empezaron a desarrollar un tipo de geometría aún más flexible; tan flexible, de hecho, que a menudo es caracterizada como la «geometría de la lámina elástica». Conocida más propiamente como topología, ésta es la geometría de las formas que pueden ser deformadas o distorsionadas de maneras extraordinariamente complicadas. Las rectas pueden curvarse, contraerse o estirarse; los círculos pueden aplastarse de modo que se convierten en triángulos o cuadrados. Todo lo que cuenta aquí es la continuidad.
Sigue habiendo un vestigio de pensamiento métrico: «cerrado» es un concepto métrico. Pero a principios del siglo XX, incluso este vestigio había sido eliminado, y las transformaciones topológicas cobraron vida propia. El estatus de la topología creció rápidamente hasta ocupar el centro de la escena en matemáticas, incluso si de entrada parecía muy extraño y prácticamente libre de contenido. Con transformaciones tan flexibles, ¿qué podía ser invariante? Resultó que la respuesta era «mucho». Pero el tipo de invariante que se empezó a descubrir no se parecía a nada antes considerado en geometría. Conectividad: ¿cuántas piezas tiene este objeto? Agujeros: ¿es un bloque macizo o está atravesado por túneles? Nudos: ¿cómo está entrelazado, y cómo pueden deshacerse los nudos? Para un topólogo, un donut y una taza de café son idénticos; sin embargo, ambos son diferentes de una bola redonda. Un nudo as de guía es diferente de un nudo de rizo, pero demostrarlo requería todo un nuevo tipo de maquinaria, y durante mucho tiempo nadie pudo demostrar que los nudos existían siquiera.
Parece extraordinario que algo tan difuso y extraño pudiera tener alguna importancia. Pero las apariencias engañan. La continuidad es uno de los aspectos básicos del mundo natural, y cualquier estudio profundo de la continuidad lleva a la topología. Incluso hoy utilizamos básicamente la topología de forma indirecta, como una técnica entre muchas. No encontramos nada topológico en nuestra cocina, al menos no de forma obvia. (Sin embargo, podemos encontrar ocasionalmente cosas tales como un lavaplatos caótico, que utiliza la extraña dinámica de dos brazos rotatorios para limpiar platos de forma más eficiente. Y nuestra comprensión del fenómeno del caos descansa en la topología.) Los principales «usuarios» prácticos de la topología son los teóricos de campos cuánticos; un uso nuevo de la palabra «práctico», quizá, pero un área importante de la física. Otra aplicación de las ideas topológicas se da en biología molecular, donde describir y analizar las torsiones y vueltas de la molécula de ADN requiere conceptos topológicos.
Entre bastidores, la topología está presente en todas las matemáticas de la corriente principal y permite el desarrollo de otras técnicas con usos prácticos más obvios. Es un estudio riguroso de aspectos geométricos cualitativos, frente a aspectos cuantitativos como longitudes. Por esto es por lo que los matemáticos dan gran importancia a la topología, mientras que el resto del mundo apenas ha oído hablar de ella.
§. Los poliedros y los puentes de Königsberg.
Aunque la topología sólo empezó a «despegar» alrededor de 1900, hizo apariciones ocasionales en las matemáticas anteriores. Dos elementos en la «prehistoria» de la topología fueron introducidos por Euler: su fórmula para los poliedros y su solución al rompecabezas de los puentes de Königsberg.
En 1639 Descartes había advertido una curiosa característica de la numerología de los sólidos regulares. Consideremos, por ejemplo, un cubo. Este tiene 6 caras, 12 aristas y 8 vértices. Sumamos 6 y 8 y obtenemos 14, que supera en 2 a 12. ¿Qué pasa con el dodecaedro? Ahora tenemos 12 caras, 30 aristas y 20 vértices. Y 12 + 20 = 32, que supera en 2 a 30. Lo mismo sucede con el tetraedro y el icosaedro. De hecho, la misma relación parecía funcionar para casi cualquier poliedro. Si un sólido tiene C caras, A aristas y V vértices, entonces C + V = A + 2, que podemos reescribir como
C - A + V = 2.
Descartes no publicó su descubrimiento, pero lo dejó escrito y su manuscrito fue leído por Leibniz en 1675.
Euler fue el primero en publicar esta relación, en 1750. Luego dio una demostración en 1751. Estaba interesado en la relación porque había estado tratando de clasificar poliedros.
Poliedro con un agujero
Cualquier fenómeno general como éste tenía que ser tenido en cuenta al realizar dicha clasificación.
Demostración de Cauchy de la fórmula de Descartes-EulerEliminamos una cara y extendemos la superficie del sólido en un plano. Esto reduce C en 1-, de modo que tenemos que demostrar que la configuración plana resultante de caras, líneas y puntos tiene C - A + V = 1. Para conseguirlo, convertimos primero todas las caras en triángulos dibujando diagonales. Cada nueva diagonal deja V inalterado, pero aumenta A y C en 1, de modo que C - A + V sigue valiendo lo mismo que antes. Ahora empezamos a borrar aristas, partiendo del exterior. Cada borrado reduce C y A en 1, de modo que C - A + V sigue una vez más sin cambios. Cuando ya no hay más caras que borrar, nos quedamos con un «árbol» de aristas y vértices que no contiene lazos cerrados.
Ejemplo de demostración de CauchyUno a uno, borramos los vértices terminales, junto con la arista que los une. Ahora A y V decrecen en 1, y de nuevo C-A + V queda inalterado. Finalmente este proceso se para al llegar a un vértice solitario. Ahora C = 0, A=0 y V = 1, de modo que C - A + V = 1, como se requería.
¿Es válida la fórmula para todos los poliedros? No del todo. Un poliedro con la forma de un marco de fotos, con secciones cuadradas e ingletes, tiene 16 caras, 32 aristas y 16 vértices, de modo que aquí C + V - A = 0. La razón de la discrepancia resulta ser la presencia de un «agujero». De hecho, si un poliedro tiene g agujeros, entonces
C + V - A = 2 - 2g.
¿Qué es exactamente un agujero? Esta pregunta es más difícil de lo que parece. En primer lugar, estamos hablando de la superficie del poliedro, no de su interior macizo. En la vida real hacemos un agujero en algo taladrando su interior macizo, pero la fórmula anterior no se refiere al interior del poliedro, sino sólo a las caras que constituyen sus superficies, junto con sus aristas y vértices. Todo lo que cuenta yace en la superficie. En segundo lugar, los únicos agujeros que cambian la numerología son los que atraviesan por completo el poliedro: túneles con dos extremos, por así decir, no agujeros como los que cavan los obreros en la carretera. En tercer lugar, tales agujeros no están «en» la superficie, aunque están de algún modo delimitados por ella. Cuando compramos un donut, también compramos su agujero, incluso si en este caso también compramos el interior macizo del donut.
Es más fácil definir lo que significa «sin agujeros». Un poliedro no tiene agujeros si puede ser deformado de forma continua, creando caras y aristas curvas, de modo que se convierta en (la superficie de) una esfera. Para estas superficies, C + V - E es siempre 2. Y también es válida la recíproca: si C + V - E = 2, entonces el poliedro puede deformarse para dar una esfera.
Problema de los puentes de Königsberg
El poliedro del marco de fotos no tiene el aspecto de poder ser deformado para dar una esfera; ¿dónde podría ir el agujero? Para una demostración rigurosa de la imposibilidad no necesitamos buscar más lejos que el hecho de que para este poliedro C + V - E = 0. Esta relación es imposible para superficies que puedan deformarse hasta dar esferas. Por ello, la numerología de los poliedros nos dice propiedades importantes de su geometría, y dichas propiedades pueden ser invariantes topológicos, inalterados bajo deformaciones.
La fórmula de Euler se ve ahora como un indicio significativo de un vínculo útil entre aspectos combinatorios de los poliedros, tales como número de caras, y aspectos topológicos. De hecho, resulta más fácil trabajar hacia atrás. Para descubrir cuántos agujeros tiene una superficie, calculamos C + V - E - 2, lo dividimos por 2 y lo cambiamos de signo:
g = - (C + V - A - 2)/2
Una consecuencia curiosa: ahora podemos definir cuántos agujeros tiene un poliedro sin definir «agujero».
Una ventaja de este procedimiento es que es intrínseco al poliedro.
No es necesario visualizar el poliedro en un espacio tridimensional circundante, que es como nuestros ojos «ven» naturalmente el agujero.
Una hormiga suficientemente inteligente que viviera en la superficie del poliedro podría calcular que tiene un agujero aunque todo lo que pudiera ver fuera la superficie. Este punto de vista intrínseco es natural en topología. Estudia las formas de los objetos en sí mismas, no como parte de algo más.
A primera vista, el problema de los puentes de Königsberg no guarda relación con la combinatoria de los poliedros. La ciudad de Königsberg, entonces en Rusia, estaba situada a ambas orillas del río Pregelarme, en el que había dos islas. Las islas estaban unidas a las orillas, y entre sí, por siete puentes. Y, al parecer, los ciudadanos de Königsberg llevaban mucho tiempo preguntándose si era posible dar un paseo que cruzara cada puente exactamente una vez.
En 1735 Euler resolvió el rompecabezas; mejor dicho, demostró que no tiene solución, y explicó por qué. Hizo dos contribuciones importantes: simplificó el problema hasta reducirlo a su esencia, y luego lo generalizó para tratar todos los rompecabezas del mismo tipo. Señaló que lo que importa no es el tamaño y la forma de las islas, sino cómo están conectadas las islas, las orillas y los puentes. El problema entero puede reducirse a un simple diagrama de puntos (vértices) unidos por líneas (aristas), que aquí se muestran superpuestas en un mapa.
Para formar este diagrama colocamos un vértice en cada masa de tierra: orilla norte, orilla sur y las dos islas. Unimos dos vértices por una arista cuando existe un puente que une las correspondientes masas de tierra. Aquí terminamos con cuatro vértices A, B, C, D y siete aristas, una por cada puente.
El rompecabezas es entonces equivalente a uno más simple sobre el diagrama. ¿Es posible encontrar un camino -una secuencia de aristas conectadas- que incluya a cada arista exactamente una vez?
Euler distinguió dos tipos de caminos: un trayecto abierto, que empieza y termina en vértices diferentes, y un trayecto cerrado, que empieza y termina en el mismo vértice. Demostró que para este diagrama particular no existía ninguno de los dos tipos de trayecto.
La cinta de MöbiusLa topología tiene algunas sorpresas. La más conocida es la cinta de Möbius (o banda de Möbius) que puede formarse tomando una larga cinta de papel y uniendo los extremos tras darles medio giro. Sin este giro, obtenemos un cilindro. La diferencia entre estas dos superficies se hace patente si tratamos de pintarlas. Podemos pintar de rojo la superficie exterior de un cilindro y de azul la interior. Pero si empezamos a pintar una cinta de Möbius de rojo por un lado, y continuamos hasta que ha sido cubierta toda la parte de la superficie que está conectada con la región roja, terminamos pos cubrir toda la cinta de pintura roja.
La superficie «interior» está conectada con la «exterior», gracias al medio giro.
Otra diferencia aparece si cortamos la cinta a lo largo de la línea central. El cilindro se divide en dos piezas; la cinta de Möbius sigue estando conectada.
La clave para el rompecabezas es considerar la «valencia» de cada vértice: cuántas aristas se encuentran en dicho vértice. En primer lugar, pensemos en un trayecto cerrado. Aquí, cada arista por la que un trayecto entra en un vértice empalma con otra, la arista siguiente, por la que el trayecto sale de dicho vértice. Si es posible un trayecto cerrado, entonces el número de aristas en un vértice dado debe ser par. En resumen, cada vértice debe tener valencia par. Pero el diagrama tiene tres vértices de valencia 3 y uno de valencia 5: todos números impares. Por lo tanto, no existen trayectos cerrados.
Un criterio similar se aplica a trayectos abiertos, pero ahora habrá exactamente dos vértices de valencia impar: uno al principio del trayecto y otro al final. Puesto que el diagrama de Königsberg tiene cuatro vértices de valencia impar, tampoco hay ningún trayecto abierto.
Euler dio un paso más: demostró que estas condiciones necesarias para la existencia de un trayecto son también suficientes con tal de que el diagrama sea conexo (dos vértices cualesquiera están unidos por un camino). Este hecho general es un poco más complicado de demostrar, y Euler tardó algún tiempo en establecer su demostración. Hoy podemos dar una demostración en unas pocas líneas.
§. Propiedades geométricas de los diagramas
Los dos descubrimientos de Euler parecen pertenecer a áreas de las matemáticas completamente diferentes, pero un examen más detallado revela que tienen elementos en común. Ambos tratan de la combinatoria de diagramas poliédricos. Uno cuenta caras, aristas y vértices; el otro cuenta valencias; uno trata de una relación universal entre tres números, el otro de una relación que debe darse si existe un trayecto. Pero es evidente que tienen un aire similar. Visto con más profundidad, y esto pasó inadvertido durante más de un siglo, ambos son invariantes bajo transformaciones continuas.
Las posiciones de los vértices y aristas no importan: lo que cuenta es cómo se conectan entre sí. Ambos problemas parecerían «el mismo» si los diagramas se dibujaran en una lámina elástica y la lámina fuera distorsionada. La única manera de crear diferencias significativas sería cortar o rasgar la lámina, o pegar unas partes a otras, pero estas operaciones destruyen la continuidad.
El germen de una teoría fue evidente para Gauss, que de cuando en cuando causaba un gran revuelo insistiendo en la necesidad de una teoría de las «propiedades geométricas básicas» de los diagramas. También desarrolló un nuevo invariante topológico, que ahora llamamos el índice o número de enlace, en un trabajo sobre magnetismo. Este número determina cómo se enrolla una curva cerrada alrededor de otra. Gauss dio una fórmula para calcular el número de enlace a partir de expresiones analíticas para las curvas.
Un invariante similar, el número de giros de una curva cerrada con respecto a un punto, estaba implícito en una de sus demostraciones del Teorema Fundamental del Álgebra.
La influencia más importante de Gauss en el desarrollo de la topología llegó a través de uno de sus estudiantes, Johann Listing, y su ayudante Augustus Möbius. Listing estudió con Gauss en 1834, y su obra Vorstudien zur Topologie introdujo la palabra «topología». El propio Listing habría preferido llamar a la disciplina «geometría de posición», pero esta expresión ya había sido propuesta por Karl von Staudt para dar a entender «geometría proyectiva», de modo que Listing tuvo que encontrar otra palabra. Entre otras cosas, Listing buscó generalizaciones de la fórmula de Euler para poliedros.
Fue Möbius quien hizo explícito el papel de las transformaciones continuas. Möbius no era el más productivo de los matemáticos, pero tendía a pensar todo de manera muy detallada y completa. En particular, advirtió que las superficies no siempre tienen dos caras distintas, y puso como ejemplo la famosa cinta de Möbius. Esta superficie fue descubierta independientemente por Möbius y Listing en 1858. Listing lo publicó en Der Census raumlicher Complexe, y Möbius lo hizo en un artículo sobre superficies.
Durante mucho tiempo las ideas de Euler sobre poliedros fueron algo marginal en matemáticas, pero varios matemáticos destacados empezaron a vislumbrar una nueva aproximación a la geometría, a la que llamaron «analysis situs»: el análisis de la posición. Lo que tenían en mente era una teoría cualitativa de la forma, por sí misma, para complementar la más tradicional teoría cuantitativa de longitudes, ángulos, áreas y volúmenes. Esta visión empezó a ganar terreno cuando cuestiones de este tipo emergieron de las investigaciones tradicionales en las matemáticas de la corriente principal. Un paso clave fue el descubrimiento de conexiones entre el análisis complejo y la geometría de superficies, y el innovador fue Riemann.
§. La esfera de Riemann
La forma obvia de pensar en una función compleja f es interpretarla como una aplicación de un plano complejo en otro. La fórmula básica w = f(z) para una función semejante nos dice que tomemos cualquier número complejo z, le apliquemos f y deduzcamos otro número complejo w asociado con z. Desde el punto de vista geométrico, z pertenece al plano complejo y w pertenece a lo que es de hecho una segunda copia del plano complejo, independiente de la primera.
Sin embargo, este punto de vista no resulta ser el más útil, y la razón está en las singularidades. Las funciones complejas suelen tener puntos «interesantes» en los que el comportamiento normal y cómodo se hace terriblemente inadecuado. Por ejemplo, la función f(z) = 1/z se comporta bien para todo z excepto 0. Cuando z = 0, el valor de la función es 1/0, que no tiene sentido como un número complejo ordinario, pero con un esfuerzo de imaginación puede considerarse como «infinito» con el símbolo ∞. En concreto, si z se aproxima mucho a 0, entonces 1/z se hace muy grande. En este sentido, infinito no es un número sino un término que describe un proceso numérico: «hacerse tan grande como uno quiera». Gauss ya había advertido que los infinitos de este tipo crean nuevos tipos de comportamiento en la integración compleja. Ellos importaban.
Riemann encontró útil incluir ∞ entre los números complejos, y encontró una bella forma geométrica de hacerlo. Coloquemos una esfera unidad de modo que esté situada sobre el plano complejo. Ahora asociamos puntos en el plano con puntos en la esfera por «proyección estereográfica».
Es decir, unimos con una recta el punto en el plano con el Polo Norte de la esfera, y vemos dónde dicha recta corta a la esfera.
Esta construcción se denomina la esfera de Riemann. El nuevo «punto en el infinito» es el Polo Norte de la esfera, el único punto que no corresponde a un punto en el plano complejo. Sorprendentemente, esta construcción encaja maravillosamente en los cálculos estándar en análisis complejo, y ahora ecuaciones como 1/0 = ∞, tienen perfecto sentido. Los puntos en los que una función compleja f toma el valor x se llaman polos, y resulta que se puede aprender mucho sobre f si se sabe dónde están sus polos.
La esfera de Riemann solamente no habría atraído la atención hacia las cuestiones topológicas en análisis complejo, pero un segundo tipo de singularidad, llamada un punto rama, hacía esencial la topología. El ejemplo más simple es la función raíz cuadrada compleja f(z) = √z.
La mayoría de los números complejos tienen dos raíces cuadradas distintas, como sucede con los números reales.
La esfera de Riemann y el plano complejo
Estas raíces cuadradas difieren sólo en su signo: una es menos la otra. Por ejemplo, las raíces cuadradas de 2i resultan ser (1 + i) y (-1 - i), igual que las raíces cuadradas reales de 4 son 2 y -2. Sin embargo, hay un número complejo con sólo una raíz cuadrada, a saber 0. ¿Por qué? Porque +0 y -0 son iguales.
Para ver por qué 0 es un punto rama de la función raíz cuadrada imaginemos que partimos del punto 1 del plano complejo y escogemos una de las dos raíces cuadradas. La elección obvia es también 1. Ahora movemos poco a poco el punto a lo largo del círculo unidad, y mientras lo hacemos, nos fijamos en la raíz cuadrada que sigue variando de forma continua. Cuando hemos recorrido la mitad del círculo, hasta - 1, la raíz cuadrada sólo ha recorrido una cuarta parte del camino, hasta +i, desde √-1 = +i ó -i. Continuando hasta completar el camino, volvemos al punto de partida 1. Pero la raíz cuadrada, que se mueve a la mitad de la velocidad, termina en -1. Para que la raíz cuadrada vuelva a su valor inicial el punto tiene que recorrer el círculo dos veces.
Riemann encontró una manera de domesticar este tipo de singularidad, desdoblando la esfera de Riemann en dos capas. Dichas capas están separadas excepto en los puntos 0 y ∞, que es un segundo punto rama. En estos dos puntos las capas se unen; o, pensándolo al revés, se «ramifican» a partir de las capas únicas en 0 y ∞. Cerca de estos puntos especiales la geometría de las capas es como una escalera de caracol, con la característica inusual de que si subimos dos vueltas completas por la escalera, volvemos a donde empezamos. La geometría de esta superficie nos dice mucho sobre la función raíz cuadrada, y la misma idea puede extenderse a otras funciones complejas.
Esfera, Toro y Toro con dos agujeros
La descripción de la superficie es más bien indirecta, y podemos preguntar: «¿qué forma tiene?». Aquí es donde la topología entra en juego. Podemos deformar continuamente la descripción «escalera de caracol» para dar algo más fácil de visualizar. El análisis complejo encuentra que, topológicamente, toda superficie de Riemann es o una esfera, o un toro, o un toro con dos agujeros, o un toro con tres agujeros, etc. El número de agujeros g se conoce como el género de la superficie, y es el mismo g que aparece en la generalización de la fórmula de Euler a las superficies.
§. Superficies orientables
El género resultó ser importante por varias cuestiones profundas en análisis complejo, que a su vez atrajeron la atención sobre la topología de superficies. Resultó entonces que hay una segunda clase de superficies, que difieren de los toros g-agujereados pero están íntimamente relacionadas con ellos.
La diferencia es que los toros g-agujereados son superficies «orientables», lo que intuitivamente significa que tienen dos caras distintas. Heredan esta propiedad del plano complejo, que tiene una «cara superior» y una «cara inferior», porque las escaleras de caracol se unen de una forma que conserva esta distinción. Si en su lugar unimos dos «pisos» de la escalera poniendo un piso del revés, las caras aparentemente diferentes se empalman.
Jules Henri Poincaré
Henri Poincaré nació en Nancy, Francia. Su padre Léon era catedrático de medicina en la Universidad de Nancy, y su madre era Eugénie (nacida Launois). Su primo, Raymond Poincaré, llegó a ser primer ministro francés y fue presidente de la República francesa durante la Primera Guerra Mundial. Henri fue el primero en todas las materias en la escuela y era absolutamente formidable en matemáticas. Tenía una memoria excelente y podía visualizar formas complicadas en tres dimensiones, lo que le ayudaba a compensar una vista tan deficiente que apenas podía ver la pizarra y mucho menos lo que estaba escrito en ella.
Su primer puesto universitario fue en Caen en 1879, pero en 1881 se había asegurado un puesto mucho más prestigioso en la Universidad de París. Allí se convirtió en uno de los matemáticos más destacados de su época. Trabajaba sistemáticamente cuatro horas al día en dos periodos de dos horas, por la mañana y a última hora de la tarde. Pero sus procesos mentales eran menos organizados, y a menudo empezaba a escribir un artículo de investigación antes de que supiera cómo iba a terminar o a dónde llevaría.
Era muy intuitivo, y sus mejores ideas solían llegar cuando estaba pensando en alguna otra cosa.
Trabajó en la mayor parte de las matemáticas de su tiempo, incluidas la teoría de funciones complejas, las ecuaciones diferenciales, la geometría no euclidiana y la topología (que prácticamente fundó). También trabajó en aplicaciones: electricidad, elasticidad, óptica, termodinámica, relatividad, teoría cuántica, mecánica celeste y cosmología.
Ganó un premio importante en un concurso convocado en 1887 por el rey Oscar II de Suecia y Noruega. El tema era el problema de tres cuerpos: el movimiento de tres cuerpos gravitantes. El trabajo que presentó contenía un error importante, que rápidamente corrigió. Como resultado descubrió la posibilidad de lo que ahora llamamos caos: movimiento irregular e impredecible en un sistema gobernado por leyes deterministas. También escribió varios libros de divulgación científica: La ciencia y la hipótesis (1901), El valor de la ciencia (1905) y Ciencia y método (1908).
La posibilidad de este tipo de unión fue resaltada por primera vez por Möbius, cuya cinta de Möbius tiene una sola cara y un solo borde. Klein fue un paso más allá y pegó idealmente un disco circular a lo largo del borde de la cinta de Möbius para eliminar por completo el borde. La superficie resultante, bautizada jocosamente como botella de Klein, tiene una única cara y ningún borde. Si tratamos de dibujarla dentro del espacio tridimensional normal, tiene que atravesarse a sí misma.
La botella de Klein. La aparente auto-intersección es un artificio de su representación en el espacio tridimensional
Pero como superficie abstracta por sí misma (o como una superficie dentro de mi espacio tetradimensional) esta autointersección no se da.
El teorema sobre toros g-agujereados puede reformularse así: cualquier superficie orientable (de extensión finita sin bordes) es topológicamente equivalente a una esfera con g asas extra (donde g podría ser 0). Hay una clasificación similar de las superficies no orientables (de una cara): pueden formarse a partir de una superficie llamada el plano proyectivo añadiendo g asas. La botella de Klein es un plano proyectivo con un asa.
La combinación de estos dos resultados se llama Teorema de Clasificación de Superficies. Nos da, salvo equivalencia topológica, todas las superficies posibles (de extensión finita sin bordes).
Con la demostración de este teorema la topología de espacios bidimensionales -superficies- podía considerarse «conocida». Eso no significaba que cualquier cuestión posible sobre superficies pudiera resolverse sin más esfuerzo, pero daba un punto de partida razonable para considerar cuestiones más complicadas. El Teorema de Clasificación de Superficies es una herramienta muy potente en topología bidimensional.
Cuando pensamos en topología suele ser útil suponer que el espacio en cuestión es todo lo que existe. No hay necesidad de «insertarlo» en un espacio circundante. Actuando así se centra la atención en las propiedades intrínsecas del espacio. Una imagen vivida es la de una minúscula criatura que vive en, digamos, una superficie topológica. ¿Cómo podría tal criatura, ignorante de cualquier espacio circundante, descubrir en qué superficie habita? ¿Cómo podemos caracterizar intrínsecamente tales superficies?
En 1900 se entendió que una manera de responder a tales preguntas es considerar lazos cerrados en la superficie y cómo pueden deformarse estos lazos. Por ejemplo, en una esfera cualquier lazo cerrado puede ser deformado de forma continua hasta ser reducido, o «contraído», a un punto. Por ejemplo, el círculo del ecuador puede ser desplazado poco a poco hacia el Polo Norte, haciéndose cada vez más pequeño hasta que coincide con el propio Polo Norte.
Por el contrario, toda superficie que no es equivalente a una esfera contiene lazos que no pueden deformarse hasta puntos. Tales lazos «pasan a través de un agujero» y el agujero les impide contraerse. Por ello, la esfera puede caracterizarse como la única superficie en la que cualquier lazo cerrado puede contraerse hasta un punto.
Para qué les servía la topologíaUno de los invariantes topológicos más simples fue ideado por Gauss. En un estudio de los campos eléctrico y magnético, él se interesó en cómo pueden unirse dos lazos cerrados. Inventó el número o índice de enlace, que mide cuántas veces un lazo se enrolla alrededor del otro.
Si el número de enlace es distinto de cero, entonces los lazos no pueden ser separados por una transformación topológica. Sin embargo, este invariante no resuelve por completo el problema de determinar cuándo dos lazos unidos no pueden ser separados, porque a veces el invariante de enlace es cero pero los enlaces no pueden ser separados.
A la izquierda, lazos con número de enlazamiento 3; a la derecha, estos lazos no pueden separarse topológicamente, incluso si tienen número de enlazamiento 0.Él obtuvo incluso una fórmula analítica para este número, integrando una magnitud apropiada a lo largo de la curva en cuestión. Los descubrimientos de Gauss proporcionaron un anticipo de lo que es ahora una enorme área de las matemáticas, la topología algebraica.
§. Topología en tres dimensiones
Después de las superficies -espacios topológicos bidimensionales- es natural pasar a tres dimensiones. Ahora los objetos de estudio son variedades en el sentido de Riemann, salvo que se ignoran las nociones de distancia.
En 1904 Henri Poincaré, uno de los más grandes matemáticos de todos los tiempos, estaba tratando de entender las variedades tridimensionales. Introdujo varias técnicas para conseguir este objetivo. Una de ellas, la homología, estudia las relaciones entre regiones en la variedad y sus fronteras. Otra, la homotopía, examina lo que sucede con los lazos cerrados en la variedad cuando los lazos se deforman.
La homotopía está íntimamente relacionada con los métodos que tan bien habían servido para las superficies, y Poincaré buscó resultados análogos en tres dimensiones. Aquí se vio llevado a una de las preguntas más famosas de todas las matemáticas.
El conocía la caracterización de la esfera como la única superficie en la que cualquier lazo puede contraerse. ¿Funcionaba una caracterización similar en tres dimensiones? Durante un tiempo él supuso que sí lo hacía; de hecho, parecía tan obvio que ni siquiera advirtió que estaba formulando una hipótesis. Más tarde se dio cuenta de que una versión plausible de esta afirmación es realmente falsa, mientras que otra formulación íntimamente relacionada parecía difícil de demostrar pero muy bien podría ser verdadera. Planteó una cuestión, más tarde reinterpretada como la «Conjetura de Poincaré»: si una variedad tridimensional (sin frontera, de extensión finita, y todo lo demás) tiene la propiedad de que cualquier lazo cerrado en ella pueda contraerse hasta un punto, entonces la variedad debe ser topológicamente equivalente a la 3-esfera (un análogo tridimensional de una esfera).
Intentos posteriores de demostrar la conjetura tuvieron éxito para generalizaciones a cuatro o más dimensiones. Los topólogos siguieron luchando con la conjetura original de Poincaré, en tres dimensiones, sin éxito.
En los años ochenta del siglo XX William Thurston dio con una idea que posibilitaría un acercamiento a la Conjetura de Poincaré con un plan más ambicioso. Su conjetura de geometrización va más lejos y se aplica a todas las variedades tridimensionales, no sólo a aquellas en las que todos los lazos pueden contraerse. Parte de una interpretación de la clasificación de las superficies en términos de geometría no euclidiana.
El toro puede obtenerse tomando un cuadrado en el plano euclidiano e identificando bordes opuestos. Como tal, es plano: tiene curvatura cero.
La esfera tiene curvatura constante positiva. Un toro con dos o más agujeros puede representarse como una superficie de curvatura constante negativa. Por eso, la topología de superficies puede representarse en términos de tres tipos de geometría, una euclidiana y dos no euclidianas, a saber, la propia geometría euclidiana, la geometría elíptica (curvatura positiva) y la geometría hiperbólica (curvatura negativa).
Grigori PerelmanPerelman nació en 1966 en lo que entonces era la Unión Soviética.
Como estudiante fue miembro del equipo de la URSS que compitió en la Olimpiada Internacional de Matemáticas y ganó una medalla de oro con una puntuación del 100 por 100. Ha trabajado en los Estados Unidos y en el Instituto Steklov de San Petersburgo pero actualmente no ocupa ningún puesto académico concreto. Su carácter cada vez más retraído ha sumado una dimensión humana inusual a la historia matemática. ¡Lástima que esta historia refuerce el estereotipo del matemático excéntrico!
¿Podría valer algo similar en tres dimensiones? Thurston señaló algunas complicaciones: hay ocho tipos de geometría que considerar, no tres. Y ya no es posible utilizar una sola geometría para una variedad dada: en su lugar, la variedad debe cortarse en varias piezas, utilizando una geometría para cada mía.
Él formuló su conjetura de geometrización: siempre hay una manera sistemática de cortar una variedad tridimensional en piezas, cada una de ellas correspondiente a una de las ocho geometrías.
La conjetura de Poincaré sería una consecuencia inmediata, porque la condición de que todos los lazos se contraigan descarta siete geometrías, dejando sólo la geometría de curvatura constante positiva: la de la 3-esfera.
“La esfera tiene curvatura constante positiva.”
Una aproximación alternativa surgió de la geometría riemanniana. En 1982 Richard Hamilton introdujo una nueva técnica en el área, basada en ideas matemáticas utilizadas por Albert Einstein en la relatividad general. Según Einstein, el espacio-tiempo puede considerarse curvado, y la curvatura describe la fuerza de la gravedad.
La curvatura se mide por el denominado tensor de curvatura, y éste tiene mi pariente más sencillo conocido como tensor de Ricci, por su inventor Gregorio Ricci-Curbastro. Los cambios en la geometría del universo con el tiempo están gobernados por las ecuaciones de Einstein, que dicen que el tensor de tensiones es proporcional a la curvatura. En efecto, la curvatura gravitatoria del universo trata de alisarlo conforme pasa el tiempo, y las ecuaciones de Einstein cuantifican esta idea.
Para qué nos sirve la topologíaEn 1956 James Watson y Francis Crick descubrieron el «secreto de la vida», la estructura de doble hélice de la molécula de ADN, la columna vertebral en la que se almacena y manipula la información genética. Hoy la topología de nudos se está utilizando para entender cómo se desenredan las dos hebras de la hélice cuando el plano genético controla el desarrollo de una criatura viva.
La hélice de ADN es como una cuerda de dos hebras, cada una de las cuales se retuerce repetidamente alrededor de la otra.
Hebras anudadas de ADNCuando una célula se divide, la información genética se transfiere a las nuevas células: las hebras se separan, se copian y luego se emparejan las nuevas con las viejas. Cualquiera que haya tratado de separar las hebras de un largo trozo de cuerda sabe lo difícil que es este proceso: las hebras se enredan cuando uno trata de separarlas. El ADN es mucho peor: las propias hélices están «superenrolladas», como si la propia cuerda se hubiera enrollado en una bobina. Imaginemos varios kilómetros de cable fino apretados en una pelota y nos haremos una idea de cuán enredado debe estar el ADN en una célula.
La bioquímica genética debe enredar y desenredar este cable enmarañado, y hacerlo de forma rápida, repetida e infalible; la misma cadena de la vida depende de ello. ¿Cómo? Los biólogos abordan el problema utilizando enzimas para romper la cadena de ADN en piezas suficientemente pequeñas para ser estudiadas en detalle. Un segmento de ADN es un nudo molecular complicado, y el mismo nudo puede parecer muy diferente después de que algunos pliegues y vueltas hayan distorsionado su apariencia.
Las nuevas técnicas para estudiar nudos abren nuevas líneas de ataque en genética molecular. Ya no es un juego de los matemáticos puros; la topología de nudos se está convirtiendo en una cuestión práctica en biología. Un descubrimiento reciente es una conexión matemática entre la cantidad de torsión en la hélice de ADN y la cantidad de superenrollamiento.
El mismo juego puede jugarse utilizando la versión de Ricci de la curvatura, y lleva al mismo tipo de comportamiento: una superficie que obedece a las ecuaciones para el «flujo de Ricci» tenderá de forma natural a simplificar su propia geometría redistribuyendo la curvatura de forma más equitativa. Hamilton demostró que la Conjetura de Poincaré bidimensional puede demostrarse utilizando el flujo de Ricci. Lo que sucede, básicamente, es que una superficie en la que todos los lazos se contraen se simplifica tamo cuando sigue el flujo de Ricci que termina como una esfera perfecta. Hamilton sugirió también generalizar esta aproximación a tres dimensiones e hizo progresos en esta dirección, pero tropezó con algunos obstáculos difíciles.
§. Perelman
En 2002 Grigori Perelman causó sensación al colocar varios artículos en los arXiv, una página web para investigación en física y matemáticas que permite a los investigadores ofrecer acceso público a trabajos que no han pasado la «revisión por los pares», y que con frecuencia están aún en curso.
(El objetivo de la página web es evitar las largas demoras que se producen mientras los artículos están siendo sometidos a revisión para su publicación oficial. Anteriormente este papel lo desempeñaban los «preprints» informales.) Estos artículos trataban evidentemente del flujo de Ricci, pero quedaba claro que si el trabajo era correcto implicaría la conjetura de geometrización, y con ello la de Poincaré.
La idea básica es la sugerida por Hamilton. Empezar con una variedad tridimensional arbitraria, equiparla con una noción de distancia para que tenga sentido el flujo de Ricci, y dejar que la variedad siga el flujo y se simplifique. La complicación principal es que pueden aparecer singularidades en donde la variedad se estrangula y deja de ser suave.
En las singularidades el método propuesto deja de ser válido. La nueva idea consiste en cortarla cerca de una singularidad semejante, tapar los agujeros resultantes y dejar que el flujo continúe. Si la variedad consigue simplificarse por completo cuando tan sólo ha aparecido un número finito de singularidades, cada pieza soportará precisamente una de las ocho geometrías, y la inversión de las operaciones de corte («cirugía») nos dice cómo pegar de nuevo esas piezas para reconstruir la variedad.
La Conjetura de Poincaré es famosa por otra razón: es uno de los ocho Problemas Matemáticos del Milenio seleccionados por el Instituto Clay, y como tal, su solución -adecuadamente verificada- conlleva un premio de un millón de dólares. Sin embargo, Perelman tenía sus propias razones para no querer el premio -de hecho, no buscaba ninguna recompensa salvo la solución misma- y por consiguiente no tenía ninguna razón fuerte para ampliar sus a veces crípticos artículos en los arXiv para dar algo más adecuado para su publicación.
Por consiguiente, los expertos en el área desarrollaron sus propias versiones de las ideas, tratando de llenar cualquier laguna aparente en el argumento y, en general, ordenar el trabajo para hacerlo aceptable como una demostración genuina. Se publicaron varios de estos intentos, y ahora una versión global y definitiva de la demostración de Perelman ha sido aceptada por la comunidad topológica. En 2006 se le concedió una medalla Fields por su trabajo en esta área, que el rechazó. No todo el mundo ansia la fama universal.
§. La topología y el mundo real
La topología fue inventada porque las matemáticas no podían funcionar sin ella, estimulada por varias preguntas básicas en áreas como el análisis complejo. Aborda la pregunta «¿qué forma tiene esto?» de una manera muy simple pero profunda. Muchos conceptos geométricos convencionales, tales como longitudes, pueden verse como añadir detalles extra a la información básica recogida por la topología.
Existen unos pocos precursores tempranos de la topología, pero ésta no empezó a despegar realmente como una rama de las matemáticas con su propia identidad y potencia hasta mediados del siglo XIX, cuando los matemáticos adquirieron una comprensión bastante completa de la topología de superficies, formas bidimensionales. La extensión a dimensiones más altas recibió un enorme impulso a finales del siglo XIX y principios del XX, en particular con las investigaciones de Henri Poincaré. Más avances se produjeron en los años veinte del siglo XX; la disciplina despegó realmente en los años sesenta aunque, irónicamente, perdió casi todo el contacto con la ciencia aplicada.
Para confusión de los críticos de la abstracción de las matemáticas «puras» del siglo XX, la teoría resultante es ahora vital para varias áreas de la física matemática. Incluso su obstáculo intratable, la Conjetura de Poincaré, ha sido superada. Visto en retrospectiva, las dificultades principales para desarrollar la topología eran internas, mejor resueltas por medios abstractos; las conexiones con el mundo real tendrían que esperar hasta que las técnicas estuvieran ordenadas adecuadamente.
Capítulo 16
La cuarta dimensión
Geometría fuera de este mundo
En su novela de ciencia ficción La máquina del tiempo, Herbert George Wells describía la naturaleza subyacente del espacio y el tiempo de una forma que ahora encontramos familiar, pero que debió de producir de asombro a sus lectores Victorianos: «Hay realmente cuatro dimensiones, tres que llamamos los tres planos del espacio, y una cuarta, el tiempo». Para fijar el contexto de su historia, añadía: «Hay, sin embargo, una tendencia a trazar una distinción irreal entre las tres primeras dimensiones y la última, porque sucede que nuestra consciencia se mueve a lo largo de la última en una misma dirección y de forma algo irregular desde el principio hasta el final de nuestra vida. Pero algunos filósofos se han estado preguntando por qué tres dimensiones en particular -¿por qué no otra dirección a ángulos rectos respecto a las tres?- e incluso han tratado de construir una geometría tetradimensional».
Su protagonista va más lejos, supera las supuestas limitaciones de la consciencia humana y viaja en la cuarta dimensión del tiempo como si fuera una dimensión normal del espacio.
§. La cuarta dimensión
El arte del escritor de ciencia ficción está en eliminar la incredulidad, y Wells la consiguió informando a sus lectores de que «el profesor Simón Newcomb estaba exponiendo esto ante la Sociedad Matemática de Nueva York hace tan sólo un mes». Aquí Wells se estaba refiriendo probablemente a un suceso real; sabemos que aproximadamente en esas fechas, Newcomb, un astrónomo prominente, dio una conferencia sobre el espacio tetradimesional. Su conferencia reflejaba un cambio importante en el pensamiento matemático y científico, pues liberaba a estas disciplinas de la hipótesis tradicional de que el espacio debe tener siempre tres dimensiones. Esto no implica que el viaje en el tiempo sea posible, pero daba a Wells una excusa para hacer observaciones penetrantes sobre la naturaleza humana actual llevando a su viajero en el tiempo a un futuro perturbador.
“La cuarta dimensión era defendida por charlatanes, explotada por novelistas...”
La máquina del tiempo, publicada en 1895, sintonizaba con una obsesión victoriana con la cuarta dimensión, que invocaba una dimensión adicional e invisible del espacio como un lugar donde residían fantasmas, espíritus o incluso Dios. La cuarta dimensión era defendida por charlatanes, explotada por novelistas, objeto de especulación para científicos y formalizada por matemáticos. En sólo unas décadas, el espacio tetradimensional no sólo era estándar en matemáticas: también lo eran espacios con cualquier número de dimensiones -cinco, diez, mil millones, incluso infinito. Las técnicas y tópicos de la geometría multidimensional eran utilizados rutinariamente en todas las ramas de la ciencia, incluso en la biología y la economía.
Los espacios de dimensiones más altas siguen siendo casi desconocidos fuera de la comunidad científica, pero muy pocas áreas del pensamiento humano podrían funcionar ahora eficazmente sin estas técnicas, por remotas que puedan parecer de los asuntos humanos ordinarios. Los científicos que tratan de unificar las dos grandes teorías del universo físico, la relatividad y la mecánica cuántica, especulan con que el espacio puede tener realmente nueve dimensiones, o diez, en lugar de las tres que normalmente percibimos. Recordando el revuelo causado por la geometría no euclidiana, el espacio de tres dimensiones es visto cada vez más como una posibilidad entre muchas, en lugar del único tipo de espacio que es posible.
Estos cambios se han producido porque la interpretación que se da ahora a términos como «espacio» y «dimensión» es más general: coincide con los significados usuales del diccionario en los contextos familiares de una pantalla de televisor o nuestros entornos normales, pero abre nuevas posibilidades. Para los matemáticos, un espacio es una colección de objetos junto con una noción de «distancia» entre dos cualesquiera de dichos objetos. Siguiendo la idea de coordenadas de Descartes, podemos definir la dimensión de dicho espacio como cuántos números se requieren para especificar un objeto. Si como objetos tomamos los puntos, y utilizamos la noción usual de distancia en el plano o en el espacio, encontramos que el plano tiene dos dimensiones y el espacio tiene tres. Sin embargo, otras colecciones de objetos pueden tener cuatro dimensiones, o más, dependiendo de cuáles sean los objetos.
Supongamos, por ejemplo, que los objetos son esferas en el espacio tridimensional. Se necesitan cuatro números (x, y, z, r) para especificar una esfera: tres coordenadas (x, y, z) para su centro, más el radio r. Por lo tanto, el «espacio» de todas las esferas en el espacio ordinario tiene cuatro dimensiones. Ejemplos como éste muestran que cuestiones matemáticas naturales pueden llevar fácilmente a espacios de dimensiones superiores.
En realidad, las matemáticas modernas van más lejos. En abstracto, el espacio de cuatro dimensiones se define como el conjunto de todas las cuádruplas (x1, x2, x3, x4) de números. Más en general, el espacio de n dimensiones -para cualquier entero n- se define como el conjunto de todas las n-tuplas (x1, x2…xn) de números. En cierto sentido, en eso consiste todo; la noción intrigante y desconcertante de muchas dimensiones se reduce a una trivialidad: largas listas de números.
Este punto de vista es ahora claro, pero históricamente se necesitó mucho tiempo para quedar establecido. Los matemáticos discutían, a veces con vehemencia, sobre el significado y la realidad de espacios de dimensiones superiores. Se necesitó casi un siglo para que las ideas llegaran a ser ampliamente aceptadas. Pero las aplicaciones de tales espacios, y la imaginería geométrica que conllevaban, se mostraron tan útiles que las cuestiones matemáticas subyacentes dejaron de ser controvertidas.
§. El espacio tri- o tetra-dimensional
Es irónico que la concepción actual de espacios de dimensiones superiores surgiera del álgebra, y no de la geometría, como consecuencia de un intento fallido de desarrollar un sistema de números tridimensional, análogo al sistema bidimensional de los números complejos.
La distinción entre dos y tres dimensiones se remonta a los Elementos de Euclides.
La primera parte del libro trata de la geometría del plano, un espacio de dos dimensiones.
La segunda parte trata de la geometría sólida: la geometría del espacio tridimensional. Hasta el siglo XIX la palabra «dimensión» se limitaba a estos contextos familiares.
La geometría griega era una formalización de los sentidos humanos de la vista y el tacto, que permiten a nuestros cerebros construir modelos internos de relaciones de posición en el mundo exterior. Estaba restringida por las limitaciones de nuestros propios sentidos y las del mundo en que vivimos. Los griegos pensaban que la geometría describía el espacio real en el que vivimos, y suponían que el espacio físico tenía que ser euclidiano. La pregunta matemática «¿puede existir un espacio tetradimensional en un sentido conceptual?» se confundía con la pregunta física «¿puede existir un espacio real con cuatro dimensiones?».
William Rowan Hamilton
1805-1865
Hamilton fue tan precoz en matemáticas que fue nombrado catedrático de Astronomía en el Trinity College de Dublín a la edad de 21 años cuando aún era estudiante. Este nombramiento le convertía en el astrónomo real de Irlanda. Hizo numerosas contribuciones a las matemáticas, pero aquella que él mismo consideraba más importante fue la invención de los cuaterniones. Él nos dice que «Los cuaterniones ... empezaron su vida, plenamente formados, el 16 de octubre de 1843, cuando yo caminaba con Lady Hamilton hacia Dublín, y llegamos al Puente Brougham. Es decir, yo sentí entonces que se cerraba el circuito galvánico del pensamiento, y las chispas que saltaron eran las ecuaciones fundamentales entre I, j, k; exactamente tales como las he utilizado desde entonces. Saqué, al momento, una libreta, que aún existe, e hice un apunte de lo que, en ese mismo instante, sentí que era algo en lo que valdría la pena trabajar al menos durante los diez (o podrían ser quince) años siguientes. Sentí que en ese momento había resuelto un problema, que había aliviado una necesidad intelectual que me perseguía desde hacía al menos quince años». Hamilton grabó inmediatamente la ecuación
i2 = j2 = k2 = ijk - 1
en la mampostería del puente.
Y esa pregunta se confundía además con «¿puede haber cuatro dimensiones dentro de nuestro propio espacio familiar?», para la que la respuesta es «no». Por ello era una creencia general que el espacio tetradimensional es imposible.
La geometría empezó a liberarse de este punto de vista restringido cuando los algebristas del Renacimiento en Italia tropezaron sin querer con una profunda ampliación del concepto de número, al aceptar la existencia de una raíz cuadrada de menos uno. Wallis, Wessel, Argand y Gauss estudiaron cómo interpretar los números complejos resultantes como puntos en un plano, liberando a los números de las ataduras unidimensionales de la recta real. En 1837, el matemático irlandés William Rowan Hamilton redujo todo el tema al álgebra, definiendo un número complejo x + iy como un par de números reales (x,y). Además definió la suma y la multiplicación de pares mediante las regla
(x, y) + (u, v) = (x + u, y + v)
(x, y) (u, v) = (xu - yv, xv + yu),
En esta aproximación, un par de la forma (x,0) se comporta exactamente igual que el número real x, y el par especial (0,1) se comporta como i. La idea es simple, pero apreciarla requiere un concepto sofisticado de la existencia matemática.
Luego Hamilton se fijó en algo más ambicioso. Era bien sabido que los números complejos hacen posible resolver muchos problemas de física matemática de sistemas en el plano, utilizando métodos simples y elegantes. Un truco similar para el espacio tridimensional tendría un valor incalculable. Por ello trató de inventar un sistema de números tridimensional, con la esperanza de que el cálculo infinitesimal asociado resolvería problemas importantes de física matemática en el espacio tridimensional. Supuso tácitamente que este sistema satisfaría todas las leyes usuales del álgebra.
Pero pese a sus heroicos esfuerzos, no pudo encontrar un sistema semejante.
Con el tiempo descubrió por qué. Es imposible.
Entre las «leyes usuales del álgebra» está la ley conmutativa de la multiplicación, que afirma que ab = ba. Hamilton había estado luchando durante años por concebir mi álgebra efectiva para tres dimensiones. Finalmente encontró una, un sistema de números a los que llamó cuaterniones. Pero era un álgebra de cuatro dimensiones, no tres, y su multiplicación no era conmutativa.
Los cuaterniones se parecen a los números complejos, pero en lugar de un «nuevo» número i hay tres: i, j, k. Un cuaternión es una combinación de éstos, por ejemplo 7 + 8i - 2j + 4k. De la misma forma que los números complejos son bidimensionales, construidos a partir de dos cantidades independientes 1 e i, los cuaterniones son tetradimensionales, construidos a partir de cuatro cantidades independientes 1, i, j y k. Pueden formalizarse algebraicamente como cuádruplas de números reales, con reglas particulares para la suma y la multiplicación.
§. Espacios de dimensión superior
Cuando Hamilton presentó su idea fundamental los matemáticos ya eran conscientes de que los espacios de alta dimensión aparecen de forma completamente natural, y tienen interpretaciones físicas razonables, cuando los elementos básicos del espacio son alguna otra cosa que puntos.
“Su presentación era mística y bastante y abstracta...”
En 1846 Julius Plücker señaló que se necesitan cuatro números para especificar una recta en el espacio. Dos de dichos números determinan dónde corta la recta a un plano fijo; los otros dos determinan su dirección con respecto al plano.
Así, considerado como una colección de rectas, nuestro espacio familiar ya tiene cuatro dimensiones, no tres. Sin embargo, había una vaga sensación de que esta construcción era bastante artificial, y que los espacios hechos de puntos por valor de cuatro dimensiones no eran naturales.
Los cuaterniones de Hamilton tenían una interpretación natural como rotaciones, y su álgebra era convincente. Eran tan naturales como los números complejos, de modo que el espacio tetradimensional era tan natural como un plano.
La idea se extendió rápidamente a más de cuatro dimensiones. Mientras Hamilton estaba promocionando sus queridos cuaterniones, un profesor de matemáticas llamado Hermann Günther Grassmann estaba descubriendo una ampliación del sistema de números a espacios con cualquier número de dimensiones. Publicó su idea en 1844 como Lecciones sobre extensión lineal.
Su presentación era mística y bastante abstracta, por lo que el trabajo atrajo poca atención. En 1862, para combatir la falta de interés, publicó una versión revisada, con frecuencia traducida como El cálculo de extensiones, que pretendía ser más comprensible. Por desgracia no lo era.
Pese a su fría recepción, el trabajo de Grassmann era de importancia fundamental. El comprendió que era posible reemplazar las cuatro unidades 1, i, j y k de los cuaterniones por cualquier número de unidades. Llamó a las combinaciones de tales unidades hipernúmeros. Él entendía que su enfoque tenía limitaciones. Hay que tener mucho cuidado en no esperar demasiado de la aritmética de hipernúmeros; seguir servilmente las leyes tradicionales del álgebra difícilmente lleva a ninguna parte.
Mientras tanto, los físicos estaban desarrollando sus propias nociones de espacios de dimensiones superiores, motivados no por la geometría sino por las ecuaciones de Maxwell para el electromagnetismo. Aquí los campos eléctrico y magnético son vectores; tienen una dirección en el espacio tridimensional tanto como magnitud. Los vectores son flechas, por así decir, alineadas con el campo eléctrico o el magnético. La longitud de la flecha muestra la intensidad del campo, y su dirección muestra hacia dónde apunta el campo.
“Los físicos estaban desarrollando sus propias nociones de espacios...”
En la notación de la época las ecuaciones de Maxwell eran ocho, pero incluían dos grupos de tres ecuaciones, una por cada componente del campo eléctrico (o magnético) en cada una de las tres dimensiones del espacio. Haría la vida mucho más fácil idear un formalismo que recogiese cada uno de estos tríos en una única ecuación vectorial. Maxwell lo consiguió utilizando cuaterniones, pero su enfoque era algo tosco.
Independientemente, el físico Josiah Willard Gibbs y el ingeniero Oliver Heaviside encontraron una manera más simple de representar vectores algebraicamente.
En 1881 Gibbs editó un librito privado, Elementos de análisis vectorial, para ayudar a sus estudiantes. Explicaba que sus ideas habían sido desarrolladas por conveniencia de uso antes que por elegancia matemática. Sus notas fueron desarrolladas por Edwin Wilson, y ambos publicaron un libro conjunto Análisis vectorial en 1901. Heaviside dio con las mismas ideas generales en el primer volumen de su Teoría electromagnética en 1893 (los otros dos volúmenes aparecieron en 1899 y 1912).
Los diversos sistemas -cuaterniones de Hamilton, números hipercomplejos de Grassmann y vectores de Gibbs- convergieron rápidamente hacia la misma descripción matemática de un vector: es una tripleta de números (x, y, z).
Al cabo de 250 años, los matemáticos y físicos del mundo habían vuelto a Descartes -pero ahora la notación de coordenadas era sólo parte de la historia. Las tripletas no sólo representaban puntos: representaban magnitudes dirigidas. Eso suponía una enorme diferencia- no para el formalismo, sino para su interpretación, su significado físico.
Los matemáticos se preguntaban cuántos sistemas de números hipercomplejos podría haber. Para ellos la pregunta no era «¿son útiles?», sino «¿son interesantes?». Por eso, los matemáticos se centraron principalmente en las propiedades algebraicas de sistemas de números hipercomplejos, para cualquier n. Había, de hecho, espacios n-dimensionales, pero de entrada todo el mundo pensaba algebraicamente y los aspectos geométricos eran minimizados.
§. Geometría diferencial
Los geómetras respondieron a la invasión de su territorio por parte de los algebristas reinterpretando geométricamente los números hipercomplejos.
La figura clave en esto fue Riemann. El estaba trabajando para su «Habilitación», que le daría derecho a cobrar tasas de matrícula a sus estudiantes. Los candidatos a la Habilitación debían dar una lección especial sobre su propia investigación. Siguiendo el procedimiento habitual, Gauss pidió a Riemann que propusiera varios temas, entre los que Gauss haría la elección final. Una de las propuestas de Riemann fue «Sobre las hipótesis que yacen en los fundamentos de la geometría», y Gauss, que había estado pensando sobre la misma cuestión, eligió ese tema. Riemann estaba aterrorizado; le disgustaba hablar en público y no había elaborado por completo sus ideas. Pero lo que tenía en mente era explosivo: una geometría de n dimensiones, por lo que entendía un sistema de n coordenadas (x1, x2,..., xn), equipado con una noción de distancia entre puntos próximos. Llamaba a tal espacio una variedad.
Esta propuesta ya era suficientemente radical, pero había otra característica aún más radical: las variedades podían estar curvadas. Gauss había estado estudiando la curvatura de superficies y había obtenido una bella fórmula que representaba la curvatura intrínsecamente, es decir, en términos de la superficie sola, no del espacio en el que está inmersa.
“Riemann estaba aterrorizado; le disgustaba hablar en público y no había elaborado por completo sus ideas.”
Riemann había intentado desarrollar una fórmula similar para la curvatura de una variedad, generalizando la fórmula de Gauss a n dimensiones.
Esta fórmula sería también intrínseca a la variedad, no haría uso explícito de ningún espacio continente. Los esfuerzos de Riemann por desarrollar la noción de curvatura en un espacio de n dimensiones le llevaron al borde de un ataque de nervios. Lo que empeoraba las cosas era que al mismo tiempo estaba ayudando a Weber, el colega de Gauss, que estaba tratando de entender la electricidad. Riemann siguió luchando, y el intercambio entre fuerzas eléctrica y magnética le llevó a un nuevo concepto de «fuerza» basado en la geometría. Tuvo la misma intuición que décadas después llevó a Einstein a la relatividad general: las fuerzas pueden ser reemplazadas por la curvatura del espacio.
En la mecánica tradicional los cuerpos viajan en línea recta a menos que sean desviados por una fuerza. En geometrías curvas, las líneas rectas no tienen por qué existir y las trayectorias son curvas. Si el espacio es curvo, lo que se experimenta cuando se está obligado a desviarse de una línea recta se siente como una fuerza. Ahora Riemann tuvo la intuición que necesitaba para elaborar su lección, que dio en 1854. Fue un triunfo importante. Las ideas se difundieron rápidamente. Pronto los científicos estaban dando charlas de divulgación sobre la nueva geometría. Entre ellos estaba Hermann von Helmholtz, quien dio charlas sobre seres que vivían en una esfera o alguna otra superficie curva.
Los aspectos técnicos de la geometría de variedades de Riemann, ahora llamada geometría diferencial, fueron desarrollados por Eugenio Beltrami, Elwin Bruno Christoffel y la escuela italiana de Gregorio Ricci y Tulio Levi- Civita. Más tarde, su trabajo iba a ser precisamente lo que Einstein necesitaba para la relatividad general.
§. Álgebra matricial
También los algebristas habían estado ocupados, desarrollando técnicas computacionales para álgebras de n-variables -el simbolismo formal del espacio n-dimensional. Una de estas técnicas era el álgebra de matrices, tablas rectangulares de números, introducidas por Cayley en 1855.
Para qué les servía la geometría de alta dimensiónAlrededor de 1907 el matemático Hermann Minkowski formuló la teoría de la relatividad especial de Einstein en términos de un espacio-tiempo tetradimensional, que combinaba un tiempo unidimensional y el espacio tridimensional en un único objeto matemático.
Éste se conoce como espacio-tiempo de Minkowski.
Los requisitos de la relatividad implican que la «métrica» natural en el espacio-tiempo de Minkowski no es la determinada por el teorema de Pitágoras, en la que el cuadrado de la distancia de un punto (x,t) al origen es x2 + t2.
Esta representación geométrica es utilizada casi universalmente por los físicos modernos.En su lugar, esta expresión debería ser reemplazada por el intervalo x2 - c2t2, donde c es la velocidad de la luz. El cambio crucial aquí es el signo menos, lo que implica que los sucesos en el espacio-tiempo están asociados con dos conos. Un cono (aquí un triángulo porque el espacio ha sido reducido a una dimensión) representa el futuro del suceso, y el otro el pasado.
Este formalismo surgía de manera natural de la idea de un cambio de coordenadas. Se había hecho un lugar común simplificar fórmulas algebraicas reemplazando variables tales como x e y por combinaciones lineales, por ejemplo
u = ax + by
v = ex + dy
para a, b, c, d constantes. Cayley representaba el par (x,y) como un «vector columna», y los coeficientes por una tabla, o matriz, 2x2. Con una adecuada definición de multiplicación, podía reescribir el cambio de coordenadas como
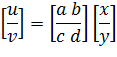
El método se extendía fácilmente a tablas con cualquier número de filas y columnas que representaban cambios lineales en cualquier número de coordenadas.
El álgebra matricial hacía posible calcular en el espacio n-dimensional.
A medida que cuajaban las nuevas ideas nació un lenguaje geométrico para el espacio n-dimensional, apoyado por un sistema de cálculo algebraico formal. Cayley pensaba que su idea no era más que una conveniencia notacional y predijo que nunca tendría aplicaciones. Hoy es indispensable en cualquier rama de la ciencia, especialmente en áreas como la estadística. Los ensayos médicos hacen un uso abundante de las matrices, que se utilizan para calcular qué asociaciones entre causa y efecto son estadísticamente significativas.
La imaginería geométrica hacía más fácil demostrar teoremas. Los críticos respondían que estas «geometrías» modernas se referían a espacios que no existían. Los algebristas replicaban señalando que el álgebra de n variables existía con toda certeza, y algo que servía para el avance en muchas áreas diferentes de las matemáticas debía ser por fuerza interesante. George Salmón escribió: «Ya he discutido por completo este problema [resolver cierto sistema de ecuaciones] cuando se nos dan tres ecuaciones en tres variables. La pregunta que tenemos ahora ante nosotros puede formularse como el problema correspondiente en el espacio de p dimensiones. Pero la consideramos como una pregunta puramente algebraica, alejada de cualquier consideración geométrica. No obstante, retendremos un poco de lenguaje geométrico... porque así podemos ver más directamente como aplicar a un sistema de p ecuaciones procesos análogos a los que hemos utilizado en un sistema de tres».
§. Espacio «real»
¿Existen las dimensiones superiores? La respuesta depende, por supuesto, de lo que entendemos por «existe», pero la gente no suele entender este tipo de cosas, especialmente cuando despiertan sus emociones. La cuestión pasó a primer plano en 1869. En un famoso discurso en la Asociación Británica, más tarde reimpreso como Un ruego para el matemático, James Joseph Sylvester señaló que la generalización es una manera importante de avanzar en matemáticas. Lo que importa, decía Sylvester, es lo que es concebible, no lo que corresponde directamente a la experiencia física. Añadía que con algo de práctica es perfectamente posible visualizar cuatro dimensiones, de modo que el espacio tetradimensional es concebible.
Esto enfureció tanto al erudito shakespeariano Clement Ingleby que éste invocó al gran filósofo Immanuel Kant para demostrar que la tridimensional es una propiedad esencial del espacio, eludiendo por completo la observación de Sylvester.
“La naturaleza del espacio real es irrelevante para las cuestiones matemáticas.”
La naturaleza del espacio real es irrelevante para las cuestiones matemáticas. De todas formas, durante algún tiempo la mayoría de los matemáticos británicos se pusieron del lado de Ingleby. Pero algunos matemáticos del continente no lo hicieron. Grassmann dijo: «Los teoremas del cálculo de extensiones no son meras traducciones de resultados geométricos a un lenguaje abstracto; tienen una importancia mucho más general, pues mientras la geometría ordinaria sigue limitada a tres dimensiones del espacio [físico], la ciencia abstracta está libre de esta limitación».
Sylvester defendió su postura: «Hay muchos que consideran la supuesta noción de un espacio generalizado sólo como una forma enmascarada de formalización algebraica; pero lo mismo podría decirse con igual verdad de nuestra noción de infinito, o de líneas imposibles, o de rectas que forman un ángulo cero en geometría, y nadie discutirá la utilidad de trabajar con ellas. El Dr. Salmón en su extensión a las superficies de la teoría de Chasles de las características, Mr. Clifford en una cuestión sobre probabilidad, y yo mismo en la teoría de particiones, y también en mi artículo sobre proyección baricéntrica, hemos sentido y dado pruebas de la utilidad práctica de manejar el espacio de cuatro dimensiones como si fuera espacio concebible».
§. Espacios multi-dimensionales
Al final, Sylvester ganó el debate. Hoy día los matemáticos consideran que algo «existe» si no es lógicamente contradictorio. Puede contradecir la experiencia física, pero eso es irrelevante para la existencia matemática. En este sentido, los espacios multidimensionales son tan reales como los familiares espacios de tres dimensiones, porque es igual de fácil dar una definición formal.
Las matemáticas de los espacios multidimensionales, tal como ahora se conciben, son puramente algebraicas y basadas en generalizaciones «obvias» de espacios de baja dimensión. Por ejemplo, todo punto en el plano (un espacio bidimensional) puede especificarse por sus dos coordenadas, y todo punto en el espacio tridimensional puede especificarse por sus tres coordenadas. Sólo hace falta un corto paso para definir un punto en el espacio tetradimensional como un conjunto de cuatro coordenadas y, más en general, para definir un punto en un espacio n-dimensional como una lista de n coordenadas. Entonces el propio espacio n-dimensional (o n-espacio para abreviar) es simplemente el conjunto de todos esos puntos.
Manipulaciones algebraicas similares nos dan la distancia entre dos puntos cualesquiera en el n-espacio, el ángulo entre dos rectas, y demás. A partir de ello, es cuestión de imaginación: las formas geométricas más razonables en dos o tres dimensiones tienen análogas directas en n dimensiones, y la manera de encontrarlas consiste en describir las formas familiares utilizando el álgebra de coordenadas y luego extender dicha descripción a n coordenadas.
Por ejemplo, un círculo en el plano, o una esfera en el 3-espacio, consiste en todos los puntos que se encuentran a una distancia fija (el radio) de un punto escogido (el centro). El análogo obvio en el n-espacio es considerar todos los puntos que se encuentran a una distancia fija de un punto escogido. Utilizando la fórmula para distancias, esto se convierte en una condición puramente algebraica, y el «objeto» resultante se conoce como una hiperesfera (n-1)-dimensional, o (n-1)-esfera para abreviar. La dimensión baja de n a n-1 porque, por ejemplo, un círculo en el 2-espacio es una curva, que es un objeto unidimensional; análogamente, una esfera en el espacio es una superficie bidimensional. Una hiperesfera maciza en n dimensiones se llama una n-bola. Por lo tanto, la Tierra es una 3-bola y su superficie es una 2-esfera.
Hoy día, este punto de vista se denomina álgebra lineal. Se utiliza en todas las materias de las matemáticas y de la ciencia, especialmente en ingeniería y estadística. Es también una técnica estándar en economía. Cayley afirmaba que era poco probable que sus matrices tuvieran aplicación práctica alguna vez. No podría haber estado más equivocado.
En 1900 las predicciones de Sylvester se estaban confirmando, con una explosión de áreas matemáticas y físicas donde el concepto de espacio multidimensional estaba teniendo un serio impacto. Una de estas áreas era la relatividad de Einstein, que puede considerarse mejor como un tipo especial de geometría espacio-temporal multidimensional. En 1908 Hermann Minkowski comprendió que las tres coordenadas del espacio ordinario, junto con una coordenada extra para el tiempo, forman un espacio-tiempo tetra- dimensional. Cualquier «punto» en el espacio-tiempo se llama un suceso: es como una partícula puntual que aparece un instante en el tiempo y al momento desaparece. La relatividad trata realmente sobre la física de sucesos.
En mecánica tradicional una partícula que se mueve en el espacio ocupa coordenadas [x(t), y(t), z(t)] en el instante t, y esta posición cambia conforme pasa el tiempo.
Desde el punto de vista del espacio-tiempo de Minkowski, la colección de todos esos puntos es una curva en el espacio-tiempo, la línea de universo de la partícula, y es un solo objeto por sí mismo que existe en todo tiempo.
Un hipercubo tetradimensional proyectado en el plano
En relatividad, «la» cuarta dimensión tiene una única y determinada interpretación: tiempo.
La incorporación posterior de la gravedad, conseguida en la relatividad general, hacía un fuerte uso de las geometrías revolucionarias de Riemann, aunque modificadas para adaptarse a la representación de Minkowski de la geometría del espacio-tiempo plano, es decir, lo que hacen el espacio y el tiempo cuando no hay presente ninguna masa para provocar distorsión gravitatoria, que Einstein modeló como curvatura.
Desde el punto de vista del espacio-tiempo de Minkowski, la colección de todos esos puntos es una curva en el espacio-tiempo, la línea de universo de la partícula, y es un solo objeto por sí mismo que existe en todo tiempo.
“Hoy día, este punto de vista se denomina álgebra lineal.”
Los matemáticos preferían una noción más flexible de dimensionalidad y «espacio», y cuando el siglo XIX estaba dando paso al siglo XX las propias matemáticas parecían exigir, de forma creciente, la aceptación de la geometría multidimensional. La teoría de funciones de dos variables complejas, una extensión natural del análisis complejo, requería pensar en el espacio de dos dimensiones complejas -pero cada dimensión compleja se reduce a dos reales, de modo que, guste o no, estamos mirando un espacio tetradimensional-. Las variedades de Riemann y el álgebra de muchas variables ofrecían una motivación adicional.
§. Coordenadas generalizadas
Otro estímulo para la geometría multidimensional fue la reformulación que hizo Hamilton en 1835 de la mecánica en términos de «coordenadas generalizadas», un desarrollo iniciado por Lagrange en su Mecánica analítica de 1788. Un sistema mecánico tiene tantas de estas coordenadas como «grados de libertad», es decir, maneras de cambiar su estado. De hecho, «número de grados de libertad» es sólo una manera disfrazada de decir «dimensión».
Por ejemplo, se necesitan seis coordenadas generalizadas para especificar la configuración de una bicicleta rudimentaria: una para especificar el ángulo del manillar con respecto al cuadro, una para cada una de las posiciones angulares de las dos ruedas, otra para el eje de los pedales, dos más para las posiciones rotacionales de los propios pedales. Una bicicleta es, por supuesto, un objeto tridimensional, pero el espacio de las configuraciones posibles de la bicicleta es seis-dimensional, que es una de las razones por las que aprender a ir en bicicleta es difícil hasta que se coge el tranquillo. El cerebro tiene que construir una representación interna de cómo interaccionan estas seis variables -tiene que aprender a navegar en la geometría seis-dimensional del espacio-bicicleta. En el caso de una bicicleta en movimiento hay también seis correspondientes velocidades de las que ocuparse: la dinámica es, en esencia, doce-dimensional.
Hacia 1920 esta concurrencia de física, matemáticas y mecánica había triunfado, y el uso del lenguaje geométrico para problemas de muchas variables -geometría multidimensional- había dejado de sorprender, excepto quizá a los filósofos. En 1950 el proceso había ido tan lejos que la tendencia natural de los matemáticos era formular todo en n dimensiones desde el principio. Limitar las teorías a dos o tres dimensiones parecía un confinamiento anticuado y ridículo.
El lenguaje del espacio de dimensiones superiores se difundió rápidamente a todas las áreas de la ciencia, e incluso invadió disciplinas como la economía y la genética. Los virólogos actuales, por ejemplo, consideran los virus como «puntos» en un espacio de secuencias de ADN que fácilmente podría tener varios centenares de dimensiones. Por esto entienden que los genomas de dichos virus tienen una longitud de varios centenares de bases de ADN; pero la imagen geométrica va más allá de la mera metáfora: proporciona un modo eficaz de pensar el problema.
Nada de esto significa, no obstante, que exista el mundo de los espíritus, que los fantasmas tengan ahora un hogar creíble, o que un día podamos (como en Planilandia de Edwin Abbot) recibir la visita de la Hiperesfera, una criatura de la Cuarta Dimensión, que se nos manifestaría como una esfera cuyo tamaño cambiara misteriosamente, capaz de contraerse hasta un punto y desaparecer de nuestro universo. Sin embargo, los físicos que trabajan actualmente en la teoría de supercuerdas piensan que nuestro universo realmente puede tener diez dimensiones, no cuatro. Ahora piensan que nunca advertiremos las seis dimensiones extra porque están enrolladas de una forma demasiado apretada para que las podamos detectar.
“Nuestro universo realmente puede tener diez dimensiones.”
La geometría multidimensional es una de las áreas más espectaculares en que las matemáticas parecen perder todo contacto con la realidad. Puesto que el espacio físico es tridimensional, ¿cómo pueden existir espacios de cuatro o más dimensiones? E incluso si pueden definirse matemáticamente, ¿cómo pueden ser útiles?
El error aquí está en esperar que las matemáticas sean una traducción literal y obvia de la realidad, observada de la forma más directa. Estamos rodeados de objetos que pueden describirse mejor por un gran número de variables, los «grados de libertad» de dichos objetos. Por ejemplo, para fijar la posición de un esqueleto humano se requieren al menos 100 variables. Desde el punto de vista matemático, la descripción natural de tales objetos es en términos de espacios de alta dimensión con una dimensión para cada variable.
Los matemáticos necesitaron mucho tiempo para formalizar tales descripciones, y todavía más tiempo para convencer a todos los demás de que eran útiles. Hoy día se han introducido tanto en el pensamiento científico que su uso se ha convertido en un acto reflejo. Son algo estándar en economía, biología, física, ingeniería, astronomía...; la lista es interminable.
La ventaja de la geometría de altas dimensiones es que acude a las capacidades visuales humanas para tratar problemas que inicialmente no son nada visuales. Puesto que nuestros cerebros están adaptados al pensamiento visual, esta formulación puede llevar con frecuencia a intuiciones insospechadas, no fácilmente obtenibles por otros métodos. A veces, conceptos matemáticos que no tienen una conexión directa con el mundo real tienen conexiones indirectas más profundas. Son esos vínculos ocultos los que hacen tan útiles las matemáticas.
Para qué nos sirve la geometría de alta dimensiónNuestro teléfono móvil hace un uso esencial de espacios multidimensionales. También lo hace la conexión a internet, la televisión por satélite o cable y prácticamente cualquier otra pieza de tecnología que envíe o reciba mensajes. Las comunicaciones modernas son «digitales». Todos los mensajes, incluidos los mensajes telefónicos de voz, se convierten en pautas de 0 y 1: números binarios.
Geometría de pares de dígitos binariosLas comunicaciones no son de mucha utilidad a menos que sean fiables; el mensaje que se recibe debería ser exactamente el mismo que el que se envió. El hardware electrónico no puede garantizar esta precisión, pues las interferencias, o incluso un rayo cósmico incidente, pueden producir errores. Por ello, los ingenieros electrónicos utilizan técnicas matemáticas para codificar las señales de tal forma que los errores puedan detectarse, e incluso corregirse. La base de estos códigos está en las matemáticas de espacios multidimensionales.
Tales espacios aparecen porque una cadena de, digamos, diez dígitos binarios, o bits, tal como 1001011100, puede verse ventajosamente como un punto en un espacio decadimensional con coordenadas restringidas a 0 o a 1. Muchas preguntas importantes sobre códigos de detección y corrección de errores se abordan mejor en términos de la geometría de dicho espacio.
Por ejemplo, podemos detectar (pero no corregir) un único error si codificamos cada mensaje reemplazando cada 0 por 00 y cada 1 por 11. Entonces, un mensaje tal como 110100 se codifica como 111100110000. Si esto se recibe como 111000110000, con un error en el cuarto bit, sabemos que algo está mal porque el par 10 no debería aparecer. Pero no sabemos si debería haber sido 00 o 11. Esto puede ilustrarse claramente con una figura bidimensional (que corresponde a la longitud 2 de las palabras de código 00 y 11).
Considerando los bits en las palabras del código como coordenadas con respecto a dos ejes (correspondientes al primero y segundo dígito de la palabra del código, respectivamente) podemos dibujar una imagen en la que las palabras de código válidas 00 y 11 son esquinas opuestas diagonalmente de un cuadrado.
Cualquier error único las cambia en palabras de código en las otras dos esquinas, que no son palabras de código válidas.
Código de corrección de errores que utiliza cadenas de longitudSin embargo, puesto que estas esquinas son adyacentes a las dos palabras del código válidas, errores diferentes pueden llevar al mismo resultado. Para obtener un código de corrección de errores podemos utilizar palabras de código de longitud tres y codificar 0 como 000 y 1 como 111. Ahora las palabras del código viven en las esquinas de un cubo en un espacio tridimensional. Cualquier error único da como resultado una palabra de código adyacente; además, cada una de estas palabras de código inválidas es adyacente a solo una de las palabras del código válidas 000 o 111.
Esta aproximación a la codificación de mensajes digitales fue avanzada por Richard Hamming en 1947. La interpretación geométrica llegó poco después, y se ha mostrado crucial para el desarrollo de códigos más eficientes.
Capítulo 17
La forma de la lógica
Asentar firmemente los cimientos de las matemáticas
Mientras la superestructura de las matemáticas se hacía cada vez más grande, un pequeño número de matemáticos empezaron a preguntarse si los cimientos podían soportar su peso. Una serie de crisis de fundamentos -en particular las controversias sobre los conceptos básicos del cálculo infinitesimal y la confusión general sobre las series de Fourier- habían dejado claro que los conceptos matemáticos deben definirse con mucho cuidado y precisión para evitar escollos lógicos. De lo contrario las torres de deducción de la disciplina podrían colapsar fácilmente en contradicciones lógicas, debido a alguna vaguedad o ambigüedad subyacentes.
Inicialmente, tales preocupaciones se centraban en ideas complicadas y sofisticadas tales como las series de Fourier. Pero poco a poco el mundo matemático llegó a darse cuenta de que también ideas muy básicas podían ser sospechosas. Fundamental entre ellas era el concepto de número.
La terrible verdad era que los matemáticos habían dedicado tanto esfuerzo al descubrimiento de propiedades profundas de los números que habían olvidado preguntar qué eran los números. Y cuando se trató de dar una definición lógica, ellos no sabían hacerlo.
§. Dedekind
En 1858, mientras impartía un curso sobre la materia, Dedekind se preocupó por la base del cálculo infinitesimal. No por su uso de los límites, sino por el sistema de los números reales. Publicó sus pensamientos en 1872 como Stetigkeit und Irracionales Zahlen, en donde señalaba que propiedades aparentemente obvias de los números reales nunca habían sido demostradas de una manera rigurosa. Como ejemplo citaba la ecuación √2×√3 = √6.
«Obviamente» este hecho se deduce elevando al cuadrado ambos miembros de la ecuación -salvo que la multiplicación de números irracionales nunca había sido realmente definida-. En su libro de 1888 Was Sind und was Sollen die Zahlen? (¿Qué son los números, y qué significan?), puso de manifiesto serias lagunas en los fundamentos lógicos del sistema de los números reales. Nadie había probado realmente que existieran los números reales.
“Nadie había probado realmente que existieran los números reales.”
También propuso una forma de llenar estas lagunas, utilizando lo que ahora llamamos cortaduras de Dedekind. La idea consistía en partir de un sistema de números establecido, los números racionales, y entonces «tirar de» este sistema para obtener el sistema más rico de los números reales.
Su aproximación consistía en partir de las propiedades requeridas de los números reales, encontrar alguna manera de reformularlas únicamente en términos de números racionales y luego invertir el procedimiento, interpretando dichas características de los números racionales como una definición de los reales. Este tipo de «ingeniería inversa» de nuevos conceptos a partir de los viejos ha sido ampliamente utilizado desde entonces.
Supongamos, de momento, que los números reales existen. ¿Cómo se relacionan con los números racionales? Algunos reales no son racionales; un ejemplo obvio es √2. Ahora bien, aunque no es una fracción exacta, puede aproximarse tanto como queramos por racionales. De algún modo está situada en una posición concreta, emparedada entre la densa formación de todos los racionales posibles. Pero ¿cómo podemos especificar dicha posición? Dedekind se dio cuenta de que divide limpiamente el conjunto de los números racionales en dos partes: los que son menores que √2 y los que son mayores.
En cierto sentido, esta división -o cortadura- define el número √2 en términos de racionales. La única pega es que hacemos uso de √2 para definir las dos partes de la cortadura.
Sin embargo, hay una escapatoria. Los números racionales mayores que √2 son precisamente los que son positivos y cuyos cuadrados son mayores que 2. Los números racionales menores que √2 son todos los demás. Estos dos conjuntos de números racionales están ahora definidos sin ningún uso explícito de √2, pero especifican de forma precisa su localización en la «recta de números reales».
Dedekind demostró que si, por razón del argumento, suponemos que existen los números reales, entonces con cualquier número real puede asociarse una cortadura que satisface estas dos propiedades, formando el conjunto R de todos los racionales que son mayores que el número real y el conjunto L de todos los racionales que son menores o iguales que dicho número real. (La condición final es necesaria para asociar una cortadura con cualquier número racional. No queremos dejarlos fuera.) Aquí «L» y «R» pueden leerse como «izquierda» y «derecha» en la imagen habitual de la recta de números reales.
Estos dos conjuntos L y R obedecen a algunas condiciones bastante restrictivas. En primer lugar, todo número racional pertenece a exactamente uno de ellos. En segundo lugar, todo número en R es mayor que cualquier número en L. Finalmente, hay una condición técnica que se ocupa de los propios números racionales: L puede o no puede tener un miembro máximo, pero R nunca tiene un miembro mínimo. Llamamos una cortadura a cualquier par de subconjuntos de los racionales con estas propiedades.
Con ingeniería inversa no necesitamos suponer que los números reales existen. En su lugar, podemos utilizar cortaduras para definir números reales, de modo que un número real es efectivamente una cortadura. Habitualmente no es así como pensamos en un número real, pero Dedekind comprendió que podemos hacerlo si queremos. La tarea principal consiste en definir la suma y la multiplicación de cortaduras, de modo que tenga sentido la aritmética de números reales. Esto resulta fácil. Para sumar dos cortaduras (L1, R1) y (L2, R2), definimos L1 + L2 como el conjunto de todos los números que se pueden obtener sumando un número en L1 con un número en L2 y de forma similar definimos R1 + R2. Entonces la suma de las dos cortaduras es la cortadura (L1 + L2) = (R1 + R2). La multiplicación es similar, pero los números positivos y los negativos se comportan de forma ligeramente diferente.
Finalmente tenemos que verificar que la aritmética de cortaduras tiene todas las propiedades que esperamos de los números reales. Éstas incluyen las leyes estándar del álgebra, que se siguen de propiedades análogas de los números racionales. La propiedad crucial, que distingue los reales de los racionales, es que existe el límite de una secuencia infinita de cortaduras (bajo ciertas condiciones técnicas). De forma equivalente, hay una cortadura correspondiente a cualquier expansión decimal infinita. Esto es también bastante sencillo.
Suponiendo que todo esto pueda hacerse, veamos como Dedekind puede demostrar que √2×√3 = √6. Hemos visto que √2 corresponde a la cortadura (L1, R2), donde R2 consiste en todos los racionales positivos cuyo cuadrado es mayor que 2. Análogamente, √3 corresponde a la cortadura (L2, R2), donde R2 consiste en todos los racionales positivos cuyo cuadrado es mayor que 3.
Se demuestra fácilmente que el producto de estas cortaduras es (L3, R3) donde R3 consiste en todos los racionales positivos cuyo cuadrado es mayor que 6. Pero ésta es la cortadura correspondiente a √6. ¡Hecho!
La belleza de la aproximación de Dedekind reside en que reduce todas las cuestiones concernientes a números reales a cuestiones correspondientes sobre números racionales -en concreto sobre pares de conjuntos de números racionales-. Por consiguiente, define los números reales puramente en términos de números racionales y operaciones sobre dichos números.
El resultado es que los números reales existen (en un sentido matemático) con tal de que existan los números racionales.
Hay un pequeño precio que pagar: un número real «es» un par de conjuntos de racionales, que no es como lo consideramos habitualmente. Si esto suena extraño, tengamos en cuenta que la representación habitual de un número real como un decimal infinito requiere una secuencia infinita de dígitos decimales 0-9. Es realmente muy complicado definir la suma o producto de dos decimales infinitos, porque los métodos aritméticos usuales para sumar o multiplicar decimales «empiezan por el extremo derecho», y cuando un decimal es infinito, no tiene un extremo derecho.
§. Axiomas para los números naturales
El libro de Dedekind estaba muy bien como ejercicio fundacional, pero a medida que calaba la cuestión sobre la definición de los términos se advirtió que lo que había hecho el libro era desplazar la atención de los reales a los racionales. ¿Cómo sabemos que los números racionales existen? Bien, si suponemos que los enteros existen, esto es fácil: definimos un racional p/q como un par de enteros (p, q) y elaboramos las sumas y productos. Si los enteros existen, también lo hacen los pares de enteros.
“¿Cómo sabemos que los enteros existen?”
Sí, pero ¿cómo sabemos que los enteros existen?
Aparte de un signo más o un signo menos, los enteros son números naturales ordinarios. Tener en cuenta los signos es fácil. Por eso los enteros existen con tal de que existan los números naturales.
Aún no hemos acabado, no obstante. Estamos tan familiarizados con los números naturales que nunca se nos ocurre preguntar si los números familiares 0, 1, 2, 3 y así sucesivamente, existen realmente. Y si lo hacen, ¿qué son?
En 1889, Giuseppe Peano planteó la cuestión de la existencia siguiendo el ejemplo del libro de Euclides. En lugar de discutir la existencia de puntos, rectas, triángulos y similares, Euclides simplemente escribía una lista de axiomas: propiedades que se daban por supuestas. No importa si puntos y demás existen; una pregunta más interesante es: si existieran, ¿qué propiedades se seguirían de ello? De este modo, Peano escribió una lista de axiomas para los números naturales. Las propiedades principales eran:
- Existe un número 0.
- Todo número n tiene un sucesor s(n) (al que designamos n + 1).
- Si P(n) es una propiedad de los números, tal que P(0) es verdadera, y si cada vez que P(n) es verdadera entonces P(s(n)) es verdadera, entonces P(n) es verdadera para todo n (principio de inducción matemática).
Luego definió los números 1, 2 y así sucesivamente en términos de dichos axiomas, esencialmente haciendo
- 1 = s(0)
- 2 = s(s(0))
y así sucesivamente. También definió las operaciones básicas de la aritmética y demostró que obedecen las leyes habituales. En su sistema, 2 + 2 = 4 es un teorema demostrable, enunciado como
s(s(0)) + s(s(0)) = s(s(s(s(0)))).
Una gran ventaja de esta aproximación axiomática es que señala exactamente lo que tenemos que demostrar si queremos probar, por un medio u otro, que los «números naturales» existen. Sólo tenemos que construir un sistema que satisfaga todos los axiomas de Peano.
La cuestión profunda aquí es el significado de «existe» en matemáticas.
En el mundo real algo existe si podemos observarlo o, si esto falla, si podemos inferir su presencia necesaria a partir de cosas que pueden observarse. Sabemos que la gravedad existe porque podemos observar sus efectos, incluso si nadie puede ver la gravedad. Por lo tanto, en el mundo real podemos hablar razonablemente de la existencia de dos gatos, dos bicicletas o dos barras de pan. Sin embargo, el número «2» no es así. No es una cosa, sino una construcción conceptual. Nunca encontramos el número «2» en el mundo real. Lo más cerca a lo que llegamos es a un símbolo, 2, escrito o impreso en papel, o mostrado en una pantalla de ordenador. Sin embargo, nadie piensa que un símbolo es lo mismo que la cosa que representa. La palabra «gato» escrita en tinta no es un gato. Tampoco el símbolo «2» es el número «2».
El significado de «número» es un problema filosófico y conceptual sorprendentemente difícil. Todo es más frustrante por el hecho de que todos conocemos perfectamente cómo utilizar los números. Sabemos cómo se comportan, pero no sabemos lo que son.
§. Conjuntos y clases
En los años ochenta del siglo XIX Gottlob Frege trató de resolver esta cuestión conceptual construyendo números naturales a partir de objetos aún más simples; a saber, conjuntos, o «clases» como él les llamaba. Su punto de partida era la asociación estándar de los números con la actividad de contar. Según Frege, «dos» es una propiedad de aquellos conjuntos -y sólo aquellos- para los que se puede establecer una correspondencia uno-a-uno con un conjunto estándar (a, b) que tiene miembros diferentes a y b. Por lo tanto
{un gato, otro gato}
{una bicicleta, otra bicicleta}
{una barra de pan, otra barra de pan}
pueden hacerse corresponder con {a, b}, de modo que todos «determinan»
-cualquier cosa que eso signifique- el mismo número.
Por desgracia, utilizar una lista de conjuntos estándar como números parece una petición de principio; es muy parecido a confundir un símbolo con lo que representa. Pues ¿cómo podemos caracterizar «una propiedad de aquellos conjuntos que pueden emparejarse uno a uno con el conjunto estándar»?
¿Qué es una «propiedad»? Frege tuvo una intuición maravillosa. Hay un conjunto bien definido que está asociado con cualquier «propiedad», a saber, el conjunto que consiste en todo lo que posee dicha propiedad. La propiedad «primo» está asociada con el conjunto de todos los números primos; la propiedad «isósceles» está asociada con el conjunto de todos los triángulos isósceles, y así sucesivamente.
La paradoja de RussellUna versión menos formal de la paradoja propuesta por Russell es la del barbero del pueblo, que afeita a todos los que no se afeitan a sí mismos. ¿Quién afeita al barbero? Si él no se afeita a sí mismo, entonces por definición es afeitado por el barbero del pueblo: ¡él mismo!
Si él se afeita a sí mismo, entonces es afeitado por el barbero: que, una vez más, es él mismo.
Aparte de varios «amaños» -el barbero es una mujer, por ejemplo-, la única conclusión posible es que no existe tal barbero. Russell reformuló esta paradoja en términos de conjuntos. Definimos un conjunto X que consiste en todos los conjuntos que no son miembros de sí mismos. ¿Es X un miembro de sí mismo, o no lo es? Si no lo es, entonces por definición pertenece a X: él mismo. Si lo es, un miembro de sí mismo, entonces como todos los miembros de X, no es un miembro de sí mismo. Esta vez no hay salida; los conjuntos femeninos no son aún parte de la empresa matemática.
Por ello Frege propuso que el número «dos» es el conjunto que comprende todos los conjuntos para los que puede establecerse una correspondencia uno-a-uno con el conjunto estándar (a,b). Más en general, un número es el conjunto de todos los conjuntos para los que puede establecerse una correspondencia uno-a-uno con cualquier conjunto dado. Así, por ejemplo, el número 3 es el conjunto
{... {a, b, c}, {un gato, otro gato, otro gato más}, {X, Y, Z},...}
aunque probablemente es mejor utilizar objetos matemáticos en lugar de gatos o letras.
Con esta idea, Frege descubrió que podía poner toda la aritmética de los números naturales sobre una base lógica. Todo se reducía a propiedades obvias de conjuntos. Lo desarrolló todo en su obra maestra Die Grunlagen der Arithmetik (Los fundamentos de la aritmética) de 1884, pero, para su amarga decepción, Georg Cantor, despachó el libro como una obra de poco valor. En 1893 Frege, impasible, publicó el primer volumen de otro libro, Die Grundgesetze der Arithmetik (Las leyes básicas de la aritmética) en el que ofrecía un sistema intuitivamente plausible de axiomas para la aritmética. Peano hizo una recensión, pero todos los demás lo ignoraron. Diez años más tarde todo estaba listo para la publicación del segundo volumen del libro, pero para entonces Frege ya era consciente de un fallo básico en sus axiomas. Otros también lo advirtieron. El desastre ocurrió mientras el segundo volumen estaba en prensa. Frege recibió una carta del matemático-filósofo Bertrand Russell, a quien había enviado un ejemplar preliminar de su libro. En resumen, la carta decía aproximadamente esto:
«Querido Gottlob, considere el conjunto de todos los conjuntos que no son miembros de sí mismos. Suyo, Bertrand».
Frege era un lógico soberbio e inmediatamente captó la idea de Russell; de hecho, ya era consciente de las dificultades que podía entrañar. La aproximación general de Frege había supuesto, sin demostración, que cualquier propiedad «razonable» definía un conjunto significativo, consistente en todos los objetos que poseen la propiedad en cuestión. Pero aquí había una propiedad aparentemente razonable, «no ser miembro de sí mismo», que manifiestamente no correspondía a un conjunto.
Un desolado Frege escribió un apéndice a su opus magnum en el que discutía la objeción de Russell. Encontró una corrección de urgencia: eliminemos del dominio de los conjuntos a cualesquiera que sean miembros de sí mismos. Pero nunca se sintió realmente satisfecho con esta propuesta.
Russell, por su parte, trató de reparar la laguna que había en la construcción de Frege de los números naturales a partir de conjuntos. Su idea consistía en restringir el tipo de propiedades que podían utilizarse para definir un conjunto. Por supuesto, él tenía que encontrar una demostración de que este tipo restringido de propiedad nunca llevaba a una paradoja. En colaboración con Alfred North Whitehead, llegó a una complicada y técnica «teoría de tipos» que conseguía ese objetivo. Escribieron su aproximación en los tres tomos de Principia Mathematica, de 1910 - 1913. La definición del número 2 en el primer volumen y el teorema 1 + 1 = 2 se demuestra el segundo. Sin embargo, los Principia Mathematica no acabaron con el debate sobre los fundamentos. La propia teoría de tipos era cuestionable. Se requería algo más simple y más intuitivo.
§. Cantor
Estos análisis del papel fundamental del acto de contar como base de los números llevaron a uno de los más audaces descubrimientos en todas las matemáticas: la teoría de Cantor de los números transfinitos: diferentes tamaños de infinito.
El infinito, con diferentes máscaras, parece inevitable en matemáticas.
No hay un número natural máximo -porque añadir uno siempre produce un número aún más grande- de modo que hay infinitos números naturales.
La geometría de Euclides tiene lugar en un plano infinito, y él demostró también que hay infinitos números primos. En la carrera hacia el cálculo infinitesimal, varias personas, entre ellas Arquímedes, encontraron útil considerar un área o un volumen como la suma de muchas rebanadas infinitamente delgadas. En los primeros días del cálculo infinitesimal la misma imagen de áreas y volúmenes fue utilizada con fines heurísticos, incluso si las demostraciones reales tomaban una forma diferente. Estas apariciones del infinito podían parafrasearse en términos finitos para evitar varias dificultades filosóficas. En lugar de decir «hay infinitos números naturales», por ejemplo, podemos decir «no hay un número natural máximo». En esencia, infinito se está considerando aquí como un proceso que puede prolongarse sin ningún límite concreto, pero que no está completado realmente. Los filósofos llaman a este tipo de infinito «infinito potencial». Por el contrario, el uso explícito de infinito como objeto matemático en sí mismo es el «infinito actual».
Los matemáticos anteriores a Cantor habían advertido que los infinitos actuales tenían características paradójicas. En 1632 Galileo escribió sus Diálogos sobre los dos sistemas máximos del mundo, en donde dos personajes de ficción, el sagaz Salviati y el profano inteligente Sagredo, discuten las causas de las mareas a partir de los puntos de vista geocéntrico y heliocéntrico. Toda mención de las mareas fue eliminada a requerimiento de las autoridades de la Iglesia, lo que convertía el libro en un ejercicio hipotético que en cualquier caso constituía un poderoso argumento a favor de la teoría heliocéntrica de Copérnico.
De paso, los dos personajes discuten algunas de las paradojas del infinito. Sagredo pregunta «¿hay más números que cuadrados?» y señala que puesto que la mayoría de los números naturales no son cuadrados perfectos, la respuesta debe ser «sí». Salviati responde que a todo número se le puede hacer corresponder su cuadrado:
Por consiguiente debe haber tantos números naturales como cuadrados, de modo que la respuesta es «no».
Cantor resolvió estas dificultades al reconocer que, en el diálogo, el adverbio «más» se está utilizando de dos maneras diferentes. Sagredo está señalando que el conjunto de todos los cuadrados es un subconjunto propio del conjunto de todos los números naturales. La postura de Salviati es más sutil: hay una correspondencia uno-a-uno entre el conjunto de los cuadrados y el conjunto de todos los números naturales. Los dos enunciados son diferentes, y ambos pueden ser verdaderos sin llevar a ninguna contradicción.
Siguiendo esta línea de pensamiento, Cantor se vio llevado a la invención de una «aritmética del infinito» que explicaba las paradojas anteriores mientras introducía algunas nuevas. Cantor empezó a pensar en conjuntos debido a algunas cuestiones difíciles que se planteaban en análisis de Fourier, de modo que las ideas estaban enraizadas en teorías matemáticas convencionales. Pero las respuestas que descubrió eran tan extrañas que muchos matemáticos de la época las rechazaron de plano. Otros, no obstante, comprendieron su valor, en especial David Hilbert, quien afirmó: «Nadie nos expulsará del paraíso que ha creado Cantor».
§. Tamaño de conjuntos
El punto de partida de Cantor era el concepto ingenuo de mi conjunto, que es una colección de objetos, sus miembros. Una manera de especificar un conjunto es hacer una lista de sus miembros, poniéndolos simplemente entre paréntesis. Por ejemplo, el conjunto de todos los números naturales entre 1 y 6 se escribe
{1, 2, 3,4, 5, 6}
De forma alternativa, un conjunto puede especificarse enunciando la regla para ser miembro:
{n : 1 ≤ ≤n 6 y n es un número natural}
Los dos conjuntos antes especificados son idénticos. La primera notación está limitada a conjuntos finitos, pero la segunda no. Así, los conjuntos
{n : n es un número natural}
{n : n es un cuadrado perfecto}
están especificados de forma precisa, y ambos son infinitos.
Resulta muy sencillo contar los miembros de un conjunto es contar sus miembros. ¿Qué tamaño tiene? El conjunto {1, 2, 3, 4, 5, 6} tiene seis miembros. También tiene seis miembros el conjunto {1, 4, 9, 16, 25, 36} que consta de los correspondientes cuadrados. Decimos que la cardinalidad del conjunto es 6, y llamamos a 6 un número cardinal. (El adjetivo «cardinal» no es superfluo aquí, porque existe un concepto diferente, el número ordinal, asociado con poner números en orden). El conjunto de todos los números naturales no puede contarse de esta manera, pero Cantor advirtió que a pesar de ello podemos colocar el conjunto de todos los números naturales y el de todos los cuadrados en una correspondencia uno a uno, utilizando el mismo esquema que Galileo. Cada número natural está emparejado con su cuadrado n2.
Cantor definió que dos conjuntos son equinumerosos (la palabra no es suya) si existe una correspondencia uno a uno entre ellos. Si los conjuntos son finitos, esta propiedad es equivalente a «tener el mismo número de miembros». Pero si los conjuntos son infinitos, aparentemente no tiene sentido hablar del «número de miembros»; sin embargo, el concepto de equinumerosidad tiene perfecto sentido. Pero Cantor fue más lejos. Introdujo un sistema de números transfinitos, o cardinales infinitos, que hacía posible decir cuántos miembros tiene un conjunto infinito. Además, dos conjuntos son equinumerosos si y sólo si tienen el mismo número de miembros: el mismo cardinal.
El punto de partida era un nuevo tipo de número, que denotó por el símbolo א0. Esta era la letra hebrea aleph con un subíndice cero, leída hoy como «aleph subcero». Este «número» se define como la cardinalidad del conjunto de todos los números naturales. Insistiendo en que los conjuntos equinumerosos tienen la misma cardinalidad. Cantor exigió entonces que cualquier conjunto que puede ponerse en correspondencia uno-a-uno con el conjunto de los números naturales también tiene cardinalidad אn. Por ejemplo, el conjunto de todos los cuadrados tiene cardinalidad א0. También la tiene el conjunto de todos los números pares:
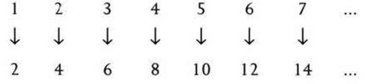
y también el conjunto de todos los números impares
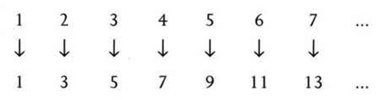
Una consecuencia de estas definiciones es que un conjunto «más pequeño» puede tener la misma cardinalidad que uno «más grande». Pero no hay en esto ninguna contradicción lógica con las definiciones de Cantor, de modo que él consideró que esta característica es una consecuencia natural de su montaje, y un precio que valía la pena pagar. Sólo hay que tener cuidado en no suponer que los cardinales infinitos se comportan igual que los finitos. ¿Por qué deberían hacerlo? ¡Ellos no son finitos!
¿Existen «más» enteros (positivos o negativos) que números naturales? ¿Son el doble? No, porque podemos emparejar los dos conjuntos de este modo:
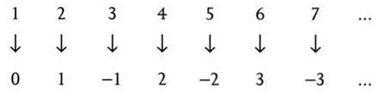
La aritmética de los cardinales infinitos es también extraña. Por ejemplo, acabamos de ver que los conjuntos de números naturales pares e impares tienen cardinal א0. Puesto que estos conjuntos no tienen miembros en común, el cardinal de su unión -el conjunto formado al combinarlos- debería ser, por analogía con los conjuntos finitos, א0 + א0. Pero sabemos cuál es la unión: son los números naturales, con cardinal א0. Por lo tanto
א0 + א0 = א0
Y así son las cosas. Pero una vez más, no hay contradicción: no podemos dividir por א0 y deducir que 1 + 1 = 1, porque no es un número natural y la división no ha sido definida, y mucho menos se ha demostrado que tenga sentido. De hecho, esta ecuación muestra que la división por א0 no siempre tiene sentido. Pero lo aceptamos como el precio del progreso.
Todo esto está muy bien, pero parece como si fuera sólo un símbolo fantasioso para el viejo ∞ y no se aportara nada nuevo. ¿No tienen todos los conjuntos infinitos cardinal א0? ¿No es cierto que todos los infinitos son iguales?
Un candidato para un cardinal infinito mayor que א0 -es decir, un conjunto infinito que no puede ponerse en correspondencia uno-a-uno con el conjunto de todos los números naturales- es el conjunto de todos los números racionales, que normalmente se denota por Q. Después de todo, hay infinitos números racionales en el intervalo entre dos enteros consecutivos, y el truco que utilizamos para los enteros ya no funciona.
Sin embargo, en 1873 Cantor demostró que también Q tiene cardinal א0. La correspondencia uno-a-uno establecida barajaba los números casi por completo, pero nadie había dicho que tuvieran que permanecer en orden numérico. Daba la impresión de que todo conjunto infinito tenía cardinal א0.
Ese mismo año, no obstante, Cantor tuvo una idea trascendental. Demostró que el conjunto R de todos los números reales no tiene cardinal א0, un teorema sorprendente que él publicó en 1874. Por ello, incluso en el sentido especial de Cantor, hay más reales que enteros. Un infinito puede ser mayor que otro infinito.
¿Qué tamaño tiene el cardinal de los reales? Cantor esperaba que fuera א1 el siguiente cardinal más grande después de א0. Pero no pudo demostrarlo, de modo que llamó al nuevo cardinal c, de «continuum».
La supuesta ecuación c = א1 recibió el nombre de hipótesis del continuo. Hasta 1960 los matemáticos no descubrieron la relación entre c y א1, cuando Paul Cohen demostró que la respuesta depende de qué axiomas escojamos para la teoría de conjuntos. Con unos axiomas razonables, los dos cardinales son iguales. Pero con otros axiomas, igualmente razonables, son diferentes.
David Hilbert
1862- 1943David Hilbert se graduó en la Universidad de Königsberg en 1885 con una tesis sobre teoría de invariantes. Pasó a formar parte del gobierno de la universidad hasta que asumió una cátedra en Gotinga en 1895. Siguió trabajando en la teoría de invariantes, demostrando su teorema de base finita en 1888.
Sus métodos eran más abstractos que los entonces de moda, y una de las figuras destacadas del campo, Paul Gordan, encontró el trabajo insatisfactorio. Hilbert revisó el artículo para su publicación en los Annalen, y Klein lo calificó como «el trabajo más importante sobre álgebra general que [la revista] ha publicado nunca».
En 1893 Hilbert empezó un informe general sobre teoría de números, el Zahibericht. Aunque pretendía resumir el estado de la teoría, Hilbert incluyó mucho material original, base de lo que ahora llamamos teoría de campos de clases.
En 1899 había cambiado de nuevo de campo de investigación, y ahora estudiaba los fundamentos axiomáticos de la geometría euclidiana. En 1900, en el Segundo Congreso Internacional de Matemáticos en Paris, presentó una lista de 23 problemas importantes no resueltos. Estos problemas de Hilbert tuvieron un tremendo efecto en la dirección posterior de la investigación matemática.
Alrededor de 1909 su trabajo sobre ecuaciones integrales llevó a la formulación de los espacios de Hilbert, ahora básicos para la mecánica cuántica. También estuvo muy cerca de descubrir las ecuaciones de Einstein para la relatividad general en un artículo de 1915. Añadió una nota en pruebas al efecto de que el artículo era consistente con las ecuaciones de Einstein, lo que dio lugar a la errónea creencia de que Hilbert podría haberse anticipado a Einstein.
En 1930, con ocasión de su retiro, Hilbert fue nombrado ciudadano honorario de Königsberg.
Su discurso de aceptación terminaba con las palabras «Wir Müssen wissen, wir werden wissen» (Debemos saber, sabremos), que recogen su creencia en el poder de las matemáticas y su determinación para resolver incluso los problemas más difíciles.
Aunque la validez de la ecuación c = א1 depende de los axiomas escogidos, hay una igualdad asociada con ella que es independiente de la elección. Esta es c = 2א0. Para cualquier cardinal A podemos definir 2A como el cardinal del conjunto de todos los subconjuntos de A. Y podemos demostrar, muy fácilmente, que 2A es siempre mayor que A. Eso no sólo significa que hay unos infinitos más grandes que otros; también significa que no hay ningún cardinal infinito máximo.
Para qué les servía la lógicaCharles Lutwidge Dodgson, más conocido como Lewis Carroll, utilizó su propia formulación de una rama de la lógica matemática, ahora conocida como cálculo de proposiciones, para enunciar y resolver rompecabezas lógicos. Un ejemplo típico de su Lógica simbólica (1896) es:
- Nadie que realmente aprecie a Beethoven deja de guardar silencio mientras se está interpretando la sonata «Claro de Luna».
- Los conejillos de Indias ignoran la música.
- Nadie que ignore desesperantemente la música guarda silencio mientras se interpreta la sonata «Claro de Luna».
- Por tanto, ningún conejillo de Indias aprecia a Beethoven.
Esta forma de argumento lógico se denomina silogismo, y se remonta a la Grecia clásica.
§. Contradicciones
Pero la tarea mayor de las matemáticas fundacionales no era demostrar que los conceptos matemáticos existen: era demostrar que las matemáticas son lógicamente consistentes. En efecto, todos los matemáticos sabían -en realidad, todos saben hoy- que podría haber una secuencia de pasos lógicos, todos ellos perfectamente correctos, que llevaran a una conclusión absurda. Quizá se podría demostrar que 2 + 2 = 5, ó 1 = 0, por ejemplo. O que 6 es primo, o π = 3.
Podría parecer que una contradicción mínima tendría consecuencias limitadas. En la vida cotidiana la gente suele operar cómodamente dentro de un marco contradictorio: tan pronto uno afirma que, digamos, el calentamiento global está destrozando el planeta como, un momento después, que las líneas aéreas de bajo coste son un gran invento. Pero en matemáticas las consecuencias no están limitadas, y no se pueden evitar las contradicciones lógicas ignorándolas. En matemáticas, una vez que algo está demostrado puede utilizarse en otras demostraciones. Si se ha demostrado 0 = 1, entonces se siguen cosas mucho más desagradables. Por ejemplo, que todos los números son iguales. En efecto, si x es un número cualquiera, partimos de 0 = 1 y multiplicamos por x. Entonces 0 = x. Análogamente, si y es cualquier otro número, 0 = y. Luego x = y.
Peor aún, el método estándar de «demostración por contradicción» significa que cualquier cosa puede ser demostrada una vez que hemos demostrado 0 = 1. Para demostrar el Último Teorema de Fermat, por ejemplo, argumentamos así:
- Supongamos que el Último Teorema de Fermat es falso.
- Entonces 0 = 1.
- Contradicción.
- Luego el Último Teorema de Fermat es verdadero.
Aparte de ser insatisfactorio, este método también demuestra que el Último Teorema de Fermat es falso:
- Supongamos que el Último Teorema de Fermat es verdadero.
- Entonces 0 = 1.
- Contradicción.
- Luego el Último Teorema de Fermat es falso
Si todo es verdadero -y también falso- no puede decirse nada con significado. El conjunto de las matemáticas sería un juego estúpido, sin contenido.
§. Hilbert
El siguiente paso fundacional importante fue dado por David Hilbert, probablemente el matemático más destacado de su época. Hilbert tenía la costumbre de trabajar en un área de las matemáticas durante unos diez años, puliendo los problemas principales, y pasar luego a una nueva área. Hilbert se convenció de que debía ser posible demostrar que las matemáticas nunca pueden llevar a una contradicción lógica. También comprendió que la intuición física no sería útil en este proyecto. Si las matemáticas son contradictorias, debe ser posible demostrar que 0 = 1; en tal caso hay una interpretación física: 0 vacas = 1 vaca, de modo que las vacas pueden desaparecer en un montón de humo. Esto parece poco probable. Sin embargo, no hay garantía de que las matemáticas de los números naturales encajen realmente con la física de las vacas, y es al menos concebible que una vaca pudiera desaparecer repentinamente. Hay un límite al número de vacas en un universo finito, pero no hay límite al tamaño de los enteros matemáticos. Por lo tanto, la intuición física podría ser engañosa, y debería ser ignorada.
Hilbert llegó a este punto de vista en su trabajo sobre la base axiomática de la geometría de Euclides. Él descubrió fallos lógicos en el sistema de axiomas de Euclides, y comprendió que estos fallos habían aparecido porque Euclides había sido confundido por su imaginería visual. Puesto que él sabía que una recta era un objeto largo y fino, un círculo era redondo y un punto era una mota, supuso inadvertidamente ciertas propiedades de estos objetos, sin establecerlas como axiomas. Tras varios intentos, Hilbert presentó una lista de 21 axiomas y discutió su papel en la geometría euclidiana en su Grundlagen der Geometrie (Fundamentos de Geometría) en 1899.
Hilbert sostenía que una deducción lógica debe ser válida independientemente de la interpretación que se le imponga. Todo lo basado en una interpretación particular de los axiomas que falle en otras interpretaciones implica un error lógico. Es esta visión de la axiomática, la más importante influencia de Hilbert sobre los fundamentos de las matemáticas. De hecho, el mismo punto de vista influyó también en el contenido de las matemáticas, lo que hace mucho más fácil -y más respetable- inventar nuevos conceptos dando listas de axiomas para ellos. Muchas de las abstracciones de las matemáticas de principios del siglo XX derivaban del punto de vista de Hilbert.
Se dice a veces que Hilbert defendía la idea de que las matemáticas son un juego sin significado jugado con símbolos, pero esto exagera su postura.
Su idea era que para colocar la disciplina sobre una base lógica firme hay que pensar en ella como si fuera un juego sin significado jugado con símbolos.
Todo lo demás es irrelevante para la estructura lógica. Pero nadie que examine seriamente los descubrimientos matemáticos de Hilbert, y su profundo compromiso con la disciplina, puede deducir razonablemente que él pensaba que estaba jugando a un juego sin significado.
Kurt Gödel
1906-1978En 1923, cuando Gödel fue a la Universidad de Viena, todavía no estaba seguro de si iba a estudiar matemáticas o física.
Su decisión estuvo influida por las lecciones de un matemático seriamente discapacitado, Philipp Furtwängler (hermano de Wilhelm, el famoso director de orquesta y compositor). La propia salud de Gödel era frágil, y la voluntad de Furtwängler para superar sus dificultades le causó una gran impresión. En un seminario impartido por Moritz Schlick, Gödel empezó a estudiar la Introducción a la Filosofía Matemática de Russell, y tuvo claro que su futuro estaba en la lógica matemática.
Su tesis doctoral de 1929 demostraba que un sistema lógico restringido, el cálculo proposicional de primer orden, es completo: todo teorema verdadero puede ser demostrado y todo teorema falso puede ser refutado. Él es más conocido por su demostración de los «Teoremas de Incompletitud de Gödel». En 1931 Gödel publicó su épico artículo «Über formal unentscheidbare Sátze der Principia Matemática und verwandter Systeme». En él demostraba que ningún sistema de axiomas suficientemente rico para formalizar las matemáticas puede ser lógicamente completo.
En 1931 discutió su trabajo con el lógico Ernst Zermelo, pero el encuentro terminó de mala manera, posiblemente porque Zermelo ya había hecho descubrimientos similares pero no los había publicado.
En 1936 Schlick fue asesinado por un estudiante nazi, y Gödel sufrió un trastorno mental (el segundo). Cuando se recuperó visitó Princeton. En 1938 se casó con Adele Porkert, contra los deseos de su madre, y volvió a Princeton inmediatamente después de que Austria fuera anexionada a Alemania. Cuando empezó la Segunda Guerra Mundial le preocupó la posibilidad de ser llamado al ejército alemán, de modo que emigró a Estados Unidos, atravesando Rusia y Japón.
En 1940 produjo un segundo trabajo seminal, una demostración de que la hipótesis del continuo de Cantor es compatible con los axiomas usuales para las matemáticas.
Se convirtió en ciudadano estadounidense en 1948 y pasó el resto de su vida en Princeton. Hacia el final de su vida estaba cada vez más preocupado por su salud, y con el tiempo llegó a convencerse de que alguien estaba tratando de envenenarle.
Se negaba a comer y murió en el hospital. Hasta el final le gustó discutir sobre filosofía con sus visitantes.
Tras su éxito en geometría, Hilbert se propuso un proyecto mucho más ambicioso: colocar el conjunto de las matemáticas sobre una sólida base lógica. Siguió de cerca el trabajo de lógicos destacados, y desarrolló un programa explícito para ordenar los fundamentos de las matemáticas de una vez por todas.
Para qué nos sirve la lógicaUna variante profunda del teorema de incompletitud de Gödel fue descubierta por Alan Turing en un análisis de qué computaciones son factibles publicado en 1936 como Sobre números computables, con una aplicación al Entscheidungsproblem. Turing empezaba formalizando una computación algorítmica -una que sigue una receta preestablecida- en términos de una denominada máquina de Turing. Ésta es una idealización matemática de un dispositivo que escribe símbolos 0 y 1 en una cinta móvil de acuerdo con reglas específicas. Él demostró que el problema de la parada para máquinas de Turing -¿llega a detenerse con el tiempo la computación para un input dado?- es indecidible. Esto significa que no hay un algoritmo que pueda predecir si la computación se para o no. Turing demostró su resultado suponiendo que el problema de la parada era decidible y construyendo una computación que se para si y sólo si no se para, una contradicción. Su resultado demuestra que hay límites a la computabilidad. Algunos filósofos han extendido estas ideas para determinar límites al pensamiento racional, y se ha sugerido que una mente consciente no puede funcionar algorítmicamente. Sin embargo, los argumentos no son concluyentes por ahora. Demuestran que es ingenuo pensar que un cerebro funciona de forma muy parecida a un computador moderno, pero esto no implica que un computador no pueda simular un cerebro.
Además de demostrar que las matemáticas estaban libres de contradicción, también creía que en principio todo problema podía resolverse, que todo enunciado matemático podía ser demostrado o refutado. Varios éxitos iniciales le convencieron de que estaba siguiendo el camino correcto y que el éxito no estaba muy lejos.
§. Gödel
Había un lógico, sin embargo, que no quedó convencido por la propuesta de Hilbert de demostrar que las matemáticas son lógicamente consistentes.
Su nombre era Kurt Gödel, y sus reservas hacia el programa de Hilbert cambiaron para siempre nuestra visión de la verdad matemática.
Antes de Gödel, simplemente se pensaba que las matemáticas eran verdaderas y eran el ejemplo máximo de verdad, porque la verdad de un enunciado como 2 + 2 = 4 pertenecía al dominio del pensamiento puro, independiente de nuestro mundo físico. Las verdades matemáticas no eran cosas que pudieran ser refutadas por experimentos posteriores. En esto eran superiores a las verdades físicas, tales como la ley de la inversa del cuadrado de la gravedad de Newton, que fue refutada por observaciones del movimiento del perihelio de Mercurio que apoyan la nueva teoría gravitatoria sugerida por Einstein.
Después de Gödel, la verdad matemática resultó ser una ilusión. Lo que existía eran las demostraciones matemáticas, cuya lógica interna muy bien podría ser intachable, pero existían en un contexto más amplio -matemáticas fundacionales- donde no podía haber garantía de que todo el juego tuviera siquiera significado. Gödel no sólo afirmaba esto: lo demostró. De hecho, hizo dos cosas que juntas echaban por tierra el cuidadoso y optimista programa de Hilbert.
Gödel demostró que si las matemáticas son lógicamente consistentes, entonces es imposible demostrarlo. No es sólo que él no pudiera encontrar una demostración, sino que no existe demostración. Por ello, y esto es notable, si se consigue demostrar que las matemáticas son consistentes, se sigue inmediatamente que no lo son. Él demostró también que algunos enunciados matemáticos no pueden ser demostrados ni refutados. Una vez más, no es sólo que él no pudiera conseguirlo, sino que es imposible. Tales enunciados se llaman indecidibles.
Inicialmente, Gödel demostró estos teoremas dentro de una particular formulación lógica de las matemáticas, la adoptada por Russell y Whitehead en sus Principia Mathematica. Al principio Hilbert pensaba que podría haber una escapatoria: encontrar una formulación mejor. Pero cuando los lógicos estudiaron el trabajo de Gödel, rápidamente se hizo patente que las mismas ideas funcionarían en cualquier fundamentación lógica de las matemáticas suficientemente fuerte para expresar los conceptos básicos de la aritmética.
Una consecuencia intrigante de los descubrimientos de Gödel es que cualquier sistema axiomático para las matemáticas debe ser incompleto: nunca se puede elaborar una lista completa de axiomas que determinen de forma unívoca todos los teoremas verdaderos o falsos. No hay escapatoria: el programa de Hilbert no puede funcionar. Se dice que cuando Hilbert supo por primera vez del trabajo de Gödel se puso «extraordinariamente furioso». Su furia muy bien podría haber estado dirigida hacia sí mismo, porque la idea básica en el trabajo de Gödel es simple. (La implementación técnica de dicha idea es bastante difícil, pero Hilbert era bueno con las cuestiones técnicas.)
Es probable que Hilbert se diera cuenta de que debería haber visto venir los teoremas de Gödel.
Russell demolió el libro de Frege con una paradoja lógica, la paradoja del barbero del pueblo que afeita a todos los que no se afeitan a sí mismos:
«el conjunto de todos los conjuntos que no son miembros de sí mismos». Gödel demolió el programa de Hilbert con otra paradoja lógica, la paradoja de alguien que dice «este enunciado es mentira». Pues en efecto, el enunciado indecidible de Gödel -sobre el que se basa todo lo demás- es un teorema T que afirma «este teorema no puede ser demostrado».
Si todo teorema puede ser demostrado o refutado, entonces el enunciado T de Gödel es contradictorio en uno u otro caso. Supongamos que T puede ser demostrado: entonces T afirma que T no puede ser demostrado, una contradicción. Por el contrario, si T puede ser refutado, entonces T es falso, de modo que es falso afirmar que T no puede ser demostrado. Por consiguiente, T puede ser demostrado, otra contradicción. Por ello, la hipótesis de que todo teorema no puede ser ni demostrado ni refutado nos dice que T puede ser demostrado si y sólo si no puede ser demostrado.
§. ¿Dónde estamos ahora?
Los teoremas de Gödel cambiaron la forma en que vemos los fundamentos lógicos de las matemáticas. Implican que problemas actualmente no resueltos pueden no tener solución: no son verdaderos ni falsos, sino que están en el limbo de la indecibilidad. Y se ha demostrado que muchos problemas interesantes son indecidibles.
Sin embargo, el efecto del trabajo de Gödel no se ha extendido, en la práctica, mucho más allá del área de los fundamentos donde tuvo lugar. Correcta o erróneamente, los matemáticos que trabajan en la conjetura de Poincaré, o en la hipótesis de Riemann, dedican su tiempo a buscar demostraciones o refutaciones.
“Los teoremas de Gödel cambiaron la forma en que vemos los fundamentos lógicos de las matemáticas.”
Ellos son conscientes de que el problema puede ser indecidible, e incluso podrían buscar una demostración de indecidibilidad si pudieran ver dónde empezar. Pero la mayoría de los problemas indecidibles conocidos tienen un sabor «auto-referencial» y, sin eso, una demostración de indecidibilidad parece inalcanzable.
A medida que la disciplina construía teorías cada vez más complicadas sobre las anteriores, la superestructura de las matemáticas empezó a descomponerse debido a hipótesis no reconocidas que resultaban falsas.
Se hacía necesario un trabajo serio que cimentara bien todo el edificio.
Las investigaciones posteriores ahondaron en la verdadera naturaleza de los números, trabajando hacia atrás desde los números complejos a los reales, a los racionales y luego a los naturales. Pero el proceso no se detuvo ahí. En su lugar, los propios sistemas de números fueron reinterpretados en términos de ingredientes aún más simples, los conjuntos.
La teoría de conjuntos llevó a avances importantes, incluido un sistema razonable, aunque heterodoxo, de números infinitos. También reveló algunas paradojas fundamentales relacionadas con la noción de un conjunto.
La resolución de dichas paradojas no fue, como Hilbert esperaba, una reivindicación completa de las matemáticas axiomáticas y una demostración de su consistencia lógica. En su lugar, fue una demostración de que las matemáticas tienen limitaciones inherentes y de que algunos problemas no tienen solución. El resultado fue un cambio profundo en la forma de pensar sobre la verdad y la certeza matemática. Es mejor ser conscientes de nuestras limitaciones que vivir en el paraíso de un loco.
Capítulo 18
¿Cuán probable es eso?
La aproximación racional al azar
El crecimiento de las matemáticas en el siglo XX y principios del XXI ha sido explosivo. Se han descubierto más nuevas matemáticas en los últimos 100 años (pie en toda la historia anterior de la humanidad. Esbozar someramente estos descubrimientos requeriría miles de páginas, así que nos vemos forzados a examinar unos pocos ejemplos de entre la enorme cantidad de material disponible.
Una rama de las matemáticas especialmente novedosa es la teoría de la probabilidad, que estudia las probabilidades asociadas a sucesos aleatorios. Son las matemáticas de la incertidumbre.
Las épocas anteriores escarbaron la superficie, con cálculos combinatorios de posibilidades en juegos de azar y métodos para mejorar la precisión de las observaciones astronómicas pese a los errores observacionales, pero sólo a comienzos del siglo XX emergió la teoría de probabilidades como una disciplina por sí misma.
§. La teoría de probabilidades
Hoy día, la teoría de probabilidades es un área mayor de las matemáticas, y su ala aplicada, la estadística, tiene un efecto importante en nuestra vida cotidiana, posiblemente más importante que cualquier otra área individual de las matemáticas. La estadística es una de las principales técnicas analíticas de la profesión médica. Ningún medicamento sale al mercado, y ningún tratamiento se permite en un hospital, a menos que los ensayos clínicos hayan asegurado que es suficientemente seguro y que es efectivo.
La seguridad es aquí un concepto relativo: en casos de pacientes extremadamente graves pueden utilizarse tratamientos cuya escasa probabilidad de éxito no los hace aconsejables para enfermedades menos dañinas.
La teoría de probabilidades quizá es también el área de las matemáticas peor entendida y peor utilizada. Pero utilizada adecuada e inteligentemente, contribuye de forma importante al bienestar humano.
§. Juegos de probabilidad
Algunas cuestiones probabilísticas se remontan a la antigüedad. En la Edad Media encontramos estudios sobre las posibilidades de sacar números diversos al lanzar dos dados. Para ver cómo funciona esto, empecemos con un dado. Suponiendo que el dado no está cargado -lo que resulta ser un concepto difícil de establecer- cada uno de sus seis números 1,2, 3, 4, 5 y 6 debería salir, «a la larga», con la misma frecuencia. A corto plazo, la igualdad es imposible: por ejemplo, en la primera tirada debe salir sólo uno de esos números. Pero en una larga serie de lanzamientos, o «ensayos», esperamos que cada número salga aproximadamente una vez de cada seis; es decir, con probabilidad 1/6. Si esto no sucediera, el dado estaría con toda probabilidad cargado o sesgado.
Un suceso de probabilidad 1 es «seguro», y uno con probabilidad 0 es imposible. Todas las probabilidades están entre 0 o 1, y la probabilidad de un suceso representa la proporción de ensayos en los que ocurre el suceso en cuestión.
Volvamos a la pregunta medieval. Supongamos que lanzamos dos dados simultáneamente (como en numerosos juegos desde los dados al Monopoly). ¿Cuál es la probabilidad de que su suma sea 5? El resultado de numerosos estudios, y algunos experimentos, es que la respuesta es 1/9. ¿Por qué? Supongamos que distinguimos los dos dados, coloreando uno de azul y el otro de rojo. Cada dado puede dar independientemente seis números distintos, lo que da un total de 36 pares de números posibles, todos igualmente probables. Las combinaciones (azul + rojo) que dan 5 son 1 +4, 2 + 3, 3 + 2, 4 + 1; son casos distintos porque el dado azul da resultados distintos en cada caso, y lo mismo hace el dado rojo. Por ello, a largo plazo esperamos encontrar una suma de 5 en cuatro ocasiones de 36, una probabilidad de 4/36 = 1/9.
Otro problema antiguo, con una evidente aplicación práctica, es cómo dividir las apuestas en un juego de azar si el juego se interrumpe por alguna razón. Los algebristas del Renacimiento, Pacioli, Cardano y Tartaglia, escribieron sobre la cuestión. Más tarde el Caballero de Mere planteó a Pascal la misma pregunta, y Pascal y Fermat intercambiaron varias cartas sobre el tema.
De este trabajo inicial salió una comprensión implícita de lo que son las probabilidades y cómo calcularlas. Pero todo estaba muy confuso y mal definido.
§. Combinaciones
Una definición operativa de la probabilidad de un suceso es la proporción de ocasiones en que sucederá. Si lanzamos un dado, y las seis caras son igualmente probables, entonces la probabilidad de que salga una cara concreta es 1/6. Mucho trabajo anterior sobre probabilidades se basaba en calcular de cuántas maneras podía ocurrir un suceso y dividirlas por el número total de posibilidades.
Un problema básico aquí es el de las combinaciones. Dado, digamos, un mazo de seis cartas, ¿cuántos conjuntos diferentes de cuatro cartas hay? Un método consiste en hacer la lista de tales subconjuntos: si las cartas son 1-6, entonces son
| 1234 | 1235 | 1236 | 1245 | 1246 |
| 1256 | 1345 | 1346 | 1356 | 1456 |
| 2345 | 2346 | 2356 | 2456 | 3456 |
de modo que hay 15. Pero este método falla para números grandes, y se necesita algo más sistemático.
Imaginemos que escogemos los miembros del subconjunto, de uno en uno. Podemos escoger el primero de seis maneras, el segundo de sólo cinco (puesto que uno ya está descartado), el tercero de cuatro maneras, el cuarto de tres maneras. El número total de elecciones, en este orden, es 6×5 × 4 × 3 = 360. Sin embargo, cada subconjunto se cuenta 24 veces: además de 1234 encontramos 1243, 2134 y demás, y hay 24 maneras de reordenar cuatro objetos. Por lo tanto, la respuesta correcta es 360/24, que es igual a 15.
Este argumento muestra que el número de maneras de escoger m objetos de entre un total de n objetos es
Estas expresiones se llaman coeficientes binomiales, porque también aparecen en álgebra. Si los disponemos en una tabla, de modo que la n-ésima fila contiene los coeficientes binomiales,
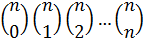
entonces el resultado es el siguiente:
En la sexta fila vemos los números 1, 6, 15, 20, 15, 6, 1. Comparémoslo con la fórmula
(x + 1)6 = x6 + 6x5 + 15x4 + 20x3 + 15x2 + 6x + 1
y vemos que los mismos números aparecen como coeficientes. Esto no es una coincidencia.
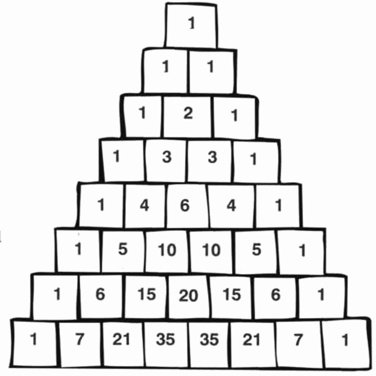
Triángulo de Pascal
El triángulo de números se denomina Triángulo de Pascal porque fue estudiado por Pascal en 1655. Sin embargo, era conocido mucho antes; se remonta a aproximadamente el año 950 en un comentario sobre un antiguo libro indio llamado el Chandas Sastra. También era conocido por los matemáticos persas Al-Karaji y Omar Khayyam, y se conoce como el «triángulo de Khayyam» en el Irán moderno.
§. Teoría de la probabilidad
Los coeficientes binomiales se utilizaban con buen efecto en el primer libro sobre probabilidades: el Ars Conjectandi (Arte de conjeturar) escrito por Jakob Bernoulli en 1713. El curioso título se explica en el libro:
«Definimos el arte de la conjetura, o arte estocástico, como el arte de evaluar lo más exactamente posible las probabilidades de las cosas, de modo que en nuestros juicios y acciones podamos siempre basarnos en lo que se ha encontrado que es lo mejor, lo más apropiado, lo más seguro, lo más aconsejado; éste es el único objeto de la sabiduría del filósofo y la prudencia del gobernante».
Por eso, una traducción más precisa podría ser El Arte de la Conjetura.
Bernoulli daba por supuesto que un número cada vez mayor de ensayos llevaba a estimaciones de la probabilidad cada vez mejores. «Supongamos que, sin saberlo nosotros, hay ocultas en una urna 3.000 canicas blancas y 2.000 canicas negras, y para tratar de determinar los números de estas canicas sacamos una canica detrás de otra (volviendo a meter de nuevo la canica...) y que observamos con qué frecuencia sacamos una canica blanca y con qué frecuencia sacamos una canica negra ... ¿Puede hacerse esto tan a menudo que se haga diez veces, cien veces, mil veces, etc., más probable ... que los números de canicas blancas y negras escogidas estén en la misma razón 3:2 que las canicas en la urna, y no una razón diferente?»
Aquí Bernoulli planteaba una pregunta fundamental, y también inventó un ejemplo ilustrativo estándar, el de las bolas en urnas. Evidentemente creía que una razón 3:2 era el resultado razonable, aunque también reconocía que los experimentos reales sólo se aproximarían a esta razón. Pero creía que con suficientes ensayos esta aproximación se haría cada vez mejor.
Aquí se plantea una dificultad que impidió el avance de la disciplina durante un tiempo. En un experimento semejante es ciertamente posible que por puro azar todas las canicas sacadas fueran blancas. Por lo tanto, no hay ninguna garantía férrea de que la razón deba tender siempre a 3:2.
Para qué les servía la probabilidadEn 1710 John Arbuthnot presentó un artículo a la Royal Society en el que utilizaba la teoría de probabilidades como prueba de la existencia de Dios. Analizó el número anual de bautizos de niños y niñas durante el periodo 1629-1710 y encontró que había ligeramente más niños que niñas. Además, la cifra era prácticamente la misma todos los años. Este hecho ya era bien conocido, pero Arbuthnot procedió a calcular la probabilidad de que la proporción fuera constante. Su resultado era muy pequeño 2-40. Entonces señaló que si el mismo efecto se daba en todos los países, y en todos los tiempos a lo largo de la historia, entonces las probabilidades son aún más pequeñas, y concluyó que la responsable debía ser la divina providencia, y no el azar.
Por el contrario, en 1872 Francis Galton utilizó las probabilidades para estimar la eficacia de la oración, advirtiendo que muchas personas rezaban todos los días por la salud de la familia real. Recogió datos y tabuló la «edad promedio alcanzada por varones de varias clases que hubieran superado los 30 años, desde 1758 a 1843», añadiendo que «se excluyen muertes por accidente». Estas clases eran hombres eminentes, realeza, clero, abogados, médicos, aristócratas, clase alta, hombres de negocios, oficiales navales, literatos y científicos, oficiales del ejército, artistas. Encontró que «Los soberanos son literalmente los de más corta vida de todos los que poseen riqueza material. Por lo tanto, la oración no tiene eficacia, a menos que se plantee la hipótesis muy cuestionable de que las condiciones de vida de la realeza puedan ser de forma natural más fatales, y que su influencia está parcialmente, aunque no totalmente, neutralizada por los efectos de las oraciones públicas».
Lo más que podemos decir es que, con muy alta probabilidad, los números deberían acercarse a dicha razón. Pero ahora hay un peligro de lógica circular: utilizamos razones observadas en ensayos para inferir probabilidades, pero también utilizamos probabilidades para realizar la inferencia. ¿Cómo podemos observar que la probabilidad de que todas las canicas sean blancas es muy pequeña? Si lo hacemos con montones de ensayos, tenemos que hacer frente a la posibilidad de que el resultado sea equívoco, por la misma razón; y parece que la única salida es hacer aún más ensayos para mostrar que este suceso es altamente poco probable. Estamos atrapados en lo que se parece mucho a un regreso infinito.
Por fortuna, los primeros investigadores en teoría de probabilidades no permitieron que esta dificultad lógica les detuviera. Como en el caso del cálculo infinitesimal, ellos «sabían» lo que querían hacer y cómo hacerlo. La justificación filosófica era menos interesante que calcular las respuestas.
El libro de Bernoulli contenía una riqueza de ideas y resultados importantes. Uno, la Ley de los Grandes Números, decía exactamente en qué sentido las razones de largas observaciones en ensayos corresponden a probabilidades. Básicamente demuestra que la probabilidad de que la razón no se aproxime mucho a la probabilidad correcta tiende a cero cuando el número de ensayos aumenta sin límite.
Otro teorema básico puede verse en términos de lanzamientos repetidos de una moneda sesgada, con una probabilidad p de salir cara y q = 1 - p de salir cruz. Si la moneda se lanza dos veces, ¿cuál es la probabilidad de que salgan exactamente 2, 1 ó 0 caras? La respuesta de Bernoulli era p2, 2pq y q2. Estos son los términos que aparecen en el desarrollo de (p + q)2 como era p2 + 2pq + q2. Del mismo modo, si la moneda se lanza tres veces, las probabilidades de 3, 2, 1 ó 0 caras son los términos sucesivos en (p + q)3 = p3 + 3p2q + 3q2p + q3.
Más en general, si la moneda se lanza n veces, la probabilidad de sacar exactamente m caras es igual a
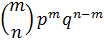
el término correspondiente en el desarrollo de (p + q)n.
Entre 1730 y 1738 Abraham De Moivre extendió el trabajo de Bernoulli a monedas sesgadas. Cuando m y n son grandes es difícil calcular los coeficientes binomiales exactamente, y De Moivre dedujo una fórmula aproximada que relaciona la «distribución binomial» de Bernoulli con lo que ahora llamamos la función error o distribución normal
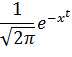
De Moivre fue presumiblemente el primero en hacer explícita esta conexión, que iba a mostrarse fundamental para el desarrollo de la teoría de probabilidades y de la estadística.
§. Definiendo la probabilidad
Un problema conceptual importante en la teoría de probabilidades era definir la probabilidad. Incluso los ejemplos simples -cuya respuesta era conocida por todos- presentaban dificultades lógicas. Si lanzamos una moneda, esperamos obtener «a la larga» números iguales de caras y cruces, y la probabilidad de cada una es ½. Más exactamente, ésta es la probabilidad si la moneda es «limpia». Una moneda sesgada podría salir siempre cara.
Pero ¿qué significa «limpia»? Presumiblemente, que caras y cruces son igualmente probables. Pero la expresión «igualmente probables» hace referencia a las probabilidades. La lógica parece circular. Para definir la probabilidad necesitamos saber qué es la probabilidad.
La salida de este punto muerto es una que se remonta a Euclides, y fue llevada a la perfección por los algebristas de finales del siglo XIX y principios del XX. Axiomatizar. Dejar de preocuparnos por lo que son las probabilidades. Escribir las propiedades que queremos que posean las probabilidades y considerar que son axiomas. Y deducir de ellos todo lo demás.
La pregunta era: ¿cuáles son los axiomas correctos? Cuando las probabilidades se refieren a conjuntos de sucesos finitos, esta pregunta tiene una respuesta relativamente fácil. Pero las aplicaciones de la teoría de la relatividad implican con frecuencia elecciones entre conjuntos de posibilidades potencialmente infinitos. Si medimos el ángulo entre dos estrellas, pongamos por caso, ése puede ser en teoría cualquier número real entre 0º y 180º. Hay infinitos números reales. Si lanzamos un dardo contra una tabla, de tal manera que a la larga tenga la misma probabilidad de dar en cada punto de la tabla, entonces la probabilidad de dar en una región dada debería ser el área de dicha región dividida por el área total de la tabla. Pero hay infinitos puntos en la tabla, e infinitas regiones.
Estas dificultades generaban todo tipo de problemas y todo tipo de paradojas. Finalmente fueron resueltas por una idea nueva procedente del análisis, el concepto de medida.
Los analistas que trabajaban en la teoría de la integración encontraron necesario ir más allá de Newton y definir nociones cada vez más sofisticadas de lo que constituye una función «integrable» y lo que es una integral. Tras una serie de intentos por parte de varios matemáticos, Henri Lebesgue consiguió definir un tipo muy general de integral, ahora llamada integral de Lebesgue, con muchas propiedades analíticas agradables y útiles.
La clave para su definición era la medida de Lebesgue, que es una manera de asignar un concepto de longitud a subconjuntos muy complicados de la recta real. Supongamos que el conjunto consiste en intervalos no solapados de longitudes 1, ½, ¼, ⅛ y así sucesivamente. Estos números forman una serie convergente con suma 2. Por ello, Lebesgue insistió en que este conjunto tiene medida 2. El concepto de Lebesgue tiene una nueva característica: es aditivo numerable. Si juntamos una colección infinita de conjuntos que no se solapan, y si esta colección es numerable en el sentido de Cantor, con cardinal א0 entonces la medida del conjunto total es la suma de la serie infinita formada por las medidas de los conjuntos individuales.
En muchos aspectos la idea de medida era más importante que la integral a la que llevaba.
En particular, la probabilidad es una medida. Esta propiedad fue explicitada en los años treinta del siglo XX por Andrei Kolmogorov, que estableció axiomas para la probabilidad.
Más exactamente, él definió un espacio de probabilidades. Este comprende un conjunto X, una colección B de subconjuntos de X llamados sucesos, y una medida m sobre B. Los axiomas afirman que m es una medida, y que m(X) = 1 (es decir, la probabilidad de que suceda algo es siempre 1).
También se requiere que la colección B tenga algunas propiedades de teoría de conjuntos que le permitan soportar una medida.
En el caso de un dado, el conjunto X consiste en los números 1-6, y el conjunto B contiene cada subconjunto de X. La medida de cualquier conjunto Y en B es el número de miembros de Y dividido por 6. Esta medida es compatible con la idea intuitiva de que cada una de las caras del dado tiene probabilidad ‘/6 de salir. Pero el uso de una medida nos exige considerar no sólo caras, sino conjuntos de caras. La probabilidad asociada con uno de tales conjuntos Y es la probabilidad de que salga una cara en Y. Intuitivamente, esto es el tamaño de Y dividido por 6.
Con esta simple idea, Kolmogorov resolvió varios siglos de controversia, a menudo acalorada, y creó una teoría de probabilidades rigurosa.
§. Datos estadísticos
El brazo aplicado de la teoría de probabilidades es la estadística, que utiliza las probabilidades para analizar datos del mundo real. Surgió de la astronomía del siglo XVIII, cuando había que tener en cuenta los errores observacionales.
Para qué nos sirve la probabilidadUn uso muy importante de la teoría de probabilidades se da en los ensayos médicos de nuevos medicamentos. Estos ensayos recogen datos de los efectos de los medicamentos: ¿parecen curar algún trastorno, o tienen efectos adversos indeseados? Cualquier cosa que las cifras parezcan indicar, la gran pregunta aquí es si los datos son estadísticamente significativos. Es decir, ¿son los datos el resultado de un efecto genuino del medicamento o son el resultado del puro azar? El problema se resuelve utilizando métodos estadísticos conocidos como comprobación de hipótesis. Estos métodos comparan los datos con un modelo estadístico y estiman la probabilidad de que el resultado aparezca por azar.
Si, pongamos por caso, dicha probabilidad es menor que 0,01, entonces con probabilidad 0,99 los datos no se deben al azar.
Es decir, el efecto es significativo a un nivel del 99 por 100.
Tales métodos hacen posible determinar con un considerable nivel de confianza qué tratamientos son efectivos, o cuáles producen efectos adversos y no deberían utilizarse.
Empírica y teóricamente, tales errores se distribuyen de acuerdo con la función error o distribución normal, a veces llamada la curva de campana debido a su forma.
La curva de campana
Aquí el error se mide en horizontal, con error cero en el centro, y la altura de la curva representa la probabilidad de un error de tamaño dado. Los errores pequeños son bastante probables, mientras que los grandes son muy improbables.
En 1835 Adolphe Quetelet defendió la utilización de la curva de campana para modelar datos sociales: nacimientos, muertes, divorcios, crímenes y suicidios.
Gráfica de Quetelet de cuántas personas tienen una altura dada: la altura está representada en el eje horizontal y el número de personas, en el vertical
Descubrió que aunque tales sucesos son impredecibles para individuos, tienen pautas estadísticas cuando se observan para una población entera. Personificó esta idea en términos del «hombre medio», un individuo ficticio que era un promedio en todos los aspectos. Para Quetelet, el hombre medio no era sólo un concepto matemático: era el objetivo de la justicia social.
A partir de 1880, aproximadamente, las ciencias sociales empezaron a hacer un amplio uso de ideas estadísticas, en especial de la curva de campana, como sustituto de los experimentos. En 1865 Francis Galton hizo un estudio de la herencia humana. ¿Cómo está relacionada la altura de un niño con la de sus padres? ¿Qué pasa con el peso, o con la capacidad intelectual?
El adoptó la curva de Quetelet, pero la veía como un método para separar poblaciones distintas, no como un imperativo moral. Si algunos datos mostraban dos picos, en lugar del único máximo de la curva de campana, entonces dicha población debía estar compuesta de dos sub-poblaciones diferentes, cada una de ellas con su propia curva de campana. En 1877 las investigaciones de Galton le llevaron a inventar el análisis de regresión, una forma de relacionar dos conjuntos de datos para encontrar la relación más probable.
Otra figura clave fue Ysidor Edgeworth. Edgeworth carecía de la visión de Galton, pero le superaba en técnica y puso las ideas de Galton sobre una firme base matemática. Una tercera figura fue Karl Pearson, quien desarrolló considerablemente las matemáticas. Pero el papel más efectivo de Pearson fue el de propagandista: él convenció al mundo exterior de que la estadística era útil.
Newton y sus sucesores demostraron que las matemáticas pueden ser un modo muy efectivo de entender las regularidades de la naturaleza.
La invención de la teoría de probabilidades, y su ala aplicada, la estadística, hizo lo mismo para las irregularidades de la naturaleza. Es curioso que existan pautas numéricas en los sucesos de azar. Pero estas pautas se manifiestan sólo en magnitudes estadísticas tales como promedios y tendencias a largo plazo. Hacen predicciones, pero éstas predicen las probabilidades de que algo suceda o no suceda. No predicen cuándo sucederá. Pese a ello, las probabilidades son ahora una de las técnicas matemáticas más ampliamente utilizadas, y se emplean en ciencia y medicina para asegurar que deducciones hechas a partir de observaciones son significativas y no pautas aparentes resultado de asociaciones casuales.
Capítulo 19
Mascando Números
Máquinas de calcular y matemáticas computacionales
Los matemáticos han soñado siempre con construir máquinas para reducir la pesadez de los cálculos rutinarios.
Cuanto menos tiempo se gasta en cálculos, más tiempo se puede dedicar a pensar. Desde tiempos prehistóricos se utilizaron palos y guijarros como ayuda para hacer recuentos, y las pilas de guijarros llevaron con el tiempo al ábaco, en el que unas cuentas que deslizan a lo largo de varillas representan los dígitos de los números. Especialmente perfeccionado por los japoneses, el ábaco podía realizar aritmética básica de forma rápida y precisa en manos de un experto. Alrededor de 1950 un ábaco japonés superaba a una calculadora mecánica manual.
§. ¿Un sueño que se cumple?
En el siglo XXI, la llegada de los computadores electrónicos y la amplia disponibilidad de los circuitos integrados («chips») dieron a las máquinas una enorme ventaja. Eran mucho más rápidas que un cerebro humano o un dispositivo mecánico; miles de millones o billones de operaciones por segundo son ahora un lugar común. El más rápido cuando escribo esto. Blue Gene/L de IBM, puede realizar mil billones de cálculos («operaciones de coma flotante») por segundo. Los computadores actuales también tienen una enorme memoria, que puede almacenar el equivalente a centenares de libros listos para un acceso casi instantáneo. Los gráficos en color han llegado a un máximo de calidad.
§. La aparición del computador
Las máquinas anteriores eran más modestas, pero ahorraban mucho tiempo y esfuerzo. El primer avance después del ábaco fue probablemente los huesos de Napier, o piedra de Napier, un sistema de varas marcadas que inventó Napier antes de dar con los logaritmos. En esencia eran componentes «universales» de la «larga multiplicación» tradicional. Las varas podían utilizarse en lugar de lápiz y papel, lo que ahorraba el tiempo de escribir numerales, pero imitaban los cálculos manuales.
En 1642 Pascal inventó la primera calculadora genuinamente mecánica, la Máquina Aritmética, para ayudar a su padre en sus cuentas. Podía realizar sumas y restas, pero no multiplicaciones ni divisiones. Tenía ocho discos rotatorios, por lo que trabajaba efectivamente con números de ocho cifras.
En la década siguiente Pascal construyó cincuenta máquinas similares, muchas de las cuales se conservan hoy en museos.
En 1671 Leibniz diseñó una máquina para multiplicar, y construyó una en 1694, pues decía él:
«No es digno de hombres excelentes perder horas como esclavos en la labor de cálculo, que podría ser relegada con seguridad a cualquiera si se utilizaran máquinas».
Llamó a su máquina el Staffelwalze (calculador por pasos). Su idea principal fue ampliamente utilizada por sus sucesores.
Una de las propuestas más ambiciosas para una máquina de calcular fue hecha por Charles Babbage. Este contaba que, en 1812:
«Estaba sentado en la sala de la Sociedad Analítica, en Cambridge, con la cabeza inclinada hacia la mesa en un estado de somnolencia, con una tabla de logaritmos abierta ante mí. Otro miembro, al entrar en la habitación y verme medio dormido, gritó,
«Bien, Babbage, ¿en qué estas soñando? a lo que respondí:
«Estoy pensando que todas estas tablas -señalando los logaritmos- podrían calcularse con una máquina».
Babbage persiguió este sueño durante el resto de su vida, y construyó un prototipo llamado motor de diferencias. Buscó financiación del gobierno para máquinas más elaboradas. Su proyecto más ambicioso, el motor analítico, era de hecho un computador mecánicos programable.
No se llegó a construir ninguna de estas máquinas, aunque se hicieron varios componentes. Una reconstrucción moderna del motor de diferencias se encuentra en el Museo de la Ciencia de Londres, y funciona. Augusta Ada Lovelace contribuyó al trabajo de Babbage con el desarrollo de algunos de los primeros «programas informáticos» escritos.
La primera calculadora producida en masa, el «Arithmometer», fue fabricada por Thomas de Colmar en 1820. Empleaba un mecanismo de «tambor dentado» y todavía se producía en 1920. El siguiente paso importante fue el mecanismo de «rueda perforada» del inventor sueco Willgodt T. Odhner. Su calculadora fijó la pauta para docenas, si no centenares, de máquinas similares, construidas por diversos fabricantes.
Método de Newton para resolver numéricamente una ecuación
La potencia motriz era suministrada por el operador, que giraba una manivela que movía una serie de discos rotatorios en los que se mostraban los dígitos 0-9. Con práctica podían realizarse cálculos complicados a gran velocidad. Los cálculos científicos y de ingeniería del Proyecto Manhattan de la Segunda Guerra Mundial, cuyo objetivo era construir la primera bomba atómica, se realizaron con estas máquinas manejadas por un escuadrón de «calculadores», principalmente mujeres jóvenes. La llegada de potentes calculadoras electrónicas baratas en los años ochenta hizo obsoletas las calculadoras mecánicas, pero su uso en los negocios y el cálculo científico era generalizado hasta entonces.
Las máquinas de calcular aportan más que simple aritmética, porque muchos cálculos científicos pueden ser implementados numéricamente como largas series de operaciones aritméticas. Uno de los primeros «métodos numéricos», que resuelve ecuaciones con una precisión arbitrariamente grande, fue inventado por Newton, y por ello se conoce como método de Newton. Resuelve una ecuación f(x) = 0 mediante el cálculo de una serie de aproximaciones sucesivas a una solución, cada una de las cuales se basa en la anterior y la mejora.
Augusta Ada King, condesa de Lovelace
1815-1852Augusta Ada era hija del poeta Lord Byron y de Anne Milbanke. Sus padres se separaron un mes después de que naciera, y ella nunca volvió a ver a su padre.
La niña demostró aptitud para las matemáticas, y Lady Byron, una excepción en su tiempo, pensó que las matemáticas eran una buena formación para la mente y animó a su hija a que las estudiara. En 1833 Ada conoció a Charles Babbage en una fiesta, y poco después éste le mostró su prototipo de motor de diferencias; ella lo encontró fascinante y rápidamente entendió su funcionamiento.
Se convirtió en condesa de Lovelace cuando su marido William fue nombrado conde en 1838.
En su traducción de 1843 de las Notions sur la Machine Analytique de Charles Babbage, de Luigi Menabrea, Ada añadió programas que ella misma había desarrollado. Escribió que «La característica distintiva del Motor Analítico ... es la introducción en el mismo del principio que Jacquard concibió para regular, por medio de tarjetas perforadas, las pautas más complicadas en la fabricación de brocados ... Podemos decir muy adecuadamente que el Motor Analítico teje pautas algebraicas igual que el buzo de Jacquard teje flores y hojas».
A los 36 años se le manifestó un cáncer de útero, y murió tras un largo período de intensos dolores, cuidada hasta la muerte por sus doctores.
A partir de una conjetura inicial x0, se obtienen aproximaciones mejoradas xn utilizando la fórmula
donde f' es la derivada de f. El método se basa en la geometría de la curva y = f(x) cerca de la solución. El punto xn+1 es el punto donde la tangente corta al eje-x. Como muestra el diagrama, éste está más cerca de x que el punto original.
Una segunda aplicación importante de los métodos numéricos es a las ecuaciones diferenciales. Supongamos que queremos resolver la ecuación diferencial
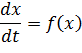
con la condición inicial x(0) = x0 en el instante t = 0. El método más simple, debido a Euler, consiste en aproximar dx/dt por
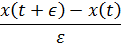
donde ε es muy pequeño. Entonces, una aproximación a la ecuación diferencial toma la forma
x(t + ε) = x(t) + εf(x(t))
Partiendo de x(0) = x0 deducimos sucesivamente los valores f(ε), f(2ε) y, f(3ε), en general, f(nε) para cualquier entero n > 0. Un valor típico para ε podría ser, digamos, 10-6. Un millón de iteraciones de la fórmula nos da x(1), otro millón lleva a x(2) y así sucesivamente. Con los computadores actuales un millón de cálculos son algo trivial, y esto se convierte en un método muy práctico.
Sin embargo, el método de Euler es demasiado simple para ser completamente satisfactorio, y se han concebido muchas mejoras.
Las más conocidas son toda una clase de métodos Runge-Kutta, llamados así por los matemáticos alemanes Carl Runge y Martin Kutta, quienes idearon el primero de dichos métodos en 1901.
Para qué les servía el análisis numéricoNewton no sólo tenía que hallar pautas en la naturaleza: tenía que desarrollar métodos efectivos de cálculo. Hizo un amplio uso de las series de potencias para representar funciones porque podía diferenciar e integrar tales series término a término. Él también las utilizó para calcular valores de funciones, un método numérico primitivo aún
en uso hoy. Una página de sus manuscritos, que data de 1665, muestra un cálculo numérico del área bajo una hipérbola, que ahora reconocemos como la función logarítmica. Sumó los términos de una serie infinita, trabajando con unas increíbles 55 cifras decimales.
Cálculo de Newton del área bajo una hipérbola
Uno de éstos, el denominado método de Runge-Kutta de cuarto orden, es ampliamente utilizado en ingeniería, ciencia y matemáticas teóricas.
Las necesidades de la dinámica no lineal moderna han generado varios métodos sofisticados que evitan la acumulación de errores durante largos periodos de tiempo exigiendo que se conserve cierta estructura asociada a la solución exacta. Por ejemplo, en un sistema mecánico sin fricción la energía total se conserva. Es posible fijar el método numérico de modo que en cada paso la energía se conserve exactamente. Este procedimiento evita la posibilidad de que la solución calculada se desvíe poco a poco de la exacta, como un péndulo que se acerca lentamente al reposo a medida que pierde energía.
Más sofisticados aún son los integradores simplécticos, que resuelven sistemas mecánicos de ecuaciones diferenciales conservando explícita y exactamente la «estructura simpléctica» de las ecuaciones de Hamilton: un tipo de geometría curiosa pero enormemente importante hecha a medida para los dos tipos de variables, posición y momento. Los integradores simplécticos son especialmente importantes en mecánica celeste, donde -por ejemplo- los astrónomos desean seguir los movimientos de los planetas en el sistema solar durante miles de millones de años. Utilizando integradores simplécticos, Jack Wisdom, Jacques Laskar y otros han demostrado que el comportamiento a largo plazo del sistema solar es caótico, que Urano y Neptuno estuvieron tiempo atrás mucho más cerca del Sol de lo que están ahora, y que con el tiempo la órbita de Mercurio se desplazará hacia la de Venus, de modo que uno u otro planeta pueden ser expulsados del sistema solar. Sólo los integradores simplécticos ofrecen garantías de que los resultados sobre grandes periodos de tiempo son precisos.
§. Los computadores necesitan matemáticas
Además de utilizar computadores como ayuda en las matemáticas, podemos utilizar las matemáticas como ayuda para los computadores. De hecho, los principios matemáticos fueron importantes en todos los primeros diseños de computadores, bien como prueba de concepto o bien como aspectos clave del diseño.
Todos los computadores digitales hoy en uso trabajan en notación binaria, en la que los números se representan como cadenas de sólo dos dígitos: 0 y 1. La ventaja principal de lo binario es que corresponde a una conmutación: 0 es «off» y 1 es «on». Ó 0 es «ausencia de voltaje» y 1 es «5 voltios», o cualquier patrón que se utilice en el diseño de circuitos. Los símbolos 0 y 1 también pueden interpretarse dentro de la lógica matemática como valores de verdad: 0 significa falso y 1 significa verdadero. Por eso los computadores pueden realizar cálculos lógicos tanto como aritméticos. De hecho, las operaciones lógicas son más básicas, y las operaciones aritméticas pueden verse como secuencias de operaciones lógicas. La aproximación algebraica de Boole a las matemáticas de 0 y 1 en Las leyes del pensamiento proporciona un formalismo efectivo para la lógica de los cálculos por computador. Los motores de búsqueda en internet realizan «búsquedas booleanas», es decir, buscan ítems definidos por una combinación de criterios lógicos, tales como «contener la palabra “gato” pero no contener “perro”».
§. Algoritmos
Las matemáticas han ayudado a las ciencias de la computación, pero a cambio las ciencias de la computación han sido motivo de nuevas y fascinantes matemáticas. La noción de algoritmo -un procedimiento sistemático para resolver un problema- es una de ellas. (El nombre proviene del algebrista árabe al-Khwarizmi.) Una pregunta especialmente interesante es, ¿cómo depende el tiempo de ejecución de un algoritmo del tamaño de los datos de entrada?
Por ejemplo, el algoritmo de Euclides para encontrar el máximo común divisor de dos números naturales m y n, con m s n, es como sigue:
- Dividir n por m para obtener el resto r.
- Si r = 0, entonces el máximo común divisor es m: STOP.
- Si r > 0, entonces reemplazar n por m y m por r y volver a empezar.
Puede demostrarse que si n tiene d cifras decimales (una medida del tamaño de los datos de entrada para el algoritmo), entonces el algoritmo se detiene después de un máximo de 5d pasos. Eso significa, por ejemplo, que si se nos dan dos números de 1000 dígitos, podemos calcular su máximo común divisor en 5000 pasos como máximo; en lo que se tarda una fracción de segundo en un computador moderno.
El algoritmo de Euclides tiene «tiempo de ejecución lineal»: la longitud de la computación es proporcional al tamaño (en dígitos) de los datos de entrada. Más en general, un algoritmo tiene un tiempo de ejecución polinómico, o es de clase P, si su tiempo de ejecución es proporcional a una potencia fija (tal como el cuadrado o el cubo) del tamaño de los datos de entrada. Por el contrario, todos los algoritmos conocidos para encontrar los factores primos de un número tienen tiempo de ejecución exponencial: una constante fija elevada a la potencia del tamaño de los datos de entrada. En esto se basa la seguridad del criptosistema RSA.
Hablando en términos generales, los algoritmos con tiempo de ejecución exponencial llevan a computaciones prácticas en los computadores actuales, mientras que algoritmos con tiempo de ejecución exponencial no lo hacen, y por ello las computaciones correspondientes no pueden realizarse en la práctica, incluso para datos iniciales de muy pequeño tamaño. Esta distinción es una regla aproximada: un algoritmo polinómico podría implicar una potencia tan alta que no sería práctico, mientras que algunos algoritmos con tiempos de ejecución peor que polinómico aún podrían resultar útiles.
“No tenemos idea de si cualquier problema «razonable» es no-P.”
Ahora surge la principal dificultad teórica. Dado un algoritmo específico, es (bastante) fácil calcular cómo depende el tiempo de ejecución del tamaño de los datos de entrada y determinar si es de clase P o no. Sin embargo, es extraordinariamente difícil decidir si podría existir un algoritmo más eficiente para resolver el mismo problema de forma más rápida. Por lo tanto, aunque sabemos que muchos problemas pueden resolverse por un algoritmo de clase P, no tenemos idea de si cualquier problema «razonable» es no-P.
«Razonable» tiene aquí un significado técnico. Algunos problemas deben ser no-P, simplemente porque sacar la respuesta requiere un tiempo de ejecución no-P. Por ejemplo «listar todas las maneras posibles de ordenar n símbolos». Para descartar problemas tan obviamente no-P, se necesita otro concepto: la clase NP de algoritmos no polinómicos deterministas.
Para qué nos sirve el análisis numéricoEl análisis numérico desempeña un papel central en el diseño de los aviones modernos. No hace mucho tiempo, los ingenieros calculaban como fluiría el aire que rozaba las alas y el fuselaje de un avión utilizando túneles de viento. Colocaban un modelo del avión en el túnel, soplaban aire con un sistema de ventiladores y observaban las pautas de flujo. Ecuaciones como las de Navier-Stokes proporcionaban varias ideas teóricas, pero era imposible resolverlas para aviones reales debido a su forma complicada.
Los computadores actuales son tan potentes, y los métodos numéricos para resolver EDP en computadores se han hecho tan efectivos, que en muchos casos la aproximación del túnel de viento ha sido descartada en favor del «túnel de viento numérico», es decir, un modelo por computador del avión.
Las ecuaciones de Navier-Stokes son tan precisas que pueden ser utilizadas de esta manera con seguridad. La ventaja de la aproximación por computador es que puede analizarse y visualizarse cualquier característica deseada del flujo.
Computación numérica del flujo de aire cerca de un avión
Un algoritmo es NP si una respuesta conjeturada puede comprobarse en un tiempo proporcional a una potencia fija del tamaño de los datos de entrada. Por ejemplo, puede comprobarse si un número es un factor primo de un número grande sin más que hacer una simple división.
Un problema de clase P es automáticamente NP. Se sabe que muchos problemas importantes, para los que no se conocen algoritmos P, también son NP Y ahora llegamos al problema no resuelto más profundo y más difícil en esta área, cuya solución conllevaría un premio de un millón de dólares ofrecido por el Instituto Clay de Matemáticas. ¿Son lo mismo P y NP? La respuesta más plausible es «no», porque P = NP significaría que un montón de cálculos aparentemente muy difíciles son realmente fáciles; existe un atajo en el que todavía no hemos pensado.
El problema ¿P = NP? se hace más difícil por un fenómeno fascinante llamado NP-completitud. Muchos problemas NP son tales que si realmente son de clase P, entonces todo problema NP es también de clase P. Se dice que dicho problema es NP-completo. Si puede demostrarse que cualquier problema NP-completo particular es P, entonces P = NP. Por el contrario, si puede demostrarse que cualquier problema NP-completo particular es no-P, entonces P no es lo mismo que NP. Un problema NP-completo que atrajo la atención recientemente está asociado con el juego de ordenador Buscaminas. Uno más matemático es el Problema de Satisfacibilidad Booleana: dado un enunciado en lógica matemática, ¿puede ser verdadero para alguna asignación de valores de verdad (verdadero o falso) para sus variables?
§. Análisis numérico
Las matemáticas implican mucho más que cálculos, pero los cálculos son un acompañamiento inevitable de investigaciones más conceptuales.
“La solución conllevaría un premio de un millón de dólares.”
Desde los tiempos más primitivos, los matemáticos han buscado ayudas mecánicas para liberarse de la pesadez del cálculo y mejorar la probabilidad de resultados precisos. Los matemáticos del pasado habrían envidiado nuestro acceso a los computadores electrónicos y se habrían maravillado por su velocidad y precisión.
Las máquinas de calcular han hecho por las matemáticas mucho más que actuar como sirvientes. Su diseño y funcionamiento han planteado nuevas preguntas teóricas a los matemáticos. Estas preguntas van desde justificar métodos numéricos aproximados para resolver ecuaciones hasta cuestiones profundas sobre los fundamentos de la computación.
Cuando empieza el siglo XXI los matemáticos tienen acceso a software potente, que hace posible no sólo realizar cálculos numéricos en computadores sino realizar también cálculos algebraicos y analíticos. Estas herramientas han abierto nuevas áreas, han ayudado a resolver antiguos problemas y han liberado tiempo para la reflexión conceptual. Como resultado, las matemáticas se han enriquecido, y también se han hecho aplicables a problemas mucho más prácticos. Euler tenía las herramientas conceptuales para estudiar el flujo de fluidos alrededor de objetos de formas complicadas, e incluso si no se había inventado el avión, había muchos problemas interesantes sobre barcos en el agua. Pero él no tenía ningún método práctico para implementar dichas técnicas.
Un nuevo desarrollo, no mencionado hasta ahora, es el uso de computadores como una ayuda para la demostración. Varios teoremas importantes, demostrados en años recientes, se basan en cálculos rutinarios pero en masa realizados por computador. Se ha dicho que las demostraciones asistidas por computador cambian la naturaleza fundamental de la demostración, al eliminar el requisito de que la demostración pueda ser verificada por una mente humana. Esta afirmación es discutible, pero incluso si fuera verdadera, el resultado del cambio es hacer de las matemáticas una ayuda aún más poderosa para el pensamiento humano.
Capítulo 20
Caos y complejidad
Las irregularidades también siguen pautas
A mediados del siglo XX las matemáticas estaban experimentando una fase de rápido crecimiento, estimuladas por la amplia extensión de sus aplicaciones y por sus nuevos y potentes métodos. Una historia general de la era moderna de las matemáticas ocuparía al menos tanto espacio como un tratamiento de todo lo que llevó a este periodo. Lo más que podemos conseguir son unas pocas muestras representativas para demostrar que la originalidad y la creatividad en matemáticas siguen vivas y en buen estado. Uno de estos temas, que alcanzó prominencia pública en los años setenta y ochenta, es la «teoría del caos», el nombre que dan los medios de comunicación a la dinámica no lineal. Este tema se desarrolló de forma natural a partir de modelos tradicionales que utilizan el cálculo infinitesimal. Otro tema lo constituyen los «sistemas complejos», que utilizan maneras menos ortodoxas de pensar y están estimulando nuevas matemáticas tanto como nueva ciencia.
§. Caos
Antes de los años sesenta del siglo XX la palabra «caos» sólo tenía un significado: desorden informe. Pero desde entonces, descubrimientos fundamentales en ciencia y matemáticas le han dotado de un segundo significado más sutil, un significado que combina aspectos de desorden con aspectos de forma. Los Principios matemáticos de la filosofía natural de Newton habían reducido el «sistema del mundo» a ecuaciones diferenciales, y éstas son deterministas. Es decir, una vez que se conoce el estado inicial del sistema, su estado futuro en cualquier instante está determinado unívocamente.
La visión de Newton es la de un universo mecánico que, una vez puesto en marcha por la mano del Creador, sigue un curso único e inevitable.
Es una visión que nos ha sido muy útil, gracias a la cual tenemos la radio, la televisión, los teléfonos móviles, los aviones comerciales, los satélites de comunicaciones, las fibras artificiales, los plásticos y los computadores.
El crecimiento del determinismo científico estuvo también acompañado por una creencia vaga pero profundamente arraigada en la «conservación de la complejidad». Esta es la hipótesis de que causas simples deben producir efectos simples, lo que implica que los efectos complejos deben tener causas complejas. Esta creencia nos hace examinar un objeto o sistema complejo y preguntar «de dónde procede la complejidad». ¿De dónde, por ejemplo, procede la complejidad de la vida, dado que debe haberse originado en un planeta sin vida? Difícilmente se nos ocurre que la complejidad podría aparecer por sí misma, pero eso es lo que indican las últimas técnicas matemáticas.
§. ¿Una solución única?
El determinismo de las leyes de la física se sigue de un hecho matemático simple: hay como máximo una solución para una ecuación diferencial con condiciones iniciales dadas.
“Esta complejidad se ve ahora como un ejemplo clásico de caos.”
En la Guía de la galaxia de Hitchhiker de Douglas Adams, el supercomputador Pensamiento Profundo se embarcaba en una búsqueda de cinco millones de años de duración en pos de la respuesta a la gran pregunta de la vida, el universo y todo lo que hay, y la respuesta que obtenía es bien conocida: «42». Este incidente es una parodia de la famosa afirmación en la que Laplace resumió la visión matemática del determinismo:
«Supongamos mi intelecto que en un momento dado conociera todas las fuerzas que animan la naturaleza y las posiciones mutuas de los seres que comprende; si este intelecto fuera suficientemente grande para someter sus datos a análisis, podría condensar en una única fórmula el movimiento de los cuerpos más grandes del universo y del átomo más ligero; para un intelecto semejante nada podría ser incierto, y el futuro tanto como el pasado estarían presentes ante sus ojos».
Luego devolvía de golpe a sus lectores a la tierra, al añadir:
«La mente humana ofrece un pálido esbozo de esta inteligencia en la perfección que ha sido capaz de dar a la astronomía».
Resulta irónico que fuera en la mecánica celeste, la parte de la física más evidentemente determinista, donde el determinismo laplaciano se pusiera en cuestión. En 1886 el rey Oscar II de Suecia (quien también regía Noruega) ofreció un premio por resolver el problema de la estabilidad del sistema solar. ¿Seguiría nuestro pequeño rincón del universo mecánico marchando para siempre, o sería posible que un planeta se aplastara contra el Sol o escapara al espacio interestelar? Las leyes físicas de conservación de la energía y el momento no prohíben ninguna de las dos eventualidades; pero ¿podría arrojar más luz la dinámica detallada del sistema solar?
El patinazo de PoincaréJune Barrow-Green, investigando en los archivos del Instituto Mittag-Lefler en Estocolmo, descubrió recientemente una historia embarazosa que previamente se había mantenido en secreto. El trabajo con el que Poincaré había ganado el premio contenía un serio error. Lejos de descubrir el caos, como se había supuesto, él había pretendido demostrar que no existía. El envío original «demostraba» que todos los movimientos del problema de tres cuerpos son regulares y tienen buen comportamiento.
Tras la concesión del premio. Poincaré detectó un error, e inmediatamente descubrió que echaba por tierra su demostración. Pero la memoria ganadora del premio ya había sido publicada como un número de la revista del Instituto. La revista fue retirada y Poincaré pagó una nueva reimpresión, que incluía su descubrimiento de enredos homoclínicos y lo que ahora llamamos caos. Esto le costó mucho más que el dinero que había ganado con su Memoria fallida. Casi todas las copias de la versión incorrecta fueron recuperadas y destruidas, pero una, conservada en los archivos del Instituto, se escapó de la red.
Poincaré estaba decidido a ganar el premio, y como precalentamiento se centró en un problema más simple, un sistema de tres cuerpos celestes.
Las ecuaciones para tres cuerpos no son mucho peores que para dos, y tienen la misma forma general. Sin embargo, el precalentamiento con tres cuerpos resultó ser sorprendentemente difícil, y Poincaré descubrió algo perturbador. Las soluciones de dichas ecuaciones eran completamente diferentes de las del caso de dos cuerpos. De hecho, las soluciones eran tan complicadas que no podían expresarse como una fórmula matemática cerrada. Peor aún, él pudo entender lo suficiente de la geometría -mejor dicho, la topología- de la solución para demostrar, más allá de cualquier sombra de duda, que los movimientos representados por dichas soluciones podrían ser a veces muy desordenados e irregulares. «Uno queda perplejo», escribía Poincaré, «ante la complejidad de esta figura que ni siquiera intento dibujar. Nada puede dar una idea mejor de la complejidad del problema de tres cuerpos». Esta complejidad se ve ahora como un ejemplo clásico de caos.
Su trabajo ganó el premio del rey Oscar II, incluso si no resolvía el problema por completo. Unos años más tarde desencadenó una revolución en nuestra forma de ver el universo y su relación con las matemáticas.
En 1926-1927 el ingeniero holandés Balthazar van der Pol construyó un circuito electrónico para simular un modelo matemático del corazón, y descubrió que en ciertas circunstancias la oscilación resultante no es periódica, como un latido cardiaco normal, sino irregular. Su trabajo recibió una sólida base matemática durante la Segunda Guerra Mundial por parte de John Littlewood y Mary Cartwright, en un estudio que tuvo su origen en la electrónica del radar. Se necesitaron más de 40 años para que se hiciera patente la gran trascendencia de su trabajo.
§. Dinámicas no lineales
A comienzos de los años sesenta el matemático norteamericano Stephen Smale abrió la era moderna de la teoría de sistemas dinámicos buscando una clasificación de los tipos de comportamiento. Inicialmente esperaba que la respuesta consistiría en combinaciones de movimientos periódicos, pero rápidamente comprendió que es posible un comportamiento mucho más complicado. En particular, él desarrolló el descubrimiento de Poincaré del movimiento complejo en el sistema restringido de tres cuerpos, simplificando la geometría para dar un sistema conocido como la «herradura de Smale». Demostró que el sistema herradura, aunque determinista, tiene algunas características aleatorias. Otros ejemplos de tales fenómenos fueron desarrollados por las escuelas de dinámica rusa y americana, con contribuciones especialmente notables de Oleksandr Sharkovskii y Vladimir Arnold, y empezó a surgir una teoría general. El término «caos» fue introducido por James Yorke y Tien-Yien Li en 1975, en un breve artículo que simplificaba uno de los resultados de la escuela rusa: el «teorema de Sharkovskii» de 1964, que describía una curiosa pauta en las soluciones periódicas de un sistema dinámico discreto: un sistema en el que el tiempo transcurre a saltos en lugar de ser continuo.
Mientras tanto, los sistemas caóticos estaban apareciendo esporádicamente en la literatura aplicada --una vez más, prácticamente desapercibidos por la comunidad científica más amplia-. El más conocido fue introducido por el meteorólogo Edward Lorenz en 1963. Lorenz se propuso modelar la convección atmosférica aproximando las complejas ecuaciones para este fenómeno por ecuaciones mucho más simples con tres variables.
El atractor de Lorenz
Al resolverlas numéricamente con un computador, descubrió que la solución oscilaba de una manera irregular, casi aleatoria. También descubrió que si las mismas ecuaciones se resuelven utilizando valores iniciales de las variables ligeramente diferentes, las diferencias se van amplificando hasta que la nueva solución es completamente diferente de la original. Su descripción de este fenómeno en conferencias posteriores llevó al término actualmente popular «efecto mariposa», según el cual el aleteo de una mariposa conduce, un mes más tarde, a un huracán en el otro extremo del globo.
Este extraño escenario es genuino, aunque lo es en un sentido bastante sutil. Supongamos que se pudieran obtener dos versiones del tiempo meteorológico: una vez con la mariposa y otra vez sin ella. Entonces encontraríamos diferencias importantes; es muy posible que una de ellas incluyera un huracán y la otra no. Exactamente este efecto aparece en simulaciones por computador de las ecuaciones habitualmente utilizadas para predecir el tiempo, y el efecto causa grandes problemas en la predicción meteorológica. Pero sería un error concluir que la mariposa provocó el huracán. En el mundo real, el tiempo no está influido por una mariposa sino por las características estadísticas de billones de mariposas y otras minúsculas perturbaciones. En conjunto, éstas tienen una influencia definida sobre dónde y cuándo se forman los huracanes, y dónde van posteriormente.
Utilizando métodos topológicos, Smale, Arnold y sus colaboradores demostraron que las soluciones extrañas observadas por Poincaré eran la consecuencia inevitable de atractores extraños en las ecuaciones. Un atractor extraño es un movimiento complejo que el sistema alberga inevitablemente. Puede visualizarse como una figura en el «espacio de fases» formado por las variables que describen el sistema. El atractor de Lorenz, que describe las ecuaciones de Lorenz de esta manera, se parece un poco al antifaz del Llanero Solitario, pero cada «superficie» aparente tiene infinitas capas.
Mary Lucy Cartwright
1900 - 1998Mary Cartwright se graduó en la Universidad de Oxford en 1923, una de las únicas cinco mujeres que estudiaban matemáticas en la universidad. Tras un corto periodo como profesora, hizo un doctorado en Cambridge, nominalmente con Godfrey Hardy pero en realidad con Edward Titchmarsh porque Hardy estaba en Princeton. Su tema de tesis era el análisis complejo.
En 1934 fue nombrada profesora ayudante en Cambridge, y en 1936 fue nombrada directora de estudios en Girton College.
En 1938, en colaboración con John Littlewood, emprendió una investigación para el Departamento de Investigación Científica e Industrial sobre ecuaciones diferenciales relacionadas con el radar. Descubrieron que estas ecuaciones tenían soluciones muy complicadas, una primera anticipación del fenómeno del caos. Por este trabajo se convirtió en la primera mujer matemática en ser elegida Fellow de la Royal Society, en 1947. En 1948 fue nombrada Mistress of Girton, y de 1959 a 1968 fue lectora en la Universidad de Cambridge.
Recibió muchos honores, y fue nombrada dama del Imperio Británico en 1969.
La estructura de los atractores explica una curiosa característica de los sistemas caóticos: pueden predecirse a corto plazo (a diferencia, digamos, de lanzar un dado) pero no a largo plazo. ¿Por qué no pueden encadenarse varias predicciones a corto plazo para dar una predicción a largo plazo? Porque la precisión con que podemos describir un sistema caótico se deteriora con el tiempo, a un ritmo cada vez mayor, de modo que hay un «horizonte de predicción» más allá del cual no podemos penetrar. Sin embargo, el sistema permanece en el mismo atractor extraño; pero su trayectoria sobre el atractor cambia significativamente.
Esto modifica nuestra visión del efecto mariposa. Todo lo que las mariposas pueden hacer es desplazar el tiempo meteorológico alrededor del mismo atractor extraño, de modo que siempre parece un tiempo perfectamente plausible. Es sólo un poco diferente del que habría sido sin todas esas mariposas.
David Ruelle y FlorisTakens encontraron rápidamente una aplicación potencial de los atractores extraños en física: el desconcertante problema del flujo turbulento en un fluido.
Las ecuaciones estándar para el flujo de los fluidos, llamadas ecuaciones de Navier-Stokes, son ecuaciones en derivadas parciales, y como tal son deterministas. Un tipo común de flujo fluido, el flujo «laminar», es suave y regular, justo lo que se esperaría de una teoría determinista. Pero otro tipo, el flujo turbulento, es irregular, casi aleatorio. Las teorías anteriores, o bien afirmaban que la turbulencia era mía combinación extraordinariamente complicada de pautas que individualmente eran muy simples y regulares, o bien que las ecuaciones de Navier-Stokes dejaban de ser válidas en el régimen turbulento. Pero Ruelle y Takens tenían una tercera teoría. Sugirieron que la turbulencia es un ejemplo físico de un atractor extraño.
Inicialmente la teoría fue recibida con cierto escepticismo, pero ahora sabemos que era correcta en espíritu, incluso si algunos detalles eran bastante cuestionables. Siguieron otras aplicaciones satisfactorias, y la palabra «caos» fue reclutada como un nombre conveniente para todos estos comportamientos.
§. Monstruos teóricos
Un segundo tema entra ahora en nuestra historia. Entre 1870 y 1930, un grupo variopinto de matemáticos heterodoxos inventaron una serie de formas extrañas cuyo único propósito era poner de manifiesto las limitaciones del análisis clásico. Durante el desarrollo inicial del cálculo infinitesimal, los matemáticos habían supuesto que cualquier cantidad que variara de forma continua debía tener una tasa de cambio bien definida «casi por doquier».
Etapas en la construcción de la curva de Hilbert que llena todo el espacio, y de la alfombra de Sierpinski
Por ejemplo, un objeto que se está moviendo de forma continua a través del espacio tiene una velocidad bien definida, excepto en los instantes relativamente escasos en que su velocidad cambia abruptamente. Sin embargo, en 1872 Weierstrass demostró que esta vieja hipótesis es falsa. Un objeto puede moverse de una forma continua pero de manera tan irregular que -en la práctica- su velocidad cambia abruptamente en todo instante de tiempo. Esto significa que en realidad no tiene siquiera una velocidad razonable.
Otras aportaciones a este extraño zoo de anomalías incluían una curva que llena toda una región del espacio (una fue encontrada por Peano en 1890, otra por Hilbert en 1891), una curva que se cruza consigo misma en todo punto (descubierta por Waclaw Serpinski en 1915) y una curva de longitud infinita que encierra un área finita. Este último ejemplo de rareza geométrica, ideado por Helge von Koch en 1906, es la curva copo de nieve, y se construye de la forma siguiente. Empezamos con un triángulo equilátero y añadimos promontorios triangulares en medio de cada lado para crear una estrella de seis puntas.
Luego se añaden promontorios más pequeños en medio de los doce lados de la estrella, y continuamos este procedimiento indefinidamente. Debido a su simetría séxtuple, el resultado final se parece a un copo de nieve complicado. Los copos de nieve reales crecen por otras reglas, pero ésa es otra historia.
La corriente principal de las matemáticas denunció inmediatamente estas anomalías como «patología» y como «galería de monstruos», pero a medida que pasaban los años varios fiascos embarazosos resaltaron la necesidad de ser cautos, y el punto de vista de los heterodoxos fue ganando terreno. La lógica que hay detrás del análisis es tan sutil que saltar a una conclusión plausible es peligroso: los «monstruos» nos advierten de lo que puede ir mal. Por eso, llegado el cambio de siglo los matemáticos se habían hecho a la existencia de nuevos artículos en la tienda de curiosidades de los heterodoxos -se restringían a la teoría sin tener ningún serio impacto en las aplicaciones-. De hecho, en 1900 Hilbert podía referirse al área total como un «paraíso» sin provocar disturbios.
La curva copo de nieve
En los años sesenta, frente a toda expectativa, la galería de monstruos teóricos recibió un impulso inesperado en la dirección de la ciencia aplicada. Benoit Mandelbrot se dio cuenta de que estas curvas monstruosas son la clave para una teoría muy general de las irregularidades en la naturaleza. El las rebautizó como fractales. Hasta entonces, la ciencia se había contentado con atenerse a formas geométricas tradicionales como rectángulos y esferas, pero Mandelbrot insistía en que esta aproximación era demasiado restrictiva. El mundo natural está plagado de estructuras complejas e irregulares -líneas de costa, montañas, nubes, árboles, glaciares, sistemas hidrológicos, ondas oceánicas, cráteres, coliflores- sobre las que la geometría tradicional permanece muda. Es necesaria una nueva geometría de la naturaleza.
Hoy, los científicos han asimilado los fractales en sus modos de pensamiento habituales, igual que sus predecesores hicieron al final del siglo XIX con esas monstruosidades matemáticas heterodoxas. La segunda parte del artículo «La difusión atmosférica mostrada en un gráfico a corta distancia», que escribió Lewis Fry Richardson en 1926, lleva el título «¿Tiene el viento una velocidad?». Esto se ve ahora como una pregunta completamente razonable.
El flujo atmosférico es turbulento, la turbulencia es fractal y los fractales pueden comportarse como la función monstruosa de Weierstrass: moviéndose continuamente pero sin tener una velocidad bien definida. Mandelbrot encontró ejemplos de fractales en muchas áreas dentro y fuera de la ciencia: la forma de un árbol, la ramificación de un río, los movimientos del mercado de valores.
¡Caos por todas partes!
Desde el punto de vista geométrico, los atractores extraños de los matemáticos resultaron ser fractales, y las dos líneas de pensamiento se entretejieron en lo que ahora se conoce popularmente como teoría del caos.
El caos puede encontrarse en prácticamente cualquier área de la ciencia. Jack Wisdom y Jacques Laskar han encontrado que la dinámica del sistema solar es caótica. Conocemos todas las ecuaciones, masas y velocidades que se requieren para predecir el movimiento futuro para siempre, pero hay un horizonte de predicción de unos diez millones de años debido al caos dinámico. Por lo tanto, si queremos saber en qué lado del Sol estará Plutón en el 10.000.000 d.C. ...olvidémoslo. Estos astrónomos han demostrado también que las mareas lunares estabilizan la Tierra frente a influencias que de otra manera llevarían a un movimiento caótico, provocando rápidos cambios de clima de periodos calientes a eras glaciares y vuelta; por ello, la teoría del caos demuestra que, sin la Luna, la Tierra sería un lugar muy desagradable en donde vivir.
El caos aparece en casi todos los modelos matemáticos de poblaciones biológicas, y experimentos recientes (cría de escarabajos en condiciones controladas) indican que también aparece en poblaciones biológicas reales.
Los ecosistemas no se asientan normalmente en una especie de «equilibrio de la naturaleza» estático: en su lugar deambulan por atractores extraños, donde normalmente tienen una apariencia similar pero siempre cambian.
Para qué les servía la dinámica no linealHasta que la dinámica no lineal se convirtió en algo importante en la modelización científica, su papel era principalmente teórico. El trabajo más profundo fue el de Poincaré sobre el problema de tres cuerpos en mecánica celeste. Éste predecía la existencia de órbitas muy complejas, pero daba muy poca idea de qué aspecto tenían. El objetivo principal del trabajo era demostrar que ecuaciones sencillas pueden no tener soluciones sencillas, que la complejidad no se conserva, sino que puede tener orígenes más simples.
Los computadores modernos pueden calcular órbitas complicadas en el problema de tres cuerpos.
El no haber comprendido la dinámica sutil del ecosistema es una razón por la que las pesquerías del mundo están próximas al desastre.
§. Complejidad
Del caos, nos volvemos a la complejidad. Muchos de los problemas a los que se enfrenta hoy la ciencia son extraordinariamente complicados.
Para gestionar un arrecife coralino, una selva o una pesquería es necesario entender un ecosistema altamente complejo, en el que cambios aparentemente inocuos pueden desencadenar problemas inesperados. El mundo real es tan complicado, y puede ser tan difícil de medir, que los métodos de modelización convencionales son difíciles de establecer y aún más difíciles de verificar. En respuesta a estos desafíos, un número creciente de científicos han llegado a creer que se necesitan cambios fundamentales en la manera en que modelamos nuestro mundo.
A comienzos de los años ochenta George Cowan, anteriormente jefe de investigación en Los Alamos, decidió que un camino hacia delante está en las teorías recién desarrolladas de la dinámica no lineal. Aquí causas pequeñas pueden crear efectos enormes, reglas rígidas pueden llevar a anarquía y el todo suele tener capacidades que no existen, ni siquiera en forma rudimentaria, en sus componentes. En términos generales, éstas son exactamente las características observadas en el mundo real. Pero ¿es esta similitud suficientemente profunda para proporcionar una comprensión genuina?
Cowan concibió la idea de un nuevo instituto de investigación dedicado a aplicaciones interdisciplinarias y desarrollo de la dinámica no lineal. Se le unió Murray Gell-Mann, físico de partículas ganador de un Premio Nobel, y en 1984 crearon lo que entonces se llamaba el Instituto de Río Grande. Hoy es el Instituto Santa Fe, un centro internacional para el estudio de los sistemas complejos.
La teoría de la complejidad ha aportado nuevos métodos y puntos de vista matemáticos que explotan los computadores para crear modelos digitales de la naturaleza. Explota la potencia del computador para analizar dichos modelos y deduce características sorprendentes de los sistemas complejos. Y utiliza la dinámica no lineal y otras áreas de las matemáticas para entender lo que los computadores revelan.
§. Autómatas celulares
En un nuevo tipo de modelo matemático, conocido como un autómata celular, cosas tales como árboles, aves y ardillas son representadas como minúsculos cuadrados coloreados. Compiten con sus vecinos en un juego de ordenador matemático. Las gráficas quizá no dicen mucho, pero la simplicidad es engañosa; estos juegos están en el filo de la ciencia moderna.
Autómata celular
Los autómatas celulares adquirieron prominencia en los años cincuenta, cuando John von Newmann estaba tratando de entender la capacidad de la vida para replicarse. Stanislaw Ulam sugirió utilizar un sistema introducido por el pionero del computador Konrad Zuse en los años cuarenta. Imaginemos un universo compuesto de una gran mafia de cuadrados, llamados celdas, como un tablero de ajedrez gigante.
En cualquier momento, un cuadrado dado puede existir en un estado. Este universo-tablero-de-ajedrez está equipado con sus propias «leyes de la naturaleza», que describen cómo debe cambiar el estado de cada celda cuando el tiempo salta al próximo instante. Es útil representar estos estados mediante colores. Entonces las reglas serían enunciados como: «si una celda es roja y tiene dos celdas azules adyacentes, debe convertirse en amarilla». Un sistema semejante se denomina un autómata celular: celular debido a la malla; autómata porque obedece ciegamente cualesquiera reglas que haya en la lista.
Para modelar la característica más fundamental de las criaturas vivas, Von Newmann creó mía configuración de celdas que podía replicarse, hacer copias de sí misma. Tenía 200.000 celdas y utilizaba 29 colores diferentes para llevar a cabo una descripción codificada de sí misma. Esta descripción podía ser copiada ciegamente y utilizada como un plano para construir otras configuraciones del mismo tipo. Von Newmann no publicó su trabajo hasta 1966, cuando Crick y Watson ya habían descubierto la estructura del ADN y resultaba claro cómo la vida realiza realmente su truco de replicación. Los autómatas celulares fueron ignorados durante otros 30 años.
Para qué nos sirve la dinámica no linealPodría parecer que el caos no tiene aplicaciones prácticas, al ser irregular, impredecible y altamente sensible a pequeñas perturbaciones. Sin embargo, puesto que el caos se basa en leyes deterministas, resulta ser útil precisamente debido a estas características.
Una de las aplicaciones potencialmente más importantes es el control caótico. Alrededor de 1950 el matemático John von Newmann sugirió que la inestabilidad del tiempo meteorológico podría un día convertirse en una ventaja, porque implica que un efecto muy deseado puede ser generado por una perturbación muy pequeña. En 1979 Edward Belbruno se dio cuenta de que este efecto podía ser utilizado en astronáutica para mover naves espaciales a través de largas distancias con muy poco gasto de combustible. Sin embargo, las órbitas resultantes necesitan mucho tiempo -dos años de la Tierra a la Luna, por ejemplo- y la NASA perdió interés en la idea.
La sonda Génesis (NASA)En 1990 Japón lanzó una pequeña sonda lunar, Hagoromo, que se separó de una sonda mayor, Hiten, que permanecía en órbita terrestre. Pero la radio de Hagoromo falló, dejando a Hiten sin ningún papel que desempeñar. Japón quería salvar algo de la misión, pero Hiten sólo tenía un 10 por 100 del combustible necesario para llegar a la Luna utilizando una órbita convencional. Un ingeniero del proyecto recordó la idea de Belbruno y le pidió ayuda. En menos de diez meses Hiten estaba en camino a la Luna y más allá, en busca de partículas atrapadas de polvo interestelar, utilizando sólo la mitad del combustible que le quedaba. La técnica se ha utilizado repetidamente desde su primer éxito, en particular por la sonda Génesis para tomar muestras del viento solar, y la misión SMARTONE de la ESA.
La técnica se aplica en la Tierra tanto como en el espacio. En 1990 Celso Grebogi, Edward Ott y James Yorke publicaron un esquema teórico general para explotar el efecto mariposa en el control de sistemas caóticos.
El método ha sido utilizado para sincronizar un banco de láseres; para controlar irregularidades del latido cardiaco, abriendo la posibilidad de un marcapasos inteligente; para controlar ondas eléctricas en el cerebro, lo que podría ayudar a suprimir ataques epilépticos; y para suavizar el movimiento de un fluido turbulento, lo que en el futuro podría hacer a los aviones más eficientes en el consumo del combustible.
En los años ochenta, sin embargo, había un interés creciente en sistemas compuestos de un gran número de partes simples que interaccionan para producir un todo complicado.
“Los sistemas complejos apoyan la idea de (pie con química suficientemente compleja puede aparecer espontáneamente la vida.”
Tradicionalmente, la mejor manera de modelar matemáticamente un sistema es incluir tantos detalles como sea posible: cuanto más cerca está el modelo del objeto real, mejor. Pero esta aproximación con gran detalle falla en el caso de sistemas muy complejos. Supongamos, por ejemplo, que queremos entender el crecimiento de una población de conejos. No necesitamos modelar la longitud del pelo de los conejos, cómo son sus orejas o cómo funciona su sistema inmune. Sólo necesitamos unos pocos hechos básicos sobre cada conejo: qué edad tiene, cuál es su sexo y, caso de ser hembra, si está preñada. Entonces podemos centrar los recursos informáticos en lo que realmente importa.
Para este tipo de sistema, los autómatas celulares son muy efectivos. Nos permiten ignorar detalles innecesarios sobre los componentes individuales y centrarnos en su lugar en cómo se interrelacionan dichos componentes. Esta resulta ser una manera excelente de calcular qué factores son importantes y de revelar ideas generales sobre por qué los sistemas complejos hacen lo que hacen.
§. Geología y biología
Un sistema complejo que desafía el análisis mediante técnicas de modelización tradicionales es la formación de cuencas y deltas de ríos. Peter Burrough ha utilizado autómatas celulares para explicar por qué estos accidentes naturales adoptan las formas que toman. El autómata modela las interacciones entre agua, tierra y sedimentos. Los resultados explican cómo afectan los diferentes ritmos de erosión del suelo a las formas de los ríos, y cómo los ríos arrastran el suelo, cuestiones importantes para la ingeniería y la gestión hidráulica. Las ideas son también interesantes para las compañías petrolíferas, porque el petróleo y el gas se encuentran con frecuencia en estratos geológicos que originalmente se depositaron como sedimentos.
Otra bella aplicación de los autómatas celulares se da en biología. Hans Meinhardt ha utilizado autómatas celulares para modelizar la formación de pautas en animales, desde conchas marinas a cebras. Los factores clave son concentraciones de sustancias químicas. Las interacciones consisten en reacciones dentro de una celda dada y difusión entre celdas vecinas.
Los dos tipos de interacción se combinan para dar las reglas reales para el estado siguiente. Los resultados proporcionan ideas útiles sobre las pautas de activación e inhibición que activan y desactivan dinámicamente los genes que producen pigmentos durante el crecimiento animal.
Stuart Kauffman ha aplicado varias técnicas de teoría de la complejidad a otro rompecabezas importante en biología: el desarrollo de la forma orgánica. El crecimiento y desarrollo de un organismo debe implicar mucha dinámica, y no puede ser simplemente una cuestión de traducir en forma orgánica la «información» contenida en el ADN. Una vía prometedora consiste en formular desarrollos sobre la dinámica de un sistema no lineal complejo.
Los autómatas celulares han completado ahora el círculo y nos han dado una nueva perspectiva sobre los orígenes de la vida. El autómata auto-replicante de Von Newmann es muy especial, hecho a medida cuidadosamente para hacer copias de una configuración inicial altamente compleja. ¿Es esto típico de los autómatas autorreplicantes o podemos obtener replicación sin partir de una configuración muy especial? En 1993 Hui-Hsien Chou y James Reggia desarrollaron un autómata celular con 29 estados para los que un estado inicial escogido aleatoriamente, o «sopa primordial», conduce a estructuras autorreplicantes más del 98 por 100 de las veces.
En este autómata, las entidades autorreplicantes son una certeza virtual.
Los sistemas complejos apoyan la idea de que en un planeta sin vida y con química suficientemente compleja, la vida puede aparecer espontáneamente y organizarse en formas cada vez más complejas y sofisticadas. Lo que queda por entender es qué tipo de reglas llevan a la emergencia espontánea de configuraciones en nuestro propio Universo; en resumen, qué tipo de leyes físicas hacen que este primer paso crucial hacia la vida sea no sólo posible, sino inevitable.
§. Cómo se crearon las matemáticas
La historia de las matemáticas es larga y complicada. Los pioneros de las matemáticas hacían avances extraordinarios, pero también se adentraban en callejones sin salida, a veces durante siglos. Este es el sino de los pioneros.
Si es obvio dónde hay que ir a continuación, cualquiera puede hacerlo. Y así, durante cuatro milenios, nació la elegante y elaborada estructura que llamamos matemáticas. Apareció de forma intermitente, con estallidos de actividad seguidos de periodos de estancamiento; el centro de actividad se desplazó por el globo terrestre siguiendo el ascenso y caída de las culturas humanas.
A veces creció de acuerdo con las necesidades prácticas de dicha cultura; otras veces la disciplina siguió su propia dirección, cuando sus practicantes jugaban a lo que para todos los demás parecían ser meros juegos intelectuales. Y con sorprendente frecuencia, dichos juegos dieron beneficios al cabo del tiempo en el mundo real, estimulando el desarrollo de nuevas técnicas, nuevos puntos de vista y nueva comprensión.
Las matemáticas no se han detenido. Nuevas aplicaciones demandan nuevas matemáticas, y los matemáticos están respondiendo. La biología, en especial, plantea nuevos desafíos a la modelización y la comprensión matemáticas. Los requisitos internos de las matemáticas siguen estimulando nuevas ideas, nuevas teorías. Muchas conjeturas importantes siguen sin resolver, pero los matemáticos están trabajando en ellas.
Durante su larga historia, las matemáticas se han inspirado en estas dos fuentes: el mundo real y el mundo de la imaginación humana. ¿Cuál es más importante? Ninguno de los dos; lo que importa es la combinación. El método histórico deja claro que las matemáticas extraen su poder, y su belleza, de ambos. La época de los antiguos griegos se suele ver como una Edad de Oro histórica, cuando la lógica, las matemáticas y la filosofía empezaron a influir en la condición humana. Pero los avances hechos por los griegos son sólo parte de una historia en curso. Las matemáticas nunca han estado tan activas, nunca han sido tan diversas y nunca han sido tan vitales para nuestra sociedad.
Bienvenidos a la Edad de Oro de las matemáticas
Libros y artículos
- E. Belbruno: Fly Me to the Moon, Princeton University Press, Princeton, 2007.
- E. T. Bell: Men of Mathematics (2 vols.), Pelican, Harmondsworth, 1953.
- E. T. Bell: The Development of Mathematics, (reed.), Dover, Nueva York, 2000.
- R. Bourgne y J. P. Azra: Écrits et mémoires mathématiques d’Évariste Galois, Gauthier- Villars, París, 1962.
- C. B. Boyer: History of Mathematics, Wiley, Nueva York, 1968. [Hay traducción castellana: Historia de la Matemática, Alianza Editorial, Madrid, 1999.]
- W K. Bühler: Gauss, a Biographical Study, Springer, Berlín, 1981.
- J. Cardan: The Book of My Life (traducido por Jean Stoner), Dent, Londres, 1931. [Hay traducción castellana del original: Mi Vida, Alianza Editorial, Madrid, 1991.]
- G. Cardano: The Great Art or the Rules of Algebra (traducido por T. Richard Witmer), MIT Press, Cambridge, MA, 1968.
- J. Coolidge: The Mathematics of Great Amateurs, Dover, Nueva York, 1963.
- T. Dantzig: Number: the Language of Science (ed. J. Mazur), Pi Press, Nueva York, 2005.
- Euclides: TheThirteen Books of Euclid’s Elements (3 vols., traducido por sirThomas L. Heath), Dover, Nueva York. [Hay traducción castellana del original: Elementos, Gredos, Madrid.]
- J. Fauvel y J. Gray: The History of Mathematics: a Reader, Macmillan Education, Basingstoke, 1987.
- D. H. Fowler: The Mathematics of Plato’s Academy, Clarendon Press, Oxford, 1987.
- C. F. Gauss: Disquisitiones Arithmeticae, Leipzig, 1801 (traducido por A. A. Clarke), Yale University Press, New Haven, CT, 1965. [Hay traducción castellana: Disquisitiones Arithmeticae, Academia Colombiana de Ciencias Exactas, Físicas y Naturales, 1995; también hay una traducción parcial de las Secciones III y IV en Dios creó los números, Crítica, Barcelona, 2006.]
- Hyman: Charles Babbage, Oxford University Press, Oxford, 1984.
- G. G. Joseph: The Crest of the Peacock: non-European Roots of Mathematics, Penguin, Harmondsworth, 2000.
- V. J. Katz: A History of Mathematics (2.a ed.), Addison-Wesley, Reading, MA, 1998.
- M. Kline: Mathematical Thought fron Ancient to Modern Times, Oxford University Press, Oxford, 1972. [Hay traducción castellana: El pensamiento matemático de la antigüedad a nuestros días, Alianza Editorial, Madrid, 1992.]
- H. Koblitz: A Convergence of Lives: Sofia Kowaleskaia, Birkháuser, Boston, 1983.
- H. Koblitz: A Course in Number Theory and Cryptography (2.a ed.), Springer, Nueva York, 1994.
- M. Livio: The Golden Ratio, Broadway, Nueva York, 2002
- M. Livio: The Equation That Couldn’t Be Solved, Simón & Schuster, Nueva York, 2005.
- M. Livio: The: the Story of a Number, Princeton University Press, Princeton, 1994.
- M. Livio: Trigonometric Delights, Princeton University Press, Princeton, 1998.
- D. MacHale: George Boole, Boole Press, Dublín, 1985.
- O. Neugebauer: A History of Ancient Mathematical Astronomy (3 vols.), Springer, Nueva York, 1975.
- Ore: Niels Hendrik Abel: Mathematician Extraordinary, University of Minnesota Press, Minneapolis, 1957.
- Reid: Hilbert, Springer, Nueva York, 1970.
- T. Rothman: «The sort life of Évariste Galois», Scientific American (abril de 1982), pp. 112-120. Recopilado en T. Rothman, A Physicist on Madison Avenue, Princeton University Press, Princeton, 1991.
- Sobel, Dava: Longitude (ed. 100 aniversario), Harper Perennial, Nueva York, 2005; [Hay traducción castellana: Longitud, Anagrama, Barcelona, 2006.]
- Stewart, Ian: Does God Play Dice? The New Mathematics of Chaos, (2.a ed.) Penguin, Harmondsworth, 1997. [Hay traducción castellana: ¿Juega Dios a los dados?; la nueva matemática del caos, Crítica, Barcelona, 2007.]
- Stewart, Ian: Why Beauty isTruth, Basic Books, Nueva York, 2007. [Hay traducción castellana: Belleza y verdad, Crítica, Barcelona, 2008.]
- S. M. Stigler: The History of Statistics, Harvard University Press, Cambridge, MA, 1986.
- L. Van der Waerden: A History of Algebra, Springer-Verlag, Nueva York, 1994.
- D. Welsh: Codes and Cryptography, Oxford University Press, Oxford, 1988.
Páginas web
La mayoría de los temas pueden localizarse fácilmente utilizando un motor de búsqueda. Hay páginas generales muy buenas:
- El archivo MacTutor de Historia de las Matemáticas: http://www-groups.dcs.st-and.ac.uk/~history/index.html
- Wolfram MathWorld, un compendio de información sobre temas matemáticos: http://mathworld.wolfram.com
- Wikipedia, la enciclopedia libre: http://en.wikipedia.org/wiki/Main_Page