
Juegos matemáticos recreativos
E. Ya. Guik
El libro de E. Ya. Guik, matemático, Candidato a Doctor en Ciencias y Maestro en ajedrez, está dedicado a juegos por los que sienten afición las personas con inclinación por las matemáticas o juegos con un análisis matemático rico en contenido. Será también de interés para los amantes de problemas lógicos, rompecabezas y crucigramas.
El libro posee las siguientes tres particularidades. Esta es la primera edición dedicada íntegramente a juegos recreativos en los cuales pueden participar varios jugadores. El conocimiento del libro puede impulsar a algunos lectores a pasar del recrea- miento a ocuparse de las matemáticas y de la cibernética. Los propios juegos intelectuales desarrollan también la capacidad necesaria para resolver problemas de ingeniería, de dirección y de economía. El libro analiza conocidos problemas y rompecabezas, no siempre fáciles de resolver, del área de las matemáticas recreativas, como, por ejemplo: cómo ganar al ganapierde, jugando con todas las fichas contra una sola; cómo dar mate lo antes posible, practicando un juego simétrico y qué hacer para no perder a las cruces y los ceros. En el libro también hay no pocos inventos del autor. Queda decir que el libro está escrito de una manera recreativa, igual que los múltiples artículos y libros de E. Ya. Guik sobre ajedrez y «matemática ajedrecística».
A. L. Brudno
Doctor en Ciencias Fisicomatemáticas, Profesor
§. Toros y vacas
§. Acertar la palabra
§. Combate marino
El afán de acertar las distintas adivinanzas y descubrir los secretos es propio de personas de todas las edades. ¿Quién de nosotros no jugó en su infancia al juego «frío-caliente», no acertó adivinanzas en forma de poesías, no se rompió la cabeza tratando de resolver un problema ingenioso?
La pasión infantil por los juegos y rompecabezas a veces infunde en el joven el deseo de dedicarse de lleno a las matemáticas, física, biología con la finalidad de poder «resolver» problemas y acertijos científicos de mayor importancia. Suele ocurrir que los mejores acertantes con el tiempo crean teorías matemáticas, descifran antiguos papiros o descubren nuevas leyes de la naturaleza. Y esto es broma sólo a medias. Indudablemente que los juegos que requieren acertar algo desarrollan la capacidad creativa de la persona, su manera lógica de pensar, les enseña a plantear problemas importantes y hallar la respuesta a los mismos.
Los juegos que precisan acertar algo se parecen mucho entre sí: un jugador plantea algún acertijo, piensa o distribuye algo y el otro hace preguntas y escucha las respuestas, por las cuales debe acertar lo que pensó el primero, adivinar el objeto pensado. En este capítulo examinaremos tres juegos que contienen determinados elementos matemáticos y lógicos. En el primer juego, «toros y vacas», se precisa determinar un número, en el segundo, «acertar la palabra», averiguar la palabra ideada por el contrario y en el tercero, «combate marino», detectar la disposición de los barcos. En los tres juegos, basados en preguntas y respuestas, el adivinador, de cada jugada, extrae cierta información sobre el objeto ideado y, tras formular una serie de preguntas, lo acierta (es decir, determina el número pensado, la palabra o la disposición de los barcos). La finalidad del juego consiste en determinar el objeto, formulando un mínimo de preguntas. Ambos jugadores, tanto el que propone el acertijo como el adivinador, se turnan y el ganador se determina por el resultado de varios encuentros.
El autor, antes que nada, asocia los juegos que se ofrecen con los testes (probablemente el lector comprenda este sentimiento después de leer el relato sobre el «combate marino»). Los testes con frecuencia se utilizan en las investigaciones psicológicas, son de gran importancia en la cibernética, un apartado especial de la cual se denomina teoría de la composición de testes. En esencia el test es un conjunto de preguntas que permiten descifrar unívocamente un objeto o ciertas propiedades del mismo. Al componer un test, uno siempre se plantea la tarea de hacerlo más corto, es decir, formular el menor número de preguntas. Por ello hemos considerado que estos tres juegos pertenecen a la categoría de juegos test.
En muchos juegos recreativos y de mesa surge la necesidad de plantear un enigma y acertar el objeto. En el ajedrez nosotros tratamos también de acertar el pensamiento del contrario, su plan de acción, pero desgraciadamente no se permite dirigir al contrario preguntas. El ajedrez es un juego con información completa: el resultado de la partida en cualquier posición teóricamente está determinado de manera unívoca y no requiere preguntas. Sin embargo, los juegos test son juegos típicos de información incompleta y su esencia consiste precisamente en las preguntas y las respuestas.
El «combate marino» es un juego que se conoce desde tiempos remotos. En lo que respecta a los otros dos juegos, éstos tienen una historia bastante modesta y en la literatura están insuficientemente reflejados. Haremos una descripción detallada de los tres juegos y examinaremos una serie de ejemplos y problemas interesantes relacionados con ellos.
§. Toros y vacas
Este juego combinatorio y lógico, ideado hace relativamente poco, en los años 70, se ganó una gran popularidad en muchos países. Su variante más difundida se conoce con el nombre «Master Mind» que literalmente significa mente relevante. Pero comencemos el relato por los «toros y vacas».
Los jugadores son dos. Cada uno de ellos piensa un número de cuatro dígitos, con cifras distintas, que el contrario debe acertar (la primera cifra puede ser también un cero). La jugada consiste en que uno de los jugadores, tratando de acertar el número del contrario, dice un número de cuatro dígitos con cifras diferentes. Si el número propuesto tiene cifras comunes con el que pensó el contrario, situadas en el mismo lugar, tal situación se denomina «toro» (en adelante se escribirá «t»). Si existen cifras comunes pero en puestos diferentes, esta situación se denomina «vaca» (en adelante se escribirá «v»).
En respuesta a la jugada del contrario, el primer jugador compara su número con el propuesto por el oponente y comunica el número de «toros» y el de «vacas» que obtuvo aquél. Por ejemplo, si el número ideado por el primer jugador es el 5239 y le propusieron como respuesta el 2735, el acertante consiguió «1 toro y 2 vacas» (1t, 2v). El tres se encuentra en ambos números y además en un mismo lugar (1t), el 2 y el 5 son comunes en los dos números pero sus lugares no coinciden por lo que se obtiene (2v), el 7 y el 9 no son comunes para ambos números.
Después de jugar y obtener la respuesta, el acertador adquiere cierta información sobre el número ideado por el contrario y al fin lo adivina. El juego termina cuando en respuesta a su jugada consecutiva, el acertador obtiene la contestación 4t, es decir, el número pensado por su oponente. Gana el que acierte antes el número ideado por el contrario. He aquí un ejemplo. Anotemos las jugadas y las respuestas en la tabla 1.

Supongamos que el contrario ideó el número 3594 que debemos acertar. Nuestra primera jugada 1568 obtuvo la respuesta 1t. Esto significa que en el número pensado sólo hay una cifra de las nombradas y además dispuesta en el mismo lugar. Trataremos de acertarla, sin utilizar otras cifras para no enredarnos. Hacemos la segunda con el número 1586. La respuesta 1t nos indica que las cifras 1 o 5 se encuentran en su lugar. Nuestra tercera jugada con el número 1658 y la respuesta 1v nos muestra que en el segundo lugar del número pensado se encuentra la cifra 5, mientras que las cifras 1, 6 y 8 en él no existen. Con la jugada 2570 trataremos de aclarar si el número pensado contiene las cifras 2, 7 y 0. La respuesta 1t es muy afortunada, por cuanto nos conviene que estas cifras no existan en el número ideado. Por lo tanto, resulta claro que el número pensado contiene las cifras 3, 4, 5 y 9 con la particularidad de que el 5 se encuentra en el segundo lugar. Hacemos la siguiente jugada, 4539. La respuesta 1t, 3v nos indica que fue ideado el número 3594 o el 9543. Si la primera cifra es un 3, entonces el 9 sólo puede ocupar el tercer lugar en el número y si la primera cifra es el 9, entonces el 3 sólo puede estar en el cuarto lugar. La jugada 3594 y la respuesta 4t significa que el fin fue alcanzado; la respuesta 1t, 3v nos indicaría que el número pensado es el 9543 y en este caso la partida sería una jugada más larga.
¿Cuál es la diferencia entre el juego «toros y vacas» y el «Master Mind»? En el Master Mind en lugar de cifras se utilizan jalones de seis colores (rojo (R), amarillo (Am), azul (Az), verde (F), blanco (B) y negro (N)); éstos se introducen en orificios que hay en una tabla, cuyo aspecto es aproximadamente el que muestra la figura 1. El conjunto ideado de jalones de codificación, de cifras, (en la parte superior de la tabla) se tapa con unas puertas especiales de manera que el descifrador no lo vea. Para cada jugada están previstos también cuatro orificios, así como otros cuatro orificios, más pequeños, situados a la izquierda para las respuestas al conjunto ideado. La jugada consiste en que el acertador introduce cuatro jalones de colores en los orificios y el contrario en respuesta expone unos jalones pequeños que sirven de clave de dos colores (negros y blancos) que introduce en los orificios a la izquierda de los de las jugadas (en cualquier orden). Los jalones negros corresponden a los «toros» y los blancos, a las «vacas». Si no fueron acertados todos los colores, algunos de los orificios quedan vacíos.
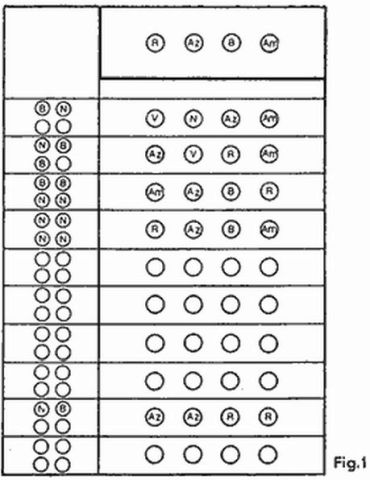
En el ejemplo de la figura 1 se muestra el cifrado R, Az, B, Am. Siendo la primera jugada V, N, Az, Am se produjo una coincidencia total del color (Am) y otro de los colores (Az) fue a parar a un lugar distinto del que ocupa en el cifrado. De este modo la respuesta es B, N (en el otro juego 1t, 1v). La respuesta a la segunda jugada es N, B, B, a la tercera, B, B, N, N (se acertaron los cuatro colores) y a la cuarta, N, N, N, N. Aquí termina el juego. La partida duró cuatro jugadas. En general, como podemos apreciar, la tabla tiene capacidad para diez jugadas (sólo a jugadores demasiado inexpertos no les alcanza esta cantidad de jugadas).
Traducido el Master Mind al idioma del juego «toros y vacas» obtenemos que el número pensado y los números de las jugadas se pueden formar sólo de seis cifras (seis jalones de colores). Mas el color de los jalones en el cifrado y en las jugadas pueden repetirse (a diferencia del juego «toros y vacas» donde todas las cifras deben ser diferentes). Así, por ejemplo, en el renglón nueve de la figura 1, se jugó Az, Az, R, R. La respuesta fue N, B (el azul se encuentra en su lugar y el rojo no). Ambos colores se consideran sólo una vez. Siendo el cifrado R, R, B, Am y la misma jugada Az, Az, R, R, el color rojo se consideraría dos veces y la respuesta sería B, B.
Formulemos más exactamente cómo se responde a cada jugada en el Master Mind. Primero se comparan los colores de los primeros jalones del cifrado y de la jugada. Si coinciden ponemos un jalón negro del código (1 «toro») y los primeros jalones del cifrado y de la jugada se eliminan del análisis. Si son diferentes, se compara el color del primer jalón del cifrado con el del segundo jalón de la jugada. En caso de coincidencia se pone un jalón blanco del código (1 «vaca») y el primer jalón del cifrado y el segundo de la jugada se excluyen del análisis. Si los colores son distintos, se comparan los colores del primer jalón del cifrado y el tercero de la jugada, etc. Cuando el primer jalón del cifrado se excluye del análisis (sea por sí solo, sea por una de las coincidencias de colores con el correspondiente jalón de la jugada), del mismo modo se comparan sucesivamente el color del segundo jalón del cifrado con los colores de los jalones de la jugada y después, por analogía, el tercero y el cuarto jalones del cifrado. Por lo visto para el cifrado y las jugadas mostradas en la figura 1 nuestro proceder dará las mismas respuestas.
Aún cuando la descripción ocupa bastante lugar, en realidad la respuesta se formula en unos segundos.
El Master Mind se caracteriza por su aspecto atractivo: una tabla bonita, jalones de colores, las puertas, etc. No obstante el juego de los «toros y vacas» posee otras ventajas: para jugar sólo se precisa de papel y lápiz.
Más adelante haremos un comentario sobre ciertos logros que nos ofrece la computación de los juegos que examinamos. Al componer el programa de máquina para el Master Mind, los distintos colores, antes que nada, han de ser codificados por medio de números, o sea, de un modo u otro nos vemos ante la necesidad de recurrir al idioma de las cifras del juego «toros y vacas».
Para acertar un número en el juego «toros y vacas» o el cifrado en el Master Mind, el contrario se ve ante la necesidad de formular cierto test. De esta manera nuestros dos juegos pertenecen a la categoría de juegos test.
Proponiendo como enigma un número en el juego «toros y vacas», la primera cifra se puede elegir de diez maneras, la segunda de nueve (una de las cifras ya está ocupada), la tercera, de ocho, y, por último, la cuarta, de siete. En total tenemos 10 × 9 × 8 × 7 = 5040 distintos números. En el Master Mind en cada lugar puede encontrarse un jalón de cualquier color (de seis posibles), es decir, en total 64 = 1296 variantes.
Así pues, en el juego «toros y vacas» hay 5040 números diferentes que pueden ser pensados y con los cuales se puede hacer una jugada. Y ¿cuál es el número de posibles respuestas?
Todas ellas están indicadas en la segunda columna de la tabla 2, en total son 14 (es evidente que la respuesta 3t, 1v no es posible). Las líneas horizontales de la tabla separan los casos de acierto de cuatro, tres, dos, una y ninguna cifra. En la tercera columna se indica la cantidad de cifras que pueden dar la correspondiente respuesta en la primera jugada. La respuesta que más agrada es, claro está, 4t con la que inmediatamente termina el juego. Como podemos apreciar la mayor variedad de números posibles sigue siendo la que corresponde a la respuesta 1v, que es de 1440 números.
Por supuesto que el resultado del juego, es decir, la cantidad de jugadas necesarias para averiguar el número ideado, en cierta medida, es casual. Pero mucho se debe también al arte de los jugadores. Aquí surge la pregunta: ¿qué debe entenderse por maestría en el juego «toros y vacas»? Pues, incluso un principiante, ya en su primera jugada puede acertar el número pensado, mas esto aún no demuestra su destreza.
Supongamos que los jugadores A y B jugaron un encuentro de tres partidas. El jugador A en las tres partidas acertó el número del jugador B en 5 jugadas. El jugador B en dos partidas acertó el número en 4 jugadas y en la tercera, en 9. ¿Quién de ellos juega mejor? El jugador B ganó el encuentro por 2 a 1, no obstante que el número total de jugadas que hizo fue mayor. Si, digamos, lo que importa en el ajedrez es el número de victorias independientemente de lo que duran las partidas, en el juego de «toros y vacas» lo es precisamente la velocidad con que se acierta, la cantidad de jugadas hechas, la que compone el resultado del juego.
Veamos los dos conceptos más interesantes para la valoración del buen juego a los «toros y vacas». Sea la cantidad de jugadas que consume uno de los jugadores en acertar el número de orden i (i recorre los valores desde 1 hasta 5040). Introduzcamos dos características de la fuerza de su juego:
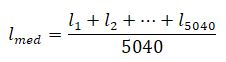
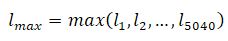
donde lmed es la cantidad media de jugadas que utiliza el jugador para acertar el número y lmáx, la cantidad de jugadas que le garantiza el descubrimiento del número cifrado. El jugador averigua cualquier número, como máximo, en lmáx jugadas. Cada una de estas características, a voluntad, puede servir para la valoración de la fuerza de juego. Por lo visto en el Master Mind las magnitudes lmed y lmáx se determinan exactamente igual, sólo que en las fórmulas figurará otro número, el 1296.

Cuando juegan dos personas siempre es fácil determinar quién juega mejor. Otra cosa es cuando se trata de un ordenador. Para una estrategia arbitraria de juego, formulada en forma de cierto algoritmo, se pueden determinar los números lmed y lmáx y por lo tanto, en función del criterio, determinar cuál de los programas es mejor para el ordenador.
Cabe destacar que este tipo de juego representa un objeto de investigación bastante interesante para el ordenador. Basta decir que en la redacción del programa para el juego «toros y vacas» tomó parte uno de los más grandes especialistas del mundo en programación, el norteamericano D. Knuth. En la URSS un grupo de estudiantes de la cátedra de cibernética del instituto del Acero y las Aleaciones de Moscú dirigido por el docente M. Guendler obtuvo ciertos resultados en esta esfera.
El problema que más atrae la atención de matemáticos y programadores es hallar el algoritmo óptimo, es decir, tal estrategia de juego, para la cual el número lmed o respectivamente lmáx tome su magnitud mínima. Hablando de lmed, aquí no todo aún está claro. Fueron halladas estrategias que para el Master Mind dieron valores de lmed algo mayores de 3 y menores de 4, y para el juego «toros y vacas», algo mayores de 5, pero la cuestión de los algoritmos óptimos sigue abierta.
En lo que concierne al número lmáx que es el que presenta mayor interés, el problema está totalmente resuelto. Para el Master Mind fue construido el mejor algoritmo de juego que permite descifrar cualquier número del cifrador no más tarde de la quinta jugada y está demostrado que para cualquier otro algoritmo (estrategia) se hallará por lo menos un número que para averiguarlo se necesitarán no menos de cinco jugadas. Así pues lmáx = 5.
Varios años atrás, estudiantes del Instituto del Acero y las Aleaciones de Moscú desarrollaron una estrategia para el juego «toros y vacas» que garantiza el acierto de cualquier número en siete jugadas y establecieron que lmáx ≥ 6. Pero no se conseguía, de ninguna manera, acercar estas fronteras. Recientemente, por medio de unos razonamientos combinatorios ingeniosos y una utilización sutil de las posibilidades del ordenador, dichos estudiantes determinaron que lmáx = 7. En otras palabras, construyeron un algoritmo para el juego «toros y vacas» que permitirá acertar en siete jugadas cualquier número memorizado y demostraron que no existe estrategia de seis jugadas.
A propósito, en el ejemplo mostrado al principio, el número pensado fue acertado precisamente en siete jugadas (aunque el ejemplo tenía carácter de estudio y no perseguía el objetivo de hacer un juego óptimo).
Claro que no nos debe sorprender el hecho de que para el juego «toros y vacas» los números lmed y lmáx sean mayores que para el juego Master Mind, pues en el primer caso la cantidad de posibles variantes del cifrado es casi 4 veces mayor. No obstante, se conoce una variante más complicada del juego, el Super Master Mind, que en lugar de cuatro orificios para la codificación utiliza cinco y en vez de jalones de 6 colores utiliza jalones de ocho colores.
Veamos ahora unas cuantas partidas (más preciso sería decir, utilizando la terminología ajedrecística, terminaciones o estudios) presentadas en forma de problemas. Si las examina usted obtendrá una buena ilustración de los detalles del juego «toros y vacas». Serán examinadas todas las situaciones en que la respuesta del contrario a nuestra primera jugada, para mayor precisión el número 1234, coincida con uno de los primeros cinco números de la tabla 2. Si la respuesta es 4t, la partida dura sólo una jugada, y para cada uno de los otros cuatro casos indicaremos el procedimiento de juego que garantiza el acierto del número ideado en un mínimo de jugadas. En otras palabras, en este número de jugadas nosotros acertamos con precisión el número del adversario, cualquiera que sea éste y, si su cantidad es menor, nosotros podemos, en todo momento, no tener suerte, el número cifrado puede quedar sin acertar.
Partida 1. A la primera jugada 1234 el contrario contestó 2t, 2v. ¿Qué cantidad mínima de jugadas garantiza el acierto del número ideado?

Es fácil comprobar que sólo seis números pensados pueden obtener la respuesta 2t, 2v (tabla 3, primera columna) y cualquiera que sea la segunda por lo menos tres de estos seis darán igual respuesta.
Hacemos nuestra segunda jugada 1356 (en lugar del 5 y el 6 se podrían tomar también otras cifras diferentes del 1, 2, 3 y 4). Las posibles respuestas se encuentran escritas en la segunda columna de la tabla. La respuesta 2t determina inmediatamente el número pensado, el 1324 (otros números tienen otras respuestas), la respuesta 1t, 1v nos deja dos variantes, mientras que la respuesta 2v nos deja 3 variantes. La tercera jugada 3256 (teniendo en cuenta la segunda) pone todo en claro, los cinco números-candidatos dan diferentes pares de respuestas. La raya en la tabla 3 (y en todas las tablas sucesivas) significa que con la correspondiente jugada la «reacción» respecto a ella del número dado ya no nos interesa. Así pues la cuarta jugada tiene garantizada la respuesta 4t y la partida dura no más de cuatro jugadas.
Un error típico y poco evidente que cometen muchos de los que intentan resolver este problema consiste en utilizar para el juego números que contienen únicamente las cifras 1, 2, 3 y 4. La lógica aquí es simple, puesto que se conocen todas las cifras, ¿qué necesidad hay de incluir otras? Sin embargo, con este enfoque el número pensado se determina con garantía a la quinta jugada (la respuesta 4t).
Partida 2. La misma pregunta que en la primera partida, pero la respuesta a la primera jugada es 1t, 3v.
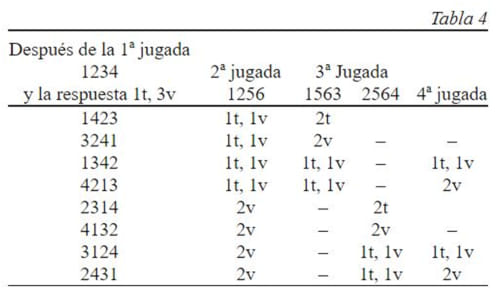
A la primera jugada 1234 ocho números pueden producir la respuesta 1t, 3v (tabla 4). Sea cual fuere la segunda jugada por lo menos cuatro números dan la misma respuesta y para aclarar la situación se requerirán otras dos jugadas. A la segunda jugada 1256 los números se dividen en dos grupos; para los del primer grupo (respuesta 1t, 1v) la tercera jugada es 1563 y para los del segundo grupo (respuesta 2v), 2564. Después de esto quedan dos pares de números en cada grupo que requieren una jugada más, y la cuarta jugada 1564 aclara totalmente el cuadro. Así pues, la segunda partida dura no más de cinco jugadas.
Partida 3. La misma pregunta que en las dos primeras partidas, pero la respuesta a la jugada inicial es 4v.
Como respuesta a la primera jugada 1234 nueve números pueden producir la respuesta 4v (tabla 5). La segunda jugada 3102 descifra dos números y los siete restantes los divide en dos grupos, en uno de los cuales resuelve la jugada 4153 y en el otro, la jugada 2456. Finaliza la partida la cuarta jugada (se obtendrá la respuesta 4t).

Partida 4. La misma pregunta que en las tres partidas anteriores, pero la respuesta a la primera jugada es 3t.
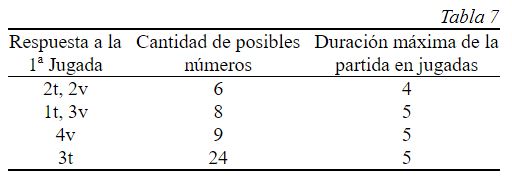
La respuesta 3t a la primera jugada 1234 da 24 números. Realmente tres cifras se pueden fijar en sus lugares de cuatro maneras y para la cuarta existen seis posibilidades 0, 5, 6, 7, 8 y 9, es decir, un total de 4 × 6 = 24 variantes. Es curioso que hallar, en esta partida, el número pensado entre 24 se consigue con la misma cantidad de jugadas con la que se hallan los 8 números en la segunda partida.
Analicemos la tabla 6a. En sus primeros cuatro renglones a sustituye a cualquiera de las cifras 8, 9 o 0. De esta manera aquí se presentan las 24 posibilidades. Hagamos la segunda jugada 1567. La respuesta 0t, 0v mantiene la elección de los tres números sin acertar, para los cuales sirve la tercera jugada 8934 (tabla 6b). Si la respuesta es 2t se puede jugar 1506 (tabla 6c) y siendo esta 1v, se podría continuar con la jugada 5634.
Para los nueve números de la tabla 6a con respuesta 1t componemos la tabla 6c (aquí también a puede tomar una de las tres cifras 8, 9 o 0). La tercera jugada 3564 los divide en tres grupos iguales, la cuarta jugada identifica los números y la quinta pone punto final al juego (respuesta 4t).
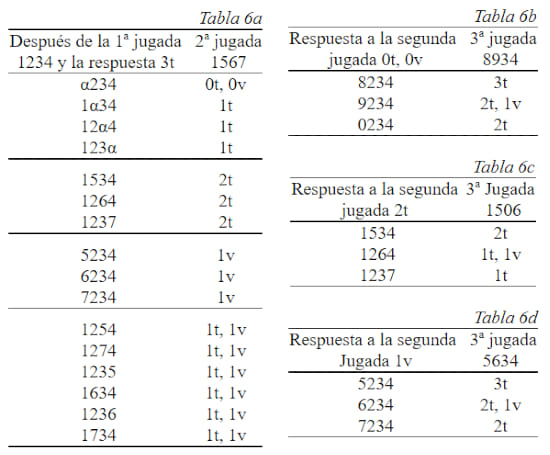
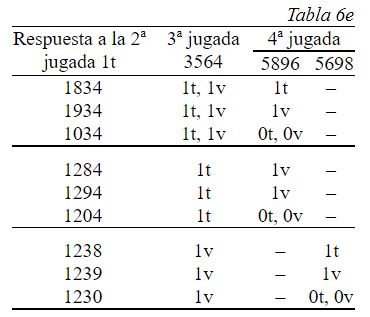
Nos quedaron otros seis números en los renglones de abajo de la tabla 6a; anotémoslos aparte (tabla 6f). Con estos seis también se logra resolver el asunto con dos jugadas adicionales. Así pues, nuevamente la partida no dura más de cinco jugadas.
Los ejemplos analizados muestran que el juego hábil a los «toros y vacas» requiere de un preciso cálculo matemático.
§. Acertar la palabra[1]
Este juego apareció a principios de los años 70, casi al mismo tiempo que el de «toros y vacas», y se asemeja mucho a él. Aunque el juego es de palabras, para tener éxito no sólo es importante poseer un amplio vocabulario, sino también pensar lógicamente. Así pues, este juego representa una mezcla de juego de palabras con uno matemático.
Juegan dos. Uno de ellos piensa una palabra de cinco letras diferentes y el segundo debe acertarla. Para ello nombra, una tras otra, palabras con una cantidad arbitraria de letras y no obligatoriamente diferentes, a cada una de las cuales el adversario, en respuesta, le comunica una cifra que significa el número de veces que las letras de la palabra ideada se encuentran en la palabra propuesta; además cada letra de la palabra pensada se considera tantas veces en la respuesta, cuantas ella se encuentra en la palabra propuesta.
Expongamos un ejemplo. Supongamos que nuestro adversario imaginario pensó la palabra RETAL y nosotros le propusimos la palabra ALAMEDA. En este caso aquél deberá responder 5. Realmente las letras R y T de la palabra ideada no entran en la palabra propuesta (o de otra manera, entran 0 veces), la letra A entra tres veces y las letras E y L, por una vez. En total 0 + l + 0 + 3 + l = 5.
Por la palabra nombrada y la respuesta nosotros cada vez sacamos determinadas conclusiones respecto a la palabra ideada. De esta manera la respuesta 5 del adversario a la palabra ALAMEDA propuesta por nosotros significa que la palabra ideada, aún desconocida para nosotros, obligatoriamente contiene la letra A, de lo contrario la respuesta máxima sería 4, así como dos letras de cuatro, L, M, D, E. Examinemos otras posibilidades. La respuesta 0 certificaría que en la palabra que queremos acertar no hay ninguna de las cinco letras de que consta la palabra ALAMEDA; la respuesta 1 o 2, que en dicha palabra hay, respectivamente, una o dos letras de las cuatro L, M, D, E y no existe la letra A; la respuesta 3 indica que la palabra contiene la letra A y no posee las otras cuatro o por el contrario tiene tres de las letras L, M, D, E y no posee la letra A; y finalmente cuando la respuesta es 4, la conclusión es que la palabra ideada contiene la letra A más una de las cuatro restantes o tiene estas cuatro letras, pero entonces no contiene la letra A.
Extrayendo de cada jugada tal o cual información sobre la palabra ideada por el adversario, nosotros hacemos la siguiente jugada, etc., hasta obtener la respuesta «acertado».
Examinemos esta «partida» hasta el final. En la segunda jugada proponemos la palabra ARA, la respuesta es 3. Sacamos la conclusión de que en la palabra pensada existe la letra R (y la letra A, acertada anteriormente). Nuestra tercera jugada, MANDA, obtiene la respuesta 2.
De esta manera, por cuanto en la palabra pensada existe la letra A, la misma no contiene las letras M, N y D.
Teniendo en cuenta la respuesta a la primera jugada, obtenemos que la palabra ideada contiene las letras L y E. De esta manera la palabra tiene las letras A, R, L y E.
La cuarta jugada, AORTA, nos da la respuesta 4. Conclusión: la quinta letra es la T, o bien la O. Nuestra quinta jugada es OSO y la respuesta 0. Por tanto la palabra contiene la letra T. Con las cinco letras halladas formamos la palabra RETAL y la proponemos como sexta jugada. La respuesta «acertado» nos indica el fin de la partida. Esta duró seis jugadas.
Lógicamente que los dos jugadores piensan las palabras de manera que resulte más difícil acertarlas. Gana el que acierte la palabra del contrario, es decir, obtenga la respuesta «acertado» en menor número de jugadas.
Como en la mayoría de los juegos con palabras, tanto la palabra pensada como las «jugadas» deben ser nombres sustantivos en singular. Para evitar discusiones innecesarias es preferible ponerse de acuerdo desde el principio sobre los diccionarios que se admite utilizar.
Por lo visto el «acertar la palabra» y el «toros y vacas» son juegos test. La elección de las palabras-jugadas, con las que se consigue el objetivo, en esencia, es un test para acertar la palabra (cifrado) pensada por el adversario y por tanto la tarea del jugador consiste en hacerlos lo más corto posible. Por supuesto que el juego es fácil de generalizar, permitiendo pensar palabras de mayor número de letras, más cinco letras es la cantidad óptima (similar a las cuatro cifras en el juego de «toros y vacas»): la diversidad de palabras con cinco letras es muy grande y acertarlas no es nada fácil.
No es obligatorio hacer las jugadas (nombrar las palabras test) por turno, lo importante es la cantidad total de jugadas. En el caso de jugarse muchas partidas, en cada una de ellas se puede tener en cuenta no sólo quién utilizó menor número de palabras, sino también en cuántas jugadas lo hizo antes.
Es de subrayar que, si ya se han encontrado las cinco letras, no significa esto que la partida ha terminado. Pues no está excluido que de estas cinco letras se pueda componer más de una palabra. Las palabras formadas con las mismas letras se llaman anagramas y el conjunto de estas palabras, bloque de anagramas. Si una vez determinadas las cinco letras «tropezamos» con un bloque de anagramas, habrá que hacer jugadas adicionales con el fin de aclarar cuál de las palabras de este bloque ha sido ideada.
En el juego «acertar la palabra» surgen problemas interesantes y originales. Examinemos algunos de estos problemas.
Según las reglas del juego, las jugadas representan palabras de un mismo idioma. Mas ¿qué cambiará si retiramos esta limitación, es decir, permitimos jugadas, por así decirlo, con palabras abstractas, compuestas de un conjunto arbitrario de letras? Puede parecer que tal modificación de las reglas no tiene importancia, no obstante de la resolución del siguiente problema se deduce que en este caso el juego se «degenera».
Problema 1. ¿En cuántas jugadas se puede acertar la palabra (o cinco letras del anagrama), si permitimos jugar palabras «abstractas»?
Este problema tiene carácter puramente matemático y la respuesta a él es bastante inesperada: ¡se requiere solamente una jugada! Esta puede ser, por ejemplo, así:
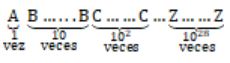
Dicha «palabra» contiene las 29 letras del alfabeto español, además la letra A – una vez (100), la letra B – 10 veces (101), etc., la letra Z – 1028 veces. La respuesta a la jugada, formulada de esta manera, permite determinar inmediatamente las cinco letras. Realmente, si en la palabra pensada existe la letra A, la última cifra de la respuesta será el 1, si por el contrario la letra A no se encuentra presente, en el final se encontrará un cero. Si la palabra contiene la letra B, en el segundo lugar por la derecha (cantidad de decenas) se encontrará un 1, de lo contrario, un 0. Si la palabra lleva la letra C, en el tercer lugar por la derecha (cantidad de centenas) se hallará un 1, de lo contrario, un cero, etc. De esta manera el número que obtengamos en respuesta a nuestra jugada tendrá muchos ceros (24, si la palabra contiene la letra Z) y exactamente cinco unos que serán los que determinen las cinco letras necesarias.
Expongamos un ejemplo. Supongamos que en respuesta a nuestra palabra abstracta se obtuvo el número 1001000100011. Esto significa que la palabra pensada contiene las letras: A (1 en el extremo derecho), B (1 en el segundo lugar por la derecha), E (1 en el sexto lugar por la derecha), I (1 en el décimo lugar por la derecha) y L (1 en el treceavo lugar por la derecha). Por tanto la palabra pensada es BAILE.
La palabra «mágica» tiene una longitud astronómica, pero en este problema es importante la existencia misma de la jugada universal. Tracemos un paralelo entre este juego de palabras y el ya examinado juego numérico «toros y vacas». Los dos juegos test precisan acertar el cifrado que ideó el adversario: en un caso qué número, en el otro, qué palabra; además en cada jugada se extrae cierta información sobre el número o la palabra ideados. Cada juego tiene sus particularidades que son las que le dan un carácter creativo. En el «toros y vacas» las jugadas son conjuntos arbitrarios de cuatro cifras y en el «acertar la palabra», conjuntos de letras de longitud arbitraria, pero que obligatoriamente forman palabras.
Por supuesto que «toros y vacas» es un juego lógico, mientras que «acertar la palabra» es un juego de palabras. Se puede hacer un híbrido de estos dos juegos, utilizando, tanto para el cifrado como también para las jugadas, palabras con igual cantidad de letras diferentes y las respuestas formularlas como en el juego «toros y vacas». Sin embargo, parece que este híbrido será menos interesante que cada uno de estos juegos por separado.
Volvamos a la variante habitual del juego «acertar la palabra». Con frecuencia al meditar la respuesta surge la necesidad de determinar si contiene el cifrado tal o cual letra concreta. De acuerdo con esto es curioso el siguiente problema.
Problema 2. ¿La presencia o no de qué letras del alfabeto puede determinarse de una jugada en la palabra pensada?
En este caso se supone que no disponemos de información sobre la palabra pensada. Resulta que, por ejemplo, en el idioma ruso 20 letras de las 33 que tiene su alfabeto precisan sólo de una jugada para esclarecer la cuestión de su presencia en la palabra ideada. La idea de adivinar la letra es muy simple: la letra «sospechosa» debe distinguirse por el número de entradas en la palabra test. Lo más sencillo es jugar con una palabra de tres letras de las que una entra dos veces. La respuesta a esta jugada nos indica directamente si contiene o no la palabra pensada dicha letra. Supongamos que la jugada es con la palabra OJO. Si la respuesta es 0, la palabra pensada no contiene ni la O ni la J. Si es 1, contiene la J y no la O. Si la respuesta es 2, en este caso existe la O y no se encuentra la J. Y, por fin, la respuesta 3 nos indica que tanto la O como la J forman parte de la palabra pensada. De esta manera, si nos interesa la información sobre la letra O o bien la J, la palabra OJO nos satisface plenamente. En total con palabras de tres letras en el idioma ruso se consigue determinar 10, en español, 12 letras. Otras 10 letras se pueden buscar con palabras de mayor longitud. Las nueve palabras test están compuestas de la siguiente manera: la letra sospechosa y dos pares de letras más. Como resultado la respuesta impar (1, 3 o 5) nos indica la presencia de dicha letra en la palabra pensada, mientras que la respuesta par (0, 2 o 4) es señal de su ausencia (por ejemplo, SALSA).
Problema 3. Para cada letra del alfabeto hállese el número mínimo necesario de jugadas para determinar si se encuentra o no dicha letra en la palabra pensada.
Resulta que cualquier letra del idioma ruso se puede hallar, como más, en dos jugadas. El par necesario para acertar las 13 letras más «complejas» se puede formar así: una de las dos palabras se compone de las letras que contiene la otra palabra, añadiéndole la letra que se desea determinar. Las respuestas iguales a estas dos palabras nos indican que en la palabra pensada no existe la letra que buscamos y las respuestas diferentes nos revelan su presencia. Por ejemplo, las respuestas iguales a las jugadas MAS y AS nos indican que en la palabra pensada no se encuentra la letra M y las respuestas diferentes (estas se pueden diferenciar sólo en 1) nos señalan que dicha letra existe.
Ofrecemos al lector determinar individualmente la cantidad de letras del alfabeto español que se pueden «revelar» en una jugada y la cantidad que se puede acertar en dos. Para las letras que se aciertan sólo en dos jugadas puede plantearse el problema de hallar tal par de palabras (que resuelven la cuestión de la presencia de una letra) cuya longitud es mínima. En la práctica rara vez se pretende hallar una letra determinada de la palabra pensada. En el transcurso del juego surgen diferentes situaciones y no hay necesidad de perseguir una letra, sino hacer jugadas que permitan conseguir el máximo de información sobre la palabra ideada por el adversario.
Problema 4. Encontrar una palabra, lo más larga posible, que de la primera jugada (en el caso si la respuesta del oponente nos favorece) nos permita acertar la palabra ideada.
Problema 5. Encontrar una palabra, lo más corta posible, que de la primera jugada (en el caso de que la respuesta del adversario nos favorezca) nos permita acertar la palabra pensada.
Este problema parece ser el contrario al número 4 y nos recuerda el juego al «cernícalo» (véase el juego 12 al final del libro). Realmente, proponiendo una palabra corta en nuestra primera jugada, debemos acertar tres o cuatro letras, las cuales después se completarán unívocamente hasta la palabra pensada.
Problema 6, ¿Qué máximo de letras puede determinarse de una sola jugada, es decir, establecer cuál de estas letras, precisamente, (una sola) pertenece a la palabra pensada?
Problema 7. Idear una partida en cuya primera jugada se acierten cuatro letras de la palabra pensada por el oponente, quedando para la quinta el máximo de posibilidades y todas ellas queden acertadas en una segunda jugada.
A diferencia del problema 6 en éste se precisa no sólo acertar de una jugada el mayor número posible de letras, sino hacerlo de tal modo que el correspondiente conjunto parezca surgir durante el juego, o sea, después de la primera jugada.
Deseándolo, se puede inventar también otros problemas y ejercicios del fascinante juego «acertar la palabra». Por lo visto muchos de ellos no se conseguirán resolver sin la utilización de un potente ordenador, además de diccionarios. En todo caso del siguiente problema esto se puede afirmar con toda seguridad.
Problema 8. ¿Cuál es el número mínimo de jugadas que resulta suficiente para acertar, con toda seguridad, la palabra ideada por el adversario, cualquiera que ésta sea?
La experiencia del juego muestra que, actuando con inteligencia y atención, la palabra que tiene en mente el contrario puede acertarse, por regla general, en 5-7 jugadas, pero no nos atrevemos demostrar este hecho.
§. Combate marino
No todo lector tuvo la oportunidad de jugar a los «toros y vacas» o a «acertar la palabra», pero encontrar una persona que no haya jugado en su vida al «combate marino» es imposible. A pesar de su aparente sencillez, este juego tan popular y sus variantes contienen no pocos detalles.
Combate marino clásico. Comencemos por la variante más difundida en muchos países del combate marino. Ambos jugadores dibujan en un papel cuadriculado dos tableros de 10 × 10. En el primero se disponen los barcos propios y en el otro se anotan los barcos acertados del contrario. La flotilla consta de diez barcos: un portaaviones (4 × 1), dos cruceros (3 × 1), tres destructores (2 × 1) y cuatro submarinos (1 × 1). Los barcos pueden ocupar cualesquiera casillas del tablero, pero no deben tocarse entre sí con sus lados ni con sus ángulos.
Después de situar la flota, los jugadores empiezan a disparar sobre el acuatorio enemigo, es decir, nombrar, turnándose, las casillas del tablero: a3, b7, i9, etc., (indicaremos las horizontales de los tableros con números desde el 1 hasta el 10, y las verticales con letras desde la a hasta la j, véanse las fig. 6 y 7). Después de cada disparo el primer jugador obtiene del segundo la siguiente información: «tocado», si el disparo dio en una casilla donde se encuentra el barco; «hundido», si ésta es la última casilla del barco (en las otras casillas del barco se hizo blanco en jugadas anteriores), y finalmente «agua», si la casilla está vacía. En los dos primeros casos el jugador hace un disparo adicional y así hasta el primer fallo, después de lo cual el turno de jugar pasa al adversario. Gana el que hunda antes los barcos del contrario.
Así pues, en este juego test el cifrado es el conjunto de rectángulos situados en el tablero y el test, los disparos. Por lo común el disparo en el combate marino se marca con un punto y en el caso de tocar el barco el punto se sustituye por una cruce- cita (el barco hundido se contornea). Lógicamente que también se puntean las casillas que con seguridad se sabe que no pueden formar parte de un barco (se encuentran en diagonal respecto a las casillas donde fue tocado el barco o rodean un barco hundido).
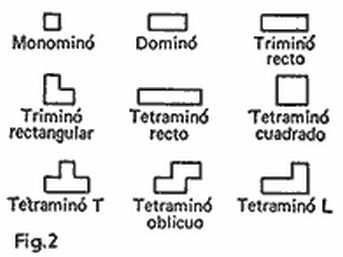
Diferentes tableros y barcos.
Es evidente que la forma del tablero para el combate marino, el aspecto de los barcos y la composición de la flotilla no tiene gran importancia. Así, por ejemplo, los ajedrecistas preferirán el tablero de 8 × 8. Señalemos que en los términos del juego «poliominó» nuestros barcos reciben los siguientes nombres: el submarino es monominó, el destructor es dominó, el crucero es triminó recto, el portaaviones es tetraminó recto (fig. 2). Como buques en este juego pueden utilizarse también otros tipos de poliominó. La figura 2 muestra los nueve barcos que contienen no más de cuatro casillas.
El combate puede tener lugar no sólo en el mar sino también en tierra. Para ello tenemos que dividir el tablero en dos partes, las correspondientes al mar y a la tierra. Los jugadores tienen a su disposición una flota (los barcos pueden hallarse sólo en el mar), un ejército de tierra (emplazado sólo en tierra) y aviones que se encuentran tanto sobre tierra como sobre el mar. En el juego pueden utilizarse, por ejemplo, 20 unidades de combate: incluir en la flotilla diez barcos como en el combate marino clásico, en el ejército de tierra, dos tetraminós en L, dos en T, dos cuadrados, dos oblicuos y finalmente convertir en aviones dos triminós rectangulares.
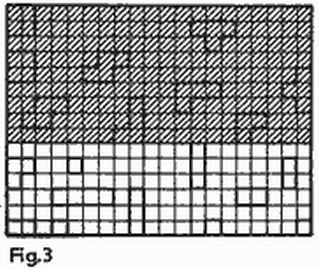
La figura 3 muestra un ejemplo de disposición de todos los tipos de ejércitos en un tablero de 20 × 15 (en el dibujo la parte correspondiente a la tierra está rayada). Como debe ser, la flota se encuentra en el mar, los ejércitos de tierra están emplazados en tierra, un avión vuela sobre el mar y el otro sobre la tierra.
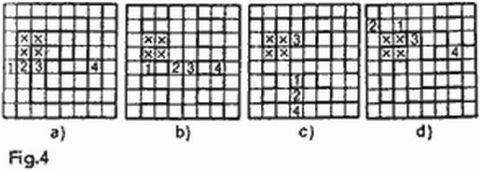
He aquí otra variedad del combate marino. El juego se desarrolla sobre tableros de ajedrez de 8 × 8; cada jugador divide el suyo en cuatro partes de forma arbitraria, compuestas de un número igual de casillas, 16 cada una. La figura 4 presenta cuatro variantes de división del tablero. La jugada comprende cuatro disparos simultáneos sobre casillas del tablero que forman un cuadrado cualquiera de 2 × 2, por ejemplo, b5, b6, c5, c6 (en la figura 4 las casillas de este cuadrado están marcadas con cruces). El jugador sometido a los disparos comunica los números de las partes que fueron alcanzadas por los disparos, sin indicar qué casillas pertenecen a cual de las cuatro partes. Para nuestros cuadrados las respuestas serán las siguientes: 2, 2, 2, 3 (fig. 4a); 1, 1, 2, 2 (fig. 4b); 2, 2, 3, 4 (fig. 4c); 2, 2, 3, 3 (fig. 4d). Después de cada jugada los dos jugadores sacan determinadas conclusiones sobre la posible división del tablero y sobre su base se eligen las siguientes jugadas. Gana el jugador que averigüe antes las cuatro partes en que está dividido el tablero del contrario.
Estrategia de juego al combate marino.
Volvamos al combate marino clásico sobre tableros de 10 × 10. Es obvio que aquí el éxito, igual que en otros juegos test, dependa, en cierta medida, de la fortuna. Es posible asestar golpes desordenados por el acuatorio enemigo y además destruir sin fallar todos los buques enemigos. Pero seguramente no merece la pena orientarse a esto.
Hablando del arte de juego al combate marino, surgen dos preguntas: 1) ¿cómo disparar para aumentar la probabilidad de tocar los barcos enemigos? 2) ¿cómo ubicar sus propios barcos con el fin de que al contrario le cueste más hundirlos?
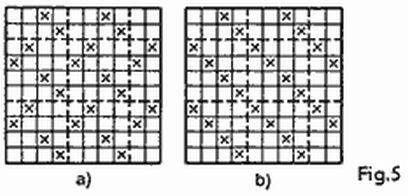
Supongamos que deseamos tocar el portaaviones enemigo. Si disparamos sucesivamente primero por las casillas de la primera horizontal (de izquierda a derecha), luego por las casillas de la segunda, y así sucesivamente, no está excluido que lo detectemos sólo después del disparo 97 (si este barco ocupa las casillas desde g10 hasta k10). No obstante, disparando sobre las casillas marcadas con cruces en las figuras 5a o 5b, nosotros con seguridad tocaremos el portaaviones no más tarde del disparo 24 (24 cruces siguen una tras otra cada cuarta casilla a lo largo de cada vertical u horizontal).
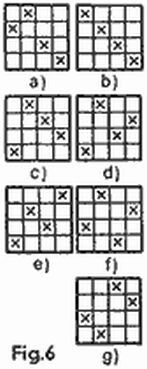
Examinemos un caso más general. Supongamos que en un tablero n × n sólo hay un barco k × 1 (k-minó). Llamemos estrategia al cúmulo de disparos que nos garantiza la posibilidad de tocar este barco. Llamemos óptima a la estrategia que contiene un mínimo de disparos; designemos con s (n,k) el número de disparos en la estrategia óptima.
Por lo visto s (4, 4) = 4; las siete estrategias óptimas para un tablero de 4 × 4 se pueden ver en la figura 6 (nosotros no diferenciamos las estrategias que coinciden, al girar el tablero y en su representación especular). Corriendo los disparos cuatro casillas vertical y horizontalmente obtendremos siete estrategias en un tablero de 10 × 10. Pero sólo dos de ellas son óptimas (compárense las figs. 5a y 5b con las figs. 6a y 6b), con la particularidad de que s (10,4) = 24.
Es evidente que para tocar el barco k × 1, ubicado en un tablero n × n los disparos deben estar separados unos de otros k casillas vertical y horizontalmente. Esto significa que en cada línea hay aproximadamente n/k disparos de estrategia óptima y obtenemos la fórmula aproximada s (n, k) ≈ n2/k.
Los jugadores experimentados, por lo general, actúan de la siguiente manera. Primero, haciendo uso de una de las estrategias de la figura 5, detectan el único portaaviones que tiene el contrario. Cuando acaban con él, comienzan la búsqueda de los cruceros. A partir de este momento los golpes se aplicarán una casilla sí, dos no, vertical y horizontalmente en lugar de uno sí tres no. Después de hundir los dos cruceros, se ocupan de los destructores. Cuando queden sólo los submarinos la elección de las casillas para el disparo no tendrá importancia y queda sólo confiar en la suerte. Por supuesto que los barcos «ligeros» pueden ser detectados también durante la caza de los «pesados».
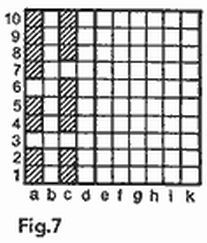
Así pues, lo más difícil es detectar los submarinos, para lo cual no se puede inventar una estrategia efectiva. Por esta razón, al distribuir su propia flotilla, hay que situar los barcos grandes de la manera más densa posible» proporcionando al contrario el mayor espacio libre posible para la búsqueda de los submarinos. En este sentido la disposición más ventajosa se puede ver en la figura 7. Aún cuando el contrario haya hundido nuestros seis barcos grandes, para dar con los cuatro submarinos él dispondrá de un acuatorio con un área máxima, 60 casillas (en la figura, a la derecha de la raya).
Combate de gran tensión. Examinemos un «final de partida» en el que una imprecisión decide inmediatamente la partida (este ejemplo lo propuso V. Chvánov).
En la figura 8 usted puede ver la posición que surgió en el curso de un juego. Hacia este momento las dos flotillas, tanto la nuestra (fig. 8a) como la del contrario (fig. 8b) sufrieron pérdidas iguales. Ambos tenemos hundidos el portaaviones, un crucero y un destructor; continúan el combate un crucero, dos destructores y los cuatro submarinos por cada bando. El contrario ya conoce la disposición de nuestros barcos (en la fig. 8a estos barcos están marcados con líneas de puntos) y cuando le toque jugar él los destruirá sin fallos.
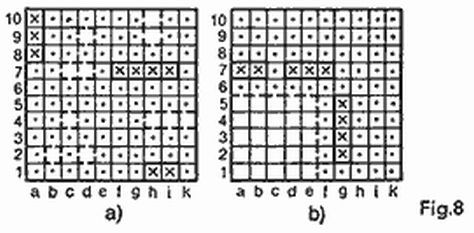

Por suerte jugamos nosotros y la fortuna de la partida está en nuestras manos. Debemos hundir uno a uno sus siete barcos concentrados en un cuadrado 5 × 5. Para hallar la combinación de la victoria en esta refriega de gran tensión se requiere, antes que nada, realizar un análisis lógico de la situación.
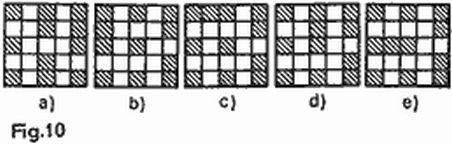
Según las reglas, cualesquiera dos barcos distan uno de otro por lo menos una casilla. Rodeemos cada barco con una orla de media casilla de ancho (fig. 9), llamaremos al rectángulo formado dotación adicional de dicho barco. Hallemos ahora el área de la dotación adicional de los siete barcos que nos proponemos hundir. La dotación adicional de un submarino es de 4 casillas (2 × 2), la del destructor, 6 casillas (3 × 2) y la del crucero, 8 casillas (4 × 2). El área total de las dotaciones supone 36 casillas. Pero el área de la dotación del tablero (el tablero con una orla de media casilla) también es de 36 casillas, de lo cual se deduce que las casillas de los ángulos del tablero 5 × 5 obligatoriamente están ocupadas por barcos (de lo contrario el área del ángulo de la dotación adicional del tablero se «pierde»). Analicemos todas las posiciones posibles de los barcos. En total son cinco (fig. 10a-e), los giros y el reflejo especular del tablero no se tienen en cuenta.
El análisis realizado permite terminar eficazmente el juego. Los primeros cuatro disparos han de lanzarse a los ángulos del tablero 5 × 5. Como nos hemos convencido, todos ellos dan en el blanco. Si al efectuar estos cuatro disparos se logran hundir tres submarinos (fig. 10a), la disposición de los demás barcos se determina unívocamente. Supongamos que se logró hundir sólo un submarino (fig. 10b-c). Por cuanto la dotación adicional de los barcos cubre densamente la del tablero, el quinto y sexto disparos se pueden hacer sin riesgo sobre los escaques a3 y el que se encuentran a dos casillas del de la esquina ocupado por el submarino hundido. De los resultados de estos dos disparos depende cuál de las variantes «b» y «c» tiene lugar. Si los disparos contra las esquinas produjeran el hundimiento de dos submarinos (fig. 10d-e), los golpes sobre las casillas a3 y c5 permitirían aclarar inmediatamente cuál de las variantes eligió el contrario.
Así, después de seis disparos, nosotros disponemos de una información completa sobre la ubicación de los barcos enemigos y con los siguientes cinco disparos acabaremos victoriosos esta batalla tan tensa. El ejemplo examinado muestra que en una situación crítica de los participantes en este juego se requiere suficiente maestría y firmeza.
Andanada. Hasta aquí cada disparo se efectuaba sobre una casilla del tablero. Una modalidad interesante del combate marino es el juego en el cual una jugada consta de varios disparos simultáneos, se produce, por decirlo así, un fuego masivo sobre la flota enemiga. El otro jugador comunica los resultados generales obtenidos, sin indicar el barco averiado y la casilla donde esto se produjo. Por ejemplo, las respuestas a tres disparos simultáneos pueden ser las siguientes: tres veces agua; dos veces agua y una vez tocado; una vez agua y una vez hundido, etc., (la última respuesta significa que dos disparos de tres dieron en un barco y lo hundieron). Las demás reglas del juego se mantienen invariables. Después de cada jugada y su correspondiente respuesta los jugadores obtienen determinada información acerca de la disposición de los barcos enemigos y en lo sucesivo tratan de utilizarla.
En otra variante de este juego cada participante tiene el derecho de disparar simultáneamente sobre tantas casillas del tablero enemigo cuantos barcos le queden sin hundir. El jugador, sobre cuya flota se dispara, comunica nuevamente al contrario sólo las veces que los disparos dieron en el agua, tocaron o hundieron barcos. Si la flotilla es la común, de diez barcos, la primera jugada constará de diez disparos. Si un barco o más resultan hundidos, el número de disparos en la próxima jugada será menor. Cuando todos los barcos hayan sido hundidos, el jugador pierde el derecho a jugar (0 disparos), pero él ya no necesita dicho derecho pues ha perdido.
Veamos otra variante interesante del combate marino sobre un tablero cuadrado arbitrario. En esta variante también pueden realizarse series de disparos. Vamos a considerar que las flotillas de ambos jugadores se componen de barcos de un solo tipo: submarinos, destructores, cruceros, portaaviones o en general, barcos k × 1 (k-minó) sobre un tablero n × n (k ≤ n). El número k se acuerda antes de comenzar el juego.
Cada jugador puede dibujar en el tablero cualquier cantidad de barcos, se puede también no poner ninguno, sin comunicar esto al adversario.
El juego consta de una sola jugada que consiste en el disparo simultáneo sobre una serie de casillas del tablero (andanada). En respuesta el jugador recibe una información sobre cada casilla del tablero, si el disparo dio en el barco o en el agua (sobre los barcos hundidos no se informa). Después de analizar las respuestas del adversario, hay que determinar la situación de toda su flotilla. Gana el jugador cuya andanada contenga menor número de disparos.
Andanada test. Entre los tres juegos test analizados por nosotros (toros y vacas, combate marino, acertar la palabra) más próximo a las matemáticas se encuentra el combate marino y sus diferentes modalidades. La teoría de los testes representa una de las partes modernas de la cibernética y de ella se ocupan muchos matemáticos. Por test se entiende cierto experimento que permite obtener una información completa sobre el objeto analizado. Por cuanto el experimento para su realización siempre requiere determinado gasto, es necesario que el mismo resulte más simple y barato. En este sentido los descritos son juegos test típicos. En adelante, al examinar la última variante del combate marino, para mayor comodidad, utilizaremos la terminología de los testes.
Como antes, llamaremos andanada al conjunto de disparos que se realizan simultáneamente sobre los escaques del tablero del adversario. Si la andanada alcanza el blanco, para cualesquiera respuestas del adversario permite determinar unívocamente el emplazamiento de todos sus barcos, la llamamos test. Los correspondientes disparos y las casillas sobre las cuales se realizan éstos, serán disparos test y casillas test.
El juego descrito, aún cuando es excepcionalmente corto (¡dura solamente una jugada!), es muy original y poco común. La cosa es que una andanada «débil», de escaso número de disparos, está sujeta a cierto riesgo de que no podamos determinar unívocamente la ubicación de los barcos del adversario. Al mismo tiempo si la andanada es «fuerte», cuando el número de disparos es grande y cualquier respuesta del contrario nos garantiza el descifrado de todos sus barcos, existe el riesgo de que nosotros, simplemente, perdamos por el número de disparos en la andanada. A propósito en este juego, como vemos, es muy importante el turno de las jugadas, por lo que hay que jugar una partida con las «blancas» y otra, con las «negras».
Al juego se le puede dar un carácter más riguroso, excluyendo de él el elemento de bluf. Y precisamente exigiremos que cada andanada de los jugadores sea un test, es decir, asegure el reconocimiento unívoco de los buques adversarios cualquiera que sea la respuesta. En adelante vamos a examinar sólo esta variante de juego.
Es evidente que para ser invencible en esta variante del combate marino es suficiente para cualesquiera valores de n y k resolver el siguiente problema.
¿Sobre qué mínimo de casillas del tablero n × n ha de producirse la andanada test para que, cualesquiera que sean las respuestas del adversario, pueda determinarse unívocamente la disposición de todos sus barcos k × 1 (y, por consiguiente, también su número)?
Llamemos mínima a la andanada que ha de determinarse en este problema test y designemos el número de disparos test en ella por t (n, k).
Examinemos primeramente un caso elemental en el que los jugadores marcan en sus tableros solamente submarinos (k = 1). Evidentemente t (n, 1) = n2. Si aunque sea una de las casillas del tablero no es abarcada por la andanada test, a la respuesta «agua» en todos los disparos test nosotros no podremos resolver si se encuentra o no el submarino en dicha casilla.
Si k >1, el problema se complica aún más. En todo caso el autor conoce solamente la solución de los casos extremos: k = 2 y k = n. A continuación formularemos estas dos soluciones en forma de problemas independientes.
Andanada test mínima. Problema 1. En un tablero n × n se encuentra cierta cantidad de destructores (buques 2 × 1), los cuales tienen prohibido cualquier contacto entre sí. ¿Cuál es la cantidad mínima de casillas sobre las cuales han de hacerse los disparos para que, al recibir la respuesta del adversario sobre los resultados de la andanada, se pueda determinar unívocamente la disposición de todos sus destructores?

La resolución de este problema se puede hallar en el libro de I. Soloviov «Los testes» mencionado en la bibliografía. La respuesta aproximada en ésta: t (n, 2) ≈ 4/5 n2 y, por lo tanto, la andanada test mínima debe producirse aproximadamente sobre 4/5 del área del tablero. Para el tablero habitual (10 × 10) la respuesta es precisa: t (10,2) = 4/5 × 102 = 80. La andanada test mínima para este caso puede verse en la figura 11, con la particularidad de que son testes todas las casillas del tablero a excepción de las rayadas.
Problema 2. En un tablero n × n se encuentra cierta cantidad de buques n × 1 que no se tocan entre sí. ¿Cuál es la cantidad mínima de casillas, sobre las cuales hay que disparar simultáneamente, para que, una vez obtenida la respuesta del adversario sobre los resultados del ataque, pueda determinarse unívocamente la disposición de todos sus buques?

Demostremos que para un tablero habitual de 10 × 10 la andanada test mínima consta de 14 disparos. Para ello es suficiente establecer que, en primer lugar, el conjunto de casillas indicadas en la figura 12 con crucecitas es un conjunto test y, en segundo lugar, que no es posible conseguir esto con un número menor de disparos.
Convenzámonos de que la andanada que muestra la figura 12 es una andanada test. Examinemos, una tras otra, todas las horizontales del tablero. Supongamos que sobre una horizontal dada se produjeron dos disparos. Si uno de ellos o ambos dieron en el agua, esto quiere decir que en esta horizontal no hay barcos. Si los dos disparos dan en el blanco esto es señal de que existe un barco horizontal, de lo contrario tendríamos dos barcos verticales con frontera común, lo cual es inadmisible. Examinemos ahora una horizontal con una casilla test. Si el disparo sobre esta casilla da en el agua esto nos indicará que no hay barcos en la horizontal. Si se alcanza el blanco, hay que ver la casilla test vecina verticalmente con aquella. En caso de que el disparo dé en el agua puede afirmarse que el barco es horizontal y en caso de tocar el buque nuestra conclusión será que dicho barco es vertical. Así pues, a cualesquiera respuestas del adversario nosotros determinamos unívocamente la disposición de todos los barcos 10 × 1 (no son más de cinco, además sólo verticales o sólo horizontales).
Queda por mostrar que nuestra andanada test es mínima. Supongamos lo contrario, que t (10,10) ≤ 13. Por cuanto cada horizontal del tablero contiene aunque sea una casilla test (de lo contrario, en caso de que todos los disparos den en el agua, nosotros no podremos determinar si está o no ocupada dicha horizontal por un barco), y el número total de tales casillas no es superior a 13, entonces como mínimo siete horizontales poseen exactamente una casilla test; llamemos solitarias a todas estas casillas (horizontalmente). Además de éstas hay no más de 13 – 7 = 6 casillas test que ocupan un máximo de 6 verticales. Las otras cuatro (o más) verticales pueden disponer sólo de casillas solitarias (horizontalmente), además no son más de siete. Esto indica que por lo menos una vertical del tablero contiene exactamente una casilla test y además ésta es solitaria (horizontalmente).
De esta manera nosotros hallamos una casilla test solitaria, tanto horizontal, como también verticalmente. Si la andanada test alcanza esta casilla y falla en las demás, nosotros no podemos determinar qué tipo de barco (horizontal o vertical) pasa por dicha casilla. Así pues, nuestra andanada no es una andanada test, lo cual es una contradicción.
En el caso general el método de construcción de la andanada test mínima para detectar los barcos n × 1 se deduce de la figura 12. A tres casillas test de cada uno de los cuadrados marcados de 3 × 3 les toca una cuarta casilla (para el tablero 10 × 10 es preciso tomar otras dos casillas en el ángulo superior derecho). De esta manera tenemos una fórmula aproximada t (n,n) ≈ 4/3 n. La respuesta precisa depende del resto que se obtiene después de dividir n por 3 y se escribe de una manera compacta como sigue: t (n, n) = [(4n + 2)/3], donde los corchetes representan la parte entera del número. Para n = 10 nuevamente se obtiene t = 14.

El último problema sobre la andanada test mínima fue propuesto por el autor del libro para la revista de problemas «Kvant», pero cuando abrió la revista recién aparecida inesperadamente descubrió que la condición de que los barcos no deben tocarse entre sí fue omitida del texto a consecuencia de lo cual se obtuvo un problema distinto. En particular, si el tablero en su totalidad está repleto de barcos, con ningún número de disparos es posible discernir cuáles de los n barcos ubicados en el tablero n × n son verticales u horizontales. Por otra parte si prohibimos una distribución tan densa, el nuevo problema tendrá solución. El número de disparos esta vez deberá ser aumentado, la andanada test mínima deberá producirse sobre (2n – 1) casillas, por ejemplo, como se indica en la figura 13. El redactor de la revista de problemas «Kvant» N. Vasíliev que se vio ante la necesidad de resolver este nuevo problema, nacido de una errata en su revista, de paso halló también una solución aún más efectiva al problema inicial, sobre los barcos que no deben tocarse entre sí. Expongámosla.
Supongamos que, como antes, t = t (n,n) es el número de casillas sobre las cuales se produce la andanada test mínima, A, el conjunto mismo de casillas. Demostremos que t ≥ 4/3 n. Por lo visto cada línea del tablero contiene por lo menos una de las A casillas y en una horizontal o vertical con ellas hay además no menos de una de estas casillas. Anotemos en las casillas A unos y doses de colores azul y rojo de la siguiente manera.
Si la horizontal tiene más de una de las A casillas, pongamos en cada una de ellas un dos rojo. Hacemos lo mismo con las verticales del tablero y ponemos en las A casillas unos y doses azules. Como resultado cada casilla A tendrá escrito un uno con un dos, o dos unos y, por consiguiente, la suma p de todos los números inscritos no será mayor de 3t. Por cuanto en cada línea del tablero hemos anotado números de «color», cuyas sumas no son menores de 2, entonces p ≥ 4n. Así pues, 3t ≥ p ≥ 4n, de donde t ≥ 4n/3. Si n se divide entre 3, entonces la respuesta precisa, como sabemos, es t = 4n/3. La fórmula general es t (n,n) = [(4n + 2)/3].
Usted, seguramente, habrá prestado atención a que la andanada test, en la última variante del combate marino, es análoga a la estrategia del juego clásico. Sin embargo, si la estrategia garantiza solamente el impacto sobre el único barco k × 1 del tablero, la andanada test permitirá determinar unívocamente la disposición de toda la flotilla de barcos. Haciendo uso de cierta estrategia en el combate marino clásico, al dar en el blanco, nos queda sólo hundir el barco. En lo que se refiere a la andanada test, independientemente del éxito obtenido con algunos disparos, es necesario realizarlos todos como uno. La andanada test mínima es una analogía de la estrategia óptima. Los que deseen desarrollar más profundamente la teoría de este juego pueden investigarla para otros valores de k, a saber 2 < k < n.
Capítulo 2
Juegos ajedrecísticos
§. Juegos sobre tableros singulares
§. Ajedrez de fantasía
§. Juegos matemáticos sobre tableros ajedrecísticos
El presente capítulo, igual que los que le siguen, está dedicado a juegos, cuyos atributos obligatorios son un tablero y figuras (piezas del juego de damas, fichas). Existen cientos de juegos que utilizan un tablero y figuras, por lo que difícilmente podríamos comentarlos todos. En el presente libro examinaremos los de mayor divulgación, así como sus variadas modificaciones. Se trata de juegos ajedrecísticos, de damas, juegos como el de tres en raya, o el go. Algunos de estos juegos están muy divulgados y muchas personas tienen gran afición por ellos, otros son de carácter matemático o recreativo. La mayoría de los juegos sobre tableros tienen una historia multisecular; la literatura dedicada a estos juegos realmente no tiene límites. Decenas de miles de títulos cuentan tan solo las ediciones de ajedrez. Es muy amplia también la literatura dedicada al juego de damas, rendsiu, go. La teoría de los distintos juegos que se desarrollan sobre tableros cuadrados y rectangulares ocupa un espacio importante en serios trabajos de matemáticas. Juegos más simples se describen en numerosos libros de matemáticas recreativas, así como en libros de teoría de los juegos, teoría de grafos combinatoria.
El presente capítulo está dedicado a los juegos ajedrecísticos y el que le sigue, a los juegos con fichas. Por cuanto muchas de las variantes examinadas se distinguen notoriamente del ajedrez y del juego de fichas que nosotros tenemos costumbre de practicar, hay que precisar qué es lo que entendemos por juegos ajedrecísticos y de fichas.
Tanto en el ajedrez como en el juego de fichas son imprescindibles un tablero y figuras. En los juegos de damas estas figuras se llaman peones, fichas o piezas. Éstas no se diferencian por su aspecto o por sus movimientos, únicamente tienen distinto el color (generalmente son blancas y negras). Las piezas pueden transformarse en damas, torres u otras figuras, pero en principio no hay gran diferencia entre las jugadas de las figuras nuevas y las viejas.
En lo que respecta al ajedrez, en él el surtido de figuras es mucho más amplio, cada una de ellas tiene sus propiedades características, difieren en el aspecto y sus movimientos son distintos. En el ajedrez se juega por todo el tablero mientras que en el juego de damas, por regla general, sólo por las casillas de un mismo color. A propósito en el rendsiu y el go con fichas se rellenan todas las casillas del tablero. Estos juegos de fichas se encuentran un poco a un lado del juego de damas tradicional y viven su vida independiente. Por esta misma razón en nuestro libro ellos ocupan dos capítulos independientes.
Los juegos de fichas tienen una historia más antigua y un surtido más amplio que los ajedrecísticos. No obstante el autor de este libro, siendo maestro de ajedrez, no podía permitirse poner el juego de damas por delante del ajedrez. Primero, como puede ver el lector, va un capítulo dedicado a los juegos ajedrecísticos y sólo después otro dedicado a los de fichas.
Existen muchos libros sobre el ajedrez, manuales de estudio y de consulta que contienen las reglas del juego, cuestiones de estrategia y de táctica. Lo mismo existe para el juego de damas tradicional, tanto el ruso como el de cien casillas. Nosotros suponemos que estos juegos son tan populares, que el lector los conoce muy bien, por lo que hacemos hincapié en otras variantes del juego menos conocidas y habituales.
§. Juegos sobre tableros singulares
El ajedrez fue creándose en el curso de muchos siglos y sus reglas de juego se modificaron multitud de veces. Desde el punto de vista de las matemáticas la diferencia en las reglas de juego, el modo de jugar sus figuras y la forma del tablero no son de gran importancia.
Se conocen no pocas variantes tan solo nacionales del ajedrez. El juego ajedrecístico más antiguo se considera el chaturanga que llegó de la India y más tarde se transformó en el schatrang de los árabes y el schatrandsch de los persas. Hasta hoy día se juega al ajedrez japonés (shogi), chino (tséung-k’i), coreano (tjyang-keui), armenio (tama), etc. Estos juegos (su lista puede continuarse) pertenecen más a la historia del ajedrez que a las matemáticas y no se exponen en el libro.
Más adelante examinaremos una serie de juegos ajedrecísticos singulares que contienen tales o cuales elementos matemáticos o son de carácter recreativo. Ante todo subrayemos que estos juegos pueden diferenciarse del ajedrez verdadero, en primer lugar por su tablero singular, en segundo, por sus figuras fuera de lo común y en tercer lugar por sus reglas particulares. Por supuesto que es posible la presencia de dos de las «singularidades» e incluso de las tres simultáneamente.
En esta parte del capítulo hablaremos principalmente de los juegos que se obtienen variando la forma del tablero. Otras modalidades de los juegos ajedrecísticos singulares se examinan en otros apartados. Por fin en un tercer apartado se explican juegos en los que predominan elementos matemáticos.
En nuestro libro damos preferencia a la narración acerca de juegos populares en vez de ocuparnos de su clasificación desde el punto de vista de la teoría matemática de los juegos. Pero, no obstante, merece la pena, por lo visto, utilizar algunos términos científicos.
El ajedrez, el juego de damas y la mayoría de sus modalidades pertenecen a la categoría de juegos estratégicos que tienen fin y con información completa. En este sentido ellos en nada se diferencian del juego elemental de tres en raya sobre un tablero de 3 × 3. La estructura de este tipo de juego, teóricamente, es absolutamente clara. En cada posición ambas partes tienen igual número de jugadas. El conjunto de sucesiones de las jugadas forma el llamado árbol del juego. En cualquier posición existe la mejor jugada, puede también que no sea la única. La secuencia de mejores jugadas por ambas partes (cierta rama del árbol) conduce la partida imaginaria a un resultado unívoco, y por ello el fin del juego a partir de cualquier posición, incluyendo el comienzo del juego, está predeterminado. Más si en el juego elemental de tres en raya, haciendo las mayores jugadas por ambas partes, la partida termina en tablas, en otros juegos y antes que nada en el ajedrez tradicional, la cuestión acerca de a quién favorece la posición inicial, por lo visto quedará para siempre abierta.
El procedimiento que proporciona la trayectoria óptima en el árbol del juego se denomina minimax. Éste constituye la base de muchos problemas de selección que surgen no sólo al investigar los juegos, sino también al resolver importantes problemas prácticos relacionados con la selección de entre un gran número de variantes. Estos problemas, de por sí, se estudian en la cibernética, por ejemplo, en su apartado «intelecto artificial». Los juegos más populares, principalmente el ajedrez clásico, son un modelo cómodo para las investigaciones científicas y por esto con frecuencia se pueden leer en la literatura sobre cibernética.
La resolución exitosa de los problemas de selección es posible sólo con ayuda de potentes ordenadores y de los modernos métodos de programación. No es casual que en los libros de programación se encuentre la descripción de los juegos y su análisis matemático. Especial popularidad tiene el ajedrez.
Miniajedrez y maxiajedrez. El procedimiento más simple para obtener un nuevo juego ajedrecístico consiste en variar las dimensiones del tablero, aumentarlo o disminuirlo. A los que desean jugar al ajedrez durante el corto receso en el trabajo M. Gardner les propone el miniajedrez. 5 × 5 son las dimensiones mínimas que permiten ubicar en el tablero la totalidad de las figuras del ajedrez. La disposición inicial es la siguiente: blancas Ra1, Db1, Te1, Ac1, Cd1, peones a2, b2, c2, d2, e2; negras Ra5, Db5, Te5, Ac5, Cd5, peones a4, b4, c4, d4, e4. Los movimientos de las figuras son los mismos, sólo que los peones tienen prohibido adelantar dos casillas. Es curioso que incluso con un tablero tan pequeño es muy difícil determinar si la posición inicial termina en empate o una de las partes debe ganar.
No existen limitaciones de ningún tipo para aumentar las dimensiones del tablero. Se pueden examinar distintos juegos y problemas matemáticos y ajedrecísticos sobre tableros rectangulares m × n, cuadrados n × n e incluso sobre tableros infinitamente grandes. Hay pocos aficionados a jugar con estos tipos de tableros, estos juegos se utilizan, por lo general, para idear interesantes problemas matemáticos sobre las rutas de algunas figuras, sobre la disposición y movimientos de éstas.
Hablando de los tableros rectangulares, el récord pertenece al de dimensiones 16 × 12. Precisamente este maxiajedrez fue propuesto en su tiempo por el campeón mundial José Raúl Capablanca con el fin de superar, como le parecía, la «muerte del ajedrez por empates».
Sobre este maxitablero se juega con doble cantidad de figuras, además en su primera jugada el peón puede adelantar cuatro escaques (desde la segunda horizontal hasta la sexta para las figuras blancas y desde la undécima hasta la séptima para las negras). Para alcanzar la victoria es suficiente dar mate a cualquiera de los reyes del contrario.
El match de Capablanca con el gran maestro húngaro Marocsy al maxiajedrez, celebrado en 1929, terminó con la victoria del autor del juego por 3:1. Las partidas de más de 100 movimientos duraron más de 10 horas cada una. Como mostró la vida, el peligro de «muerte por empates» no existe y el descubrimiento de Capablanca no tuvo divulgación.
Entre los tableros de grandes dimensiones puede mencionarse el de 12 × 12 para jugar al llamado gran ajedrez, que tiene su origen en la India. Cada jugador disponía de 12 figuras y 12 peones, con la particularidad de que las figuras llevaban nombres exóticos: cocodrilos, jirafas, leones, unicornios.
El famoso conquistador Tamerlán, apasionado admirador del ajedrez, consideraba insuficientes las dimensiones habituales del tablero. Para el ajedrez de su sistema particular, denominado ejemplar, fue fabricado un tablero especial de 11 × 10; once tipos de figuras (general, camello, caballero, etc.) se disponían sobre él en tres filas.
Ajedrez sobre tableros paralelos. La idea de los «mundos paralelos» que utilizan con frecuencia los escritores de obras de ciencia ficción no escapó tampoco de la atención de los compositores de fantasías ajedrecísticas. Se juega sobre dos tableros simultáneamente situados uno sobre el otro. En cada plano las jugadas son habituales pero las figuras pueden desplazarse también, por el espacio, de un tablero a otro. La figura 14 muestra cómo pasan desde el plano inferior (1) al plano superior (2) el rey, la torre, el caballo, el alfil y el peón. La dama juega en el espacio igual que el rey, los peones pueden cambiar de plano sólo al tomar alguna figura o peón. El que desee jugar una partida puede limitarse a un tablero, poniendo las figuras que se dirigen al segundo plano sobre vasos o soportes transparentes puestos sobre el tablero. Esperamos, por otra parte, que la imaginación geométrica les permita comprender los problemas que examinamos sin necesidad de dispositivos especiales.
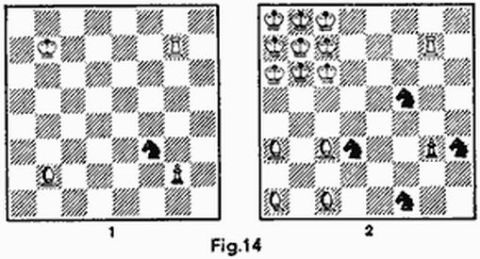
En el problema que muestra la figura 15 las blancas comienzan y dan mate en dos jugadas. l.Th7 (1) – h8(1). La única respuesta es esperar los acontecimientos. El rey de las negras no puede moverse, por lo que éstas sólo pueden jugar con el caballo o con el peón. Si retrocede el caballo (a cualquier plano), se retira la presión sobre la casilla h5 y resuelve la jugada 2.Th8 (1) – h5 (1) × !: el caballo blanco apoya a la torre. A la jugada 1... h4 (2) – h3 (2) le sigue 2.h2 (1) – h4 (1) × !, lo cual no presenta peligro inmediato por cuanto se come al paso.
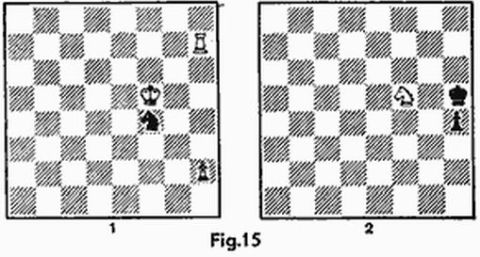
Para resolver el problema de la figura 16, las blancas empiezan y dan mate en 4 jugadas, es necesario examinar atentamente el espacio. Presentemos la variante principal.
1. Ce5 (2) – c5 (1)! amenazando con 2. Cc5 (1) – b3 (1) × . Si 1 ... b6 (1): c5 (1); 2. Rc 1 (2) – c2 (1) Ta7 (1) – a7 (2). La torre negra sale de su escondite, pero inmediatamente la torre blanca pasa al otro plano. 3.Tb2 (2) – b2 (1) Ta7 (2) – a2 (2); 4. Tb2 (1) – b1 (1) × , o bien 3... Ra1 (1) – a2 (2); 4. Tb2 (1) – a2 (1) × . Analicemos, como ejemplo, la posición final en la segunda variante. Al rey negro que se encuentra en la casilla a2 (2) desde el plano inferior le pone mate la torre a2 (1). Realmente la torre ataca al rey, y ella misma se halla bajo vigilancia del caballo c2 (2), los escaques b1, b2, b3 (de ambos planos), bajo control del rey blanco, las casillas a1 y a3 del primer plano bajo control de la torre, mientras que las del segundo están amenazadas por el caballo.
Ajedrez cilíndrico y toroidal. La mayor parte de los tableros que examinamos son planos. Toda una clase de tableros singulares se obtiene cuando entran en «juego» las matemáticas. Ayudados por las diferentes transformaciones geométricas y topológicas del tablero estandartizado no resulta difícil construir tableros de formas más fantásticas. Se puede jugar sobre tableros cilíndricos y esféricos, toroidales, conoidales e incluso sobre la banda de Möbius (un tablero habitual retorcido a media vuelta y pegado por sus extremos). Un tablero en forma de esfera fue exhibido cierta vez en una exposición de pintores vanguardistas.
Claro está que serán muy pocos los que deseen jugar sobre los tableros enumerados, no obstante algunos de ellos tienen una buena aceptación entre los compositores de fantasías ajedrecísticas. Al componer y resolver problemas sobre estos tableros, no es obligatorio armarse de tijeras y cola, las transformaciones geométricas necesarias se pueden realizar mentalmente.
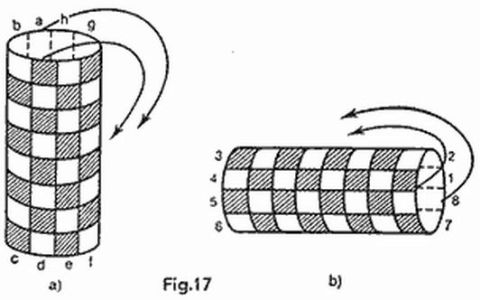
Especial divulgación tiene el ajedrez cilíndrico. De un tablero habitual se hacen dos cilíndricos, uno vertical y el otro horizontal. El primero se obtiene pegando los bordes verticales del tablero normal y el segundo, pegando los horizontales (fig. 17a-b). En los tableros cilíndricos no se obtiene todo lo que es posible obtener en un tablero normal. Por ejemplo, el rey y una torre, por regla general, no son capaces de dar mate al rey solitario del contrario. Por otra parte aquí se abren posibilidades verdaderamente extraordinarias.

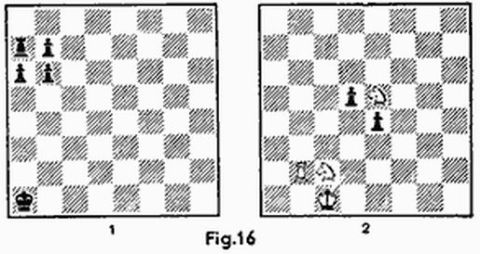
El problema de la figura 18 tiene dos tareas. Las blancas dan mate en dos jugadas: a) sobre un tablero habitual; b) sobre un tablero cilíndrico vertical. En el primer caso todo es muy sencillo: 1. T: a6 Rc1; 2. Ta1 × . Pero en el cilindro después de 1.Ta5:a6 se pierde la torre: 1... h7:a6! (las verticales «a» y «h» están pegadas). Mas si la torre abandona a5, las negras mueven el peón y no se da mate. Resuelve el problema la jugada 1.Ta5 – a5!!: la torre da una «vuelta de honor» y regresa a su lugar inicial. A la jugada obligada 1... Rb1 – c1 le sigue 2.Ta5 – a1 × .

El problema de la figura 19 tiene ya tres tareas. Las blancas dan mate en una jugada sobre tres tableros: a) el habitual; b) el cilíndrico vertical; c) el cilíndrico horizontal.
En el tablero habitual se resuelve con la jugada 1.De2 – e8 × ; en el cilindro vertical con esta jugada no se da mate a causa de la respuesta 1... Ra8 – h7!, y se puede poner fin sólo con la jugada 1.De2 – g8 × ! (la dama blanca hace el recorrido e2 – a6 – h7 – g8); en el cilindro horizontal la aparición de la dama en e8 igualmente no resuelve nada a causa de 1... Ra8 – a1 (b1), y la que resuelve es 1.De2 – a2 × !

En el problema examinado el rey negro está restringido por un proceder un poco rudo. No le queda ni la más mínima libertad y sólo queda darle el puntillazo. La búsqueda de una construcción inicial más refinada condujo a la posición que muestra la figura 20. La tarea es la misma: dar mate en una jugada sobre cada uno de los tres tableros. En comparación con el problema anterior el rey negro se siente más libre y el caballo, que es más dinámico, sustituye al peón b7. No obstante en cualquiera de los tableros el rey al instante recibe jaque mate.
En el tablero habitual: 1.Da6 × . Las otras dos maniobras de la dama ya las conocemos: 1.Dg8 × en el cilindro vertical y 1.Da2 × , en el horizontal. El encanto de los mates consiste en que son dobles: la dama ataca al rey de dos lados, y taparse jugando 1 ... Cd8 (h8) en el primer caso y 1... Ca5 (a1) en el segundo no resuelve la situación.
Cambiando ligeramente la disposición de las figuras blancas, conseguimos diferentes problemas gemelos. Así, por ejemplo, al retirar el rey blanco a la casilla e4 y la dama a f1, los dos finales son los mismos que en la posición examinada, y en el cilindro horizontal la dama da mate desde el centro del tablero: 1.Dd3 × ! La dama ataca al rey por la diagonal d3 – b1 – a8 y la casilla a7, en este caso, se encuentra bajo control del alfil por la diagonal f4 – c1 – b8 – a7 (el rey está desplazado de e3 para no obstruirle el camino al alfil).
Las sucesivas «meditaciones cilíndricas» permitieron establecer que el caballo negro está de sobra...

En la figura 21 nuevamente tenemos tres tareas: las blancas dan mate en una jugada sobre los tres tableros: a) el habitual; b) el vertical cilíndrico; c) el horizontal cilíndrico.
Esta posición es una representación ideal del tema de los «tres problemas sobre cilindros». Realmente, sobre el tablero hay sólo cuatro figuras, además la disposición de éstas es muy ligera, elegante: las figuras blancas están alejadas del rey negro y parece que del mate en una jugada no hay nada que hablar. Para penetrar más profundamente en la esencia geométrica del ajedrez cilíndrico estudiemos atentamente la resolución de este problema.
a) En el tablero habitual, como antes, hacia el mate sólo conduce la jugada 1.Da6 × . A la jugada 1.Da2 (c8, e4) + las negras responden con 1... Rb7 (a7, a7)!
b) En el cilindro vertical las líneas «a» y «h» están pegadas entre sí y 2.Da6 (e4) + se refuta mediante la jugada 1... Rh8! Contra la jugada 1.Dc8 (g8, h7) + existe la respuesta l... Rh7 (b7, h7). Pero da mate la jugada 1.Dc4 – a2 – h1 × ! La dama somete a control cuatro casillas a la vez en la región del rey negro (incluyendo la que ella misma ocupa): b7, a8 por la diagonal h1 – a8 y h7, h8 por la vertical «h». Es curioso que desde más cerca quitarle tantas casillas al rey, sin poner la dama en una casilla amenazada, no es posible tanto en el tablero cilíndrico como en el habitual. Otras dos casillas a las que podría retroceder el rey, a7 y b8, se encuentran bajo control del alfil por la diagonal c1 – h6 – a7 – b8. Así pues, ¡sobre el tablero tenemos un jaque-mate verdadero!
Préstese atención a que en los tableros cilíndricos todas las diagonales son iguales y contienen, igual que las líneas rectas, por ocho casillas, con la particularidad de que geométricamente cada diagonal adquiere la forma de una espira. Es por esto que en el cilindro vertical se encuentran en los extremos de una de estas espiras las casillas b8 y h1, en los extremos de otra espira, las casillas b8 y a1, en la tercera, c8 y b1, etc. En dirección perpendicular tenemos las espiras diagonales con los extremos en a8 y b1, b8 y el, c8 y d1, etc.
c) En el cilindro horizontal están pegadas la primera y octava líneas y contra la jugada 1.Da6 + el rey posee la respuesta l... Ra8 – b1! Resuelve sólo la jugada 1.Dc4 – f1 – g8 – h7 × ! Nuevamente la dama le quita al rey cuatro casillas: a8, b1 por la diagonal h7 – b1 – a8 y a7, b7 por la séptima horizontal. Las casillas b8, al están dominadas por el alfil situado en la diagonal h2 – b8 – a1. Aquí como antes otros jaques de la dama no dan mate, puesto que el rey se marcha a las casillas a7, b1 o b7. Si retiramos el rey blanco de la línea del alfil, entonces los jaques 1.Dc8 (e4, h1) + se convierten en mates a causa de que la casilla a7 se torna inaccesible para el rey negro. Es extraño pero el rey blanco, aún estando en la retaguardia de sus figuras, de una manera original participa en la resolución: ¡molesta a sus propias figuras dar mate! Ésta también es una propiedad específica del cilindro: de que el rey blanco es inútil estaba claro, desde el principio, pero el que su juego sea perjudicial se reveló inesperadamente...
Es muy interesante que los dos últimos problemas pueden ser unidos. Para ello hay que inscribir debajo del último diagrama otras tres tareas: lo mismo, ¡pero con la condición de agregar un caballo negro en la casilla b7! En tal caso las resoluciones de los problemas-gemelos, como hemos visto, se distinguen uno de otro.

Un problema, con la misma relación de fuerzas y una tarea muy singular, se puede ver en la figura 22: las blancas dan mate en... 0 jugadas. Por ahora, a propósito, ante nosotros vemos un tablero habitual.
En este problema-broma el mate realmente se anuncia en 0 jugadas, además de dos maneras. Las blancas, como es preciso, no tocan ninguna de sus figuras, no obstante... convierten el tablero en un cilindro. En cualquiera de los tableros, el horizontal o el vertical, el rey negro inmediatamente recibe mate. Supongamos que están pegadas entre sí las horizontales extremas. En este caso la casilla a1 se adosa del lado izquierdo a la diagonal b8 – h2 y las casillas b8, c7 se ven amenazadas por el alfil. Además de esto las diagonales a6 – c8 y d1 – h5 se funden en una sola (a6 y h5 son las casillas extremas de esta nueva diagonal) y como resultado la dama ataca al rey negro, quitándole simultáneamente la casilla b7. Pero las casillas d7 y d8 son inaccesibles para el rey en cualquiera de los tableros. ¡Mate! En el cilindro vertical la casilla al nuevamente se une a la diagonal b8 – h2, pero por debajo, se funden en una sola las diagonales d1 – h5 y a6 – c8 (los extremos de la nueva diagonal son d1 y c8). Y una vez más el rey negro se ve atrapado en la posición de jaque-mate.

En todos nuestros ejemplos las tareas estaban mezcladas, tanto en el tablero común como en los cilíndricos. En el problema puramente cilíndrico que ofrece la figura, por regla general, se recortan las fronteras correspondientes. En la figura 23 las blancas dan mate en tres movimientos sobre un tablero cilíndrico vertical.
Nuevamente tenemos ante nosotros un cuarteto con una relación de fuerzas conocida. 1.Rf2! Rc8; 2.Ah2 Rd8; 3.Dd1 × ; l...Ra8; 2.Ad2 Rh8; 3.Dh1 × .
En el problema de la figura 24 vemos una tarea medio en serio, medio en broma: las blancas comienzan y hacen tablas.

Ante nosotros tenemos un tablero habitual y la esperanza para las blancas de empatar el juego no es muy buena, que digamos. El peón negro avanza sin obstáculos hasta convertirse en dama. Pero hay salvación.
En su desesperación las Blancas pegan las horizontales extremas del tablero, convirtiendo éste en un cilindro. Como resultado el peón de manera totalmente inesperada perdió su perspectiva: la transformación en dama se suspende. Móvil perpetuo...
Al pasar a los tableros nuevos no sólo surgen problemas originales con argumento ajedrecístico, sino también interesantes problemas matemáticos.
Muchos conocen el «problema de las 8 damas», del que se ocupó en su tiempo el gran matemático G. Gauss: ¿de cuántas maneras se pueden colocar sobre el tablero ocho damas sin amenazarse entre sí?
Resulta que, si en el tablero normal hay 92 maneras de colocarlas, en el tablero cilíndrico no hay ninguna. Demostremos lo dicho para el tablero cilíndrico vertical. Tomemos un tablero habitual, teniendo presente que sus bordes están pegados. Esto, en particular, significa que las casillas desde d1 hasta a4 y desde h5 hasta e8 forman una misma diagonal. Anotemos en cada casilla del tablero 3 cifras correspondientes al número de la vertical, al de la horizontal y al de la diagonal (paralela a a8 – h1) que pasan por dicha casilla (fig. 25).
Si 8 damas no se amenazan mutuamente, en las 8 casillas que ocupan éstas, las primeras cifras son diferentes y, por consiguiente, forman el conjunto de cifras 1, 2, ..., 8. Lo mismo se puede afirmar para las segundas y las terceras cifras de estas casillas. Por tanto la suma de las 24 cifras escritas en las casillas que ocupan las damas será (1 + ... + 8) 3 = 108. Por cuanto la suma de cifras de cada casilla se divide entre 8, por tanto la suma determinada debe dividirse entre 8, pero 108 no se divide entre 8, lo cual es una contradicción.

El tablero toroidal se obtiene como resultado de pegar dos a dos cuatro bordes del tablero común (véanse las flechas en la fig. 17a-b). En un tablero así no pueden dar mate al rey solitario ni siquiera dama y rey; aquí simplemente no existe posición de mate.
La figura 26 muestra un problema sobre un tablero ajedrecístico toroidal. Las blancas comienzan y dan mate en 4 jugadas. Después de 1.Df5-h7! a disposición de las negras hay 2 jugadas: a) l... Re8-f8 (las casillas d1, e1 y f1 se encuentran bajo control del rey blanco desde la casilla e2: en el toro actúan las reglas del cilindro horizontal) 2.Dh7-g6 Rf8-e7; 3.Rc2-e1 Re7-d7 (las casillas d8 y f8 están controladas por el rey blanco desde la casilla e1) 4.Dg6-e8 × !; b) 1... Re8-d8; 2.Dh7-c7 + Rd8-e8; 3.Cb5-h6! (el caballo se mueve por el toro como por un cilindro vertical) 3... Re8-f8; 4.Dc7-e1 × ! (las casillas f7 y g8 junto al rey negro están controladas por el caballo blanco y las demás, por la dama).
Ajedrez proyectivo. A este ajedrez se juega sobre un tablero proyectivo. Las reglas del juego se basan en las propiedades de las líneas rectas que se estudian en la geometría proyectiva, en la que se supone que cualquier familia de rectas paralelas se corta en un punto infinitamente alejado. Conforme a esto el tablero para el ajedrez proyectivo se obtiene de un tablero infinito (que se extiende por todo el plano), añadiéndole cuatro casillas infinitamente alejadas: Ph – intersección de las horizontales, Pv – intersección de las verticales, Pd1 – intersección de las diagonales paralelas a a1-h8, Pd2 – intersección de las diagonales paralelas a a8-h1.
En el ajedrez proyectivo se conservan muchas reglas del ajedrez habitual y los cambios esenciales consisten en que las figuras de largo alcance pueden desplazarse a una de las casillas infinitamente alejadas (manteniendo sus movimientos) y desde allí volver a una casilla finita del tablero.

Examinemos un problema sobre el tablero proyectivo de ajedrez (fig. 27). Las blancas comienzan y dan mate en dos jugadas. La primera jugada de la solución es 1.Rh2-g1! El rey negro aquí tiene varias respuestas. Si ocupa la casilla e4, es la dama la que le da mate, alejándose al infinito por a5: Dc5-Ph × . Realmente desde la casilla Ph la dama ataca al rey negro y controla todas las casillas a su alrededor: e3 y f3 por h3; d4, e4 y f4 por h4; d5, e5 y f5 por a5. La jugada 2.Dc5-Ph da también mate en el caso de 1… Rf4-f3. Las casillas e4, f4 y g4 en este caso se encuentran bajo control de la dama por h3; e3, f3 y g3 por h3 y e2, f2 y g2 por h2 (el rey blanco previsiblemente abandonó la casilla h2).
Al retirarse el rey negro a la línea «g», así como en el caso de 1... d3-d2, se da mate con la jugada 2.Dc5-Pd1 × (la dama se retira al infinito por la diagonal c5-a3). Por ejemplo, después de 1... Rf4-g5; 2.Dc5–Pd1 × la dama controla las casillas f4, g5 y h6 por c1; la casilla f6, por a1; la casilla f5, por h7; las casillas g4 y h5, por d1; y la casilla h4, por e1.
Quedan por examinar las jugadas de los caballos negros. A cualquiera de las jugadas del caballo b6 se responde 2.Dc5-Pd2 × y a cualquier jugada del caballo c7 se contesta 2.Dc5-Pv × (en el primer caso la dama se retira al infinito por la casilla a7, en el segundo, por c8).
En el problema de dos jugadas no sólo importa la existencia de una solución, sino también el que ésta sea única. No es difícil convencernos de que, si la primera jugada de las blancas es otra, éstas no podrán dar mate en dos jugadas. Así por ejemplo, después de 1.Dc5-Ph + el rey negro se refugia en la casilla g5 y después de 1.Dc5-Pd1 +, en la casilla e4; desde la casilla Pd2 la dama tan siquiera da jaque y la jugada Dc5-Pv no existe (la vertical «c» está obstruida en ambas direcciones). Es curioso que para la resolución del problema se usaran las cuatro casillas infinitamente alejadas del tablero adjedrecístico proyectivo.
Ajedrez tridimensional. Las casillas que hemos utilizado hasta aquí se determinaban mediante dos coordenadas, es decir, se utilizaba la notación habitual ajedrecística (sólo en el juego con tableros paralelos las designaciones eran algo más complicadas). En el ajedrez tridimensional (espacial) esto es distinto.
Este juego se practica sobre un tablero tridimensional que no es sino un paralelepípedo m × n × k (como caso particular, un cubo n × n × n), cuyos pequeños cubos unitarios forman las «casillas» del tablero. Estas casillas en este caso se anotan mediante tres coordenadas. Tomemos, por ejemplo, el tablero volumétrico 4 × 4 × 4 que contiene, igual que el tablero común, 64 casillas, pero volumétricas (64 pequeños cubos). Si numeramos las cuatro capas horizontales de un tablero así con los números 1, 2, 3 y 4, entonces la columna izquierda más cercana contiene las casillas a11, a12, a13 y a14, etc. Los movimientos por una capa del tablero volumétrico corresponden a los de un tablero habitual, pero las figuras pueden pasar de una capa a otra. Así, por ejemplo, la dama desde la casilla a11 está en condiciones de moverse no sólo por las rutas habituales hasta las casillas a41 y h11, sino puede también llegar a la capa superior del tablero, a la casilla a14 o pasar por su diagonal grande a11-h44. El caballo en el tablero volumétrico se mueve en T; una casilla en una capa y dos en la perpendicular.
Ya hemos hablado del problema «acerca de las ocho damas» por el que se interesó en su tiempo C. Gauss. Otro gran matemático, L. Euler, se vio atraído por otro problema matemático sobre el tablero ajedrecístico: «acerca del movimiento del caballo». Se precisa recorrer con el caballo todas las casillas de un tablero habitual de manera que ninguna de ellas se visite dos veces. Se conocen muchos métodos para recorrer el tablero de esta manera incluyendo el propuesto por Euler, sin embargo, el número total de rutas no está determinado hasta hoy día (está demostrado que este número supera los 30 millones).
El siguiente problema generaliza el problema clásico sobre el movimiento del caballo. Recorrer con el caballo todas las casillas del tablero ajedrecístico volumétrico 4 × 4 × 4, visitando una sola vez cada una de ellas.

Hallar el recorrido del caballo por el tablero volumétrico es similar a numerar consecutivamente todas sus casillas desde 1 hasta 64 de tal modo que cada dos casillas con números consecutivos se encuentren enlazadas por el movimiento del caballo. La figura 28 muestra las proyecciones de las cuatro capas horizontales del tablero volumétrico sobre un tablero plano de 4 × 4 (las capas tienen los números 1, 2, 3 y 4).
No cuesta trabajo convencernos de que, partiendo de la casilla b33 (con el número 1) y moviéndonos con el caballo en la secuencia indicada, nosotros recorreremos todas las casillas del tablero 4 × 4 × 4.
Ajedrez hexagonal. Rara vez se utilizan tableros no estandarizados en juegos serios; estos tableros más bien son instrumentos para la creación de nuevos juegos. Pero existe también una excepción, el ajedrez hexagonal. El tablero, al igual que las casillas, tienen forma de hexágono y las figuras adquieren mayor campo de acción. Se inventaron dos variantes de este juego, una la del geólogo soviético I. Shafrán y otra la del ingeniero polaco V. Glinski. El ajedrez polaco recibió una difusión bastante amplia en el mundo. Examinemos primero este ajedrez.
El tablero hexagonal contiene 91 casilla de 3 colores: blanco, negro y gris; tiene 11 verticales desde «a» hasta «l» (exceptuando «j»), las casillas de cada vertical se numeran desde abajo hacia arriba (fig. 29). Las verticales de los extremos tienen por 6 casillas y la central, 11. Las veces de horizontales las cumplen las diagonales, a la izquierda de la línea «f», paralelas a a1-f1 y, a la derecha de ella, paralelas a f1-l1. Las figuras de cada jugador se complementan con un alfil que se mueve por las casillas grises y un peón. La disposición inicial de las figuras se muestra en la figura 29 y los movimientos de las mismas, en la figura 30.
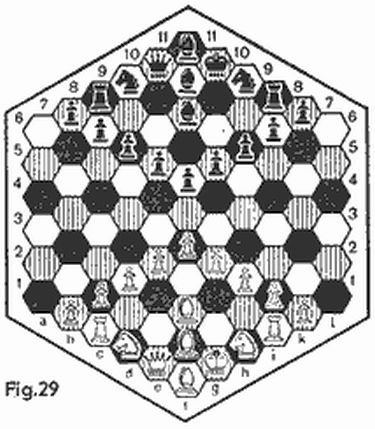
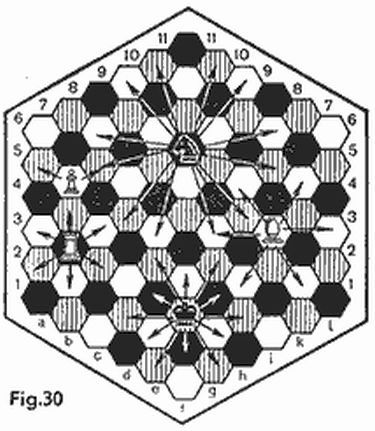
El rey, como debe ser, puede moverse a todas las casillas adyacentes: no sólo a las que contactan directamente con la que ocupa, sino también a las casillas próximas a él del mismo color. Así pues, desde la casilla f3 el rey puede desplazarse a cada una de las 12 casillas indicadas con flechitas. De la misma cantidad de casillas dispone el caballo situado en f8. La torre y el alfil se mueven a cualquier número de casillas en una de las seis direcciones (diferentes para estas figuras). La dama, que reúne los movimientos de la torre y el alfil, se desplaza en las mismas 12 direcciones que el rey pero a un número arbitrario de casillas. Claro que, más cerca de los límites del tablero, el número de jugadas para todas las figuras disminuye. Los peones avanzan una casilla verticalmente (desde la posición inicial pueden avanzar dos casillas) y capturan en diagonal: de b5 toman en a5 y c6 (fig. 30). Se conserva también la toma al paso: en respuesta a c2-c4 el peón negro en d3 puede tomar el peón blanco d3:c3. Al alcanzar la última casilla de la vertical, el peón se transforma en cualquier figura. No están previstos los enroques por cuanto los reyes se encuentran en casillas suficientemente seguras y la torre en dos jugadas se suma al ataque o a la defensa. El resto de las reglas, incluyendo la finalidad del juego, de dar mate al rey contrario, no varía.
El tablero para jugar al ajedrez de Shafrán puede verse en la figura 31, se obtiene de la variante polaca, retirando las líneas f1-l1, f11-l6 y las dos verticales de la derecha k1-k7 y l1-l6; el número de casillas se reduce hasta 70.
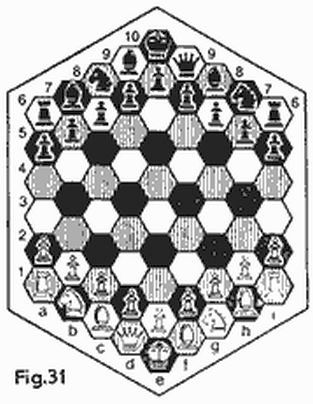
La disposición inicial (fig. 31) recuerda el ajedrez habitual y las figuras se mueven como se indican en la figura 30, con la única excepción de que el peón toma a 60°: desde b5 toma en a6 y c7. Los tres peones centrales pueden adelantar tres casillas en su primer movimiento, los demás sólo pueden adelantar dos. En este juego los enroques son posibles: el corto, si la torre se acerca al rey y éste pasa al otro lado de la misma, y el largo, si el rey se acerca a la torre y ésta pasa al otro lado del mismo.
En el ajedrez polaco el tablero representa un hexágono regular y, probablemente, esta precisión geométrica ayudó a Glinski «superar» a Shafrán en la popularidad de su juego. En el ajedrez de Shafrán la partida puede acabar en la tercera jugada: 1.Cb1-c4 Cc8-d6; 2.Dd1-e3 b6-b5 (las negras quieren espantar al caballo del contrario, pero les espera una amarga desilusión) 3.Cc4-d7 × ! En el ajedrez de Glinski sólo es posible el «mate del estudiante» en 4 jugadas: 1.De1-c3 De10-c6; 2.Ch1-i3 Ch9-i6; 3.Ci3-g6, e7-e6; 4.Dc3: f9 × , o 3 ...Ci6-g5; 4.e4-e5 Dc6: f3 × . Es curioso que en este juego se puede dar jaque en la primera jugada: 1.Rg1-g2 Af10-d6 +.
En el ajedrez clásico las aperturas están estudiadas en profundidad, la creación individual, con frecuencia, comienza sólo después de hacer 15–20 jugadas. La teoría del ajedrez hexagonal casi no está elaborada, además la diversidad de jugadas y variantes es tan grande que acertar la respuesta del adversario es más difícil que en el ajedrez habitual. Aumentaron las dimensiones del tablero y como consecuencia se incrementó la movilidad de las figuras, lo cual, a su vez, proporcionó mayores posibilidades de combinación a los aficionados de la táctica.
Un poco de crónica. En 1953 el ajedrez polaco fue presentado en la exposición mundial de París. El primer campeonato de Europa se celebró en Londres en 1980. Por eso entonces fue organizado en la URSS el club nacional de las «6 aristas» que desde 1982 organiza competiciones. En 1984 en Hungría se organizó el segundo campeonato de Europa, en el que participaron 26 jugadores de 7 países. A los vencedores del primer certamen, el polaco. M. Matskoviak, y del segundo, el húngaro L. Rudolf, les concedieron el título de gran maestro internacional en ajedrez hexagonal.
La geometría del tablero hexagonal es muy singular. Así pues, la vertical «f» es su eje de simetría y la casilla f6, su casilla central (en el tablero estándar el centro consta de cuatro casillas: d4, d5, e4 y e5). Aún cuando el tablero es mayor que el habitual, el caballo cubre la distancia entre dos casillas arbitrarias en no más de cuatro jugadas (en el tablero 8 × 8 el caballo recorre la distancia entre a1 y h8 en 6 jugadas). En el tablero hexagonal cualquier figura puede hacer una jugada manteniendo el control de las casillas que controlaba antes. Esta propiedad se revela especialmente interesante en el caballo. Por ejemplo, desde g9 el caballo controla la casilla e7, pero después de saltar a d9 o h6 sigue manteniendo el control de dicha casilla. Resulta que el caballo es capaz de recorrer un triángulo, ganándole tiempo al contrario. En el ajedrez clásico utilizar el caballo para estos fines resulta imposible.
He aquí algunos puntos de diferencia entre el ajedrez polaco y el tradicional. En el tablero hexagonal el rey sólo puede ahogar al rey contrario, si este se encuentra en uno de los ángulos. Por ejemplo, el rey blanco en f3 impide totalmente los movimientos del rey negro en f1. De esto se deduce que el rey con cualquier otra figura puede dar mate al rey adversario. Por otra parte obligar al rey contrario a meterse en uno de los ángulos es difícil incluso con dos piezas ligeras; para ganar se necesita una tercera pieza. En cambio la dama sin ayuda alguna puede dar jaque-mate, digamos, desde esa misma casilla f3 al rey en f1.
Examinemos tres problemas en el tablero hexagonal polaco.
En el problema que muestra la figura 32 las blancas comienzan y dan mate en cuatro jugadas.
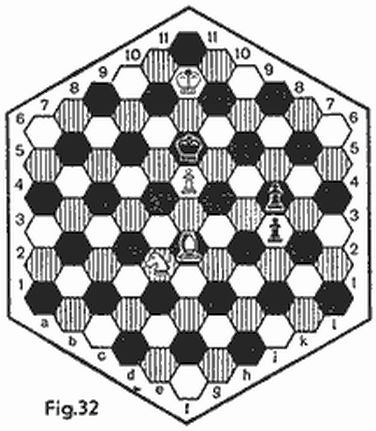
En el ajedrez habitual, al abandonar una casilla, el caballo pierde el control sobre las casillas que hasta ese momento se encontraban vigiladas por él. Muy distinto es en el ajedrez hexagonal...
En la posición presentada el rey negro está ahogado: las casillas e6, g6, d7 y h7 están bajo control del alfil blanco; e7 y g7 están dominadas por el peón; e8, e9, f7, g7 y g8, por el rey y el peón f7 se encuentra protegido por el caballo. Pero a pesar de ello las blancas han de jugar...
1.Ce4-c5! El caballo se retira de su lugar pero mantiene el control del peón en f7, procedimiento habilidoso ya mencionado antes. 1... i4-i3; 2.Cc5-d8! Nuevamente el peón se ve protegido por el caballo. No es buena la jugada 2. Ce4? por cuanto 2… i4! y ya no se da mate, pero no 2… i2; 3.Ch4 y 4.Ci6 × .
2… i3-i2; 3.Cd8-g9 i2-i1D; 4. Cg9-i6 × ! El caballo hizo cuatro jugadas seguidas pero el peón no dejó de estar protegido por él.
Desplazando ligeramente las figuras, se puede obtener un interesante problema gemelo. Blancas: Rd6, Ad1, Ce1 y pd3; negras: Rd4 y pf7. Parece una posición desplazada hacia la parte inferior del tablero, además el material se redujo en un peón.
1.Cg3! f5! Pero no 1... f6?; 2. Ce1! (2.C:f6 tablas por ahogado) 2… f5 (las negras se ven obligadas a hacer jugadas forzadas); 3.Ac2 × ! (la casilla f5 está bloqueada por su propio peón).
2.Cf6! f4; 3.Cc2 × . En el presente ejemplo hexagonal se ilustran simultáneamente varios temas populares de problemas: tablas por ahogado, zugzwang o jugadas forzadas y bloqueo.
En el problema que presenta la figura 33 las blancas empiezan y dan mate en 2 jugadas. A primera vista parece que el rey negro tiene suficiente libertad y que en 2 jugadas no es posible darle mate.
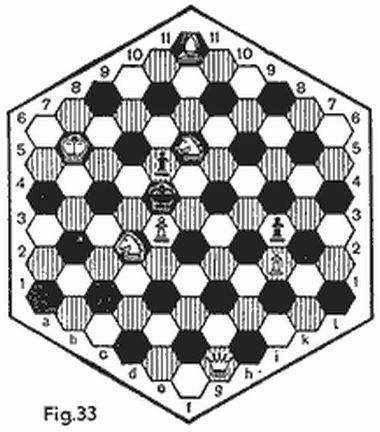
1. Af11-l1! Un inesperado desplazamiento del alfil desde un ángulo del tablero hexagonal a otro resuelve el problema. Las negras se encuentran en zugzwang. Cualquier jugada de su rey conduce a un jaque mate muy bonito con la dama en el centro del tablero. l... Re6:d4; 2.Dg1-c2 × . Resultó útil el alfil que apuntaba contra la casilla c2. 1... Re6: f8; 2. Dg1-g9 × . La casilla g7 también se encuentra bajo control del alfil oculto lejos del foco de las acciones principales. 1... ReG-f5; 2.Dg1-g3 × . La casilla g3 también se halla dominada por el alfil. l... Re6-d6; 2.Dg1-cG × . En esta última variante la dama blanca se encuentra apoyada por el rey.
En la figura 34 las blancas también comienzan y dan mate en dos jugadas. Este problema ilustra el tema geométrico de Novotny (obstrucción) bastante difundido en la composición ajedrecística habitual. Difiere sólo en las líneas de acción de las figuras.
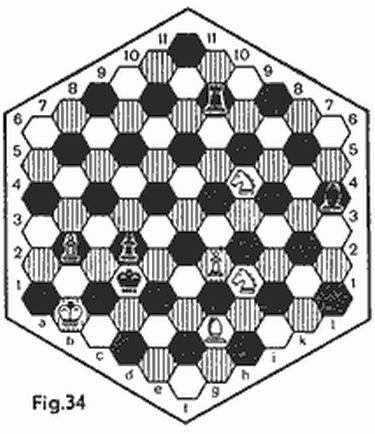
1.g4-g6! El peón comienza adelantando dos casillas. De paso surge otro elemento en los problemas, la liberación de la casilla para otras figuras. Ahora el peón se vio ubicado en la intersección de las líneas g1-g10 y a4-l1 que se encuentran a disposición de la torre y del alfil respectivamente. l... Ah4-g6. La trayectoria de la torre está obstruida y 2.Ch6-g4 × . l... Tg9:g6. La trayectoria del alfil se encuentra obstruida (la línea a4-l4 no es de la competencia de la torre) y 2. Ch6-e6 × .
Ajedrez para más de dos jugadores. Casi todos los juegos examinados en este libro, incluyendo el ajedrez, de acuerdo con la terminología de la teoría matemática de juego son juegos para dos, es decir, en el juego participan dos personas. En las modalidades del ajedrez examinadas basta aquí se suponía la existencia de dos participantes, no obstante se conocen no pocos juegos ajedrecísticos en los cuales pueden jugar simultáneamente tres o cuatro jugadores. Así, por ejemplo, en una de las variantes del ajedrez «para tres» el tablero representa un hexágono con 96 casillas y las figuras son de tres colores: blancas, negras y rojas. Gana el que tome los reyes de sus dos oponentes. El juego se desarrolla de tal modo que dos de los participantes puedan agrupar sus esfuerzos contra el más fuerte.
Es interesante que en su origen el ajedrez estaba destinado a la participación de cuatro jugadores. Estamos hablando del antiguo juego chaturanga al que se jugaba dos contra dos (las amarillas y las rojas competían contra las negras y las verdes). Dudo que merezca la pena explicar aquí las reglas del chaturanga, por cuanto en nuestros días este juego sólo conserva interés histórico.
Al antiguo «juego de reyes», cuyo tablero tenía forma de cruz y representaba un sistema de líneas que se intersecaban por las verticales, horizontales y diagonales, también jugaban 4 personas. Hoy día el «juego de reyes» está olvidado por completo, y el nombre se conservó como sinónimo del ajedrez clásico.
De un juego con cuatro participantes, el ajedrez se convirtió paulatinamente en un juego para dos personas. Aún cuando el ajedrez moderno se ganó el reconocimiento general, el juego para cuatro no está totalmente olvidado. Al llamado ajedrez para cuatro se juega sobre un tablero de 160 casillas que se obtiene del tablero de 8 × 8, añadiéndole tres filas en cada uno de los cuatro lados; en las dos filas finales se colocan las figuras, como en el ajedrez normal, en total se utilizan cuatro juegos de figuras habituales. Juegan dos contra dos, con la particularidad de que los compañeros de juego se pueden sentar uno frente al otro o uno al lado del otro. Se conocen distintos tipos de ajedrez para cuatro que se diferencian no sólo en la manera de sentar a los participantes alrededor del tablero, sino también por las reglas del juego, por el área del tablero en el que está autorizado actuar, por el color de las figuras.
Es curioso que en una de las variantes de este juego el rey que recibe jaque-mate se retira del tablero, en otra no, y puede ser liberado del mate por el compañero de juego. El ajedrez para cuatro está reconocido oficialmente en la URSS e incluso se organizaron varios campeonatos de la capital.
Si en su casa se reunió un grupo de cuatro aficionados y todos ansían jugar y al alcance de la mano no hay más que un tablero normal, no se decepcione. Jueguen dos contra dos un partido habitual, pero las jugadas háganlas turnándose uno a uno con los contrarios. Este es un juego muy divertido y no importa si uno de los compañeros de juego idea una buena combinación y el otro la echa a perder inmediatamente.
Así pues, para cuatro jugadores fueron inventados muchos juegos ajedrecísticos. Pero el record de participantes pertenece al «ajedrez astronómico» muy difundido en la antigüedad. A este juego jugaban siete personas sobre un tablero redondo y las figuras eran los planetas y las estrellas (la Luna, el Sol, Venus, Marte, etc.).
§. Ajedrez de fantasía
En el apartado anterior hemos comentado sobre los distintos juegos, relacionados con tal o cual transformación del tablero. No obstante, para obtener juegos nuevos, no es obligado utilizar tableros especiales, basta con cambiar las reglas del juego sobre el tablero 8 × 8 o introducir figuras singulares. Precisamente sobre juegos de este tipo acentuaremos nuestra atención en este apartado. Los creadores de juegos ajedrecísticos consideran que las variedades de juegos de ajedrez con jugadas insólitas de sus figuras y reglas singulares pertenecen al género de juegos ajedrecísticos mágicos o de fantasía y utilizan esta «singularidad» para componer posiciones y problemas interesantes y originales.
Ajedrez con jaques y sin ellos. En el juego «hasta el primer jaque» todo va como en el ajedrez verdadero, pero gana no el que dé antes el mate, sino el que dé antes jaque. Cuando la posición inicial es la habitual, las blancas fuerzan el juego y ganan, además no más allá de la quinta jugada.
1.Cc3. Amenaza la jugada del caballo a e4, d5 o b5 con el inevitable jaque, las negras tienen como única respuesta l... e6 (l... e5; 2.Cd5 y 3.Cfb +) y después de 2.Ce4 Re7; 3.Cf3 el segundo caballo blanco con un efecto decisivo entra en juego: 3... De8 (3... d6; 4.Cd4) 4.Ce5 y en la siguiente jugada se da jaque.
Para hacer el juego más vivo es preciso cambiar de alguna manera la posición inicial, por ejemplo, desplazar el peón blanco de c2 a c3 y el negro de c7 a c6. Así ya no es posible hacer la primera jugada 1.Cc3 y ya no se percibe forzar el juego hasta ganar; después de 1. Db3 d5; 2. Db4 Db6!; 3. Da4 Ad7; 4. Dh4 Cf6 el rey negro sigue protegido y con suficiente seguridad contra posibles jaques.
En el «ajedrez sin jaques» las figuras se mueven como en el ajedrez normal, prohibiéndose los jaques: el primer jaque simultáneamente debe ser también mate. En el «ajedrez con jaques» las reglas son otras: la partida continúa, como en el ajedrez clásico, hasta el mate, pero el jaque es obligatorio, si éste es posible (por cualquier procedimiento).
A propósito, el excampeón mundial de ajedrez «normal», A. Kárpov, en su infancia gustaba de practicar el juego «quien da antes tres jaques» y siempre salía vencedor.
Ajedrez de dos movimientos. En este juego cada movimiento de las blancas y de las negras consta de dos jugadas habituales (después del primer movimiento, «ciclo», el rey puede encontrarse en posición de jaque). Esta modificación de las reglas de juego permite demostrar el siguiente fenómeno inesperado.
Jugando correctamente al ajedrez de dos movimientos, las blancas, por lo menos, tienen garantizado el empate.
Intentemos demostrar esto a partir de lo contrario. Supongamos que las blancas, cuan bien no jueguen, siempre pierden. En tal caso después del movimiento 1. Cb1-c3-b1 se mantiene la posición inicial, pero el primer movimiento ya pasó a las negras. A partir de este momento las negras cumplen la función de las blancas de comenzar el juego y de acuerdo con la suposición inicial también pierden. Esta es una contracción.
Todo parece cierto. Sin embargo, esta demostración no es del todo exacta. Después de la primera jugada de las blancas la posición sobre el tablero realmente se repite, pero la situación es distinta. Así, por ejemplo, después de jugar l... Cg8-f6-g8; 2.Cb1-c3-b1 las blancas no pueden exigir tablas y las negras sí, por cuanto 2... Cg8-f6- g8 conduce a la triple repetición de la posición inicial. De esta manera después de la jugada 1.Cb1-c3-b1 no es posible considerar que las negras juegan con las blancas: las posibilidades de ambas partes difieren. Un ejemplo análogo se puede presentar también para el caso de la «regla de las 50 jugadas». Curiosamente fue el eminente matemático soviético, académico A. Kolmogórov, quien llamó la atención sobre este sutil error en la demostración.
Expongamos ahora la demostración precisa. Nuevamente haremos la suposición de que como quiera que jueguen las blancas al ajedrez de dos movimientos siempre han de perder. Juguemos simultáneamente con un adversario imaginario dos partidas sobre dos tableros. En el primer tablero iniciemos la partida jugando 1.Cb1-c3-b1 (sin cambiar la disposición de las figuras sobre el tablero). Utilicemos la respuesta de las negras a nuestra jugada de espera como jugada de las blancas en el segundo tablero (digamos, si las negras juegan en el primer tablero 1... e7-e5, d7-d5, nuestra primera jugada en el segundo será 1.e2-e4, d2-d4). Seguidamente repetimos la respuesta del contrario en el segundo tablero para jugar con las blancas en el primero, la jugada de las negras en el primero para jugar con las blancas en el segundo, etc. A nuestra manera de ver las negras, tarde o temprano, han de ganar las dos partidas y por consiguiente debe llegar el momento en que sobre el primer tablero, en su jugada siguiente, den mate al rey blanco. Pero entonces en el segundo tablero, al repetir las blancas esta jugada surge una posición en la que es el rey negro quien recibe mate. Nuevamente nos vemos ante una contradicción.
Nuestra demostración, como dirían los matemáticos, no es constructiva. Hemos demostrado que las blancas pueden no perder jugando al ajedrez de dos movimientos, mas no hemos aclarado cómo deben jugar. Más aún, si se demuestra que las blancas, forzando la partida, ganan (como, por ejemplo, en el juego hasta el primer jaque), entonces resulta evidente que la primera jugada de las blancas 1.Cb1-c3-b1 conduce a la pérdida del juego. Así pues, no está descartado que nuestra demostración de que las blancas no pierden parte de una jugada que pierde.

He aquí una de las modificaciones examinadas del ajedrez de dos movimientos. Uno de los participantes tiene todas las figuras que se mueven como en el ajedrez clásico y el otro dispone sólo del rey y unos cuantos peones, pero éstos hacen dos jugadas de una vez. El objetivo de la parte más débil consiste en ganar al rey contrario. Este juego es bastante interesante: el que acaba de conocer este juego siempre elige las figuras con movimientos normales y... pierde rápidamente. En el ajedrez de dos movimientos el rey desnudo es capaz, ya en la cuarta jugada, de dar mate al adversario que posee un ejército completo de figuras (fig. 35): 1.Re1-e2-e3 (primer movimiento doble) 1... e7-e5 (el movimiento de las negras es unitario); 2.Re3-e4: e5 Dd8-e7 +; 3.Re5-d6:c7 + y en la siguiente jugada el rey negro se retira del tablero.
Si en cierta posición cualquier jugada de las blancas pierde, nosotros afirmamos que ellas se encuentran en zugzwang (si pierde también cualquier jugada de las negras, el zugzwang es mutuo). El «ajedrez sin zugzwang» se distingue del habitual añadiendo sólo una jugada, una jugada sin salirse del sitio. En este ajedrez ya no hay zugzwang por cuanto siempre se puede ceder el turno de juego al contrario.
La demostración antes expuesta de que, jugando correctamente al ajedrez de dos movimientos, las blancas tienen garantizado el empate es también justa en su totalidad para el ajedrez sin zugzwang. No obstante, a diferencia del ajedrez de dos movimientos, la búsqueda directa del mate aquí es inútil. Recordemos que en el ajedrez clásico, donde las posibilidades de las blancas, a juzgar por las estadísticas, son notoriamente más altas, no se puede considerar demostrado que incluso en el caso de jugar su mejor partida tengan asegurado aunque sea el empate.
Ganapierde. Más difundido está el ganapierde del juego de damas, del cual hablaremos en el siguiente capítulo, sin embargo, su variante ajedrecística es también bastante interesante. La tarea principal de los jugadores en ambos juegos consiste en deshacerse de todas sus figuras. Claro que, si en el juego de damas el objetivo del juego habitual (directo) y el contrario son totalmente opuestos, en el ajedrez la situación es algo distinta: el concepto de mate aquí no existe y gana el que entregue antes al adversario todas sus figuras o las ahogue. Igual que en el juego de damas, es obligatorio tomar la figura ofrecida, mas si se puede elegir, se puede tomar cualquiera de ellas incluyendo el rey.
Es curioso que el ganapierde ajedrecístico tiene su teoría no muy habitual ni muy sencilla. Cuan paradójico no sea, pero ya la primera jugada puede resultar un error decisivo. Está demostrado que las jugadas 1.e4 y 1.d4 (las más utilizadas en las aperturas del ajedrez normal) permiten a las negras forzar el juego y ganar: las negras logran entregar todas sus figuras al contrario. He aquí como las negras consiguen su propósito, al avanzar las blancas el peón del rey dos casillas.
1.e4? b5!; 2.A:b5 Cf6 (jugada lenta); 3.A:d7 C:e4; 4.A:c8 (la posibilidad de jugar 4.A:e8 se examina más adelante) 4... C:d2; 5.A:d2 D:d2; 6.D:d2 Ca6; 7.A:a6 Tc8; 8.A:c8 f5; 9.A:f5 Tg8; 10.A:h7 c5; 11.A:g8 e6; 12.A:e6 c4; 13.A:c4 a6; 14.A:a6 g5; 15.D:g5 Rd8; 16.D:d8 Ae7; 17.D:e7 y sobre el tablero quedan sólo figuras blancas . A la jugada 4.A:e8 resuelve la jugada 4... D:d2; 5.D:d2 (5.A:f7 D:e1; 6.D:e1 C:f2; 7. R:f2, Tg8 etc.) 5... C:d2; 6. R:d2, Tg8; 7.A:f7 c5; 8.A:g8 g6; 9.A:h7 e5; 10.A:g6 e4; 11.A:e4 Cc6; 12.A:c6 Ab7; 13.A:b7 Tc8; 14.A:c8 a6; 15.A:a6 c4; 16.A:c4 Aa3; 17.C:a3 y las negras salen ganadoras al ganapierde.
De manera más simple se «refuta» la primera jugada con el peón de dama: 1.d4? e5!; 2. de Dg5!; 3. D:d7 A:d7 (este cambio en d7 puede producirse también más tarde); 4.A:g5 Rd8; 5.A:d8 a6; 6.A:c7 Ta7; 7.A:b8 b6; 8.A:a7 a5; 9.A:b6 g6; 10.A:a5 Ab4; 11.A:b4 Ce7; 12.A:e7 Tf8; 13.A:f8 h6; 14.A:h6 g5; 15.A:g5 f6; 16.A:f6 Ah3; 17.C:h3. ¡Ganan las negras!

Ideas originales e inesperadas tienen lugar también en los problemas relacionados con el ganapierde ajedrecístico. En la posición que presenta la figura 36 las blancas tratan de ganar el ganapierde, es decir, deshacerse de su único peón. Una posición más simple sobre el tablero es difícil imaginar, pero observen cuántos detalles contiene.
1.a3! Las blancas entregan el ritmo al adversario: procedimiento muy utilizado en el ajedrez normal. 1... h5; 2.a4 h4; 3.a5 h3; 4.a6 h2; 5.a7 h1T! Si las negras transforman su peón en dama o alfil, al transformar las blancas su peón en cualquier figura, aquéllas se verán obligadas a tomar inmediatamente la figura blanca. A la jugada 5... h1C se responde 6.a8D y 7.Dh1! Si sobre el tablero aparece el rey negro, o sea 5... h1R, entonces no se puede jugar 6.a8D ni 6.a8A por cuanto 6... Rg2, la transformación 6.a8R conduce al empate: tampoco sirve 6.a8C; en este caso la solución es 6.a8T! Rg2; 7.Ta4 Rf2; 8.Td4 Rg2; 9. Te4 Rh2; 10. Tf4 Rh1; 11. Tf3 Rg2; 12. Tf2 R:f2 y las blancas consiguen su objetivo.

6.a8A! Las blancas ponen sobre el tablero una figura aún más débil. En caso de otras transformaciones las negras fácilmente se deshacen de su torre. Ahora, a cualquier jugada que haga, le sigue 7.Ah1!, y el ganapierde ajedrecístico termina a favor de las blancas.
En la posición original que muestra la figura 37 las blancas se deshacen de unas figuras y ahogan las demás: 1.Th6! A:a2; 2.Tg6 A:b1; 3.g5 A:c2; 4.g4 A:d3; 5.Ah4! A:e4; 6.g3 A:g6. Las blancas ganan el ganapierde por cuanto no tienen con que jugar.
Modificación de la posición inicial. Obtener un juego nuevo sobre un tablero de ajedrez es posible sin necesidad de introducir reglas nuevas, es suficiente cambiar de posición algunas figuras. Efectivamente, como resultado de este procedimiento, los profundos conocimientos de la teoría clásica de las aperturas e incluso del medio juego pierden su sentido. Al cambiar la posición inicial en el tablero, los peones, por lo general, se mantienen en su lugar y las figuras tras la barrera de peones se cambian. Los cálculos muestran que la cantidad total de posiciones iniciales es (7!)2 = 25.401.600. Así pues, si consideramos diferentes todos los juegos que se distinguen por la posición inicial de sus figuras entonces del ajedrez habitual, sin dificultad, se puede obtener más de 25 millones de juegos nuevos.
Algunos innovadores no muy radicales suponen que para crear un juego nuevo es suficiente cambiar de lugar en ambos lados al rey con la dama. Es una suposición bastante ingenua. Aunque el juego que se obtiene en este caso es bastante insólito, no obstante en nada se diferencia del ajedrez habitual. Para convencerse de ello es suficiente cambiar mentalmente de color las casillas del tablero y junto a este (a derecha o a izquierda) colocar un espejo y mirando en él mover las figuras. El reflejo en el espejo de nuestra posición coincide con la disposición habitual de las figuras antes de iniciar el juego. Si nuestro adversario no juega muy bien al ajedrez normal, aquí también puede recibir rápidamente el «mate del estudiante»: 1.d4 d5; 2.Af4 Cf6; 3.Da5 Cc6; 4.D:c7 × .
Para la obtención de la disposición inicial de las figuras se utilizan distintos procedimientos divertidos. Por ejemplo, se puede proceder así. Las blancas ponen en una casilla cualquiera de la horizontal extrema una de sus figuras, las negras ponen una figura similar enfrente a aquella y a su vez eligen la casilla para la siguiente figura. Ahora son ya las blancas quien colocan la correspondiente figura enfrente, etc. Por este procedimiento ninguno de los jugadores tiene base para considerar que sus figuras en la posición inicial están peor situadas.
Existe también otro procedimiento más atrayente de disponer las figuras. En el centro del tablero se coloca una pantalla y ambos participantes del encuentro, en secreto del adversario, colocan sus figuras como les venga en gana. Colocadas las figuras, se retira la pantalla del tablero y se inicia el juego (por las reglas habituales) que se llama ajedrez a ciegas.
Un torneo muy curioso fue organizado en Ámsterdam en 1909. Este transcurrió por unas reglas singulares: antes de comenzar las partidas los participantes retiraban del tablero sus caballos de dama y en adelante introducían en el combate la «caballería de reserva» en el momento más apropiado. Este debería llamarse juego con el «caballo oculto».
Maharajá. Hasta aquí hemos analizado juegos con reglas singulares, pero sus figuras se movían como en el ajedrez real. Un mar sin límites de juegos, problemas e ideas fuera de lo corriente surgen con la introducción en el juego de figuras fantásticas. Tomemos como ejemplo la figura del maharajá (en otras fuentes, la amazona) que reúne en sí los movimientos de la dama y del caballo. Esta figura es el personaje principal en el siguiente juego.
Uno de los jugadores tiene el conjunto completo de figuras dispuestas en sus lugares iniciales, el otro sólo tiene el maharajá que puede poner en la casilla que quiera. El maharajá pierde si se consigue tomarlo y gana si da mate al rey contrario.
En este juego se prohíbe transformar los peones por cuanto de lo contrario la victoria se conseguiría de manera demasiado fácil: pasando los dos peones extremos y convirtiéndolos en damas, después de lo cual tres damas y dos torres sin dificultad rodean al maharajá. Con la restricción impuesta, el maharajá ofrece una tenaz resistencia, y un jugador inexperto incluso pierde rápidamente (es la misma situación que en el juego cuando un conjunto completo de figuras se opone al rey y los peones que pueden hacer por dos jugadas). Y con todo ello existe un procedimiento que permite, de manera forzada, vencer al maharajá. Gardner propuso un plan para cercarlo en 25 jugadas. No obstante el objetivo se alcanza, por lo menos, diez jugadas antes.

Sin prestar atención a los movimientos del maharajá, las blancas deben hacer los siguientes 14 movimientos seguidos: a4, h4, Cc3, Cf3, Ta3, Th3, Tb3, Tg3, d4, Dd3, De4, Tb7, Dd5, Tg8. Jugando así el maharajá no puede tomar ni una sola figura blanca y a partir de este momento sólo dispone de dos casillas libres, a6 y f6. En la casilla a6 (fig. 38) él sucumbe después de 15.Ag5, y en la casilla f6, después de 15.e4.
Figuras de fantasía. El maharajá es solamente una de las varias decenas de figuras de fantasía inventadas por aficionados a los juegos insólitos y por los compositores de fantasías ajedrecísticas. Distintos personajes de cuentos se obtienen a partir del caballo generalizado (a,b), eligiendo tales o cuales valores de a y b. Si a = 1 y b = 2 tenemos el caballo normal del ajedrez. Al caballo (1,3) lo llaman camello y su movimiento es una casilla en dirección de una línea y tres a lo largo de la otra. Al caballo (1,4) le llaman jirafa y al caballo (2,3), cebra. Si una de las cifras a o b es igual a cero se obtiene una torre de movimientos limitados a un número determinado de casillas, y cuando a = b se obtiene un alfil con la misma propiedad. El caballo que en una jugada da varios saltos seguidos recibe el nombre de jinete.
Hay que decir que las figuras-animales pueblan muchos juegos de fantasía sobre tableros ajedrecísticos. Así, por ejemplo, en el juego llamado «jungla» (forma antigua del ajedrez chino e indio) participan perros, lobos, gatos, panteras, ratas...
Muchas de las figuras, a semejanza del maharajá, son combinadas. La emperatriz reúne los movimientos de la torre y el caballo, el dragón, los del peón y el caballo, el centauro, los del alfil y el caballo. En los juegos antiguos tropezamos con sabios, bufones, obispos y otras personalidades exóticas.
Muchas figuras ajedrecísticas poseen distintos cargos y grados militares: granaderos, zapadores, soldados, oficiales, generales. Después de la Primera Guerra Mundial sobre el tablero aparecieron figuras tan terribles como tanques y aviones, y después de la SGM fue inventada la «bomba atómica», en la que se transforma el peón que alcanza la última horizontal. Esta temible figura se coloca en cualquiera de las casillas del tablero y se hace «estallar» destruyendo todo alrededor en determinado radio.
He aquí otras cuantas figuras sorprendentes que se pueden ver en el mundo de las fantasías ajedrecísticas. El grillo se mueve como la dama y salta por encima de figuras ajenas y propias, deteniéndose directamente detrás de ellas. El león, a diferencia del grillo, salta a cualquier casilla situada detrás de la figura sobre la cual saltó. El superelefante se mueve igual que el elefante, pero además puede rebotar de los bordes del tablero, a semejanza de una bola de billar. En el fútbol ajedrecístico las figuras actúan de acuerdo con las reglas del fútbol y la finalidad del juego no es dar mate al rey adversario, sino marcar un gol... Con las figuras neutrales pueden jugar tanto las blancas como las negras y las figuras golpeadoras sólo pueden jugar tomando otra figura. El caballo golpeador es un hipopótamo, y la dama golpeadora, un dinosaurio. Las figuras radiológicas ejercen influencia sobre las casillas del tablero a través de otras figuras. El diplomático es una figura que no se mueve y además no puede ser tomada por otra; las figuras de un mismo color que se encuentran junto al diplomático son inmunes, mientras que las figuras de los kamikazes (suicidas) se retiran del tablero junto con la figura tomada.
No son pocas las variedades de peones fantásticos. El peón-camaleón, al tomar una figura del contrario se transforma en dicha figura pero de su color. El superpeón se desplaza a cualquier número de casillas verticalmente y captura en diagonal a cualquier número de casillas. El peón-taxi se mueve hacia delante y hacia atrás. El peón berlinés se mueve en diagonal y toma verticalmente. El peón inmóvil no se desplaza y no toma otras figuras pero él mismo puede ser tomado. El peón de acción lenta se transforma sólo en la figura tomada, pero si no las hay, él espera el momento oportuno.
Juego combinado de damas y ajedrez. Así pues, hemos presentado, al detalle, los juegos ajedrecísticos sobre tableros no estandarizados, con reglas singulares y figuras de fantasía. En este juego inventado por el matemático norteamericano S. Golomb, se utilizan simultáneamente los tres elementos singulares.

Realmente este juego representa una mezcla del juego de damas con el ajedrez: las figuras son como en el ajedrez, pero se desplazan sólo por las casillas negras del tablero, como en el juego de damas.
La disposición de las figuras antes de empezar el juego se ve en la figura 39. Como vemos la composición de figuras en este juego difiere algo de la del ajedrez. Cada una de las partes tiene dos reyes que se mueven a las casillas negras adyacentes. El alfil en este juego no se diferencia en nada del que se utiliza en el ajedrez y los peones se mueven como las fichas. Por cuanto el caballo habitual (1,2) no puede hacer una sola jugada sobre el tablero del juego de damas (inmediatamente va a parar a una casilla blanca en las que está prohibido detenerse), por esto lo sustituimos por el camello (1,3) que se mueve sólo por casillas de un mismo color. La toma con los peones y los reyes es igual que en el juego de damas (saltando por encima de la figura) y la toma con el alfil y el camello, como en el ajedrez (ocupando la casilla en la que se encuentra la figura). La toma con los peones y los reyes es obligatoria y la elección entre la toma ajedrecística o como en el juego de damas, si tal se produce, es libre. El peón que llega a la última horizontal se transforma en cualquiera de las tres figuras. Gana el que tome antes a los dos reyes del contrario.
§. Juegos matemáticos sobre tableros ajedrecísticos
Juegos singulares sobre tableros de ajedrez inventan no sólo los compositores de fantasías ajedrecísticas, sino también los matemáticos. Pero estos últimos prefieren juegos que permitan el análisis matemático, expresados en forma de problemas; éstos se ofrecen en las olimpiadas matemáticas o se incluyen en las diferentes colecciones de problemas.
En los juegos matemáticos el interés consiste en hallar un algoritmo preciso que garantice la victoria o el empate. Pero si el algoritmo ya fue hallado, el juego pierde su carácter creativo que tanto nos atrae en los juegos intelectuales.
Es curioso que en la época del Renacimiento era muy popular un juego especial matemático-ajedrecístico llamado «ajedrez aritmético» o de otra manera, ritmomaquia. Sobre un tablero de 16 × 8 se movían tres tipos de figuras: en forma de círculo, de triángulo y de rectángulo. Cada figura tenía números inscritos, cuyas combinaciones determinaban las jugadas, capturas y los mates. El juego requería cálculos matemáticos demasiado complicados y poco a poco fue olvidado.
El caballo y el camello. En una de las esquinas de un tablero n × n (n ≥ 4) se encuentra un caballo, con el que ambos participantes juegan alternándose. El primer jugador lo desplaza como a un caballo habitual, pero en dos movimientos (como en el ajedrez de dos movimientos) y el segundo lo mueve como a un camello, es decir, tres casillas a lo largo de una línea y una casilla, a lo largo de otra. Las «blancas» comienzan y tratan de situar la figura en el rincón opuesto del tablero y las «negras» pretenden impedírselo. ¿Como terminará el juego?
En esta competencia, un poco rara, del caballo con el camello (más preciso sería decir del camaleón que se transforma ora en una, ora en otra figura) sale vencedor el caballo normal. Si nuestra figura se encuentra en la diagonal grande que pasa por la casilla inicial de la esquina, a cualquier retroceso del camello de esta diagonal el caballo vuelve a ella, con la particularidad de que se acerca por ella como mínimo en una casilla al objetivo final. A fin de cuentas el caballo llega a la esquina contraria.
Los gatos y el ratón. El primer jugador sólo tiene una figura, un ratón, y el otro, varias figuras, gatos. El ratón y los gatos tienen los mismos movimientos, una casilla vertical u horizontalmente, es decir, se obtienen a partir del caballo (a,b) cuando a = 0, b = 1. Si el ratón se halla en el extremo del tablero, al siguiente movimiento salta del tablero y escapa a la persecución de los gatos; si el ratón y un gato van a parar a una misma casilla, el gato se come al ratón.
La lucha de los gatos contra el ratón transcurre sobre un tablero normal, con la particularidad de que los jugadores mueven sus figuras alternándose, pero el segundo en una jugada mueve todos sus gatos (en cualesquiera direcciones). Comienza el ratón tratando de saltar del tablero y los gatos hacen todo lo posible para comérselo. Son posibles dos variantes del juego, para cada una de las cuales formularemos un problema interesante.
a) Los gatos son sólo dos y el ratón se encuentra en una casilla interior del tablero. ¿Se pueden situar los gatos en los extremos del tablero de manera que al fin y al cabo logren comerse al ratón?
b) Los gatos son tres y se encuentran en cualesquiera casillas, pero por otra parte el ratón en su primera jugada hace dos movimientos seguidos. ¿Podrá escapar el ratón a la persecución de los gatos?
Mostremos que en el primer caso el ratón no logra escapar y en el segundo, por el contrario, se escapa felizmente de los gatos.
a) Trazamos una diagonal por la casilla en que se encuentra el ratón y colocamos a los gatos en sus extremos. A cada jugada del ratón, los gatos se desplazan de tal manera que las tres figuras nuevamente se encuentren en una misma diagonal y las distancias entre los gatos disminuyan en una casilla (por la diagonal). Tal estrategia permite a los gatos en breve comerse al ratón.
b) Examinemos dos diagonales del tablero que pasan por la casilla que ocupa el ratón. Si la casilla no es extrema (de lo contrario el ratón inmediatamente salta del tablero), entonces estas diagonales dividen el tablero en cuatro partes. Por cuanto los gatos son tres, en una de las partes no hay gatos. Tracemos una línea (horizontal o vertical) que una al ratón con el extremo del tablero dentro de esta parte. Es evidente que si el ratón se dirige por esta línea hacia el extremo del tablero los gatos no lo atraparán.

La dama al rincón. Sobre el tablero se encuentra una dama que los dos jugadores, turnándose, mueven a cualquier número de casillas hacia arriba, hacia la derecha o diagonalmente hacia arriba y a la derecha (es decir, no se puede retroceder con la dama). Gana el que consiga antes meterla en el rincón superior derecho del tablero, o sea en la casilla h8.
Mostremos que el resultado del juego se determina automáticamente según la figura 40. Si la dama se encuentra en una casilla con un signo más, gana el que juega primero y si ocupa una casilla con el signo menos, el que gana es el contrario. En este juego no hay empates. Supongamos que la dama se halla en la octava horizontal, en la vertical «h» o en la diagonal a1–h8 (a excepción de la casilla h8), en este caso las blancas, en su primera jugada, ponen la dama en el rincón y ganan. En adelante razonamos así. Si de esta casilla del tablero la dama se ve obligada a desplazarse a otra casilla que tenga el signo más, ella, naturalmente, obtiene un menos y si la puede mover a una casilla con el signo «menos», obtiene un más, etc. Al fin y al cabo en todas las casillas del tablero se anotarán los signos. Resulta que las siete casillas son tales que el que empieza por ellas pierde el juego, el resto dan la victoria al que comienza por ellas, además, la dama va a parar al rincón deseado no más tarde de la tercera jugada. Pongamos que la dama, al empezar el juego, se encuentra en b1 (véase la fig. 40), en tal caso la «partida» puede desarrollarse del modo siguiente: 1.Db1 – d1 (conduce más rápido al objetivo la jugada 1.Dg6!) 1... Dd2; 2.Dd3! (única jugada) 2... Dd7; 3.Df7! Dh7; 4.Dh8, alcanzando la victoria.
El principio indicado de disposición de los mases y los menos se traslada a cualquier tablero rectangular, es decir, en cada uno de estos tableros el juego se somete a un esmerado análisis.
Tomemos ahora una torre en sustitución de la dama y examinemos el juego «la torre al rincón». ¡Las reglas de este juego son similares a las del anterior y su algoritmo recuerda el juego «el caballo y el camello»! Los jugadores, turnándose, mueven la torre por las horizontales (hacia la derecha) y por las verticales (hacia arriba) y gana quien ocupe antes la casilla del rincón (h8).
Nuevamente en la casilla h8 se pone un menos y las demás casillas de la octava horizontal y las de la vertical «h» reciben el signo más. Cuando la torre se halla en la casilla g7 el que comienza pierde, se pone un menos, y en las demás casillas de la séptima horizontal gana, ponemos un más, etc.
Como resultado obtenemos que las «blancas» ganan si su torre no se encuentra en la diagonal a1–h8. El método que conduce a la victoria es el mismo que en el juego de «el caballo y el camello». En la primera jugada hay que ocupar la diagonal «grande», después de la retirada forzosa del contrario hay que volverá ella, y así hasta llegar al rincón. La partida más larga, empezando con la torre en las casillas a2 o en b1 consta de siete movimientos: 1.Tb1 – b2! Tc2; 2.Tc3 Tc4; 3.Td4! Te4; 4.Te5! Te6; 5.Tf6! Tg6; 6.Tg7 Tg8; 7.Th8.
De manera análoga se analizan los juegos «el caballo al rincón» y «el rey al rincón». La teoría de estos juegos se traslada fácilmente a cualesquiera tableros. Para valorar la posición basta con poner correctamente sobre el tablero los signos más y menos.
El ajedrez y el «nim». He aquí otro juego con torres. Tomemos un tablero arbitrario m × n. Pongamos en la primera horizontal las torres blancas y en la última, las negras. Los jugadores turnándose mueven sus torres verticalmente (hacia adelante y hacia atrás) y gana el que consigue bloquear las m torres del contrario contra el extremo del tablero.
Distraigámonos un poco y analicemos otro juego para «dos personas». Tenemos varios montones de piedrecitas y cada jugada consiste en que el jugador toma de uno de los montones cierto número de piedrecitas. Juegan turnándose y gana el que tome las últimas piedrecitas. Este juego antiguo se llama nim y su descripción puede encontrarse en muchos libros de matemáticas recreativas. Este juego tiene una gran cantidad de variantes. En unos de estos juegos se imponen limitaciones al número de piedrecitas que se pueden tomar de una vez, en otros se permite trasladar piedrecitas de un montón a otro, en otros, las piedrecitas se pueden tomar de distintos montones al mismo tiempo, etc. En el juego nimbi hay tres montones con 3, 4 y 5 piedrecitas. Estas doce piedrecitas se disponen en las cuadrículas de un tablero especial y se pueden tomar, siguiendo reglas especiales. En el juego de Bachet las piedras se toman de un solo montón pero no más de la cantidad fijada, en el juego tsy czang szi los montones son dos y las piedras pueden tomarse no sólo como en el nim habitual (cualquier cantidad de un montón), sino también de dos al mismo tiempo: en este caso un número igual. Como regla en cada una de las variantes del nim se consigue realizar un análisis matemático sutil y hallar el método correcto de juego.
He aquí la variante «infantil» del nim con un solo montón de piedrecitas (cerillas) que fácilmente asimilan también los preescolares. Dos personas, por turno, toman del montón una, dos o tres piedras. Gana el que logre tomar la última piedrecita. Por lo visto si usted le deja al contrario 4 piedras y antes de esto 8, 12, etc., la victoria será suya. De esta manera el que empieza gana, si el número de piedras en el montón no se divide por 4, si por el contrario es múltiplo de 4, gana el segundo jugador.
El lector seguramente ya se dio cuenta que el juego con las torres representa una de las modalidades del nim. El papel de los montones de piedrecitas lo desempeñan las verticales del tablero y la cantidad de piedrecitas en el montón es igual al número de casillas entre las torres en la vertical correspondiente. De esta manera, al comenzar el juego, nosotros en esencia disponemos de m montones y en cada uno de ellos n – 2 piedrecitas. El movimiento de la torre no es otra cosa que la retirada de varias piedrecitas del montón (si nuestra torre se acerca a la del adversario) o la añadidura de piedrecitas (si nuestra torre se aleja de la del contrario).
Resulta que para valorar el resultado del juego en esta variante del nim sólo tiene importancia el número de verticales que tiene el tablero, pero la cantidad de horizontales no tiene importancia (con tal que no sean dos, por cuanto las blancas perderían sin comenzar el juego). Si el número de verticales no es par, ganan las blancas, y si es par, las negras. Si el tablero está compuesto de una sola vertical, las blancas con su primera jugada bloquean la torre del adversario (toman todas las piedrecitas del montón) y la partida termina a su favor. Supongamos que las verticales son dos: a y b. Entonces a cualquier jugada de la torre blanca hacia adelante las negras responden con una jugada simétrica respecto al centro y esta estrategia les permite alcanzar su objetivo. Por ejemplo: 1.Ta3 Tb6!; 2.Tb4 Ta5!; 3.Ta4 Tb5! Ahora las torres blancas se ven obligadas a retroceder perseguidas por las negras hasta el fin victorioso (claro que, al retroceder las torres blancas, las negras no tienen necesidad de respetar la simetría). Sobre el tablero 3x8 las blancas juegan 1.Tc7! y reducen el juego al caso anterior, siendo ahora la jugada del contrario. La actuación simétrica en las dos primeras verticales les proporciona la victoria. Sobre el tablero 4x8 nuevamente ganan las negras, etc.
Hablemos otra vez sobre el nim. Si son dos el número de montones, entonces el análisis es simple. Supongamos que en uno de los montones hay s piedrecitas y en el otro, t (s > t). Cuando nos toque jugar, tomemos del primer montón s – t piedrecitas, es decir, igualemos la cantidad en ambos montones. A continuación actuaremos simétricamente: tomaremos del segundo montón la misma cantidad de piedrecitas que el adversario del primero, etc.
Resulta evidente que si al comenzar el juego s = t y nosotros empezamos, las cosas se nos ponen mal.
Este juego casi no se distingue del de las torres. Cuando s > t, el que comienza, en su primera jugada, reduce el juego al desplazamiento de las torres sobre el tablero 2 × (t + 2), siendo la jugada del contrario, y gana. Claro que en este caso, no es obligatorio remitirse al ajedrez. Pero en el siguiente juego esto es muy útil.
Pongamos que siguen siendo dos montones, pero las piedras se pueden tomar no solo de uno de ello, sino de ambos a la vez, pero en este caso obligatoriamente de los dos por igual, o sea, obtenemos una variante del nim llamada tsy czang szi. Supongamos que el primer montón contiene siete piedras y el segundo, seis. Tomemos entonces un tablero de ajedrez y pongamos en la casilla b1 la dama (fig. 40). Como se puede ver, por encima de la dama hay siete horizontales y a su derecha seis verticales.
Establezcamos la relación entre las jugadas en nuestros dos juegos: el tsy szang szi y el de «la dama al rincón». La toma de cierta cantidad de piedrecitas del primer montón corresponde al movimiento de la dama a una misma cantidad de casillas verticalmente y la toma del segundo montón, al desplazamiento de la dama, horizontalmente; por fin si tomamos de ambos montones igual cantidad de piedrecitas, la dama se mueve por la diagonal a la misma cantidad de casillas. En el momento en que no quede una sola piedrecita en ambos montones la dama fue a parar al rincón del tablero.
Así pues, no hay necesidad de desarrollar una teoría para el tsy szang szi, sino que utilizaremos la del juego «la dama al rincón». En nuestro caso la dama se encuentra en una casilla con el signo más y por esta razón el que comienza gana. En el caso general, siendo arbitrarias las cantidades de piedrecitas en los montones, para valorar la posición en el tsy szang szi es suficiente «traspasarla» al tablero de ajedrez y mirar ¿en qué casilla se encuentra, en este caso, la dama (otra cosa es si es o no visible tal tablero)!
Por lo tanto la diferencia entre los dos juegos examinados es superficial: las posiciones y las jugadas en uno de ellos corresponden a las posiciones y las jugadas del segundo. Matemáticamente estos juegos se llaman isomorfos.
El eminente matemático soviético I. Guelfand inventó un juego con piedrecitas parecido a aquéllos. Nuevamente tenemos dos montones de piedrecitas, pero en este caso se puede tomar una piedrecita de un montón, una piedrecita del segundo, una piedrecita de cada montón o finalmente no coger ninguna piedra, sino trasladar una piedrecita de un montón a otro. Aquí también gana el que toma la última piedrecita.
Este juego es también isomorfo a uno ajedrecístico similar al juego «la dama al rincón», solo que las funciones de la dama, como es fácil ver, las desempeña el rey. Anotando debidamente los mases y los menos en el tablero 8 × 8 es fácil llevar a cabo un análisis minucioso del juego.
Dominó sobre un tablero de ajedrez. Por su naturaleza el dominó tiene una relación más próxima a las matemáticas que muchos otros juegos descritos en este libro. Los números representados por puntos en las fichas del dominó están presentes en forma evidente. En los libros dedicados a las matemáticas recreativas se pueden hallar decenas de problemas combinatorios, rompecabezas, trucos y juegos con el dominó. Especialmente populares son las «cuadrillas», colocación sobre la mesa de las fichas del dominó con tales o cuales propiedades ingeniosas.
Por ejemplo, es interesante el siguiente juego. Dos jugadores, de manera que no lo vea el adversario, colocan las 28 fichas, formando rectángulos de 8 × 7. Después copian la disposición de sus números en una hoja de papel y se intercambian estos papeles.
Los límites entre las fichas del dominó desaparecen y los jugadores deben determinar cómo las tenía colocadas el adversario, es decir, dividir el rectángulo numérico de 8 × 7 en 28 rectángulos de 2 × 1, que forman el conjunto de fichas del dominó.
Por supuesto que este juego y todo género de «cuadrillas» no tienen relación directa con el dominó clásico el cual contiene no pocos detalles, existen también sus maestros. Sin embargo, el éxito, a nuestro parecer, depende antes que nada de la capacidad de observación (quien a «qué» juega) y no de la capacidad matemática. Es de señalar que se conocen muchos juegos diferentes del dominó tradicional. He aquí algunos de ellos: relámpago (de una jugada se pueden poner varias fichas una tras otra de números iguales en uno de los cuadrados); dominó a ciegas (los jugadores no ven sus propias fichas y las descubren, una tras otra, en el curso del juego); bergen (en cada jugada los participantes reciben determinado número de puntos y gana el que alcance primero la cifra fijada); dominó quíntuple, dominó triple, sevastópol, dominó chino, jubileo, cuarenta y dos, matador, etc.
Expongamos el famoso rompecabezas en el que participan simultáneamente el tablero de ajedrez y el dominó.
De un tablero cuadrado de 8 × 8 recortaron las dos casillas angulares ubicadas una contra la otra, al y h8. ¿Se puede cubrir la parte restante del tablero con 31 fichas de dominó (es decir con rectangulares 2 × 1)?
Se podrían utilizar razonamientos algebraicos, pero la resolución «ajedrecística» es más simple y más elegante. Pintemos nuestro cuadrado con recortes en blanco y negro escaqueadamente. Ahora prestemos atención a que el tablero resultante tiene recortadas dos casillas del mismo color y en él el número de casillas negras es en dos unidades menor que el de casillas blancas. Pero cada ficha de dominó cubre una casilla blanca y una casilla negra y por tanto no se produce la cobertura total del tablero.
Claro que este problema tiene una relación lejana con los juegos, pero fue difícil abstenerse de presentar un ejemplo de tal efecto...
A propósito, precisamente este problema dio origen a toda una clase de diversiones matemáticas: el poliminó, mencionado por nosotros en el relato sobre el combate marino. Poliminó no sólo son rompecabezas atractivos, en los cuales hay que cubrir tableros singulares con figuras rectangulares sino también juegos para dos personas. Recordemos primero el siguiente juego-problema divertido.
Sobre una mesa perfectamente redonda dos jugadores, turnándose, ponen monedas de cualquier valor. Pierde el que en su jugada de turno no puede depositar la moneda sin montar sobre otras ni sobrepasar los límites de la mesa.
El resultado de este juego está predeterminado antes de comenzarlo. Gana el que comienza y además le asegura la victoria la estrategia simétrica. El primer jugador comienza poniendo una moneda cualquiera en el centro de la mesa, después de lo cual le resta copiar las jugadas del contrario: en respuesta a la jugada de éste poner una moneda de mismo valor en el lugar simétrico respecto al centro. Si el segundo jugador se encuentra en condiciones de poner una moneda cualquiera sobre la mesa, para una moneda del mismo valor del primer jugador se encontrará sobre la mesa el correspondiente lugar simétrico respecto al centro. Al fin y al cabo llegará el momento cuando el segundo jugador no podrá hacer su jugada y la partida terminará con su derrota.
Por lo visto esta estrategia simétrica conduce al objetivo no sólo al jugar sobre una mesa redonda sino también sobre una mesa cuadrada, rectangular y en general sobre una mesa de cualquier forma simétrica respecto al centro. En lugar de monedas pueden utilizarse fichas arbitrarias con la única condición de que su cantidad sea suficiente.
Es evidente que el juego con las monedas, recién descrito, tiene, por decirlo así, un carácter especulativo. Es difícil imaginar a dos jugadores provistos de voluminosos monederos colocando por turno monedas sobre una mesa...

Más seriedad hay en los poliminós sobre tableros de ajedrez de m × n. Dos jugadores, turnándose, ponen fichas de dominó sobre un tablero, cubriendo con cada ficha dos casillas de éste. Igual que en el juego con las monedas pierde el que no pueda hacer su jugada siguiente. También en este juego la idea de la simetría, conocida por nosotros, tiene una importancia decisiva. Tomemos un tablero de 10 × 6. La estrategia de juego aquí es la misma que en el juego con las monedas, pero en este caso el que empieza pierde. El segundo jugador no tiene de que preocuparse, le es suficiente copiar (simétricamente respecto del centro) las jugadas del adversario. Así, por ejemplo, si el primero hace la jugada 1 (fig. 41a), el segundo pone la ficha 2; a la jugada 3 responde con 4, a la jugada 5 responde con la jugada 6, etc., hasta que el primer jugador no pueda hacer su jugada.
Si uno de los lados del tablero es par y el otro impar, gana el primer jugador. Por ejemplo, sobre el tablero 11 × 6 el primer jugador empieza con la jugada 1, poniendo la ficha en el centro del tablero, y después sigue por el método descrito, manteniendo enteramente la simetría. Las primeras jugadas se muestran en la figura 41b; nuevamente los números impares pertenecen al primer jugador y los pares, al segundo.
Señalemos que si los dos lados del tablero son impares, la acción simétrica ya no garantiza el éxito. La estrategia óptima para tal tablero no es conocida por nosotros. A propósito, si jugamos al dominó (o cualquier conjunto de poliminós) sobre un tablero no dividido en cuadrados (casillas) y, por consiguiente, se permite poner las fichas en cualquier lugar, entonces este juego ya en nada se diferenciará del juego con las monedas. El que empieza siempre gana, independientemente de la paridad de los lados del tablero: para él es suficiente en su primera jugada ocupar con una ficha el centro del tablero y a partir de aquí, como siempre, acogerse a la estrategia de la simetría respecto al centro.
La simetría en el ajedrez. En una serie de ejemplos ya nos hemos convencido (poliminó, juego de las torres) de que la estrategia de la simetría con frecuencia conduce a la victoria. Y ¿qué ocurre en el caso del propio ajedrez? ¿Sería suficiente para las negras simplemente copiar las jugadas de las blancas como para que esta estrategia les garantice el empate? Como muestra la siguiente partida interesante, las negras inesperadamente pueden tener suerte.
1.e4 e5. Por lo visto en la partida de ajedrez sólo es posible la simetría axial: la posición inicial es simétrica respecto a la recta que divide las partes superior e inferior del tablero. 2.Re2 Re7; 3.Re3 Re6; 4.Df3 Df6; 5.Ce2 Ce7; 6.b3 b6; 7.Aa3 Aa6; 8.Cd4 +. Al rey negro le dieron jaque. No hay otra alternativa, las negras se ven obligadas a romper la simetría y... dar mate después de 8... ed × !
La partida resultó interesante, pero, como usted comprenderá, si las negras, copiando las jugadas del adversario, pudieran ganar o aunque sea hacer tablas, sería poco probable que se celebrara con tanta frecuencia el campeonato del mundo de ajedrez.
Se conoce la siguiente interesante historia. Alguien llegó a un club de ajedrez y anunció que encontró una manera fija de no perder con las negras. «¿De qué manera?»– le preguntaron–. «Muy sencillo –contestó el huésped –, ¡repitiendo las jugadas del contrario!» Sam Loyd se ofreció para jugar con el ingenuo inventor. La partida duró solamente cuatro jugadas: 1.c4 c5; 2.Da4 Da5; 3.Dc6 Dc3; 4.D:c8 × . Posiblemente que si los jugadores se sentaran nuevamente a jugar, la partida terminaría de una manera un poco distinta: 1.d4 d5; 2.Dd3 Dd6; 3.Dh3 Dh6 4.D:c8 × .
Semejantes «duelos» ajedrecísticos, en los que las negras copian enteramente los movimientos del contrario y finalmente reciben mate se llaman partidas de monos. En los ejemplos mencionados el mate lo daba la dama blanca y cumplir antes su tarea no podía. Y ¿cuáles son los records en las partidas de monos en las que el mate lo dan otras figuras: la torre, alfil, caballo y peón?
A principios de siglo de este asunto se interesó K. Traksler, autor de composiciones ajedrecísticas. Compuso partidas simétricas en las que la torre daba mate en 9 jugadas, el alfil, en 8, el caballo, en 7 y el peón, en 15. Estos records fueron mejorados más de una vez y en lo sucesivo fueron inventadas partidas en las que la torre daba mate en 6 jugadas, el alfil, en 7, el caballo, en 6 y el peón, en 7. He aquí las partidas de monos más cortas:
Da mate la torre: 1.Cf3 Cf6; 2.Cg5 Cg4; 3.C:h7 C:h2; 4.C:f8 C:fl 5.Cg6 Cg3. Aquí termina la danza de los caballos. 6.T:h8 × .
Da mate el caballo: 1.Cc3 Cc6; 2.Ce4 Ce5; 3.e3 e6; 4.Ce2 Ce7; 5.g3 gG; 6.Cf6 × (o bien 5.c3 c6 6.Cd6 x.)
Da mate el alfil de casillas blancas: 1.e4 e5; 2.f4 f5; 3.ef ef; 4.f6 f3; 5.fg fg; 6.Ae2 Ae7; 7.Ah5 × , y ahora da mate el alfil de casillas negras: 1.d4 d5; 2.Rd2 Rd7; 3.Rd3 Rd6; 4.Ae3 Ae6; 5.c3 c6; 6.Dd2 Dd7; 7.Af4 × .
Da mate el peón: 1.g4 g5; 2.h4 b5; 3.Cf3 Cf6; 4.Ce5 Ce4; 5.hg hg; 6.g6 g3; 7.gf × ; o bien 1.f4 f5; 2.g4 g5; 3.gf gf; 4.f6 f3; 5.Ch3 Ch6; 6.Cg5 Gg4; 7.f7 × .
Nuestra digresión lírica acerca de las partidas de monos pertenece, más bien, al género humorístico aunque, como ya hemos visto, también aquí se encuentra presente la simetría.
Entre los juegos inventados hace relativamente poco hay que subrayar dos clases interesantes: juegos topológicos y juegos sobre grafos. La aparición de estos juegos, por lo visto, se debe al impetuoso desarrollo de dos partes modernas de las matemáticas, la topología y la teoría de los grafos. Por desgracia estos juegos no se inscriben bien en la estructura de este libro (teniendo en cuenta su volumen). Por lo visto estos juegos tampoco tienen relación con el ajedrez. Su mención en este capítulo se debe a que la estrategia óptima en ellos con frecuencia es la simetría. Tomemos, como ejemplo, el juego bridg-it. La figura 42a muestra el «tablero» para este juego. Los participantes, turnándose, trazan líneas verticales y horizontales, uniendo los puntos de su color. Las líneas de los adversarios no deben intersecarse. Gana el que construya antes una quebrada de su color que conecte los dos lados contrarios del tablero (en la fig. 42 a ganaron las blancas).
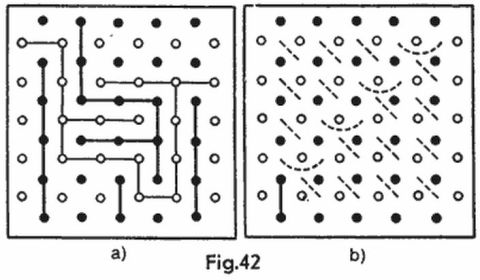
La estrategia óptima que garantiza la victoria de las blancas en este juego fue descubierta por O. Gross, especialista en teoría de juegos. Esta estrategia es tan efectiva como sencilla. Utilicemos la figura 42b. Como primera jugada unamos dos puntos en la esquina inferior izquierda. En adelante se debe jugar así: cada vez que la línea trazada por el contrario interseque el extremo de alguna de las curvas de puntos habrá de trazarse una línea que interseque el otro extremo de esta curva y así basta conseguir la victoria. Esta estrategia ingeniosa se generaliza fácilmente para cualquier tablero.
Préstese atención a que en la figura de antemano no están previstas las líneas que unen los puntos extremos del tablero. Las reglas del juego no prohíben tales líneas pero es absurdo trazarlas; si el adversario traza de pronto una línea a lo largo del extremo del tablero, hay que hacer una contrajugada, uniendo dos puntos extremos o bien, si gusta más, uniendo dos puntos cualesquiera del tablero. Puede resultar que precisamente esta jugada casual será más adelante condicionada por la estrategia, entonces, por cuanto usted ya la ha hecho, trace cualquier otra línea, una línea de más en el tablero nunca molesta. Lógicamente, ahora, cuando se conoce la estrategia óptima para el primer jugador, el bridg-it pierde su atractivo.
Por desgracia debemos dejar a un lado juegos topológicos y de grafos tan interesantes como «col de bruselas», «hex», «juego a los puntos», «juego de conmutación de Shannon», etc.
Para terminar el capítulo indiquemos que las estrategias examinadas por nosotros, cuando a la jugada de uno de los jugadores automáticamente le sigue la jugada del otro (¡y esta jugada le acerca a su objetivo!), en la teoría de juegos se denominan pares.
Ejemplos curiosos de juegos simétricos y de estrategias pares se exponen en sucesivos capítulos.
Contenido:§. Ganapierde
§. Esquinas chinas
§. Reversi
Como ya liemos dicho los juegos de fichas se diferencian de los ajedrecísticos en que las figuras presentes en el tablero son de un solo tipo (aun cuando de dos colores). En lugar de fichas se pueden utilizar bolitas, botones, piedrecitas.
En muchos países están difundidos los juegos de fichas con sus particularidades y sus reglas.
Se conocen los juegos de damas rusas, americanas, inglesas, españolas, italianas, alemanas, francesas, escocesas, etc. En estos juegos se utiliza el tablero habitual de 8 × 8 y 12 fichas por cada jugador. Se diferencian entre sí por la disposición inicial, por las leyes respecto a los movimientos y capturas.
Pero, por ejemplo, el juego de damas turco no tiene nada en común con el juego clásico. Ambos adversarios disponen de 16 fichas cada uno: las blancas en su posición inicial ocupan la segunda y tercera horizontales, las negras, respectivamente, la sexta y séptima. Las fichas se mueven una casilla hacia adelante, a izquierda y a derecha, la dama además puede moverse hacia atrás y en las demás direcciones a cualquier número de casillas. Los movimientos diagonales no existen por lo que el color de las casillas no tiene importancia, se puede combatir sobre un papel cuadriculado. Las demás reglas (captura, transformación, etc.) son iguales que en el juego de damas de 8 × 8.
Además de los tipos nacionales del juego de damas sobre tableros de 8 × 8, existen juegos sobre tableros de mayores dimensiones. Así por ejemplo, en el juego de damas canadiense se utiliza un tablero de 12 × 12.
La diferencia en las reglas de juego en los distintos países molestaba a los mejores jugadores competir entre sí. A mediados del siglo pasado las relaciones internacionales entre los ajedrecistas se agilizaron mucho y los jugadores a las damas quisieron también hallar un lenguaje común para celebrar sus campeonatos. Como resultado de ello nació el juego de damas internacional o, llamado de otra manera, de las cien casillas, al que se juega sobre un tablero de 10 × 10. En la posición inicial cada una de las partes coloca sus fichas en cuatro horizontales por las casillas negras. Así pues tanto las blancas como las negras tienen por 20 fichas, lo cual hace el juego más complicado y más variado que el juego de damas ruso.
En la actualidad las damas internacionales adquirieron gran divulgación, se organizan muchas competencias de este juego, se editan libros y revistas. Claro que las cuestiones de la teoría no serán expuestas aquí, pero explicar la diferencia entre las damas de cien casillas y el juego de damas ruso creemos que merece la pena. En realidad, diferentes son sólo tres reglas de captura:
1) cuando se tienen varias posibilidades, hay que tomar la mayor cantidad posible de fichas:
2) una ficha simple, después de alcanzar la última horizontal como resultado de una captura se convierte en dama pero el derecho a tomar como tal lo adquiere sólo a partir del siguiente movimiento;
3) cuando una ficha simple alcanza la última horizontal como resultado de una captura y está obligada a tomar otras fichas como simple, sigue siendo una ficha simple.
En el juego de damas de cien casillas, a diferencia de las damas rusas (y del ajedrez), se utiliza la notación numérica, pero esto ya se refiere al apunte de las partidas y con las reglas del juego no tiene relación alguna.
Una generalización interesante de las damas rusas son las fichas-postes o torres. La diferencia respecto del juego habitual consiste en que, al tomar la ficha del contrario, ésta no se retira del tablero, sino que se coloca debajo de la ficha que la tomó. Si se capturan varias fichas del adversario, todas ellas se recogen una tras otra y en la última casilla se forma una «torre» o un «poste». De aquí el nombre del juego. La torre se mueve completa y juega por las reglas de la ficha de arriba, como una ficha simple o una dama. La torre, igual que una ficha solitaria, puede pasar a dama, en la cual se convierte sólo la ficha superior. Al capturar una torre, de ella se retira solo la ficha superior y la ficha situada debajo de ella entra en su derecho. Como resultado el jugador puede liberar su ficha o dama, capturada anteriormente por el adversario. Cuando de la torre se retira una dama y debajo de esta se encuentra una ficha simple del mismo color, la torre se convierte en simple y juega como tal hasta que no se produzcan nuevos cambios.
Este juego antiguo es muy peculiar y no tiene semejanza con otras modalidades del juego de damas. Así pues, en este juego, desde el comienzo hasta el fin, sobre el tablero se encuentran las 24 fichas, aunque se pueden disponer en los distintos pisos de las torres y estar recluidas en sus sótanos. A propósito, E. Lasker, el rey del ajedrez, era aficionado a este juego y una de sus variantes lleva su nombre.
En el juego llamado «prestidigitación» las fichas capturadas tampoco se retiran del tablero y se convierten en material de construcción para la torre. Pero aquí hay demasiadas singularidades: un tablero en forma de cruz, movimientos de las fichas horizontal y verticalmente, y el número de casillas a las que se puede jugar se determina por la altura de la torre.
En el capítulo dedicado al ajedrez hemos descrito modalidades del juego para más de dos jugadores. Hoy día también existen juegos de damas para tres jugadores, de manera que en este sentido el juego de damas trata de no ir a la zaga del ajedrez...
A la par con los juegos tradicionales de fichas, en los que para ganar hay que comer todas las fichas del contrario (o privarlas de movilidad), se conocen muchos juegos en los que los objetivos de sus jugadores son totalmente diferentes. Antes que nada merece la pena hablar sobre el ganapierde. La popularidad de este juego no ofrece duda, pero en la literatura especial hasta hoy día no se le presta la debida atención. Nosotros hemos decidido dedicar al ganapierde un apartado especial.
Otro apartado de este capítulo está dedicado al juego de las esquinas chinas y otros juegos similares. En estos juegos las reglas son totalmente diferentes: las fichas no se toman, sino que se adelantan desde su territorio al del contrario y el que haga esto antes gana. De la gran cantidad de juegos de fichas nuestra elección recayó sobre el juego de las esquinas chinas por el hecho de que en él se detectó un hecho inesperado...
Muy original es el juego llamado reversi, en el cual las fichas no se toman, sino que se dan la vuelta, cambiando su color. Este juego, hacia el cual aumenta de año en año el interés, se describe en el último apartado de este capítulo.
El rendsiu representa una generalización del juego de cruces y ceros y sobre él se hablará en el capítulo siguiente. Ligeramente a un lado se encuentra el go. El número de adictos a este juego aumenta constantemente, se fabrica y se celebran competiciones de go, pero literatura sobre este juego aún hay poca. Por eso decidimos dedicarle un capítulo especial.
Otro juego de fichas es también el nard muy difundido en Transcaucasia. Por desgracia este juego queda algo fuera del género de este libro... Es que éste pertenece al tipo de juegos de probabilidades, de casualidad, pues en él tiene importancia no sólo el arte de los jugadores, sino también la suerte. Nosotros, en primer lugar, examinamos juegos determinados, en los que cada jugada se hace conscientemente y no depende de factores casuales.
Por el contrario en el nard es elemento obligatorio el lanzamiento de dados y sólo después en función del número de puntos conseguidos, se mueven las fichas a tal o cual cantidad de casillas. (Claro que después del lanzamiento de los dados queda suficiente campo para elegir, de lo contrario el juego estaría privado de carga intelectual.) Así pues, en cualquier posición la mejor jugada puede ser hecha solamente con cierta probabilidad.
En los juegos determinados teóricamente en cualquier posición existe la mejor jugada. A decir verdad, en los juegos test, examinados en el primer capítulo, mucho igualmente depende de la suerte, pero en ellos los jugadores toman decisiones unívocas basadas en la información de que disponen y todo se soluciona sin intervención de la fortuna (lanzamiento de dados).
Por esa misma causa «probabilística» hemos dejado a un lado las diferentes variantes del nard: el tryktrak, backgammon, jacquet, etc. Quedaron también fuera de nuestro campo de visión los naipes, que representan juegos de azar clásicos. Así por ejemplo, es curioso que al póquer le dedicaran gran número de trabajos matemáticos serios (en la teoría matemática de los juegos). Semejantes juegos simulan distintas situaciones prácticas, en las que tales o cuales condiciones se cumplen con determinada probabilidad y por eso son muy interesantes para las matemáticas aplicadas.
Existe otra clase de juegos que tampoco encontraron lugar en el presente libro. Estos juegos: wari, kalaj, chisolo, toguzkumalak, etc., requieren atributos especiales, tableros con hoyos o ahondamientos y conjuntos de piedras. Las jugadas consisten en tomar piedras de unos hoyos, y, siguiendo determinadas reglas, distribuirlas por los otros hoyos. Pierde el que se encuentre antes con sus hoyos vacíos.
Al lector le puede surgir una pregunta lógica: ¿no es demasiado larga la lista de juegos que no se incluyeron en este libro, teniendo motivos para estarlo?
En el libro de L. Pijanowski «Guía de los juegos», editado en Polonia, se hace mención de más de 300 juegos y 800 variantes de los mismos. La lista de libros compuesta por Pijanowski contiene 330 títulos. Y en el prólogo el autor presenta sus escusas por el hecho de que en el libro... no encontraron lugar muchos de los juegos. De esta manera el tema es totalmente inagotable y tanto más resulta imposible esperar una plenitud especial en un libro tan pequeño. Hay que tener también en cuenta que nosotros no teníamos el propósito de sorprender al lector enumerando gran cantidad de juegos, sino que queríamos describir más detalladamente sólo algunos de ellos, los más populares.
§. Ganapierde
Las reglas del juego son simples y conocidas por todos. Gana el que consiga entregar antes todas sus piezas o queda con algunas de ellas encerradas. El juego del ganapierde tiene una historia bastante rica. El primer teórico ruso del juego de damas, el maestro de ajedrez A. Petrov, ya en su tiempo se ocupaba del ganapierde y escribió que este juego requiere un cálculo mayor que el juego de damas habitual. En la actualidad este juego tiene muchos aficionados, en Moscú en 1978 fue incluso organizado un club nacional «Shashechnitsa» en el que se celebran competencias de ganapierde y se estudia la teoría. Este apartado contiene, en particular, una serie de ideas y hallazgos que pertenecen a miembros de este club.
En el «Diccionario de la lengua rusa» de V. Dal del ganapierde se dice que es un juego de damas en el que «ganador se considera al que pierde». Es una determinación precisa, subraya con acierto que la esencia del ganapierde y el juego de damas es la misma: las reglas son iguales y se puede decir que coinciden con una precisión hasta el resultado final. Pero he aquí una formulación distinta: el ganapierde es un juego habitual, con la diferencia de que los jugadores mueven las piezas del adversario.
Al ganapierde también lo llaman juego de damas al revés, por cuanto se obtiene de este juego por medio de la conversión: los conceptos de «victoria» y «derrota» se invierten. La conversión es simétrica puesto que el ganapierde invertido es el juego de damas.
Formalmente se puede invertir cualquier juego, pero en realidad pocos de ellos son convertibles. Por ejemplo, las partidas al ajedrez invertido generalmente terminarían en tablas, por cuanto para dar el mate al revés se necesita una amplia ventaja material imposible en un juego de ajedrecistas de más o menos un mismo nivel. (El ganapierde ajedrecístico examinado en el capítulo anterior es un juego singular que no puede ser considerado como ajedrez invertido. Las reglas están esencialmente modificadas: los reyes pueden ocupar casillas amenazadas y retirarse del tablero como las demás figuras.)
Por lo visto son convertibles todos los juegos deportivos: la transformación del fútbol o del hockey cambiaría muy pocas cosas (sólo cambiarían de lugar los porteros), invertir el boxeo es totalmente imposible, etc. Esta rara propiedad de conversión es propia del juego de damas gracias a la regla de captura obligatoria, sin la cual jugar al ganapierde es imposible.
La unidad entre el juego de damas y el ganapierde a veces no se percibe incluso por jugadores de categoría. Un gran maestro en el juego de damas, hábil jugador al ganapierde, propuso cierta vez a sus colegas celebrar una simultánea, prometiéndoles que ganaría exactamente la mitad de las partidas y perdería las demás. El gran maestro se proponía llevar a cabo dicho propósito incluso contra maestros que aceptaran el desafío convencidos de que entre las partidas que el retador pretende ganar ellos serán capaces de hacer aunque sea unas tablas. Sin embargo, los conocedores del juego de damas clásico no se percataron de que su adversario podía evadirse de la amenaza de tablas, pasando en dicha partida al ganapierde en el que jugar con el fin de hacer tablas no tiene sentido, aunque el desenlace pacífico a veces se da.
Algunas veces no existe diferencia entre el juego de damas rusas y el ganapierde. Tomemos, por ejemplo, los problemas «cooperativos» que en el juego de damas, a diferencia del ajedrez, casi no se componen. Es interesante la siguiente pregunta: ¿cuál es el número menor de jugadas que puede durar una partida a las damas? Por lo visto no hay ningún sentido aclarar cuál de los dos juegos se tiene en cuenta: el simple o el invertido. He aquí la partida record que consta de diez movimientos: 1.ed4 de5; 2.de3 ed6; 3.cd2 dc5; 4.ab4 c:c1; 5.ef4 c:g5; 6.fe3 g:b4; 7.ab2 e:a1; 8.ed2 b:h4; 9.gf2 h:e;1 10.hg3 e:h4. Mejorar este resultado, por lo visto, es imposible (aunque no está demostrado).
Otra situación singular puede llamarse así: «Tablas y sólo tablas». Por lo general las tablas en las damas rusas y en el ganapierde son dos cosas diferentes, por cuanto en el juego habitual se trata de «tablas por lo menos» (si las tablas están garantizadas, merece la pena pensar en la victoria). Un problema totalmente diferente se le presentó al barón Münchhausen que se vio ante la necesidad de jugar a las damas, estando prisionero, en condiciones penosas: tanto la victoria como la derrota se castigaba igual, con la pena de muerte, sólo las tablas le permitían conservar la vida y le devolvían la libertad.
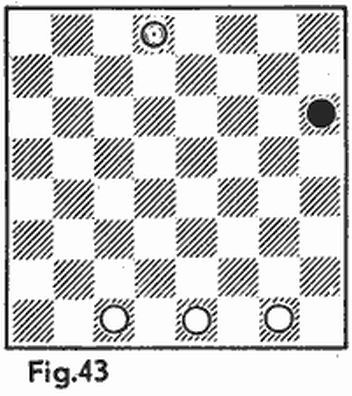
Su ingenio extraordinario tampoco le falló en esta ocasión, en la posición surgida (fig. 43) en el transcurso del combate «a muerte», el barón, que jugaba con las blancas, mostró un amor excepcional por la vida: 1.db6 hg5; 2.cd2 gf4; 3.be3 fg3; 4.gf2 gh2; 5.ef4 hg1; 6.de3 gh2; 7.f2 – g3 hg1; 8.ef2 gh2; 9.ed4 hg1; 10.f4 – e3 gh2; 11.ef4 y las negras no pueden ni perder ni ganar (algo así como un empate posicional en el ajedrez).
Entre los jugadores de damas está difundida la opinión de que el ganapierde por su contenido es inferior al juego común de damas. Sin embargo, existen no pocos argumentos en defensa del ganapierde, incluyendo argumentos de carácter cuantitativo. Para esto hay que establecer las propiedades que reflejan la riqueza de contenido expresadas numéricamente. Ante todo en una posición llena de contenido debe haber un número suficientemente grande de jugadas erróneas (si estas no existieran no habría en que pensar). De aquí el primer signo de abundancia de contenido: la relación entre el número de jugadas erróneas y el de jugadas posibles. A continuación las situaciones del juego deben presentar determinada dificultad en la valoración general realizada sin un cálculo preciso. Esta circunstancia se aprecia del siguiente modo. Supongamos que cierta posición es ganable para las blancas. Introduzcamos cambios en ella. La posición nueva será nuevamente ganable para las blancas o bien no lo será. En el segundo caso se debe, por lo visto, considerar que la posición inicial requiere un examen más atento y considerarla más llena de contenido. Es natural considerar como pequeños cambios, en primer lugar, la entrega de la jugada al contrario, en segundo lugar, el traslado de una pieza (horizontalmente) a la casilla negra más cercana. Esto da dos indicios de plenitud de contenido que se miden por el porciento de posiciones a partir de las cuales cambia el resultado entre todas las posiciones cambiadas. La entrega de la jugada al contrario presenta una posición nueva, de manera que el segundo indicio puede tomar los valores 0 o bien 1, y el tercero, la sensibilidad a los pequeños cambios de la posición, varía dentro de estos mismos límites.
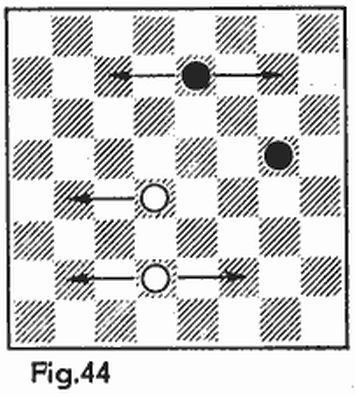
Expliquemos lo dicho en un ejemplo (fig. 44).
Jugando a las damas rusas cualquiera de las cuatro jugadas de las blancas conduce a tablas por cuanto no hay jugadas erróneas. En el ganapierde se gana sólo con 1.de5 y hay tres jugadas erróneas de cuatro. Al entregar la jugada a las negras en el juego simple se conservan las tablas, mientras que en el ganapierde las blancas ya no ganan: 1... gf4; 2.dc3 ef6; 3.dc5 fe5; 4.cd6 e:c7; 5.cd4 fg3; 6.de5 cd6; 7.e:c7 gf2; 8.cb8 fg1. Tablas. Trasladar una de las piezas horizontalmente a la casilla negra más cercana (sin destruir la discontinuidad de la posición) se puede hacer por cinco procedimientos, como lo muestran las flechas. En el juego de damas rusas ninguna de las cinco modificaciones influye sobre el resultado. En el ganapierde en dos de los casos las blancas consiguen solamente tablas. Así pues, los valores de los indicios de plenitud de contenido de esta posición en las damas rusas es de 0, 0, 0, y en el ganapierde, 3/4, 1, 2/5. De por sí estas cifras no dicen nada, pues la unicidad de la jugada puede ser evidente igual que la variación de la situación después de un cambio ligero de la posición. Con todo eso la veracidad de este enfoque es más verosímil.

Claro que el procedimiento expuesto de valoración sólo se puede aplicar a varias posiciones a la vez. Esto precisamente fue hecho para varios cientos de posiciones elegidas arbitrariamente con un número pequeño de piezas simples. Los resultados de la valoración de los diferentes tipos de posiciones mostraron una buena estabilidad: por los indicios primero y tercero el ganapierde supera en algo al juego de damas rusas y por el segundo lo supera dos veces. Esto, realmente, no es la demostración, sino un argumento serio a favor del ganapierde, especialmente en las composiciones en las que se valoran los problemas conjugadas únicas. Aquí son posibles, en particular, posiciones de género especial, de las cuales escribe el conocido matemático polaco G. Steingaus en su «Caleidoscopio matemático». En el apartado dedicado a las matemáticas ajedrecísticas el autor propone hallar la posición en la que todas las jugadas, por ambas partes, fueran únicas y no conducentes a la derrota. Parece que tanto en el ajedrez como en las damas rusas no existen tales posiciones. A su vez en el ganapierde éstas son muchas. He aquí una posición record en duración, hallada por M. Debetz (fig. 45). Juegan las blancas. 1.c:a5 de3; 2.d:f4 g:e3; 3.ab2 ed2; 4.e:c3 hg5; 5.ab6 a:c5; 6.gf2 cb4; 7.c:a5 gh4; 8.ba3 de5; 9.ab6 ef4; 10.fg3 h:f2; 11.bc7 fg1; 12.cd8 gd4; 13.db6 d:a7; 14.ab4 ac5; 15.b:d6 fe3; 16.dc7 ef2; 17.db8 fg1. Tablas.
¿Cuál es la técnica de juego al ganapierde? Muchos de los principios y procedimientos se basan en las consideraciones generales y coinciden con las recomendaciones en las damas rusas y no sólo en este juego. Conviene dominar el centro, por cuanto en los extremos del tablero las piezas tienen menos movilidad.
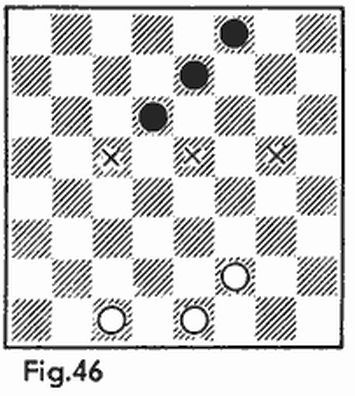
Es esencial la acción conjunta de los flancos. Hay que preocuparse del desarrollo del resto de las piezas (de a1 y h2 para las blancas). Son elementos importantes las restricciones y las amenazas. En la posición que muestra la figura 46 después de la jugada 1. fe3, si aunque sea en una de las casillas marcadas con una cruz aparece una pieza negra, las blancas inmediatamente terminan el juego a su favor.
En opinión del matemático N. Bronshtein, que reflexionó bastante sobre el ganapierde, esta idea de restricción de las piezas del contrario se formaliza fácilmente y puede ser utilizada al preparar programas de máquina para ordenadores. En nuestro ejemplo después de 1... ef6; 2.cd2 fg7; 3.ef2 gh6; 4.fg3 y las blancas ganan. En tres movimientos las blancas restringen a las piezas negras y ahora hay que ir a una de las casillas indicadas (4... fg5; 5.ef4 g:c1; 6.gf4 c:g5; 4... de5; 5.ed4 e:h4).

Ahora mostremos un ejemplo de amenaza (fig. 47). 1.hg3 ¡jaque! La utilización de un término ajedrecístico aquí es muy oportuno. Realmente, la amenaza de entregar inmediatamente todas las piezas es análoga a la amenaza de «comer» al rey. 1... ab2; 2.a:c3 gf6; 3.cd4 + (jaque) fg5 (3… cd6; 4.dc5 d:b4; 5.gf4 + fg5; 6.f:h6, etc.) 4.ef4 g:c5; 5.gf4 cb4; 6.fe5 + cb6; 7.ed6 + bc5; 8.dc7 y la dama blanca que aparece sobre el tablero rápidamente se sitúa en una casilla amenazada.
El juego en la posición que muestra la figura 46 recuerda una emboscada y la que muestra la figura 47, una persecución. Por así decirlo, los métodos del perro y el gato. En una partida real, a propósito, no siempre se logra diferenciar estos dos procedimientos. Subrayemos que en el ganapierde, igual que en las damas rusas (pero a diferencia del ajedrez), la restricción desempeña el papel principal y la amenaza, el secundario.
La superioridad material en el juego invertido, por paradójico que parezca, hasta cierto momento conviene. En el juego de damas habitual la superioridad numérica, por lo visto, aproxima al jugador hacia su objetivo final. ¿Por qué entonces esto es útil también en el ganapierde? He aquí la explicación. Cuanto mayor es el número de piezas, tanto más amplia es la elección de jugadas y tanto mayor es la probabilidad de que entre estas jugadas se encuentren las que aseguren la victoria. En las damas rusas los factores numéricos y de movilidad actúan en una misma dirección, mientras que en el ganapierde, en diferentes, pero el papel de la movilidad sigue siendo el mismo. La adición de las causas, puede decirse, se sustituye por la resta, pero el factor de movilidad es más importante. La esencia de la paradoja consiste, precisamente, en este hecho inesperado establecido por la práctica de juego. A decir verdad, del hecho de que la superioridad numérica es conveniente no se deduce que una mayor superioridad da mayores ventajas.
Jugar a las damas rusas sin una pieza es igual que al ajedrez sin una figura. Esta consideración intuitiva se verifica con el siguiente cálculo. La suma de la fuerza ajedrecística es: 9 (la dama) + 2 × 4,5 (las torres) + 2 × 3,5 (los alfiles) + 2 × 3 (los caballos) + 3 (el rey) +8 × 1 (los peones) = 42; y la doceava parte de esta suma representa 3,5 unidades, es decir, la fuerza de un alfil. Pero una de las 12 piezas del juego de damas también representa una doceava parte. En lo que se refiere al ganapierde, es dificilísimo determinar a favor de quién será la retirada del tablero de una pieza.
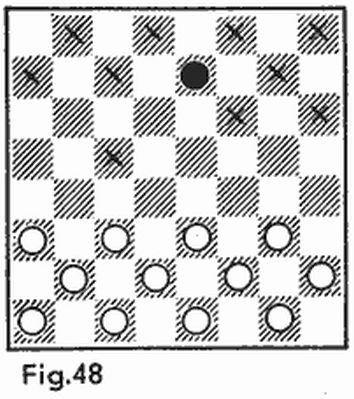
Un ejemplo interesante de conveniencia de la superioridad numérica es el juego con las 12 piezas contra una sola pieza del contrario. Las blancas ganan al ganapierde si la pieza única del contrario ocupa una de las casillas marcadas con una cruz en la figura 48. Para ganar se precisa no más de 18 jugadas. La posición record es la que se da cuando una pieza negra se encuentra en e7. He aquí la variante principal: 1.cb! ed6; 2.ba5 de5; 3.ef4 ed4; 4.fe5 d:f6; 5.de3 fe5; 6.ef4 ed4; 7.fe3 d:h4; 8.ab4 hg3; 9.bc5 g:e5; 10.cd6 e:c7; 11.ab6 c:a5; 12.cd2 ab4; 13.bc3 ba3; 14.hg3 ab2; 15.gf2 b:d4; 16.fe3 d:h4; 17.ab2 hg3; 18. ef2 g:a1.

La figura 49 muestra en qué casos se resuelven problemas análogos al de ganar al ganapierde sobre un tablero de 100 casillas, jugando 20 piezas blancas contra una negra. Es curioso que la correspondiente demostración fue publicada por la Academia de Ciencias de Bélgica ya en 1852, además su autor examinó más de 800 variantes.
Jugando correctamente al ganapierde, tarde o temprano llega el momento crítico cuando hay que entregar el material ganado. No obstante, entregar las piezas por el mero hecho de que queden menos es irracional en cualquier etapa del juego; en todo momento hay que preparar las condiciones para deshacerse de todas las piezas a la vez. Si la conveniencia de entregar el material no se logra demostrar analíticamente, entonces esto es un sacrificio. Por ejemplo, después de 1.ed4 bc5; 2.d:b6 c:a5; 3.cb4 a:c3; 4.b:d4 ab6; 5.fe3 ba5 (fig. 50) las blancas con frecuencia sacrifican una pieza: 6.ab4 a:e5; 7.dc3 ed4; 8.c:c7. A las negras les toca resolver problemas complicados de desarrollo.
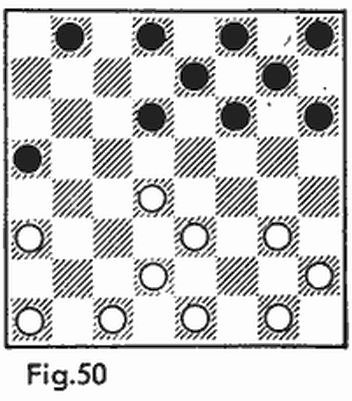
Otro importante procedimiento de juego consiste en encerrar las piezas del contrario. En el momento preciso éstas se dejan en libertad y la partida termina con la victoria del que supo encerrarlas a tiempo.
Un ejemplo de que el ganapierde no es un juego estrictamente de cálculo (muchos piensan precisamente así) es la partida entre Boldin y Bronshtein. 1.gh4 hg5; 2.ef4 g:e3; 3.f:d4 bc5; 4.d:b6 c:a5 (una apertura muy difundida); 5.gf2 fe5 (escapando del encierre en h4); 6.cb4 a:c3; 7.b:f6 g:e5; 8.dc3 (fijando la pieza débil en e5); 8... bc7 (correcta es la jugada 8... ed4, aquí las negras se ven obligadas a hacer jugadas forzadas); 9.ab2 hg7; 10.ab4 ab6; 11.cd2 ef6; 12.hg5 f:h4; 13.cd4 e:a5; 14.hg3 ab4; 15.dc3 b:d2; 16.e:c3 gf6; 17.cb4 y las blancas una tras otra entregan todas sus piezas.

En el ganapierde las tablas son muy raras. Las damas de distinto color en las casillas b8 y g1 es un empate frecuente. La posición de tablas con un número record de piezas se dio en la partida entre Larin y Rodzianko (fig. 51); jugando las blancas, los únicos desplazamientos con los que no se pierde son: 1. cd6 bc5 2. dc7 cb6, etc.
En el juego de damas habitual, en una posición ganada, lo más probable es que entre las jugadas erróneas se hallen también las que conducen a tablas. En el ganapierde el error, por lo general, conduce a la derrota, es decir, la franja de tablas entre las zonas de victorias y de derrotas puede no existir.
Por esta razón no se puede evitar el riesgo, apartándose de las posiciones complicadas y agudas, es decir, en las posiciones a primera vista simples y tranquilas el riesgo no es menor. A propósito, la ausencia de una franja de tablas crea dificultades al comentarista de las partidas. La apreciación estándar «con ventaja para...» significa que la ventaja puede no ser suficiente para alcanzar la victoria, de lo contrario habría que decir «con la victoria para...». En el ganapierde la imposibilidad de ganar con frecuencia corre el peligro de la derrota, en tales casos hablar de ventajas seguramente no es oportuno. Consideraciones análogas surgen también respecto a la valoración «con un juego aproximadamente igual». Así es que de la «muerte por empate» el ganapierde, por lo visto, está sólidamente asegurado.
La teoría de las aperturas del juego invertido se desarrolla paulatinamente, nos limitaremos a una breve información. De las siete posibles jugadas iniciales con más frecuencia se juega 1. ed4 y 1. gh4, les sigue 1. ab4. Puede considerarse demostrado que las aperturas 1. ef4 y 1. gf4 conducen, después de la respuesta 1... hg5, a la derrota forzada de las blancas. Las jugadas 1.cb4 y 1.cd4 son posibles, pero la estadística de encuentros entre jugadores de categoría muestra que el juego con más frecuencia se inclina a favor de las negras.
Al ganapierde sobre un tablero de cien casillas se juega, naturalmente, siguiendo las reglas del juego de damas internacional. Las diferencias que surgen al pasar al tablero grande en este caso son más importantes que en el simple juego de damas, pero este ya es otro tema…:
¿Por qué razón el ganapierde es inferior en popularidad al juego de damas habitual! Por lo visto la causa reside en la percepción tradicional del juego de damas como modelo de las acciones militares. El deseo de destruir o coger prisioneras a las fuerzas enemigas es característico para la mayoría de los juegos, incluyendo el de damas, y es más atractivo por su vitalidad. Por otra parte, releyendo los «Ensayos» de M. Montaigne, encontramos un episodio histórico que puede considerarse como una analogía real del juego invertido...
«Alejandro tenia sitiada cierta ciudad en la India. Sus habitantes llevados al extremo, con firmeza decidieron privarle de la alegría por la victoria; quemaron la ciudad y junto con ella perecieron devorados por las llamas, expresando así su desprecio hacia la generosidad del vencedor. Comenzó una nueva batalla: el enemigo luchaba por salvarles la vida y los habitantes de la ciudad, por la posibilidad de dar fin a sus vidas, además para ello se esforzaban igual que las personas cuando tratan de salvar sus vidas».
§. Esquinas chinas
Empecemos por la variante clásica de las esquinas chinas conocidas por todos. En dos ángulos opuestos de un tablero de 8 × 8 se colocan diez piezas blancas en uno y diez piezas negras en el otro (fig. 52).

Los jugadores hacen sus jugadas turnándose, además las jugadas pueden ser de dos tipos: 1) desplazamiento de la pieza a la casilla libre adyacente vertical u horizontalmente (¡pero no por la diagonal!); 2) saltos sucesivos con una de las piezas por encima de propias o contrarias por las casillas libres, por las verticales y las horizontales del tablero (cada salto en el curso de estas jugadas puede realizarse sólo por encima de una pieza, «aterrizando» en la casilla inmediata a la recién saltada).
Gana el que consiga antes ocupar con sus piezas las casillas que ocupaba inicialmente el contrario en la esquina opuesta. A propósito, si las blancas ya ocuparon la esquina del contrario, esto aún no es «mate».

Si en la jugada siguiente las negras también ocupan el ángulo contrario, la partida se reconoce empatada (los jugadores hicieron igual número de jugadas).
Examinemos la posición que muestra la figura 53. La pieza b5 puede mover a la casilla a5, ésta es una jugada del primer tipo; puede desplazarse a las casillas b7, d5, d7, f5, f7, h5 y h7, éstas son jugadas del segundo tipo. Observemos que una misma jugada puede, a veces, realizarse de diferente manera, en nuestro ejemplo la pieza b5 puede llegar a la casilla h7 por dos trayectorias: b5-b7-d7-f7-h7 o bien b5-d5-f5-h5-h7.
Si uno de los jugadores no mueve de su posición inicial una o varias piezas, entonces, por lo visto, el contrario nunca podrá alcanzar su objetivo y la partida pierde su sentido. Por esta razón en el juego de las esquinas chinas se introduce una regla según la cual ambos jugadores deben dejar libre su ángulo antes de hacer, por ejemplo, 40 jugadas.
Da la impresión de que después de introducir esta última regla el juego se hizo más divertido. Sin embargo, esto no es del todo así. Como veremos más adelante, las negras, sin esfuerzo alguno, pueden conseguir el empate y por tanto el juego pierde notoriamente su interés deportivo.
En realidad esto ocurrió así. Un colega del autor de este libro, el matemático D. Poliak durante largo tiempo observó cómo su hija quinceañera «jugaba apasionadamente» con sus amigas a las esquinas chinas. Por fin, este pasatiempo ocioso empezó a disgustarle (mejor sería que jugaran al ajedrez –pensó él). Precisamente entonces ideó el algoritmo del empate para las negras. Hay que decir que las chicas estaban algo desilusionadas, pero dejaron de jugar a las esquinas chinas y se ocuparon de cosas más intelectuales.
Ahora nuevamente nos ocuparemos de las ideas de la simetría, a la cual se dedicó mucha atención en el capítulo anterior. El algoritmo del juego para las negras es simple: a cada jugada de las blancas, para las negras es suficiente responder con una jugada simétrica respecto al centro del tablero, el punto 0 en la figura 52.
Utilicemos, para mayor comodidad, un sistema numérico de coordenadas: la casilla (i,j) se encuentra en el cruce de la vertical i con la horizontal j. Por lo visto la casilla simétrica respecto a (i,j) es la (9 – i,9 – j). Por lo tanto si las blancas juegan su pieza de la casilla (i, j) a la casilla (k, l), las negras deberán responder con la jugada de (9 – i,9 – j) a (9 – k,9 – l). Por ejemplo, en la figura 53 en respuesta a la jugada de las blancas b6-d6 las negras juegan g3-e3.
En la estrategia descrita de las negras, después de cada una de sus jugadas, la disposición simétrica de las piezas sobre el tablero respecto al centro se mantiene y en el momento en que las blancas ocupen con sus piezas la esquina contraria del tablero, las negras con su jugada de respuesta igualmente ocuparán la esquina y la partida terminará en tablas.
Se sobreentiende que aún hay que demostrar que a cualquier jugada de las blancas es posible la respuesta simétrica de las negras. Examinemos una posición simétrica, en la que a cada pieza blanca le corresponde una pieza simétrica negra y al revés. De aquí se deduce que cada casilla sin ocupar tiene simétricamente otra casilla vacía.
Por lo visto, en el caso de simetría respecto al centro, a la vertical (horizontal) con el número i le corresponde la vertical (horizontal) con el número 9 – i, y las casillas vecinas por la vertical (horizontal) pasan a las casillas igualmente vecinas por la vertical (horizontal).
Supongamos que en su turno de juego la pieza blanca se movió a la casilla vacía de al lado. Simétricamente respecto a esta casilla hay una vacía vecina con la pieza negra que era simétrica a la blanca antes de que ésta jugara. Por esto en su próxima jugada la pieza negra puede ocupar igualmente dicha casilla vacía.
Supongamos que ahora la pieza blanca hace una jugada de salto. Llamemos las casillas ocupadas, por encima de las cuales se salta, casillas de apoyo. Examinemos la posición sobre el tablero anterior a esta jugada de la pieza blanca. La pieza negra, simétrica a la blanca, en este momento podía desplazarse por una trayectoria simétrica, por cuanto a las casillas de apoyo les corresponden las de apoyo, a las libres, las libres y la «vecindad» entre ellas se mantiene. Demostremos que esta jugada de las negras es posible igualmente después de la jugada de las blancas. La jugada de la pieza blanca podría molestar a la jugada simétrica de las negras en uno de estos dos casos: 1) después de su jugada, la pieza blanca ocupó una casilla en la trayectoria de la pieza negra; 2) antes de su jugada la pieza blanca era de apoyo en la trayectoria de la pieza negra. Mostremos que estos dos casos son imposibles.
Supongamos que la pieza blanca tiene las coordenadas (i,j), entonces las coordenadas de la pieza negra simétrica son (9 – i,9 – j). A cada salto de la pieza por encima de la casilla de apoyo, la paridad de sus coordenadas se conserva, es decir, las coordenadas de todas las casillas libres de la trayectoria tienen la misma paridad que las coordenadas de la casilla inicial. Pero si el número i es par, el número 9 – i es impar y viceversa. Por esto la pieza blanca después de su jugada no puede llegar a la casilla libre de la trayectoria de las negras. En adelante una de las coordenadas de la casilla de apoyo coincide con la coordenada de la casilla libre junto a la trayectoria y, por consiguiente, tiene la misma paridad que la correspondiente coordenada de la casilla inicial. Pero los números de cada par (i,9 – i) y (j,9 – j) tienen distinta paridad y por esta razón la casilla (i,j) no puede ser de apoyo para la pieza (9 – i,9 – j);
Así pues, los dos casos están refutados y después de la jugada de las blancas, la jugada simétrica de las negras es posible. Por cuanto la posición inicial es simétrica respecto al centro y se mantiene igual después de cada respuesta de las negras, su estrategia de empate triunfa.
Es curioso que la «teoría» de las esquinas chinas examinada por nosotros resulta incorrecta, si permitimos los saltos diagonales de las piezas. En este caso la pieza blanca, antes de su jugada, podía ser de apoyo sobre la trayectoria de la pieza simétrica negra. Así, por ejemplo, en la figura 53, después de la jugada de las blancas d4-f6, las negras no están en condiciones de copiar la jugada del adversario.
Nosotros suponíamos hasta ahora que el juego se desarrolla sobre un tablero habitual de 8 × 8. Estos mismos razonamientos son verídicos también para cualquier tablero con lados pares y para una posición inicial arbitraria simétrica respecto al centro (en particular las piezas se pueden situar en la esquina del tablero en forma de cuadrados de 3 × 3). No obstante el método de juego que garantiza a las negras el empate ya no es válido para un tablero que tenga aunque sea uno de sus lados impar.
Así pues, las negras, jugando a las esquinas chinas, fácilmente hacen tablas. Pero, cuan extraño no parezca, es difícil demostrar que en este juego «aburrido» las blancas también tienen garantizadas las tablas. Pensamos que este problema no es de los fáciles. De esta manera en la variante más simple de las esquinas, con una pieza blanca en la casilla a1 y otra negra en la h8, las blancas sólo tienen dos formas de hacer tablas: su pieza debe desplazarse por la primera horizontal desde a1 hasta h1 y seguidamente por la vertical desde hl hasta h8 o bien primero por la vertical desde al hasta a8 y luego por la horizontal desde a8 hasta h8. En ambos casos el juego termina en tablas en el movimiento 14 y toda desviación de la pieza blanca del borde del tablero, como es fácil notar, conduce a la pérdida del juego.
Aún cuando hemos criticado el juego de las esquinas chinas, nosotros mismos hemos indicado que sobre tableros de dimensiones determinadas es posible un verdadero combate y el algoritmo del empate, y con más razón, el de la victoria se desconocen. A propósito, en el mercado se venden distintos juegos («a las cuatro esquinas», «labirinto», «a sus lugares») que se parecen al de las esquinas chinas. Estos juegos se practican sobre tableros no habituales, las reglas que rigen los movimientos de las piezas son diferentes, pero la finalidad en todos ellos es la misma: ocupar con sus piezas el territorio del contrario y el que lo consiga antes, gana.
La particularidad esencial de los juegos del tipo de las esquinas consiste en que las piezas blancas y las negras se cambian de lugar. Por esta razón estos juegos pueden llamarse juegos de conmutación. Se conocen muchos juegos y distracciones de conmutación, el más famoso de los cuales es el «juego del 15» o «taken» inventado por Sam Loyd. Este no es exactamente un juego, sino un rompecabezas (aquí no hay adversario) y no tiene relación directa con el tema de nuestro libro, pero es demasiado famoso como para no dedicarle aunque sea unas líneas.
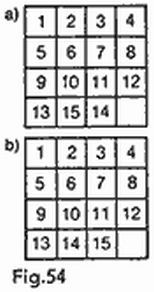
Dentro de una cajita de 4 × 4 hay quince fichas numeradas desde el 1 hasta el 15 (una de las posibles disposiciones de las fichas se puede ver en la figura 54a). Se precisa, sin extraer ninguna ficha, ir desplazándolas hasta conseguir su posición normal (fig. 54b).
Loyd asignó un premio monetario grande al que solucionase el rompecabezas, cuya posición inicial muestra la figura 54a). Claro que él no arriesgaba nada, ya que de antemano había demostrado que esta tarea es irrealizable. Existen en total 16! distintas disposiciones de las fichas y todas ellas se dividen en dos clases de igual cantidad. Las disposiciones de una de las clases se transforma por medio de desplazamientos en la disposición inicial (véase la fig. 54b), y las disposiciones de la segunda clase se consiguen transformar solamente en la posición indicada en la figura 54a, es decir, con las fichas 14 y 15 invertidas.
¿Cómo averiguar la pertenencia de una posición determinada a cada una de las clases? Para averiguarlo hay que calcular el número de conmutaciones en dicha posición. Dicen que dos fichas forman una conmutación, si la ficha con el número mayor está delante de la ficha cuyo número es menor. Si el número de conmutaciones es par, la posición pertenece a la primera clase (en la fig. 54b dicho número es igual a cero), y si, por el contrario, es impar, entonces pertenece a la segunda clase (en la fig. 54a hay una sola conmutación).
Semejante análisis del juego se puede hallar en muchos libros dedicados a las matemáticas recreativas.
Mostremos otro rompecabezas antiguo, en el cual se cambian de lugar figuras de colores diferentes. Para ello volvamos nuevamente al ajedrez.
En las esquinas de un tablero de ajedrez de 3 × 3 se encuentran dos caballos blancos y dos caballos negros (fig. 55a). Es preciso cambiar de lugar los caballos blancos con los negros en un número mínimo de movimientos.
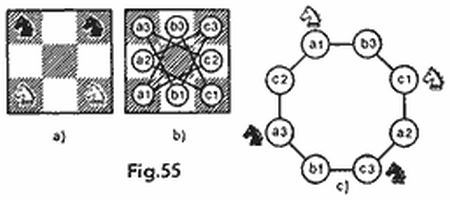
Los aficionados a las matemáticas recreativas conocen bien este problema inventado por el italiano Guarini en el siglo XVI. Se resuelve elegantemente por el «método de botones e hilos» que propuso el famoso maestro en rompecabezas, el inglés H. Dudeney.
En cada casilla de nuestro pequeño tablero, a excepción de la central (a esta casilla no pueden saltar ninguno de los caballos) colocamos un botón (en la fig. 55b están sustituidos por pequeños círculos). Si entre dos casillas es posible el movimiento del caballo, los botones ubicados en ellas se unen con un hilo (en la figura los hilos están representados por líneas que unen los dos círculos). Desenredemos el ovillo de botones e hilos obtenido de tal manera que todos los botones se dispongan en círculo (fig. 55c).
A partir de aquí el problema se resuelve casi automáticamente. Se elige en la circunferencia una de las direcciones y se desplazan por ella los caballos hasta que éstos se cambien de lugar. El desplazamiento de los caballos por el tablero se consigue sustituyendo los botones por las respectivas casillas. No cuesta trabajo convencerse de que la solución consta de 16 saltos de los caballos (ocho de los caballos blancos y ocho de los negros), con la particularidad de que los caballos de diferente color pueden moverse turnándose. Si planteamos condiciones adicionales, de que los caballos de diferente color no se amenacen entre sí (en este caso la secuencia de los movimientos puede ser alterada), entonces la solución se obtiene también desenredando el ovillo. Sólo es preciso observar que en el ovillo los caballos de diferente color no se encuentren uno al lado del otro. Si los movimientos por el círculo (en dirección de las agujas del reloj) lo inicia el caballo blanco en al, la solución será la siguiente: Ca1-b3, Ca3-c2, Cc3-b1-a3, Cc1-a2-c3, Cb3-c1-a2, Cc2-a1-b3, Ca3-c2-a1, Cc3-b1-a3, Ca2-c3, Cb3-c1.
El método de los botones e hilos se interpreta fácilmente en los mismos términos que la teoría de los grafos. Realmente, a nuestro problema de conmutación de los caballos se le puede comparar con el grafo, cuyos vértices corresponden a las casillas del tablero (a los botones) y las aristas, a los movimientos posibles (a los hilos). En este caso el desenrollado del ovillo de botones e hilos, en esencia, significa solamente una disposición más evidente del grafo construido. Es de suponer que el método de botones e hilos puede ser utilizado no sólo para resolver el problema de Guarini, sino también toda una clase de juegos, problemas y rompecabezas de conmutación (no obligatoriamente ajedrecísticos).
Los rompecabezas de conmutación surgen también en el juego de las esquinas clásico por el cual empezamos este apartado. He aquí varios problemas inventados por F. Barténiev.
Utilizando un número mínimo de movimientos y guiándose por las reglas del juego de las esquinas chinas conmutar cuatro piezas desde la esquina inferior izquierda del tablero, las casillas a1, a2, b1, b2, a la esquina superior derecha.
La solución consta de 13 movimientos: 1.a2-c2; 2.a1-c1-c3; 3.b1-b3-d3; 4.b2-d2-d4; 5.c2-c4-e4; 6.c3-e3-e5; 7.d3-d5-f5; 8.d4-f4-f6; 9.e4-e6-g6; 10.e5-g5-g7; 11.f5-f7-h7; 12.f6-h6-h8; 13.g6-g8.
Cuatro piezas dispuestas en el centro (en las casillas d4, e4, d5 y e5) pueden desplazarse hacia las cuatro esquinas del tablero en 22 movimientos. Tres piezas en 19 movimientos pueden trasladarse desde las casillas a1, b1 y el hasta las casillas f6, g6 y h6 y en 20 movimientos desde las casillas al, a2 y b1 hasta las casillas g8, h7 y h8.
En el juego habitual de las esquinas chinas las piezas se mueven vertical y horizontalmente por un tablero de 8 × 8, pasando ora por una casilla blanca, ora por una casilla negra. No obstante, se puede también jugar a las esquinas chinas, siguiendo las reglas normales del juego de damas, es decir, en la posición inicial del juego, como siempre, se colocan las piezas de ambos colores sobre las casillas negras de las 3 horizontales extremas (12 fichas en cada lado), pero se mueven en diagonal a la casilla adyacente o saltan por encima de piezas propias y contrarias. Nuevamente se anuncia vencedor al que, con sus piezas, ocupe antes el territorio del contrario.
Este juego representa una de las variantes del «halma» en el que se utilizan los más diversos tableros. Por cuanto en la presente variante de juego las piezas se mueven en diagonal, el algoritmo del empate no funciona aunque la posición inicial de sus piezas es simétrica respecto al centro.
Otro juego, mezcla del juego de damas con el ganapierde, se conoce con el nombre «salta». Este juego se considera inventado por uno de los participantes del torneo internacional de ajedrez, celebrado en Montecarlo en 1900. A decir verdad, este juego se practica sobre un tablero de 10 × 10, con la particularidad de que sus piezas (15 por bando; al comienzo del juego se colocan en las tres horizontales extremas del tablero) tienen símbolos distintivos que representan una estrella, la luna y el sol. El juego tal vez sea demasiado artificial y por ello no lo describiremos al detalle.
Para concluir este apartado presentaremos un «ejercicio» para el halma sobre un tablero de 8 × 8. Es preciso conmutar lo antes posible 12 piezas blancas de su territorio al territorio vacío del contrario.
El objetivo se consigue en 20 movimientos: 1.a3-b4; 2.c1-a3-c5; 3.b2-d4-b6; 4.a1-b2; 5. b2-d4 6.c3-a5-c7; 7.b4-d6-b8; 8.e1-c3-e5; 9.d2-f4-d6; 10.h2-f4; 11.c5-a7; 12.e3-c5-e7; 13.d4-f6-d8; 14.g1-e3-g5; 15.f2-h4-f6; 16.e5-g7; 17.g7-h8; 18.g3-e5-g7; 19.f4-h6-f8; 20.g5-h6.
Reducir esta solución, por lo visto, es imposible, aún cuando tampoco es fácil demostrarlo. Únicamente se conoce la simple demostración de que el problema no puede resolverse en menos de 16 movimientos. ¡Expongamos esta demostración! En la posición inicial ocho piezas ocupan horizontales impares, la primera y la tercera, y cuatro piezas ocupan la segunda horizontal. En la posición final ocho piezas ocupan dos horizontales pares, la sexta y la octava, y cuatro, una impar, la séptima. Así pues, cuatro piezas cambiaron la paridad de sus horizontales. Para llegar a su destino, cada una de estas piezas debe, aunque sea una sola vez, pasar a la casilla de al lado (para cambiar la paridad) y, aunque sea una sola vez, saltar por encima de otras piezas (para penetrar en el campamento ajeno). Las otras ocho piezas hacen, aunque sea, por un movimiento. En total 4 × 2 + 8 × 1 = 16.
§. Reversi
El juego reversi (del inglés to reverse, transformar) últimamente adquirió gran popularidad. En EE.UU. pasó a un segundo lugar después del ajedrez, en el Japón, al segundo lugar después del go. Se celebran muchos torneos, campeonatos, incluso con la participación de ordenadores. El juego atrae por la simplicidad de sus reglas, son más simples que en el ajedrez y en el juego de damas, y un admirable dinamismo. La situación sobre el tablero cambia instantáneamente y todo lo alcanzado por uno de los jugadores puede pasar en una sola jugada al contrario.
El reversi se conoce desde los tiempos remotos y hace 15 años fue descubierto nuevamente por el japonés Hasedjawa. Las trampas pérfidas y las situaciones inesperadas que distinguen este juego le infundieron asociaciones con el Othelo de Shakespeare y como resultado le fue cambiado el nombre por el de «Othelo». El tablero de este juego está forrado con paño azul (como en el billar) y para las fichas hay unos ahondamientos especiales que se cubren con tapaderas de plástico. Así que es un placer jugar...
Los atributos de este juego son un tablero de 8 × 8 y 64 fichas (32 para cada jugador) por un lado blancas, por el otro, negras. Se puede tomar un tablero normal de ajedrez, pero el color de las casillas no tiene importancia. Si usted todavía no adquirió este juego, las fichas se pueden hacer de la siguiente manera: pegar entre sí dos piezas de distinto color del juego de damas o pintar de dos colores 64 botones iguales. Por lo visto en el juego se utilizan fichas no reales, sino algo así como fichas-camaleones que cambian de color.
El que juega con las blancas pone una ficha con el color blanco hacia arriba y el que juega con las negras pone su ficha con el color negro hacia arriba. Al empezar, ambos jugadores ponen en el centro del tablero por dos fichas como se puede ver en la figura 56.
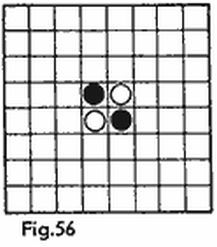
A diferencia del ajedrez y del juego de damas, en éste empiezan las negras. Los adversarios, por turno, ponen las fichas en las casillas libres del tablero obligatoriamente junto a fichas del color contrario, de manera que, junto con otras fichas de su propio color, se pueda rodear una o varias fichas del contrario horizontal, vertical o diagonalmente. En otras palabras, la ficha se coloca en una línea con otra ficha del mismo color que ya se encuentra sobre el tablero, con la particularidad de que entre ellas debe encontrarse una o varias fichas del contrario y no deben haber casillas libres. Las fichas rodeadas caen prisioneras, pero no se retiran del tablero, sino se dan la vuelta, como cambiando de «dueño». Si el cerco se produce simultáneamente por varias líneas, se dan la vuelta todas las cadenas de fichas capturadas. De esta manera las fichas que se pusieron sobre el tablero ya no se retiran de él, pero se pueden dar vuelta todas las veces que sea necesario.

Como ilustración examinemos la posición simétrica de la figura 57. Juegan las negras y, poniendo su ficha en la casilla de la esquina al, rodean de una vez 18 fichas blancas en tres direcciones posibles. Las fichas de la vertical «a» desde a2 hasta a7 están rodeadas de fichas negras al y a8; las fichas de la primera horizontal desde b1 hasta g1, por las fichas a1 y h1, y finalmente por la diagonal grande las fichas desde b2 hasta g7; las blancas están rodeadas por las fichas a1 y h8. Este ejemplo es el récord: la mayor cantidad de fichas que pueden ser capturadas y volteadas en una jugada es de 18.
Si usted no puede hacer una jugada, siguiendo las reglas (no está en condiciones de rodear ninguna de las fichas del contrario), entonces deja pasar una jugada. Si en este momento el contrario ya utilizó todas sus fichas, a él se le permite tomar una de vuestras fichas. Por otra parte, en el juego reversi cada una de las partes tiene por dos fichas adicionales y esto resulta suficiente para arreglárselas.
El juego continúa mientras no se rellenen las 64 casillas del tablero, o hasta que uno de los jugadores no pueda hacer más movimientos siguiendo las reglas. Al término de la partida se hace el recuento de las fichas blancas y negras. Gana el que disponga de mayor número de fichas sobre el tablero. Por lo visto la partida dura no más de 60 jugadas.
Volviendo a la figura 57, podemos observar que la jugada de las negras a la casilla al fue la última de la partida puesto que todo el tablero se llenó de fichas. Habiendo dado la vuelta a 18 fichas, las negras se salvaron por milagro y el juego terminó en tablas 32:32
Hagamos, como ejemplo, cinco jugadas. Por cuanto comienzan las negras, los números impares corresponden a sus jugadas y los pares a las de las blancas (a diferencia de otros juegos cada jugada de las blancas y de las negras tienen su numeración aparte; examinando la partida al final de esta narración nos convenceremos de la comodidad de esta forma de numeración).
1.c4 (la ficha d4 está rodeada por las negras c4 y e4 y por tanto se da la vuelta y de blanca se convierte en negra); 2.c3 (la ficha d4 cambia de color); 3.d3 (la ficha d4 nuevamente se vuelve negra); 4.e3 (ahora están rodeadas las fichas d3 y e4, ambas se dan la vuelta y cambian de color); 5.f3 (la ficha e4 se torna negra); 6.c5 (c4 y d4 son blancas); 7.b3 (la ficha c4 ha sido rodeada mediante d5, y la fila c3, d3, e3, por medio de la jugada f3; todas las fichas se dan la vuelta y se convierten en negras); 8.d6 (d5 es blanca); 9.d7 (d4, d5 y d6 son negras); 10.f2 (d4 y e3 son blancas). Surgió la posición de la figura 58. La iniciativa pertenece a las negras por tener más fichas.
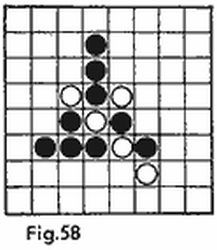
Mas es temprano alegrarse. La situación en el reversi cambia como en un caleidoscopio, las fichas, en cualquier momento, «cambian de color» y lo importante es de qué color serán al final del juego.
Jugando al reversi usted puede ponerle una trampa, suponiendo que a las pocas jugadas podrán capturar muchas fichas del contrario, pero, después de alcanzar la posición prefijada, descubre que usted mismo cayó en ella. Esta dinámica singular del juego, como ya hemos mencionado, lo hace excepcionalmente atractivo. Así, por ejemplo, a diferencia del ajedrez, donde en el final del juego la ventaja material, por lo general, decide el resultado final del juego, en el reversi el jugador que posee mayor número de fichas puede de súbito quedarse a dos velas.
Se comprende que si en cierto momento uno de los jugadores se queda sin fichas, pierde la partida.
M. Gardner presenta partidas que termina después de la cuarta jugada de las negras («mate del estudiante» del reversi), mas cuando la disposición inicial es otra, las blancas: d5 y e5; las negras: d4 y e4. He aquí una partida récord: 1.e6; 2.f5; 3.g4; 4.d3; 5.c4; 6.e3; 7.e2 y sobre el tablero quedan solamente fichas negras. La partida más corta que comienza en una posición estándar, por lo visto dura 2 jugadas más: 1.c4; 2.c5; 3.e6; 4.e3; 5.e2; 6.d6; 7.c6; 8.f4; 9.g4! Las negras ganan 13:0.
La teoría del reversi aún está poco desarrollada, no obstante algunos principios importantes los jugadores los descubren para sí con bastante rapidez. Por lo visto capturar la ficha del contrario ubicada en el centro del tablero es más fácil que la que se encuentra en el borde. Por esta razón siempre hay que tratar de ocupar con sus fichas el borde del tablero e impedir esto al contrario. Especialmente importante es ocupar las casillas de las esquinas. Las fichas que alcanzaron estas casillas no pueden ser dadas la vuelta: simplemente no hay con qué capturarlas. El que ocupe primero la esquina, por lo general, adquiere una importante ventaja, y si esto se logra al principio del juego o a mediados del mismo esta ventaja puede ser decisiva. Por esta razón es muy peligroso poner las fichas cerca de las casillas angulares, sobre todo en las casillas b2, b7, g2 y g7.

El adversario puede realizar una combinación no muy complicada y ocupar la esquina. He aquí un ejemplo convincente que ilustra la fuerza de las fichas de las esquinas (fig. 59). Hay que reconocer que esta posición difícilmente puede producirse en una partida real. Parecería que llegó el momento preciso para rendirse, ¡sólo les queda una ficha contra 54 del contrario! No obstante las blancas ganan fácilmente. He aquí como puede terminar la partida:
1. Las blancas juegan a8 (aún cuando ahora le toque jugar a las negras, ellas de todos modos han de dejar pasar su turno); toda la vertical «a» se torna blanca y las negras, como antes, no tienen jugadas que hacer. 2.h8; ahora se dan vuelta las fichas negras b8-g8 por la horizontal y b2-g7 por la diagonal, a las negras les aparece la jugada 3.h7. A continuación 4.h1; 5.h2; 6.h6; 7.h5; 8.h4; 9.h3. Así pues, a pesar de que la posición inicial parecía difícil, las blancas ganaron con un tanteo de 40:24. Es curioso que, si retiramos la ficha negra a7 de la posición inicial, las blancas pueden ganar 64:0! (compruébelo).
Los jugadores experimentados empiezan el juego luchando por dominar el centro, el cuadrado c3-c6-f6-f3, para de esta manera no permitir al adversario alcanzar el borde del tablero. Seguidamente las blancas y las negras, una ficha tras otra, alcanzan las verticales y horizontales extremas y hay que estar atento de no permitirle al contrario llegar a la esquina. Hacia el final del juego quedan menos variantes y los jugadores hábiles calculan muchas jugadas hacia adelante. Aquí la cesión de las esquinas ya no es tan peligrosa.
Mostremos una partida interesante del reversi jugada entre una persona (con las negras) y un ordenador (con las blancas).
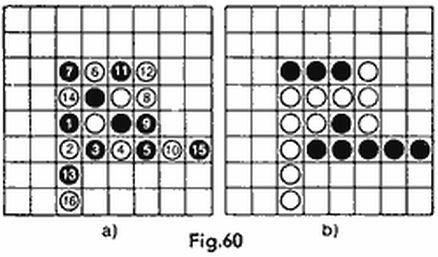

La figura 60 a presenta las primeras 16 jugadas de negras y blancas en el orden que fueron hechas. El color de las fichas numeradas indica cuál de las partes hizo la jugada correspondiente. La posición surgida está representada en la figura 60b. Primero se ocupo todo el centro del tablero, después los jugadores salieron a su extremo (las negras, en la jugada 15 y las blancas, en la 16). En esto termina la apertura. El medio juego, o sea las jugadas 17 – 42, se muestra en la figura 61. Cada vez mayor es el número de fichas que aparece en las líneas extremas, pero a las esquinas del tablero los adversarios no dejan pasar uno al otro. Aquí la iniciativa pertenece al ordenador, pero al final de la partida las negras pasan al ataque decisivo (fig. 62a, jugadas 43 – 60). Para ello las negras se deciden a una astucia: entregan la esquina inferior izquierda (la máquina la ocupa con la jugada 46), pero con las jugadas 47 y 49 penetran en la esquina inferior derecha, ganando suficiente espacio en la parte inferior del tablero. Las posibilidades se nivelan, pero con la jugada 50 el ordenador se equivoca y la persona se hace con otra de las esquinas, la superior derecha.
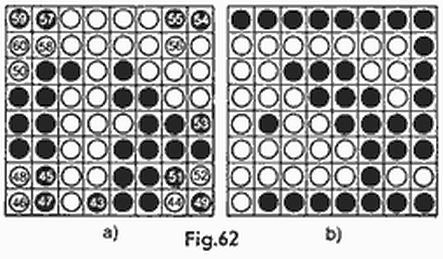
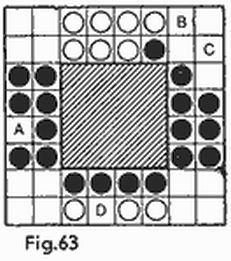
Después de la jugada 53 de las negras, las blancas no están en condiciones de poner una ficha nueva sobre el tablero y se ven obligadas a dejar pasar una jugada y después otra (por eso los números de las jugadas 53, 54 y 55 en la figura 62 a están pintados de negro). Unas cuantas jugadas más tarde la partida terminó con la victoria de las negras con una ventaja mínima de 33:31 (fig. 62b).
Señalemos otros elementos estratégicos del reversi. Los jugadores experimentados en el medio juego forman con acierto unas casillas sobre el tablero a las que ellos pueden desplazarse y el contrario no. Las cuatro situaciones fundamentales con la posible jugada de las blancas al extremo del tablero, las situaciones A, B, C y D, se indican en la figura 63. Teniendo una segunda ficha de apoyo en el centro del tablero (en la figura está sombreado) las blancas pueden poner su ficha en una de estas casillas; para las negras por el contrario estas casillas son inaccesibles cualquiera que sea la situación en el centro. Por lo visto, la presencia de tales casillas de «reserva» para uno de los bandos, en este caso para las blancas, es muy importante.
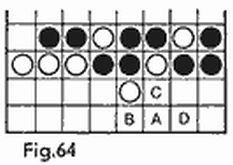
Algunos consideran que en el reversi lo más importante es el cálculo total de las variantes, sin embargo, esto no es precisamente así. Con frecuencia se dan situaciones en las que la lucha tiene carácter local, se toca sólo una parte determinada del tablero. Veamos la figura 64. Hay que reconocer que las blancas salieron mal del centro: las negras pueden formar una casilla, a la cual ellas pueden jugar y las blancas no. Para esto las negras ponen su ficha en la casilla A, después de lo cual tratan de no ocupar durante el mayor tiempo posible la casilla C. Si en cierto momento las blancas la ocupan, a las negras les aparecerá la casilla D, en la que pueden poner su ficha y el adversario no.
Supongamos ahora que las negras en su primera jugada pusieron su ficha en B. En tal caso las blancas adquirirían la posibilidad de realizar una combinación simple: las blancas juegan a la casilla A (ahora a nosotros no nos interesa la disposición de las fichas en la mitad superior del tablero, pero se supone que en b5 se encuentra una ficha blanca), las negras juegan a D, las blancas a C y ahora les toca jugar a las negras. Por cuanto ocupar la casilla g2 sería un suicidio, las negras deben trasladarse a otro lugar del tablero.
¿Cuál es el sentido de la combinación de las blancas o, hablando con más precisión, de la «maniobra»? Para explicarlo hay que tocar algunos principios generales. En cualquier situación sobre el tablero la cantidad de jugadas es finita y cada jugador tiene a su disposición, digamos, un conjunto × de jugadas malas y un con junto Y de jugadas neutrales. Nuestra tarea consiste en obligar al contrario a utilizar todas las jugadas neutrales y al fin y al cabo hacer una jugada mala. El procedimiento más común consiste en ceder el turno de la jugada. Esta situación local se resuelve de manera que, después de terminada, la jugada sea del contrario. Precisamente este procedimiento es el que se ha utilizado en la operación que muestra la figura 64. Después de una imprecisión de las negras y una correcta jugada de las blancas, el adversario se ve obligado a jugar fuera del ángulo inferior derecho.
Conociendo las posiciones estándar en los extremos (fig. 63), a qué aspirar y qué evitar, hacia la jugada 30 ya se puede pronosticar el resultado del juego. El juego correcto del «lado» del tablero es una especie de analogía con el juego posicional en el ajedrez. Si usted consiguió obtener en un lado del tablero una casilla de reserva, esto se puede valorar en el lenguaje ajedrecístico, por ejemplo, como la posesión de una línea abierta o la posesión de un peón pasado... Si por el contrario en esta situación local usted hizo dos jugadas y el adversario una, puede considerar que lo adelantó en el desarrollo de las figuras. Por supuesto que igual que en el ajedrez la ventaja en la posición y tanto más la material (su influencia en el reversi es escasa) no garantizan la victoria aún cuando un «tiempo» de más (una casilla de reserva) aumentan las posibilidades de ganar la partida.
Han sido desarrollados también otros principios estratégicos aplicables a tales o cuales posiciones, por ejemplo: «desarrolla el punto común», «captura menos», «no ocupes todos los lados», «protege la diagonal», etc. La exposición detallada de la teoría del reversi no forma parte de nuestros planes.
Igual que en otros juegos, en el reversi existen problemas y combinaciones interesantes. Expongamos un problema único (en el idioma ajedrecístico, un estudio) propuesto por O. Stepánov. En la figura 65 las blancas comienzan y ganan.
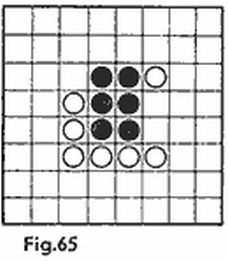
Esta perla se resuelve con la jugada 1.e7!! Veamos qué puede ocurrir más adelante. Las fichas negras d6 y e4-e6 se dan la vuelta y vivas quedan sólo las fichas d4 y d5. ¿Cómo deben jugar ahora las negras? Después de la jugada d2 o d7 y de la correspondiente respuesta d1 o d8 sobre el tablero, como podemos ver, quedan sólo fichas blancas, es decir, en esto el juego ha terminado. En el caso de una de las jugadas b2, b4, b5, b6, f7, f5, f4, f2 y la correspondiente respuesta al, a4, a5, a7, a8, g5, g4, g1 a las negras les queda sólo una ficha, que se halla rodeada y en la siguiente jugada las blancas terminan el juego con la aniquilación total de las fuerzas enemigas.
Así pues, las negras tienen la respuesta forzada 1... g2, cediendo el ángulo del tablero. Las blancas juegan, por ejemplo, 2.f4 (en e4 aparece una ficha blanca) con la jugada inevitable 3.hl. Como resultado el ángulo inferior derecho ha sido ganado, lo cual en un estado tan prematuro del juego equivale a la victoria.
Probablemente que ésta sea la única posición (con exactitud hasta la simetría) con material tan escaso y aproximadamente igual, de la cual se puede afirmar que una de las partes comienza y gana.
Para finalizar observemos que la idea de la captura de fichas al adversario por ambos jugadores se da en los diferentes juegos (patrunculi, tablut y otros), pero en estos juegos las fichas rodeadas se comen, retirándolas del tablero. Después de conocer el reversi esta operación estándar de retirar las fichas del tablero puede parecer muy aburrida.
Capítulo 4
Desde el tres en raya hasta el rendsiu
§. Tres en raya
§. Cuatro y cinco en raya
§. n en raya
§. Rendsiu
En este capítulo nuevamente trataremos sobre un juego de fichas, pero muy diferente de los examinados hasta ahora. Para ganar no se precisa capturar las figuras del adversario o darle jaque-mate, sino es suficiente disponer sus fichas en determinada línea (tres, cuatro o cinco en raya). A pesar de que las reglas son muy sencillas, lo cual de ninguna manera indica que el juego también sea elemental, comenzaremos el capítulo por el juego «infantil» «tres en raya» 3 × 3 y lo terminaremos con el rendsiu, uno de los juegos más complejos y atractivos. El nombre de tres en raya no nos debe turbar, pues en lugar de cruces y ceros se pueden utilizar piezas blancas y negras del juego de damas. No obstante en aquellos casos cuando se acostumbra a jugar al tres en raya, no vamos a abandonar la terminología admitida por todos.
§. Tres en raya
Así pues, el juego más simple es el tres en raya sobre un tablero de 3 × 3. Los jugadores, por turno, ponen sobre las casillas del cuadrado (tablero) cruces y ceros y gana el que ponga antes sus tres signos en raya. Lógicamente la partida tiene una duración no mayor de 10 jugadas. Si ninguno de los jugadores logra su objetivo, la partida termina en tablas.
Es interesante que incluso en un ejemplo tan simple se pueden ilustrar muchos conceptos importantes de la teoría matemática de los juegos. El tres en raya pertenece a la categoría de juegos finitos, determinados, de selección, estratégicos, que juegan dos personas y posee información completa. Vamos a señalar con vértices (puntos) las «posiciones» que surgen en el curso del juego (disposición de las cruces y los ceros). Pongamos que empiecen las cruces. Unamos el vértice inicial (tablero vacío) con aquellos nueve que corresponden a la primera jugada de las cruces. Unamos cada uno de ellos con ocho vértices que corresponden a las jugadas de los ceros, etc. Como resultado obtenemos el árbol del juego (árbol de selección). El vértice inicial, raíz del árbol, longitud máxima de la rama (profundidad de la selección) en este caso es igual a nueve. Después de analizar el árbol por el llamado procedimiento minimax, nosotros determinaremos con precisión matemática, cómo debe terminar la partida haciendo ambas partes sus mejores jugadas.
Todos los términos enumerados se pasan fácilmente a la mayoría de los juegos examinados en este libro, con la particularidad de que desde el punto de vista de la teoría de los juegos, el «tres en raya» no se diferencia en nada del ajedrez, a no ser por la profundidad de la selección. En el ajedrez el árbol es tan grande que no existe esperanza de analizarlo íntegramente, incluso con ordenador. En estos casos el árbol de selección completo se sustituye por un árbol truncado y el juego «preciso» se transforma en «aproximado».
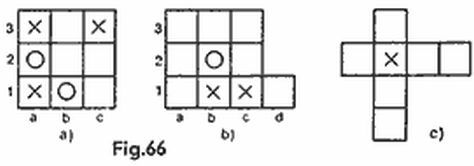
Claro que para analizar el «tres en raya» podemos pasar sin métodos especiales: no ocupará más de una hora de juego. Es fácil detectar que, jugando correctamente ambos jugadores, la partida termina en tablas. Su solución se decide ya en la primera jugada. Las cruces tienen tres maneras de comenzar a ocupar la esquina, el centro o una casilla lateral del tablero. El mayor peligro para las cruces es empezar por la casilla del rincón (a1 en la fig. 66). De las ocho posibles respuestas, la correcta para los ceros es solamente jugar al centro del tablero. Después de esto las tablas se logran sin dificultad. Supongamos que el cero jugó de otra manera: a la jugada al respondió con b1. Entonces sigue a3; la única respuesta es a2, contra lo cual se resuelve con la jugada c3, poniendo un «tenedor», es decir, con doble amenaza en b2 o b3 (fig. 66a). En su siguiente jugada las cruces ponen su tercer signo y ganan. Con el «tenedor» termina también la partida en otras variantes.
Abstraigámonos un poco y examinemos el siguiente juego. En nueve cartulinas escribimos otras tantas palabras: viga, útil, cien, voz, zeta, coz, ver, tur, car. Dos jugadores, turnándose, van tomando de la mesa las cartulinas y gana el que consiga coger antes tres cartulinas con una letra común.
El lector puede sorprenderse, ¿por qué razón nos liemos desviado hacia un juego de palabras? Precisamente porque este juego de palabras, en principio, no se diferencia del «tres en raya» habitual. Compongamos la siguiente tabla:

En realidad hemos dispuesto nuestras nueve palabras en las casillas de un tablero de 3 × 3. Cualesquiera tres palabras que se encuentran en un mismo renglón, en una columna o en una de las diagonales grandes de la tabla tienen una letra común. Al mismo tiempo cualesquiera otras tres palabras no tienen letras comunes. De esta manera para ganar es suficiente tomar tres cartulinas con las palabras situadas en la tabla a lo largo de una de las líneas. Y por tanto, si usted juega bien al tres en raya, componiendo mentalmente esta tabla, se volverá invencible en este juego de palabras. Claro que también aquí seleccionando correctamente las cartulinas, la partida siempre terminará en tablas.
Por tanto, como dicen los matemáticos, los dos juegos examinados, tres en raya y el de las palabras, son isomorfos, es decir, entre sus reglas puede establecerse tal relación que los juegos en nada se distinguirán uno de otro. El isomorfismo es un concepto matemático importante que permite, al estudiar unos objetos, pasar a otros, ya investigados.
Añadamos ahora al tablero habitual de 3 × 3 una sola casilla, la d1 (fig. 66b). ¿Cómo terminará el juego en este caso? En este tablero las cruces rápidamente ganan. Resuelve la jugada c1. Si los ceros no juegan a la casilla b2, como ya sabemos, pierden sobre el tablero habitual de 3 × 3 (se resuelve sin necesidad de la casilla adicional). Si por el contrario, los ceros ocupan la casilla b2, entonces después de b1, sigue la jugada de las cruces a la casilla al o bien a la casilla d1 (fig. 66b).
Así pues, tenemos un tablero de 10 casillas en el cual las cruces forzadamente obtienen la victoria. Pero esto no es un récord. Sobre un tablero de siete casillas, compuesto por dos filas de 4 × 1 que se cruzan en una de las casillas interiores (fig. 66c), la victoria se consigue en la tercera jugada. La primera cruz se marca en la intersección de ambas filas, la segunda, en una de las casillas interiores vecinas, después de lo cual los ceros se vuelven indefensos. No cuesta trabajo convencerse de que cualquiera que sea el tablero con un número de casillas inferior a siete el resultado del juego será de tablas.
Volvamos al tres en raya sobre un tablero de 3 × 3. Parecerá curioso, pero sobre este tablero se puede jugar al ganapierde. El que rellene antes una fila de tres signos se considera vencido. A diferencia del juego «directo», en el «inverso» la iniciativa pertenece a los ceros. No obstante, las cruces tienen una estrategia segura para hacer tablas: en el primer movimiento ellas deben ocupar el centro y luego repetir simétricamente las jugadas del adversario.
La siguiente variante del tres en raya certifica que incluso un tablero tan pequeño como el de 3 × 3 puede representar una fuente inagotable para los inventores de juegos. De las reglas del tres en raya, las de esta variante se diferencian en que cada jugador, cuando le toca jugar, puede poner a voluntad tanto una cruz como un cero. Gana el que consiga terminar antes una fila de tres signos iguales, indiferentemente de cuales.
En el juego habitual, e incluso en el ganapierde, si los jugadores no cometen errores, la partida termina en tablas. En la variante dada, por el contrario, gana el que comienza el juego. En su primera jugada éste ocupa el centro, la casilla b2, pone, como de costumbre, una cruz (fig. 67a). El segundo jugador puede ocupar ya sea la casilla del rincón, ya sea la lateral del tablero y para no perder inmediatamente, debe poner un cero. Si la casilla del rincón al está ocupada, el primer jugador dibuja un cero en el vértice contrario, c3, y, donde quiera que ponga ahora el contrario una cruz o un cero, él con su jugada siguiente termina respectivamente la fila de cruces o de ceros. Si el segundo jugador con su primera jugada ocupa la casilla lateral a2, el primero pone un cero en una misma línea con los dos signos ya inscritos, es decir, en la casilla c2. Al segundo jugador no le queda nada mejor que poner otro cero en b1 y después de la respuesta con un cuarto cero en b3, no le queda más opción que rendirse (fig. 67a).
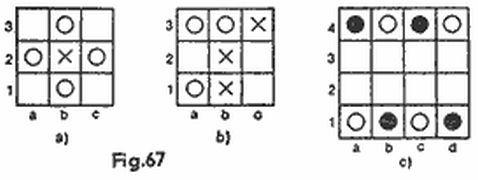
He aquí otra variante del juego sobre un tablero de 3 × 3. Ambos jugadores, turnándose, ponen sobre el tablero tres cruces y tres ceros, después de lo cual ya no se dibujan signos nuevos. Si en este momento ninguno de los jugadores logra poner tres signos en fila, el juego continúa. Ahora en cada jugada los jugadores pueden trasladar uno de sus signos a una casilla adyacente vertical u horizontalmente. Gana nuevamente quien coloque antes tres signos en fila.
Igual que en el juego anterior, el derecho a la primera jugada aquí es decisivo. El que comienza debe poner su crucecita en el centro del tablero. Si como respuesta el cero se pone en una de las esquinas, por ejemplo, en la casilla a3, el primer jugador pone una cruz en la casilla b1. La respuesta viene forzada, b3. A ésta le sigue c3; la respuesta nuevamente es obligada, a1. En esto termina la apertura de la partida (fig. 67b). En sus dos jugadas siguientes el primer jugador traslada las cruces de b2 a c2 y de b1 a e1 y gana la partida. Si en su primera jugada el segundo jugador ocupa una casilla lateral, por ejemplo, la b3, el primero juega a la casilla al, el segundo responde a c3, entonces el primero pone su signo en a3 y el contrario, en a2. Todos los signos están ubicados, ahora el primer jugador traslada la cruz situada en al, primero a b1 y después a e1, ganando la partida.
Si los jugadores acuerdan que el que empieza, en su primera jugada, no debe ocupar la casilla central, entonces, jugando correctamente los dos jugadores, ninguno de ellos podrá conseguir su objetivo y la partida termina en tablas.
Claro que en este último juego es más cómodo sustituir las cruces y los ceros por fichas blancas y negras. Este juego puede considerarse como introducción a una clase de juego que representa un híbrido del «tres en raya» con el «juego de damas». Este mismo juego pero sobre un tablero de 4 × 4 se llama tak-tikl. En él cada una de las partes tiene cuatro fichas (fig. 67c). Los jugadores las mueven por turno a una casilla vertical u horizontalmente y gana el que logre poner tres fichas en fila.
He aquí, como ejemplo, una partida al tak-tikl: 1.c1-c2 d1-c1 2.b4-b3 b1-b2; 3.b3-a3 (existía la amenaza 3... a4-a3) 3... a4-b4; 4.a1-b1 y ganan las blancas por cuanto las negras no pueden oponerse a la maniobra. 5.d4-d3. Con ayuda de un ordenador se ha demostrado que el juego tak-tikl termina en tablas, es decir, jugando con precisión, ninguno de los jugadores consigue poner tres fichas en fila.
Una generalización consecutiva de los dos últimos juegos es el «molino», uno de los juegos más antiguos en la historia de la humanidad. La figura 68 presenta varios molinos. La forma inicial del tablero (a), hasta hoy día, sigue siendo la más popular. En esta variante del juego, denominada molino simple, cada jugador dispone de nueve fichas. En el molino-caracol (b) el número de fichas aumenta hasta 12 y en el molino hexagonal (c), los oponentes disponen de 13 cada uno.
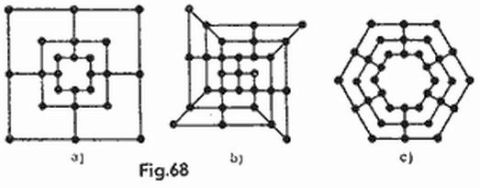
Se conocen también el molino-araña, molino-red, molino pentagonal, etc. En todas las variantes de este juego las reglas son idénticas. La partida se compone de tres etapas. La primera (apertura) consiste en ubicar las fichas sobre el tablero. Los jugadores ponen por turno sus piezas en cualesquiera de las casillas libres del tablero. Tres fichas del mismo color colocadas en fila forman una figura llamada molino. Una vez construida esta figura, el jugador retira del tablero una ficha cualquiera del contrario. Si con una jugada se logran construir dos molinos, del tablero se retiran dos fichas.
La segunda etapa (medio juego) comienza después de ubicar todas las piezas. A partir de aquí los jugadores mueven por turno sus piezas a lo largo de la línea hacia las casillas adyacentes. El objetivo es el mismo: construir un molino y retirar del tablero una ficha del contrario.
La tercera etapa (final) llega cuando a uno de los participantes le quedan sólo tres fichas. En este momento este jugador adquiere el derecho de trasladar en su jugada siguiente una ficha cualquiera a una de las casillas libres del tablero, sin prestar atención a las líneas que unen las casillas. Construyendo un molino con sus tres fichas, él retira una pieza del contrario y así hasta que a éste no le queden también tres fichas.
Gana el que consiga reducir el número de fichas del adversario a dos, impidiéndole, de esta manera, construir su molino. La partida puede también acabar antes, si en cierto momento uno de los jugadores se ve imposibilitado de hacer un movimiento, es decir, sus piezas están atascadas. Si a los dos jugadores les quedan pocas fichas (por ejemplo, por tres) y ninguno de ellos puede construir un molino, la partida termina en tablas. Está prohibido utilizar dos veces un mismo molino. Se pueden ocupar, todas las veces que se quiera, con fichas tres casillas dadas del tablero, pero la pieza del contrario se retira sólo a la primera construcción de un molino.
El bolotudu, que ligeramente recuerda al molino, se juega sobre un tablero rectangular de 6 × 5. Cada jugador tiene 12 fichas. Las van poniendo sobre el tablero por turno (dos fichas por jugada). A diferencia del molino aquí se prohíbe colocar tres fichas en fila y la apertura se desarrolla con mayor tranquilidad. La segunda etapa es igual que en el molino. Las fichas se mueven vertical y horizontalmente y una vez colocadas tres fichas en fila, se retira una pieza del contrario: la que se encuentre junto a este trío, a la derecha o a la izquierda. Se permite utilizar un mismo trío todas las veces que se quiera. Si a uno de los jugadores le quedan sólo dos fichas, al mismo se le anuncia derrotado. En este juego no existe una etapa similar a la tercera del molino. Al repetir las jugadas, la partida se reconoce empatada.
En el «tres en raya» clásico la partida termina en cuanto uno de los jugadores logra construir una fila de tres signos. En otras variantes del juego el tablero también se utiliza con escaso rendimiento. Para los que consideren esto demasiado aburrido, ha sido inventado otro juego. Sobre un tablero de 6 × 6 los jugadores, igualmente por turno, ponen sus signos (o fichas) y a cada formación de un trío vertical u horizontal obtienen un punto. Cada casilla del tablero se toma en consideración sólo dos veces: vertical y horizontalmente. Gana el que consiga mayor cantidad de puntos. En este caso termina llenando el tablero.
Hasta aquí se examinaron las diferentes variantes del tres en raya sobre tableros planos, no obstante se conocen también no pocas variantes tridimensionales del juego. La generalización más elemental de estas variantes es el juego sobre un cubo de 3 × 3 × 3. Los jugadores por turno marcan por un pequeño cubo de 1 × 1 × 1 y gana el que logre poner tres signos suyos en línea recta. No hay ni que decir que aquí un principiante gana sin ninguna dificultad. Es curioso que en el juego tridimensional, a diferencia del plano, no se producen tablas aún cuando ambas partes lo deseen. Realmente, si en un cubo de 3 × 3 × 3 marcamos 14 cubos pequeños unitarios cualesquiera (precisamente esta es la cantidad de jugadas que tienen las cruces en el transcurso del juego); aunque sea una fila vertical, horizontal o diagonal, estará compuesta exclusivamente por cruces.
Es más interesante el juego sobre un tablero de 3 × 3 × 3, en el cual gane el que ocupe primero dos filas que se intersecan. El pequeño cubo que se encuentra en la intersección de dos filas se permite marcarlo a última hora. Por cuanto la ocupación del centro del cubo conduce simplemente a la victoria, esta jugada se puede hacer sólo en dos casos: si con ella se termina victoriosamente el juego o si se impide que el contrario gane en la jugada siguiente.
§. Cuatro y cinco en raya
Son mucho más profundos e interesantes los juegos con cruces y ceros, en los cuales la victoria se consigue no por la colocación de tres signos en fila, sino por cuatro o por cinco. En el juego «4 en raya» sobre un tablero de 4 × 4 a los ceros les resulta aún más simple hacer tablas que en la variante clásica de 3 × 3. Este juego fue programado en ordenador para un tablero de 5 × 5. La máquina actuaba meticulosamente: conseguía tablas jugando con cualquiera de los dos colores, y cuando la persona no prestaba suficiente atención, ganaba. A propósito, está demostrado que sobre un tablero de 5x5 este juego también termina en tablas.
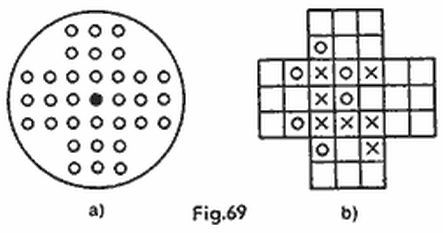
Al «4 en raya» se juega también sobre el tablero que presenta la figura 69a, el cual se usa para el solitario. Este tablero tiene 33 casillas con orificios en cada una de ellas. Unos jalones hacen las veces de fichas, introduciéndolos en los orificios. La variante principal del solitario, muy popular en el siglo pasado, consiste en lo siguiente. En todas las casillas del tablero se colocan fichas de un mismo color y una de ellas se retira, dejando una casilla libre. La jugada representa un salto que da una ficha cualquier vertical u horizontalmente por encima de la ficha adyacente a la casilla libre, la cual, en este caso, a diferencia del juego de las esquinas, se retira del tablero. Igual que en el juego de las esquinas, una ficha puede hacer en una jugada varios saltos y todas las fichas, por encima de las cuales se salte, se retiran del tablero.
Si no existen más jugadas, la partida termina. La finalidad del juego consiste en no dejar sobre el tablero más que una pieza. Está demostrado que, cualquiera que sea la ficha retirada del tablero, el objetivo se consigue, además la solución más corta contiene 15 jugadas.
El solitario clásico (a él le dedicaron muchos libros), en esencia es un rompecabezas. En la URSS este juego se vende (con el nombre de yoga) ligeramente ampliado. Teniendo en cuenta que a la gente le gusta más practicar juegos que resolver rompecabezas, el yoga contiene tres juegos más. Para ello las fichas-jalones tienen sus extremos de diferente color (como en el reversi) y cada jugador utiliza el suyo. El primer juego es el de las esquinas chinas. Los participantes colocan seis fichas en dos rectángulos de 3 × 3 opuestos y, siguiendo las reglas del juego de las esquinas chinas (se admiten también jugadas diagonales), tratan de ocupar el territorio del adversario.
En el otro juego, igual que en el solitario tradicional, sobre el tablero se colocan 32 fichas de un mismo color, con la particularidad de que se permite saltar por encima de un número cualquiera de fichas sin espacios libres entre ellas y todas se retiran del tablero (hay que detenerse inmediatamente detrás de dichas fichas). Los participantes juegan por turno y gana quien al final del juego reúna una mayor cosecha de fichas.
Y por fin, el tercer juego, gracias al cual nosotros precisamente nos acordamos del solitario, es el «4 en raya». En lugar de cruces y ceros en él se utilizan fichas de dos colores.
En la figura 69b las cruces crearon un tenedor y ganan en la jugada siguiente, poniendo su signo en una de las casillas marcadas. Sin embargo, cuando se juega correctamente al tres en raya sobre el tablero que se utiliza para el solitario se consiguen tablas.
El «cuadrado» (su otro nombre es «tiko») es un juego que representa una combinación del «4 en raya» y el «bolotudu». Se juega sobre un tablero de 5 × 5 y cada jugador dispone de 4 fichas. El objetivo del juego es formar las fichas de su color a lo largo de una línea o en forma de un cuadrado de 2 × 2. Antes que nada los oponentes colocan, por turno, todas sus fichas (se prohíbe formar grupos de a cuatro), después de lo cual las desplazan a cualesquiera de las casillas adyacentes (vertical, horizontal o diagonalmente).
El juego «4 en raya» sobre un tablero de 4 × 4 × 4 se llama tik-tak-tow. Durante mucho tiempo se consideró que este juego termina en tablas, pero no hace mucho por medio de un ordenador se estableció que el jugador que comienza la partida tiene una estrategia que le garantiza la victoria.
Ahora, por fin, le llegó el turno al juego de mayor popularidad de los que se juegan con cruces y ceros. Sobre un campo ilimitado (una hoja de papel cuadriculado) dos personas ponen por turno sus signos. Gana el que consiga construir antes cinco signos en fila (por la vertical, horizontal o diagonal). Si ninguno de los dos consigue este objetivo el juego termina en tablas. Claro que las condiciones deben ser acordadas, así como el número de movimientos que puede durar la partida.
Aunque teóricamente el juego se desarrolla sobre un plano infinito, en realidad el tablero tiene dimensiones finitas. Por lo común, es una simple hoja de papel cuadriculado. Teniendo a mano papel y lápiz, al «5 en raya» con gusto juegan escolares, estudiantes e incluso candidatos a doctor y doctores en ciencias. Este juego fue inventado cuatro mil años atrás, muchos años antes de que aparecieran los primeros cuadernos de papel cuadriculado... A propósito, los juegos antiguos go-bang y gomoku se distinguen del «5 en raya» sólo en la utilización de tableros especiales de 19 × 19 (como en el go) o de 15 × 15, así como también de fichas en lugar de signos.
En la mayor parte de los juegos examinados en este apartado los ceros luchan por hacer tablas. Se tiene en cuenta que las cruces (la parte que inicia el juego) siempre pueden conseguirlas. Esta idea intuitiva se confirma mediante el siguiente teorema.
Jugando correctamente al «5 en raya» o, en general, al m en raya», para cualquier valor de n, el que comienza la partida tiene garantizadas las tablas.
Demostremos esto por oposición. Supongamos que, jueguen como jueguen las cruces, los ceros, utilizando su mejor estrategia, ganan. Entonces el que empieza, después de poner su primera cruz en una casilla cualquiera, a continuación debe acogerse a la estrategia del adversario, cambiando mentalmente de signo: las cruces y los ceros. Si, de acuerdo con esta estrategia, en una de las jugadas le toca ocupar la casilla en la cual se encuentra la primera cruz, él nuevamente pone su signo en una casilla cualquiera, etc. Está claro que a nadie molestará una cruz de más. A nuestra manera de ver, los ceros deben ganar. Mas la estrategia de las cruces es tal que ellas juegan como si fuera con los ceros, pero con un signo de más, por tanto también ganan. Llegamos a una contradicción, lo cual demuestra el teorema.
Esta demostración es casi igual a la del juego ajedrecístico «dos jugadas seguidas». Como verán, aquí nuevamente hemos utilizado las ideas de la simetría. A propósito, el teorema es válido tanto para los tableros infinitos, como también para los de dimensiones dadas.
Aunque hemos citado algunos juegos, en los que gana el que juega segundo, por lo general, el derecho a la primera jugada proporciona cierta ventaja. Además en el ajedrez y en el juego de damas esta ventaja no es demasiado grande, mientras que en el «3 en raya» y el «4 en raya», es decisiva (en el primer caso, añadiendo una casilla al tablero de 3 × 3, y en el segundo, sobre un tablero de 6 × 6 y más). ¿Cuál es la situación en el «5 en raya», existe o no la victoria forzada por el jugador que empieza el juego? La práctica muestra que una notable iniciativa pertenece a las cruces, pero no son pocos los casos en que los ceros toman la delantera. Mas como aseguran los conocedores del rendsiu (sobre esta variedad del juego de cruces y ceros se hablará en el apartado siguiente), en libros japoneses se dan variantes exhaustivas de cómo ganar dando comienzo al juego. Para su décima jugada las cruces adquieren una ventaja decisiva y para la jugada quince terminan la construcción del quinteto.
Aunque es raro que estos razonamientos teóricos asusten a los aficionados a los juegos de cruces y ceros, con todo ello no hay necesidad de hablar de competiciones serias, si está demostrada la victoria de una de las partes. Por esta razón precisamente fueron ideadas ciertas modificaciones, con las cuales el resultado del juego se hacía no tan determinado. Pero antes de hablar del juego de fichas rendsiu examinemos otras dos variantes del de cruces y ceros con fichas. He aquí el juego en el cual se tiene en cuenta cualquier número de fichas dispuestas en fila. Sobre un tablero de ajedrez (se puede coger también un tablero de menores dimensiones) dos personas ponen por turno por dos fichas de su color, tratando de construir con ellas filas horizontales o verticales lo más largas posible. Una fila de dos fichas de un mismo color proporciona al dueño de éstas 4 puntos, una de tres, 9 puntos, una de cuatro, 16 puntos, etc., (es posible, claro está, asignar otros tipos de valoración). Una ficha que pertenece simultáneamente a dos filas se tiene en cuenta una sola vez. Después de rellenar todo el tablero se contabilizan los puntos. El que tenga mayor cantidad de puntos, es el que gana.
El hasami shogi contiene simultáneamente elementos de varios juegos: del de cruces y ceros, del de las esquinas chinas y del juego de damas. Se juega sobre un tablero de 9 × 9. Cada uno de los jugadores tiene 18 fichas que disponen en las horizontales extremas (las blancas de un lado y las negras del contrario). El objetivo del juego consiste en poner antes que el contrario, cinco de sus fichas en fila en cualquiera de las cinco líneas intermedias. Las fichas pueden avanzar vertical u horizontal- mente una casilla o saltar una ficha adyacente, ocupando la casilla libre situada inmediatamente detrás de aquélla. Si uno de los jugadores bloquea una de las fichas del contrario (en una vertical, horizontal o diagonal) entre dos de las suyas, la misma se retira del tablero; al propio tiempo la ficha puede pasar sin peligro entre dos fichas del adversario. En el mercado existen juegos que representan variantes más simples. El tablero es de 8 × 8, los jugadores disponen de 16 fichas cada uno y gana el que consiga formar una fila de cuatro fichas en lugar de cinco.
§. n en raya
Como generalización del juego de cruces y ceros es interesante analizar los juegos «n en raya» sobre planos ilimitados para los distintos valores de n. Por lo visto, como antes, gana el que logra construir primero n de sus signos en una fila. Como ya sabemos, cuando n = 5 la victoria (teóricamente) está del lado del que comienza el juego, es decir, de las cruces. Ganan con gran facilidad para cualquier n < 5. Mas ¿qué se puede decir sobre el juego «n en raya» cuando n > 5?
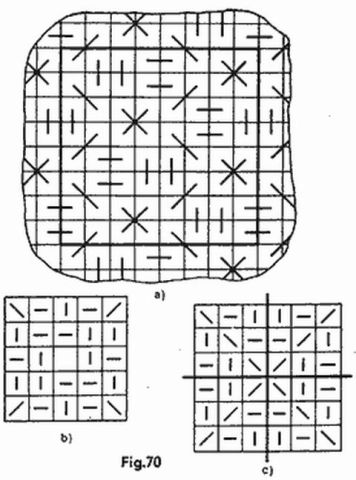
Ya en 1954 G. Pollack y C. Shannon, este último uno de los fundadores de la cibernética, demostraron que cuando n ≥ 9 el segundo jugador tiene una estrategia según la cual no pierde. Más adelante varios matemáticos compusieron un algoritmo de juego muy simple y efectivo para lograr tablas. El tablero infinito se divide mentalmente en cuadrados de 8 × 8 y se rellenan con líneas, como se indica en la figura 70. Ahora cualquiera que sea la casilla que ocupe el primer jugador, el segundo debe ocupar la casilla que se halla al otro extremo de la línea.
Mostremos que este procedimiento de juego garantiza las tablas. Examinemos para ello una fila arbitraria de nueve casillas adyacentes de un plano infinito. Nuestro cuadrado posee la propiedad de que entre estas nueve casillas siempre habrán dos relacionadas entre sí por una línea. Esto significa que si una de las casillas de este par está ocupada por una cruz, en la otra obligatoriamente hay un cero. De esta manera nueve casillas seleccionadas no pueden ser llenadas con un mismo signo, es decir, el que comienza nunca pondrá nueve signos en fila (y con más razón cuando son más de nueve), incluso si el juego es de duración infinita.
El lector se habrá fijado que nosotros nuevamente hemos utilizado con éxito la estrategia par que ya nos condujo, en su tiempo, al objetivo en juegos como el bridg-it y el de las esquinas chinas. En este caso esta estrategia obtuvo éxito sobre un tablero infinito.
Los matemáticos norteamericanos A. Heils y R. Juitte inventaron el cuadrado que muestra la figura 70. Curiosamente los matemáticos leningradenses A. Davlitsárov y O. Stepánov hallaron semejante cuadrado con ayuda de un ordenador.
Por desgracia la estrategia examinada, que se distingue por su elegancia, no sirve para los valores n ≤ 8. Sin embargo, está demostrado (por un procedimiento más complicado) que el juego «8 en raya» sobre un tablero ilimitado igualmente termina en tablas. En lo que se refiere al resultado de los juegos «7 en raya» y «6 en raya» el resultado aún no está aclarado. A propósito A. Davlitsárov y O. Stepánov demostraron que los juegos inventados por ellos de las cruces y los ceros «ecuatoriales» «7 en raya» terminan en tablas: sobre un plano se elige una dirección determinada, esta es el ecuador y la construcción paralelamente a ella de siete signos iguales en fila no se considera victoriosa.
Como conclusión volvamos al juego «5 en raya» pero sobre un tablero de dimensiones limitadas de 5 × 5. En esta variante los ceros consiguen tablas con mucha facilidad. Para ello deben utilizar nuevamente el método de Heils y Juitte. Después de cada jugada de las cruces a cualquiera de los cuadrados marcados en la figura 70b el cero debe ponerse en un cuadrado con una marca igual y en la dirección indicada por ella misma. En este caso los ceros pueden dar un avance al adversario, permitiendo al principio del juego ocupar el cuadrado central y hacer otra jugada a cualquier lugar. Al final del juego en cada fila posible de cinco casillas habrá aunque sea un cero.
De manera parecida se consiguen tablas en el juego «6 en raya» sobre un tablero de 6 × 6. La figura 70c se parece a la 70b con la única diferencia de que la respuesta de los ceros por la diagonal puede ser cualquiera. La «cubierta de Heils y Juitte» en el caso dado se caracteriza por su simetría especular por las dos líneas más gruesas.
§. Rendsiu
En 1980 apareció en la revista soviética «Nauka y zhizn» (Ciencia y vida) un artículo de V. Saprónov que causó una gran sorpresa entre los aficionados al juego de las cruces y los ceros. Quién pudiera pensar que desde tiempos remotos existe un juego atractivo de fichas, llamado rendsiu, que casi no se diferencia del «5 en raya» y al mismo tiempo representa uno de los deportes más practicados en Japón y en otros países. Este juego tiene una historia muy antigua (según los cronistas a finales del siglo XVII y comienzos del XVIII en Japón al rendsiu jugaba casi todo el mundo, desde los pequeños hasta los mayores), sobre él se escribieron muchos libros, existen sus clubes, se organizan campeonatos, se conceden categorías deportivas, etc. En pocas palabras, ¡un juego tan ingenuo como el de las cruces y los ceros representa una ocupación muy seria! Subrayemos que, tras V. Saprónov, una serie de interesantes artículos sobre el rendsiu publicó el Doctor en ciencias fisicomatemáticas A. Sokolski.
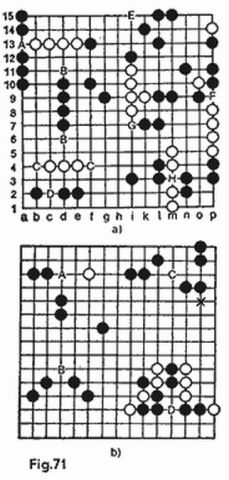
¿En qué se diferencia el rendsiu del juego de las cruces y los ceros «5 en raya»? Para el juego se precisa un tablero con 14 verticales y otras tantas horizontales (no es obligatorio pintar las casillas), así como fichas blancas y negras. Las fichas se colocan en las intersecciones de las líneas y no en las casillas, como en la mayoría de los juegos (fig. 71); en realidad el juego se desarrolla sobre un tablero de 15 × 15. Las intersecciones de las líneas se llaman puntos. El número de fichas no está limitado (aunque más de 225 no harán falta).
Empiezan el juego las negras (como en el reversi) con la jugada al centro del tablero. Ambas partes ponen sus fichas por turno y el objetivo del juego consiste en construir una fila de cinco fichas propias (por la horizontal, vertical o diagonal) formando un «hilo de perlas» (así se traduce del japonés la palabra «rendsiu»). Por ahora todo es igual que en el juego de las cruces y los ceros «5 en raya». Las fichas blancas y negras sustituyen dos tipos de signos y la limitación del tablero no es tan importante. Las reglas adicionales se deben a ciertas limitaciones para las negras (que son las que empiezan el juego). Pero antes de formularlas introduzcamos una serie de definiciones simples, que precisan los términos antes utilizados intuitivamente.
La disposición de cinco fichas seguidas de un mismo color en fila forma un quinteto (en la terminología ajedrecística, el mate). La finalidad del juego consiste precisamente en construir un quinteto. Una fila de cuatro fichas que con una jugada puede ser convertida en quinteto es llamada por nosotros cuarteto (jaque). Si éste puede ser convertido en quinteto añadiendo una ficha por cualquiera de los dos extremos, el mismo se llama cuarteto abierto (fig. 71a, punto B). Trío es una fila de tres fichas que en una jugada puede ser convertida, añadiendo una ficha, en cuarteto abierto (semijaque). Los tríos pueden ser de dos tipos: continuos (C) y con intervalo (D). La construcción de un cuarteto no abierto o un trío no es tan peligrosa. Pero si en su jugada siguiente uno de los jugadores forma dos o más cuartetos, tríos (jaques, semijaques) o combinaciones de estos (que se intersecan en el punto de aparición de la ficha), el contrario cae en una situación difícil y su única esperanza esta relacionada con el contraataque. Tales jugadas se llaman tenedores (tenedor se llama también a la situación creada sobre el tablero).
Ahora, por fin, se pueden indicar las prohibiciones introducidas en el rendsiu en comparación con el juego «5 en raya». Las negras, que son las que comienzan el juego, tienen prohibida la creación en una jugada de cualesquiera tenedores con dos y más tríos o dos y más cuartetos, así como la construcción de una fila larga de seis o más fichas. La formación de uno de estos tenedores se llama falta. Es importante subrayar que el tenedor compuesto de dos filas, una de las cuales es un cuarteto y la otra un trío, no está prohibido, al igual que los tenedores que surgen sobre el tablero en el momento cuando las negras dan mate (terminan la construcción de un quinteto). Para las blancas no existen jugadas prohibidas y la fila larga, igual que el quinteto, les proporciona la victoria.
Si sobre el tablero ya no puede surgir ningún quinteto (para esto no es obligatorio que se pongan todas las fichas), la partida termina en tablas. Los jugadores pueden hacer también tablas antes, si consideran que éstas son inevitables. Durante el juego cada uno de los adversarios tiene derecho a pasar algunas jugadas. Las negras recurren a ello cuando les amenaza una falta y las blancas, para mantener esta amenaza sobre las negras. Si ambos jugadores, uno tras otro, se niegan a poner sus fichas, la partida automáticamente se considera empatada. En esto las reglas del rendsiu quedan agotadas.
Como ilustración de las jugadas prohibidas véase nuevamente la figura 71a. Las blancas amenazan poner una quinta ficha en el punto A y las negras no pueden salvarse por cuanto, ocupando este punto, forman una fila prohibida de seis fichas (falta). Las negras no pueden evitar la formación de quintetos en otros lugares del tablero. Ocupando el punto F, las negras forman un tenedor 4 × 4 (dos cuartetos), ocupando el punto G, forman un tenedor 3 × 3 (dos tríos) y ocupando el punto H, forman un tenedor 4 × 4 × 3. Por cuanto a las negras no se les prohíbe construir el tenedor 4 × 3 (jaque-semijaque) –al formarse este tenedor no existen ni dos tríos, ni dos cuartetos– la jugada al punto E la tienen autorizada.
Examinemos la figura 71b. En ella se ven las posiciones que sólo recuerdan las faltas 3 × 3. No obstante tres fichas sobre una horizontal (punto A) están bloqueadas por una ficha blanca y no se transforman en cuarteto abierto, es decir, no representan un trío. Una de las filas diagonales que se cruzan en el punto B puede transformarse solamente en sexteto; la jugada al punto G no es una falta 3 × 3, puesto que las negras no amenazan con poner su ficha en el punto X (en este caso las negras tropiezan con la falta 4 × 4); y por fin, terminando con la jugada D de construir el quinteto, las negras ganan: los tenedores prohibidos que surgen y las filas largas ya no tienen importancia. Por tanto en la figura 71b las negras tienen a su disposición cualquiera de las jugadas A, B, C y D.
Como ya hemos dicho el rendsiu es popular en muchos países. En la URSS también se han creado círculos de aficionados, se organizan competiciones. La experiencia de medio siglo del rendsiu moderno mostró que la introducción de las faltas aproximadamente nivela las posibilidades de ambas partes, más aún, esta regla enriquece tácticamente el juego, le proporciona una belleza y finura sin igual. Es esencial que la invencibilidad de las negras (bando que comienza el juego) ya no se puede demostrar por los métodos de la simetría, por cuanto el rendsiu no posee esta propiedad.
Indiquemos además que han sido inventadas muchas variantes del rendsiu, pero ninguna de ellas adquirió una difusión tan amplia. He aquí algunas variantes del juego.
El gomoku es parecido al «5 en raya» pero se juega, como ya se ha dicho, con fichas comunes sobre un tablero de 15 × 15. En sustitución de las faltas introducidas en el rendsiu exigiremos que la segunda jugada de las negras se haga fuera del cuadrado central de 5 × 5. Tal juego lleva el nombre de «gomoku con el cuadrado central prohibido». En el «gomoku con el campo central común» también se juega sin faltas sobre un tablero de 15 × 15 (5 en raya), pero parece como si la primera ficha, la central, todo el tiempo cambiara de color, jugando las negras, se considera negra y, al jugar las blancas, blanca.
En el antirendsiu (tablero de 15 × 15) la falta se produce sólo en el caso de construir un cuarteto abierto y en el «viejo rendsiu» (tablero de 19 × 19), sólo al producir un tenedor 3 × 3. En el gomokunarabe (tablero de 15 × 15) a ambos jugadores se les prohíbe construir tenedores 3 × 3; a cada uno se le entregan 35 fichas y si las negras utilizan todas sus fichas y no logran construir un quinteto, se consideran derrotadas.
El penta se diferencia del rendsiu más que otros juegos. El tablero es de 15 × 15, no existen faltas y la regla adicional (obligatoria para ambos jugadores) consiste en que, tapando dos fichas del adversario por dos lados, el jugador las retira del tablero, anunciándolas «presa». Gana el que consiga construir antes un quinteto, o (¡novedad!) consiga primero hacer cinco «presas».
Volvamos al rendsiu tradicional. Éste tiene una teoría suficientemente desarrollada (igual que en el ajedrez, están estudiadas las aperturas), contiene bastantes procedimientos estratégicos y tácticos (juego posicional y combinatorio), pero el estudio desarrollado del juego no forma parte de nuestros planes. Limitémonos al examen de seis problemas (fig. 72) de complejidad creciente que ilustran algunos procedimientos del rendsiu.
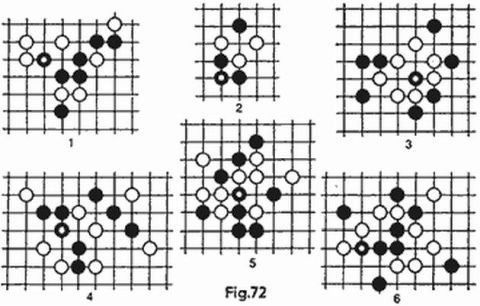
Por cuanto lo que tenemos ante nosotros son fragmentos de un tablero real, para orientarnos hacia donde se puede jugar, la ficha negra que hizo la primera jugada está marcada con un punto blanco.
Estos problemas fueron compuestos por A. Sokolski y por el campeón del mundo de este juego por correspondencia, A. Nosovski. En cada uno de ellos la victoria es forzada; en los problemas 2 y 3 las blancas empiezan y ganan, y en los otros ganan las negras. Las soluciones se pueden ver en la figura 73, comentémoslas (la numeración de las jugadas en el rendsiu es continua: en las figuras los números están indicados directamente sobre la ficha).
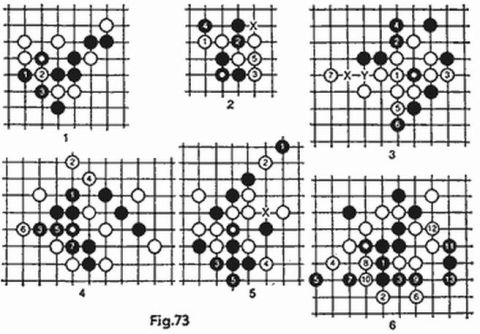
El primer problema es el más simple. Con su jugada 1 las negras construyen un trío y como quiera que lo cierre el contrario, con la jugada 3 ellas construyen el tenedor de la victoria 4 × 3. En el segundo problema las blancas con los semijaques 1 y 3 prepararon el ataque decisivo. Las negras, cualesquiera que sean las respuestas, se verán obligadas a ocupar los puntos 2 y 4, después de lo cual el punto × se convierte en prohibitivo para ellas (falta 3 × 3). A partir de aquí las blancas construyen sin obstáculos su quinteto. Semejante método de ganar es denominado por los jugadores al rendsiu de manera breve: victoria por faltas.
En el tercer problema las blancas nuevamente ganan preparando las faltas de las negras con las jugadas 1, 3 y 5 (obligando a las negras a ocupar los puntos 2, 4 y 6). Aquí hay dos puntos prohibitivos, X e Y, en los que se hacen faltas 3 × 3. Después de hacer las blancas la jugada 7, las negras no pueden ocupar ninguno de estos puntos, y su posición no tiene arreglo. En el cuarto problema la jugada 2 es la defensa más oportuna; ella transforma el trío negro, construido con la jugada 1, en seudotrío (él no puede convertirse en cuarteto abierto). Pero las blancas se ven obligadas a capitular a causa del tenedor victorioso 4x3 preparado con los semijaques 3 y 5.
El quinto problema ilustra un procedimiento muy útil: incluso al atacar no hay que olvidar la defensa. Si las negras no hicieran la jugada intermedia 1 y directamente ocuparan el punto 3, las blancas se harían con la iniciativa y ganarían dando jaques preparatorios de la falta 3 × 3 de las negras en el punto X. En el sexto problema con su jugada 4 las blancas se defienden de la amenaza directa (si en la jugada 4 se pone la ficha en el punto 2, entonces en la jugada 5 se pondrá en el punto 7, es decir, se construirá un tenedor 4 × 3). Después de las jugadas 4 y 5 esta amenaza queda neutralizada, por cuanto la jugada 9 al punto 10 puede conducir solamente a la construcción, por las negras, de una fila larga, la cual está prohibida. Pero con todo ello las negras encuentran la victoria. Con la jugada 11 las negras conectan las fichas del «flanco superior» y ganan construyendo el tenedor 4 × 3.
El go es uno de los juegos más antiguos y más sabios en la historia de la humanidad. En la URSS este juego sólo desde hace poco empezó a ganar popularidad: se inauguran clubes, se celebran torneos; este juego se puede comprar en las tiendas. Es curiosa la opinión sobre el go del rey del ajedrez, E. Lasker: «Este juego, por la sencillez de sus reglas, supera al ajedrez, sin ser inferior que éste en la riqueza de la fantasía».
A pesar de la expresión aforística de Lasker, el go no es tan sencillo y el autor del libro no se arriesgaría describirlo sin un compañero de juego. Este capítulo está escrito con la participación activa del matemático y excelente jugador moscovita A. Goncharov, el cual está trabajando sobre la preparación de un programa del go para el ordenador.
Datos históricos. A juzgar por los hallazgos arqueológicos el go apareció hace cuatro mil años. La espesa neblina del tiempo ocultó de nosotros el secreto de su aparición. Aunque el juego es antiguo, pero por los problemas que plantea ante nuestro intelecto, parece un juego bastante moderno. La trayectoria de su difusión, que abarcó los países de Oriente, hoy día se extendió por casi todo Occidente.
Primeramente el go (con unos u otros nombres) se utilizaba como instrumento de la astrología. De acuerdo con el horóscopo de la persona que quiere conocer su futuro, sobre el tablero (cielo) se colocaban piedras (estrellas). Las piedras blancas simbolizan el bien y las negras, el mal. El «juego» comenzaba por su destino. De esta forma tan insólita para nosotros se expresaba el hecho de que cada persona es creadora de su destino. Poco a poco el go salió de los pañales astrológicos y de místico se transformó en un juego intelectual.
Para comienzos del primer milenio de nuestra era el go se puso de moda en los círculos de allegados a los imperadores y se igualaba a las artes reconocidas por aquel entonces de caligrafía y de arreglo de flores. Después de llamar la atención de Confucio, todos los sabios orientales consideraron digno dedicarse seriamente a este juego.
El siglo XVII se caracterizó por el desarrollo impetuoso del go, cuando el joven monje japonés Honinbo Sans abandonó el monasterio budista y encabezó la primera academia estatal de go. Lograda la posibilidad de dedicarse al arte del go, los mejores jugadores de aquellos tiempos empezaron a abrir escuelas con sus líderes y sus estilos de juego. La escuela japonesa de Honinbo durante trescientos años fue la mejor del mundo y por lo visto ésta es la causa de que el go generalmente se relacione con el Japón, llamándolo a veces damas japonesas.
El interés por el juego sigue creciendo, hoy día en los go-clubes del Japón tienen registrados millones de miembros, se editan libros y revistas, se organizan muchas competiciones. Ya tuvieron lugar seis campeonatos del mundo entre aficionados. En el último participaron más de cuarenta países. Los profesionales celebran sus competiciones aparte de los aficionados. En la URSS también hay muchos jugadores buenos y los mejores de ellos compiten, de igual a igual, con los maestros japoneses del go que visitaron varias veces la Unión Soviética.
La clasificación de los jugadores del go es diferente de la del ajedrez. En lugar de títulos y categorías en este juego se utilizan los ku y los dan. El escalón más bajo es el de 20 ku, tras él va el 19, etc., hasta el primero. A renglón seguido se adjudican los dan, desde el primero hasta el noveno. Para que dos jugadores de diferente categoría jueguen con interés entre sí, se utiliza el sistema del hándicap, es decir, en función de la diferencia en la clase de juego, el jugador más experimentado le da un avance al contrario de varias piedras, que éste pone sobre el tablero antes de comenzar el juego. La numeración de las categorías puede continuarse más allá de 20 ku. Entonces el juego del principiante se valora aproximadamente en 35 ku. Subrayemos que con el primer programa de máquina para el go ésta jugaba al nivel de 30 ku.
Es curioso que desde la introducción del go en Occidente, sus primeras «víctimas» fueron representantes de las ciencias exactas, a los cuales el juego les atrajo por la sencillez de sus reglas y al mismo tiempo por su original capacidad matemática. Con un análisis más profundo se descubren diferentes aspectos paralelos entre el go y tales partes de las matemáticas modernas, como la teoría de los grafos y la de reconocimiento de caracteres. No es casual que los especialistas en ordenadores se hayan interesado seriamente por este juego. A decir verdad el éxito de las máquinas en el go aún no es tan grande como en el ajedrez.
Descripción del fuego. Para jugar al go hay que disponer de un tablero y piedras de dos colores, blancas y negras. El tablero estándar se puede ver en la figura 74 (las cuadrículas no se pintan de colores). El campo sobre el que se juega está formado por 19 líneas verticales y 19 horizontales que se cruzan (en este juego se considera que el tablero es de 19 × 19, aunque, hablando ajedrecísticamente, sus dimensiones reales son de 18 × 18). Las líneas rectas se cruzan en 361 puntos (como en el rendsiu), sobre estos puntos precisamente se colocan las piedras.
Por lo general se utilizan 360 piedras, 180 de cada color, pero en la práctica son suficientes 150 por jugador. Algunas veces se utilizan tableros de menores dimensiones, así, por ejemplo, en la URSS se juega sobre un tablero de 13 × 13 y 90 piedras por jugador. Si usted no dispone de un juego especial, en lugar de piedras puede tomar fichas blancas y negras o botones de dos colores. Es muy fácil dibujar el tablero en una hoja de papel gruesa o sobre cartón.
Igual que en el reversi y en el rendsiu, en el go comienzan las negras. Los jugadores se turnan en sus movimientos, poniendo en uno de los puntos libres del tablero una piedra de su color. Las piedras, una vez puestas no se mueven de su lugar, pero pueden ser hechas prisioneras. El go es un juego «territorial», su finalidad consiste en ocupar el máximo de espacio sobre el tablero. Para ello los jugadores con sus piedras forman sobre el tablero cadenas, de las cuales después se componen los grupos.
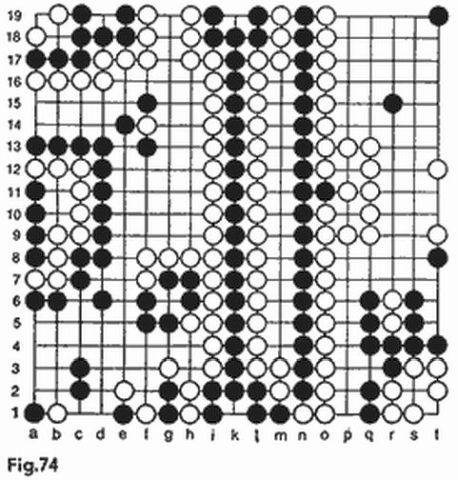
Una cadena es un conjunto arbitrario de piedras de un mismo color unidas entre sí (las piezas deben unirse por las líneas del tablero). Por ejemplo, en la figura 74 la línea n junto con la piedra o11 forma una cadena de 19 piedras negras y en las líneas desde i hasta m se forma una cadena de 25 piedras de ese mismo color.
Para cada piedra y cada cadena existe el concepto de grado de libertad. El número de grados de libertad de una piedra es igual a la cantidad de puntos libres vertical y horizontalmente adyacentes a la piedra. El número de grados de libertad de una cadena es igual a la suma de grados de libertad de sus piedras. Cuando queda sólo un grado de libertad, se dice que la piedra (o la cadena) se encuentra en posición atari.
En adelante acompañaremos las reglas con la descripción de algunos momentos del juego. Veamos el ejemplo de la figura 74. La piedra negra t19 en la esquina del tablero tiene dos grados de libertad: t18 y s19 y la piedra blanca t12, tres: t11, t13 y s12. La mayor cantidad posible de grados de libertad que puede tener una piedra es de cuatro, como, por ejemplo, el de la piedra negra r15. Si dos piedras, una negra y otra blanca, se encuentran sobre puntos adyacentes, el número de grados de libertad de cada una de las piedras disminuirá: se quitaron mutuamente un grado de libertad; ejemplo de ello son las piedras t9 y t8.
La cadena de dos piedras negras c2, c3 tienen seis grados de libertad y la cadena de piedras blancas r5, r6 se encuentran en posición atari, ésta sólo tiene un punto libre, el r7. Sólo un grado de libertad tiene también la cadena g7, h6, h7. Junto a ella se encuentra otra cadena de tres piedras negras, pero dichas cadenas no están unidas entre sí, por cuanto pasar por las piedras adyacentes de una cadena a otra no está permitido por las reglas.
Algunas cadenas situadas cerca, pero no relacionadas entre sí, pueden ser separadas con seguridad por piedras o cadenas del contrario. En este caso se dice que están separadas una de otra. Así en la figura 74 la cadena negra sobre la línea n está separada de la cadena negra en la línea k. Por arriba no se pueden unir, por cuanto las blancas ocupan el punto m19, y por abajo existe un corte diagonal. Sin embargo, habiendo dividido las fuerzas de las negras, la cadena blanca también se seccionó a sí misma respecto de sus piedras.
Si una cadena (o piedra) cualquiera se encuentra totalmente rodeada por las piedras del contrario, es decir, no le queda un solo grado de libertad, la misma se considera prisionera y se retira del tablero. Las piedras prisioneras se convierten en propiedad del contrario. En la figura 74, al poner una piedra blanca en d1, cae prisionera la piedra negra en el que se encuentra en posición atari (sobre el punto libre se pueden poner otras piedras). Si las negras juegan a f2, cae prisionera la piedra f1. De manera análoga caen prisioneras dos cadenas blancas (de dos piedras cada una), al poner piedras negras en los puntos h3 y r7, y en el caso cuando las blancas juegan a g7, caen prisioneras tres piedras negras.
Este último ejemplo debe ser examinado más atentamente. Si la piedra blanca se encuentra en g6, este «paracaidista» no adquiere ningún grado de libertad. Esta jugada está permitida solamente cuando la piedra colocada elimina el último grado de libertad de las piedras contrarias, es decir, las hace prisioneras. Si por el contrario, las mismas no caen prisioneras, la cadena atacada no se encuentra en atari, está prohibido ocupar un punto totalmente cercado. Por ejemplo, las negras no pueden ocupar los puntos ti y s2. Obsérvese que en nuestro ejemplo, después de retirar del tablero las piedras negras prisioneras g7, h6 y h7, la blanca en g6 queda libre.
Las cadenas y las piedras, sobre las cuales se cierne la amenaza de prisión, pueden salvarse añadiéndoles piedras nuevas. Digamos, la jugada de las blancas a r7 saca del estado de atari una cadena de dos piedras blancas, por cuanto la cadena larga formada ya tiene tres grados de libertad. De manera similar, poniendo una piedra en g6, las negras salvan tres de sus piedras, uniéndolas a otras tres. Como resultado se forma una cadena compuesta de siete piedras negras con cuatro grados de libertad y ya no resulta tan fácil rodearlas.
Una unión más importante de piedras es el grupo. Es el caso de una o varias cadenas que cercan aunque sea un punto del tablero. El espacio cercado por un grupo se llama ojo. Un mismo grupo puede rodear también varios ojos. Como podemos convencernos ahora, una condición suficiente de la capacidad de vida de un grupo es la presencia en él de por lo menos dos ojos cercados. Los grados de libertad de un grupo pueden dividirse en interiores y exteriores, pues el grupo no es una simple «valla» sino una cerca que rodea determinado espacio.
Con las piedras pueden ocuparse puntos que se encuentran tanto fuera del grupo como dentro de él. Un grupo cae prisionero, si en su jugada inmediata el adversario le deja sin grados de libertad. Pero si el grupo contiene dos ojos, prácticamente resulta imposible hacerlo prisionero. La figura 74 muestra un enorme grupo negro con dos ojos en k1 y k19 cercado por fuera. Más ¿cómo cercarlo por dentro? La jugada k1 no es posible por cuanto la piedra blanca que ataca se convertirá en presa de las negras. Por la misma razón tampoco se consigue aprisionar el grupo blanco con ojos en s2 y t1.
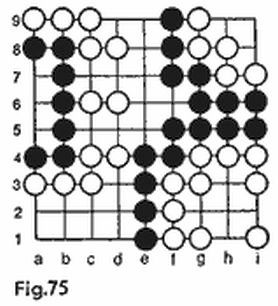
Para un grupo con un solo ojo no existe regla común de ataque y defensa. Examinemos algunos grupos «de un solo ojo» que se presentan con frecuencia, representados, para simplificar, sobre un tablero de 9 × 9 (fig. 75). En su lado izquierdo se encuentra un grupo negro con cinco grados de libertad: dos, c5 y c7, por fuera y tres, a5, a6 y a7, por dentro. Las blancas crearon un cerco seguro, oprimiendo a las piedras negras contra el borde del tablero. Los grados de libertad exteriores se liquidan con facilidad y el destino del grupo depende íntegramente del espacio interior. Las blancas pueden jugar a a6, después de lo cual al grupo negro le quedarán dos puntos libres, a5 y a7. Si las negras ocupan uno de estos puntos, las blancas, habiendo ocupado antes los puntos c5 y c7, ponen su piedra en el último punto libre y hacen prisionero a todo el grupo negro. Por lo visto las negras no tratarán de autodestruirse. En este caso las blancas harán la jugada al penúltimo punto interior libre. Las negras ocuparán el último grado de libertad común y aprisionarán dos piedras blancas. Pero esta es solamente una salvación temporal del grupo negro. El ojo disminuyó, en él quedaron sólo dos puntos libres, digamos el a5 y el a6. En la etapa posterior del ataque blanco se producirá el desembarco de una nueva tropa en el punto a6. Nuevamente al grupo negro le quedará un solo grado de libertad. Las negras aprisionarán una piedra blanca con la jugada a5, mas esto no varía nada, por cuanto el número de grados de libertad no aumenta. Una vez más las blancas pondrán sus piedras en el interior del grupo y lo retirarán íntegramente del tablero, consiguiendo nueve piedras negras prisioneras y espacio libre adicional. Estas adquisiciones, por lo visto, compensan plenamente la pérdida de tres piedras.
Hemos descrito con tanto detalle el ataque sobre un grupo de piedras con un solo ojo por cuanto representa parte de la base sobre la cual se configura la táctica del go. En el presente ejemplo la jugada de las negras a a6 garantiza la existencia del grupo, aún cuando el espacio interior de las negras disminuye. Puntos similares al a6 se llaman críticos. En función del turno de jugada, los jugadores, poniendo sus piedras, forman sus ojos o bien, por el contrario, tratan de evitar que el contrario los forme.
La figura 75 presenta dos grupos blancos con puntos críticos en i9 y h2. Sea de quien sea la jugada, uno de estos grupos perece y el otro se salva (cuando la jugada es de las negras, éstas, por supuesto, captarán al grupo mayor).
Si uno de los jugadores no logra formar un grupo con dos ojos en una cadena, puede intentar unir varias cadenas. Examinemos un grupo de seis piedras blancas con ojos en los puntos t1 y s2 (fig. 74). Dos cadenas no se unen entre sí, mas sin embargo, rodean con gran seguridad dos puntos libres.
Una situación especial, llamada ko, prohíbe la repetición de posiciones sobre el tablero. Presentemos un ejemplo. En la figura 76 la piedra negra a9 puede ser aprisionada con la jugada de las blancas a a8. Parecerá que ahora las negras, a su vez, continuando con la jugada a a9, pueden tomar la piedra blanca en a8. No obstante, de conformidad con la regla ko, esta jugada está prohibida, por cuanto después de realizarla la posición sobre el tablero se repite íntegramente. Solo apareciendo una piedra cualquiera en otro lugar del tablero, las negras podrán situar su piedra en a9.
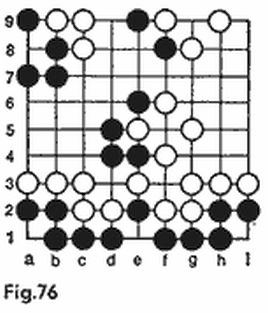
La figura 76 presenta las principales variedades de situaciones ko: el ko ya examinado en una esquina, el ko en el centro del tablero y dos variantes de ko en los lados del tablero. Examinemos atentamente el lado inferior del tablero en el que se forma el ko después de la jugada de las blancas a e1. A diferencia de los otros tres casos, aquí se decide el destino de un grupo grande de piedras. Si el punto e1 es ocupado por las negras, éstas obtendrán un sólido grupo con ojos. Supongamos que ahora le toque jugar a las blancas. Haciéndolo a e1 ellas retiran del tablero la piedra e2 y dividen las negras en dos grupos con escasa capacidad de vida. De acuerdo con la regla ko las negras no pueden responder inmediatamente a e2. Su misión es desviar la atención del adversario hacia otro lugar del tablero, después de lo cual, de todas las maneras, jugar a e2. Si por el contrario las blancas se hacen fuertes en el, al adversario se le forman dos grupos con un ojo cada uno condenado a la muerte. Semejante lucha por los puntos se denomina lucha ko y la regla ko se utiliza como un medio táctico muy fuerte. Con un ejemplo de la lucha ko volveremos a tropezar, al examinar una partida de go.
Conozcamos otra situación que se da con frecuencia sobre el tablero. La situación seki es la existencia pacífica obligada de cadenas con colores contrarios: el ataque por parte de una de ellas termina con su derrota. Los grados de libertad en la zona de seki son neutrales, no pertenecen a ninguno de los dos colores. Las dos variedades principales de seki se pueden ver en la figura 74. En uno de los casos son cadenas mutuamente rodeadas con dos grados de libertad comunes, b10 y b11, en el extremo izquierdo del tablero, en el otro, los grupos rodeados tienen un ojo cada uno y un grado de libertad común, b 18. En el segundo caso la situación presenta un seki, por cuanto jugar a los puntos a19 y b19 equivale al suicidio. La jugada bl8 también destruye al que la haga aún cuando no contradiga las reglas del juego. La figura 74 muestra otro ejemplo de equilibrio de fuerzas: dos cadenas con toda una línea de grados de libertad comunes, desde m4 hasta ml6. En cuanto queden los dos últimos puntos se cesará de ocupar los puntos libres de la línea m. Por consiguiente los 13 puntos sin ocupar son neutrales.
¿Cómo acaba la partida al go? En el curso del juego sobre el tablero se colocan, una tras otra, las piedras blancas y las negras. Algunas de ellas se hacen prisioneras y otras forman grupos activos. Por fin llega el momento en que uno de los jugadores se da cuenta de que su próxima jugada no le proporciona nada (piedras aprisionadas o puntos del territorio), sino todo lo contrario solo le puede ocasionar pérdidas. En tal caso dicho jugador pasa, es decir, se niega de su próxima jugada. Después de contestar el adversario, él puede volver a poner piedras. Pero, si el segundo jugador pasa inmediatamente después del primero, la partida termina y ambos jugadores pasan al recuento de los puntos. Los jugadores con experiencia, por supuesto, pasan solamente cuando ven que el juego en adelante no ofrece cambios esenciales sobre el tablero. Por lo general esto significa que el tablero está dividido en los territorios blanco y negro.
Para hacer el recuento de los puntos primero, con las piedras no expuestas, se rellenan los puntos neutrales colindantes tanto con las piedras blancas como con las negras (estos puntos no se tienen en cuenta para el recuento). Después de esto sobre el tablero quedan sin rellenar sólo los puntos que presentan los ojos de los grupos. Por cada uno de estos puntos dentro de los ojos de un mismo color al jugador se le adjudica un punto, también le proporciona un punto cada una de las piedras presas. Gana el que contabilice mayor número de puntos. Para no contar por separado los puntos vacíos del territorio de los adversarios y las piedras aprisionadas, se procede así. Los puntos vacíos del territorio que ocupan las blancas se rellena con las piedras blancas aprisionadas y sobre el territorio que ocupan las negras se colocan, respectivamente, las piedras negras aprisionadas por las blancas. Como resultado el recuento se simplifica. Un ejemplo de recuento de los puntos obtenidos será dado en la partida que se expondrá más adelante.
La estadística del go sobre tableros de 19 × 19 muestra que si la fuerza de los jugadores es aproximadamente igual, las negras, que son las que comienzan la partida, como promedio ganan con una ventaja de 5 puntos. Por esto, de conformidad con las reglas modernas, a las blancas se les añade cinco puntos durante el recuento de éstos. Al jugar con puntos de ventaja, en el caso de igualdad de puntos, gana el que dio el avance. Así pues, en el go no existen tablas.
Repitamos brevemente las reglas del juego.
1. Comienzan las negras. Las jugadas se hacen por turno (el pase también es una jugada).
2. Se prohíben jugadas que conduzcan a la repetición de las posiciones sobre el tablero (se tiene en cuenta no solo la disposición de las piedras, sino también el orden de las jugadas). En la mayoría de los casos esto se relaciona con la situación ko.
3. La piedra (o el grupo de piedras) sin grados de libertad se retira del tablero, al ocupar el último grado de libertad.
4. No se permite liquidar el último grado de libertad de sus propias piedras, si en este caso no se aprisionan las del adversario.
5. El juego termina después de pasar dos veces seguidas.
6. Gana el que obtenga la mayor parte del territorio (después de colocar las piedras aprisionadas sobre el territorio del contrario).
Para mejorar la comprensión de las reglas y los momentos del juego que hemos mencionado examinemos unos problemas interesantes (fig. 77) compuestos por el japonés Maeda Nobuaki, jugador de noveno dan (grado superior de maestría).
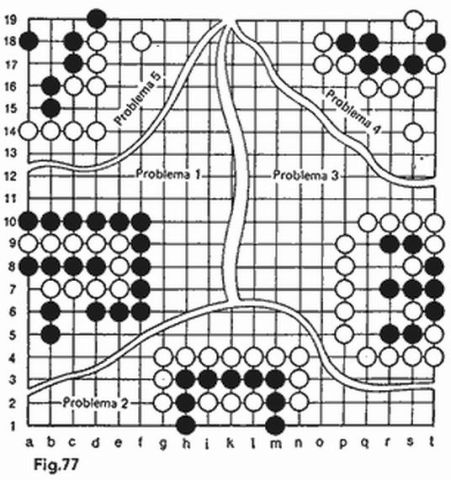
Problema 1. Jugada de las negras. ¿Cómo aprisionar una cadena blanca que rodea cuatro piedras negras?
Solución. 1.a7; 2.a6; 3.a7; 4.a8; 5.c8. Ahora el grupo de piedras blancas no se encuentra en condiciones de formar dos ojos, por cuanto el punto c8 es crítico y el punto a7 no es un ojo.
Problema 2. Jugada de las negras. ¿Cómo eludir el aprisionamiento?
Solución. 1.k1! Única jugada. Las negras formaron varios seki y a pesar de que dentro de su grupo se encuentran tres piedras blancas, el adversario no puede sacrificarlas. La cadena sacrificada resultará encorvada, lo cual permitirá a las negras construir dos ojos.
Problema 3. Jugada de las blancas. ¿Cómo aprisionar todas las piezas negras?
Solución, 1.q7; 2.r8; 3.r6; 4.g6; 5.r6. Las negras no pueden salvarse, a la jugada 6.q5 resuelve la jugada 7.s6; y a la 6.s6, 7.g5. En este problema la primera jugada de las blancas no es única.
Problema 4. Jugada de las negras. ¿Cómo salvar el juego?
Solución. 1.r19; 2.s18; 3.p19; 4.t19; 5.r18; 6.t16; 7.t18. Las negras formaron dos ojos, q19 y s18, s19, t19. Si las blancas en su jugada seis unieran sus tres piedras a la piedra t17 jugando a t18, entonces después de 7.t16 el adversario aprisionaría cinco piedras en vez de tres.
Problema 5. Jugada de las blancas. ¿Cómo aprisionar el grupo negro?
Solución. 1.b17; 2.a17; 3.a15; 4.a16; 5.b19! Si ahora las negras juegan 6.b18, le sigue la respuesta 7.c19 y, sacrificando dos piezas, b19 y c19, las blancas liquidan un ojo de las negras. Si las negras cierran inmediatamente la salida de su grupo mediante cl9, las blancas con su jugada a b18 reúnen tres de sus piedras y, después de aprisionarlas, la jugada b18 les conducirá a la posición con un punto crítico, igual que en el problema 1.
Partida entre dos jugadores inexpertos. En el ejemplo de una partida sobre un tablero de estudio de 9 × 9 explicaremos algunas reglas del go. Para la anotación de la partida es cómodo mostrar los números de las jugadas directamente sobre las piedras. Por cuanto la numeración es corrida, las jugadas de las negras siempre son números impares y las de las blancas, números pares (a excepción del juego con cesión de puntos, en el que comienzan las blancas). Si la jugada se hace al punto que antes estaba ocupado por otra piedra, ambos números se anotan juntos debajo del diagrama.
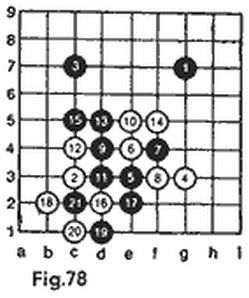
Las jugadas 1 – 21 están indicadas en la figura 78. Las primeras cuatro piedras fueron puestas por los jugadores en diferentes ángulos del tablero. Realmente, hacerse con el territorio en las zonas de los ángulos es más fácil, pues ayudan los extremos del tablero. Después de la quinta jugada se presentan complicaciones. Con su jugada a e3 las negras penetran en el dominio potencial de las blancas, con el fin de molestar al adversario en el rodeo de la parte inferior del tablero. Las blancas emplean una defensa activa, «sorprendiendo» una piedra negra con su jugada 6. Con sus jugadas 7 y 9 las negras muestran que no tienen objeción de que el juego se desarrolle así, esperando obtener buenas posibilidades de cercar el centro del tablero. No obstante con la jugada 10 las blancas no entregan la piedra 6. Las negras se ven obligadas a unir en cadena sus piedras con la jugada 11. Ahora las blancas deben defender el ángulo inferior izquierdo contra las fuerzas superiores de las negras (cadena 9, 11, 5). Las blancas comienzan la construcción de la cadena con la jugada 12, tratando de defender con ello el ángulo inferior izquierdo. Las negras con su jugada 13 alargan su cadena, persiguiendo tres fines: hallarse más cerca de la piedra 3 que se encuentra en el ángulo, salir del flanco izquierdo, si las blancas responden por la derecha, y salir hacia el flanco derecho, si es que las blancas responden por la izquierda. Las blancas estabilizan el flanco derecho. Como resultado de ello, la piedra 7 cae en la posición atari. Con su jugada 15 las negras salen al flanco izquierdo. La posición de las blancas se torna peligrosa y con sus próximas jugadas tratan de colocar sus piedras de tal manera que puedan obtener un grupo en acción. Por ahora las blancas no lo consiguen y después de la jugada 21 surge la amenaza de ko y la situación del grupo ahora depende de quién gane en la lucha ko.
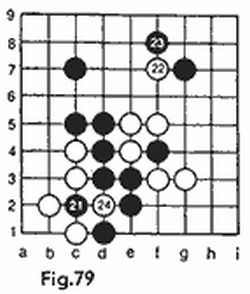
Jugadas 21 – 24 (fig. 79). Según la regla ko las blancas no pueden con su jugada 22 hacer prisionera a la piedra 21, la cual molesta a la formación de ojos y con la jugada 22 crean la amenaza ko, atacando la piedra negra que se encuentra en el ángulo. Con la jugada 23, las negras defienden el rincón, pero las blancas en respuesta hacen prisionera la piedra 21.

Jugadas 24 – 31 (fig. 80). Después de crear la amenaza ko con la jugada 25, la piedra blanca 17 se verá en la posición atari. Y con todo ello no es muy acertado, para las negras sería mejor crear la amenaza ko con la jugada g4, pretendiendo jugar a g5 y dominar la mitad superior del tablero. Las blancas con su jugada 26 alargan la cadena e4, e5, f5 y las negras se verán en' peligro. Para no preocuparse de la parte superior del tablero, para las negras sería mejor poner en la jugada 27 su piedra en e7, haciendo prisionera la piedra blanca. Mas ellas se entretienen con la lucha ko y toman la piedra inferior. Las blancas se aprovechan de ello: después de hacer prisionera la piedra negra f6, con la jugada 28 crean una agrupación fuerte en el flanco derecho. Además resulta que dos piedras negras en el ángulo superior derecho no cumplen su función defensiva y necesitan refuerzo.
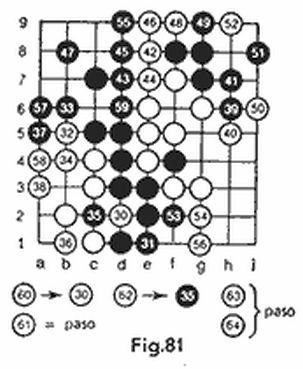
Con la jugada 29 las negras tratan de arreglar la situación. Las blancas aprisionan la piedra 27 (con la jugada 30 al sitio 24), y las negras, esta vez, sin una fuerte amenaza ko se defienden con la jugada 31.
Jugadas 32 – 64 (fig. 81). Aprovechando la imprecisión en la jugada de las negras, las blancas tratan de estabilizar su grupo de la esquina con la jugada 32. La jugada 33 obstaculiza el avance de las blancas hacia arriba y crea el peligro de separación de la piedra blanca b5. Las blancas reaccionan con la jugada 34. Ahora las negras por medio de una amenaza ko tratan de impedir la formación de ojos. Las blancas defienden la piedra el con la jugada 36, lo cual es un gran error. En este momento de gran responsabilidad debía jugar 36.a3. En este caso el grupo blanco conservaría la posibilidad de sobrevivir, ganando la lucha ko en el ángulo inferior izquierdo (por ejemplo, 36.a3; 37.b1; 38.a5; 39.a2; 40.a1 o bien 37.a5; 38.b1 y el grupo se conserva sin lucha ko). Ahora las negras podrían hacer prisionero el grupo blanco en la esquina, pero no encontraron la combinación. La jugada 37 reduce los ojos del grupo, sin destruir éste. Había que poner una piedra en el punto a3. Las blancas ocupan este punto crítico y esperan.
Para las negras resulta claro que el grupo blanco aguantó la presión y con la jugada 39 inician la formación de su propio grupo en la esquina contraria del tablero. Sin embargo, esta jugada es demasiado pasiva, conduce a la pérdida de la iniciativa. Las blancas limitan fácilmente la propagación de las negras y realizan la importante jugada 42 con la que se ataca simultáneamente dos grupos negros que aún no tienen ojos. Las negras fortalecen el ángulo izquierdo superior, pero la jugada 46 no les permite unirse en el ángulo derecho. La jugada 47 es de la categoría de pavorosas, mejor sería obtener un ojo, seguido de d6. Por otra parte, la jugada 46 es igualmente imprecisa: más lógico sería incluir el intercambio de jugadas: las blancas d6, las negras c6. Después de la jugada 48 el grupo de las negras está condenado a la derrota, aún cuando intentan defenderse con la jugada 51. Mas con la jugada 52 las blancas ocupan el segundo punto crítico, h9.
Habiéndose resignado con las pérdidas, las negras intentan, en su jugada 53, desplazar la posible frontera hacia las zonas restantes del tablero, pero ellas tenían una jugada mucho más efectiva para disminuir el territorio de las blancas en el lugar dado, y más precisamente la jugada h2! Las blancas no están en condiciones de rechazar esta piedra negra, y el territorio de las blancas en la esquina se reduce mucho. Mejor que la jugada 55 sería g1 (55.g1; 56.h1; 57.f1; 58.h2). En la jugada 56 las blancas seguidas de las negras se negaron equivocadamente de d6. En respuesta a la jugada 57, las blancas, por supuesto, ponen su piedra en a4. Por fin se hace la jugada 59.d6. Con la jugada 60 (al lugar 30) las blancas hacen prisionera la piedra 35.
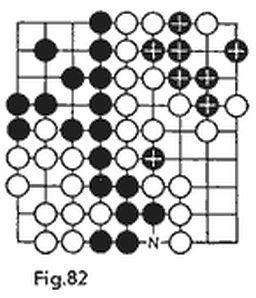
Las negras pasan, suponiendo que ninguna de sus jugadas mejora la situación, aunque 61.g5 permitiría ganar un punto en la lucha ko. Las blancas cierran la lucha ko con la jugada 62. Las fronteras están formadas, el juego terminó. Resta llevar el tablero a un aspecto cómodo para el recuento de los puntos y contar éstos.
La figura 82 presenta el tablero después de hecha la última jugada. Con la letra N está indicado el punto neutro (no pertenece a nadie), por ello se puede ocupar con una piedra cualquiera. Las piedras marcadas con el signo «más» están condenadas a la prisión, se permite retirarlas del tablero y sumarlas a las piedras ya capturadas.
Hagamos el resumen de la partida jugada al go (fig. 83). Las negras aprisionaron tres piedras blancas y las blancas cuatro piedras negras. Otras ocho piedras están condenadas (están marcadas con el signo «más»), es decir, la relación de piedras prisioneras es de 12:3 a favor de las blancas.
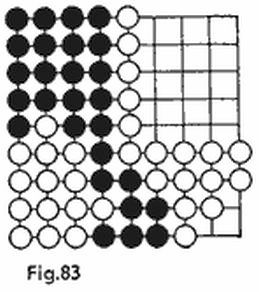
Las negras ponen las piedras prisioneras sobre el territorio de las blancas, y las blancas hacen lo propio en el territorio de las negras. A las blancas les quedaron otras cuatro piedras prisioneras que el territorio de las negras no pudo ubicar. Así pues, el territorio de las blancas consiste de 23 puntos, las negras a su vez, en general, no tienen conquistas. Las blancas tienen también cuatro piedras prisioneras y aún sin considerar los 5,5 puntos ellas ganaron con una ventaja de 27 puntos.
Capítulo 6
Treinta juegos para finalizar
| § 1. Taktix | § 16. Tome una cantidad par |
| § 2. Chasqueo | § 17. Bolos |
| § 3. ¿Quién tiene menos? | § 18. Twopins |
| § 4. «Mediocridad» | § 19. Es barato, caro o razonable |
| § 5. Sim | § 20. Trihex |
| § 6. Plantón | § 21. Temor al cuadrado |
| § 7. Cuatro colores | § 22. Marel |
| § 8. Oua | § 23. Coche de la policía |
| § 9. Cerco de la tropa de desembarco | § 24. Black |
| § 10. Los lobos y las ovejas | § 25. En camino |
| § 11. Cajista | § 26. Diez y cinco kopeks |
| § 12. Cernícalo | § 27. Juego militar francés |
| § 13. Cernícalo real | § 28. Vacas y leopardos |
| § 14. Lotería de palabras | § 29. Focus |
| § 15. Erudit | § 30. Ajedrez de Dawson |
Los juegos matemáticos recreativos, de los cuales hemos hablado hasta aquí, están clasificados, sistematizados y divididos por nosotros en seis tipos, seis grupos (en algunos casos esta división es condicional). No obstante muchos juegos existentes no están descritos por nosotros, en algunos casos se describen de pasada, en otros no caben en nuestra clasificación; la fuerza y carácter inagotable de los juegos intelectuales no permite limitarlos con ciertos marcos rígidos dados. Como conclusión presentaremos precisamente treinta juegos diferentes, para los cuales no se halló lugar en los cinco capítulos principales del libro.
§ 1. Taktix
Sobre un tablero de n × n casillas se colocan fichas iguales, una sobre cada casilla. Los jugadores, cogen por turno las fichas de cualquier fila vertical u horizontal, además, obligatoriamente, seguidas, no se permite dejar pasar las casillas vacías. Pierde el que coja la última ficha.
Ya en el caso de valores pequeños de n el juego resulta bastante complejo. Para un tablero de 3 × 3 es fácil convencernos de que el primer jugador gana si coge la ficha central o la de uno de los ángulos o toda la fila central. El análisis del juego sobre un tablero de 4 × 4 no es tan simple, está demostrado que el segundo jugador dispone de una estrategia que gana. El taktix se asemeja al nim pero el análisis del juego, cuando n > 4 se complica grandemente a causa de la utilización de filas de fichas que se cruzan.
§ 2. Chasqueo
En este juego las fichas llenan un tablero arbitrario m × n. La jugada consiste en lo siguiente. Uno de los jugadores elige una casilla cualquiera del tablero, traza mentalmente por esta casilla dos rayos mutuamente perpendiculares hacia arriba y a la derecha y después retira del tablero todas las fichas que se encuentran dentro del ángulo recto, las «corta». Pierde el que se vea obligado a «cortar» la ficha del ángulo inferior izquierdo.
Para dos casos particulares de este juego se conocen las estrategias que conducen a la victoria. Sobre el tablero n × n el primer jugador gana si «corta» un cuadrado cuyos lados son de n – 1. En el rectángulo 2 × n el que empieza consigue la victoria, si «corta» la ficha situada en el ángulo inferior derecho. En la fila inferior, en tal caso, quedará en una ficha más que en el superior y el primer jugador debe restablecer esta relación en cada jugada que hace.
§ 3. ¿Quién tiene menos?
Cada jugador piensa un número desde el 1 hasta el 5 y los comparan. Si coinciden o se diferencian en más de una unidad, cada jugador recibe un número de puntos coincidente con el número que pensó. Si por el contrario los números se diferencian en una unidad, en este caso el jugador con el número menor recibe una cantidad de puntos igual a la suma de los números pensados. El juego dura diez rondas y después de cada una de ellas se suman los puntos. Gana el que acumule mayor número de puntos.
Para analizar este complicado juego estratégico es preciso componer una matriz especial: la tabla de las posibles variantes de las jugadas y de la correspondiente distribución de los puntos. El plan de acción óptimo se halla por los métodos de la teoría matemática de juegos.
§ 4. «Mediocridad»
Este es un ejemplo de juego para tres personas. En cada ronda los tres participantes eligen un número compuesto de determinado conjunto de cifras, además los puntos se apuntan sólo al jugador que haya elegido el número intermedio de los tres, al más «mediocre». El número de puntos que se le adjudica coincide con el pensado. El juego dura diez rondas y gana el que consiga la cantidad intermedia de puntos. La estrategia de este juego es muy compleja.
§ 5. Sim
Sobre una hoja de papel en redondo se dibujan varios puntos. En su jugada de turno cada uno de los jugadores traza una línea de su color que une cualesquiera dos puntos. Pierde el jugador que se vea obligado a construir un triángulo de su color con los vértices en estos puntos.
Si el número de puntos es inferior a 5, el juego termina muy rápido en tablas. Teóricamente las tablas son posibles también cuando los puntos son cinco pero el juego ya es bastante interesante. En el caso de seis puntos se ha encontrado la estrategia victoriosa para el segundo jugador. Si el número de puntos es mayor de seis, el análisis del juego resulta muy complicado. Está demostrado que las tablas están excluidas, pero la cuestión de las estrategias victoriosas sigue abierto.
El sim es un juego sobre grafos y para su investigación detallada se utiliza la teoría matemática de los grafos.
§ 6. Plantón
Sobre una hoja de papel se dibujan varios puntos, a partir de los cuales comienzan a crecer los «plantones». En su jugada consecutiva cada uno de los jugadores traza una línea (el «plantón germina») que une un punto con otro o bien describe un lazo y vuelve al punto inicial. Además dibuja sobre la línea un punto nuevo. La línea no debe tener intersecciones consigo mismo, cruces con líneas trazadas anteriormente, ni pasar por puntos que no le sirvieron de inicial o final. Por fin, de cada punto no se deben trazar más de tres líneas (gérmenes). Pierde el que no pueda trazar una línea sin infringir las reglas.
El «plantón» es un juego clásico de grafos; al buscar estrategias ganadoras, se utilizan también algunas propiedades topológicas del plano. Está demostrado que la partida dura no más de 3n – 1 jugadas, donde n es el número de puntos al iniciarse el juego. No cuesta trabajo convencerse, de que seleccionando las variantes, cuando n = 1, 3, 4 o 5 y jugando correctamente, siempre gana el primer jugador y cuando n = 2, el segundo. Para el caso de n ≥ 6 aún no se pudo aclarar todo incluso con ordenador.
§ 7. Cuatro colores
Para jugar se necesitan cuatro lápices de colores. El primer jugador dibuja un área arbitraria. El segundo pinta esta área de cualquier color y le adjunta otra área. El primer jugador pinta esta área nueva y añade otra, etc. De esta manera en cada jugada uno de los participantes pinta el área marcada por el adversario y traza la suya. Además las áreas adyacentes, con frontera común deben quedar pintadas de diferente color. Pierde el que en su jugada consecutiva, para pintar correctamente, se vea obligado a utilizar un quinto color.
Este juego tiene relación con el antiguo «problema de los colores», del cual se ocuparon muchos matemáticos: cuál es la cantidad mínima de colores necesarios para pintar un mapa geográfico cualquiera con la condición de que los países fronterizos siempre resulten pintados de diferente color. Hace relativamente poco tiempo los matemáticos norteamericanos T. Appel y M. Jeiken, con ayuda de un ordenador, demostraron que para pintar un mapa cualquiera es suficiente disponer de cuatro colores. De manera que, en principio, este juego puede continuar hasta el infinito. Mas una cosa es la teoría y otra, completamente diferente, es la práctica...
§ 8. Oua
Uno de los juegos más simples, en el que se trasladan bolas (piedras); más populares son el kalaj y el chisolo. Dos jugadores disponen de una fila de siete hoyos cada uno, en cada uno de los cuales hay por cuatro bolas. La jugada consiste en sacar todas las bolas de cualquiera de los hoyos de su fila y repartirlas de uno en uno en el resto de los hoyos (suyos y ajenos) moviéndose en dirección de las agujas del reloj. Si en una de las jugadas de un hoyo se extrajeron 12 y más bolas, entonces en el caso de la distribución en redondo, al llegar a este hoyo hay que dejarlo pasar, dejarlo vacío. Si durante la distribución de las bolas por los hoyos, la última se deposita en el hoyo extremo derecho de su parte o en cualquier hoyo de la parte adversaria y además en el hoyo habían 2 o 3 bolas, entonces el jugador de turno recoge del hoyo todas las bolas como «presas». Él recoge también sucesivamente todas las bolas de los hoyos anteriores del contrario, en los cuales también hay 2 o 3 bolas, pero no más allá del hoyo en el que hay una cantidad distinta de bolas. El juego termina si la cantidad de bolas sobre el tablero es insuficiente para formar una «presa». Se convierte en ganador el que tenga una «presa» mayor. El juego termina también, si uno de los jugadores se encuentra con los hoyos vacíos, en tal caso éste pierde.
§ 9. Cerco de la tropa de desembarco
El juego que ofrecemos es otra variante del juego de cruces y ceros sobre un tablero infinito (sobre una hoja de papel cuadriculado). El primer jugador dibuja una cruz en cualquiera de las cuadrículas. A continuación, en cada una de sus jugadas, pone una nueva cruz sobre una cuadrícula vacía, adyacente con la cruz antes marcada (las vecinas tienen un lado o el vértice común). El segundo jugador tiene permitido poner dos ceros en una jugada en cualesquiera dos cuadrículas adyacentes. Su misión es conseguir que el adversario no pueda poner su sucesiva cruz. El primer jugador, por lo visto, cada vez trata de escapar a la presión de los ceros.
§ 10. Los lobos y las ovejas
Este juego de fichas es uno de los más simples y más populares. En la primera horizontal de un tablero común hay cuatro fichas blancas (los lobos), en la última, una ficha negra (la oveja). En una jugada cualquiera de las fichas puede desplazarse a la casilla negra adyacente diagonalmente, pero los lobos tienen prohibido el retroceso. La oveja trata de alcanzar la primera diagonal y los lobos, por el contrario, intentan cazar a la oveja, es decir, encerrarla, de manera que a la ficha no le queden jugadas que hacer. Está demostrado que, actuando correctamente, el éxito corresponde a los lobos, o sea ganan las blancas.
§ 11. Cajista
El juego test «acertar la palabra» que examinamos en el capítulo primero es uno de los muchos juegos conocidos de palabras, aunque se distingue de entre ellos por sus propiedades lógicas y combinatorias. Los juegos y diversiones con palabras, por su popularidad, ocupan unos de los primeros puestos entre otras formas de ocio. ¿Quién de nosotros, en sus horas de descanso, no resolvió con entusiasmo crucigramas, charadas, jeroglíficos, criptogramas y otros rompecabezas de palabras? Los juegos de palabras desarrollan la cultura del habla, aumenta la erudición y el horizonte intelectual, enseñan a utilizar los diccionarios. No poca importancia tienen ellos también para el desarrollo del pensamiento y del lenguaje, por esta razón los utilizan con frecuencia los educadores. Estos juegos no sólo permiten entrenar la memoria y revelar la erudición, sino también profundizar en las particularidades del idioma, comprender la estructura de la formación de las palabras. No es casual que en su «Libro sobre el idioma», excelente obra perteneciente a la pluma del conocido filólogo popularizador norteamericano F. Folsom, se pueden hallar juegos y pasatiempos de palabras.
El «cajista» es uno de los más difundidos entre los juegos de palabras. Se toma una palabra cualquiera y con sus letras se componen otras palabras. Como de costumbre se utilizan sólo nombres sustantivos comunes en su forma inicial, en singular, en el caso nominativo y nada de palabras cariñosas y en diminutivo. Gana el que consiga componer mayor número de palabras. A propósito, con frecuencia se tiene en consideración la originalidad de las palabras y la cantidad de letras en ellas. Por ejemplo, si son cuatro los que juegan, la palabra hallada por solo uno de los participantes se valora en 3 puntos, la hallada por dos, en 2 puntos y la hallada por tres, en un punto, pero si la anotan todos los jugadores, esta palabra simplemente se tacha (0 puntos).
De los jugadores al «cajista», además de erudición y gran reserva de palabras, se requieren hábitos de combinación pues han de realizarse no pocas combinaciones de letras y palabras. Puede ser que por eso en los encuentros entre personas con estudios técnicos superiores y personas con estudios humanitarios los primeros ganen con mayor frecuencia...
§ 12. Cernícalo
En este juego de palabras, quizás el más popular, podemos arreglárnoslas sin papel y lápiz, y jugar, como dirían los ajedrecistas, a ciegas. El primer jugador nombra una letra arbitraria, el segundo añade una letra a la derecha o a la izquierda de aquélla, teniendo en mente una palabra determinada. El siguiente (o nuevamente el primero, si son dos los que juegan) igualmente añade una letra por uno de los lados, teniendo en cuenta su propia palabra, etc. El que en su jugada consecutiva se vea obligado a terminar la palabra, o simplemente no tiene letra que poner (por cuanto no acierta a continuar las letras ya escritas hasta una palabra) pierde su baza y como castigo recibe la letra «c». En su segunda derrota la «c» se transforma en «ce», luego en «cer» y finalmente uno de ellos se convierte en «cernícalo».
En este juego se acostumbra poner las letras en sus extremos, pero nada nos impide ponerlas en el interior del «semifabricado». Precisamente así se juega al «anticernícalo». En este juego todo es al revés, cada participante trata de terminar la palabra, además hacer esto la mayor cantidad posible de veces. En el momento en que los contrincantes no ven la posibilidad de continuar la última palabra, el juego se detiene y se hace el recuento de los puntos.
§ 13. Cernícalo real
El juego habitual al cernícalo permite las distintas generalizaciones. Una de ellas, el anticernícalo, ya la hemos expuesto. En algunos casos se juega, poniendo las letras no sólo por la derecha y por la izquierda, sino también por arriba, por abajo y en diagonal. Si el juego tradicional es lineal, en estos casos se obtiene una variante plana. E. Iodkovski propuso llamar esta modalidad interesante del juego cernícalo real.
Sobre un cuadrado de 5 × 5 se escribe en su horizontal media una palabra de cinco letras. A continuación los participantes del juego, por turno, van escribiendo por una letra en las casillas vacías del «tablero» adyacentes con una o varias casillas en las que ya hay letras. Con las letras escritas (no todas, obligatoriamente) debe formarse una palabra nueva que se lee como una serie de jugadas del rey del ajedrez por el tablero. La cadena de letras de las que se forma la palabra es ininterrumpible y no se interseca consigo mismo, es decir, el rey no pasa por una misma casilla dos veces. Por cada palabra que se forma en la jugada dada se asigna un punto. Después de formar veinte palabras (el número de casillas libres sobre el tablero) el juego termina, pasando al recuento de los puntos.
En este juego se ha tomado del «cernícalo» tradicional el principio fundamental, la adición de letras, y del ajedrez, la formación de palabras mediante las jugadas del rey. Esto es un híbrido curioso del ajedrez con el juego de palabras.
Al cernícalo real pueden jugar dos, cuatro o cinco, por cuanto la división de la cifra 20 por 2, 4 y 5 es exacta y por consiguiente, los oponentes tendrán igual cantidad de palabras. Para jugar tres personas el tablero debe ser mayor, 6 × 6 y la palabra inicial de seis letras, en este caso cada jugador tendrá al final 10 palabras. Por supuesto que para ganar en este juego en cada jugada hay que idear palabras lo más largas posible, utilizando un número máximo de letras ya inscritas.
§ 14. Lotería de palabras
En nuestro siglo impetuoso, en que queda tan poco tiempo para relacionarse, la lotería numérica clásica puede ofrecerse como un buen medio para los encuentros amistosos. Rellenando sin prisas los cartones con números, se
puede discutir alguna cuestión interesante, como lo hacen los héroes de las obras de Chéjov. Mas como actividad intelectual, la lotería no es la mejor muestra, aquí no hay que romperse la cabeza. Otra cosa es la lotería de palabras. Igual que en el cernícalo real, sobre una hoja de papel se dibuja un cuadrado, por ejemplo, de 6 × 6. En el curso del juego sus casillas se rellenan con letras de tal manera que vertical y horizontalmente se pueda leer un mayor número de palabras. En su jugada uno de los participantes pronuncia una letra cualquiera y los demás jugadores la apuntan en las casillas vacías del cuadrado. El juego sigue hasta llenar todo el cuadrado, después de lo cual se hace el recuento de puntos. Para estimular palabras más largas, se introduce la siguiente escala: por una palabra de seis letras, 20 puntos, por una de cinco 10 puntos, por una de cuatro, 5 puntos, por una de tres, 2 puntos. Las palabras de dos letras, así como las que forman parte de otras más largas, no se consideran para la puntuación.
§ 15. Erudit
Este juego basado en el «scrable» norteamericano seguramente es uno de los juegos de palabras más interesantes, que engloba momentos lógicos y combinatorios con elementos de los crucigramas e incluso del dominó.
Se juega sobre un tablero de 15 × 15. La «banca» dispone de 131 fichas, cada una de las cuales tiene dibujada una letra y una cifra que la valora. Igual que en el dominó, cada jugador toma siete fichas y las tiene en secreto de los otros jugadores. En una jugada se pueden componer varias palabras (por las verticales y las horizontales del tablero) con las fichas disponibles y las ubicadas sobre el tablero. No se puede formar una palabra sin tomar en consideración las anteriores, es decir, debe obtenerse de ciertas letras de las palabras ya escritas más una letra adicional. De esta manera, todas las palabras se cruzan igual que en un crucigrama. Una vez hecha la jugada, igual que en el dominó, el jugador completa sus fichas hasta la cantidad de siete, que toma de la banca.
Por cada nueva palabra se asigna tal cantidad de puntos, cuantos llevan escritos todas las letras que forman dicha palabra. El tablero dispone de ciertas casillas de color que modifican la valoración de las fichas. A la letra que ocupe la casilla verde se le dobla el número de puntos y a la que se halle en la amarilla, se le triplica. Si una de las letras ocupa la casilla azul se duplica la suma de puntos de toda la palabra y si ocupa la roja se triplica. El juego continúa o bien hasta cierto número de puntos, por ejemplo, hasta 200, o bien hasta acabar con la banca. No presentamos aquí el dibujo del tablero por cuanto este juego se encuentra en el mercado y seguramente usted no intentará hacerlo por su cuenta.
Es curioso que en la elaboración del «erudit» no se pudo evitar la injerencia de las matemáticas. Al resolver la cuestión sobre la cantidad de fichas de tal o cual letra que debe tener la banca y qué precios deben tener las letras, debe realizarse un análisis de frecuencia del diccionario de la lengua. Como material para este tipo de investigación se utilizan diferentes textos sobre la base de los cuales se juzga acerca de la frecuencia con que se repiten las distintas letras. Existen muchos trabajos sobre este tema, incluso fueron creados diccionarios especiales para estos fines. Sin embargo, utilizarlos para jugar al «erudit» no es tan simple. Pues además de la frecuencia de las letras hay que tener en cuenta su posición dentro de la palabra: unas letras se encuentran con más frecuencia al principio de la palabra, otras al final. Además en este juego se admiten sólo nombres sustantivos en singular y en nominativo. Por otra parte la distribución de las palabras en estas partes de la oración se distingue de la de otras que no se permiten utilizar en este juego. Todas estas particularidades fueron tomadas en cuenta al elaborar el «erudit».
§ 16. Tome una cantidad par
Es una variante no habitual del nim que se describió anteriormente. En un montón hay n piedrecitas y dos jugadores por turno toman de él no más de m piedrecitas (m < n). Gana el que al final del juego tenga acumulado un número par de piedrecitas. Merece la pena analizar más detalladamente el caso n = 13, m = 4.
§ 17. Bolos
Las fichas (bolos) se colocan sobre la mesa en varias filas. Haciendo su jugada sucesiva, un jugador puede tomar una ficha o dos vecinas de una fila. Gana el que «tumbe» el último bolo. El juego se complica a partir de tres filas de a 5, 6 o 7 bolos en cada una.
Esta complicación del nim fue propuesta por Dudeney. La idea y el nombre los adoptó de un juego muy popular en el siglo XVI. Esta diversión antigua consistía en tumbar con una bola los bolos colocados en una fila, con la particularidad de que se permitía tumbar uno o dos bolos situados al lado. Este juego se somete a análisis por medio de un sistema doble aunque más complejo que en el nim. El estudio matemático profundo de semejantes juegos no es el objetivo de este libro.
§ 18. Twopins
El nombre del juego viene del inglés y significa dos bolos. Los bolos (fichas) se colocan en filas y en columnas. Cada columna consta de uno o dos bolos. Los jugadores retiran por turno cualquiera de las columnas de dos bolos o dos columnas vecinas (retirar columnas de una sola ficha no está permitido). El que tumbe el último bolo, gana. Al final del juego, por lo visto, puede quedar alguna que otra ficha.
El análisis de este juego, inventado por E. Berlekamp, es muy complejo, por cuanto para cada columna existen dos variantes: 1 o 2 bolos; el número total de posiciones iniciales a partir de n columnas es de 2, pero muchas de ellas son equivalentes.
§ 19. Es barato, caro o razonable
En un papel se escriben las palabras «barato», «caro» y «razonable». Debajo de estas palabras se escriben respectivamente tres grupos de cifras: «1, 2, 3», «4, 5, 6» y «7, 8, 9». El primer jugador apunta, sin que lo vea el contrario, una de estas cifras. Después le dice al segundo: «Mi padre compró en la feria un caballo». El segundo le pregunta: «¿Barato, caro o por un precio razonable?» Le sigue la respuesta, de la cual el segundo jugador se entera de qué grupo es la cifra pensada. Ahora él trata de acertarla. Por ejemplo, si el primero pensó la cifra 5 (y por consiguiente a la pregunta del oponente contestó «caro») y el segundo la acierta, en tal caso este jugador recibe un número de puntos igual a la cifra acertada, es decir, 5 puntos. Si el segundo jugador nombró la cifra 4 o 6, los 5 puntos los recibe el primero. Después de esto la cifra 5 se tacha y el turno pasa al segundo jugador. Gana el que acumule mayor número de puntos.
Esta antigua diversión escocesa nos presentó otra muestra de juego test. Su investigación puede realizarse utilizando para ello la teoría matemática de juegos. El análisis preciso del juego se debe a V. Jvatal y muestra que si ambos jugadores se atienen a la estrategia óptima, en el caso de gran cantidad de partidas el segundo jugador puede calcular obtener un promedio de 24,4 puntos y el primero, 20,6. Por supuesto que aquí nosotros no tenemos en cuenta el factor psicológico (digamos, uno de los jugadores, para no exponerse a la derrota, puede renunciar a la mejor estrategia y el otro no se percata de ello rápidamente y empieza a perder).
§ 20. Trihex
Dos jugadores tienen por cuatro fichas de su color. Ellos, por turno, las colocan sobre un tablero original, inventado por el matemático O’Beirn (fig. 84).
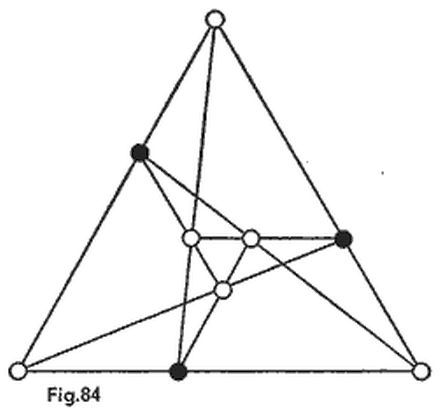
Se reconoce ganador al que consiga ocupar antes tres círculos dispuestos en una línea.
Ante nosotros tenemos otro juego, una variante totalmente insólita del tres en raya. Distraigámonos un poco del juego y observemos que el cuadrado habitual de 3 × 3 puede ser considerado como una configuración de 9 casillas (cuadrículas) dispuestas en ocho filas (por tres casillas en cada fila): tres verticales, tres horizontales y dos diagonales. El inventor del trihex, O'Beirn encontró una configuración de nueve «casillas» situadas en 9 filas (son fáciles de ver en la fig. 84). Esta configuración entretenida posee una propiedad métrica curiosa: cualquier segmento de recta que cojamos de los que pasan por tres círculos, el círculo central divide dicho segmento en partes, cuyas longitudes se hallan en relación de «oro»[2]). La existencia de una fila «de más» cambia la situación y a diferencia del juego habitual de tres en raya, en este juego el que comienza tiene garantizada la victoria, si éste hace su primera jugada a uno de los círculos negros de la figura 84. Independientemente de la respuesta del adversario, la segunda jugada del primer jugador provoca una reacción única y en su tercera jugada forma el tenedor de la victoria. De esta manera el que comienza no gana tan fácil en el tablero nuevo y termina el juego casi al instante, en la cuarta jugada.
Si la primera jugada es otra, la partida, jugando sin errores, termina en tablas, pero del segundo jugador se requiere precisión. En respuesta a la primera jugada a la esquina del tablero, el contrario también debe ir a la casilla del rincón. Si por el contrario el primer jugador, comenzando la partida, ocupa uno de los vértices del triángulo equilátero, situado en el interior de un triángulo grande, el segundo debe responder ocupando uno de los vértices de ese mismo triángulo pequeño.
§ 21. Temor al cuadrado
Sobre un tablero de 6 × 6 dos jugadores, por turno, colocan las fichas de su color en cualesquiera casillas libres (cada jugador dispone de 18 fichas; se pueden utilizar también las cruces y los ceros). Si las fichas de uno de los jugadores llegan a ocupar los vértices de cierto cuadrado, a este jugador se le considera derrotado. El cuadrado puede ser de cualquier dimensión e inclinado a cualquier ángulo respecto al cuadrado inicial (fig. 85a).
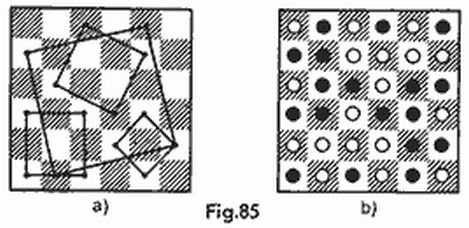
M. Gardner, inventor de este juego, suponía primero que éste no podía terminar en tablas. Pero más tarde fue demostrado que la terminación pacífica, sin embargo, era posible. Se consiguió dividir el tablero en dos grupos de a 18 casillas de manera que ningunas cuatro casillas de un mismo grupo se conviertan en vértices de un mismo cuadrado. Este juego terminado en tablas pueden verse en la figura 85b. Fácilmente podemos convencernos de que ninguno de los 105 cuadrados posibles posee cuatro vértices de un mismo color.
El tablero 6 × 6 es el más grande, sobre el cual se puede hacer tablas. R. Juitte demostró que las tablas no son posibles sobre un tablero de 7 × 7 y por cuanto todos los tableros mayores contienen cuadrados interiores a 7 × 7, por tanto las tablas tampoco son posibles en estos tableros.
Así pues, cuando n < 6 el juego «temor al cuadrado» sobre un tablero n × n siempre termina a favor de alguno de los dos. Pero ¿quién gana? Podría parecer extraño, pero a diferencia de la mayoría de los juegos, aquí el que empieza, si las respuestas del contrario son correctas, no puede alcanzar ni siquiera tablas. El segundo jugador elige una de las estrategias simétricas, lo cual le garantiza la victoria. Este método también conduce al objetivo si se juega sobre un tablero par arbitrario n × n (n > 6). En lo referente a los tableros impares (n = 7, 9, ...), aunque las tablas no son posibles, aún no está establecido (incluso con ordenador) cuál de los jugadores, el primero o el segundo, se impondrá, si los dos juegan con racionalidad.
Por lo que se conoce, la posibilidad de colocar las fichas sobre un tablero triangular sin formar triángulos (temor al triángulo) no se ha investigado.
§ 22. Marel
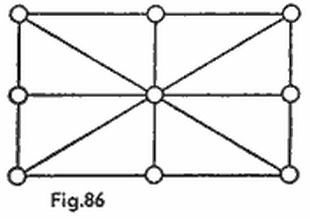
Dos jugadores con tres fichas cada uno que colocan, turnándose, sobre un tablero-rejilla 3 × 3 (fig. 86). Cuando se coloquen todas, los jugadores moverán sus fichas a lo largo de cualquiera de los 16 segmentos, siempre que el segundo extremo del segmento esté libre. Ganador se considera al que coloque primero sus fichas sobre una recta.
Este antiguo juego estuvo difundido en Oriente con el nombre «juego de los tres caminos» (nosotros expusimos un juego parecido en el capítulo dedicado a las cruces y los ceros, pero en aquella variante se prohibía jugar diagonalmente). El que empieza tiene una estrategia que le conduce a la victoria. La primera jugada ha de hacerse al centro del tablero y a partir de aquí todo es simple. Si por el contrario prohibimos al primero jugar al centro del tablero, la partida terminará en tablas. Supongamos que en estas condiciones el segundo jugador pone su primera ficha precisamente en la casilla central. ¿Cómo terminará la partida? La importancia del centro es tal que el primer jugador puede alcanzar las tablas solamente en el caso si en sus dos primeras jugadas ocupa con sus fichas dos esquinas vecinas del tablero.
§ 23. Coche de la policía
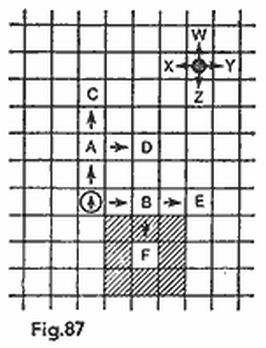
Este juego inventado por el eminente especialista en la investigación de operaciones, R. Aizaks, pertenece a la clase de juegos de persecución. La persecución se produce sobre un tablero de ajedrez infinito. Los jugadores, el «coche de la policía» (un circulito con una flecha) y el coche de los delincuentes (un circulito simple rayado), mueven sus fichas por turno y además en línea recta como la torre (por la vertical y la horizontal, pero no por la diagonal). El coche de los delincuentes se puede mover de casilla en casilla en cualquier dirección y el de la policía, de dos en dos, es decir es más veloz. Mas los guardianes del orden deben observar las leyes de circulación que por otra parte incumplen los malhechores (siete pecados y una penitencia). Las reglas prohíben doblar a la izquierda y dar la vuelta (girar en U) en los cruces. Por esto en cada jugada el coche de la policía puede pasar el cruce en sentido directo (en el de la flecha en el «coche»), o bien girar a la derecha. La figura 87 nos muestra cómo mueven los jugadores sus fichas. El coche de la policía en su primera jugada puede trasladarse a las casillas A y B, a continuación de A a G y D, y de B a E y P, etc. (después de cada jugada es más cómodo girar el coche de la policía de tal manera que la flecha indique la dirección en que se movió). El coche de los delincuentes puede ir desde su casilla a cualquiera de las casillas X, Y, Z y W.
Después de colocar los dos coches en su posición inicial sobre el tablero, el coche de la policía comienza la persecución. Si, por ejemplo, el coche de la policía ocupa la casilla F y la de los delincuentes se encuentra en esa misma casilla o bien en cualquiera de las ocho casillas que la rodean (en la figura están rayadas) los delincuentes están capturados.
En el caso cuando el coche de la policía se encuentra en una posición arbitraria fijada, existe una zona que, si se encuentran en ella, los delincuentes están perdidos, es decir, una persecución inteligente termina capturándolos. Fuera de la zona fatal los delincuentes, maniobrando con destreza, burlan la persecución. Construyendo para cada casilla las zonas que conducen a la victoria se puede determinar en qué cantidad de jugadas, precisamente, se detiene a los delincuentes, con la condición de que ambos bandos actúan de manera óptima. Este juego es de la familia de juegos de diferenciación, nos deja un amplio terreno para las deliberaciones...
§ 24. Black
Juegan dos personas sobre un tablero cuadrado de 4 × 4 (véase la fig. 88). Los participantes del juego dibujan en las casillas del tablero una de las tres «figuras» representadas en la parte inferior de la figura 88, es decir, una cruz, dos arcos cruzados que unen los centros de los lados. Uno de los jugadores empieza la partida poniendo una cruz en el ángulo izquierdo superior y el segundo continúa la línea dibujando cierta figura en la casilla adyacente. Los jugadores, por turno, deben continuar la curva a una de las casillas vecinas, de manera que dicha curva no se cruce con el extremo del tablero. El que con su jugada se vea obligado a salirse de estas fronteras, pierde la partida. Gana el jugador que con su jugada lleva la «trayectoria» continua basta el ángulo inferior derecho, es decir, cruza esta casilla (en la figura está rayada).
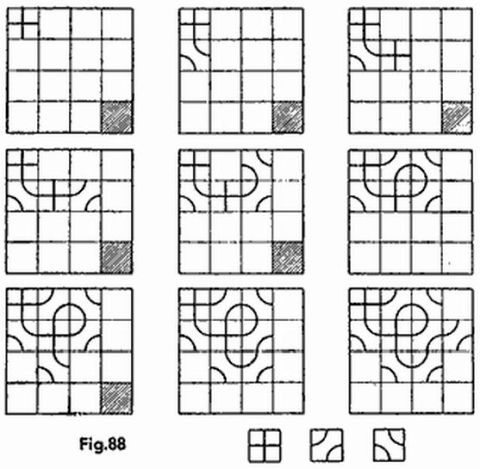
Una partida de black sobre un tablero de 4 × 4 puede verse en la figura 88. Habiendo arrinconado al contrario en la novena jugada en el ángulo superior derecho, el primer jugador obtiene la victoria, por cuanto independientemente de la continuación que elija el adversario, la curva alcanza el extremo del tablero. (Observemos que la cruz tiene como continuación de la curva sólo uno de los segmentos que la forman, sin embargo en el transcurso del juego el segundo segmento también puede convertirse en parte de la trayectoria).
Este juego fue inventado por el matemático norteamericano W. Black al cual se debe su nombre. E. Berlekamp, colega de Black descubrió una estrategia que garantiza la victoria de uno de los jugadores. Todo depende de la paridad del tablero, además el método de juego se extiende a un tablero rectangular cualquiera m × n (m, n ≥ 2). Si la cantidad total de casillas mn es impar (incluyendo el ángulo rayado), jugando correctamente gana el primer jugador y si es par, el segundo (excepción es el tablero de 2 × 2).
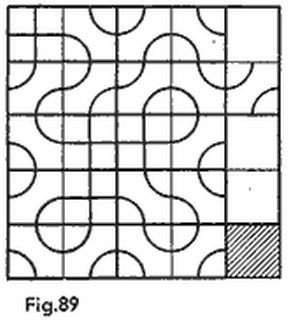
Mostremos cómo gana el que comienza la partida sobre un tablero de 5 × 5 (fig. 89) Para ello éste debe imaginarse que todo el tablero, a excepción del ángulo rayado, está cubierto con fichas del dominó (con rectangulares de 2 × 1). El jugador que da comienzo a la partida pone su primera cruz en el ángulo superior izquierdo del tablero y el contrario continúa la trayectoria sobre una de las fichas del dominó. A partir de aquí el primer jugador hace que el extremo de la trayectoria quede dentro de la ficha en cuya frontera acaba de encontrarse el segundo jugador. En tal caso éste nuevamente deberá pasar a otra ficha y el primero, otra vez, se «afianzará» en ella. Al fin y al cabo el segundo jugador se verá obligado salirse de los límites del tablero o bien a la frontera del ángulo inferior derecho. Tanto Jo uno como lo otro, como sabemos, equivale a la derrota. La estrategia victoriosa para el segundo jugador, sobre un tablero par, también se basa en las ideas del dominó, pero es un poco más compleja.
§ 25. En camino
He aquí otro juego test, aunque no es del todo matemático. El que lleva el juego escribe en una hoja de papel la regla que determina qué cosas se pueden coger para el camino. Después anuncia: «Preparándome para el camino yo cogeré conmigo...» y nombra una prenda que según la regla él puede llevarse. El resto de los participantes (estos pueden ser varios) preguntan por turno si pueden o no coger consigo tal o cual objeto y aquél contesta si se puede hacer esto o no según la regla. Gana el que acierte antes la regla ideada por el primero.
Las reglas pueden ser simples y complejas y no siempre son fáciles de formalizar.
Por cuanto este juego es más de distracción que matemático es poco probable que merezca la pena imponer limitaciones rígidas a la selección de palabras que determinan la regla. He aquí dos reglas simples pero lo suficientemente ingeniosas: a) denominación de objeto y apellido del que lo coge consigo para el camino empiezan por una misma letra; b) la prenda cabe en la cartera.
§ 26. Diez y cinco kopeks
Este igual que los dos siguientes pertenece al tipo de juego en que uno de los jugadores pretende privar al adversario de la libertad de movimiento. Antes ya se han descrito semejantes juegos: «cerco de la tropa de desembarco» y «los lobos y las ovejas».
El juego se desarrolla sobre el tablero que muestra la figura 90. Primero los cinco kopeks se encuentran sobre el círculo 2 y la moneda de diez en el círculo 15. Uno de los jugadores mueve la moneda de cinco kopeks y el otro la de diez. En cada jugada la moneda se mueve por una línea hacia el círculo adyacente. Empieza la partida el de la moneda de cinco kopeks. Este pretende capturar la moneda de diez, para lo cual debe alcanzar el mismo círculo. Si después de seis jugadas, la moneda de cinco kopeks no lo logra, pierde.
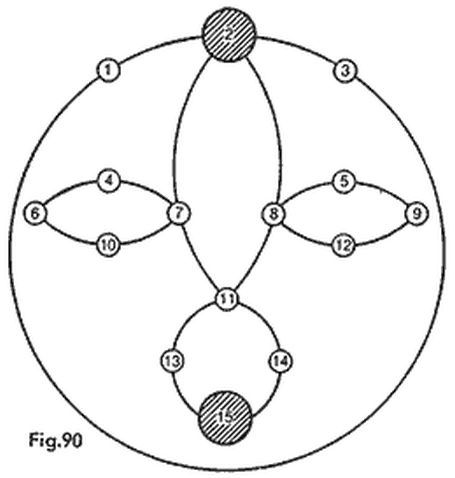
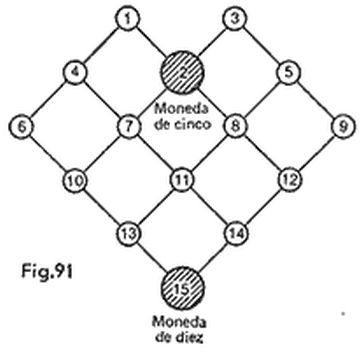
El que comienza este juego tiene una estrategia simple que le permite vencer. Para mayor claridad, transformemos la complicada red que forma el campo de juego, en un tablero «normal» con líneas rectas (fig. 91). Este procedimiento se asemeja al «método de los botones y el hilo» que hemos utilizado para resolver el problema de Guarini. En este caso el método nos sirvió para este juego.
Sobre el tablero transformado es muy fácil describir el plan que conduce a la victoria. La moneda de cinco kopeks empieza jugando a la casilla 1 o 3 y después se desplaza al encuentro de la moneda de diez. Ilustremos una partida: 1.(2, 3)! (15, 13); 2.(3, 1)! (13, 10); 3.(1, 4)! (10, 13); 4.(4, 7)! (13, 15); 5.(7, 11)! y para dondequiera que vaya la moneda de diez kopeks en la siguiente jugada la moneda de cinco la tomará. Es fácil convencerse de que si la moneda de cinco kopeks en su primera jugada se dirigiese hacia la casilla 15, la moneda de diez se encontraría a salvo. Este método de juego, seguramente recordará a los ajedrecistas el principio de juego de las terminaciones de peones (teoría de las casillas correspondientes). La lucha de la moneda de cinco kopeks con la de diez se asemeja a la oposición de los reyes que tratan de conseguir cada bando.
§ 27. Juego militar francés
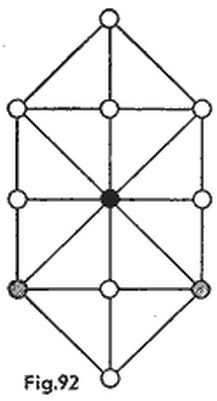
El primer jugador (las blancas) tiene tres fichas que primeramente se encuentran sobre los círculos rayados (fig. 92). El segundo jugador (las negras) sólo tiene una ficha que pone en un lugar libre (en la variante estándar del juego, sobre una casilla negra). La ficha negra puede jugar a cualquier casilla vecina y las blancas tienen prohibido retroceder, es decir, la ficha blanca puede mover hacia la izquierda, derecha o cualquier casilla hacia adelante. Comienzan las blancas. Ellas ganan si consiguen encerrar a la ficha blanca. En caso contrario ganan las negras.
Claro que es necesario introducir limitaciones sobre el número de movimientos (del tipo de la «regla de las 50 jugadas» en el ajedrez). En este juego para cualquier casilla inicial de la ficha negra, las blancas tienen una estrategia para ganar, aún cuando es muy complicada.
§ 28. Vacas y leopardos
Se juega sobre un tablero como el que muestra la figura 93. El primer jugador tiene dos leopardos, el segundo, 24 vacas. El primer jugador empieza poniendo uno de sus leopardos en el centro del tablero. El segundo pone una vaca en cualquier casilla libre. Ahora sobre una casilla libre se pone un leopardo y luego otra vaca. Los leopardos comienzan la caza y las vacas pueden jugar sólo después de que todo el rebaño se encuentre sobre el tablero. En una jugada los «animales» se trasladan a las casillas vecinas. El leopardo mata una vaca saltando por encima a una casilla libre tras de ella. Los leopardos ganan después de matar ocho vacas. Las vacas ganan si encierran a los dos leopardos.
§ 29. Focus
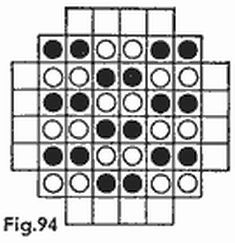
Cada uno de los jugadores tiene 18 fichas de su color. Ellos las colocan sobre un tablero especial de 8 × 8 con tres casillas recortadas en cada una de las esquinas (la posición inicial puede verse en la fig. 94). En cada movimiento los jugadores desplazan columnas de fichas (por supuesto que al comienzo del juego las columnas constan de una sola ficha) a un número de casillas igual al de fichas en dicha columna. Se puede jugar sólo vertical y horizontalmente. Mueve la columna el jugador cuya ficha se encuentre arriba de la columna. Si en las casillas pasadas hay fichas, todas ellas caen bajo la columna en movimiento.
Construir columnas de más de cinco fichas está prohibido. Cuando aparece una columna de más de cinco fichas, de su base se retiran todas las fichas sobrantes. Si las fichas retiradas son del contrario éstas se hacen prisioneras y se retiran del tablero. Si dichas fichas pertenecen al jugador que hizo la jugada, éste las pone a un lado, formando con ellas una reserva. En un momento dado del juego el que posee una reserva puede tomar de ella una ficha y colocarla en cualquiera de las casillas ocupadas o libres del tablero (en el primer caso la columna elegida se hace ligeramente más alta y pertenece al que puso la ficha de encima). La introducción de la ficha de reserva se considera jugada hecha. El jugador tiene derecho a jugar menor cantidad de casillas de las que se permiten por la cantidad de fichas en la columna. Para ello debe retirar del «tejado» una cantidad de fichas igual a la cantidad de casillas a la que quiere desplazar la columna. En este caso todas las fichas sobrantes quedan en su lugar y pertenecen al dueño de la ficha superior. Si al jugador no le queda ni reserva, ni columnas, pierde.
El focus –su autor es S. Sackson– tiene semejanza con los peones-postes (torres), pero contiene un mayor número de elementos singulares.
§ 30. Ajedrez de Dawson
El autor del libro es maestro de ajedrez y, lógicamente, siente por el ajedrez y juegos afines una simpatía especial. A esto se debe también el que el capítulo dedicado al ajedrez sea el más amplio. Pero también desea terminar esta lista de juegos con el tema del ajedrez...
El ajedrez inventado por T. Dawson se juega sobre un tablero de 3 × n (en la fig. 95 n = 8). Los peones situados en las horizontales extremas, en este caso se mueven y comen como en el ajedrez normal. Mas las transformaciones no se permiten, pero comer es obligatorio. Pierde el que no pueda hacer su jugada consecutiva, es decir, todos los peones que le quedan están ahogados.
Supongamos que la primera jugada de las blancas es 1.a2, entonces las negras se ven obligadas a responder l... ba. Después de 2.ba, los dos peones «a» se inmovilizan pero el turno de jugar es de las negras. Si juegan 2... f2, las blancas deben mover 3.ef o 3.gf. Después de cambiar tres peones blancos y tres peones negros quedan sólo dos, taponados en la vertical «f» y le toca jugar nuevamente a las blancas. Así pues, cualquiera de las jugadas conduce a una serie de cambios y a la liberación de las verticales vecinas. En este caso el turno de juego pasa al adversario.
El análisis del juego sobre un tablero de 3 × n en el caso de valores arbitrarios de n representa un problema matemático muy complejo. Examinemos los valores de n desde 1 hasta 8. Cuando n = 1, después de 1.a2 el peón negro queda ahogado y ganan las blancas. Ganan también cuando n = 2 (1.a2 ba; 2.ba) y cuando n = 3 (1.b2 ab; 2 ab cb; 3.cb, pero no 1.a2? ba; 2.ba c2). Cuando n = 4 se imponen las negras; he aquí las dos variantes principales: 1.a2 ba; 2.ba c2; 3.de de; o 1.b2 ab; 2.ab cb; 3.cb d2. Es fácil comprobar que para los tres valores siguientes (n = 5, 6, 7) nuevamente ganan las blancas y para n = 8 (fig. 95) ya no pueden evitar la derrota. A causa de la simetría es suficiente examinar cuatro «debuts».
1) 1.a2 ba; 2.ba e2; 3.de de; 4.fe fe; 5.g2 hg; 6.hg c2;
2) 1.b2 ab; 2.ab cb; 3.cb f2!; 4.ef ef; 5.fg fg; 6.d2 h2;
3) 1.c2 be; 2.be de; 3.de e2; 4.fe fe; 5.g2 hg; 6.hg a2;
4) 1.d2 cd; 2.cd ed; 3.ed f2; 4.gf gf; 5.a2 ba; 6.ba h2.
En todas las variantes, el juego termina con que ninguno de los peones blancos puede jugar.
En principio se pueden deducir las relaciones recurrentes para determinar el resultado del juego sobre un tablero de 3 × n para diferentes valores de n, pero no existe una regla simple que permita revelar al vencedor para un valor de n dado. Aún más complicado es el análisis de una «miserable» forma de ajedrez de Dawson (precisamente ésta fue propuesta por el autor del juego): pierde el que hace la última jugada.
Así pues, en este libro usted pudo conocer los más diversos juegos: antiguos y muy recientes, simples y complejos, muy populares y menos conocidos. Por desgracia no hemos dicho nada sobre muchos de los juegos. Casi no fue tocado un tema muy atractivo, relacionado con la historia y aparición de los juegos. Es imposible imaginar el volumen de un libro que contenga todos los juegos del mundo, los juegos llamados de mesa, lógicos, recreativos, intelectuales, matemáticos.
En la famosa novela de García Márquez «Cien años de soledad» podemos leer este interesante pasillo.
«Cierta vez el padre Nicanor trajo una caja con fichas y un tablero de juego y propuso a José Arcadio Buendía jugar una partida, éste se negó porque, como él mismo explicó, no ve sentido en la lucha entre dos adversarios que en lo esencial están de acuerdo entre sí. El padre Nicanor, que nunca antes examinó el juego de damas desde este punto de vista, no pudo convencerlo...»
Y con todo ello es difícil estar de acuerdo con la opinión del personaje de García Márquez. Pasando el tiempo sobre una partida de ajedrez, un combate al go o a las damas, jugando al tres en raya, nosotros, como se acostumbra decir, combinamos lo útil con lo agradable. Dos personas que luchan a un juego interesante y atractivo reciben una gran satisfacción creativa y a veces también estética. Pues bien, las victorias y las derrotas, las ideas ingeniosas y las trampas astutas de los adversarios no les impiden ser amigos y «revelar sus relaciones» sólo colocando las figuras sobre el tablero.
«Las personas, más que nada, muestran su inventiva en el juego –indicó el gran matemático G. Leibniz– y, por consiguiente, los juegos matemáticos merecen atención, no solo de por sí, sino también gracias a que desarrollan la ingeniosidad».
Como ya hemos dicho, en el libro de L. Pijanowski «Guía de los juegos», editado en Varsovia, se da una lista de libros de 330 títulos. Pero esta lista no es muy completa. Solamente libros sobre el ajedrez y el juego de damas en el mundo existen decenas de miles. Tales juegos como el combate marino, el molino, el tres en raya, están descritos en diferentes tipos de libros recreativos. A propósito, los dos primeros libros de M. Gardner que mencionamos contienen cerca de 300 ediciones sobre matemáticas recreativas, así como libros sobre ordenadores, teoría de grafos, análisis combinatorio, que tiene relación con nuestro tema. Si añadimos además una enorme cantidad de publicaciones sobre juegos en periódicos y revistas quedará claro que una bibliografía más amplia sobre juegos, si ésta en realidad es posible, necesitaría no menos espacio que la edición que les hemos presentado. Con dolor tenemos que constatar que casi cada libro sobre juegos, inmediatamente después de su aparición se convierte en rareza bibliográfica.
- Martin Gardner. Mathematical puzzles and diversions. London.
- Martin Gardner. New mathematical from scientific american. New York, Simon and Schuster, 1966.
- The unexpected hanging and other mathematical diversions. New York, Simon and Schuster, 1969.
- Mathematical games from scientific american.
- E. Ya. Guik. Matemáticas sobre un tablero de ajedrez. M.: Nauka, 1976 (en ruso).
- E. Ya. Guik. El ajedrez y las matemáticas. M.: Nauka, 1983 (en ruso).
- Solomon W. Golomb. Polyminoes. New York, Charles Scribner’s Sons.
- Henry E. Dudeney. The Canterbury puzzles and other curious problems. New York, Dover Publications, Inc. 1958.
- Juegos matemáticos/ Colección en tres partes. Krasnoyarsk Editorial KGU, 1985 (en ruso).
- The mathematical gardner/ David A. Klarner, Prindle, Weber and Schmidt. Boston, Massachusetts/.
- N. V. Soloviov. Tests (teoría, composición, utilización). Novosibirsk: Nauka, 1978 (en ruso).
- ¿Juego? ¡Juego!/ por V.N. Belov, L.: Lenizdat, 1987 (en ruso).
- Marie Berrondo. Les jeux mathématiques (Teureka
- E. R. Berlekamp, J. H. Conway, R. K. Guy. Winning Ways. 1982, Academic Press.