
La Aritmética del Ábaco es un determinado método de cálculo en el que los números están representados por bolas de madera, Estas bolas están sistemáticamente colocadas en una tablilla conocida con el nombre de Ábaco Chino. El término Aritmética del ábaco se usa para distinguirla de otros tipos de aritmética en los que se usan representaciones escritas. Se le podría denominar ciencia de los números pero ya que se usa comúnmente en la vida comercial, es más apropiado hablar de ella como arte del cálculo.
Historia
La historia de este objeto es poco conocida. Los antiguos chinos usaban para calcular tallos de bambú o trocitos de madera en la actualidad usan el ábaco. No se sabe quién inventó este aparato ni se conoce cuando hizo su aparición por vez primera este ingenioso instrumento. En Cease Farming Sketch Book de Dao Nan Tsang, se mencionan casualmente los términos estructura de bolas móviles y estructura de bolas corredizas. (Enciclopedia China). Este libro fue escrito durante la dinastía Yuan, la cual gobernó durante el siglo XIV, de lo que se deduce que el ábaco está en uso desde hace seiscientos años.
Ventajas del Ábaco
Para resolver cualquier problema en aritmética, aunque sea simple, debemos usar dos elementos de nuestro poder mental como son las facultades de cálculo y de memoria. Ambas son usadas cuando sumamos uno y dos; para sumar debemos primeramente retener el número uno en nuestra mente, después fijamos nuestra atención sobre el otro número, dos, y finalmente calculamos cuánto son uno y dos. Estas operaciones resultan fáciles cuando usamos número simples. Sin embargo cuando las operaciones son más complicadas, pronto alcanzamos el límite de nuestra capacidad mental. Al tratar problemas más difíciles debemos hallar otros medios con que aliviar a la memoria del esfuerzo del cálculo. Podemos considerarnos afortunados ya que sabios de generaciones pasadas hallaron estos medios para nosotros. Ahora debemos aprender solamente cómo usarlos: Entre estos medios están los tallos de bambú o las fichas usadas en los tiempos antiguos, y el Abarco Chino. No es una máquina automática como las calculadoras usuales (en muchos aspectos es superior a estas calculadoras) pero aún así nos ofrece un servicio no menor como agente memorizador en el cálculo. Usando este instrumento podemos dedicar enteramente nuestra atención a la exactitud del cálculo dejando el trabajo de la memoria a la tablilla.
Ventajas y desventajas de la aritmética del ábaco en comparación con la aritmética escrita
Comparando la aritmética del ábaco y la aritmética escrita o aritmética del lápiz, como se la llama en China, ambas presentan sus puntos débiles y sus puntos fuertes. Al tratar con problemas complejos la aritmética del lápiz es más práctica pero para la mayoría de las operaciones contables habituales, es mucho más conveniente la aritmética del ábaco. Su mayor ventaja sobre la aritmética del lápiz, es la economía de tiempo. Se puede decir con certeza que para resolver cualquier problema con las operaciones fundamentales de la aritmética necesitaremos la mitad del tiempo usando el ábaco, del que necesitaríamos usando la numeración escrita. Esto es especialmente cierto en la suma. Por ejemplo, si dos personas fueran a resolver el mismo problema empezando al mismo tiempo pero usando distintos métodos, el resultado sería sin duda que cuando uno apenas habría acabado de anotar los números de la pregunta, el otro ya habría obtenido la respuesta en la tablilla. La aritmética del ábaco a pesar de su superioridad no carece de algunas desventajas. Un operador no cualificado está sujeto a error porque las bolas de las varillas pueden desplazarse con facilidad sin advertirlo. Sin embargo esto puede evitarse usándolo cuidadosamente.
Amplia repercusión de la aritmética del ábaco.
Debido a sus ventajas, el ábaco es ampliamente usado en China y en sus países vecinos. En casi todos los hogares a lo largo y ancho de la Tierra Celestial se encuentra el ábaco. Es más, en las dinastías pasadas era el único método con que contaban los Astrónomos Reales para contar las estaciones y los días, los Tesoreros para llevar a cabo las cuentas del Estado y los conocidos Cabezas peladas para realizar sus negocios. Es considerado tan importante para los comerciantes en China que su uso se ha hecho imprescindible. Un comerciante chino no olvida nunca de mencionar en sus anuncios: "Sólo los que poseen una gran habilidad necesitan recurrir al ábaco". Pronto se introdujo en Japón y Corea convirtiéndose en un objeto muy común. Recientemente lo han adoptado muchos occidentales que han sabido apreciar su utilidad. Cualquier hombre que sepa valorar la importancia del tiempo en los negocios y quiera duplicar su capacidad de trabajo, hallará en la aritmética del ábaco un medio seguro para doblar su rendimiento.
Campo de acción de la aritmética del ábaco.
Algunos de nuestros amigos extranjeros parecen considerar el ábaco chino como un instrumento apto sólo para sumar, o como máximo para sumar y restar. Sólo unos pocos han comprendido que el ábaco no es solamente capaz de resolver problemas de sumar y restar sino también de multiplicación y división. De hecho puede usarse para realizar cualquier tipo de operación aritmética. Aunque en algunos casos presenta algunos inconvenientes el uso del ábaco, especialmente en operaciones que conlleven complicadas fracciones, incluso en estos casos su uso es posible. En otros casos los procedimientos usados con el ábaco son mucho más simples. Por ejemplo para extraer raíces cuadradas y cúbicas, el proceso es simplemente una cuestión de resta.
Como ciencia, la aritmética del ábaco no está tan desarrollada como la aritmética escrita. En los libros chinos en general se le presta una considerable atención al ábaco para los problemas de la industria, comercio, impuestos y medidas. Pero desde el punto de vista científico la literatura es muy pobre.
Alcance de este libro
Este folleto explica solamente las operaciones fundamentales de la aritmética del ábaco. Sus posibilidades van mucho más allá. La intención del escritor es familiarizara los lectores de habla hispana con este antiguo e ingenioso instrumento que ha sido durante tanto tiempo de dominio exclusivo de los chinos. Espera, de aquí en adelante muchas más personas puedan beneficiarse de sus ventajas.
CAPITULO 1
INSTRUCCIONES GENERALES
El ábaco, tal como aparece en la figura, consiste en una tablilla rectangular de madera dividida longitudinalmente en dos partes iguales por una varilla horizontal. Puede poseer nueve, once, trece o más columnas de bolas móviles hechas generalmente de madera. El número de bolas en cada columna es de siete; dos por encima de la varilla horizontal y cinco por debajo de ella. A las bolas situadas en la parte superior de la varilla se las llama altobolas y a las que están situadas eh la parte inferior se las llama hipobolas. Una altobola equivale a cinco hipobolas. Existe un tipo de ábaco que posee solamente seis bolas móviles en cada columna, una altobola y cinco hipobolas.

Swanpan o ábaco chino
Valor según su colocación
El valor de la bola depende de la columna que tomemos como unidad. Las bolas de la columna situada a mano izquierda tienen más valor que las situadas en la columna de la derecha. Una unidad de la columna del lado izquierdo posee diez veces más valor que su equivalente situada en la columna del lado derecho. De este modo si tomamos como unidad la primera columna del lado derecho de la varilla, una hipobola de la segunda columna tendrá el valor de diez unidades; una de la tercera columna será igual a cien unidades, etc.
Digitación
Se ha comprobado que la mejor forma de mover las hipobolas es usando los dedos pulgar e índice, y las altobolas usando el dedo medio. Si se usan el pulgar y el medio para mover las hipobolas, el dedo índice no realizará ninguna función y podría hacernos cometer errores.
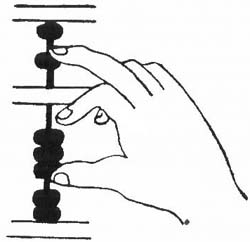
Forma correcta de mover las bolas en las columnas
Antes de empezar a usar el ábaco, todas las altobolas deben ser colocadas en el extremo superior de la tablilla y las hipobolas en el extremo inferior. Una vez colocadas así, están en disposición de ser movidas hacia arriba o hacia abajo para registrar cualquier número. La varilla de en medio es el eje al lado del cual se van colocando las bolas que vamos usando. Las bolas que permanecen inactivas o neutrales, deben ser colocadas en los lados.
Para sumar y restar no es necesario mover la altobola que está en el extremo superior ni la última de las hipobolas. Ya que una altobola equivale a cinco hipobolas, en vez de mover la última hipobola para contar hasta cinco podemos usar una altobola y devolver a la posición neutral o de inactividad a las cuatro hipobolas restantes. Del mismo modo ya que una hipobola situada en la columna de la izquierda es igual a dos de las altobolas adyacentes situadas en la columna de la derecha, en vez de usar la altobola del extremo superior para sumar diez, podemos usar una hipobola de la columna izquierda y devolver a su posición neutral a la altobola del extremo inferior.
Comprobación
Es aconsejable, sobre todo para los principiantes, comprobar los resultados de un cálculo. Para ello pueden usarse uno o dos métodos. Suma, resta, multiplicación y división nos permiten verificar a través de ellas su operación opuesta. Así por ejemplo el resultado de una suma puede ser comprobado con una resta y viceversa, lo mismo ocurre con la multiplicación y división. Sin embargo el método usado generalmente por los expertos en el uso del ábaco es repetirle operación.
Ejercicios
Representar los siguientes números en el ábaco:
1,427
7,543
500,005
137,005
10,010
16,896
Se llama suma al proceso de combinar dos o más números dados para obtener uno igual a la totalidad de los mismos.
Tratar de sumar 73, 49, 21 y 58 primero usando el ábaco, y después a través de los números escritos. Comprobar el resultado obtenido en ambos casos y el tiempo empleado en cada uno de ellos. Estos números pueden ser sumados con el ábaco pero se verá que presenta algún inconveniente hacerlo porque el tiempo empleado será mayor que el que emplearíamos para hacerlo por el sistema escrito ordinario. Esto es cierto, pero se debe, amigo lector, a que usted no está todavía familiarizado con el tema y le falta agilidad en sus manos y en su mente. Para el principiante se han establecido una serie de guías o indicaciones denominadas secretas en los libros chinos, que enseñan cómo sumar los números que van a ser posteriormente sumados en el ábaco. Esta serie de guías serán las que nos harán más fácil y rápido el proceso de la operación que vayamos a realizar, por esto debemos conocerlos y guardarlos cuidadosamente en nuestra memoria. Facilitamos a continuación 17 de estas guías que han sido condensadas en frases muy simples para ser retenidas mejor en nuestra memoria. Algunas de las palabras usadas necesitan ser explicadas. Por ejemplo bajar cinco significa desplazar hacia el eje central una altobola; anular significa sacar una bola que había sido antes colocada junto al eje central; elevar significa desplaza, hacia el centro una hipobola, adelantar diez significa desplazar hacia arriba una hipobola de la columna de la izquierda. En cada guía, el primer número indica el número que ha de ser sumado a otro que está ya en una varilla, lo demás nos dice cómo proceder. Por ejemplo, el número cuatro está ya en la varilla de una columna, a este número le queremos sumar otro, el uno, ¿cómo proceder? Tomamos la primera guía: uno, bajar cinco anular cuatro, desplazamos hacia abajo en la misma columna cinco, es decir una altobola, y quitamos cuatro, es decir cuatro hipobolas.
Guías para sumar
Estas son las diecisiete guías o reglas mencionadas anteriormente:
| Uno Dos Tres Cuatro Uno Dos Tres Cuatro Cinco Seis Siete Ocho Nueve Seis Siete Ocho Nueve | bajar cinco, anular cuatro bajar cinco, anular tres bajar cinco, anular dos bajar cinco, anular uno anular nueve, adelantar diez anular ocho, adelantar diez anular siete, adelantar diez anular seis, adelantar diez anular cinco, adelantar diez anular cuatro, adelantar diez anular tres, adelantar diez anular dos, adelantar diez anular uno, adelantar diez elevar uno, anular cinco, adelantar diez elevar dos, anular cinco, adelantar diez elevar tres, anular cinco, adelantar diez elevar cuatro, anular cinco, adelantar diez. |
Ejemplo 1
¿Cuántos dólares son tres más cuatro?
Para sumar colocamos primero el número tres en la varilla desplazando hacia arriba tres hipobolas de la primera columna de la derecha (esta columna ha sido tomada, para nuestra conveniencia, como unidad). A este número se le ha de sumar el 4. Como ya hemos utilizado tres hipobolas de la primera columna y las otras dos bolas que dejamos no son suficientes para sumar cuatro, debemos en este momento recordar la cuarta guía, cuatro: bajar cinco, anidar uno. Así pues desplazamos hacia abajo una altobola y quitamos una hipobola. De este modo, la altobola y las dos hipobolas que permanecen en medio junto a la varilla central suman siete, el resultado deseado.
Ejemplo 2
¿Cuántos metros son 24 más 36?
Del mismo modo, colocamos el número 24 elevando dos hipobolas de la segunda columna y cuatro de la primera y procedemos a sumar. Aquí es preciso hacer una distinción entre la aritmética del ábaco y la escrita. En la aritmética escrita, empezamos a sumar desde la derecha, pero en la aritmética del ábaco empezamos a hacerlo desde el lado izquierdo. Así empezamos desde la izquierda a sumar: en la segunda columna, tres: bajar cinco, anular dos. En la primera columna, seis: anular cuatro, adelantar diez. Todos juntos suman 60, es decir el resultado es de 60 metros.
Ejemplo 3
Averiguar la suma de 783, 275, 14, 5.697 y 34.
Primero sumar la primera y segunda cantidad, después tomar la tercera, la cuarta y finalmente la última. Prestar atención a sumar las centenas con centenas, decenas con decenas etc. La suma total debe ser 6.803.
Ejercicios
Sumar, comprobando después el resultado, en orden inverso. Intentar hacerlo con rapidez y comprobar el tiempo empleado para obtener el resultado correcto. Repetir la misma operación tantas veces como sea necesario hasta ser capaz de sumar con exactitud y rapidez.
- 1, 2, 3, 4, 5, 6, 7, 8, 9.
- 45, 1, 2, 3, 4, 5, 6, 7, 8, 9.
- 90, 1, 2, 3, 4, 5, 6, 7, 8, 9.
- 312'75 ptas., 95'75 ptas., 21'03 ptas., 2.304'69 ptas.
- En una ciudad hay cuatro escuelas, la primera tiene 396 alumnos, la segunda 683, la tercera tantos como la primera ,y segunda juntas, y la cuarta tantos como las otras tres juntas. ¿Cuántos alumnos tiene la tercera escuela? ¿Cuántos tiene la cuarta? ¿Cuántos alumnos hay entre las cuatro escuelas juntas?
Restar es el proceso por el cual averiguamos la diferencia entre dos números o bien averiguamos cuántos números debemos quitarle a un número determinado para obtener una parte del mismo. El número del cual ha de restarse otro se llama minuendo, y el número que ha de restarse de otro se llama sustraendo. Al resultado obtenido de tomar uno de otro se le llama residuo.
Usando el ábaco restar 498 de 884
Al igual que en la suma, aquí existen también 17 reglas o guías para restar. El lector verá enseguida que son el reverso de las guías dadas para sumar. En cada guía el primer número es el número que ha de ser restado, y lo que sigue nos indica como proceder. Por ejemplo en la primera guía: Uno anular cinco, devolver cuatro, el número uno es el que ha de ser restado de otro número que está ya en la varilla (minuendo). Sabemos que cinco menos uno es cuatro, pero ¿cómo vamos a restar en la tablilla? La guía nos habla de cancelar cinco y devolver cuatro, esto es sumar cuatro. Memorizar estas guías constituirá el secreto para el uso eficiente del ábaco.
Guías para restar
| Uno Dos Tres Cuatro Uno Dos Tres Cuatro Cinco Seis Siete Ocho Nueve Seis Siete Ocho Nueve | anular cinco, devolver cuatro. anular cinco, devolver tres. anular cinco, devolver dos anular cinco, devolver uno. anular diez (sacar una hipobola de la columna de la izquierda), devolver nueve. anular diez, devolver ocho. anular diez, devolver siete. anular diez, devolver seis. anular diez, devolver cinco. anular diez, devolver cuatro. anular diez, devolver tres. anular diez, devolver dos. anular diez, devolver uno. anular diez, devolver cinco, anular uno. anular diez, devolver cinco, anular. anular diez, devolver cinco, anular tres anular diez, devolver cinco, anular cuatro. |
Ejemplo
De 884 restar 498.
Colocar el minuendo 884 en el ábaco. Como en la suma, empezamos a restar por, la izquierda, las centenas de las centenas, las decenas de las decenas, y las unidades de las unidades. Así para restar cuatro de ocho de la columna de las centenas, recordamos: Cuatro cinco, anular, devolver uno. Cuatro son dejadas en la columna. Para restar nueve de ocho en la columna de las decenas recordamos: Nueve, anular diez, devolver uno (desplazar hacia abajo una hipobola de la columna de las centenas y añadir una ala columna de las decenas). Nueve son dejadas en la columna de las decenas. Para restar 8 de 4 en la columna de las unidades recordamos: Ocho, anular diez, devolver cinco, anular tres. (Desplazamos hacia abajo una hipobola de la columna de las decenas, añadimos una altobola de la columna de las unidades y anulamos tres hipobolas de la misma columna. Seis son dejadas en la columna de las unidades.
El número total dejado en la varilla es 386.386. Este es el resultado.
Prueba
386 el resultado más 498 el sustraendo es igual a 884 el minuendo. La operación es correcta.
Ejercicios
Resolver las, siguientes operaciones comprobando después el resultado con la suma. Controlar el tiempo.
- De 45 restar 1,2,3,4,5,6,7,8, y 9 sucesivamente.
- De 90 restar los mismos números consecutivamente.
- De 135 restar lo mismo.
- Averiguar la diferencia entre 3,402,731 y 1,924,005.
- Si compramos en un colmado chino, té por valor de 78 pts. arroz por 26 pts. y azúcar por tanto como la diferencia entre las sumas pagadas por el té y el arroz, y damos para pagar dos billetes de 100 pts. ¿Cuánto cambio tendrán que devolvernos?
Multiplicar es el proceso por el cual tomamos un número tantas veces como unidades tiene otro, o es un proceso rápido para averiguar la suma de varios números iguales. El multiplicando es el número tomado o multiplicado; el multiplicador es el número que nos dice cuantas veces ha de ser tomado el multiplicando, y el producto es el resultado de la multiplicación.
Tratar de multiplicar 68 por 32 en el ábaco
El requisito fundamental para este, proceso es tener un conocimiento exacto de una multiplicación simple, es decir de una multiplicación en la que tanto el multiplicando como el multiplicador estén formados por un solo número. Ya sabemos cómo multiplicar números como 3 x 4, 6 x 7, 7 x 9. Es preciso recordar la tabla de multiplicar. En la tablilla, los números que están en la columna de la izquierda se consideran como los multiplicadores y los que están al otro lado de la parte superior como los multiplicandos. Los números que están en las filas horizontales opuestos a los multiplicadores y debajo de los multiplicandos son los productos. Debe leerse 2 x 2 = 4, 2 x 3 = 6, 2 x 4 = 8, 3 x 2 = 6, 3 x 3 = 9, etc.
1 2 3 4 5 6 7 8 9 | 1 1 2 3 4 5 6 7 8 9 | 2 2 4 6 8 10 12 14 16 18 | 3 3 6 9 12 15 18 21 24 27 | 4 4 8 12 16 20 24 28 32 36 | 5 5 10 15 20 25 30 35 40 45 | 6 6 12 18 24 30 36 42 48 54 | 7 7 14 21 28 35 42 49 56 63 | 8 8 16 24 32 40 48 56 64 72 | 9 9 18 27 36 45 54 63 72 81 |
Ejercicios
Repetir con rapidez el resultado de las siguientes, aplicaciones, multiplicaciones.
2x3 | 5x7 | 7x3 | 8x9 | 8x5 | 5x8 |
Lugar que ocupan el multiplicando, multiplicador y producto en el ábaco
Para mayor comodidad el multiplicador se coloca en el lado izquierdo de la tablilla y el multiplicando en el derecho.
Sin embargo, la columna de la derecha (es decir la primera columna de la derecha) no puede ser tomada como unidad del multiplicando. Esta columna se utiliza como unidad del producto.
Cuando el multiplicador está expresado por un solo número, la columna del lado derecho situada junto a la que hemos tomado como unidad del multiplicando, será la unidad del producto.
Cuando el multiplicador está representado por dos números, la segunda columna desde la columna unidad del multiplicando (es decir, la segunda columna de la derecha) es la unidad del producto; cuando está representado por tres números la tercera columna, y así sucesivamente.
De este modo cuando el multiplicador sea un número dígito, el multiplicando puede colocarse en e. lado derecho de la tablilla, dejando un espacio vacante a la derecha para la unidad del producto; cuando el multiplicador sea dos números dígitos dejar dos columnas vacantes, si es de tres números dejar tres columnas. etc. Este sistema es para uso de los principiantes. Los números pueden ser colocados en cualquier sitio tal que dejemos un espacio para el producto multiplicador no se coloca en la tablilla cuando está compuesto por un solo número dígito.
Cuando el multiplicador está expresado por un solo número
Ejemplo 1 .
¿Cuántas veces son cuatro veces 316? Colocar el multiplicando, 316, al lado derecho de la tablilla, dejando una columna de la derecha libre. Empezar por la derecha a multiplicar de la siguiente manera:
- 4 x 6 igual 24. Pero 24 está compuesto por dos decenas y cuatro unidades. Así pues el número cuatro se colocará en la columna de la unidad del producto (la columna siguiente ala derecha después de la columna de la unidad del multiplicando, es decir la columna situada en la parte extrema de la derecha) y anulamos el número de la unidad del multiplicando que es 6 y en su lugar ponemos el número dos.
- 4 x 1 igual 4. Aquí el número cuatro significa cuatro decenas, el producto de 4 veces una decena. Así pues, el número 4 se coloca en el lugar de las decenas del producto; es decir añadimos un 4 a las decenas del producto parcial anterior (2 más 4 igual 6). El lugar de las decenas del producto debe ahora marcar 6. Anular inmediatamente el 1 en el lugar de las decenas del multiplicando.
- 4 x 3 igual 12. Se coloca el 2 en la columna de las centenas del producto y el número multiplicando, 3, se anula y en su lugar se coloca el número 1. Así pues el resultado o producto es 1264.
Nota 1. Del ejemplo anterior se puede deducir que el número de la columna de las decenas es un producto parcial y se coloca en la columna del número que acabamos de multiplicar, y que el número de la columna de la unidad se coloca en la columna de la derecha al lado de la columna de la unidad del multiplicando. En cada operación el número del multiplicando que acaba de ser multiplicado debe ser anulado inmediatamente, y así el multiplicando se convierte en el producto.
Nota 2. Al método usado para resolver el ejemplo anterior se le llama en los libros chinos métodos de abertura fina/ porque empezamos a multiplicar por el final del lado derecho del número. El otro método en el que empezamos a multiplicar por la izquierda es llamado método de abertura inicial. Está probado que el primero es mejor que el segundo. Por esta razón sólo hablaremos del primero en este libro.
Ejemplo 2
Multiplicar 617,283,945 x 2. Colocar el multiplicando 617,283,945 en la varilla y empezar a multiplicar de la siguiente manera:
- 5: 2 x 5 igual 10: Cambiar 5 por 1.
- 4: 2 x 4 igual 8: Anular el número 4 acabado de multiplicar y añadir un 8 ala columna de la derecha.
- 9: 2 x 9 igual 18: Cambiar 9 por 1 y añadir un 8 a la columna de la derecha.
- 3: 2 x 3 igual 6: Anular el 3 y añadir un 6 a la columna de la derecha
- 2: 2 x 8 igual 16: Cambiar 8 por 1 y añadir un 6 a la columna de la derecha.
- 2: 2 x 2 igual 4: Anular el dos y añadir un 4 a la columna de la derecha.
- 7: 2 x 7 igual 14: Cambiar 7 por 1 y añadir un 4 a la columna de la derecha.
- 1: 2 x 1 igual 2: Anular el 1 y añadir un 2 a la columna de la derecha.
- 6: 2 x 6 igual 12: Cambiar 6 por 1 y añadir un 2 a la columna de la derecha.
El resultado será: 1,234,567,890.
Ejercicios
Hallar el resultado de las siguientes operaciones:
- 3 x 41,152,263.
- 4 x 3,086,419,725.
- 5 x 246,913,574.
- 6 x 205,761,315.
- 7 x 17,636,684.
- 8 x 15,432,096,625.
- 9 x 13,716,421.
- Un semillero forestal produjo el año pasado 675.984 semillas de distintas especies. A este ritmo, ¿cuántas producirá en 7 años?
- Un mercader chino vende 34,579 metros de satín de Hangchow al precio de 200 pts. el palmo. ¿Cuánto cobrará por su venta?
- Si una pieza de lino de Kiangsi contiene 50 metros y el coste de un metro es de 400 pts. ¿cuánto habrá que pagar por 7,296 piezas?
La multiplicación de un numero por 10,100,1000 ó 1, por cualquier número de ceros añadidos, se resuelve añadiendo al multiplicando tantos ceros como tenga el multiplicador .
Cuando el multiplicador esta formado por mas de un numero
Cuando el multiplicador está formado por más de un número, el número de su izquierda es considerado como el primer número, el siguiente el segundo, etc.
El número de la derecha de cualquier producto parcial de cualquier multiplicando por el primer número del multiplicador, se coloca en la primera columna de la derecha del número multiplicado, el segundo número del multiplicador se coloca en la segunda columna de la derecha, el tercero en la tercera columna, etc.
Ejemplo 1.
Multiplicar 68 por 32.
Para nuestra conveniencia, colocaremos el multiplicador junto al lado izquierdo del ábaco ya que así puede ser recordado, y el multiplicando se coloca junto al lado derecho dejando dos columnas para el producto (ya que hay dos números en el multiplicador).Ya que no podemos multiplicar 68 por 32 en una sola operación, multiplicamos parte del 68, es decir 8 unidades y 6 decenas o 60 y al mismo tiempo sumamos los productos.
Así, 2 x 8 igual 16. Colocamos un 1 en la primera columna a la derecha del multiplicando y un 6 en la segunda columna a la derecha del número multiplicado que es 8. 3 x 8 igual 24. Anulamos de inmediato el número multiplicado, 8, y ponemos en su lugar un dos y añadimos un 4 ala siguiente columna de la derecha (4 más 1).
2 x 6 igual 12. Añadimos un 1 a la primera columna de la derecha y un 2 ala segunda. 3 x 6 igual 18. Anulamos inmediatamente el 6 y ponemos un 1 en su lugar y añadimos un 8 a la siguiente columna de la derechas (Guía: ocho anular dos, adelantar diez). El resultado será 2176.
Nota: Puede ser más aconsejable usar en la primera operación 8 del multiplicando, 68 para multiplicar primero 2 y después 3 del multiplicador 32, y en la segunda operación usar 6 del 68 para multiplicar el multiplicador por el mismo orden. Los productos quedan así registrados en sus propios lugares tal como hemos dicho antes. En este caso, el multiplicando se convierte en el multiplicador y el multiplicador en el multiplicando.
Ejemplo 2
Hallar el producto de 4,567 x 4,325.
Para la primera operación multiplicamos el 7 del multiplicando 4567 por el multiplicador 4325 tomando, como hemos explicado anteriormente, 5, 2, 3, 4 número tras número; para la segunda operación multiplicamos 6 por los mismos números; para la tercera multiplicamos 5, y por último para la última multiplicamos 4. Hemos de asegurarnos de que el producto de cualquier número del multiplicando por el cuarto número del multiplicador quede colocado en la cuarta columna a la derecha del número multiplicado que el tercer número quede en la tercera columna, etc. Por ejemplo, en la primera operación: 5 (cuarto número del multiplicador) x 7 igual 35. El número 5 del producto se coloca en la cuarta columna a la derecha del número multiplicado (7). El resultado de la operación total es: 19,752,275.
Nota 1: Para la multiplicación de un número por un multiplicador de más de dos números, el método descrito en los libros antiguos chinos es multiplicar el número primero por el segundo número del multiplicador, después por el tercero, cuarto, quinto, etc., y finalmente por el primero. Este método está simplemente tomado de las guías dadas para la multiplicación. Como las antiguas guías no han sido adaptadas al proceso descrito en este libro, este método no se usa.
Nota 2: Cuando el multiplicador contiene un cero el número es multiplicado sólo por los otros números distintos a cero, pero hay que tener cuidado en colocar el número del lado derecho de cada producto parcial en su lugar apropiado.
Ejercicios
Multiplicar:
- 345 x 27
- 369 x 63
- 5,241 x 345
- 5,234 x 739
- 38,613 x 206
- 58,325 x 5,802
- Un día tiene 1,440 minutos. ¿Cuántos minutos tiene un año?
- Una milla tiene 5,280 pies. ¿Cuántos pies tienen 73 millas?
- Un hombre compra 327 sacos de arroz.
- ¿Cuánto tiene que pagar teniendo en cuenta que cada saco pesa 50 kg y que cada kilo vale 25 pts.?
- Un buque navega a una velocidad de 63 millas por horas. Si otro buque saliese del mismo puerto a la misma hora pero en dirección opuesta a una velocidad de 45 millas por hora, ¿a qué distancia estarían uno de otro después de navegar 6 días y medio? ¿A qué distancia estarían si hubiesen navegado en la misma dirección?
Colocar el número 10 en el ábaco y restarle 2 tantas veces como sea posible. ¿Cuántas veces es posible realizar esta operación? Del mismo número restar 3 tantas veces como sea posible. ¿Cuántas veces es posible? ¿Cuántos quedan? Cuánto es 2 x 5? ¿Cuántas veces está 2 contenido en 10, 5 en 10? ¿Cuánto es la mitad de diez?
La división es una forma rápida de restar. Es el proceso contrario a la multiplicación y se la ha definido como la operación a través de la cual dándonos el producto de dos números y uno de ellos, hemos de averiguar cuál es el otro número. El número dado o el producto que ha de ser dividido, se llama dividendo, y el otro número que nos dice en cuántas partes iguales el número dado ha de ser dividido, es llamado divisor. La parte del dividendo que queda cuando la división no es exacta, se llama resto.
División simple.
Cuando la división se puede resolver sin usar la multiplicación, se la llama división simple. Esto ocurre solamente cedo el divisor es inferior a 10. El proceso es muy fácil si conservamos bien en nuestra memoria las guías.
Guías para la división simple .
Nos muestran cómo manipular las bolas:
- Dividir por uno. Uno por uno, adelantamos uno. Dos por uno, adelantamos dos. Tres por uno, adelantamos tres... nueve por uno, adelantamos nueve.
- Dividir por dos. Uno por dos es cinco. Dos por dos, adelantar uno. Cuatro por dos, adelantar dos. Seis por dos, adelantar tres. Ocho por dos, adelantar cuatro.
- Dividir por tres. Uno por tres es tres, más uno. Dos por tres es seis, más dos. Tres por tres adelantar uno. Nueve por tres adelantar tres.
- Dividir por cuatro. Uno por cuatro, es dos más dos. Dos por cuatro es cinco. Tres por cuatro es siete, más dos. Cuatro por cuatro, adelantar uno. Ocho por cuatro, adelantar dos.
- Dividir por cinco. Uno por cinco es dos. Dos por cinco es cuatro. Tres por cinco es seis. Cuatro por cinco es ocho. Cinco por cinco, adelantar uno.
- Dividir por seis Uno por seis es uno más cuatro Dos por seis es tres más dos. Tres por seis es cinco. Cuatro por seis es cuatro más cuatro. Cinco por seis es ocho más dos. Seis por seis adelantar uno.
- Dividir por siete. Uno por siete es uno más tres. Dos por siete es dos más seis. Tres por siete es cuatro más dos. Cuatro por siete es cinco, más cinco. Cinco por siete es siete más uno. Seis por siete es ocho, más cuatro. Siete por siete, adelantar uno.
- Dividir por ocho. Uno por ocho es uno más dos. Dos por ocho es dos, más cuatro. Tres por ocho es tres, más dos. Dos por ocho es dos más cuatro. Tres por ocho es tres, más seis, Cuatro por ocho es cinco. Cinco por ocho es seis, más dos. Seis por ocho es siete, más cuatro. Siete por ocho es ocho, más seis. Ocho por ocho, adelantar uno.
- Dividir por nueve. Uno por nueve es uno, más uno. Dos por nueve es dos más doy Tres por nueve es tres, más tres. Ocho por nueve es ocho más ocho. Nueve por nueve adelantar uno.
Dividir por uno. Uno por uno igual uno. Dos por uno igual dos. Como ya sabemos, cualquier número dividido por uno es exactamente iguala este número, así pues parece que no necesitemos una guía para este caso. Sin embargo sí que podemos necesitarla cuando este uno es un número situado a la izquierda de un divisor con más de un número. En este caso el cociente no puede ser igual al dividendo.
Con añadir uno queremos decir desplazar hacia arriba una hipobola de la columna de la izquierda junto al número dividido. La división en el ábaco difiere de la multiplicación en que empezamos por la izquierda, y en que el lugar de la unidad en el cociente es la columna de la izquierda junto al lugar de la unidad en el dividendo (cuando el divisor es de un sólo número). De este modo el número en la guía precedido por adelantar ésta en el lugar de la unidad en cociente y es por este motivo integral. Según esta guía, si queremos dividir uno por uno, después de poner el dividendo en la tablilla, registramos uno en la fila izquierda junto al número dividido. El número que va a ser dividido, cono ocurre siempre en la Aritmética del ábaco, se quita , o anula. El número registrado es el cociente. Las frases restantes pueden ser aplicadas de la misma manera.
Dividir por dos. Al decir uno por dos es cinco queremos decir que al dividir uno por dos después de colocar el dividendo en la varilla hemos de cambiar el número dividido uno, por cinco, en la misma columna. Ya que el lugar de la unidad en el cociente es la columna de la izquierda junto al número del dividendo, el número cinco registrado allí como cociente, estará situado en el lugar de las décimas del cociente. En otras palabras, si uno es dividido por dos, una mitad o cinco décimas partes serán el cociente y así sucesivamente.
Las guías para el divisor tres y demás números pueden ser explicadas de la misma manera, sólo teniendo en cuenta que el resto si lo hay, ha de ser añadido al número del dividendo a la columna de la derecha junto al cociente. Por ejemplo en la guía Uno por tres es tres más uno, además de cambiar el número uno en tres como cociente, añadimos el resto, uno (lo que significa una décima parte) en la columna de la derecha junto al tres.
Ejemplo 1.
Dividir 1,497 por 2.
Colocar el dividendo 1,497 en la varilla junto al lado izquierdo, dejando una columna libre para el número del cociente. Recordar inmediatamente el número divisor, o si no se puede recordar, colocarlo en la varilla junto al lado derecho del ábaco.
Empezar a dividir por la izquierda tal como sigue: "uno (ejemplo 1,000) por dos es cinco", inmediatamente anular el primer número y cambiarlo por cinco.
"Cuatro por dos, adelantar dos" inmediatamente anular cuatro y desplazar hacia arriba dos, en la columna de la izquierda.
A continuación en la siguiente columna tenemos un nueve. No hay una guía especial para este número. Pero nueve es igual a 8 más 1; así pues dividimos primero 8 y después tomamos el resto, uno. "Ocho por dos, adelantar cuatro", anular ocho del nueve y adelantar cuatro en, la columna de la izquierda. "Uno por dos es cinco", anular el uno y colocar un cinco en la misma columna.
Hasta aquí hemos dejado sin dividir solamente el último número del dividendo. Este número está en el lugar de, la unidad del dividendo y por lo tanto cualquier número situado en la columna de la izquierda junto a él, está en el lugar de la unidad en el cociente y aquí esta columna es el lugar de las décimas. Del mismo modo que dividimos el 9, dividimos el 7. "Seis por dos adelantar tres", anular seis y adelantar tres en la columna de la izquierda, dejando uno enfila columna de la unidad del dividendo. A continuación "Uno por dos es cinco" anular el uno y colocar un 5 en la misma columna. Así el cociente es 748,5 con un resto de 1.
Prueba.
748,5 el cociente, multiplicado por 2, el divisor, es igual a 1,497 el dividendo. Así pues la operación es correcta.
A la división de este tipo que acaba con un resto se le llama inexacta, si no queda resto la división es exacta.
Ejemplo 2.
Dividir 123,456,789 por 3.
Después de colocar el dividendo en el ábaco empezamos a dividir por la izquierda, tal como sigue:
- 1: 3, más 1. Cambiar 2 por 3 y añadir 1 a la columna siguiente a la derecha.
- 3: 3, adelantar 1. Anular el 3, adelantar 1 en la columna de la izquierda.
- 3: 3, adelantar 1. Anular el tres, adelantar 1 en la columna de la izquierda.
- 3: 3, adelantar 1. Anular tres de cuatro adelantar 1 en la columna de la izquierda. 1 por es tres más uno, cambiar 1 por 3 y añadir 1 a la columna siguiente de la derecha.
- 6: 3, adelantar 2. Anular el 6 y adelantar 2 e la columna de la izquierda.
- 6: 3, adelantar 2. Anular el 6 y adelantar 2 en la columna de la izquierda.
- 6: 3, adelantar 2. Anular 6 de 7 y adelantar 2 en la columna de la izquierda. 1 por 3 es 3 más 1: Cambiar 1 por 3 y ,añadir 1 a la siguiente columna de la derecha.
- 9: 3, adelantar 3. Anular 9 y adelantar 3 en la columna de la izquierda.
- 9: 3, adelantar 3. Anular el 9 y adelantar 3 en la columna de la izquierda.
Así pues el cociente será 41, 152, 263.
Ejercicios
- Dividir 123,456,789 por 4, 5, 6, 7, 8, y 9 respectivamente.
- Dividir 3,936 por 4.
- Dividir 4,986 por 9.
- El coste total de cuatro carretas de arroz es de 15,442 pts. Cuál es el coste de un saco teniendo en cuenta que cada carreta contiene 6 sacos?
- Si una hectárea (10,000 m 2 ) de tierra va a ser plantada de árboles con una distancia entre cada 2 de dos metros, cuántos árboles vamos a necesitar?
Cuando el divisor es mayor de 10
Cuando el divisor está representado por más de un número el proceso de división en el ábaco es completamente distinto. E1 proceso para resolver este problema es una combinación de división simple, multiplicación y resta. En este proceso empezamos por la izquierda y dividimos primero el número del dividendo por el número situado al lado izquierdo del divisor, después multiplicamos el conciente parcial así obtenido por el resto del divisor y finalmente restamos el producto del dividendo. Esto se va repitiendo hasta que el número completo está dividido. El número situado a la izquierda del divisor aparece, en los antiguos libros chinos, como el divisor y el resto como el multiplicador, al proceso completo se le llama división resta.
Ejemplo.
Dividir 1,536 por 12.
Colocamos primero 1,536 junto al lado izquierdo de la tablilla, dejando vacante una columna, y el divisor junto al lado derecho de la tablilla. Después, usando las guías dividimos primero el primer número del dividendo, 1, por el primer número del divisor; multiplicamos el cociente así obtenido por el segundo número del divisor, 2, y restamos el producto obtenido del dividendo en la segunda columna del número cociente. Repetimos la misma operación hasta que acabamos todo el dividendo.
Aquí puede estar indicada la regla general que muestra en qué columna ha de ser restado el producto del número cociente por cualquier número del divisor. El producto de cualquier número del cociente por- el segundo número del divisor debe ser restado del dividendo en la segunda columna del número del cociente; el número del cociente por el tercer número del divisor restado en la tercera columna del número del cociente; por el cuarto número en la cuarta columna, etc.
"Uno por uno, adelantar uno". 2 (el segundo número del divisor) x 1 (el número cociente) igual 2.5 (número dividendo en la segunda columna del número cociente) menos 2 igual 2.336 es lo que queda todavía sin dividir.
A continuación podemos dividir el nuevo número del dividendo situado a la izquierda, por el primer número del divisor y proceder como antes. Sin embargo, el producto 6 obtenido de esta forma será demasiado alto para ser restado del número del dividendo 3, en la columna adecuada, así pues debemos tomar una parte de aquel número, dejando el resto del minuendo, término que puede ser usado por conveniencia, para el número o números del dividendo de los que va a ser restado el producto. Así, "Dos por uno, adelantar dos", inmediatamente anulamos dos de tres y adelantamos 2 en la columna de la izquierda. 2 x 2 (número cociente) igual 4.13 menos 4 igual 9. 96 queda sin dividir.
Del mismo modo, "ocho por uno, adelantar ocho". Anulamos 8 de 9 y adelantamos 8 en la columna de la izquierda. 2 x 8 igual 16. 16 menos 16 igual 0. Así pues el cociente es 128.
División larga
La división en la que se usa la multiplicación es llamada división larga. La división larga es el proceso que usamos cuando el divisor es mayor de 10.
Como complemento a las guías dadas para la división corta tenemos 18 más para la división larga. Se usan cuando el número de la izquierda del dividendo siendo igual al del divisor, si lo dividimos de la forma ordinaria, no hay minuendo para restar el producto del número del cociente por el resto del divisor; o cuando el minuendo es demasiado bajo para el producto.
Guías para la división larga
Dividir por uno. Uno por uno, si no hay minuendo, es 9 más 1, i.e. cambiar el número del dividendo, 1, por 9 y añadir 1 a la columna de la derecha. Si el minuendo es insuficiente (para mayor comodidad en el resto de las guías diremos sólo insuficiente) restar 1 del número cociente y añadir uno al número del dividendo en la siguiente columna. (Para nuestra comodidad diremos simplemente restar 1, restituir 1).
- Dividir por dos. 2 por 2, si no hay minuendo, es 9 más 2. Insuficiente, restar 1 restituir 2.
- Dividir por tres. 3 por 3, si no hay minuendo es: 9 más 3. Insuficiente, restar 1 restituir 3.
- Dividir por cuatro. 4 por 4, si no hay minuendo, es 9 más 3. Insuficiente, restar 1 restituir 4.
- Dividir por cinco. 5 por 5, si no hay minuendo, es 9 más 5. Insuficiente, restar 1. Restituir 5.
- Dividir por seis. 6 por 6, si no hay minuendo, es 9 más 6. Insuficiente, restar 1, restituir 6.
- Dividir por siete. 7 por 7, si no hay minuendo, es 9 más 7. Insuficiente, restar 1 restituir 7.
- Dividir por ocho. 8 por 8, si no hay minuendo, es 9 más 8. Insuficiente, restar 1, restituir 8.
- Dividir por nueve. 9 por 9, si no hay minuendo, es 9 más 9. Insuficiente, restar 1 restituir 9.
Ejemplo 1 .
Si 136 sacos de harina valen 1028,16 pts. ¿Cuánto costará un saco?
Como hemos hecho anteriormente, después de colocar el número en la tablilla, empezamos por la izquierda a dividir por el primer número del divisor, multiplicamos el número cociente así obtenido por el segundo y tercer números del divisor, en operaciones separadas y restamos sus respectivos productos de los números del dividendo en la segunda y tercera columnas del número del cociente.
Primera operación
Si vamos a dividir por el sistema ordinario usando "Uno por uno, adelantar uno" no habría minuendo para el producto. En cambio, usamos "Uno por uno, si no hay minuendo, es 9 más 1 ". Así pues cambiamos el número del dividendo 1, por 9 y desplazamos hacia arriba un 1 en la columna de la derecha. Como el minuendo 12, es todavía insuficiente para el producto de 9 x 3, basándonos en otra guía restamos del número cociente y añadimos un 1 al número del dividendo en la siguiente columna, obteniendo así el minuendo 22. Pero de nuevo vemos que este número es demasiado bajo para el producto de 3 x 8, por lo que restamos otra vez 1 del cociente y añadimos otro 1 al dividendo obteniendo así el número cociente 7, y el minuendo 32 el cual ya es ahora suficientemente alto para que podamos usarlo. 3 x 7 igual 21. 32 menos 21 igual 11.6, el tercer número del divisor, por 7 igual 42. 118, los números del dividendo en la tercera columna del número del cociente, menos 42 igual 76. Nos queda 76.16 sin dividir.
Segunda operación.
"5 (parte de 7) por 1, adelantar 5". 3 x 5 (número cociente) igual 15. 26 menos 15 igual 11. 6 x 5 igual 30. 111 menos 30 igual 81. 8.16 queda sin dividir.
Ultima operación.
"6 por 1, adelantar 6". 3 x 6 igual 18. 21 menos 18 igual 3. 6 x 6 igual 36. 36 menos 36 igual 0. Así pues el coste de un saco de harina es de 756 pts.
La columna de la unidad del cociente
Cuando la división es exacta y los números son integrales, es fácil saber en qué lugar estará colocado cada número cociente. Pero, cuando las condiciones son otras, como en la operación anterior, es algo difícil para un principiante acertar qué columna es el lugar de la unidad en el cociente. Hay sin embargo una regla general para ello. Invariablemente cuando el divisor tiene un solo número (integral, naturalmente) la primera columna a la izquierda de la columna de la unidad en el dividendo, es la columna de la unidad del cociente; cuando el divisor tiene dos números es la segunda columna, cuando tiene tres es la tercera, y así sucesivamente.
Ejemplo 2.
Dividir 18,144 a partes iguales entre 56 personas.
Procedemos a dividir por 5 y usamos 6 como multiplicador tal como sigue: "Uno por cinco es dos". 6 x 2 igual 12. 81 menos 12 igual 69. Pero el resto 69, es mayor que el divisor 56, así pues debemos tomarlo de nuevo.
"Cinco (parte de 6) por cinco, adelantar 1 ", añadirlo al número del cociente 2. 6 x 1 (cociente acabado de obtener) igual 6. 19 menos 6 igual 13.
"Uno por cinco es dos". 6 x 2 igual 12. 34 menos 12 igual 22.
"Dos por cinco es cuatro" 6 x 4 igual 24. 24 menos 24 igual 0. Así pues el cociente es 324.
Ejemplo 3
El coste de 894 cajas de té es de 8000. Averiguar el coste de una caja.
El dividendo es 8000, el divisor 894.
"8 por 8, si no hay minuendo, es 6 más 8. Insuficiente, restar 1, restituir 8". Aquí para registrar 16 en una columna, tomamos una altobola para representar 10 y una hipobola 2. Si como ocurre a menudo esta cantidad todavía no satisface nuestras demandas, tomamos prestadas bolas de la columna de la derecha. 9 x 8 igual 72 160 menos 72 igual 88. 4 x 8 igual 32. 880 menos 32 igual 848.
"8 por 8, si no hay minuendo, es 8". 9 x 9 igual 81. 128 menos 81 igual 47. 4 x 9 igual 36. 470 menos 36 igual 434. Así pues el cociente es 89 con un resto de 434. El precio de cada caja será de
89 * 434/894
EjerciciosHallar el cociente de:
- 1,386 dividido por 21.
- 6,473 dividido por 37.
- 749,653 dividido por 721.
- 563,217 dividido por 721.
- 150,475 dividido por 5,122.
- 4,820,805 dividido por 62,413.
- 344,40 dividido por 28.
- 8383.20 dividido por 65.
- En una colecta cada persona contribuye con 72 pts. Si la suma total conseguida es de 59112 pts. ¿Cuántas personas han contribuido?
- El cociente es 432 y el dividendo 15984.¿Cuál es el divisor?
CAPITULO 6
ABREVIACIONES CORTAS Y EJERCICIOS RECORDATORIOS
Para la suma
La suma de una serie de números consecutivos, o números cuya diferencia entre cada par sucesivo de términos esa igual, es equivalente a la mitad del producto de la suma de los números primero y último de la serie, multiplicado por el número de términos en la serie. Así pues, 15 más 16, más 17, más 18, más 30 igual 360 igual 1/2 (15 más 30) x 16.
Para la multiplicación
- Multiplicación por 5. Añadir un cero al multiplicando y dividir por 2. Así pues 5 x 12 igual 120 dividido por 12 igual 60.
- Por 0.5. Dividir el multiplicando por 2.
- Por 25. Añadir dos ceros al multiplicando y dividirlo por 4.
- Por 0.25. Dividir el multiplicando por 4.
- Por 125. Añadir tres ceros al multiplicando y dividirlo por 8.
- Por 1.25. Añadir un cero al multiplicando y dividirlo por 8.
- Por 9. Añadir un cero al multiplicando y restarle el mismo multiplicando. Así pues 35 x 9 igual 350 menos 35.
- Por 0.9. Restar del multiplicando una décima parte del mismo, así pues 35 x 0.9 igual 35 menos 35.
- Por 11. Añadir un cero al multiplicando y restarle el mismo multiplicando.
- Por 99. Añadir dos ceros al multiplicando y restarle el mismo multiplicando.
- Por 9.9. Añadir dos ceros al multiplicando y restarle una décima parte del multiplicando.
- Por 0.99. Añadir dos ceros al multiplicando y restarle una centésima parte del multiplicando.
- Por 98. Añadir dos ceros al multiplicando y retarle el doble del mismo multiplicando. Así pues 98 x 172 igual 17200 menos 344 0 17200 menos 172 menos 172.
- Por 95. Añadir dos ceros al multiplicando y restarle cinco veces el multiplicando.
Por ejemplo, al multiplicar 55 x 13 multiplicar solamente por 3, pero hay que tener en cuenta que el número 5 del multiplicando no debe ser cambiado sino que el 1 del producto parcial 15, debe ser añadido.
Para la división
- Dividir por 5. Marcar un decimal en el dividendo y a continuación multiplicarlo por 2. Así tenemos que 125 dividido por 5 es igual a 12.5 x 2.
- Por 0.5. Multiplicar el dividendo por 2.
- Por 25. Marcar dos decimales en el dividendo y multiplicarlo por 4.
- Por 2.5. Marcar un decimal en el dividendo y multiplicarlo y dividirlo por 4 y 3 respectivamente.
Ejercicios
Resolver los siguientes ejercicios usando las "abreviaciones cortas".
- 27.50 más 28 más 28.50 más 29 más... más 40.
- 25,000 menos 317, menos 347 menos 377 menos... 917.
- 968 multiplicado por 5, 125 y 17.
- 163 x 5,954,
- 167, 250 dividido por 12.5 y por 0.75.
Ejercicios recordatorios
Hallar el valor de las siguientes operaciones:
Nota: El paréntesis ( ), guión - -, o corchetes [ ] nos dicen que los números que están en su interior han de ser considerados como un solo número.
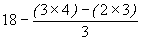
- (99 - 3) dividido por 8 - (86 más 10) dividido por 12.
- 78 - 2 (igual 78 x 78) - 146 - 147 - 148 - ... 170.
- [(82 x 76) dividido por (193 - 11)] dividido por 42.
- (5 más 2 más 6) x 4 - (7 más 8 - 3) dividido por (6 más 10).
- Un hombre pagó 8.750 pts. por un piano, 830 por transporte y 200 por afinarlo. Después lo alquiló durante 7 trimestres a razón de 500 pts. por trimestre, y finalmente lo vendió por 8.250 pts. ¿Ganó o perdió con la venta? ¿Cuánto?
- Un albañil puede construir una casa en 25 días, pero con la ayuda de su hijo puede construirla en 15 días. ¿Cuántos días necesitaría su hijo para construirla él solo?
- Dos muchachos empiezan a correr desde el mismo lugar y en la misma dirección, alrededor de un estanque cuya circunferencia es de 36 metros. Uno corre a razón de 50 metros por minuto y el otro a razón de 43. ¿A qué distancia estarán uno de otro después de 5 minutos?
- Si los muchachos del problema anterior corriesen en direcciones opuestas, ¿en qué distancia estarían uno de otro después de 5 minutos?
- 20 hombres pueden construir una escuela en 56 días. ¿En cuántos días podrían construirla 70 hombres?
CAPITULO 7
RAICES CUADRADAS Y CUBICAS
Procedimiento para extraer una raíz cuadrada
- Colocar el número al lado derecho del ábaco (para nuestra comodidad le llamaremos "número cuadrado") y separarlo en grupos de dos números o columnas, empezando por el punto decimal, al igual que en la aritmética escrita.
- Marcar un uno (1) al lado izquierdo de la tablilla (llamándole "número raíz") y restarlo del grupo del número cuadrado situado a la izquierda.
- Añadir un dos (2) al número raíz y restar de nuevo la suma del grupo del número cuadrado situado a la izquierda. Añadir de nuevo un 2 al número raíz y de nuevo restar la suma del mismo grupo repitiendo esta operación hasta que el número raíz (que va aumentando después de cada operación) sea mayor que el número de este grupo.
- A continuación, bajando al grupo siguiente, le añadimos un cero al número raíz y le sumamos 11, y restamos la suma total del nuevo grupo. Repetimos el proceso explicado en el apartado 3 hasta que el número raíz sea de nuevo demasiado alto para ser restado de este grupo. Seguidamente repetimos la operación explicada al principio de este apartado (4) sumando y restando hasta que terminemos con todo el número.
- Si, como ocurre a menudo, después de pajar el siguiente grupo el número raíz es demasiado alto para ser restado, bajad otro grupo, pero en vez de añadir un cero al número raíz y de sumar 11, añadimos dos ceros y sumamos 101, y a continuación procedemos según lo explicado en los apartados 3 y 4.
- Después que terminemos con la totalidad del número cuadrado, añadimos un uno (1) al número raíz final y dividimos la totalidad por dos (2). El resultado es la raíz cuadrada del número dado.
Ejemplo 1 .
Hallar la raíz cuadrada de 625.
De acuerdo con el método explicado, después de colocar el número 625 al lado derecho de la tablilla, lo separamos en dos grupos conteniendo uno de ellos el número 6 y el segundo los números 25. Estos dos grupos de números nos indican que habrá también 2 grupos en la raíz cuadrada.
Marcamos un uno al lado izquierdo de la tablilla que será el número raíz, y lo restamos del grupo situado a la izquierda, 6, quedándonos así un 5.
A continuación le sumamos 2 al número raíz que se convierte así en 3 y seguidamente lo restamos del grupo situado al lado izquierdo, 5, quedándonos así en 2.
El número raíz es ahora mayor que el número, cuadrado. Por consiguiente añadimos un cero al número raíz 3, convirtiéndose en 30 y le sumamos 11 obteniendo así 41. Restamos 41 (la suma total) del siguiente grupo del número cuadrado 225, quedando 184. Procediendo según el método indicado, 41 el número raíz más 2 igual 43, y 184 menos 43 igual 141. Número raíz 43 más 2 igual 45. Número raíz 45 más 2 igual 47. Número cuadrado 96 menos 47 igual 49. Número raíz 47 más 2 igual 49. Número cuadrado 49 menos 49 igual 0.
Por consiguiente el número es perfectamente cuadrado.
El número raíz final más 1 será igual a 50 (49 más 1) 50 dividido por 2 igual 25 que es la raíz cuadrada del número 625.
Ejemplo 2.
Hallar la raíz cuadrada de 363,690.
Procediendo como hemos explicado anteriormente, después de haber acabado la operación con el primer número (o grupo), tendremos 11 como número raíz y 36 en el grupo siguiente. Si le sumamos 11 a 110 (número raíz más 0) tendríamos que la suma total sería mayor que 36. Por consiguiente, sabemos que tenemos un cero en la raíz cuadrada. De este modo, bajamos otro grupo convirtiéndose así el número cuadrado en 3609. Sin embargo, no restaremos 125 sino 1201 que es la suma de 1100 y 101 (ver el párrafo 5 del apartado Procedimiento). A continuación procedemos como de costumbre. 3609 menos 1201 igual 2408, .etc. Cuando acabamos con el número cuadrado nos queda 1205 como número raíz final. Sumándole 1 y dividiéndolo por 2 será igual a 603 que es la raíz cuadrada de 363,609.
Procedimiento para extraer una raíz cubica
- Colocar el número al lado derecho del ábaco (para nuestra comodidad le llamaremos "número cúbico") y separarlo en grupos de tres números cada uno, empezando por el punto, decimal.
- Poner un 1 al lado izquierdo de la tablilla (le llamaremos "número raíz") y restarlo del grupo del número cúbico situado ala izquierda. Marcar asimismo un 1 en medio de la tablilla y llamarle "número cuadrado".
- Añadirle un 1 al número raíz y añadir la suma total al número cuadrado. Añadir de nuevo un 2 al número raíz y añadirla suma total al número cuadrado. Restar la suma del número cuadrado del grupo situado ala izquierda. Repetir el mismo proceso hasta que el número cuadrado sea mayor que el número cúbico de este grupo.
- Seguidamente, bajar el siguiente grupo, añadirle un 1 al número raíz y añadir la suma total al número cuadrado. Después añadir un cero al número raíz y un 11; de nuevo le añadimos la suma total al número cuadrado, situado en la segunda columna a la derecha del grupo situado al lado derecho. Restar la suma total del nuevo grupo del número cúbico. A continuación proceder como en los apartados (3) o (4) si es necesario.
- Si después de bajar el siguiente grupo el número cuadrado es todavía demasiado alto, tomaremos el grupo siguiente pero en vez de añadirle un cero y sumarle 11, le añadiremos dos ceros y le sumaremos 101 al número raíz. La suma total se añadirá pues al número cuadrado en la cuarta columna a la derecha del grupo situado a su vez en la derecha. A continuación procedemos según lo explicado en los párrafos (3) o (4).
- Cuando hemos acabado con todo el número le añadiremos un 2 al número raíz final y lo dividiremos por 3. El resultado será la raíz cúbica.
Hallar la raíz cúbica de 42,875.
Nota: Para resolver este tipo de operaciones se necesita por lo menos un ábaco de 15 columnas o bien podemos anotar el número cuadrado en un papel o también usar dos ábacos .
Después de colocar el número cúbico 42,875 al lado derecho de la tablilla lo separamos en grupos de tres números cada uno. Habrá dos grupos, e1 primero será 42 y el segundo 875.
Marcamos un 1 en el lado izquierdo de la tablilla que será el número raíz y lo restamos del grupo del número cúbico situado a la izquierda, 42, quedándonos así 41. De nuevo marcamos un 1 en medio de la tablilla que será el número cuadrado. Añadimos un. 1 al número raíz y la suma total la añadimos al número cuadrado, obteniendo así un total de 3. De nuevo le añadimos un 2 al número raíz 2, obteniendo así un 4 el cual será a su vez añadido al número cuadrado 3, obteniendo así un total de 7. A continuación restamos la suma total del primer grupo del número cúbico 41, quedándonos en 34.
Repitiendo el mismo proceso, el número raíz 1 más 1 igual 5. 5 más 7, el número cuadrado, igual 12. Número raíz 5 más 2 igual 7. 7 más 12, el número cuadrado, igual 19. El primer grupo del número cúbico 34 menos 19 igual 15 el cual será así más bajo que el número cuadrado.
Por consiguiente, bajamos el siguiente grupo quedándonos así el número cúbico 15,875.
Según el apartado 4 del método de Procedimiento le añadimos un 1 al número raíz quedándonos en un 8 que es a su vez añadido al número cuadrado 19, obteniendo así 27. Seguidamente añadimos un cero al número raíz convirtiéndose en 80 y le añadimos 11. La suma total 91 se añade al número cuadrado en la segunda columna a su derecha obteniendo así 2791. Restamos este número del número cúbico 15,875 quedándonos 13,084. A continuación procedemos de la siguiente manera:
- Número raíz 91 más 1 es 92. Número cuadrado 2791 más 92 igual 2883. Número raíz 92 más 2 igual 94. Número cuadrado 2883 más 94 es igual a 2977. Número cúbico 13084 menos 2977 es 10107.
- Número raíz 94 más 1 es 95. Número cuadrado 2977 más 95 es 3072.
- Número raíz 95 más 2 es 97. Número cuadrado 3072 más 97 es 3169. .
- Número cúbico 10107 menos 3169 igual 6938.
- Número raíz 97 más 1 es 98. Número cuadrado 3169 más 98 es 3267.
- Número raíz 98 más 2 es 100. Número cuadrado 3267 más 100 es 3367. Número cúbico 6938 menos 3367 es 3571.
- Número raíz 100 más 1 es 101. Número cuadrado 3367 más 101 es 3468.
- Número raíz 101 más 2 es 103. Número cuadrado 3468 más 103 es 3571.
- Número cúbico 3571 menos número cuadrado 3571 igual 0. Por consiguiente el número es perfectamente cúbico. El número raíz final 103 más 2 igual 105. 105 dividido por 3 igual 35. Por consiguiente 35 es la raíz cúbica de 42,875.
Hallar la raíz cúbica de 28,934,443.
Procediendo según lo explicado anteriormente, al tomar el segundo grupo nos encontraremos con que el número cuadrado que será 2791, será mayor que el número cúbico de este grupo que será 1934. Por consiguiente tomaremos el tercer grupo. Pero le añadiremos dos ceros y le sumaremos 101 (en vez de añadirle un cero y sumarle 11 al número raíz 27) a la cuarta columna de su derecha obteniendo así 270901, el cual ha de ser restado del número cúbico. A continuación procederemos como hemos hecho en ejercicios anteriores. La raíz cúbica será 207.
Tabla de Números Binarios y Fracciones Decimales | |||
1/64 1/32 3/64 1/16 5/64 3/32 7/64 1/8 9/64 5/32 11/64 3/16 13/64 7/32 15/64 1/4 17/64 9/32 19/64 5/16 21/64 11/32 23/64 3/8 25/64 13/32 27/64 7/16 29/64 15/32 31/64 1/2 | 0.015625 0.031250 0.046875 0.062500 0.078125 0.093750 0.109375 0.125000 0.140625 0.156250 0.171875 0.187500 0.203125 0.218750 0.234375 0.250000 0.265625 0.281250 0.296875 0.312500 0.328125 0.343750 0.359375 0.375000 0.390625 0.406250 0.421875 0.437500 0.453125 0.468750 0.484375 0.500000 | 33/64 17/32 35/64 9/16 37/64 19/32 39/64 5/8 41/64 21/32 43/64 11/16 45/64 23/32 47/64 3/4 49/64 25/32 51/64 13/16 53/64 27/32 55/64 7/8 57/64 29/32 59/64 15/16 61/64 31/32 63/64 1 | 0.515625 0.531250 0.546875 0.562500 0.578125 0.593750 0.609375 0.625000 0.640625 0.656250 0.671875 0.687500 0.703125 0.718750 0.734375 0.750000 0.765625 0.781250 0.796875 0.812500 0.828125 0.843750 0.859375 0.875000 0.890625 0.906250 0.921875 0.937500 0.953125 0.968750 0.984375 1.000000 |
Los números romanos sirven para expresar todos los números a través de estas 7 letras: I uno; V cinco; X diez; L cincuenta; C cien; D quinientos; M mil.
La repetición de una letra repite su valor; así II significa dos; XXX treinta, etc. V y L no se repiten nunca.
| Árabe | Romano | Árabe | Romano |
| 1 | I | 30 | XXX |
| 2 | II | 40 | XL |
| 3 | III | 50 | L |
| 4 | IV | 60 | LX |
| 5 | V | 70 | LXX |
| 6 | VI | 80 | LXXX |
| 7 | VII | 90 | XC |
| 8 | VIII | 100 | C |
| 9 | IX | 200 | CC |
| 10 | X | 300 | CCC |
| 11 | XI | 400 | CD |
| 12 | XII | 500 | D |
| 13 | XIII | 600 | DC |
| 14 | XIV | 1000 | M |
| 15 | XV | 2000 | MM |
| 16 | XVI | 5000 | |
| 17 | XVII | 10000 | |
| 18 | XVIII | 50000 | |
| 19 | XIX | 100000 | |
| 20 | XX | ||
| 21 | XXI | ||
| 22 | XXII |
Cuando una letra de menor valor se coloca delante de otra de mayor valor, el valor de la menor ha de ser restado de la letra más alta. Si se coloca después, el valor de la letra menor se ha de sumar al de la mayor.